matlab二维图形的绘制
MATLAB二维函数绘图、数据标准化、归一化处理
网络均值 bp） 。奇异样本数据存在所引起的网络训练时间增加，并可能引起网 络无法收敛，所以对于训练样本存在奇异样本数据的数据集在训练之前，最好 先进形归一化，若不存在奇异样本数据，则不需要事先归一化。 一个小程序： p=[1.3711 1.3802 1.3636 1.3598 1.3502 1.3404 1.3284 1.3160 1.3118 1.3032 1.2989 1.2945 1.2923 1.2923 1.2856 1.2788 1.2742 1.2672 1.2577 1.2279 1.1903 1.0864 0.9956 ]; t=[0 1.38 1.68 1.98 2.08 2.23 2.53 2.83 2.93 3.13 3.23 3.33 3.43 3.53 3.63 3.73 3.83 3.93 4.03 4.13 4.23 4.33 4.43]; u=p; tt=t; p=(p-min(p))/(max(p)-min(p));%g 归一化 t=(t-min(t))/(max(t)-min(t)); net=newff(minmax(p),[23 1],{'tansig' 'purelin'},'traingdx'); net.trainParam.epochs=1000; net.trainParam.goal=0.001; net.trainParam.show=10; net.trainParam.lr=0.05; [net,tr,Y,E]=train(net,p,t); a=sim(net,p); out=a*(max(tt)-min(tt))+min(tt);%反归一化 x=u; y=tt; figure(1) plot(x,y,'k*',x,y,'-k',u,out,'ko') title('70°EPDM 的压缩永久变形') legend('*试验数据 o 预测结果') xlabel('压缩变形保持率') ylabel('时间的对数 log10（t）') grid on
Matlab二维图形和三维图形的创建
二维图形和三维图形的创建1．生成1×10维的随机数向量a，在同一幅图片上分别用红、黄、蓝、绿色绘出其连线图、脉冲图、阶梯图和条形图，并分别标出标题“连线图”、“脉冲图”、“阶梯图”、“条形图”。
2．绘制向量x=[1 3 0.5 2.5 2]的饼形图，并把3对应的部分分离出来。
3．用hold on命令在同一个窗口绘制曲线y=sin(t)，y1=sin(t+0.25) y2=sin(t+0.5)，其中t=[0 10]。
t=0:1/100:10;y=sin(t);plot(t,y,'-r')hold ony1=sin(t+0.25);plot(t,y1,'--b')y2=sin(t+0.5);plot(t,y2,'-y')4．绘制曲线 x=tcos(3t)y=tsin2t 其中-π≤t≤π，步长取π/100。
要求：要图形注解、标题、坐标轴标签, 并在曲线上截取一点，将相对应的坐标值文本标注出来(ginput())。
；5．在三个子图像中，分别绘制三维曲线，三维曲面，三维网格的半径为6，坐标为（6,7,6）的由900个面构成的球面（sphere()），对每个图形标注标题6．（1）绘一个圆柱螺旋线（形似弹簧）图。
圆柱截面直径为10，高度为5，每圈上升高度为1。
如左图所示。
（2）利用（1）的结果，对程序做少许修改，得到如右图所示图形。
思考题：如果要绘制出如图所示的图形，请先指出这四个图形分别对应哪副图，以及请正确填写下列空格subplot(6 ,4 ,[2 3 4 6 7 8] );plot(1:10);grid on;subplot( 6 ,4 ,[10 11 14 15] );plot(peaks);grid on;subplot(6 ,4 ,[5 9]);plot(membrane);grid on;subplot(6, 4,[17 18 21 22]);surf(membrane);grid on;。
实验二MATLAB绘制图形
grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下：
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
（2）plot(x,y)： 基本格式，x和y可为向量或矩阵. 1. 如果x，y是同维向量，以x元素为横坐标，以y元素 为纵坐标绘图. 2. 如果x是向量，y是有一维与x元素数量相等的矩阵， 则以x为共同横坐标， y元素为纵坐标绘图，曲线数目 为y的另一维数. 3. 如果x，y是同维矩阵，则按列以x，y对应列元素为 横、纵坐标绘图，曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
MATLAB4二维图形绘制
y3=cos(t);y4=cos(t+0.25);y5=cos(t+0.5); plot(t,y3);hold on; plot(t,y4); plot(t,y5);
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 1 2 3 4 5 6 7
0
figure(1) title('\fontsize{16}y(\omega)=\int^{\infty }_{0}y(t)e^{-j\omegat}dt')
二、绘制曲线的一般步骤
步骤 1 表 4.1 绘制二维、三维图形的一般步骤 内容 曲线数据准备： 对于二维曲线，横坐标和纵坐标数据变量； 对于三维曲面，矩阵参变量和对应的函数值。 指定图形窗口和子图位置： 默认时，打开 Figure No.1 窗口或当前窗口、当前子图； 也可以打开指定的图形窗口和子图。 设置曲线的绘制方式： 线型、色彩、数据点形。 设置坐标轴： 坐标的范围、刻度和坐标分格线 图形注释： 图名、坐标名、图例、文字说明 着色、明暗、灯光、材质处理(仅对三维图形使用) 视点、三度(横、纵、高)比(仅对三维图形使用) 图形的精细修饰(图形句柄操作)： 利用对象属性值设置； 利用图形窗工具条进行设置。
x=peaks;plot(x) x=1:length(peaks);y=peaks;plot(x,y)
10 8 6 4 2 0 -2 -4 -6 -8
0
5
10
15
20
25
30
35
40
45
50
3. 单窗口多曲线分图绘图 subplot(1,3,1); plot(t,y) subplot(1,3,2); plot(t,y3) subplot(1,3,3); plot(t,y2)
实验五 MATLAB二维、三维图形的绘制
实验五 MATLAB二维、三维图形的绘制一、实验目的1.掌握二维、三维图形的绘制；2.掌握特殊二维图形的绘制；3.掌握绘图参数的设置；4.了解并学习简单动画的制作。
二、实验内容1.运行下列程序，学会并掌握标题、坐标轴标签和网格线的设置方法x=0:1:10;y=x.^2-10*x+6;plot(x,y);title ('Plot of y=x.^2-10*x+6');xlabel ('x');ylabel ('y');grid on;2.运行下列程序，学会并掌握线型、点型、颜色的设置方法x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,y1,'bo',x,y2,'r:');title('线型、点型和颜色');xlabel('时间'),ylabel('Y');grid on;3.同一坐标系内多条曲线的绘制1）使用 plot(x,[y1;y2;…])x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,[y1;y2]);legend('sin x','cos x');2）使用hold命令x = -pi:pi/20:pi;y1 = sin(x);y2 = cos(x);plot(x,y1);hold on;plot(x,y2,‘r’);3）在plot后使用多输入变量x = -2*pi:pi/20:2*pi;y1 = 2*sin(x);y2 = 2*cos(x);plot(x,y1,'ro',x,y2,'b:');title('线型、点型和颜色');xlabel('时间'),ylabel('Y');4) 使用plotyy命令x = -pi:pi/20:pi;y1 = sin(x);y2 = 5*cos(x);plotyy(x,y1,x,y2);grid on;gtext(‘sinx’) ; gtext(‘5cosx’) ;4.子图形窗口的绘制subplot(2,1,1);x= -pi:pi/20:pi;y=sin(x);plot(x,y) ; grid on;title('正弦曲线');subplot(2,1,2);x= -pi:pi/20:pi;y=cos(x);plot(x,y); grid on;title('余弦曲线');5.对数坐标图形x=0:0.1:10;y=x.^2 -10.*x +25;subplot(2,2,1);plot(x,y); grid on;xlabel('a) x、y轴线性刻度');subplot(2,2,2);semilogx(x,y); grid on;xlabel('b) x轴对数刻度、y轴线性刻度');subplot(2,2,3);semilogy(x,y); grid on;xlabel('c) x轴线性刻度、y轴对数刻度');subplot(2,2,4);loglog(x,y); grid on;xlabel(‘d) x、y轴对数刻度');6.极坐标下的绘图theta = 0:pi/20:2*pi;r = 0.5+cos(theta);polar(theta,r);7.复数的绘图，并比较下面几种情况的不同1）t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(y);grid on ;title('Plot of Complex Function vs Time');xlabel('Real Part');ylabel('Imaginary Part');2）t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(t, y);grid on ;title('Plot of Complex Function vs Time');xlabel('t');ylabel('y(t)');3）t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));plot(t, real(y),'b-');grid on;hold on;plot(t, imag(y),'r-');title('Plot of Complex Function vs Time');xlabel('t');ylabel('y(t)');legend('real','imaginary');hold off;4）t = 0:pi/20:6*pi;y = exp(0.1*t) .* (cos(t) + i * sin(t));polar(angle(y),abs(y));title('Plot of Complex Function');8.特殊二维图形的绘制1）x = [1 2 3 4 5 6];y = [2 6 8 7 8 5];stem(x,y);title('Example of a Stem Plot');xlabel('x');ylabel('y');axis([0 7 0 10]);将上述程序中的stem语句换为stairs、bar、barh和compass，即可实现阶梯图、条形图、罗盘图的绘制。
Matlab建模训练3 图形绘制
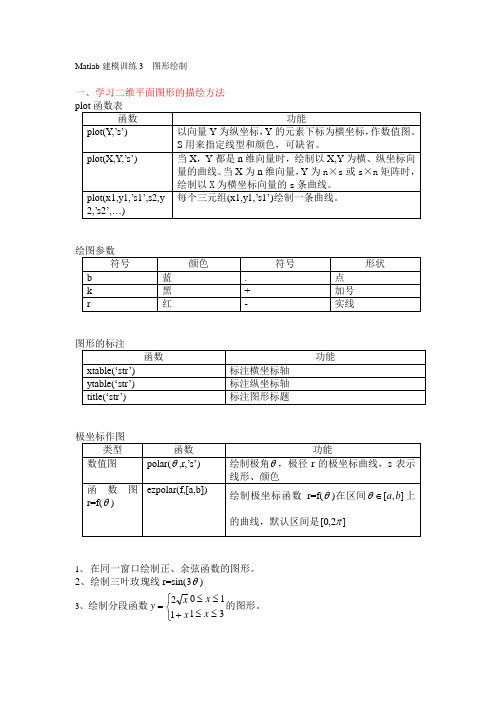
Matlab 建模训练3 图形绘制一、学习二维平面图形的描绘方法1、 在同一窗口绘制正、余弦函数的图形。
2、绘制三叶玫瑰线r=sin(3θ)3、绘制分段函数311012≤≤≤≤⎩⎨⎧+=x x xx y 的图形。
二、学习空间曲线的绘制1、sin cos cos ,06sin ,06.x t t x t ty t t t y t t t z t z tππ==⎧⎧⎪⎪=≤≤=≤≤⎨⎨==⎪⎪⎩⎩及2、 绘制空间曲线sin ,cos ,x t t y t z ===三、学习空间曲面的绘制例 绘制函数sin z x =4个子图的不同特征。
[X,Y]=meshgrid(-4:0.2:4); Z=X.*sin(sqrt(X.^2+Y .^2)); subplot(2,2,1) mesh(Z)subplot(2,2,2) mesh(X,Y ,Z) subplot(2,2,3)surf(X,Y,Z)subplot(2,2,4)surfc(X,Y,Z)ezsurf命令彩色表面图，调用格式与ezmesh相同。
二维图形的视例 分别用命令ezmesh(22,22x y -≤≤-≤≤)和ezsurf(04,14x y ≤≤-≤≤)作函数例 绘制函数22xy z xe --=的图形，并在各坐标设置点观察图形。
功能在默认区域0,2x y π≤≤上画z=f(x,y)高线图,a x y b ≤≤上画z=f(x,y)的等高线图,a x b c y d ≤≤≤≤上画z=f(x,y)例 绘制函数sin cos(),,,,2222z x x y x y ππππ⎡⎤⎡⎤=++∈-∈-⎢⎥⎢⎥⎣⎦⎣⎦的二维等高线和填充等高线。
例 绘制多峰函数()()()222222211351311053x y x y x y x z x ex y e e--+-+---⎛⎫=----- ⎪⎝⎭，在[][],,,x y ππππ∈-∈-上的图形以及二维等高线、二维填充等高线和三维等高线的图形。
第5章matlab绘制二维图形及三维图形的方法
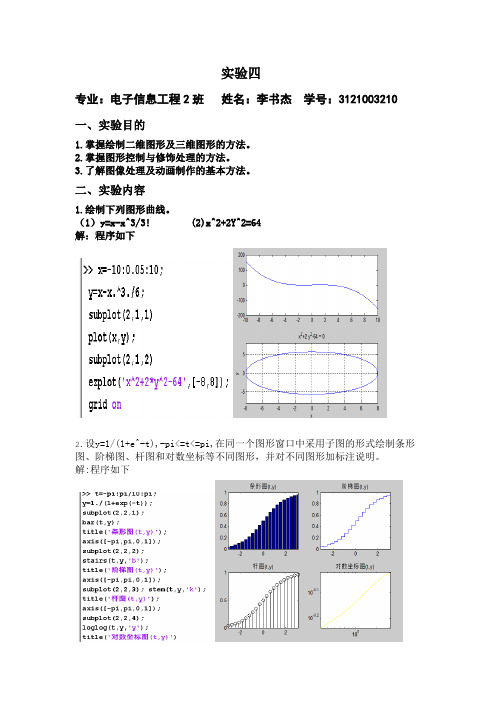
实验四
专业：电子信息工程2班姓名：李书杰学号：3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。
2.掌握图形控制与修饰处理的方法。
3.了解图像处理及动画制作的基本方法。
二、实验内容
1.绘制下列图形曲线。
（1）y=x-x^3/3! (2)x^2+2Y^2=64
解：程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形，并对不同图形加标注说明。
解:程序如下
3.绘制下列极坐标图。
（1）ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解：程序如下
思考练习：
2.绘制下列曲线
（1）y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解：程序如下
（1）
结果如下：
（2）
结果如下：
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。
（1）y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解：程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线，分析两曲线的差别。
解：程序如下
结果如下：
5.绘制下列极坐标图：
(1）p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解：程序如下
结果如下：。
二维图形的绘制
依次输入如下指令，观察输出的图形.
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定，也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
x=0:0.01:4*pi; y1=exp(-0.5*x); y2=-exp(-0.5*x); y3=exp(-0.5*x).*sin(5*x); plot(x,y1,x,y2,x,y3)
函数线条会自动设 置成不同颜色
数组间的乘法用.*
习题 使用plot函数绘制
y 10*exp((0.2 pi)* x), x 0,10
例2 使用plot(x,y)命令绘制y=cosx在[-4π,4π]的图形.
Matlab作图步骤：
给出离散点列： x=-4*pi:0.1:4*pi 计算函数值： y=cos(x) 画图：用 matlab 二维绘图命令 plot 作出函数图形
plot(x,y)
作图命令：x=-4*pi:0.1:4*pi; y=cos(x); plot(x,y)
>> x=0:0.01:10; >> y=10*exp((-0.2+pi)*x); >> plot(x,y)
Matlab 作图
2、Matlab作图命令： （2）plot(x,y,'LineSpec')
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
matlab二维图形的绘制(2006-11-20 20:38:35)转载▼分类：matlab基础（电子方向）常用的二维图形命令:plot：绘制二维图形loglog：用全对数坐标绘图semilogx：用半对数坐标（X）绘图semilogy：用半对数坐标（Y）绘图fill：绘制二维多边填充图形polar：绘极坐标图bar：画条形图stem：画离散序列数据图stairs：画阶梯图errorbar：画误差条形图hist：画直方图fplot：画函数图title：为图形加标题xlabel：在X轴下做文本标记ylabel：在Y轴下做文本标记zlabel：在Z轴下做文本标记text：文本注释grid：对二维三维图形加格栅绘制单根二维曲线plot函数，基本调用格式为：plot(x,y)其中x和y为长度相同的向量，分别用于存储x坐标和y坐标数据。
例如：在区间内，绘制曲线y=2e-0.5xcos(4πx)程序如下：x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x);plot(x,y)plot函数最简单的调用格式是只包含一个输入参数：plot(x)在这种情况下，当x是实向量时，以该向量元素的下标为横坐标，元素值为纵坐标画出一条连续曲线，这实际上是绘制折线图。
p=[22,60,88,95,56,23,9,10,14,81,56,23];plot(p)绘制多根二维曲线1．plot函数的输入参数是矩阵形式(1) 当x是向量，y是有一维与x同维的矩阵时，则绘制出多根不同颜色的曲线。
曲线条数等于y矩阵的另一维数，x被作为这些曲线共同的横坐标。
(2) 当x,y是同维矩阵时，则以x,y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
(3) 对只包含一个输入参数的plot函数，当输入参数是实矩阵时，则按列绘制每列元素值相对其下标的曲线，曲线条数等于输入参数矩阵的列数。
当输入参数是复数矩阵时，则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
2．含多个输入参数的plot函数调用格式为：plot(x1,y1,x2,y2,…,xn,yn)(1) 当输入参数都为向量时，x1和y1，x2和y2，…，xn和yn分别组成一组向量对，每一组向量对的长度可以不同。
每一向量对可以绘制出一条曲线，这样可以在同一坐标内绘制出多条曲线。
(2) 当输入参数有矩阵形式时，配对的x,y 按对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
例如：分析下列程序绘制的曲线。
x1=linspace(0,2*pi,100);x2=linspace(0,3*pi,100);x3=linspace(0,4*pi,100);y1=sin(x1);y2=1+sin(x2);y3=2+sin(x3);x=[x1;x2;x3]';y=[y1;y2;y3]';plot(x,y,x1,y1-1)3．具有两个纵坐标标度的图形在MATLAB中，如果需要绘制出具有不同纵坐标标度的两个图形，可以使用plotyy绘图函数。
调用格式为：plotyy(x1,y1,x2,y2)其中x1，y1对应一条曲线，x2，y2对应另一条曲线。
横坐标的标度相同，纵坐标有两个，左纵坐标用于x1，y1数据对，右纵坐标用于x2，y2数据对。
例如：用不同标度在同一坐标内绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)。
程序如下：x=0:pi/100:2*pi;y1=0.2*exp(-0.5*x).*cos(4*pi*x);y2=2*exp(-0.5*x).*cos(pi*x);plotyy(x,y1,x,y2);4．图形保持hold on/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换。
例如：采用图形保持，在同一坐标内绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)。
程序如下：x=0:pi/100:2*pi;y1=0.2*exp(-0.5*x).*cos(4*pi*x); plot(x,y1)hold ony2=2*exp(-0.5*x).*cos(pi*x); plot(x,y2);hold off设置曲线样式MATLAB提供了一些绘图选项，用于确定所绘曲线的线型、颜色和数据点标记符号，它们可以组合使用。
例如，“b-.”表示蓝色点划线，“y:d”表示黄色虚线并用菱形符标记数据点。
当选项省略时，MATLAB规定，线型一律用实线，颜色将根据曲线的先后顺序依次。
要设置曲线样式可以在plot函数中加绘图选项，其调用格式为：plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)例如：在同一坐标内，分别用不同线型和颜色绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)，标记两曲线交叉点。
程序如下：x=linspace(0,2*pi,1000);y1=0.2*exp(-0.5*x).*cos(4*pi*x);y2=2*exp(-0.5*x).*cos(pi*x);k=find(abs(y1-y2)<1e-2); %查找y1与y2相等点(近似相等)的下标x1=x(k); %取y1与y2相等点的x坐标y3=0.2*exp(-0.5*x1).*cos(4*pi*x1); %求y1与y2值相等点的y坐标plot(x,y1,x,y2,'k:',x1,y3,'bp');图形标注与坐标控制1．图形标注有关图形标注函数的调用格式为：title(图形名称)xlabel(x轴说明)ylabel(y轴说明)text(x,y,图形说明)legend(图例1,图例2,…)函数中的说明文字，除使用标准的ASCII字符外，还可使用LaTeX格式的控制字符，这样就可以在图形上添加希腊字母、数学符号及公式等内容。
例如，text(0.3,0.5,‘sin({\omega}t+{\beta})’)将得到标注效果sin(ωt+β)。
例如：在区间内，绘制曲线y1=2e-0.5x和y2=cos(4πx)，并给图形添加图形标注。
程序如下：x=0:pi/100:2*pi;y1=2*exp(-0.5*x);y2=cos(4*pi*x);plot(x,y1,x,y2)title('x from 0 to 2{\pi}'); %加图形标题xlabel('Variable X'); %加X轴说明ylabel('Variable Y'); %加Y轴说明text(0.8,1.5,'曲线y1=2e^{-0.5x}'); %在指定位置添加图形说明text(2.5,1.1,'曲线y2=cos(4{\pi}x)'); legend(‘y1’,’y2’) %加图例2．坐标控制axis函数的调用格式为：axis([xmin xmax ymin ymax zmin zmax]) axis函数功能丰富，常用的格式还有：axis equal：纵、横坐标轴采用等长刻度。
axis square：产生正方形坐标系(缺省为矩形)。
axis auto：使用缺省设置。
axis off：取消坐标轴。
axis on：显示坐标轴。
例如：给坐标加网格线用grid命令来控制。
grid on/off命令控制是画还是不画网格线，不带参数的grid命令在两种状态之间进行切换。
给坐标加边框用box命令来控制。
box on/off 命令控制是加还是不加边框线，不带参数的box命令在两种状态之间进行切换在同一坐标中，可以绘制3个同心圆，并加坐标控制。
程序如下：t=0:0.01:2*pi;x=exp(i*t);y=[x;2*x;3*x]';plot(y)grid on; %加网格线box on; %加坐标边框axis equal %坐标轴采用等刻度图形窗口的分割subplot函数的调用格式为：subplot(m,n,p)该函数将当前图形窗口分成m×n个绘图区，即每行n个，共m行，区号按行优先编号，且选定第p个区为当前活动区。
在每一个绘图区允许以不同的坐标系单独绘制图形。
例如：在一个图形窗口中以子图形式同时绘制正弦、余弦、正切、余切曲线。
程序如下：x=linspace(0,2*pi,60);y=sin(x);z=cos(x);t=sin(x)./(cos(x)+eps);ct=cos(x)./(sin(x)+eps);subplot(2,2,1);plot(x,y);title('sin(x)');axis([0,2*pi,-1,1]);subplot(2,2,2);plot(x,z);title('cos(x)');axis ([0,2*pi,-1,1]);subplot(2,2,3);plot(x,t);title('tangent(x)');axis ([0,2*pi,-40,40]);subplot(2,2,4);plot(x,ct);title('cotangent(x)');axis ([0,2*pi,-40,40]);其他二维图形其他坐标系下的二维数据曲线图1．对数坐标图形MATLAB提供了绘制对数和半对数坐标曲线的函数，调用格式为：semilogx(x1,y1,选项1,x2,y2,选项2,…) semilogy(x1,y1,选项1,x2,y2,选项2,…) loglog(x1,y1,选项1,x2,y2,选项2,…)例绘制y=10x2的对数坐标图并与直角线性坐标图进行比较。
程序如下：x=0:0.1:10;y=10*x.*x;subplot(2,2,1);plot(x,y);title('plot(x,y)');grid on;subplot(2,2,2);semilogx(x,y);title('semilogx (x,y)');grid on;subplot(2,2,3);semilogy(x,y);title('semilogy (x,y)');grid on;subplot(2,2,4);loglog(x,y);title('loglog(x,y)'); grid on;2．极坐标图polar函数用来绘制极坐标图，其调用格式为：polar(theta,rho,选项)其中theta为极坐标极角，rho为极坐标矢径，选项的内容与plot函数相似。
例4-11 绘制r=sin(t)cos(t)的极坐标图，并标记数据点。