利用相似三角形测高专题训练
利用相似三角形测高

《利用相似三角形测高》同步练习一、选择题1.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为()A.10m B.12m C.13m D.15m2.如图所示,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,则电线杆的高度为()A.2.4m B.24m C.0.6m D.6m第2题第6题3.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是()A.15m B.60m C.20m D.10m4.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出()A.仰角B.树的影长C.标杆的影长D.都不需要5.一斜坡长70米,它的高为5米,将重物从斜坡起点推到坡上20米处停下,停下地点的高度为()A.米B.米C.米D.米6.如图,有点光源S在平面镜上方,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24cm,点光源S到平面镜的距离即SA的长度为()A.11cm B.12cm C.13cm D.14cm7.某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为()A.5.3米B.4.8米C.4.0米D.2.7米8.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是()A.()m B.()mC.m D.4m二、填空题9.高6m的旗杆在水平面上的影长为8m,此时测得一建筑物的影长为48m,则该建筑的高度为m.10.如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为米.(不计宣传栏的厚度)第10题第11题11.铁道上的栏杆的短臂长为1.25m,长臂为17.5m,如图要使长臂端点升高16m,则短臂端点要下降m.12.如图,要测量A、B两点间距离,在O点设桩,取OA中点C,OB中点D,测得CD=30m,则AB= m.第12题第14题13.高为3m的木条,在地面上的影长为12m,这时,测得一建筑物的影长为36m,则该建筑物的高度是m.14.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为米.15.如图,小明从路灯下,向前走了5米,发现自己在地面上的影子长DE是2米.如果小明的身高为1.6米,那么路灯高地面的高度AB是米.第15题第16题16.一油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油面的高度为m.17.如图,小华在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离EB=20米,镜子与小华的距离ED=2米时,小华刚好从镜子中看到铁塔顶端点A.已知小华的眼睛距地面的高度CD=1.5米,则铁塔AB的高度是米.。
北师大版九年级上册 4.6 利用相似三角形测高专题(包含答案)

2019-2020利用相似三角形测高专题(含答案)一、单选题1.如图,小雅同学在利用标杆BE 测量建筑物的高度时,测得标杆BE 高1.2m ,又知:1:8AB BC =,则建筑物CD 的高是( )A .9.6mB .10.8mC .12mD .14m2.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根 长为 1 米的竹竿的影长为 0.4 米,同时另一名同学测量树的高度时, 发现树的影子不全落在地面上,有一部分落在教学楼的第一级台 阶水平面上,测得此影子长为 0.2 米,一级台阶高为 0.3 米,如图 所示,若此时落在地面上的影长为 4.4 米,则树高为( )A.11.8 米B.11.75 米C.12.3 米D.12.25 米3.《孙子算经》是我国古代重要的数学著作,其下卷有题如下:“今有竿不知长短,度其影得一丈五尺.别立一表,长一尺五寸,影得五寸.问竿长几何?”译文:“有一根竹竿不知道它的长短,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长是五寸,则这根竹竿的长度为多少尺?”可得这根竹竿的长度为( ) (提示:1丈10=尺,1尺10=寸)A.五丈B.四丈五尺C.五尺D.四尺五寸4.如图,为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底B端8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树AB的高度约为()A.4.2米B.4.8米C.6.4米D.16.8米5.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为()A.4.5mB.4.8mC.5.5mD.6 m二、填空题6.某同学要测量某烟囱的高度,他将一面镜子放在他与烟囱之间的地面上某一位置,然后站到与镜子、烟囱成一条直线的地方,刚好从镜中看到烟囱的顶部,如果这名同学身高为1.65米,他到镜子的距离是2米,测得镜面到烟囱的距离为20米,烟囱的高度_____ 米.7.如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高CD =1.2m ,CE =0.6m ,CA =30m (点A 、E 、C 在同一直线上).已知小明身高EF 是1.6m ,则楼高AB 为______m .8.如图,在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆2AB m =,它的影子1.6BC m =,木杆PQ 的影子有一部分落在了墙上, 1.2PM m =,0.8MN m =,则木杆PQ 的长度为______m .9.为了测量校园水平地面上一棵树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B )8.4米的点E 处,然后沿着直线BE 后退到点D ,这时恰好在镜子里看到树梢顶点A ,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树AB 的高度为 米.三、解答题10.如图,晚上小明由路灯AD走向路灯BC,当他行至点P处时,发现他在路灯BC下的影长为2m,且影子的顶端恰好在A点,接着他又走了6.5m至点Q处,此时他在路灯AD下的影子的顶端恰好在B点,已知小明的身高为1.8m,路灯BC的高度为9m.(1)计算小明站在点Q处时在路灯AD下影子的长度;(2)计算路灯AD的高度。
北师大版九年级上册数学 4.6利用相似三角形测高 同步习题(含解析)
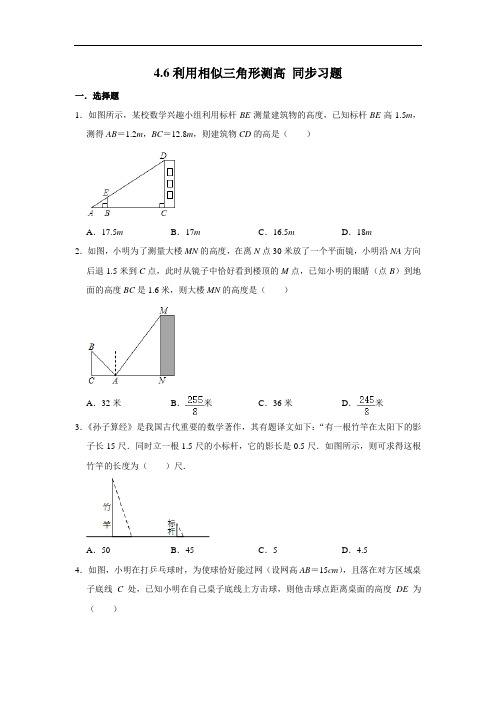
4.6利用相似三角形测高同步习题一.选择题1.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是()A.17.5m B.17m C.16.5m D.18m2.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是()A.32米B.米C.36米D.米3.《孙子算经》是我国古代重要的数学著作,其有题译文如下:“有一根竹竿在太阳下的影子长15尺.同时立一根1.5尺的小标杆,它的影长是0.5尺.如图所示,则可求得这根竹竿的长度为()尺.A.50B.45C.5D.4.54.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为()A.15cm B.20cm C.25cm D.30cm5.数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为()A.32米B.28米C.24米D.16米6.如图,某同学拿着一把12cm长的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子恰好遮住电线杆,已知臂长60cm,则电线杆的高度是()A.2.4m B.24m C.0.6m D.6m7.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面()A.2.4米B.8米C.3米D.必须知道两根电线杆的距离才能求出点P离地面距离8.已知:如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.6m,并测得BC=2.2m,CA=0.8m,那么树DB的高度是()A.6m B.5.6m C.5.4m D.4.4m9.如图,A,B两点被一河隔开,为了测量A,B两点间的距离,小明过点B作BF⊥AB,在BF上取两点C,D,使BC=2CD,过点D作DE⊥BF且使点A,C,E在同一条直线上,测得DE=20m,则A,B两点间的距离是()A.60m B.50m C.40m D.30m10.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为()A.4 m B.m C.5m D.m二.填空题11.在某一时刻,测得一根高为2m的竹竿的影长为1m,同时测得一栋建筑物的影长为12m,那么这栋建筑物的高度为m.12.小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是.13.利用标杆CD测量建筑物的高度的示意图如图所示,若标杆CD的高为1.5米,测得DE=2米,BD=18米,则建筑物的高AB为米.14.根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表.如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是.15.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB=米.三.解答题16.如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.17.随着人们对生活环境的要求逐渐提高,环境保护问题受到越来越多人的关注,环保宣传也随处可见.如图,小云想要测量窗外的环保宣传牌AB的高度,她发现早上阳光恰好从窗户的最高点C处射进房间的地板F处,中午阳光恰好从窗户的最低点处射进房间的地板E处,小云测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF =3m.请根据以上测量数据,求环保宣传牌AB的高度.参考答案1.解:∵EB⊥AC,DC⊥AC,∴EB∥DC,∴△ABE∽△ACD,∴,∵BE=1.5m,AB=1.2m,BC=12.8m,∴AC=AB+BC=14m,∴,解得,DC=17.5,即建筑物CD的高是17.5m,故选:A.2.解:∵BC⊥CA,MN⊥AN,∴∠C=∠MNA=90°,∵∠BAC=∠MAN,∴△BCA∽△MNA.∴=,即=,∴MN=32(m),答:楼房MN的高度为32m.故选:A.3.解:设竹竿的长度为x尺,由题意得:=,解得:x=45,答:竹竿的长度为45尺,故选:B.4.解:∵AB∥DE,∴△CAB∽△CDE,而BC=BE,∴DE=2AB=2×15=30(cm).故选:D.5.解:根据题意,易得到△ABP∽△PDC.即=故CD=×AB=×1=32米;那么该大厦的高度是32米.故选:A.6.解:作AN⊥EF于N,交BC于M,∵BC∥EF,∴AM⊥BC于M,∴△ABC∽△AEF,∴=,∵AM=0.6,AN=30,BC=0.12,∴EF===6(m).故选:D.7.解:作PE⊥BC于E.∵CD∥AB,∴△APB∽△CDP,∴====,∵CD∥PE,∴△BPE∽△BDC,∴=,解得PE=2.4.故选:A.8.解:∵EC∥AB,BD⊥AB,∴EC∥BD,∠ACE=∠ABD=90°,在Rt△ACE∽Rt△ABD中,∠A=∠A,∠ACE=∠ABD=90°,∴Rt△ACE∽Rt△ABD,∴=,即=,解得BD=6m.故选:A.9.解:∵AB⊥BF,ED⊥BF,∴AB∥DE,∴△ABC∽△EDC,∴,即,解得:AB=40,故选:C.10.解:∵AB∥CD,∴△ABM∽△DCM,∴===,(相似三角形对应高的比等于相似比),∵MH∥AB,∴△MCH∽△ACB,∴==,解得MH=.故选:B.11.解:设这栋建筑物的高度为xm,由题意得,=,解得x=24,即这栋建筑物的高度为24m.故答案为:24.12.解:设教学楼高度为xm,列方程得:解得x=19.2,故教学楼的高度为19.2m.故答案为:19.2m.13.解:∵AB∥CD,∴△EBA∽△ECD,∴=,即,∴AB=15(米).故答案为:15.14.解:根据题意得=,所以b=×3.6=2.16(cm).故答案为2.16.15.解:根据题意可得:∠AEB=∠CED,∠BAE=∠DCE=90°,∴△ABE∽△CDE,∴=,∴,∴AB=6(米),故答案为:6.16.解:∵CD∥AB,∴△EAB∽△ECD,∴=,即=①,∵FG∥AB,∴△HFG∽△HAB,∴=,即=②,由①②得=,解得BD=15,∴=,解得AB=10.2.答:路灯A离地面的高度为10.2m.17.解:∵DO⊥BF,∴∠DOE=90°,∵OD=1m,OE=1m,∴∠DEB=45°,∵AB⊥BF,∴∠BAE=45°,∴AB=BE,设AB=EB=xm,∵AB⊥BF,CO⊥BF,∴AB∥CO,∴△ABF∽△COF ,∴=,=,解得:x=10.经检验:x=10是原方程的解.答:AB的高度是10m.。
利用相似三角形测高基础训练含详细答案

利用相似三角形测高基础训练一.选择题(共8小题)1.《孙子算经》是我国古代重要的数学著作,其有题译文如下:“有一根竹竿在太阳下的影子长15尺.同时立一根1.5尺的小标杆,它的影长是0.5尺.如图所示,则可求得这根竹竿的长度为()尺.A.50B.45C.5D.4.52.如图,小卓利用标杆EF测量旗杆AB的高度,测得小桌的身高CD=1.8米,标杆EF=2.4米,DF=1米,BF=11米,则旗杆AB的高度是()A.6.4米B.7.2米C.9米D.9.6米3.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是()A.32米B.米C.36米D.米4.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是()A.17.5m B.17m C.16.5m D.18m5.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为()A.15cm B.20cm C.25cm D.30cm6.数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为()A.32米B.28米C.24米D.16米7.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB 的高为(保留到整数,1丈=10尺)()A.162丈B.163丈C.164丈D.165丈8.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为()A.4.5m B.4.8m C.5.5m D.6 m二.填空题(共5小题)9.如图,利用镜子M的反射(入射角等于反射角),来测量旗杆CD的长度,在镜子上作一个标记,观测者AB看着镜子来回移动,直到看到旗杆顶端在镜子中的像与镜子上的标记相重合,若观测者AB的身高为1.6m,量得BM:DM=2:11,则旗杆的高度为m.10.如图,有一个广告牌OE,小明站在距广告牌OE10米远的A处观察广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为米.11.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.5m,测得AB=2m,BC=6m,则建筑物CD的高是m.12.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为米.13.小明用这样的方法来测量某建筑物的高度:如图,在地面上放一面镜子,调整位置,直至刚好能从镜子中看到建筑物的顶端.如果此时小明与镜子的距离是2m,镜子与建筑物的距离是20m.他的眼睛距地面1.5m,那么该建筑物的高是.三.解答题(共3小题)14.福建省会福州拥有“三山两塔一条江”,其中报恩定光多宝塔(别名白塔),位于山风景区,利用标杆可以估算白塔的高度.如图,标杆BE高1.5m,测得AB=0.9m,BC=39.1m,求白塔的高CD.15.如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是?16.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.利用相似三角形测高基础训练参考答案与试题解析一.选择题(共8小题)1.《孙子算经》是我国古代重要的数学著作,其有题译文如下:“有一根竹竿在太阳下的影子长15尺.同时立一根1.5尺的小标杆,它的影长是0.5尺.如图所示,则可求得这根竹竿的长度为()尺.A.50B.45C.5D.4.5【答案】B【解答】解:设竹竿的长度为x尺,由题意得:=,解得:x=45,答:竹竿的长度为45尺,故选:B.2.如图,小卓利用标杆EF测量旗杆AB的高度,测得小桌的身高CD=1.8米,标杆EF=2.4米,DF=1米,BF=11米,则旗杆AB的高度是()A.6.4米B.7.2米C.9米D.9.6米【答案】C【解答】解:CG的延长线交AB于H,如图,易得GF=BH=CD=1.8m,CG=DF=1m,GH=BF=11m,∴EG=EF﹣GF=2.4m﹣1.8m=0.6m,∵EG∥AH,∴△CGE∽△CHA,∴=,即=,∴AH=7.2,∴AB=AH+BH=7.2+1.8=9(m),即旗杆AB的高度是9m.故选:C.3.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是()A.32米B.米C.36米D.米【答案】A【解答】解:∵BC⊥CA,MN⊥AN,∴∠C=∠MNA=90°,∵∠BAC=∠MAN,∴△BCA∽△MNA.∴=,即=,∴MN=32(m),答:楼房MN的高度为32m.故选:A.4.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是()A.17.5m B.17m C.16.5m D.18m【答案】A【解答】解:∵EB⊥AC,DC⊥AC,∴EB∥DC,∴△ABE∽△ACD,∴,∵BE=1.5m,AB=1.2m,BC=12.8m,∴AC=AB+BC=14m,∴,解得,DC=17.5,即建筑物CD的高是17.5m,故选:A.5.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为()A.15cm B.20cm C.25cm D.30cm【答案】D【解答】解:∵AB∥DE,∴△CAB∽△CDE,∴=,而BC=BE,∴DE=2AB=2×15=30(cm).故选:D.6.数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为()A.32米B.28米C.24米D.16米【答案】A【解答】解:根据题意,易得到△ABP∽△PDC.即=故CD=×AB=×1=32米;那么该大厦的高度是32米.故选:A.7.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB 的高为(保留到整数,1丈=10尺)()A.162丈B.163丈C.164丈D.165丈【答案】D【解答】解:由题意得,BD=53里CD=95尺,EF=7尺,DF=3里,过E作EG⊥AB于G,交CD于H,则BG=DH=EF=7尺,GH=BD=53里,HE=DF=3里,∵CD∥AB,∴△ECH∽△EAG,∴=,∴=,∴AG≈164.2丈,AB=AG+0.7=164.9≈165丈.答:山AB的高为165丈.故选:D.8.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为()A.4.5m B.4.8m C.5.5m D.6 m【答案】D【解答】解:由题意可得:AE=2m,CE=0.5m,DC=1.5m,∵△ABE∽△EDC,∴=,即=,解得:AB=6,故选:D.二.填空题(共5小题)9.如图,利用镜子M的反射(入射角等于反射角),来测量旗杆CD的长度,在镜子上作一个标记,观测者AB看着镜子来回移动,直到看到旗杆顶端在镜子中的像与镜子上的标记相重合,若观测者AB的身高为1.6m,量得BM:DM=2:11,则旗杆的高度为8.8 m.【答案】见试题解答内容【解答】解:根据题意得:△ABM∽△CDM,∴AB:CD=BM:DM,∵AB=1.6m,BM:DM=2:11,∴1.6:CD=2:11,解得:CD=8.8m,故答案为:8.8.10.如图,有一个广告牌OE,小明站在距广告牌OE10米远的A处观察广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为2.5米.【答案】见试题解答内容【解答】解:作BF⊥OE于点F交CD于点G,根据题意得:AB=CG=OF=1.5米,BF=10米,BG=5米,DG=CD﹣CG=2﹣1.5=0.5米,∵DG∥EF,∴,∴,解得:EF=1,∴EO=EF+OF=1+1.5=2.5(米),故答案为:2.5.11.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.5m,测得AB=2m,BC=6m,则建筑物CD的高是6m.【答案】6.【解答】解:由题意可得:BE∥DC,则△ABE∽△ACD,故=,∵标杆BE高1.5m,AB=2m,BC=6m,∴=,解得:DC=6.故答案为:6.12.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为9米.【答案】见试题解答内容【解答】解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,则BE=BC+CE=10米,∵CD∥AB,∴△ECD∽△EBA∴=,即=,解得AB=9(米),即路灯的高AB为9米;故答案为:9.13.小明用这样的方法来测量某建筑物的高度:如图,在地面上放一面镜子,调整位置,直至刚好能从镜子中看到建筑物的顶端.如果此时小明与镜子的距离是2m,镜子与建筑物的距离是20m.他的眼睛距地面1.5m,那么该建筑物的高是15m.【答案】见试题解答内容【解答】解:∵∠APB=∠CPD,∠ABP=∠CDP,∴△ABP∽△CDP∴=,即:,解得:CD=15(米).故答案为:15.三.解答题(共3小题)14.福建省会福州拥有“三山两塔一条江”,其中报恩定光多宝塔(别名白塔),位于山风景区,利用标杆可以估算白塔的高度.如图,标杆BE高1.5m,测得AB=0.9m,BC=39.1m,求白塔的高CD.【答案】见试题解答内容【解答】解:∵EB⊥AC,DC⊥AC,∴EB∥DC,∴△ABE∽△ACD,∴=,∵BE=1.5,AB=0.9,BC=39.1,∴AC=16,∴=,∴CD=.∴白塔的高CD为米.15.如图是小明设计利用光线来测量某古城墙CD高度的示意图,如果镜子P与古城墙的距离PD=12米,镜子P与小明的距离BP=1.5米,小明刚好从镜子中看到古城墙顶端点C,小明眼睛距地面的高度AB=1.2米,那么该古城墙的高度是?【答案】见试题解答内容【解答】解:∵∠APB=∠CPD,∠ABP=∠CDP,∴△ABP∽△CDP∴=,即:=,解得:PD=9.6(米).答:该古城墙的高度是9.6m.16.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.【答案】见试题解答内容【解答】解:过点A作AM⊥EF于点M,交CD于点N,由题意可得:AN=2m,CN=2﹣1.65=0.35(m),MN=40m,∵CN∥EM,∴△ACN∽△AEM,∴=,∴=,解得:EM=7.35,∵AB=MF=1.65m,故城楼的高度为:7.35+1.65﹣1.7=7.3(米),答:城楼的高度为7.3m.。
利用相似三角形测高经典例题

第四章图形的相似一 、利用相似三角形测高知识点1:利用阳光下的影子来测量旗杆的高度操作方法:一名学生在直立于旗杆影子的顶端处测出该同学的_________和此时旗杆的_______.(点拨:把太阳的光线看成是平行的.)∵太阳的光线是_________的,∴________∥_________,∴∠AEB =∠CBD ,∵人与旗杆是________于地面的,∴∠ABE =∠CDB=_____°, ∴△_______∽△_______ ∴BD BE CD AB = 即CD=BE BD AB ⋅ 因此,只要测量出人的影长BE ,旗杆的影长DB ,再知道人的身高AB ,就可以求出旗杆CD 的高度了.知识点2:利用标杆测量旗杆的高度操作方法:选一名学生为观测者,在他和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在____________时,分别测出他的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度.如图,过点A 作AN ⊥DC 于N ,交EF 于M .点拨:∵人、标杆和旗杆都_______于地面,∴∠ABF =∠EFD=∠CDH =_______°∴人、标杆和旗杆是互相_______的.∵EF ∥CN ,∴∠_____=∠_____,∵∠3=∠3,∴△______∽△______,∴CN EM AN AM ∵人与标杆的距离、人与旗杆的距离,标杆与人的身高的差EM都已测量出,∴能求出CN ,∵∠ABF =∠CDF =∠AND =90°,∴四边形ABND为________.∴DN =_______,∴能求出旗杆CD 的长度.知识点3:利用镜子的反射操作方法:选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆_______.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.点拨:入射角=反射角∵入射角=反射角 ∴∠________=∠________∵人、旗杆都_________于地面 ∴∠B =∠D =_______°∴△________∽△________,∴DE BE CD AB 因此,测量出人与镜子的距离BE ,旗杆与镜子的距离DE ,再知道人的身高AB ,就可以求出旗杆CD 的高度.二、例题精讲例1:如图,有一路灯杆AB (底部B 不能直接到达),在灯光下,小华在点D 处测得自己的影长DF=3m ,沿BD 方向到达点F 处再测得自己的影长FG=4m ,如果小华的身高为1.5m ,求路灯杆AB 的高度。
4.6 利用相似三角形测高(分层练习)(解析版)

第四章 图形的相似4.6 利用相似三角形测高精选练习一、单选题1.(2020·浙江嘉兴·八年级期末)直角三角形两条直角边长分别是5和12,则斜边上的高是( )A .3013B .6013C .132D .120132.(2021·云南省个旧市第二中学八年级期中)如图,在△ABC 中,∠C =90°,D ,E 是AC 上两点,且AE =DE ,BD 平分∠EBC ,那么下列说法中不正确的是( )A .BE 是△ABD 的中线B .BD 是△BCE 的角平分线C .∠1=∠2=∠3D .BC 是△ABE 的高【答案】C【分析】根据三角形的高、中线、角平分线的定义对各选项分析判断后利用排除法求解.【详解】解:A 、AE DE =Q ,BE \是ABD D 的中线,正确;B 、BD Q 平分EBC Ð,BD \是EBC D 的角平分线,正确;C 、BD Q 是EBC D 的角平分线,EBD CBD \Ð=Ð,BE Q 是中线,EBD ABE \йÐ,123\Ð=Ð=Ð不正确,符合题意;D 、90C Ð=°Q ,BC \是ABE D 的高,正确.故选:C .【点睛】本题考查了三角形的角平分线,高线,中线的定义,熟记概念并准确识图是解题的关键.3.(2022·江苏·灌南县新知双语学校七年级阶段练习)如图,ABC V 中,AE 是中线,AD 是角平分线,AF 是高,则下列说法中错误的是( )A .BE CE=B .C CAF 90ÐÐ+=°C .BAE CAE Ð=ÐD .ABC ABES 2S =△△【答案】C 【分析】由中线的性质可得BE CE =,ABC ABE S 2S =△△,由角平分线的定义可得BAD CAD Ð=Ð;由AF 是ABC V 的高,可得C CAF 90ÐÐ+=°.【详解】解:AE Q 是中线,BE CE \=,ABC ABE S 2S =△△,故A 、D 说法正确;AD Q 是角平分线,BAD CAD ÐÐ\=,BAE CAE ÐÐ\¹,故C 说法错误;AF Q 是ABC V 的高,AFC 90Ð\=°,C CAF 90ÐÐ\+=°,故B 说法正确;故选:C .【点睛】本题考查了三角形的面积,三角形的角平分线,中线和高,明确概念是本题的关键.4.(2022·全国·九年级课时练习)如图,ABC V 的高CD 、BE 相交于O ,如果55A Ð=°,那么BOC Ð的大小为( )A .35°B .105°C .125°D .135°【答案】C 【分析】先根据三角形的内角和定理结合高的定义求得∠ABC+∠ACB 、∠ABE 、∠ACD 的度数,即可求得∠OBC+∠OCB 的度数,从而可以求得结果.【详解】解:∵∠A=55°,CD 、BE 是高∴∠ABC+∠ACB=125°,∠AEB=∠ADC=90°∴∠ABE=180°-∠AEB -∠A=35°,∠ACD=180°-∠ADC -∠A=35°∴∠OBC+∠OCB=(∠ABC+∠ACB )-(∠ABE +∠ACD )=55°∴∠BOC=180º-(∠OBC+∠OCB )=125°故选C .【点睛】此题考查的是三角形的内角和定理和高,三角形的内角和定理是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.5.(2021·全国·八年级专题练习)如图,在ABC V 中,AD ,AE 分别是边BC 上的中线与高,8AE =,ABC V 的面积为24,则CD 的长为( )A.2B.3C.4D.56.(2021·全国·九年级专题练习)如图,△ABC中,AD是高,角平分线BE交AD于点F,若∠BAC=60°,∠C=70°,则∠DFB的度数为( )A.75°B.65°C.60°D.55°高线定义,余角关系性质是解题关键.二、填空题7.(2020·山东·胶州市第七中学九年级阶段练习)小明和小红在太阳光下行走,小明身高1.5m,他的影长2.0m,小红比小明矮30cm,此刻小红的影长为______m.8.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = ______米;【答案】80【分析】过点C作CE⊥AB后,图中将有两个直角三角形.先在△BCE中,利用已知角的正切值求出CE,然后在△CEA中,利用已知角的正切值求出AE即可解决问题.【详解】9.我军侦察员在距敌方100m的地方发现敌方的一座建筑物,但不知其高度又不能靠近建筑物物测量,机灵的侦察员将自己的食E指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离约为40cm,食指的长约为8cm,则敌方建筑物的高度约是_______m.【答案】20【分析】由题意知△ABC∽△ADE,然后根据相似三角形对边的比与对应高的比相等列式求解即可.【详解】解:∵40cm=0.4m,8cm=0.08m∵BC∥DE,AG⊥BC,AF⊥DE.∴△ABC∽△ADE,∴BC:DE=AG:AF,∴0.08:DE=0.4:100,∴DE=20m.故答案为20.【点睛】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的对应高的比等于相似比,列出方程,通过解方程求解即可.此题是实际应用题,解题时首先要理解题意,将实际问题转化为三角形相似问题求解;相似三角形的对应边成比例.10.(2022·全国·九年级单元测试)如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DE=8cm,DF=10cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m.三、解答题11.(2022·全国·九年级专题练习)如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与直线PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,求PQ的长.12.(2022·全国·九年级课时练习)下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.题目测量小河的宽度测量目标示意图相关数据BC=1m,DE=1.5m,BD=5m【答案】10m【分析】利用BC//DE,可得到△ABC∽△ADE,利用相似三角形的对应边成比例,可求出AB的长.一、填空题1.(2021·山东泰安·九年级期末)小明和他的同学在太阳下行走,小明身高1.4米,他的影长为1.75米,他同学的身高为1.6米,则此时他的同学的影长为__________米.2.(2022·全国·九年级单元测试)贺哲同学的身高1.86米,影子长3米,同一时刻金老师的影子长2.7米,则金老师的身高为________米(结果保留两位小数)。
【最新】九年级数学-4.6 利用相似三角形测高--精选练习
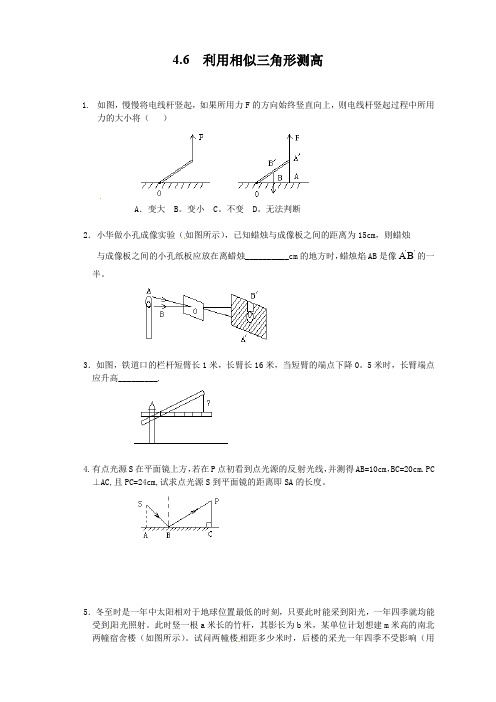
4.6 利用相似三角形测高1. 如图,慢慢将电线杆竖起,如果所用力F 的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )A .变大B 。
变小C 。
不变D 。
无法判断2.小华做小孔成像实验(如图所示),已知蜡烛与成像板之间的距离为15cm ,则蜡烛 与成像板之间的小孔纸板应放在离蜡烛__________cm 的地方时,蜡烛焰AB 是像''B A 的一半。
3.如图,铁道口的栏杆短臂长1米,长臂长16米,当短臂的端点下降0。
5米时,长臂端点应升高_________.4.有点光源S 在平面镜上方,若在P 点初看到点光源的反射光线,并测得AB=10cm ,BC=20cm.PC ⊥AC,且PC=24cm,试求点光源S 到平面镜的距离即SA 的长度。
5.冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射。
此时竖一根a 米长的竹杆,其影长为b 米,某单位计划想建m 米高的南北两幢宿舍楼(如图所示)。
试问两幢楼相距多少米时,后楼的采光一年四季不受影响(用m,a,b表示)6.一位同学想利用树影测出树高,他在某时刻测得直立的标杆高1米,影长是0.9米,但他去测树影时,发现树影的上半部分落在墙CD上,(如图所示)他测得BC=2.7米,CD=1.2米。
你能帮他求出树高为多少米吗?7.我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。
若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。
8.如图,阳光透过窗口照到室内,在地面上留下2.7米宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7米,窗口高AB=1.8 米,试求窗口下底与地面之间的距离B C的大小。
答案:1.C 2.5 3.8 4.由.12,201024cm SA SA BC AB PC SA ===故知 5.由米故abm ,==BC BC AB b a 。
利用相似三角形测高训练题

利用相似三角形测高训练题1.XXX用自制的直角三角形纸板DEF测量树的高度AB。
他调整自己的位置,使斜边DF保持水平,边DE与点B在同一直线上。
已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m。
求树高AB。
2.在同一时刻,两根木竿在太阳光下的影子如图所示。
其中木竿AB=2米,它的影子BC=1.6米。
木竿PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米。
求木竿PQ的长度。
3.某校数学兴趣小组利用自制的直角三角形小硬纸板DEF 来测量操场旗杆AB的高度。
他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上。
已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米。
求旗杆的高度为多少米?4.数学兴趣小组的同学们想利用树影测量树高。
课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,但当他们马上测量树高时,发现树的影子不落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处。
同学们认为继续量也可以求出树高,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米(每级台阶的宽度相同)。
请你和他们一起算一下,树高为多少。
(假设两次测量时太阳光线是平行的)5.如图,是一个照相机成像的示意图,像高MN,景物高度AB、CD为水平视线。
根据物体成像原理知:XXX,CD⊥XXX。
1)如果像高MN是35mm,焦距CL是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物的距离LD是多少?2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少毫米?6.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm。
动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(<t<2),连接PQ。
北师大版九年级上册 4.6 利用相似三角形测高专题(含答案)

∴AG:GF=AB:BC=物高:影长=1:0.4
∴GF=0.4AG
又∵GF=GE+EF,BD=GE,GE=4.4m,EF=0.2m,
∴GF=4.6
∴AG=11.5
∴AB=AG+GB=11.8,即树高为11.8米.
【点睛】
此题考查相似三角形的应用,解题关键在于画出图形.
∵△ABC∽△EDC,
∴ ,
即 ,
解得:AB=6,
故选:D.
【点睛】
本题考查的是相似三角形在实际生活中的应用,根据题意得出△ABE∽△CDE是解答此题的关键入射角等于反射角,以及人与被测量物体都与地面垂直,故可构造相似三角形利用这种方法测量物体的高度是通过判定两个物体与地面以及镜子所构成的两个三角形相似,利用相似三角形对应边成比例得到比例式,从而解答此类问题例如本题,结合题意画出图形,根据分析结果即可得到△ABE∽△CDE,据此即可得到解答此题的关键: .
A.4.5mB.4.8mC.5.5mD.6m
二、填空题
6.某同学要测量某烟囱的高度,他将一面镜子放在他与烟囱之间的地面上某一位置,然后站到与镜子、烟囱成一条直线的地方,刚好从镜中看到烟囱的顶部,如果这名同学身高为1.65米,他到镜子的距离是2米,测得镜面到烟囱的距离为20米,烟囱的高度_____米.
【详解】
解:过点D作DN⊥AB,垂足为N.交EF于M点,
∴四边形CDME、ACDN是矩形,
17.如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
利用相似三角形测高练习题

利用相似三角形测高练习题
一、基础训练
1、高4米的旗杆在水平地面上的影子长为6米,此时测得附近一个建筑物的影长为24米,则该建筑物的高度是______________米.
2、如图是小明设计用手电筒测量某建筑物高度的示意图,点P 处放一水平的平面镜,光线从点A 出发经平面镜反射后刚好射到该建筑物CD 的顶端C 处,已知AB ⊥BD ,CD ⊥BD ,且测得AB=1.2米,BP=1.8米,PD=12米,那么该建筑物的高度是()
A 6米
B 8米
C 18米
D 24米
3、如图,利用标杆BE 测量建筑物DC 的高度,
如果标杆BE 的长为1.2米,测得AB=1.6米, BC=8.4米,则楼高CD=___________米. 二、、提高训练:
4、如图所示,从点A (0,2)发出的一束光,经x 轴反射,过点B (4,3),则这束光从点A 到点B 所经过路径的长为 。
5、如图,某测量工作人员与标杆顶端F 、电视塔顶端在同一直线上,已知此人眼睛距地面
1.5米,标杆为3米,且BC=1米,CD=6米,求电视塔的高ED 。
A B
6、如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1米,已知某一时刻BC在地面的影长CN=1.5米,AC在地面的影长CM=4.5米,求窗户的高度.
7、一位同学想利用树影测量树高AB,他在某一时刻测得小树高为1米,树影长0.9
米,但当他马上测量树影时,因树靠近建筑物,影子不全落在地上,有一部分落在
墙上,如图,他先测得地面部分的影子长2.7米,又测得墙上的影高CD为1.2米,
试问树有多高?。
专题15利用相似三角形测高(3个知识点2种题型1种中考考法)(原卷版)-初中数学北师大版9年级上册

整自己的位置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知纸板的两条边 DE=8cm,
DF=10cm,测得边 DF 离地面的高度 AC=1.5m,CD=8m,则树高 AB=
m.
【变式】如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通
过竹杆的顶端刚好看到塔顶,若小明眼睛离地面1.6m ,竹杆顶端离地面 2.4m ,小明到竹杆的距离 DF 2m , 竹杆到塔底的距离 DB 33m ,求这座古塔的高度.
【学习目标】
1. 掌握几种测量物体高度的方法与原理,能综合运用相似三角形的判定定理和相似三角形的定义解决问题。 2. 通过设计测量旗杆高度的方案,学会将实物图形抽象成几何图形的方法,体会将实际问题转化成数学模 型的转化思想。
【知识导图】
【倍速学习四种方法】
【方法一】脉络梳理法
知识点 1.利用阳光下的影子测量旗杆的高度(重点)
为12m , CF 为1.8m , CF 为 3.84m ,求树高. 【变式 1】(2022 秋·九年级课时练习)每年的秋冬季节,青竹湖湘一外国语学校的银杏大道是学校最为靓丽
的一条风景线,数学彭老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜 子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树 (AB)8 m 的点 E 处,然后观测者沿着直线 BE 后 退到点 D ,这时恰好在镜子里看到树梢顶点 A ,再用皮尺量得 DE 2 m,观测者目高 CD 1.75 m,则树高 AB 约是多少米?
2.(2022 秋·九年级课时练习)如图,在斜坡的顶部有一铁塔 AB,B 是 CD 的中点,CD 是水平的,在阳光的 照射下,塔影 DE 留在坡面上.若铁塔底座宽 CD=12m,塔影长 DE 18 m,小明和小华的身高都是 1.6m,同 一时刻小明站在点 E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为 2m 和 1m,
人教版九年级数学上《利用相似三角形测高》同步练习(含解析)

北师大版数学九年级上册第三章第6节利用相似三角形测高同步检测一、选择题1、如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,长臂外端B升高()A、2mB、4mC、4.5mD、8m2、如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC,则梯子的长为()A、3.5mB、3.85mC、4mD、4.2m3、某一时刻,身髙1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得某旗杆的影长是5m,则该旗杆的高度是()A、1.25mB、10mC、20mD、8m4、小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为()A、10米B、12米C、15米D、22.5米5、如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为()A、12mB、10mC、8mD、7m6、如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是()A、6米B、8米C、18米D、24米7、一个油桶高0.8m,桶内有油,一根长lm的木棒从桶盖小口插入桶内,一端到达桶底,另一端恰好在小口处,抽出木棒量得浸油部分长0.8m,则油桶内的油的高度是()A、0.8mB、0.64mC、1mD、0.7m8、小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O,准星A,目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到,若OA=0.2米,OB=40米,=0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为()A、3米B、0.3米C、0.03米D、0.2米9、如图,测量小玻璃管口径的量具ABC,AB的长为12cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是()A、8cmB、10cmC、20cmD、60cm10、已知如图,小明在打网球时,要使球恰好能打过网,而且落在离网5m的位置上,则球拍击球的高度h应为()A、2.7mB、1.8mC、0.9mD、2.5m11、如图所示,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,则电线杆的高度为()A、2.4mB、24mC、0.6mD、6m12、如图所示的测量旗杆的方法,已知AB是标杆,BC表示AB在太阳光下的影子,叙述错误的是()A、可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高B、只需测量出标杆和旗杆的影长就可计算出旗杆的高C、可以利用△ABC∽△EDB,来计算旗杆的高D、需要测量出A B、BC和DB的长,才能计算出旗杆的高13、如图,在针孔成像问题中,根据图形尺寸可知像的长是物AB长的()A、3倍B、不知AB的长度,无法计算C、D、14、如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为()米.(不计宣传栏的厚度)A、4B、5C、6D、815、数学兴趣小组的小明想测量教学楼前的一棵树的高度.下午课外活动时他测得一根长为1m的竹竿的影长是0.8m.但当他马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图).他先测得留在墙壁上的树影高为1.2m,又测得地面的影长为2.6m,请你帮他算一下,下列哪个数字最接近树高()m.A、3.04B、4.45C、4.75D、3.8二、填空题16、为测量池塘边两点A,B之间的距离,小明设计了如下的方案:在地面取一点O,使A C、BD交于点O,且CD∥AB.若测得OB:OD=3:2,CD=40米,则A,B两点之间的距离为________米.17、如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,=50cm,则这个三角尺的面积与它在墙上所形成影子图形的面积之比是________。
相似三角形的应用综合(五大类型)(题型专练)(原卷版)

专题03 相似三角形的应用综合(五大类型)【题型1 利用相似三角形测量高度-平面镜测量法】【题型2 利用相似三角形测量高度-影子测量法】【题型3 利用相似三角形测量高度-手臂测量法】【题型4 利用相似三角形测量高度-标杆测量法】【题型5 利用相似三角形测量距离】【题型1 利用相似三角形测量高度-平面镜测量法】1.(2022秋•郑州期末)如图,小明探究“利用镜子反射测量旗杆的高度”.小明作为观测者,在旗杆和小明之间的地面上平放一面镜子,在镜子上作一个标记,小明看着镜子来回移动,当看到旗杆顶端在镜子中的像与镜子上的标记重合时,通过测量得到以下数据:小明的眼睛到地面的距离为1.5m,小明的站的位置到镜子上标记的距离是3.2m,旗杆的底部到小明的位置是19.2m,则旗杆的高度为()A.19.2B.16C.9D.7.5 2.(2023•龙华区一模)数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1米,BP=1.5米,PD=48米,那么该大厦的高度约为()A.32米B.28米C.24米D.16米3.(2023•深圳模拟)如图,九年级(1)班课外活动小组利用平面镜测量学校旗杆的高度,在观测员与旗杆AB之间的地面上平放一面镜子,在镜子上做一个标记E,当观测到旗杆顶端在镜子中的像与镜子上的标记重合时,测得观测员的眼睛到地面的高度CD为1.6m,观测员到标记E的距离CE为2m,旗杆底部到标记E的距离AE为16m,则旗杆AB的高度约是()A.22.5m B.20m C.14.4m D.12.8m 4.(2023•青原区校级一模)为了测量校园内一棵树的高度,学校数学应用实践小组做了如下的探索实践.根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树(AB)9m的水平地面点E处,然后一同学沿着直线BE后退到点D,这时该同学恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3m,该同学身高CD=1.6m.请你计算树(AB)的高度.5.(2023•新城区校级一模)【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.【同题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E 到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,本板到墙的水平距离为CD=4m.图中点A,B,C,D在同一条直线上.(1)求BC的长;(2)求灯泡到地面的高度AG.6.(2023•灞桥区校级模拟)小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.小明同学对该塔进行了测量,测量方法如下,如图所示,先在点A处放一平面镜,从A处沿NA方向后退1米到点B处,恰好在平面镜中看到塔的顶部点M,再将平面镜沿NA方向继续向后移动15米放在D处(即AD=15米),从点D处向后退1.6米,到达点E处,恰好再次在平面镜中看到塔的顶部点M、已知小明眼睛到地面的距离CB=EF=1.74米,请根据题中提供的相关信息,求出小雁塔的高度MN﹒(平面镜的大小忽略不计)7.(2022秋•大名县校级期末)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得∠ACD=135°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF =1.6米,测量器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(小平面镜的大小忽略不计)【题型2 利用相似三角形测量高度-影子测量法】8.(2021秋•蓝山县期末)如图,某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为米.9.(2022•兴化市模拟)如图,电线杆上的路灯距离地面8m,身高1.6m的小明(AB)站在距离电线杆的底部(点O)20m的A处,则小明的影子AM为m.【题型3 利用相似三角形测量高度-手臂测量法】10.(2022秋•房山区期中)在设计“利用相似三角形的知识测量树高”的综合实践方案时,晓君想到了素描课上老师教的方法,如图,请一位同学右手握笔,手臂向前伸直保持笔杆与地面垂直,前后移动调整自己的位置,直到看见笔杆露出的部分刚好遮住树的主干,这时测量同学眼睛到笔的距离AB、同学到树干的距离AC,以及露出笔的长度DE,就可通过计算得到树的高度,这种实践方案主要应用了相似三角形的性质定理:相似三角形对应高的比等于相似比.(填写定理内容)11.(2022•姑苏区一模)小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处时恰好能看到铁塔的顶部B 和底部A(如图).设小明的手臂长l=50cm,小尺长a=20cm,点D到铁塔底部的距离AD=20m,则铁塔的高度为m.12.(2023•长安区校级二模)如图,是位于西安市长安区香积寺内的善导塔,善导塔为楼阁式砖塔,塔身全用青砖砌成,平面呈正方形,原为十三层,现存十一层,建筑形式独具一格.数学兴趣小组测量善导塔的高度AB,有以下两种方案:方案一:如图1,在距离塔底B点45m远的D处竖立一根高1.5m的标杆CD,小明在F处蹲下,他的眼睛所在位置E、标杆的顶端C和塔顶点A三点在一条直线上.已知小明的眼睛到地面的距离EF=0.8m,DF=1m,AB⊥BM,CD ⊥BM,EF⊥BM,点B、D、F、M在同一直线上.方案二:如图2,小华拿着一把长为22cm的直尺CD站在离善导塔45m的地方(即点E到AB的距离为45m).他把手臂向前伸,尺子竖直,CD∥AB,尺子两端恰好遮住善导塔(即A、C、E在一条直线上,B、D、E在一条直线上),已知点E到直尺CD的距离为30cm.请你结合上述两个方案,选择其中的一个方案求善导塔的高度AB.我选择方案.【题型4 利用相似三角形测量高度-标杆测量法】13.(2023•费县二模)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=10.8m,则建筑物CD 的高是m.14.(2021秋•吉林期末)小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为.15.(2022秋•花都区期末)如图,利用标杆BE测量建筑物的高度,如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?16.(2023•雁塔区一模)为测量一棵大树的高度,设计的测量方案如图所示:标杆高度CD=3m,人的眼睛A、标杆的顶端C和大树顶端M在一条直线上,标杆与大树的水平距离DN=14m,人的眼睛与地面的高度AB=1.6m,人与标杆CD的水平距离BD=2m,B、D、N三点共线,AB⊥BN,CD⊥BN,MN⊥BN,求大树MN的高度.17.(2023•碑林区校级一模)某数学兴趣小组决定利用所学知识测量一古建筑的高度.如图2,古建筑的高度为AB,在地面BC上取E,G两点,分别竖立两根高为1.5m的标杆EF和GH,两标杆间隔EG为26m,并且古建筑AB,标杆EF和GH在同一竖直平面内.从标杆EF后退2m到D处(即ED=2m),从D处观察A点,A,F,D在一直线上;从标杆GH后退4m到C处(即CG =4m),从C处观察A点,A、H、C三点也成一线.已知B、E、D、G、C 在同一直线上,AB⊥BC,EF⊥BC,GH⊥BC,请你根据以上测量数据,帮助兴趣小组求出该古建筑AB的高度.18.(2022秋•高新区期末)某校同学参与“项目式学习”综合实践活动,小明所在的数学活动小组利用所学知识测量旗杆EF的高度,他在距离旗杆40米的D处立下一根3米高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4米时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6米,求旗杆EF的高度.19.(2023•碑林区一模)杭州市西湖风景区的雷峰塔又名“皇妃塔”,某校社会实践小组为了测量雷峰塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,雷峰塔的塔尖点B正好在同一直线上,测得EC=3米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,雷峰塔的塔尖点B正好又在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=5米,GC=60米,请你根据以上数据,计算雷峰塔的高度AB.20.(2022秋•益阳期末)大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=1.28米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.92米,CG=20米,请你根据以上数据,计算古塔的高度AB.21.(2022秋•雁塔区校级期中)青龙寺是西安最著名的樱花观赏地,品种达到了13种之多,每年3、4月陆续开放的樱花让这里成为了花的海洋,一天,小明和小刚去青龙守游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米;然后,小明在地面上放一个镜子,恰好在G处时,小刚刚好能从镜子里看到树的顶端B.已知EF=3.2米,CF =3米,CG=2米,点小C、F、G在一条直线上,CD⊥AC,EF⊥AC,AB ⊥AC.根据以上测量过程及测量数据,请你求出这棵樱花树AB的高度.【题型5 利用相似三角形测量距离】22.(2022秋•开封期末)如图,某“综合实践”小组为估算开封护城河的宽度,可以在河对岸选定一个目标点P,在近岸取点A和点C,使AC=30m,且AC ⊥AP,再过点C作CD⊥BC,且CD=20m,PD与AC交于点B,若测得AB =20m,则河宽AP的宽度为()A.40m B.30m C.20m D.10m 23.(2022秋•上海月考)如图,A,B是河边上的两根水泥电线杆,C,D是河对岸不远处的两根木质电话线杆,且电线、电话线及河两边都是平行的.O 是A、B对岸河边上一点,且O与A、C在同一直线上,与B、D也在同一直线上,已知AB=35m,CD=20m,OD=20m,根据所给的已知条件是否一定能求出河的大约宽度能(填能或不能或不一定).24.(2023•山西模拟)如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,在近岸取点B和点C,观察者在点E.适当调整,使得AB与EC 都与河岸BC垂直.此时AE与BC相交于点D,若测得BD=100m,DC=50m,EC=45m,请利用这些数据计算河的宽度.25.(2022秋•济南期末)如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.(1)求证:△BEF∽△CDF;(2)求CF的长.26.(2023•西吉县一模)如图,A,B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于点N,量得MN=38m,求AB的长.27.(2023•莲湖区模拟)如图,为了测量平静的河面的宽度(EP),在离河岸D点3m远的B点,立一根长为1.5m的标杆AB,已知河岸高出水面0.6m,即DE=0.6m.在河对岸的水里有一棵高出水面4.6m的大树MP,大树的顶端M在河里的倒影为点N,即PM=PN.经测量此时A,D,N三点在同一直线上,并且点M,P,N共线,若AB,DE,MP均垂直于河面EP,则河宽EP 是多少米?。
专题4-6利用相似三角形测高-(解析版)

2020-2021学年九年级数学上册尖子生同步培优题典【北师大版】专题4.6利用相似三角形测高姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020•宛城区一模)如图,顽皮的小聪在小芳的作业本上用红笔画了个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),A、B、C、D、O都在横格线上,且线段AD、BC交于点O.若线段AB=4cm,则线段CD长为()A.4cm B.5cm C.6cm D.8cm【分析】过点O作OE⊥AB于点E,OF⊥CD于点F,则由相似三角形(△AOB∽△DOC),根据平行线分线段成比例可得,代入计算即可解答.【解析】如图,过点O作OE⊥AB于点E,OF⊥CD于点F,则OE、OF分别是△AOB、△DOC的高线,∵练习本中的横格线都平行,∴△AOB∽△DOC,∴,即,∴CD=6cm.故选:C.2.(2020•新宾县四模)如图,有一块直角边AB=4cm,BC=3cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为()A.B.C.D.【分析】过点B作BP⊥AC,垂足为P,BP交DE于Q,三角形的面积公式求出BP的长度,由相似三角形的判定定理得出△BDE∽△BAC,设边长DE=x,根据相似三角形的对应边成比例求出x的长度可得.【解析】如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.∵S△ABC•AB•BC•AC•BP,∴BP.∵DE∥AC,∴∠BDE=∠A,∠BED=∠C,∴△BDE∽△BAC,∴.设DE=x,则有:,解得x,故选:D.3.(2020•天水)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是()A.17.5m B.17m C.16.5m D.18m【分析】根据题意和图形,利用三角形相似,可以计算出CD的长,从而可以解答本题.【解析】∵EB⊥AC,DC⊥AC,∴EB∥DC,∴△ABE∽△ACD,∴,∵BE=1.5m,AB=1.2m,BC=12.8m,∴AC=AB+BC=14m,∴,解得,DC=17.5,即建筑物CD的高是17.5m,故选:A.4.(2019秋•南岸区期末)如图,在一块斜边长60cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若CD:CB=1:3,则这块木板截取正方形CDEF 后,剩余部分的面积为()A.202.5cm2B.320cm2C.400cm2D.405cm2【分析】设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.【解析】∵四边形CDEF为正方形,∴EF∥BC,∴△AEF∽△ABC,∵CD:CB=1:3,∴,设AF=x,则AC=3x,EF=CF=2x,∴BC=6x,在Rt△ABC中,AB2=AC2+BC2,即602=(3x)2+(6x)2,解得,x=4,∴AC=12,BC=24,∴剩余部分的面积241288400(cm2),故选:C.5.(2019秋•鹿城区校级月考)如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为()A.4 m B.m C.5m D.m【分析】根据已知易得△ABM∽△DCM,可得对应高BH与HD之比,易得MH∥AB,可得△MDH∽△ADB,利用对应边成比例可得比例式,把相关数值代入求解即可.【解析】∵AB∥CD,∴△ABM∽△DCM,∴,(相似三角形对应高的比等于相似比),∵MH∥AB,∴△MCH∽△ACB,∴,∴,解得MH.故选:B.6.(2018秋•嘉兴期末)如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为()A.60mm B.mm C.20mm D.mm【分析】利用相似三角形的性质构建方程即可解决问题.【解析】如图,设AD交PN于点K.∵PM:PQ=3:2,∴可以假设MP=3k,PQ=2k.∵四边形PQNM是矩形,∴PM∥BC,∴△APM∽△ABC,∵AD⊥BC,BC∥PM,∴AD⊥PM,∴,∴,解得k=20mm,∴PM=3k=60mm,故选:A.7.(2019秋•永春县期中)我国古代数学著作中记载了一个问题:“今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”其大意是:一座正方形城池,西、北边正中各开一道门,从北门往正北方向走40步后刚好有一树木,若从西门往正西方向走810步后正好看到树木,则正方形城池的边长为()步.A.360 B.270 C.180 D.90【分析】设正方形城池的边长为x步,则AE=CE x,证明Rt△BEA∽Rt△EDC,利用相似比得到,然后利用比例性质求出x即可.【解析】如图,设正方形城池的边长为x步,则AE=CE x,∵AE∥CD,∴∠BEA=∠EDC,∴Rt△BEA∽Rt△EDC,∴,即,∴x=360,即正方形城池的边长为360步.故选:A.8.(2020•成都模拟)如图是用卡钳测量容器内径的示意图,现量得卡钳上A,D两个端点之间的距离为10m,,则容器的内径是()A.5cm B.10cm C.15cm D.20cm【分析】首先连接AD、BC,然后判定△AOD∽△BOC,根据相似三角形的性质可得,进而可得答案.【解析】连接AD、BC,∵,∠AOD=∠BOC,∴△AOD∽△BOC,∴,∵A,D两个端点之间的距离为10m,∴BC=15m,故选:C.9.(2020春•武邑县校级月考)如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是()A.5m B.6m C.125m D.4m【分析】先求出△ABC∽△AEF,再根据三角形对应高的比等于对应边的比,这样就可以求出电线杆EF 的高.【解析】作AN⊥EF于N,交BC于M,∵BC∥EF,∴AM⊥BC于M,∴△ABC∽△AEF,∴,∵AM=0.7m,AN=25m,BC=0.14m,∴EF5(m).故选:A.10.(2019•毕节市)如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF 后,剩余部分的面积为()A.100cm2B.150cm2C.170cm2D.200cm2【分析】设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.【解析】设AF=x,则AC=3x,∵四边形CDEF为正方形,∴EF=CF=2x,EF∥BC,∴△AEF∽△ABC,∴,∴BC=6x,在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,解得,x=2,∴AC=6,BC=12,∴剩余部分的面积12644100(cm2),故选:A.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2017秋•嘉兴期末)某公司门口的栏杆如图,AB=1.2m,BC=15m.要使栏杆C端从栏杆水平位置上升到垂直距离(CE)5m处,栏杆A应下降的垂直距离(AD)为0.4m.【分析】证明∴△BAD∽△BCE,然后利用相似比计算AD的长.【解析】∵AD∥CE,∴△BAD∽△BCE,∴AD:CE=BA:BC,即AD:5=1.2:15,解得AD=0.4(m).故答案为0.4.12.(2020•衡阳模拟)如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF 后,剩余部分的面积为100cm2.【分析】设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.【解析】设AF=x,则AC=3x,∵四边形CDEF为正方形,∴EF=CF=2x,EF∥BC,∴△AEF∽△ABC,∴,∴BC=6x,在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,解得,x=2,∴AC=6,BC=12,∴剩余部分的面积12644100(cm2),故答案为:100cm2.13.(2020•晋安区一模)如图,利用镜子M的反射(入射角等于反射角),来测量旗杆CD的长度,在镜子上作一个标记,观测者AB看着镜子来回移动,直到看到旗杆顶端在镜子中的像与镜子上的标记相重合,若观测者AB的身高为1.6m,量得BM:DM=2:11,则旗杆的高度为8.8m.【分析】根据题意抽象出相似三角形,然后利用相似三角形的对应边的比相等列式计算即可.【解析】根据题意得:△ABM∽△CDM,∴AB:CD=BM:DM,∵AB=1.6m,BM:DM=2:11,∴1.6:CD=2:11,解得:CD=8.8m,故答案为:8.8.14.(2019秋•山西期末)太原市某学校门口的栏杆如图所示,栏杆从水平位置AB绕定点O旋转到DC位置,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m.支柱OE的高为0.5m,则栏杆D端离地面的距离为 2.3m.【分析】过D作DG⊥AB于G,过C作CH⊥AB于H,则DG∥CH,根据相似三角形的性质即可得到结论.【解析】过D作DG⊥AB于G,过C作CH⊥AB于H,则DG∥CH,∴△ODG∽△OCH,∴,∵栏杆从水平位置AB绕固定点O旋转到位置DC,∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,∴OC=0.5m,∴,∴DG=1.8m,∵OE=0.5m,∴栏杆D端离地面的距离为1.8+0.5=2.3m.故答案是:2.3m.15.(2019秋•西城区期末)在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量,如图所示.若a1=1米,a2=10米,h=1.5米,则这个学校教学楼的高度为15米.【分析】直接利用相似三角形的判定与性质进而得出教学楼的高度.【解析】由镜面反射原理可得,∠1=∠2,△ACB∽△ADE,故,则,解得:ED=15(m),即这个学校教学楼的高度为15米.故答案为:15.16.(2020春•沙坪坝区校级期末)我军边防部队沿加勒万河谷巡逻时发现,对岸我方领土上有Y国军队在活动,为了估算其与我军距离,侦察员手臂向前伸,将食指竖直,通过前后移动,使食指恰好将对岸我方树立的旗杆遮住,如图所示.若此时眼睛到食指距离l约为63cm,食指AB长约为7cm,旗杆CD高度为28米,则对方与我军距离d约为252米.【分析】将实际问题转化为三角形相似问题求解进而得出答案.【解析】63cm=0.63m,AB=7cm=0.07m,∵AB∥CD,∴△ABO∽△CDO,∴,即,d=252(m),故答案为:252.17.(2020•上海)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么AC为7米.【分析】根据相似三角形的判定和性质定理即可得到结论.【解析】∵BD⊥AB,AC⊥AB,∴BD∥AC,∴△ACE∽△BDE,∴,∴,∴AC=7(米),故答案为:7.18.(2020•温州)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为15米,BC为20米.【分析】根据已知条件得到△ANE和△BNF是等腰直角三角形,求得AE=EN=15+2+8=25(米),BF =FN=2+8=10(米),于是得到AB=AN﹣BN=15(米);过C作CH⊥l于H,过B作PQ∥l交AE 于P,交CH于Q,根据矩形的性质得到PE=BF=QH=10,PB=EF=15,BQ=FH,根据相似三角形的性质即可得到结论.【解析】∵AE⊥l,BF⊥l,∵∠ANE=45°,∴△ANE和△BNF是等腰直角三角形,∴AE=EN,BF=FN,∴EF=15米,FM=2米,MN=8米,∴AE=EN=15+2+8=25(米),BF=FN=2+8=10(米),∴AN=25,BN=10,∴AB=AN﹣BN=15(米);过C作CH⊥l于H,过B作PQ∥l交AE于P,交CH于Q,∴AE∥CH,∴四边形PEHQ和四边形PEFB是矩形,∴PE=BF=QH=10,PB=EF=15,BQ=FH,∵∠1=∠2,∠AEF=∠CHM=90°,∴△AEF∽△CHM,∴,∴设MH=3x,CH=5x,∴CQ=5x﹣10,BQ=FH=3x+2,∵∠APB=∠ABC=∠CQB=90°,∴∠ABP+∠P AB=∠ABP+∠CBQ=90°,∴∠P AB=∠CBQ,∴△APB∽△BQC,∴,∴,∴x=6,∴BQ=CQ=20,∴BC=20,故答案为:15,20.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020•雁塔区校级模拟)《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看一到位于A处的树木(即点D在直线AC上).【分析】证明△CDK∽△DAH,利用相似三角形的性质得,然后利用比例性质可求出CK的长.【解析】DH=100,DK=100,AH=15,∵AH∥DK,∴∠CDK=∠A,而∠CKD=∠AHD,∴△CDK∽△DAH,∴,即,∴CK.答:出南门步恰好看一到位于A处的树木.20.(2020春•莱州市期末)如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上已知纸板的两条直角边DE=40cm,EF =30cm,测得AM=10m,边DF离地面的高度DM=1.5m,求树高AB.【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.【解析】∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB,∴,∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,∴,∴BC=7.5米,∴AB=AC+BC=1.5+7.5=9米,∴树高为9米.21.(2020•山西一模)“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走2.8米,到达点D 处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上).若测得FM=1.5米,DN=1.1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.【分析】设NB的长为x米,则MB=x+1.1+2.8﹣1.5=(x+2.4)米.通过△CND∽△ANB和△EMF∽△AMB的性质求得x的值,然后结合求得大树的高.【解析】设NB的长为x米,则MB=x+1.1+2.8﹣1.5=(x+2.4)米.由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,∴△CND∽△ANB,∴.同理,△EMF∽△AMB,∴.∵EF=CD,∴,即.解得x=6.6,∵,∴.解得AB=9.6.答:大树AB的高度为9.6米.22.(2019春•西湖区校级月考)如图,一位同学通过调整自己的位置,设法使三角板的斜边保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面AC=1.5m,CD=8m,求树高.【分析】利用Rt△DEF和Rt△BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.【解析】∵∠DEF=∠DCB=90°,∠D=∠D,∴△DEF∽△DCB∴,∵DE=0.4m,EF=0.2m,CD=8m,∴,∴CB=4(m),∴AB=AC+BC=1.5+4=5.5(米).答:树高为5.5米.23.(2019秋•绥德县期末)如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根3米高的标杆(CD)竖直放在某一位置,有一名同学站在F处与标杆底端(D)、旗杆底端(B)成一条直线,此时他看到标杆顶端C与旗杆顶端A重合,另外一名同学测得站立(EF)的同学离标杆(CD)3米,离旗杆(AB)30米.如果站立(EF)的同学的眼睛距地面1.6米,过点E作EH⊥AB于点H,交CD于点G(EF∥AB,CD∥AB,EH∥FB),求旗杆AB的高度.【分析】过点E作EH⊥AB于点H,交CD于点G得出△EGC∽△EHA,进而求出AH的长,进而求出AB的长.【解析】过点E作EH⊥AB于点H,交CD于点G.由题意可得,四边形EFDG、GDHB都是矩形,AB∥CD∥EF.∴△ECG∽△EAH.∴.由题意可得:EG=FD=3m,EH=BF=30m,CG=CD﹣GD=CD﹣EF=3﹣1.6=1.4(m).∴,∴AH=14(米),∴AB=AH+HB=14+1.6=15.6(米).答:旗杆的高度为15.6米.24.(2012•茂南区校级一模)在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:(1)用含t的代数式表示Rt△CPQ的面积S;(2)当t=3时,P、Q两点之间的距离是多少?(3)当t为多少时,以点C、P、Q为顶点的三角形与△ABC相似?【分析】(1)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP、CQ用含t的表达式求出,代入直角三角形面积公式S△CPQ CP×CQ求解;(2)在Rt△CPQ中,由(1)可知CP、CQ的长,运用勾股定理可将PQ的长求出;(3)应分两种情况,当Rt△CPQ∽Rt△CAB时,根据,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据,可求出时间t.【解析】(1)由题意得AP=4t,CQ=2t,则CP=20﹣4t,因此Rt△CPQ的面积为S cm2;(2)当t=3时,CP=20﹣4t=8cm,CQ=2t=6cm,由勾股定理得PQ;(3)分两种情况:①当Rt△CPQ∽Rt△CAB时,,即,解得t=3;②当Rt△CPQ∽Rt△CBA时,,即,解得t.因此t=3或t时,以点C、P、Q为顶点的三角形与△ABC相似.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用相似三角形测高
基础题
知识点1 利用阳光下的影子测量高度
1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )
A.仰角B.树的影长
C.标杆的影长D.都不需要
2.小玲和爸爸正在散步,爸爸身高1.8 m,他在地面上的影长为2.1 m,若小玲比爸爸矮0.3 m,则她的影长为( )
A.1.3 m B.1.65 m
C.1.75 m D.1.8 m
3.如图,夏季的一天,身高为1.6 m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2 m,CA=0.8 m,于是得出树的高度为( )
A.8 m
B.6.4 m
C.4.8 m
D.10 m
4.(北京中考)在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为________m.
5.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,请你计算DE的长.
知识点2 利用标杆测量高度
6.(娄底中考)如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为________m.
7.如图,一天早上,小张正向着教学楼AB走去,他发现教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了”心里很是纳闷.经过了解,教学楼、水塔的高分别为20 m和30 m,它们之间的距离为30 m,小张身高为1.6 m.小张要想看到水塔,他与教学楼的距离至少应有多少米?
知识点3 利用镜子的反射测量高度
8.(天水中考)如图是一位学生设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A发出经平面镜反射后刚好到古城墙CD的顶端C 处,已知AB⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是________米.
9.如图,球从A处射出,经球台边挡板CD反射到B,已知AC=10 cm,BD=15 cm,CD=50 cm,则点E到点C的距离是________cm.
中档题
10.小刚身高1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,测得影子长为1.1 m,那么小刚举起的手臂超出头顶( )
A.0.5 m B.0.55 m
C.0.6 m D.2.2 m
11.(巴中中考)如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为________米.
12.(陕西中考)晚饭后,小聪和小军在社区广场散步.小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
综合题
13.为了测量一棵大树的高度,准备了如下测量工具:①镜子,②皮尺,③长为2 m 的标杆,④高为1.5 m的测角仪.请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中.选用的测量工具是________;(用工具序号填写)
(2)画出测量方案示意图;
(3)你需要测量示意图中哪些数据,并用a、b、c、α、β等字母表示测得的数据;
(4)写出求树高的算式:AB=________m.(用a、b、c、α、β等字母表示)
参考答案
1.B 2.C 3.A 4.15 5.(1)略.(2)设DE 的长为x ,依题意,=,即=.解AB BC DE x 53x 6
得x =10,即DE 的长为10 m . 6.
9
7.如图所示,AH =18.4,DG =28.4,HG =30,由△EAH ∽△EDG ,得=,代EH EG AH DG
入数据,得=.解得EH =55.2.答:他与教学楼的距离至少应有55.2米. EH EH +3018.428.4
8.8 9.20 10.A 11.1.5 12.由题意得∠CAD =∠MND =90°,∠CDA =∠MDN.∴△CAD ∽△MND.∴=.∴=.∴MN =9.6.又∵∠EBF =∠MNF CA MN AD ND 1.6MN 1×0.8(5+1)×0.8
=90°,∠EFB =∠MFN ,∴△EBF ∽△MNF.∴=.∴=.∴EB MN BF NF EB 9.62×0.8(2+9)×0.8
EB≈1.75.∴小军的身高约为1.75米. 13.方法一:(1)①②.(2)测量示意图如图1所示.(3)MB(镜子离树的距离)=a.MD(人与镜子的距离)=b ,CD(眼睛与地面的距离)=
c(单位:m).(4).ac
b
方法二:(1)②③④.(2)测量示意图如图2所示.(3)DF(标杆与测角仪的距离)=a ,
BD(标杆到树底面的距离)=b(单位:m).(4)(+2).b 2a。
