空间几何体结构练习题
专题14 空间几何体的结构、面积与体积(练)【解析版】

第一篇热点、难点突破篇专题14空间几何体的结构、面积与体积(练)【对点演练】一、单选题1.(2022秋·北京·高三统考阶段练习)已知圆柱的上、下底面的中心分别为1O,2O,过直O O的平面截该圆柱所得的截面是面积为12的正方形,则该圆柱的体积为()线12A.B.12πC.D.则该圆台的体积为()A.36πB.40πC.42πD.45πOO的长度===,1O为ABC的外接圆的圆心,球O的表面积为64π,则1AB BC AC为()B.2C.D.3A【答案】C【分析】由已知求得球O的半径4r=,即可求R=,根据正弦定理求出ABC外接圆半径2出结果.O的半径为r,球O的半径为R.【详解】设圆1依题意得ABC 为等边三角形,则由正弦定理得O 的表面积为如图,根据球的截面性质得2d OA ==的扇形,则该圆锥的侧面积为( ) A .π B .3π2C D .点作球O 的截面,则最小截面的面积为( ) A .3π B .4πC .5πD .6π子,其形状可以看成一个正四面体.广东流行粽子里放蛋黄,现需要在四角状粽子内部放入一个蛋黄,蛋黄的形状近似地看成球,当这个蛋黄的表面积是9π时,则该正四面体的高的最小值为()A.4B.6C.8D.10实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为()A.3:2B.5:4C.5:3D.4:3一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为,则该圆锥的体积为( )A .B .C .D .9π中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),若458h r =,则S 占地球表面积的百分比约为( ) A .26% B .34% C .42% D .50%【答案】C【分析】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,得AOC α∠=,在直角三角形中求出cos α后,可计算两者面积比.【详解】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,如图,则AOC α∠=,r OE =,CE h =,OA CA ⊥,二、填空题10.(2022秋·江苏徐州·高三期末)已知圆柱的高为8,该圆柱内能容纳半径最大的球的表面积为36π,则圆柱的体积为______.【答案】72π【分析】先分析半径最大的球不可能为圆柱的内切球,所以此球是与圆柱侧面与下底面相切的球,就能求出圆柱底面半径,然后根据圆柱的体积公式可得.【详解】圆柱内能容纳半径最大的球的表面积为36π,设此球半径为r,则24π36π3r r=⇒=如果圆柱有内切球,又因为圆柱的高为8,所以内切球半径为43>,说明这个圆柱内能容纳半径最大的球,与圆柱侧面和下底面相切,与上底面相离,易得圆柱底面半径为3,圆柱的体积为2π3872π⋅⨯=故答案为:72π【冲刺提升】一、单选题1.(2022秋·广东东莞·高三统考期末)已知一个装满水的圆台形容器的上底半径为6,下底半径为1,高为,若将一个铁球放入该容器中,使得铁球完全没入水中,则可放入的铁球的体积的最大值为()A.B.C D.108π【答案】B【分析】作出体积最大时的剖面图,分析出此时圆与上底,两腰相切,建立合适直角坐标系,()53,05<<t=-533)32332=模拟预测)某工厂要生产容积为为侧面成本的2倍,为使成本最小,则圆柱的高与底面半径之比应为()A.1B.1C.2D.4 2圆柱上下底的总面积为3.(2022·浙江·模拟预测)如图,正方体1111的棱长为1,,E F 分别为棱BC ,11的中点,则三棱锥1B AEF -的体积为( )A .524B .316C .29D .181AB ES =因为正方体ABCD A B C D -的棱长为1, 所以111(,1,0),(0,1,1),(1,22AE AB AF =-==-的法向量为(,,)n x y z =112n AE x n AB y z ⎧⋅=-⎪⎨⎪⋅=+⎩所以(2,1,1)n =-,F 平面1AB E 的距离为2AF n n-+⋅=又因为1AB =,121122AB EAB S⎫==⋅⎪⎭所以三棱锥故选:AF ,G ,H 分别是SA ,SB ,BC ,AC 的中点,则四边形EFGH 面积的取值范围是( ) A .()0,∞+ B .⎫∞⎪⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭D .1,2⎛⎫+∞ ⎪⎝⎭【答案】B【分析】画出图形,求出,EF HG ,说明EFHG 是矩形,结合图形,说明S 点在ABC 平面时,面积最小,求出即可得到范围 【详解】如图所示:由正三棱锥S ABC -的底面边长是2,因为E 、F 、G 、H 分别是SA 、SB 、BC 、AC 的中点,设ABC 的中心为SC OA >=所以EFGH 所以四边形且4BC =,6BD =,面ABC 与面BCD 夹角正弦值为1,则空间四边形ABCD 外接球与内切球的表面积之比为( )A B C D 【答案】C【分析】根据空间四边形ABCD 的线面关系可得DB ⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱中,根据圆柱的外接球半径求得空间四边形ABCD 的外接球半径R ,又根据内切球的几何性质用等体积法可求得空间四边形ABCD 的内切球半径r ,即可得空间四边形ABCD 外接球与内切球的表面积之比.【详解】解:面ABC 与面BCD 夹角正弦值为1,∴面ABC ⊥面BCD ,又面ABC ⋂面BCD BC =,DB BC DB ⊥⊂面BCD ,DB ∴⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱12O O 中,如下图所示:点在上底面圆周上,ABC三个顶点在下底面圆周上,则圆柱O O的外接球即空间四边连接OA,则球心为为正ABC4sin6032BC=︒1111333ABC ABD ADC BCDS r S r S r S r⋅+⋅+⋅+⋅,,所以()22142132832ADCS=⨯⨯-=,44612ABC ABD ADC BCDS S S S⨯⨯⨯=+++⨯外接球与内切球的表面积之比为6.(2022秋·湖南长沙·高三长郡中学校考阶段练习)三棱锥A BCD -中,AB BC AD CD BD AC ======,则三棱锥A BCD -的外接球的表面积为( )A .20πB .28πC .32πD .36π23AB AD ==且E 为BD 中点,AE BD ∴⊥,AE AB ∴=又AE CE =120, 过BCD △的外心作平面同理过ABD △l l O ''=,易知连接O E ',O 为BCD △又在OO E '中,603=,∴得27O C O O ''=,即外接球半径7=,故外接球表面积28π=.故选:B7.(2022秋·天津河东·高三统考期末)一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的两个底面和三个侧面都相切,若棱柱的体积为)A.16πB.4πC.8πD.32π8.(2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.则该截角四面体的表面积是______.正六边形每个内角均为2π111A B C 中,点P 在棱1BB 上,且1PA PC ⊥,当1APC 的面积取最小值时,三棱锥-P ABC 的外接球的表面积为______.【答案】28π时,1APC 面积取得最小值,补形后三棱锥的外接球,求出外接球半径和表面积【详解】由勾股定理得:AB =,则16PA =(7x y ++1APC S =2169y +,即2x =其中长方体的外接球的直径为,平面PAB ⊥平面PCD ,则P ABCD -体积的最大值为__________.PO ⊥平面ABCD ,PE CD⊥CD平面POE∴⊥,CD OE底面ABCD是边长为∴⊥,CD BCOE⊂平面ABCD OE BC∴,同理可得:OF∥O E F三点共线故,,∥,且有EF BC设平面PAB⋂平面∥AB CD AB,∴∥∥l AB⊥PE CD平面PAB∴⊥平面PEPF⊂平面∴⊥PE PF不妨设PE22∴+x y且2OP=-即2y m11.(2023·广西梧州·统考一模)边长为1的正方形ABCD 中,点M ,N 分别是DC ,BC 的中点,现将ABN ,ADM △分别沿AN ,AM 折起,使得B ,D 两点重合于点P ,连接PC ,得到四棱锥P AMCN -.(1)证明:平面APN ⊥平面PMN ;(2)求四棱锥P AMCN -的体积. ,所以PMN 为直角三角形,即PMN S=111111222AMN ABN ADM CMN ABCD S S S S S =---=-⨯⨯⨯-⨯正方形设点P 到平面AMN 的距离为h ,由A PMN P V V --=1133PMN AMN S PA S h ⋅=⋅△△,即13188h ⨯=,得h =)AMN MCN S S h +=AMCN 的体积为全国·高三对口高考)如题图,是圆锥底面的圆心,ABC 是底面的内接正三角形.P 为DO 上一点,90APC ∠=︒.(1)求证:PC ⊥平面PAB ;(2)若DO =.求三棱锥-P ABC 的体积. 因为ABC 是底面的内接正三角形,CO AB ⊥,PO OC ⋂AB ⊥平面PC ⊂平面AB PC ⊥,PA AB A =,⊥平面PAB(2)解:设圆锥的母线为l,底面半径为r,则圆锥的侧面积为ππ,即,=603所以,在等腰直角三角形APC。
空间几何体(经典习题)
正视图 俯视图侧视图空间几何体(经典习题)一、选择题:1、半径为R 的半圆卷成一个圆锥,则它的体积为( )A .3R B .3R C .3R D .3R 2、一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ) A. 28cm π B. 212cmπC. 216cmπD. 220cm π3、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则 圆台较小底面的半径为( )A . 7 B. 6 C. 5 D. 34、棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( ) A . 1:7 B. 2:7 C. 7:19 D. 5:165、一简单组合体的三视图及尺寸如图示(单位: cm )则该组合 体的体积为( )A. 720003cmB. 640003cmC. 560003cmD. 440003cm62的等腰三角形,俯视图是半径为1的半圆,则该几何体的 体积是( )A. C 7、如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,//EF AB ,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )A .92B. 5 C. 6 D. 152侧视图俯视图8、一个棱锥的三视图如图,则该棱锥的体积是( ) C.4 D.89、如图是一个空间几何体的三视图,则该几何体的侧面积为( )第8题 第9题10、如图为一平面图形的直观图,则此平面图形可能是选项中的( )11、棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8 个三棱锥后,剩下的凸多面体的体积是( )A、23 B 、76 C 、45 D 、5612、在一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D 、E 、F ,且知SD :DA=SE :EB=CF :FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )A 、2923 B 、2719 C 、3130 D 、2723 13、 一空间几何体的三视图如图所示,A.2π+B. 4π+C. 23π+D. 43π+俯视图14、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为( ).(A )(B )(C )(D )15、正六棱锥P-ABCDEF 中,G 为PB 的中点,则三棱锥D-GAC 与三棱锥P-GAC 体积之比为( )(A )1:1 (B) 1:2 (C) 2:1 (D) 3:216、如右图,某几何体的正视图与侧视图都是边长为1的正方形, 且体积为12。
构成空间几何体的练习题

构成空间几何体的练习题一、选择题1. 下列几何体中,哪一个不是由平面图形构成的空间几何体?A. 正方体B. 圆柱体C. 三棱锥D. 球体2. 一个正方体的六个面都是正方形,下列关于正方体的说法正确的是?A. 正方体的六个面面积相等B. 正方体的六个面都是相同大小的正方形C. 正方体的六个面都是矩形D. 正方体的六个面都是平行四边形3. 下列哪个几何体的底面是圆形?A. 圆柱体B. 三棱锥C. 四棱锥D. 立方体二、填空题1. 由六个完全相同的正方形组成的几何体是______体。
2. 一个圆柱体的底面半径为r,高为h,则其体积为______。
3. 一个正方体的棱长为a,则其对角线长度为______。
三、判断题1. 两个完全相同的正方体可以组成一个长方体。
()2. 圆锥体的底面一定是圆形。
()3. 任何多面体的侧面都是平面图形。
()四、作图题1. 请画出由两个正方形和四个等边三角形组成的几何体的三视图。
2. 请画出底面半径为2cm,高为3cm的圆柱体的直观图。
五、解答题1. 一个正方体的棱长为2cm,求其对角线长度。
2. 一个圆锥体的底面半径为3cm,高为4cm,求其体积。
3. 两个完全相同的正方体组成一个长方体,求该长方体的表面积。
4. 一个三棱锥的底面是一个边长为3cm的正三角形,高为4cm,求其体积。
5. 请描述一个球体的特征,并求出半径为5cm的球体的表面积和体积。
六、相似与全等几何体的判断两个棱长为3cm的正方体。
两个底面半径为2cm,高为4cm的圆柱体。
两个底面边长为4cm,侧棱长为5cm的正四棱锥。
一个棱长为2cm的正方体和一个棱长为4cm的正方体。
一个底面半径为3cm,高为5cm的圆锥体和一个底面半径为6cm,高为10cm的圆锥体。
一个底面边长为6cm,高为8cm的正三棱锥和一个底面边长为9cm,高为12cm的正三棱锥。
七、几何体的展开与折叠一个正方体。
一个正四棱锥。
一个圆锥体。
2. 根据给出的展开图,判断下列几何体能否折叠成立体图形:一个由四个相同大小的正方形和两个相同大小的等腰直角三角形组成的图形。
必修二_1.3_空间几何体的表面积和体积同步练习和详细答案

1.3空间几何体的表面积和体积【知识总结】1. 多面体的面积和体积公式名称 侧面积(S 侧) 全面积(S 全)体积(V )棱 棱柱 直截面周长x IS 侧+2S 底S底• h=S 直截面• h柱直棱柱 chS 底• h「棱锥棱锥 各侧面积之和1S 底• h3 正棱锥 1『 —ch 2S 侧+S 底棱台各侧面面积之和1—h(S 上底+S 下底+3棱 台正棱台1一 (c+c ' )h '2S 侧+S 上底+S 下底S 下底’S 下底)表中表示面积,'、分别表示上、下底面周长,表斜咼,'表示斜咼,表示侧棱长。
2 .旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧 2 n rl n rl n (r 1+「2)lS 全 2 n r(l+r) n r(l+r) 2 2n (r 1+r 2)l+ n (r 1+r24 n RVn r 2h(即 n r 2l)1r 2h —n r h312 2—n h(r 1+r 1「2+r 2)3 43—n R3 表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径,r i 、「2分别表示圆台上、下底面半径,R 表示半径。
【知能训练】A:多面体的表面积和体积 一•选择题1.如图,在直三棱柱 ABC-ABC i 中,AA=AB=2 BC=1, / ABC=90,若规 定主(正)视方向垂直平面 ACCA ,则此三棱柱的左视图的面积为 ( )A.—— B . 2 - C . 4 D . 22•某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底 边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、 高为4的等腰三角形,则该几何体的表面积为()3.—个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1: 2,则截面把棱锥的一条侧棱分成的两段之比是()A . 1 : 4B . 1 : 2C . 1 : ( "- 1 )D . 1: ( 一+1 ) 4.正六棱台的两底边长分别为1cm, 2cm,高是1cm,它的侧面积为()A . 80B . 24 一+88C. 24 一+40 D . 118A .9 ~ 2cm2B . 9 cmC. - cm 22D. 3 cm5. 要制作一个容积为 4卅,高为1m 的无盖长方体容器,已知该容器的底面造价是每平方米 20元,侧面造价是每平方米 10元,则该容器的最低总造价是( )A . 80 元B . 120 元C . 160 元D. 240 元6. (文) 四棱锥S-ABCD 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱 锥及其三视图如图(AB 平行于主视图投影平面)则四棱锥 A . 24 B . 18 C . - - D . 87. 某空间组合体的三视图如图所示,则该组合体的体积为( A . 48B . 56C . 64D. 72&各棱长均为a 的三棱锥的表面积为( )A. 4 _a 2B . 3 "a 2C .2 _a 2D9.已知一个四棱锥的高为 3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为()10. 如图,在三棱柱 ABC-ABC 中,D, E , F 分别是AB, AC, AA 的中点,设三棱锥 F-ADE的体积为V 1,三棱柱 ABG-ABC 的体积为V 2,则V 1: V ___________________________________ .11. _______ 将边长为2的正方形沿对角线 AC 折起,以A, B, C, D 为顶点的三棱锥的体积最大值等 于 ____ .12.如图,一个三棱柱形容器中盛有水,且侧棱AA=8.若AAB 1B 水平放置时,液面恰好过AC BC, AC , BC 的中点,则当底面 ABC 水平放置时,液面的高为 _________________ . 13. 四棱锥P-ABCD 的底面ABCE 为正方形,且PD 垂直于底面 ABCD N 为PB 中点,则三棱锥 P-ANC 与四棱锥P-ABCD 的体积比为 ________________ .14.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为S-ABCD 的体积=( )A .B . 6C. -D . 2直角三角形,则它的体积为_________________15.如图所示,在三棱柱ABC-ABQ 中,AB=AC=AA=2, BC=2 ;且/ AAB=/ A i AC=60,则该三棱柱的体积是_________________________ .B:旋转体的表面积和体积1•如果圆锥的底面半径为,高为2,那么它的侧面积是()A. 4 n B . 2 n C . 2 n D . 4 n2.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A. 5 nB. 4 nC. 3 nD. 2 n3•如果圆锥的轴截面是正三角形(此圆锥也称等边圆锥),则此圆锥的侧面积与全面积的比是()A. 1 : 2 B. 2: 3 C. 1 : 一 D. 2: _4•圆锥侧面积为全面积的,则圆锥的侧面展开图圆心角等于()A. - nB. nC. 2 nD.以上都不对5.圆台的上、下底面半径和高的比为 1 : 4: 4,母线长为10,则圆台的侧面积为()A. 81 nB. 100 nC. 14 nD. 169 n6.已知球的直径SC=8 A, B是该球球面上的两点,AB=2 ,/ SCAN SCB=60,则三棱锥S-ABC 的体积为()A. 2 ~B. 4 ~C. 6 ~D. 8 ~7.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S、S,则S:Sa=()A. 1 : 1B. 2: 1C. 3: 2D. 4: 1&若两个球的表面积之比为1: 4,则这两个球的体积之比为()A. 1 : 2B. 1 : 4C. 1 : 8D. 1 : 169.体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S , S, S3,那么它们的大小关系为()A. S1 v S2 v S3B. S1 v S3V S2C. S2V S3 v S1D. S2 v S1 v S3二.填空题(共5小题)10.圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为________________n和n的矩形, 11 .已知一个圆柱的侧面展开图是一个长和宽分别为则该圆柱的体积是____________________12.在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S= cm 2.13.球的体积与其表面积的数值相等,则球的半径等于14•已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O的表面积为15.已知A, B, C是球面上三点,且AB=AC=4cm/ BAC=90,若球心O到平面ABC的距离为2 ,则该球的表面积为cm3.11.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD7卜接球表面积为三.解答题(共3小题)16•如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成•已知球的直径是6cm,圆柱筒长2cm.(1)这种“浮球”的体积是多少cm (结果精确到0.1 ) ?(2 )要在这样2500个“浮球”表面涂一层胶质,如果每平方米需要涂胶100克,共需胶多少?17.(文)如图,球O的半径长为10(1)求球O的表面积;(2)求球O的体积;(3)若球O的小圆直径AB=3Q求A、B两点的球面距离.18.设底面直径和高都是4厘米的圆柱的内切球为O.(1)求球O的体积和表面积;(2)与底面距离为1的平面和球的截面圆为M AB是圆M内的一条弦,其长为2 ,求AB 两点间的球面距离.参考答案: A:I、A 2、B 3、C 4、A 5、C 6、D 7、C 8、D 9、D10、解:因芮D,E,分S]是Ab肌的中自所以血虫DE;S AA BC=1:仆又F是宜納的中点,所以A T aS面的范离H为F到虧面距离h的2倍• 即三複栓盘卩1门-2匚的壽是三棱穩F-ME高的7倍-斷以如;畑空兰空=4T=1:西.故答案为1; 24.II、铅:妇也肪示,评正方也就口叭対術钱M * 3DSt + iO>甲n折更启的位豈为F・连揺即‘ *苛一TAZJLBC,AC l-BD* - BaflD- QrO--ACX 耶®IT g匡b> =楼帕的作祗対V D -kBC"v^EOC' -^Vc-BCC~ ;BCD' k AO*j52kBOD' x J S^ISOD_卞航:王方世的迪丢为2・可J?■■- BOD ft AH - To LABC谜劉昴尢值■*:S/\ 二 0D* =? x j^x忑小血乂目□力'二w in上aoii *’,丄i ?rv「.q-TTY-M' l「=丄工」•王5V.怡巧「此t」导.乂RJ农虻-土故告案为;半12、解:不妨令此三棱柱为直三棱柱,如图当侧面AA1B1B水平放置时,水的形状为四棱柱形,底面是梯形.设△ ABC的面积为S,贝U S梯形ABFE= S,V水=S? AA1=6S .当底面ABC水平放置时,水的形状为三棱柱形,设水面高为h,则有V水=Sh,••• 6S=Sh,.•• h=6 .故当底面ABC水平放置时,液面高为6 .故答案为:613、1:4 14、15、2解:團柱的側面展开囹星长利员务别为和TT的矩用,当毋线为戈氏时,區1桂的庙面半襌是扌此时囿桂体粮是(l)1 2Ttx3it=^;当母线为H时,圆柱酌展面半轻是学此时圆柱的体釈是(芥II"二竺匕£-t 4综上所求圈柱的体稅杲:—16、解:(1 )T该“浮球”的圆柱筒直径d=6cm ,•••半球的直径也是6cm,可得半径R=3cm,•两个半球的体积之和为V球=-冗R = - n ? 27 = 6 n cm3 * S 6…(2分)斗412、解:将相同的两个几何体,对接为圆柱,则圆柱的侧面展开,侧面展开图的面积 S=[ ( 50+80) X 20 n x 2]/2=2600 n cm2. 故答案为:2600 n13、 3 14、8 n 15、64 n学习参考而V 圆柱=n R ? h= n X 9X = n cm3…(2 分)•该“浮球”的体积是:V=V球+V圆柱=36 n +18 n =54 n" 169.6cm 3…(4分)(2)根据题意,上下两个半球的表面积是S 球表= n R = Xn X 9= 6 n cm?…(6 分)而“浮球”的圆柱筒侧面积为:S圆柱侧=2 n Rh=2 Xn X 3 X 2=12 n cm2…(8分)6 n n n• 1个“浮球”的表面积为S = —0一= —m因此,2500个“浮球”的表面积的和为2500 S = 00 X —= n m2…(10分)•/每平方米需要涂胶100克,•总共需要胶的质量为:100 X 12 n =1200 n (克)…(12分)答:这种浮球的体积约为169.6cm 3;供需胶1200 n克.…(13分)17、解:(1)球的表面积为4 n r 2=1200 n ; …(4分)(2)球的体积V=-n r3= 4000 _n ; …(8 分)(3)设球心为O,在△ AOB中,球O的小圆直径AB=30,球O的半径长为10解得Z AOB=",所以A、B两点的球面距离为0 n n . …(15分)18、解:(1)•••底面直径和高都是4厘米的圆柱的内切球为O,•球O的半径为2cm,.•.球O的体积为-n ? 2=,表面积4 n ? 22=16 n ;(2)•/ AB是圆M内的一条弦,其长为2 ,• Z AOB= n , • AB两点间的球面距离为".。
2023年高考数学一轮复习精讲精练(新高考专用)专题33:空间几何体(练习版)

专题33:空间几何体精讲温故知新一.空间几何体的结构1.多面体一般地,由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
2.旋转体一条平面曲线,包括直线,绕它所在平面内的一条定直线旋转所成的曲面叫做旋转面。
封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
3.棱柱一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
在棱柱中,两个互相平行的面叫做棱柱的底面,它们是全等的多边形,其余各面叫做棱柱的侧面,它们都是平行四边形,相邻两边的公共边叫做棱柱的侧棱,侧面和底面的公共顶点叫做棱柱的顶点。
棱柱的底面可以是三角形、四边形、五边形,我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱。
一般地,我们把侧面垂直于底面的棱柱叫做直棱柱,侧面不垂直于底面的棱柱叫做斜棱柱,底面是正多边形的,直棱柱叫做正棱柱,底面是平行四边形的四棱柱,也叫做平行六面体。
4.棱锥一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
这个多边形面叫做棱锥的底面,有公共顶点的各个三角形面叫做棱锥的侧面,相邻两边的公共边叫做棱锥的侧棱,这侧面的公共顶点叫做棱锥的顶点。
棱锥,用表示顶点和各面各顶点的字母来表示,其中三棱锥又叫四面体,底面是正多边形并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。
5.棱台用一个平行于圆锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台。
在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面面,类似于棱柱、棱锥,棱台也有侧面、侧棱和顶点。
6.圆柱与矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱。
旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面,叫做圆柱的底面,平行的边旋转而成的曲面叫做圆柱的侧面,无论旋转到什么位置,平行于轴的边叫做圆柱侧面的母线。
高中数学空间几何体知识点归纳与常考题型专题练习(附解析)

( 7)球体:定义: 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体
几何特征: ①球的截面是圆;②球面上任意一点到球心的距离等于半径。
2、空间几何体的三视图 定义三视图:正视图(光线从几何体的前面向后面正投影) 俯视图(从上向下)
;侧视图(从左向右) 、
注:正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;
B.
C. D.
29.如图是某几何体的三视图,则该几何体的体积为(
)
A. 1 B. C. D. 30.某几何体的三视图如图所示,且该几何体的体积是 是( )
,则正视图中的 x 的值
A. 2 B. C. D.3
31.将边长为 a 的正方形 ABCD 沿对角线 AC 折起,使得 BD=a,则三棱锥 D﹣ ABC 的体积为( )
设三棱锥 F﹣ADE 的体积为 V 1,三棱柱 A 1B1C1﹣ ABC 的体积为 V 2,则 V 1:
V2=
.
39.如图,在圆柱 O1O2 内有一个球 O,该球与圆柱的上、下底面及母线均相切,
记圆柱 O1O2 的体积为 V 1,球 O 的体积为 V 2,则 的值是
.
40.若某几何体的三视图(单位: cm3.
( 1)要使倾斜后容器内的溶液不会溢出,角 α的最大值是多少; ( 2)现需要倒出不少于 3000cm3 的溶液,当 α=60°时,能实现要求吗?请说明 理由. 47.如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为 32cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ的两底面对角线 EG, E1G1 的长分别为 14cm 和 62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为 12cm.现有一根玻璃棒 l,其长度为 40cm.(容器厚度、 玻璃棒粗细均忽略不计) ( 1)将 l 放在容器Ⅰ中, l 的一端置于点 A 处,另一端置于侧棱 CC1 上,求 l
2022年高考数学空间几何体的直观图与三视图知识点专项练习含答案

专题28 空间几何体的直观图与三视图一、单选题(本大题共12小题,共60分)1.已知一个几何体的正视图和侧视图如图(1)所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示),则此几何体的体积为()A. 1B. √2C. 2D. 2√22.正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图(如图),则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm3.一个几何体的三视图如图所示,则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√324.某几何体的三视图如图所示,则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√35.已知某几何体的一条棱长为l,该棱在正视图中的投影长为√2020,在侧视图与俯视图中的投影长为a与b,且a+b=2√1011,则l的最小值为()A. √20212B. √40422C. √2021D. 20216.已知一几何体的三视图如图所示,则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+47.某圆柱的正视图是如图所示的边长为2的正方形,圆柱表面上的点A,B,C,D,F在正视图中分别对应点A,B,C,E,F.其中E,F分别为AB,BC的中点,则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √638.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π39.如图,网络纸上小正方形的边长为1,粗实线画出的某几何体的三视图,则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π10.如图所是某一容器三视图,现容中匀速注水,容器中的度h随时间变可能图象是()A. B. C. D.11.如图是一个四棱锥的三视图,则该几何体的体积为()A. 403B. 323C. 163D. 28312.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3二、单空题(本大题共4小题,共20分)13.某组合体的正视图和侧视图如图(1)所示,它的俯视图的直观图是图(2)中粗线所表示的平面图形,其中四边形O′A′B′C′为平行四边形,D′为C′B′的中点,则图(2)中平行四边形O′A′B′C′的面积为___________.14.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和附视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可).15.在棱长为1的正方体ABCD−A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为.16.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影,如图所示,在三棱锥A−BCD中,BC⊥DC,AD⊥DC,BC⊥AB,BC= CD=4,AC=4√3,则△ADB在平面ABC上的射影的面积是________.三、解答题(本大题共2小题,共20分)13.设某几何体的三视图如图(尺寸的长度单位为cm),(1)用斜二测画法画出该几何体的直观图(不写画法);(2)求该几何体最长的棱长.14.设一正方形纸片ABCD边长为4厘米,切去阴影部分所示的四个全等的等腰三角形,剩余为一正方形纸片和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥,O为正四棱锥底面中心.,(粘接损耗不计),图中AH PQ(1)若正四棱锥的棱长都相等,请求出它的棱长并画出它的直观图示意图;(2)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积表示为x的函数,并求S范围.专题28 空间几何体的直观图与三视图一、单选题(本大题共12小题,共60分)17.已知一个几何体的正视图和侧视图如图(1)所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图(2)所示),则此几何体的体积为()A. 1B. √2C. 2D. 2√2【答案】B【解析】解:根据直观图可得该几何体的俯视图是一个直角边长分别是2和√2的直角三角形,根据三视图可知该几何体是一个三棱锥,且三棱锥的高为3,所以体积V=13×(12×2×√2)×3=√2.故选B.18.正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图(如图),则原图形的周长是()A. 6cmB. 8cmC. (2+3√2)cmD. (2+2√3)cm【答案】B【解析】解:如图,OA=1cm,在Rt△OAB中,OB=2√2 cm,∴AB=√OA2+OB2=3cm.∴四边形OABC的周长为8cm.故选B.19.一个几何体的三视图如图所示,则该几何体的表面积为()A. 3π2+1+√32B. 3π+12+√32C. 3π+1+√32D. 3π+1+√32【答案】C【解析】解:由三视图可知几何体上部为三棱锥,下部为半球,三棱锥的底面和2个侧面均为等腰直角三角形,直角边为1,另一个侧面为边长为√2的等边三角形,半球的直径2r=√2,故r=√22.∴S表面积=12×1×1×2+√34×(√2)2+12×4π×(√22)2+π×(√22)2−12×1×1=12+√32+3π2.故选:C.20.某几何体的三视图如图所示,则该几何体的表面积为()A. 3π+4+√3B. 3π+5+√3C. 52π+6+√3 D. 52π+4+√3【答案】A【解析】解:由已知中的三视图可得:该几何体是一个半圆柱和三棱锥的组合体半圆柱的半径为1高2,所以该组合体的面积故选A.21.已知某几何体的一条棱长为l,该棱在正视图中的投影长为√2020,在侧视图与俯视图中的投影长为a与b,且a+b=2√1011,则l的最小值为()A. √20212B. √40422C. √2021D. 2021【答案】C【解析】解:如图所示:设长方体中AB=m,BD为正投影,BE为侧投影,AC为俯视图的投影.故:BD=√2020,BE=a,AC=b,设AE=x,CE=y,BC=z,则:x2+y2+z2=l2,x2+y2=b2,y2+z2=a2,x2+z2=2020,所以2(x2+y2+z2)=a2+b2+2020,故:2l2=a2+b2+2020,因为a2+b2≥(a+b)22=2022,所以2l2≥2022+2020,则l≥√2021.故l的最小值为√2021.故选C.22.已知一几何体的三视图如图所示,则该几何体的表面积为()A. √24π+72B. √24π+4 C. 1+√24π+72D. 1+√24π+4【答案】D【解析】解:几何体左边为四分之一圆锥,圆锥的半径为1,高为1,右边为三棱锥,三棱锥底面是直角边长为1和2的直角三角形,高为1,所以几何体的表面积为:+12×(2+1)×1+12×√2×√(√5)2−(√22)2,故选D.23.某圆柱的正视图是如图所示的边长为2的正方形,圆柱表面上的点A,B,C,D,F在正视图中分别对应点A,B,C,E,F.其中E,F分别为AB,BC的中点,则异面直线AC与DF所成角的余弦值为()A. 13B. √23C. √33D. √63【答案】D【解析】解:如图所示,连结DE,EF,易知EF//AC,所以异面直线AC与DF所成角为∠DFE,由正视图可知,DE⊥平面ABC,所以DE⊥EF.由于AB=BC=2,所以EF=√2,又DE=1,所以DF=√3,在RtΔEFM中,cos∠DFE=√2√3=√63,故选D.24.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A. 22π3B. 28π3C. 34π3D. 40π3【答案】C【解析】解:根据几何体得三视图转换为几何体为:该几何体是由一个底面半径为2,高为3的半圆柱和一个半径为2的半球组成,故:V=12⋅π×22×3+12×43×π×23=34π3.故选C.25.如图,网络纸上小正方形的边长为1,粗实线画出的某几何体的三视图,则该几何体的体积是()A. 18πB. 21πC. 27πD. 36π【答案】A【解析】解:该几何体是一个四分之一的圆和圆锥的组合体,如图:有题意知该圆的直径为6cm,圆锥的高为3cm,则该几何体的体积为13×π×32×3+1 4×43π×33=18π,故选A.26.如图所是某一容器三视图,现容中匀速注水,容器中的度h随时间变可能图象是()A. B. C. D.【答案】B【解析】解:三视图表示的容器倒的圆锥,下细,上面,刚开始度增加的相快些.曲越竖直”,后,高度增加来越慢,图越平稳.故B.27.如图是一个四棱锥的三视图,则该几何体的体积为()A. 403B. 323C. 163D. 283【答案】A【解析】解:由三视图得到其直观图(下图所示),则体积为:13×[12(1+4)×4]×4=403,故选A .28.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为A. 64−8√2π3B. 64−4√2π3C. 64−8π3D. 64−4π3【答案】A【解析】解:这是一个有一条侧棱垂直于底面的四棱锥内部挖去了一个八分之一的球,四棱锥的底面边长和高都等于4,八分之一球的半径为2√2,,故选A .二、单空题(本大题共4小题,共20分)29. 某组合体的正视图和侧视图如图(1)所示,它的俯视图的直观图是图(2)中粗线所表示的平面图形,其中四边形O ′A ′B ′C ′为平行四边形,D ′为C ′B ′的中点,则图(2)中平行四边形O ′A ′B ′C ′的面积为___________.【答案】3√2【解析】解:由正视图和侧视图可得俯视图如下:∴|O′A′|=4,|O′C′|=32,∠A′O′C′=45°,∴S ΔA′O′C′=12|O′A′|·|O′C′|·sin∠A′O′C′ =12×4×32×√22=3√22, ∴S ▱O′A′B′C′=2S △A′O′C′=3√2, 故答案为3√2.30.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和附视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_____________(写出符合求的一组答案即可).【答案】②⑤或③④【解析】解:由高度可知,侧视图只能为②或③,侧视图为②,如图(1)平面PAC⊥平面ABC,PA=PC=√2,BA=BC=√5,AC=2,俯视图为⑤;侧视图为③,如图(2),PA⊥平面ABC,PA=1,AC=AB=√5,BC=2,俯视图为④.故答案为②⑤或③④.31.在棱长为1的正方体ABCD−A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为.【答案】712【解析】解:直线MN分别与直线A1D1,A1B1交于E,F两点,连接AE,AF,分别与棱DD1,BB1交于G,H两点,连接GN,MH,得到截面五边形AGNMH,向平面ADD1A1作投影,得到五边形AH1M1D1G,由点M,N分别是棱B1C1,C1D1的中点,可得D1E=D1N=12,由△D1EG∽△DAG,可得DG=2D1G=23,同理BH=2B1H=23,则AH1=2A1H1=23,A1M1=D1M1=12,则S AH1M1D1G =1−S A1H1M1−S ADG=1−12×12×13−12×1×23=712,故答案为:712.32.把平面图形α上的所有点在另一个平面上的射影所构成的图形β称为图形α在这个平面上的射影,如图所示,在三棱锥A−BCD中,BC⊥DC,AD⊥DC,BC⊥AB,BC= CD=4,AC=4√3,则△ADB在平面ABC上的射影的面积是________.【答案】8√2【解析】解:因为BC⊥DC,AD⊥DC,BC⊥AB,BC=CD=4,AC=4√3,把三棱锥A−BCD放入如图所示的棱长为4的正方体中,过点D作CE的垂线DF,垂足为F,连接AF,BF,因为BC⊥平面CE,DF⊂平面CE,故BC⊥DF又BC∩CE=C,BC,CE⊂平面ABC则DF⊥平面ABC,故△ADB在平面ABC上的射影为△AFB,因为AB=√42+42=4√2,×4×4√2=8√2,所以△AFB的面积为12即△ADB在平面ABC上的射影的面积为8√2.故答案为8√2.三、解答题(本大题共2小题,共20分)13.设某几何体的三视图如图(尺寸的长度单位为cm),(1)用斜二测画法画出该几何体的直观图(不写画法);(2)求该几何体最长的棱长.【答案】(1)答案见解析;(2)4cm.【解析】(1)(2)如下图,SE⊥面ABC,线段AC中点为D2,3,1,4,2,=1======,BD AC SE cm AE cm CE cm AC cm AD DC cm DE cm⊥,=,3BD cm在等腰ABC中,AB AC=在Rt SEA△中,SA=在Rt SEC△中,SC△中,BE==在Rt BDE∴⊥SE⊥面ABC,SE BE在Rt SEB△中,SB=<==<<,在三梭锥S-ABC中,SC AB AC SA SB AC所以最长的棱为AC ,长为4cm14.设一正方形纸片ABCD 边长为4厘米,切去阴影部分所示的四个全等的等腰三角形,剩余为一正方形纸片和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中AH PQ ⊥,O 为正四棱锥底面中心.,(1)若正四棱锥的棱长都相等,请求出它的棱长并画出它的直观图示意图;(2)设等腰三角形APQ 的底角为x ,试把正四棱锥的侧面积表示为x 的函数,并求S 范围.【答案】(1),画图见解析;(2)161tan 2tan S x x=++,()0,4.【解析】(1)由题意,设正四棱锥的棱长为a,则AH =,2a AC a +===(2)设PH b =,则tan AH b x =,由2tan 2a x a ⋅+=a =,从而22116tan 442tan 2(tan 1)APQ x S S PQ AH a x x ==⋅⋅⋅==+△,其中(tan 1),x ∈+∞,∴16(0,4)1tan 2tan S x x=∈++。
高一数学必修2__1.1空间几何体的结构(练习题)
必修2 1.1空间几何体的结构(练习题)一、选择题1.在棱柱中()A.只有两个面平行 B.所有的棱都平行C.所有的面都是平行四边形 D.两底面平行,且各侧棱也互相平行2.将图1所示的三角形线直线l旋转一周,可以得到如图2所示的几何体的是哪一个三角形()3.若一个平行六面体的四个侧面都是正方形,则这个平行六面体是()A.正方体 B.正四棱锥C.长方体D.直平行六面体4.下面命题中,正确的是()①底面是正方形,侧面都是等腰三角形的棱锥是正四棱锥;②对角线相等的四棱柱必是直棱柱;③底面边长相等的直四棱柱为正四棱柱;④四个面都是全等的三角形的几何体是正四面体5.如图一个封闭的立方体,它6个表面各标出1、2、3、4、5、6这6个数字,现放成下面3个不同的位置,则数字l、2、3对面的数字是()A.4、5、6 B.6、4、5 C.5、4、6 D.5、6、46.如图,能推断这个几何体可能是三棱台的是()A.A1B1=2,AB=3,B1C1=3,BC=4B.A1B l=1,AB=2,B l C l=1.5,BC=3,A1C1=2,AC=3C.A l B l=1,AB=2,B1C l=1.5,BC=3,A l C l=2,AC=4D.AB=A1B1,BC=B1C1,CA=C1A17.有下列命题(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;(3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;(4)圆柱的任意两条母线所在的直线是互相平行的.其中正确的是()A.(1)(2) B.(2)(3) C.(1)(3) D.(2)(4)8.下列命题中错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.圆锥的轴截面是所有过顶点的截面中面积最大的一个C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面是全等的等腰三角形9.一个三棱锥四个面中,是直角三角形的最多有()A.1个 B.2个 C.3个 D.4个10.图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是_______________.(注:把你认为正确的命题的序号都填上)11.高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是_______________.三、解答题12.察以下几何体的变化,通过比较,说出他们的特征.13.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,母线长为10cm,求圆锥的母线长__________.。
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
2023年新高考数学一轮复习8-2 空间几何体的表面积和体积(真题测试)解析版

专题8.2 空间几何体的表面积和体积(真题测试)一、单选题1.(2020·天津·高考真题)若棱长为 ) A .12π B .24π C .36π D .144π【答案】C【解析】【分析】求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.【详解】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R =,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C.2.(2020·北京·高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(). A .63+ B .623+ C .123+ D .1223+【答案】D【解析】【分析】首先确定几何体的结构特征,然后求解其表面积即可.【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+ ⎪⎝⎭故选:D.【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.3.(2022·浙江·高考真题)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .22πB .8πC .22π3D .16π3【答案】C【解析】【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可根据球,圆柱,圆台的体积公式求出.【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的底面半径,圆台的上底面半径都为1cm ,圆台的下底面半径为2cm ,所以该几何体的体积(322214122ππ1π122π2π12333V =⨯⨯+⨯⨯+⨯⨯⨯+⨯=3cm .故选:C .4.(2022·全国·高考真题)已知正三棱台的高为1,上、下底面边长分别为面上,则该球的表面积为( )A .100πB .128πC .144πD .192π【答案】A【解析】【分析】根据题意可求出正三棱台上下底面所在圆面的半径12,r r ,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积.【详解】设正三棱台上下底面所在圆面的半径12,r r ,所以123432,260sin 60r r ==,即123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d =2d =121d d -=或121d d +=,即1=1,解得225R =符合题意,所以球的表面积为24π100πS R ==. 故选:A .5.(2021·浙江·高考真题)某几何体的三视图如图所示,则该几何体的体积是( )A .32B .3C .2D .【答案】A【解析】【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【详解】几何体为如图所示的四棱柱1111ABCD A B C D -,其高为1,底面为等腰梯形ABCD ,1=故1111131222ABCD A B C D V -=⨯⨯=, 故选:A. 6.(2021·全国·高考真题(理))已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为( )A B C D A 【解析】【分析】由题可得ABC 为等腰直角三角形,得出ABC 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.【详解】,1AC BC AC BC ⊥==,ABC ∴为等腰直角三角形,AB ∴=,则ABC 1, 设O 到平面ABC 的距离为d ,则2d =所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯= 故选:A.7.(2022·全国·高考真题(文))已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( )A .13B .12CD 【答案】C【解析】【分析】先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α, 则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅= (当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r又22r h 1+=则2123O ABCDV r h -=⋅⋅=当且仅当222r h =即h 时等号成立,故选:C8.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤ ) A .8118,4⎡⎤⎢⎥⎣⎦ B .2781,44⎡⎤⎢⎥⎣⎦ C .2764,43⎡⎤⎢⎥⎣⎦ D .[18,27]【答案】C【解析】【分析】设正四棱锥的高为h ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围.【详解】∵ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =- 所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭, 所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l ≤0V '<,所以当l =V 取最大值,最大值为643,又3l =时,274V =,l =814V =, 所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,. 故选:C.二、多选题9.(2022·广东茂名·二模)某一时段内,从天空降落到地面上的液态或固态的水,未经蒸发,而在水平面上积聚的深度称为这段时间的降雨量.24h 降雨量的等级划分如下:在一次暴雨降雨过程中,小明用一个大容量烧杯(如图,瓶身直径大于瓶口直径,瓶身高度为50cm ,瓶口高度为3cm )收集雨水,容器内雨水的高度可能是( )A .20cmB .22cmC .25cmD .29cm【答案】CD【解析】【分析】设降雨量为x ,容器内雨水高度为h,根据雨水的体积相等关系可得到h,x 之间的关系49h x =,结合题意可得4200400[,)999x ∈,由此判断出答案. 【详解】设降雨量为x ,容器内雨水高度为h,根据体积相等关系可得:22π100π150x h ⨯=⨯,解得49h x = , 由于[50,100)x ∈ ,故4200400[,)999x ∈, 故20040020040020,22[,),25,29[,)9999∉∈故选:CD .10.(2023·湖北·高三阶段练习)折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧,DE AC 所在圆的半径分别是3和9,且120ABC ∠=,则该圆台的( )A .高为42B .体积为5023π C .表面积为34πD .上底面积、下底面积和侧面积之比为1:9:22【答案】AC【解析】 【分析】设圆台的上底面半径为r ,下底面半径为R ,求出1,3r R ==,即可判断选项A 正确;利用公式计算即可判断选项BCD 的真假得解.【详解】解:设圆台的上底面半径为r ,下底面半径为R ,则11223,22933r R ππππ=⨯⨯=⨯⨯,解得1,3r R ==.圆台的母线长6l =,圆台的高为h ==,则选项A 正确;圆台的体积()22133113π=⨯+⨯+=,则选项B 错误; 圆台的上底面积为π,下底面积为9π,侧面积为()13624ππ+⨯=,则圆台的表面积为92434ππππ++=,则C 正确;由前面可知上底面积、下底面积和侧面积之比为1:9:24,则选项D 错误.故选:AC .11.(2022·湖南·长沙一中模拟预测)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则( )A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165π C .四面体CDEF 的体积的取值范围为3203⎛⎤ ⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为2⎡+⎣【答案】BCD【解析】【分析】利用球的表面积公式及圆柱的表面积公式可判断A ,由题可得O 到平面DEF 的距离为1d 平面DEF 截得球的截面面积最小值可判断B ,由题可得四面体CDEF 的体积等于12E DCO V -可判断C ,设P 在底面的射影为P ',设2t P E '=,PE PF +PE PF +的取值范围可判断D.【详解】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积为24r π,圆柱的表面积222226r r r r πππ+⋅=, 所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得12OG == 设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=, 所以平面DEF 截得球的截面面积最小值为165π,故B 正确; 由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈, 又114482DCO S =⨯⨯=,所以123228(0,]33E DCO V d -=⨯∈,故C 正确; 由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ', 则2222222,2,2,16PP PE P E PF P F P E P F '''''==+=++=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,PE PF +所以()2224PE PF +==+2424⎡⎤=++⎣⎦,所以2PE PF ⎡+∈+⎣,故D 正确.故选:BCD.12.(2022·全国·高考真题)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则( )A .322V V =B .31V V =C .312V V V =+D .3123V V =【答案】CD【解析】【分析】直接由体积公式计算12,V V ,连接BD 交AC 于点M ,连接,EM FM ,由3A EFM C EFM V V V --=+计算出3V ,依次判断选项即可.【详解】设22AB ED FB a ===,因为ED ⊥平面ABCD ,FB ED ,则()2311114223323ACD V ED S a a a =⋅⋅=⋅⋅⋅=, ()232111223323ABC V FB S a a a =⋅⋅=⋅⋅⋅=,连接BD 交AC 于点M ,连接,EM FM ,易得BD AC ⊥, 又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED AC ⊥,又ED BD D =,,ED BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又12BM DM BD ==,过F 作FG DE ⊥于G ,易得四边形BDGF 为矩形,则,FG BD EG a ===,则,EM FM ===,3EF a =,222EM FM EF +=,则EM FM ⊥,212EFM SEM FM =⋅=,AC =, 则33123A EFM C EFM EFM V V V AC S a --=+=⋅=,则3123V V =,323V V =,312V V V =+,故A 、B 错误;C 、D 正确.故选:CD.三、填空题 13.(2021·全国·高考真题(文))已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.【答案】39π【解析】【分析】利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.【详解】∵216303V h ππ=⋅=∴52h =∴132l =∴136392S rl πππ==⨯⨯=侧. 故答案为:39π.14.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,则此六角螺帽毛坯的体积是 ____ cm 3. 【答案】1232π-【解析】【分析】先求正六棱柱体积,再求圆柱体积,相减得结果.【详解】正六棱柱体积为262⨯ 圆柱体积为21()222ππ⋅=所求几何体体积为2π故答案为: 2π15.(2019·天津·高考真题(文)若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________. 【答案】4π. 【解析】【分析】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.【详解】借助勾股定理,2=,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为12,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,故圆柱的体积为21124ππ⎛⎫⨯⨯= ⎪⎝⎭. 16.(2022·吉林·长春市第二实验中学高三阶段练习)在三棱锥P ABC -中,点P 在底面的射影是ABC 的外心,2,3BAC BC PA π∠===___________. 【答案】12548π 【解析】【分析】先由正弦定理得,ABC 外接圆的半径,再由勾股定理,即可求出半径,从而可得外接球体积.【详解】解:设ABC 的外心为1O ,连接1PO ,则球心O 在1PO 上,连接1O A ,则1O A 为ABC 外接圆的半径r ,连接OA ,设外接球的半径为R ,则OA OP R ==,在ABC 中,由正弦定理得2,BC r sin BAC ==∠解得1r =,即11O A =, 在1Rt PAO 中,12,PO =在1Rt AOO ,中22211OO AO AO +=,即()22221R R -+=,解得:54R =, 所以外接球的体积为:3344125334854R V πππ⎛⎫⋅ ⎪⎝⎭===, 故答案为:12548π 四、解答题17.(2022·安徽芜湖·高一期末)如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终不离开桌面,设直径AB 所在直线与桌面所成的角为α.要使倾斜后容器内的溶液不会溢出,求α的最大值. 【答案】4π【解析】【分析】当水杯倾斜过程中,溶液恰好不溢出时,此时α最大;在这个临界条件下,结合溶液的体积不变,可以得到关于α的一个不等式,即可求出α的取值范围,得到最大值.【详解】如图所示,在Rt △CDE 中20tan DE α=,()2221020tan 103020tan 10202παπαπ⨯⨯⨯⨯-+≥⨯⨯解得tan 1α≤,即α的最大值4π. 18.(2022·全国·南宁二中高三期末(文))图1是由矩形ABGF ,Rt ADE △和菱形ABCD 组成的一个平面图形,其中2AB =,1==AE AF ,60BAD ∠=︒,将该图形沿AB ,AD 折起使得AE 与AF 重合,连接CG ,如图2.(1)证明:图2中的C ,D ,E ,G 四点共面;(2)求图2中三棱锥C BDG -的体积.【答案】(1)证明见解析【解析】【分析】(1)依题意可得//AB FG ,//AB CD ,即可得到//AB GE ,从而得到//CD EG ,即可得证;(2)依题意可得AE AD ⊥、AE AB ⊥,即可得到AE ⊥平面ABCD 从而得到BG ⊥平面ABCD ,再根据13C BDG G BCD BCD V V BG S --==⋅计算可得;(1)证明:在矩形ABGF 和菱形ABCD 中,//AB FG ,//AB CD ,所以//AB GE ,所以//CD EG ,所以C 、D 、E 、G 四点共面;(2)解:在Rt ADE △中AE AD ⊥,矩形ABGE 中AE AB ⊥,AD AB A ⋂=,,AD AB ⊂平面ABCD ,所以AE ⊥平面ABCD ,又//BG EA ,所以BG ⊥平面ABCD ,又11sin 2222BCD S BC CD BCD =⋅⋅∠=⨯⨯=所以11133C BDG G BCD BCD V V BG S --==⋅=⨯ 19.(2022·山西吕梁·高一期末)如图是某种水箱用的“浮球”,它是由两个半球和一个圆柱筒组成.已知球的半径是2cm ,圆柱筒的高是2cm .(1)求这种“浮球”的体积;(2)要在100个这种“浮球”的表面涂一层防水漆,每平方厘米需要防水漆0.5g ,共需多少防水漆?【答案】(1)356(cm)3π (2)1200g π【解析】【分析】(1)由球的体积公式和圆柱的体积公式求解即可;(2)由球的表面积公式和圆柱的侧面积公式求解即可.(1)因为该“浮球”的圆柱筒底面半径和半球的半径2cm r =,圆柱筒的高为2cm ,所以两个半球的体积之和为331432(cm)33V r ππ==, 圆柱的体积2328(cm)V r h ππ==,∴该“浮球”的体积是31256(cm)3V V V π=+=; (2)根据题意,上下两个半球的表面积是221416(cm)S r ππ==,而“浮球”的圆柱筒侧面积为2228(cm)S rh ππ==,∴“浮球”的表面积为21224(cm)S S S π=+=;所以给100个这种浮球的表面涂一层防水漆需要100240.51200g ππ⨯⨯=.20.(2022·全国·高三专题练习)如图1,在直角梯形ABCD 中,//AD BC ,∠BAD =90°,12AB BC AD a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图2中1A BE 的位置,使平面1A BE ⊥平面BCDE ,得到四棱锥1A BCDE -.当四棱锥1A BCDE -的体积为a 的值.【答案】6a =.【解析】【分析】在直角梯形ABCD 中,证明BE AC ⊥,在四棱锥1A BCDE -中,由面面垂直的性质证得1A O ⊥平面BCDE ,再利用锥体体积公式计算作答.【详解】如图,在直角梯形ABCD 中,连接CE ,因E 是AD 的中点,12BC AD a ,有//,AE BC AE BC =,则四边形ABCE 是平行四边形,又,90BAD AB BC ∠==,于是得ABCE 是正方形,BE AC ⊥,在四棱锥1A BCDE -中,1BE AO ⊥,因平面1A BE ⊥平面BCDE ,且平面1A BE 平面BCDE BE =,1A O ⊂平面1A BE ,因此1A O ⊥平面BCDE ,即1A O 是四棱锥1A BCDE -的高,显然112AO AO CO AC ====,平行四边形BCDE 的面积2S CO BE a =⋅==,因此,四棱锥1A BCDE -的体积为2311133V S AO a =⋅===6a =, 所以a 的值是6.21.(2022·北京·高一期末)《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑 (四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中,已知3AB =,4BC =,5AC =.当阳马111C ABB A -体积等于24时, 求:(1)堑堵111ABC A B C -的侧棱长;(2)鳖臑1C ABC -的体积;(3)阳马111C ABB A -的表面积.【答案】(1)6(2)12 (3)51313【解析】【分析】(1)设堑堵111ABC A B C -的侧棱长为x ,根据阳马111C ABB A -体积等于24求解即可;(2)根据棱锥的体积计算即可;(3)分别计算111C ABB A -的侧面积与底面积即可(1)因为3AB =,4BC =,5AC =,所以222AB BC AC +=.所以△ABC 为直角三角形.设堑堵111ABC A B C -的侧棱长为x ,则113A ABB S x 矩形,则111143243AA BB V x C , 所以6x =,所以堑堵111ABC A B C -的侧棱长为6.(2)因为13462ABC S =⨯⨯=△, 所以1111661233ABC ABC V S CC C . 所以鳖臑1C ABC -的体积为12.(3) 因为11113462A B C S,11164122BB C S , 11165152AA C S ,1132133132ABC S , 113618A ABB S 矩形,所以阳马111C ABB A -的表面积的表面积为612151831351313. 22.(2022·重庆市巫山大昌中学校高一期末)如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5,3AB BC CD ===,(1)求该圆柱的表面积;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求ACD △的三边在旋转过程中所围成的几何体的体积.【答案】(1)75π2(2)15π【解析】【分析】(1)由题意求出柱的底面圆的半径即可求解;(2)ACD △绕AB 旋转一周而成的封闭几何体的体积为两个圆锥的体积之差,结合圆锥体积公式求解即可(1)由题意知AB 是圆柱OO '的一条母线,BC 过底面圆心O ,且5AB BC ==, 可得圆柱的底面圆的半径为52R =, 则圆柱的底面积为221525πππ24S R ⎛⎫==⨯= ⎪⎝⎭, 圆柱的侧面积为252π2π525π2S Rl ==⨯⨯= 所以圆柱的表面积为12257522π25ππ42S S S =+=⨯+=. (2) 由线段AC 绕AB 旋转一周所得几何体为以BC 为底面半径,以AB 为高的圆锥,线段AD 绕AB 旋转一周所得的几何体为BD 为底面半径,以AB 为高的圆锥,所以以ACD △绕AB 旋转一周而成的封闭几何体的体积为:22221111πππ55π4515π3333V BC AB BD AB =⋅⋅-⋅⋅=⋅⋅-⋅⋅=.。
从易到难分析立体几何常见题型及练习

立体几何常见类型题题型一、空间几何体三视图与直观图 (1)由实物图画三视图1.如图甲所示,在正方体1111D C B A ABCD -中,E 、F 分别是1AA 、11D C 的中点,G 是正方形11B BCC 的中心,则四边形AGFE 在该正方体的各个面上的投影可能是图乙中的_______________。
(2)三视图还原实物图2..某空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B. 423π+ C. 2323π+D. 2343π+ (3)斜二测画法有关的计算问题(S S 42'=) 3.等腰梯形ABCD ,上底1=CD ,腰2==BC AD ,下底,3=AB 以下底所在直线为x 轴,则由斜二侧画法画出的直观图''''D C B A 的面积是 ________ 题型二、空间几何体的表面积与侧面积 (1)空间几何体的表面积与体积4.已知某几何体的俯视图如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形。
(1)画出几何体的直观图 (2)求该几何体的侧面积S 。
(3)求该几何体的体积V ;(2)空间几何体展开图及面积计算5.已知圆锥的侧面展开图是右图所示的扇形,半径为1,圆心角为ο120, 则圆锥的表面积和体积分别是多少?(3)割补法和等体积法求体积6.如图,正方体''''D C B A ABCD -的棱长为2,E 是AB 的中点, 求:(1)三棱锥EC A B '-的体积V . (2)求B 点到平面EC A '的距离。
类型三.证明线面平行1.在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。
2.正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证: C1O ∥面11AB D ; 考点:法1:利用平行四边形 法2:利用面面平行的性质类型四.证明面面平行1. 正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .2.在正方体1111ABCD A B C D -中,E 、F 、G分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .A ED 1CB 1DCBAD 1ODBAC 1B 1A 1C A 1AB 1C 1 CD 1D G EF类型五.证明线面垂直1. 正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面. (考点:线面垂直的判定定理)2. ,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD . 考点:线面垂直的判定,运用勾股定理寻求线线垂直3. 已知ABC ∆中90ACB ∠=o ,SA ⊥面ABC ,AD SC ⊥, 求证:AD ⊥面SBC .4. 四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =,90BDC ∠=o ,求证:BD ⊥平面ACD5. 如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠= 且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂 直于底面ABCD . G 为AD 的中点,求证:BG ⊥平面PAD ; (考点:利用面面垂直性质定理)类型六.证明面面垂直1. 如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. 求证:平面1A AC ⊥平面BDE . (考点:面面垂直的判定)ABD CA ’D ’B ’C ’SDCBA2.如图,过S 引三条长度相等但不共面的线段SA 、SB 、SC ,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC ⊥平面BSC . 考点:面面垂直的判定(证二面角是直二面角)类型七.证明线线垂直1. 在正方体ABCD-A ’B ’C ’D ’中,M 为DD ’的中点,O 为AC 的中点,AB=2 证明:B ’O ⊥AC 考点:法1:线面垂直→线线垂直 法2:勾股定理法3:等腰三角形三线合一。
超实用高考数学:空间几何体知识点解析(含历年真题专项练习)

空间几何体[考情分析] 几何体的结构特征是立体几何的基础,空间几何体的表面积与体积是高考题的重点与热点,多以小题的形式进行考查,属于中等难度. 考点一 表面积与体积 核心提炼1.旋转体的侧面积和表面积(1)S 圆柱侧=2πrl ,S 圆柱表=2πr (r +l )(r 为底面半径,l 为母线长). (2)S 圆锥侧=πrl ,S 圆锥表=πr (r +l )(r 为底面半径,l 为母线长). (3)S 球表=4πR 2(R 为球的半径). 2.空间几何体的体积公式 V 柱=Sh (S 为底面面积,h 为高); V 锥=13Sh (S 为底面面积,h 为高);V 球=43πR 3(R 为球的半径).例1 (1)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________. 答案 402π解析 因为母线SA 与圆锥底面所成的角为45°, 所以圆锥的轴截面为等腰直角三角形. 设底面圆的半径为r ,则母线长l =2r .在△SAB 中,cos ∠ASB =78,所以sin ∠ASB =158.因为△SAB 的面积为515,即12SA ·SB sin ∠ASB=12×2r ×2r ×158=515, 所以r 2=40,故圆锥的侧面积为πrl =2πr 2=402π.(2)如图,已知正三棱柱ABC -A 1B 1C 1的各棱长均为2,点D 在棱AA 1上,则三棱锥D -BB 1C 1的体积为________.答案 233解析 如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2, ∴AC =2,OC =1,则AO = 3. ∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为 3. 又11BB C S=12×2×2=2, ∴11D BB C V =13×2×3=233.易错提醒 (1)计算表面积时,有些面的面积没有计算到(或重复计算). (2)一些不规则几何体的体积不会采用分割法或补形思想转化求解. (3)求几何体体积的最值时,不注意使用基本不等式或求导等确定最值.跟踪演练1 (1)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A .122π B .12π C .82π D .10π答案 B解析 设圆柱的底面半径为r ,高为h ,由题意可知2r =h =22,∴圆柱的表面积S =2πr 2+2πr ·h =4π+8π=12π.故选B.(2)如图,在Rt △ABC 中,AB =BC =1,D 和E 分别是边BC 和AC 上异于端点的点,DE ⊥BC ,将△CDE 沿DE 折起,使点C 到点P 的位置,得到四棱锥P -ABDE ,则四棱锥P -ABDE 的体积的最大值为________.答案327解析 设CD =DE =x (0<x <1),则四边形ABDE 的面积S =12(1+x )(1-x )=12(1-x 2),当平面PDE ⊥平面ABDE 时,四棱锥P -ABDE 的体积最大,此时PD ⊥平面ABDE ,且PD =CD =x ,故四棱锥P -ABDE 的体积V =13S ·PD =16(x -x 3),则V ′=16(1-3x 2).当x ∈⎝⎛⎭⎫0,33时,V ′>0;当x ∈⎝⎛⎭⎫33,1时,V ′<0.∴当x =33时,V max =327. 考点二 多面体与球 核心提炼解决多面体与球问题的两种思路(1)利用构造长方体、正四面体等确定直径.(2)利用球心O 与截面圆的圆心O 1的连线垂直于截面圆的性质确定球心.例2 (1)已知三棱锥P -ABC 满足平面P AB ⊥平面ABC ,AC ⊥BC ,AB =4,∠APB =30°,则该三棱锥的外接球的表面积为__________. 答案 64π解析 因为AC ⊥BC ,所以△ABC 的外心为斜边AB 的中点,因为平面P AB ⊥平面ABC ,所以三棱锥P -ABC 的外接球球心在平面P AB 上, 即球心就是△P AB 的外心,根据正弦定理ABsin ∠APB =2R ,解得R =4,所以外接球的表面积为4πR 2=64π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________. 答案23π 解析 圆锥内半径最大的球即为圆锥的内切球,设其半径为r .作出圆锥的轴截面P AB ,如图所示,则△P AB 的内切圆为圆锥的内切球的大圆.在△P AB 中,P A =PB =3,D 为AB 的中点,AB =2,E 为切点,则PD =22,△PEO ∽△PDB , 故PO PB =OE DB ,即22-r 3=r 1,解得r =22, 故内切球的体积为43π⎝⎛⎭⎫223=23π.规律方法 (1)长方体的外接球直径等于长方体的体对角线长.(2)三棱锥S -ABC 的外接球球心O 的确定方法:先找到△ABC 的外心O 1,然后找到过O 1的平面ABC 的垂线l ,在l 上找点O ,使OS =OA ,点O 即为三棱锥S -ABC 的外接球的球心. (3)多面体的内切球可利用等积法求半径.跟踪演练2 (1)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36π B .64π C .144π D .256π 答案 C解析 如图所示,设球O 的半径为R ,因为∠AOB =90°, 所以S △AOB =12R 2,因为V O -ABC =V C -AOB , 而△AOB 的面积为定值,当点C 位于垂直于平面AOB 的直径端点时,三棱锥O -ABC 的体积最大, 此时V O -ABC =V C -AOB =13×12R 2×R =16R 3=36,故R =6,则球O 的表面积为S =4πR 2=144π.(2)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知P A ⊥平面ABCE ,四边形ABCD 为正方形,AD =5,ED =3,若鳖臑P -ADE 的外接球的体积为92π,则阳马P -ABCD 的外接球的表面积为________.答案 20π解析 ∵四边形ABCD 是正方形,∴AD ⊥CD ,即AD ⊥CE ,且AD =5,ED =3, ∴△ADE 的外接圆半径为r 1=AE2=AD 2+ED 22=2, 设鳖臑P -ADE 的外接球的半径为R 1, 则43πR 31=92π,解得R 1=322. ∵P A ⊥平面ADE ,∴R 1=⎝⎛⎭⎫P A 22+r 21, 可得P A 2=R 21-r 21=102,∴P A =10. 正方形ABCD 的外接圆直径为2r 2=AC =2AD =10, ∴r 2=102, ∵P A ⊥平面ABCD ,∴阳马P -ABCD 的外接球半径R 2=⎝⎛⎭⎫P A 22+r 22=5, ∴阳马P -ABCD 的外接球的表面积为4πR 22=20π. 专题强化练一、单项选择题1.水平放置的△ABC 的直观图如图,其中B ′O ′=C ′O ′=1,A ′O ′=32,那么原△ABC 是一个( )A .等边三角形B .直角三角形C .三边中只有两边相等的等腰三角形D .三边互不相等的三角形 答案 A解析 AO =2A ′O ′=2×32=3,BC =B ′O ′+C ′O ′=1+1=2.在Rt △AOB 中,AB =12+(3)2=2,同理AC =2,所以原△ABC 是等边三角形.2.(2020·全国Ⅰ)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5-14 B.5-12 C.5+14 D.5+12答案 C解析 设正四棱锥的底面正方形的边长为a ,高为h , 侧面三角形底边上的高(斜高)为h ′, 则由已知得h 2=12ah ′.如图,设O 为正四棱锥S -ABCD 底面的中心,E 为BC 的中点,则在Rt △SOE 中,h ′2=h 2+⎝⎛⎭⎫a 22, ∴h ′2=12ah ′+14a 2,∴⎝⎛⎭⎫h ′a 2-12·h ′a -14=0,解得h ′a =5+14(负值舍去).3.已知一个圆锥的侧面积是底面积的2倍,记该圆锥的内切球的表面积为S 1,外接球的表面积为S 2,则S 1S 2等于( )A.12B.13C.14D.18 答案 C 解析 如图,由已知圆锥侧面积是底面积的2倍,不妨设底面圆半径为r ,l 为底面圆周长,R 为母线长, 则12lR =2πr 2, 即12·2π·r ·R =2πr 2, 解得R =2r ,故∠ADC =30°,则△DEF 为等边三角形, 设B 为△DEF 的重心,过B 作BC ⊥DF ,则DB 为圆锥的外接球半径,BC 为圆锥的内切球半径,则BC BD =12,∴r 内r 外=12,故S 1S 2=14. 4.(2020·大连模拟)一件刚出土的珍贵文物要在博物馆大厅中央展出,如图,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1 000元,则气体的费用最少为( )A .4 500元B .4 000元C .2 880元D .2 380元 答案 B解析 因为文物底部是直径为0.9米的圆形,文物底部与玻璃罩底边至少间隔0.3米,所以由正方形与圆的位置关系可知,底面正方形的边长为0.9+2×0.3=1.5米,又文物高1.8米,文物顶部与玻璃罩上底面至少间隔0.2(米),所以正四棱柱的高为1.8+0.2=2(米),则正四棱柱的体积V =1.52×2=4.5(立方米).因为文物的体积为0.5立方米,所以罩内空气的体积为4.5-0.5=4(立方米),因为气体每立方米1 000元,所以气体的费用最少为4×1 000=4 000(元),故选B.5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,动点E 在BB 1上,动点F 在A 1C 1上,O 为底面ABCD 的中心,若BE =x ,A 1F =y ,则三棱锥O -AEF 的体积( )A .与x ,y 都有关B .与x ,y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关 答案 B解析 由已知得V 三棱锥O -AEF =V 三棱锥E -OAF =13S △AOF ·h (h 为点E 到平面AOF 的距离).连接OC ,因为BB 1∥平面ACC 1A 1,所以点E 到平面AOF 的距离为定值.又AO ∥A 1C 1,OA 为定值,点F 到直线AO 的距离也为定值,所以△AOF 的面积是定值,所以三棱锥O -AEF 的体积与x ,y 都无关.6.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3 B.4π3 C.5π3 D .2π 答案 C解析 如图,过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,该几何体的体积为V =V 圆柱-V 圆锥=π·AB2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3.7.(2020·全国Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为( ) A .64π B .48π C .36π D .32π 答案 A解析 如图,设圆O 1的半径为r ,球的半径为R ,正三角形ABC 的边长为a .由πr 2=4π,得r =2, 则33a =2,a =23, OO 1=a =2 3.在Rt △OO 1A 中,由勾股定理得R 2=r 2+OO 21=22+(23)2=16,所以S 球=4πR 2=4π×16=64π.8.(2020·武汉调研)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上,若AB =AC =1,AA 1=23,∠BAC =2π3,则球O 的体积为( )A.32π3 B .3π C.4π3 D .8π 答案 A解析 设△ABC 外接圆圆心为O 1,半径为r ,连接O 1O ,如图,易得O 1O ⊥平面ABC ,∵AB =AC =1,AA 1=23,∠BAC =2π3,∴2r =AB sin ∠ACB =112=2,即O 1A =1,O 1O =12AA 1=3,∴OA =O 1O 2+O 1A 2=3+1=2,∴球O 的体积V =43π·OA 3=32π3.故选A.9.如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成,在该封闭的几何体内部放入一个小圆柱体,且小圆柱体的上、下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为( )A.2 000π9B.4 000π27C .81πD .128π答案 B解析 小圆柱的高分为上、下两部分,上部分的高同大圆柱的高相等,为5,下部分深入底部半球内.设小圆柱下部分的高为h (0<h <5),底面半径为r (0<r <5).由于r ,h 和球的半径构成直角三角形,即r 2+h 2=52,所以小圆柱的体积V =πr 2(h +5)=π(25-h 2)(h +5)(0<h <5),把V 看成是关于h 的函数,求导得V ′=-π(3h -5)(h +5).当0<h <53时,V ′>0,V 单调递增;当53<h <5时,V ′<0,V 单调递减.所以当h =53时,小圆柱的体积取得最大值.即V max =π⎝⎛⎭⎫25-259×⎝⎛⎭⎫53+5=4 000π27,故选B. 10.已知在三棱锥P -ABC 中,P A ,PB ,PC 两两垂直,且长度相等.若点P ,A ,B ,C 都在半径为1的球面上,则球心到平面ABC 的距离为( ) A.36 B.12 C.13 D.32答案 C解析 ∵在三棱锥P -ABC 中,P A ,PB ,PC 两两垂直,且长度相等, ∴此三棱锥的外接球即以P A ,PB ,PC 为三边的正方体的外接球O , ∵球O 的半径为1,∴正方体的边长为233,即P A =PB =PC =233,球心到截面ABC 的距离即正方体中心到截面ABC 的距离,设P 到截面ABC 的距离为h ,则正三棱锥P -ABC 的体积V =13S △ABC ×h =13 S △P AB ×PC =13×12×⎝⎛⎭⎫2333, ∵△ABC 为边长为263的正三角形,S △ABC =233,∴h =23, ∴球心(即正方体中心)O 到截面ABC 的距离为13.二、多项选择题11.(2020·枣庄模拟)如图,透明塑料制成的长方体容器ABCD -A 1B 1C 1D 1内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的是( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜度的不同,A 1C 1始终与水面所在平面平行D .当容器倾斜如图③所示时,AE ·AH 为定值 答案 AD解析 由于AB 固定,所以在倾斜的过程中,始终有CD ∥HG ∥EF ∥AB ,且平面AEHD ∥平面BFGC ,故水的部分始终呈棱柱形(三棱柱或四棱柱),且AB 为棱柱的一条侧棱,没有水的部分也始终呈棱柱形,故A 正确;因为水面EFGH 所在四边形,从图②,图③可以看出,EF ,GH 长度不变,而EH ,FG 的长度随倾斜度变化而变化,所以水面EFGH 所在四边形的面积是变化的,故B 错;假设A 1C 1与水面所在的平面始终平行,又A 1B 1与水面所在的平面始终平行,则长方体上底面A 1B 1C 1D 1与水面所在的平面始终平行,这就与倾斜时两个平面不平行矛盾,故C 错;水量不变时,棱柱AEH -BFG 的体积是定值,又该棱柱的高AB 不变,且V AEH -BFG =12·AE ·AH ·AB ,所以AE ·AH =2V AEH -BFG AB ,即AE ·AH 是定值,故D 正确.12. (2020·青岛检测)已知四棱台ABCD -A 1B 1C 1D 1的上、下底面均为正方形,其中AB =22,A 1B 1=2,AA 1=BB 1=CC 1=DD 1=2,则下列叙述正确的是( )A .该四棱台的高为 3B .AA 1⊥CC 1C .该四棱台的表面积为26D .该四棱台外接球的表面积为16π 答案 AD解析 将四棱台补为如图所示的四棱锥P -ABCD ,并取E ,E 1分别为BC ,B 1C 1的中点,记四棱台上、下底面中心分别为O 1,O ,连接AC ,BD ,A 1C 1,B 1D 1,A 1O ,OE ,OP ,PE .由条件知A 1,B 1,C 1,D 1分别为四棱锥的侧棱P A ,PB ,PC ,PD 的中点,则P A =2AA 1=4,OA =2,所以OO 1=12PO =12P A 2-OA 2=3,故该四棱台的高为3,故A 正确;由P A =PC=4,AC =4,得△P AC 为正三角形,则AA 1与CC 1所成角为60°,故B 不正确;四棱台的斜高h ′=12PE =12PO 2+OE 2=12×(23)2+(2)2=142,所以该四棱台的表面积为(22)2+(2)2+4×2+222×142=10+67,故C 不正确;易知OA 1=OB 1=OC 1=OD 1=O 1A 21+O 1O 2=2=OA =OB =OC =OD ,所以O 为四棱台外接球的球心,所以外接球的半径为2,外接球表面积为4π×22=16π,故D 正确.三、填空题13.(2020·浙江)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是________. 答案 1解析 如图,设圆锥的母线长为l ,底面半径为r ,则圆锥的侧面积S 侧=πrl =2π,即r·l=2.由于侧面展开图为半圆,可知12πl2=2π,可得l=2,因此r=1.14.在如图所示的斜截圆柱中,已知圆柱的底面直径为40 cm,母线长最短50 cm,最长80 cm,则斜截圆柱的侧面面积S=________cm2.答案 2 600π解析将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S=12×(π×40)×(50+80)=2 600π(cm2).15.已知球O与棱长为4的正四面体的各棱相切,则球O的体积为________.答案82 3π解析将正四面体补成正方体,则正四面体的棱为正方体面上的对角线,因为正四面体的棱长为4,所以正方体的棱长为2 2.因为球O与正四面体的各棱都相切,所以球O为正方体的内切球,即球O的直径2R=22,则球O的体积V=43πR3=823π.16.(2020·新高考全国Ⅰ)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心,5为半径的球面与侧面BCC1B1的交线长为________.答案2π2解析如图,设B1C1的中点为E,球面与棱BB1,CC1的交点分别为P,Q,连接DB,D1B1,D1P,D1E,EP,EQ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r , 则r =R 2球-D 1E 2=5-3= 2.又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5, ∴B 1P =D 1P 2-D 1B 21=1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ 的长为π2×2=2π2,即交线长为2π2.。
2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】

2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练一、基本技能练1.下列说法中,正确的是()A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形,则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等2.如图所示的等腰梯形是一个几何图形的斜二测直观图,其底角为45°,上底和腰均为1,下底为2+1,则此直观图对应的平面图形的面积为()A.1+2B.2+2C.2+22D.4+223.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.4B.43D.3C.234.已知在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,则将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为() A.(5+2)π B.(4+2)πC.(5+22)πD.(3+2)π5.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为()A.3∶2B.2∶2C.3∶3D.3∶46.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P 的截面与底面交于CD ,若∠COD =90°(O 为底面圆心),且S △PCD =72,则这个等边圆锥的表面积为()A.2π+2πB.3πC.2π+3πD.π+3π7.如图,四边形ABCD 是边长为2的正方形,ED ⊥平面ABCD ,FC ⊥平面ABCD ,ED =2FC =2,则四面体ABEF 的体积为()A.13B.23C.1D.438.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为5-12,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比.在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金比,且它们夹角的余弦值为黄金比值,那么这个三角形一定是直角三角形,且这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为()A.5-12B.5+12C.1D.149.如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F,G分别是棱A′B′,B′C′,CD的中点,则由点E,F,G确定的平面截正方体所得的截面多边形的面积等于________.10.已知圆锥的顶点为S,底面圆周上的两点A,B满足△SAB为等边三角形,且面积为43,又知圆锥轴截面的面积为8,则圆锥的侧面积为________.11.如图,已知正三棱柱ABC-A1B1C1的各棱长均为2,点D在棱AA1上,则三棱锥D-BB1C1的体积为________.12.已知三棱锥S-ABC中,∠SAB=∠ABC=π2,SB=4,SC=213,AB=2,BC =6,则三棱锥S-ABC的体积为________.二、创新拓展练13.(多选)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ,这个角接近30°.若取θ=30°,侧棱长为21米,则()A.正四棱锥的底面边长为6米B.正四棱锥的底面边长为3米C.正四棱锥的侧面积为243平方米D.正四棱锥的侧面积为123平方米14.(多选)如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=12,则下列结论中错误的是()A.AC⊥AFB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.△AEF的面积与△BEF的面积相等15.(多选)《九章算术》是《算经十书》中最重要的一部,其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”,则()A.“羡除”有且仅有两个面为三角形B.“羡除”一定不是台体C.不存在有两个面为平行四边形的“羡除”D.“羡除”至多有两个面为梯形16.(多选)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则()A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1参考答案与解析一、基本技能练1.答案C解析棱柱的侧面都是平行四边形,选项A错误;其他侧面可能是平行四边形,选项B错误;棱柱的侧棱与底面边长并不一定相等,选项D错误;易知选项C正确.2.答案B解析∵平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,∴平面图形为直角梯形,且直角腰长为2,上底边长为1,下底边长为2+1,∴平面图形的面积S=1+1+22×2=2+ 2.故选B.3.答案B解析易知该几何体是由上、下两个全等的正四棱锥组成的,其中正四棱锥底面边长为2,棱锥的高为1,所以该多面体的体积V =2×13×(2)2×1=43.4.答案A解析因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周得到的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥后剩余的部分,如图所示.所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.5.答案D解析设塔顶是正四棱锥P -ABCD (如图),PO 是正四棱锥的高.设正四棱锥底面边长为a ,则底面面积S 1=a 2,因为AO =22a ,∠PAO =45°,所以PA =2×22a =a ,所以△PAB 是正三角形,其面积为S 2=34a 2,所以S 2∶S 1=34a 2∶a 2=3∶4.6.答案B解析如图,连接PO ,设圆锥的母线长为2a ,则圆锥的底面圆的半径为a ,高为PO =3a .由已知得CD =2a ,PC =PD =2a ,则S △PCD =12×2a ×(3a )2+22a 2=72,从而可得a =1,圆锥的表面积为πa ×2a +πa 2=3πa 2=3π.7.答案B解析∵ED ⊥平面ABCD 且AD ⊂平面ABCD ,∴ED ⊥AD .∵在正方形ABCD 中,AD ⊥DC ,又DC ∩ED =D ,DC ,ED ⊂平面CDEF ,∴AD ⊥平面CDEF .易知FC =ED2=1,V A -BEF =V ABCDEF -V F -ABCD -V A -DEF .∵V E -ABCD =13·ED ·S 正方形ABCD =13×2×2×2=83,V B -EFC =13·BC ·S △EFC =13×2×2×1×12=23,∴V ABCDEF =V E -ABCD +V B -EFC =83+23=103.又V F -ABCD =13·FC ·S 正方形ABCD =13×1×2×2=43,V A -DEF =13·AD ·S △DEF =13×2×2×2×12=43,∴V A -BEF =V ABCDEF -V F -ABCD -V A -DEF =103-43-43=23.故选B.8.答案D解析如图,在黄金分割正四棱锥P -ABCD 中,O 是正方形ABCD 的中心,PE 是正四棱锥的斜高,设OE =a ,则CD =2a ,∴Rt△POE为黄金分割直角三角形,则OEPE=5-12,∴PE=5+12,则PO=PE2-OE2=1+52a,∴以该正四棱锥的高为边长的正方形的面积S=PO2=1+52a2,又正四棱锥的四个侧面是全等的,∴S侧=4S△PCD=4×12×CD×PE=2(1+5)a2,∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为1 4 .9.答案332解析分别取AD,CC′和AA′的中点为P,M,N,可得出过E,F,G三点的平面截正方体所得截面为正六边形EFMGPN,则正六边形的边长MG=CG2+CM2=222+2221,故截面多边形的面积S=6×34×12=332.10.答案82π解析设圆锥的母线长为l,由△SAB为等边三角形,且面积为43,所以12l 2sin π3=43,解得l =4;又设圆锥底面半径为r ,高为h ,则由轴截面的面积为8,得rh =8;又r 2+h 2=l 2=16,解得r =h =22,所以圆锥的侧面积S =πrl =π·22·4=82π.11.答案233解析如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2,∴AC =2,OC =1,则AO = 3.∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为3.又S △BB 1C 1=12×2×2=2,∴V D -BB 1C 1=13×2×3=233.12.答案43解析∵∠ABC =π2,AB =2,BC =6,∴AC =AB 2+BC 2=22+62=210.∵∠SAB =π2,AB =2,SB =4,∴AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,∴AC ⊥AS .又∵SA ⊥AB ,AC ∩AB =A ,AC ,AB ⊂平面ABC ,∴AS ⊥平面ABC .∴AS 为三棱锥S -ABC 的高,∴V 三棱锥S -ABC =13×12×2×6×23=4 3.二、创新拓展练13.答案AC解析如图,在正四棱锥S -ABCD 中,O 为正方形ABCD 的中心,H 为AB 的中点,则∠SHO 为侧面SAB 与底面ABCD 所成的锐二面角,且SH ⊥AB ,∠SHO =30°,设底面边长为2a ,所以OH =AH =a ,OS =33a ,SH =233.在Rt △SAH 中,a 2=21,解得a =3,所以正四棱锥的底面边长为6米,侧面积为S =12×6×23×4=243(平方米).14.答案AD解析由题意及图形知,当点F 与点B 1重合时,∠CAF =60°,故A 错误;由正方体ABCD -A 1B 1C 1D 1的两个底面平行,EF ⊂平面A 1B 1C 1D 1,知EF ∥平面ABCD ,故B 正确;由几何体的性质及图形知,三角形BEF 的面积是定值,点A 到平面DD 1B 1B 的距离是定值,故可得三棱锥A -BEF 的体积为定值,故C 正确;由图形可以看出,B 到直线EF 的距离与A 到直线EF 的距离不相等,故△AEF 的面积与△BEF 的面积不相等,故D 错误.故选AD.15.答案ABC解析由题意知AE ∥BF ∥CD ,四边形ACDE 为梯形,如图所示.选项A ,由题意知“羡除”有且仅有两个面为三角形,故A 正确;选项B ,因为AE ∥BF ∥CD ,所以“羡除”一定不是台体,故B 正确;选项C ,假设四边形ABFE 和四边形BCDF 为平行四边形,则AE ∥BF ∥CD ,且AE =BF =CD ,即四边形ACDE 为平行四边形,与已知四边形ACDE 为梯形矛盾,故不存在,故C 正确;选项D ,若AE ≠BF ≠CD ,则“羡除”有三个面为梯形,故D 错误.故选ABC.16.答案CD 解析如图,连接BD 交AC 于O ,连接OE ,OF .设AB =ED =2FB =2,则AB =BC =CD =AD =2,FB =1.因为ED ⊥平面ABCD ,FB ∥ED ,所以FB ⊥平面ABCD ,所以V 1=V E -ACD =13S △ACD ·ED =13×12AD ·CD ·ED =13×12×2×2×2=43,V 2=V F -ABC =13S △ABC ·FB =13×12AB ·BC ·FB =13×12×2×2×1=23.因为ED ⊥平面ABCD ,AC ⊂平面ABCD ,所以ED ⊥AC ,又AC ⊥BD ,且ED ∩BD =D ,ED ,BD ⊂平面BDEF ,所以AC ⊥平面BDEF .因为OE ,OF ⊂平面BDEF ,所以AC ⊥OE ,AC ⊥OF .易知AC=BD=2AB=22,OB=OD=12BD=2,OF=OB2+FB2=3,OE=OD2+ED2=6,EF=BD2+(ED-FB)2=(22)2+(2-1)2=3,所以EF2=OE2+OF2,所以OF⊥OE.又OE∩AC=O,OE,AC⊂平面ACE,所以OF⊥平面ACE,所以V3=V F-ACE=13S△ACE·OF=13×12AC·OE·OF=13×12×22×6×3=2,所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,所以选项A,B不正确,选项C,D正确.故选CD.。
高二数学同步单元练习(必修2) 专题01 空间几何体的结构(AB卷) Word版含解析

(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列图形中,不是三棱柱的展开图的是()答案:C2.有两个面平行的多面体不可能是()A.棱柱B.棱锥C.棱台D.以上都错解析:选B棱柱、棱台的上、下底面是平行的,而棱锥的任意两面均不平行.3.关于棱柱,下列说法正确的是()A.只有两个面平行B.所有的棱都相等C.所有的面都是平行四边形D.两底面平行,侧棱也互相平行4.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有()A.20 B.15C.12 D.10解析:选D从正五棱柱的上底面1个顶点与下底面不与此点在同一侧面上的两个顶点相连可得2条对角线,故共有5×2=10条对角线.5.下列命题中正确的是()A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.两个底面平行且相似,其余各面都是梯形的多面体是棱台C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点解析:选D A中的平面不一定平行于底面,故A错;B中侧棱不一定交于一点;C中底面不一定是正方形.6.观察如图的四个几何体,其中判断不正确的是()A.①是棱柱B.②不是棱锥C.③不是棱锥D.④是棱台解析:结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.答案:B7.纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一条棱将正方体剪开,外面朝上展平得到右侧的平面图形,则标“△”的面的方位是()A.南B.北C.西D.下答案:B8.如图,在三棱台A'B'C'-ABC中,截去三棱锥A'-ABC,则剩余部分是()A.三棱锥B.四棱锥C.三棱柱D.三棱台解析:剩余部分是四棱锥A'-BCC'B'.答案:B9.棱锥的侧面和底面可以都是()A.三角形B.四边形C.五边形D.六边形解析:三棱锥的侧面和底面均是三角形.答案:A10.在下列四个平面图形中,每个小四边形皆为正方形,其中可以沿相邻正方形的公共边折叠围成一个正方体的图形是()解析:动手将四个选项中的平面图形折叠,看哪一个可以折叠围成正方体即可.答案:C11.如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定形状.答案:A12.用一个平面去截四棱锥,不可能得到()A.棱锥B.棱柱C.棱台D.四面体解析:根据棱椎的特点,侧棱不平行,所以肯定得不到棱柱答案:B第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.面数最少的棱柱为________棱柱,共有________个面围成.解析:棱柱有相互平行的两个底面,其侧面至少有3个,故面数最少的棱柱为三棱柱,共有五个面围成.答案:三 514.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A 到点M的最短路程是________ cm.答案:1315.侧棱垂直于底面的棱柱叫做直棱柱.侧棱不垂直于底面的棱柱叫做斜棱柱.底面是正多边形的直棱柱叫做正棱柱.底面是平行四边形的四棱柱叫做平行六面体.侧棱与底面垂直的平行六面体叫做直平行六面体.底面是矩形的直平行六面体叫做长方体.棱长都相等的长方体叫做正方体.请根据上述定义,回答下面的问题:(1)直四棱柱________是长方体;(2)正四棱柱________是正方体.(填“一定”、“不一定”、“一定不”)解析:根据上述定义知:长方体一定是直四棱柱,但是直四棱柱不一定是长方体;正方体一定是正四棱柱,但是正四棱柱不一定是正方体.答案:(1)不一定(2)不一定16.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为cm.解析:n棱柱有2n个顶点,因为此棱柱有10个顶点,所以此棱柱为五棱柱.又棱柱的侧棱都相等,五条侧棱长的和为60 cm,可知每条侧棱长为12 cm.答案:12三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.18.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.解:如图(1)所示,沿正三角形三边中点连线折起,可拼得一个底面为正三角形的三棱锥.如图(2)所示,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的14,有一组对角为直角,余下部分按虚线折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底. 19.按下列条件分割三棱台ABC-A 1B 1C 1(不需要画图,各写出一种分割方法即可). (1)一个三棱柱和一个多面体; (2)三个三棱锥.20.正三棱台的上、下底面边长及高分别为1,2,2,则它的斜高是多少? 解析:如图,MF=OF-O'E=. 在Rt △EMF 中,∵EM=2, ∴EF=.所以斜高是21.如图,在棱锥A-BCD中,截面EFG平行于底面,且AE∶AB=1∶3,已知△DBC的周长是18,求△EFG的周长.解:由已知得EF∥BD,FG∥CD,EG∥BC,∴△EFG∽△BDC.∴.又,∴.∴△EFG的周长=18×=6.22.如图,在长方体ABCD-A1B1C1D1中,AB=3,BC=4,A1A=5,现有一只甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.观察如图所示的4个几何体,其中判断正确的是( )A.①是棱台 B.②是圆台C.③是棱锥 D.④不是棱柱2.下列关于母线的叙述正确的是( )①在圆柱上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.A.①② B.②③C.①③ D.②④D ①③中两点的连线可能不在侧面上,因此不一定是母线;②中两点的连线符合母线的条件;④中圆柱任意一条母线与圆柱的轴所在的直线平行,因此圆柱的任意两条母线所在的直线是互相平行的.3.下列判断正确的是( )A.棱柱中只能有两个面互相平行B.底面是正方形的直四棱柱是正四棱柱C.底面是正六边形的棱台是正六棱台D.底面是正方形的四棱锥是正四棱锥B A错误,比如四棱柱;B正确;C错误,还应满足正棱台上下底面中心的连线垂直于底面;D错误,还应满足顶点在底面的投影为底面的中心.4.若一正方体沿着表面几条棱裁开放平得到如图L112所示的展开图,则在原正方体中( )A.AB∥CD B.AB∥EFC.CD∥GH D. AB∥GHC 折回原正方体如图所示,则C与E重合,D与B重合,显然CD∥GH.5.如图所示的四个长方体中,由如图所示的纸板折成的是( )D 根据纸板的折叠情况及特殊面的阴影部分可以判断正确选项是D.6.给出下列三个命题:①底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱;②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;③棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确命题的个数是( )A.0 B.1 C.2 D.37.如图所示,若Ω是长方体ABCDA1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱 D.Ω是棱台D 根据棱台的定义(侧棱的延长线必交于一点,即棱台可以还原成棱锥)可知,几何体Ω不是棱台.8.下列命题正确的是( )A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的投影可能平行D.一条线段中点的平行投影仍是这条线段投影的中点9.如图所示的一个几何体,哪一个是该几何体的俯视图( )答案:C10.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①② B.①③ C.①④ D.②④D11.一个长方体去掉一个小长方体,所得几何体的正视图与侧视图分别如图所示,则该几何体的俯视图为( )答案:C12.如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )答案:D第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.关于如图所示的几何体的正确说法为________.(填序号)图L116①这是一个六面体;②这是一个四棱台;③这是一个四棱柱;④这是一个被截去一个三棱柱的四棱柱①③④由图易知①③④正确.14.一个无盖的正方体盒子展开后的平面图如图L117所示,A,B,C是展开图上的三点,则在正方体盒子中∠ABC=________.15.下列说法中错误的是__________.(填序号)①圆柱的轴截面是过母线的截面中面积最大的;②球的所有截面中过球心的截面的面积最大;③圆台的所有平行于底面的截面都是圆面;④圆锥的所有轴截面都是全等的等腰直角三角形.④根据旋转体的定义可知,圆锥的所有轴截面是全等的等腰三角形.16.若一个三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.答案:2 4解析三棱柱的高同侧视图的高,侧视图的宽度恰为底面正三角形的高,故底边长为4.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在下面图形中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求).18.如图是截去一角的长方体,画出它的三视图.解该图形的三视图如图所示.19.如图,螺栓是棱柱和圆柱的组合体,画出它的三视图.解该物体是由一个正六棱柱和一个圆柱组合而成的,正视图反映正六棱柱的三个侧面和圆柱侧面,侧视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).它的三视图如图所示.20.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?解由于正视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块.而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字,其他方框内的数字可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块.21.有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?备特征③.22.如图所示,四边形ABCD绕边AD所在的直线EF旋转,其中AD∥BC,AD⊥CD.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,比较其不同点.(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列说法正确的是()A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的平行投影可能平行D.若一条线段的平行投影是一条线段,则中点的平行投影仍为这条线段投影的中点答案:D2.在一个几何体的三视图中,正视图和俯视图如图,则相应的侧视图可以为()解析:此空间几何体是由一个半圆锥和一个三棱锥拼接而成的一个简单组合体,由其正视图和俯视图可知其相应的侧视图可为D.答案:D3.(2016山西大同一中高二月考)如果用表示1个立方体,用表示2个立方体叠加,用表示3个立方体叠加,那么如图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是()解析:由题意和图可知,左边和右边各为1个正方体,用表示;当中为3个正方体,用表示;上面为2个正方体,用表示.故选B.答案:B4.(2016山西太原五中高二月考)一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是()A.①B.②C.③D.④解析:其俯视图若为圆,则正视图中的长度与侧视图中的宽度应一样,由图中可知其正视图与侧视图的宽度不一样,因此其俯视图不可能是圆.故选C.答案:C5.(2016安徽蚌埠一中高二期中)已知正六棱柱的底面边长和侧棱长均为2 cm,其三视图中的俯视图如图所示,则其侧视图的面积是()A.4 cm2B.2 cm2C.8 cm2D.4 cm2答案:A6.关于几何体的三视图,下列说法正确的是( )A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽答案:C 由三视图的特点可知选项C正确.7.在原来的图形中,两条线段平行且相等,则在直观图中对应的两条线段( )A.平行且相等 B.平行不相等C.相等不平行 D.既不平行也不相等答案:A 由斜二测画法规则知平行性是不变的,长度的变化在平行时相同,故仍平行且相等.8.一个几何体的三视图如图L121所示,这个几何体可能是一个( )A.三棱锥B.底面不规则的四棱锥C.三棱柱D.底面为正方形的四棱锥答案:C 根据三视图,几何体为一个倒放的三棱柱.9.如图是水平放置的三角形的直观图,D′是△A′B′C′中B′C′边的中点,A′B′,A′D′,A′C′三条线段对应原图形中的线段AB,AD,AC,那么( )A.最短的是ACB.最短的是ABC.最短的是ADD.无法确定谁最短10.如图L123所示,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的周长为( )A.2 2 B.6 C.8 D.4 2+2图L123图L12411.图L124为水平放置的正方形ABCO,在直角坐标系中点B的坐标为(2,2),则用斜二测画法画出的正方形的直观图中,点B′到O′x′轴的距离为( )A.12B.22C. 1D.2答案:B 因为BC垂直于x轴,所以在直观图中B′C′的长度是1,且与O′x′轴的夹角是45°,所以B′到O′x′轴的距离是22.12.用斜二测画法画出的某平面图形的直观图如图L125所示,AB平行于y′轴,BC,AD平行于x′轴.已知四边形ABCD的面积为2 2 cm2,则原平面图形的面积为( )图L125A.4 cm2B.4 2 cm2C.8 cm2D.8 2 cm2答案:C 依题意可知∠BAD=45°,则原平面图形为直角梯形,且上下底边的长分别与BC,AD相等,高为梯形ABCD的高的2 2倍,所以原平面图形的面积为8 cm2.第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.太阳光线与地面成60°的角,照射在地面上的一个皮球上,皮球在地面上的投影长是10,则皮球的直径是.解析:直径d=10sin 60°=15.答案:1514.在棱长为1的正方体ABCD-A1B1C1D1中,对角线AC1在六个面上的正投影长度总和是.解析:正方体的对角线AC1在各个面上的正投影是正方体各个面上的对角线,因而其长度都为,所以所求总和为6.答案:615.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的.(填入所有可能的几何体前的编号)①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.答案:①②③⑤16.(2012·杭州检测)如图Rt△O′A′B′是一平面图形的直观图,直角边O′B′=1,则这个平面图形的面积是________.解析:∵O′B′=1,∴O′A′=2,∴在Rt△OAB中,∠AOB=90°,OB=1,OA=22,∴S △AOB =12×1×22= 2.答案: 2三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,原平面图形的面积为________.答案:2+2218.画出下列几何体的三视图.解:几何体的三视图如图所示:19.如图,该几何体是由一个长方体木块锯成的. (1)判断该几何体是否为棱柱;(2)画出它的三视图.解:(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.(2)该几何体的三视图如图.20.如图是某圆锥的三视图,求其底面积和母线长.21.已知正三棱锥VABC的正视图、侧视图和俯视图如图L1215所示.(1)画出该三棱锥的直观图;(2)求出侧视图的面积.图L1215解:(1)三棱锥的直观图如图所示. (2)根据三视图间的关系可得BC =2 3. 由俯视图可知三棱锥底面三角形的高为2 3×32=3. ∵三棱锥的高在底面上的投影是底面的中心,且其到点A 的距离为底面△ABC 高的23,∴底面中心到点A 的距离为23×3=2,∴侧视图中VA =42-22=2 3,∴S △VBC =12×2 3×2 3=6.22.如图所示,画出水平放置的四边形OBCD 的直观图.。
高考复习 第8篇 第1讲 空间几何体及其表面积与体积知识点+例题+练习 含答案
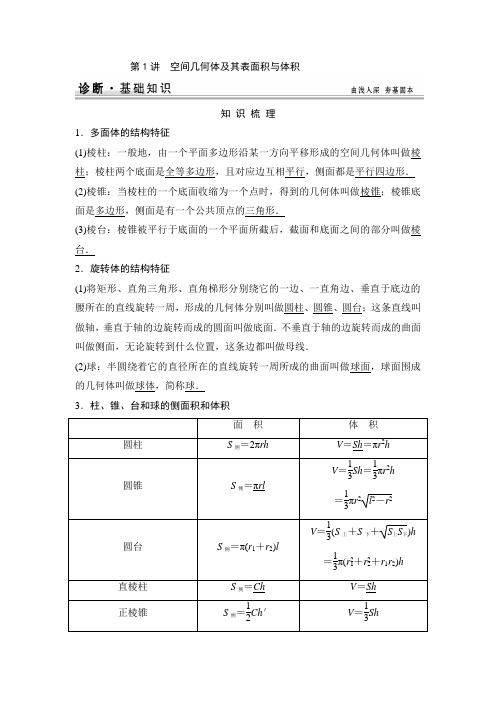
第1讲空间几何体及其表面积与体积知识梳理1.多面体的结构特征(1)棱柱:一般地,由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱;棱柱两个底面是全等多边形,且对应边互相平行,侧面都是平行四边形.(2)棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥;棱锥底面是多边形,侧面是有一个公共顶点的三角形.(3)棱台:棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台.2.旋转体的结构特征(1)将矩形、直角三角形、直角梯形分别绕它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台;这条直线叫做轴,垂直于轴的边旋转而成的圆面叫做底面.不垂直于轴的边旋转而成的曲面叫做侧面,无论旋转到什么位置,这条边都叫做母线.(2)球:半圆绕着它的直径所在的直线旋转一周所成的曲面叫做球面,球面围成的几何体叫做球体,简称球.3.柱、锥、台和球的侧面积和体积面积体积圆柱S侧=2πrh V=Sh=πr2h圆锥S侧=πrlV=13Sh=13πr2h=13πr2l2-r2圆台S侧=π(r1+r2)lV=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h直棱柱S侧=Ch V=Sh正棱锥S侧=12Ch′V=13Sh续表4.(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和.辨析感悟1.柱体、锥体、台体与球的面积(1)圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.(×)(2)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为3πa2.(×)2.柱体、锥体、台体的体积(3)(教材练习改编)若一个球的体积为43π,则它的表面积为12π.(√)(4)在△ABC中,AB=2,BC=3,∠ABC=120°,使△ABC绕直线BC旋转一周所形成的几何体的体积为9π.(×)3.柱体、锥体、台体的展开与折叠(5)将圆心角为2π3,面积为3π的扇形作为圆锥的侧面,则圆锥的表面积等于4π.(√)(6)(2014·青州模拟改编)将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为312a3.(×)[感悟·提升]两点注意一是求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.二是几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.考点一空间几何体的结构特征【例1】给出下列四个命题:①有两个侧面是矩形的棱柱是直棱柱②侧面都是等腰三角形的棱锥是正棱锥③侧面都是矩形的直四棱柱是长方体④底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱其中不正确的命题为________.解析对于①,平行六面体的两个相对侧面也可能是矩形,故①错;对于②,对等腰三角形的腰是否为侧棱未作说明(如图),故②错;对于③,若底面不是矩形,则③错;④正确.答案①②③规律方法解决该类题目需准确理解几何体的定义,要真正把握几何体的结构特征,并且学会通过举反例对概念进行辨析,即要说明一个命题是错误的,设法举出一个反例即可.【训练1】设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体;④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.解析命题①符合平行六面体的定义,故命题①是正确的.底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②是错误的.因为直四棱柱的底面不一定是平行四边形,故命题③是错误的.命题④由棱台的定义知是正确的. 答案 ①④考点二 几何体的表面积与体积【例2】 如图所示,四棱锥P -ABCD 的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,∠ABD =60°,∠BDC =45°, △ADP ∽△BAD . (1)求线段PD 的长;(2)若PC =11R ,求三棱锥P -ABC 的体积. 解 (1)∵BD 是圆的直径,∴∠BAD =90°, 又∵△ADP ∽△BAD ,∴AD BA =DP AD , ∠PDA =∠BAD =90°, DP =AD 2BA =(BD sin 60°)2BD sin 30°=4R 2×342R ×12=3R . ∴DP 的长为3R .(2)在Rt △BCD 中,BC =CD =BD cos 45°=2R , ∵PD 2+CD 2=9R 2+2R 2=11R 2=PC 2,∴PD ⊥CD , 又∠PDA =90°,AD ∩CD =D ,∴PD ⊥底面ABCD , 则S △ABC =12AB ·BC sin(60°+45°) =12R ·2R ⎝ ⎛⎭⎪⎫32×22+12×22=3+14R 2.所以三棱锥P -ABC 的体积为V P -ABC =13·S △ABC ·PD =13·3+14R 2·3R =3+14R 3.规律方法 求几何体的体积问题,可以多角度、全方位地考虑问题,常采用的方法有“换底法”、“分割法”、“补体法”等,尤其是“等积转化”的数学思想方法应高度重视.【训练2】 (2014·苏州模拟)一个正三棱台的上、下底面边长分别是3 cm 和6 cm ,高是32 cm.(1)求三棱台的斜高;(2)求三棱台的侧面积和表面积. 解(1)设O 1、O 分别为正三棱台ABC -A 1B 1C 1的上、下底面正三角形的中心,如图所示,则O 1O =32,过O 1作O 1D 1⊥B 1C 1,OD ⊥BC ,则D 1D 为三棱台的斜高;过D 1作D 1E ⊥AD 于E ,则D 1E =O 1O =32, 因O 1D 1=36×3=32,OD =36×6=3,则DE =OD -O 1D 1=3-32=32.在Rt △D 1DE 中, D 1D =D 1E 2+ED 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322=3(cm). (2)设c 、c ′分别为上、下底的周长,h ′为斜高, S 侧=12(c +c ′)h ′=12(3×3+3×6)×3=2732(cm 2),S 表=S 侧+S 上+S 下=2732+34×32+34×62=9934(cm 2).故三棱台斜高为 3 cm ,侧面积为2732 cm 2,表面积为9934 cm 2.考点三 球与空间几何体的接、切问题【例3】 (1)(2013·新课标全国Ⅱ卷)已知正四棱锥O -ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.(2)(2013·辽宁卷改编)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为________.审题路线 (1)根据正四棱锥的体积求高⇒求底面正方形的对角线长⇒由勾股定理求OA ⇒由球的表面积公式求解.(2)BC 为过底面ABC 的截面圆的直径⇒取BC 中点D ,则球心在BC 的垂直平分线上,再由对称性求解. 解析 (1)设正四棱锥的高为h , 则13×(3)2×h =322,解得h =322. 又底面正方形的对角线长为2×3= 6. 所以OA =⎝ ⎛⎭⎪⎫3222+⎝ ⎛⎭⎪⎫622= 6. 故球的表面积为S 球=4π×(6)2=24π.(2)因为在直三棱柱中AB =3,AC =4,AA 1=12,AB ⊥AC ,所以BC =5,且BC 为过底面ABC 的截面圆的直径,取BC 中点D ,则OD ⊥底面ABC ,则O 在侧面BCC 1B 1内,矩形BCC 1B 1的对角线长即为球的直径,所以2r =122+52=13,即r =132.答案 (1)24π (2)132规律方法 解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.【训练3】(2012·辽宁卷)已知点P,A,B,C,D是球O表面上的点,P A⊥平面ABCD,四边形ABCD是边长为23的正方形.若P A=26,则△OAB的面积为________.解析根据球的内接四棱锥的性质求解.如图所示,线段PC就是球的直径,设球的半径为R,因为AB=BC=23,所以AC=2 6.又P A=26,所以PC2=P A2+AC2=24+24=48,所以PC=43,所以OA=OB=23,所以△AOB是正三角形,所以S=12×23×23×32=3 3.答案3 3考点四几何体的展开与折叠问题【例4】(1)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC,OD折叠,使OA,OB重合,则以A,B,C,D,O为顶点的四面体的体积为________.(2)如图所示,在直三棱柱ABC-A1B1C1中,△ABC为直角三角形,∠ACB=90°,AC=4,BC=CC1=3.P是BC1上一动点,沿棱柱表面使CP+P A1最小,则最小值为________.解析 (1)折叠后的四面体如图所示.OA ,OC ,OD 两两相互垂直,且OA =OC =OD =22,体积V =13 S △OCD ·OA =13×12×(22)3=823.(2)由题意知,A 1P 在几何体内部,把面BB 1C 1C 沿BB 1展开与面AA 1B 1B 在一个平面上,如图所示,连接A 1C 即可. 则A 1、P 、C 三点共线时,CP +P A 1最小, ∵∠ACB =90°,AC =4,BC =C 1C =3,∴A 1B 1=AB =42+32=5,∴A 1C 1=5+3=8,∴A 1C =82+32=73.故CP +P A 1的最小值为73.答案 (1)823 (2)73规律方法 (1)有关折叠问题,一定要分清折叠前后两图形(折前的平面图形和折叠后的空间图形)各元素间的位置和数量关系,哪些变,哪些不变.(2)研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.【训练4】如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q共线,点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.解析由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图所示),其中PD⊥平面ABCD,因此该四棱锥的体积V=13×6×6×6=72,而棱长为6=3个这样的几何体,才能拼成的正方体的体积V=6×6×6=216,故需要21672一个棱长为6的正方体.答案 31.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决.2.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.3.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.方法优化5——特殊点在求解几何体的体积中的应用【典例】 (2012·山东卷)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为________.[一般解法] 三棱锥D 1-EDF 的体积即为三棱锥F -DD 1E 的体积.因为E ,F 分别为AA 1,B 1C 上的点,所以在正方体ABCD -A 1B 1C 1D 1中△EDD 1的面积为定值12,F 到平面AA 1D 1D 的距离为定值1,所以VF -DD 1E =13×12×1=16. [优美解法] E 点移到A 点,F 点移到C 点,则VD 1-EDF =VD 1-ADC =13×12×1×1×1=16. [答案] 16[反思感悟] (1)一般解法利用了转化思想,把三棱锥D 1-EDF 的体积转化为三棱锥F -DD 1E 的体积,但这种解法还是难度稍大,不如采用特殊点的解法易理解、也简单易求.(2)在求几何体体积时还经常用到等积法、割补法. 【自主体验】 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为________.解析补形法将三棱柱补成四棱柱,如图所示.记A1到平面BCC1B1的距离为d,则d=2.则V三棱柱=12V四棱柱=12S四边形BCC1B1·d=12×4×2=4.答案 4基础巩固题组(建议用时:40分钟)一、填空题1.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数是________.解析命题①错,因为这条边若是直角三角形的斜边,则得不到圆锥.命题②题,因这条腰必须是垂直于两底的腰.命题③对.命题④错,必须用平行于圆锥底面的平面截圆锥才行.答案 12.在正方体上任意选择4个顶点,它们可能是如下各种几何形体的四个顶点,这些几何形体是________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.解析①显然可能;②不可能;③取一个顶点处的三条棱,连接各棱端点构成的四面体;④取正方体中对面上的两条异面对角线的四个端点构成的几何体;⑤正方体ABCD-A1B1C1D1中,三棱锥D1-DBC满足条件.答案①③④⑤3.在三棱锥S-ABC中,面SAB,SBC,SAC都是以S为直角顶点的等腰直角三角形,且AB=BC=CA=2,则三棱锥S-ABC的表面积是________.解析设侧棱长为a,则2a=2,a=2,侧面积为3×12×a2=3,底面积为34×22=3,表面积为3+ 3.答案3+ 34.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为________.解析 设圆锥的底面圆半径为r ,高为h ,母线长为l ,则⎩⎪⎨⎪⎧ πrl =2π,πr 2=π,∴⎩⎪⎨⎪⎧r =1,l =2.∴h =l 2-r 2=22-12= 3.∴圆锥的体积V =13π·12·3=33π. 答案 33π5.(2012·新课标全国卷改编)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为________. 解析如图,设截面圆的圆心为O ′,M 为截面圆上任一点,则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3,∴V =43π(3)3=43π.答案 43π 6.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 答案 267.(2013·天津卷)已知一个正方体的所有顶点在一个球面上,若球的体积为9π2,则正方体的棱长为________.解析 设正方体的棱长为a ,外接球的半径为R ,由题意知43πR 3=9π2,∴R 3=278,而R =32.由于3a 2=4R 2,∴a 2=43R 2=43×⎝ ⎛⎭⎪⎫322=3,∴a = 3.答案 38.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为________.解析 如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,容易求得EG =HF =12,AG =GD =BH =HC =32,∴S △AGD =S △BHC =12×22×1=24,∴V =V E -ADG +V F -BHC +V AGD -BHC =2V E -ADG +V AGD -BHC =13×24×12×2+24×1=23. 答案 23 二、解答题 9.如图,在三棱锥P -ABC 中,AC =BC =2,∠ACB =90°,AP =BP =AB ,PC ⊥AC .(1)求证:PC ⊥AB ;(2)求点C 到平面APB 的距离. (1)证明 取AB 中点D ,连接PD ,CD .因为AP =BP ,所以PD ⊥AB , 因为AC =BC ,所以CD ⊥AB .因为PD ∩CD =D ,所以AB ⊥平面PCD .因为PC ⊂平面PCD ,所以PC ⊥AB . (2)解 设C 到平面APB 的距离为h ,则由题意,得AP =PB =AB =AC 2+BC 2=22, 所以PC =AP 2-AC 2=2.因为CD =12AB =2,PD =32PB =6, 所以PC 2+CD 2=PD 2,所以PC ⊥CD .由(1)得AB ⊥平面PCD ,于是由V C -APB =V A -PDC +V B -PDC , 得13·h ·S △APB =13AB ·S △PDC ,所以h =AB ·S △PDCS △APB=22×12×2×234×(22)2=233.故点C 到平面APB 的距离为233.10.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解 如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r ,水面半径BC 的长为3r ,则容器内水的体积为 V =V 圆锥-V 球=13π(3r )2·3r - 43πr 3=53πr 3,将球取出后,设容器中水的深度为h , 则水面圆的半径为33h ,从而容器内水的体积为 V ′=13π⎝ ⎛⎭⎪⎫33h 2h =19πh 3,由V =V ′,得h =315r .能力提升题组 (建议用时:25分钟)一、填空题1.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S -ABC 的体积为________.解析 由题意知,如图所示,在棱锥S -ABC 中,△SAC ,△SBC 都是有一个角为30°的直角三角形,其中AB =3,SC =4,所以SA =SB =23,AC =BC =2,作BD ⊥SC 于D 点,连接AD ,易证SC ⊥平面ABD ,因此V S -ABC =13×34×(3)2×4= 3. 答案 32.(2014·南京模拟)如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,AC =5,AA 1=3,M 为线段B 1B 上的一动点,则当AM +MC 1最小时,△AMC 1的面积为________.解析 如图,当AM +MC 1最小时,BM =1,所以AM 2=2,C 1M 2=8,AC 21=14,于是由余弦定理,得cos ∠AMC 1=AM 2+MC 21-AC 212AM ·MC 1=-12,所以sin ∠AMC 1=32,S △AMC 1=12×2×22×32= 3. 答案 33.如图,已知正三棱柱ABC -A 1B 1C 1的底面边长为2 cm 、高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为________cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 cm.答案 13 二、解答题4.如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D -ABC ,如图2所示.(1)求证:BC ⊥平面ACD ; (2)求几何体D -ABC 的体积.(1)证明 在图中,可得AC =BC =22, 从而AC 2+BC 2=AB 2, 故AC ⊥BC ,又平面ADC ⊥平面ABC , 平面ADC ∩平面ABC =AC , BC ⊂平面ABC , ∴BC ⊥平面ACD .(2)解 由(1)可知,BC 为三棱锥B -ACD 的高,BC =22,S △ACD =2,∴V B -ACD =13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体D -ABC 的体积为423.。
空间几何体练习题及参考答案

A空间几何体部分1、如果一个水平放置的图形的斜二测直观图是一个底面为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A. 2+1+2、半径为R 的半圆卷成一个圆锥,则它的体积为() 3R 3R 3R 3R 3、一个棱柱是正四棱柱的条件是A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C 、底面是菱形,且有一个顶点处的三条棱两两垂直D 、每个侧面都是全等矩形的四棱柱4.有一个几何体的三视图如下图所示,这个几何体应是一个A 、棱台B 、棱锥C 、棱柱D 、都不对5.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后 ,剩下的几何体的体积是( )A.23 B. 76 C. 45D. 566.长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是A 、25πB 、50πC 、125πD 、都不对 7.正方体的内切球和外接球的半径之比为()A.B.2 C. 2 D.38.在△ABC 中,AB=2,BC=1.5,∠A BC=120o,若使绕直线BC 旋转一周,则所形成的几何体的体积是A. 92π B. 72π C. 52π D. 32π9、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为A 、7B 、6C 、5D 、3 10.直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在 侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2VB 、3VC 、4VD 、5V 11、如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正 方形,EF ∥AB,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )正视图侧视图俯视图_ A _BBB 1DCC 1AEE 1D 1A 1FF 1A 、92 、5 C 、6 D 、15212、如右图所示,正三棱锥V-ABC中,D,E,F分别是VC ,VA,AC 的中点,P为VB上任意一点,则直线DE与PF 所成的角的大小是( )A6π B 2π C 3πD 随P点的变化而变化。
高考数学一轮复习《空间几何体》练习题(含答案)

高考数学一轮复习《空间几何体》练习题(含答案)一、单选题1.降水量(precipitation[amount]):从天空降落到地面上的液态或固态(经融化后)水,未经蒸发、渗透、流失,而在水平面上积聚的深度.降水量以mm 为单位,气象观测中一般取一位小数,现某地10分钟的降雨量为13.1mm ,小王在此地此时间段内用口径为10cm 的圆柱型量筒收集的雨水体积约为( )(其中π 3.14≈)A .331.0210mm ⨯B .331.0310mm ⨯C .531.0210mm ⨯D .531.0310mm ⨯2.某几何体的三视图如图所示(单位:cm ),则该几何体的表面积(单位:2cm )是( )A .()256122cm +B .()248162cm + C .()280122cm + D .()272162cm + 3.阿基米德(Archimedes ,公元前287年-公元前212年)是古希腊伟大的数学家,物理学家和天文学家,在他墓碑上刻着的一个圆柱容器里放了一个球,该球与圆柱的两个底面及侧面均相切,如图所示,则在该几何体中,圆柱表面积与球表面积的比值为( )A .32B .43C .32或23D .234.已知一个几何体的三视图如图所示,则这个几何体的表面积为( )A .33πB .2πC .3πD .4π5.某圆锥的母线长为2,高为423,其三视图如下图所示,圆锥表面上的点M 在正视图上的对应点为A ,圆锥表面上的点N 在侧视图上的对应点为B ,则在此圆锥侧面上,从M 到N 的路径中,最短路径的长度为A .2B .22C .823+D .223- 6.已知某空间几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .323B .163C .4D .87.已知正方体的六个面的中心可构成一个正八面体,现从正方体内部任取一个点,则该点落在这个正八面体内部的概率为( )A .12B .13C .16D .1128.某几何体的三视图如图所示,则该几何体的表面积为( )A .810+16B .40C .810++24D .489.棱长为1的正方体1111ABCD A B C D -中,点E 是侧面11CC B B 上的一个动点(包含边界),则下面结论正确的有( )①若点E 满足1AE B C ⊥,则动点E 的轨迹是线段;②若点E 满足130EA C ∠=,则动点E 的轨迹是椭圆的一部分;③在线段1BC 上存在点E ,使直线1A E 与CD .所成的角为30;④当E 在棱1BB 上移动时,1EC ED +的最小值是352+. A .1个 B .2个 C .3个 D .4个10.某锥体的正视图和侧视图均为如图所示的等腰三角形,则该几何体的体积最小值为A .4πB .12C .1D .211.已知四棱锥S ABCD -的所有顶点都在同一球面上,底面ABCD 是正方形且和球心O 在同一平面内,当此四棱锥体积取得最大值时,其表面积等于443+,则球O 的体积等于( )A .3223πB .1623πC .823πD .423π 12.一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为A .36B .48C .64D .72二、填空题13.如果用半径为r 的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高等于____. 14.点A ,B ,C ,D 在同一个球的球面上,3AB BC AC ==,若四面体ABCD 体积的3________.15.“方锥”,在《九章算术》卷商功中解释为正四棱锥.现有“方锥”S ABCD -,其中4AB =,SA 与平面ABCD 32,则此“方锥”的外接球表面积为________. 16.棱长为6的正方体内有一个棱长为x 的正四面体,正四面体的中心(正四面体的中心就是该四面体外接球的球心)与正方体的中心重合,且该四面体可以在正方体内任意转动,则x 的最大值为______.三、解答题17.如图,已知直三棱柱111ABC A B C ,其底面是等腰直角三角形,且22AB BC ==14AC AA ==.(1)求该几何体的表面积;(2)若把两个这样的直三棱柱拼成一个大棱柱,求拼得的棱柱表面积的最小值.18.如图是一个以111A B C为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知11112A B B C==,11190A B C∠=︒,14AA=,13BB=,12CC=,求该几何体的体积.19.如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.(单位:cm)20.如图所示,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 是矩形,2PA AB ==,2AD =,过点B 作BE ⊥AC ,交AD 于点E ,点F ,G 分别为线段PD ,DC 的中点.(1)证明:AC ⊥平面BEF ;(2)求三棱锥F -BGE 的体积.21.如图,多面体ABCDEF 中,四边形ABCD 是边长为2的菱形,AC =23,△ADE 为等腰直角三角形,∠AED =90°,平面ADE ⊥平面ABCD ,且EF //AB ,EF =1.(1)证明:AC ⊥平面BDF ;(2)若G 为棱BF 的中点,求三棱锥G —DEF 的体积.22.如图,在三棱锥-P ABC 中,2AB BC ==,22PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC =2MB ,求点C 到平面POM 的距离.23.如图,在三棱锥S -ABC 中,SA =SC ,D 为AC 的中点,SD ⊥AB .(1)证明:平面SAC ⊥平面ABC ;(2)若△BCD 是边长为3的等边三角形,点P 在棱SC 上,PC =2SP ,且932S ABC V -=,求三棱锥A -PBC 的体积.24.如图,在四棱锥P ABCD -中,底面ABCD 是边长为4的菱形,60DAB ∠=︒,7PA PD ==,O F 、分别为AD AB 、的中点,PF AC ⊥.(1)求证:面POF ⊥面ABCD ;(2)求三棱锥B PCF -的体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的结构
.判断正误
1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;()2)圆锥顶点与底面圆周上任意一点的线段是圆锥的母线;(对)
3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;()
4)圆柱的任意两条母线所在的直线是互相平行的.(对)
5)棱垂直于底面的棱柱是直棱柱(对)
6)底面是正多边形的棱柱是正棱柱
7)棱柱的侧面都是平行四边形.(对)
8)有两个面平行,其余各面都是平行四边形的几何体叫棱柱
9)有一个面是多边形,其余各面都是三角形的几何体叫棱锥
10)由五个面围成的多面体一定是四棱锥
11 )棱台各侧棱的延长线交于一点(对)
12)棱柱的侧棱都相等,侧面都是全等的平行四边形;
13 )存在每个面都是直角三角形的四面体;(对)
14 )棱台的侧棱延长后交于一点.(对)15)棱柱的侧面可以是三角形
16 )正方体和长方体都是特殊的四棱柱(对)
17)棱柱的各条棱都相等18)所有的几何体的表面都展成平面图形
19 )有两个平面互相平行,其余各面都是四边形的多面体一定是棱柱;
20)有一个面是多边形,其余各面都是三角形的多面体一定是棱锥;
21)用一个面去截棱锥,底面与截面之间的部分叫棱台;
22)侧面都是长方形的棱柱叫长方体.
23 )多面体至少有四个面(对)
24)有两个侧面是矩形的棱柱是直棱柱;
25)各侧面都是正方形的棱柱一定是正棱柱;
26)一个三棱锥四个面可以都为直角三角形.对)
(27)有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的
几何体叫棱柱(对)
(28)直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
(29)以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;
(30 )一个平面截圆锥,得到一个圆锥和一个圆台.
(31)两底面互相平行,其余各面都是梯形,侧棱延长线交于一点的几何体是棱台(对)(32)如图,在透明塑料制成的长方体ABCD- A1B1C1D1容器内装进一些水,将容器底面一边BC固定于底面上,再将容器倾斜,随着倾斜度的不同,有下列三个说法:①水的形状
始终是棱柱形状;②水面形成的四边形EFGH的面积不改变;③当E€ AA1时,AE+BF是定值•其中正确说法是.(写出所以正确说法的序号)
【答案】①③
(33)若正棱锥底面边长与侧棱长相等,则该棱锥一定不是()
A.三棱锥
B.四棱锥
C.五棱锥
D.六棱锥
【答案】D
二.多面体和旋转体表面上的最短距离问题
1•已知侧棱长为2的正三棱锥S- ABC如图所示,其侧面是顶角为20。
的等腰三角形,一只蚂蚁从点A出发,围绕棱锥侧面爬行两周后又回到点A,则蚂蚁爬行的最短路程为—.
2.如图所示,在三棱柱ABC- A1B1C1中,AA i丄底面A i BiG,底面为直角三角形,
/ ACB=90 , AC=2 BC=1, CC=E, P 是BC 上一动点,则A i P+PC的最小值是
3.如图:已知正三棱锥P-ABC,侧棱PA PB, PC的长为2,且/APB=30, E,F
段BB1 上的一动点,则当AM MC1最小时,△ AMC1的面积为_____________ 。
5. 如图,三棱柱ABR DCC1 中,BC 面ABB1, ABB1 90 , AB 4 , BC 2 ,
CG 2,棱CD上有一动点P,贝U APG周长的最小值为
【答案】2V3
4.如图,直三棱柱ABC A1B1C1中,AB 1 , BC 2 , AC 5 , AA1 3 , M 为线【答案】3
A. 4.2 2.6
B. 4.526
C. 3_2 2 6
D. ^2 4 6
【答案】A
6. 如图,长方体ABCD- A1B1C1D1中,AB=3, BC=4, CG=5,则沿着长方体表面从
A到C i的最短路线长为
【答案】■
7. 如图,在直三棱柱ABC- A1B1C1 中,AB=BC=t , BBi=2,Z ABC=90 , E、F
分别为AA i、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为.
B
【答案】■:
8. 长方体ABCD- A i B i C i D i中,AB=2, BC=3 AA i=5,则一只小虫从A点沿长方体的表面爬到C i点的最短距离是_.
【答案】’“
三.截面问题
1•用一个平面截正方体和正四面体,给出下列结论:
①正方体的截面不可能是直角三角形;
②正四面体的截面不可能是直角三角形;
③正方体的截面可能是直角梯形;
④若正四面体的截面是梯形,则一定是等腰梯形.
其中,所有正确结论的序号是()
A.②③
B.①②④
C.①③
D.①④
【答案】D
2用一个平面去截正方体,则截面不可能是()
A.正三角形
B.正方形C正五边形 D.正六边形
【答案】C
3•正方体ABCD A I B I C I D I , P , Q , R为别是AB , AD , B i C i的中点,则正方体过P , Q ,
R三点的截面图形是().
A.三角形
B.四边形
C.五边形
D.六边形
【答案】D
4•在如图所示的棱长为2的正方体ABCDA i BiGD i中,作与平面ACD平行的截面,则截得的 ;截得的
平面图形中,面积最大的值是
【答案】2 .3 ; 3 3
5•如图,正方体ABCDA i B i C i D i的棱长为1, P为BC的中点,Q为线段CG上的动点,过点A,
P, Q的平面截该正方体所得截面记为S,则下列命题正确的是________________
1
①当0 CQ 时,S为四边形;
2
3
②当CQ —时,S为五边形;
4
3
③当CQ 1时,S为六边形;
4
A . 1 cm B. 2 cm C.
cm
④ 当CQ 1时,S 为菱形.
B
c r>
【答案】D
7.—个棱柱的底面是正六边形,侧面都是正方形,用至少过该棱柱三个顶点(不在同一侧面 或同一底面内)的平面去截这个棱柱,所得截面的形状不可以是 ()
(A )等腰三角形 (B )等腰梯形 (C )五边形 (D )正六边形
【答案】D
8.设正方体ABCD AiB i C i D i 的棱长为2, 为过直线BD i 的平面,贝U
截该正方体的截
面面积的取值范围是 _________ . 【答案】 2,2 6
9.在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一 条侧棱和高作截面,正确的截面图形是(
)
四. 简单计算问题
1.
用一个半径为2cm 的半圆围成一个圆锥,则圆锥底面圆的半径为( 【答案】 ①②④
6•—个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为
(
【答案】B
【答案】A
2•已知圆锥的侧面展开图是一个半径为2的半圆,则这个圆锥的高是 _____ .
【答案】.:
3•设正三棱台的上下底面的边长分别为2cm和5cm,侧棱长为5cm,求这个棱台的高.
【答案】.■■:
4•把一个圆锥截成圆台,已知圆台的上、下底面半径之比为1: 2,母线长为6cm,则圆锥的
母线长为____ cm.
【答案】12
5. 如图所示的正四棱台的上底面边长为2,下底面边长为8,高为3.2,则它的侧棱长
为_____ .
【答案】6
6. 若圆锥的侧面积是底面积的2倍,则其母线与轴所成角的大小是
【答案】30°
7. 半径为R的半圆卷成底面最大的圆锥,所得圆锥的高为()
一、.3 —、..2
A. R
B. R
C. -.2 R
D. R
【答案】B
22。
