离散数学试卷及答案一
离散数学考试模拟试题及详细参考答案共四套

离散模拟答案11命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.一、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))↔(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)∀x∃y(x+y=4)b)∃y∀x (x+y=4)3.求∀x(F(x)→G(x))→(∃xF(x)→∃xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A⋃B)-C=(A-B) ⋃(A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)二、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→⌝F)→⌝C, B→(A∧⌝S)⇒B→Eb)∀x(P(x)→⌝Q(x)), ∀x(Q(x)∨R(x)),∃x⌝R(x) ⇒∃x⌝P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠∅且B≠∅,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
离散数学试题及答案

离散数学试题及答案一、选择题1. 设A、B、C为三个集合,下列哪个式子是成立的?A) \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)B) \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)C) \(A \cup (B \cup C) = (A \cup B) \cup (A \cup C)\)答案:B2. 对于一个有n个元素的集合S,S的幂集中包含多少个元素?A) \(n\)B) \(2^n\)C) \(2 \times n\)答案:B二、判断题1. 对于两个关系R和S,若S是自反的,则R ∩ S也是自反的。
答案:错误2. 若一个关系R是反对称的,则R一定是反自反的。
答案:正确三、填空题1. 有一个集合A,其中包含元素1、2、3、4和5,求集合A的幂集的大小。
答案:322. 设a和b是实数,若a \(\neq\) b,则a和b之间的关系是\(\__\_\)关系。
答案:不等四、解答题1. 证明:如果关系R是自反且传递的,则R一定是反自反的。
解答:假设关系R是自反的且传递的,即对于集合A中的任意元素x,都有(x, x) ∈ R,并且当(x, y) ∈ R和(y, z) ∈ R时,(x, z) ∈ R。
反证法:假设R不是反自反的,即存在一个元素a∈A,使得(a, a) ∉ R。
由于R是自反的,所以(a, a) ∈ R,与假设矛盾。
因此,R一定是反自反的。
答案完整证明了该结论。
2. 已知集合A={1, 2, 3},集合B={2, 3, 4},求集合A和B的笛卡尔积。
解答:集合A和B的笛卡尔积定义为{(a, b) | a∈A,b∈B}。
所以,集合A和B的笛卡尔积为{(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)}。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1, 2, 3, 4}中,子集{1, 2}的补集是()。
A. {3, 4}B. {1, 3, 4}C. {2, 3, 4}D. {1, 2, 3, 4}答案:A2. 命题“若x > 0,则x² > 0”的逆否命题是()。
A. 若x² ≤ 0,则x ≤ 0B. 若x² > 0,则x > 0C. 若x ≤ 0,则x² ≤ 0D. 若x² ≤ 0,则x < 0答案:C3. 函数f(x) = x² + 2x + 1的值域是()。
A. {x | x ≥ 0}B. {x | x ≥ 1}C. {x | x ≥ 2}D. {x | x ≥ -1}答案:B4. 以下哪个图是无向图()。
A. 有向图B. 无向图C. 有向树D. 无向树答案:B5. 以下哪个图是二分图()。
A. 完全图B. 非完全图C. 任意两个顶点都相连的图D. 任意两个顶点都不相连的图答案:C6. 以下哪个是哈密顿回路()。
A. 经过每个顶点恰好一次的回路B. 经过每个顶点至少一次的回路C. 经过每个顶点恰好两次的回路D. 经过每个顶点至少两次的回路答案:A7. 以下哪个是欧拉回路()。
A. 经过每条边恰好一次的回路B. 经过每条边至少一次的回路C. 经过每条边恰好两次的回路D. 经过每条边至少两次的回路答案:A8. 以下哪个是二进制数()。
A. 1010B. 1020C. 1102D. 1120答案:A9. 以下哪个是格雷码()。
A. 0101B. 1010C. 1100D. 1110答案:B10. 以下哪个是素数()。
A. 4B. 6C. 7D. 8答案:C二、填空题(每题2分,共20分)11. 集合{1, 2, 3}与{2, 3, 4}的交集是______。
答案:{2, 3}12. 命题“若x > 0,则x² > 0”的逆命题是:若x² > 0,则______。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中,元素(2,4)是否存在?A. 存在B. 不存在C. 无法确定D. 以上都不对2. 函数f: A→B是单射的,当且仅当对于任意的a1, a2∈A,若f(a1)=f(a2),则a1=a2。
A. 正确B. 错误C. 无法确定D. 以上都不对3. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 有些狗不会游泳。
C. 所有的狗都不会游泳。
D. 以上都不是真命题。
4. 如果p蕴含q为假,那么p和q的真值可以是?A. p为真,q为假B. p为假,q为真C. p为真,q为真D. p为假,q为假5. 以下哪个图是连通图?A. 一个孤立点B. 两个不相连的点C. 一个包含三个点且每对点都相连的图D. 以上都不是连通图6. 在有向图中,如果存在从顶点u到顶点v的路径,那么称v是u的后继顶点。
A. 正确B. 错误C. 无法确定D. 以上都不对7. 以下哪个等价关系是集合{1,2,3}上的?A. {(1,1), (2,2), (3,3)}B. {(1,2), (2,1), (2,2), (3,3)}C. {(1,1), (2,3), (3,2), (3,3)}D. {(1,1), (2,2), (3,3), (1,3)}8. 以下哪个命题是假命题?A. 所有的鸟都有羽毛。
B. 有些鸟不会飞。
C. 所有的哺乳动物都是温血动物。
D. 以上都不是假命题。
9. 在图论中,一个图的生成树是包含图中所有顶点的最小连通子图。
A. 正确B. 错误C. 无法确定D. 以上都不对10. 如果命题p和q互为逆否命题,那么它们具有相同的真值。
A. 正确B. 错误C. 无法确定D. 以上都不对二、填空题(每题2分,共20分)1. 集合{1,2,3}和{3,4,5}的并集是________。
2. 函数f: A→B是满射的,当且仅当对于任意的b∈B,存在a∈A,使得f(a)=________。
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学考试题目及答案

离散数学考试题目及答案一、单项选择题(每题2分,共20分)1. 集合A={1,2,3},集合B={3,4,5},则A∩B的元素个数为:A. 0B. 1C. 2D. 3答案:B2. 函数f: X→Y是一个双射,当且仅当:A. f是单射且满射B. f是单射C. f是满射D. f是双射答案:A3. 命题p: "x是偶数",命题q: "x是3的倍数",下列逻辑运算中,表示"x是6的倍数"的是:A. p∧qB. p∨qC. ¬p∧¬qD. ¬p∨¬q答案:A4. 有向图G中,若存在从顶点u到顶点v的有向路径,则称顶点u可达顶点v。
若G中任意两个顶点都相互可达,则称G为:A. 强连通图B. 弱连通图C. 无向图D. 有向无环图答案:A5. 在二进制数系统中,下列哪个数的值最大?A. 1010B. 1100C. 1110D. 1101答案:C6. 布尔代数中,逻辑或运算符表示为:A. ∧B. ∨C. ¬D. →答案:B7. 有限自动机中,状态q0是初始状态,状态q1是接受状态。
若存在从q0到q1的ε-转移,则该自动机:A. 仅在输入为空时接受B. 仅在输入非空时接受C. 无论输入为何都接受D. 无法确定是否接受答案:C8. 命题逻辑中,若命题p和q都为真,则p∧q的真值是:A. 真B. 假C. 可能为真,也可能为假D. 无法确定答案:A9. 集合{1,2,3}的子集个数为:A. 4B. 6C. 7D. 8答案:D10. 若关系R在集合A上是自反的,则对于A中的任意元素a,有:A. (a,a)∈RB. (a,a)∉RC. (a,a)是R的自反对D. (a,a)不是R的自反对答案:A二、填空题(每题3分,共15分)1. 集合A={1,2,3}的幂集包含__个元素。
答案:82. 若函数f: X→Y是满射,则对于Y中的任意元素y,至少存在X中的一个元素x,使得f(x)=__。
大学离散数学试卷一及答案

大学离散数学试卷一及答案一、单项选择题(本大题共10小题,每小题2分,共20分)1.下列不是命题的是[ C ]。
A.7能被3整除.B.5是素数当且仅当太阳从西边升起.C.x加7小于0.D.华东交通大学位于南昌北区.2. 设p:王平努力学习,q:王平取得好成绩,命题“除非王平努力学习,否则他不能取得好成绩”的符号化形式为[ D ]。
A. p→qB. ⌝p→qC. ⌝q→pD. q→p3. 下面4个推理定律中,不正确的为[ D ]。
A.A=>(A∨B) (附加律)B. (A∨B)∧⌝A=>B (析取三段论)C. (A→B)∧A=>B (假言推理)D. (A→B)∧⌝B=>A (拒取式)4. 设解释I如下,个体域D={1,2},F(1,1)=(2,2)=0,F(1,2)=F(2,1)=1,在解释I下,下列公式中真值为1的是[ A ]。
A.∀x ∃yF(x,y)B. ∃x∀yF(x,y)C. ∀x∀yF(x,y)D. ⌝∃x∃yF(x,y)5. 下列四个命题中哪一个为真?[ D ]。
A. ∅∈∅B. ∅∈{a}C. ∅∈{{∅}}D. ∅⊆∅6. 设S={a,b,c,d},R={<a,a>,<b,b>,<d,d>},则R的性质是[ B ]。
A.自反、对称、传递的B. 对称、反对称、传递的C.自反、对称、反对称的D. 只有对称性7.设A={a,b,c},则下列是集合A的划分的是[ D ]。
A.{{b,c},{c}}B.{{a,b},{a,c}}C.{{a,b},c}D.{{a},{b,c}}8. 设集合})关于普通数的乘法,不正确的有[ C ]。
ab+=aQ∈2,{)2(QbA. 结合律成立B. 有幺元C. 任意元素有逆元D. 交换律成立9.设A是非空集合,P(A)是A的幂集,∩是集合交运算,则代数系统〈P(A),∩〉的幺元是[ C ]。
A. P(A)B. φC. AD. E10.下列四组数据中,不能成为任何4阶无向简单图的度数序列的为[ C ]。
离散数学试卷及答案
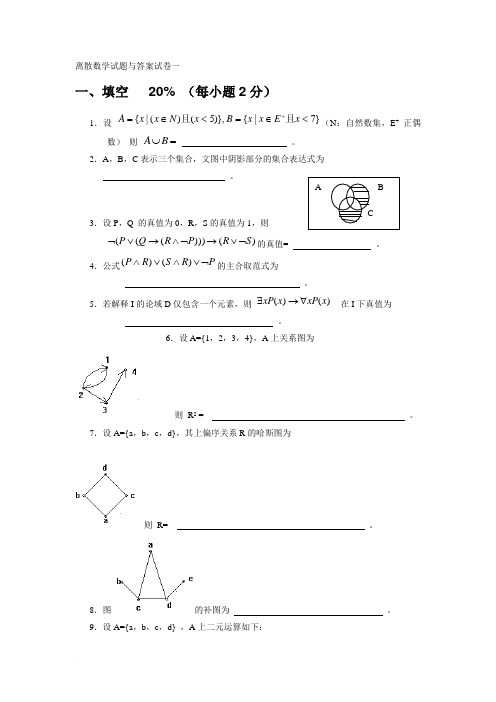
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有()个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
5、设A={1,2,3,4},P(A)(A的幂集)上规定二元系如下t st spR=∈=则P(A)/ R=()<A∧>)(||||}s({t,,|A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
大学《离散数学》期末考试试卷及答案(1)

大学《离散数学》期末考试试卷及答案(1)一、选择题1. 离散数学的主要研究对象是()。
A. 连续的数学结构B. 有限的数学结构C. 数学的综合应用D. 数学的哲学思考2. 命题逻辑是离散数学的一个重要组成部分,它主要研究()。
A. 命题之间的真假关系B. 变量之间的关系C. 函数之间的关系D. 集合之间的关系3. 集合的基本运算包括()。
A. 并、交、差、补B. 加、减、乘、除C. 包含、相等、不等、自反D. 大于、小于、等于、不等于二、填空题1. 若集合A={m|2m-1>3},则A中的元素为______。
2. 有一个集合A={1,2,3},则集合A的幂集为______。
3. 若命题p为真,命题q为假,则复合命题“p∧q”的真值为______。
三、解答题1. 请写出离散数学中常用的数学符号及其含义。
2. 请解释命题逻辑中的充分必要条件及其符号表示,并给出一个例子。
3. 请定义集合的笛卡尔积,并给出两个集合进行笛卡尔积运算的例子。
四、问答题1. 离散数学在计算机科学中有着重要的应用,请列举三个与计算机科学相关的离散数学应用领域并简要介绍。
2. 请简要解释归纳法在离散数学中的作用,并给出一个使用归纳法证明的例子。
3. 什么是有向图?请给出一个有向图的例子,并解释该图中的关系。
参考答案:一、选择题1. B2. A3. A二、填空题1. A={m|2m-1>3}2. {{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}3. 假三、解答题1. 常用数学符号及含义:- ∪:并,表示集合的合并操作。
- ∩:交,表示集合的交集操作。
- ∖:差,表示减去一个集合中的元素。
- ⊆:包含,表示一个集合包含于另一个集合。
- =:相等,表示两个集合具有相同的元素。
2. 充分必要条件是指一个命题的成立与另一个命题的成立互为必要条件,若A是B的充分必要条件,那么当A成立时B一定成立,且当A不成立时B也一定不成立。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个符号表示属于关系?A. ∈B. ∉C. ⊆D. ∩答案:A2. 对于命题逻辑,下列哪个是真值表的表示方法?A. 真值表B. 逻辑图C. 布尔代数D. 集合论答案:A3. 以下哪个是图论中的基本单位?A. 点B. 线C. 面D. 体答案:A4. 函数f(x) = x^2 + 3x + 2在x=-1处的值是:A. 0C. 4D. 6答案:C5. 在关系数据库中,以下哪个操作用于删除表中的记录?A. SELECTB. INSERTC. UPDATED. DELETE答案:D6. 以下哪个是离散数学中的归纳法证明方法?A. 直接证明法B. 反证法C. 归纳法D. 构造性证明法答案:C7. 在逻辑中,以下哪个是析取命题?A. P ∧ QB. P ∨ QC. ¬PD. P → Q答案:B8. 以下哪个是图的遍历算法?B. BFSC. Dijkstra算法D. Floyd算法答案:B9. 在集合{1, 2, 3}上,以下哪个是幂集?A. {∅, {1}}B. {1, 2}C. {1, 2, 3}D. 所有选项答案:D10. 以下哪个是递归算法的特点?A. 不能自我调用B. 必须有一个终止条件C. 必须有一个基本情况D. 所有选项答案:D二、填空题(每空2分,共20分)1. 在离散数学中,_________ 表示一个命题的否定。
答案:¬P2. 如果集合A和集合B的交集为空集,那么A和B被称为_________。
答案:不相交3. 一个函数f: A → B是_________,如果对于集合B中的每个元素b,集合A中至少有一个元素a与之对应。
答案:满射4. 在图论中,一个没有环的连通图被称为_________。
答案:树5. 一个命题逻辑公式是_________,如果它在所有可能的真值分配下都是真的。
答案:重言式6. 一个关系R在集合A上是_________,如果对于A中的任意两个元素a和b,如果(a, b)属于R,则(b, a)也属于R。
《离散数学》期末练习题考试卷和答案

a , b, c , d , e, f , g,那么 所对应的 19. 设集合 A a , b , c , d , e , f , g , A 上有一个划分
等价关系 R 应有( )个序偶。 )。
20. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
等价关系 R 应有( )个序偶。 )。
25. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
26. 一个(
)称为布尔代数。
27.P Q P Q 的主析取范式是
。(写出一般
5
表示形式即可) 28.设集合 A a , b , c , d , R 是 A 上的二元关系,且 R a , b , b , a , b , c , c , d , a , c , 则 R 的传递闭包 t R 。
C. x x是正整数, x 5
D. x x是有理数, x 5
。
6.下面有关集合之间的包含和属于关系的说法,正确的是 Ⅰ. Ⅲ.
Ⅱ. , ,
Ⅳ.
a, b a, b, a, b
B.Ⅰ和Ⅲ
a, b a, b, a, b, c
二、填空题 1.设 A 为非空集合,且 A n ,则 A 上不同的二元关系的个数为 为 。 时, P Q 的真值为 1。 , A 上不同的映射的个数
2.设 P 、 Q 为两个命题,当且仅当
3. 在运算表中的空白处填入适当符号,使 a , b , c, * 成为群。 *
a a
a b c
4. 当 n 为 数时, K n n 3 必为欧拉图。
国家开放大学电大本科《离散数学》2024-2025期末试题及答案(试卷号:1009)

国家开放大学电大本科《离散数学》2024-2025期末试题及答案(试卷号:1009)一、单项选择题(每小题3分,本题共16分)若集合A = {1,2,3,4},则下列表述不正确的是( ).A.{2,3)€AB.AU{1,2,3,4}C. <1,2,3,4)QAD. 16A2.若无向图G的结点度数之和为20,则G的边数为( ).A.10B. 20C. 30D. 53.无向图G是棵树,结点数为10,则G的边数为( ).A. 5B. 10C.9D. 114.设A(x):x是人,B(x):x是学生,则命题“有的人是学生”可符号化为( )•A.Vx)(A(x)-*B(x»B.(3x)(A(x)AB(x))C.(Vx)(A(x)AB(x»D.-«(3x)(A(x)A -B(x»5.下面的推理正确的是( ).A.(l)(Vx)F(x)->G(x) 前提引入(2)F(>-)-*G(y) US(1).B.(1)( 3 x)F(x)-*G(x) 前提引入(2)F(y)-*G(y) US(1),C.(l)(3x)(F(x)->G(x»前提引入(2)F(y)-*G(x) ES(1).D.(l)(3x)(F(x)-*G(x)) 前提引入(2)F(y)-*G(y) ESQ).二、填空题(每小题3分,本题共15分)6.设A = {1,2),H = {1,2,3},则A到B上不同的函数个数为________________ .7.有&个结点的无向完全图的边数为 ____________ .8.若无向图G中存在欧拉路但不存在欧拉回路,则G的奇数度数的结点有________ 个.9.设G是有10个结点的无向连通图,结点的度数之和为30,则从G中删去条边后使之变成树.10.设个体域£> = {1,2,3,4},则谓词公式(*)人(了)消去量词后的等值式为三、逻辑公式翻译(每小题6分,本息共12分)11.将语句“昨天下甬“翻译成命题公式.12.将语句“小王今天上午或者去看电彩或者去打球”翻译成命JS公式.四、判断说明题(判断各题正误,并说明理由.每小题7分,本黑共14分)13.存在集合A与B,使得A6B与AUB同时成立.14.完全图K<是平面图.五、计算题(每小题12分,本题共36分)15.设偏序集VA,R>的哈斯图如下,B为A的子集,其中B = 试(1)写出R的关系表达式;(2)画出关系R的关系图;(3)求出B的最大元、极大元、上界.16.设图G — <V,E>,V={vj f v it v t,Vi»v s)»(v2, v3)»(v3»vs)}»试(1)画出G的图形表示;(2)写出其邻接矩阵;(3)求出每个结点的度数;(4)画出图G的补图的图形,17.求P TQ代R)的合取范式与主合取范式.六、证明题(本题共8分)18.设A.B是任意集合,试证明:若AXA=BXB,^ A = B.M答杖松标准(仅辩者)一、单项选择题(每小题3分,本题共15分)1. A2. A3. C4.B5. D二、填空题(每小题3分,本题共]5分)6.97.”3 — 1)/2(或庆)8.210. A(l) VA(2) V A(3) V A(4)三、 逻辑公式翻译(每小题6分,本题共】2分)H,设P :昨天下雨. 则命题公式为:P ,12. 设P :小王今天上午去看电影 Q :小王今天上午去打球 则命题公式为:r (PiQ ). 或者(rPAQ )V 〈PA rQ )四、 判断说明题(每小题7分,本题共14分)13. 正确.例:设 A = {a} t H — {a,{a}) 则有且ACI3.说明:举出符合条件的例均给分. 14. 正确.完全图K 〈是平面图, 如K,可以如下图示嵌入平面.(7分)五、计算题(每小题12分,本题共36分)15. (l )R = {Va ,a>,Vb,Q>,Vc,c>,Vd,d>・Va0>・Va ・c>,V&,d>,VQ,d >}. (4 分)(2)关系图(8分)(3)集合B 无最大元,极大元为6与c.无上界. 16, 解: (1)关系图(2分) (6分)(2分)(6分)(3分) (517. P TQAR) 5PV(QAR) 0(rPVQ 〉A(rPVR)合取范式<=>(-PVQ)V(K A rR)A(rPVR) 0("VQ)V(& A rR)A(" VR)V(QA -Q)D(rPVQVR)A(rPVQVA("VR VQ) A(-、PVR V -Q) c=>(-PVQV7?)A(-'PVQV-R)A(-PV-QVR) 主合取范式 六、证明题(本意共8分)18. 证明:V2(2)邻接矩阵bioir 101001001 1 00 0(6分)(3) deg(vi)=,3deg(v t )—2 <ieg(v 3)~2 deg顷)=1 deg(v s )=2 (4) 补图(9分)(】2分)(2分) (5分)(7分〉设x€A,则Vx,x>€AXA,(1 分)因AXA = BXB,故V X,X>€BXB,则有xGB, (3 分)因此AGB. (5分)设xQB,则Vx,x>€BXB,(6 分)因AXA-BXB,故Vx,x>eAXA,则有因此BWA. (7 分)故得A=B. (8分)。
《离散数学》试题及答案

一、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A - B={3} ; ρ(A) - ρ(B)={3},{1,3},{2,3},{1,2,3}} .2. 设有限集合A, |A| = n, 则|ρ(A×A)| = 22n.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是α1= {(a,1), (b,1)}, α2= {(a,2), (b,2)},α3= {(a,1), (b,2)}, α4= {(a,2), (b,1)}, 其中双射的是α3, α4 .4. 已知命题公式G=⌝(P→Q)∧R,则G的主析取范式是(P∧⌝Q∧R)5.设G是完全二叉树,G有7个点,其中4个叶点,则G的总度数为12,分枝点数为3.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A⋂B={4} ; A⋃B={1,2,3,4};A-B={1,2} .7.设R是集合A上的等价关系,则R所具有的关系的三个特性是自反性, 对称性传递性.8. 设命题公式G=⌝(P→(Q∧R)),则使公式G为真的解释有(1, 0, 0), (1, 0, 1),(1, 1, 0)9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)}, R2 = {(2,1),(3,2),(4,3)}, 则R1∙R2 ={(1,3),(2,2),(3,1)} , R2∙R1 = {(2,4),(3,3),(4,2)} _R12 ={(2,2),(3,3).10. 设有限集A, B,|A| = m, |B| = n, 则| |ρ(A⨯B)| = .11设A,B,R是三个集合,其中R是实数集,A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B = -1<=x<0 , B-A = {x | 1 < x < 2, x∈R} ,A∩B ={x | 0≤x≤1, x∈R} , .13.设集合A={2, 3, 4, 5, 6},R是A上的整除关系,则R以集合形式(列举法)记为{(2, 2),(2, 4),(2, 6),(3, 3),(3, 6),(4, 4),(5, 5),(6, 6)} .14. 设一阶逻辑公式G = ∀xP(x)→∃xQ(x),则G的前束范式是∃x(⌝P(x)∨Q(x)) .15.设G是具有8个顶点的树,则G中增加21 条边才能把G变成完全图。
离散数学考试试题及答案

离散数学考试试题及答案一、单项选择题(每题5分,共20分)1. 在离散数学中,以下哪个概念不是布尔代数的基本元素?A. 逻辑与B. 逻辑或C. 逻辑非D. 逻辑异或答案:D2. 下列哪个命题不是命题逻辑中的命题?A. 所有学生都是勤奋的B. 有些学生是勤奋的C. 学生是勤奋的D. 勤奋的学生答案:D3. 在集合论中,以下哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 以下哪个图不是无向图?A. 简单图B. 完全图C. 有向图D. 多重图答案:C二、填空题(每题5分,共20分)1. 如果一个命题的逆否命题为真,则原命题的________为真。
答案:逆命题2. 在图论中,如果一个图的任意两个顶点都由一条边连接,则称这个图为________图。
答案:完全3. 一个集合的幂集是指包含该集合的所有________的集合。
答案:子集4. 如果一个函数的定义域和值域都是有限集合,那么这个函数被称为________函数。
答案:有限三、简答题(每题10分,共30分)1. 请简述什么是图的欧拉路径。
答案:欧拉路径是一条通过图中每条边恰好一次的路径。
2. 解释什么是二元关系,并给出一个例子。
答案:二元关系是指定义在两个集合之间的关系,它将第一个集合中的元素与第二个集合中的元素联系起来。
例如,小于关系就是一个二元关系。
3. 请说明什么是递归函数,并给出一个简单的例子。
答案:递归函数是一种通过自身定义来计算函数值的函数。
例如,阶乘函数就是一个递归函数,定义为:n! = n * (n-1)!,其中n! = 1当n=0时。
四、计算题(每题10分,共30分)1. 计算以下逻辑表达式:(P ∧ Q) ∨ ¬R答案:首先计算P ∧ Q,然后计算¬R,最后计算两者的逻辑或。
2. 给定集合A = {1, 2, 3},B = {2, 3, 4},求A ∪ B。
答案:A ∪ B = {1, 2, 3, 4}3. 已知函数f(x) = 2x + 3,求f(5)。
《离散数学》试卷及答案精选全文完整版

H(x):x是身体健康的;
S(x):x是科学家
C(x):x是事业获得成功的人
置换规则。
3、设集合|A|=101,S ,且|S|为奇数,则这样的S有2101/2或2100个。
4、设mi是公式G的的主析取范式中的一个极小项,则mi的对偶式不一定是(填“是”/“不是”/“不一定是” ) G的主合取范式中的一个极大项。
5、由3个元素组成的有限集上所有的等价关系有5个
6、给定解释I如下: (1) Di:={2,3}; (2) a=3; (3) 函数f(x)为f(2)=2,f(3)=3; (4) 谓词:F(x)为F(2):=1,F(3):=0;G(x,y)为当i=j时,G(i,j):=1;当i≠j时,G(i,j):=0;其中i,j=2,3;
ac>0并且cu>0
若u>0,则c>0,a>0,因此有ac>0;
若u<0,则c<0,a<0, 也有ac>0;
因此有(a+bi)R(u+vi)
所以R在C*是传递的。所以R是C*上的等价关系。
2、在一阶逻辑自然推理系统F中,构造下面推理的证明。个体域是人的集合。
“每位科学家都是勤奋的,每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以,存在着事业获得成功的人。”(15分)
2.设A={1,2,3…10},定义A上的二元关系R={<x,y>|x,y∈A∩x+y=10},试讨论R关于关系的五个方面的性质并说明理由(5分)
解答:R={<1,9>,<9,1>,<2,8>,<8, 2 >,<3,7>,<7,3>,<4,6>,<6, 4 >,<5, 5 >}
离散数学试题及答案解析

离散数学试题及答案解析一、单项选择题(每题2分,共10分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B等于:A. {1,2,3}B. {2,3}C. {1,4}D. {3,4}答案:B2. 以下哪个命题是真命题?A. 所有天鹅都是白色的。
B. 有些天鹅不是白色的。
C. 所有天鹅都不是白色的。
D. 没有天鹅是白色的。
答案:B3. 函数f: A→B的定义域是A,值域是B,那么f是:A. 单射B. 满射C. 双射D. 既不是单射也不是满射答案:D4. 逻辑表达式(p∧q)→r的逆否命题是:A. ¬r→¬(p∧q)B. ¬r→¬p∨¬qC. r→(p∧q)D. ¬r∧¬p∨¬q答案:B5. 有限集合A={a, b, c}的子集个数为:A. 3B. 4C. 7D. 8答案:D二、填空题(每题3分,共15分)1. 如果一个关系R在集合A上是自反的,那么对于A中的每一个元素a,都有___________。
答案:(a, a)∈R2. 命题逻辑中,合取(AND)的逻辑运算符用___________表示。
答案:∧3. 在图论中,一个连通图是指图中任意两个顶点之间都存在___________。
答案:路径4. 集合{1, 2, 3}的幂集包含___________个元素。
答案:85. 如果一个函数f是单射,那么对于任意的x1, x2∈A,如果f(x1)=f(x2),则x1___________x2。
答案:=三、解答题(每题10分,共20分)1. 证明:若p是q的充分条件,q是r的充分条件,则p是r的充分条件。
证明:假设p成立,由于p是q的充分条件,所以q成立。
又因为q是r的充分条件,所以r成立。
因此,p成立可以推出r成立,即p是r的充分条件。
2. 给定一个有向图,其中包含顶点A、B、C、D,边为(A, B),(B, C),(C, D),(D, A),(A, C)。
离散数学本科试题及答案

离散数学本科试题及答案一、选择题(每题5分,共20分)1. 在集合论中,空集的定义是:A. 包含所有集合的集合B. 不包含任何元素的集合C. 包含所有非空集合的集合D. 包含所有有限集合的集合答案:B2. 在逻辑运算中,非运算的符号是:A. ∧B. ∨C. ¬D. →答案:C3. 以下哪个选项是图的邻接矩阵表示法?A. 邻接表B. 顶点列表C. 边列表D. 所有选项都是答案:A4. 以下哪个命题是真命题?A. 所有的偶数都是整数B. 所有的整数都是偶数C. 所有的奇数都是整数D. 所有的整数都是奇数答案:A二、填空题(每题5分,共20分)1. 在布尔代数中,逻辑与运算的符号是________。
答案:∧2. 如果一个图是无向图且任意两个顶点都相连,则称这个图是________。
答案:完全图3. 在关系数据库中,关系模式的属性名集合称为________。
答案:关系模式4. 一个命题的逆否命题与其原命题的________是相同的。
答案:真假性三、简答题(每题10分,共30分)1. 描述什么是二元关系,并举例说明。
答案:二元关系是定义在两个集合上的一个关系,它由有序对组成,每个有序对的第一个元素来自第一个集合,第二个元素来自第二个集合。
例如,小于关系是实数集上的一个二元关系,因为对于任意两个实数a和b,如果a小于b,那么有序对(a, b)属于这个关系。
2. 解释什么是图的哈密顿回路,并给出一个例子。
答案:图的哈密顿回路是一条通过图中每个顶点恰好一次的闭合路径。
例如,在一个五边形的顶点上,可以画出一条哈密顿回路,即从任一顶点出发,依次经过其他顶点,最后回到起始顶点。
3. 什么是正规文法?请给出一个例子。
答案:正规文法是一种形式文法,它能够生成正规集合,即可以被有限自动机接受的字符串集合。
例如,正规文法可以定义为:S -> aSb| ε,其中S是开始符号,a和b是字母,ε表示空字符串。
这个文法生成的字符串集合是所有长度为偶数的字符串,其中a和b交替出现。
离散数学期末考试试题及答案

离散数学期末考试试题及答案一、选择题(每题5分,共25分)1. 设A={1,2,3,4,5},B={2,3,5,7,11},则A∩B等于()A. {1,2,3,4,5}B. {2,3,5}C. {1,4}D. {2,3,5,7,11}2. 下面哪一个图是连通图?()A. 无向图B. 有向图C. 平面图D. 连通图3. 若一个图G有n个顶点,e条边,则以下哪个条件是图G 为连通图的必要条件?()A. n ≥ eB. n ≤ eC. n = eD. n + e = 24. 在一个简单图中,若每个顶点的度数都等于n-1,则该图是()A. 无向图B. 有向图C. 完全图D. 平面图5. 以下哪一个命题是正确的?()A. 每个图都有欧拉回路B. 每个连通图都有哈密顿回路C. 每个图都有哈密顿路径D. 每个连通图都有欧拉路径二、填空题(每题5分,共25分)6. 设A={a,b,c},B={1,2,3},则A×B的结果是______。
7. 一个连通图的生成树包含______条边。
8. 在一个n阶完全图中,任意两个不同顶点之间的距离是______。
9. 一个图G的顶点集为V,边集为E,则图G的邻接矩阵表示为______。
10. 在一个简单图中,若每个顶点的度数都等于n-1,则该图的边数是______。
三、判断题(每题5分,共25分)11. 一个图的子图包含原图的所有顶点和边。
()12. 一个连通图的所有顶点都连通。
()13. 在一个简单图中,每个顶点的度数都小于等于n-1。
()14. 每个图都有哈密顿路径。
()15. 一个图G的生成树是原图G的子图。
()四、解答题(共50分)16. (10分)设A={1,2,3,4,5},B={2,3,5,7,11},求A∪B 和A-B。
17. (10分)证明:一个连通图的每个顶点的度数都大于等于2。
18. (10分)给定一个图G,顶点集V={a,b,c,d,e},边集E={ab,bc,cd,de,ac,ad},求图G的所有连通分支。
离散数学试题及答案1

离散数学总分:100 考试时间:100分钟一、单项选择题1、一个无向图G是一个二元组〈V,E〉,V代表(正确答案:B,答题答案:)A、边集B、顶点集C、环D、路径2、最佳前缀码可由()算法求出(正确答案:A,答题答案:)A、HuffmanB、PERTC、DijkstraD、Kruskal3、带权为2、3、5、7、8、9的最优树T,权W(T)=()(正确答案:B,答题答案:)A、82B、83C、84D、854、设n阶无向连通图G有m条边,则()(正确答案:A,答题答案:)A、m≥n-1B、m≤n-1C、m=n-1D、m≥n5、经过图中每条边一次且仅一次并且行遍图中每个顶点的通路(回路),称为()(正确答案:A,答题答案:)A、欧拉通路B、简单通路C、初级通路D、哈密尔顿通路6、入度为0的顶点称为()(正确答案:B,答题答案:)A、树根B、树叶C、边D、顶点7、按中序行遍法,其行遍结果为((dce)bf)a(gih),则按后序行遍法其结果为()(正确答案:A,答题答案:)A、a(b(cde) )(igh)fB、a(b(cde) f)(igh)C、((dec)fb)(ghi) aD、(b(cde) f)(igh)a8、设T=〈V,E〉是n阶非平凡树,则T中至少有()片树叶.(正确答案:C,答题答案:)A、1B、2C、3D、49、设有向简单图D的度数列为2,2,3,3,入度列为0,0,2,3,D的出度列为().(正确答案:B,答题答案:)A、2,2,1,0B、2,2,3,3C、0,0,2,3D、2,2,5,610、设G=〈V,E〉是n阶无向简单图,若G中任何顶点都与其余的n-1个顶点相邻,则称G为n阶()(正确答案:A,答题答案:)A、无向图B、无向完全图C、完全图D、有向简单图二、多项选择题1、简单图为()(正确答案:AB,答题答案:)A、不含平行边B、不含环C、不含顶点D、不含单边2、下面给出的符号串集合中,哪些是前缀码?(正确答案:ABD,答题答案:)A、B1={0,10,110,1111}B、B2={1,01,001,000}C、B3={1,11,101,001,0011}D、B4={b,c,aa,ac,aba,abb,abc }3、树的行遍法有()(正确答案:ABC,答题答案:)A、中序B、前序C、后序D、顺序4、无向图G为欧拉图,则()(正确答案:ABC,答题答案:)A、G是连通的B、G中无奇度顶点C、所有顶点的入度等于出度D、奇数个顶点5、无向图G具有欧拉通路,当且仅当G是()(正确答案:AB,答题答案:)A、连通图B、有零个或两个奇度顶点C、回路D、奇数个顶点6、根据边是否有方向,图可分为()(正确答案:CD,答题答案:)A、连通图B、树C、有向图D、无向图7、两图同构,则()(正确答案:ABC,答题答案:)A、顶点个数相同B、边的条数相同C、每个顶点的度相同D、有多重边8、特殊的图有()(正确答案:ABCD,答题答案:)A、二部图B、欧拉图C、哈密尔顿图D、平面图9、下列各组数中,哪些能够成无向图的度数列?(正确答案:ABC,答题答案:)A、1,1,1,2,3B、2,2,2,2,2C、3,3,3,3D、1,2,3,4,510、若图G中任意两个结点u和v,都有从u到v和从v到u的通路,则称G是()(正确答案:A,答题答案:)A、强连通图B、弱连通图C、单向连通图D、连通图三、判断题1、强连通图一定是单向连通图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个选项中只有 一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1•一个连通的无向图 G ,如果它的所有结点的度数都是偶数,那么它具有一条 ( )A.汉密尔顿回路 B.欧拉回路 C.汉密尔顿通路 D.初级回路2. 设G 是连通简单平面图, G 中有11个顶点5个面,则G 中的边是() A.10B.12C.16 D .143. 在布尔代数L 中,表达式(a A b) V (a A b A c)V (b A c)的等价式是( )A. b A (a V c)B. (a A b) V (a'A b)C. (a V b) A (a V b V c) A (b V c)D. (b V c)A (a V c)4. 设i 是虚数,•是复数乘法运算,则 G=<{1,-1,i,-i}, • >是群,下列是 G 的子群是( )A.<{1}, • > B.〈 {-1}, •C. < {i}, •>D.〈 {-i}, •>5. 设Z 为整数集,A 为集合,A 的幕集为P(A),+、-、/为数的加、减、除运算,门为集合的交 运算,下列系统中是代数系统的有 ()A. < Z , + , />B. C. <Z , -, /> D.6.下列各代数系统中不含有零元素的是 (( )A. ( - x)( -y)( - z)(A(x,y))宀A(f(x,z),f(y,z))B. ( _x)A(f(a,x),a)C. ( -x)( -y) (A(f(x,y),x))<乙/ >〈P(A),门〉A. B. C. D. 〈Q , * > Q 是全体有理数集, 〈Mn(R),* > ,Mn(R)是全体n 阶实矩阵集合, 〈Z , : >, Z 是整数集, 淀义为x :xy=xy, 〈Z , + >, Z 是整数集,+是数的加法运算 *是数的乘法运算 *是矩阵乘法运算 -x,y € Z7. 设A={1,2,3} , A 上二元关系R 的关系图如下: R 具有的性质是 A. 自反性 B. 对称性 C. 传递性 D. 反自反性 8.设A={a,b,c} ,A 上二元关系 R={ < a,a>, < b,b 〉,〈a,c 〉},则关系 R 的对称闭包 S(R)是( )C.R U { < c,a > }D.R n I A 9.设 X-{a,b,c},lx 是 X 上恒等关系,要使 Ix U { < a,b>, < b,c>,等价关系,R 应取()A. {〈 c,a >, < a,c >}B.{ < c,b>, < b,a > }C.{ < c,a >, < b,a > }D.{ < a,c 〉,< c,b > }10. 下列式子正确的是()A..一 € ..B. • 一 Fc.{ - } -D.{ - } € .一F 列公式在R 下为真的是A.R U I AB.R 〈c,a 〉,< b,a > } U R 为 X 上的11.设解释R 如下:论域 D 为实数集a=O,f(x,y)=x-y,A(x,y):x<y.D. ( —x)( —y)(A(x,y) A(f(x,a),a))12. 设B是不含变元x的公式,谓词公式(-x)(A(x) T B)等价于()A.( x)A(x) T BB.(-X)A(X)T BC.A(x) T BD.(- x)A(x) T (- X)B13. 谓词公式(-x)(P(x,y)) T ( -iz)Q(x,z) A (- y)R(x,y)中变元x( )A. 是自由变元但不是约束变元B. 既不是自由变元又不是约束变元C. 既是自由变元又是约束变元D. 是约束变元但不是自由变元14. 若P:他聪明;Q:他用功;则“他虽聪明,但不用功”,可符号化为()A.P V QB.P An QC.P Tn QD.P Vn Q15.以下命题公式中,为永假式的是( )A.p T (p V q V r)B.(P Tn p) 7 pC.n (q T q) A pD.n (q Vn p)T(p An p)、填空题(每空1分,共20分)16. 在一棵根树中,仅有一个结点的入度为—0 ____ ,称为树根,其余结点的入度均为—1。
17. A={1,2,3,4}上二元关系R={〈2,4 >,〈3,3 >,〈4,2 >},R 的关系矩阵M R中m24= __ 1 __ ,m 34= __ 0 __ 。
18. ___________________________________ 设〈s,*>是群,则那么s中除—幺元外,不可能有别的幕等元;若〈s,*>有零元,则|s|=—1—。
19. ____________________________________________________________________________ 设A为集合,P(A)为A的幕集,则〈P(A) ,9 >是格,若x,y € P(A),则x,y最大下界是_____________ 最小上界是 ______ 。
20. 设函数f:X T Y,如果对X中的任意两个不同的X1和X2,它们的象y1和y2也不同,我们说f是—入射—函数,如果ranf=Y,则称f是___满射___函数。
21. 设R为非空集合A上的等价关系,其等价类记为〔x〕R。
-x,y € A,若〈x,y >€ R,贝卩〔x〕R与〔y〕R的关系是 ____ ,而若〈x,y >世R,则〔x〕R Q〔y〕R= ________ 。
22. 使公式(Fx)( ry)(A(x) A B(y))二(三x)A(x) A ( ^y)B(y)成立的条件是 ______________ 不含有y,______ 不含有x。
23. 设M(x):x是人,D(s):x是要死的,则命题“所有的人都是要死的”可符号化为(Fx) _______ ,其中量词(\/ x)的辖域是_______ 。
24. 若H1A H2A-A H n 是_________ ,则称H1,H2,…Hn 是相容的,若H1 A H2A-A H n 是__________ ,则称H1,H2,…H n是不相容的。
25. 判断一个语句是否为命题,首先要看它是否为________________ ,然后再看它是否具有唯一的 ______ 。
三、计算题(共30分)26. (4分)设有向图G=(V,E)如下图所示,试用邻接矩阵方法求长度为2的路的总数和回路总数。
27. (5)设A={a,b},P(A)是A的幂集,::.:是对称差运算,可以验证<P(A),:F >是群。
设n是正整数,求({a} -1{b}{a}) n二{a} -n{b} n{a} n28. (6分)设A={1,2,3,4,5},A 上偏序关系R={ 〈1,2>,〈3,2〉,〈4,1 >,〈4,2>,〈4,3〉,〈3,5>,〈4,5>} U I A;(1) 作出偏序关系R的哈斯图⑵令B={1,2,3,5},求B的最大,最小元,极大、极小元,上界,下确界,下界,下确界。
29. (6分)求「(P f Q)=(PQ)的主合取范式并给出所有使命题为真的赋值。
30. (5分)设带权无向图G如下,求G的最小生成树T及T的权总和,要求写出解的过程。
31. (4 分)求公式n (( -x)F(x,y) f ( y)G(x,y)) V ( x)H(x)的前束范式。
四、证明题(共20分)32. (6分)设T是非平凡的无向树,T中度数最大的顶点有2个,它们的度数为k(k >2),证明T 中至少有2k-2片树叶。
33. (8分)设A是非空集合,F是所有从A到A的双射函数的集合,:是函数复合运算。
证明:〈F,:〉是群。
34. (6分)在个体域D={a 1,a2,…,a n}中证明等价式:(-!x)(A(x) f B(x)) (一x)A(x) f ( x)B(x)五、应用题洪15分)35. (9分)如果他是计算机系本科生或者是计算机系研究生,那么他一定学过DELPHI语言而且学过C++语言。
只要他学过DELPHI语言或者C++语言,那么他就会编程序。
因此如果他是计算机系本科生,那么他就会编程序。
请用命题逻辑推理方法,证明该推理的有效结论。
36. (6分)一次学术会议的理事会共有20个人参加,他们之间有的相互认识但有的相互不认识。
但对任意两个人,他们各自认识的人的数目之和不小于20。
问能否把这20个人排在圆桌旁,使得任意一个人认识其旁边的两个人?根据是什么?参考答案1.B2.D3.A6.D7.D8.C11.A 12.A 13.C二、填空题16.0 117.1 018.单位元 119. x A y20.入射满射x U y21. : X] R= [y] R22.A(x) B(y)23.(M(x) T D(x)) M(x) T D(x)24.可满足式永假式(或矛盾式)25.陈述句真值15小题,每小题、单项选择题(本大题共二、计算题1分,共15分)4.A9.D14.B5.D10.B15.C1126. M= s1十221211111111111121111=18,G中长度为2的路总数为18,长度为2的回路总数为6。
{a} n=•_ 二({a}-1 )n{b} n{a} 1—:.•一当n是奇数时,({a} -1{b} { a )n - {a} -n{b}n{a} n={a} -1{b} ■{a}二({a} -1)n{b}n{a} n={a} -1{b} ■{a}- {a} -1{b} {a}=..27•当n 是偶数时,- x € P(A),x n=.一当n是奇数时,- x € P(A),x n=x于是:当n 是偶数,({ a} -1{b} {a} )n二{a「n{ b} n28.(1)偏序关系R的哈斯图为(2) B的最大元:无,最小元:无;极大元:2, 5,极小元:1 , 3 下界:4,下确界4;上界:无,上确界:无29. 原式二(n(P T Q)T (P^n Q)) A ((P Q) = (P~ Q))((P T Q) V (P^n Q)) A (n (P^n Q) J (P T Q)) (n P V Q Vn P Vn Q)A (n (n P Vn Q) V (P An Q))(n (P An Q) V (P An Q))(P A Q) V (P An Q) P A (Q Vn Q) P V (Q An Q) (P V Q) A (P Vn Q)命题为真的赋值是P=1,Q=0和P=1,Q=130. 令e i=(v i,V3), e2=(V4,V6)e3=(V2,V5), e4=(V3,V6)e5=(V2,V3), e6=(V1,V2)e7=(V1,V4), e8=(V4,V3)e9=(V3,V5), e i0 =(V5,V6)令a i为e上的权,则a i<a2<a3<a4<a5=a6=a7=a8<a9=a io取a i 的e i € T,a2 的e2 € T,a3 的e3 € T,a4 的e4 € T,a5 的e5 € T,即,T 的总权和=1+2+3+4+5=1531. 原式n (一x i F(x i,y) T T y i G(x,y i)) V T x2H(x2)(换名)―n x i y i(F(x i,y)T G(x,y i)) V X2H(X2)= _x i _y i n (F(x i,y i)T G(x,y i)) V T x2H(X2)=-x i-y i T x2(n (F(x i,y i)T G(x,y i))V H(x2)四、证明题32. 设T中有x片树叶,y个分支点。
