后方交会 前方交会
空间后方交会与前方交会求解地面点坐标的计算方法

双像解析计算的空间后交-前交方法当我们通过航空摄影,获得地面的一个立体像对时,采用双像解析计算的空间后交-前交方法计算地面点的空间点位。
这种方法首先由单片后方交会求出左、右像片的外方位元素,再用空间前方交会公式求出待定点坐标,其具体的作业步骤如下:● 像片野外控制测量一个立体像对采用空间后方交会-前方交会法计算点的地面坐标时,像对内必须具有一定数量的地面控制点坐标。
一般情况下,在一个像对的重叠范围四个角上,找出四个明显地物点,在野外判识出地面的实际位置,并准确地在像片上刺出各点的位置,要求在像片的背面绘出各点与周围地物关系的点位略图,加注记说明。
然后用普通测量计算方法,求出四个控制点的地面坐标X,Y,Z 。
● 用立体坐标量测仪测像点的坐标像片在仪器上归心定向后,测出四个控制点的像片坐标()11y ,x 与()22y ,x ,然后测出所需要解求的地面点坐标()11y ,x 和()22y ,x 。
● 空间后方交会法计算像片外方位元素利用控制点分别计算每个像片的六个外方位元素,包括:S1X ,S1Y ,S1Z ,1ϕ,1ω,1κ和S2X ,S2Y ,S2Z ,2ϕ,2ω,2κ。
● 空间前方交会计算所求点的地面坐标1. 用各自像片的角元素,计算出左、右像片的旋转矩阵1R 与2R 。
2. 根据左、右像片的外方位线元素计算摄影基线分量X B ,Y B ,Z B :⎪⎭⎪⎬⎫-=-=-=S1S2Z S1S2Y S1S2X Z Z B Y Y B X X B3. 逐点计算像点的像空间辅助坐标:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡f y x R Z Y X 111111,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡f y x R Z Y X 1111114. 计算点投影系数:⎪⎪⎭⎪⎪⎬⎫--=--=12211121221221Z X Z X X B Z B N Z X Z X X B Z B N Z X Z X5. 计算所求点的地面摄影测量坐标:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡222222111222222222111111111Z N Y N X N B B B Z Y X Z N Y N X N Z Y X Z N Y N X N Z Y X Z Y X Z Y X S S S S S S S S S A A A 6. 重复3-5步骤完成所有点地面坐标的计算。
摄影测量解析基础(后方交会前方交会)

06
结果输出
输出目标点的三维坐标数据。
前方交会方法的优缺点分析
优点 不需要地面控制点,可以在未知环境中进行测量。
可以快速获取大范围的三维空间信息。
前方交会方法的优缺点分析
• 适用于动态目标和快速测量场景。
前方交会方法的优缺点分析
01
缺点
02
03
04
对光照条件敏感,光照变化会 影响测量精度。
对摄影图像的质量要求较高, 需要清晰、分辨率高的图像。
随着科技的不断发展,摄影测量技术也在不断进步和完善,其在各个领域的应用 也日益广泛和深入。
摄影测量的历史与发展
01
摄影测量起源于19世纪中叶,当时人 们开始使用胶片相机进行地形测量。 随着技术的发展,数字相机逐渐取代 了胶片相机,使得摄影测量更加便捷 和高效。
02
近年来,随着计算机技术和人工智能 的飞速发展,摄影测量技术也取得了 重大突破。例如,无人机技术的兴起 使得摄影测量更加灵活、快速和安全 ;计算机视觉和深度学习技术的应用 则提高了影像解析的自动化和智能化 水平。
在复杂地形和遮挡严重的环境 中,前方交会方法可能会失效
。
05 实际应用案例
Hale Waihona Puke 后方交会方法应用案例总结词
通过已知的摄影站和地面控制点,解算出摄影中心和地面点的空间坐标。
详细描述
后方交会方法常用于地图更新、地籍测量和城市三维建模等领域。例如,在城市三维建模中,利用后方交会方法 可以快速准确地获取建筑物表面的空间坐标,为构建真实感强的城市三维模型提供数据支持。
图像获取
获取至少两幅不同角度的摄影图像。
01
02
像片处理
对图像进行预处理,包括图像校正、去噪等 操作。
测量放样后方交会法

后方交会
后方交会是指仅在待定点上设站,向三个已知控制点观测两个水平夹角a、b,从而计算待定点的坐标,称为后方交会。
交会测量是加密控制点常用的方法,它可以在数个已知控制点上设站,分别向待定点观测方向或距离,也可以在待定点上设站向数个已知控制点观测方向或距离,而后计算待定点的坐标。
常用的交会测量方法有前方交会、后方交会、侧边交会和自由设站法。
如下图所示,已知 A、B、C 三点的坐标,通过测量三个角度α、β、γ 即可求出这三个角度顶点 P 的坐标。
此即为后方交会。
计算公式一
后方交会有如下计算公式:
实际测量时一般是使用全站仪测量三个方向角 PA、PB、PC。
根据这三个方向角计算如下六个变量,然后再代入上面的公式计算点P 的坐标。
计算公式二
全站仪测量三个方向角 PA、PB、PC。
根据这三个方向角计算点P坐标的公式如下:
危险圆
点 P 在三角形 ABC 的外接圆上时,α、β、γ 将保持不变。
如此一来,点 P 的坐标将有无穷个——外接圆上的任意一点均可以是点 P。
此时,使用计算公式计算点 P 坐标时,可能会因为除以零而得到无效解。
点 P 靠近外接圆时,很小的观测误差都会引起点 P 位置的较大偏差。
因此,称三角形 ABC 的外接圆为危险圆。
后方交会时,应避免点 P 离危险圆很近。
精度假定水平方位角的观测中误差为
,则有:
点P的定位精度为:
定向精度为:
上面两个公式中的
按下面的公式计算
注意:当点P在危险圆上时
将等于零,于是定位精度与定向精度将为无穷大。
摄影测量-空间前交、后交【精选文档】

空间后交—前交程序设计(实验报告)姓名:班级:学号:时间:空间后交-前交程序设计一、实验目的用 C 、VB或MATLAB语言编写空间后方交会-空间前方交会程序⑴提交实习报告:程序框图、程序源代码、计算结果、体会⑵计算结果:像点坐标、地面坐标、单位权中误差、外方位元素及其精度二、实验数据f=150。
000mm,x0=0,y0=0三、实验思路1。
利用空间后方交会求左右像片的外方位元素(1).获取m(于像片中选取两点,于地面摄影测量坐标系中选取同点,分别计算距离,距离比值即为m),x,y,f,X,Y,Z(2).确定未知数初始值Xs,Ys,Zs,q,w,k(3).计算旋转矩阵R(4).逐点计算像点坐标的近似值(x),(y)(5)。
组成误差方程式(6)。
组成法方程式(7).解求外方位元素(8)。
检查是否收敛,即将求得的外方位元素的改正数与规定限差比较,小于限差即终止;否则用新的近似值重复步骤(3)-(7)2。
利用求出的外方位元素进行空间前交,求出待定点地面坐标(1).用各自像片的角元素计算出左、右像片的方向余弦值,组成旋转矩阵R1,R2(2)。
根据左、右像片的外方位元素,计算摄影基线分量Bx,By,Bz(3)。
计算像点的像空间辅助坐标(X1,Y1,Z1)和(X2,Y2,Z2)(4).计算点投影系数N1和N2(5)。
计算未知点的地面摄影测量坐标四、实验过程⑴程序框图函数AandL%求间接平差时需要的系数%%%已知%a=像点坐标x,b=像点坐标y,f内方位元素主距%φ=q,ψ=w,κ=k%像空间坐标系X,Y,Z%地面摄影测量坐标系Xs,Ys,Zsfunction [A1,L1,A2,L2]=AandL(a,b,f,q,w,k,X,Y,Z,Xs,Ys,Zs) %%%%%%%%%%%选择矩阵元素a1=cos(q)*cos(k)—sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)—sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=—sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=—sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);%%%%%%%共线方程的分子分母X_=a1*(X—Xs)+b1*(Y-Ys)+c1*(Z-Zs);Y_=a2*(X-Xs)+b2*(Y—Ys)+c2*(Z-Zs);Z_=a3*(X—Xs)+b3*(Y—Ys)+c3*(Z-Zs);%%%%%%%近似值x=-f*X_/Z_;y=-f*Y_/Z_;%%%%%%%A组成L组成a11=1/Z_*(a1*f+a3*x);a12=1/Z_*(b1*f+b3*x);a13=1/Z_*(c1*f+c3*x);a21=1/Z_*(a2*f+a3*y);a22=1/Z_*(b2*f+b3*y);a23=1/Z_*(c2*f+c3*y);a14=y*sin(w)-(x/f*(x*cos(k)—y*sin(k))+f*cos(k))*cos(w);a15=-f*sin(k)—x/f*(x*sin(k)+y*cos(k));a16=y;a24=—x*sin(w)-(y/f*(x*cos(k)-y*sin(k))—f*sin(k))*cos(w);a25=-f*cos(k)-y/f*(x*sin(k)+y*cos(k));a26=-x;lx=a—x;ly=b-y;%%%%%%%%%组成一个矩阵,并返回A1=[a11,a12,a13,a14,a15,a16];A2=[a21,a22,a23,a24,a25,a26];L1=lx;L2=ly;函数deg2dms%%%%%%%%角度转度分秒function y=deg2dms(x)a=floor(x);b=floor((x-a)*60);c=(x-a—b/60)*3600;y=a+(b/100)+(c/10000);函数dms2deg%%%%%度分秒转度function y=dms2deg(x)a=floor(x);b=floor((x-a)*100);c=(x-a—b/100)*10000;y=a+b/60+c/3600;函数ok%%%%%%%%%%%%%%目的是为了保证各取的值的有效值%%xy为n*1,a为1*nfunction result=ok(xy,a)format short gi=size(xy,1);for n=1:io=xy(n)—floor(xy(n,1));o=round(o*(10^a(n)))/(10^a(n));xy(n,1)=floor(xy(n,1))+o;endformat long gresult=xy;函数rad2dmsxy%%%%求度分秒表现形式的三个外方位元素,三个角度function xydms=rad2dmsxy(xy)[a,b,c,d,e,f]=testvar(xy);d=deg2dms(rad2deg(d));e=deg2dms(rad2deg(e));f=deg2dms(rad2deg(f));xydms=[a,b,c,d,e,f]';函数spacehoujiao%%%%%%%空间后交%%% f%%输入p(2*n,1)%%像点坐标x,y,X,Y,Z,均为(n,1)function [xy,m,R]=spacehoujiao(p,x,y,f,X,Y,Z)format long;%%%%%权的矢量化,这是等精度时的,如果非,将函数参数改为PP=diag(p);%%求nj=size(X,2);%%初始化Xs=0;Ys=0;Zs=0;for n=1:jXs=Xs+X(n);Ys=Ys+Y(n);Zs=Zs+Z(n);endSx=sqrt((x(2)-x(1))^2+(y(2)—y(1))^2);%%%%两像点之间距离Sd=sqrt((X(2)-X(1))^2+(Y(2)-Y(1))^2);%%%%两地面控制点之间距离m=Sd/Sx; %%%%图像比例系数Xs=Xs/j;Ys=Ys/j;Zs=m*f+Zs/j;m0=0;q=0;w=0;k=0;i=0;a=rand(2*j,6);l=rand(2*j,1);%%%%for n=1:j[a(2*n—1,:),l(2*n—1,1),a(2*n,:),l(2*n,1)]=AandL(x(n),y(n),f,q,w,k,X(n),Y(n),Z(n),Xs,Ys,Zs);enddet=inv(a’*P*a)*transpose(a)*P*l;%%%%%%%%%循环体while 1%%%%%%%%%%%%%%%%[dXs,dYs,dZs,dq,dw,dk]=testvar(det);detXs=abs(dXs);detYs=abs(dYs);detZs=abs(dZs);detq=abs(dq);detw=abs(dw);detk=abs(dk);%%%%%%%%%if ((detXs<0。
前方交会。后方交会

一、交会法概述
是一种经常采用的加密控制点的方法。
常用的几种方法有:前方交会、是一种经常采用的加密控制点的方法。
常用的几种方法有:前方交会、侧方交会、侧方交会、侧方交会、后方后方交会。
1.前方交会
如果已知A 、B 两点的坐标,为了计算未知点P 的坐标,只要观测∠A 和∠B 即可。
这种测定未知点P 的平面坐标的方法称为前方交会。
2.侧方交会
若观测∠A 和∠P 或∠B 和∠P ,同样可以测定未知点P 的平面坐标,这种方法称为侧方交会。
3.后方交会
若在未知点P 上瞄准A 、B 、C 三个已知点,测得∠α和∠β,也可确定
未知点P的平面坐标,这种方法称为后方交会。
二、前方交会法加密控制点
已知条件A、B两点坐标分别为(x A,y B)、(x B,y B),求p点的坐标。
待求数据p点的坐标(X p,Y p) 观测数据
为确定P点的位置,经纬仪分别安置A、B两点,用测回法观测∠A、∠B 坐标计算
根据A、B两点的坐标和∠A、∠B,P点坐标为
Welcome To
Download
欢迎您的下载,资料仅供参考!。
后方交会

后方交会-解释是工程测量中一种比较常用的一种测量方法.主要是通过两个或多已知点测量一个未知点.测角定位-正文利用测角仪器观测角度,以确定被测点位置的一种方法。
一般观测两个角,则有两条位置线,两线交点即为被测点位置。
在海洋测量中,测角定位通常使用的方法有:后方交会法,一般使用三标两角法,有时使用四标三角法,即在被测点上使用测角仪器观测3个或4个已知目标之间的夹角来确定点位;前方交会法,在两个或两个以上已知点上用测角仪器同时观测各已知点到某一被测点的夹角来确定点位;侧方交会法,综合使用后方交会法和前方交会法来实现定位的方法。
另外,还有一距离一方位法,也是通过测角测定方位和距离实现定位的。
因为测角仪器大部分是目视光学仪器,所以作用距离近,只适于近岸测量使用。
控制测量-正文在一定的区域内为地形测图或工程测量建立控制网(区域控制网)所进行的测量工作。
分为平面控制测量和高程控制测量。
平面控制网与高程控制网一般分别单独布设,也可以布设成三维控制网。
控制网具有控制全局,限制测量误差累积的作用,是各项测量工作的依据。
对于地形测图,等级控制是扩展图根控制的基础,以保证所测地形图能互相拼接成为一个整体。
对于工程测量,常需布设专用控制网,作为施工放样和变形观测的依据。
平面控制网常用三角测量、导线测量、三边测量和边角测量等方法建立。
三角测量是建立平面控制网的基本方法之一。
但三角网(锁)要求每点与较多的邻点相互通视,在隐蔽地区常需建造较高的觇标。
导线测量布设简单,每点仅需与前后两点通视,选点方便,特别是在隐蔽地区和建筑物多而通视困难的城市,应用起来方便灵活。
随着电磁波测距仪的发展,导线测量的应用日益广泛。
三边测量要求丈量网中所有的边长。
应用电磁波测距仪测定边长后即可进行解算。
此法检核条件少,推算方位角的精度较低。
边角测量法既观测控制网的角度,又测量边长。
测角有利于控制方向误差,测边有利于控制长度误差。
边角共测可充分发挥两者的优点,提高点位精度。
摄影测量学3-3

要将空中摄站及影像放到整个的加密网中,起到 点的传递和构网作用,故被称为空中三角测量。
目的:用摄影测量解析法确定区域内所有影像的外方位元素。
摄影测 量 加密
一、 空中三角测量意义:
(1)不需直接触及被量测的目标或物体.凡是在影像上可 以看到的目标,不受地面通视条件限制,均可以测定其位 臵和几何形状; (2)可以快速地在大范围内同时进行点位测定,从而可节 省大量的野外测量工作; (3)摄影测量平差计算时,加密区域内部精度均匀,且很 少受区域大小的影响;
4个平高控制点:4 4 16
n 各待求点:
4 n 4n
3n 12 未知数的个数:
两张像片的外方位元素:
t1
t2
多余观测数: 6 n
n
2 6 12 各待求点: 3 n 3n
3.9光束法双像解析摄影测量
按未知数的类型将误差方程式写成矩阵形式:
V1 A1 V 0 2 0 A2 t1 B1 l1 t 2 B2 l 2 X
• 要点: 1) 空间后方交会-空间前方交会:由于空间后方交会至少需要3 个平高控制点,通常采用4 个平高控制点,按最小二乘平差 方法解算单张像片6 个外方位元素。故该方法不适合; 2) 相对定向-绝对定向:相对定向完成后,绝对定向通常采用3
个平高控制点按最小二乘平差方法解算7 个绝对定向元素。
上述问题中,控制点数量不足以解决该绝对定向问题。故该 方法不适合; • 3) 光束法:上述问题中,2 个平高控制点和1 个高程控制点 可以确定平差的基准,多余观测个数r=(2×6×2)(6×2+3×3)=3>0,故可用该方法解决上述问题。
N12 ) X (u2 N N
前方、后方和侧方交会

前方交会和侧方交会由正弦定理得出:D AP/D AB=sinβ/sinγ=sinβ/sin(α+β)则:(D AP/D AB)sinα=(sinβsinα)/sin(α+β)=1/(ctgα+ctgβ)前方交会和侧方交会中P点坐标计算公式:X P=(X A ctgβ+X B ctgα+(Y B-Y A)÷(ctgα+ctgβ)Y P=(Y A ctgβ+Y B ctgα+(X A-X B)÷(ctgα+ctgβ)上式常称为余切公式。
注意使用上述公式时,A、B、P的编号应是反时针方向的。
P点坐标算出后,可将A、P作为已知点,用计算B点坐标来校核:校核计算公式:X B=(X p ctgα+X A ctgγ+(Y A-Y P)÷(ctgα+ctgγ)Y B=(Y p ctgα+Y A ctgγ+(X P-X A)÷(ctgα+ctgγ)本公式只能检查计算本身是否有错,不能发现角度侧错以及已知数据是否用错、抄错等错误,也不能提高计算精度。
运用此公式的技术要求:为保证计算结果和提高交会精度,规定如下:1、前方交会和侧方交会应有三个大地点,困难时应有两个大地点。
2、交会角不应小于30°,并不应大于150°,困难时亦不应小于20°,并应不大于160°。
3、水平角应观测两个测回,根据测点数量可用全测回法或方向观测法。
4、三个大地点的前方交会,可通过两个三角形(ΔABP,ΔBCP)求出P点的两组坐标值P(X P1、Y P1),(X P2、Y P2),两组算得的点位较差不大于两倍的比例尺精度,即:ΔD=√δx2+δy2≤2×0.1M(mm)式中δx,δy—δx= X P1- X P2,δy= Y P1 -Y P2M—比例尺分母。
后方交会B如图所示,A、B、C是已知三角点,P点是导线点,将仪器安置在P点上,观测P至A、B、C各个方向之间的水平夹角α、β,然后根据已知三角点的坐标,可解算P点坐标。
5摄影测量解析基础(后方交会+前方交会)

内定向通常采用多项式变换公式。假设框标在以像主点为原点的像平
面坐标系中的理论坐标为(x,y),在量测坐标系(框标坐标系、扫描 坐标系)的量测坐标为(I,J),则常用的多项式变换公式有:
线性正形变换公式
x a0 a1 I a2 J y b0 b1 I b2 J
仿射变形公式
x f
a10 X X S 0 b10 Y YS 0 c10 Z Z S 0
0 0 Z Z S 0 a0 X X b Y Y c S 0 S 0 3 3 3 0 0 Z Z S 0 a0 X X b Y Y c S0 S0 2 2 2 0 0 Z Z S 0 a0 X X b Y Y c S 0 S 0 3 3 3
•
已知值 影像的内方位元素x0,y0,f 和 m(像片摄影比例尺的分母)
以及物点坐标(X,Y,Z)
•
• •
观测值 像点坐标 x,y(观测值)
未知数 像片的外方位元素XS,YS,ZS,,, 泰勒级数展开
泰勒级数展开的概念:
Z f X1, X 2 ,, X n
设X有近似值X0 则按泰勒公式在点
误差方程的矩阵形式:
v1 1 v 2 1 v 3 0 v 4 0 v 5 0 0 0 1 0 1 0 1 1 0 1 0 dX B 23 dX C 0 dX D 14 0 0 0 0 2.9 0 0 3.7 0 0 0 Pi 10 / S i 0 0 2.5 0 0 0 0 0 3 . 3 0 0 0 0 4.0 0
摄影测量解析基础后方交会前方交会实用教案

Ys Zs
第第1十9九页页,/共共464页6。页
偏导数(dǎo shù) 1
x X s
f Z
2
( X X s
Z
Z X s
X)
f Z 2 (a1Z a3 X )
1 Z
(a1
f
f
X Z
a3 )
1 Z
a1 f
a3(x
x0 )
第第2二0十页页,/共共464页6。页
x X s
1 Z
a1 f
y
o
x
坐标(zhí jiǎo zuò biāo)系
中。
I y'
在解析摄影测量和数字
摄影测量中,内定向是通
(x1,y1) (x2,y2)
过输入像片主距和量测影 像框标并进行相应的计算 来完成的,其目的就是恢 o 第第4四页页,/共共464页6。页
(x3,y3) (x4,y4)
x'
二、内定向(dìnɡ xiànɡ) 的作业过程
)
H
A
第第1一页页,/共共464页6。页
h2 C
h4
h1 h2 h3
v1 v2 v3
(
X
0 B
(
X
0 B
dXB ) dXB )
(
X
0 C
(
X
0 C
dXC dXC
) )
HA HA
h4 v4
(
X
0 C
dX
C
)
(
X
0 D
dXD )
h5 v5
(X
0 D
dX D
)
H
A
v1 dX B
§5-1 影像(yǐnɡ xiànɡ)内定向
单像空间后方交会和双像解析空间后方-前方交会的算法程序实现

单像空间后方交会和双像解析空间后方-前方交会的算法程序实现遥感科学与技术摘要:如果已知每张像片的6个外方位元素,就能确定被摄物体与航摄像片的关系。
因此,利用单像空间后方交会的方法,可以迅速的算出每张像片的6个外方位元素。
而前方交会的计算,可以算出像片上点对应于地面点的三维坐标。
基于这两点,利用计算机强大的运算能力,可以代替人脑快速的完成复杂的计算过程。
关键词:后方交会,前方交会,外方位元素,C++编程0.引言:单张像片空间后方交会是摄影测量基本问题之一,是由若干控制点及其相应像点坐标求解摄站参数(X S,Y S,ZS,ψ、ω、κ)。
单像空间后方交会主要有三种方法:基于共线条件方程的平差解法、角锥法、基于直接线性变换的解法。
而本文将介绍第一种方法,基于共线条件方程反求象片的外方位元素。
而空间前方交会先以单张像片为单位进行空间后方交会,分别求出两张像片的外方位元素,再根据待定点的一对像点坐标,用空间前方交会的方法求解待定点的地面坐标。
可以说,这种求解地面点的坐标的方法是以单张像片空间后方交会为基础的,因此,单张像片空间后方交会成为解决这两个问题以及算法程序实现的关键。
1.单像空间后方交会的算法程序实现:(1)空间后方交会的基本原理:对于遥感影像,如何获取像片的外方位元素,一直是摄影测量工作者探讨的问题,其方法有:利用雷达(Radar)、全球定位系统(GPS)、惯性导航系统(I N S)以及星像摄影机来获取像片的外方位元素;也可以利用一定数量的地面控制点,根据共线方程,反求像片的外方位元素,这种方法称为单像空间后方交会(如图1所示)。
图中,地面坐标X i、Yi、Zi和对应的像点坐标x i、yi是已知的,外方位元素XS、Y S、ZS(摄站点坐标),ψ、ω、κ(像片姿态角)是待求的。
(2)空间后方交会数学模型:空间后方交会的数学模型是共线方程, 即中心投影的构像方程:式中X、Y、Z是地面某点在地面摄影测量坐标系中的坐标,x,y是该地面点在像片上的构像点的像片坐标,对于空间后方交会而言它们是已知的,还有主距f是已知的。
后方交会的原理

后方交会的原理后方交会是测量学中一种常用的方法,可以用来确定点的位置,尤其是在地图制图、土地测量、建筑设计等领域中。
本文将从定义、原理、步骤、误差分析等方面详细介绍后方交会的原理。
一、定义后方交会是一种测量学方法,通过已知控制点的坐标、方位角等信息,对未知点进行定位。
它是一种基于三角测量原理的方法,通过三角形相似原理计算出未知点的坐标。
后方交会可以用来测量平面坐标、高程、方位角等,适用于各种地形和地貌。
二、原理后方交会的原理基于三角测量原理,即以三个已知点为顶点的三角形,其内部所有角度和三个顶点的距离都是已知的。
通过测量三角形内角和三边长度,可以计算出未知点的坐标。
具体来说,后方交会的原理可以分为以下几个步骤:1.测量控制点的坐标和方位角首先需要测量控制点的坐标和方位角,以确定已知点的位置和方向。
控制点可以是已知点,也可以是通过前方交会计算出的点。
2.测量未知点与控制点之间的距离和方位角接下来需要测量未知点与控制点之间的距离和方位角。
距离可以通过测距仪、激光测距仪等设备进行测量,方位角可以通过经纬仪或罗盘进行测量。
3.计算三角形内角和三边长度通过测量三角形内角和三边长度,可以计算出未知点的坐标。
其中,内角可以通过三角函数计算,三边长度可以通过勾股定理计算。
4.检验后方交会的精度最后需要对后方交会的精度进行检验,可以通过误差分析等方法进行评估。
如果误差较大,可以通过增加控制点、提高测量精度等方式进行调整。
三、步骤后方交会的步骤可以总结为以下几个:1.确定控制点的位置和方向,测量其坐标和方位角。
2.测量未知点与控制点之间的距离和方位角。
3.计算三角形内角和三边长度,确定未知点的坐标。
4.检验后方交会的精度,评估误差。
四、误差分析后方交会的精度受到多种因素的影响,如测量仪器精度、控制点布设精度、天气环境等。
误差分析可以通过以下几种方法进行: 1.重复测量法重复测量法是通过多次测量同一点来评估测量精度的方法。
后方交会

※内容概述:地势平坦的常采用经纬仪导线建立测图控制点。
在山区或地形复杂的地区往往采用经纬仪交会点来加密测图控制。
经纬仪交会法按其布设形式的不同,可分为前方交会法、侧方交会法和后方交会法。
在两个已知控制点上,分别观测两个角度,以求得待定点的坐标称为前方交会法,在待定点上照准三个已知控制点的方向,观测其间的两个角度,求待定点的坐标就是后方交会法。
除此之外还有侧方交会法。
※教学目的:通过本讲的学习,掌握前方交会法的原理,并会运用相应的公式进行计算;掌握后方交会法的原理,并会运用相应的公式进行计算;了解侧边交会的原理,并会进行计算。
※内容详述:§6.1 前方交会前方交会是采用经纬仪在已知点A、B上分别向新点P观测水平角α和β,从而可以计算P点的坐标。
但是为检核,有时从三个已知点A、B、C上分别向新点P进行角度观测,由两个三角形分别解算P点的坐标。
同时为了提高交会点的精度,选择P点时,应尽可能使交会角r接近于90°,并保证30°≤r≤150°。
图6-1 前方交会1、P点坐标的计算公式P点坐标计算可采用前方交会法的余切公式,用计算器进行计算。
要求A、B、P和B、C、P的注字方向是逆时针的。
2、测量精度的检核由于角度观测有误差,由两组值推算的P点坐标不会完全相同。
《规范》规定:在图根测量中,由两组计算同一点的坐标较差e,不得大于M/5000m,M为比例尺的分母。
表6-1 前方交会计算(正切公式)§6.2 后方交会图6-2 后方交会如图6-2,设A、B、C为已知点,P为未知点。
为了测定P点的坐标,将仪器安置在P点,测出α、β角,同时测出检验角ε(K点为已知点)。
利用α、β角值及A、B、C三个已知点的坐标,就可算出P点的坐标,同时也可用检核角检验测量成果的精度。
后方交会法的应用条件是,需要有四个高级控制点,且P点不在A、B、C三点所构成的圆周上或该圆周的附近,否则将算不出结果或计算结果误差很大,所以称这个圆为危险圆。
后方交会

01 图上定位
目录
02 测绘
03 危险圆
04 精度
05 放样方法应用
图上定位
如果目的是在一张二维地图上大致确定自己的横纵位置(不考虑误差问题),按照如下步骤: 第一步:标定地图真北。 第二步:选取图上两个显眼的定位点A,B,并在实地找到此二点。 第三步:用指北针瞄准定位点A,读出指北针方位角。 第四步:在图上用指北针的尺边或三棱尺切准定位点A,作沿着既读方位角的双方向直线 第五步-第六步:对定位点B重复第三第四步 此时图上的交点O就是当前所站位置。测量和绘制两步可能产生各类误差,这些误差造成的线簇 会形成一个任意四边形(如“误差一览”图所示),实际所站位置就在此四边形之中。
测边后方交会放样方法简介
(1)测边后方交会放样方法
郑西客运专线新渭南车站施工放样利用Leica TCA1800型全站仪,测角精度为1″,测距精度为 1ppm+2ppm。LeicaTC系列的全站仪本身自带的程序里就有后方交会(自由设站法)。
具体步骤如下:在任意点P进行仪器整平→选择后方交会程序→输入任意点P点名→输入已知点A信 息(点名、坐标值)→盘左后视已知点A并测距→盘右后视已知点A并测距→输入已知点B信息(点名、 坐标值)→盘左后视已知点B并测距→盘右后视已知点B并测距→设置P点为测站点→测量或放样点 位。
该车站设计采用高架桥结构,在我国为首例。
一般放样方法的局限性
图1侧边后方交会自由设站放样承台示意图
在两级控制(CPⅠ,CPⅡ)建立起来以后,郑西客运专线渭南高架车站桥面系以下的施工测量工作 主要包括:定期进行控制复测,钻孔桩放样,放样承台边线,放样墩身,放样垫石边线,放样现 浇梁中线,调整悬灌模板,变形(沉降)监测等等。一般工程建筑物平面位置的测设方法有:直角 坐标法、极坐标法、角度交会法、距离交会法等。随着科技的发展,测量仪器日益先进,全站仪 在工程建设领域的应用已经十分普及,建筑物平面位置的测设一般多采用全站仪极坐标法进行放 样。但是,为了避免施工过程中对控制点的破坏,更好的保护控制点,线性工程的控制一般沿线 路走向,布设在线路的两侧,导线控制点距离线路中心100m~200m。
交会测量(前方、后方、侧方交会测量)

前方交会法1.前方交会法定义自两已知坐标之三角点上,观测一欲测点之水平角,以推算其坐标位置,称之前方交会法。
图-1,前方交会法。
图-2,前方交会点。
图-1 前方交会法图-2 前方交会点2.前方交会点此种补点(前方交会点),通常为无法设置仪器之测点,如塔尖、避雷针、烟囱等等。
3.前方交会法适用场合:A.具两已知三角点。
B.三点(两已知点及欲测点)间可以通视。
C.两已知点可以架设仪器,但欲测点不方便架设仪器。
D.有数个欲测点待测定时。
图-3,为数个欲测点图-3 数个欲测点4.前方交会法施作步骤:A.经纬仪分别整置于A、B 两三角点上。
B.照准P 点,分别测得α、β两水平角。
C.以计算方法,求P 点坐标。
图-4,为量测角度。
图-4 量测角度5.已知、量测、计算之数据:A.已知:xA、yA、xB、yB。
B.量测:α、β。
C.计算:xP、yP。
图-5,为前方交会法相关角度位置图-5 前方交会法相关角度位置6.限制:α、β、γ三内角均必须介于30°~120°之间。
图-6 ,为角度限制。
图-6 为角度限制7.计算法前方交会法计算方法有三种:A.三角形法; B.角度法; C.方位角法8.三角形法19()()3891802890--++=---= βφφαφφABBP AB AP ()()()()()689cos sin cos 589sin cos sin 48922222---=-==---=-==---+-=∆+∆= ABAB AB AB AB AB A B AB A B A B y y AB ABy y x x AB ABx x y y x x AB y x AB φθφφθφ()()789sin sin sin sin sin sin --+===βαβγβγβAB AB AP ABAP γβαABP AB AB y y y -=∆ABNB.求方位角ψAP 、ψBP :C.求各邊邊長:①AB 邊長:有三種方法可求得②AP 邊長:()[](βαβαγγβα+=+-==++sin 180sin sin 180γβαsin sin sin AB AP BP ==20()()1289cos 1189sin --+=--+= BPB P BP B P BP y y BP x x φφ()()889sin sin sin sin sin sin --+===βααγαγαAB AB BP ABBP ()()1089cos 989sin --+=--+= APA P AP A P AP y y AP x x φφAPAP l φcos A Py yPBy y BPy y l y BP x x l x yy y x x x BP BP BP B P BP BP B P B P -=∆==-=∆=-=∆+=∆+=φφφφcos cos sin sin ③BP 邊長:D.求P 座標x P 、y P :①由A 點求P 點②由B 點求P 點9.角度法A.由上法直接代入:將(9-8-2)式與(9-8-7)式代入(9-8-9)式中,可得:yy y x x x A P A P ∆+=∆+=APy y l y AP x x l x AP AP AP AP AP AP -=∆=-=∆=φφcos sin21()()()1389sin sin sin sin ---++=+= αφβαβφAB A APA P AB x AP x x ()αφαφαφsin cos cos sin sin AB AB AB -=-()()()1489cos sin sin cos ---++=+= αφβαβφAB A APA P AB y AP y y ()αααφsin cos sin ABy y AB x x AB A B AB ---=-()()()()()1589sin sin sin sin sin cos --+--+-+= βαβαβαβαA B A B A P y y x x x x ()()()()()1789cot cot cot sin cos sin 1689tan tan tan sin cos sin 1cot cot 1tan tan sin cos sin cos cos sin sin cos sin --+=+--+=++=+=+=+ αβαβαβαββαβαβααββαβαβαβαβαβα或將(9-8-2)式與(9-8-7)式代入(9-8-9)式中,可得:B.化簡x P :由和差化積公式:將(9-8-5)式與(9-8-6)式代入,可得:再之代入(9-8-13)式中,可得:由和差化積公式:化簡下式,可得:()βαβαβαcos cos cos sin sin +=+22()2289cot cot cot cot --++-+=βααβBA B A P x x y y y ()()()()ABPB PA APBA BP A B A P APA B A P y y y y y y x x φφφφφφφcos sin cos sin tan ---+=-+=()()()()2089tan tan tan tan tan tan tan tan tan tan tan tan tan --+--+=+--+-+= βαβαβαβαβαβαβA B B A P A B A B A P y y x x x y y x x x x ()()()()()1989cot cot sin sin sin 1889tan tan tan tan sin sin sin tan 1tan 1sin sin sin cos cos sin sin sin sin --+=+--+=++=+=+ βαβαβαβαβαβαβααββαβαβαβαβα或()()()2189cot cot cot cot cot cot 1cot cot cot --+-++=+--+-+= βααββαβααBA B A P A B A B A P y y x x x y y x x x x 同理,化簡下式,可得:將(9-8-16)式與(9-8-18)式代入(9-8-15)式中,可得:或將(9-8-17)式與(9-8-19)式代入(9-8-15)式中,可得:C.化簡y P :(推演過程省略)D.角度法所得公式(9-18-21)式與(9-18-22)式,適於計算機使用,唯應注意:左A ,右B ;左α,右β。
后方交会
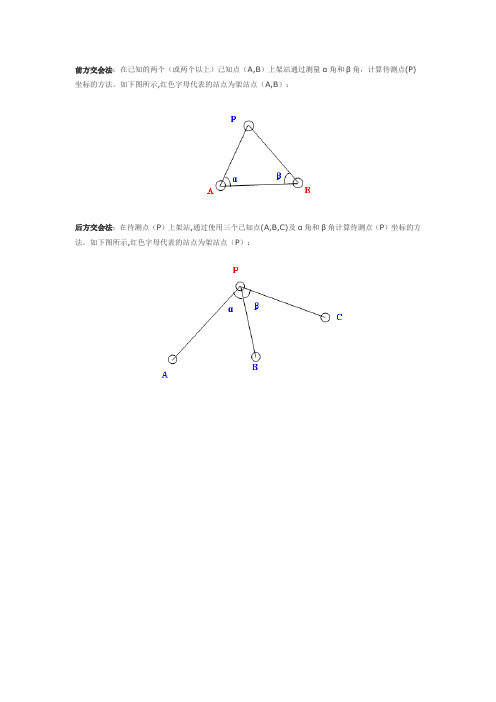
前方交会法:在己知的两个(或两个以上)己知点(A,B)上架站通过测量α角和β角,计算待测点(P)坐标的方法。
如下图所示,红色字母代表的站点为架站点(A,B):后方交会法:在待测点(P)上架站,通过使用三个己知点(A,B,C)及α角和β角计算待测点(P)坐标的方法。
如下图所示,红色字母代表的站点为架站点(P):一、引言在工程测量中,内业资料计算占有很重要的比重,内业资料计算的准确无误与速度直接决定了测量工作是否能够快速、顺利地完成。
而内业资料的计算方法及其所需达到的精度,则又直接取决于外业所用仪器及具体的放样目标和内业计算所用到的办公软件和计算方法。
计算机辅助设计(Computer Aid Design 简写CAD,常称AutoCAD)是20世纪80年代初发展起来的一门新兴技术型应用软件。
如今在各个领域均得到了普遍的应用。
它大大提高了工程技术人员的工作效率。
AutoCAD配合AutoLisp语言,还可以编制一些常用的计算程序,得到计算结果。
AutoCAD的特性提供了测量内业资料计算的另外一种全新直观明了的图形计算方法。
结合我们现正使用的徕卡全站仪的情况,其可以很方便地进行三维坐标的测量,通过AutoCAD的内业计算,①、在放样的过程中,可以用编程计算器结合全站仪,非常方便地、快速地进行作业;②、运用AutoCAD进行计算结果的验证;③、随着全站仪的推广和普及,极坐标的放样越来越成为众多放样方法中备受测量人员青睐的一种,而坐标计算又是极坐标放样中的重点和难点,由于一般的红线放样,工程放样中的元素多为点、直线(段)、圆(弧)等,故可以充分利用AutoCAD的设定坐标系、绘图和取点的功能,以及结合我们外业所用计算器的功能,从而大大减轻我们外业的工作强度及内业的工作量。
以下以冶勒电站厂区枢纽工程的一些实例来说明三者在工程测量中的应用。
二、测区概况冶勒电站厂址位于石棉县李子坪乡南桠村,距坝址11KM,距石棉县城40KM。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y2 y1 (Q Q0 )
X 0,Y0,P0,Q0是仪器零位置读数
左右视差:同名像点在各自的像平面坐标系的x坐标之差
p x1 x2
上下视差:同名像点在各自的像平面坐标系的y坐标之差
q y1 y2
(1)摄影测量--通过摄影进行测量--问题:如何恢复影
像的方位;
(2)什么是影像的方位? --内方位元素、外方位元素 (3)怎样恢复外方位元素?
x
(y) f
y
a20 ( X a30 ( X
X s0 ) b20 (Y X s0 ) b30 (Y
Ys0 ) c20 (Z Zs0 ) Ys0 ) c30 (Z Zs0 )
X s
偏导数,系数
dX S,dYS,dZS,d,d,d 外方位元素初始值的改正数,待求未知数
误差方程
vx a11dX s a12dYs a13dZs a14d a15d a16d lx
y cos )
y
a26 x
在竖直摄影的情况下,角元素都很小(<3度),各系数可 简化为:
0 sin 0 cos 1 a1 cos cos sin sin sin 1 a3 sin cos 0
Z ZS H
x 1
f
a11 X s Z (a1 f a3x) H
令
Y
a2
b2
c2
Y
Ys
R 1
Y
Ys
Z a3 b3 c3 Z Zs
Z Zs
X
Y Z
0
a1c2
a2c1
a1c3 a3c1
a2c1 a1c2 0
a2c3 a3c2
a3c1 a3c2
a1c3 a2c3
X Y
0
Z
进一步简化 R是正交阵当 R 1 时,各元素等于其代数余子式
a14
y sin
[
x f
(x cos
y sin )
f
cos ]cos
f
(1
x2 f 2)
a24
x sin
[
y f
(x cos
y sin )
f
sin ]cos
xy f
x 1
f
a11 X s Z (a1 f a3x) H
x a12 0 a13 H
x2 a14 f (1 f 2 )
f (x)
f (x0 )
f (x0 )(x x0 )
f
( x0 2!
)
(
x
x0
)2
...
f
(n) (x0 n!
)
(x
x0
)n
Rn (x)
Rn (x)
f (n1) ( )
(n 1)!
(
x
x0
)n1
注意 (x x0 ) 的含义
观测值:像点坐标
x
vx
(x)
x X s
dX s
x Ys
dYs
x Zs
xy a15 f
a16 y
a21 0
a22
-
f H
y a23 H
a24
xy f
a25
f
(1
y2 f 2)
a26 x
N个点的误差方程式的矩阵形式:
间接平差:V AX L
V vx
T
vy
A
a11
a12
a13
a14
1
ctgA ctg
1
xp
PA
•
xA PB • xB PA PB
PC PC
•
xC
yp
PA
•
yA PB • yB PA PB
PC PC
•
yC
PB PC
ctgB ctg
1
ctgC ctg
摄影测量的后方交会 关系式?
像片的外方位元
摄影测量的空间后方交会
当已知(至少)三个空间已知点 A、B 、 C, 与它们在影像上的三个对应点 a、b 、 c,就 能求得影像的 6 个外方位元素。
S (XS、YS、ZS)
c
b
Z
a
C
YA
B
X
其理论基础为:共线方程,
一个点有两个方程,已知三 个点可列6个方程,因此可以
解得6个外方位元素。
二、误差方程式和法方程式(通常在像片的四个角上选取四个地 面控制点)
一个控制点可以列两个方程,至少要三个控制点解六个外 方位元素,有多余观测用平差的方法计算
非线性函数模型。 线性化:按泰勒公式展开,取小值一次项
§5-2 单像空间后方交会
获取六个外方位元素的方法? ✓雷达、GPS、INS、星象相机 ✓地面控制点反算(单像空间后方交会)
POS系统
一、空间后方交会的定义 利用一定数量的地面控制点,根据共线条件方程式,解求像片 外方位元素的过程
z
y
x s(Xs, Ys, Zs)
Z a
bc
Y
A
C
B
X
后方交会
PA
vy
a21dX s
a22dYs
a23dZs
a24d
a25d
a26d
l
y
lx x (x)
ly y (y)
X a1 b1 c1 X X s
X Xs
推导偏导数
令
Y
a2
b2
c2
Y
Ys
R 1
Y
Ys
Z a3 b3 c3 Z Zs
Z Zs
a24
y
( f Y Z
)
f Z2
( Y
Z
Z
Y
)
x sin [ y (x cos y sin ) f sin ]cos
f
a21
y X s
1 Z
(a2 f
a3 y)
a22
y Ys
1 Z
(b2 f
b3 y)
y 1 a23 Zs Z (c2 f c3 y)
a25
y
f
cos
y f
(x sin
第五章 摄影测量解析基础
P(X、Y)
S1
A(xA, yA )
B(xB , yB )
A
a1 a2
S2
观测值:水平角
同名像点坐标?
§5-1 像点坐标量测 同名像点坐标
像点量测
左片像点坐标( x1, y1) 右片像点坐标( x2 , y2 )
x1 X X 0
x2 x1 (P P0 )
y1 Y Y0
xf X Z
yf Y Z
导数四则运算法则: (u ) uv uv
v
v2
x X s
( f X Z
X s
)
f Z
2
X ( X s
Z
Z X s
X)
f Z2
(a1Z
a3
X
)
1 Z
(a1
f
f
X Z
a3 )
1 Z
a1 f
a3x
a24
y
( f Y Z
)
X a1 b1 c1 X X s
X Xs
dZs
x
d
x
d
x
d
y
vy
( y)
y X s
dX s
y Ys
dYs
y Zs
dZs
y
d
y
d
y
d
dX S,dYS,dZS,d,d,d
外方位元素初始值的改正数,能给定合 适的初值才能保证函数展开的准确性
(x),( y) 像点坐标近似值,将外方位元素的初始值代入共线条件方程的计算值
f (x0 )
(x) f a10 ( X X s0 ) b10 (Y Ys0 ) c10 (Z Zs0 ) a30 ( X X s0 ) b30 (Y Ys0 ) c30 (Z Zs0 )
