计数问题竞赛讲义题二
小学奥数数论讲义 第十九讲 数论在方程、计数、最值、行程等问题的应用竞赛篇

第十九讲数论在方程、计数、最值、行程等问题的应用竞赛篇
【例1】
一个正整数A,若满足:A,2×A,3×A,…,99×A这99个数除以100的余数各不相同,则称A为“末尾好数”。
1,2,3,…,2010中有______个“末尾好数”。
【例2】(2008年实验中学考题)
在1,2,3,…,7,8的任意排列中,使得相邻两数互质的排列方式共有____种。
【例3】
甲,乙,丙同时从山脚开始爬山,到达山顶后立即下山,不断往返运动。
已知山坡长360米,甲、乙、丙的速度比为6:5:4,并且甲、乙、丙的下山速度都是各自上山速度的1.5倍。
经过一段时间后,甲到达山顶时,看见乙正在下山,此时乙距离山脚不到180米(乙不在山脚)。
求此时丙离山顶的距离。
2020年初中数学竞赛讲义:计数问题

【难度】★★
【解析】A,
无论是这三种情况中的哪一种,以这6个点为顶点作出所有不重叠的三角形个数都是7个,即 .
故选A.
3.
【难度】★★★
【解析】19,
本题虽然以计算为载体,但首先要有试验观察的能力.
经计算 ,知十位数字为奇数的只有 .
然后,对两位数 ,有 .
其十位数字为 的十位数字加上一个偶数,
所以所组成的数是3的倍数的概率是 .故选C
9.
【难度】★★★
【解析】不妨设 ,由已知等式可得
①
令 , ,则 ,其中 , 均为自然数.
于是,等式①变为 ,即
②
由于 , 均为自然数,判断易知,使得等式②成立的 , 只有两组:
和
⑴当 , 时, , .
又 , , 为三角形的三边长,所以 ,
即 ,解得 .
又因为三角形的周长不超过30,即 ,
, ,
二、
13.
A. B. C. D.
【难度】★★
【解析】B,
设摸出的15个球中有 个红球、 个黑球、 个白球,则 , , 都是正整数,且 , , , .因为 ,所以 可取值2,3,4,5.
当 时,只有一种可能,即 , ;
当 时, ,有2种可能, , 或 , ;
当 时, ,有3种可能, , 或 ,或 , ;
到 ,结果都只各占4个数位,共占 个数位;
到 ,结果都只各占5个数位,共占 个数位;
此时还差 个数位.
到 ,结果都只各占6个数位,共占 个数位.
所以,排在第2008个位置的数字恰好应该是 的个位数字,即为1.
当 时, ,有4种可能, , 或 , 或 , 或 , .
因此,共有 种可能的摸球结果,其中摸出的球中恰好有3个红球的结果有2种,所以所求的概率为 .故选B.
小学四年级奥数竞赛班讲义 第41讲:几何计数
1
【例5】(★★★★) 在下图中只包含一个★的长方形有多少个?
★ ★
【例6】(★★★★) 如图,用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡 皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为 1的三角形有多少个?
【例7】(★★★★★) 图中一共有多少个三角形?
本讲总结 枚举法——按照大小和位置 对应法——找到对应关系 容斥原理——不重不漏 和面积相关——熟悉公式 利用图形对称性 重点例题:例4,例5,例6
几何计数
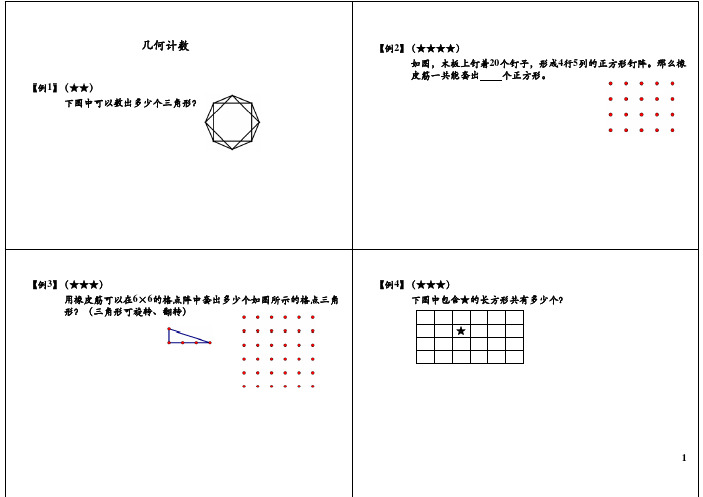
【例1】(★★) 下图中可以数出多少个三角形?
【例2】(★★★★) 如图,木板上钉着20个钉子,形成4行5列的正方形钉阵。那么橡 皮筋一共能套出 个正方形。
【例3】(★★★) 用橡皮筋可以在6×6的格点阵中套出多少个如图所示的格点三角 形?(三角形可旋转、翻转)
【例4】(★★★) 下图中包含★的长方形共有多少个?
2
【竞赛题】人教版小学五年级下册数学第05讲《计数综合》竞赛试题(含详解)

第五讲计数综合从三年级开始到现在,我们已经学了很多有关计数的讲次,其中包括枚举法、加乘原理、排列组合、容斥原理等.我们先来做一个简单的小结和复习.枚举法是万能的方法,只要有足够多的时间和精力.并且往往在一些复杂棘手的题目中,别的方法都不能适用,此时就能体会到枚举法的“威力”.使用枚举法时一定要注意有序思考..... 加法原理强调的是分类,计数时我们只需选择其中的某一类即可以满足要求,类与类之间可以相互替代.乘法原理强调的是分步,每一步只是整个事情的一部分,必须全部完成才能满足结论,缺一不可.在乘法原理中,步骤顺序的安排往往非常重要.排列与组合:排列的计算公式由乘法原理推导而来,组合的计算公式由排列公式推导而来.从n 个不同的元素中取出m 个(m n ≤),并按照一定的顺序排成一列,其方法数叫做从n 个不同元素中取出m 个的排列数,记作m n A .()()()()!121!m n n A n n n n m n m ==⨯-⨯-⨯⨯-+- 从n 个不同元素中取出m 个(m n ≤)作为一组(不计顺序),可选择的方法数叫做从n 个不同元素中取出m 个的组合数,记作m n C .()()()()()121!121m mn nn n n n m A C m m m m ⨯-⨯-⨯⨯-+==⨯-⨯-⨯⨯ 在运用排列组合时,有特殊要求的我们往往优先考虑,有时还会用到“捆绑法”和“插空法”.我们今天主要来学习计数中的分类思想,以及正面分类和反面排除的合理选择.分类讨论是一种重要的数学思想方法,当问题所给对象不能进行统一研究时,就需要对研究的对象进行分类,将整体问题划分为局部问题,把复杂问题转化为单一问题,然后分而治之、各个击破,最后综合各类的结果得到整个问题的解答.例题1.五张卡片上分别写有0、1、2、3、5,每张卡片各用一次可以组成一些五位数.其中5的倍数有多少个?4的倍数有多少个?分析:一个数是5的倍数,它要满足什么条件?4的倍数呢?练习1.五张卡片上分别写有0、1、2、3、5,每张卡片只能用一次可以组成多少个三位偶数?例题2.(1)用2个1、2个2和1个3可以组成多少个不同的五位数?(2)用1个0、2个1和2个2可以组成多少个不同的五位数?(3)用1个0、2个1和2个2可以组成多少个不同的四位数?分析:先选好1的位置,再选好2的位置,最后选好3的位置,就可以组成五位数.那么有多少种不同的选法?练习2.(1)用1个1、1个2、2个3可以组成多少个不同的四位数?(2)用1个0、1个2、2个3可以组成多少个不同的四位数?(3)用1个0、1个2、2个3可以组成多少个不同的三位数?例题3.数1447、1225、1031有某些相同的特点,每一个数都是以1为首的四位数,且每个数恰好只有两个数字相同(1112,1222,1122这样的数不算),这样的数共有多少个?分析:根据题意可知这样的四位数由三种数字组成,其中有一种数字出现了2次.那么可以根据这个数字所在的数位来分类.练习3.用1、2、3、4这4个数字组成四位数,至多允许有1个数字重复一次.例如1234、1233和2434是满足条件的,而1212、3331和4444就是不满足条件的.那么,所有这样的四位数共有多少个?例题4和2468相加至少会发生一次进位的四位数有多少个?分析:和2486相加发生进位有好多种情况,比如发生一次进位、发生两次进位、发生三次进位等等,不同的类型太多了.这时不妨考虑下反面.练习4.和250相加至少会发生一次进位的三位数有多少个?例题5.有10名外语翻译,其中5名是英语翻译,4名日语翻译,另外1名英语和日语都很精通,从中找出7人,使他们可以组成两个翻译小组,其中4人翻译英语,另3人翻译日语,这两个小组能同时工作,则不同的分配方案共有多少种?分析:这个英语和日语都很精通的人很麻烦,应该优先考虑他.例题6.将右图中的“○”分别用四种颜色染色,只要求有实线段连接的两个相邻的“○”都涂成不同的颜色,共有多少种涂法?如果还要求虚线段连接的两个“○”也涂成不同的颜色,共有多少种涂法?分析:染色时顺序很重要,要遵循“前不影响后”的原则.四色定理四色定理指出每个可以画出来的无飞地地图(飞地是指与本土不相连的土地)都可以至多用4种颜色来上色,而且没有两个相邻的区域会是相同的颜色.被称为相邻的两个区域是指它们共有一段边界,而不是一个点.这一定理最初是由Francis Guthrie 在1853年提出的猜想.很明显,3种颜色不会满足条件,而且也不难证明5种颜色满足条件且绰绰有余.但是,直到1977年四色猜想才最终由Kenneth Appel 和Wolfgang Haken 证明.他们得到了J. Koch 在算法工作上的支持.证明方法将地图上的无限种可能情况减少为1,936种状态(稍后减少为1,476种),这些状态由计算机一个挨一个的进行检查.这一工作由不同的程序和计算机独立的进行了复检.在1996年,Neil Robertson 、Daniel Sanders 、Paul Seymour 和Robin Thomas 使用了一种类似的证明方法,检查了633种特殊的情况.这一新证明也使用了计算机,如果由人工来检查的话是不切实际的.四色定理是第一个主要由计算机证明的理论,这一证明并不被所有的数学家接受,因为它不能由人工直接验证.最终,人们必须对计算机编译的正确性以及运行这一程序的硬件设备充分信任.参见实验数学.缺乏数学应有的规范成为了另一个方面;以至于有人这样评论“一个好的数学证明应当像一首诗——而这纯粹是一本电话簿!”虽然四色定理证明了任何地图可以只用四种颜色着色,但是这个结论对于现实中的应用却相当有限.现实中的地图常会出现飞地,即两个不相连的土地属于同一个国家的情况(例如美国的阿拉斯加州),而制作地图时我们仍会要求这两个区域被涂上同样的颜色,在这种情况下,四个颜色将会是不够用的.作业1. 计算:(1) 38C =_________; (2) 48A =_________;作业2. (3) 810C =_________; (4)012345555555C C C C C C +++++=_________. 作业3. 王老师家装修新房,需要2个木匠和2个电工.现有木匠3人、电工4人,另有1人既能做木匠也能做电工.要从这8人中挑选出4人完成这项工作,共有多少种不同的选法?作业4. 用2个3、3个1和1个0可以组成多少个不同的六位数?作业5. 用2个5、1个2和1个0可以组成多少个不同的三位数?作业6. 与1357相加会发生进位的四位数有多少个?俗话说,兴趣是最好的老师。
奥数杯赛-第2讲-专题2-计数综合-学生版

奥数杯赛-第2讲-专题2-计数综合本讲主要内容:1、乘法计数原理;分步完成用乘法;2、图形的计数:分类枚举法、有序枚举法、公式法、容斥原理;3、组合计数;4、排列计数;本讲设计25道题,课后作业5道题。
【1】【2】【3】【4】一个两位数减去它的倒序数(如92的倒序数是29,30的倒序数是3),其差大于0且能被9整除.那么,这样的两位数共有___个.【补充--人大附中考试题】(标数法)图9-1,是小明家和学校的示意图,要求只能向上或者向左行走,那么小明从家到学校的路线中,长度相等的共有()条。
【5】【6】【7】【8】用红黄蓝绿4种颜色对下列字母"XESXSC"进行染色,要求相同字母相同颜色,相邻字母不同颜色,那么,共有()种不同的染色方法。
【9】已知300=2×2×3×5×5,则300有______个不同的约数.【10】在从1到20的自然数中选出2个自然数,使它们的乘积是10的倍数,有_______种选法.【11】将1到10这10个自然数排成一行,使得每相邻3个数的和都是3的倍数.有_________种排法。
【12】如果一个四位数与一个三位数的和是1999,并且这两个数由7个不同的数字组成,那么,这样的四位数有____个.【13】在一个圆上有10个点,以这样的点为端点或顶点,可以画出不同的(1)直线段有()条;(2)三角形有()个;(3)四边形有()个。
【15】用5种不同的颜色给一个正方体涂色,要求相邻的面异色,共有_________种不同的涂色方法.【16】计算:(1)35A (2)28482A -A (3)66A【17】用1、2、3、4、5、6、7、8,可以组成多少个没有重复数字的五位数?【18】幼儿园的6名小朋友去坐3把不同的椅子,有多少种坐法?【提示】3把椅子看作3个位置。
6个小朋友看作6个元素,还有顺序的问题。
So,用排列解释。
初中数学竞赛:计数的方法与原理(含例题练习及答案)

初中数学竞赛:计数的方法与原理计数方法与原理是组合数学的主要课题之一,本讲介绍一些计数的基本方法及计数的基本原理。
一、枚举法一位旅客要从武汉乘火车去北京,他要了解所有可供乘坐的车次共有多少,一个最易行的办法是找一张全国列车运行时刻表,将所有从武汉到北京的车次逐一挑出来,共有多少次车也就数出来了,这种计数方法就是枚举法。
所谓枚举法,就是把所要求计数的所有对象一一列举出来,最后计算总数的方法。
运用枚举法进行列举时,必须注意无一重复,也无一遗漏。
例1四个学生每人做了一张贺年片,放在桌子上,然后每人去拿一张,但不能拿自己做的一张。
问:一共有多少种不同的方法?解:设四个学生分别是A,B,C,D,他们做的贺年片分别是a,b,c,d。
先考虑A拿B做的贺年片b的情况(如下表),一共有3种方法。
同样,A拿C或D做的贺年片也有3种方法。
一共有3+3+3=9(种)不同的方法。
例2甲、乙二人打乒乓球,谁先连胜两局谁赢,若没有人连胜头两局,则谁先胜三局谁赢,打到决出输赢为止。
问:一共有多少种可能的情况?解:如下图,我们先考虑甲胜第一局的情况:图中打√的为胜者,一共有7种可能的情况。
同理,乙胜第一局也有 7种可能的情况。
一共有 7+7=14(种)可能的情况。
二、加法原理如果完成一件事情有n类方法,而每一类方法中分别有m1,m2,…,mn种方法,而不论采用这些方法中的任何一种,都能单独地完成这件事情,那么要完成这件事情共有:N=m1+m2+…mn种方法。
这是我们所熟知的加法原理,也是利用分类法计数的依据。
例 3 一个自然数,如果它顺着数和倒着数都是一样的,则称这个数为“回文数”。
例如1331,7,202都是回文数,而220则不是回文数。
问:1到6位的回文数一共有多少个?按从小到大排,第2000个回文数是多少?解:一位回文数有:1,2,…,9,共9个;二位回文数有:11,22,…,99,共9个;三位回文数有:101,111,…,999,共90个;四位回文数有:1001,1111,…,9999,共90个;五位回文数有:10001,10101,…,99999,共900个;六位回文数有:100001,101101,…,999999,共900个。
第2讲 计数问题

第2讲计数问题一、知识堤要近年来各类试题中频繁出现计数问题,尤其是几何图形计数问题,图形计数顾思义就是数某种图形的个数.数图形的过程中为了避免重数或者漏数,一般先对图形进行分类,分类的时候一是要“全”,不遗漏;二是“不要重”,然后按方位顺序分类进行计数,边数边做记号.常用的计数方法和原理有:枚举法、加法原理、乘法原理、抽屉原理和容斥原理.1,枚举法,枚举法就是将计数的对象一一列举出来.有一些需要计算总数或种类的题.因其数量关系比较隐蔽,很难找到“正统”的方式解答,此时,我们可以先初步估计其数目的大小,若数目不是太大,可按照一定的顺序一一列举出所有的可能情况,要做到不重复、不遗漏(简称:不重不溺),为此,我们的思考就要遵循某种规律,或者说采取某种“有序”的规则。
枚举法,可用文字表述,也可用树形图表示,所得的结果完整、直观,一目了然,但是当题目中的数据较大时,,枚举法的优越性就没有了.2.加法原理完成一件事有k类方法,第一类方法中有种不同的方法,第二类方法中有种不同的方法,……,第k类方法中有种不同的方法.那么,完成这件事共有(种)不同的方法.3.乘法原理如果完成一件事需要n个步骤,其中,做第一步有种不同的方法,做第二步有种不同的方法,……,第n步有种不同的方法,那么完成这件事一共有种不同的方法.乘法原理运用的范围:这件事的规个步骤彼此独立,互不影响.在应用乘法原理时,要注意乘法原理的应用条件:“n个步骤”缺一不可,如果缺少了步骤,那么就不能完成这件事了.4.抽屉原理桌子上有10个苹果,要把这10个苹果放到9个抽屉里,我们发现无论怎样放,至少会有一个抽屉里面放2个苹果.这一现象被称为“抽屉原理”(或鸽巢原理),这是组合数学中一个重要的原理,(1)将多于n个的物体放到n个抽屉里,则至少有一个抽屉里有2个或2个以上的物体.(2)将多于mn+1个的物体放到n个抽屉里,则至少有一个抽屉里有m+1个或多于m+l个的物体。
初中竞赛数学28.计数方法(含答案)

28.计数方法知识纵横所谓计数,通俗地说就是数数,即把我们研究的对象的个数数出来.当研究的对象比较简单,且数目也不大时,枚举法是最基本而又简单的方法,•即把对象的所有可能一一列举出来,数出总数即可.当研究的对象比较复杂,且数目较大时,计数时常常要用到如下两原理: 加法原理:做一件事,完成它可以有n 类办法,在第一类办法中有m 1种不同的方法,在第二类办法中有m 2种不同的方法…,在第n 类办法中有m n 种不同的方法,那么完成这件事共有N=m 1+m 2+…m n 种不同的方法.乘法原理:做一件事,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法……做第n 步有m n 种不同的方法,那么完成这件事共有N=m 1·m 2·…m n 种不同的方法.例题求解 【例1】如图,从甲地到乙地共有4条路可走,从乙地到丙地有3条路可走,从甲地到丙地有5条路可走,那么从甲地到丙地共有_______条. (2000年重庆市竞赛题)思路点拨 从甲地到丙地可分两类办法:直达和转乙地. 解:17 提示:共有3×4+5=17(条)路可走【例2】右图中的小方格是边长为1的正方形,则从图中一共可以数出( )个正方形.A.24B.210C.50D.90(2001年“五羊杯”邀请赛题)思路点拨 图中的正方形可以分成边长为1,边长为2,边长为3,边长为4这4种类型,分别求出每种规格的正方形个数.解:选C 提示:边长为1的正方形为4×6个,边长为2的正方形有3×5个,边长为3的正方形有2×4个,边长为4的正方形有1×3个,共有4×6+3×5+2×4+1×3=50(个)【例3】我们知道,两条直线相交,有且只有一个交点,三条直线相交,•最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n 条直线最多有多少个交点?说明理由.思路点拨 从特殊情况入手,由简到繁,深入思考,从中发现规律.解:提示:三条直线的情形:若平面上已有两条直线,再添一条直线,•则这条直线和原来平面上的两条直线各有一个交点,所以有1+2个交点,同理,4•条直线的情形为在原来三条直线的基础上添加一条直线,共多出3个交点,所以有1+2+3个交点.•一般地,n 条直线两丙乙甲B n+1B i+1B i A n+1A n两相交,其交点数为1+2+…+(n-1)= (1)2n n 个. 【例4】由0、1、2、3、4、5、6这7个数字,可以组成(1)多少个四位数,其中有多少个奇数,有多少个偶数?(2)多少个没有重复数字的四位数,其中有多少个奇数,有多少个偶数?思路点拨 要确定四位数,必须一位一位来考虑,显然计数时,需要用乘法原理,(2)问与(1)问的差别在于,增加了“没有重复”的限制.解:提示:(1)这个四位数的最高位不是0,故最高位有6种选法(即选1~6•中的任一个数字),其余各位,可以从0~6这7个数字中任选,故共有6×7×7×7=2058个四位数,在这些四位数中,奇数的个数也可用类似方法获得,有6×7×7×3=882•个,•偶数2058-882=1176个.(2)同理,没有重复数字的四位数有6×6×5×4=720个,其中奇数有3×5×5×4=300个,其中偶数有720-300=420个.【例5】两条平行直线上各有n 个点,用这n 对点按如下规则连接线段:•①同一直线上的点之间不连接,②连接的任意两条线段可以有共同的端点,但不得有其他的交点.(1)画图说明当n=1,2,3时,连接的线段最多各有多少米?(2)由(1)猜想n(n 为正整数)对点之间连接的线段最多有多少条,证明你的结论;(3)当n=2003时,所连接的线段最多有多少条? (第14•届“希望杯”邀请赛试题) 思路点拨 把直线标记为L 1,L 2,它们上面的点从左到右分别为A 1,A 2,A 3,…A n 和B 1,B 2,•B 3,…B n ,设这n 对点之间连接的直线段最多有p n 条,解题的关键是探讨p n+1与p n 的关系.解:(1)由下图①可以看出,n=1时,最多可以连接1条线段,n=2时,•最多可以连接3条线段,n=3时,最多可以连接5条线段.n=1n=2n=3图① 图②(2)猜想:对于正整数n,这n 对点之间连接的直线段最多有2n-1条.证明:将直线标记为L 1、L 2,它们上面的点从左到右排列分别为A 1,A 2,A 3,…A n 和B 1,B 2,•B 3,…,B n ,设这n 对点之间连接的直线段最多有P n 条,显然,其中必有A n B n 这一条,否则,P n 就不是最多的数.当在L 1、L 2上分别加上第n+1个点时,不妨设这两个点在A n 与B n 的右侧,•那么除了原来已经有的P n 条直线段外,还可以连接A n+1Bn,A n+1B n+1这两条线段,或连接A n B n+1,A n+1B n+1这两条线段.所以P n+1≥P n +2,另一方面,设对于n+1对点有另一种连法:考虑图②中以A n+1为端点的线段,若以A n+1为端点的线段的条数大于1,•则一定可以找到一个i ≤n,使得对于任意的j<i,A n+1B j 都不在所画的线段中,这时,B i+1,B i+2,…,B n+1只能与A n+1连接,不妨设A n+1B i+1,A n+1B i+2,…,A n+1B n+1都已连接,此时图中的线段数为P n+1,我们做如下操作:去掉A n+1B i,连接A n B i+1,得到新的连接图,而新的连接图满足要求且线段总数不变,将此操作一直进行下去,直到与A n+1连接的线段只有一条A n+1B n+1为止.最后图中,与点B n+1相关的线段只剩两条,即A n B n+1,A n+1B n+1,去掉这两条线段,则剩余P n+1-2条线段,而图形恰是n•对点的连接图,所以P n+1-2≤P n.由此我们得到P n+1=P n+2,而P1=1,P2=3,所以P n=1+2×(n-1)=2n-1.(3)当n=2003时,P2003=4005(条).学力训练一、基础夯实1.第一个口袋中装2个球,第二个口袋中装4个球,第三个口袋中装5个球,所有三个口袋中的球各不相同.(1)从口袋中任取一个球,共有______种不同的取法.(2)从三个口袋中各取一个球,有_______种不同的取法.2.如图,在四个正方形拼接成的图形中...,以A1、A2、A3…、A10这十个点中任意三点为顶,共能组成______个等腰直角三角形. (2003年泉州市中考题)(第2题)(第4题)3.画一条直线,可将平面分成2个部分,画2条直线,最多可将平面分成4个部分,•那么,画6条直线最多可将平面分成______个部分. (第14届“希望杯”邀请赛试题)4.一条信息可通过如图的网络线由上(A点)往下向各站点传送.例如信息到b2•点可由经a1的站点送达,也可由经a2的站点送达,共有两条途径传送,则信息由A•点到达d3的不同途径共有( ).A.3条B.4条C.6条D.12条 (2003年南宁市中考题)5.如图,图中不同的线段的条数有( ).A.52条B.63条C.141条D.154条(第5题)(第7题)6.平面内的7条直线任两条都相交,交点数最多有a个,最少有b个,则a+b等于( • ).A.42B.41C.21D.22 (2003年北京市竞赛题)7.如图,在表板上有4个开关,如果相邻的2个开关不能同时是关的,•那么所有不同的状态有( ).A.4种B.6种C.8种D.12种 (第15届江苏省竞赛题)8.如图,左右相邻两点,上下相邻两点之间距离都等于1厘米,把这些点连接起来,作为三角形的顶点,那么可以组成多少个直角三角形?9.用数字0,1,2,3,4可以组成多少个(1)四位数? (2)四位偶数?(3)没有重复数字的四位数?(4)没有重复数字的四位偶数?二、能力拓展10.5人站成一排照相,其中一人必须站在中间,有_____种站法.11.在1到300这300个自然数中,不含有数字3的自然数有_______个.12.跳格游戏:如图,人从格外只能进入第1格;在格中,每次可向前跳1格或2格,•那么人从格外跳到第6格可以有______种方法. (第15届江苏省竞赛题)(第12题) (第13题)13.如图,由18个边长相等的正方形组成的长方形ABCD 中,•包含“※”在内的长方形及正方形一共有_____个. (北京市“迎春杯”竞赛题)14.如图,正方形被分成9个相同的小正方形,一共16个顶点,•以其中不在同一直线上的3个顶点为顶点,可以构成三角形,在这些三角形中,与阴影面积相等的三角形有_______个.(第14题) (第15题) (第16题)15.如图,一共能数出( )个长方形(正方形也算作长方形).A.64B.63C.60D.48 (2000年“五羊杯”竞赛题)16.如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指数轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,•右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b 恰好偶数的不同数对的个数为m,则m n等于( ). A. 12 B. 16 C. 512 D. 34 (2000年山东省竞赛题) 17. (2002年重庆市竞赛题)如图,从A 点B 点(只从左向右,从上到下),共有( )种不同的走法.A.24B.20C.16D.12A18.平面上5个圆最多能把平面分成多少个部分?一般地,n•个圆最多能把平面分成多少个部分?19.5个人站成一排照相.(1)若甲、乙两人必须相邻,则有多少不同的站队方法?(2)若甲、乙两人必不相邻,则有多少不同的站队方法?三、综合创新20. (第11届“希望杯”邀请赛试题)将编号为1,2,3,4,5的5个小球放入编号为1,2,3,4,5的5个盒子中,每个盒子中只放入一个.(1)一共有多少种不同的方法?(2)若编号为1的球恰好放在1号盒子中,共有多少种不同的放法?(3)若至少有一个球放入了同号的盒子中(即对号放入)共有多少种不同的放法?答案1.2+4+5=11(种),2×4×5=40(种)2.243.22 提示:一般地n条直线最多将平面分为2+2+3+…+n=1+1+2+…+n=12(n2+2n+2)部分. 4.C5.D 提示:水平方向上的一类线段共有(6+5+4+3+2+1)×4=84(条)(只考虑线段BC上共有多少条不同的线段),同理,斜方向上的线段共有(4+3+2+1)×7=70条.6.D7.C8.将图中的每一点作为直角三角形的直角顶点时,•这样的直角三角形个数一一算出,注意图形的对称性,共有4×4+5×4+8×1=44(个)9.(1)4×5×5=500(个);(2)4×5×5×3=300(个);(3)4×4×3×2=96(个);(•4)96-2×3×3×2=60(个).10.24 提示:4×3×2×1=24(种)11.242 提示:按数的位数分类:不含3的一位数有8个,不含3的二位数有72个,•不含3的三位数有162个.12.每次跳1格,有惟一的跳法,仅有一次跳2格,其余各次跳1格,有4种跳法,有两次跳2格,其余各次跳1格,有3种跳法,共有1+4+3=8种跳法.13.3614.48 提示:图中等积三角形可分为:底长为3,高长为2的一类三角形有24个;•底长为2,高长为3一类的三角形有32个,扣除其中重复的,故有48个.15.B 提示:不包括第一行的三个小正方形时,可数出(1+2)(1+2+3+4+5)=45•个长方形;包括时,可数出3×(1+2+3)=18个长方形,共计63个.16.C17.B 提示:从A→A n点的走法数量,等于从A到A n•左边一个点的走法数量加上从A到A n上边一个点的走法数量A→B=(A→a14)+(A→a11)=10+10=20(种),•这种计数方法称为逐点标数累计法.18.提示:1个圆最多能把平面分成2个部分,2个圆最多能把平面分成4个部分;•3个圆最多能把平面分成8个部分;现在加入第4个圆,为了使分成的部分最多,第4个圆必须与前面3个圆都有两个交点,如图所示,因此得6个交点,这6个交点将第4•个圆的圆周分成6段圆弧,而每一段圆弧将原来的部分一分为二,即增加了一个部分,•于是4个圆最多将平面分成8+6=14个部分.同理,5个圆最多将平面分成14+8=22个部分,•一般地,n个圆最多分平面为:2+1×2+2×2+…+(n-1)×2=2+[1+2+…+(n-1)]=n2-n+2•个平面.19.提示:(1)把甲、乙两人看成一个整体,与剩下的3人看成4个对象,这4个对象站成一排,共有4×3×2×1×2=48种不同的站队方法(注:甲、•乙两人可以甲在乙左边或右边两种情况).(2)从5个人自由站队总数中减去甲、乙两人必须相邻的情况,剩下的就是甲、•乙两人必不相邻的情况,5个人自由站队总数是5×4×3×2×1=120种,故甲、乙两必不相邻的站队方法有120-48=72种.20.提示:(1)将第一个球先放入,有5种不同的放法;再放入第二个球,这时有4种不同的放法;依此类推,放入第三、四、五个球时,分别有3、2、1种放法,•所以总共有5×4×3×2×1=120种不同的放法.(2)将1号球放在1号盒子中,其余的4个球随意放,它们依次有4、3、2、1•种不同的放法,这样共有4×3×2×1=24种不同的放法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计数问题竞赛讲义二解排列、组合题的基本策略与方法(1)合理分类与准确分步(2)有序排列,无序组合(3)排列、组合混合问题先选后排(4)特殊元素、特殊位置优先(5)正难则反,等价转化(6)相邻问题捆绑处理(7)不相邻问题插空处理策略(8)定序问题除法处理(9)分排问题直排处理(10)构造模型的策略一.有条件限制的排列组合问题例1.甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学。
若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )例 2. 甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是(用数字作答)A.150种B.180种C.300种D.345种例3.有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标数字之和等于10,则不同的排法共有________________种(用数字作答).例4.某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两人至少有一人参加.当甲乙同时参加时,他们两人的发言不能相邻.那么不同的发言顺序的种数为()A.360 B.520 C.600 D.720例5.由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是()A. 36B. 32C.28D.24例6.把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是( ).A168.B96.C72.D144例7.将2个a和2个b共4个字母填在如图所示的16个小方格内,每个小方格内至多填1个字母,若使相同字母既不同行也不同列,则不同的填法共有多少种?(用数字作答)。
解:使2个a既不同行也不同列的填法有C42A42=72种,同样,使2个b既不同行也不同列的填法也有C42A42=72种,故由乘法原理,这样的填法共有722种,其中不符合要求的有两种情况:2个a所在的方格内都填有b 的情况有72种;2个a所在的方格内仅有1个方格内填有b的情况有C161A92=16×72种。
所以,符合题设条件的填法共有722−72−16×72=3960种。
例8.有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共有______________种(用数字作答).二.鞋子配对问题例1.现有5双型号不同的鞋,从中任取4只,按下列条件各有多少种不同的取法?(1)互不配对(2)恰有1双配对(3)恰有2双配对例2.某电视台邀请了6位同学的父母共12人,请这12人中的4位介绍对子女的教育情况,如果这4位中恰有一对是夫妻,那么不同的选择方法有多少?三.分组分配问题本类问题主要集中了三类问题:分组问题,不定向分配问题,定向分配问题例1.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有多少种(用数字作答)?例2.将5名志愿者分配到3个不同的奥运场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为A. 540B. 300C. 180D. 150例3.星期天,有3家人约好外出自驾游,每家都有三口人(两个大人一个孩子),现在他们准备开A,B,C 三辆车,并且规定:(1)每辆车限坐4人;(2)每辆必须有一个大人开车;(3)三个孩子不能乘坐同一辆车。
问满足上述三个条件的乘车方法有多少种?(9180)四.插空处理题型例1.马路上有编号为1~10的十盏路灯,为节电又不影响照明,可以将其中的三盏关掉,但不能同时关掉相邻的两盏或三盏,也不能关掉两端的路灯,问有多少满足条件的关灯方案?(20)例2.某仪表显示屏上有7个小孔,每个小孔可显示0或1,若每次显示其中三个小孔,但相邻两孔不能同时显示,则这个显示屏可以显示多少不同的信号?(80)例3. 一排有14个具有编号的座位,现3个人来坐,要求他们都不坐两边且两人之间必须至少有1个空位,问有多少种不同的坐法?(720)例4. 一排有14个具有编号的座位,现3个人来坐,要求他们每两人之间必须至少有3个空位,问有多少种不同的坐法?(336)例5.5个数码1和4个数码0组成一个二进制的9位数.(1)其中奇数有多少个? (70) (2)数码0不排在一起的偶数有多少个?(10)(3)恰有两个0连在一起,其余0不连在一起的有多少个?(20)例6.某停车场有连成一排的9个停车位,现有5辆不同型号的车需要停放,按下列要求各有多少种停法?(1)5辆车停放的位置连在一起; (2)有且仅有两车连在一起;(3)为方便车辆进出,要求任何3辆车不能在一起.五.隔板模型问题不定方程)(21k n n x x x k ≥=+++ 的正整数解的组数为11--k n C ,非负整数解的组数为11--+k k n C例1.将20个完全相同的小球放入编号为1,2,3,4,5的5个不同的盒子,每个盒中至少有一个小球,那么这20个球有多少种不同的投放方案?例2.将20个完全相同的小球放入编号为1,2,3,4,5的5个不同的盒子,每个盒子的小球数不小于编号数,那么这20个球有多少种不同的投放方案?例3.将24个志愿者名额分配给3个学校,则每校至少有一个名额,则不同的分配方法共有多少种? 例4.(2008)将24个志愿者名额分配给3个学校,则每校至少有一个名额且各校名额互不相同的分配方法共有多少种?解析:设分配给3个学校的名额数分别为123,,x x x ,则每校至少有一个名额的分法数为不定方程:12324x x x ++=.的正整数解的个数,253223=C .又在“每校至少有一个名额的分法”中“至少有两个学校的名额数相同”的分配方法有31种. 综上知,满足条件的分配方法共有253-31=222种.例5.设两个集合},,,,{15321a a a a A =,},,,,{10321b b b b B =,若从A 到B 的映射f 使得B 中的每一个元素都有原象,且)()()(1521a f a f a f ≤≤≤ ,则这样的映射共有多少个?例6.在1,2,3,…,14中,按数从小到大的顺序取出321,,a a a ,使同时满足412≥-a a ,423≥-a a ,则满足条件的不同取法有多少种?例7.求不等式10<++z y x 的正整数解的个数.(84)例8.方程3210321=++++x x x x 有多少个非负整数解.(174)解析:注意到1x 是重根,且只能取1,或2.例9.(2005)如果自然数a 的各位数字之和等于7,那么称a 为“吉祥数”.将所有“吉祥数”从小到大排成一列,,,,321 a a a 若2005=n a ,则=n a 5 。
六.容斥原理:设全集U 是有限集合,n A A A ,,,21 是U 的子集,则有(1)n A A A 21()n n n k j i k j i n i j i j ii A A A A A A A A A 2111111||+<<≤=≤<≤-+-+-=∑∑∑(2)n A A A 21=n A A A 21=U -n A A A 21特别地,当2=n 时,212121A A A A A A -+=;当3=n 时,321A A A =323121321A A A A A A A A A ---+++321A A A . 例1.一次会议有2001位数学家参加,每人至少有1335位合作者,证明:可以找到4位数学家,他们中每两位都合作过。
解析:设与i a 合作过的数学家的集合为i A ,并且设数学家21a a 与合作过,则0200113351335||||||||212121>-+≥-+=A A A A A A所以有数学家213A A a ∈,即213,a a a 与都合作过。
又因为||||||||321321321A A A A A A A A A -+=|||||||||32121321A A A A A A A A --++=32001213353=⨯-⨯≥所以必有3214A A A a ∈,即4a 与321,,a a a 都合作过。
所以总有4位数学家,他们中每两位都合作过。
例2.由数字1,2,3组成的n 位数中,要求1,2,3每个数字至少出现一次,求所有这种n 位数的个数. 解析:由数字1,2,3组成的n 位数的集合记作S ,nS 3||=。
设S 中所有不含k 的n 位数的集合记作)3,2,1(=k A k ,则k A 是S 中所有含有数字k 的n 位数的集合。
321A A A 即是S 中同时含有数字1,2和3的n 位数的全体构成的集合,有公式2得:321A A A ||||||||||||||||321313221321A A A A A A A A A A A A S -+++---= 因为k A 是S 中所有不含k 的n 位数的集合,所以nk A 2||= j i A A 是所有不含数字j i ,的n 位数的集合,所以31,1||≤<≤=j i A A j i因为0||321=A A A 所以满足条件的n 位数的个数为3233||321+⨯-=nn A A A例3.有4对夫妇站成一排,没有任何一对夫妇相邻的站法有多少种? 解析:记}8{人的全排列=S ,),4,3,2,1}{==i i S A i (对夫妇相邻的排列中第则,||88A S =7722||A A A i ⋅=,原题即求||4321A A A A ,易算得:)41(||662222≤<≤⋅⋅=j i A A A A A j i)41(||55222222≤<<≤⋅⋅⋅=k j i A A A A A A A k j i444224321)(||A A A A A A ⋅= 所以由公式可算得13824||4321=A A A A例4.(贝努利装错信封问题)若(1,2,…,n )的一个排列(1i ,2i ,…,n i )满足11≠i ,22≠i ,…,n i n ≠,则称(1i ,2i ,…,n i )为(1,2,…,n )的一个错位排列.试求(1,2,…,n )的所有错位排列的个数. 解析:)!1)1(!31!21!111(!n n n -++-+- . 例5.设)(n ϕ(n 为正整数)表示小于n 且与n 互素的数的个数,求)(n ϕ.分析:1)2(=ϕ,2)3(=ϕ,2)4(=ϕ,4)10(=ϕ,当p 是素数时,1)(-=p p ϕ注意到算术基本定理:对任意不小于2的正整数n 都可以唯一表示为k k p p p n ααα 2121=,其中i p 为n 的质因数,i α是正整数解:由算术基本定理可得 k k p p p n ααα 2121=,其中i p 为n 的质因数,i α是正整数,设U ={1,2,3,…,n },{}U a p a a A i i ∈==),(mod 0,=i 1,2,3,…,k ,注意i A 实际上是i p 的倍数的集合,则i A 是指不是i p 的倍数的集合,k A A A 21即表示从1到n 中与n 互素的数的个数,注意到 ii p n A =,j i j i p p n A A ⋅= ,…,k k p p p n A A A 2121= 于是)(n ϕ=n A A A 21=n A A A 21=U -n A A A 21=n -k k j i j i k i i A A A A A A2111)1(-+-+∑∑≤<≤= =k k k j i j i k i i p p p n p p n p n n 2111)1(-+-⋅+-∑∑≤<≤==)11()11)(11(21kp p p n --- . 七.递推方法1.(斐波那契数列)一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一 对小兔子来.如果所有兔都不死,那么刚出生的一对小兔子一年以后通过繁殖可以得到多少对兔子?理解:每月的大兔子数为上月的兔子数,每月的小兔子数为上月的大兔子数,即上上月的兔子数,相加.2.(汉诺塔问题)设有5个银圈,大小不同,从大到小排列在三根金棒中的一根.这些银圈要搬到另一根金棒上,每次搬一个.第三根金棒作为银圈暂时摆放用.在搬动过程中,仍要保持大圈在下,小圈在上,问至少要搬动多少次,才能将所有银圈从一根棒搬到另一根,且搬完后银圈相对位置不变?(121+=-n n a a )3.(贝努利装错信封问题)推导(1,2,…,n )的所有错位排列的个数为)!1)1(!31!21!111(!n n n -++-+-. 提示:))(1(21--+-=n n n a a n a ,其中01=a ,12=a ,23=a4.(环形涂色问题)一个圆形花坛分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n ),3(+∈≥N n n 份,种植m 种不同颜色的花,要求相邻两部分种植不同颜色的花.(1)如图1,圆环分成的3等份为321,,a a a ,有多少不同的种植方法?如图2,圆环分成的4等份为4321,,,a a a a ,有多少不同的种植方法?(2)如图3,圆环分成的n 等份为n a a a a ,,,,321 ,有多少不同的种植方法?分析可得:⎪⎩⎪⎨⎧--=--==-+nn n m a m m a m m m A a 1133)1()2)(1( ])1()1)[(1(1n n n m m a -+--=-]八.其它的排列组合1.圆排列(1)由},,,,{321n a a a a A =的n 个元素中,每次取出r 个元素排在一个圆环上,叫做一个圆排列(或叫环状排列).(2)圆排列有三个特点:(i )无头无尾;(ii )按照同一方向转换后仍是同一排列;(iii )两个圆排列只有在元素不同或者元素虽然相同,但元素之间的顺序不同,才是不同的圆排列.(3)在},,,,{321n a a a a A =的n 个元素中,每次取出k 个不同的元素进行圆排列,圆排列数为kA k n . 例1.有5对夫妻围圆桌就座,任何一对夫妻都必须相邻,问有多少种不同的入座方法?(768)例2.用F E D C B A ,,,,,六种不同的颜色给正方体的各个面涂色,并使相邻面必须涂不同的颜色,共有多少种不同的涂色方式?(230)2.不尽相异元素的全排列如果n 个元素中,有1p 个元素相同,又有2p 个元素相同,…,又有s p 个元素相同(n p p p s ≤+++ 21),这n 个元素全部取出的排列叫做不尽相异的n 个元素的全排列,它的排列数是!!!!21s p p p n ⋅⋅⋅ 例3.现有10张卡片,每张卡片上写有1、2、3、4、5中的某个数字,其中3张1,3张2,2张3,1张4,1张5,任意取出4张,可组成多少个不同的四位数?3.可重复组合(1)从n 个元素,每次取出允许重复的k 个元素,并成一组叫从n 个元素取出k 个的可重复组合.(2)定理:从n 个元素每次取出k 个元素有重复的组合数为:k k n k n C H )1(-+=.。
