重庆市中考数学压轴题及答案15例
重庆市合川区第一中学2020年中考九年级数学典型压轴题专练:二次函数(包含答案)

重庆市合川区第一中学2020 年中考九年级数学典型压轴题专练:二次函数1、已知二次函数y=ax 2﹣ 2ax+c ( a> 0)的图象与 x 轴的负半轴和正半轴分别交于A、 B 两点,与 y 轴交于点C,它的极点为P,直线 CP与过点 B 且垂直于x 轴的直线交于点D,且CP: PD=2: 3(1)求 A、 B 两点的坐标;(2)若 tan ∠ PDB= ,求这个二次函数的关系式.2、已知二次函数y=x 2+bx+c 的图象与y 轴交于点C( 0,﹣ 6),与 x 轴的一个交点坐标是 A (﹣ 2, 0).(1)求二次函数的分析式,并写出极点 D 的坐标;(2)将二次函数的图象沿x 轴向左平移个单位长度,当y < 0 时,求 x 的取值范围.3、如图,已知抛物线y= ﹣ x2+mx+3与 x 轴交于 A, B 两点,与 y 轴交于点C,点 B 的坐标为(3, 0)(1)求 m的值及抛物线的极点坐标.(2)点 P 是抛物线对称轴l 上的一个动点,当PA+PC的值最小时,求点P 的坐标.4、如图,抛物线y=ax 2+bx﹣ 3( a≠ 0)的极点为E,该抛物线与x 轴交于 A、 B 两点,与y 轴交于点C,且 BO=OC=3AO,直线 y=﹣x+1 与 y 轴交于点D.(1)求抛物线的分析式;(2)证明:△ DBO∽△ EBC;(3)在抛物线的对称轴上能否存在点 P,使△ PBC是等腰三角形?若存在,请直接写出切合条件的 P 点坐标,若不存在,请说明原因.5、课本中有一个例题:有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,假如制作窗框的资料总长为6m,怎样设计这个窗户,使透光面积最大?这个例题的答案是:当窗户半圆的半径约为0.35m 时,透光面积最大值约为 1.05m2.我们假如改变这个窗户的形状,上部改为由两个正方形构成的矩形,如图2,资料总长仍为6m,利用图3,解答以下问题:(1)若 AB为 1m,求此时窗户的透光面积?(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请经过计算说明.6、正方形OABC的边长为 4,对角线订交于点P,抛物线L 经过 O、 P、 A 三点,点E 是正方形内的抛物线上的动点.(1)成立适合的平面直角坐标系,①直接写出 O、P、 A 三点坐标;②求抛物线 L 的分析式;(2)求△ OAE与△ OCE面积之和的最大值.[ 根源 :]7、如图,抛物线y=ax 2+bx﹣ 5( a≠ 0)与x 轴交于点A(﹣ 5, 0)和点B(3, 0),与y 轴交于点 C.(1)求该抛物线的分析式;(2)若点 E 为 x 轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点 E 的坐标;(3)在( 2)的条件下,抛物线上能否存在点P,使∠BAP=∠ CAE?若存在,求出点P 的横坐标;若不存在,请说明原因.8、如图,已知抛物线y=ax 2+bx+c( a≠ 0)经过 A(﹣ 1,0)、B( 3,0)、C( 0,﹣ 3)三点,直线 l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当点P 到点A、点 B 的距离之和最短时,求点P 的坐标;l 上的动点,且△MAC为等腰三角形,请直接写出全部切合条件的点M (3)点M也是直线的坐标.9、如图1,在平面直角坐标系xOy 中,抛物线y=ax 2+1 经过点A( 4,﹣ 3),极点为点B,点 P 为抛物线上的一个动点,l 是过点(0,2)且垂直于y 轴的直线,过P 作PH⊥ l ,垂足为 H,连结PO.(1)求抛物线的分析式,并写出其极点 B 的坐标;(2)①当P 点运动到 A 点处时,计算: PO= ,PH= ,由此发现,PO PH(填“>” 、“<”或“=”);②当 P 点在抛物线上运动时,猜想PO与 PH有什么数目关系,并证明你的猜想;(3)如图 2,设点 C( 1,﹣ 2),问能否存在点 P,使得以 P,O,H为极点的三角形与△ ABC 相像?若存在,求出 P 点的坐标;若不存在,请说明原因.10 、如图,已知抛物线与 x 轴交于 A(﹣ 1 , 0 ), B( 4 , 0 ),与 y 轴交于 C ( 0 ,﹣ 2 ).(1 )求抛物线的解析式;(2 ) H 是 C 关于 x 轴的对称点, P 是抛物线上的一点,当△ PBH 与△ AOC 相似时,求符合条件的 P 点的坐标(求出两点即可);(3 )过点 C 作 CD∥ AB, CD 交抛物线于点 D,点 M 是线段 CD 上的一动点,作直线 MN 与线段 AC 交于点 N,与 x 轴交于点 E,且∠ BME=∠ BDC,当 CN 的值最大时,求点 E 的坐标.11、如图,对称轴为直线 x=2 的抛物线 y=x 2+bx+c 与 x 轴交于点 A 和点 B,与 y 轴交于点 C,且点A 的坐标为(﹣ 1, 0)(1)求抛物线的分析式;(2)直接写出 B、 C 两点的坐标;(3)求过 O, B, C 三点的圆的面积.(结果用含π的代数式表示)注:二次函数y=ax2+bx+c ( a≠ 0)的极点坐标为(﹣,)12、在平面直角坐标系中,平行四边形ABOC如图搁置,点A、C 的坐标分别是(0,4)、(﹣1, 0),将此平行四边形绕点O顺时针旋转90°,获得平行四边形A′B′ OC′.(1)若抛物线经过点C、 A、A′,求此抛物线的分析式;(2)点 M时第一象限内抛物线上的一动点,问:当点M在哪处时,△ AMA′的面积最大?最大面积是多少?并求出此时M的坐标;(3)若 P 为抛物线上一动点,N 为 x 轴上的一动点,点Q坐标为( 1, 0),当 P、N、 B、 Q 构成平行四边形时,求点P 的坐标,当这个平行四边形为矩形时,求点N 的坐标.13、在平面直角坐标系xOy 中,抛物线y=ax2+bx+2 过 B(﹣ 2, 6), C( 2, 2)两点.(1)试求抛物线的分析式;(2)记抛物线极点为 D,求△ BCD的面积;(3)若直线 y=﹣x 向上平移 b 个单位所得的直线与抛物线段BDC(包含端点B、 C)部分有两个交点,求 b 的取值范围.14、如图 1(注:与图 2 完整同样),二次函数y= x2+bx+c 的图象与x 轴交于 A( 3,0),B (﹣ 1, 0)两点,与y 轴交于点C.(1)求该二次函数的分析式;(2)设该抛物线的极点为 D,求△ ACD的面积(请在图 1 中探究);(3)若点 P, Q同时从 A 点出发,都以每秒 1 个单位长度的速度分别沿AB,AC边运动,其中一点抵达端点时,另一点也随之停止运动,当P,Q运动到 t 秒时,△ APQ沿 PQ所在的直线翻折,点 A 恰巧落在抛物线上 E 点处,请直接判断此时四边形 APEQ的形状,并求出 E 点坐标(请在图 2 中探究).15、如图,矩形的边 OA在 x 轴上,边 OC在 y 轴上,点 B 的坐标为( 10, 8),沿直线 OD 折叠矩形,使点 A 正好落在 BC上的 E 处, E 点坐标为( 6,8),抛物线 y=ax2+bx+c 经过 O、A、 E 三点.(1)求此抛物线的分析式;(2)求 AD 的长;(3)点 P 是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P 的坐标.16、如图,抛物线 L: y=ax 2+bx+c 与 x 轴交于 A、 B( 3, 0)两点( A 在 B 的左边),与 y 轴交于点 C( 0, 3),已知对称轴 x=1.(1)求抛物线L 的分析式;(2)将抛物线L 向下平移h 个单位长度,使平移后所得抛物线的极点落在△OBC内(包含△OBC的界限),求 h 的取值范围;(3)设点 P 是抛物线L 上任一点,点Q在直线 l :x=﹣ 3 上,△ PBQ可否成为以点P 为直角极点的等腰直角三角形?若能,求出切合条件的点P 的坐标;若不可以,请说明原因.参照答案 :1、解:( 1)过点 P 作 PE⊥ x 轴于点 E,∵y=ax 2﹣ 2ax+c ,∴该二次函数的对称轴为: x=1,∴O E=1∵OC∥ BD,∴CP: PD=OE:EB,∴OE: EB=2: 3,∴E B= ,∴O B=OE+EB=,∴B(,0)∵A 与 B 对于直线x=1 对称,∴A(﹣,0);(2)过点 C 作 CF⊥ BD于点 F,交 PE于点 G,令 x=1 代入 y=ax 2﹣2ax+c ,∴y=c ﹣ a,令 x=0 代入 y=ax 2﹣2ax+c ,∴y=c∴P G=a,∵CF=OB= ,∴t an ∠ PDB= ,∴F D=2,∵PG∥ BD∴△ CPG∽△ CDF,∴= =∴PG= ,∴a=,∴y= x2﹣ x+c ,把 A(﹣,0)代入y=x2﹣x+c, [ 根源 : ]∴解得: c=﹣ 1,∴该二次函数分析式为:y= x2﹣x﹣ 1.2、解:( 1)∵把 C( 0,﹣ 6)代入抛物线的分析式得:C=﹣6,把 A(﹣ 2,0)代入 y=x 2+bx ﹣6得: b=﹣ 1,∴抛物线的分析式为 y=x 2﹣ x﹣6.∴y= ( x﹣)2﹣.∴抛物线的极点坐标D(,﹣).(2)二次函数的图形沿x 轴向左平移个单位长度得:y=( x+2)2﹣.令 y=0 得:( x+2)2﹣=0,解得: x1=,x2=﹣.∵a> 0,∴当 y< 0 时, x 的取值范围是﹣<x<.3、解:( 1)把点 B 的坐标为( 3, 0)代入抛物线y=﹣x2+mx+3得: 0=﹣ 32 +3m+3,解得: m=2,∴y= ﹣ x2+2x+3=﹣( x﹣ 1)2+4,∴极点坐标为:( 1, 4).(2)连结 BC交抛物线对称轴 l 于点 P,则此时 PA+PC的值最小,设直线 BC的分析式为: y=kx+b ,∵点 C( 0, 3),点 B( 3,0),∴,解得:,∴直线 BC的分析式为:y= ﹣x+3,当x=1 时, y=﹣1+3=2,∴当 PA+PC的值最小时,求点P 的坐标为:(1, 2).4、解:( 1)∵抛物线y=ax2 +bx﹣ 3,∴c= ﹣ 3,∴C( 0,﹣ 3),∴O C=3,∵BO=OC=3AO,∴BO=3, AO=1,∴B( 3, 0), A(﹣ 1, 0),∵该抛物线与x 轴交于 A、 B 两点,∴,∴,∴抛物线分析式为y=x 2﹣ 2x﹣3,(2)由( 1)知,抛物线分析式为 y=x2 ﹣2x﹣ 3=( x﹣ 1)2﹣4,∴E( 1,﹣ 4),∵B( 3, 0), A(﹣ 1, 0), C( 0,﹣3),∴BC=3 , BE=2 ,CE= ,∵直线 y=﹣ x+1 与 y 轴交于点 D,∴D( 0, 1),∵B( 3, 0),∴O D=1, OB=3,BD=,∴,,,∴,∴△ BCE∽△ BDO,(3)存在,原因:设P( 1,m),∵B( 3, 0), C( 0,﹣ 3),∴BC=3,PB=,PC=,∵△ PBC是等腰三角形,①当 PB=PC时,∴=,∴m=﹣ 1,∴P( 1,﹣ 1),②当 PB=BC时,∴3=,∴m=±,∴P( 1,)或P(1,﹣),③当 PC=BC时,∴3 = ,∴m=﹣ 3±,∴P( 1,﹣ 3+ )或 P( 1,﹣ 3﹣),∴切合条件的P点坐标为 P( 1,﹣ 1)或 P( 1,)或 P( 1,﹣)或 P( 1,﹣ 3+ )或 P( 1,﹣ 3﹣)5、解:( 1)由已知可得: AD= ,则 S=1×2 m,(2)设 AB=xm,则 AD=3﹣m,∵,∴,设窗户面积为S,由已知得:,当 x= m时,且 x= m在的范围内,,∴与课本中的例题比较,此刻窗户透光面积的最大值变大.6、解:( 1)以 O点为原点,线段OA所在的直线为x 轴,线段OC所在的直线为y 轴成立直角坐标系,以下图.①∵正方形OABC的边长为 4,对角线订交于点P,∴点 O的坐标为( 0, 0),点 A 的坐标为( 4, 0),点 P 的坐标为( 2,2).②设抛物线L 的分析式为y=ax 2+bx+c ,∵抛物线L 经过 O、 P、 A 三点,∴有,解得:,∴抛物线L 的分析式为y=﹣+2x.(2)∵点 E 是正方形内的抛物线上的动点,∴设点 E 的坐标为( m,﹣+2m)( 0 < m< 4),∴S +S = OA?y + 2 2OC?x =﹣m+4m+2m=﹣( m﹣ 3) +9,△ OAE OCE E E∴当 m=3时,△ OAE与△ OCE面积之和最大,最大值为9.7、解:(1)把 A、 B 两点坐标代入分析式可得,解得,∴抛物线分析式为y= x2+x﹣ 5;2(2)在 y= x + x﹣ 5 中,令 x=0 可得 y=﹣ 5,∴C( 0,﹣ 5),∵S△ABE=S△ABC,且 E 点在 x 轴下方,∴E 点纵坐标和 C 点纵坐标同样,当 y=﹣ 5 时,代入可得x2+ x=﹣ 5,解得 x=﹣ 2 或 x=0(舍去), [ 根源 : ] ∴E 点坐标为(﹣2,﹣ 5);(3)假定存在知足条件的 P 点,其坐标为( m, m2+ m﹣ 5),如图,连结 AP、CE、 AE,过 E 作 ED⊥ AC于点 D,过 P作 PQ⊥ x 轴于点 Q,则 AQ=AO+OQ=5+m,PQ=| m2+m﹣ 5| ,在 Rt △ AOC中, OA=OC=5,则 AC=5,∠ ACO=∠ DCE=45°,由( 2)可得 EC=2,在 Rt △ EDC中,可得 DE=DC=,∴AD=AC﹣ DC=5﹣=4,当∠ BAP=∠ CAE时,则△ EDA∽△ PQA,∴=,即=,∴2( 5+m)或2m+ m﹣5= m+ m﹣ 5=﹣(5+m),当2m﹣5= ( 5+m)时,整理可得2或 m=﹣ 5(与 A 点重合,m+ 4m﹣ 5m﹣ 75=0,解得 m=舍去),当2m﹣5=﹣( 5+m)时,整理可得2或 m=﹣ 5(与 A 点重合,m+ 4m+11m﹣ 45=0,解得 m=舍去),8、解:( 1)将 A(﹣ 1, 0)、B( 3, 0)、 C( 0,﹣ 3)代入抛物线y=ax2 +bx+c 中,得:,解得:故抛物线的分析式:y=x2﹣ 2x﹣3.(2)当 P 点在 x 轴上, P,A,B 三点在一条直线上时,点P 到点 A、点 B的距离之和最短,此时 x=﹣=1,故 P( 1, 0);(3)以下图:抛物线的对称轴为:x=﹣=1,设 M( 1, m),已知 A(﹣ 1, 0)、C( 0,﹣3),则:22222 2MA=m+4,MC=( 3+m) +1=m+6m+10, AC=10;2 2①若 MA=MC,则 MA=MC,得:2 2m+4=m+6m+10,解得: m=﹣ 1,2 2②若 MA=AC,则 MA=AC,得:2m+4=10,得: m=±;2 2③若 MC=AC,则 MC=AC,得:2m+6m+10=10,得: m1=0,m2=﹣ 6;当 m=﹣ 6 时, M、 A、 C 三点共线,构不可三角形,不合题意,故舍去;综上可知,切合条件的M点,且坐标为M(1,)(1,﹣)(1,﹣1)(1,0).9、( 1)解:∵抛物线y=ax2 +1 经过点 A( 4,﹣ 3),∴﹣ 3=16a+1,∴a=﹣, [ 根源 : 学 , 科 , 网 Z,X,X,K]∴抛物线分析式为y=﹣x2+1,极点 B( 0, 1).(2)①当 P 点运动到 A 点处时,∵ PO=5, PH=5,∴PO=PH,故答案分别为 5, 5, =.②结论: PO=PH.原因:设点 P 坐标( m,﹣ m2+1),∵PH=2﹣(﹣m2+1) =m2+1PO=2 = m+1,∴PO=PH.(3)∵ BC==,AC==,AB==4 ∴BC=AC,∵PO=PH,又∵以 P, O, H为极点的三角形与△ABC相像,∴PH与 BC, PO与 AC是对应边,∴=,设点P(m,﹣m2+1),∴=,解得 m=± 1,∴点 P 坐标( 1,)或(﹣1,).10 、解:( 1 )∵抛物线与 x 轴交于 A(﹣ 1, 0), B( 4 , 0),∴设抛物线的解析式为: y=a ( x+1 )( x ﹣ 4 ),把( 0 ,﹣ 2 )代入 y=a ( x+1 )( x ﹣ 4 ),∴a= ,∴抛物线的解析式为: y= x 2﹣x ﹣ 2 ;(2 )当△ PBH 与△ AOC 相似时,∴ △ AOC 是直角三角形,∴ △ PBH 也是直角三角形,由题意知: H( 0 ,2 ),∴ OH=2,∵ A(﹣ 1 , 0 ), B( 4 ,0 ),∴ OA=1, OB=4 ,∴∵ ∠ AOH=∠ BOH,∴ △ AOH∽ △ BOH,∴ ∠ AHO=∠ HBO,∴ ∠ AHO+∠ BHO=∠ HBO+∠ BHO=90 °,∴ ∠ AHB=90 °,设直线 AH 的解析式为: y=kx+b,把A(﹣ 1 , 0 )和 H( 0 , 2 )代入 y=kx+b ,∴,∴ 解得,∴直线 AH 的解析式为: y=2x+2,联立,解得: x=1或x=﹣8,当x= ﹣ 1 时,y=0 ,当x=8 时,y=18∴ P 的坐标为(﹣ 1 , 0 )或( 8, 18 )( 3 )过点 M 作 MF⊥ x 轴于点 F,设点 E 的坐标为( n , 0 ), M 的坐标为( m, 0 ),∵ ∠ BME=∠ BDC,∴ ∠ EMC+∠ BME=∠ BDC+∠ MBD,∴ ∠ EMC=∠ MBD,∵CD∥ x 轴,∴ D 的纵坐标为﹣ 2 ,令 y= ﹣ 2 代入 y= x 2﹣x ﹣ 2 ,∴ x=0或x=3,∴ D( 3,﹣ 2 ),∵ B( 4, 0),∴由勾股定理可求得: BD=,∵ M( m, 0),∴MD=3﹣ m, CM=m( 0 ≤ m≤ 3 )∴由抛物线的对称性可知:∠ NCM=∠ BDC,∴△ NCM∽ △ MDB,∴,∴,∴ CN= =﹣( m﹣)2+ ,∴当 m= 时, CN 可取得最大值,∴此时 M 的坐标为(,﹣ 2 ),∴ MF=2, BF= , MD=∴由勾股定理可求得: MB= ,∵E( n, 0),∴ EB=4 ﹣ n,∵CD∥ x 轴,∴ ∠ NMC=∠ BEM,∠ EBM=∠ BMD,∴ △ EMB∽ △ BDM,∴,∴MB2 =MD? EB,∴= ×( 4 ﹣ n ),∴n= ﹣,∴ E 的坐标为(﹣, 0 ).11、解:( 1)由 A(﹣ 1, 0),对称轴为 x=2,可得,解得,∴抛物线分析式为y=x 2﹣ 4x﹣5;(2)由 A 点坐标为(﹣ 1,0),且对称轴方程为 x=2,可知 AB=6,∴OB=5,∴B 点坐标为( 5, 0),∵y=x 2﹣ 4x﹣ 5,∴C 点坐标为( 0,﹣ 5);(3)如图,连结BC,则△ OBC是直角三角形,∴过 O、 B、 C 三点的圆的直径是线段BC的长度,在Rt △ OBC中, OB=OC=5,∴BC=5 ,∴圆的半径为,∴圆的面积为π()2=π.12、解:( 1)∵平行四边形 ABOC绕点 O顺时针旋转 90°,获得平行四边形 A′ B′OC′,且点 A 的坐标是( 0, 4),∴点 A′的坐标为:( 4, 0),∵点 A、 C的坐标分别是(0, 4)、(﹣ 1, 0),抛物线经过点C、 A、 A′,设抛物线的分析式为:y=ax2+bx+c,∴,解得:,∴此抛物线的分析式为:y=﹣ x2+3x+4;(2)连结 AA′,设直线AA′的分析式为:y=kx+b ,∴,解得:,∴直线 AA′的分析式为:y=﹣ x+4,设点 M的坐标为:( x,﹣ x2+3x+4),则S△AMA′= × 4×[ ﹣ x2+3x+4﹣(﹣ x+4) ]= ﹣ 2x2+8x=﹣2( x﹣ 2)2+8,S△AMA′ =8,∴当 x=2 时,△ AMA′的面积最大,最大值∴M的坐标为:(2, 6);(3)设点 P 的坐标为( x,﹣ x2+3x+4),当 P, N, B, Q构成平行四边形时,∵平行四边形 ABOC中,点 A、 C的坐标分别是( 0, 4)、(﹣ 1, 0),∴点 B 的坐标为( 1, 4),∵点 Q坐标为( 1, 0), P 为抛物线上一动点, N为 x 轴上的一动点,①当 BQ为边时, PN∥ BQ, PN=BQ,∵BQ=4,∴﹣ x2+3x+4= ± 4,当﹣ x2+3x+4=4 时,解得: x1=0, x2=3,∴P1( 0, 4), P2( 3,4);2 ﹣ 4 时,解得: x = , x = ,当﹣ x +3x+4=3 2∴P3(,﹣ 4), P4(,﹣ 4);②当 PQ为对角线时, BP∥ QN, BP=QN,此时 P 与 P , P 重合;1 2综上可得:点P 的坐标为: P1( 0, 4), P2( 3,4), P3(,﹣ 4), P4(,﹣4);如图 2,当这个平行四边形为矩形时,点N的坐标为:(0, 0)或( 3, 0).13、解:( 1)由题意解得,∴抛物线分析式为y=x2﹣ x+2.(2)∵ y= x2﹣ x+2= ( x﹣1)2+ .∴极点坐标(1,),∵直线 BC为 y=﹣ x+4,∴对称轴与BC的交点 H( 1, 3),∴S△BDC=S△BDH+S△DHC=?3+?1=3.(3)由消去y获得x2﹣x+4﹣2b=0,当△ =0 时,直线与抛物线相切,1﹣ 4( 4﹣2b) =0,∴b= ,当直线 y=﹣x+b 经过点 C 时, b=3,当直线 y=﹣x+b 经过点 B 时, b=5,∵直线 y=﹣x 向上平移 b 个单位所得的直线与抛物线段BDC(包含端点B、C)部分有两个交点,∴<b≤ 3.[ 根源 : ZXXK]14、解:( 1)∵二次函数y=x2+bx+c 的图象与 x 轴交于 A( 3, 0), B(﹣ 1, 0),∴,解得:,∴y= x2﹣ x﹣ 4;(2)过点 D 作 DM⊥ y 轴于点 M,∵y= x2﹣x﹣ 4=(x﹣1)2﹣,∴点 D( 1,﹣)、点C(0,﹣4),则S△ACD=S 梯形AOMD﹣ S△CDM﹣ S△AOC= ×( 1+3)×﹣×(﹣4)× 1﹣× 3× 4=4;(3)四边形APEQ为菱形, E 点坐标为(﹣,﹣).原因以下如图 2, E 点对于 PQ与 A 点对称,过点Q作, QF⊥ AP于 F,∵A P=AQ=t, AP=EP, AQ=EQ∴A P=AQ=QE=EP,∴四边形 AQEP为菱形,∵FQ∥ OC,∴== ,∴==∴AF= t , FQ= t ?∴Q( 3﹣t ,﹣t ),∵E Q=AP=t,∴E( 3﹣t ﹣ t ,﹣t ),∵E 在二次函数y= x2﹣x﹣ 4 上,∴﹣t=(3﹣t )2﹣(3﹣t )﹣ 4,∴t=,或t=0(与A重合,舍去),∴E(﹣,﹣).15、解:( 1)∵四边形ABCD是矩形, B( 10, 8),∴A( 10, 0),又抛物线经过A、 E、 O三点,把点的坐标代入抛物线分析式可得,解得,∴抛物线的分析式为y=﹣x2+x;(2)由题意可知: AD=DE,BE=10﹣ 6=4, AB=8,设AD=x,则 ED=x, BD=AB﹣ AD=8﹣ x,在 Rt △ BDE中,由勾股定理可知2 2 2 2 2 2,解得 x=5,ED=EB+BD,即 x =4 +( 8﹣ x)∴AD=5;(3)∵ y=﹣∴其对称轴为x2+x=5,x,∵A、 O两点对于对称轴对称,∴PA=PO,当P、 O、 D 三点在一条直线上时, PA+PD=PO+PD=OD,此时△ PAD的周长最小,如图,连结 OD交对称轴于点 P,则该点即为知足条件的点 P,由( 2)可知 D点的坐标为(10, 5),设直线 OD分析式为y=kx ,把 D 点坐标代入可得5=10k,解得 k=,∴直线 OD分析式为y= x,令x=5,可得 y= ,∴P 点坐标为( 5,).16、解:( 1)∵抛物线的对称轴x=1, B(3, 0),∴A(﹣ 1, 0)∵抛物线y=ax 2+bx+c 过点 C( 0,3)∴当 x=0 时, c=3.又∵抛物线y=ax 2+bx+c 过点 A(﹣ 1, 0), B( 3, 0)∴,∴∴抛物线的分析式为:y=﹣x2+2x+3;(2)∵C(0,3),B(3,0),∴直线BC分析式为y= ﹣x+3,∵y= ﹣ x2+2x+3=﹣( x﹣ 1)2+4,∴极点坐标为( 1, 4)∵对于直线BC:y=﹣ x+1,当 x=1 时, y=2;将抛物线L 向下平移h 个单位长度, [ 根源 : 学 * 科*网 ]∴当 h=2 时,抛物线极点落在BC上;当 h=4 时,抛物线极点落在OB上,∴将抛物线L 向下平移h 个单位长度,使平移后所得抛物线的极点落在△的界限),OBC内(包含△OBC则 2≤ h≤ 4;(3)设 P( m,﹣ m2+2m+3), Q(﹣ 3, n),①当 P 点在 x 轴上方时,过 P 点作 PM垂直于 y 轴,交 y 轴与 M点,过 B 点作 BN垂直于 MP 的延伸线于 N 点,以下图:∵B( 3, 0),∵△ PBQ是以点 P 为直角极点的等腰直角三角形,∴∠ BPQ=90°, BP=PQ,则∠ PMQ=∠ BNP=90°,∠ MPQ=∠ NBP,在△ PQM和△ BPN中,,∴△ PQM≌△ BPN( AAS),∴PM=BN,∵PM=BN=﹣ m2+2m+3,依据 B 点坐标可得PN=3﹣m,且 PM+PN=6,重庆市合川区第一中学2020年中考九年级数学典型压轴题专练:二次函数(包含答案)2∴﹣ m+2m+3+3﹣ m=6,解得: m=1或 m=0,∴P( 1, 4)或 P( 0, 3).②当 P 点在 x 轴下方时,过 P 点作 PM垂直于 l 于 M点,过 B 点作 BN垂直于 MP的延伸线与N 点,同理可得△ PQM≌△ BPN,∴PM=BN,2∴PM=6﹣( 3﹣m) =3+m, BN=m﹣2m﹣ 3,2则 3+m=m﹣ 2m﹣ 3,解得 m=或.∴P(,)或(,).综上可得,切合条件的点P 的坐标是( 1,4),( 0,3),(,)和(,).。
2009-2012年重庆市中考压轴题及答案

1、.(2009年)已知:如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3.过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E . (1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为65,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.1.解:(1)由已知,得(30)C ,,(22)D ,,90AD E C D B BC D ∠=-∠=∠ °, 1tan 2tan 212A E A D A D E B C D ∴=∠=⨯∠=⨯= .∴(01)E ,. ··········································································································· (1分) 设过点E D C 、、的抛物线的解析式为2(0)y ax bx c a =++≠. 将点E 的坐标代入,得1c =.将1c =和点D C 、的坐标分别代入,得42129310.a b a b ++=⎧⎨++=⎩,··································································································· (2分) 解这个方程组,得56136a b ⎧=-⎪⎪⎨⎪=⎪⎩故抛物线的解析式为2513166y x x =-++.··························································· (3分)(2)2E F G O =成立. ························································································ (4分)26题图x点M 在该抛物线上,且它的横坐标为65,∴点M 的纵坐标为125. ······················································································· (5分)设D M 的解析式为1(0)y kx b k =+≠, 将点D M 、的坐标分别代入,得1122612.55k b k b +=⎧⎪⎨+=⎪⎩, 解得1123k b ⎧=-⎪⎨⎪=⎩,. ∴D M 的解析式为132y x =-+. ········································································ (6分) ∴(03)F ,,2E F =. ·························································································· (7分) 过点D 作D K O C ⊥于点K ,则D A D K =.90A D K F D G ∠=∠= °, F D A G D K ∴∠=∠.又90F A D G K D ∠=∠= °,D AF D K G ∴△≌△. 1K G A F ∴==.1G O ∴=. ··········································································································· (8分) 2E F G O ∴=.(3) 点P 在AB 上,(10)G ,,(30)C ,,则设(12)P ,.∴222(1)2PG t =-+,222(3)2PC t =-+,2G C =.①若P G P C =,则2222(1)2(3)2t t -+=-+,解得2t =.∴(22)P ,,此时点Q 与点P 重合.∴(22)Q ,. ·········································································································· (9分) ②若PG G C =,则22(1)22t 2-+=,解得 1t =,(12)P ∴,,此时G P x ⊥轴.G P 与该抛物线在第一象限内的交点Q 的横坐标为1,∴点Q 的纵坐标为73.∴713Q ⎛⎫⎪⎝⎭,. ·······································································································(10分)x③若P C G C =,则222(3)22t -+=,解得3t =,(32)P ∴,,此时2PC G C ==,PC G △是等腰直角三角形. 过点Q 作QH x ⊥轴于点H ,则QH GH =,设QH h =,(1)Q h h ∴+,. 2513(1)(1)166h h h ∴-++++=.解得12725h h ==-,(舍去). 12755Q ⎛⎫∴ ⎪⎝⎭,. ··········································· (12分) 综上所述,存在三个满足条件的点Q ,即(22)Q ,或713Q ⎛⎫ ⎪⎝⎭,或12755Q ⎛⎫⎪⎝⎭,.x2(2010年).已知:如图(1),在平面直角坐标xOy 中,边长为2的等边△OAB 的顶点B在第一象限,顶点A 在x 轴的正半轴上.另一等腰△OCA 的顶点C 在第四象限,OC =AC ,∠C =120°.现有两动点P 、Q 分别从A 、O 两点同时出发,点Q 以每秒1个单位的速度沿OC 向点C 运动,点P 以每秒3个单位的速度沿A →O →B 运动,当其中一个点到达终点时,另一个点也随即停止.(1)求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系,并写出自变量t 的取值范围;(2)在等边△OAB 的边上(点A 除外)存在点D ,使得△OCD 为等腰三角形,请直接写出所有符合条件的点D 的坐标;(3)如图(2),现有∠MCN =60°,其两边分别与OB 、AB 交于点M 、N ,连接MN .将∠MCN 绕着C 点旋转(0°<旋转角<60°),使得M 、N 始终在边OB 和边AB 上.试判断在这一过程中,△BMN 的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.图2图1解:(1)如图,过点Q 作QE 垂直x 轴,垂足为E ,过点C 作CF 垂直x 轴,垂足为F ,在Rt ⊿OQE 中,∵OQ =t ,∠EOQ =30°,sin 30QEOQ︒=,∴sin 302t O E Q O =⨯︒=第一种情况,点P 运动到O 点前: 在⊿OQP 中∵OP =2-3t ,∴11(3)(3)2224O P Q t t t S O P Q E t ∆-=⨯=⨯-=(0<t <23)第二种情况,点Q 运动到C 点前:在⊿OQP 中,∵∠AOQ =30°, ∠BOA =60°,∴∠POQ =90°∴11(32)(32)222O P Q t tS O P O Q t t ∆-=⨯=⨯-=(23<t <3)(2)如图可以看到有三个点:1D (23,0),2D 3,1),3D (433(3)如图将C N A ∆绕着点C 旋转120°(A '与O 重合)使得C N A ∆落到C N A ''∆处.则C N A ∆≌C N A ''∆(旋转的性质)∴C N '=CN , A N ''=AN ,∠NCA =∠N C A '',∴∠NCM =∠N C M '在M C N ∆和C N M '∆中∠NCM =∠N C M ',C N '=CN ,CM =CM ,∴M C N ∆≌C N M '∆,∴M N =N M ',即M N =A N ''+A M ',∴M N =AN +OM , 则△BMN 的周长为:BM +BN +MN =BM +BN +AN +OM =OB +AB =4 所以则△BMN 的周长为定值,这个定值是4.3、(2011•重庆)如图,矩形ABCD中,AB=6,BC=23,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AO H是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由.考点:相似三角形的判定与性质;根据实际问题列二次函数关系式;等腰三角形的性质;等边三角形的性质;矩形的性质;解直角三角形。
重庆市合川中学2019-2020年中考九年级数学典型压轴题专练:一次函数与反比例函数(含答案)

重庆市合川中学2019-2020 学年中考九年级数学典型压轴题专练:一次函数与反比率函数1、如,在平面直角坐系xOy 中,双曲y=与直y=2x+2 交于点 A( 1,a).(1)求 a, m的;(2)求双曲与直 y= 2x+2 另一个交点 B 的坐.2、如,已知直y1=x+1 与 x 交于点A,与直y2=x 交于点 B.(1)求△ AOB的面;( 2)求 y1> y2x 的取范.3、在平面直角坐系中,把横坐都是整数的点称“整点”.(1)直接写出函数 y= 象上的全部“整点” A1, A2, A3,⋯的坐;(2)在( 1)的全部整点中任取两点,用状或列表法求出两点对于原点称的概率.4、环保局对某公司排污状况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超出最高同意的 1.0mg/L .环保局要求该公司立刻整顿,在15 天之内(含15 天)排污达标.整悔过程中,所排污水中硫化物的浓度y( mg/L)与时间x(天)的变化规律如图所示,此中线段AB表示前 3 天的变化规律,从第 3 天起,所排污水中硫化物的浓度y 与时间 x 成反比率关系.(1)求整悔过程中硫化物的浓度y 与时间 x 的函数表达式;(2)该公司所排污水中硫化物的浓度,可否在15天之内不超出最高同意的1.0mg/L ?为什么?5、如图,在平面直角坐标xOy 中,正比率函数y=kx 的图象与反比率函数y=的图象都经过点 A( 2,﹣ 2).(1)分别求这两个函数的表达式;(2)将直线 OA向上平移 3 个单位长度后与 y 轴交于点 B,与反比率函数图象在第四象限内的交点为 C,连结 AB, AC,求点 C 的坐标及△ ABC的面积.6、请用学过的方法研究一类新函数y=(k为常数,k≠ 0)的图象和性质.(1)在给出的平面直角坐标系中画出函数y=的图象;(2)对于函数y=,当自变量x 的值增大时,函数值y 如何变化?7、△ ABC的极点坐标为 A(﹣ 2,3)、B(﹣ 3,1)、C(﹣ 1,2),以坐标原点 O为旋转中心,顺时针旋转 90°,获得△ A′B′ C′,点 B′、 C′分别是点 B、 C 的对应点.(1)求过点 B′的反比率函数分析式;(2)求线段 CC′的长.8、如图,已知一次函数y= x+b 的图象与反比率函数y=(x<0)的图象交于点A(﹣ 1,2)和点 B,点 C 在 y 轴上.(1)当△ ABC的周长最小时,求点 C 的坐标;(2)当x+b<时,请直接写出x 的取值范围.9 、如图,直线 AB 与坐标轴分别交于 A(﹣ 2 , 0 ), B( 0 , 1 )两点,与反比率函数的图象在第一象限交于点 C( 4 , n ),求一次函数和反比例函数的解析式.10、如图,在平面直角坐标系中,直线AB与 x 轴交于点B,与 y 轴交于点A,与反比率函数 y=的图象在第二象限交于点C, CE⊥ x 轴,垂足为点E, tan ∠ ABO= , OB=4,OE=2.(1)求反比率函数的分析式;(2)若点 D 是反比率函数图象在第四象限上的点,过点 D 作 DF⊥y 轴,垂足为点F,连结OD、 BF.假如 S△BAF=4S△DFO,求点 D的坐标.11、如图,直线y=x﹣与x,y轴分别交于点A, B,与反比率函数y=(k>0)图象交于点 C, D,过点 A 作 x 轴的垂线交该反比率函数图象于点E.(1)求点 A 的坐标.(2)若 AE=AC.①求 k 的值.②试判断点 E 与点 D 能否对于原点 O成中心对称?并说明原因.12、在平面直角坐标系中,一次函数y=ax+b( a≠ 0)的图形与反比率函数y=(k≠ 0)的图象交于第二、四象限内的A、 B 两点,与 y 轴交于 C 点,过点 A 作 AH⊥ y 轴,垂足为H,OH=3, tan ∠ AOH= ,点 B 的坐标为( m,﹣ 2).(1)求△ AHO的周长;(2)求该反比率函数和一次函数的分析式.13、如图, Rt△ ABO的极点 O在座标原点,点B在 x 轴上,∠ ABO=90°,∠ AOB=30°, OB=2,反比率函数y=(x>0)的图象经过OA的中点 C,交 AB于点 D.(1)求反比率函数的关系式;(2)连结 CD,求四边形CDBO的面积.14、如图,直线y=ax+b 与反比率函数y=(x>0)的图象交于A( 1, 4), B( 4, n)两点,与 x 轴、 y 轴分别交于C、 D 两点.(1) m= x2,则 y1 ,n=;若M(x1,y1),N(x2,y2)是反比率函数图象上两点,且y2(填“<”或“ =”或“>”);0< x1<(2)若线段CD上的点 P 到 x 轴、 y 轴的距离相等,求点P 的坐标.15、如图,直线y=x+与两坐标轴分别交于A、 B 两点.(1)求∠ ABO的度数;(2)过 A 的直线 l 交 x 轴半轴于 C, AB=AC,求直线 l 的函数分析式.16、如图,点A( m, 4), B(﹣ 4, n)在反比率函数y=(k>0)的图象上,经过点A、 B的直线与x 轴订交于点C,与 y 轴订交于点D.(1)若 m=2,求 n 的值;(2)求 m+n的值;(3)连结 OA、OB,若 tan ∠ AOD+tan∠ BOC=1,求直线 AB的函数关系式.17、如图 1 所示,已知:点A(﹣ 2,﹣ 1)在双曲线C: y=上,直线l 1: y=﹣ x+2,直线l 2与 l 1对于原点成中心对称,F1( 2, 2), F2(﹣ 2,﹣ 2)两点间的连线与曲线C在第一象限内的交点为B, P 是曲线 C 上第一象限内异于 B 的一动点,过P 作 x 轴平行线分别交l 1,l 2于 M, N 两点.(1)求双曲线 C 及直线l 2的分析式;(2)求证:PF2﹣PF1=MN=4;(3)如图 2 所示,△ PF1F2的内切圆与F1F2,PF1,PF2三边分别相切于点Q,R,S,求证:点Q与点 B 重合.(参照公式:在平面坐标系中,如有点A( x1, y1), B( x2,y2),则 A、 B 两点间的距离公式为AB= .)参照答案:1、解:( 1)∵点 A 的坐标是(﹣1, a),在直线y=﹣2x+2 上, [ 根源 :Z 。
重庆初中考数学压轴题——二次函数专题

于A与B点,交y轴交于C点,顶点为D,连接AD。
(1)如图1,P是抛物线的对称轴上的一点,当 时,求P的坐标。
(2)在(1)的条件下,在直线AP上方、对称轴右侧的抛物线上找一点Q,过Q作
,交直线AP于H,过Q作 在抛物线的对称轴上找一点M,使 最大,并求这个最大值及此时M点的坐标。
(3)
,另一边交直线DB于R,是否存在这样的R点,使
(3)如图2, 为 轴上一动点( 不与点 、 重合),作 交直线 于点 ,连接 ,是否存在点 使 ,若存在,请直接写出点 的坐标,若不存在,请说明理由。
图1图2
9.已知抛物线y=﹣x2+2x+c与x轴交于A、B两点,其中点A(﹣1,0).抛物线与y轴交于点C,顶点为D,点N在抛物线上,其横坐标为 .
⑶如图2,直线DN:y=mx+2(m≠0)经过点D,交y轴于点N,点R是已知抛物线上一动点,过点R作直线DN的垂线RH,垂足为H,直线RH交x轴与点Q,当∠DRH=∠ACO时,求点Q的坐标。
4.已知抛物线 与x轴交点A、B,与y轴交于点C,抛物线的顶点为D,点F 是y轴正半轴上一点,
(1)点E是线段BC上一点,连接FB、FE,若△FEB的面积为 ,求点E的坐标;
(3)点Q是线段BD上的动点,将△DEQ延边EQ翻折得到△D′EQ,是否存在点Q使得△D′EQ与△BEQ的重叠部分图形为直角三角形?若存在,请求出BQ的长,若不存在,请说明理由.
8.在直角坐标系 中,抛物线 源自 轴交于 两点,与 轴交于点 连接 。
(1)求 的正弦值。
(2)如图1, 为第一象限内抛物线上一点,记点 横坐标为 ,作 交 于点 轴交于 于点 ,请用含 的代数式表示线段 的长,并求出当 时线段 的长。
重庆历届中考数学压轴题汇总及答案

重庆历届中考数学压轴题汇总及答案(2020年26题.)如图,在中,,,点是边上一动点,连接,把绕点逆时针旋转90°,得到,连接,.点是的中点,连接. (1)求证:; (2)如图2所示,在点运动的过程中,当时,分别延长,,相交于点,猜想与存在的数量关系,并证明你猜想的结论;(3)在点运动的过程中,在线段上存在一点,使的值最小.当的值取得最小值时,的长为,请直接用含的式子表示的Rt ABC △°90BAC ∠=AB AC =D BC AD AD A AE CE DE F DE CF CF AD =D 2BD CD =CF BA G AG BC D AD P PA PB PC ++PA PB PC ++AP m m CE(2019年26题.)(8分)如图,在平面直角坐标系中,抛物线223y x x --=与x 轴交于点A ,B (点A 在点B 的左侧),交y 轴于点C ,点D 为抛物线的顶点,对称轴与x 轴交于点E .(1)连结BD ,点M 是线段BD 上一动点(点M 不与端点B ,D 重合),过点M 作MN BD ⊥,交抛物线于点N (点N 在对称轴的右侧),过点N 作NH x ⊥轴,垂足为H ,交BD 于点F ,点P 是线段OC 上一动点,当MN 取得最大值时,求13HF FP PC ++的最小值;(2)在(1)中,当MN 取得最大值,13HF FP PC ++取得最小值时,把点P 向上平移个单位得到点Q ,连结AQ ,把AOQ △绕点O 顺时针旋转一定的角度α0360α︒︒<<,得到A OQ ''△,其中边A Q ''交坐标轴于点G .在旋转过程中,是否存在一点G ,使得''Q Q OG ∠=∠?若存在,请直接写出所有满足条件的点Q '的坐标;若不存在,请说明理由.(2018年26题)(本小题满分12分)如图,在平面直角坐标系中,点A 在抛物线24y x x =-+上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当PBE △的面积最大时,求12PH HF FO ++的最小值; (3)在(2)中,12PH HF FO ++取得最小值时,将CFH △绕点C 顺时针旋转60后得到CF H ''△,过点F '作CF '的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标;若不存在,请说明理由.(2016年26题.)(本小题满分12分)3在点B 的左侧),与y 轴交于点C ,抛物线的顶点为点E .(1)判断ABC △的形状,并说明理由;(2)经过B ,C 两点的直线交抛物线的对称轴于点D ,点P 为直线BC 上方抛物线上的一动点,当PCD △的面积最大时,点Q 从点P 出发,先沿适当的路径运动到抛物线的对称轴上点M 处,再沿垂直于抛物线对称轴的方向运动到y 轴上的点N 处,最后沿适当的路径运动到点A 处停止.当点Q 的运动路径最短时,求点N 的坐标及点Q 经过的最短路径的长;(3)如图2,平移抛物线,使抛物线的顶点E 在射线AE 上移动,点E 平移后的对应点为点E ',点A 的对应点为点A '.将AOC △绕点O 顺时针旋转至11AOC △的位置,点A ,C 的对应点分别为点1A ,1C ,且点1A 恰好落在AC 上,连接1C A ',1C E '.1A C E ''△是否能为等腰三角形?若能,请求出所有符合条件的点E '的坐标;若不能,请说明理由.(2015年26题) (本小题满分12分)在点B 的左侧),交y 轴于点W ,顶点为C ,抛物线的对称轴与x 轴的交点为D .(1)求直线BC 的解析式;(2)点(,0)E m ,(2,0)F m +为x 轴上两点,其中24m <<.EE ',FF '分别垂直于x 轴,交抛物线于点E ',F ',交BC 于点M ,N .当ME NF ''+的值最大时,在y 轴上找一点R ,使||RF RE ''-的值最大,请求出点R 的坐标及||RF RE ''-的最大值;(3)如图2,已知x 轴上的一点P 9(,0)2,现以P 为顶点,23为边长在x 轴上方作等边三角形QPG ,使QP x ⊥轴,现将QPG △沿PA 方向以每秒1个单位长度的速度平移,当点P 到达点A 时停止.记平移后的QPG △为Q P G '''△,设Q P G '''△与ADC △的重叠部分面积为s .当点Q '到x 轴的距离与点Q '到直线AW 的距离相等时,求s 的值.(2020年)26.【答案】(1)2CF AD =,证明如下:90BAC DAE ︒∠=∠=∵,BAD CAE ∠=∠∴,AB AC =∵,AD AE =,∴在ABD △和ACE △中BAD CAE AB ACAD AE =∠⎧⎪=⎨⎪=⎩, ABD ACE ≅∴△△,45ABD ACE ︒∠=∠=∴,90DCE ACB ACE ︒∠=∠+∠=∴,在Rt ADE △中,F 为DE 中点(同时AD AE =),45ADE AED ︒∠=∠=,AF DE ⊥∴,即Rt ADF △为等腰直角三角形,AF DF AD ==∴, CF DF =∵,CF AD =∴; (2)由(1)得ABD ACE ≅△△,CE BD =,°45ACE ABD ∠=∠=,454590DCB BCA ACE ︒︒︒∠=∠+∠=+=∴,在Rt DCB △中,()2DE BD CE CD ==,F ∵为DE 中点,12DE EF DE ===∴, 在四边形ADCE 中,有90CAG DCE ︒∠=∠=,180CZG DCE ︒∠+∠=,∴点A ,D ,C ,E 四点共圆, F ∵为DE 中点,F ∴为圆心,则CF AF =,在Rt AGC △中,CF AF =∵,F ∴为CG中点,即2CG CF ==,22AG AC DC ⎛⎫== ⎪ ⎪⎝⎭∴,即BC =;(3)设点P 存在,由费马定理可得120APB BPC CPA ︒∠=∠=∠=,60BPD ︒∠=∴,设PD 为a ,BD =∴,又AD BD =,a m +∴, )1m a =a又BD CE =CE ∴. 【解析】(1)先证BAD CAE ≅△△,可得°45ABD ACE ∠=∠=,可求°90BCE ∠=,由直角三角形的性质和等腰直角三角形的性质可得结论.具体解题过程参照答案.(2)由(1)得ABD ACE △≌△,CE BD =,°45ACE ABD ∠=∠=,推出°°°454590DCB BCA ACE ∠=∠+∠=+=,然后根据现有条件说明在Rt DCB △中,DE ==,点A ,D ,C ,E 四点共圆,F 为圆心,则CF AF =,在Rt AGC △中,推出AG ==,即可得出答案.具体解题过程参照答案.(3)设点P 存在,由费马定理可得°120APB BPC CPA ∠=∠=∠=,设PD 为a ,得出BD =,AD BD ==,得出a m +=,解出a ,根据BD CE =即可得出答案.具体解题过程参照答案.【考点】全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,锐角三角函数(2019年26题)【答案】解:(1)如图1∵抛物线223y x x --=与x 轴交于点A ,B (点A 在点B 的左侧),交y 轴于点C ∴令0y =解得:11x =-,23x =,令0x =,解得:3y =-, ∴()1,0A -,()3,0B ,()0,3C -∵点D 为抛物线的顶点,且2122b a --=-=,()2413444441ac b a ⨯⨯---==-⨯∴点D 的坐标为()1,4D -∴直线BD 的解析式为:26y x -=,由题意,可设点2,23N m m m --(),则点26F m m -(,)∴22262343NF m m m m m --+--=()-()=-∴当22bm a=-=时,NF 取到最大值,此时MN 取到最大值,此时2HF =,此时,()2,3N -,()2,2F -,()2,0H在x 轴上找一点K ⎛⎫⎪ ⎪⎝⎭,连接CK ,过点F 作CK 的垂线交CK 于点J 点,交y 轴于点P ,∴1sin 3OCK ∠=,直线KC 的解析式为:3y =--,且点()2,2F -,∴13PJ PC =,直线FJ 的解析式为:442y x +=-∴点J ⎝⎭∴13FP PC +的最小值即为FJ 的长,且1||33FJ =+∴min 1||3HF FP PC ++=;(2)由(1)知,点0,P ⎛ ⎝⎭,∵把点P 个单位得到点Q ∴点()0,2Q -∴在Rt AOQ △中,90AOG ︒∠=,AQ ,取AQ 的中点G ,连接OG ,则12OG GQ AQ ==,此时,AQO GOQ ∠=∠ 把AOQ △绕点O 顺时针旋转一定的角度()0360αα︒︒<<,得到A OQ ''△,其中边A Q ''交坐标轴于点G ①如图2G 点落在y 轴的负半轴,则0,G ⎛ ⎝⎭,过点'Q 作'Q I x ⊥轴交x 轴于点I ,且''GOQ Q ∠=∠则'''IOQ OA Q OAQ ∠=∠=∠,∵sinOQ OAQ AQ ∠=∴sin '2IQ IQ IOQ OQ ''∠'===IO =∴在'Rt OIQ △中根据勾股定理可得OI =∴点'Q 的坐标为'Q ⎝⎭;②如图3,当G 点落在x 轴的正半轴上时,同理可得'Q ⎝⎭③如图4当G 点落在y 轴的正半轴上时,同理可得'Q ⎛ ⎝⎭ ④如图5当G 点落在x 轴的负半轴上时,同理可得'Q ⎛ ⎝⎭综上所述,所有满足条件的点'Q 的坐标为:⎝⎭,⎝⎭,⎛ ⎝⎭,⎛ ⎝⎭【考点】二次函数图象与坐标轴的交点求法,直角三角形的中线性质.(2018年26题)【答案】(1)2(2(3)点S 的坐标为(5,3)或(1,3-+或(1,3-或(1,8)-. 【解析】解:(1)抛物线的对称轴为422(1)x =-=⨯-.令1x =,得3y =.∴点A 的坐标为(1,3). 由抛物线的对称性可得,点B 的坐标为(3,3), ∴线段AB 的长为2.(2)过点E 作EN PH ⊥,交PH 的延长线于点N ,PN 交BE 于点M ,如图1所示.点(1,1)E ,点(3,3)B , ∴直线BE 的解析式为y x =.设点P 的坐标为2(4)(13)t t t t -+,<<, 则点M 的坐标为(,)t t . 则2211221()21(4)(31)3.2PBE PBM PEMS S S PM BH PM EN PM BH EN t t t t t =+=+=+=-++-⨯-=-△△△ 当32t =时,PBE △面积取得最大值,此时点P 的坐标为315,24⎛⎫ ⎪⎝⎭.H 的坐标为3,32⎛⎫ ⎪⎝⎭.3.4PH ∴=过原点O 在y 轴左侧作射线OJ ,使30COJ ∠=,如图2所示,过点H 作HG OJ ⊥,垂足为G ,HG 与y 轴的交点为K ,当点F 与点K 重合时,12FO HF +取得最小值,此时11.22FO HF OK KH KG KH HG +=+=+=3060.GOK OKG CKH ∠=∴∠=∠=,在Rt CHK △中,3602CH CKH =∠=,,30CHK ∴∠=. 3tan302CK CH KH CK ∴=⨯===3OK ∴= 在Rt GOK △中,11322KG OK ⎛==⨯= ⎝⎭HG KG KH ∴=+=+=12PH HF FO ∴++的最小值为34PH HG +==(3)点S 的坐标为(5,3)或(1,3-或(1,3-或(1,8)-.【提示】(1)根据抛物线解析式求出对称轴,并求出点A 的坐标,由对称性得点B 的坐标,从而求出AB 的长;(2)过E 点作PH 的垂线,根据B ,E 两点坐标求出直线BE 的解析式,根据抛物线解析式设点P 的坐标,根据三角形的面积公式求出三角形面积关于P 点横坐标的函数解析式,利用二次函数的性质求得面积的最大值,从而求出点P ,H 的坐标,即可求出PH 的长,然后确定线段和取得最小值的条件,根据条件结合锐角三角函数求出线段的长,从而求出线段和的最小值; (3)根据(2)的结果,结合旋转的性质,根据抛物线的解析式设出点的坐标,表示出线段的长,根据菱形的四边相等,分情况讨论,列出方程,求出待定系数的值,从而求出满足条件的点的坐标.【考点】抛物线的性质、特殊角的三角函数、旋转的性质、菱形的判定和性质.(2016年26题)【答案】(1)△ABC 为直角三角形.理由如下:当y =0时,即21303x -+=,解这个方程,得1x =2x =∴点A (0),B (0).OA ∴=OB =当x =0时,y =3,∴点C (0,3),3OC ∴=.在Rt △AOC 中,22222312AC OA OC =+=+=.在Rt △BOC 中,22222336BC OB OC =+=+=.又2248AB ⎡⎤==⎣⎦,1236=48+,222AC BC AB ∴+=.△ABC 为直角三角形.(2)如图1,点B (0),C (0,3).图1∴直线BC 的解析式为3y =+. 过点P 做PG ∥y 轴交直线BC 于点G .设点P (a ,2133a -+),则点G (a ,3+),21(3)(3)3PG a ∴=-+-+21=3a -+.设D 点横坐标为D x ,C 点横坐标为C x .1()2PCDD C Sx x PG =⨯-⨯211()23a =-2=628a --+.0a <<∴当a =PCD 的面积最大,此时点P ,154).如图1,将点P 'P ,连接'AP 交y 轴于点N ,过点N 做NM ⊥抛物线对称轴于点M ,连接PM .点Q 沿P M N A →→→运动,所走的路径最短,即最短路径的长为PM +MN +NA 的长.又点A (0),∴ 直线'AP 的解析式为52y =+. 当x =0时,52y =,点N (0,52).过'P 作'P H ⊥x 轴于点H ,则有HA =15'4P H =,'AP =.∴点Q 运动的最短路径的长为PM MN AN ++=(3)如图2,在Rt △AOC 中,图2tanOC OAC OA ∠===60OAC ∴∠=︒.1OA OA =,1OAA ∴为等边三角形,1=60AOA ∠︒. 130BOC ∠=︒.又由13OC OC ==,得点1C (2,32).点A (0),E 4),AE ∴=.''A E AE ∴==直线AE 的解析式为2y x =+,设点'E (a 2+),则点A (a -2-).22213'(2)2C E a ∴=++-27=733a -+22213A'(2)2C a =-+--27=4933a -+若1'''C A A E =,则有221'''C A A E =,即22777=4933a a ++.解这个方程,得a =∴点'E ,5) 若1'''A C A E =,则有221'''A C A E =即2749=2833a a -+解这个方程,得1a =,2a =.∴点'E 7+或7.若1'''E A E C =,则有221'''E A E C =,即277=283a +.解这个方程,得12a ,22a (舍去).∴点'E ,3+.综上所述,符合条件的点'E 的坐标为,5)或7或,7或,3+. 【考点】直角三角形的判定,利用待定系数法求一次函数、二次函数的解析式,轴对称的性质,等腰三角形的性质(2015年26题)【答案】(1)y =+(2)R ,max '-'4RF RE =(3)S =【解析】(1)y =+ (2)22'(E M =++=+-2'F N =+故:2''E M F N +=+-当3m ==时,''E M F N +最大,此时E F∵'':E F y =+∵(0R ,max '-'4RF RE =(3)由题意,Q 点在CAB ∠的角平分线或外角平分线上 ①当Q 点在CAB ∠的角平分线上时,如图''Q M Q N ==,CW ='RMQ RNC ∆∆∽,故'RQRN =+△CRN ∵△CWO,故CN =∵4DN CD CN =-=故S =∵当Q 点在的外角平分线上时,如图'Q RN WCO △∽△,故'Q R =RM =RCM WCO △∽△,故CM =在''Rt Q MP ∆中,''3AM M ==,故''3CP MP CM =-=-在'Rt CP S ∆中,'P S =故S =综上所述,当点Q '到x 轴的距离与Q '到直线AW的距离相等时,S =S =.【提示】(1)求出抛物线与x 轴的交点坐标和顶点坐标,用待定系数法求解析式即可; (2)先求出E′、F′的坐标表示,然后求出E′M 、F′N ,用二次函数的顶点坐标求出当3m =时,''ME NF +的值最大,得到E′、F′的坐标,再求出E′F′的解析式,当点R 在直线E′F′与y 轴的交点时,||RF RE ''﹣的最大值,从而求出R 点的坐标及||RF RE ''﹣的最大值; (3)分类讨论Q 点在∠CAB 的角平分线或外角平分线上时,运用三角形相似求出相应线段,在求出△Q′P′G′与△ADC 的重叠部分面积为S . 【考点】二次函数综合题。
2020-2021重庆备战中考数学压轴题专题一元二次方程组的经典综合题

2020-2021重庆备战中考数学压轴题专题一元二次方程组的经典综合题2020-2021重庆备战中考数学压轴题专题一元二次方程组的经典综合题一、一元二次方程1.随着经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,汽车消费成为新亮点.抽样调查显示,截止2008年底全市汽车拥有量为14.4万辆.已知2006年底全市汽车拥有量为10万辆.(1)求2006年底至2008年底我市汽车拥有量的年平均增长率;(2)为保护城市环境,要求我市到2010年底汽车拥有量不超过15.464万辆,据估计从2008年底起,此后每年报废的汽车数量是上年底汽车拥有量的10%,那么每年新增汽车数量最多不超过多少辆?(假定每年新增汽车数量相同)【答案】详见解析【解析】试题分析:(1)主要考查增长率问题,一般用增长后的量=增长前的量×(1+增长率)解决问题;(2)参照增长率问题的一般规律,表示出2010年的汽车拥有量,然后根据关键语列出不等式来判断正确的解.试题解析:(1)设年平均增长率为x ,根据题意得:10(1+x )2=14.4,解得x=﹣2.2(不合题意舍去)x=0.2,答:年平均增长率为20%;(2)设每年新增汽车数量最多不超过y 万辆,根据题意得:2009年底汽车数量为14.4×90%+y ,2010年底汽车数量为(14.4×90%+y )×90%+y ,∴(14.4×90%+y )×90%+y≤15.464,∴y≤2.答:每年新增汽车数量最多不超过2万辆.考点:一元二次方程—增长率的问题2.某建材销售公司在2019年第一季度销售,A B 两种品牌的建材共126件,A 种品牌的建材售价为每件6000元,B 种品牌的建材售价为每件9000元.(1)若该销售公司在第一季度售完两种建材后总销售额不低于96.6万元,求至多销售A 种品牌的建材多少件?(2)该销售公司决定在2019年第二季度调整价格,将A 种品牌的建材在上一个季度的基础上下调%a ,B 种品牌的建材在上一个季度的基础上上涨%a ;同时,与(1)问中最低销售额的销售量相比,A 种品牌的建材的销售量增加了1%2a ,B 种品牌的建材的销售量减少了2%3a ,结果2019年第二季度的销售额比(1)问中最低销售额增加2%23a ,求a 的值.【答案】(1)至多销售A 品牌的建材56件;(2)a 的值是30.【解析】【分析】(1)设销售A 品牌的建材x 件,根据售完两种建材后总销售额不低于96.6万元,列不等式求解;(2)根据题意列出方程求解即可.【详解】(1)设销售A 品牌的建材x 件.根据题意,得()60009000126966000x x +-≥,解这个不等式,得56x ≤,答:至多销售A 品牌的建材56件.(2)在(1)中销售额最低时,B 品牌的建材70件,根据题意,得()()()12260001%561%90001%701%6000569000701%2323a a a a a -?+++?-=?+?+ ? ? ?,令%a y =,整理这个方程,得21030y y -=,解这个方程,得1230,10y y ==,∴10a =(舍去),230a =,即a 的值是30.【点睛】本题考查了一元二次方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.3.已知关于x 的一元二次方程x 2﹣x+a ﹣1=0.(1)当a=﹣11时,解这个方程;(2)若这个方程有两个实数根x 1,x 2,求a 的取值范围;(3)若方程两个实数根x 1,x 2满足[2+x 1(1﹣x 1)][2+x 2(1﹣x 2)]=9,求a 的值.【答案】(1)123,4x x =-=(2)54a ≤(3)-4【解析】分析:(1)根据一元二次方程的解法即可求出答案;(2)根据判别式即可求出a 的范围;(3)根据根与系数的关系即可求出答案.详解:(1)把a =﹣11代入方程,得x 2﹣x ﹣12=0,(x +3)(x ﹣4)=0,x +3=0或x ﹣4=0,∴x 1=﹣3,x 2=4;(2)∵方程有两个实数根12x x ,,∴△≥0,即(﹣1)2﹣4×1×(a ﹣1)≥0,解得54a ≤:;(3)∵12x x ,是方程的两个实数根,222211221122101011x x a x x a x x a x x a -+-=-+-=∴-=--=-,,,.∵[2+x 1(1﹣x 1)][2+x 2(1﹣x 2)]=9,∴221122229x x x x +-+-=,把22112211x x a x x a -=--=-,代入,得:[2+a ﹣1][2+a ﹣1]=9,即(1+a )2=9,解得:a =﹣4,a =2(舍去),所以a 的值为﹣4.点睛:本题考查了一元二次方程,解题的关键是熟练运用判别式以及根与系数的关系.4.“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨52m %,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了920m 元,购买数量在原计划基础上增加15m %,最终,在两个网站的实际消费总额比原计划的预算总额增加了152m %,求出m 的值.【答案】(1)120;(2)20.【解析】试题分析:(1)本题介绍两种解法:解法一:设标价为x 元,列不等式为0.8x ?80≤7680,解出即可;解法二:根据单价=总价÷数量先求出1个礼盒最多花费,再除以折扣可求出每个礼盒在花店的最高标价;(2)先假设学生会计划在这两个网站上分别购买的礼盒数为a 个礼盒,表示在“大众点评”网上的购买实际消费总额:120a (1﹣25%)(1+52m %),在“美团”网上的购买实际消费总额:a [120(1﹣25%)﹣920m ](1+15m %);根据“在两个网站的实际消费总额比原计划的预算总额增加了152m %”列方程解出即可.试题解析:(1)解:解法一:设标价为x 元,列不等式为0.8x ?80≤7680,x ≤120;解法二:7680÷80÷0.8=96÷0.8=120(元).答:每个礼盒在花店的最高标价是120元;(2)解:假设学生会计划在这两个网站上分别购买的礼盒数为a 个礼盒,由题意得:。
2024年重庆市中考数学压轴题

2024年重庆市中考数学压轴题一、在直角三角形ABC中,角C为直角,AC等于3,BC等于4,以点C为圆心,半径为2的圆与AB边的位置关系是?A. 相离B. 相切C. 相交D. 无法确定(答案)B。
解析:首先利用勾股定理计算出斜边AB的长度,AB等于根号下(AC平方加BC 平方)等于5。
接着计算点C到AB边的距离,即直角三角形ABC的面积除以AB边的一半,面积等于二分之一乘以AC乘以BC等于6,所以点C到AB边的距离为6除以5等于1.2,小于圆的半径2,但圆的半径又小于AB边的一半(5除以2等于2.5),因此圆与AB边相切。
二、已知二次函数y等于ax平方加bx加c的图像经过点(1,0),(2,0),(0,2),则a的值为?A. 1B. -1C. 2D. -2(答案)B。
解析:将三个点的坐标代入二次函数,可以得到三个方程:a加b加c等于0,4a加2b加c等于0,c等于2。
解这个方程组,可以得到a等于-1,b等于1,c等于2。
三、一个正方体的内切球半径为2,则这个正方体的体积为?A. 8B. 32C. 64D. 128(答案)C。
解析:正方体的内切球半径等于正方体边长的一半,所以正方体的边长为4,体积为边长的三次方,即4的三次方等于64。
四、在平行四边形ABCD中,E为AD的中点,F为BC上的一点,且BF等于四分之一BC,连接EF,与对角线AC相交于点G,则AG与GC的比值为?A. 1:2B. 1:3C. 2:3D. 3:4(答案)C。
解析:过E做BC的平行线,交AC于H,则EH等于四分之一BC,且EH平行于FC,所以三角形EHG与三角形CFG相似,且相似比为1:3,所以AG与GC的比值为2:3。
五、已知等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为?A. 9B. 12C. 15D. 18(答案)C。
解析:等腰三角形的两边长相等,且大于第三边,所以腰长为6,底边长为3,周长为6加6加3等于15。
重庆市合川中学2019-2020学年中考九年级数学典型压轴题专练:统计初步(含答案解析)

重庆市合川区第一中学2020年中考九年级数学典型压轴题专练:统计初步1、根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图:(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;(2)求这天5路公共汽车平均每班的载客量;(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.2、为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):根据统计图中的信息,解答下列问题:(1)求本次被调查的学生人数.(2)将条形统计图补充完整.(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.3、为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:(1)求“非常了解”的人数的百分比.(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?4、某校八年级学生在学习《数据的分析》后,进行了检测.现将该校八年级(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).(1)补全条形统计图;(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?(4)小明的成绩为88分,他的成绩如何,为什么?【逐步提示】(1)在表格中查到得96的人数是6,据此不全条形图;(2)根据众数、中位数的定义求解;(3)用500乘以96分以上(含96分)的人数所占的百分比即可得解;(4)把小明的成绩和平均数、中位数、众数作对比,即可对小明的成绩做出判断.5、秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:分数段频数频率60≤x<70 9 a70≤x<80 36 0.480≤x<90 27 b90≤x≤100 c 0.2请根据上述统计图表,解答下列问题:(1)在表中,a= ,b= ,c= ;(2)补全频数直方图;(3)根据以上选取的数据,计算七年级学生的平均成绩.(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?6、某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.请你根据以上提供的信息,解答下列问题:(1)补全上面的条形统计图和扇形统计图;(2)所抽取学生对数学学习喜欢程度的众数是;(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?7、某校为了解该校九年级学生适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:(说明:A等级:135分﹣150分 B等级:120分﹣135分,C等级:90分﹣120分,D等级:0分﹣90分)(1)此次抽查的学生人数为;(2)把条形统计图和扇形统计图补充完整;(3)若该校九年级有学生1200人,请估计在这次适应性考试中数学成绩达到120分(包含120分)以上的学生人数.8、中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:抽取的200名学生海选成绩分组表组别海选成绩xA组50≤x<60B组60≤x<70C组70≤x<80D组80≤x<90E组90≤x<100请根据所给信息,解答下列问题:(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为15 ,表示C组扇形的圆心角θ的度数为度;(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?9、海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?10、为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)节目类型新闻体育动画娱乐戏曲人数36 90 a b 27根据表、图提供的信息,解决以下问题:(1)计算出表中a、b的值;(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?11、在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m ),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(Ⅰ)图1中a 的值为 ;(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m 的运动员能否进入复赛.12、某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图:请你根据以上的信息,回答下列问题:(1) 本次共调查了_____名学生,其中最喜爱戏曲的有_____人;在扇形统计图中,最喜爱30%8%6%动画新闻体育娱乐戏曲体育的对应扇形的圆心角大小是______;(2) 根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.13、某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;(1)这次抽样调查的样本容量是,并补全条形图;(2)D等级学生人数占被调查人数的百分比为8% ,在扇形统计图中C等级所对应的圆心角为°;(3)该校九年级学生有1500人,请你估计其中A等级的学生人数.14、为了解七年级学生上学期参加社会实践活动的情况,随机抽查A市七年级部分学生参加社会实践活动天数,并根据抽查结果制作了如下不完整的频数分布表和条形统计图.A市七年级部分学生参加社会实践活动天数的频数分布表天数频数频率3 20 0.104 30 0.155 60 0.306 a 0.257 40 0.20A市七年级部分学生参加社会实践活动天数的条形统计图根据以上信息,解答下列问题;(1)求出频数分布表中a的值,并补全条形统计图.(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.15、为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.分组频数4.0≤x<4.2 24.2≤x<4.4 34.4≤x<4.6 54.6≤x<4.8 84.8≤x<5.0 175.0≤x<5.2 5(1)求所抽取的学生人数;(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.16、某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为个小组打,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:小组研究报告小组展示答辩甲91 80 78乙81 74 85丙79 83 90(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?17、为了解某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:(1)该市场6月上半月共销售这三种荔枝多少吨?(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?18、某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:(1)本次抽取样本容量为,扇形统计图中A类所对的圆心角是度;(2)请补全统计图;(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?19、为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对概念机学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.20、某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图:设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.(1)若n=9,求y与x的函数关系式;(2)若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.答案:1、、【解答】解:(1)A组对应扇形圆心角度数为:360°×=72°;这天载客量的中位数在B组;(2)各组组中值为:A: =10,B: =30;C: =50;D: =70;==38(人),答:这天5路公共汽车平均每班的载客量是38人;(3)可以估计,一个月的总载客量约为38×50×30=57000=5.7×104(人),答:5路公共汽车一个月的总载客量约为5.7×104人.2、【解答】解:(1)60÷30%=200(人),即本次被调查的学生有200人;(2)选择文学的学生有:200×15%=30(人),选择体育的学生有:200﹣24﹣60﹣30﹣16=70(人),补全的条形统计图如下图所示,(3)1600×(人).3、【解答】解:(1)由题意可得,“非常了解”的人数的百分比为:,即“非常了解”的人数的百分比为20%;(2)由题意可得,对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有:1200×=600(人),即对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有600人.4、解:(1)补全条形统计图如下:(2)该班学生成绩的中位数为90分,众数为90分;(3)∵6+540×500≈138.∴估计有138名学生的成绩在96分以上(含96分).(4)小明的成绩为88分,他的成绩处于中偏下水平,因为小明的成绩比班级平均成绩高,但比班级学生成绩的中位数和众数低.5、【解答】解:(1)抽查的学生数:36÷0.4=90,a=9÷90=0.1,b=27÷90=0.3,c=90×0.2=18,故答案为:0.1,0.3,18;(2)补全的频数分布直方图如右图所示,(3)∵=81,即七年级学生的平均成绩是81分;(4)∵800×(0.3+0.2)=800×0.5=400,即“优秀”等次的学生约有400人.6、【解答】解:(1)由题意可得,调查的学生有:30÷25%=120(人),选B的学生有:120﹣18﹣30﹣6=66(人),B所占的百分比是:66÷120×100%=55%,D所占的百分比是:6÷120×100%=5%,故补全的条形统计图与扇形统计图如右图所示,(2)由(1)中补全的条形统计图可知,所抽取学生对数学学习喜欢程度的众数是:比较喜欢,故答案为:比较喜欢;(3)由(1)中补全的扇形统计图可得,该年级学生中对数学学习“不太喜欢”的有:960×25%=240(人),即该年级学生中对数学学习“不太喜欢”的有240人.7、【解答】解:(1)由题意可得,此次抽查的学生有:36÷24%=150(人),故答案为:150;(2)A等级的学生数是:150×20%=30,B等级占的百分比是:69÷150×100%=46%,D等级占的百分比是:15÷150×100%=10%,故补全的条形统计图和扇形统计图如右图所示,(3)1200×(46%+20%)=792(人),即这次适应性考试中数学成绩达到120分(包含120分)以上的学生有792人.11118、【解答】解:(1)D的人数是:200﹣10﹣30﹣40﹣70=50(人),补图如下:(2)B组人数所占的百分比是×100%=15%,则a的值是15;C组扇形的圆心角θ的度数为360×=72°;故答案为:15,72;(3)根据题意得:2000×=700(人),答:估计该校参加这次海选比赛的2000名学生中成绩“优等”的有700人.9、【解答】解:(1)12÷20%=60,答:共调查了60名学生.(2)60﹣12﹣9﹣6﹣24=9,答:最喜爱的教师职业人数为9人.如图所示:(3)×1500=150(名)答:该中学最喜爱律师职业的学生有150名.10、【解答】解:(1)∵喜欢体育的人数是90人,占总人数的20%,∴总人数==450(人).∵娱乐人数占36%,∴a=450×36%=162(人),∴b=450﹣162﹣36﹣90﹣27=135(人);(2)∵喜欢动画的人数是135人,∴×360°=108°;(3)∵喜爱新闻类人数的百分比=×100%=8%,∴47500×8%=3800(人).答:该地区七年级学生中喜爱“新闻”类电视节目的学生有3800人.11、【解答】解:(Ⅰ)根据题意得:1﹣20%﹣10%﹣15%﹣30%=25%;则a的值是25;故答案为:25;(Ⅱ)观察条形统计图得:==1.61;∵在这组数据中,1.65出现了6次,出现的次数最多,∴这组数据的众数是1.65;将这组数据从小到大排列为,其中处于中间的两个数都是1.60,则这组数据的中位数是1.60.(Ⅲ)能;∵共有20个人,中位数是第10、11个数的平均数,∴根据中位数可以判断出能否进入前9名;∵1.65m>1.60m,∴能进入复赛.12、【答案】(1)50,3,72°;(2)160人【解析】(1)本次共调查学生:4÷8%=50(人),最喜爱戏曲的人数为:50×6%=3(人),∵“娱乐”类人数占被调查人数的百分比为:18100%36% 50⨯=,∴“体育”类人数占被调查人数的百分比为:1-8%-30%-36%-6%=20%,在扇形统计图中,最喜爱体育的对应扇形圆心角大小事360°×20%=72°;(2)2000×8%=160(人).13、【解答】解:(1)由条形统计图和扇形统计图可知总人数=16÷32%=50人,所以B等级的人数=50﹣16﹣10﹣4=20人,故答案为:50;补全条形图如图所示:(2)D等级学生人数占被调查人数的百分比=×100%=8%;在扇形统计图中C等级所对应的圆心角=8%×360°=28.8°,故答案为:8%,28.8;(3)该校九年级学生有1500人,估计其中A等级的学生人数=1500×32%=480人.14、【解答】解:(1)由题意可得:a=20÷01×0.25=50(人),如图所示:;(2)由题意可得:20000×(0.30+0.25+0.20)=15000(人),答:该市七年级学生参加社会实践活动不少于5天的人数约为15000人.15、【解答】解:(1)∵频数之和=40,∴所抽取的学生人数40人.(2)活动前该校学生的视力达标率==37.5%.(3)①视力4.2≤x<4.4之间活动前有6人,活动后只有3人,人数明显减少.②活动前合格率37.5%,活动后合格率55%,视力保健活动的效果比较好.16、【解答】解:(1)由题意可得,甲组的平均成绩是:乙组的平均成绩是:丙组的平均成绩是:从高分到低分小组的排名顺序是:丙>甲>乙;(2)由题意可得,甲组的平均成绩是:乙组的平均成绩是:丙组的平均成绩是:由上可得,甲组的成绩最高.17、【解答】解:(1)120÷30%=400(吨).[来源:学§科§网Z§X§X§K] 答:该市场6月上半月共销售这三种荔枝400吨;(2)500×=300(千克).答:该商场应购进C品种荔枝300千克比较合理.18、【解答】解:(1)由题意可得,抽取的学生数为:10÷20%=50,扇形统计图中A类所对的圆心角是:360°×20%=72°,故答案为:50,72;(2)C类学生数为:50﹣10﹣22﹣3=15,C类占抽取样本的百分比为:15÷50×100%=30%,D类占抽取样本的百分比为:3÷50×100%=6%,补全的统计图如图所示,(3)300×30%=90(名)即该校九年级男生“引体向上”项目成绩为C类的有90名.19、【解答】解:根据题意,阅读了6本的人数为100×30%=30(人),阅读了7本的人数为:100﹣20﹣30﹣﹣15=35(人),补全条形图如图:∵平均每位学生的阅读数量为: =6.45(本),∴估计该校七年级全体学生在2015年全年阅读中外名著的总本数为800×6.45=5160本,答:估计该校七年级全体学生在2015年全年阅读中外名著的总本数约为5160本.20、【解答】解:(1)当n=9时,y==;(2)根据题意,“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,则“更换笔芯的个数不大于同时购买笔芯的个数”的频数大于30×0.5=15,根据统计图可得,需要更换笔芯的个数为7个对应的频数为4,8个对应的频数为6,9个对应的频数为8,因此当n=9时,“更换笔芯的个数不大于同时购买笔芯的个数”的频数=4+6+8=18>15.因此n的最小值为9.(3)若每支笔同时购买9个笔芯,则所需费用总和=(4+6+8)×3×9+7×(3×9+5×1)+5×(3×9+5×2)=895,若每支笔同时购买10个笔芯,则所需费用总和=(4+6+8+7)×3×10+5×(3×10+5×1)=925,因此应购买9个笔芯.。
2023重庆中考数学b卷压轴题26题

2023重庆中考数学b卷压轴题26题题目:已知二次函数y=x²-2x-3一、对题目进行分析,这道题主要考察二次函数的性质和图像,需要理解二次函数的表达式,掌握其对称轴和开口方向等信息。
二、解题步骤:1. 根据二次函数表达式,我们可以得到对称轴为直线x=1,开口向上。
2. 在B卷压轴题中,通常需要考生进行一些复杂的计算和推理。
首先,我们需要找到函数图像与x轴的交点,这可以通过令y=0来求解。
解方程x²-2x-3=0,得到x₁=3,x₂=-1。
也就是说,函数图像与x轴有两个交点(-1,0)和(3,0)。
3. 将已知的两个交点坐标代入图像中,可以得到图像大致呈抛物线形状,开口向上,与x轴有两个交点(-1,0)和(3,0)。
对称轴为直线x=1。
4. 接下来,我们需要根据题目要求,求出函数图像与直线y=4的交点坐标。
将直线y=4代入二次函数表达式中,得到一元二次方程x²-2x-7=0。
解得,该方程的两个解分别为x₃=5和x₄=-2。
也就是说,图像与直线y=4有两个交点(5,4)和(-2,4)。
5. 最后,根据题目要求,求出图像与直线y=-2的交点与对称轴的间距。
由于题目中未给出具体的坐标值,因此需要进行一些简单的代数计算。
综上,通过以上步骤的推理和计算,我们可以得出以下结论:当x=1时,y=2当x=-2时,y=-5当x=5时,y=4因此,函数图像与直线y=-2的交点坐标为(5,4),该点与对称轴的距离为4。
三、总结:这道题考察了二次函数的性质和图像,需要考生具备一定的数学基础和推理能力。
解题的关键在于理解二次函数的表达式,掌握其对称轴和开口方向等信息,并能够进行一些复杂的计算和推理。
同时,考生还需要注意题目中的细节和要求,确保解题的准确性和完整性。
备战2023年重庆中考数学二轮复习知识点精练14 二次函数压轴题(含详解)

精练14--二次函数压轴题1.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC、BC.(1)求抛物线的函数表达式;(2)点P为直线BC下方抛物线上一动点,连接OP交BC于点E,当的值最大时,求点P的坐标和的最大值;(3)把抛物线y=x2+bx+c向右平移1个单位,再向下平移2个单位,得到新抛物线y′,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,请直接写出所有符合条件的N点的坐标,并任选其中一个N点,写出求N点的坐标的过程.2.如图1,二次函数y =ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、点B(点A在点B左侧),与y轴交于点C(0,3),tan∠CBO=.(1)求二次函数解析式;(2)如图2,点P是直线BC上方抛物线上一点,PD∥y轴交BC于D,PE∥BC交x 轴于点E,求PD+BE的最大值及此时点P的坐标;(3)在(2)的条件下,当PD+BE取最大值时,连接PC,将△PCD绕原点O顺时针旋转90°至△P'C'D';将原抛物线沿射线CA方向平移个单位长度得到新抛物线,点M在新抛物线的对称轴上,点N为平面内任意一点,当以点M,N,C′,D′为顶点的四边形是矩形时,请直接写出点N的坐标.3.如图,已知直线BC的解析式为y=x﹣3,抛物线y=x2+bx+c与坐标轴交于A、B、C三点.(1)求抛物线的解析式;(2)如图1,若M(m,y1),N(4﹣m,y2)是第四象限内抛物线上的两个动点,且m <2.分别过点M,N作x轴的垂线,交线段BC于点D、E.通过计算证明四边形MDEN 是平行四边形,并求其周长的最大值;(3)抛物线y=x2+bx+c沿射线CB方向平移个单位,得到新抛物线y1,点F为y1的对称轴上任意一点,若以点B,C,F为顶点的三角形是以BC为腰的等腰三角形,直接写出所有符合条件的点F的坐标.4.如图,已知抛物线y=ax2+bx+2的图象与x轴交于A,B两点,与y轴交于点C.﹣1,3是关于x的一元二次方程ax2+bx+2=0的两个根.(1)求该抛物线的解析式;(2)过点A作AD∥BC交抛物线于点D,AD与y轴交于点E,P为直线BC上方抛物线上的一个动点,连接P A交BC于点F,求S△PEF的最大值及此时点P的坐标;(3)在(2)的条件下,点M为抛物线上一动点,在平面内找一点N,是否存在以点A,M,N,P为顶点的四边形是以P A为边的矩形?若存在,请直接写出点N的坐标,若不存在,请说明理由.5.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中A(﹣1,0),OB=4OA,tan∠CAB=3,连接AC、BC.(1)求该抛物线的解析式;(2)如图2,过A作AD∥BC,交抛物线于点D,点P为直线BC下方抛物线上任意一点,连接DP,与BC交于点E,连接AE,当△APE面积最大时,求点P的坐标及△APE 面积的最大值;(3)如图3,在(2)的条件下,将抛物线先向右平移个单位,再向上平移3个单位后与x轴交于点F、G(点F在点G的左侧),点Q为直线AC上一点,连接QP、QG、PG,当△QPG是以PG为腰的等腰三角形时,请直接写出点Q的坐标.6.如图1,在平面直角坐标系xOy中,抛物线y=x2+bx+c(b、c为常数)与y轴交于点C,对称轴为直线x=﹣3,点N(﹣4,﹣5)在该抛物线上.(1)求该抛物线的函数表达式;(2)连接CN,点P是直线CN下方抛物线上一动点,过点P作PH∥y轴交直线CN于点H,在射线CH上有一点G使得PH=PG.当△PGH周长取得最大值时,求点P的坐标和△PGH周长的最大值;(3)如图2,在(2)的条件下,直线l:y=x﹣与x轴、y轴分别交于点E、F,将原抛物线沿着射线FE方向平移,平移后的抛物线与x轴的右交点恰好为点E,动点M 在平移后的抛物线上,点T是平面内任意一点,是否存在菱形METP,若存在,请直接写出点T的横坐标,若不存在,请说明理由.7.如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的图象与x轴交于点A(1,0)、B两点,与y轴交于点C(0,﹣3),且抛物线的对称轴为直线x=﹣1.(1)求抛物线的解析式;(2)在直线BC下方的抛物线上有一动点P,过点P作PM⊥x轴,垂足为点M,交直线BC于点N,求PN+CN的最大值,并求出此时点P的坐标;(3)如图2,若抛物线沿射线AC方向平移个单位长度得到抛物线y',点E为新抛物线y'上一点,点F为原抛物线对称轴上一点,取(2)中最大值时点P,是否存在以点B、P、E、F构成的平行四边形?若存在,直接写出点E的坐标,若不存在,请说明理由.8.如图1,抛物线y=ax2+bx+4交x轴于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC,BC.(1)求此抛物线的解析式;(2)P是抛物线上位于直线BC上方的一个动点,过点P作PQ∥y轴交BC于点Q;过点P作PE⊥BC于点E,过点E作EF⊥y轴于点F,求出2PQ+EF的最大值及此时点P 的坐标;(3)如图2,将抛物线y=ax2+bx+4沿着射线CB的方向平移,使得新抛物线y′过点(3,1),点D为原抛物线y与新抛物线y′的交点,若点G为原抛物线的对称轴上一动点,点H为新抛物线y′上一动点,直接写出所有使得以A,D,G,H为顶点的四边形为平行四边形的点H的坐标,并把求其中一个点H的坐标的过程写出来.9.在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式;(2)如图1,点P是直线上方抛物线上的一点,过点P作PD∥AC交BC于E,交x轴于点D,求PE+BE的最大值以及此时点P的坐标;(3)在(2)的条件下,将抛物线沿着射线CA方向平移个单位长度得到新抛物线y1,新抛物线y1和原抛物线相交于点F.新抛物线y1的顶点为点G,点M是直线FG上的一动点,点N为平面内一点.若以P、G、M、N四点为顶点的四边形为菱形,请直接写出点N的坐标,并写出求解其中一个N点的过程.10.如图,在平面直角坐标系xOy中,抛物线y=x2+x﹣2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A的坐标;(2)如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为S1,△AEO的面积为S2,求S1﹣S2的最大值及此时点D的坐标;(3)如图2,将抛物线沿射线CB方向平移个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线与y轴的交点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.11.如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与直线交于x轴上的点B,y轴上的点C,且其对称轴为直线.该抛物线与x轴的另一交点为点A,顶点为M.(1)求抛物线的解析式及顶点M的坐标;(2)如图2,长度为的线段DF在线段BC上滑动(点D在点F的左侧),过D,F 分别作y轴的平行线,交抛物线于E,P两点,连接PE.求四边形PFDE面积的最大值及此时点P坐标;(3)在(2)问条件下,当四边形PFDE面积有最大值时,记四边形PFDE为四边形P1F1D1E1.将四边形P1F1D1E1沿直线BC平移,点P1,E1关于直线BC的对称点分别是点P2,E2.在平移过程中,当点P2,E2中有一点落到抛物线上时,请直接写出点P2,E2的坐标.1 2.如图,抛物线y=x2+bx+c与x轴相交于点A(﹣1,0)和点B,交y轴于点C,.(1)求抛物线的解析式;(2)如图1,P点为一象限内抛物线上的一个动点,D点是BC中点,连接PD,BD,PB.求△BDP面积的最大值以及此时P点坐标;(3)如图2,将抛物线向左平移1个单位长度,得到新的抛物线y1,M为新抛物线对称轴上一点,N为直线AC上一动点,在(2)的条件下,是否存在点M,使得以点P、B、M、N为顶点的四边形为平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于点A(﹣6,0),B(4,0),与y 轴交于点C.(1)求该抛物线的解析式;(2)如图1,点D与点C关于抛物线的对称轴对称,连接BD交y轴于点G,作直线OD,点P为线段BD上方的抛物线上任意一点,过点P作PE∥y轴交BD于点E,过点P作PF⊥直线OD于点F.当PE+PF为最大时,求这个最大值及此时点P的坐标;(3)如图2,连接BC,CD,将△OCD绕点O顺时针旋转α(0°<α<90°)得到△OC'D',使得C'D'∥BC,将线段OD'沿射线C'O平移得到O'D″,连接AO′,AD″,请问在平移过程中,是否存在△AO'D″是以O'D″为直角边的直角三角形,若存在,请直接写出D″的坐标,若不存在,请说明理由.14.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0),交y轴于点C,且OC=3.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;(3)把抛物线y=ax2+bx+c平移,使得新抛物线的顶点为(2)中求得的点P,R为新抛物线上一点,S是新抛物线对称轴上一点,直接写出所有使得以点A,C,R,S为顶点的四边形是平行四边形的点R的坐标,并把其中一个求点R的坐标过程写出来.15.如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(﹣2,0),直线BC的解析式为y=x﹣4.(1)求抛物线的解析式.(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标.(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.16.如图,在平面直角坐标系中,抛物线交x轴于A、B两点(点A在点B左侧),交y轴于点C,一次函数y=kx+b(k≠0)与抛物线交于B、D两点,已知cos∠ABD=.(1)求点D的坐标;(2)点F是抛物线的顶点,连接BF.P是抛物线上F、D两点之间的任意一点,过点P 作PE∥BF交BD于点E,连接PF、PD、FE.求四边形PFED面积的最大值及相应的点P的坐标;(3)连接AC,将抛物线沿射线AC方向平移个单位长度得到新抛物线y',新抛物线与原抛物线交于点G.S是原抛物线对称轴上一点,T是平面内任意一点,G、S、A、T四点能否构成以AS为边的菱形?若能,请直接写出点T的坐标;若不能,请说明理由.精练14--二次函数压轴题1.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC、BC.(1)求抛物线的函数表达式;(2)点P为直线BC下方抛物线上一动点,连接OP交BC于点E,当的值最大时,求点P的坐标和的最大值;(3)把抛物线y=x2+bx+c向右平移1个单位,再向下平移2个单位,得到新抛物线y′,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,请直接写出所有符合条件的N点的坐标,并任选其中一个N点,写出求N点的坐标的过程.【解答】解:(1)将A(﹣2,0),B(4,0)代入y=x2+bx+c,得,解得,∴抛物线的函数表达式为y=x2﹣x﹣4.(2)如图1,作PG⊥x轴于点G,交BC与点F,抛物线y=x2﹣x﹣4,当x=0时,y=﹣4,∴C(0,﹣4),设直线BC的函数表达式为y=kx﹣4,则4k﹣4=0,解得k=1,∴直线BC的函数表达式为y=x﹣4,设P(x,x2﹣x﹣4),则F(x,x﹣4),∴PF=x﹣4﹣(x2﹣x﹣4)=﹣x2+2x,∵PF∥OC,∴△PEF∽△OEC,∴==(﹣x2+2x)=﹣(x﹣2)2+,∴当x=2时,的值最大,最大值为,此时P(2,﹣4),∴点P的坐标为(2,﹣4),的最大值为.(3)∵y=x2﹣x﹣4=(x﹣1)2﹣,∴该抛物线向右平移1个单位,再向下平移2个单位,得到的新抛物线为y′=(x﹣2)2﹣,即y′=x2﹣2x﹣,该抛物线的对称轴为直线x=2,顶点坐标为(2,﹣),如图2,BC的中点为Q(2,﹣2),当点M与抛物线的顶点重合时,则点N与点M(2,﹣)关于点Q(2,﹣2)对称,∵BQ=CQ,MQ=NQ,∴四边形BMCN是平行四边形,此时N(2,);如图3,四边形BCMN是平行四边形,且点M在直线x=2的左侧,过点M作直线x=2的垂线,垂足为点R,∵MN∥BC,QN∥y轴,∴∠MNR=∠BQN=∠BCO,∵MN=BC,∠MRN=∠BOC=90°,∴△MRN≌△BOC(AAS),∴RN=OC=4,RM=OB=4,∴点M的横坐标为﹣2,抛物线y′=x2﹣2x﹣,当x=﹣2时,y′=,∴M(﹣2,),R(2,),∴y N=+4=,∴N(2,);如图4,四边形BCNM是平行四边形,且点M在直线x=2的右侧,过点M作直线x=2的垂线,垂足为点H,∵MN∥BC,QN∥y轴,∴∠MNH=∠BQH=∠BCO,∵MN=BC,∠MHN=∠BOC=90°,∴△MHN≌△BOC(AAS),∴HN=OC=4,HM=OB=4,∴点M的横坐标为6,抛物线y′=x2﹣2x﹣,当x=6时,y′=,∴M(6,),H(2,),∴y N=﹣4=﹣,∴N(2,﹣),综上所述,点N的坐标为(2,)或(2,)或(2,﹣).2.如图1,二次函数y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、点B(点A在点B左侧),与y轴交于点C(0,3),tan∠CBO=.(1)求二次函数解析式;(2)如图2,点P是直线BC上方抛物线上一点,PD∥y轴交BC于D,PE∥BC交x 轴于点E,求PD+BE的最大值及此时点P的坐标;(3)在(2)的条件下,当PD+BE取最大值时,连接PC,将△PCD绕原点O顺时针旋转90°至△P'C'D';将原抛物线沿射线CA方向平移个单位长度得到新抛物线,点M在新抛物线的对称轴上,点N为平面内任意一点,当以点M,N,C′,D′为顶点的四边形是矩形时,请直接写出点N的坐标.【解答】解:(1)∵点C的坐标为(0,3),∴OC=3,∵tan∠CBO==,∴OB=6,∴点B的坐标为(6,0),由抛物线经过点A(﹣2,0),B(6,0)设抛物线的解析式为y=a(x+2)(x﹣6),将点C(0,3)代入解析式为a×(0+2)×(0﹣6)=3,∴a=﹣,∴抛物线的解析式为y=﹣(x+2)(x﹣6)=﹣x2+x+3.(2)过点P作PF∥x轴交BC于点F,∵PE∥BC,∴四边形PEBF为平行四边形,∴PF=BE,∴PD+BE=PD+PF,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=﹣x+3,设点P的坐标为(m,﹣m2+m+3),则点D的坐标为(m,﹣m+3),∴PD=﹣m2+m+3﹣(﹣m+3)=﹣m2+m,∵PF∥x轴,∴点F和点P的纵坐标相等,即﹣x+3=﹣m2+m+3,∴x=m2﹣2m,∴点F的坐标为(m2﹣2m,﹣m2+m+3),∴PF=m﹣(m2﹣2m)=﹣m2+3m,∴PD+BE=﹣m2+m+(﹣m2+3m)=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,PD+BE的最大值为,此时,点P的坐标为(3,);(3)由(2)中得,点P的坐标为(3,),∴点D的坐标为(3,),∵△PCD绕着点O顺时针旋转90°得到△P'C'D',C(0,3),∴点C'的坐标为(3,0),点D'的坐标为(,﹣3),∵A(﹣2,0),C(0,3),∴AC==,∵抛物线沿射线CA方向平移,∴抛物线向左平移了1个单位长度,向下平移了个单位长度,∴平移后抛物线的对称轴为直线x==1,设点M(1,y),N(a,b),C'(3,0),D'(,﹣3),①以MN为对角线时,如图①,有x M+x N=x C'+x D',y M+y N=y C'+y D',C'M2+C'N2=MN2,∴,解得:或,∴点N的坐标为(,﹣+)或(,﹣﹣);②以MC'为对角线时,如图②,有x M+x C'=x N+x D',y M+y C'=y N+y D',C'M2=C'N2+MN2,∴,解得:,∴点N的坐标为(,);③以MD'为对角线时,如图③,有x M+x D'=x N+x C',y M+y D'=y N+y C',C'M2+MN2=C'N2,∴,解得:,∴点N的坐标为(﹣,﹣2);综上所述,当以点M,N,C′,D′为顶点的四边形是矩形时,点N的坐标为(,﹣+)或(,﹣﹣)或(,)或(﹣,﹣2).3.如图,已知直线BC的解析式为y=x﹣3,抛物线y =x2+bx+c与坐标轴交于A、B、C三点.(1)求抛物线的解析式;(2)如图1,若M(m,y1),N(4﹣m,y2)是第四象限内抛物线上的两个动点,且m <2.分别过点M,N作x轴的垂线,交线段BC于点D、E.通过计算证明四边形MDEN 是平行四边形,并求其周长的最大值;(3)抛物线y=x2+bx+c沿射线CB方向平移个单位,得到新抛物线y1,点F为y1的对称轴上任意一点,若以点B,C,F为顶点的三角形是以BC为腰的等腰三角形,直接写出所有符合条件的点F的坐标.【解答】解:(1)∵直线BC的解析式为y=x﹣3,令y=0,则x=4,即点B是(4,0)令x=0,则y=﹣3,即点C是(0,﹣3).把点B(4,0),点C(0,﹣3).代入到抛物线y=x2+bx+c中.得.∴抛物线的解析式为y=x2﹣x﹣3(2)∵若M(m,y1),N(4﹣m,y2)是第四象限内抛物线上的两个动点,∴y1=m2−m−3,y2=(4﹣m)2−(4﹣m)−3.∵直线BC的解析式为y=x﹣3.∵过点M,N作x轴的垂线,分别交线段BC于点D,E,∴D(m,m−3),E(4﹣m,﹣m).∴MD=﹣(m2﹣m﹣3)﹣(3﹣m)=﹣m2+4m,∴EN=﹣(4﹣m)2+4(4﹣m)=﹣m2+4m.∴MD=EN.∵过点M,N作x轴的垂线,分别交线段BC于点D,E,∴MD∥EN.∴四边形MDEN为平行四边形.过D作DF⊥NE于F,则DF=4﹣2m,如图,∵B(4,0),C(0,﹣3).∴OB=4,OC=3.∴BC=5.∵DF∥OB.∴∠EDF=∠OBC.∵∠COB=∠DFE=90°,∴△DFE∽△BOC.∴=.∴=.∴DE=(2﹣m).∴平行四边形MDEN的周长=2MD+2DE=2(﹣m2+4m)+2×(2﹣m)=﹣2m2+3m+10.∵﹣2m2+3m+10=﹣2(m−)2+,又﹣2<0,∴当m=时,四边形MDEN的周长有最大值.(3)设平移后的抛物线的解析式为:y1=x2+b1x+c1,点C平移后对应的点C1的坐标为(t,t﹣3),点B平移后对应的点B1的坐标为(s,t﹣3),其中,t>0,s>4.∵抛物线y=x2+bx+c沿射线CB方向平移个单位,C(0,﹣3),B(4,0),∴CC1==,BB1==.解得:t=,s=.∴C1的坐标为(,﹣),B1的坐标为(,﹣).∴,解得:.∴y1=x2﹣6x+.∴抛物线的对称轴为直线:x=3.∵点F为y1的对称轴上任意一点,∴设点F的坐标为(3,n).∵B(4,0),C(0,﹣3),∴BC=.∵以点B,C,F为顶点的三角形是以BC为腰的等腰三角形,∴当BF=BC时,=5,解得:n=+2.∴点F的坐标为(3,2)或(3,﹣2).当CF=BC时,=5,解得:n=1或﹣7.∴点F的坐标为(3,1)或(3﹣7).综上所述:符合条件的点F的坐标为(3,2)或(3,﹣2)或(3,1)或(3,﹣7).4.如图,已知抛物线y=ax2+bx+2的图象与x轴交于A,B两点,与y轴交于点C.﹣1,3是关于x的一元二次方程ax2+bx+2=0的两个根.(1)求该抛物线的解析式;(2)过点A作AD∥BC交抛物线于点D,AD与y轴交于点E,P为直线BC上方抛物线上的一个动点,连接P A交BC于点F,求S△PEF的最大值及此时点P的坐标;(3)在(2)的条件下,点M为抛物线上一动点,在平面内找一点N,是否存在以点A,M,N,P为顶点的四边形是以P A为边的矩形?若存在,请直接写出点N的坐标,若不存在,请说明理由.【解答】解:(1)∵﹣1,3是关于x的一元二次方程ax2+bx+2=0的两个根,∴,解得,∴该抛物线的解析式为y=x2+x+2.(2)如图1,作PH⊥x轴,交AD于点H,作PG⊥AD于点G,作BK⊥AD于点K.当y=0时,x1=﹣1,x2=3,则A(﹣1,0)、B(3,0);当x=0时,y=2,则C(0,2).设直线BC的解析式为y=kx+2,则3k+2=0,解得k=,∴y=x+2;设直线AD的解析式为y=x+c,则+c=0,解得c=,∴y=x,E(0,),∵OA=1,OE=,∠AOE=90°,∴AE==,∴OE:OA:AE=2:3:.∴BK=AB•sin∠OAE=(3+1)×=,∴S△AEF=××=,设P(x,x2+x+2),则H(x,x),∴PH=x2+x+2+x+=x2+2x+,∵PH∥y轴,∴∠PHG=∠AEO,∴PG=PH•sin∠AEO=(x2+2x+),∴S△PEF=××(x2+2x+)=x2+x=(x)2+,∴当x=时,S△PEF的面积最大,最大值为,此时P(,).(3)存在.如图2,设直线AP交y轴于点R,直线AM交y轴于点Q,直线AP的解析式为y=px+q,由(1)得P(,),则,解得,∴y=x+1,R(0,1),OA=OR=1.当矩形AMNP以AP、AM为邻边时,则∠RAQ=90°,PN∥AM,MN∥AP.∵∠OAR=∠ORA=45°,∠AOR=∠AOQ=90°,∴∠OAQ=∠OQA=45°,∴OQ=OA=1,Q(0,﹣1);设直线AM的解析式为y=mx﹣1,则﹣m﹣1=0,解得m=﹣1,∴y=﹣x﹣1;设直线PN的解析式为y=﹣x+n,则+n=,解得n=4,∴y=﹣x+4.由,得,,∴M(,);设直线MN的解析式为y=x+r,则+r=,解得r=﹣10,∴y=x﹣10,由,得,∴N(7,﹣3);设PN交抛物线于另一点M′,作M′N′∥AP交AM于点N′.由,得,,∴M′(2,2),设直线M′N′的解析式为y=x+d,则2+d=2,解得d=0,∴y=x,由,得,当矩形AN′M′P以AP、PM′为邻边,则N′(,).综上所述,点N的坐标为(7,﹣3)或(,).5.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中A(﹣1,0),OB=4OA,tan∠CAB=3,连接AC、BC.(1)求该抛物线的解析式;(2)如图2,过A作AD∥BC,交抛物线于点D,点P为直线BC下方抛物线上任意一点,连接DP,与BC交于点E,连接AE,当△APE面积最大时,求点P的坐标及△APE 面积的最大值;(3)如图3,在(2)的条件下,将抛物线先向右平移个单位,再向上平移3个单位后与x轴交于点F、G(点F在点G的左侧),点Q为直线AC上一点,连接QP、QG、PG,当△QPG是以PG为腰的等腰三角形时,请直接写出点Q的坐标.【解答】解:(1)∵A(﹣1,0),OB=4OA,∴B(4,0),∵tan∠CAB=3,∴=3,∴C(0,﹣3),将A(﹣1,0),B(4,0),C(0,﹣3)代入y=ax2+bx+c得:,解得,∴抛物线的解析式为y=x2﹣x﹣3;(2)过P作PF∥AD交x轴于F,连接DF,如图:设经过B(4,0),C(0,﹣3)的直线为y=dx+e,则,解得,∴直线BC为y=x﹣3,由AD∥BC,设直线AD为y=x+f,把A(﹣1,0)代入得:0=﹣+f,解得f=,∴直线AD为y=x+,解得或,∴D(5,),∵AD∥BC,∴S△ADE=S△ADB,而S△ADB=AB•|y D|=×5×=,∴S△ADE=,设P(m,m2﹣m﹣3),而PF∥AD,设直线PF为y=x+g,则m2﹣m﹣3=m+g,解得g=m2﹣3m﹣3,∴直线PF为y=x+m2﹣3m﹣3,令y=0得x=﹣m2+4m+4,∴F(﹣m2+4m+4,0),∵PF∥AD,∴S△ADF=S△ADP,而S△ADF=AF•|y D|==[﹣m2+4m+4﹣(﹣1)]•=﹣m2+9m+,∴S△ADP=﹣m2+9m+,∴S△APE=S△ADP﹣S△ADE=﹣m2+9m=﹣(m﹣2)2+9,∴m=2时,S△APE最大,最大值为9,∴P(2,﹣);(3)将抛物线y=x2﹣x﹣3先向右平移个单位,再向上平移3个单位,得到的抛物线解析式为y=(x﹣)2﹣(x﹣)﹣3+3=x2﹣3x+,令y=0得x=或x=,∴G(,0),∵A(﹣1,0),C(0,﹣3),∴直线AC的解析式为y=﹣3x﹣3,设Q(n,﹣3n﹣3),则QG2=(n﹣)2+(﹣3n﹣3)2,QP2=(n﹣2)2+(﹣3n﹣3+)2,PG2=(﹣2)2+()2=,△QPG是以PG为腰的等腰三角形,分两种情况:①PG=QG时,(n﹣)2+(﹣3n﹣3)2=,解得n=或n=,∴Q(,)或(,);②PG=QP时,(n﹣2)2+(﹣3n﹣3+)2=,解得n=或n=,∴Q(,)或(,),综上所述,Q的坐标为:(,)或(,)或(,)或(,).6.如图1,在平面直角坐标系xOy中,抛物线y=x2+bx+c(b、c为常数)与y轴交于点C,对称轴为直线x=﹣3,点N(﹣4,﹣5)在该抛物线上.(1)求该抛物线的函数表达式;(2)连接CN,点P是直线CN下方抛物线上一动点,过点P作PH∥y轴交直线CN于点H,在射线CH上有一点G使得PH=PG.当△PGH周长取得最大值时,求点P的坐标和△PGH周长的最大值;(3)如图2,在(2)的条件下,直线l:y=x﹣与x轴、y轴分别交于点E、F,将原抛物线沿着射线FE方向平移,平移后的抛物线与x轴的右交点恰好为点E,动点M 在平移后的抛物线上,点T是平面内任意一点,是否存在菱形METP,若存在,请直接写出点T的横坐标,若不存在,请说明理由.【解答】解:(1)根据题意得:,解得:,∴该抛物线的函数表达式为y=x2+6x+3;(2)如图1,过点P作PK⊥CN于点K,设直线CN交x轴于点M,令x=0,得y=3,∴C(0,3),设直线CN的解析式为y=kx+n,把C(0,3)、N(﹣4,﹣5)代入得:,解得:,∴直线CN的解析式为y=2x+3,令y=0,得2x+3=0,解得:x=﹣,∴M(﹣,0),∴OM=,∵C(0,3),∴OC=3,在Rt△CMO中,CM===,设P(t,t2+6t+3),则H(t,2t+3),∴PH=(2t+3)﹣(t2+6t+3)=﹣t2﹣4t,∴PG=﹣t2﹣4t,∵PH=PG,PK⊥HG,∴HG=2HK,∵PK⊥CN,∴∠PKH=∠MOC=90°,∵PH∥y轴,∴∠PHK=∠MCO,∴△PHK∽△MCO,∴=,即=∴HK=(﹣t2﹣4t),∴HG=(﹣t2﹣4t),∴△PGH周长=PH+PG+HG=(﹣t2﹣4t)+(﹣t2﹣4t)+(﹣t2﹣4t)=﹣(t2+4t)=﹣(t+2)2+,∵﹣<0,﹣4<t<0,∴当t=﹣2时,△PGH周长取得最大值,此时点P的坐标为(﹣2,﹣5);(3)联立方程组得,解得:,,∴E′(﹣1,﹣2),在y=x﹣中,令y=0,得x﹣=0,解得:x=3,∴E(3,0),∵原抛物线上的点E′(﹣1,﹣2)平移后得到E(3,0),∴原抛物线向右平移4个单位,向上平移2个单位,∵原抛物线y=x2+6x+3=(x+3)2﹣6,顶点坐标为(﹣3,﹣6),∴平移后的抛物线顶点坐标为(1,﹣4),∴平移后的抛物线解析式为:y=(x﹣1)2﹣4=x2﹣2x﹣3,∵动点M在平移后的抛物线上,∴设M(m,m2﹣2m﹣3),∵菱形METP,∴PE和MT为对角线,∴MP=ME,∵P(﹣2,﹣5),E(3,0),∴MP2=[m﹣(﹣2)]2+[m2﹣2m﹣3﹣(﹣5)]2ME2=(m﹣3)2+(m2﹣2m﹣3﹣0)2,∵MP=ME,∴MP2=ME2,解得m=或,∴m2﹣2m﹣3=或∴M点的坐标为(,)或(,),①当M点的坐标为(,)时:如图所示,过点M作MJ⊥x轴于J,过T作y轴的平行线与过P点且平行于x轴的平行线交点L,过点M作MV∥x轴与ET交点V,则J(,0),MV∥PL,∴JE=3﹣=,MJ=,∠JEM=∠EMV,∵四边形METP为菱形,∴ME=PT,ME∥PT,∴∠EMV=∠TPL,∴∠MEJ=∠TPL,在△MJE和△TLP中,,∴△MJE≌△TLP(AAS),∴MJ=TL=,PL=JE=,∴点T的横坐标为﹣2+=,纵坐标为﹣5+=,∴T点的坐标为(,﹣),②当M点的坐标为(,)时:同理①可得T点的坐标为(,),综上所述,T点的坐标为(,)或(,).7.如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的图象与x轴交于点A(1,0)、B两点,与y轴交于点C(0,﹣3),且抛物线的对称轴为直线x=﹣1.(1)求抛物线的解析式;(2)在直线BC下方的抛物线上有一动点P,过点P作PM⊥x轴,垂足为点M,交直线BC于点N,求PN+CN的最大值,并求出此时点P的坐标;(3)如图2,若抛物线沿射线AC方向平移个单位长度得到抛物线y',点E为新抛物线y'上一点,点F为原抛物线对称轴上一点,取(2)中最大值时点P,是否存在以点B、P、E、F构成的平行四边形?若存在,直接写出点E的坐标,若不存在,请说明理由.【解答】解:(1)将点A(1,0),C(0,﹣3)分别代入y=ax2+bx+c得,,解得:b=﹣a+3,∵函数的对称轴为直线x=﹣1,∴﹣=﹣1,即b=2a,∴﹣a+3=2a,∴a=1,b=2,c=﹣3,∴二次函数的解析式为y=x2+2x﹣3.(2)当y=0时,x2+2x﹣3=0,解得:x=1或x=﹣3,∴B(﹣3,0),过点C作直线PM的垂线,垂足为点H,∵点B(﹣3,0),点C(0,﹣3),∴OB=OC=3,∴△OBC是等腰直角三角形,∴△CHN是等腰直角三角形,∴CN=CH,∴PN+CN=PN+2CH,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=﹣x﹣3,设点P的坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),∴PN=﹣x﹣3﹣(x2+2x﹣3)=﹣x2﹣3x,CH=﹣x,∴PN+CN=﹣x2﹣3x+2(﹣x)=﹣x2﹣5x=﹣(x+)2+,∴PN+CN的最大值为,此时点P的坐标为(﹣,﹣).(3)∵点A(1,0),点C(0,﹣3),∴OA=1,OC=3,∴AC=,∵抛物线沿射线AC方向平移个单位长度得到抛物线y',∴抛物线先向左平移个单位长度,再向下平移个单位长度得到y',∴抛物线y'的解析式为y=(x+)2+2(x+)﹣3﹣=x2+3x﹣,设点E(e,e2+3e﹣),点F(﹣1,f),B(﹣3,0),P(﹣,﹣),①以FE为对角线时,,解得:,∴点E的坐标为(﹣,);②以FP为对角线时,,解得:,∴点E的坐标为(﹣,﹣);③以FB为对角线时,,解得:,∴点E的坐标为(﹣,﹣);综上所述,点E的坐标为(﹣,)或(﹣,﹣)或(﹣,﹣).8.如图1,抛物线y=ax2+bx+4交x轴于A(﹣2,0),B(4,0)两点,与y轴交于点C,连接AC,BC.(1)求此抛物线的解析式;(2)P是抛物线上位于直线BC上方的一个动点,过点P 作PQ∥y轴交BC于点Q;过点P作PE⊥BC于点E,过点E作EF⊥y轴于点F,求出2PQ+EF的最大值及此时点P的坐标;(3)如图2,将抛物线y=ax2+bx+4沿着射线CB的方向平移,使得新抛物线y′过点(3,1),点D为原抛物线y与新抛物线y′的交点,若点G为原抛物线的对称轴上一动点,点H为新抛物线y′上一动点,直接写出所有使得以A,D,G,H为顶点的四边形为平行四边形的点H的坐标,并把求其中一个点H的坐标的过程写出来.【解答】解:(1)∵抛物线y=ax2+bx+4交x轴于A(﹣2,0),B(4,0)两点,∴,解得:,∴此抛物线的解析式为y=x2+x+4;(2)如图1,延长FE交PQ于点G,则FG⊥PQ,∵抛物线y=x2+x+4与y轴交于点C,∴C(0,4),∵B(4,0),∴OB=OC=4,∵∠BOC=90°,∴△BOC是等腰直角三角形,∠CBO=∠BCO=45°,设直线AC的解析式为y=kx+n,将B(4,0),C(0,4)代入得,解得:,∴直线AC的解析式为y=﹣x+4,∵点P在抛物线上,PQ∥y轴交BC于点Q,∴设P(m,m2+m+4),则Q(m,﹣m+4),其中0<m<4,∴PQ=m2+m+4﹣(﹣m+4)=m2+2m,∵PE⊥BC,PQ∥y轴,∴∠PEQ=90°,∠PQE=∠BCO=45°,∴△PEQ是等腰直角三角形,∵EG⊥PQ,∴EG=PQ=×(m2+2m)=﹣m2+m,∴EF=FG﹣EG=m﹣(﹣m2+m)=m2,∴2PQ+EF=2×(m2+2m)+m2=﹣m2+4m=﹣(m﹣)2+,∵﹣<0,∴当m=时,2PQ+EF最大值为,此时P(,);(3)∵B(4,0),C(0,4),y=x2+x+4=(x﹣1)2+,∴将抛物线y=x2+x+4沿着射线CB的方向平移,即向右平移t个单位,向下平移t 个单位,∴平移后的新抛物线解析式为y=(x﹣1﹣t)2+﹣t,∵新抛物线y′过点(3,1),∴1=(3﹣1﹣t)2+﹣t,解得:t=﹣1(不符合题意,舍去)或t=3,∴新抛物线的解析式为y=(x﹣4)2+=x2+4x﹣,由得,∴D(,),∵点G为原抛物线的对称轴上一动点,点H为新抛物线y′上一动点,∴设G(1,s),H(r,r2+4r﹣),而A(﹣2,0),①以AH、DG为对角线时,则,解得:r=,∴r2+4r﹣=﹣×()2+4×﹣=﹣,∴H(,﹣);②以AG、DH为对角线时,则,解得:r=,∴r2+4r﹣=﹣×(﹣)2+4×(﹣)﹣=﹣,∴H(,);③以AD、GH为对角线时,则,解得:r=,∴r2+4r﹣=﹣×()2+4×﹣=﹣,∴H(,﹣);综上所述,H的坐标为:H(,﹣)或H(,)或H(,﹣).9.在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A(﹣1,0),B(3,0),与y 轴交于点C.(1)求抛物线的解析式;(2)如图1,点P是直线上方抛物线上的一点,过点P作PD∥AC交BC于E,交x轴于点D,求PE+BE的最大值以及此时点P的坐标;(3)在(2)的条件下,将抛物线沿着射线CA方向平移个单位长度得到新抛物线y1,新抛物线y1和原抛物线相交于点F.新抛物线y1的顶点为点G,点M是直线FG上的一动点,点N为平面内一点.若以P、G、M、N四点为顶点的四边形为菱形,请直接写出点N的坐标,并写出求解其中一个N点的过程.【解答】解:(1)将A(﹣1,0),B(3,0)代入,得,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,过点E作x轴的平行线,过点P作PJ⊥x轴于J,并与过E点的平行线交点H,过点B作BK⊥EH的延长线于K,则可得四边形HKBJ为矩形,由(1)可得C(0,3),则有Rt△AOC中,CO=3,OA=1,AC=,∵AC∥DP,EK∥x轴,KB⊥x轴,CO⊥x轴,∴∠CAO=∠PDJ=∠PEH,∠OCB=∠EBK,∴,,∴,,∴PH=,,∴+=PH+BK=PH+HJ=PJ,∵当P在抛物线的顶点时,有PJ的最大值,∴当P在抛物线顶点时,有+最大值,∵抛物线的解析式为y=﹣x2+2x+3,求得抛物线的顶点坐标为(1,4),∵当P点坐标为(1,4)时,PJ=4,∴当+最大时,P点坐标为(1,4),∴=2•(+)=8,此时点P的坐标为(1,4).(3)∵抛物线沿射线CA方向平移个单位得到新的抛物线y1,且CA=,∴平移之后原来的C点到了A点的位置,∴原抛物线的平移可看作先向下平移3个单位长度,再向左平移1个单位长度,∵新抛物线的解析式为,∴y1的顶点坐标为G(0,1),∵﹣x2+1=﹣x2+2x+3,解得x=﹣1,则﹣x2+1=0,∴F(﹣1,0),①当P,G,M,N四点为顶点的菱形如图所示时(PG=PN):∵M为平面内任意一点,∴此情况时,只要求PN=PG即可,∵F(﹣1,0),G(0,1),∴可求出FG的解析式为y=x+1,∴设N(n,n+1)∵P(1,4),G(0,1),PG=PN,∴PG===PN=,求得n=4,∴n+1=5,∴N坐标为(4,5).②当P,G,M,N四点为顶点的菱形如图所示时(GP=GN):同理①可求出N(),③当P,G,M,N四点为顶点的菱形如图所示时(GP=GN):同理①可求出N(),④当P,G,M,N四点为顶点的菱形如图所示时(NP=NG):同理①可求出N(),综上所述,N坐标为(4,5)或()或()或().10.如图,在平面直角坐标系xOy中,抛物线y=x2+x﹣2与x轴交于A、B两点(点A 在点B的左侧),与y轴交于点C.(1)求点A的坐标;(2)如图1,连接AC,点D为线段AC下方抛物线上一动点,过点D作DE∥y轴交线段AC于E点,连接EO,记△ADC的面积为S1,△AEO的面积为S2,求S1﹣S2的最大值及此时点D的坐标;(3)如图2,将抛物线沿射线CB方向平移个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线与y轴的交点,当△AMN为以AM为腰的等腰三角形时,请直接写出点N的坐标.【解答】解:(1)∵抛物线,与x轴交于A、B两点,令y=0,得,解得x1=﹣3,x2=1,∵点A在点B的左侧,∴点A的坐标为(﹣3,0);(2)如图1,延长DE交x轴于点K,∵抛物线与y轴交于点C,∴C(0,﹣2),设直线AC的函数表达式为y=kx+n(k≠0),∵A(﹣3,0),C(0,﹣2),∴,解得,∴直线AC的函数表达式为,设,其中﹣3<t<0,∴,K(t,0),∴DE=﹣t2﹣2t,∵=(﹣t2﹣2t)=﹣t2﹣3t,=(t+2)=t+3,∴S1﹣S2=﹣t2﹣3t﹣t﹣3=﹣t2﹣4t﹣3=﹣(t+2)2+1,∴当t=﹣2时,S1﹣S2取得最大值,最大值为1,此时点D的坐标为(﹣2,﹣2);(3)∵C(0,﹣2),B(1,0),∴=,∵抛物线沿射线CB方向平移个单位长度,∴抛物线向右平移个单位长度,向上平移3个单位长度,。
2024年重庆市中考数学b卷压轴题

2024年重庆市中考数学b卷压轴题一、在直角坐标系中,点A(3,4)关于x轴对称的点B的坐标是?A. (-3,4)B. (3,-4)C. (4,3)D. (-3,-4)(答案)B解析:点关于x轴对称,横坐标不变,纵坐标互为相反数。
所以点A(3,4)关于x轴对称的点B的坐标是(3,-4)。
二、若一元二次方程x² - 2x - 3 = 0的两个根为x₁和x₂,则x₁ + x₂的值为?A. -2B. 2C. -3D. 3(答案)B解析:根据一元二次方程的根与系数的关系,x₁ + x₂ = -(-2) = 2。
三、一个正六边形的内角和为?A. 360°B. 540°C. 720°D. 900°(答案)C解析:正六边形可以被划分成4个三角形,每个三角形的内角和为180°,所以正六边形的内角和为4 × 180° = 720°。
四、函数y = 2x - 1与y = -x + 4的交点坐标是?A. (1,3)B. (2,3)C. (3,1)D. (3,5)(答案)C解析:联立两个方程2x - 1 = -x + 4,解得x = 3,代入任一方程得y = 1,所以交点坐标为(3,1)。
五、若一个长方形的长是宽的2倍,且面积为128平方厘米,则长方形的长为?A. 8厘米B. 16厘米C. 32厘米D. 64厘米(答案)B解析:设长方形的宽为x厘米,则长为2x厘米,根据面积公式得x × 2x = 128,解得x = 8,所以长为2x = 16厘米。
六、下列哪个数不是有理数?A. √4B. √5C. 3.14D. -2/3(答案)B解析:√4 = 2,3.14和-2/3都可以表示为两个整数的比,所以它们都是有理数。
而√5不能表示为两个整数的比,所以它是无理数。
七、一个圆锥的底面半径为3厘米,高为4厘米,则它的体积为?A. 12π立方厘米B. 36π立方厘米C. 48π立方厘米D. 144π立方厘米(答案)B解析:圆锥的体积公式为V = (1/3)πr²h,代入r = 3厘米,h = 4厘米,得V = (1/3)π× 3²× 4 = 36π立方厘米。
重庆中考数学压轴题训练

一.压轴题专题训练1.问题:如图1,在等边三角形ABC 内有一点P,且PA=2,PB= 3,PC=1.求∠BPC度数的大小和等边三角形ABC 的边长.李明同学的思路是:将△BPC 绕点B 逆时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′B P是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证).所以∠AP′B=150°,而∠BPC=∠AP′B=150°.进而求出等边△ABC 的边长为7 .问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD 内有一点P,且PA= 5 ,BP= 2 ,PC=1.求∠BPC 度数的大小和正方形ABCD 的边长.图3图1 图22.阅读下列材料,并解决后面的问题.在锐角△A BC 中,∠ A 、∠B、∠C 的对边分别是a、b、c.过 A 作AD ⊥BC 于D(如图),则s inB= A D ,sinc= AD ,即AD=csinB ,AD=bsinC ,c b于是csinB=bsinC ,即 bsin Bcsin Cc a a b.同理有,sin C sin A sin A sin B.a b c∴⋯⋯⋯⋯⋯⋯(*)sin A sin B sin C即:在一个三角形中,各边和它所对角的正弦的比相等.(1)在锐角三角形中,若已知三个元素a、b、∠A ,运用上述结论(* )和有关定理就可以求出其余三个未知元素c、∠B、∠C,请你按照下列步骤填空,完成求解过程:用关系式求出第一步,由条件∠B;用关系式求出第二步,由条件∠C;用关系式求出第三步,由条件c.o(2)一货轮在 C 处测得灯塔A 在货轮的北偏西30 的方向上,随后货轮以28.4o海里/时的速度按北偏东45 的方向航行,半小时后到达B处,此时又测得灯塔A 在货轮的北偏西o70 的方向上(如图11),求此时货轮距灯塔A 的距离AB (结果精确到0.1.参考数据:sin 40o =0.643,sin 65o =0.906,sin70o =0.904,sin 75o =0.966).3. 对于三个数a、b、c,M|a,b,c|表示这三个数的平均数,min { a,b,c}表示a、b、c这三个数中最小的数,如:M{ -1,2,3} 1 23343,min {-1,2,3} =-1;M{ -1,2,a} =1 2 a a3 31,m{ -1,2,a} =a(a1(a1),1),解决下列问题:(1)填空:min { sin30°,cos45°,tan30°} =________;若min { 2,2x+2,4-2x} =2,则x 的取值范围是________;(2)①若M{ 2,x+1,2x} =min { 2,x+1,2x} ,那么x=________;②根据①,你发现结论“若M {a,b,c} =min{ a,b,c},那么________”(填a,b,c 大小关系);③运用②,填空:若M{ 2x+y+2,x+2y,2x-y} =min { 2x+y+2,x+2y,2x-y} ,则x+y=________;2,y=2-x 的图 (3)在同一直角坐标系中作出函数y=x+1,y=(x-1)象(不需列表,描点),通过图象,得出min { x+1,(x-1)2,2-x}最大值为________.4.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S.△BCD应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.(1)求证:△AOB和△AOE是“友好三角形”;(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,1 将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的,4 请直接写出△ABC的面积.2bx a6.如图1,在平面直角坐标系中,抛物线y ax8(0)与x轴交于A、B两点、与月y轴交于点C经过点B的直线y x4与y轴交于点D,点P在抛物线的对称轴上,且P点的横坐标是1.(1)求该抛物线的解析式;(2)在第一象限的抛物线上有一个动点M,过点M作直线MN x轴于点N,交直线BD 于点E,若点M到直线BD的距离与BN的长度之比为22:1,求点M坐标;(3)如图2,若点P位于x轴上方,且PAB60,点Q是对称轴上的一个动点,将BPQ绕点P顺时针旋转60°得到船B'PQ'(B的对应点为B',Q的对应点为Q'),是否存在点Q,使BQQ'的面积是34,若存在,请求出PQ的长:若不存在,说明理由.全等三角形问题中常见的辅助线的作法三角形辅助线做法图中有角平分线,可向两边作垂线。
2023年重庆中考第26题压轴题专题:几何变换综合题
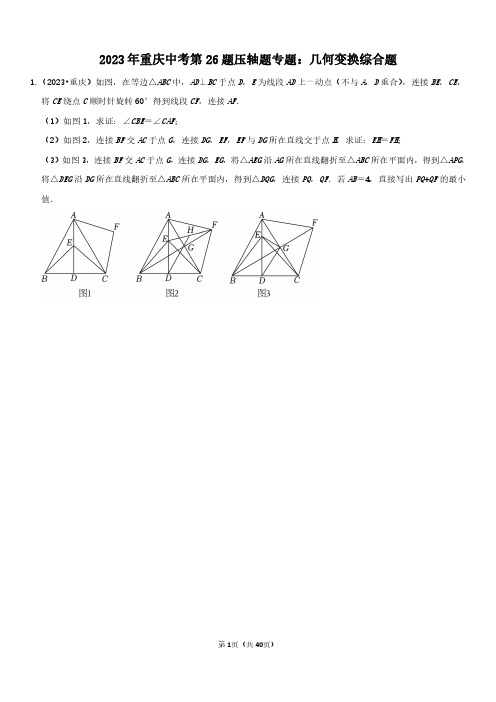
2023年重庆中考第26题压轴题专题:几何变换综合题1.(2023•重庆)如图,在等边△ABC中,AD⊥BC于点D,E为线段AD上一动点(不与A,D重合),连接BE,CE,将CE绕点C顺时针旋转60°得到线段CF,连接AF.(1)如图1,求证:∠CBE=∠CAF;(2)如图2,连接BF交AC于点G,连接DG,EF,EF与DG所在直线交于点H,求证:EH=FH;(3)如图3,连接BF交AC于点G,连接DG,EG,将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,连接PQ,QF.若AB=4,直接写出PQ+QF的最小值.2.(2023•渝中区校级二模)如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,D为AB边上一点,连接CD,AE ⊥CD于E点.(1)如图1,过B作BF⊥AB交AE的延长线于点F.若BD=1,BF=2,求AE的长度;(2)如图2,将AE绕A点逆时针旋转90°到AF,连接BF交AE于点H,猜想AH和CE之间存在的数量关系,并证明你的猜想;(3)如图3,在第(2)问的条件下,将△ABH沿着AB翻折得到△ABP,连接PC,当线段PC取得最大值,请直接写出的值.3.(2023•渝中区校级一模)如图,△ABC是等边三角形,D为AB上一点,连接CD,将CD绕点C顺时针旋转120°至CE,连接BE,分别交AC、CD于点F、G.(1)若AD=3,BD=1,求△BCE的面积;(2)请猜想线段AF,BD,CF之间的数量关系,并证明你的猜想;(3)当△BCE周长最小时,请直接写出的值.4.(2023•沙坪坝区校级一模)在等腰三角形ABC中,AB=AC.点E为AC上一点,连接BE.(1)如图1,若∠BAC=90°,过点C作CD⊥BE交BE延长线于点D,连接AD,过点A作AF⊥AD交BD于点F,连接CF,求证:FC2=FB2+2FA2;(2)如图2,过A作AD∥BC交BE延长线于点D,将AD绕着点A逆时针旋转至AN,连接DN,使得DN⊥AC于点G,AN与BD交于点M,若点M为BD的中点,且∠DAM=∠DMA,猜想线段AM与DE之间的数量关系,并证明你的猜想;(3)如图3,若∠BAC=60°,,将AC沿着AP翻折得到AC′(∠CAC′<120°),点C′落在BE延长线上,BC′交AP于点P,点Q、R分别是射线AC、AB上的点,连接CP、PQ、QR,满足,当BP取得最大值时,直接写出的最小值的平方.。
2020-2021重庆备战中考数学压轴题专题二次函数的经典综合题

2020-2021重庆备战中考数学压轴题专题二次函数的经典综合题一、二次函数1.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式;()2求ABC V 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC V 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-V 当时,有最大值,点P 的坐标是153,4P ⎛⎫--⎪⎝⎭. 【解析】【分析】 (1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC V 的面积计算拆分为APF CPF S S +V V 即可.【详解】()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-,又∵函数图象经过点()6,0A -,∴20(62)4a =-+- 解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-;()2∵点C 是函数2134y x x =+-的图象与y 轴的交点, ∴点C 的坐标是()0,3-,又当0y =时,有21304y x x =+-=, 解得16x =-,22x =,∴点B 的坐标是()2,0,则11831222ABC S AB OC =⋅=⨯⨯=V ; ()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+, ∵直线AC 过点()6,0A -,()0,3C -,∴603k b b -+=⎧⎨-=⎩, 解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅V V V 2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S V 有最大值274,此时点P的坐标是153,4P⎛⎫--⎪⎝⎭.【点睛】本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF最大进行理解.2.如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求点A、B、C的坐标;(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=22DQ,求点F的坐标.【答案】(1)A(﹣3,0),B(1,0);C(0,3) ;(2)矩形PMNQ的周长=﹣2m2﹣8m+2;(3) m=﹣2;S=12;(4)F(﹣4,﹣5)或(1,0).【解析】【分析】(1)利用函数图象与坐标轴的交点的求法,求出点A,B,C的坐标;(2)先确定出抛物线对称轴,用m表示出PM,MN即可;(3)由(2)得到的结论判断出矩形周长最大时,确定出m,进而求出直线AC解析式,即可;(4)在(3)的基础上,判断出N应与原点重合,Q点与C点重合,求出DQ=DC=2,再建立方程(n+3)﹣(﹣n2﹣2n+3)=4即可.【详解】(1)由抛物线y=﹣x2﹣2x+3可知,C(0,3).令y=0,则0=﹣x2﹣2x+3,解得,x=﹣3或x=l,∴A(﹣3,0),B(1,0).(2)由抛物线y=﹣x2﹣2x+3可知,对称轴为x=﹣1.∵M(m,0),∴PM=﹣m2﹣2m+3,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(﹣m2﹣2m+3﹣2m﹣2)×2=﹣2m2﹣8m+2.(3)∵﹣2m2﹣8m+2=﹣2(m+2)2+10,∴矩形的周长最大时,m=﹣2.∵A(﹣3,0),C(0,3),设直线AC的解析式y=kx+b,∴303k bb-+=⎧⎨=⎩解得k=l,b=3,∴解析式y=x+3,令x=﹣2,则y=1,∴E(﹣2,1),∴EM=1,AM=1,∴S=12AM×EM=12.(4)∵M(﹣2,0),抛物线的对称轴为x=﹣l,∴N应与原点重合,Q点与C点重合,∴DQ=DC,把x=﹣1代入y=﹣x2﹣2x+3,解得y=4,∴D(﹣1,4),∴DQ=DC∵FG=,∴FG=4.设F(n,﹣n2﹣2n+3),则G(n,n+3),∵点G在点F的上方且FG=4,∴(n+3)﹣(﹣n2﹣2n+3)=4.解得n=﹣4或n=1,∴F(﹣4,﹣5)或(1,0).【点睛】此题是二次函数综合题,主要考查了函数图象与坐标轴的交点的求法,待定系数法求函数解析式,函数极值的确定,解本题的关键是用m表示出矩形PMNQ的周长.3.童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价x元,每星期的销售量为y件.(1)降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?【答案】(1)这一星期中每件童装降价20元;(2)每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【解析】【分析】(1)根据售量与售价x (元/件)之间的关系列方程即可得到结论.(2)设每星期利润为W 元,构建二次函数利用二次函数性质解决问题.【详解】解:(1)根据题意得,(60﹣x )×10+100=3×100,解得:x =40,60﹣40=20元,答:这一星期中每件童装降价20元;(2)设利润为w ,根据题意得,w =(x ﹣30)[(60﹣x )×10+100]=﹣10x 2+1000x ﹣21000=﹣10(x ﹣50)2+4000,答:每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【点睛】本题考查二次函数的应用,一元二次不等式,解题的关键是构建二次函数解决最值问题,利用图象法解一元二次不等式,属于中考常考题型.4.已知,m ,n 是一元二次方程x 2+4x +3=0的两个实数根,且|m |<|n |,抛物线y =x 2+bx +c 的图象经过点A (m ,0),B (0,n ),如图所示.(1)求这个抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一个交点为抛物线的顶点为D ,求出点C ,D 的坐标,并判断△BCD 的形状;(3)点P 是直线BC 上的一个动点(点P 不与点B 和点C 重合),过点P 作x 轴的垂线,交抛物线于点M ,点Q 在直线BC 上,距离点P 为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.【答案】(1)223y x x =--;(2)C (3,0),D (1,﹣4),△BCD 是直角三角形;(3)2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩<<<或> 【解析】试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;(2)先解方程求出抛物线与x 轴的交点,再判断出△BOC 和△BED 都是等腰直角三角形,从而得到结论;(3)先求出QF=1,再分两种情况,当点P 在点M 上方和下方,分别计算即可. 试题解析:解(1)∵2+430x x +=,∴11x =-,23x =-,∵m ,n 是一元二次方程2+430x x +=的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线223y x x =--的图象经过点A (m ,0),B (0,n ),∴10{3b c c -+==-,∴2{3b c =-=-,∴抛物线解析式为223y x x =--;(2)令y=0,则2230x x --=,∴11x =-,23x =,∴C (3,0),∵223y x x =--=2(1)4x --,∴顶点坐标D (1,﹣4),过点D 作DE ⊥y 轴,∵OB=OC=3,∴BE=DE=1,∴△BOC 和△BED 都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD 是直角三角形;(3)如图,∵B (0,﹣3),C (3,0),∴直线BC 解析式为y=x ﹣3,∵点P 的横坐标为t ,PM ⊥x 轴,∴点M 的横坐标为t ,∵点P 在直线BC 上,点M 在抛物线上,∴P (t ,t ﹣3),M (t ,223t t --),过点Q 作QF ⊥PM ,∴△PQF 是等腰直角三角形,∵,∴QF=1.①当点P 在点M 上方时,即0<t <3时,PM=t ﹣3﹣(223t t --)=23t t -+,∴S=12PM×QF=21(3)2t t -+=21322t t -+,②如图3,当点P 在点M 下方时,即t <0或t >3时,PM=223t t --﹣(t ﹣3)=23t t -,∴S=12PM×QF=12(23t t -)=21322t t -. 综上所述,S=2213 (03)22{13 (03)22t t t t t t t 或-+<<-.考点:二次函数综合题;分类讨论.5.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);(3)符合条件的点P的坐标为(73,209)或(103,﹣139),【解析】分析:(1)设交点式y=a(x+1)(x-3),展开得到-2a=2,然后求出a即可得到抛物线解析式;再确定C(0,3),然后利用待定系数法求直线AC的解析式;(2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3);(3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC 的解析式为y=3x+3,∴直线PC 的解析式可设为y=﹣13x+b , 把C (0,3)代入得b=3,∴直线PC 的解析式为y=﹣13x+3, 解方程组223133y x x y x ⎧-++⎪⎨-+⎪⎩==,解得03x y =⎧⎨=⎩或73209x y ⎧=⎪⎪⎨⎪=⎪⎩,则此时P 点坐标为(73,209); 过点A 作AC 的垂线交抛物线于另一点P ,直线PC 的解析式可设为y=﹣x+b , 把A (﹣1,0)代入得13+b=0,解得b=﹣13, ∴直线PC 的解析式为y=﹣13x ﹣13, 解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩==,解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩,则此时P 点坐标为(103,﹣139). 综上所述,符合条件的点P 的坐标为(73,209)或(103,﹣139). 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.6.已知抛物线26y x x c =-++.(1)若该抛物线与x 轴有公共点,求c 的取值范围;(Ⅱ)设该抛物线与直线21y x =+交于M ,N 两点,若25MN =C 的值;(Ⅲ)点P ,点Q 是抛物线上位于第一象限的不同两点,,PA QB 都垂直于x 轴,垂足分别为A ,B ,若OPA OQB ∆≅∆,求c 的取值范围.【答案】(I )9c -…;(Ⅱ)2c =-;(Ⅲ)c 的取值范围是2174c -<< 【解析】【分析】(1) 抛物线与x 轴有公共点,则判别式为非负数,列不等式求解即可;(2)求出二次函数与直线的交点,并根据勾股定理求出MN 的长度,列方程即可求解;(3)由OPA OQB ∆≅∆可知,P ,Q 两点的坐标特点,设坐标得到设点P 的坐标为(, )m n ,则点Q 的坐标为(,)n m ,代入二次函数,得到n,m 的关系,则只需保证该方程有正根即可求解.【详解】解:(I )∵抛物线26y x x c =-++与x 轴有交点, ∴一元二次方程260x x c -++=有实根。
重庆市中考数学压轴题(华师版)

重庆市2019中考数学压轴题训练(华师版)1. (2018•绍兴)小敏思考解决如下问题:原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.(1)小敏进行探索,若将点P,Q的位置特殊化;把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2.此时她证明了AE=AF,请你证明.(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明.(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).2.(2018•重庆A卷)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=√2CG.(m为常数,m>1,3.(2018.长沙)如图,在平面直角坐标系xOy中,函数y=mxx>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.(1)求∠OCD的度数;(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.5. (2018•重庆A卷)如图,在平面直角坐标系中,点A在抛物线y=-x2+4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,FO的最小值;点F为y轴上一点,当△PBE的面积最大时,求PH+HF+12FO取得最小值时,将△CFH绕点C顺时针旋转60°后(3)在(2)中,PH+HF+12得到△CF′H′,过点F'作CF′的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.6.(2018•重庆B卷)抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B 2 C的位置,再将△O2B2C绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.7.(2018.安徽) 如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB 于点E.点M为BD中点,CM的延长线交AB于点F.(1)求证:CM=EM;(2)若∠BAC=50°,求∠EMF的大小;(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.10.(2018.泰安)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.(1)求二次函数的表达式;(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标,若不存在请说明理由.11. (2018.泰安)如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF∥AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;(2)找出图中与△AGB相似的三角形,并证明;(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MF•MH.12. (2018.聊城)如图,已知反比例函数y=k1x (x >0)的图象与反比例函数y=k2x (x <0)的图象关于y 轴对称,A (1,4),B (4,m )是函数y=k1x (x >0)图象上的两点,连接AB ,点C (-2,n )是函数y=k2x (x <0)图象上的一点,连接AC ,BC .(1)求m ,n 的值;(2)求AB 所在直线的表达式; (3)求△ABC 的面积.14.(2018聊城) 如图,已知抛物线y=ax2+bx 与x 轴分别交于原点O 和点F (10,0),与对称轴l 交于点E (5,5).矩形ABCD 的边AB 在x 轴正半轴上,且AB=1,边AD ,BC 与抛物线分别交于点M ,N .当矩形ABCD 沿x 轴正方向平移,点M ,N 位于对称轴l 的同侧时,连接MN ,此时,四边形ABNM 的面积记为S ;点M ,N 位于对称轴l 的两侧时,连接EM ,EN ,此时五边形ABNEM 的面积记为S .将点A 与点O 重合的位置作为矩形ABCD 平移的起点,设矩形ABCD 平移的长度为t (0≤t ≤5).(1)求出这条抛物线的表达式; (2)当t=0时,求S △OBN 的值;(3)当矩形ABCD 沿着x 轴的正方向平移时,求S 关于t (0<t ≤5)的函数表达式,并求出t 为何值时,S 有最大值,最大值是多少?15.(2018.东莞)如图,已知顶点为C (0,-3)的抛物线y=ax ²+b (a ≠0)与x 轴交于A ,B 两点,直线y=x+m 过顶点C 和点B . (1)求m 的值;(2)求函数y=ax ²+b (a ≠0)的解析式;(3)抛物线上是否存在点M ,使得∠MCB=15°?若存在,求出点M 的坐标;若不存在,请说明理由.19.(2018.武汉)已知点A (a ,m )在双曲线y= 8x 上且m <0,过点A 作x 轴的垂线,垂足为B .(1)如图1,当a=-2时,P (t ,0)是x 轴上的动点,将点B 绕点P 顺时针旋转90°至点C .①若t=1,直接写出点C 的坐标; ②若双曲线y= 8x 经过点C ,求t 的值.(2)如图2,将图1中的双曲线y= 8x (x >0)沿y 轴折叠得到双曲线y=- 8x (x <0),将线段OA 绕点O 旋转,点A 刚好落在双曲线y=- 8x (x <0)上的点D (d ,n )处,求m 和n 的数量关系.。
重庆市2019中考数学压轴题及解析答案(华师版)

1. (2018•绍兴)小敏思考解决如下问题:原题:如图1,点P ,Q 分别在菱形ABCD 的边BC ,CD 上,∠PAQ=∠B ,求证:AP=AQ . (1)小敏进行探索,若将点P ,Q 的位置特殊化;把∠PAQ 绕点A 旋转得到∠EAF ,使AE ⊥BC ,点E ,F 分别在边BC ,CD 上,如图2.此时她证明了AE=AF ,请你证明.(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作AE ⊥BC ,AF ⊥CD ,垂足分别为E ,F .请你继续完成原题的证明.(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).【考点】.【专题】几何综合题.【分析】(1)根据菱形的性质、结合已知得到AF ⊥CD ,证明△AEB ≌△AFD ,根据全等三角形的性质证明;(2)由(1)的结论得到∠EAP=∠FAQ ,证明△AEP ≌△AFQ ,根据全等三角形的性质证明;(3)根据菱形的面积公式、结合(2)的结论解答. 【解答】(1)证明:∵四边形ABCD 是菱形, ∴∠B+∠C=180°,∠B=∠D ,AB=AD , ∵∠EAF=∠B ,∴∠EAF+∠C=180°, ∴∠AEC+∠AFC=180°, ∵AE ⊥BC , ∴AF ⊥CD ,在△AEB 和△AFD 中,{∠AEB =∠AFD∠B =∠D AB =AD,∴△AEB ≌△AFD , ∴AE=AF ;(2)证明:由(1)得,∠PAQ=∠EAF=∠B ,AE=AF , ∴∠EAP=∠FAQ ,在△AEP 和△AFQ 中,{∠AEP =∠AFQ =90°AE =AF ∠EAP =∠FAQ,∴△AEP ≌△AFQ , ∴AP=AQ ;(3)解:已知:AB=4,∠B=60°, 求四边形APCQ 的面积, 解:连接AC 、BD 交于O , ∵∠ABC=60°,BA=BC , ∴△ABC 为等边三角形, ∵AE ⊥BC , ∴BE=EC ,同理,CF=FD ,∴四边形AECF 的面积= 12×四边形ABCD 的面积, 由(2)得,四边形APCQ 的面积=四边形AECF 的面积, OA= 12AB=2,OB=√32AB=2√3, ∴四边形ABCD 的面积=12×2×2√3×4=8√3, ∴四边形APCQ 的面积=4√3.【点评】本题考查的是菱形的性质、全等三角形的判定和性质,掌握菱形的性质、全等三角形的判定定理和性质定理是解题的关键.2.(2018•重庆A 卷)如图,在平行四边形ABCD 中,点O 是对角线AC 的中点,点E 是BC 上一点,且AB=AE ,连接EO 并延长交AD 于点F .过点B 作AE 的垂线,垂足为H ,交AC 于点G .(1)若AH=3,HE=1,求△ABE 的面积; (2)若∠ACB=45°,求证:DF=√2CG . 【考点】;.【专题】多边形与平行四边形.【分析】(1)利用勾股定理即可得出BH 的长,进而运用公式得出△ABE 的面积;(2)过A 作AM ⊥BC 于M ,交BG 于K ,过G 作GN ⊥BC 于N ,判定△AME ≌△BNG (AAS ),可得ME=NG ,进而得出BE=√2GC ,再判定△AFO ≌△CEO (AAS ),可得AF=CE ,即可得到DF=BE=√2CG . 【解答】解:(1)∵AH=3,HE=1, ∴AB=AE=4,又∵Rt △ABH 中,BH=√AB 2−AH 2=√7, ∴S △ABE = 12AE ×BH =12×4×√7=2√7;(2)如图,过A 作AM ⊥BC 于M ,交BG 于K ,过G 作GN ⊥BC 于N ,则∠AMB=∠AME=∠BNG=90°, ∵∠ACB=45°,∴∠MAC=∠NGC=45°,∵AB=AE , ∴BM=EM=12BE ,∠BAM=∠EAM ,又∵AE ⊥BG ,∴∠AHK=90°=∠BMK ,而∠AKH=∠BKM ,∴∠MAE=∠NBG,设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,∴AB=BG,∴AE=BG,在△AME和△BNG中,{∠AME=∠BNG ∠MAE=∠NBGAE=BG,∴△AME≌△BNG(AAS),∴ME=NG,在等腰Rt△CNG中,NG=NC,∴GC=√2NG=√2ME=√22BE,∴BE=√2GC,∵O是AC的中点,∴OA=OC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠OAF=∠OCE,∠AFO=∠CEO,∴△AFO≌△CEO(AAS),∴AF=CE,∴AD-AF=BC-EC,即DF=BE,∴DF=BE=√2CG.【点评】本题主要考查了平行四边形的性质,全等三角形的判定与性质,等腰直角三角形的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造全等三角形以及等腰直角三角形,利用全等三角形的对应边相等得出结论.3.(2018.长沙)如图,在平面直角坐标系xOy中,函数y=mx(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.(1)求∠OCD的度数;(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.【考点】.【专题】代数几何综合题.【分析】(1)想办法证明OC=OD即可解决问题;①1<x<5时,如图1中,∴E(1X ,5X),F(x,15x),5. (2018•重庆A 卷) 如图,在平面直角坐标系中,点A 在抛物线y=-x2+4x 上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长; (2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当△PBE 的面积最大时,求PH+HF+12FO 的最小值; (3)在(2)中,PH+HF+12FO 取得最小值时,将△CFH 绕点C 顺时针旋转60°后得到△CF ′H ′,过点F'作CF ′的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.【考点】.【专题】代数几何综合题.【分析】(1)求出A 、B 两点坐标,即可解决问题;(2)如图1中,设P (m ,-m2+4m ),作PN ∥y 轴交BE 于N .构建二次函数利用二次函数的性质求出满足条件的点P 坐标,作直线OG 交AB 于G ,使得∠COG=30°,作HK ⊥OG 于K 交OC 于F ,因为FK=12OF ,推出PH+HF+12FO=PH+FH+Fk=PH+HK ,此时PH+HF+OF 的值最小,解直角三角形即可解决问题; (3)分两种情形分别求解即可; 【解答】解:(1)由题意A (1,3),B (3,3), ∴AB=2.(2)如图1中,设P (m ,-m ²+4m ),作PN ∥y 轴J 交BE 于N .∵直线BE 的解析式为y=x , ∴N (m ,m ),∴S △PEB = 12×2×(-m ²+3m )=-m ²+3m , ∴当m=32时,△PEB 的面积最大,此时P ( 32, 154 ),H (32 ,3),属于中考压轴题.6.(2018•重庆B卷)抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B 2 C的位置,再将△O2B2C绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN 是以MN 为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O 2M 的长;若不存在,请说明理由.【考点】HF :二次函数综合题. 【专题】16:压轴题.【分析】(1)分别表示C 和D 的坐标,利用勾股定理可得CD 的长; (2)令y=0,可求得A (﹣3,0),B (,0),利用待定系数法可计算直线AC 的解析式为:y=,设E (x ,),P (x ,﹣x 2﹣x+),表示PE 的长,利用勾股定理计算AC 的长,发现∠CAO=30°,得AE=2EF=,计算PE+EC ,利用配方法可得当PE+EC 的值最大时,x=﹣2,此时P (﹣2,),确定要使四边形PO 1B 1C 周长的最小,即PO 1+B 1C 的值最小,将点P 向右平移个单位长度得点P 1(﹣,),连接P 1B 1,则PO 1=P 1B 1,再作点P 1关于x 轴的对称点P 2(﹣,﹣),可得结论;(3)先确定对折后O 2C 落在AC 上,△AMN 是以MN 为腰的等腰三角形存在四种情况:①如图4,AN=MN ,证明△C 1EC ≌△B 2O 2M ,可计算O 2M 的长; ②如图5,AM=MN ,此时M 与C 重合,O 2M=O 2C=;③如图6,AM=MN ,N 和H 、C 1重合,可得结论;④如图7,AN=MN ,过C 1作C 1E ⊥AC 于E 证明四边形C 1EO 2B 2是矩形,根据O 2M=EO 2+EM 可得结论.【解答】解:(1)如图1,过点D 作DK ⊥y 轴于K , 当x=0时,y=,∴C (0,),y=﹣x 2﹣x+=﹣(x+)2+,∴D (﹣,), ∴DK=,CK=﹣=,∴CD===;(4分)(2)在y=﹣x 2﹣x+中,令y=0,则﹣x 2﹣x+=0,解得:x 1=﹣3,x 2=,∴A (﹣3,0),B (,0),∵C (0,),易得直线AC 的解析式为:y=, 设E (x ,),P (x ,﹣x 2﹣x+),∴PF=﹣x 2﹣x+,EF=,Rt △ACO 中,AO=3,OC=,∴AC=2,∴∠CAO=30°, ∴AE=2EF=, ∴PE+EC=(﹣x 2﹣x+)﹣(x+)+(AC ﹣AE ),=﹣﹣x+[2﹣()],=﹣﹣x ﹣x ,=﹣(x+2)2+,(5分)∴当PE+EC 的值最大时,x=﹣2,此时P (﹣2,),(6分)∴PC=2, ∵O 1B 1=OB=,∴要使四边形PO 1B 1C 周长的最小,即PO 1+B 1C 的值最小, 如图2,将点P 向右平移个单位长度得点P 1(﹣,),连接P 1B 1,则PO 1=P 1B 1,再作点P 1关于x 轴的对称点P 2(﹣,﹣),则P 1B 1=P 2B 1,∴PO 1+B 1C=P 2B 1+B 1C ,∴连接P 2C 与x 轴的交点即为使PO 1+B 1C 的值最小时的点B 1, ∴B 1(﹣,0),将B 1向左平移个单位长度即得点O 1,此时PO1+B1C=P2C==,对应的点O1的坐标为(﹣,0),(7分)∴四边形PO1B1C周长的最小值为+3;(8分)(3)O2M的长度为或或2+或2.(12分)理由是:如图3,∵H是AB的中点,∴OH=,∵OC=,∴CH=BC=2,∴∠HCO=∠BCO=30°,∵∠ACO=60°,∴将CO沿CH对折后落在直线AC上,即O2在AC上,∴∠B2CA=∠CAB=30°,∴B2C∥AB,∴B2(﹣2,),①如图4,AN=MN,∴∠MAN=∠AMN=30°=∠O2B2O3,由旋转得:∠CB2C1=∠O2B2O3=30°,B2C=B2C1,∴∠B2CC1=∠B2C1C=75°,过C1作C1E⊥B2C于E,∵B2C=B2C1=2,∴=B2O2,B2E=,∵∠O2MB2=∠B2MO3=75°=∠B2CC1,∠B2O2M=∠C1EC=90°,∴△C1EC≌△B2O2M,∴O2M=CE=B2C﹣B2E=2﹣;②如图5,AM=MN,此时M与C重合,O2M=O2C=,③如图6,AM=MN,∵B2C=B2C1=2=B2H,即N和H、C1重合,∴∠CAO=∠AHM=∠MHO2=30°,∴O2M=AO2=;④如图7,AN=MN,过C1作C1E⊥AC于E,∴∠NMA=∠NAM=30°,∵∠O3C1B2=30°=∠O3MA,∴C1B2∥AC,∴∠C1B2O2=∠AO2B2=90°,∵∠C1EC=90°,∴四边形C1EO2B2是矩形,∴EO2=C1B2=2,,∴EM=,∴O2M=EO2+EM=2+,综上所述,O2M的长是或或2+或2.【点评】本题考查二次函数综合题、一次函数的应用、轴对称变换、勾股定理、等腰三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,学会构建轴对称解决最值问题,对于第3问等腰三角形的判定要注意利用数形结合的思想,属于中考压轴题.7.(2018.安徽) 如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB 于点E.点M为BD中点,CM的延长线交AB于点F.(1)求证:CM=EM;(2)若∠BAC=50°,求∠EMF的大小;(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.【考点】.【专题】几何综合题.【分析】(1)利用直角三角形斜边中线的性质定理即可证明;(2)利用四边形内角和定理求出∠CME即可解决问题;(3)首先证明△ADE 是等腰直角三角形,△DEM 是等边三角形,设FM=a ,则AE=CM=EM=√3a ,EF=2a ,推出 FMMN =2√33 ,EFAE=2√33,由此即可解决问题; 【解答】(1)证明:如图1中,∵DE ⊥AB ,∴∠DEB=∠DCB=90°, ∵DM=MB ,∴CM=12DB ,EM=12DB ,∴CM=EM .(2)解:∵∠AED=90°,∠A=50°, ∴∠ADE=40°,∠CDE=140°, ∵CM=DM=ME ,∴∠MCD=∠MDC ,∠MDE=∠MED , ∴∠CME=360°-2×140°=80°, ∴∠EMF=180°-∠CME=100°.(3)证明:如图2中,设FM=a .∵△DAE ≌△CEM ,CM=EM ,∴AE=ED=EM=CM=DM ,∠AED=∠CME=90°∴△ADE 是等腰直角三角形,△DEM 是等边三角形, ∴∠DEM=60°,∠MEF=30°, ∴AE=CM=EM=√3 a ,EF=2a , ∵CN=NM , ∴MN=2√33a , ∴FM MN =2√33 ,EFAE =2√33, ∴FMMN =EF AE ,∴EM ∥AN .(也可以连接AM 利用等腰三角形的三线合一的性质证明)【点评】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、等边三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考压轴题. 10.(2018.泰安) 如图,在平面直角坐标系中,二次函数y=ax 2+bx+c 交x 轴于点A (-4,0)、B (2,0),交y 轴于点C (0,6),在y 轴上有一点E (0,-2),连接AE .(1)求二次函数的表达式;(2)若点D 为抛物线在x 轴负半轴上方的一个动点,求△ADE 面积的最大值; (3)抛物线对称轴上是否存在点P ,使△AEP 为等腰三角形?若存在,请直接写出所有P 点的坐标,若不存在请说明理由. 【考点】.【专题】压轴题.【分析】(1)把已知点坐标代入函数解析式,得出方程组求解即可;(2)根据函数解析式设出点D 坐标,过点D 作DG ⊥x 轴,交AE 于点F ,表示△ADE 的面积,运用二次函数分析最值即可;(3)设出点P 坐标,分PA=PE ,PA=AE ,PE=AE 三种情况讨论分析即可.【解答】解:(1)∵二次函数y=ax 2+bx+c 经过点A (-4,0)、B (2,0),C (0,6),∴ {16a −4b +c =04a +2b +c =0c =6,(2)由A (-4,0),E (0,-2),可求AE 所在直线解析式为y=−12x−2, 过点D 作DN ⊥x 轴,交AE 于点F ,交x 轴于点G ,过点E 作EH ⊥DF ,垂足为H ,如图设D (m ,−34m 2−32m+6),则点F (m ,−12m −2), ∴DF=−34m 2−32m+6-(−12m −2)=−34m 2−m+8 ,论; (3)先判断出BM=DM ,∠ADM=∠ABM ,进而得出∠ADM=∠H ,判断出△MFD ∽△MDH ,即可得出结论,【解答】解:(1)∠DEF=∠AEF , 理由:∵EF ∥AB ,∴∠DEF=∠EBA ,∠AEF=∠EAB , ∵∠EAB=∠EBA , ∴∠DEF=∠AEF ;(2)△EOA ∽△AGB ,理由:∵四边形ABCD 是菱形, ∴AB=AD ,AC ⊥BD ,∴∠GAB=∠ABE+∠ADB=2∠ABE , ∵∠AEO=∠ABE+∠BAE=2∠ABE ,∵∠GAB=∠AEO ,∠AGB=∠AOE=90°, ∴△EOA ∽△AGB ;(3)如图,连接DM ,∵四边形ABCD 是菱形, 由对称性可知,BM=DM ,∠ADM=∠ABM , ∵AB ∥CH , ∴∠ABM=∠H , ∴∠ADM=∠H , ∵∠DMH=∠FMD , ∴△MFD ∽△MDH , ∴DMMH=MFDM , ∴DM 2=MF •MH , ∴BM 2=MF •MH .【点评】此题是相似形综合题,主要考查了菱形的性质,对称性,相似三角形的判定和性质,判断出△EOA ∽△AGB 是解本题的关键.12. (2018.聊城)如图,已知反比例函数y=k1x (x >0)的图象与反比例函数y=k2x (x <0)的图象关于y 轴对称,A (1,4),B (4,m )是函数y=k1x (x >0)图象上的两点,连接AB ,点C (-2,n )是函数y=k2x (x <0)图象上的一点,连接AC ,BC .(1)求m ,n 的值;(2)求AB 所在直线的表达式; (3)求△ABC 的面积. 【考点】;;. 【专题】常规题型. 【分析】(1)先由点A 确定k ,再求m 的值,根据关于y 轴对称,确定k2再求n ;(2)先设出函数表达式,再代入A 、B 两点,得直线AB 的表达式;(3)过点A 、B 作x 轴的平行线,过点C 、B 作y 轴的平行线构造矩形,△ABC 的面积=矩形面积-3个直角三角形的面积.【解答】解:(1)因为点A 、点B 在反比例函数y=k1x (x >0)的图象上, ∴k1=1×4=4, ∴m ×4=k1=4, ∴m=1∵反比例函数y=k1x (x >0)的图象与反比例函数y=k2x (x <0)的图象关于y 轴对称.∴k2=-k1=-4 ∴-2×n=-4, ∴n=2(2)设直线AB 所在的直线表达式为y=kx+b 把A (1,4),B (4,1)代入,得 {4=k +b 1=4k +b解得 {k =−1b =5∴AB 所在直线的表达式为:y=-x+5(3)如图所示:过点A 、B 作x 轴的平行线,过点C 、B 作y 轴的平行线,它们的交点分别是E 、F 、B 、G . ∴四边形EFBG 是矩形.则AF=3,BF=3,AE=3,EC=2,CG=1,GB=6,EG=3 ∴S △ABC =S 矩形EFBG-S △AFB -S △AEC -S △CBG =BG ×EG-12AF ×FB- 12AE ×EC-12BG ×CG =18- 92-3-3 =152【点评】本题考查了反比例函数的图形及性质、待定系数法确定一次函数解析式及面积的和差关系.题目具有综合性.注意图形的面积可以用割补法也可以用规则的几何图形求和差. 14.(2018聊城) 如图,已知抛物线y=ax2+bx 与x 轴分别交于原点O 和点F (10,0),与对称轴l 交于点E (5,5).矩形ABCD 的边AB 在x 轴正半轴上,且AB=1,边AD ,BC 与抛物线分别交于点M ,N .当矩形ABCD 沿x 轴正方向平移,点M ,N 位于对称轴l 的同侧时,连接MN ,此时,四边形ABNM 的面积记为S ;点M ,N 位于对称轴l 的两侧时,连接EM ,EN ,此时五边形ABNEM 的面积记为S .将点A 与点O 重合的位置作为矩形ABCD 平移的起点,设矩形ABCD 平移的长度为t (0≤t ≤5).(1)求出这条抛物线的表达式; (2)当t=0时,求S △OBN 的值;(3)当矩形ABCD 沿着x 轴的正方向平移时,求S 关于t (0<t ≤5)的函数表达式,并求出t 为何值时,S 有最大值,最大值是多少? 【考点】.【专题】函数的综合应用.【分析】(1)根据点E 、F 的坐标,利用待定系数法即可求出抛物线的表达式; (2)找出当t=0时,点B 、N 的坐标,进而可得出OB 、BN 的长度,再根据三角形的面积公式可求出S △OBN 的值; (3)分0<t ≤4和4<t ≤5两种情况考虑:①当0<t ≤4时(图1),找出点A 、B 、M 、N 的坐标,进而可得出AM 、BN 的长度,利用梯形的面积公式即可找出S 关于t 的函数关系式,再利用二次函数的性质即可求出S 的最大值;②当4<t ≤5时,找出点A 、B 、M 、N 的坐标,进而可得出AM 、BN 的长度,将五边形分成两个梯形,利用梯形的面积公式即可找出S 关于t 的函数关系式,再利用二次函数的性质即可求出S 的最大值.将①②中的S 的最大值进行比较,即可得出结论. 【解答】解:(1)将E (5,5)、F (10,0)代入y=ax ²+bx , {25a +5b =5100a +10b =0, 解得: {a =15b =2,(2)当t=0时,点B 的坐标为(1,0),点N 的坐标为(1 , 95 ),∴BN= 95,OB=1, ∴S △OBN = 12BN •OB= 910.(3)①当0<t ≤4时(图1),点A 的坐标为(t ,0),点B 的坐标为(t+1,0),∴点M 的坐标为(t ,−15t 2+2t ),点N 的坐标为(t+1,−15(t +1)2+2(t +1), ∴AM=−15t 2+2t ,BN=−15(t +1)2+2(t +1),∴S= 12(AM+BN )•AB= 12×1×[−15t 2+2t −15(t +1)2+2(t +1)],=−15t 2+95t +910, =−15(t −92)2+9920, ∵−15<0,∴当t=4时,S 取最大值,最大值为9910;②当4<t ≤5时(图2),点A 的坐标为(t ,0),点B 的坐标为(t+1,0), ∴点M 的坐标为(t ,−15t 2+2t ),点N 的坐标为(t+1,−15(t +1)2+2(t +1)),∴AM=−15t 2+2t ,BN=−15(t +1)2+2(t +1), ∴S= 12(5-t )(−15t 2+2t )+ 12(t-4)[5-−15(t +1)2+2(t +1)], = −310t 2+2710t −1110 =−310(t −92)2+19940,∵−310<0,∴当t=92时,S 取最大值,最大值为19940. ∵4910= 19640<19940, ∴当t= =92时,S 有最大值,最大值是 19940.【点评】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、二次函数的性质、梯形的面积以及三角形的面积,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数关系式;(2)利用二次函数图象上点的坐标特征求出当t=0时点N 的坐标;(3)分0<t ≤4和4<t ≤5两种情况找出S 关于t 的函数关系式.15.(2018.东莞)如图,已知顶点为C (0,-3)的抛物线y=ax ²+b (a ≠0)与x 轴交于A ,B 两点,直线y=x+m 过顶点C 和点B . (1)求m 的值;(2)求函数y=ax ²+b (a ≠0)的解析式;(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.【考点】.【专题】函数及其图象.【分析】(1)把C(0,-3)代入直线y=x+m中解答即可;(2)把y=0代入直线解析式得出点B的坐标,再利用待定系数法确定函数关系式即可;(3)分M在BC上方和下方两种情况进行解答即可.【解答】解:(1)将(0,-3)代入y=x+m,可得:m=-3;(2)将y=0代入y=x-3得:x=3,所以点B的坐标为(3,0),将(0,-3)、(3,0)代入y=ax²+b中,可得:{b=−3 9a+b=0解得:{a=13 b=−3,所以二次函数的解析式为:y=13x²-3;(3)存在,分以下两种情况:①若M在B上方,设MC交x轴于点D,则∠ODC=45°+15°=60°,∴OD=OC•tan30°= √3,设DC为y=kx-3,代入(√3,0),可得:k= √3,联立两个方程可得:{y=√3x−3y=13x²−3,解得:{x1=0y1=−3 ,{x2=3√3y2=6所以M1(3√3,6);②若M 在B 下方,设MC 交x 轴于点E ,则∠OEC=45°+15°=60°,综上所述M 的坐标为(3√3,6)或(√3,-2).【点评】此题主要考查了二次函数的综合题,需要掌握待定系数法求二次函数解析式,待定系数法求一次函数解析式等知识是解题关键.19.(2018.武汉)已知点A (a ,m )在双曲线y= 8x 上且m <0,过点A 作x 轴的垂线,垂足为B .(1)如图1,当a=-2时,P (t ,0)是x 轴上的动点,将点B 绕点P 顺时针旋转90°至点C .①若t=1,直接写出点C 的坐标; ②若双曲线y= 8x 经过点C ,求t 的值.(2)如图2,将图1中的双曲线y= 8x (x >0)沿y 轴折叠得到双曲线y=- 8x (x <0),将线段OA 绕点O 旋转,点A 刚好落在双曲线y=- 8x (x <0)上的点D (d ,n )处,求m 和n 的数量关系.【考点】.【专题】代数几何综合题.如对你有帮助,请购买下载打赏,谢谢!【分析】(1)①如图1-1中,求出PB、PC的长即可解决问题;②图1-2中,由题意C(t,t+2),理由待定系数法,把问题转化为方程解决即可;(2)分两种情形①当点A与点D关于x轴对称时,A(a,m),D(d,n),可得m+n=0.上,作D′H⊥y轴,则②当点A绕点O旋转90°时,得到D′,D′在y=-8x△ABO≌△D′HO,推出OB=OH,AB=D′H,由A(a,m),推出D′(m,-a),上,可得mn=-8;即D′(m,n),由D′在y=-8x【解答】解:(1)①如图1-1中,由题意:B(-2,0),P(1,0),PB=PC=3,∴C(1,3).②图1-2中,由题意C(t,t+2),上,∵点C在y=8x∴t(t+2)=8,∴t=-4 或2,(2)如图2中,①当点A与点D关于x轴对称时,A(a,m),D(d,n),∴m+n=0.上,②当点A绕点O旋转90°时,得到D′,D′在y=-8x作D′H⊥y轴,则△ABO≌△D′HO,∴OB=OH,AB=D′H,∵A(a,m),∴D′(m,-a),即D′(m,n),上,∵D′在y=-8x∴mn=-8,综上所述,满足条件的m、n的关系是m+n=0或mn=-8.【点评】本题考查反比例函数综合题、旋转变换、待定系数法、全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加辅助线,构造全等三角形解决问题,属于中考压轴题.。
重庆巴蜀中学九年级上册压轴题数学模拟试卷含详细答案

重庆巴蜀中学九年级上册压轴题数学模拟试卷含详细答案一、压轴题1.如图,抛物线23y ax bx =++经过点A (1,0),B (4,0)与y 轴交于点C .(1)求抛物线的解析式;(2)如图①,在抛物线的对称轴上是否存在点P ,使得四边形PAOC 的周长最小?若存在,求出四边形PAOC 周长的最小值;若不存在,请说明理由.(3)如图②,点Q 是线段OB 上一动点,连接BC ,在线段BC 上是否存在这样的点M ,使△CQM 为等腰三角形且△BQM 为直角三角形?若存在,求M 的坐标;若不存在,请说明理由.2.二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ,顶点为P ,直线PA 与x 轴交于点B .(1)当m =1时,求顶点P 的坐标;(2)若点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上,且0b m ->,试求a 的取值范围;(3)在第一象限内,以AB 为边作正方形ABCD .①求点D 的坐标(用含m 的代数式表示);②若该二次函数的图象与正方形ABCD 的边CD 有公共点,请直接写出符合条件的整数m 的值.3.在平面直角坐标系中,O 是坐标原点,抛物线2115:L y x bx a a=+-的顶点D 在第四象限,且经过(1,)A m n +,(1,)(0,0)B m n m n ->>两点直线AB 与y 轴交于点C ,与抛物线的1L 对称轴交于点E ,8AC BC ⋅=,点E 的纵坐标为1.(1)求抛物线1L 所对应的函数表达式;(2)若将直线AB 绕着点E 旋转,直线AB 与抛物线1L 有一个交点Q 在第三象限,另一个交点记为P ,抛物线2L 与抛物线1L 关于点P 成中心对称,抛物线2L 的顶点记为1D . ①若点Q 的横坐标为-1,抛物线1L 与抛物线2L 所对应的两个函数y 的值都随着x 的增大而增大,求相应的x 的取值范围;②若直线PQ 与抛物线2L 的另一个交点记为Q ,连接1PD ,11Q D ,试间:在旋转的过程中,1PDQ ∠的度数会不会发生变化?请说明理由. 4.如图,A 是以BC 为直径的圆O 上一点,AD ⊥BC 于点D ,过点B 作圆O 的切线,与CA 的延长线相交于点E ,G 是AD 的中点,连接并延长CG 与BE 相交于点F ,连接并延长AF 与CB 的延长线相交于点P .(1)求证:BF =EF ;(2)求证:PA 是圆O 的切线;(3)若FG =EF =3,求圆O 的半径和BD 的长度.5.如图1,在平面直角坐标系中,抛物线与x 轴交于点 A (-1,0) ,B (点A 在点B 的左侧),交y 轴与点(0,-3),抛物线的对称轴为直线x =1,点D 为抛物线的顶点. (1)求该抛物线的解析式;(2)已知经过点A 的直线y =kx +b (k >0)与抛物线在第一象限交于点E ,连接AD ,DE ,BE ,当2ADE ABE S S ∆∆=时,求点E 的坐标.(3)如图2,在(2)中直线AE 与y 轴交于点F ,将点F 向下平移233+到Q ,连接QB .将△OQB 绕点O 逆时针旋转一定的角度α(0°<α<360°)得到OQ B '',直线B Q ''与x 轴交于点G .问在旋转过程中是否存在某个位置使得OQ G '是等腰三角形?若存在,请直接写出所有满足条件的点Q '的坐标;若不存在,请说明理由.6.在平面直角坐标系xOy 中,函数1F 和2F 的图象关于y 轴对称,它们与直线(0)x t t =>分别相交于点,P Q .(1)如图,函数1F 为1y x =+,当2t =时,PQ 的长为_____; (2)函数1F 为3y x=,当6PQ =时,t 的值为______; (3)函数1F 为2(0)y ax bx c a =++≠, ①当b t b=时,求OPQ △的面积; ②若0c >,函数1F 和2F 的图象与x 轴正半轴分别交于点(5,0),(1,0)A B ,当1c x c ≤≤+时,设函数1F 的最大值和函数2F 的最小值的差为h ,求h 关于c 的函数解析式,并直接写出自变量c 的取值范围.7.已知抛物线y =ax 2+bx+c(a >0),顶点D 在y 轴上,与x 轴的一个交点的横坐标为6. (1)求a 、c 满足的关系式;(2)若直线y =kx-2a 与抛物线交于A 、B 两点(点A 在点B 左侧),以AB 为直径的圆恒过点D .①求抛物线的解析式;②设直线y =kx-2a 与y 轴交于点M 、直线l 1:y =px+q 过点B ,且与抛物线只有一个公共点,过点D 作x 轴的平行线l 2,l 1与l 2交于点N .分别记BDM 、NDM 的面积为S 1,S 2,求12S S . 8.公司经销某种商品,经研究发现,这种商品在未来40天的销售单价1y (元/千克)关于时间t 的函数关系式分别为11602y t =-+(040t <≤,且t 为整数); ()()21030,3033040,20t t t y t t ⎧<≤-+⎪=⎨<≤⎪⎩且为整数且为整数,他们的图像如图1所示,未来40天的销售量m (千克)关于时间t 的函数关系如图2的点列所示.(1)求m 关于t 的函数关系式;(2)那一天的销售利润最大,最大利润是多少?(3)若在最后10天,公司决定每销售1千克产品就捐赠a 元给“环保公益项目”,且希望扣除捐赠后每日的利润不低于3600元以维持各种开支,求a 的最大值(精确到0.01元).9.将一个直角三角形纸片OAB 放置在平面直角坐标系中,点()0,0O ,点()2,0A ,点B 在第一象限,90OAB ∠=︒,30B ∠=︒,点P 在边OB 上(点P 不与点,O B 重合).(1)如图①,当1OP =时,求点P 的坐标;(2)折叠该纸片,使折痕所在的直线经过点P ,并与x 轴的正半轴相交于点Q ,且OQ OP =,点O 的对应点为O ',设OP t =.①如图②,若折叠后O PQ '与OAB 重叠部分为四边形,,O P O Q ''分别与边AB 相交于点,C D ,试用含有t 的式子表示O D '的长,并直接写出t 的取值范围;②若折叠后O PQ '与OAB 重叠部分的面积为S ,当13t ≤≤时,求S 的取值范围(直接写出结果即可).10.如图1 ,一次函数1y kx b =+(k,b 为常数,k≠0)的图象与反比例函数2m y x =(m 为常数,m≠0)的图象相交于点M(1,4)和点N (4,n ).(1)填空:①反比例函数的解析式是 ; ②根据图象写出12y y <时自变量x 的取值范围是 ;(2) 若将直线MN 向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点,求a 的值;(3) 如图2,函数2m y x=的图象(x >0)上有一个动点C ,若先将直线MN 平移使它过点C ,再绕点C 旋转得到直线PQ ,PQ 交轴于点A ,交轴点B ,若BC =2CA , 求OA·OB 的值.11.在Rt△ABC中,∠ACB=90°,AC=1,记∠ABC=α,点D为射线BC上的动点,连接AD,将射线DA绕点D顺时针旋转α角后得到射线DE,过点A作AD的垂线,与射线DE 交于点P,点B关于点D的对称点为Q,连接PQ.(1)当△ABD为等边三角形时,①依题意补全图1;②PQ的长为;(2)如图2,当α=45°,且BD=43时,求证:PD=PQ;(3)设BC=t,当PD=PQ时,直接写出BD的长.(用含t的代数式表示)12.如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.(1)求直线AB的函数表达式;(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G 的坐标;若不存在,请说明理由.13.在直角坐标平面内,O为原点,点A的坐标为(10),,点C的坐标为(0)4,,直线CM x∥轴(如图所示).点B与点A关于原点对称,直线y x b=+(b为常数)经过点B,且与直线CM相交于点D,联结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若POD是等腰三角形,求点P的坐标;14.如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=2.(1)求抛物线的解析式;(2)E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;(3)设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.15.如图1,抛物线M1:y=﹣x2+4x交x正半轴于点A,将抛物线M1先向右平移3个单位,再向上平移3个单位得到抛物线M2,M1与M2交于点B,直线OB交M2于点C.(1)求抛物线M2的解析式;(2)点P是抛物线M1上AB间的一点,作PQ⊥x轴交抛物线M2于点Q,连接CP,CQ.设点P的横坐标为m,当m为何值时,使△CPQ的面积最大,并求出最大值;(3)如图2,将直线OB向下平移,交抛物线M1于点E,F,交抛物线M2于点G,H,则EG的值是否为定值,证明你的结论.HF16.如图,已知矩形ABCD 中,AB=8,AD=6, 点E 是边CD 上一个动点,连接AE ,将△AED 沿直线AE 翻折得△AEF.(1) 当点C 落在射线AF 上时,求DE 的长;(2)以F 为圆心,FB 长为半径作圆F ,当AD 与圆F 相切时,求cos ∠FAB 的值;(3)若P 为AB 边上一点,当边CD 上有且仅有一点Q 满∠BQP=45°,直接写出线段BP 长的取值范围.17.在平面直角坐标系中,抛物线2y ax bx c =++经过点A 、B 、C ,已知A (-1,0),B (3,0),C (0,-3).(1)求此抛物线的函数表达式;(2)若P 为线段BC 上一点,过点P 作y 轴的平行线,交抛物线于点D ,当△BCD 面积最大时,求点P 的坐标;(3)若M (m ,0)是x 轴上一个动点,请求出CM+12MB 的最小值以及此时点M 的坐标.18.如图,在直角坐标系中,点C 在第一象限,CB x ⊥轴于B ,CA y ⊥轴于A ,3CB =,6CA =,有一反比例函数图象刚好过点C .(1)分别求出过点C 的反比例函数和过A ,B 两点的一次函数的函数表达式;(2)直线l x ⊥轴,并从y 轴出发,以每秒1个单位长度的速度向x 轴正方向运动,交反比例函数图象于点D ,交AC 于点E ,交直线AB 于点F ,当直线l 运动到经过点B 时,停止运动.设运动时间为t (秒).①问:是否存在t 的值,使四边形DFBC 为平行四边形?若存在,求出t 的值;若不存在,说明理由;②若直线l 从y 轴出发的同时,有一动点Q 从点B 出发,沿射线BC 方向,以每秒3个单位长度的速度运动.是否存在t 的值,使以点D ,E ,Q ,C 为顶点的四边形为平行四边形;若存在,求出t 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.19.在平面直角坐标系中,经过点()0,2A 且与33y x =-平行的直线,交x 轴于点B ,如图1所示.(1)试求B 点坐标,并直接写出ABO ∠的度数;(2)过()1,0M 的直线与AB 成45︒夹角,试求该直线与AB 交点的横坐标;(3)如图2,现有点(,)C m n 在线段AB 上运动,点,(320)D m -+在x 轴上,N 为线段CD 的中点.①试求点N 的纵坐标y 关于横坐标x 的函数关系式;②直接写出N 点的运动轨迹长度为 .20.对于⊙C 与⊙C 上的一点A ,若平面内的点P 满足:射线..AP 与⊙C 交于点Q (点Q 可以与点P 重合),且12PA QA≤≤,则点P 称为点A 关于⊙C 的“生长点”.已知点O 为坐标原点,⊙O 的半径为1,点A (-1,0).(1)若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标________;(2)若点B 是点A 关于⊙O 的“生长点”,且满足1tan BAO 2∠=,求点B 的纵坐标t 的取值范围;(3)直线3y x b =+与x 轴交于点M ,与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是_____________________________.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)2315344y x x =-+;(2)9;(3)存在点M 的坐标为(315,28)或(1212,77)使△CQM 为等腰三角形且△BQM 为直角三角形【解析】【分析】(1)根据抛物线经过A 、B 两点,带入解析式,即可求得a 、b 的值.(2)根据PA=PB ,要求四边形PAOC 的周长最小,只要P 、B 、C 三点在同一直线上,因此很容易计算出最小周长.(3)首先根据△BQM 为直角三角形,便可分为两种情况QM ⊥BC 和QM ⊥BO ,再结合△QBM ∽△CBO ,根据相似比例便可求解.【详解】解:(1)将点A (1,0),B (4,0)代入抛物线23y ax bx =++中,得:3016430a b a b ++=⎧⎨++=⎩ 解得:34154a b ⎧=⎪⎪⎨⎪=-⎪⎩所以抛物线的解析式为2315344y x x =-+.(2)由(1)可知,抛物线的对称轴为直线52x =.连接BC ,交抛物线的对称轴为点P ,此时四边形PAOC 的周长最小,最小值为OA+OC+BC=1+3+5=9.(3) 当QM ⊥BC 时,易证△QBM ∽△CBO 所以 QM BM OC OB =, 又因为△CQM 为等腰三角形 ,所以QM=CM.设CM=x , 则BM=5- x所以534x x -= 所以157x .所以QM=CM=157,BM=5- x=207,所以BM:CM=4:3. 过点M 作NM ⊥O B 于N ,则MN//OC, 所以 NM BM BN OC CB OB ==, 即4374NM BN == ,所以1216,77MN BN ==, 127ON OB BN =-= 所以点M 的坐标为(1212,77) 当QM ⊥BO 时, 则MQ//OC, 所以 QM BQ OC OB =, 即34QM BQ = 设QM=3t , 则BQ=4t , 又因为△CQM 为等腰三角形 ,所以QM=CM=3t,BM=5-3t 又因为QM 2+QB 2=BM 2, 所以(3t )2+(4t )2=(5-3t )2, 解得58t =MQ=3t=158,32OQ OB BQ =-=, 所以点M 的坐标为(315,28). 综上所述,存在点M 的坐标为(315,28)或(1212,77)使△CQM 为等腰三角形且△BQM 为直角三角形【点睛】本题是一道二次函数的综合型题目,难度系数较高,关键在于根据图形化简问题,这道题涉及到一种分类讨论的思想,这是这道题的难点所在,分类讨论思想的关键在于根据直角三角形的直角进行分类的.2.(1)P (2,13);(2)a 的取值范围为:a <0或a >4;(3)①D (m ,m +3); ②2,3,4.【解析】【分析】(1)把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中,进而求顶点P 的坐标即可;(2)把点Q (a ,b )代入二次函数22(0)63m m y x x m m =-+>解析式中,根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组,解出a 的取值范围即可; (3)①过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,求出二次函数与y 轴的交点A 的坐标,得到OA 的长,再根据待定系数法求出直线AP 的解析式,进而求出与x 轴的交点B 的坐标,得到OB 的长;通过证明△ADF ≌△ABO ,得到AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,求出点D 的坐标;②因为二次函数的图象与正方形ABCD 的边CD 有公共点,由①同理可得:C (m+3,3),分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况,进行讨论m 可能取的整数值即可.【详解】解:(1)当m =1时,二次函数为212163y x x =-+, ∴顶点P 的坐标为(2,13); (2)∵点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上, ∴2263m m b a a m =-+, 即:2263m m b m a a -=- ∵0b m ->, ∴2263m m a a ->0, ∵m >0,∴2263a a ->0,解得:a <0或a >4,∴a 的取值范围为:a <0或a >4;(3)①如下图,过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,∵二次函数的解析式为2263m m y x x m =-+, ∴顶点P (2,3m ), 当x=0时,y=m ,∴点A (0,m ),∴OA=m ;设直线AP 的解析式为y=kx+b(k≠0),把点A (0,m ),点P (2,3m )代入,得: 23m b m k b =⎧⎪⎨=+⎪⎩, 解得:3m k b m⎧=-⎪⎨⎪=⎩,∴直线AP 的解析式为y=3m -x+m , 当y=0时,x=3,∴点B (3,0);∴OB=3;∵四边形ABCD 是正方形,∴AD=AB ,∠DAF+∠FAB=90°,且∠OAB+∠FAB =90°,∴∠DAF=∠OAB ,在△ADF 和△ABO 中,DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADF ≌△ABO (AAS ),∴AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,∴点D 的坐标为:(m ,m+3);②由①同理可得:C (m+3,3),∵二次函数的图象与正方形ABCD 的边CD 有公共点,∴当x =m 时,3y m ≤+,可得322363m m m m -+≤+,化简得:32418m m -≤. ∵0m >,∴2184m m m -≤,∴218(2)4m m--≤, 显然:m =1,2,3,4是上述不等式的解,当5m ≥时,2(2)45m --≥,18 3.6m ≤,此时,218(2)4m m-->, ∴符合条件的正整数m =1,2,3,4; 当x = m +3时,y ≥3,可得2(3)2(3)363m m m m m ++-+≥, ∵0m >,∴21823m m m ++≥,即218(1)2m m++≥, 显然:m =1不是上述不等式的解,当2m ≥时,2(1)211m ++≥,189m ≤,此时,218(1)2m m++>恒成立, ∴符合条件的正整数m =2,3,4;综上:符合条件的整数m 的值为2,3,4.【点睛】本题考查二次函数与几何问题的综合运用,熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键.3.(1)2125333y x x =--;(2)①110x ≤≤;②不会发生变化,理由见解析 【解析】【分析】(1)根据点A ,B 坐标求出对称轴为1x =,得到2b a=-,代入抛物线解析式得到216(1)y x a a =--,写出顶点61,D a ⎛⎫- ⎪⎝⎭,根据其位置,得出0a >,根据A ,B 坐标表示出AC ,BC 长度,结合AC ·BC=8,求得m 的值,代入点A ,B 得其坐标,将A 坐标代入抛物线解析式得a 的值,即可得到抛物线的解析式;(2)①将1x =-代入2125333y x x =--,求得21,3Q ⎛⎫-- ⎪⎝⎭,结合点E 求得PQ 解析式,联立2125333y x x =--,解得点P 的坐标,根据中心对称的性质,得到点1D 的横坐标为10,可得x 的取值范围;②过,P Q 分别作直线1x =的垂线,垂足分别为,F G ,设出点P ,Q 坐标,求出PQ 的解析式,联立2125333y x x =--,得到1212,x x x x +⋅,由tan 1tan DPF QDG ∠=∠,得到DPF QDG ∠=∠,结合90DPF PDF ︒∠+∠=,得到90PDQ ︒∠=,可证得结果.【详解】解:(1)∵抛物线212y x bx a a=+-过(1,),(1,)(0)A m n B m n n +->两点, ∴由抛物线对称性知:抛物线对称轴为直线1x =, 112b a∴-=⨯ 2b a∴=- 2212516(1)y x x x a a a a a ∴=--=-- 61,D a ⎛⎫∴- ⎪⎝⎭ 又∵顶点D 在第四象限,60a ∴-<,解得:10,0a a>> 0,0m n >>,∴抛物线的开口向上,其图象如图所示,1,|1|,8AC m BC m AC BC =+=-⋅=,(1)(1)8m m ∴+-=±,解得:3m =±0m >,3m ∴=,由题意可知,点E 在线段AB 上,而点E 的纵坐标为1,(4,1),(2,1)A B ∴-,把(4,1)A 代入216(1)y x a a =--得,2161(41)a a =--解得:113a = ∴抛物线1L 所对应的函数表达式为2125333y x x =-- (2)①把1x =-代入2125333y x x =--得,23y =- 21,3Q ⎛⎫∴-- ⎪⎝⎭ (1,1)E ,∴直线PQ 的解析式为5166y x =+ 由25166125333y x y x x ⎧=+⎪⎪⎨⎪=--⎪⎩可得,21255133366x x x --=+, 解得:12111,2x x =-= ∴点P 的横坐标为112由中心对称的性质可得,点1D 的横坐标为10,即抛物线2L 的对称轴为直线10x =, 结合图象:可得,x 的范围为110x ≤≤;②在旋转的过程中,1PDQ ∠的度数不会发生变化,理由如下: 连接,PD QD ,由中心对称的性质可得,11PD Q PDQ ∠=∠.过,P Q 分别作直线1x =的垂线,垂足分别为,F G ,如图所示,设()()1122,,,P x y Q x y ,直线PQ 的解析式为y kx b '=+,则∵直线PQ 过(1,1)E ,1k b '∴=+,可得,1b k '=-,∴直线PQ 的解析式为(1)y kx k =+- 由2(1)125333y kx k y x x =+-⎧⎪⎨=--⎪⎩得,2125(1)333x x kx k --=+- 整理得,2(32)(38)0x k x k -++-=121232,38x x k x x k ∴+=+⋅=-21111125(2)1333tan 13x x x DF DPF PF x -----∠===-,2222213tan 1251(2)333x QDG x x x -∠==-----, ()()()121212111tan (38)(32)11tan 999x x x x x x DPF k k QDG ---⋅++-∠--++-∴====∠ tan tan DPF QDG ∴∠=∠DPF QDG ∴∠=∠又90DPF PDF ︒∠+∠=90QDG PDF ︒∴∠+∠=90PDQ ︒∴∠=1190PDQ ︒∴∠=,即在旋转的过程中,PDQ ∠的度数不会发生变化. 【点睛】本题考查了二次函数与几何图形的综合应用,熟知其设计的知识点及相关关系,是解题的关键.4.(1)详见解析;(2)详见解析;(3)BD=22,r=32.【解析】【分析】(1)根据已知条件得到∠EBC=∠ADC=90°,根据平行线分线段成比例定理得出AG CG GD==EF CF BF,等量代换即可得到结论;(2)证明∠PAO=90°,连接AO,AB,根根据直角三角形斜边中线的性质,切线的性质和等量代换,就可得出结论;(3)连接AB,根据圆周角定理得到∠BAC=∠BAE=90°,推出FA=FB=FE=FG=3,过点F作FH⊥AG交AG于点H,推出四边形FBDH是矩形,得到FB=DH=3,根据勾股定理得到FH=22,设半径为r,根据勾股定理列方程即可得到结论.【详解】解:(1)∵EB是切线,AD⊥BC,∴∠EBC=∠ADC=90°,∴AD∥EB,(同位角相等,两直线平行)∴AG CG GD==EF CF BF,(平行线分线段成比例)∵G是AD的中点,∴AG=GD,∴EF=FB;(2)证明:连接AO,AB,∵BC是⊙O的直径,∴∠BAC=90°,(直径所对圆周角为直角)在Rt△BAE中,由(1)知,F是斜边BE的中点,直角三角形斜边中线为斜边一半,∴AF=FB=EF,且等边对等角,∴∠FBA=∠FAB,又∵OA=OB,∴∠ABO=∠BAO,∵BE是⊙O的切线,∴∠EBO=90°,∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,∴PA是⊙O的切线;(3)如图2,连接AB,AO,∵BC 是直径,∴∠BAC =∠BAE =90°,∵EF =FB ,∴FA =FB =FE =FG =3,过点F 作FH ⊥AG 交AG 于点H ,∵FA =FG ,FH ⊥AG ,∴AH =HG ,∵∠FBD =∠BDH =∠FHD =90°,∴四边形FBDH 是矩形,∴FB =DH =3,∵AG =GD ,∴AH =HG =1,GD =2,FH 2222AF AH =31=22--,∴BD =22设半径为r ,在Rt ADO 中,∵222AO =AD +OD , ∴222r =4+(r-22),解得:r =32综上所示:BD =22r =32【点睛】本题主要考察了平行线的性质及定理、平行线分线段成比例定理、等边对等角、直角三角形斜边中线的性质、圆周角定理、勾股定理及圆的切线及其性质,该题较为综合,解题的关键是在于掌握以上这些定理,并熟练地将其结合应用.5.(1)223y x x =--;(2)点E 的坐标为(113,289);(3)存在;点Q '的坐标为:(3232-)或(32,32)或(3,32)或(32-,3 【解析】【分析】(1)利用待定系数法代入计算,结合对称轴,即可求出解析式;(2)取AD 中点M ,连接BM ,过点A 作AE ∥BM ,交抛物线于点E ;然后求出直线AE 的解析式,结合抛物线的解析式,即可求出点E 的坐标;(3)由题意,先求出点F 的坐标,然后得到点Q 的坐标,得到OQ 和OB 的长度,然后结合等腰三角形的性质进行分类讨论,可分为四种情况进行分析,分别求出点Q '的坐标即可.【详解】解:(1)根据题意,设二次函数的解析式为2y ax bx c =++, ∵对称轴为12b x a=-=,则2b a =-, 把点(-1,0),点(0,-3)代入,有03a b c c -+=⎧⎨=-⎩, 又∵2b a =-,∴1a =,2b =-,3b =-,∴抛物线的解析式为:223y x x =--;(2)由(1)223y x x =--可知,顶点D 的坐标为(1,4-),点B 为(3,0),∵点A 为(1-,0),∴AD 的中点M 的坐标为(0,-2);如图,连接AD ,DE ,BE ,取AD 中点M ,连接BM ,过点A 作AE ∥BM ,交抛物线于点E ;此时点D 到直线AE 的距离等于点B 到直线AE 距离的2倍,即2ADE ABE S S ∆∆=,设直线BM 为y kx h =+,把点B 、点M 代入,有302k h h +=⎧⎨=-⎩, ∴直线BM 为223y x =-, ∴直线AE 的斜率为23, ∵点A 为(1-,0),∴直线AE 为2233y x =+, ∴2223323y x y x x ⎧=+⎪⎨⎪=--⎩,解得:10x y =-⎧⎨=⎩(舍去)或113289x y ⎧=⎪⎪⎨⎪=⎪⎩; ∴点E 的坐标为(113,289); (3)由(2)可知,直线AE 为2233y x =+, ∴点F 的坐标为(0,23), ∵将点F 向下平移233+个单位长度得到Q , ∴点Q 的坐标为(0,3-),∴3OQ =,∵点B 为(3,0),则OB=3,在Rt △OBQ 中,3tan 33OB OQB OQ ∠===, ∴60OQB ∠=︒,由旋转的性质,得60Q OQB '∠=∠=︒,3OQ OQ '==,①当3OG OQ '==时,OQ G '∆是等边三角形,如图:∴点G 30),∴点Q '的横坐标为32, ∴点Q '的坐标为(32,32-);②当3OQ Q G ''==,OQ G '∆是等腰三角形,如图:∵60OQ B ''∠=︒,∴30Q OG '∠=︒,∵3OQ '=,∴点Q '的坐标为(32,32); ③当3OG OQ '==时,OQ G '∆是等边三角形,如图:此时点G 的坐标为(3-0),∴点Q '的坐标为(332); ④当3Q G OQ ''=时,OQ G '∆是等腰三角形,如图:此时30Q OG '∠=︒,∴点Q '的坐标为(32-,3); 综合上述,点Q '的坐标为:(32,32-)或(32,32)或(332)或(32-,3). 【点睛】本题考查了二次函数的综合问题,也考查了解直角三角形,旋转的性质,等边三角形的性质,等腰三角形的性质,一次函数的性质,以及坐标与图形,解题的关键是熟练掌握图形的运动问题,正确的确定点Q '的位置是关键;注意运用数形结合的思想,分类讨论的思想进行解题.6.(1)4;(2)1;(3)①1OPQS ∆=;②322169(02)5552(2)c c c c h c c c ⎧++<≤⎪=⎨⎪+>⎩. 【解析】【分析】(1)由题意,先求出2F 的解析式,再求出P 、Q 两点的坐标,即可求出PQ 的长度; (2)由题意,先求出2F 的解析式,结合PQ 的长度,即可求出t 的值;(3)①根据题意,先求出2F 的解析式,然后求出点P 和点Q 的纵坐标,得到PQ 的长度,利用三角形的面积公式即可求出面积;②根据题意,先求出函数1F 和2F 的解析式,然后求出两个函数的对称轴,利用二次函数的对称性和增减性进行分类讨论:当02c <≤时,以及当2>c 时,分别求出h 与c 的关系式即可.【详解】解:(1)∵函数1F 为1y x =+,函数1F 和2F 的图象关于y 轴对称, ∴函数2F 为1y x =-+,当2x t ==时,有121=3y =+;2211y =-+=-;∴点P 为(2,3),点Q 为(2,1-),∴PQ 的长为3(1)4PQ =--=;故答案为:4;(2)∵函数1F 为3y x =,函数1F 和2F 的图象关于y 轴对称, ∴函数2F 为3y x =-; ∵(0)x t t =>,∴点P 在第一象限,点Q 在第四象限,设点P 为(t ,3t ),点Q 为(t ,3t -), ∵6PQ =, ∴33()6t t--=, 解得:1t =;故答案为:1;(3)①∵函数1F 为2(0)y ax bx c a =++≠,函数1F 和2F 的图象关于y 轴对称,∴函数2F 为:2()()y a x b x c =•-+•-+,即2y ax bx c =-+;∵t =,∴把t =1F ,则2a y a b c c b =•+=+;把t =代入函数2F ,则2a y a b c c b =•+=-;∴()a a PQ c c b b=+-=∴112OPQ S ∆==; ②由①可知,函数1F 为2y ax bx c =++,函数2F 为2y ax bx c =-+,∵函数1F 和2F 的图象与x 轴正半轴分别交于点(5,0),(1,0)A B ,∴25500a b c a b c ++=⎧⎨-+=⎩,解得:1545a c b c ⎧=-⎪⎪⎨⎪=⎪⎩, ∴函数1F 可化为:2455c c y x x c =-++,函数2F 可化为:2455c c y x x c -=-+; ∴函数1F 的对称轴为:4522()5c x c =-=⨯-, 函数2F 的对称轴为:4522()5cx c -=-=-⨯-, ∵0c >,则05a c =-<, 则函数1F ,函数2F 均是开口向下;∴函数1F 在02x <<上,y 随x 增大而增大,在2x >上是y 随x 增大而减小; 函数2F 在2x >-上,y 随x 增大而减小;∵1c x c ≤≤+,0c >,当02c <≤时,则函数1F 在2x =时取到最大值;函数2F 在1x c =+时取到最小值,则 ∴244(42)[(1)(1)]5555c c c c h c c c c =-⨯+⨯+--•+-•++, 即32169555h c c c =++(02c <≤); 当2>c 时,则函数1F 在x c =时取到最大值;函数2F 在1x c =+时取到最小值,则2244()[(1)(1)]5555c c c c h c c c c c c =-•+•+--•+-•++, 即22h c c =+(2>c );综合上述,h 关于c 的函数解析式为:322169(02)5552(2)c c c c h c c c ⎧++<≤⎪=⎨⎪+>⎩. 【点睛】本题考查了二次函数的综合问题,考查了二次函数的对称性、增减性,也考查了一次函数的图像和性质,待定系数法求函数的解析式,以及两点之间的距离,求三角形的面积等知识,解题的关键是熟练掌握二次函数和一次函数的性质进行解题,注意运用数形结合、分类讨论的思想进行分析,从而进行解题.7.(1)6c a =-;(2)①2132y x =-;②2. 【解析】【分析】(1)先根据二次函数的对称性求出抛物线与x 轴的另一个交点的横坐标,然后根据二次函数与一元二次方程的联系、一元二次方程的根与系数的关系即可得;(2)①先根据(1)可得抛物线的解析式和顶点D 的坐标,再设11222),(2)(,,A x k a B k x x a x --,从而可得直线AD 、BD 解析式中的一次项系数,然后根据一元二次方程的根与系数的关系可得12k x x a+=,124x x =-,最后根据圆周角定理可得AD BD ⊥,从而可得1212144x x k a k a x x +⋅=-+,化简可求出a 的值,由此即可得出答案;②先求出点B 、D 的坐标,再根据直线1l 与抛物线只有一个交点可得出2213,2q p x p --==,然后联立直线1l 与2l 求出点N 的坐标,最后利用三角形的面积公式分别求出12,S S ,由此即可得.【详解】(1)抛物线2(0)y ax bx c a =++>,顶点D 在y 轴上,∴抛物线的对称轴为y 轴,即0x =,0b ∴=,抛物线与x∴抛物线与x轴的另一个交点的横坐标为是关于x 的一元二次方程20(0)ax bx c a ++=>的两根,(c a∴=, 即6c a =-;(2)①由(1)可得:抛物线的解析式为26y ax a =-,顶点D 的坐标为(0,6)D a -,由题意,设点A 、B 的坐标分别为11222),(2)(,,A x k a B k x x a x --,且21x x >,由点A 、D 的坐标得:直线AD 解析式中的一次项系数为11112064x a x x k x a k a -=-++, 由点B 、D 的坐标得:直线BD 解析式中的一次项系数为22222064x a x x k x a k a -=-++,联立262y ax a y kx a⎧=-⎨=-⎩可得240ax kx a --=, 则1x 与2x 是关于x 的一元二次方程240ax kx a --=的两根, 由根与系数的关系得:1212,4k x x x x a+==-, 以AB 为直径的圆恒过点D , 90ADB ∴∠=︒,即AD BD ⊥, 则1212144x x k a k a x x +⋅=-+, 整理得:2164a =, 解得12a =或102a =-<(不符题意,舍去), 故抛物线的解析式为2132y x =-; ②由①可知,222(0,3),(,31)2D x x B --, 则直线2l 的解析式为3y =-, 联立2132y x y px q⎧=-⎪⎨⎪=+⎩可得22260px x q ---=, 1l 与抛物线只有一个公共点,∴方程22260px x q ---=只有一个实数根2x ,∴其根的判别式244(26)0p q ∆=++=,且2222260x px q ---=, 解得2132q p --=, 将2132q p --=代入2222260x px q ---=得:2x p =, 联立3y y px q =-⎧⎨=+⎩,解得33q x p y --⎧=⎪⎨⎪=-⎩, 即点N 的坐标为3(,3)q N p---, 21322p q p DN p p --∴===,121122S DM x DM p =⋅=⋅,21112224p S DM DN DM DM p =⋅=⋅=⋅, 1212124DM S p M p S D ⋅⋅∴==. 【点睛】本题考查了二次函数与一元二次方程的联系、一元二次方程的根与系数的关系以及根的判别式、二次函数的对称性、圆周角定理等知识点,较难的是题(2)①,利用圆周角定理得出AD BD ⊥,从而利用一次函数的性质建立等式是解题关键.8.(1)m=()()21200304603040t t t t +≤≤⎧⎪⎨+<≤⎪⎩, (2) t=40时w 最大=13200,(3)a 的最大值是85=2a . 【解析】【分析】(1)由图2知m 与t 是一次函数关系,设0≤t≤30时的解析式为m=k 1t+b 1,由图形的点(0,120),(30,180)在函数图像上代入解析式即可,设3040t <≤时的解析式为m=k 2t+b 2,由图形的点(40,220),(30,180)在函数图像上 代入解析式即可,(2)由商品没有成本价,为此只要商品的销售额最大,利润就最大,设y 1的总价为w 1,y 2的总价为w 2,总价=销售单价×销售量m 即可列出, w 1=2260720022103600t t t t ⎧-++⎨-++⎩与w 2=222036003801200t t t ⎧-++⎪⎨⎪+⎩两种总销售w=w 1+w 2,把w 函数配方讨论当030t ≤≤,第一段w 最大与3040t <≤,在第二段,w 最大经比较即可(3)根据题意决定每销售1千克产品就捐赠a 元给“环保公益项目”,则捐赠额a(4t+60)后10天每日销售额Q=w-am=-2t 2+(290-4a)t+4800-60a ,Q≥3600,构造抛物线Q 在Q=3600直线上方有解即可,在-2<0,开口向下,在3600上方取值,且满足3040t ≤≤,对称轴=2904-24b a a -=,只要对称轴介于30与40之间即可. 【详解】 (1)由图2知m 与t 是一次函数关系,设0≤t≤30时的解析式为m=k 1t+b 1,由图形的点(0,120),(30,180)在函数图像上,则11112030180b k b =⎧⎨+=⎩①②,解得112120k b =⎧⎨=⎩, m=2t+120,设3040t <≤时的解析式为m=k 2t+b 2,由图形的点(40,220),(30,180)在函数图像上, 则22224022030180k b k b +=⎧⎨+=⎩③④, 解得22460k b =⎧⎨=⎩, m=4t+60,m=()()21200304603040t t t t ⎧+≤≤⎪⎨+<≤⎪⎩,(2)由商品没有成本价,为此只要商品的销售总值最大,利润就最大,设y 1的总价为w 1,y 2的总价为w 2,w 1=()()1-60212021-604602t t t t ⎧⎛⎫++ ⎪⎪⎪⎝⎭⎨⎛⎫⎪++ ⎪⎪⎝⎭⎩, 整理得w 1=2260720022103600t t t t ⎧-++⎨-++⎩, w 2=()()1-302120320460t t t ⎧⎛⎫++⎪ ⎪⎝⎭⎨⎪+⎩, 整理得w 2=222036003801200t t t ⎧-++⎪⎨⎪+⎩,总销售w=w 1+w 2=22580108003-22904800t t t t ⎧-++⎪⎨⎪++⎩, 配方得w=()225-24117603145215312.52t t ⎧-+⎪⎪⎨⎛⎫⎪--+ ⎪⎪⎝⎭⎩, 当030t ≤≤,第一段w 最大=11760,而3040t <≤,145=2t >40,在第二段,w 随t 的增大而增大,t=40,w 最大=13200,经比较11760<13200,t=40时w 最大=13200,(3)根据题意决定每销售1千克产品就捐赠a 元给“环保公益项目”,则捐赠额a(4t+60), 后10天每日销售额Q=w-am=-2t 2+(290-4a)t+4800-60a ,则Q-3600=-2t 2+(290-4a)t+1200-60a ,∵-2<0,开口向下,在3600上方取值,且满足3040t ≤≤,对称轴为t=2904-24b a a -=只要3040t ≤≤, 290430404a -≤≤, 658522a ≤≤, a 的最大值是85=2a .【点睛】本题考查分段函数的解析式的求法与利用,两图象结合并利用,求日销售最大利润,抛物线顶点式,分段比较,在最后又利用捐赠构造新函数,求对称轴,利用对称轴解决问题,此题难度较大,综合能力强,必须掌握好函数的各方面的知识.9.(1)点P 的坐标为132⎛ ⎝⎭;(2)①34O D t '=-,t 的取值范围是423t <<;S ≤≤ 【解析】【分析】(1)过点P 作PH x ⊥轴,则90OHP ∠=︒,因为90OAB ∠=︒,30B ∠=︒,可得60BOA ∠=︒,进而得30OPH ∠=︒,由30°所对的直角边等于斜边的一半可得1122OH OP ==,进而用勾股定理可得2HP ==,点P 的坐标即求出; (2)①由折叠知,O PQ OPQ '≌,所以O P OP '=,O Q OQ '=;再根据OQ OP =,即可根据菱形的定义“四条边相等的四边形是菱形”可证四边形OQO P '为菱形,所以//QO OB ',可得30ADQ B ∠=∠=︒;根据点A 的坐标可知2OA =,加之OP t =,从而有2QA OA OQ t =-=-;而在Rt QAD 中,242QD QA t ==-, 又因为O D O Q QD ''=-,所以得34O D t '=-,由34O D t '=-和2QA t =-的取值范围可得t 的范围是423t <<; ②由①知,'POQ 为等边三角形,由(1)四边形OQO P '为菱形,所以'AB PQ ⊥,三角形DCQ 为直角三角形,∠Q=60°,从而11(34)22CQ DQ t ==-,(34)22CD DQ t ==-,进而可得222''3124))47POQ CDQ S S S t t =-=-=-+,又已知t 的取值范围是13t ≤≤S ≤≤ 【详解】解:(1)如图,过点P 作PH x ⊥轴,垂足为H ,则90OHP ∠=︒.90OAB ∠=︒,30B ∠=︒9060BOA B ∴∠=︒-∠=︒.9030OPH POH ∴∠=-∠=︒.在Rt OHP △中,1OP =,1122OH OP =∴=,HP =.∴点P 的坐标为12⎛ ⎝⎭.。
8 重庆中考之几何压轴题(25题)

如图,在平行四边形 ABCD 中,点 O 是对角线 AC 的中点,点 E 是 BC 上一点,且 AB=AE, 连接 EO 并延长交 AD 于点 F. 过点 B 作 AE 的垂线,垂足为 H,交 AC 于点 G.
(1)若 AH=3,HE=1,求△ABE 的面积 (2)若∠ACB=45°,求证: DF 2CG
14
已知,在矩形 ABCD 中,E 为 BC 边上一点 , AE DE ,AB=12,BE=16,F 为线段 BE 上一点, EF=7,连接 AF.如图 1,现有一张硬质纸片 GMN ,NGM 900 ,NG=6,MG=8,斜边 MN 与 边 BC 在同一直线上,点 N 与点 E 重合,点 G 在线段 DE 上.如图 2,GMN 从图 1 的位置
10
在平行四边形 ABCD 中,BE 平分∠ABC 交 AD 于点 E.
(1)如图 1,若∠D=30°,AB= 6 ,求△ABE 的面积;
(2)如图 2,过点 A 作 AF⊥DC,交 DC 的延长线于点 F,分别交 BE,BC 于点 G,H,且 AB=AF. 求证:ED-AG=FC.
A
ED
A G
E
6
如图,△ABC 中,∠ACB=90°,AC=BC,点 E 是 AC 上一点,连接 BE. (1)如图 1,若 AB=4 ,BE=5,求 AE 的长; (2)如图 2,点 D 是线段 BE 延长线上一点,过点 A 作 AF⊥BD 于点 F,连接 CD、 CF,当 AF=DF 时,求证:DC=BC.
15
16
请说明理由。
A
G
A
B
B
G
E F
D
H
C
图1
(E)
D
H
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市中考数学压轴题及答案15例1.如图,已知与x 轴交于点(10)A ,和(50)B ,的抛物线1l 的顶点为(34)C ,,抛物线2l 与1l 关于x 轴对称,顶点为C '.(1)求抛物线2l 的函数关系式;(2)已知原点O ,定点(04)D ,,2l 上的点P 与1l 上的点P '始终关于x 轴对称,则当点P 运动到何处时,以点D O P P ',,,为顶点的四边形是平行四边形?(3)在2l 上是否存在点M ,使ABM △是以AB 为斜边且一个角为30的直角三角形?若存,求出点M 的坐标;若不存在,说明理由.解:(1)由题意知点C '的坐标为(34)-,. 设2l 的函数关系式为2(3)4y a x =--. 又点(10)A ,在抛物线2(3)4y a x =--上,2(13)40a ∴--=,解得1a =.∴抛物线2l 的函数关系式为2(3)4y x =--(或265y x x =-+).(2)P 与P '始终关于x 轴对称,PP '∴与y 轴平行.设点P 的横坐标为m ,则其纵坐标为265m m -+,4OD =,22654m m ∴-+=,即2652m m -+=±.当2652m m -+=时,解得36m =± 当2652m m -+=-时,解得32m =.∴当点P 运动到(362)-,或(362)+,或(322)--,或(322)+-,时, P P OD ' ∥,以点D O P P ',,,为顶点的四边形是平行四边形.(3)满足条件的点M 不存在.理由如下:若存在满足条件的点M 在2l 上,则90AMB ∠=,30BAM ∠=(或30ABM ∠=),114222BM AB ∴==⨯=. 过点M 作ME AB ⊥于点E ,可得30BME BAM ∠=∠=.112122EB BM ∴==⨯=,3EM =,4OE =. ∴点M 的坐标为(43)-,. 但是,当4x =时,246451624533y =-⨯+=-+=-≠∴不存在这样的点M 构成满足条件的直角三角形.2.如图,抛物线y =-x 2+bx +c 与x 轴交于A (1,0),B (-3,0)两点. (1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出点Q 的坐标;若不存在,请说明理由; (3)在(1)中的抛物线上的第二象限内是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值;若不存在,请说明理由.解:(1)将A (1,0),B (-3,0)代入y =-x 2+bx +c 得⎩⎨⎧03901=+--=++-c b c b ············································································ 2分 解得⎩⎨⎧32==-c b ························································································ 3分 ∴该抛物线的解析式为y =-x 2-2x +3. ············································ 4分 (2)存在. ································································································· 5分该抛物线的对称轴为x =-)(--122⨯=-1∵抛物线交x 轴于A 、B 两点,∴A 、B 两点关于抛物线的对称轴x =-1对称. 由轴对称的性质可知,直线BC 与x =-1的交点即为所求的Q 点,此时△QAC 的周长最小,如图1.将x =0代入y =-x 2-2x +3,得y =3. ∴点C 的坐标为(0,3).设直线BC 的解析式为y =kx +b 1,将B (-3,0),C (0,3)代入,得⎩⎨⎧30311==+-b b k 解得⎩⎨⎧311==b k ∴直线BC 的解析式为y =x +3. ··············· 6分 联立⎩⎨⎧31+==-x x y 解得⎩⎨⎧21==-y x∴点Q 的坐标为(-1,2). ································································· 7分 (3)存在. ································································································· 8分设P 点的坐标为(x ,-x 2-2x +3)(-3<x <0),如图2. ∵S △PBC =S 四边形PBOC -S △BOC =S 四边形PBOC -21×3×3=S 四边形PBOC -29当S 四边形PBOC 有最大值时,S △PBC 就最大.∵S 四边形PBOC =S Rt △PBE +S 直角梯形PEOC ························································· 9分=21BE ·PE +21(PE +OC )·OE =21(x +3)(-x 2-2x +3)+21(-x 2-2x +3+3)(-x ) =-23(x +23)2+29+827当x =-23时,S 四边形PBOC 最大值为29+827.∴S △PBC 最大值=29+827-29=827. ·············· 10分当x =-23时,-x 2-2x +3=-(-23)2-2×(-23)+3=415.∴点P 的坐标为(-23,415). ···························································· 11分3.如图,已知抛物线y =a (x -1)2+33(a ≠0)经过点A (-2,0),抛物线的顶点为D ,过O 作射线OM ∥AD .过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为t (s ).问:当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC =OB ,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t (s ),连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.解:(1)把A (-2,0)代入y =a (x -1)2+33,得0=a (-2-1)2+33.∴a =-33 ························································································· 1分 ∴该抛物线的解析式为y =-33(x -1)2+33 即y =-33x 2+332x +338. ·························································· 3分 (2)设点D 的坐标为(x D ,y D ),由于D 为抛物线的顶点∴x D =-)(-332332 =1,y D =-33×1 2+332×1+338=33. ∴点D 的坐标为(1,33).如图,过点D 作DN ⊥x 轴于N ,则DN =33,AN =3,∴AD =22333)+(=6.∴∠DAO =60° ··················································································· 4分 ∵OM ∥AD①当AD =OP 时,四边形DAOP 为平行四边形. ∴OP =6∴t =6(s ) ······························································ 5分 ②当DP ⊥OM 时,四边形DAOP 为直角梯形. 过点O 作OE ⊥AD 轴于E .在Rt △AOE 中,∵AO =2,∠EAO =60°,∴AE =1. (注:也可通过Rt △AOE ∽Rt △AND 求出AE =1) ∵四边形DEOP 为矩形,∴OP =DE =6-1=5.∴t =5(s ) ························································································· 6分 ③当PD =OA 时,四边形DAOP 为等腰梯形,此时OP =AD -2AE =6-2=4. ∴t =4(s )综上所述,当t =6s 、5s 、4s 时,四边形DAOP 分别为平行四边形、直角梯形、等腰梯形.····················································································· 7分(3)∵∠DAO =60°,OM ∥AD ,∴∠COB =60°.又∵OC =OB ,∴△COB 是等边三角形,∴OB =OC =AD =6.∵BQ =2t ,∴OQ =6-2t (0<t <3) 过点P 作PF ⊥x 轴于F ,则PF =23t . ··············································· 8分 ∴S 四边形BCPQ =S △COB -S △POQ=21×6×33-21×(6-2t )×23t=23(t -23)2+8363 ····················································· 9分 ∴当t =23(s )时,S 四边形BCPQ 的最小值为8363. ······························ 10分此时OQ =6-2t =6-2×23=3,OP =23,OF =43,∴QF =3-43=49,PF =433.∴PQ =22QF PF +=2249433)+()(=233 ····································· 11分 4.如图,已知直线y =-21x +1交坐标轴于A 、B 两点,以线段AB 为边向上作正方形ABCD ,过点A ,D ,C 的抛物线与直线另一个交点为E .(1)请直接写出点C ,D 的坐标; (2)求抛物线的解析式;(3)若正方形以每秒5个单位长度的速度沿射线AB 下滑,直至顶点D 落在x 轴上时停止.设正方形落在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围;(4)在(3)的条件下,抛物线与正方形一起平移,直至顶点D 落在x 轴上时停止,求抛物线上C 、E 两点间的抛物线弧所扫过的面积.解:(1)C (3,2),D (1,3); ·············································································· 2分(2)设抛物线的解析式为y =ax 2+bx +c ,把A (0,1),D (1,3),C (3,2)代入得⎪⎩⎪⎨⎧23931=++=++=c b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧161765===-c b a ················································· 4分∴抛物线的解析式为y =-65x 2+617x +1; ······································· 5分(3)①当点A 运动到点F (F 为原B 点的位置)时∵AF =2221+=5,∴t =55=1(秒).当0< t ≤1时,如图1. B ′F =AA ′=5t∵Rt △AOF ∽Rt △∠GB ′F ,∴OFOA =F B GB ''. ∴B ′G =OFOA ·B ′F =21×5t =25t正方形落在x 轴下方部分的面积为S 即为△B ′FG 的面积S △B ′FG∴S =S △B ′FG =21B ′F ·B ′G =21×5t ×25t =45t 2 ······························ 7分②当点C 运动到x 轴上时∵Rt △BCC ′∽Rt △∠AOB ,∴BC CC =OAOB. ∴CC ′=OA OB ·BC =12×5=52,∴t =552=2(秒). 当1< t ≤2时,如图2.∵A ′B ′=AB =5,∴A ′F =5t -5. ∴A ′G =255-t ∵B ′H =25t∴S =S 梯形A ′B ′HG =21(A ′G +B ′H )·A ′B ′ =21(255-t +25t )·5 =25t -45 ··································································· 9分 ③当点D 运动到x 轴上时DD ′=53 t =553=3(秒)当2< t ≤3时,如图3.∵A ′G =255-t∴GD ′=5-255-t =2553t- ∴D ′H =53-t 5 ∴S △D ′GH =21(2553t -)(53-t 5)=(2553t -)2∴S =S 正方形A ′B ′C ′D ′ -S △D ′GH=(5)2-(2553t -)2=-45t 2+215t -425 ··································································· 11分(4)如图4,抛物线上C 、E 两点间的抛物线弧所扫过的面积为图中阴影部分的面积.∵t =3,BB ′=AA ′=DD ′=53∴S 阴影=S 矩形BB ′C ′C ············································································ 13分=BB ′·BC =53×5=15 ······················································································· 14分5.已知:抛物线y =x 2-2x +a (a <0)与y 轴相交于点A ,顶点为M .直线y =21x -a 分别与x轴,y 轴相交于B ,C 两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则M ( , ),N ( , ); (2)如图,将△NAC 沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连结CD ,求a 的值和四边形ADCN 的面积; (3)在抛物线y =x 2-2x +a (a <0)上是否存在一点P ,使得以P ,A ,C ,N 为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.解:(1)M (1,a -1),N (34a ,-31a ). ······························································ 4分(2)∵点N ′是△NAC 沿y 轴翻折后点N 的对应点∴点N ′与点N 关于y 轴对称,∴N ′(-34a ,-31a ).将N ′(-34a ,-31a )代入y =x 2-2x +a ,得-31a =(-34a )2-2×(-34a )+a整理得4a 2+9a =0,解得a 1=0(不合题意,舍去),a 2=-49. ···· 6分∴N ′(3,34),∴点N 到y 轴的距离为3.∵a =-49,抛物线y =x 2-2x +a 与y 轴相交于点A ,∴A (0,-49).∴直线AN ′的解析式为y =x -49,将y =0代入,得x =49.∴D (49,0),∴点D 到y 轴的距离为49. ∴S 四边形ADCN =S △ACN +S △ACN =21×29×3+21×29×49=16189············· 8分(3)如图,当点P 在y 轴的左侧时,若四边形ACPN 是平行四边形,则PN 平行且等于AC .∴将点N 向上平移-2a 个单位可得到点P ,其坐标为(34a ,-37a ),代入抛物线的解析式,得:-37a =(34a )2-2×34a +a ,整理得8a 2+3a =0.解得a 1=0(不合题意,舍去),a 2=-83.∴P (-21,87) ················································································· 10分当点P 在y 轴的右侧时,若四边形APCN 是平行四边形, 则AC 与PN 互相平分.∴OA =OC ,OP =ON ,点P 与点N 关于原点对称.∴P (-34a ,31a ),代入y =x 2-2x +a ,得31a =(-34a )2-2×(-34a )+a ,整理得8a 2+15a =0.解得a 1=0(不合题意,舍去),a 2=-815. ∴P (25,-85) ·················································································· 12分∴存在这样的点P ,使得以P ,A ,C ,N 为顶点的四边形是平行四边形,点P 的坐标为(-21,87)或(25,-85).43 x 的图6.如图,已知一次函数y = - x +7与正比例函数y =象交于点A , 且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y轴. 动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.【答案】(1)根据题意,得⎩⎪⎨⎪⎧y =-x +7y=43x ,解得 ⎩⎨⎧x =3y =4,∴A (3,令y =-x +7=0,得x =7.∴B (7,0). (2)①当P 在OC 上运动时,0≤t <4. 由S △APR =S 梯形COBA -S △ACP -S △P OR -S △ARB =8,得 12(3+7)×4-12×3×(4-t )- 12t(7-t )- 12t ×4=8 ly APlRP C AB Oyx整理,得t2-8t +12=0, 解之得t1=2,t2=6(舍)当P在CA上运动,4≤t<7.由S△APR= 12×(7-t) ×4=8,得t=3(舍)∴当t=2时,以A、P、R为顶点的三角形的面积为8.②当P在OC上运动时,0≤t<4. 此时直线l交AB于Q。
