BM模式匹配算法图解

合集下载

串匹配BM算法KMP算法BF算法

串匹配BM算法KMP算法BF算法串匹配算法是一种用于在一个主串中查找一个子串的方法。

主串是一个较大的字符串，而子串是一个较小的字符串。

串匹配算法的目的是在主串中找到子串的出现位置或者确定子串不在主串中出现。

三种常见的串匹配算法是BF算法（Brute Force算法），KMP算法（Knuth-Morris-Pratt算法）和BM算法（Boyer-Moore算法）。

1. BF算法（Brute Force算法）：BF算法是最简单直观的串匹配算法，也是最基础的算法。

它的思想是从主串的第一个字符开始，逐个与子串进行匹配，如果子串中的所有字符都与主串中的字符相等，则匹配成功；否则，主串向后移动一个位置，子串从头开始重新匹配，直到找到匹配或主串结束。

BF算法的时间复杂度是O(n*m)，其中n是主串的长度，m是子串的长度。

在最坏情况下，需要完全比较所有字符。

2. KMP算法（Knuth-Morris-Pratt算法）：KMP算法是一种改进的串匹配算法，它利用已经匹配过的部分信息来避免不必要的字符比较，从而提高匹配效率。

KMP算法的核心思想是构建一个next数组，该数组存储了在子串中，在一些字符之前具有相同前缀和后缀的最大长度。

KMP算法在匹配过程中，主串和子串的指针分别从头开始遍历。

如果当前字符匹配成功，则两个指针同时后移；如果匹配失败，则利用next 数组的信息将子串的指针向后移动到一个合适的位置继续匹配。

KMP算法的时间复杂度是O(n+m)，其中n是主串的长度，m是子串的长度。

它通过构建next数组，避免了不必要的字符比较，提高了匹配效率。

3. BM算法（Boyer-Moore算法）：BM算法是一种基于启发式的串匹配算法，它通过利用模式串的特点，在匹配过程中跳跃性地移动主串的指针，从而提高匹配效率。

BM算法的核心思想是从模式串的末尾到开头进行匹配，并根据不匹配字符的位置进行跳跃。

BM算法分为两个主要步骤：坏字符规则和好后缀规则。

BF算法KMP算法BM算法

BF算法KMP算法BM算法BF算法（Brute-Force算法）是一种简单直接的字符串匹配算法。

它的基本思想是从主串的第一个字符开始，逐个与模式串的字符进行比较，如果匹配失败，则主串的指针向右移动一位，继续从下一个字符开始匹配。

重复这个过程，直到找到匹配的子串或者主串遍历完毕。

BF算法的时间复杂度是O(n*m)，其中n和m分别是主串和模式串的长度。

当模式串较长时，算法的效率较低。

但是BF算法的实现简单，易于理解，对于较短的模式串和主串，仍然是一种可行的匹配算法。

KMP算法（Knuth-Morris-Pratt算法）是一种改进的字符串匹配算法，它利用了模式串内部的信息，避免了不必要的比较。

KMP算法引入了一个next数组，用于记录模式串中每个位置对应的最长可匹配前缀子串的长度。

KMP算法的基本思想是，当匹配失败时，不是简单地将主串指针右移一位，而是利用next数组将模式串的指针向右移动若干位，使得主串和模式串中已经匹配的部分保持一致，减少比较次数。

通过预处理模式串，计算出next数组，可以在O(n+m)的时间复杂度内完成匹配。

BM算法（Boyer-Moore算法）是一种高效的字符串匹配算法，它结合了坏字符规则和好后缀规则。

BM算法从模式串的末尾开始匹配，根据坏字符规则，如果在匹配过程中发现了不匹配的字符，可以直接将模式串向右滑动到该字符在模式串中最右出现的位置。

BM算法还利用了好后缀规则，当发现坏字符后，可以根据好后缀的位置和模式串的后缀子串进行匹配，从而减少不必要的比较。

通过预处理模式串，计算出坏字符规则和好后缀规则对应的滑动距离，可以在最坏情况下实现O(n/m)的时间复杂度。

总结来说，BF算法是一种简单直接的字符串匹配算法，适用于较短的模式串和主串；KMP算法通过预处理模式串，利用next数组减少比较次数，提高了匹配效率；BM算法结合了坏字符规则和好后缀规则，利用了更多的信息，是一种高效的字符串匹配算法。

BM算法详解

BM算法详解BM算法后缀匹配，是指模式串的⽐较从右到左，模式串的移动也是从左到右的匹配过程，经典的BM算法其实是对后缀蛮⼒匹配算法的改进。

为了实现更快移动模式串，BM算法定义了两个规则，好后缀规则和坏字符规则，如下图可以清晰的看出他们的含义。

利⽤好后缀和坏字符可以⼤⼤加快模式串的移动距离，不是简单的++j，⽽是j+=max (shift(好后缀), shift(坏字符)) 先来看如何根据坏字符来移动模式串，shift(坏字符)分为两种情况：坏字符没出现在模式串中，这时可以把模式串移动到坏字符的下⼀个字符，继续⽐较，如下图：坏字符出现在模式串中，这时可以把模式串第⼀个出现的坏字符和母串的坏字符对齐，当然，这样可能造成模式串倒退移动，如下图：此处配的图是不准确的，因为显然加粗的那个b并不是”最靠右的”b。

⽽且也与下⾯给出的代码冲突！我看了论⽂，论⽂的意思是最右边的。

当然了，尽管⼀时⼤意图配错了，论述还是没有问题的，我们可以把图改正⼀下，把圈圈中的b改为字母f就好了。

接下来的图就不再更改了，⼤家⼼⾥有数就好。

为了⽤代码来描述上述的两种情况，设计⼀个数组bmBc['k']，表⽰坏字符‘k’在模式串中出现的位置距离模式串末尾的最⼤长度，那么当遇到坏字符的时候，模式串可以移动距离为： shift(坏字符) = bmBc[T[i]]-（m-1-i)。

如下图：数组bmBc的创建⾮常简单，直接贴出代码如下：1 void preBmBc(char *x, int m, int bmBc[]) {23 int i;45 for (i = 0; i < ASIZE; ++i)67 bmBc[i] = m;89 for (i = 0; i <= m - 1; ++i)1011 bmBc[x[i]] = m - i - 1;1213 } 代码分析：ASIZE是指字符种类个数，为了⽅便起见，就直接把ASCII表中的256个字符全表⽰了，哈哈，这样就不会漏掉哪个字符了。

BM立体匹配算法的参数详解

BM立体匹配算法的参数详解1. 最小视差（Minimum Disparity）：表示在计算深度图时允许的最小视差值，即物体最近处的深度差异。

选择合适的最小视差值对于过滤无意义的区域非常重要。

2. 最大视差（Maximum Disparity）：表示在计算深度图时允许的最大视差值，即物体最远处的深度差异。

选择合适的最大视差值可以防止视差计算的误差。

3. 视差窗口大小（Disparity Window Size）：表示计算每个像素的视差时，使用的窗口大小。

较大的窗口尺寸可以提供更准确的深度信息，但也会增加计算时间。

通常情况下，窗口大小是一个奇数，最常见的是3、5或74. 匹配代价度量（Matching Cost Metric）：用于计算两个像素之间的匹配代价的度量方法。

最常见的度量方法是灰度差异和绝对差异，也可以根据特定的应用选择适当的度量方法。

5. 匹配代价聚合（Matching Cost Aggregation）：用于减少匹配代价图像中的噪声和不一致性的技术。

常用的方法包括平均代价和双边滤波。

6. 视差图优化（Disparity Map Optimization）：通过优化视差图像，减少错误匹配和噪声，并提高深度估计的准确性。

常用的方法包括视差图扩张、视差图填充和视差图平滑。

7. 左右一致性检查（Left-Right Consistency Check）：用于消除左右图像之间不一致匹配的误差。

该步骤通过检查左右视图之间的匹配来得到更准确的视差图。

8. 剔除无效区域（Invalid Region Exclusion）：根据特定应用需求，去除由于遮挡、反射等原因导致的无效区域。

可以使用其他传感器信息或额外的图像处理技术来实现。

9. 空洞填充（Occlusion Filling）：通过使用图像分割或插值算法填充由遮挡产生的空洞。

这可以提供更完整和连贯的深度图像。

10. 算法效率（Algorithm Efficiency）：BM算法的计算效率对于实时应用很重要。

最详细最容易理解的BM算法简介PPT共37页

• Shift = 6
-2
Case 2a
• 坏字符在模式串中
• *******NLE********
• NEEDLE
•
NEEDLE
• Shift =最右的坏字符位置–position(坏)
• Shift = 5
-2
Case 2b
• 坏字符在模式串中
• *******ELE********
•
NEEDLE
好后缀算法
• 模式串中没有子串匹配上好后缀，并且在模式串中找不到最长前缀，让该前缀等于好后缀的后缀时
• S= *******BABCDE******** • T= AACDEFGBCDE
好后缀算法
• 模式串中没有子串匹配上好后缀，并且在模式串中找不到最长前缀，让该前缀等于好后缀的后缀时
• S= *******BABCDE********
}
预处理-坏字符
• void preBmBc(char *S, int m, int bmBc[]) { int i; for (i = 0; i < ASIZE; ++i) //ASIZE=256 bmBc[i] = m; for (i = 0; i <=m - 1; ++i) bmBc[S[i]] = m - i - 1;
} • 这是会有倒退的算法设计，优点在于能够
对模式串预处理
预处理-坏字符
• void preBmBc(char *S, int m, int bmBc[]) { int i;
for (i = 0; i < ASIZE; ++i) //ASIZE=256
bmBc[i] = m;

BM算法

1.简单的字符串匹配算法
模式匹配问题的简单直接算法是，将其看成是以模式作为关键字的查找问题，它将长度为n的正文T划分为n-m+1个长度为 m的子字符串，检查比较每个这样的子串是否于长度为m的模式p相匹配。
2.boyer-moore串匹配算法
• 算法主要是采用试控法来减少模式串与文本串的字符比较次数，也就是说，算法在沿着文本串进行匹配时，利用已知的模式串的信息跳过一些没有必要的比较。算法的实现分为两个步骤：
每次比较从↓开始，从右至左移动。
2.boyer-moore串匹配算法
匹配比较过程中，不少情形是前面的许多字符都匹配而最后的若干个字符不匹配，这时若采取从左到右的方式扫描的话将浪费很多时间，因此改为自右至左的方式扫描模式和正文，这样，一旦发现当正文中出现模式中没有的字符时就可以将模式、正文大幅度地“滑过”一段距离。
几种பைடு நூலகம்要的模式匹配算法
在对数据包的有效载荷进行攻击检测时，对数据包的载荷进行攻击检测的过程从本质上讲就是一个字符串的模式匹配过程。对数据包有效载荷进行攻击检测的速度已经成为最制约网络级入侵检测效率的瓶颈，所以如何为数据包有效载荷攻击检测过程找到一种快速有效实用的模式匹配方法是当前网络级入侵检测系统面临的一个重要问题。
坏字符启发示例2
移动前：模式串：－＞ one plus two 文本串：－＞ two plus three equals five
移动后：模式串：－＞文本串：－＞ one plus two two plus three equals five
每次比较从↓开始，从右至左移动。
好后缀启发示例
移动前：模式串：－＞ two plus two 文本串：－＞ count to two hundred thirty 移动后：模式串：－＞文本串：－＞ two plus two count to two hundred thirty

BM算法原理图示详细讲解

A
B
C
E
C
A
B
E
… …
… …
P
A
B
C
A
B
2010/10/29 于 HoHai University 4216
BM 算法详细图解编著：WeiSteve@ 自此，讲解完毕。
[Weisteven]
在 BM 算法匹配的过程中，取 Jump(x)与 Shift(x)中的较大者作为跳跃的距离。 BM 算法预处理时间复杂度为 O（m+s），空间复杂度为 O(s)，s 是与 P, T 相关的有限字符集长度，搜索阶段时间复杂度为 O(m*n)。最好情况下的时间复杂度为 O(n/m)，最坏情况下时间复杂度为 O(m*n)。
T
A
B
C
B
A
D
F
T
B
C
F
A
Q
P
C
B
C
A
B
C
E
A
B
C
例二（说明情况 b）：
T
A
B
C
B
A
D
F
T
B
C
F
A
Q
P
B
C
C
A
B
C
E
T
B
C
共同后缀为 TBC，寻找 P 中未匹配部分中是否出现过 TBC。发现未曾出现过。那么我们就要找 P 的最长前缀同时又是 TBC 的最大后缀的情况。发现只有 BC，那么 P 需要移动前缀 BC 至对齐 T 中的 BC。
A A
B B
C
A
B
由于 CAB 在前面 P 中未曾出现过，只能进行第二种情况的最大前缀的匹配。上图中对应的就是已经匹配的部分 CAB 字段在 P 中前方的最大重叠 AB。看出来了吧，最大的移动就是让 P 中的其实部分 AB 跟 T 中已匹配的字段 CAB 的部分进行对齐。移动后的结果如下：

【字符串匹配】BM（Boyer-Moore）字符串匹配算法详解总结（附C++实现代码）

【字符串匹配】BM（Boyer-Moore）字符串匹配算法详解总结（附C++实现代码）BM算法思想的本质上就是在进⾏模式匹配的过程中，当模式串与主串的某个字符不匹配的时候，能够跳过⼀些肯定不会匹配的情况，将模式串往后多滑动⼏位。

BM算法寻找是否能多滑动⼏位的原则有两种，分别是坏字符规则和好后缀规则。

坏字符规则：我们从模式串的末尾往前倒着匹配，当我们发现某个字符⽆法匹配时，我们把这个⽆法匹配的字符叫做坏字符（主串中的字符）。

此时记录下坏字符在模式串中的位置si，然后拿坏字符在模式串中查找，如果模式串中并不存在这个字符，那么可以将模式串直接向后滑动m位，如果坏字符在模式串中存在，则记录下其位置xi，那么模式串向后移动的位数就是si-xi，（可以在确保si>xi，执⾏减法，不会出现向前移动的情况）。

如果坏字符在模式串中多次出现，那我们在计算xi的时候，选择最靠后的那个，这样不会因为让模式串滑动过多，导致本来可能匹配的情况被略过。

好后缀规则：在我们反向匹配模式串时，遇到不匹配时，记录下当前位置j位坏字符位置。

把已经匹配的字符串叫做好后缀，记作{u}。

我们拿它在模式串中查找，如果找到了另⼀个跟{u}相匹配的字串{u*}，那么我们就将模式串滑动到字串{u*}与主串{u}对齐的位置。

如下图所⽰：如果在模式串中找不到另⼀个等于{u}的⼦串，我们就直接将模式串滑动到主串中{u}的后⾯，因为之前的任何⼀次往后滑动，都没有匹配主串中{u}的情况。

但是这种滑动做法有点太过头了，可以看下⾯的例⼦，如果直接滑动到好后缀的后⾯，可能会错过模式串与主串可以匹配的情况。

如下图：当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候，并且重回部分相等的时候，就可能会存在完全匹配的情况。

所以针对这种情况我们不仅要看好后缀在模式串中，是否有另⼀个匹配的字串，我们还要考察好后缀的后缀字串是否存在跟模式串的前缀字串匹配的情况。

如下图所⽰：最后总结如何确定模式串向后滑动的位数，我们可以分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最⼤的。

BM算法详解

BM算法详解来源在没有BM算法时，其原始算法是从后往前进⾏匹配，需要两层循环，判断以某个字符为结尾的⼦串是否和模式串相等，这种算法也称作暴搜；贴上代码：void BLS(string s, string p) {int s_len = s.size(), p_len = p.size();int j = 0, i = 0;while (j <= s_len - p_len) {for (i = p_len - 1; i >= 0 && p[i] == s[i + j]; --i) {}if (i < 0) {cout << "match: " << i + j + 1 << endl;j += p_len;}elsej++;}}算法的思想还是⽐较容易理解的，i和j分别指的是，模式串中已经匹配的位数，模式串相对于原串移动的位数；移动规则算法包含了两个重要的内容，分别是好后缀和坏字符的规则；坏字符：当模式串和原串的字符并不匹配时，原串中的字符就称为坏字符；好后缀：模式串和原串的字符相等时所有的字符串，⽐如ABCD和BCD，那么它的好后缀则包括第⼀次匹配的D，和第⼆次匹配的CD，还有第三次的BCD；例⼦：BM算法的向右移动模式串的距离就是取坏字符和好后缀算法得到的最⼤值；这两个内容分别拥有着⼏条规则，需要注意：坏字符1. 坏字符没出现在模式串中，这时可以把模式串移动到坏字符的下⼀个位置，继续⽐较；⽐如说，ABC和D，其中D和A对齐，因为不匹配，所以D会移动到和B对齐；2. 坏字符出现在模式串中，这时可以把模式串中第⼀个出现（从后往前数第⼀个出现，也就是从前往后数，最靠右出现的）的坏字符和原串的坏字符对齐；⽐如说，BCCBCAD和AAD，假如其中AAD和BCC对齐，发现D和C⽆法匹配，移动到和BCA匹配，此时同样不匹配，但是A存在于模式串中，所以移动到模式串中坏字符出现的上⼀次位置，也就是向后移⼀位，和CAD对齐；当⾸次⽐较就⽆法匹配时，那么肯定是运⽤坏字符规则，因为并不存在好后缀；所以我们发现坏字符的移动规则公式为：后移位数＝坏字符的位置－模式串中的上⼀次出现位置那⽤代码表⽰则是void preBmBc(string x, vector<int>& bmBc) {int i = 0;int len = (int)x.size();// 全部更新为⾃⼰的长度for (i = 0; i < ASIZE; ++i) {bmBc[i] = len;}// 计算字符串中每个字符距离字符串尾部的长度for (i = 0; i < x.size() - 1; ++i) {bmBc[x[i]] = len - i - 1;}}⾸先应该知道的是，bmBc存储的是坏字符出现的位置距离模式串末尾的最⼤长度；前⼀个循环⽤来处理第⼀种规则，因为遇见不匹配时，直接移动模式串的长度；后⼀个循环处理第⼆种规则，需要注意的是，因为要保证最靠右原则，所以要从头开始循环，从⽽使得当遇见相同的字符，后者可以将前者进⾏覆盖。

BM算法详解

BM算法详解/joylnwang/article/details/67857432011.091977年，Robert S.Boyer和J Strother Moore提出了另一种在O(n)时间复杂度内，完成字符串匹配的算法，其在绝大多数场合的性能表现，比KMP算法还要出色，下面我们就来详细了解一下这一出色的单模式匹配算法，在此之前推荐读者读一下我的另一篇文章《KMP 算法详解》，对于透彻理解BM算法大有裨益。

在讲解Boyer-Moore算法之前，我们还是要提一提KMP算法的老例子，当模式串与目标串匹配至如下位置时：我们发现target[13]!=pattern[7]，此时根据KMP算法的next值，我们将target[13]与pattern[5]对齐，再依次执行匹配。

这里target[13]='a'。

如果target[13]='d'，因为'd'不是模式串pattern中的字符，所以无论将target[13]与pattern中任何一个字符对齐都会匹配失败，所以当我们在匹配过程中发现target[i]是不属于模式串的字符，则我们可以直接将target[i+1]，与pattern[1]对齐，再向后执行匹配。

这样就获得了更大的跳转幅度，同时也能保证匹配的正确性。

这便是BM算法相较于KMP算法的一个重要改进。

BM算法之所以能够在单模式匹配中有更加出色的表现，主要是其使用了两个跳转表，一个是坏字符表（论文中称为delta1），一个是好后缀表（论文中称为delta2），下面我们以BM算法对目标串的一次匹配操作，来讲解这两个表的具体跳转策略，这里模式串为"AT-THAT"，目标串为"WHICH-FINALLY-HALTS.--AT-THAT-POINT"。

BM算法与KMP算法的最大的不同之处在于，当目标串与模式串在某个位置对齐之后，KMP算法是从对齐位置向后依次执行匹配（不一定是模式串的第一个元素）。

字符串匹配算法-BM

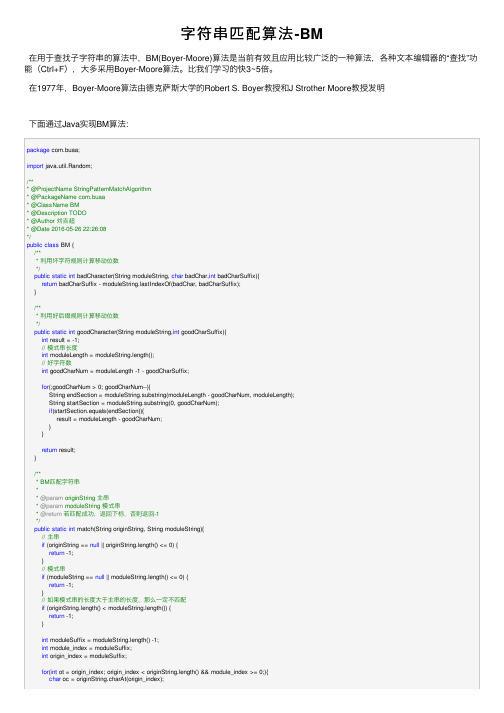
字符串匹配算法-BM在⽤于查找⼦字符串的算法中，BM(Boyer-Moore)算法是当前有效且应⽤⽐较⼴泛的⼀种算法，各种⽂本编辑器的“查找”功能（Ctrl+F），⼤多采⽤Boyer-Moore算法。

⽐我们学习的快3~5倍。

在1977年，Boyer-Moore算法由德克萨斯⼤学的Robert S. Boyer教授和J Strother Moore教授发明下⾯通过Java实现BM算法：package com.buaa;import java.util.Random;/*** @ProjectName StringPatternMatchAlgorithm* @PackageName com.buaa* @ClassName BM* @Description TODO* @Author 刘吉超* @Date 2016-05-26 22:26:08*/public class BM {/*** 利⽤坏字符规则计算移动位数*/public static int badCharacter(String moduleString, char badChar,int badCharSuffix){return badCharSuffix - stIndexOf(badChar, badCharSuffix);}/*** 利⽤好后缀规则计算移动位数*/public static int goodCharacter(String moduleString,int goodCharSuffix){int result = -1;// 模式串长度int moduleLength = moduleString.length();// 好字符数int goodCharNum = moduleLength -1 - goodCharSuffix;for(;goodCharNum > 0; goodCharNum--){String endSection = moduleString.substring(moduleLength - goodCharNum, moduleLength);String startSection = moduleString.substring(0, goodCharNum);if(startSection.equals(endSection)){result = moduleLength - goodCharNum;}}return result;}/*** BM匹配字符串** @param originString 主串* @param moduleString 模式串* @return若匹配成功，返回下标，否则返回-1*/public static int match(String originString, String moduleString){// 主串if (originString == null || originString.length() <= 0) {return -1;}// 模式串if (moduleString == null || moduleString.length() <= 0) {return -1;}// 如果模式串的长度⼤于主串的长度，那么⼀定不匹配if (originString.length() < moduleString.length()) {return -1;}int moduleSuffix = moduleString.length() -1;int module_index = moduleSuffix;int origin_index = moduleSuffix;for(int ot = origin_index; origin_index < originString.length() && module_index >= 0;){char oc = originString.charAt(origin_index);char mc = moduleString.charAt(module_index);if(oc == mc){origin_index--;module_index--;}else{// 坏字符规则int badMove = badCharacter(moduleString,oc,module_index);// 好字符规则int goodMove = goodCharacter(moduleString,module_index);// 下⾯两句代码可以这样理解，主串位置不动，模式串向右移动origin_index = ot + Math.max(badMove, goodMove);module_index = moduleSuffix;// ot就是中间变量ot = origin_index;}}if(module_index < 0){// 多减了⼀次return origin_index + 1;}return -1;}/*** 随机⽣成字符串** @param length 表⽰⽣成字符串的长度* @return String*/public static String generateString(int length) {String baseString = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789";StringBuilder result = new StringBuilder();Random random = new Random();for (int i = 0; i < length; i++) {result.append(baseString.charAt(random.nextInt(baseString.length())));}return result.toString();}public static void main(String[] args) {// 主串// String originString = generateString(10);String originString = "HERE IS A SIMPLE EXAMPLE";// 模式串// String moduleString = generateString(4);String moduleString = "EXAMPLE";// 坏字符规则表// int[] badCharacterArray = badCharacter(originString,moduleString);System.out.println("主串：" + originString);System.out.println("模式串：" + moduleString);int index = match(originString, moduleString);System.out.println("匹配的下标：" + index);}}下⾯，我来解释上⾯代码⾸先先明确两个规则：坏字符规则、好后缀规则1、坏字符规则后移位数 = 坏字符的位置 - 模式串中的坏字符上⼀次出现位置如果"坏字符"不包含在模式串之中，则上⼀次出现位置为 -1。

BM字符串匹配预处理方式及其优化效果评估

BM字符串匹配预处理方式及其优化效果评估字符串匹配是计算机科学中一个重要的问题，涉及到在一个字符串中查找给定模式的位置。

BM（Boyer-Moore）算法作为一种高效的字符串匹配算法，具备了较好的预处理方式和优化效果。

本文将探讨BM 字符串匹配预处理方式及其优化效果的评估。

一、BM算法概述BM算法是由Robert S. Boyer和J Strother Moore于1977年提出的，其主要思想是利用模式串中的信息来跳过尽可能多的字符来进行匹配。

BM算法具有两个关键步骤：坏字符规则和好后缀规则。

坏字符规则用于确定模式串的错位，好后缀规则则用于处理模式串中的后缀。

二、BM算法预处理方式BM算法的预处理过程包括两个关键步骤：坏字符规则的预处理和好后缀规则的预处理。

1. 坏字符规则的预处理坏字符规则的预处理是通过构建一个坏字符表（Bad character table），以确定模式串错误定位时可以向后滑动的距离。

坏字符表存储了字符串中的每个字符在模式串中出现的最后位置。

2. 好后缀规则的预处理好后缀规则的预处理是通过构建一个好后缀表（Good suffix table），以确定当模式串中的后缀与主串匹配失败时可以滑动的距离。

好后缀表存储了模式串中每个后缀的起始位置。

三、BM算法优化效果评估为了评估BM算法的优化效果，我们选取了一组测试数据，包括不同长度的主串和模式串，并使用BM算法进行匹配。

评估主要从以下几个方面进行：1. 匹配效率对比对比BM算法和暴力匹配算法的匹配效率，通过统计算法执行时间以及比较两者的差异，可以评估BM算法相对于暴力匹配算法的优势。

2. 预处理过程时间开销对比BM算法的预处理过程和匹配过程的时间开销，通过统计预处理过程和匹配过程的执行时间，可以评估BM算法预处理过程对匹配效率的影响。

3. 不同模式串长度对匹配效率的影响通过使用不同长度的模式串进行匹配，比较不同长度模式串的匹配时间，可以评估模式串长度对BM算法匹配效率的影响。

字符串匹配算法之BM算法

字符串匹配算法之BM算法 BM算法，全称是Boyer-Moore算法，1977年，德克萨斯⼤学的Robert S. Boyer教授和J Strother Moore教授发明了⼀种新的字符串匹配算法。

BM算法定义了两个规则：1、坏字符规则：当⽂本串中的某个字符跟模式串的某个字符不匹配时，我们称⽂本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。

此外，如果"坏字符"不包含在模式串之中，则最右出现位置为-1。

2、好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上⼀次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。

关于坏字符规则和好后缀规则的具体讲解，以及怎么移动，可以查看阮⼀峰⽼师的详细讲解：这⾥根据讲解画了两张图，⽅便⾃⼰理解坏字符规则：2019年11⽉14⽇15:38:41 修改具体代码如下：1private static final int SIZE = 256; // 全局变量或者是局部变量23/**4 * 坏字符规则哈希表构建⽅法5 *6 * @param b7 * 模式串8 * @param m9 * 模式串的长度10 * @param bc11 * 散列表12*/13private void generateBC(char[] b, int m, int[] bc) {14for (int i = 0; i < SIZE; ++i) {15 bc[i] = -1; // 初始化bc16 }1718for (int i = 0; i < m; ++i) {19int ascii = (int) b[i]; // 计算b[i]的ASCII值20 bc[ascii] = i;21 }22 }2324/**25 * 好后缀规则构建哈希表26 *27 * @param b28 * 模式串29 * @param m30 * 模式串长度31 * @param suffix32 * suffix数组的下标 k，表⽰后缀⼦串的长度，33 * 下标对应的数组值存储的是，在模式串中跟好后缀{u}相匹配的⼦串{u*}的起始下标值34 * @param prefix35 * 记录模式串的后缀⼦串是否能匹配模式串的前缀⼦串36*/37private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {38for (int i = 0; i < m; ++i) { // 初始化39 suffix[i] = -1;40 prefix[i] = false;41 }4243for (int i = 0; i < m - 1; ++i) {44int j = i;45int k = 0; // 公共后缀⼦串长度46while (j >= 0 && b[j] == b[m - 1 - k]) { // 与b[0, m-1]求公共后缀⼦串47 --j;48 ++k;49 suffix[k] = j + 1; // j+1表⽰公共后缀在b[0，i]中的起始下标50 }51if (j == -1) {52 prefix[k] = true; // 如果公共后缀⼦串也是模式串的后缀⼦串53 }54 }55 }5657/**58 * 完整的BM算法好后缀+坏字符59 *60 * @param a61 * 主串62 * @param n63 * 主串的长度64 * @param b65 * 模式串66 * @param m67 * 模式串的长度68 * @return69*/70public int bm(char[] a, int n, char[] b, int m) {71int[] bc = new int[SIZE];72 generateBC(b, m, bc); // 构建坏字符哈希表73int[] suffix = new int[m];74boolean[] prefix = new boolean[m];75 generateGS(b, m, suffix, prefix); // 构建好字符哈希表76int i = 0; // j 表⽰主串与模式串匹配的第⼀个字符77while (i < n - m) {78int j = 0;79for (j = m - 1; j >= 0; --j) {// 模式串从后向前匹配80if (a[i + j] != b[j]) {81break; // 坏字符串82 }83 }84if (j < 0) {85return i;// 匹配成功，返回主串和模式串第⼀个匹配字符的位置86 }87int x = j - bc[(int) a[i + j]];88int y = 0;89if (j < m - 1) { // 如果有好后缀的话90 y = moveByGS(j, m, suffix, prefix);91 }92 i = i + Math.max(x, y);93 }94return -1;95 }9697private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {98int k = m - 1 - j; // 好后缀的长度99if (suffix[k] != -1) {100return j - suffix[k] + 1;101 }102for (int r = j + 2; r <= m - 1; ++r) {103if (prefix[m - r] == true) {104return r;105 }106 }107return m;108 }现在再看BM算法，原来之前⾃⼰是⼀点也没弄懂！只是当做⽂章简单读了⼀遍，阿西吧！⾸先，那个坏字符的散列表的构建就没有弄懂：1、为什么在散列表数组中要初始化每⼀个值为-1？这⾥是在坏字符匹配的时候，如果主串与模式串中字符没有匹配上（把坏字符在模式串中下标记做xi），此时的xi=-12、你有没有考虑过模式串中的相同的字符的ASCII码是相同的，那样循环处理的话，只是记录模式串中相同字符中最后⾯的那个字符的下标，没有问题吗？这个是没有问题的！这⾥⽆⾮有两种情况，就是坏字符与⾮坏字符：坏字符：因为是从后向前倒序匹配，只需要知道后⾯的字符下标，就可以计算出移动距离⾮坏字符：需要去寻找坏字符或者使⽤好后缀规则2019年11⽉14⽇15:34:37 修改此⼤部分内容来⾃极客时间专栏，王争⽼师的《数据结构与算法之美》极客时间：。

那些经典算法：字符串匹配算法BM算法

那些经典算法：字符串匹配算法BM算法单模式串匹配算法中BM（Boyer-Moore）算法算是很难理解的算法了，不过性能高效，据说比KMP算法性能提升3到4倍，suricata里面的单模式匹配就是用这种算法，所以有必要学习下，再把suricata的这部分代码过一下还是不错的。

一、BM算法原理BM算法是1975年发明的,它是一种后匹配算法，我们普通的字符串匹配算法是从左向右的，BM算法是从右向做的，即先判断模式串最后一个字符是否匹配，最后判断模式串第一个字符是否匹配。

原来我们在BF算法中，如果模式串和主串不匹配，则将主串或模式串后移一位继续匹配，BM算法根据模式串的特定规律，将后移一位的步子迈的更大一些，后移几位。

来看个图简单说明下，图来自《数据结构与算法之美》课程：但是如果我们仔细观察，c字符在abd中不存在，那么abd可以直接移动到主串中c字符的后面再继续匹配：这样移动的步数变大了，匹配起来肯定更快了。

BM算法根据模式串的特定规律，这里面的特定规律有两种，一种是好后缀规则，一种是坏字符规则，初次看到这种规则的介绍后，心里嘀咕着这性能会好吗，后面才发现经典的BM算法做了不少优化，所以性能高。

下面分别介绍下好后缀规则（good suffix shift）和坏字符规则（bad character rule）。

1.1 BM坏字符规则首先在BM算法里面何谓好坏那，匹配上的，我们称为好，匹配不上的叫坏。

按照刚才说的，BM算法是倒着匹配字符串的，我们在倒着匹配字符串的过程中，当我们发现某个字符没法匹配的时候，我们把主串中这个没法匹配的字符称为坏字符。

我们发现在模式串中，字符c是不存在的，所以可以直接将模式字符串向后滑动3位继续匹配。

滑动后，我们继续匹配，发现主串中的字符a和模式串的d不匹配，这时候的情况和上一种不一样，因为主串中的坏字符a在模式串中存在，则后移动2位，让主串和模式串中的a对齐继续匹配。

那么每次后移多少位那，我们假设把匹配不到的坏字符的位置记作si，如果坏字符在模式串中存在，则坏字符在模式串中的位置记作xi，那么模式串后移为si-xi；如果坏字符在模式串中不存在，xi就为-1。

BF算法KMP算法BM算法

BF算法KMP算法BM算法1. BF算法（Brute Force Algorithm）BF算法也称为暴力匹配算法，它是一种最简单直观的字符串匹配算法。

其原理是从目标字符串的第一个字符开始，逐个与模式字符串的字符进行比较，如果匹配失败，则将目标字符串的指针向后移动一位，再继续比较。

直到找到匹配或目标字符串被遍历完。

BF算法的时间复杂度为O(n*m)，其中n为目标字符串的长度，m为模式字符串的长度。

在最坏情况下，需要进行n-m+1次比较。

BF算法的优点是实现简单，适用于简单的字符串匹配问题。

但是对于大规模文本的匹配效率较低。

2. KMP算法（Knuth–Morris–Pratt Algorithm）KMP算法是一种改进的字符串匹配算法，通过利用已经匹配的信息来避免不必要的比较。

它首先构建一个部分匹配表（Partial Match Table），用于存储模式字符串每个前缀的最长公共前后缀的长度。

然后通过这个表来指导匹配过程。

KMP算法的核心思想是，当出现不匹配的字符时，通过部分匹配表中的信息，可以将模式字符串向后移动尽可能多的位置，而不是单纯地移动一位。

这样可以大大减少不必要的比较次数，提高匹配效率。

KMP算法的时间复杂度为O(n+m)，其中n为目标字符串的长度，m为模式字符串的长度。

在构建部分匹配表时需要O(m)的时间复杂度，匹配过程需要O(n)的时间复杂度。

KMP算法的优点是在大规模文本匹配时效率较高，缺点是算法较为复杂，需要额外的存储空间来存储部分匹配表。

3. BM算法（Boyer-Moore Algorithm）BM算法是一种高效的字符串匹配算法，通过利用不匹配字符的信息来跳过尽可能多的字符，从而减少比较次数。

其核心思想是从模式字符串的末尾开始匹配，并向前移动模式字符串。

BM算法分为坏字符规则和好后缀规则两部分：-坏字符规则：当遇到不匹配的字符时，将模式字符串根据目标字符串中的字符向后移动一位，从而跳过了部分字符的比较。

BM字符串匹配算法

BM字符串匹配算法字符串匹配是一种常见的操作，可以用来判断一个字符串中是否包含另一个字符串。

比如在搜索引擎中输入一个关键字，搜索引擎会根据关键字在文本中匹配相似的内容。

在编程中，字符串匹配也是一种常见的操作。

BM字符串匹配算法是一种高效的字符串匹配算法，本文将介绍BM算法的原理、优化和应用场景。

BM字符串匹配算法的原理BM字符串匹配算法是由Boyer和Moore两个人于1977年提出的，它是一种模式匹配算法，用于在一个主串中查找一个模式串的出现位置。

BM算法是一种启发式算法，它利用了在主串中匹配失败时，模式串能够“跳过”一些已经匹配的字符的特点，从而提高匹配的效率。

BM算法的核心思想是利用两个规则：坏字符规则和好后缀规则。

坏字符规则是指如果在匹配过程中发现不匹配，就找到主串中与模式串中不匹配的那个字符相同的最右位置，将模式串向右滑动这个位置。

而好后缀规则是指如果在匹配过程中发现不匹配的位置包含一个好后缀，就将模式串向右滑动这个好后缀和主串中和它匹配的最靠右的模式串位置对齐。

BM算法的优化BM算法在实际应用中可以进一步优化。

其中一种优化是使用哈希表。

在坏字符规则中，每次需要在主串中找到不匹配的字符，在O(n)的时间复杂度内搜索。

如果主串中出现了大量相同的字符，那么哈希表可以大大减少搜索的时间。

哈希表将字符映射到桶中，桶中存储的是出现该字符的最右位置，这样就可以在O(1)的时间复杂度内找到该字符出现的最右位置。

另一种优化是使用suffix数组。

suffix数组是一个字符串排序之后的结果，它可以用于快速查找当前位置后面的所有后缀。

在好后缀规则中，需要找到与好后缀相匹配的子串，然后滑动这个子串到最右位置。

如果每次都从当前位置开始往后搜索，时间复杂度是很高的。

而使用suffix数组可以快速查找到所有与好后缀匹配的子串，然后选择离当前位置最远的那个子串进行滑动，这样可以大大提高匹配的效率。

BM算法的应用场景BM算法的应用场景非常广泛，比如在文本编辑器中查找某个单词、在搜索引擎中根据关键字搜索相似文章、在代码中查找某个变量或函数等等。

关于KMP算法和BM算法的理解

关于KMP算法和BM算法的理解自己之前没有接触到模式匹配的问题。

对于所谓的字符串匹配也只是简单的蛮力匹配。

上周刚看了《多模式匹配算法及破件实现》这篇文章。

文章中主要讲的是多模式匹配算法: AC算法和WM算法以及这两个算法的改进。

AC算法是基于KMP算法的，WM算法是基于BM算法的。

只有充分理解了单模式匹配的KMP算法和BM算法才能理解多模式匹配算法, 最后才能对模式匹配有一个深入的理解。

卜面主要说卜•自己对KMP算法和BM算法的理解。

KMP算法和BM算法，它们分别是前缀匹配和后缀匹配的经典算法。

所谓前缀匹配是指: 模式串和母串的比较从左到右，模式串的移动也是从左到右：所谓后缀匹配是指：模式串和母串的的比较从右到左，模式串的移动从左到右。

看得岀来前缀I兀配和后缀匹配的区别就仅仅在于比较的顺序不同。

KMP算法KMP算法，是由Knuth, Morris, Pratt共同提出的模式匹配算法，其对于任何模式和目标序列，都可以在线性时间内完成匹配查找，而不会发生退化，足一个非常优秀的模式匹配算法。

KMP算法对于朴素匹配算法的改进是引入了一个跳转表next[]。

但next[]刚接触时比较难于理解。

next跳转表，在进行模式匹配，实现模式串向后移动的过程中，发挥了更要作用。

这个表看似神奇，实际从原理上讲并不复杂，对于模式串而言，其前缀字符串，有町能也是模式串中的非前缀子串，这个问题我称之为前缀包含问题。

以模式串abcabcacab为例，其前缀abca,止好也是模式串的一个子串abc(abca)cab,所以当目标串与模式串执行匹配的过程中，如果直到第8个字符才匹配失败，同时也意味着目标串当前字符Z前的4个字符, 与模式串的前4个字符是相同的，所以当模式串向后移动的时候，可以直接将模式串的第5 个字符与当前字符对齐，执行比较，这样就实现了模式串一次性向前跳跃多个字符。

这里只是一个模式串移动的思想。

如何以较小的代价计算KMP算法中所用到的跳转表next,是算法的核心问题。

串匹配算法之BM算法

串匹配算法之BM算法参考资料：这⾥，我们仅仅⽤了坏字符规则定义⼀个滑动距离函数：dist（C）= 1） m – j j = max{j| tj = c && 1<= j <= m - 1}2) m 若C不出现在模式中或tm = c⽐如 T = pattern dist（a）= 7 – 2 ； dist（t） = 7 – 4 （算最后出现的）； dist（e） = 7 – 5 ； dist（r） = 7 - 6；最后⼀个dist（n） = 7 （m ，模式串T的总长度），其他的未出现的字符， dist（ch） = 7；程序如下：1: void BMDist(string str,int dist[])2: {3: int i;4: for (i = 0; i < 256; i++)5: {6: dist[i] = str.length();7: }8: for (i = 0; i < str.length() - 1; i++)//最后⼀个字符取不到9: {10: dist[str[i]] = str.length() - i - 1;11: }12: dist[str[str.length()-1]] = str.length();13:14: }15:16: int BM(string s, string t,int dist[])17: {18: int i = t.length();19: while(i <= s.length())20: {21: int j = t.length();22: while(j>0 && s[i-1]==t[j-1])23: {24: j--;25: i--;26: }27: if (j == 0)28: {29: return i + 1;30: }31: else32: {33: i = i + dist[s[i-1]];34: }35: }36: return -1;37: }测试代码：1: int main()2:3: {4:5: while(1)6: {7: clock_t start,stop;8: string Str,Tsr;9:10: int flag1,flag2,flag3;11: int dist[256];12:13: int next[1000]={0,};14: cout <<"请输⼊S串与T串：" <<endl;15: cin >> Str >> Tsr;16: cout << endl;17:18: start = clock();19: for (int i=0; i< 1000; i++)20: {21: flag1 = BF(Str,Tsr);22: }23: stop = clock();24: cout << "BF算法的执⾏时间是："<< stop - start << endl; 25:26:27: start = clock();28: for (int i=0; i< 1000; i++)29: {30: kmpNext(Tsr,next);31: flag2 = kmp(Str,Tsr,next);32: }33: stop = clock();34: cout << "KMP算法的执⾏时间是："<< stop - start << endl; 35:36:37: start = clock();38: for (int i=0; i< 1000; i++)39: {40: BMDist(Tsr,dist);41: flag3 = BM(Str,Tsr,dist);42: }43: stop = clock();44: cout << "BM算法的执⾏时间是："<< stop - start << endl; 45:46: if (flag1 == -1)47: {48: cout << "没有找到⼦串"<<endl;49: }50: else51: {52: cout << "找到⼦串的位置为"<< flag1 <<endl;53: }54: if (flag2 == -1)55: {56: cout << "没有找到⼦串"<<endl;57: }58: else59: {60: cout << "找到⼦串的位置为"<< flag2 <<endl;61: }62: if (flag3 == -1)63: {64: cout << "没有找到⼦串"<<endl;65: }66: else67: {68: cout << "找到⼦串的位置为"<< flag3 <<endl;69: }70: }71:72: return 0;73: }。