共轭方向与共轭梯度法-最优化方法
最优化方法-共轭方向和共轭梯度法

由3式可以看出
2020/3/6
16
2.共轭方向-共轭方向法
• 基本定义
利用共轭方向作为搜索方向的无约束极小化算法
• 通用步骤:
(1)任取X 0 ,以及在X 0的下降方向P0 , k 0; (1)求解一维搜索问题
min f ( X k Pk ),为最优步长,是个数值.
(3) X k1 X k k Pk ;
X
T QX
bT
X
c, Q正定,
X 0是初始点,
P0
f
(X0)
X k1 X k k Pk , k 0,1...m 1, k是最优步长,且
Pk1 f ( X k1) ak Pk (这是构造的结果)
其中ak
f
( X k1)T QPk PkT QPk
,
P0
(
X
)T
k 1
Pk
)T
PkT f ( X k1)
f ( X k1) QX k1 b Q( X k k Pk ) b, ( X k 1 X k k Pk )
f ( X k1) (QX k b) kQPk f ( X k ) kQPk
当m 2时 所以,P0,P1, Pm1是线性无关的。
P0T QP1
P0T Q f ( X 1 )
f ( X 1 )T QP0 P0T QP0
P0
P0T Qf ( X 1 ) f ( X 1 )T QP0 0
表明,P0与P1共轭。
2020/3/6
2020/3/6
4
1.共轭方向法的基本原理
• 已知 X1 点是在 X 0 点在直线 l0 上沿 P0 搜索方向的一个极小 点。(l0 与 P0 是平行的)
最优化方法第二章_线搜索算法_最速下降法
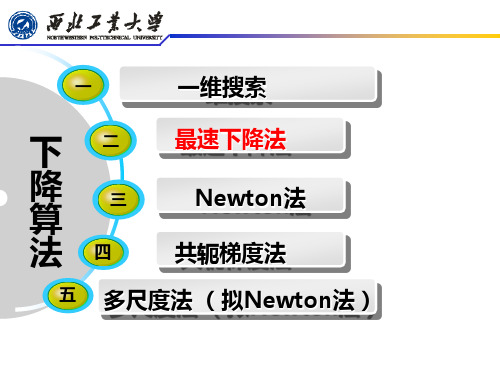
f x1 , x2 c, c>0,
2
改写为:
x12 2c 1
2 x2
2c 2
2
1
二、最速下降法
x2
这是以
2c
1
和
2c
2
为半轴的椭圆
2c
2c
2
2
从下面的分析可见 两个特征值的相对
x1
大小决定最速下降法的收敛性。
(1)当 1 2 时,等值线变为圆
2 2
4 f x , 2
2 x1 2 x2 4 f ( x) , 2 x1 +4x2
4 d = f x , 2
0 0
=40 2 20 3 令 0= ' ( ) 80 20, 得 0 =1/4,
一
一维搜索
二 三 四
下 降 算 法
五
最速下降法 Newton法 共轭梯度法
多尺度法 (拟Newton法)
二、最速下降法 假设 f 连续可微,取 线搜索方向
k
d f ( x )
k
步长k 由精确一维搜索得到。 从而得到第 k+1次迭代点,即
f ( x k k d k ) min f ( x k d k )
(推论)在收敛定理的假设下,若f (x)为凸函数,则最速下降 法或在有限迭代步后达到最小点;或得到点列 x k ,它的任 何聚点都是 f (x)的全局最小点。
二、最速下降法
最速下降法特征:相邻两次迭代的方向互相垂直。
令
( ) f ( x d ), 利用精确一维搜索,可得
最优化方法实验报告(2)

最优化方法实验报告Numerical Linear Algebra And ItsApplications学生所在学院:理学院学生所在班级:计算数学10-1学生姓名:甘纯指导教师:单锐教务处2013年5月实验三实验名称:无约束最优化方法的MATLAB实现实验时间: 2013年05月10日星期三实验成绩:一、实验目的:通过本次实验的学习,进一步熟悉掌握使用MATLAB软件,并能利用该软件进行无约束最优化方法的计算。
二、实验背景:(一)最速下降法1、算法原理最速下降法的搜索方向是目标函数的负梯度方向,最速下降法从目标函数的负梯度方向一直前进,直到到达目标函数的最低点。
2、算法步骤用最速下降法求无约束问题n R()min的算法步骤如下:xxf,a )给定初始点)0(x ,精度0>ε,并令k=0;b )计算搜索方向)()()(k k x f v -∇=,其中)()(k x f ∇表示函数)(x f 在点)(k x 处的梯度;c )若ε≤)(k v ,则停止计算;否则,从)(k x 出发,沿)(k v 进行一维搜索,即求k λ,使得)(min )()()(0)()(k k k k v x f v x f λλλ+=+≥; d )令1,)()()1(+=+=+k k v x x k k k k λ,转b )。
(二)牛顿法1、算法原理牛顿法是基于多元函数的泰勒展开而来的,它将)()]([-)(1)(2k k x f x f ∇∇-作为搜索方向,因此它的迭代公式可直接写出来:)()]([)(1)(2)()(k k k k x f x f x x ∇∇-=-2、算法步骤用牛顿法求无约束问题n R x x f ∈),(min 的算法步骤如下:a )给定初始点)0(x ,精度0>ε,并令k=0;b )若ε≤∇)()(k x f ,停止,极小点为)(k x ,否则转c );c )计算)()]([,)]([)(1)(2)(1)(2k k k k x f x f p x f ∇∇-=∇--令;d )令1,)()()1(+=+=+k k p x x k k k ,转b )。
无约束常用优化方法

步长 ,作前进(或后退)试探.如试探成功(目
标函数值有所减小),则按步长序列
,加
大步长(注意每次加大步长都是由初始点算起),直
至试探失败(目标函数值比前一次的有所增加)时,
则取其前一次的步长作为沿这个坐标轴方向搜索的最
优步长,并计算出该方向上的终止点,而后以这个终
止点为始点再进行下一坐标轴方向的搜索,并重复上
处
显然 是二次函数,并且还是正定二次函数,所以 是凸函数且存在唯一全局极小点.为求此极小点,令
即可解得
即
(5.9)
对照基本迭代公式,易知,式(5.9)中的搜索方向
步长因子
方向
是直指点 处近似二次函数
的极小点的方向.此时称此方向为从点 出发的
Newton方向.从初始点开始,每一轮从当前迭代点出发,
沿Newton方向并取步长 的算法称为Newton法.
另外,共轭梯度法不要求精确的直线搜 索.但是,不精确的直线搜索可能导致迭代 出来的向量不再共轭,从而降低方法的效 能.克服的办法是,重设初始点,即把经过 n次迭代得到的Xn作为初始点重新迭代.
五、坐标轮换法
在坐标轮换法中,沿各个坐标轴方向进行一维搜索
时,常选用最优步长法或加速步长法.加速步长法从
初始点出发,沿搜索(坐标轴)方向先取一个较小的
三、共轭方向法
1、概念
通常,我们把从任意点
出发,依次沿某组共轭
方向进行一维搜索的求解最优化问题的方法,叫做共
轭方向法.
2、特点
• 一般地,在n维空间中可以找出n个互相共轭的方向,对于n元正 定二次函数,从任意初始点出发,顺次沿这n个共轭方向最多作n 次直线搜索就可以求得目标函数的极小点.这就是共轭方向法的 算法形成的基本思想.
最优化问题的算法迭代格式

最优化问题的算法迭代格式最优化问题的算法迭代格式最优化问题是指在一定的条件下,寻找使某个目标函数取得极值(最大值或最小值)的变量取值。
解决最优化问题的方法有很多种,其中较为常见的是迭代法。
本文将介绍几种常用的最优化问题迭代算法及其格式。
一、梯度下降法梯度下降法是一种基于负梯度方向进行搜索的迭代算法,它通过不断地沿着目标函数的负梯度方向进行搜索,逐步接近极值点。
该方法具有收敛速度快、易于实现等优点,在许多应用领域中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和学习率 $\alpha$,梯度下降算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 更新当前点 $x_k$ 为 $x_{k+1}=x_k-\alpha\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则返回第 1 步。
2. 算法特点- 沿着负梯度方向进行搜索,能够快速收敛;- 学习率的选择对算法效果有重要影响;- 可能会陷入局部极小值。
二、共轭梯度法共轭梯度法是一种基于线性方程组求解的迭代算法,它通过不断地搜索与当前搜索方向共轭的新搜索方向,并在该方向上进行一维搜索,逐步接近极值点。
该方法具有收敛速度快、内存占用少等优点,在大规模问题中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和初始搜索方向 $d_0$,共轭梯度算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则进行下一步;- 计算当前搜索方向 $d_k$;- 在当前搜索方向上进行一维搜索,得到最优步长 $\alpha_k$;- 更新当前点为 $x_{k+1}=x_k+\alpha_k d_k$;- 计算新的搜索方向 $d_{k+1}$;- 返回第 2 步。
2. 算法特点- 搜索方向与前面所有搜索方向都正交,能够快速收敛;- 需要存储和计算大量中间变量,内存占用较大;- 可以用于非线性问题的求解。
4.4共轭方向法4.5 共轭梯度法

序框图如下图所示。
开始
给定 X 0、d0、
k0
X (k 1) X k ak d k ak : min f ( X k ak d k )
k k+1
YES Xk X(k+1)
结束
NO
f (X k1) <
提供新的共轭方向
共轭方向 + 精确一维搜索 = 二次终结 设 Z1 ,Z2 ,……Zm 关于正定矩阵A共轭。则从任意初 始点出发 二次型目标函数
2 0
2 9
,
2 T 3
X
2
X1
1d1
2
3
0
2
1
9 2
3
2 3
2 9
1
2 3
1
将 X 2 代入原方程,将 n 维问题化成一维问题。
令 将
(1) 1 代入
0 X2
,解得 1
式得
3 2
。
X
2
2 3
2 9
1
2 3
1
1 1
计算 X 2 点的梯度
g2
f
(
X
2
)
4 0
(0 )
(0 ) 120 4
令 (0 ) 0 ,解得
0
1 3
将
0
1 3
代入
X1
式得
X
1
20
0
2
3
0
将 X 1 代入求梯度公式
g1
f
(
X
1)
3x1 2
x2
x1
x2
x1
2 3
x2 0
0
2
3
0
g1 g0
(完整版)机械优化设计习题参考答案孙靖民第四版机械优化设计

2.黄金分割法(0.618法)
原理:提高搜索效率:1)每次只插一个值,利用一个前次的插值;2)每次的缩短率λ相同。左右对称。
程序:p52
(四)插值方法
1.抛物线法
原理:任意插3点:
算得: ; ;
要求:
设函数 用经过3点的抛物线 代替,有
解线代数方程
解得:
程序框图p57
网格法 ,缩小区间,继续搜索。
Monte Carlo方法 , ,随机数。
比较各次得到的 得解
遗传算法(专题)
(二)区间消去法(凸函数)
1.搜索区间的确定:高—低--高( )则区间内有极值。
2.区间消去法原理:在区间[a, b]内插两个点a1, b1保留有极值点区间,消去多余区间。
缩短率:
(三)0.618法
可行方向—约束允许的、函数减小的方向。(图)约束边界的切线与函数等高线的切线方向形成的区域。
数学模型
用内点法或混合法,取 ,
直接方法
(一)随机方向法
1.在可行域产生一个初始点 ,因 (约束),则
--(0,1)的随机数。
2.找k个随机方向,每个方向有n个方向余弦,要产生kn个随机数 , , ,随机方向的单位向量为
3.取一试验步长 ,计算每个方向的最优点
4.找出可行域中的最好点 得搜索方向 。以 为起点, 为搜索方向得 。最优点必须在可行域内或边界上,为此要逐步增加步长。
得
穷举下去得递推公式
3.算例
p73
4.框图p72
5.特点
作业:1. 2.
(六)变尺度法
1.引言
坐标变换
二次函数
令 为尺度变换矩阵
共轭梯度法

2 2 min f ( x ) = x1 + 2x2 x
⎛1⎞ 给定初始点 x (0) = ⎜ ⎜1⎟ ⎟。 ⎝ ⎠
13
⎛ 2 x1 ⎞ ⎛ 2 0⎞ 2 首先, ∇f ( x ) = ⎜ ⎜ 0 4⎟ ⎟ ,以下利用(4.14)确定 β k 。 ⎜ 4x ⎟ ⎟ ,H= ∇ f ( x ) = ⎜ ⎝ ⎠ ⎝ 2⎠ k=0:
0
k +1
) 与搜索方向 s 0 ," , s k 均正交。同时,利用引理 4.1 马上
设 H ∈ R n×n 是对称正定阵,s ," , s
0
n −1
0
n −1
是非零 G—共轭方向组,x ∈ R 。 若对问题(UQP),
0
n
从 x 出发,依次沿 s ," , s
0
进行最优一维搜索,最终得到 x ,则 x 是(UQP)的最优解。
为保证 H-共轭性,在 x 处必须取 s 为搜索方向,而不能取 α s (α > 0) 为搜索方向。
k k
k
利用定理 4.3,马上得到上述算法的有限终止性。 定理 4.4 设 H ∈ R n×n 是对称正定阵。若用凸二次规划的共轭梯度法求解 (UQP) 时产生迭代点
x1 ," , x K ,则 x K 是(UQP)的最优解,并且 K ≤ n 。
首先由(4.7)知, g = ∇f ( x ) ( j = 0, " , k -1)是 s ," , s 的线性组合,因此根据定理 4.2,
j j 0 j
( g k )T g j =0, j = 0, " , k -1
由于
工程优化 第4章-3

g k +1 与 g1 ,g 2 ,...,g k 正交,p k +1 与 p1 ,p 2 ,...,p k A共轭。 (a) 证明 g k +1 与 g1 ,g 2 ,...,g k 正交; 1 f ( x ), i 1, 因为 i p i i 1 f ( x ) p , i 2,..., n, i 1
共轭方向法---共轭方向的性质
性质4 设n元函数f(x)=1/2xTAx+bTx+c, A=AT正定,又设n维非零向量组p1, p2,…, pn是A 共轭向量组,从任意点x1出发,相继以p1, p2,…, pn 为搜索方向进行精确一维搜索,则
(1) ▽f(xk+1)与p1, p2,…, pk (k=1,2,…,n)正交;
共轭方向法和共轭梯度法
最速下降法,计算步骤简单,但收敛速度慢。
Newton法和阻尼Newton法都有一个优点:收敛速度快,但 需要计算Hesse矩阵和Hesse矩阵的逆矩阵,计算量和存储量都 很大。
需要寻找一种好的算法,这种算法能够兼有这两种方法的 优点,又能克服它们的缺点,即收敛速度快同时计算简单。 这就是要讨论的共轭方向法和共轭梯度法。
=0
结论(b)成立,进而结论(2)成立。
共轭梯度法
定理1:设向量组 p , p ,..., p 是由上述方法产生的向量组,向量
组 g1 , g 2 ,..., g n 是由各点的梯度生成的向量组, ( g k f ( x ) ) 则
k
1 2 n
(1) g1 , g 2 ,..., g n 是正交向量组;
( pi )T Ap j 0 (i j, j 1, 2,..., m)
最优化方法3-5共轭梯度法和共轭方向法

算法 3.5.1
设目标函数为 f (x) 1 xTGx bT x c,其中G 正定。 2
给定控制误差 。
Step1. 给定初始点 x0及初始下降方向 p0,令k 0。
Step2. 作精确一维搜索,求步长k
f
( xk
k
pk )
min
0
f
( xk
pk
)
Step3. 令 xk1 xk k pk 。
称 Fletcher-Reeves 公式,简称 FR 公式。
k 1
gkT Gpk1 pkT1Gpk 1
Gpk 1
1
k 1
(gk
g
k 1 ) ,
gkT Gpk1
1
k 1
gkT
(gk
g
k 1)
,
pkT1Gpk 1
1
k 1
(g
k1 k2
pk2 )T
(gk
g
k 1)
1
k 1
g
g T
k 1 k
1
(2)Polak-Ribiere-Polyak 公式
故
k 1
g
T k
(
gk
g
k 1)
gkT1gk 1
此式是 Polak 和 Ribiere 以及 Polyak 分别于 1969
年提出的,故称 Polak-Ribiere-Polyak 公式,简称 PRP
0,i
1,2,L
,k
(ii) xk1是二次函数在k 维超平面Hk 上的极小点。
证明 由引理 3.5.2,只需证明(i),
共轭梯度法总结

共轭梯度法(Conjugate Gradient Method)总结1. 引言共轭梯度法是一种用于求解线性方程组或优化问题的迭代算法。
它在大规模问题上具有较高的效率和收敛速度,并且不需要存储完整的矩阵。
共轭梯度法最早由Hestenes和Stiefel于1952年提出,后来经过多次改进和推广,成为求解稀疏线性方程组和优化问题的重要工具。
2. 基本原理共轭梯度法的基本思想是利用共轭方向的性质,通过一系列迭代来逼近最优解。
对于一个对称正定矩阵A和一个向量b,我们希望找到一个向量x使得Ax=b成立。
通过引入残差r=b-Ax,我们可以将问题转化为求解残差最小化的问题。
定义两个向量d和g满足以下关系:d_i^TAd_j=0 (i≠j),则称d_i与d_j是关于矩阵A共轭的。
在每次迭代中,选择与之前所有搜索方向都共轭的搜索方向,并沿着该方向进行搜索。
3. 算法流程步骤1:初始化给定初始解x_0,计算初始残差r_0=b-Ax_0,并令搜索方向d_0等于r_0。
步骤2:迭代重复以下步骤直到满足收敛条件: - 计算当前搜索方向的梯度g_k=Ad_k。
- 计算步长alpha_k=r_k Tr_k/(d_k TAd_k)。
- 更新解x_{k+1}=x_k+alpha_k d_k。
- 更新残差r_{k+1}=r_k-alpha_k Ad_k。
- 计算新的搜索方向d_{k+1}=r_{k+1}+beta_{k+1}d_k,其中beta_{k+1}=r_{k+1}^T r_{k+1}/(r_k^T*r_k)。
步骤3:输出结果返回近似解x。
4. 关键观点和发现共轭梯度法具有以下几个关键观点和发现: - 共轭方向的选择:在每次迭代中,选择与之前所有搜索方向都共轭的搜索方向。
这样可以保证每次迭代都能沿着一个新的、不再相关的搜索方向前进,从而避免了无谓的震荡和重复计算。
- 最优解性质:对于一个n维问题,共轭梯度法最多需要n步就可以达到最优解,即解决了一个n维线性方程组的问题。
最优化方法 总结

最优化方法总结
最优化方法是一种用于求解最优化问题的数学工具和技术。
最优化问题是指在给定约束条件下寻找使得目标函数取得最大或最小值的变量取值。
最优化方法主要分为两类:无约束优化和约束优化。
在无约束优化中,最优化方法包括:
1. 梯度下降法:通过不断迭代来寻找函数的最小值点,在每一步迭代中通过计算函数的梯度来确定下降的方向和步长。
2. 牛顿法:使用函数的一阶和二阶导数来近似估计最小值点,通过迭代计算来逐步逼近最小值点。
3. 拟牛顿法:使用函数的梯度信息来估计牛顿法的一阶导数信息,以减少计算二阶导数的复杂性。
4. 共轭梯度法:通过迭代来求解线性最小二乘问题,可以高效地求解大规模问题。
在约束优化中,最优化方法包括:
1. 等式约束优化:利用拉格朗日乘数法将等式约束转化为无约束优化问题,并使用无约束优化方法求解。
2. 不等式约束优化:使用罚函数、投影法或者序列二次规划等方法将不等式约束转化为无约束优化问题,并使用无约束优化方法求解。
3. 信赖域方法:通过构造信赖域来限制搜索方向和步长,以保证在搜索过程中满足约束条件。
4. 内点法:通过转化为等式约束问题,并使用迭代法来逐步逼近约束边界。
总体来说,选择适当的最优化方法取决于问题的性质和约束条件的类型。
不同的最优化方法有不同的优缺点,适用于不同的问题,因此需要在具体应用中进行选择和调整。
最优化课程练习-共轭梯度法
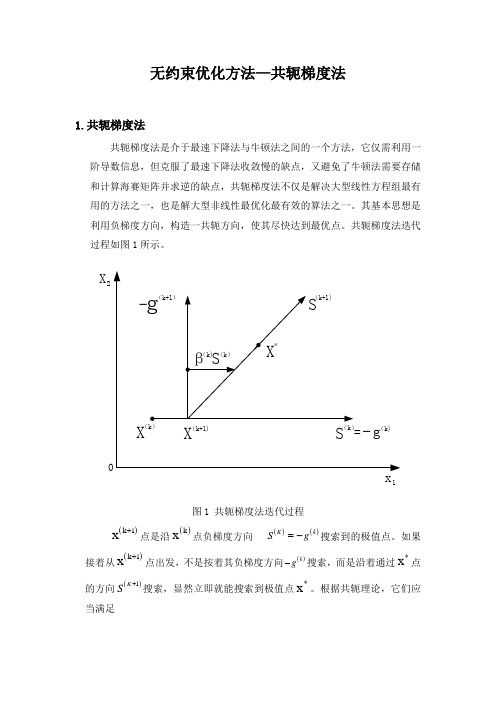
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其基本思想是利用负梯度方向,构造一共轭方向,使其尽快达到最优点。
共轭梯度法迭代过程如图1所示。
1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。
如果接着从()k 1x +点出发,不是按着其负梯度方向()kg -搜索,而是沿着通过*x 点的方向()1K S +搜索,显然立即就能搜索到极值点*x 。
根据共轭理论,它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向,新构造的共轭方向()1K S +,可由矢量合成,()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理,推到出:()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+,就可以构造一个与梯度矢量为共轭的矢量()1K S +,沿着该方向搜索,即可求得极值点。
共轭梯度法程序框图如图2所示。
图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解,其中:初始点()0[1,1]T X =。
收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结 论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。
最优化方法第三章(2).

n 维向量空间中,非零的共轭向量的
个数不超过 n 。 设 p0 , p1 , , pm1 是 R n 中的非零 Q 共轭向量。因为 线性无关,所以由它们可以张成 R n 的一个 m 维子空间, 且这个 m 维子空间中的任意一个向量 x 均可表示为
x ai pi ,
i 0 m 1
3. 共轭方向法
共轭方向法的理论基础是下面的定理。 定理3.4 假设 (1)Q 为 n n 对称正定矩阵; (2) 非零向量 p0 , p1 , , pm1是 Q 共轭向量; (3)对二次目标函数(3.36)顺次进行 m 次直线搜索
xi 1 1s xi , pi , i 0,1, , m 1
p1
因为 p1 从 其中
p1 怎样确定,它应该满足什么条件?
*
x x1 t1 p1
*
x1 直指极小点 x ,所以 x
*
可以表示为
(3.38)
t1 是最优步长因子。显然,当 x1 x*时, t1 0 。
对(3.36)求导数,有
f x Qx b .
因为
(3.39)
x 是极小点,所以有
归纳一下,对于二元二次目标函数,从任意初始点 x0 出发,沿任意下降方向 p0 做直线搜索得到 x1;再从 x1 出发,沿 p0 的共轭方向 p (可由( 3.42)确定)作直线 1 * 搜索,所得到的 x2 必是极小点 x 。
一般说来,具有二次终止性的算法,在用于一般函数 时,收敛速度是较快的。
设 Q 是 n n 对称正定矩阵。若 n 维向量 空间中的非零向量 p0 , p1 , , pm1 满足 piT Qp j 0, i, j 0,1, , m 1(i j) (3.43) 则称 p0 , p1 , , pm1是 Q 共轭向量或称向量 p0 , p1 , , pm1 是 Q共轭的(简称共轭),称 p0 , p1 , , pm1 的方向是 Q 共轭 方向。 当 Q 1(单位矩阵)时,(3.43)为 定义3.3
共轭梯度法

共轭梯度法简介共轭梯度法是一种迭代的最优化算法,用于求解线性方程组或求解非线性优化问题。
它在解决大规模线性方程组时表现出色,尤其适用于对称正定矩阵的问题。
共轭梯度法结合了最速下降法和共轭方向法的优点,能够在有限次数的迭代中快速收敛到最优解。
背景在数值计算和优化问题中,线性方程组的求解是一个常见且重要的问题。
例如,在图像处理、数据分析和机器学习等领域,我们经常需要求解一个大规模的线性方程组。
然而,传统的直接方法,如高斯消元法或LU分解,对于大规模问题往往计算量巨大,耗时较长。
因此,我们需要寻找一种高效的迭代方法来解决这些问题。
共轭梯度法的核心思想是通过一系列共轭的搜索方向来逼近最优解。
具体来说,对于一个对称正定的线性方程组Ax=b,共轭梯度法的步骤如下:1.初始化解向量x0和残差x0=x−xx0。
2.计算初始搜索方向x0=x0。
3.进行共轭梯度迭代:重复以下步骤n次或直到收敛为止。
a.计算步长$\\alpha_k=\\frac{r_k^Tr_k}{d_k^TAd_k}$。
b.更新解向量$x_{k+1}=x_k+\\alpha_kd_k$。
c.更新残差$r_{k+1}=r_k-\\alpha_kAd_k$。
d.计算新的搜索方向$d_{k+1}=r_{k+1}+\\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}d_k$。
共轭梯度法与其他迭代方法相比有以下特点:1.高效性:共轭梯度法能够在有限次数的迭代中收敛到最优解,尤其适用于对称正定矩阵。
相比于直接方法,其计算量较小,具有更高的计算效率。
2.无需存储完整矩阵:共轭梯度法只需知道矩阵A的乘法运算结果,不需要存储完整的矩阵。
这对于大规模问题是一个很大的优势。
3.不需要计算矩阵的特征值:相比于其他迭代方法,共轭梯度法不需要计算矩阵的特征值,因此在实际问题中更加实用。
算法应用共轭梯度法广泛应用于各个领域的优化问题和线性方程组求解问题,包括:1.图像处理:共轭梯度法用于图像恢复、图像去噪和图像分割等问题。
最优化理论与算法(第四章)

第四章 共轭梯度法§4.1 共轭方向法共轭方向法是无约束最优化问题的一类重要算法。
它一方面克服了最速下降法中,迭代点列呈锯齿形前进,收敛慢的缺点,同时又不像牛顿法中计算牛顿方向耗费大量的工作量,尤其是共轭方向法具有所谓二次收敛性质,即当将其用于二次函数时,具有有限终止性质。
一、共轭方向定义4.1 设G 是n n ⨯对称正定矩阵,1d ,2d 是n 维非零向量,若120T d Gd = (4.1)则称1d ,2d 是G -共轭的。
类似地,设1,,m d d 是n R 中一组非零向量。
若0T i j d Gd =()i j ≠ (4.2)则称向量组1,,m d d 是G -共轭的。
注:(1) 当G I =时,共轭性就变为正交性,故共轭是正交概念的推广。
(2) 若1,,m d d G -共轭,则它们必线性无关。
二、共轭方向法共轭方向法就是按照一组彼此共轭方向依次搜索。
模式算法:1)给出初始点0x ,计算00()g g x =,计算0d ,使000Td g <,:0k = (初始共轭方向);2)计算k α和1k x +,使得0()min ()k k k k k f x d f x d ααα≥+=+,令1k k k k x x d α+=+;3)计算1k d +,使10Tk j d Gd +=,0,1,,j k =,令:1k k =+,转2)。
三、共轭方向法的基本定理共轭方向法最重要的性质就是:当算法用于正定二次函数时,可以在有限多次迭代后终止,得到最优解(当然要执行精确一维搜索)。
定理4.2 对于正定二次函数,共轭方向法至多经过n 步精确搜索终止;且对每个1i x +,都是()f x 在线性流形00,i j j j j x x x d αα=⎧⎫⎪⎪=+∀⎨⎬⎪⎪⎩⎭∑中的极小点。
证明:首先证明对所有的1i n ≤-,都有10T i j g d +=,0,1,,j i =(即每个迭代点处的梯度与以前的搜索方向均正交)事实上,由于目标函数是二次函数,因而有()11k k k k k k g g G x x Gd α++-=-=1)当j i <时, ()1111iTT T i j j j k k j k j g d gd gg d +++=+=+-∑110iT T j j kkj k j gd dGd α+=+=+=∑2)当j i =时,由精确搜索性质知:10T i j g d +=综上所述,有 10Ti j g d += (0,1,,)j i =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (X1)T P0 0 ,所以 f (X1)T P0 1P1TQ P0 0
P1TQ P0 0
(1)
以上就是搜索方向P1所必须满足的(必要) 条件。这也是使X2是极小点的充分条件。 P1,P2称为关于Q的共轭方向。
讨论表明 对于二维的具有正定矩阵Q的 二次函数f(X),从任一初始点出发,依次沿关 于Q共轭的两个方向进行一维搜索,必可达到 f(X)的无约束精确极小点。
Pk 1
0
且对j 0,1 , k 2, 有
PjT QPk PjT Q f ( X k ) k1Pk1
PjT Qf
(X
k
)
k
PT
1 j
QPk
1
f ( X k )T QPj
f ( X k )T f ( X j1) f ( X j ) j
f ( X k1 ) QX k1 b Q( X k k Pk ) b (2)
f ( X k1 ) f ( X k ) k QPk
所以
f ( X m ) f ( X m1) m1QPm1
f ( X m2 ) m2QPm2 m1QPm1
其中1 是最优步长,1>0 .因为 X * 是无约束极小点。
故 f ( X * ) 0 即 QX * b 0
f (X1) QX1 b
Q( X * 1P1) b (QX * b) 1QP1 1QP1
又因为 X1是f(X)沿P0方向的直线l0上的极小点,故
设 X En ,
,Q为对称正定矩阵,P0,
P1,···,Pm-1是关于Q共轭的m个共轭方向,
X0为任意指定的初始点。
设 X k1 X k k Pk ,k=0,1,···,m-1
其中,k 是一维搜索的最优步长。那么,有以下结 论成立:
(1) PjT f ( X m ) 0, j=0,1,···,m-1
共轭方向与共轭梯度法
主要内容
共轭方向法的基本原理 共轭方向和共轭方向法 共轭梯度法
一、共轭方向法的基本原理
问题引入
以二维问题为例 如图,设有无约束极小值题
min f (x) 1 X TQX bT X c 2
Q是正定对称矩阵,X0是初始点,P0 是初始搜索方向,l0是过X0且与方向 P0平行的直线,X1是f(x)在l0上的极
(2)Xm是f(X)在线性流形L(X0;P0,···,Pm-1)上 的极小点。
证明:(1)因为Xm是沿Pm-1方向进行搜索所 得的极小点,所以有 f ( X m )T Pm 1 0, 当k=0,1,···,m-2时,因为Xk+1 是沿Pk方向进 行一维搜索所得的极小点,所以
PkT f ( X k 1 ) 0,
即 Xm是f(X)在L(X0;P0,···,Pm-1)上的极小点。
推论 设在定理二中m=n,则Xn是f(X)在En中的全局极小点。
2、共轭方向法
• 基本定义
利用共轭方向作为搜索方向的无约束极小化算法
• 通用步骤:
(1)任取X 0 ,以及在X 0的下降方向P0 , k 0; (1)求解一维搜索问题
min f ( X k Pk ),为最优步长,是个数值.
(3) X k1 X k k Pk ;
(4)若X
k
满足迭代终止准则,
1
输出X k1, 计算停止,
否则转下一步;
(5)根据某种共轭方向的构造方法获得搜索方向Pk 1 ,
令k k 1, 再次循环计算.
三、共轭梯度法
m1
Xm X0
k Pk L( X 0; P0 , , Pm1)
k 0
m1
现任取X L(X 0 ; P0 , , Pm1) 有 X
X 0
k Pk
因 2 f (X ) Q
k 0
由Taylor二阶展式
f
(X)
f
(X m ) f
(Xm )T
(X
jf ( X k )T Pj f ( X k )T Pj1
00 0
同理,有f ( X k )T f ( X j) 0 故PjT QPk 0, j 0,1L , k 2 又由归纳法假设条件,
有PiT QPj 0,i j.,i、j k 1 综合以上可断言P0,P1,L ,Pk1, Pk是共轭向量。
j 0
令
,
则
PkT QPj
0,当k j
{
0,当k
j
k=j P0,jT 1Q,P·j ·0·,m-1
由 Qj 的 正0 定,j=性0,1以,··及·P,jm-,1 Pk的共轭性, 表明P0,P1,···,Pm-1线性无关
推论 在n维空间,任一共轭向量组最多包含n个向量。
定义3.18 设 (线性流形) X 0 En , P0,P1,···,Pm1是En中m个线性无关向量,则称集合L (X0;P0,P1,···,Pm-1)是由点X0和向 量组(P0,P1,···,Pm-1)所生成的线性流 形。
f ( X k )T f ( X j1) f ( X k )T f ( X j ) j
由(1)式和定理3.32的结论(1)(PjTf ( X m ) 0),有
f ( X k )T f ( X j1) f ( X k )T jPj Pj1
1.52 122 0.54 62 2 124 6 22 12
令
0, 可得0
180 612
又由3 81式有f ( X k1 )T f ( X k ) 0
Pk T f ( X k ) [f ( X k ) ak1Pk1 ]T f ( X k ), ( 由3.78可知Pk T f ( X k ) ak1Pk1 )
f
(X
k
)T
f
(
X
k
(4)如果k n 1, 令X 0 X k1, k 0, 转(1),否则转下步;
(5)令ak
[
f ( X k1) f ( X k )
]2 ;
(6)如果f ( X k1)T Pk1 0, 令X 0 X k1, 转(1),否则k k 1, 转(2)步;
例 设X0 2, 4T ,用共轭梯度法求解:
如果Q取单位向量,那么Q共轭向量就是相互正交的向量。
所以可认为共轭的概念是正交概念(
xiT x j 0 )的推广。
定理3.31 组。
共轭向量组是线性无关向量
证明 m:1 设j PjQ为0 正定矩阵,P0,P1,···, Pm-j10 是Q 的共轭向量组。
m 1
j PkT QPj 0,
线性流形的几何意义
如图所示,设P0,P1是3维空
间E3中的两个线性无关向量,过点
X0做平面 与向量P0,P1都平行,定义及平面 的向
量表达方程,可知
x2
L(X0;P0,P1)=∏
x1
简单的说:线性流形是由一 点和一个向量组决定的平面
定理3.32 共轭方向的极小点
)
ak
1
Pk
T 1
f
(
X
k
)
f
(
X
k
)T
f
(
X
k
),
(Pk
T 1
f
(
X
k
)
0,
理由同上)
故ak
f ( X k1 )T f ( X k1 ) f ( X k )T f ( X k )
[
f ( X k1 ) f ( X k )
]2
f ( X k 1) f ( X k ) kQPk (3 77)
Xm)
1 (X 2
X m )T Q(X
Xm)
m1
f (X m )T (X X m ) f (X m )T ( (k k )Pk )
m1
k 0
(k k )PkT f ( X m ) 0
k 0
又由于Q正定,知 f (X ) f (X m ),当X X m 故 ( X X m )T Q( X X m ) 0,当X X m
=···
m1
f ( X k 1 )
jQPj
j k 1
m 1
PkT f ( X m ) PkT f ( X k 1)
j PkT QPj 0
j k 1
(2)因 X k1 X k k Pk ,k=0,1,···,m-1 ,
由递推关系得
表明,P0与P1共轭。
2 设当m k时,P0,P1, ,Pk-1是共轭的,即
PiT QPj 0, i j, j k 1
3 证明P0,P1, ,Pk-1,Pk也是共轭的: 首先有
PkT1QPk
PkT1Q f
(Xk )
f
( X k )T QPk 1 PkT1QPk 1
小点。
X*(X2)
f (X1)
P1
X0 P0 X1
l0
Questions
问在二维空间能否找到一个方向P1,沿着过 X1点且平行于P1的直线进行一维搜索,其极 小点X2即为f(x)的全局精确极小点X* ?若存 在这样的P1,它满足什么条件?
首先寻找满足上述要求的方向P1应满足什么条件。
令
X * X 2 X 1 1P1
定理3.34 ( 公式的简化)
在定理3.33的条件下, 可简化 为:
