蛮力法求旅行商问题
第3章 蛮力法

计 算
i 1 ji 1
i 1
i 1
机 学
(n 1) (n 2) (n 3) 3 2 1
院
黄
襄 念
结论
n(n 1) (n2 ) 2
1. 选择排序算法效率属于 (n2 ) 型
2. 元素交换次数 (n 1) (n),该特性使选择排序算法效率超过了
学 增长函数:
数
n1 ni
n1
n1
学 与
T(n) 1 [(n i 1) 1] [n i]
计 算
i 1 j1
i 1
i 1
机 学 院
n(n 1) (n2 ) 2
黄 结果讨论:
襄 念
1. 冒泡排序算法效率属于(n2 ) 类型 —— 与选择排序相同
描述:在一个包含 n 个点的点集中,找到距离最近的两个点
西 简化:二维平面上两点 Pi (xi , yi) 和 Pj (xj , yj) 的欧氏距离
华
大 学
d(Pi , Pj ) ( xi x j )2 ( yi y j )2
数 学
蛮力法:穷举计算 每一对点 的距离,然后找出距离最小的那对点。
大
学 顺序查找的蛮力法
数 学
查找键与表中元素从头至尾逐个比较。结果:找到 或 失败
与 计
限位器:把查找键添加到列表末尾—— 一定成功,避免每次循环时
算
对检查是否越界(边界检查)
机
学 院
SequentialSearch( A[0...n], K ) {
最佳效率:Tbest (n) = 1 最差效率:Tworst(n) = n + 1
邮递员问题最短路径的解法

邮递员问题最短路径的解法邮递员问题,又称旅行商问题(Traveling Salesman Problem,TSP),是一个著名的组合优化问题。
它要求找到一条路径,使得邮递员从出发点出发,经过所有的城市且仅经过一次,最后回到出发点,同时路径长度最短。
由于邮递员问题是NP-hard问题,没有多项式时间的解法。
然而,存在一些启发式和近似算法可以在可接受的时间内找到较好的解决方案:1. 蛮力法:尝试所有可能的路径组合,计算每条路径的长度,最终选择最短路径作为解。
这种方法的时间复杂度为O(n!),适用于较小规模的问题。
2. 最近邻算法:从一个起始点开始,每次选择离当前点最近的未访问过的城市作为下一个访问点,直到所有城市都被访问过,然后回到起始点。
该算法的时间复杂度为O(n^2),虽然不能保证找到最优解,但是可以在较短的时间内找到较好的解。
3. 2-opt算法:先使用最近邻算法得到一个初始解,然后对路径进行优化。
2-opt算法通过不断交换路径中的两个边来减小路径的长度,直到没有可改进的交换。
该算法可以较快地优化路径,但无法保证找到全局最优解。
4. 遗传算法:使用进化计算的思想来解决TSP问题。
通过生成初始种群,交叉、变异等操作进行迭代优化,逐渐找到更好的路径。
遗传算法可以在较短时间内找到较好的解,但是无法保证找到最优解。
上述算法只是解决TSP问题的一部分方法,具体使用哪种方法取决于问题规模和时间要求。
对于较小规模的问题,可以使用蛮力法或者最近邻算法得到较好的解。
对于更大规模的问题,可以考虑使用启发式算法,如遗传算法等。
此外,还存在其他算法和优化技术用于处理TSP问题,根据具体情况选择合适的方法。
数学帮你优化旅行路线

数学帮你优化旅行路线旅行是一种令人兴奋的体验,而优化旅行路线可以让我们更好地利用时间和资源,获得更好的旅行体验。
数学作为一门科学,可以帮助我们解决旅行中的路线规划问题,使我们的旅行更加高效和便捷。
本文将介绍数学在优化旅行路线中的应用,并提供一些实用的方法和技巧。
一、旅行销售员问题旅行销售员问题是一个经典的数学问题,它要求找到一条最短的路径,使得旅行员可以经过所有的城市并回到起点。
这个问题在实际生活中有很多应用,比如快递员送货、旅行路线规划等。
解决旅行销售员问题的方法有很多,其中最常用的是蛮力法和动态规划法。
蛮力法是一种穷举所有可能路径的方法,然后找到最短路径。
虽然这种方法可以得到最优解,但是当城市数量增加时,计算量会急剧增加,不适用于大规模问题。
动态规划法则通过将问题分解为子问题,并利用子问题的最优解来求解整个问题。
这种方法可以大大减少计算量,适用于中等规模的问题。
二、最小生成树算法最小生成树算法是另一种常用的优化旅行路线的方法。
最小生成树是指连接所有城市的最短路径,它可以帮助我们找到一条经济、高效的旅行路线。
常用的最小生成树算法有普里姆算法和克鲁斯卡尔算法。
普里姆算法从一个起始城市开始,逐步选择与当前路径最短的城市进行连接,直到所有城市都被连接为止。
克鲁斯卡尔算法则是先将所有城市看作独立的树,然后逐步合并树,直到所有城市都在同一棵树中。
三、模拟退火算法模拟退火算法是一种基于概率的优化算法,它可以帮助我们找到一个接近最优解的旅行路线。
这种算法模拟了金属退火的过程,通过不断降低温度来减少能量,最终达到稳定状态。
在旅行路线优化中,模拟退火算法可以通过随机交换城市的顺序来搜索更优的解。
算法开始时,会以一定的概率接受较差的解,以避免陷入局部最优解。
随着温度的降低,算法会逐渐减少接受较差解的概率,最终得到一个较优的旅行路线。
四、遗传算法遗传算法是一种模拟生物进化过程的优化算法,它可以帮助我们找到一个较优的旅行路线。
蛮力法

i 0 nm
1 [(m 1) 1] (n m 1)m
j 0 i 0
m 1
nm
第三章 蛮力法
3.2 最近对问题 算法:BruteForceClosetPoints(P)
//该算法实现了蛮力法球平面中距离最近的两个点 //输入:一个n个(n>1)个点的列表,P1=(X1,Y1)…… ,Pn=(Xn,Yn) //输出:最近的两个点得下标,index1和index2
C( n )
n 1 i 1
1
i 1 j i 1k 1 n n) n( n i )
j i 1
n[(n 1)(n 2) 1] n 2 ( n 1) / 2
第三章 蛮力法
3.4 旅行商问题 算法:TSP(P[1..n],V[1..n][1..n])
C( n )
i 1 n 1
j i 1
2 [2(n i)] 2[(n 1 1)(n 1)] / 2 n(n 1)
i 1
n
n 1
第三章 蛮力法
3.3 凸包问题 算法:BruteForceConvexHull(P)
//该算法实现了蛮力法求平面中距离最近的两个点 //输入:一个n个(n>1)个点的列表,P1=(X1,Y1)…… ,Pn=(Xn,Yn) //输出:最小凸集合集合S
2 3 n C( n) c11 cn cn cn 2n 1 n
第三章 蛮力法
3.4 旅行商问题 效率分析: TSP(P[1..n],V[1..n][1..n]) //对于具有n个节点的哈密顿回路而言,必须生成一个由n+1 个节点构成的序列,其入口和出口假设为节点1,那么蛮 力法必须生成所有其他的n-1个节点构成一条完整的路径 //显然,对于这样一个算法而言,蛮力法求旅行商问题总是 一个效率为θ((n-1)!)的算法
实验项目1:蛮力法与分治法应用

实验项目1:蛮力法与分治法应用1、目的与要求:实验目的:了解蛮力法和分治法的基本思想,学会运用蛮力法和分治法解决实际系统设计应用中碰到的问题。
实验要求:用蛮力法实现选择、冒泡排序,或旅行商问题、背包问题等问题(任选其中之一)。
用分治法实现合并排序或快速排序。
要求写出算法的伪代码描述,并编写程序实现之,相关算法放在函数实现,主程序给出测试用例,要设计足够多的相关测试用例,验证程序的正确性。
注意观察程序执行结果和运行的时间。
实验报告要求给出问题定义及算法的伪代码描述,程序设计的代码,算法的测试用例及结果,并分析算法的时间效率,回答指导书中的思考题。
2、实验容:(2)用分治法实现快速排序、合并排序算法。
本实验主要是用分治法实现合并排序,快速排序程序等。
合并排序算法描述:MergeSort ( A[0...p-1] )// input 待排序数组A[0..n-1]// output 非降序排列的数组A[0..n-1]if ( n>1 ) {//至少有2个元素Copy A[0.. n/2-1 ] to B[0.. n/2-1 ];Copy A[n/2..n-1 ] to C[0.. n/2-1 ];MergeSort ( B[0.. n/2-1 ] );MergeSort (C[0.. n/2-1 ]t);Merge (B, C, A); //复制回数组a快速排序算法描述:QuickSort ( A[1.. r ] ){if (l<r) s=Partition( A[l,r] ); // s 是分裂位置QuickSort ( A[l..s-1] ); //对左半段排序QuickSort ( A[s+1,r); //对右半段排序}Partition ( A[l..r] ){p=A[[l] ;i = l; j = r + 1;repeatedrepeated i=i+1; until A[i]> p // 将>= x的元素交换到左边区域repeated i=i+1; until A[i]> p // <= x的元素交换到右边区域Swap( A[i], A[j] )Until i>jSwap( A[i] = a[j] );Swap( A[l], A[j] )return j;要求先给出算法的伪代码,然后用C++或其他程序设计语言编写程序实现之,并设计相关的测试用例,验证程序的正确性。
算法论文:旅行商问题的求解方法(动态规划法和贪心法)讲解

旅行商问题的求解方法摘要旅行商问题(TSP问题)时是指旅行家要旅行n个城市然后回到出发城市,要求各个城市经历且仅经历一次,并要求所走的路程最短。
该问题又称为货郎担问题、邮递员问题、售货员问题,是图问题中最广为人知的问题。
本文主要介绍用蛮力法、动态规划法、贪心法和分支限界法求解TSP问题,其中重点讨论动态规划法和贪心法,并给出相应求解程序。
关键字:旅行商问题;动态规划法;贪心法;分支限界法1引言旅行商问题(TSP)是组合优化问题中典型的NP-完全问题,是许多领域内复杂工程优化问题的抽象形式。
研究TSP的求解方法对解决复杂工程优化问题具有重要的参考价值。
关于TSP的完全有效的算法目前尚未找到,这促使人们长期以来不断地探索并积累了大量的算法。
归纳起来,目前主要算法可分成传统优化算法和现代优化算法。
在传统优化算法中又可分为:最优解算法和近似方法。
最优解算法虽然可以得到精确解,但计算时间无法忍受,因此就产生了各种近似方法,这些近似算法虽然可以较快地求得接近最优解的可行解,但其接近最优解的程度不能令人满意。
但限于所学知识和时间限制,本文重点只讨论传统优化算法中的动态规划法、贪心法和分支限界法,并对蛮力法做简单介绍,用以比较。
2正文2.1蛮力法2.1.1蛮力法的设计思想蛮力法所依赖的基本技术是扫描技术,即采用一定的策略将待求解问题的所有元素一次处理一次,从而找出问题的解。
一次处理所有元素的是蛮力法的关键,为了避免陷入重复试探,应保证处理过的元素不再被处理。
在基本的数据结构中,一次处理每个元素的方法是遍历。
2.1.2算法讨论用蛮力法解决TSP问题,可以找出所有可能的旅行路线,从中选取路径长度最短的简单回路。
如对于图1,我们求解过程如下:(1)路径:1->2->3->4->1;路径长度:18;(2)路径:1->2->4->3->1;路径长度:11;(3)路径:1->3->2->4->1;路径长度:23;(4)路径:1->3->4->2->1;路径长度:11;(5) 路径:1->4->2->3->1;路径长度:18;(6) 路径:1->4->3->2->1;路径长度:18;从中,我们可以知道,路径(2)和(4)路径长度最短。
TSP问题

lb=((1+3)+(3+6)+(1+2)+(3+4)+(2+3))/2=14
于是,得到了目标函数的界[14, 16]。 需要强调的是,这个解并不是一个合法的选择(可能没有 构成哈密顿回路),它仅仅给出了一个参考下界。
d(1, {2, 3})=min{c12+d(2, {3}), c13+ d(3, {2})}=min{2+5, 3+11}=7(1→2) d(2, {1, 3})=min{c21+d(1, {3}), c23+ d(3, {1})}=min{4+6, 2+12}=10(2→1) d(3, {1, 2})=min{c31+d(1, {2}), c32+ d(2, {1})}=min{7+8, 5+9}=14(3→2) 最后有:
③ 边(u, v) 加入解集合S后,S中不产生分枝;
∞3 3 2 6
C= 3 ∞ 7 3 2 3 7 ∞2 5
2 3 2∞3
6 2 5 3∞
1
52
2
4
3
(a) 5城市的代价矩阵 (b) 城市1→城市4
1
2 5
22
4
3
(c) 城市5→城市2
组合优化中的旅行商问题求解

组合优化中的旅行商问题求解在组合优化领域中,旅行商问题(Traveling Salesman Problem,TSP)是一类具有重要实际应用价值和理论研究意义的问题。
该问题要求在给定一系列城市和各城市之间的距离情况下,找到一条最短路径,使得旅行商能够恰好访问每个城市一次,并最终回到出发城市。
TSP在计算机科学、运筹学和数学等多个领域都得到了广泛的关注和研究。
1. TSP的数学建模旅行商问题可以用图论中的图来描述和解决。
首先,我们将每个城市表示为图中的一个节点,城市之间的距离表示为节点之间的边。
若每对节点之间的边都有权重,表示相应城市之间的距离,旅行商问题就可以转化为求解图的最短哈密顿回路(Hamiltonian cycle)的问题。
2. 求解TSP的经典算法2.1 蛮力算法蛮力算法是最简单直观的求解TSP的方法,它遍历所有可能的路径,并计算出总的路径长度,然后选择最短路径作为解。
然而,蛮力算法的时间复杂度为O(n!),当城市数量增加时,计算时间将呈指数级增长,因此适用于城市数量较少的情况。
2.2 最邻近插入算法最邻近插入算法从一个起始城市开始,每次选择离当前城市最近的未访问城市作为下一个访问城市,直到访问完所有城市,并回到起始城市。
该算法的时间复杂度为O(n^2),但它可能会得到次优解,因为贪心策略在选择下一个城市时只考虑了当前状态,没有考虑到整体最优解。
2.3 分支限界法分支限界法是一种基于回溯的求解TSP的优化方法,其思想是通过剪枝操作,去掉一些分支,从而减少搜索空间。
该算法首先选择一个起始城市,然后逐步扩展路径,每次选择一个未访问的城市,并通过计算路径长度来更新当前最优路径。
同时,在搜索过程中,根据当前路径长度和已知的最短路径长度,进行剪枝操作,以减少无效的计算。
分支限界法可以得到较优的解,但其时间复杂度仍然较高,因此在处理大规模问题时可能会面临困难。
3. 近似算法及元启发式算法为了求解大规模问题或提高求解效率,研究者们提出了许多近似算法和元启发式算法。
旅行商问题实验报告

算法设计与分析实验报告姓名:xx班级:xxxx学号:xxxxxx实验名称:旅行商问题实验目的:1.分支限界法按广度优先策略搜索问题的解空间树,在搜索过程中,对待处理的结点根据限界函数估算目标函数的可能取值,从中选取使目标函数取得极值(极大或极小)的结点优先进行广度优先搜索,从而不断调整搜索方向,尽快找到问题的解。
2.分支限界法适用于求解最优化问题。
实验程序:输入:图G=(V, E)输出:最短哈密顿回路1.根据限界函数计算目标函数的下界down;采用贪心法得到上界up;2.计算根节点的目标函数并加入待处理的结点表PT;3.循环直到某个叶子结点的目标函数值在表PT中取得极小值3.1i=表PT中具有最小值的结点;3.2对结点i的每个孩子结点x执行下列操作;3.2.1估算结点x的目标函数值lb;3.2.2若(lb<=up),则将结点x加入表PT中,否则丢弃该结点;4.将叶子结点对应的最优值输出,回溯求得最优解的各个分量。
实验分析:问题描述:TSP 问题是指旅行家要旅行n 个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
采用贪心法求得近似解为:1→3→5→4→2→1,其路径长度为1+2+3+7+3=16,这可以作为TSP 问题的上界,把矩阵中每一行最小的两个元素相加再除以2,得到TSP 问题的下界:[(1+3)+(3+6)+(1+2)+(3+4)+(2+3)]/2=14,于是得到目标函数的界[14,16]。
一般情况下,假设当前已确定的路径为U=(r1, r2, …, rk),即路径上已确定了k 个顶点,此时,该部分解的目标函数值 的计算方法(限界函数)如下:27 156 3 1 3 4 2 5 39 8 4C = ∞ 3 1 5 8 3 ∞ 6 7 9 1 6 ∞ 4 2 5 7 4 ∞ 3 8 9 2 3∑∑∑=∉-=+++=k i Ur j i k i i i j r r r r c lb ,11112/)]][[2(行最小的两个元素素行不在路径上的最小元分支限界法求解图上机心得与体会:时间复杂性分析:分支限界法实际上属于蛮力穷举法,当然不能指望它有很好的最坏时间复杂性,遍历具有指数阶个结点的解空间树,在最坏情况下,时间复杂性肯定为指数阶。
蛮力法

/
© School of Computer Science and Technology, SWUST
11
凸包问题
定理 任意包含n>2个点(不共线)的集合S的凸包是以S 中的某些点为顶点的凸多边形。 凸包问题是为一个n个点的集合构造凸包的问题。 极点:对于任何一集合中的点为端点的线段来说,它们不 是这种线段的中点。
/
© School of Computer Science and Technology, SWUST
6
顺序查找
/
© School of Computer Science and Technology, SWUST
7
蛮力字符串匹配
http://mryang.Βιβλιοθήκη /
© School of Computer Science and Technology, SWUST
8
蛮力字符串匹配
Θ(n+m)=Θ(n)
/ © School of Computer Science and Technology, SWUST 9
对于一个n各点集合中的两 个点Pi和Pj,当且仅当该集 合中的其他点都位于穿过 这两点的直线的同一边时 它们的连线是该集合凸包 边界的一部分。 直线方程:ax+by=c a=y2-y1 , b=x1-x2, c=x1y2-y1y2
/ © School of Computer Science and Technology, SWUST 12
/
© School of Computer Science and Technology, SWUST
2
蛮力法的优点
可以用来解决广阔领域的问题 对于一些重要的问题,它可以产生一些合 理的算法 解决问题的实例很少时,它让你花费较少 的代价 可以解决一些小规模的问题 可以作为其他高效算法的衡量标准
《算法设计与分析基础》课件-3.蛮力法

if A[j] < A[min] min j
swap A[i] and A[min]
7
2017/12/31
例题:对序列 {89,45,68,90,29,34,17}用选择排序 算法进行排序
• 第1遍: {89,45,68,90,29,34,17} //求最小元素 {17,45,68,90,29,34,89} //交换
• 第5遍: {17,29,34,45,90,68,89} {17,29,34,45,68,90,89}
• 第6遍: {17,29,34,45,68,90,89} {17,29,34,45,68,89,90} //排序结束
8
CHD
(本动画中,参与排序的是R[1]到R[n],R[0]作为交换中转的空 间;变量j对应前面算法中的变量min)
2017/12/31
ALGORITHM BubbleSort(A[0,…,n – 1]) // 冒泡排序算法在数组上的应用 // 输入:数组A,数组中的元素属于某偏序集 // 输出:按升序排列的数组A for i 0 to n – 2 do
for j 0 to n – 2 – i do if A[j+1] < A[j] swap(A[j], A[j+1])
CHD
(4)对解决一些小规模的问题实例仍然有效
(5)可作为衡量其他算法的参照。
2
2017/12/31
Brute Force Examples:
1. Computing an (a > 0, n a nonnegative integer)
2. Computing n!
3. Multiplying two matrices
算法论文:旅行商问题的求解方法(动态规划法和贪心法)讲解

旅行商问题的求解方法摘要旅行商问题(TSP问题)时是指旅行家要旅行n个城市然后回到出发城市,要求各个城市经历且仅经历一次,并要求所走的路程最短。
该问题又称为货郎担问题、邮递员问题、售货员问题,是图问题中最广为人知的问题。
本文主要介绍用蛮力法、动态规划法、贪心法和分支限界法求解TSP问题,其中重点讨论动态规划法和贪心法,并给出相应求解程序。
关键字:旅行商问题;动态规划法;贪心法;分支限界法1引言旅行商问题(TSP)是组合优化问题中典型的NP-完全问题,是许多领域内复杂工程优化问题的抽象形式。
研究TSP的求解方法对解决复杂工程优化问题具有重要的参考价值。
关于TSP的完全有效的算法目前尚未找到,这促使人们长期以来不断地探索并积累了大量的算法。
归纳起来,目前主要算法可分成传统优化算法和现代优化算法。
在传统优化算法中又可分为:最优解算法和近似方法。
最优解算法虽然可以得到精确解,但计算时间无法忍受,因此就产生了各种近似方法,这些近似算法虽然可以较快地求得接近最优解的可行解,但其接近最优解的程度不能令人满意。
但限于所学知识和时间限制,本文重点只讨论传统优化算法中的动态规划法、贪心法和分支限界法,并对蛮力法做简单介绍,用以比较。
2正文2.1蛮力法2.1.1蛮力法的设计思想蛮力法所依赖的基本技术是扫描技术,即采用一定的策略将待求解问题的所有元素一次处理一次,从而找出问题的解。
一次处理所有元素的是蛮力法的关键,为了避免陷入重复试探,应保证处理过的元素不再被处理。
在基本的数据结构中,一次处理每个元素的方法是遍历。
2.1.2算法讨论用蛮力法解决TSP问题,可以找出所有可能的旅行路线,从中选取路径长度最短的简单回路。
如对于图1,我们求解过程如下:(1)路径:1->2->3->4->1;路径长度:18;(2)路径:1->2->4->3->1;路径长度:11;(3)路径:1->3->2->4->1;路径长度:23;(4)路径:1->3->4->2->1;路径长度:11;(5) 路径:1->4->2->3->1;路径长度:18;(6) 路径:1->4->3->2->1;路径长度:18;从中,我们可以知道,路径(2)和(4)路径长度最短。
蛮力法等求解背包问题报告剖析

算法综合实验报告学号:姓名:一、实验内容:分别用蛮力、动态规划、贪心及分支限界法实现对TSP问题或者0-1背包问题的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:1、蛮力法(1)数据结构:使用一维数组存储物品的价值和重量还有下标。
(2)函数组成除主函数外还有一个subset()函数,在此函数中列出所有的子集列出子集的同时求解最大价值,并且物品总重量要小于背包总容量。
(3)输入/输出设计首先通过键盘输入物品的总重量,再输入背包总容量,依次输入每个物品的重量,对应输入相应重量的价值,循环直至输入所有物品的重量和价值。
最后输出物品的最大价值。
本程序通过键盘进行输入、屏幕进行输出。
(根据实际程序情况,还可以选择随机产生输入数据、将输出数据输出到文件等其它方式)(4)符号名说明w[1001]为物品重量的集合,v[1001]为物品价值的集合,n为物品数量,m为背包总容量,x[1001]用来存储物品是否装入背包,0为不装入,1为装入。
用a[1001]来存储下标,用下标找出所有子集。
(5)算法描述采用增量构造的方法来构造出物品的所有子集,对物品的下标应用此方法进行构造,下标与物品相对应,选出子集时物品的重量加之前重量小于背包总重量时将价值加上去,最后选出能装入背包的物品的最大值。
2、 动态规划法(1)数据结构:使用一维数组存储各个物品价值,重量,使用一个二维数组存储动态规划的整体求解的表,并以背包容量为最大列号,物品个数为最大行号。
(2)函数组成:除主函数外由两个函数组成,一个是求解两个数中的大的一个的函数,另一个则是进行动态规划求解的函数,在使用动态规划方法具体求解时调用求最大值函数,在主程序之中调用动态规划函数。
(3)输入/输出设计:首先通过键盘输入物品的总重量,再输入背包总容量,依次输入每个物品的重量,对应输入相应重量的价值,循环直至输入所有物品的重量和价值。
旅行商问题_TSP_的几种求解方法

4) 禁忌表及其长度: 建议尝试 自适应 长度法, 譬 如根据 目标值更新的情况 或禁忌 频率 信息来 适当 增加 或缩短 禁忌 表长度。
5) 藐视准则: 采 用若某个 状态的性能 优于 / best so far0 状态, 则忽视其禁忌属性, 直接选 取它为当前状态。
6) 集中搜索和分散搜索策略: 分别采用在一定步数的迭 代后基于最佳状态 进行重 新初 始化并 对其 邻域 进行多 步趋
化性搜索和对算法 的重新 随机 初始化 或是 根据 频率信 息对 一些已知对象进行惩罚 。
7) 终止条件: 给定最优状态连续保持不变的最大持续迭 代步数。
大量研究表明禁忌搜索算法 具有模拟退火、遗传 算法等 智能优化算法相当的性 能, 甚至更优越。 2. 3 H op fie ld神经网络优化算法 2. 3. 1 基本思想
5) 退温函数的设计: 指数 退温 函数 是最 常用 的退 温策 略 ( tk = Ktk- 1, K为退温速率 ) 。
6) 温度修改准则和 算法 终止 准则 的设 计: 可 采用 阈值 法设计的 / 温度修改 0 和 / 算法终止 0 两准则 。 2. 2 禁忌搜索算法 2. 2. 1 基本思想
禁忌搜索 ( T abu Search或 T aboo Sea rch, 简称 T S) 是一 种亚启发式搜索技术 [ 4], 由 G lover在 1986年首次提出, 进而
3) SA 状 态 接 受 函数 的 设 计: m in{ 1, ex p( - v / t) } > random [ 0, 1] 准则是作为接受新 状态的 条件最常 用的方 案, 其中 v 为新旧状态的目标值差, t为 / 温度 0。
动态规划法-回溯法-分支限界法求解TSP问题实验报告

for(int i=1;i<=n;i++)
vis[i]=x[i];
ans=cur+mp[x[n-1]][x[n]]+mp[x[n]][1];
}
}
else
{
for(int i=t;i<=n;i++)
{
if(mp[x[t-1]][x[i]]!=-1&&(cur+mp[x[t-1]][x[i]]<ans||ans==-1))
一般情况下,假设当前已确定的路径为U=(r1,r2,…,rk),即路径上已确定了k个顶点,此时,该部分解的目标函数值的计算方法(限界函数)如下:
Lb=(2∑c[ri][r(i+1)]+∑ri行不在路径上的最小元素+∑ri行最小的两个元素)/2
算法设计
输入:图G=(V,E)
输出:最短哈密顿回路
1、根据限界函数计算目标函数的下界down;采用贪心法得到上界up;
算法设计
输入:图的代价矩阵mp[n][n]
输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度
1.初始化第0列(动态规划的边界问题)
for(i=1;i<n;i++)
dp[i][0]=mp[i][0]
2.依次处理每个子集数组x[2^n-1]
for(i=1;i<n;i++)
if(子集x[j]中不包含i)
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
using namespace std;
蛮力法求解旅行商问题
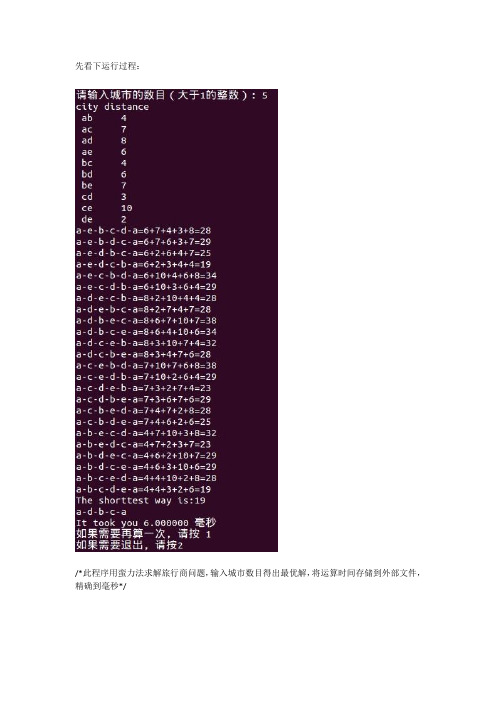
先看下运行过程:/*此程序用蛮力法求解旅行商问题,输入城市数目得出最优解,将运算时间存储到外部文件,精确到毫秒*/#include<stdio.h>#include<stdlib.h>#include<string.h>#include <time.h>#include <sys/time.h>#include <assert.h>#define MAXSIZE 99999//#define CITYNUM 5 /*4个城市的话,其实全排列的只有3个,另外一个是起点固定的*///#define TOTLE 15 /*4个城市对应的道路一共有6条*/#define MAX 32int CITYNUM=0;int TOTLE=0;char city[MAXSIZE]={0}; /*和下面这个数组组成两个城市之间的道路*/char citytwo[MAXSIZE]={0};int distance[MAXSIZE]={0}; /*存放城市间距离*/int valueall[MAXSIZE]={0}; /*最后放每次运算的路径值*/int all=0; /*对应上面的*/char backarray[MAXSIZE]={0};long int bbb=0;int ccc=0;/*文件里存了全部的道路和距离比如:ab 7,读取数据到三个数组*/void read(){int nn = 1, ii = 1;int i = 1;int p ;FILE *fp;fp = fopen("in.dat", "rb");while(!feof(fp)){p=fscanf(fp,"%c %c %d\n",&city[nn],&citytwo[nn], &distance[nn]); /*读取的时候遇到回车所以fscanf时候加\n*/if((p != EOF)){nn++;i++;TOTLE++;}else{break;}}fclose(fp);printf("city ");printf("distance\n");for(ii = 1; ii < nn;ii++){printf(" %c%c %d\n", city[ii],citytwo[ii],distance[ii]);}}/*两两互换*/void swap(int *l, int *r){int temp;temp = *l;*l = *r;*r = temp;}/*打印各种东西...*/void print(int ncount, int *val){int n=0;int i;int ii=0;int nnn=0;int sum=0; /*每次运算加起来的最后路程*/int value[MAXSIZE]={0}; /*存放每次运算上面那个结果*/printf("a-");for(;n < ncount;n++){printf("%c-", val[n]);backarray[bbb]=val[n];bbb++;}printf("a");printf("=");/*起点城市*/for(i=0;i<TOTLE;i++){if(val[0]==citytwo[i+1]&&city[i+1]=='a'){printf("%d+", distance[i+1]);value[nnn]=distance[i+1];nnn++;}}/*中间的全排列城市*/for(i=0;i<ncount;i++){for(ii=1;ii<=TOTLE;ii++){if(val[i]==city[ii] && val[i+1]==citytwo[ii]){printf("%d+", distance[ii]);value[nnn]=distance[ii];nnn++;continue;}else if(val[i]==citytwo[ii] && val[i+1]==city[ii]){printf("%d+", distance[ii]);value[nnn]=distance[ii];nnn++;continue;}}}/*最后返回起点*/for(i=0;i<TOTLE;i++){if(val[ncount-1]==citytwo[i+1] && city[i+1]=='a'){printf("%d=", distance[i+1]);value[nnn]=distance[i+1];nnn++;}}/*存放走一次的路径*/for(i=0;i<nnn;i++){sum=sum+value[i];}printf("%d", sum);/*存入数组*/valueall[all]=sum;all++;printf("\n");}/*蛮力法穷举*/void func(int ncount, int n, int *val){if(1 == n){print(ncount, val);}else{int i = 0;int *pnew = (int *)malloc(sizeof(int)*ncount);for(;i < n;i++){memcpy(pnew, val, sizeof(int)*ncount);swap(pnew +ncount -n, pnew+ncount-1-i);func(ncount, n-1, pnew);}free(pnew);}}/*自动生成文件*/void become()int i,j;FILE *fp;fp = fopen("in.dat","w");//srand(unsigned(time(NULL)));for(i=0;i<CITYNUM;i++){for(j=i+1;j<=CITYNUM;j++){fprintf(fp,"%c %c %d\n",i+'a',j+'a',rand()%10+1);}}fclose(fp);}void del(){remove("in.dat");}int main(){printf("请输入城市的数目(大于1的整数):");scanf(" %d",&CITYNUM);CITYNUM=CITYNUM-1;become();float time_usea=0;float time_useb=0;struct timeval starta;struct timeval enda;struct timeval startb;struct timeval endb;int i = 0, ncount = CITYNUM, *val = 0;int temp;int loop;int n=0,d,cnt=0;char sa[10],sb[10];int j;gettimeofday(&starta,NULL);read();val = (int *)malloc(sizeof(int)*ncount);/* a 城市是起点,从b 城市开始全排列,把所有城市存在val中*/ for(i = 0;i < ncount;i++){val[i] ='b'+i;}func(ncount, ncount, val);/*for(i=0;i<all;i++){if(i%10==0){printf("%d ",valueall[i]);printf("\n");}else{printf("%d ",valueall[i]);}}*//*找到最短路程*/temp = valueall[0];for(i=1;i<all;i++){if(temp > valueall[i]){temp=valueall[i];ccc = i;}}printf("The shorttest way is:%d\n",temp);printf("a-");for(i=ccc*(CITYNUM-1);i<ccc*(CITYNUM-1)+(CITYNUM-1);i++){printf("%c-",backarray[i]);}printf("a");printf("\n");gettimeofday(&enda,NULL);time_usea=(__sec)*1000+(__usec)/1000;//毫秒printf("It took you %f 毫秒\n",time_usea);//printf("b = %ld,all=%d,ccc=%d\n",bbb,all,ccc);free(val);FILE *fp = NULL;fp = fopen("OUT.DAT", "a+");if(NULL == fp){printf("wrong");return 0;}fprintf(fp, "蛮力: %d %f\n", n,time_usea);//fprintf(fp, "分支: %d %f\n", n,time_useb/1000);fclose(fp);del();printf("如果需要再算一次,请按1\n");printf("如果需要退出,请按2\n");scanf("%d",&loop);switch(loop){case 1:return main();case 2:return;default:return;}return 0;}。
动态规划法-回溯法-分支限界法求解TSP问题实验报告

动态规划法-回溯法-分支限界法求解TSP问题实验报告TSP问题算法实验报告指导教师:季晓慧姓名:辛瑞乾学号: 1004131114 提交日期: 2015年11月目录总述 (4)动态规划法 (4)算法问题分析 (4)算法设计 (5)实现代码 (6)输入输出截图 (10)OJ提交截图 (10)算法优化分析 (10)回溯法 (11)算法问题分析 (11)算法设计 (11)实现代码 (12)输入输出截图 (17)OJ提交截图 (17)算法优化分析 (17)分支限界法 (18)算法问题分析 (18)算法设计 (19)实现代码 (20)输入输出截图 (29)OJ提交截图 (29)算法优化分析 (29)总结 (30)总述TSP问题又称为旅行商问题,是指一个旅行商要历经所有城市一次最后又回到原来的城市,求最短路程或最小花费,解决TSP可以用好多算法,比如蛮力法,动态规划法…具体的时间复杂的也各有差异,本次实验报告包含动态规划法,回溯法以及分支限界法。
动态规划法算法问题分析假设n个顶点分别用0~n-1的数字编号,顶点之间的代价存放在数组mp[n][n]中,下面考虑从顶点0出发求解TSP问题的填表形式。
首先,按个数为1、2、…、n-1的顺序生成1~n-1个元素的子集存放在数组x[2^n-1]中,例如当n=4时,x[1]={1},x[2]={2},x[3]={3},x[4]={1,2},x[5 ]={1,3},x[6]={2,3},x[7]={1,2,3}。
设数组dp[n][2^n-1]存放迭代结果,其中dp[i][j]表示从顶点i经过子集x[j]中的顶点一次且一次,最后回到出发点0的最短路径长度,动态规划法求解TSP问题的算法如下。
算法设计输入:图的代价矩阵mp[n][n]输出:从顶点0出发经过所有顶点一次且仅一次再回到顶点0的最短路径长度1.初始化第0列(动态规划的边界问题)for(i=1;i<n;i++)dp[i][0]=mp[i][0]2.依次处理每个子集数组x[2^n-1]for(i=1;i<n;i++)if(子集x[j]中不包含i)对x[j]中的每个元素k,计算d[i][j]=min{mp[i][k]+dp[k][j-1]};3.输出最短路径长度。
Java实现旅行商问题

Java实现旅⾏商问题1 问题描述何为旅⾏商问题?按照⾮专业的说法,这个问题要求找出⼀条n个给定的城市间的最短路径,使我们在回到触发的城市之前,对每个城市都只访问⼀次。
这样该问题就可以表述为求⼀个图的最短哈密顿回路的问题。
(哈密顿回路:定义为⼀个对图的每个顶点都只穿越⼀次的回路)很容易看出来,哈密顿回路也可以定义为n+1个相邻顶点v1,v2,v3,…,vn,v1的⼀个序列。
其中,序列的第⼀个顶点和最后⼀个顶点是相同的,⽽其它n-1个顶点都是互不相同的。
并且,在不失⼀般性的前提下,可以假设,所有的回路都开始和结束于相同的特定顶点。
因此,可以通过⽣成n-1个中间城市的组合来得到所有的旅⾏线路,计算这些线路的长度,然后求取最短的线路。
下图是该问题的⼀个⼩规模实例,并⽤该⽅法得到了它的解,2 解决⽅案 2.1 蛮⼒法此处使⽤蛮⼒法解决旅⾏商问题,取的是4个城市规模,并已经定义好各个城市之间的距离(PS:该距离使⽤⼆维数组初始化定义,此处的距离是根据图1中所⽰距离定义)。
此处主要是在体验使⽤蛮⼒法解决该问题的思想,如要丰富成普遍规模问题,还请⼤家⾃⼰稍微修改⼀下哒。
对于代码中如碰到不能理解的地⽅,可以参考⽂章末尾给出的参考资料链接,以及相关代码注解~具体代码如下:package com.liuzhen.chapterThree;public class TravelingSalesman {public int count = 0; //定义全局变量,⽤于计算当前已⾏⾛⽅案次数,初始化为0public int MinDistance = 100; //定义完成⼀个⾏⾛⽅案的最短距离,初始化为100(PS:100此处表⽰⽐实际要⼤很多的距离)public int[][] distance = {{0,2,5,7},{2,0,8,3},{5,8,0,1},{7,3,1,0}}; //使⽤⼆维数组的那个⾳图的路径相关距离长度/** start为开始进⾏排序的位置* step为当前正在⾏⾛的位置* n为需要排序的总位置数* Max为n!值*/public void Arrange(int[] A,int start,int step,int n,int Max){if(step == n){ // 当正在⾏⾛的位置等于城市总个数时++count; //每完成⼀次⾏⾛⽅案,count⾃增1printArray(A); //输出⾏⾛路线⽅案及其总距离}if(count == Max)System.out.println("已完成全部⾏⾛⽅案,最短路径距离为:"+MinDistance);else{for(int i = start;i < n;i++){/*第i个数分别与它后⾯的数字交换就能得到新的排列,从⽽能够得到n!次不同排序⽅案* (PS:此处代码中递归的执⾏顺序有点抽象,具体解释详见本⼈另⼀篇博客:)*算法笔记_017:递归执⾏顺序的探讨(Java)*/swapArray(A,start,i);Arrange(A,start+1,step+1,n,Max);swapArray(A,i,start);}}}//交换数组中两个位置上的数值public void swapArray(int[] A,int p,int q){int temp = A[p];A[p] = A[q];A[q] = temp;}//输出数组A的序列,并输出当前⾏⾛序列所花距离,并得到已完成的⾏⾛⽅案中最短距离public void printArray(int[] A){for(int i = 0;i < A.length;i++) //输出当前⾏⾛⽅案的序列System.out.print(A[i]+" ");int tempDistance = distance[A[0]][A[3]]; //此处是因为,最终要返回出发地城市,所以总距离要加上最后到达的城市到出发点城市的距离for(int i = 0;i < (A.length-1);i++) //输出当前⾏⾛⽅案所花距离tempDistance += distance[A[i]][A[i+1]];if(MinDistance > tempDistance) //返回当前已完成⽅案的最短⾏⾛距离MinDistance = tempDistance;System.out.println(" ⾏⾛路程总和:"+tempDistance);}public static void main(String[] args){int[] A = {0,1,2,3};TravelingSalesman test = new TravelingSalesman();test.Arrange(A,0,0,4,24); //此处Max = 4!=24}}运⾏结果:1 2 3 ⾏⾛路程总和:181 32 ⾏⾛路程总和:112 13 ⾏⾛路程总和:232 3 1 ⾏⾛路程总和:113 2 1 ⾏⾛路程总和:183 1 2 ⾏⾛路程总和:230 2 3 ⾏⾛路程总和:110 3 2 ⾏⾛路程总和:182 03 ⾏⾛路程总和:232 3 0 ⾏⾛路程总和:183 2 0 ⾏⾛路程总和:113 0 2 ⾏⾛路程总和:231 0 3 ⾏⾛路程总和:181 3 0 ⾏⾛路程总和:230 1 3 ⾏⾛路程总和:110 3 1 ⾏⾛路程总和:233 0 1 ⾏⾛路程总和:183 1 0 ⾏⾛路程总和:111 2 0 ⾏⾛路程总和:231 02 ⾏⾛路程总和:112 1 0 ⾏⾛路程总和:182 0 1 ⾏⾛路程总和:110 2 1 ⾏⾛路程总和:230 1 2 ⾏⾛路程总和:18已完成全部⾏⾛⽅案,最短路径距离为:112.2 减治法旅⾏商问题的核⼼,就是求n个不同城市的全排列,通俗⼀点的话,就是求1n的全排列。
蛮力算法

内蒙古农业大学职业技术学院
蛮力法
算法设计1: 1)用n个空间的一维数组a[n],每个元素记录一个锁的状 态,1为被锁上,0为被打开。 2)用数学运算方便模拟开关锁的技巧,对i号锁的一次开 关锁可以转化为算术运算:a[i]=1-a[i]。 3)第一次转动的是1,2,3,……,n号牢房; 第二次转动的是2,4,6,……号牢房; 第三次转动的是3,6,9,……号牢房; ……第i次转动的是i,2i,3i,4i,……号牢房,是起点为 i,公差为i的等差数列。 4)不做其它的优化,用蛮力法通过循环模拟狱吏的开关 锁过程,最后当第i号牢房对应的数组元素a[i]为0时, 该牢房的囚犯得到大赦。算法1如下:
受速度对实例求解。
第四,即使效率通常很低,仍然可以用蛮力法解决一些小规模的问
题实例。
2 >
内蒙古农业大学职业技术学院
蛮力法
穷举法
选择排序和冒泡排序
顺序查找和蛮力字符串匹配
3 >
内蒙古农业大学职业技术学院
蛮力法
穷举查找
对于组合问题来说,穷举查找是一种简单的蛮力方法。它要求生 成问题域中的每一个元素,选出其中满足问题约束的元素,然后 再找出一个期望元素(例如,使目标函数达到最值的元素)。
I=2+8+1+7=18 I=2+3+1+5=11 I=5+8+3+7=23 I=5+1+3+2=11 I=7+3+8+5=23 最佳 最佳
adc b a I=7+1+8+2=18 用穷举查找对一个小规模旅行商问题的求解过程
内蒙古农业大学职业技术学院
蛮力法
《旅行商问题》课件

3 鲁棒性
蛮力解法和分支限界法对问题大小敏感,动 态规划法稳定,遗传算法和模拟退火算法适 应性强。
ቤተ መጻሕፍቲ ባይዱ
4 可扩展性
分支限界法和动态规划法适用于大规模问题, 其他解法在问题规模较小时表现更好。
应用场景举例
物流配送
优化快递员路径,减少时间和成本。
城市规划
优化城市道路规划,提高交通效率。
生产制造
优化零件加工顺序,增加生产效率。
分支限界法
2
通过优化子问题,逐步找到最短路径。
3
动态规划法
利用子问题的最优解构建整体最优解。
遗传算法
4
模拟进化过程,通过基因编码求解最优路
径。
5
模拟退火算法
模拟金属退火过程,通过接受劣解概率性 地跳出局部最优。
解法优缺点对比
1 时间复杂度
分支限界法和动态规划法相对较高,蛮力解 法最高。
2 精度
遗传算法和模拟退火算法可能得到次优解, 其他解法可得到最优解。
《旅行商问题》PPT课件
# 旅行商问题PPT课件 什么是旅行商问题 - 旅行商问题的定义 - 实际场景示例 - 问题的复杂度分析
问题示例:旅行商问题
旅行商问题是指一个旅行商人需要依次访问N个城市并回到起始城市,要求找到一条最短路径,使得经过每个 城市仅一次。
1
蛮力解法
穷举所有可能的路径,计算最短路径。
网络优化
优化数据传输路径,提高网络效率。
结语
旅行商问题在实际应用中的重要性
解决旅行商问题可以帮助优化各种物流和路径规划 场景,提高效率。
后续研究方向
进一步研究旅行商问题的求解算法,寻找更高效、 精确的解决方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
//如果cost<min执行
if(cost<min)
{
min=cost;
for(i=0;i<m;i++)
{
t[i]=a[i];
}
t[i]=a[0];
}
//cout<<endl;
}
if(count==Num)
//step 步数
void permutation(int a[],int start,int step,int n,int m,int Num,int *t,int **c)
{
if(n<m)
{
m=n;
}
//穷举求最小的路径
//路径存到数组中
if (step==m)
void salesman_problem(int n,int **c,int *T)
{
int Max_count=factorial(n); //全排列的数目,算法的时间复杂度
int *Array=new int[n];
for(int i=0;i<n;i++)
{
Array[i]=i;
for (int j=start; j<n; j++)
{
swap(a[step],a[j]);
permutation(a,start+1,step+1,n,m,Num,t,c);//注意实参start的值 start+1
swap(a[j],a[step]);
}
for(int i=0;i<N;i++)
{
Graph[i]=new int[N];
}
cout<<"输入费用矩阵"<<endl;
for(i=0;i<N;i++)
for(int j=0;j<N;j++)
{
cin>>Graph[i][j];
}
salesman_problem(N,Graph,T);
}
}
}
//实现n的阶乘
//输入n
//输出n的阶乘
int factorial(int n)
{
int temp=1;
for(int i=1;i<n+1;i++)
{
temp=temp*i;
}
return temp;
}
//城市个数n,费用矩阵c[][]
//旅行路线t,最小费用min
#include<iostream>
using namespace std;
const int MAX_FLOAT_NUM=65535;
static int count=0;
static int cost=0; //临时存放路径费用
static int min=MAX_FLOAT_NUM; //最下路径的初始值
{
//输出最小的路径及费用
cout<<"最短路径为:"<<min<<endl;
cout<<"旅行路线为:";
for(int i=0;i<m+1;i++)
{
cout<<t[i]<<" ";
}
cout<<endl;
}
else
{
//
//交换两个mp;x, int &y)
{
int temp;
temp = x;
x = y;
y = temp;
}
//
//permutation
//求从n取m个数的排列
//a[]为等待求组合的数组,长度为n,同时用来保存结果
//start 每轮挑选的起点
}
permutation(Array,0,0,n,n,Max_count,T,c);
}
void main()
{
int N;
cout<<"输入城市个数:";
cin>>N;
//存贮最优路径
int *T=new int[N+1];
//建立动态的费用矩阵;
int **Graph=new int *[N];
{
cost=0;
count++;
for (int i=0;i<m;i++)
{
if(i<m-1)
cost=cost+c[a[i]][a[i+1]];
else
cost=cost+c[a[i]][a[0]];
// cout<<a[i]<<" ";
