矩阵论在电路中的应用

合集下载

矩阵论在工程学中的应用讨论

矩阵论在工程学中的应用讨论矩阵论是数学中一个重要的分支，它用数值表示具有相似数学性质的物象，为各个学科提供了通用的数学方法。

在工程学中，矩阵论的应用更是发挥了重要作用，从建筑设计到机械运转，都离不开矩阵论的帮助。

一、矩阵论在结构力学中的应用结构力学作为土木工程的一个分支学科，矩阵论在其中扮演了重要角色。

利用矩阵的运算规则，可以将结构物进行离散化处理，使得其可以被抽象为矩阵的形式。

这样处理之后，我们可以应用矩阵的求解方法来计算结构物的力学特性，如位移、强度等等。

矩阵论不仅大大简化了计算流程，而且还方便了结构力学的理解和分析。

二、矩阵论在电力系统中的应用电力系统是一个涉及电机、变压器、开关等电力设备的复杂系统，它的运行在很大程度上依赖于对电源和负载电流的精确和及时地计算和控制。

矩阵论在电力系统中的应用主要集中在两个方面：一是负载流量的均衡问题，二是电力系统的稳定性问题。

利用矩阵论的方法，可以快速求解电力系统中的负载流量分配、发电机输出功率等问题，进一步优化电力系统的运行效率。

同时，矩阵论的稳定性分析方法也可以被应用于电网中的电力负荷控制和优化。

三、矩阵论在机器人技术中的应用机器人技术已经成为现今工程学中最热门的领域之一，它将机械、电子、计算机等学科融合在了一起，实现了对多种工作场合中的自动化操作和控制。

矩阵论在机器人技术中的应用非常广泛，比如运用矩阵来描述机器人的坐标系变换，描述机器人的运动学和动力学，以及设计和优化机器人控制算法等。

矩阵论的应用不仅可以提高机器人的运动和控制精度，而且还可以提高机器人的工作效率和安全性。

四、矩阵论在通信系统中的应用通信系统是现代工程技术中的一个重要分支，矩阵论在其中的应用也非常广泛。

在现代通信系统中，信号处理是一个重要的环节，而矩阵论则可以被用于信号去噪、信道等化、多输入多输出等问题的求解。

此外，矩阵论还可以被用于视频信号压缩、语音和文字识别等方面的问题求解。

矩阵论的应用为通信系统的设计和优化提供了有力的支持。

电器开关原理解读：探究开关的电流矩阵与电阻网络

电器开关原理解读：探究开关的电流矩阵与电阻网络电器开关在现代生活中扮演着至关重要的角色，它们可以控制电路中的电流流动和电器的开关状态。

在本篇文章中，我们将探究开关的电流矩阵与电阻网络原理。

首先，我们来了解一下开关的基本原理。

开关可以分为两种类型：机械开关和电子开关。

机械开关通过机械运动使电路开闭，如普通的电灯开关；而电子开关则通过电子元件的控制来实现电路的开闭，如晶体管。

在了解开关原理之前，我们先来了解一下电阻网络。

一个电阻网络是由多个电阻元件以特定的连接方式组合而成的。

电流在电阻中的流动会导致电压的降落，这种现象被称为电压降。

电阻网络可以用来控制电流的流通路径，从而实现对电路的控制。

对于一个简单的电路，我们可以使用电流矩阵的方式来描述电流的流动。

电流矩阵可以表示电路中各个支路上的电流和电源的关系。

假设电路有N个支路，我们可以用一个N维的列向量I来表示电路中各个支路上的电流，用一个N维的列向量V 来表示电路中各个支路上的电压。

电流矩阵的表达式为V = RI，其中R是电阻矩阵，它描述了电阻网络中各个支路间的电阻关系。

了解了电阻网络和电流矩阵的基本概念后，我们来看看开关是如何工作的。

当电器开关处于闭合状态时，电路中的电流可以顺利通过。

此时，我们可以将开关视为一个低电阻的通路，即可近似将开关看作一个电阻矩阵的元件。

当电器开关处于断开状态时，电路中的电流无法通过。

此时，我们可以将开关视为一个高电阻的隔离器，即可近似将开关看作一个电阻矩阵的开路。

在实际应用中，我们可以通过控制开关的状态来实现对电路的控制。

以普通的电灯开关为例，当我们将开关拨向闭合状态时，电路中的电流可以通过，灯泡亮起；当我们将开关拨向断开状态时，电路中的电流无法通过，灯泡熄灭。

在电子开关中，我们使用晶体管来实现对电路的控制。

晶体管是一种具有三个电极的半导体器件，分别是发射极、基极和集电极。

晶体管的工作原理是通过控制基极信号来控制集电极和发射极之间的电流流动。

矩阵论及工程应用

矩阵论及工程应用矩阵论是数学中的一个重要分支，它研究的是矩阵的性质、运算规则以及与线性代数的关系。

矩阵论在工程应用中发挥着重要的作用，能够帮助工程师们解决各种问题，提高工程设计的效率和精度。

矩阵论在电力系统中的应用非常广泛。

电力系统是由各种电力设备和电力线路组成的复杂网络，矩阵论可以通过建立节点矩阵和支路矩阵的关系来描述电力系统的状态。

通过求解矩阵方程，可以得到电力系统的各个节点的电压和相角，从而实现电力系统的稳态分析和电力负荷的调度控制。

矩阵论在通信系统中也有广泛的应用。

通信系统由各种设备和信道组成，矩阵论可以用于描述信道的传输特性和信号的传输过程。

通过矩阵运算和信号处理算法，可以实现信号的编码和解码、信号的滤波和调制等功能。

矩阵论还可以用于通信系统的性能分析和优化设计，提高通信系统的传输速率和抗干扰能力。

矩阵论在结构工程中也发挥着重要作用。

结构工程是研究和设计建筑物和桥梁等工程结构的学科，矩阵论可以通过建立刚度矩阵和位移矩阵的关系来描述结构的力学特性。

通过求解矩阵方程，可以得到结构的受力状态和变形情况，从而实现结构的静力分析和动力响应分析。

矩阵论还可以用于结构的优化设计和结构的损伤检测，提高结构的安全性和稳定性。

矩阵论还在图像处理和模式识别等领域有广泛的应用。

图像处理是对数字图像进行处理和分析的技术，矩阵论可以用于描述图像的像素值和颜色分布。

通过矩阵运算和图像处理算法，可以实现图像的增强和去噪、图像的压缩和编码等功能。

模式识别是指通过对输入的模式进行分析和比较，识别出模式所属的类别或特征，矩阵论可以用于描述模式的特征向量和相似度矩阵。

通过矩阵运算和模式识别算法，可以实现模式的分类和识别、模式的匹配和检索等功能。

矩阵论在工程应用中具有重要的地位和作用。

它能够帮助工程师们解决各种问题，提高工程设计的效率和精度。

无论是电力系统、通信系统、结构工程还是图像处理和模式识别，矩阵论都能够提供有效的数学工具和方法，为工程应用提供支持和指导。

我看矩阵在实际生活中的应用

矩阵在实际生活中的应用华中科技大学文华学院城市建设工程学部环境工程1班丛目录摘要 (3)实际应用举例 (4)论文总结 (15)参考文献 (16)摘要：随着现代科学的发展，数学在经济中广泛而深入的应用是当前经济学最为深刻的因素之一，马克思曾说过：“一门学科只有成功地应用了数学时，才真正达到了完善的地步”。

下面通过具体的例子来说明矩阵在经济生活中、人口流动、电阻电路、密码学、文献管理的应用。

关键词：矩阵、人口流动、电阻电路、密码学、文献管理一：矩阵在经济生活中的应用1．“活用”行列式定义定义：用符号表示的n阶行列式D指的是n!项代数和，这些项是一切可能的取自D不同行与不同列上的n个元素的乘积的符号为。

由定义可以看出。

n阶行列式是由n!项组成的，且每一项为来自于D 中不同行不同列的n个元素乘积。

实例1：某市打算在第“十一”五年规划对三座污水处理厂进行技术改造，以达到国家标准要求。

该市让中标的三个公司对每座污水处理厂技术改造费用进行报价承包，见下列表格(以1万元人民币为单位)．在这期间每个公司只能对一座污水处理厂进行技术改造，因此该市必须把三座污水处理厂指派给不同公司，为了使报价的总和最小，应指定哪个公司承包哪一座污水处理厂?设这个问题的效率矩阵为，根据题目要求，相当于从效率矩阵中选取来自不同行不同列的三个元素“和”中的最小者!从行列式定义知道，这样的三个元素之共有31=6(项)，如下：由上面分析可见报价数的围是从最小值54万元到最大值58万元。

由④得到最小报价总数54万元，因此，该城市应选定④即2．“借用”特征值和特征向量定义：“设A是F中的一个数．如果存在V中的零向量，使得，那么A就叫做的特征值，而叫做的属于本征值A的一个特征向量。

实例2：发展与环境问题已成为21世纪各国政府关注和重点，为了定量分析污染与工业发展水平的关系，有人提出了以下的工业增长模型：设是某地区目前的污染水平(以空气或河湖水质的某种污染指数为测量单位)，是目前的工业发展水平(以某种工业发展指数为测量单位)．若干年后(例如5年后)的污染水平和工业发展水平分别为和它们之间的关系为试分析若干年后的污染水平和工业发展水平。

矩阵论在电气工程中的应用

题目: 矩阵论在电气工程中的应用指导老师: xxx学生姓名：xxx所属院系：电气工程学院专业：电气工程学号：xxx完成日期：20xx年x月x日矩阵论在电气工程中的应用摘要电路分析是电气专业领域人员必需的一项能力。

该知识具有概念性强、电路分析繁杂求解计算量大的特点。

为了解决这个问题，因此引入了矩阵理论，并结合软件对矩阵分析的良好支持，以期达到优化分析电路的目的。

本文就矩阵理论中的网络拓扑知识展开，介绍了网络拓扑在电路中的应用，并以给予求解。

关键词：电路分析矩阵法网络拓扑ABSTRACT：Circuit analysis is an essential ability of professional personnel in the field of electronic. The concept of strong, complex circuit analysis calculation with the knowledge of the characteristics of large amount. In order to alleviate this problem, so we introduced matrix theory, combined with good support analysis software for matrix, in order to achieve the purpose of optimization of circuit analysis. In this paper, the network topology in matrix theory unfolds, introduces the application of network topology in circuit, and to give the solution.KEY WORDS：circuit analysis；matrix method；network topology0 前言矩阵是线性代数里的一个重要概念，在电路网络分析、工程结构分析等方面，矩阵都是一个强自力的工具，因为它能使较复杂的计算过程简化成一系列的四则运算，便于用计算机的算法语言或程序进行描述和解答。

[现代电路分析][02]电路的矩阵分析

国家电工电子教学基地
电路理论系列课程组 2005.3
↑ 支路编号
用树支电压表示支路电压的方法
1 0 0 − 1 0 1 e1 e1 0 0 e2 1 0 e 2 e1 e 3 0 1 e 3 = e 2 = 0 1 − e1 + e3 e 4 e 3 1 1 e 2 + e 3 e 5 1 0 e1 + e 2 e6
↑ 支路编号
割集矩阵输入方法
1. 画图、支路编号、画图、支路编号、选树，选树，画割集
− 6.6V 2Ω
•
3Ω 5Ω
− 4.4V
•
1
1
3 4
2
2. 割集矩的行按先树支后连支编号列按割集编号
•
4Ω
• 2Ω
•
4Ω
•
5
3
6
2
2.4A
1 1 1 2 0 3 0 D = 4 − 1 5 0 6 1
2 0 1 0 0 1 1
3 ← 切割编号 0 0 1 DT = 1 DL 1 0
3. 按支路编号顺序填写割集矩阵元素支路号被割集号切割，同向填1 支路号被割集号切割，同向填支路号被割集号切割，反向填-1 支路号被割集号切割，反向填支路号不被割集号切割，支路号不被割集号切割，填0 注意：分块矩阵注意：分块矩阵DT为单位阵
国家电工电子教学基地电路理论系列课程组 2005.3
割集法分析电路举例
2Ω
8 1
•
2 3Ω
举例说明割集法分析电路
9
1
6.6V
• •
5Ω 4Ω

矩阵理论在微波电路中的应用

矩阵理论在微波技术中的应用本人研究生所学专业为电磁场与微波技术，因此本文总结了所学矩阵理论在微波技术中的两种应用。

矩阵理论用于微波网络分析微波网络理论是微波技术中分析问题、解决问题的重要方法之一。

一般来说，对于微波结构的电特性有三种描述方法：场描述、等效电路描述和网络矩阵参数描述。

场描述原则上适用于各种微波结构，能全面描述其内部和外部特性，但实际对于复杂结构的描述是有困难的；利用等效电路能在一定程度上描述微波网络内部和外部特性，不过仅在一定频率下是准确的，而且并非所有的微波电路都适合用微波等效电路来描述。

网络参数矩阵描述，具有简练、高度概括的特点，它适用于各种微波结构，特别是复杂的微波结构，可用它只描述外部特性。

微波网络理论就是利用网络参数矩阵描述和研究微波结构的理论，主要用来解决网络分析和网络综合两方面的问题。

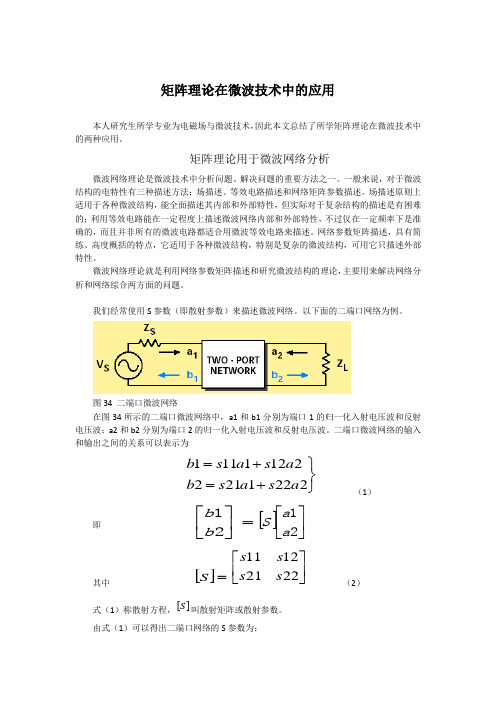
我们经常使用S 参数（即散射参数）来描述微波网络。

以下面的二端口网络为例。

图34 二端口微波网络在图34所示的二端口微波网络中，a1和b1分别为端口1的归一化入射电压波和反射电压波；a2和b2分别为端口2的归一化入射电压波和反射电压波。

二端口微波网络的输入和输出之间的关系可以表示为⎭⎬⎫+=+=22212122121111a s a s b a s a s b （1）即 =⎥⎦⎤⎢⎣⎡21b b []⎥⎦⎤⎢⎣⎡21a a S 其中[]=S ⎥⎦⎤⎢⎣⎡22211211s s s s （2）式（1）称散射方程，[]S 叫散射矩阵或散射参数。

由式（1）可以得出二端口网络的S 参数为：S11=0211=a a b ，即当端口2匹配时（ZL=Z0），端口1的反射系数； S22=0122=a a b ，即当端口1匹配时（ZS=Z0），端口2的反射系数； S12=0121=a a b ，即当端口1匹配时，端口2到端口1的传输系数；S21=0212=a a b ，即当端口2匹配时，端口1到端口2的传输系数。

矩阵论论文

西安理工大学研究生课程论文课程名称：矩阵论任课教师：XXX论文/研究报告题目：线性变换在电路方程中的应用完成日期：2014年11月5日学科：Xxxx学号：XXXXXXX姓名：XXX成绩：线性变换在电路方程中的应用摘要：电路分析中的坐标变换和复杂绕组变压器分析中所用的变压器变换都是电路方程的线性变换。

根据矩阵理论，对坐标变换和变压器变换进行了统一阐释。

坐标变换本质是一个方阵和对角阵的相似变换，变压器变换的本质是新变量对旧变量的表示，当变换矩阵的逆阵等于它的转置（共轭转置）阵时，坐标变换和变压器变换数学表示是相同的。

通过对电路方程系数矩阵和三角阵的相似变换，同时得到了三相 abc 坐标系和任意速度旋转两相 dq0 坐标系、瞬时值复数分量 120 坐标系、前进 - 后退 FB0 坐标系之间的变换矩阵。

这有助于在更加基础的理论层面上揭示和理解电路方程线性变换的本质，也为提出电路方程线性变换的新类型提供了思路。

关键词：电路方程；线性变换；坐标变换；变压器变换引言在交流电机等电路分析中，常用的坐标变换是指三相静止 abc 坐标系任意速度旋转两相 dq坐标系、瞬时值复数分量 120 坐标系、前进 - 后退 FB坐标系，以及它们对应的特殊坐标系的变量之间的相互转换。

电路方程坐标变换的主要目的是使电压、电流、磁链方程系数矩阵对角化和非时变化，从而简化数学模型，使分析和控制变得简单、准确、易行。

还有一类电路方程变换，其目的是用旧变量表示出新变量，例如变压器中由原边变量利用变比变换而来的副边变量，把这类电路方程变换称为变压器变换。

坐标变换已有很多文献进行了阐述，但这些阐述大都是基于物理概念的。

变压器变换在复杂绕组变压器的分析中得到了应用，但只是针对具体问题对其方法的具体应用，没有明确提出变压器变换的概念。

这些文献对坐标变换和变压器变换都缺乏在数学层面上予以统一论述。

这种特殊和具体的阐述，不便于将之作普遍化和一般化的理解，也就妨碍了对它的推广和发展。

电路第15章电路方程的矩阵形式

元件参数的识别
利用矩阵形式的电路方程，可以对电路中的元件参数进行识别和估计，例如通过测量节点电压和支路电流来计算元件的电阻、电容、电感等参数。
系统分析和控制
矩阵形式的电路方程可以用于系统分析和控制，例如稳定性分析、频率响应分析、最优控制等。
02 电路元件的矩阵表示
电阻元件的矩阵表示
总结词
电阻元件在矩阵形式中表示为对角线矩阵，对角线上的元素为电阻值。
矩阵元素的选取
矩阵中的元素根据电路元件的类型和连接方式进行选取，通常包括电阻、电容、电感等元件的参数。
矩阵形式的优点
矩阵形式能够简化电路的分析和计算过程，提高计算效率和精度，适用于大规模复杂电路的分析。
矩阵形式的电路方程
节点电压方程
在电路中选取节点电压作为未知量，根据基尔霍夫定律建立节点电压方程，并将其表示为矩阵形
线性
电路的输出信号与输入信号成正比，满足叠加定理。
3
时不变
电路的参数不随时间变化。
线性时不变电路的矩阵形式
矩阵形式的电路方程
将电路中的元件参数和连接关系表示为矩阵形式，以便于分析和计算。
状态变量
描述电路中电压和电流变化的变量，通常用向量表示。
状态方程
描述电路中状态变量之间关系的方程，通常表示为矩阵形式。
矩阵形式的电路方程广泛应用于电子工程、通信工程、控制工程等多个领域，尤其在处理大规模复杂电路时表现出显著的优势。
电路方程的矩阵形式的展望
01
矩阵形式的进一步研究
随着电子技术和计算机技术的不断发展，对电路方程的矩阵形式的研究将更加深入。未来研究将更加注重矩阵形式的数学基础、算法优化和数值稳定性等方面。
02 03

矩阵论及其工程应用

矩阵论及其工程应用矩阵论是数学中的一个重要分支，它研究的是矩阵的性质和运算规律。

矩阵论不仅在数学领域有着广泛的应用，而且在工程领域也有着重要的应用价值。

在数学领域，矩阵论是线性代数的重要组成部分。

矩阵论的基本概念包括矩阵的定义、矩阵的运算、矩阵的转置、矩阵的逆等。

矩阵论的应用范围非常广泛，例如在微积分、概率论、统计学、物理学、工程学等领域都有着广泛的应用。

在工程领域，矩阵论也有着重要的应用价值。

矩阵论可以用来描述和分析各种工程问题，例如电路分析、信号处理、控制系统、图像处理等。

在电路分析中，矩阵论可以用来描述电路中各个元件之间的关系，从而分析电路的性质和特点。

在信号处理中，矩阵论可以用来描述信号的变换和处理过程，从而实现信号的压缩、去噪、增强等功能。

在控制系统中，矩阵论可以用来描述系统的状态和控制器的作用，从而实现对系统的控制和优化。

在图像处理中，矩阵论可以用来描述图像的特征和变换，从而实现图像的压缩、增强、分割等功能。

除了在电路分析、信号处理、控制系统、图像处理等领域有着广泛的应用外，矩阵论还可以用来解决其他工程问题。

例如在机器学习中，矩阵论可以用来描述数据的特征和关系，从而实现对数据的分类、聚类、预测等功能。

在计算机图形学中，矩阵论可以用来描述图形的变换和投影，从而实现对图形的渲染、动画等功能。

在通信系统中，矩阵论可以用来描述信道的特性和传输的方式，从而实现对信号的传输和接收。

总之，矩阵论是一门非常重要的学科，它在数学和工程领域都有着广泛的应用。

矩阵论的应用不仅可以帮助我们更好地理解和分析各种工程问题，而且可以为我们提供更多的解决方案和创新思路。

因此，我们应该加强对矩阵论的学习和研究，不断探索其在各个领域的应用价值，为推动科技进步和社会发展做出更大的贡献。

矩阵论在电气工程中的应用

.题目: 矩阵论在电气工程中的应用指导老师: xxx学生姓名：xxx所属院系：电气工程学院专业：电气工程学号：xxx完成日期：20xx年x月x日矩阵论在电气工程中的应用摘要电路分析是电气专业领域人员必需的一项能力。

该知识具有概念性强、电路分析繁杂求解计算量大的特点。

为了解决这个问题，因此引入了矩阵理论，并结合软件对矩阵分析的良好支持，以期达到优化分析电路的目的。

本文就矩阵理论中的网络拓扑知识展开，介绍了网络拓扑在电路中的应用，并以给予求解。

《电路》第15章电路方程的矩阵形式解析

结束
2
i2 i1
i5
5
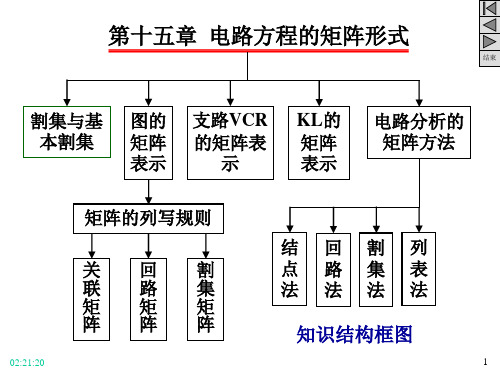
1 i1 i2 - i1 - i2 + i3 0 i3 i 4 = - i3 - i4 + i6 = 0 + i 1 + i4 + i5 0 i5 i6
结点1的KCL 矩阵形式结点 2 的 KCL [A][i] = … … 的KCL 结点(n-1)的KCL
14:45:53
[A][ i ] = 0
14:45:53 12
(3)关联矩阵A的作用
①表示矩阵形式的KCL方程；设：[ i ] = [i1 , i2 , i3 , i4 , i5 , i6 ]T 以结点④为参考结点 -1 -1 +1 0 0 0 [A][i] = 0 0 -1 -1 0 +1 +1 0 0 +1 +1 0
①
② i3 3 i6 6 ④ 4 i 4 ③
14:45:53
u1 u3 u4 u2 u5 u6
② ①
i3 3
2 5 Ⅰ ④ i1 1
i6 Ⅲ Ⅱ i2 6 i5
4 i 4
③
KVL的矩阵形式： [B][u] = 0
21
注意：连支电压可以用树支电压表示。 ② 3 4 i ul i 3 4 证 [ Bf ][ u ] =[ 1 Bt ] =0 i ① ③ 6 ut Ⅲ Ⅱ i2 6 i5 ul + Btut = 0 ul = - Btut ②用回路矩阵[B]T表示矩阵形式的KCL方程。设： [ i ] = [i1 , i3 , i4 , i2 , i5 , i6 ]T 1 0 0 0 1 0 0 0 1 -1 1 0 -1 0 -1 0 1 1 [ B ]T
注意：

(完整版)浅谈矩阵计算

浅谈矩阵计算一丶引言矩阵是高等代数学中的常见的工具。

在应用数学，物理学，计算机科学中都有很大的作用。

研究矩阵的计算，可以简化运算，并深入理解矩阵的性质。

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。

这一概念由19世纪英国数学家凯利首先提出。

矩阵常见于统计分析等应用数学学科中。

在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。

矩阵的运算是数值分析领域的重要问题。

将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。

对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。

关于矩阵相关理论的发展和应用，请参考矩阵理论。

在天体物理、量子力学等领域，也会出现无穷维的矩阵，是矩阵的一种推广。

矩阵的研究历史悠久，发展也是历久弥新，拉丁方阵和幻方在史前年代已有人研究。

作为解决线性方程的工具，矩阵也有不短的历史。

成书最迟在东汉前期的《九章算术》中，用分离系数法表示线性方程组，得到了其增广矩阵。

在消元过程中，使用的把某行乘以某一非零实数、从某行中减去另一行等运算技巧，相当于矩阵的初等变换。

但那时并没有现今理解的矩阵概念，虽然它与现有的矩阵形式上相同，但在当时只是作为线性方程组的标准表示与处理方式。

矩阵正式作为数学中的研究对象出现，则是在行列式的研究发展起来后。

逻辑上，矩阵的概念先于行列式，但在实际的历史上则恰好相反。

日本数学家关孝和（1683年）与微积分的发现者之一戈特弗里德·威廉·莱布尼茨（1693年）近乎同时地独立建立了行列式论。

其后行列式作为解线性方程组的工具逐步发展。

1750年，加布里尔·克拉默发现了克莱姆法则。

矩阵的现代概念在19世纪逐渐形成。

1800年代，高斯和威廉·若尔当建立了高斯—若尔当消去法。

1844年，德国数学家费迪南·艾森斯坦（F.Eisenstein）讨论了“变换”（矩阵）及其乘积。

矩阵论分析与应用论文

矩阵论在电路网络分析中的应用摘要：电路网络分析中，运用矩阵论的相关知识可以直观的解决一些复杂问题，比如所在支路存在无伴电压源的情况，而且矩阵运算方便进行计算机算法，在解决含大量节点的电路时是人工计算无法比拟的。

若电路中存在无伴电压源支路时，由于该支路的导纳为无穷大，这给节点电压方程和割集方程的建立带来困难。

解决这一问题的方法之一是将无伴电压源的支路电流也作为网络变量。

因此，在改进的节点方程中是以节点电压和某些支路电流作为未知量。

所述的支路电流包括无伴电压源支路电流和直接求解的支路电流。

改进节点法将网络的支路划分为三类，一类是一般支路，另两类是无伴电压源支路和直接求电流的支路。

后两类支路都可以以二端元件作为一条支路，支路电压和支路电流选择关联参考方向。

网络中的支路编号按照一般支路、无伴电压源支路和直接求电流支路，可将网络的关联矩阵A 写成如下分块矩阵形式：[]0Ex A A A A =式中A 是反映一般支路与节点之间的关联关系的子阵。

E A是反映无伴电压源支路与节点之间的关联关系子阵。

x A是反映直接求电流支路与节点之间关联关系子阵。

将支路电流向量和支路电压向量也按同样的顺序分块：[]0()()()()Tb E x I s I s I s I s =[]0()()()()Tb E x U s U s U s U s =根据基尔霍夫电流定律，有[]00()()0()Ex E x I s A A A I s I s ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦00A ()()()0E E x x I s A I s A I s ++=根据基尔霍夫电压定律,有[]000()()()()TE Ex n U s U s A A A U s U s ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦一般支路、无伴电压源支路和直接求电流支路的电流电压关系方程分别为000()Y ()()()()()()()()()U ()o s s E SE x x x I s s U s Y s U s I s U s U s I s Y s s =+-=-=将基尔霍夫电压方程带入得0000()()()()()T n s s I s Y s A U s Y U s I s =+-0000()()()()A ()T x x x n Tn I s Y s A U s Y s Y s A ==将以上方程式列写为矩阵形式为00()()()00()()()0()0n E x n n TE E SE Txx x Y s A A U s I s A I s U s Y s A E I s ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦该式即为改进节点方程的一般形式，改进的节点法是以增加网络变量数为代价，避开了写无伴电压源支路的支路导纳。

dl-15 电路矩阵

2
0 1 0
3
4 5
1 0 0 0 1 0 0 0 1
求基本割集矩阵，并画出网络图。
解
1 1 1 1 1 1 Ql B 0 0 1 0 1 0
1. A与B之间的关系
对同一有向图，支路排列次序相同时，满足：
ub A un B ub 0
T
BA u 0
T n
BA
T
0
or
AB
T
0
2. B与Q之间的关系
对同一有向图，任选一树，满足：
ib B T il Q ib 0
引入关联矩阵A的作用：
４
②
５
① 用关联矩阵A表示矩阵形式的KCL方程
①
２
３
６
设:
i i
1
i2 i3 i4 i5 i6
③
T
以④为参考节点
-1 -1 0 1 0 0 [A][ i ]= 0 0 1 -1 -1 0 1 0 0 0 1 1
④1 i1 i2 i1 i 2 i4 i3 i 3 i4 i5 0 i 4 i5 i1 i5 i6 i 6
n b
ajk
ajk=1 ajk= -1 ajk =0
支路k与结点j 关联，方向背离结点。支路k与结点j 关联，方向指向结点支路k与结点j无关
例
４ ①
２
②
５
支1 结
③
３
６ ④1
1 -1 Aa= 2 0 3 1 4 0
2 3 -1 0 0 1 0 0 1 -1
4 1 -1 0

矩阵论在电路中的应用

矩阵论在电路分析中的应用随着科学技术的迅速发展，古典的线性代数知识已不能满足现代科技的需要，矩阵的理论和方法业已成为现代科技领域必不可少的工具。

诸如数值分析、优化理论、微分方程、概率统计、控制论、力学、电子学、网络等学科领域都与矩阵理论有着密切的联系，甚至在经济管理、金融、保险、社会科学等领域，矩阵理论和方法也有着十分重要的应用。

当今电子计算机及计算技术的迅速发展为矩阵理论的应用开辟了更广阔的前景。

因此，学习和掌握矩阵的基本理论和方法，对于工科研究生来说是必不可少的。

全国的工科院校已普遍把“矩阵论”作为研究生的必修课。

对于电路与系统专业的研究生，矩阵论也显得尤为重要。

本文以电路与系统专业研究生的必修课《电网络分析与综合》为例，讲解矩阵论的重要作用。

在电路分析中，对于一个有n 个节点，b 条支路的电路图，每条支路的电压和电流均为未知，共有2b 个未知量。

根据KCL我们可以列出（b-1）个独立的方程，根据KVL 我们也可以列出（b-n+1）个独立的方程，根据每条支路所满足的欧姆定律，我们还可以可以列出b 个方程；总共2b 个方程要解出b 个支路电流变量和b 个支路电压变量。

当b 的数值比较大时，传统的解数学方程组的方法已经不再适用了，因此我们需要引入矩阵来帮助我们求解电路。

一. 电网络中最基本的三个矩阵图 1 1. 关联矩阵在电路图中，节点和支路的关联性质可以用关联矩阵][ij a A 来表示。

选取一个节点为参考节点后，矩阵A 的元素为：⎪⎩⎪⎨⎧-+=个节点无关联条支路与第第方向指向节点个节点相关联，且支路条支路与第第方向离开节点个节点相关联，且支路条支路与第第i j ii j i i j a ij 0 1 1图1中电路图的关联矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 0 1- 0 1- 1- 0 0 1- 0 0 0 1 1 0 0 0 0 0 0 1- 1-0 0 1- 1 0 0 1 A2. 基本回路矩阵在电路图中，基本回路和支路的关联性质可以用基本回路矩阵][ij f b B =来表示。

矩阵论在电气工程中的应用

题目：矩阵论在电气工程中的应用指导老师：XXX _______________________________学生姓名：XXX _____________________________所属院系：电气工程学院_______________专业：_____________ 电气工程 ________________学号: XXX _______________________完成日期：20xx 年x月x日__________________矩阵论在电气工程中的应用摘要电路分析是电气专业领域人员必需的一项能力。

该知识具有概念性强、电路分析繁杂求解计算量大的特点。

为了解决这个问题，因此引入了矩阵理论，并结合软件对矩阵分析的良好支持，以期达到优化分析电路的目的。

本文就矩阵理论中的网络拓扑知识展开，介绍了网络拓扑在电路中的应用，并以给予求解。

关键词：电路分析矩阵法网络拓扑ABSTRACTCircuit an alysis is an esse ntial ability of professi onal pers onnelin the field of electronic. The concept of strong, complex circuit an alysis calculatio n with the kno wledge of the characteristics of large amount. In order to alleviate this problem, so weintroduced matrix theory, comb ined with good support an alysis software for matrix, in order to achieve the purpose of optimization of circuit analysis. In this paper, the network topology in matrix theory unfolds, introduces the application of n etwork topology in circuit, and to give the solutio n. KEY WORDScircuit analysis ； matrix method ； network topology0前言矩阵是线性代数里的一个重要概念，在电路网络分析、工程结构分析等方面，矩阵都是一个强自力的工具，因为它能使较复杂的计算过程简化成一系列的四则运算，便于用计算机的算法语言或程序进行描述和解答。

电力系统的增广矩阵的求法

电力系统的增广矩阵的求法电力系统是现代社会不可或缺的基础设施之一，而电力系统的稳定运行离不开对其进行精确的建模和分析。

其中，增广矩阵是电力系统建模中的重要工具之一。

本文将从定义、求法和应用三个方面，对电力系统的增广矩阵进行详细介绍。

一、定义增广矩阵是指将矩阵的右侧增加一列，用于存储矩阵的常数项。

在电力系统中，增广矩阵通常用于描述节点电压和电流之间的关系。

例如，对于一个有n个节点的电力系统，其增广矩阵可以表示为：[A|B]其中，A是一个n×n的矩阵，用于描述节点电压和电流之间的关系；B是一个n×1的列向量，用于存储节点的电流注入值。

二、求法电力系统的增广矩阵求法主要有两种方法：基尔霍夫定律法和潮流方程法。

基尔霍夫定律法是指根据基尔霍夫电流定律和基尔霍夫电压定律，建立电力系统的节点方程组，然后将其转化为增广矩阵形式。

具体步骤如下：1. 根据电力系统的拓扑结构，建立节点方程组。

2. 将节点方程组转化为增广矩阵形式。

3. 对增广矩阵进行高斯消元或LU分解，求解节点电压和电流。

潮流方程法是指根据电力系统的潮流方程，建立节点方程组，然后将其转化为增广矩阵形式。

具体步骤如下：1. 根据电力系统的拓扑结构和潮流方程，建立节点方程组。

2. 将节点方程组转化为增广矩阵形式。

3. 对增广矩阵进行高斯消元或LU分解，求解节点电压和电流。

三、应用电力系统的增广矩阵在电力系统建模和分析中有着广泛的应用。

其中，最常见的应用包括：1. 潮流计算：通过求解电力系统的增广矩阵，可以计算出电力系统中各节点的电压和电流，从而实现潮流计算。

2. 稳态分析：通过对电力系统的增广矩阵进行特征值分解，可以得到电力系统的特征值和特征向量，从而实现稳态分析。

3. 短路分析：通过对电力系统的增广矩阵进行高斯消元或LU分解，可以计算出电力系统中各节点的短路电流，从而实现短路分析。

总之，电力系统的增广矩阵是电力系统建模和分析中不可或缺的工具之一。