2018年中考数学一模分类汇编 统计综合
2018届中考数学一模试卷分类汇编:综合计算及答案
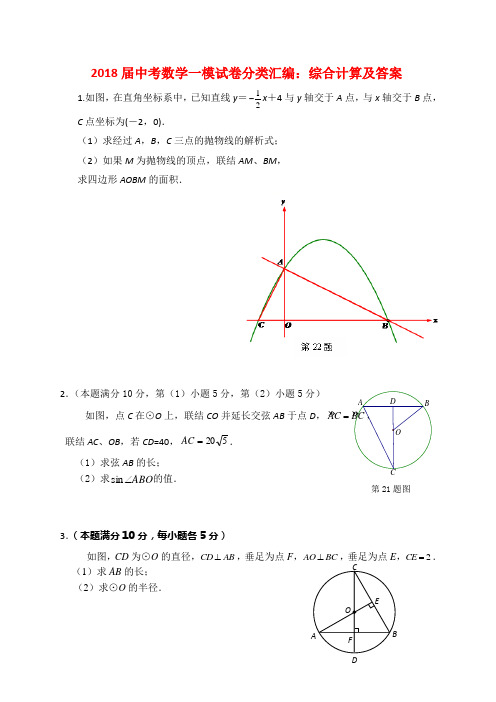
2018届中考数学一模试卷分类汇编:综合计算及答案1.如图,在直角坐标系中,已知直线y =12-x +4与y 轴交于A 点,与x 轴交于B 点, C 点坐标为(-2,0).(1)求经过A ,B ,C 三点的抛物线的解析式; (2)如果M 为抛物线的顶点,联结AM 、BM , 求四边形AOBM 的面积.2.(本题满分10分,第(1)小题5分,第(2)小题5分)如图,点C 在⊙O 上,联结CO 并延长交弦AB 于点D ,AC=联结AC 、OB ,若CD =40,520=AC . (1)求弦AB 的长; (2)求ABO ∠sin 的值.3.(本题满分10分,每小题各5分)如图,CD 为⊙O 的直径,CD AB ⊥,垂足为点F ,AO BC ⊥,垂足为点E ,2CE =. (1)求AB 的长; (2)求⊙O 的半径.第21题图D4.已知:如图,在Rt △ABC 中,∠ACB =90°,BC =,cot ABC ∠D 是AC 的中点.(1)求线段BD 的长;(2)点E 在边AB 上,且CE =CB ,求△ACE 的面积.5.如图,在△ABC 中,∠ACB =90°,AC =4,BC =3,D 是边AC 的中点,CE ⊥BD 交AB 于点E .(1)求tan ∠ACE 的值; (2)求AE ∶EB .6.如图5,在Rt △ABC 中,∠C =90°,AC =5,BC =25,以点C 为圆心,CA 长为半径的⊙C 与边AB 交于点D ,以点B 为圆心,BD 长为半径的⊙B 与⊙C 的另一个交点为点E .A BCED(1)求AD 的长.(2)求DE 的长7.(本题满分10分)如图,已知AB 是⊙O 的弦,C 是AB 的中点,AB=8,AC=O 半径的长.8.(本题满分10分, 其中第(1)小题4分,第(2)小题6分)已知:二次函数图像的顶点坐标是(3,5),且抛物线经过点A (1,3). (1)求此抛物线的表达式;(2)如果点A 关于该抛物线对称轴的对称点是B 点,且抛物线与y 轴的交点是C 点,求△ABC 的面积.9.(本题共2小题,每小题5分,满分10分)如图,已知OC 是⊙O 半径,点P 在⊙O 的直径BA 的延长线上,且OC ⊥PC ,垂足为C .弦CD 垂直平分半径AO ,垂足为E ,PA = 6.求:(1)⊙O 的半径; (2)求弦CD 的长.10.(本题满分10分,其中第(1)小题4分,第(2)小题6分)如图,已知G 、H 分别是□ABCD 对边AD 、BC 上的点,直线GH 分别交BA 和DC 的延长线于点E 、F . (1)当81=∆CDGHCFH S S 四边形时,求DGCH 的值;(2)联结BD 交EF 于点M ,求证:MG ME MF MH ⋅=⋅.11.(本题满分10分)如图8,已知⊙O 经过△ABC 的顶点A 、B ,交边BC 于点D ,点A 恰为BD 的中点,且8BD =,9AC =,1sin 3C =,求⊙O 的半径.12.(本题满分10分,第(1)小题5分,第(2)小题5分)如图6,在平面直角坐标系xOy 中,直线)0(≠+=k b kx y 与双曲线xy 6=相交于点A (m ,6)和点B (-3,n ),直线AB 与y 轴交于点C .(1)求直线AB 的表达式; (2)求:AC CB 的值.13. (本题满分10分,每小题各5分)如图,已知△ABC 中,AB AC ==BC =4.线段AB 的垂直平分线DF 分别交边AB 、ABH F CG DM图8ABCD O图6ADE。
【名师推荐-新课标】2018年北京市各区中考一模汇编《统计初步》常考题型及答案解析

北京市2018年各区中考一模汇编统计初步一、统计初步之基本概念1.【2016东城一模,第04题】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表所示选手甲乙丙丁方差 0.030 0.019 0.121 0.022 则这四人中发挥最稳定的是A 甲B 乙C 丙D 丁2.【2016东城一模,第14题】为了解一路段车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数是3.【2016丰台一模,第07题】某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是A. 18,18B. 9,9C. 9,10D. 18,94.【2016平谷一模,第07题】某校在汉字听写大赛中,10名学生得分情况分别是:人数3 4 2 1分数885995这10名学生所得分数的中位数和众数分别是A.85和80 B.80和85 C.85和85 D.85.5和80 5.【2016朝阳一模,第07题】2022年将在北京—张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了冰壶选修课,他们被分成甲、乙两组进行训练,身高(单位:cm )如下表所示:队员1 队员2 队员3 队员4 甲组 176 177 175 176 乙组178175177174设两队队员身高的平均数依次为甲x ,乙x ,方差依次为2甲s ,2乙s ,下列关系中完全正确的是A .甲x =乙x ,2甲s <2乙sB .甲x =乙x ,2甲s >2乙sC .甲x <乙x ,2甲s <2乙sD .甲x >乙x ,2甲s >2乙s6.【2016海淀一模,第07题】初三(8)班体委用划记法统计本班40名同学投掷实心球的成绩,结果如下表所示:成绩(分) 6 7 8 9 10 人数正 一正 正 一正 正正则这40名同学投掷实心球的成绩的众数和中位数分别是 A.9,8 B. 9,8.5 C. 8,8 D. 8,8.57.【2016西城一模,第07题】李阿姨是一名健步走运动爱好者,她用手机软件记录了某月(30天)每天健步走的步骤(单位:万步),将记录结果绘制成了突入所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是() A .1.2,1.3 B .1.4,1.3C .1.4,1.35D .1.3,1.38.【2016通州一模,第08题】为了弘扬优秀传统文化,通州区30所中学参加了“名著·人生”戏剧展演比赛,最后有13所中学进入决赛,他们的决赛成绩各不相同.某中学已进入决赛且知道自己的成绩,但是否进入前7名,还必须知道这13所中学成绩的 A .中位数B .平均数C .众数D .方差二、统计初步之基本应用9.【2016丰台一模,第15题】某地区有36所中学,其中九年级学生共7000名.为了了解该地区九年级学生的体重情况,请你运用所学的统计知识,将解决上述问题所要经历的几个主要步骤进行排序.①抽样调查;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.排序:.(只写序号)10.【2016平谷一模,第09题】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d 和身高h 成某种关系.下表是测得的指距与身高的一组数据:根据上表解决下面这个实际问题:姚明的身高是226厘米,可预测他的指距约为A.25.3厘米B.26.3厘米C.27.3厘米D.28.3厘米11.【2016平谷一模,第15题】在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化折线图如图所示,这个图形中折线的变化特点是,试举一个大致符合这个特点的实物实验的例子(指出关注的结果).12.【2016海淀一模,第15题】北京市2010-2015年高考报名人数统计如图所示,根据统计图中提供的信息,预估2016年北京市高考人数约为万人,你的预估理由是.指距d (cm ) 20 21 22 23身高h (cm )160169178187报名人数/万人87.87.67.47.276.86.66.4201020112012201320142015201620178.027.607.557.257.056.813.【2016西城一模,第16题】有这样一个数字游戏,将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x 代表的数字是___,此时按游戏规则填写空格,所有可能出现的结果共有__________________种.14.【2016通州一模,第13题】手机悦动圈是记录步行数和热量消耗数的工具,下表是孙老师用手机悦动圈连续记录的一周当中,每天的步行数和卡路里消耗数(热量消耗,单位:大卡)星期 一 二 三 四 五 六 日 步行数 5025 5000 4930 5208 5080 10085 1000卡路里消耗 201 200 198 210 204 405 400孙老师发现每天步行数和卡路里消耗数近似成正比例关系.孙老师想使自己的卡路里消耗数达到300大卡,预估他一天步行约为__________步.(直接写出结果,精确到个位)三、统计初步之复杂应用(大题)15.【2016东城一模,第24题】某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:阅读本数n(本) 1 2 3 4 5 6 7 8 9人数(名) 1 2 6 7 12 x7 y 1 请根据以上信息回答下列问题:(1)求出本次随机抽取的学生总人数;(2)分别求出统计表中的x,y的值;(3)估计该校九年级400名学生中为“优秀”档次的人数.16.【2016丰台一模,第25题】阅读下列材料:北京市统计局发布了2014年人口抽样调查报告,首次增加了环线人口分布数据. 调查数据显示,北京市超过一半的常住人口都住在了远离城区的五环以外. 事实上,北京市的中心城区人口从上世纪80年代起就持续下降,越来越多的人向郊区迁移根据2014年人口抽样调查结果发现,本市三环至六环间,聚集了1226.9万人的常住人口,占全市的57.1%;四环至六环间聚集了941万人的常住人口,占全市的43.8%;五环以外有1098万人的常住人口,占全市的51.1%.在进行人口分布研究时,北京通常被划分为四个区域,城市功能拓展区包括:朝阳、海淀、丰台、石景山四个区; 城市发展新区包括:通州、顺义、大兴、昌平、房山五个区和亦庄开发区; 首都功能核心区包括:东城区和西城区; 生态涵养发展区包括:门头沟、平谷、怀柔、密云、延庆五个区县.从常住人口分布上看:城市功能拓展区常住人口最多,占全市总量的49%;城市发展新区常住人口约为684万人;首都功能核心区常住人口约为221万人;生态涵养发展区常住人口约为191万人.从常住外来人口分布上看:城市功能拓展区常住外来人口最多,约为436万人;城市发展新区常住外来人口约为297万人;首都功能核心区常住外来人口约为54万人;生态涵养发展区常住外来人口约为32万人.根据以上材料回答下列问题:(1)估算2014年北京市常住人口约为___________万人.(2)选择统计表或.统计图,将2014年北京市按四个区域的常住人口和常住外来人口分布情况表示出来.17.【2016平谷一模,第25题】“世界那么大,我想去看看”是现代很多人追求的生活方式之一.根据北京市旅游发展委员会发布的信息显示, 2012——2015年连续四年,我市国内旅游市场保持了稳定向好的态势.2012年,旅游总人数约2.31亿人次,同比增长8.1%;2013年,旅游总人数约 2.52亿人次,同比增长9%;2014年,旅游总人数约 2.61亿人次,同比增长3.8%;2015年,旅游总人数2.73亿人次,同比增长4.3%;预计2016年旅游总人数与2015年同比增长5%.旅游不仅是亲近自然的好时机,同时也是和家人朋友沟通的好时机,调查显示,中秋国庆黄金假期成为人们选择旅游最佳时期,《2015年中秋国庆长假出游趋势报告》显示,人们出行的方式可以归纳为四种,即乘火车、乘汽车、坐飞机、其他.其中选择乘火车出行的人数约占47%,选择乘汽车出行的人数约占28%,选择坐飞机出行的人数约占17%.根据以上信息解答下列问题:(1)预计2016年北京市旅游总人数约亿人次(保留两位小数);(2)选择其他出行方式的人数约占;(3)请用统计图或统计表,将2012——2015年北京市旅游总人数表示出来.18.【2016朝阳一模,第25题】阅读下列材料:人口老龄化已经成为当今世界主要问题之一.北京市在上世纪90年代初就进入了老龄化社会,全市60岁及以上户籍老年人口2013年底达到279.3万人,占户籍总人口的21.2%; 2014年底比2013年底增加17.4万人,占户籍总人口的22.3%;2015年底比2014年底增加23.3万人,占户籍总人口的23%.“百善孝为先”,北京市政府越来越关注养老问题,提出养老服务新模式,计划90%的老年人在社会化服务协助下通过家庭照顾养老(即居家养老),6%的老年人在社区养老,4%的老年人入住养老服务机构.本市养老服务机构的床位总数2013年达到8.0516万张,2014年达到10.938万张,2015年达到12万张.根据以上材料回答下列问题:(1)到2014年底,本市60岁及以上户籍老年人口为__________万人; (2)选择统计表或.统计图,将2013年––2015年本市60岁及以上户籍老年人口数量和占户籍总人口的比例表示出来;(3)预测2016年本市养老服务机构的床位数约为_________万张,请你结合数据估计,能否满足4%的老年人入住养老服务机构,并说明理由.19.【2016海淀一模,第25题】 阅读下列材料:2015年中国内地电影市场票房总收入400亿元,动画电影成为了新崛起的热点,票房占比为11.25%。
【中考汇编】北京市各区2018届中考一模数学试卷精选汇编88页含答案

北京市各区2018届中考一模数学试卷精选汇编目录北京市各区2018届中考一模数学试卷精选汇编:解不等式组(含答案)北京市各区2018届中考一模数学试卷精选汇编:计算题(含答案)北京市各区2018届中考一模数学试卷精选汇编:解四边形(含答案)北京市各区2018届中考一模数学试卷精选汇编:几何证明(含答案)北京市各区2018届中考一模数学试卷精选汇编:几何综合(含答案)北京市各区2018届中考一模数学试卷精选汇编:函数计算及运用(含答案)北京市各区2018届中考一模数学试卷精选汇编:二次函数综合(含答案)北京市各区2018届中考一模数学试卷精选汇编:统计(含答案)解不等式组专题东城区18. 解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩>≥, 并写出它的所有整数解. 18. 解:4+6,23x x x x ⎧⎪⎨+⎪⎩①②>≥, 由①得,-x >2,------------------1分由②得,1x ≤, ------------------2分∴不等式组的解集为-1x 2<≤.所有整数解为-1, 0, 1. ---------------------5分西城区18.解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥,并求该不等式组的非负整数解.【解析】解①得,364x x ++≥,22x -≥,1x -≥,解②得,12x -<,3x <,∴原不等式解集为13x -<≤,∴原不等式的非负整数解为0,,2.海淀区18.解不等式组:()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解:() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①,得3x >-. …2分解不等式②,得2x <. ………4分所以 原不等式组的解集为32x -<<. ………5分18.解不等式组:341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18.解:解不等式①,得1x ≤, ……………………2分解不等式②,得1x >-. ……………………4分∴原不等式组的解集是11x -<≤.………5分石景山区18.解不等式组:3(1)45622x x x x +>++<⎧⎪⎨⎪⎩,. 18.解:原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①,得2x <-. ………………2分 解不等式②,得2x <. ………………4分 ∴原不等式组的解集为<2x -. ………………5分 朝阳区18. 解不等式组 :⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解:原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①,得 5<x . ………………………………………2分解不等式②,得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分① ②18.解不等式组:⎩⎪⎨⎪⎧x -32<1,2(x +1)≥x -1.18.解:由(1)得,x-3<2X<5 ……………………….2′(2) 得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x <5……………………….5′ 门头沟区18. 解不等式组:1031+1.x x x ⎧-<⎪⎨⎪-⎩,≤3()18.(本小题满分5分)解不等式①得,x <3, …………………………………………2分解不等式②得,x ≥﹣2, ………………………………4分所以,不等式组的解集是﹣2≤x <3. ………………5分大兴区17.解不等式组:⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解. 17. 解:⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 由①,得21-≥x . ………………………………………………………1分 由②,得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分 它的所有整数解为0,1. …………………………………………………5分① ②18.解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩,并写出它的所有整数解.... 18.解:3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①,得 x ≤2. ·········································································1 解不等式②,得 x >-1. ·······································································3 ∴原不等式组的解集为12x -<≤. ························································4 ∴适合原不等式组的整数解为0,1,2. ·······················································5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解:由①得:3x < . ………………………………………………………………………2分由②得:9x >- …………………………………………………………………………4分 原不等式组的解集为93x -<< ………………………………………………………5分 延庆区18.解不等式组:523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩, 并写出它的所有整数解. 18.解:由①得,x <4. ……1分由②得,x ≥1 . ……3分∴ 原不等式组的解集为1≤x <4. ……4分∴ 原不等式组的所有整数解为1,2,3. ……5分18.解不等式组:()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18.解不等式组:()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解:解不等式①得 x ≥3- ……………………………………………………………2分 解不等式②得 2x > ………………………………………………………………4分 不等式组的解集是 2x > …………………………………………………………5分计算题专题东城区17.计算:()2012sin 60-π-2++1-3-⎛⎫︒ ⎪⎝⎭. =217.解:原式分分西城区17114sin 3015-⎛⎫+︒- ⎪⎝⎭.【解析】原式1541)52122=+⨯-=+=. 海淀区17.计算:11()3tan 302|3-︒+. 17.解:原式=3323-⨯+- ………………4分=5- ………………5分丰台区1702cos 45(3π)|1-︒+-+-.1702cos 45(3π)|1︒+-+.=211++ ……………………4分= ……………………5分石景山区17.计算:012sin 455(3--++° 17.解:原式=2512⨯-+- ………………4分4=-- ………………5分朝阳区17. 计算:2sin30°+ .8)4()31(01+-+-π17. 解:原式 2213212+++⨯= …………………………………………………4分 225+=. ……………………………………………………………5分燕山区17.计算:4cos30°-12 + 20180 + ||1-317.4cos30°-12 + 20180 + ||1-3 =13132234-++-⨯=3 门头沟区17.计算:()201254sin 603π-⎛⎫--++-︒ ⎪⎝⎭.平谷区17.计算:(1013132sin 603-⎛⎫-+-︒ ⎪⎝⎭π.17.解:(1013132sin 603-⎛⎫-+--︒ ⎪⎝⎭π=331312-- ···········································································4 =1 ····································································································5 怀柔区17.计算:102130tan 3)3(31-︒⎪⎭⎫ ⎝⎛-+---π. 17.解:原式331132=--+ …………………………………………………4分.…………………………………………………………………5分延庆区17.计算:0113tan 301(2)()3π-︒+---.17.原式=3⨯33+3-1+1-3 ……4分=23-3 ……5分顺义区17.计算:()01312sin 452π--︒+-.17.解:()01312sin 452π--︒+-112132=-⨯+ (4)分13= ……………………………………………………………………………… 5分4=-解四边形专题东城区21.如图,已知四边形ABCD 是平行四边形,延长BA 至点E ,使AE = AB ,连接DE ,AC .(1)求证:四边形ACDE 为平行四边形;(2)连接CE 交AD 于点O . 若AC=AB =3,1cos 3B =,求线段CE 的长.21.(1) 证明:∵平行四边形ABCD ,∴=AB DC ,AB DC ∥.∵AB =AE ,∴=AE DC ,AE DC ∥.∴四边形ACDE 为平行四边形. -------------------2分(2) ∵=AB AC ,∴=AE AC .∴平行四边形ACDE 为菱形.∴AD ⊥CE .∵AD BC ∥,∴BC ⊥CE.在Rt △EBC 中,BE =6, 1cos 3BC B BE ==, ∴=2BC . 根据勾股定理,求得=42BC 分 西城区21.如图,在ABD △中,ABD ADB ∠=∠,分别以点B ,D 为圆心,AB 长为半径在BD 的右侧作弧,两弧交于点C ,分别连接BC ,DC ,AC ,记AC 与BD 的交点为O . (1)补全图形,求AOB ∠的度数并说明理由;(2)若5AB =,3cos 5ABD ∠=,求BD 的长.BDA【解析】(1)补全的图形如图所示.90AOB ∠=︒. 证明:由题意可知BC AB =,DC AB =, ∵在ABD △中,ABD ADB ∠=∠, ∴AB AD =,∴BC DC AD AB ===, ∴四边形ABCD 为菱形, ∴AC BD ⊥, ∴90AOB ∠=︒.(2)∵四边形ABCD 为菱形, ∴OB OD =.在Rt ABO △中,90AOB ∠=︒,5AB =,3cos 5ABD ∠=,∴cos 3OB AB ABD =⋅∠=, ∴26BD OB ==.ABCDO海淀区21.如图,□ABCD 的对角线,AC BD 相交于点O ,且AE ∥BD ,BE ∥AC ,OE = CD . (1)求证:四边形ABCD 是菱形;(2)若AD = 2,则当四边形ABCD 的形状是__________时,四边形AOBE 的面积取得最大值是_______.C B EOAD21.(1)证明:∵AE BD ∥,BE AC ∥,∴四边形AEBO 是平行四边形. ………………1分 ∵四边形ABCD 是平行四边形,∴DC AB =. ∵OE CD =, ∴OE AB =.∴平行四边形AEBO 是矩形. ………………2分 ∴90BOA ∠=︒. ∴AC BD ⊥.∴平行四边形ABCD 是菱形. ………………3分 (2) 正方形; ………………4分2. ………………5分丰台区21.已知:如图,菱形ABCD ,分别延长AB ,CB 到点F ,E ,使得BF = BA ,BE = BC ,连接AE ,EF ,FC ,CA .(1)求证:四边形AEFC 为矩形;(2)连接DE 交AB 于点O ,如果DE ⊥AB ,AB = 4,求DE 的长.ABCEDF21.(1)证明:∵BF =BA ,BE =BC ,∴四边形AEFC 为平行四边形. ………………………1分 ∵四边形ABCD 为菱形, ∴BA =BC .∴BE =BF .∴BA + BF = BC + BE ,即AF =EC .∴四边形AEFC 为矩形. ………………………2分(2)解:连接DB .由(1)知,AD ∥EB ,且AD =EB . ∴四边形AEBD 为平行四边形 ∵DE ⊥AB ,∴四边形AEBD 为菱形.∴AE =EB ,AB =2AG ,ED =2EG . ………………………4分 ∵矩形ABCD 中,EB =AB ,AB=4, ∴AG =2,AE =4.∴Rt △AEG 中,EG=23.∴ED=43. ………………………5分 (其他证法相应给分)石景山区21.如图,在四边形ABCD 中,90A BCD ∠=∠=°,210BC CD ==,CE AD ⊥于点E . (1)求证:AE CE =;(2)若tan 3D =,求AB 的长.BA CE D21.(1)证明:(法一)过点B 作BH ⊥CE 于H ,如图1. ∵CE ⊥AD ,∴∠BHC =∠CED =90°,190D ∠+∠=︒. ∵∠BCD =90°, ∴1290∠+∠=︒, ∴2D ∠=∠. 又BC =CD∴BHC △≌CED △. ∴BH CE =.∵BH ⊥CE ,CE ⊥AD ,∠A =90°, ∴四边形ABHE 是矩形, ∴AE BH =.∴AE CE =. ………………3分 (法二)过点C 作CH ⊥AB 交AB 的延长线于H .图略,证明略. (2)解: ∵四边形ABHE 是矩形, ∴AB HE =.∵在Rt CED △中,tan 3CE D DE==,设,3DE x CE x ==,∴10210CD x ==. ∴2x =.∴2DE =,6CE =. ………………4分 ∵2CH DE ==.∴624AB HE ==-=. ………………5分朝阳区21. 如图,在△ABC 中,D 是AB 边上任意一点,E 是BC 边中点,过点C作AB 的平行线,交DE 的延长线于点F ,连接BF ,CD . (1)求证:四边形CDBF 是平行四边形; (2)若∠FDB =30°,∠ABC =45°,BC =,求DF 的长.21.(1)证明:∵CF ∥AB ,∴∠ECF =∠EBD . ∵E 是BC 中点, ∴CE =BE .∵∠CEF =∠BED , ∴△CEF ≌△BED . ∴CF =BD .∴四边形CDBF 是平行四边形. ………………………2分(2)解:如图,作EM ⊥DB 于点M ,∵四边形CDBF 是平行四边形,BC =24,∴2221==BC BE ,DE DF 2=. 在Rt △EMB 中,2sin =∠⋅=ABC BE EM . ……………………3分在Rt △EMD 中,42==EM DE . …………………4分∴DF =8. ………………………………………………………5分燕山区23. 如图,在△ABC 错误!未找到引用源。
北京市2018年中考数学一模分类汇编 统计综合

统计综合2018西城一模23.某同学所在年级的500名学生参加“志愿北京”活动,现有以下5个志愿服务项目:A.纪念馆志愿讲解员.B.书香社区图书整理.C.学编中国结及义卖.D.家风讲解员.E.校内志愿服务.要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示).B,E,B,A,E,C,C,C,B,B,A,C,E,D,B,A,B,E,C,A,D,D,B,B,C,C,A,A,E,B,C,B,D,C,A,C,C,A,C,E,整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图.选择各志愿服务项目的人数统计表分析数据、推断结论:a:抽样的40个样本数据(志愿服务项目的编号)的众数是__________.(填A E-的字母代号)b:请你任选A E-中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.2018石景山一模24.某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分):整理、分析过程如下,请补充完整.成绩x 学生70≤x≤7475≤x≤7980≤x≤8485≤x≤8990≤x≤9495≤x≤100甲乙 1 1 4 2 1 1学生极差平均数中位数众数方差甲83.7 86 13.21 乙24 83.7 82 46.21(3)若从甲、乙两人中选择一人参加知识竞赛,你会选(填“甲”或“乙),理由为.2018平谷一模23.为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析:甲91 89 77 86 71 31 97 93 72 9181 92 85 85 95 88 88 90 44 91 乙84 93 66 69 76 87 77 82 85 8890 88 67 88 91 96 68 97 59 88 整理、描述数据分析数据两组数据的平均数、中位数、众数、方差如下表:的值是.得出结论a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .b可以推断出学校学生的数学水平较高,理由为 . (至少从两个不同的角度说明推断的合理性)2018怀柔一模24.某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:排球 10 9.5 9.5 10 8 9 9.5 97 10 4 5.5 10 9.5 9.5 10篮球 9.5 9 8.5 8.5 10 9.5 10 86 9.5 10 9.5 9 8.5 9.5 6整理、描述数据按如下分数段整理、描述这两组样本数据:(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)分析数据两组样本数据的平均数、中位数、众数如下表所示:得出结论(1)如果全校有160人选择篮球项目,达到优秀的人数约为人;(2)初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.你同意的看法,理由为.(至少从两个不同的角度说明推断的合理性)2018海淀一模24. 某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.收集数据 调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);A .抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本B .抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本C .从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本 整理、描述数据 抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:77 83 80 64 86 90 75 92 83 81 85 86 88 62 65 86 97 96 82 73 86 84 89 86 92 73 57 77 87 82 91 81 86 71 53 72 90 76 68 78 整理数据,如下表所示:2018年九年级部分学生学生的体质健康测试成绩统计表分析数据、得出结论调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,分2017年九年级部分学生体质健康成绩直方图你能从中得到的结论是_____________,你的理由是__________________________.体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有________名同学参加此项目.2018朝阳一模24. 水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:甲 26 32 40 51 44 74 44 63 73 74 81 54 6241 33 54 43 34 51 63 64 73 64 54 33乙 27 35 46 55 48 36 47 68 82 48 57 66 7527 36 57 57 66 58 61 71 38 47 46 71整理、描述数据按如下分组整理、描述这两组样本数据(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据两组样本数据的平均数、众数和方差如下表所示:得出结论a.估计乙大棚产量优秀的秧苗数为株;b.可以推断出大棚的小西红柿秧苗品种更适应市场需求,理由为.(至少从两个不同的角度说明推断的合理性)2018东城一模24.随着高铁的建设,春运期间动车组发送旅客量越来越大.相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间铁路发送旅客量情况进行了调查,具体过程如下.(I)收集、整理数据请将表格补充完整:(II)描述数据为了更直观地显示春运期间动车组发送旅客量占比的变化趋势,需要用___________(填“折线图”或“扇形图”)进行描述;(III)分析数据、做出推测预计2019年春运期间动车组发送旅客量占比约为___________,你的预估理由是_________________________________________ .2018丰台一模24.第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.【收集数据】从甲、乙两校各随机抽取20名学生,在这次竞赛中他们的成绩如下:甲 30 60 60 70 60 80 30 90 100 6060 100 80 60 70 60 60 90 60 60乙 80 90 40 60 80 80 90 40 80 5080 70 70 70 70 60 80 50 80 80【整理、描述数据】按如下分数段整理、描述这两组样本数据:(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)【分析数据】两组样本数据的平均分、中位数、众数如下表所示:其中a【得出结论】(1)小明同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是________校的学生;(填“甲”或“乙”)(2)张老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为________;(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)2018房山一模24. 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.收集数据 17 18 16 12 24 15 27 25 18 1922 17 16 19 31 29 16 14 15 2515 31 23 17 15 15 27 27 16 19整理、描述数据分析数据样本数据的平均数、众数、中位数如下表所示:得出结论(1)如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为万元.(2)如果想确定一个较高的销售目标,这个目标可以定为每月万元,理由为.2018门头沟一模24.地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态坏境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:初一: 76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二: 74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74(1)根据上表中的数据,将下列表格补充完整;整理、描述数据:(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)分析数据:(2你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).24.甲乙两组各有10名学生,进行电脑汉字输入速度比赛,现将他们的成绩进行统计,过程如下:收集数据各组参赛学生每分钟输入汉字个数统计如下表:分析数据两组数据的众数、中位数、平均数、方差如下表所示:得出结论(1)若每分钟输入汉字个数136及以上为优秀,则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?(2)请你根据所学的统计知识,从不同角度评价甲、乙两组学生的比赛成绩(至少从两个角度进行评价).23.中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次 “汉字听写”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:90,92,81,82,78,95,86,88,72,66, 62,68,89,86,93,97,100,73,76,80, 77,81,86,89,82,85,71,68,74,98, 90,97,100,84,87,73,65,92,96,60.请根据所给信息,解答下列问题:(1)a = ,b = , c = ,d = ; (2)请补全频数分布直方图;(3)若成绩在90分以上(包括90分)的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?16142607*********4681012成绩x /分频数23. 体育教师为了解本校九年级女生“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试.获取数据如下:收集数据抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:38 46 42 52 55 43 59 46 25 3835 45 51 48 57 49 47 53 58 49整理、描述数据请你按如下分组整理、描述样本数据:(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)分析数据样本数据的平均数、中位数、众数如下表所示:得出结论①估计该校九年级女生在中考体育测试中仰卧起坐项目可以得到满分的人数为;②该中学所在区县的九年级女生在1分钟仰卧起坐总体测试成绩如下:请你结合该校样本测试成绩和该区县的总体测试成绩,对该校九年级女生的“仰卧起坐”达标情况做一下评估,并提出相应建议.2018燕山一模:日期4月1日4月2日4月3日4月4日4月5日4月6日步行数(步) 10672 4927 5543 6648步行距离(公里)6.8 3.1 3.4 4.3卡路里消耗(千卡)157 79 91 127燃烧脂肪(克)20 10 12 16(1)4月5日,4月6日,豆豆妈妈没来得及作记录,只有手机图片,请你根据图片数据,帮她补全表格.(2)豆豆利用自己学习的统计知识,把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来,请你根据图中提供的信息写出结论:.(写一条即可)步行距离燃烧脂肪101520525303025燃烧脂肪(千卡)2015104月1日-6日妈妈步行距离与燃烧脂肪情况统计图步行距离(公里)(3)豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系,豆豆妈妈想使自己的卡路里消耗数达到250千卡,预估她一天步行距离为__________公里.(直接写出结果,精确到个位)。
2018届中考数学一模试卷(解析版)

中考数学一模试卷(解析版)一.选择题1.下列图形中,既是轴对称图形又是中心对称图形的有()A. 4个B. 3个C. 2个D. 1个2.如图,点D,E分别为△ABC的边AB,AC上的中点,则△ADE的面积与四边形BCED的面积的比为()A. 1:2B. 1:3C. 1:4D. 1:13.如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限.若反比例函数y= 的图象经过点B,则k的值是()A. 1B. 2C.D.4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A. =B. ∠APB=∠ABCC. =D. ∠ABP=∠C5.在△ABC中,(2cosA﹣)2+|1﹣tanB|=0,则△ABC一定是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 等腰直角三角形6.已知x=1是方程x2+bx=2的一个根,则方程的另一个根是()A. 1B. 2C. ﹣2D. ﹣17.有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y=(x>0),y=﹣(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是()A. B. C. D. 18.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()A. a>0B. 3是方程ax2+bx+c=0的一个根C. a+b+c=0D. 当x<1时,y随x的增大而减小9.如图所示,直线l和反比例函数y= (k>0)的图象的一支交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则()A. S1<S2<S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S310.如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB= ,则⊙O的半径为()A. 4B. 3C. 2D.二.填空题11.如图,若点A的坐标为,则sin∠1=________.12.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是________.13.如图,一次函数与反比例的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是________.14.在矩形ABCD中,AB=6,BC=8,AC,BD相交于O,P是边BC上一点,AP与BD交于点M,DP与AC交于点N.①若点P为BC的中点,则AM:PM=2:1;②若点P为BC的中点,则四边形OMPN的面积是8;③若点P为BC的中点,则图中阴影部分的总面积为28;④若点P在BC的运动,则图中阴影部分的总面积不变.其中正确的是________.(填序号即可)三.解答题16.解方程:x2﹣5x+3=0.四.综合题17.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心,将四边形ABCD顺时针旋转90°,得到四边形AB1C1D1;(2)以A为位似中心,将四边形ABCD作位似变换,且放大到原来的两倍,得到四边形AB2C2D2.18.如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)五.应用题19.如图,在平面直角坐标系xOy中,直线y=﹣x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.(1)求反比例函数的解析式;(2)连接OD,求△OBD的面积.(3)x取何值时,反比例函数的值大于一次函数的值.20.如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.(1)求证:AD平分∠BAC;(2)若AC=8,tan∠DAC= ,求⊙O的半径.21.在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为________,若A为随机事件,则m的取值为________;(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.22.如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB•AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=________°.(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?23.已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).(1)求抛物线l2的解析式;(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.①当四边形AMBN的面积最大时,求点P的坐标;②当CM=DN≠0时,求点P的坐标.答案解析一.<b >选择题</b>1.【答案】C【考点】轴对称图形,中心对称及中心对称图形【解析】【解答】解:左起第1个图形不是轴对称图形;左起第2个图形和第3个图形,它们旋转180°能与原图形重合,都有4条对称轴,∴这两个图形既是轴对称又是中心对称;左起第4个图形旋转180°不能与原图形重合,但它是轴对称图形,有5条对称轴故答案为:C.【分析】根据轴对称图形的定义和中心对称图形的定义去判定。
上海市16区2018届中考一模数学试卷分类汇编:押轴题(含答案)

上海市16区2018届九年级上学期期末(一模)数学试卷分类汇编押轴题专题宝山区25.(本题共14分,其中(1)(2)小题各3分,第(3)小题8分)如图,等腰梯形ABCD 中,AD //BC ,AD =7,AB =CD =15,BC =25,E 为腰AB 上一点且AE :BE =1:2,F 为BC 一动点,∠FEG =∠B ,EG 交射线BC 于G ,直线EG 交射线CA 于H . (1)求sin ∠ABC ; (2)求∠BAC 的度数;(3)设BF =x ,CH =y ,求y 与x 的函数关系式及其定义域.长宁区25.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分)已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D 重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E . 设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求 ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域; (3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.备用图备用图图1DCBA DCA F EP D CB A崇明区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分) 如图,已知ABC △中,90ACB ∠=︒,8AC =,4cos 5A =,D 是AB 边的中点,E 是AC 边上一点,联结DE ,过点D 作DF DE ⊥交BC 边于点F ,联结EF . (1)如图1,当DE AC ⊥时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,DFE ∠的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出DFE ∠的正切值;(3)如图3,联结CD 交EF 于点Q ,当CQF △是等腰三角形时,请直接写出....BF 的长.(第25题图1)ABCD FE BD FE CA(第25题图2) BD F ECA(第25题图3)奉贤区25.(本题满分14分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分6分)已知:如图,在梯形ABCD 中,AB ∥CD ,∠D =90°,AD =CD =2,点E 在边AD 上(不与点A 、D 重合),∠CEB =45°,EB 与对角线AC 相交于点F ,设DE =x . (1)用含x 的代数式表示线段CF 的长;(2)如果把△CAE 的周长记作△CAE C ,△BAF 的周长记作△BAF C ,设△△CAEBAFC y C =,求y 关于x 的函数关系式,并写出它的定义域;(3)当∠ABE 的正切值是35时,求AB 的长.虹口区25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知AB =5,AD =4,AD ∥BM ,3cos 5B =(如图),点C 、E 分别为射线BM 上的动点(点C 、E 都不与点B重合),联结AC 、AE ,使得∠DAE =∠BAC ,射线EA 交射线CD 于点F .设BC =x ,AFy AC=. (1)如图1,当x =4时,求AF 的长;(2)当点E 在点C 的右侧时,求y 关于x 的函数关系式,并写出函数的定义域; (3)联结BD 交AE 于点P ,若△ADP 是等腰三角形,直接写出x 的值.黄浦区25.(本题满分14分)如图,线段AB =5,AD =4,∠A =90°,DP ∥AB ,点C 为射线DP 上一点,BE 平分∠ABC 交线段AD 于点E (不与端点A 、D 重合).(1)当∠ABC 为锐角,且tan ∠ABC =2时,求四边形ABCD 的面积; (2)当△ABE 与△BCE 相似时,求线段CD 的长;(3)设CD =x ,DE =y ,求y 关于x 的函数关系式,并写出定义域.嘉定区25. 在正方形ABCD 中,AB =8,点P 在边CD 上,tan ∠PBC =43,点Q 是在射线BP 上的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直。
2018年广州中考数学一模统计与概率题汇编参考答案
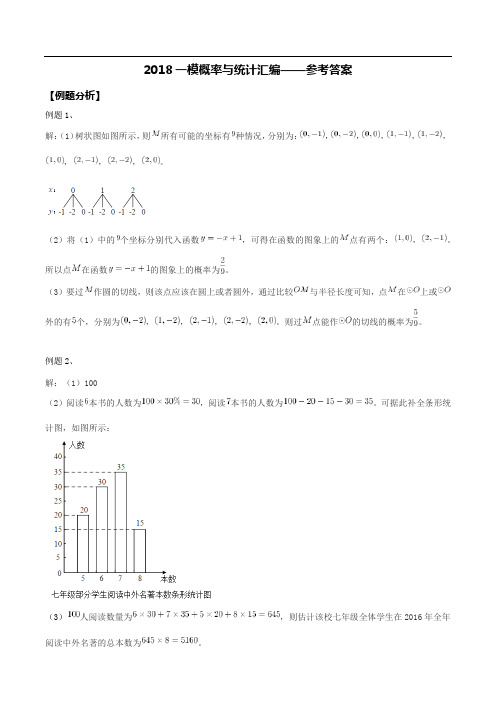
2018一模概率与统计汇编——参考答案【例题分析】例题1、解:(1)树状图如图所示,则所有可能的坐标有种情况,分别为:,,,,,,,,。
(2)将(1)中的个坐标分别代入函数,可得在函数的图象上的点有两个:,。
所以点在函数的图象上的概率为。
(3)要过作圆的切线,则该点应该在圆上或者圆外,通过比较与半径长度可知,点在上或外的有个,分别为,,,,。
则过点能作的切线的概率为。
例题2、解:(1)100(2)阅读本书的人数为,阅读本书的人数为。
可据此补全条形统计图,如图所示:(3)人阅读数量为,则估计该校七年级全体学生在2016年全年阅读中外名著的总本数为。
(4)根据题意,如图:由图可以看出,共有种可能的结果,其中甲、乙二人中至少有一个被选中有十种,所以P=1012=56 .例题3、解:(1)由两种统计表可知:总人数人,打印项目占,打印项目人数人,,,故答案为:8,3;(2)扇形统计图中机器人项目所对应扇形的圆心角度数,故答案为:144;由表格可知,共有12种可能出现的结果,并且它们都是第可能的,其中“1名男生、1名女生”有8种可能. 所以P( 1名男生、1名女生)例题4、解:(1)如图:(2)一次性打开锁,则开第一次刚好拿到第一把锁的钥匙概率是,第二次拿到第二把锁的钥匙概率是,所以一次打开所有锁的概率是:.例题5、解:(1)是,占,的人数为10人,这次被调查的学生共有:(人)。
(2)如图,C有:(人),(3)画树状图得:共有6种等可能的结果,甲、乙被选中的有2种情况, 恰好同时选中甲、乙两位同学的概率为例题6、解:(1)如图:“体育”对应扇形的圆心角是(2)人;(3)设来自甲班的两人分别为甲、甲,来自乙班的两人分别为乙、乙,画树状图如下:共有种互不相同的选取方法,每种选择的概率项都相等,满足题意的情况有种,所以(来自不同班级)。
例题7、解:(1)该班总人数是:12÷24% = 50(人)答:该班总人数是 50 人。
北京市各区2018届中考数学一模试卷精选汇编代数综合专题

代数综合专题东城区20. 已知关于x 的一元二次方程()2320x m x m -+++=.(1) 求证:无论实数m 取何值,方程总有两个实数根;(2) 若方程有一个根的平方等于4,求m 的值.20. (1)证明:()()2=+3-42m m ∆+()2=+1m∵()2+10m ≥,∴无论实数m 取何值,方程总有两个实根. -------------------2分(2)解:由求根公式,得()()1,231=2m m x +±+, ∴1=1x ,2=+2x m .∵方程有一个根的平方等于4,∴()2+24m =.解得=-4m ,或=0m . -------------------5分西城区20.已知关于x 的方程2(3)30mx m x +--=(m 为实数,0m ≠).(1)求证:此方程总有两个实数根.(2)如果此方程的两个实数根都为正整数,求整数m 的值.【解析】(1)2222(3)4(3)691269(3)0m m m m m m m m ∆=--⨯-=-++=++=+≥ ∴此方程总有两个不相等的实数根.(2)由求根公式,得(3)(3)2m m x m --±+=, ∴11x =,23x m=-(0m ≠). ∵此方程的两个实数根都为正整数,∴整数m 的值为1-或3-.海淀区20.关于x 的一元二次方程22(23)10x m x m --++=.(1)若m 是方程的一个实数根,求m 的值;(2)若m 为负数..,判断方程根的情况. 20.解:(1)∵m 是方程的一个实数根,∴()222310m m m m --++=. ………………1分 ∴13m =-. ………………3分 (2)24125b ac m ∆=-=-+.∵0m <,∴120m ->.∴1250m ∆=-+>. ………………4分∴此方程有两个不相等的实数根.丰台区20.已知:关于x 的一元二次方程x 2 - 4x + 2m = 0有两个不相等的实数根.(1)求m 的取值范围;(2)如果m 为非负整数....,且该方程的根都是整数..,求m 的值.20.解:(1)∵方程有两个不相等的实数根,∴Δ>0.∴Δ=24421680m m --⋅=->().∴2m <. ………………………2分(2)∵2m <,且m 为非负整数,∴=0m 或1. ………………………3分当m =0时,方程为240x x -=,解得方程的根为01=x ,24x =,符合题意;当m =1时,方程为2420x x -+=,它的根不是整数,不合题意,舍去.综上所述,m =0. ………………………5分石景山区20.关于x 的一元二次方程2(32)60mx m x +--=.(1)当m 为何值时,方程有两个不相等的实数根;(2)当m 为何整数时,此方程的两个根都为负整数.20.解:(1)∵24b ac ∆=-2(32)24m m =-+2(32)0m =+≥∴当0m ≠且23m ≠-时,方程有两个不相等实数根. …………… 3分 (2)解方程,得: 12x m=,23x =-. …………… 4分 ∵m 为整数,且方程的两个根均为负整数,∴1m =-或2m =-.∴1m =-或2m =-时, 此方程的两个根都为负整数. …………… 5分朝阳区20. 已知关于x 的一元二次方程0)1(2=+++k x k x .(1)求证:方程总有两个实数根;(2)若该方程有一个根是正数,求k 的取值范围.20. (1)证明:依题意,得k k 4)1(2-+=∆ …………………1分.)1(2-=k …………………………………2分∵0)1(2≥-k ,∴方程总有两个实数根. ………………………3分(2)解:由求根公式,得11-=x ,k x -=2. …………………………4分∵方程有一个根是正数,∴0>-k .∴0<k .………………………………5分燕山区21.已知关于x 的一元二次方程22(21)0x k x k k -+++=.(1)求证:方程有两个不相等的实数根;(2)当方程有一个根为1时,求k 的值.21.(1) 证明:因为[])(14)12(4222k k k ac b +⨯⨯-+-=- 01〉=所以有两个不等实根 …………3′..(2)当x=1 时,01)12(12=++⨯+-k k k 02=-k k ′1021==k k 或 ………5′门头沟区22. 已知关于x 的一元二次方程22410x x k ++-=有实数根.(1)求k 的取值范围;(2)若k 为正整数,且方程有两个非零的整数根,求k 的取值.22(本小题满分5分)解:(1)由题意得,168(1)0k ∆=--≥.………………………………………1分∴3k ≤. ………………………………………2分(2)∵k 为正整数,∴123k =,,.当1k =时,方程22410x x k ++-=有一个根为零;……………………3分当2k =时,方程22410x x k ++-=无整数根; ……………………4分当3k =时,方程22410x x k ++-=有两个非零的整数根.综上所述,1k =和2k =不合题意,舍去;3k =符合题意.……………5分大兴区20. 已知关于x 的一元二次方程01632=-+-k x x 有实数根,k 为负整数.(1)求k 的值;(2)如果这个方程有两个整数根,求出它的根.20.解:(1)根据题意,得Δ=(-6)2-4×3(1-k )≥0.解得2≥-k .……………………………………………………………1分∵k 为负整数,∴k =-1,-2.……………………………………… 2分(2)当1=-k 时,不符合题意,舍去; ………………………………… 3分当2=-k 时,符合题意,此时方程的根为121==x x .………… 5分平谷区20.关于x 的一元二次方程2210x x k ++-=有两个不相等的实数根.(1)求k 的取值范围;(2)当k 为正整数时,求此时方程的根.20.解:(1)∵关于x 的一元二次方程有两个不相等的实数根.∴()2Δ2410k =-->····················· 1 =8-4k >0.∴2k < (2)(2)∵k 为正整数,∴k =1. ··························· 3 解方程220x x +=,得120,2x x ==-. ············· 5 怀柔区20.已知关于x 的方程226990-+-=x mx m .(1)求证:此方程有两个不相等的实数根;(2)若此方程的两个根分别为x 1,x 2,其中x 1>x 2,若x 1=2x 2,求m 的值.20.(1)∵△=(-6m)2-4(9m 2-9) ……………………………………………………………………1分=36m 2-36m 2+36=36>0.∴方程有两个不相等的实数根……………………………………………………………2分(2)66332m x m ±===±.……………………………………………………3分 ∵3m+3>3m -3,∴x 1=3m+3,x 2=3m-3, …………………………………………………………………………4分 ∴3m+3=2(3m -3) .∴m=3. …………………………………………………………………………………………5分 延庆区20.已知:∠AOB 及边OB 上一点C .求作:∠OCD ,使得∠OCD=∠AOB .要求:1.尺规作图,保留作图痕迹,不写做法;(说明:作出一个..即可) 2.请你写出作图的依据.C B O A20. (1)作图(略) ……2分(2)到线段两端点距离相等的点在线段的垂直平分线上;垂直平分线上的点到线段两端点距离相等;等边对等角. ……5分顺义区20.已知关于x 的一元二次方程()21260x m x m --+-=.(1)求证:方程总有两个实数根;(2)若方程有一个根是负数,求m 的取值范围.20.(1)证明:∵()214(26)m m ⎡⎤∆=----⎣⎦221824m m m =-+-+21025m m =-+ ()25m =-≥0 …………………………………………………… 2分 ∴ 方程总有两个实数根. ………………………………………………… 3分(2)解:∵1(5)2m m x -±-==, ∴ 13x m =-,22x =. ……………………………………………… 4分 由已知得 30m -<.∴ 3m <. ………………………………………………………………… 5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计综合2018西城一模23.某同学所在年级的500名学生参加“志愿北京”活动,现有以下5个志愿服务项目:A.纪念馆志愿讲解员.B.书香社区图书整理.C.学编中国结及义卖.D.家风讲解员.E.校内志愿服务.要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示).B,E,B,A,E,C,C,C,B,B,A,C,E,D,B,A,B,E,C,A,D,D,B,B,C,C,A,A,E,B,C,B,D,C,A,C,C,A,C,E,整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图.选择各志愿服务项目的人数统计表分析数据、推断结论:a:抽样的40个样本数据(志愿服务项目的编号)的众数是__________.(填A E-的字母代号)b:请你任选A E-中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.2018石景山一模24.某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分):整理、分析过程如下,请补充完整.成绩x 学生70≤x≤7475≤x≤7980≤x≤8485≤x≤8990≤x≤9495≤x≤100甲乙 1 1 4 2 1 1学生极差平均数中位数众数方差甲83.7 86 13.21 乙24 83.7 82 46.21(3)若从甲、乙两人中选择一人参加知识竞赛,你会选(填“甲”或“乙),理由为.2018平谷一模23.为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析:甲91 89 77 86 71 31 97 93 72 9181 92 85 85 95 88 88 90 44 91 乙84 93 66 69 76 87 77 82 85 8890 88 67 88 91 96 68 97 59 88 整理、描述数据分析数据两组数据的平均数、中位数、众数、方差如下表:的值是.得出结论a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .b可以推断出学校学生的数学水平较高,理由为 . (至少从两个不同的角度说明推断的合理性)2018怀柔一模24.某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:排球 10 9.5 9.5 10 8 9 9.5 97 10 4 5.5 10 9.5 9.5 10篮球 9.5 9 8.5 8.5 10 9.5 10 86 9.5 10 9.5 9 8.5 9.5 6整理、描述数据按如下分数段整理、描述这两组样本数据:(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)分析数据两组样本数据的平均数、中位数、众数如下表所示:得出结论(1)如果全校有160人选择篮球项目,达到优秀的人数约为人;(2)初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.你同意的看法,理由为.(至少从两个不同的角度说明推断的合理性)2018海淀一模24. 某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.收集数据 调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);A .抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本B .抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本C .从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本 整理、描述数据 抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:77 83 80 64 86 90 75 92 83 81 85 86 88 62 65 86 97 96 82 73 86 84 89 86 92 73 57 77 87 82 91 81 86 71 53 72 90 76 68 78 整理数据,如下表所示:2018年九年级部分学生学生的体质健康测试成绩统计表分析数据、得出结论调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,分2017年九年级部分学生体质健康成绩直方图你能从中得到的结论是_____________,你的理由是__________________________.体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有________名同学参加此项目.2018朝阳一模24. 水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:甲 26 32 40 51 44 74 44 63 73 74 81 54 6241 33 54 43 34 51 63 64 73 64 54 33乙 27 35 46 55 48 36 47 68 82 48 57 66 7527 36 57 57 66 58 61 71 38 47 46 71整理、描述数据按如下分组整理、描述这两组样本数据(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据两组样本数据的平均数、众数和方差如下表所示:得出结论a.估计乙大棚产量优秀的秧苗数为株;b.可以推断出大棚的小西红柿秧苗品种更适应市场需求,理由为.(至少从两个不同的角度说明推断的合理性)2018东城一模24.随着高铁的建设,春运期间动车组发送旅客量越来越大.相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间铁路发送旅客量情况进行了调查,具体过程如下.(I)收集、整理数据请将表格补充完整:(II)描述数据为了更直观地显示春运期间动车组发送旅客量占比的变化趋势,需要用___________(填“折线图”或“扇形图”)进行描述;(III)分析数据、做出推测预计2019年春运期间动车组发送旅客量占比约为___________,你的预估理由是_________________________________________ .2018丰台一模24.第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.【收集数据】从甲、乙两校各随机抽取20名学生,在这次竞赛中他们的成绩如下:甲 30 60 60 70 60 80 30 90 100 6060 100 80 60 70 60 60 90 60 60乙 80 90 40 60 80 80 90 40 80 5080 70 70 70 70 60 80 50 80 80【整理、描述数据】按如下分数段整理、描述这两组样本数据:(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)【分析数据】两组样本数据的平均分、中位数、众数如下表所示:其中a【得出结论】(1)小明同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是________校的学生;(填“甲”或“乙”)(2)张老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为________;(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)2018房山一模24. 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.收集数据 17 18 16 12 24 15 27 25 18 1922 17 16 19 31 29 16 14 15 2515 31 23 17 15 15 27 27 16 19整理、描述数据分析数据样本数据的平均数、众数、中位数如下表所示:得出结论(1)如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为万元.(2)如果想确定一个较高的销售目标,这个目标可以定为每月万元,理由为.2018门头沟一模24.地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态坏境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:初一: 76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二: 74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74(1)根据上表中的数据,将下列表格补充完整;整理、描述数据:(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)分析数据:(2你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).24.甲乙两组各有10名学生,进行电脑汉字输入速度比赛,现将他们的成绩进行统计,过程如下:收集数据各组参赛学生每分钟输入汉字个数统计如下表:分析数据两组数据的众数、中位数、平均数、方差如下表所示:得出结论(1)若每分钟输入汉字个数136及以上为优秀,则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?(2)请你根据所学的统计知识,从不同角度评价甲、乙两组学生的比赛成绩(至少从两个角度进行评价).23.中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次 “汉字听写”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:90,92,81,82,78,95,86,88,72,66, 62,68,89,86,93,97,100,73,76,80, 77,81,86,89,82,85,71,68,74,98, 90,97,100,84,87,73,65,92,96,60.请根据所给信息,解答下列问题:(1)a = ,b = , c = ,d = ; (2)请补全频数分布直方图;(3)若成绩在90分以上(包括90分)的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?16142607*********4681012成绩x /分频数23. 体育教师为了解本校九年级女生“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试.获取数据如下:收集数据抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:38 46 42 52 55 43 59 46 25 3835 45 51 48 57 49 47 53 58 49整理、描述数据请你按如下分组整理、描述样本数据:(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)分析数据样本数据的平均数、中位数、众数如下表所示:得出结论①估计该校九年级女生在中考体育测试中仰卧起坐项目可以得到满分的人数为;②该中学所在区县的九年级女生在1分钟仰卧起坐总体测试成绩如下:请你结合该校样本测试成绩和该区县的总体测试成绩,对该校九年级女生的“仰卧起坐”达标情况做一下评估,并提出相应建议.2018燕山一模:日期4月1日4月2日4月3日4月4日4月5日4月6日步行数(步) 10672 4927 5543 6648步行距离(公里)6.8 3.1 3.4 4.3卡路里消耗(千卡)157 79 91 127燃烧脂肪(克)20 10 12 16(1)4月5日,4月6日,豆豆妈妈没来得及作记录,只有手机图片,请你根据图片数据,帮她补全表格.(2)豆豆利用自己学习的统计知识,把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来,请你根据图中提供的信息写出结论:.(写一条即可)步行距离燃烧脂肪101520525303025燃烧脂肪(千卡)2015104月1日-6日妈妈步行距离与燃烧脂肪情况统计图步行距离(公里)(3)豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系,豆豆妈妈想使自己的卡路里消耗数达到250千卡,预估她一天步行距离为__________公里.(直接写出结果,精确到个位)。
