四位加法器
四位加法器实验报告

四位加法器实验报告1.实验目的:掌握组合逻辑电路的基本分析与设计方法;理解半加器和全加器的工作原理并掌握利用全加器构成不同字长加法器的各种方法;学习元件例化的方式进行硬件电路设计;学会利用软件仿真实现对数字电路的逻辑功能进行验证和分析。
2.实验仪器:数字逻辑实验箱3.实验内容:A. 设计实现逐次进位加法器,进行软件仿真并在实验平台上测试。
B. 设计实现超前进位加法器,进行软件仿真并在实验平台上测试。
C.使用VHDL自带加法运算实现一个4位全加器。
4.实验代码:A. 逐次进位加法器:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity FDFA is#定义串行加法器总体接口port(A,B:in std_logic_vector(3 downto 0);Ci:in std_logic;S:out std_logic_vector(3 downto 0);Co:out std_logic);end entity;architecture struct of FDFA iscomponent fadder is#基于一位全加器port(a,b,ci:in std_logic;s,co:out std_logic);end component fadder;signal c0,c1,c2:std_logic;beginU0:fadder port map(A(0),B(0),Ci,S(0),c0);U1:fadder port map(A(1),B(1),c0,S(1),c1);U2:fadder port map(A(2),B(2),c1,S(2),c2);U3:fadder port map(A(3),B(3),c2,S(3),Co);end architecture struct;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity fadder is #定义一位全加器port(a,b,ci:in std_logic;s,co:out std_logic);end entity;architecture func of fadder isbeginco<=(a and b) or (ci and ( a xor b));s<=a xor b xor ci;end architecture func;B. 超前进位加法器:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity LAC is#定义超前进位加法器总体接口port(A,B:in std_logic_vector(3 downto 0);Ci:in std_logic;Co:out std_logic;S:out std_logic_vector(3 downto 0));end entity;architecture struct of LAC issignal wirep, wireg:std_logic_vector(3 downto 0);signal wirec:std_logic_vector(2 downto 0);component fadder is#基于一位全加器port(Ai,Bi:in std_logic;c:in std_logic;si:out std_logic;pi:out std_logic;gi:out std_logic);end component fadder;component Ker is#Ker总理进位传递信号P与进位产生信号G,以及进位信号C port(ci:in std_logic;P:in std_logic_vector(3 downto 0);G:in std_logic_vector(3 downto 0);C:out std_logic_vector(3 downto 0));end component Ker;beginU0:fadder port map(Ai=>A(0),Bi=>B(0),c=>Ci,si=>S(0),pi=>wirep(0),gi=>wireg(0));U1:fadder port map(Ai=>A(1),Bi=>B(1),c=>wirec(0),si=>S(1),pi=>wirep(1),gi=>wireg(1));U2:fadder port map(Ai=>A(2),Bi=>B(2),c=>wirec(1),si=>S(2),pi=>wirep(2),gi=>wireg(2));U3:fadder port map(Ai=>A(3),Bi=>B(3),c=>wirec(2),si=>S(3),pi=>wirep(3),gi=>wireg(3));L:Ker port map(ci=>Ci,P(0)=>wirep(0),P(1)=>wirep(1),P(2)=>wirep(2),P(3)=>wirep(3),G(0)=>wireg(0),G(1)=>wireg(1),G(2)=>w ireg(2),G(3)=>wireg(3),C(0)=>wirec(0),C(1)=>wirec(1),C(2)=>wirec(2),C(3)=>Co);end architecture struct;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity fadder is #定义一位全加器port(Ai,Bi:in std_logic;c:in std_logic;si:out std_logic;pi:out std_logic;gi:out std_logic);end entity;architecture func of fadder isbeginpi<=Ai xor Bi;gi<=Ai and Bi;si<=Ai xor Bi xor c;end architecture func;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity Ker is#定义Ker port(ci:in std_logic;P:in std_logic_vector(3 downto 0);G:in std_logic_vector(3 downto 0);C:out std_logic_vector(3 downto 0));architecture func of Ker isbeginC(0)<=G(0) or ( P(0) and ci );C(1)<=G(1) or ( P(1) and G(0) ) or ( P(1) and P(0) and ci );C(2)<=G(2) or ( P(2) and G(1) ) or ( P(2) and P(1) and G(0) ) or ( P(2) and P(1) and P(0) and ci );C(3)<=G(3) or ( P(3) and G(2) ) or ( P(3) and P(2) and G(1) ) or ( P(3) and P(2) and P(1) and G(0) ) or ( P(3) and P(2) and P(1) and P(0) and ci );end architecture func;C. VHDL自带加法运算实现4位全加器:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity VHDLAD is#定义VHDL自带加法运算实现4位全加器总体接口,如果加和比原来和少,则会进位port(A,B:in std_logic_vector(3 downto 0);Ci:in std_logic;Co:out std_logic;S:out std_logic_vector(3 downto 0));end VHDLAD;architecture bhv of VHDLAD issignal D:std_logic_vector(3 downto 0);beginprocess(A,B,Ci,D)beginD <= A + B;if(Ci = '1') thenD <= D + 1;end if;if(D >= A) thenS <= D;Co <= '0';elseS <= D;Co <= '1';end if;end process;end bhv;5.软件仿真结果说明下面图片每幅有14条信号线,从上到下依次为A的低位到高位(共4条)、B的低位到高位(共4条)、输入的进位信号、和的低位到高位(共4条)、输出进位信号。
4位加法器的设计原理

4位加法器的设计原理四位加法器是一种数字电路,用于实现四位二进制数的加法运算。
它由多个逻辑门组成,主要包括四个全加器、一个四路二选一选择器和一个四位二进制数输出。
在四位加法器中,每个全加器都负责计算两个输入位和上一位的进位的和。
全加器的原理是采用异或门(XOR)、与门(AND)和或门(OR)的组合。
具体来说,全加器有三个输入端,分别是两个输入位(A和B)和上一位的进位(Cin),两个输出端,分别是当前位的和(S)和当前位的进位(Cout)。
全加器的计算公式如下:S = (A XOR B) XOR CinCout = AB + (A XOR B)Cin其中,“XOR”代表异或操作,“AND”代表与操作,“OR”代表或操作。
全加器的设计原理是基于四位二进制数的加法运算规则。
在四位加法过程中,每一位的和由该位的两个输入位和上一位的进位确定。
进位则与上一位的输入位和上一位的进位有关。
因此,通过级联四个全加器,就可以实现四位加法运算。
除了四个全加器以外,四位加法器还包括一个四路二选一选择器。
这个选择器根据一个控制信号选择输出。
四位加法器的输出是一个四位二进制数,可以选择以原码、反码或补码的形式输出。
通过选择器的控制信号,可以选择输出形式。
四位加法器的工作原理是:首先,将四个输入数两两相加,得到每一位的和,以及进位。
然后,将每一位的和通过四个全加器计算得到最终的和,同时将进位以及控制信号传递给选择器。
最后,选择器选择要输出的结果。
总结来说,四位加法器是基于全加器的构建的数字电路,可以实现四位二进制数的加法运算。
它的设计原理是根据四位二进制数加法的规则和全加器的计算公式,通过级联四个全加器,并通过选择器控制输出形式,实现四位二进制数的加法运算。
4位加法器实验报告

硬件描述语言实验题目:四位全加器学院数学与计算机学院学科门类xxxxxxxxxx专业xxxxxxxxxx学号姓名x指导教师xxxx20xx年x 月xx日1、实验目的:练习VHDL语言设计工程的建立与仿真的步骤和方法、熟悉VHDL语言行为描述的编写方法。
2、实验环境:PC个人计算机、Windows XP操作系统、Quartus II集成开发环境软件。
3、实验要求:设计一个四位加法器,其引脚及其功能如下表。
4、实验步骤:(1)用RTL描述方式描述4位加法器①RTL描述方式是一种明确规定寄存器描述的方法,它要求在描述时要么采用寄存器硬件的一一对应的直接描述,要么采用寄存器之间的功能描述。
RTL描述方式可以进行逻辑综合,这是其他描述方式所不具备的特点。
②编辑代码这种描述方法详细描述了加法器的计算过程,即写出了每一位的计算和进位方法。
模块内部(构造体说明部分)需要定义三个连接线,定义语句为:signal c0,c1,c2 : std_logic代码如下:library ieee;use ieee.std_logic_1164.all;entity adder4 isport(a,b:in std_logic_vector(3 downto 0);ci:in std_logic;s:out std_logic_vector(3 downto 0);co:out std_logic);end entity;architecture rtl of adder4 issignal c0,c1,c2:std_logic;s(0) <= a (0) xor b(0) xor ci;c0<= (a(0) and b(0)) or (a(0) and ci) or (b(0) and ci);s(1) <= a (1) xor b(1) xor c0;c1<= (a(1) and b(1)) or (a(1) and c0) or (b(1) and c0);s(2) <= a (2) xor b(2) xor c1;c2<= (a(2) and b(2)) or (a(2) and c1) or (b(2) and c1);s(3) <= a (3) xor b(3) xor c2;co<= (a(3) and b(3)) or (a(3) and c2) or (b(3) and c2);end architecture rtl;③仿真结果(2)用行为描述方式描述4位加法器①行为描述是对系统数学模型的描述,其抽象程度比寄存器传输描述方式和结构描述方式更高。
四位超前进位加法器原理

四位超前进位加法器原理1. 输入部分:四位超前进位加法器有两个四位输入数和一个进位输入。
输入数A和B分别代表被加数和加数,每位由低位到高位分别为A0,A1,A2,A3和B0,B1,B2,B3、进位输入Cin表示上一位的进位情况。
2. 输出部分:四位超前进位加法器有一个四位输出数和一个进位输出。
输出数S代表和,每位由低位到高位分别为S0,S1,S2,S3、进位输出Cout表示本位的进位情况。
3. 逻辑运算:每位的和采用异或门(XOR)实现:Si = A ⊕ B ⊕ Cin。
每位的进位采用与门(AND)实现:Ci+1 = (A ⊕ B) ∧ Cin + A∧ B。
4. 进位传递:如果上一位的进位Cin为1,则本位需要传递进位,即Ci+1 = 1、如果上一位的进位Cin为0,则本位不需要传递进位,即Ci+1 = (A ⊕ B) ∧ Cin。
这样可以确保进位在高位传递,实现加法运算的正确性。
5. 进位溢出:最高位的进位输出Cout表示四位相加是否产生进位溢出,即Cout = A3 ∧ B3 ∧ Cin。
如果Cout为1,则表示加法运算的结果超过了四位二进制数的表示范围,发生了进位溢出。
(1)将输入的两个四位二进制数A和B依次与进位输入Cin相异或,得到每位的和Si。
(2)将输入的两个四位二进制数A和B依次与进位输入Cin相与,得到进位传递结果Di。
(3)将邻位的进位传递结果Di与当前位的和Si再次相与,得到进位输出结果Ci+1(4)将当前位的和Si输出为结果的相应位,将进位输出结果Ci+1作为下一位的进位输入。
(5)最高位的进位输出结果Cout表示加法运算是否产生进位溢出。
四位超前进位加法器的优点是速度快,可以实现高速的加法运算。
其核心原理是采用异或门进行和的计算,采用与门进行进位的计算,通过逐位运算,实现了四位二进制数的加法运算,同时处理了进位情况,确保了运算的正确性。
四位加法器
四位加法器一、实验要求掌握组合逻辑电路的基本分析和设计方法;理解半加器和全加器的工作原理,用硬件描述语言实现半加器和全加器的门级设计,并使用自己设计的半加器组件构建全加器;学会利用软件仿真和远程实验系统实现对数字电路的逻辑功能进行验证和分析。
二、实验原理半加器(Half Adder)是不考虑来自低位的进位信号,其输入为 1 bit 的被加数和加数,输出为两位:本位的和以及向高一位的进位。
考虑低位进位的1位二进制加法器称为全加器(Full Adder),其输入为被加数加数以及低一位来的进位,输出为本位的和及向高一位的进位。
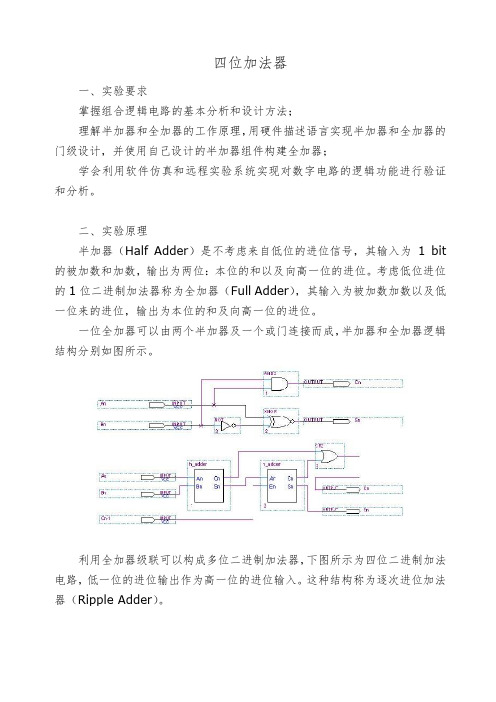
一位全加器可以由两个半加器及一个或门连接而成,半加器和全加器逻辑结构分别如图所示。
利用全加器级联可以构成多位二进制加法器,下图所示为四位二进制加法电路,低一位的进位输出作为高一位的进位输入。
这种结构称为逐次进位加法器(Ripple Adder)。
由于逐次进位加法器的进位信号是在各级间逐级传递的,所以高位的输出必须等低位的进位输入稳定后才有效,这就使得逐次进位加法器的延时比较大,速度比较慢。
为了提高加法器的运算速度,需要对加法器的结构进行改进。
引入进位传递信号和进位产生信号的概念,有{P n=A n⊕B n G n=A n B n利用这两个信号,可以把和信号与进位输出信号表示为{S n=P n⊕C n−1 C n=P n C n−1+G n根据上面给出的进位输出表达式,可得C0=G0+ P0C−1C1=G1+ P1C0=G1+ P1G0+P1P0C−1C2=G2+ P2C1=G2+ P2G1+P2P1G0+ P2P1P0C−1C3=G3+ P3C2=G3+ P3G2+P3P2G1+ P3P2P1G0+ P3P2P1P0C−1由于各级的进位传递信号和进位产生信号是同时生成的,所以各级的进位输出信号不再需要等待低一位的进位输入信号,从而大大减小了整个电路的延时,提高的加法器的运算速度。
四位加法器实验报告

四位加法器实验报告四位加法器实验报告一、引言在数字电路的学习中,加法器是一个非常重要的基础电路。
本次实验旨在通过设计和实现四位加法器,加深对数字电路原理的理解,并掌握加法器的设计方法和实现过程。
二、实验目的1. 理解加法器的原理和工作方式;2. 掌握加法器的设计方法和实现过程;3. 学会使用逻辑门电路和触发器构建加法器;4. 验证加法器的正确性和稳定性。
三、实验原理1. 半加器半加器是最基本的加法器,用于实现两个一位二进制数的相加。
其逻辑电路如下:(插入半加器电路图)2. 全加器全加器是由两个半加器和一个或门构成,用于实现三个一位二进制数的相加。
其逻辑电路如下:(插入全加器电路图)3. 四位加法器四位加法器是由四个全加器和一些其他逻辑门组成,用于实现四个四位二进制数的相加。
其逻辑电路如下:(插入四位加法器电路图)四、实验步骤1. 按照电路图连接逻辑门和触发器,搭建四位加法器电路;2. 使用开关设置输入数据,观察输出结果;3. 验证加法器的正确性,将不同的输入数据相加,并手动计算结果进行对比;4. 测试加法器的稳定性,观察输出结果是否随着时间稳定。
五、实验结果与分析通过实验,我们成功搭建了四位加法器电路,并进行了多组数据的测试。
实验结果表明,加法器能够正确地进行四个四位二进制数的相加,并输出正确的结果。
同时,实验中观察到输出结果在一段时间后稳定下来,验证了加法器的稳定性。
六、实验总结本次实验通过设计和实现四位加法器,加深了对数字电路原理的理解,并掌握了加法器的设计方法和实现过程。
通过实验验证了加法器的正确性和稳定性,提高了实际操作能力和解决问题的能力。
同时,实验中还发现了一些问题,比如电路连接错误、输入数据设置错误等,这些问题在实验中及时发现和解决,也对实验结果的准确性起到了保障作用。
在今后的学习中,我们将进一步深入研究数字电路的原理和应用,不断提高自己的实验技能和创新能力。
希望通过这次实验,能够为我们的学习和未来的工作打下坚实的基础。
4位快速加法器设计故障与调试

4位快速加法器设计故障与调试4位快速加法器设计故障与调试引言:在数字电路设计中,快速加法器是一个非常重要的组件。
它用于将两个二进制数相加,并输出其结果。
然而,在设计和实现过程中,可能会遇到一些故障或错误。
本文将介绍4位快速加法器的设计故障和调试方法。
一、4位快速加法器的基本原理1.1 二进制加法的基本概念二进制加法是指将两个二进制数相加,并按照二进制规则进行进位和求和。
当两个二进制数A=1101和B=1010相加时,其结果为C=10111。
1.2 4位快速加法器的结构4位快速加法器由四个全加器组成,每个全加器负责计算一对输入位的和以及前一位的进位。
四个全加器按照级联方式连接起来,形成一个完整的4位快速加法器。
二、常见故障与解决方法2.1 电路连接错误在设计和实现过程中,可能会出现电路连接错误导致功能无法正常工作。
这种情况下,需要检查电路连接是否正确,并进行修正。
2.2 逻辑门选择错误在选择逻辑门时,可能会选错门类型或门数量不足,导致电路无法正确计算和输出结果。
解决方法是仔细检查逻辑门的选择,并根据需要增加或更换逻辑门。
2.3 信号线延迟问题在数字电路中,信号线延迟是一个常见的问题。
当信号传输的时间超过了设计所允许的范围时,可能会导致计算结果出错。
解决方法是通过添加缓冲器或调整信号线长度来解决延迟问题。
2.4 电源供应不稳定电源供应不稳定可能导致电路工作不正常或产生噪声干扰。
为了解决这个问题,可以使用稳压器来提供稳定的电源,并添加滤波器以降低噪声干扰。
三、调试方法3.1 逐级验证在进行调试时,可以使用逐级验证的方法。
首先验证单个全加器的功能是否正常,然后再将多个全加器级联起来进行整体验证。
3.2 输入输出检查通过检查输入和输出信号是否符合预期结果,可以确定是否存在故障。
如果输入和输出不匹配,则需要检查逻辑门连接、输入数据和控制信号等方面是否有错误。
3.3 示波器测量使用示波器可以观察信号的波形和时序,从而帮助定位故障。
层次化4位加法器设计 VHDL

课程设计说明书学院专业题目学号姓名同组人员报告完成日期成绩指导教师实验一层次化4位加法器设计一.实验目的1、掌握用 VHDL 设计全加器的方法并实现。
2、熟悉设计平台及VHDL层次化设计。
二.实验仪器1、硬件:计算机Gxsoc/sops-Dev-LabCycloneII EP2C35F672C8 核心板2、软件:正版Quartus8.0三.实验设计要求学习用VHDL或原理图设计方法,掌握全加器的设计方式及表示方式,极其与二进制表示的转换方法,完成编译、综合、适配、仿真和实验箱上的硬件测试,通过数码管观察结果。
采用层次化方法实现4位加法器,完成编译,仿真,引脚锁定,下载。
四.实验原理通过动态扫描两组4BIT的二进制数据,同时还有一个单BIT 的进位,把三者按照二进制加法原理进行加,求出和及进位,并通过电路显示出各部分数据(输入,输出)。
加数、被加数、“和”显示在共阳数码管上,进位输出显示在LED上。
五.程序代码1、半加器Hadder代码LIBRARY Ieee;USE Ieee.Std_Logic_1164.all;ENTITY HADDER ISPort (a,b: In Bit;Co, So: Out Bit);END HADDER;ARCHITECTURE fh1 Of HADDER Is BEGINSo <= (a Xor b);Co <= (a And b);END fh1;2、或门ora代码LIBRARY Ieee;USE Ieee.Std_Logic_1164.all;ENTITY ora ISPort ( a: in Std_Logic;b: in Std_Logic;c: out Std_Logic);END ora;ARCHITECTURE org OF ora ISBEGINc <= a Or b;END org;3、1位全加器f_hadder代码LIBRARY Ieee;USE Ieee.Std_Logic_1164.all;ENTITY f_ADDER ISPort (x: In Std_Logic;y: In Std_Logic;cin: In Std_Logic;cout: Out Std_Logic;sum: Out Std_Logic);END f_ADDER;ARCHITECTURE fd1 Of f_ADDER Is Component HADDERPort( a,b: In Std_Logic;co,so: Out Std_Logic);END Component;Component oraPort(a,b: In Std_Logic;c: Out Std_Logic);END Component;Signal d,e,f: Std_Logic;BeginU1: HADDERPort Map(a=>X,b=>Y,Co=>d,so=>e);U2:HADDERPort Map(a=>e,b=>cin,Co=>f,so=>sum);U3:ora Port Map(a=>d,b=>f,c=>cout);END ARCHITECTURE fd1;4、4位全加器Qadd:Library ieee;Use ieee.std_logic_1164.all;Entity Qadd isPort (a:in std_logic_VECTOR(3 DOWNTO 0);b:in std_logic_VECTOR(3 DOWNTO 0);--cin:in std_logic;s:out std_logic_VECTOR(3 DOWNTO 0)); End Qadd;Architecture one of Qadd isSignal c0,c1,c2,c3 : std_logic;Component f_ADDERPort (x: In Std_Logic;y: In Std_Logic;cin: In Std_Logic;cout: Out Std_Logic;sum: Out Std_Logic);END Component;Beginu1 :F_ADDERPort map(sum=>s(0),cout=>c0,X=>a(0),Y=>b(0),cin=>'0');u2 :F_ADDERPort map(sum=>s(1),cout=>c1,X=>a(1),Y=>b(1),cin=>c0 );u3 : F_ADDERPort map(sum=>s(2),cout=>c2,X=>a(2),Y=>b(2),cin=>c1 );u4 : F_ADDERPort map(sum=>s(3),cout=>c3,X=>a(3),Y=>b(3),cin=>c2 ); END;六.仿真结果程序代码进行编译后,建立waveform文件,设定输入输出端口进行仿真,仿真结果如图1-1所示。
4位并行加法器代码

4位并行加法器代码摘要:1.4 位并行加法器的概念和原理2.4 位并行加法器的实现方法3.4 位并行加法器的应用场景正文:一、4 位并行加法器的概念和原理4 位并行加法器是一种能够同时对四个二进制数进行加法运算的电路。
在计算机系统中,数据的传输和处理通常是以二进制形式进行的。
为了提高运算速度,需要采用并行加法器,使其在同一时钟周期内完成多个二进制数的加法运算。
4 位并行加法器正是为了满足这一需求而设计的。
二、4 位并行加法器的实现方法1.采用全加器实现全加器(Full Adder)是一种能够对两个二进制数进行加法运算的电路。
通过多个全加器的级联,可以实现对多个二进制数的加法运算。
例如,实现一个4 位并行加法器,需要4 个全加器级联。
输入数据为4 个二进制数A、B、C、D,输出结果为S、C0、C1。
2.采用数据选择器实现数据选择器(Data Selector)是一种能够根据控制信号选择输入数据输出的电路。
通过使用数据选择器,可以实现对多个二进制数的加法运算。
例如,实现一个4 位并行加法器,需要4 个数据选择器级联。
输入数据为4 个二进制数A、B、C、D,输出结果为S、C0、C1。
三、4 位并行加法器的应用场景1.数据处理在数据处理系统中,例如计算机、手机等设备,4 位并行加法器可用于加速数据的加法运算,提高数据处理速度。
2.图像处理在图像处理领域,例如模式识别、图像增强等应用,4 位并行加法器可以用于加速图像的像素级加法运算,提高图像处理效果。
3.通信系统在通信系统中,例如调制解调器、信道编解码等应用,4 位并行加法器可以用于加速信号的加法运算,提高通信系统的性能。
综上所述,4 位并行加法器在多个领域具有广泛的应用前景。
4位全加器实验报告

4位全加器实验报告篇一:四位全加器实验报告实验一:四位全加器实验报告实验日期:学生姓名:陆小辉(学号:25)指导老师:黄秋萍加法器是数字系统中的基本逻辑器件,是构成算数运算电路的基本单元。
1位加法器有全加器和半加器两种。
多位加法器构成方式有并行进位方式和串行进位方式。
并行进位加法器设有并行进位产生逻辑,运算速度较快;串行进位加法器是将全加器级联构成多位加法器。
并行进位加法器通常比串行进位加法器占用更多的资源,随着位数的增多,相同位数的并行进位加法器比串行进位加法器的资源占用差距快速增大。
因此,在工程中使用加法器时,要在速度与容量之间寻求平衡。
一、设计要求:设计四位全加器,完成相应的功能。
可采用并行进位方式和串行进位方式,可采用三种常用建模方式中的任意一种。
三、测试代码如(转载自:小草范文网:4位全加器实验报告)下: module text_fulladd4; 二、设计代码如下:(此处采用数据流建模)wire [3:0]sum; module fulladd4(sum,cout,a,b,cin); wire cout; output [3:0]sum; reg [3:0]a,b; output cout; reg cin; input [3:0]a,b; fulladd4 f1(sum,cout,a,b,cin);input cin; initial assign {cout,sum}=a+b+cin; begin endmodule a=4'b0; b=4'b0; cin=1'b0; #210 $stop; end always #10 a=a+1; always #5 b=b+1; always #100 cin=cin+1;endmodule 四、仿真波形如下:续图篇二:4位全加器实验报告数电第一次实验通信1402 程杰 UXX13468【实验目的】采用ISE集成开发环境,利用verilog硬件描述语言中行为描述模式、结构描述模式或数据流描述模式设计四进制全加器。
4位加法器

可编程逻辑器件应用技术实验报告册主编魏欣班级:11041T学号:11011P02姓名:蔡丹设计工作任务书任务 名 称 4位加法器的设计任务编号CPLDSJ-3任 务 要 求按设计要求完成所有设计内容,并撰写设计报告。
设 计 设 备CPLD 实验平台 (1套) 数字万用表 (1只) 计算机 (1台)设 计 电 路一个4位加法器可以由2个1位全加器和1个1位半加器构成,加法器间的进位可以串行方式实现。
一、 四位加法器电路设计程序一、先完成半加器和全加器的设计,包括原理图输入、编译、综合、适配、仿真、实验板上的硬件测试,并将此半加器和全加器电路设置成一个硬件符号入库。
1、一位半加器电路图2、一位全加器电路图二、建立一个更高的原理图设计层次,利用以上获得的半加器和全加器构成4位全加器,并完成编译、综合、适配、仿真和硬件测试。
三、利用VHDL语言层次调用重新将4位全加器设计一遍。
1、半加器VHDL语言2、全加器VHDL语言Library ieee;Use ieee.std_logic_1164.all;Entity adder_f isPort (a2,b2,cin:in std_logic;s2,co2:out std_logic);End adder_f;Architecture full of adder_f isBeginProcess(a2,b2,cin)Begins2<=((not a2)and(not b2)and(cin)) or ((not a2)and(b2)and(not cin)) or ((a2)and(not b2)and(not cin)) or ((a2)and(b2)and(cin));co2<=((a2)and(b2)) or ((b2)and(cin)) or ((a2)and(cin));End process;End full;波形3、四位全加器的VHDL设计语言波形结论与体会通过本课程设计,自己学会了很多,以前只是完全按照书上的模式来连接电路图,现在学会。
4位快速加法器原理

4位快速加法器原理四位快速加法器是一种广泛应用于现代数字电路的基本运算模块,它可以实现对两个4位二进制数或小于4位的二进制数进行快速的加法运算。
其工作原理基于基本的逻辑门电路,包括与门、或门、非门等。
四位快速加法器由两个主要部分构成:输入部分和计算部分。
输入部分接受两个4位二进制数作为输入,其中每个二进制数按照从最低位到最高位的顺序作为输入。
计算部分执行快速加法运算,并产生输出结果。
在计算部分,首先将两个输入数的最低位输入到全加器中进行加法运算。
全加器是由一个与门、两个异或门和一个或门组成的电路。
该电路的输出结果为两个输入位和进位位的和,以及进位位的进位结果。
当进行两个二进制数的最低位的相加时,进位位的值默认为0。
然后将下一个输入位和前面的进位结果在全加器中相加,以便实现接续的进位运算。
这个过程将重复进行,直到最高位相加完成。
最终输出的结果为一个4位二进制数。
如果最高位相加的结果产生进位,则输出的结果中也会包含一个进位位。
四位快速加法器的工作原理简单直接,在现代数字电路应用中非常常见。
它可以通过级联多个四位快速加法器来实现更大数的快速相加运算。
这种级联的实现方式被称为位数扩展加法器。
例如,将两个8位二进制数相加,则可以通过级联两个四位快速加法器来实现。
在此基础上,通过不断级联可以实现更大数的加法运算。
总之,四位快速加法器是现代数字电路中非常重要的基本运算模块,可以实现快速、高效的二进制数相加运算。
其工作原理基于全加器电路,通过输入和计算两个主要部分来实现。
同时,四位快速加法器可以通过级联多个加法器实现更大数的快速加法运算。
四位并行加法器设计

四位并行加法器设计四位并行加法器是一种电子设计电路,可以执行四位二进制数的并行加法操作。
它由多个逻辑门和加法器组成,可以通过并行的方式同时对四位数进行加法计算,提高了计算速度。
本文将详细介绍四位并行加法器的设计原理和实现方法。
首先,我们需要了解二进制加法的原理。
在数字电路中,二进制加法器是一种能够对两个二进制数字进行相加运算的电路。
它的输入包括两个二进制数字和一个进位输入,输出是一个和结果和一个进位输出。
对于四位加法器来说,需要使用四个单独的加法器来执行每一位的加法运算。
每个加法器都有两个输入位和一个进位输入,以及一个和结果和一个进位输出。
这四个加法器可以并行地执行四位加法运算,从而提高计算速度。
接下来,我们将设计一个四位并行加法器的电路。
首先,我们需要一个四位完全加器。
一个四位完全加器可以由四个单独的全加器组成。
一个全加器是一种能够完成两个输入位和一个进位输入位的加法运算的电路。
它的输出包括一个和结果和一个进位输出。
为了实现四位并行加法器,我们可以将四个全加器按照并行的方式连接在一起,使得每个全加器的输入位和进位输入位都与相应的输入连接。
其中,第一个全加器的进位输入为0,其他三个全加器的进位输入位分别与前一个全加器的进位输出位相连。
这样,我们就可以实现四位加法运算。
在实际设计中,我们可以使用逻辑门和触发器来搭建完整的四位并行加法器电路。
首先,我们将使用逻辑门来实现全加器。
全加器的实现可以使用两个异或门、一个与门和一个或门来构建。
异或门用于计算两个输入位的和结果,与门用于计算两个输入位和进位输入位的交集,或门用于计算和结果的并集。
通过组合这些逻辑门,我们就可以构建一个完整的全加器。
接下来,我们将使用四个全加器和一些额外的逻辑门和触发器来构建四位并行加法器。
我们可以使用一个四输入的或门来进行四个全加器的和结果的合并。
为了实现进位输入位的传递,我们可以使用多级的触发器来实现。
具体的电路设计取决于具体的需求和实现方式。
4位快速加法器原理

4位快速加法器原理四位快速加法器是指用于执行四位数加法运算的电路。
其原理可以分为如下几个步骤:1. 位相加器(Half Adder):该电路用于执行两个二进制位相加操作。
对于输入的两个二进制位A和B,位相加器会通过异或门(XOR gate)得到它们的和S,然后通过与门(AND gate)得到它们的进位C。
比如当A为0,B为1时,S为1,C为0;当A为1,B为1时,S为0,C为12. 全加器(Full Adder):当执行三个二进制位相加操作时,需要使用全加器电路。
全加器会接受两个输入位与进位位(Cin),然后通过两个位相加器得到两个中间结果(Sn)和进位位(Cout)。
其中第一个位相加器用于计算Cin和A的和(S1),第二个位相加器用于计算S1和B的和(S2),最终结果S2和两个位相加器的进位结果相加得到最终结果Sn。
3. 四位加法器:四位加法器是由四个全加器串联而成的电路。
每个全加器都接收两个输入位和一个进位位,并生成一个输出位和一个进位位。
第一个全加器接收A0、B0和Cin,并生成S0和C1、第二个全加器接收A1、B1和C1,并生成S1和C2、第三个全加器接收A2、B2和C2,并生成S2和C3、最后一个全加器接收A3、B3和C3,并生成S3和Cout。
4. 进位传递加法器(Carry Lookahead Adder):进位传递加法器是一种优化的四位加法器电路,它通过预先计算进位位的传递情况,可以更快速地得到结果。
进位传递加法器由两个部分组成:进位生成部分和进位传递部分。
进位生成部分用于计算每一位的进位结果,进位传递部分用于计算每一位进位位的传递情况。
通过计算进位生成部分和进位传递部分的结果可以得到最终结果。
总结起来,四位快速加法器通过使用位相加器、全加器以及进位传递加法器等电路模块,实现了高效的四位加法运算。
通过预先计算进位位的传递情况,提高了加法运算的速度。
这种加法器广泛应用于计算机硬件中,可以快速进行多位数的加法运算。
4位快速加法器设计原理

4位快速加法器设计原理快速加法器是一种计算器件,可以快速地对两个二进制数进行加法运算。
相对于一般的加法器,它具有更高的速度和效率。
本文主要介绍4位快速加法器的设计原理。
1.基本概念在二进制加法中,加法器通过对两个二进制数分别进行逐位相加的方法,得到它们的和。
二进制加法的基本规则如下:0+0=0;1+0=1;0+1=1;1+1=0(进位1)。
在四位二进制数的加法中,每位相加可以得到一个位和进位两位。
4位快速加法器在计算时需要考虑到位和进位两个方面。
2.快速加法器的组成4位快速加法器可以由4个1位全加器和1个2位全加器组成。
1位全加器的输出等于输入A、B和进位C的和。
输出S等于(A xor B) xor C,进位C 等于AB+C(A xor B)。
2位全加器是由两个1位全加器和一个2选1选择器组成。
输入A和B分别与这两个全加器相连,进位C输入到这两个全加器的进位端。
选择器的选择信号是两个输入和上一个全加器的进位,选择器的输出连接到2位全加器的进位输出。
3.原理图4位快速加法器的原理图如下所示:每个1位全加器都由具有相同运算功能的逻辑门电路组成。
在1位全加器中,输入A、B和进位C分别与XOR、AND和OR门相连,这些门的输出再次进行逻辑运算得到输出S和新的进位C。
2位全加器由两个1位全加器和一个2选1选择器组成。
选择器的选择信号是上一个1位全加器的进位和两个输入的和。
这两个1位全加器的进位输出也分别与这个选择器相连。
4.流程图4位快速加法器的计算流程图如下所示:将输入的两个4位二进制数的第0位分别输入到1位全加器1和2中。
这两个全加器的进位C0均为0,得到第0位的位和(S0)和进位(C1)。
然后,将输入的两个4位二进制数的第1位分别输入到1位全加器3和4中。
全加器3的进位C1为1,因为它是在第0位加法器的进位C1的基础上进行的。
全加器4的进位C2为全加器3的进位C2与两个输入的和的2选1选择器输出的结果。
FPGA四位加法器实验报告

题目:含异步清0和同步使能的4位加法计数器一. 实验目的.学习时序电路的设计、仿真和硬件测试,进一步熟悉VHDL技术。
二.实验原理.如图是一含计数使能、异步复位和计数值并行预置功能4位加法计数器,4位锁存器;rst是异步清0信号,高电平有效;clk是锁存信号;D[3..0]是4位数据输入端。
ENA是使能信号,当ENA为'1'时,多路选择器将加1器的输出值加载于锁存器的数据端;当ENA为'0'时将"0000"加载于锁存器。
三.实验内容.设计一个含异步清0和同步使能的4位加法计数器;实现对输入时钟(clk)的计数。
任务分析:在RST=1,ENA=1时,系统对输入时钟进行计数,所计数值输出至OUTY(3 DOWNTO 0),当计数满15时,产生一个进位,输出至COUT,同时OUTY溢出归零;如果RST=1,ENA=0时,保持原来的计数值不变。
如果RST=0,置输出信号为0;1)异步复位,则输入信号有复位信号RST2)同步使能, 则输入信号有使能信号ENA3)要求同步的时序,则输入信号有时钟CLK在QuartusII上对下列程序进行编辑、编译、综合、适配、仿真。
module CNT4B(CLK,RST,ENA,CLK_1,RST_1,ENA_1,OUTY,COUT);input CLK,RST,ENA;output CLK_1,RST_1,ENA_1;output[3:0] OUTY;output COUT;reg[3:0] OUTY;reg COUT;wire CLK_1; wire RST_1; wire ENA_1;assign CLK_1 = CLK; assign RST_1 = RST; assign ENA_1 = ENA;always@(posedge CLK or negedge RST)begin if(!RST)begin OUTY<=4'b0000;COUT<=1'b0; endelse if(ENA)Begin OUTY<=OUTY+1;COUT<=OUTY[0] & OUTY[1] & OUTY[2] & OUTY[3]; end end endmodule四.实验步骤.1.在QUARTUSII软件下创建一工程,工程名为CNT4B,芯片名为EP2C35F672C6;2.新建Verilog语言文件,输入以上Verilog语言源程序,并将程序命名为CNT4B.vhd,保存在与工程相同的文件夹中;3.进行功能仿真、全编译、时序仿真,如出现错误请按照错误提示进行修改,保证设计的正确性。
四位加法器实验报告

四位加法器实验报告四位加法器实验报告引言:在现代科技高速发展的时代,计算机已经成为人们生活中不可或缺的一部分。
而计算机的核心部件之一就是加法器。
加法器是计算机中用于实现加法运算的电子电路,其功能是将两个二进制数相加并输出结果。
本实验旨在通过搭建四位加法器电路,深入了解加法器的工作原理和实现方式。
一、实验目的通过本实验,我们的目的是掌握四位加法器的原理和工作方式,了解二进制数的加法运算规则,并通过实际搭建电路进行验证。
二、实验材料1. 电路板2. 电子元件:电阻、电容、晶体管等3. 电源线、导线4. 示波器、万用表等实验仪器三、实验步骤1. 搭建四位加法器电路根据实验原理,我们需要使用多个晶体管、电阻和电容等元件来搭建四位加法器电路。
首先,将电路板连接好电源线和导线,并按照电路图的要求依次连接各个元件。
确保连接正确无误后,进行下一步操作。
2. 进行加法运算在搭建好四位加法器电路后,我们可以通过输入两个二进制数并观察输出结果来进行加法运算。
将需要相加的两个二进制数输入到电路中,然后观察输出端的显示结果。
通过比对输入和输出的二进制数,可以验证加法器电路的正确性。
3. 测试电路的稳定性和可靠性在进行加法运算的过程中,我们还需要测试电路的稳定性和可靠性。
通过不断输入不同的二进制数并观察输出结果,可以检验电路在不同情况下的工作状况。
同时,还可以通过示波器等实验仪器对电路的波形进行观察和分析,进一步验证电路的性能。
四、实验结果与分析通过实验,我们成功地搭建了四位加法器电路,并进行了加法运算测试。
实验结果显示,电路能够正确地将输入的二进制数相加,并输出相应的结果。
同时,在测试电路的稳定性和可靠性时,电路表现出了较好的工作状态,波形稳定且无明显干扰。
五、实验总结通过本次实验,我们深入了解了四位加法器的工作原理和实现方式,并通过实际搭建电路进行了验证。
实验结果表明,四位加法器电路能够准确地进行二进制数的加法运算,并具备较好的稳定性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子设计技术课程设计
四位加法器
姓名:罗鹏
学号:09325215
专业:电子信息工程
班级:093252
指导教师:黄河
2012年11月8日
目录
一、设计目的 (3)
二、设计要求 (3)
三、设计过程 (4)
1.原理图的设计 (4)
2.程序的设计 (5)
3.功能仿真设计文件 (8)
四、设计体会 (10)
附录:A 参考文献 (11)
附录:B 评分表 (12)
一、设计目的
1.学习实用EDA设计软件QuartusⅡ,了解电路描述、综合、模拟过程。
2.学习VHDL程序中数据对象、数据类型、顺序语句、并行语句的综合使用,了解VHDL程序的基本结构。
3.掌握使用EDA工具设计数字系统的设计思路和设计方法。
学习VHDL基本逻辑电路的综合设计应用。
二、设计内容
设计并调试好一个由4个1位全加器级连构成的,本级的近位输出作为下一集的近位输入。
三、设计过程
1、原理图的设计
打开QuartusⅡ,单击file,选择new ,选择BlockDiagram/Schematic类型。
在原理图编辑界面中,元件选择对话框的符号名“Symbol Name”栏目内直接输入xor,或者在“Symbol Files”栏目中,用鼠标双击“xor”元件名,即可得到异或门的元件符号。
用上述同样的方法也可以得到与门及输入端和输出端的元件符号。
用鼠标双击输入或输出元件中原来的名称,使其变黑后就可以进行名称修改,用这种方法把输入端的名称分别更改为“in3,in4,in5”,把两个输出端的名称分别更改为“led3”和“led4”,然后按照图1所示的一位加法器逻辑电路的连接方式,用鼠标将相应的输入端和输出端及电路内部连线连接好,并以“xxx.bdf”(注意后缀是.bdf)为文件名,存在自己建立的工程目录D:\xxx内。
进行存盘操作时,系统在弹出的存盘操作对话框中,自动保留了上一次存盘时的文件名和文件目录,不要随意单击“OK”按钮结束存盘,一定要填入正确的文件名并选择正确的工程目录后,才能单击“OK”按钮存盘,这是上机实验时最容易忽略和出错的地方。
图1 一位加法器原理图
四位加法器的设计中,全加器成为底层文件A0、A1、A3、A4、A5、A6、A7、A8 是8个4位二进制输入端,A2是低位来得进位输入端,T(0…3)是4位和输出端,T4是向高位进位的输出端。
原理图如图2所示。
图2 四位加法器原理图
2、程序的设计
打开QuartusⅡ,单击file,选择new ,弹出下图界面,选择Verilog HDL File。
图3
进入界面进行编程,程序:
module add_j1(sum,cout,a,b,cin);
input [3:0] a,b; input cin; output[3:0] sum; output cout;
full_add1 u0(a[0],b[0],cin,sum[0],cin1); full_add1 u1(a[1],b[1],cin1,sum[1],cin2); full_add1 u2(a[2],b[2],cin2,sum[2],cin3); full_add1 u3(a[3],b[3],cin3,sum[3],cout);
endmodule
module full_add1(a,b,cin,sum,cout);
input a,b,cin; output sum,cout; wire s1,m1,m2,m3;
and(m1,a,b),(m2,b,cin),(m3,a,cin);
xor(s1,a,b),(sum,s1,cin);
or(cout,m1,m2,m3);
endmodule
根据程序点击Tools 中Netlist Viewers 接着是RTL Viewer,出来如图4所示RTL原理图。
图4 四位加法器RTL原理图
3、功能仿真设计文件
仿真,也称为模拟(Simulation);是对电路设计的一种间接的检测方法。
对电路设计的逻辑行为和功能进行模拟检测,可以获得许多设计错误及改进方面的信息。
对于大型系统的设计,能进行可靠、快速、全面的仿真尤为重要。
(1)建立波形文件
进行仿真时需要先建立仿真文件。
在QuartusII环境执行File的New命令,再选择弹出如下图的对话框中的Vector Waveform File项,波形编辑窗口即被打开。
图5
(2)输入信号节点
选择菜单View→Utility Windows →Node Finder ,在Filter框中选择Pins:all,再单击List按钮,即在下面的Nodes Found框中国i不过出现本设计的项目所有输入输出和近位,并全部拖到波形编辑窗口。
(3)波形文件存盘
以“xxxvwf”(注意后缀是.vwf)为文件名,存在自己建立的工程目录D\xxx 内。
在波形文件存盘时,系统将本设计电路的波形文件名自动设置为“xxx.vwf”,因此可以直接单击确定按钮。
(4)进行仿真
波形文件存盘后,执行仿真器“Simulator”命令,单击弹出的“仿真开始”对话框中的“Start”按钮,即完成仿真,可通过观察仿真波形进行设计电路的功能验证。
仿真如下图5:
图6 四位加法器的波形仿真结果
四、设计体会
在本次电子设计技术课程设计中,我们遇到过很多困难,但是在组员们的努力下和指导老师的指导下,我们最终战胜了这些困难,完成了四位加法器的设计。
这一过程中我学到了很多东西,同时也感慨良多。
更加强化了自己查阅资料的能力,这有助于提高我的自学能力。
并且很好的掌握了QuartusⅡ软件的各元器件的应用仿真设计。
在编程的时候我们遇到了很多的困难,比如说:编程后程序运行的时候提示有几个错误,我们检查了很多遍没发现程序问题,我们只好咨询老师,指导老师说我们的文件名一定要一样,结果通过老师我们把这个问题解决了,我们也顺利的完成了编程,并且很好的把设计做出来了。
通过以上的问题说明了我们的专业水平还不高,一些基础的东西没有很好的应用,因此需要付出更多的时间去学习,还要付出更多的努力。
这次作品成功,给我们学到很多的东西。
不仅是我们的理论知识和实践能力,更是对我们毅力、应变能力。
我们都学到了很多在课堂里没能学到的东西,而这些东西将为我们一生受用,为我们以后的实践能力打好很好的基础。
本次课程设计更加激发了我的学习欲望,有利于我后续课程的学习,更为我们马上进入社会提供了帮助,所有实践的机会都是很宝贵的。
所以通过这次电子设计技术的课程设计我希望下次做作品的时候我们能有更好的成绩。
附A:参考文献
[1]电子技术李春茂主编科学技术文献出版社
[2]数字电子技术基础解题指南唐竞新主编清华大学出版社
[3]电子技术实验指导书李国丽,朱维勇主编,中国科技大学出版社
[4]电子技术基础模拟部分(第四版),康华光主编,高教出版社
[5]数字电子技术基础(第四版),阎石主编,高教出版社
附B:课程设计评分表
东华理工大学长江学院
课程设计评分表
学生姓名:罗鹏学号:09325215
课程设计题目:四位加法器的设计。
