利用全加器电路创建四位二进制加法器
四位二进制全加器设计

四位二进制全加器设计(总3页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除组合逻辑电路课程设计题目:用74ls283构成四位二进制全加/减器一、设计思路74ls283为四位加法器,而如果希望进行减法运算,则需要将其转化为加法,而之前学到,二进制运算,一个数减去另一个数,即等于加上其补码。
于是得到如下公式,A-B=A+(-B)=A+B’+1。
将其全部视为加法运算,即一个数加上一个正数或者一个负数,这个数为加数B。
那么,需要将加数增添一位符号位,以区分正负。
因为74ls283芯片的引脚为低位向正在运算的数的进位,所以可以将其作为加数的符号位。
当其为正数时,输入为0,即计算A+B。
而当加数为负数时候,使其输入为1,并将B取反,再加上进位1,正好与公式相符。
根据以上原理,应用输入作为符号位,进行4位被加(减)数与5位加(减)数的加法运算。
设A3-A0为被加(减)数,B3-B0为加(减)数,M0为符号位。
当M0为0时表示正数,为1时表示负数。
而当B为负数需要取反时,刚好可以利用异或门的特性来进行,即1异或B等于B’,0异或B等于B即将B的各个数位和M0通过异或门相连,即可以做到负数取反。
二、电路图如图,输入输出ABC都用LED来指示二进制的数值,开关S2控制A的数值,S1控制B的数值以及符号位。
BX1指示灯指示的是输入B经过异或门作用后的电平。
三、由于此电路进行的是加法运算,两个加数一共2的9次方中组合,所以真值表又多又显而易见,此处将不给出。
四、举例演示:(1)5+6=11如图拨动开关,A=5,B=6,可见C为11的二进制表示1011。
(2)7-3=4如图,将M0置为1以表示负数。
BX1表示的是3的反码,在74283中进行了加1的运算即变成了补码,输出结果为0100(2)=4(10)(3)1000+1000=10000由于输出只有四位,而1000+1000会产生进位。
4位二进制全加器设计

任务一4位全加器设计一、实验目的1、掌握运用Quartus II原理图编辑器进行层次电路系统设计的方法。
2、进一步熟悉利用Quartus II进行电路系统设计的一般流程。
3、掌握4位全加器原理图输入设计的基本方法及过程。
二、实验原理(1)设计一位半加器真值表:(2)设计一位全加器真值表:SOn=n n n−1;COn=(A n⨁B n)C n−1+A n B n;(2)设计多位全加器由一位全加器组合成多位全加器。
依次将低位全加器的进位输出端接到高位全加器的进位输入端,由四个一位全加器构成四位全加器。
三、实验过程1、一位半加器的设计(1)电路图①执行“Files”─>“New”─>“Block Diagram/Sch matic”─>“OK”②在编辑窗口输入“与非”门电路原理图,保存电路为“01.bdf”,如图:(2)仿真波形①执行“Files”─>“New”─>“Vector Waveform File”─>“OK”②在波形编辑窗口双击左键,执行“Insert Node or Bus”─> “New Finder”─> “List”─>“》”─>“OK”。
③保存文件为“01.vwf”。
④执行菜单“Processing”─> “Start Simulation”,如图:(3)仿真波形分析:(4)封装之后的图:设“01.bdf”为顶层文件,执行“Files”─>“Create、Update”─> “Create Symbol Files forCurrent Files”,保存。
如图:2、一位全加器(1)电路图①执行“Files”─>“New”─>“Block Diagram/Sch matic”─>“OK”②在编辑窗口输入“与非”门电路原理图,保存电路为“02.bdf”,如图:(2)仿真波形①设“02.bdf”为顶层文件。
4位2进制全加器仿真电路

4位2进制全加器仿真电路
4位2进制全加器仿真电路是一种电路设计,用于将两个二进制数相加,并输出其和。
这种电路通常由多个逻辑门组成,包括与门、或门
和异或门等。
在这个电路中,每个二进制位都被视为一个单独的电路,并且每个电路都可以独立地进行计算。
在这个电路中,每个二进制位都有三个输入:两个输入位和一个进位位。
输出也有两个:一个和位和一个进位位。
进位位是由前一位的计
算结果和当前位的输入位共同决定的。
因此,这个电路需要一个额外
的输入,即进位位,以确保正确的计算结果。
为了实现这个电路,我们需要使用逻辑门。
与门用于计算进位位,或
门用于计算和位,异或门用于计算进位位和和位之间的差异。
这些门
可以通过布尔代数表达式来表示,然后转换为逻辑门电路。
在这个电路中,我们需要使用四个单独的2位全加器电路,每个电路
都可以独立地进行计算。
这些电路可以通过级联连接来实现4位2进
制全加器电路。
在级联连接中,每个电路的输出都被连接到下一个电
路的输入,以便在整个电路中进行计算。
最终,这个电路将输出一个4位二进制数,表示两个输入数的和。
这
个电路可以用于许多应用,包括计算机中的算术运算和数字信号处理中的滤波器设计等。
总之,4位2进制全加器仿真电路是一种重要的电路设计,用于将两个二进制数相加。
这个电路由多个逻辑门组成,包括与门、或门和异或门等。
这个电路可以用于许多应用,包括计算机中的算术运算和数字信号处理中的滤波器设计等。
4位加法器的设计原理

4位加法器的设计原理四位加法器是一种数字电路,用于实现四位二进制数的加法运算。
它由多个逻辑门组成,主要包括四个全加器、一个四路二选一选择器和一个四位二进制数输出。
在四位加法器中,每个全加器都负责计算两个输入位和上一位的进位的和。
全加器的原理是采用异或门(XOR)、与门(AND)和或门(OR)的组合。
具体来说,全加器有三个输入端,分别是两个输入位(A和B)和上一位的进位(Cin),两个输出端,分别是当前位的和(S)和当前位的进位(Cout)。
全加器的计算公式如下:S = (A XOR B) XOR CinCout = AB + (A XOR B)Cin其中,“XOR”代表异或操作,“AND”代表与操作,“OR”代表或操作。
全加器的设计原理是基于四位二进制数的加法运算规则。
在四位加法过程中,每一位的和由该位的两个输入位和上一位的进位确定。
进位则与上一位的输入位和上一位的进位有关。
因此,通过级联四个全加器,就可以实现四位加法运算。
除了四个全加器以外,四位加法器还包括一个四路二选一选择器。
这个选择器根据一个控制信号选择输出。
四位加法器的输出是一个四位二进制数,可以选择以原码、反码或补码的形式输出。
通过选择器的控制信号,可以选择输出形式。
四位加法器的工作原理是:首先,将四个输入数两两相加,得到每一位的和,以及进位。
然后,将每一位的和通过四个全加器计算得到最终的和,同时将进位以及控制信号传递给选择器。
最后,选择器选择要输出的结果。
总结来说,四位加法器是基于全加器的构建的数字电路,可以实现四位二进制数的加法运算。
它的设计原理是根据四位二进制数加法的规则和全加器的计算公式,通过级联四个全加器,并通过选择器控制输出形式,实现四位二进制数的加法运算。
四位加法器
四位加法器一、实验要求掌握组合逻辑电路的基本分析和设计方法;理解半加器和全加器的工作原理,用硬件描述语言实现半加器和全加器的门级设计,并使用自己设计的半加器组件构建全加器;学会利用软件仿真和远程实验系统实现对数字电路的逻辑功能进行验证和分析。
二、实验原理半加器(Half Adder)是不考虑来自低位的进位信号,其输入为 1 bit 的被加数和加数,输出为两位:本位的和以及向高一位的进位。
考虑低位进位的1位二进制加法器称为全加器(Full Adder),其输入为被加数加数以及低一位来的进位,输出为本位的和及向高一位的进位。
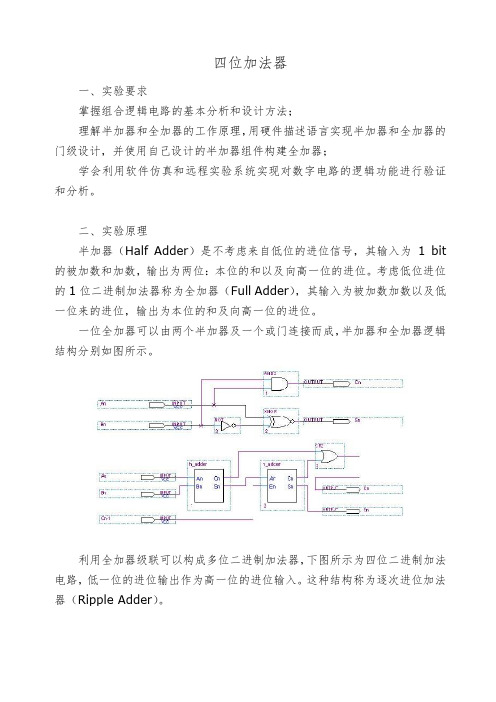
一位全加器可以由两个半加器及一个或门连接而成,半加器和全加器逻辑结构分别如图所示。
利用全加器级联可以构成多位二进制加法器,下图所示为四位二进制加法电路,低一位的进位输出作为高一位的进位输入。
这种结构称为逐次进位加法器(Ripple Adder)。
由于逐次进位加法器的进位信号是在各级间逐级传递的,所以高位的输出必须等低位的进位输入稳定后才有效,这就使得逐次进位加法器的延时比较大,速度比较慢。
为了提高加法器的运算速度,需要对加法器的结构进行改进。
引入进位传递信号和进位产生信号的概念,有{P n=A n⊕B n G n=A n B n利用这两个信号,可以把和信号与进位输出信号表示为{S n=P n⊕C n−1 C n=P n C n−1+G n根据上面给出的进位输出表达式,可得C0=G0+ P0C−1C1=G1+ P1C0=G1+ P1G0+P1P0C−1C2=G2+ P2C1=G2+ P2G1+P2P1G0+ P2P1P0C−1C3=G3+ P3C2=G3+ P3G2+P3P2G1+ P3P2P1G0+ P3P2P1P0C−1由于各级的进位传递信号和进位产生信号是同时生成的,所以各级的进位输出信号不再需要等待低一位的进位输入信号,从而大大减小了整个电路的延时,提高的加法器的运算速度。
数字电子技术项目4 4位二进制数加法数码显示

YAB AB
A1 =B=1&;A<B时,Y AY B
≥1
YAB
&
A
B
1
YAB
YAB AB
可写出逻辑函数表达式
YAB AB AB AB AB
2.多位数值比较器
如两个多位二进制数进行比较时, 则需从高位到低位逐位进行比较。 只有在高位相应的二进制数相等时, 才能进行低位数的比较。当比较到 某一位二进制数不等时,其比较结 果便为两个多位二进制数的比较结 果。
逻辑电平开关,输出端接LED电平指示,灯亮为1, 灯灭为0。 3)验证功能 输入端按真值表输入不同数值,观察输出端接 LED电平指示,
4.4 项目实施
1.4位二进制数加法数码显示电路
+5V
S1
S2
5
A1
VCC
S3
3
A2
S4
14
A3
S1
4
S5
12
A4
S2
1
S6
6
B1
S3
13
S7
2
B2
S4
S
2. 全加器
将两个多位二进制数相加时,除了将两个同位数 相加外,还应加上来自相邻低位的进位,实现这 种运算的电路称为全加器。
全加器具有三个输入端,A、B为被加数和加数, Ci-1是来自低位的进位输入,两个输出端,Ci是向 高位的进位输出,Si是本位和输出。
写出输出逻辑表达式
Ci-1
=1
Si
Si Ai Bi Ci1
Ai
Bi
Ci Ai Bi Ci1 ( Ai Bi )
=1 &
Ai
利用全加器电路创建四位二进制加法器

一.课程设计的目的:1、学习并了解MATLAB软件。
2、尝试用Simulink建模。
3、实现对数字电路的防真设计。
4、利用全加器电路创建四位二进制加法器。
二.课程设计题目描述及要求:利用所学的数字电路的基本知识和MUTLAB软件中Simulink的应用学习,完成对数字电路的仿真设计。
用各种各样的组合逻辑电路设计全加器,输出曲线,再利用全加器设计电路创建四位二进制加法器电路图,给出输出。
三.MATLAB软件简介:MATLAB是MathWorks公司于1984年推出的一套高性能的数值计算可视化软件,集数值分析、矩阵运算、信号处理和图形显示于一体。
MATLAB是由Matrix 和Laboratory单词的前三个字母组合而成的,其含义是矩阵实验室。
Simulink是MATLAB最重要的组件之一,是实现动态系统建模、仿真的一个集成环境。
它支持线性和非线性系统,连续时间、离散时间,或者两者的相结合的仿真,而且系统是多进程的。
Simulink是从底层开发的一个完整的仿真环境和图形界面,它把MATLAB的许多功能都设计成一个个直观的功能模块,把需要的功能模块连接起来就可以实现所需要的仿真功能。
Simulink仿真应用于数字电路、数字信号处理、通信仿真、电力系统仿真、宇航仿真等领域。
由于数字系统中高低电平分别用0和1表示,因此数字电路问题往往可以转化为一个数字上的逻辑问题。
MATLAB提供了逻辑运算模块和各种触发器模块,可以方便的进行数字电路的设计和仿真。
借助于组合电路仿真常用模块Logic and Bit Operations子库中的Local Operator模块,将其拖到所建的untitled窗口中,然后鼠标左键双击该模块弹出的Block Parameters/Logical Operator对话框,按Operator栏后的黑三角来选择所需要的门电路标识符,如:AND、OR、NAND、NOR、XOR、NOT中的一个,并依次设置所需的输入、输出端子个数,之后按OK 键确定。
4位二进制数加法器实验

《电子线路设计、实验、测试》实验报告实验名称:4位二进制数加法器实验院系:电子信息与通信学院专业班级:电信1401班姓名:XXX学号:xxxxxx时间:地点:南一楼指导教师:2016 年 4 月 13 日4位二进制加法器实验一.实验目的1.熟悉ISE软件的使用2.熟悉并初步掌握Verilog HDL描述电路的方法3.掌握用仿真波形验证电路功能的方法4.熟悉使用ISE软件创建文件并下载到basys2开发板上的过程二.实验内容用ISE软件对4位二进制全加器实验进行仿真,采用4位二进制数加法器的数据流描述方式,由于被加数A和加数B都是4位的,而低位的进位Cin为1位,所以运算的结果可能为5位,用{Cout,Sum}拼接起来表示。
然后对其进行仿真,最后创建约束文件,生成bit文件下载到basys2开发板上,对开发板进行操作。
三.实验原理除本位两个数相加外,还要加上从低位来的进位数,称为全加器。
图1为全加器的方框图。
图2全加器原理图。
被加数Ai、加数Bi从低位向本位进位Ci-1作为电路的输入,全加和Si与向高位的进位Ci作为电路的输出。
能实现全加运算功能的电路称为全加电路。
全加器的逻辑功能真值表如表1中所列。
表1 全加器逻辑功能真值表图1 全加器方框图图2 全加器原理图四位全加器四位全加器如图3所示,四位全加器是由半加器和一位全加器组建而成:图3四位全加器原理图四、实验步骤与要求1.创建一个子目录,并新建一个工程项目。
2.创建一个Verilog HDL文件,并将文件添加到工程项目中并编译整个项目,查看该电路所占用的逻辑单元(Logic Elements,LE)的数量。
3.对设计项目进行时序仿真,记录仿真波形图。
4.根据FPGA开发板使用说明书,对设计文件中的输入、输出信号分配引脚。
即使用开发板上的拨动开关代表电路的输入,用发光二极管(LED)代表电路的输出。
5.重新编译电路,并下载到FPGA器件中。
改变拨动开关的位置,并观察LED灯的亮、灭状态,测试电路的功能。
加法器实验实训报告

加法器实验实训报告实验目的,通过设计和实现一个加法器电路,加深对数字电路原理和逻辑门的理解,掌握数字电路的设计和实现方法。
实验原理,加法器是一种基本的数字电路,用于将两个二进制数相加得到和。
常见的加法器有半加器、全加器和多位加法器。
在本实验中,我们将使用全加器来设计一个4位二进制加法器。
实验材料和设备:1. 逻辑门集成电路(如74LS08、74LS32等)。
2. 连线材料。
3. 电源。
4. 示波器(可选)。
实验步骤:1. 根据实验要求,确定所需的加法器类型和位数。
在本实验中,我们选择使用4位全加器。
2. 根据全加器的真值表,设计电路连接图。
全加器由两个半加器和一个或门组成,其中半加器用于计算两个输入位的和,或门用于计算进位。
3. 根据电路连接图,使用逻辑门集成电路进行实验电路的搭建。
根据需要,可以使用示波器检测电路的工作情况。
4. 进行电路的调试和测试。
输入不同的二进制数,观察输出结果是否符合预期。
可以使用示波器观察信号波形,以验证电路的正确性。
5. 记录实验数据和观察结果。
包括输入的二进制数、输出的和、进位等信息。
6. 分析实验结果。
比较实验结果与预期结果的差异,找出可能存在的问题并加以解决。
7. 撰写实验报告。
包括实验目的、原理、材料和设备、步骤、数据和结果分析等内容。
实验结果分析:根据实验数据和观察结果,我们可以得出结论,通过设计和实现一个4位二进制加法器电路,我们成功地实现了二进制数的相加操作。
电路的输出结果与预期结果一致,证明电路的设计和实现是正确的。
实验总结:通过本次实验,我们深入学习了数字电路原理和逻辑门的运作方式,掌握了数字电路的设计和实现方法。
同时,我们也了解到了加法器的工作原理和实现过程。
通过实际操作和观察,我们加深了对加法器电路的理解,并提高了实验操作和数据分析的能力。
总的来说,本次实验对我们的学习和实践能力有很大的提升,使我们更加熟悉和了解数字电路的应用。
通过这次实验,我们不仅掌握了加法器的设计和实现方法,还培养了我们的动手能力和问题解决能力。
四位二进制加法器

用原理图层次化设计法设计一个4位二进制加法器一、实训目的1.掌握原理图输入法中的层次化设计方法。
2.进一步巩固原理图输入法。
二、实训器材计算机与Quartus Ⅱ工具软件。
三、实训指导(一)实训原理1.系统分析两个4位二进制数相加运算:a3 a2 a1 a0+ b3 b2 b1 b0 co s3 s2 s1 s0 其中: s0=a0+b0s1=a1+b1+进位co0s2=a2+b2+进位co1 s3=a3+b3+进位co2so=进位co3根据以上分析,4位二进制加法器可分解为4个全加器按一定方式连接而成。
2.全加器电路真值表全加器的真值表如表2-1所示。
表2-1 全加器电路真值表(二)实训步骤1.输入编辑底层原理图文件fadd.bdf(1)建立工程项目,其工程文件夹为fsdd,以fadd.bdf为顶层实体文件名。
(2)根据全加器电路的真值表建立原理图文件fsdd,bdf。
(3)编辑原理图文件fsdd.bdf。
一位全加器原理图如图2-1所示。
图2-1 一位全加器原理图2.编译仿真原理图文件fadd.bdf并生成符号文件fadd.bsf(1)编译原理图文件fadd.bdf。
若编译不过关,先双击第一个错误提示,可使鼠标出现在第一个错误处附近,检查纠正第一个错误后保存再编译,如果还有错误,重复以上操作,直至最后通过。
(2)仿真原理图文件fadd.bdf。
认真核对输入/输出波形,检查设计的电路功能正确与否。
一位全加器仿真波形如图2-2所示。
图2-2 一位全加器仿真波形图(3)生产符号文件fadd.bdf。
在原理图编辑界面下执行File→Greate/Update→Greate Symbol File for Current File命令,生成符号fadd.bsf。
3.输入编辑顶层电路原理图文件add4.bdf新建一个工程文件夹add4,把fadd.bdf、fadd.bsf文件放入其中,新建一个原理图文件,使用插入符号命令,选择fadd.bsf将它放置于原理图编辑区中。
logisim1位全加器构成4位加法器的设计过程描述

logisim1位全加器构成4位加法器的设计过程描述[logisim1位全加器构成4位加法器的设计过程描述]在数字电路设计中,加法器是最基本也是最常见的电路之一。
一个4位加法器由四个1位全加器组成,每个1位全加器都能实现两个1位二进制数的加法。
本文将以构造一个4位加法器为例,详细介绍1位全加器的设计过程及其在4位加法器中的应用。
1. 1位全加器的功能和原理:1位全加器是一种能够实现三个二进制输入数(a、b和进位cin)加和产生两个输出数(和sum和进位cout)的电路。
其最基本的真值表可以表示为:a b cin sum cout-0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1从上表中可以看出,和sum的计算结果是输入数a、b和cin的异或值;而进位cout的计算结果则是输入数a、b和cin的与运算后再与(a、b的异或结果)的或运算的结果。
2. 1位全加器的逻辑门电路设计:根据上述的真值表,我们可以设计出1位全加器的逻辑门电路。
一种常见的实现方式是使用两个异或门、一个与门和一个或门组合而成。
具体接线如下图所示:a -oooob -ooocin -oooosum cout Cin3. 构造4位加法器的步骤:一位全加器是完成二进制的加法运算的基本单元,我们可以通过将四个1位全加器按照特定的连接方式组成一个4位加法器。
下面是构造一个4位加法器的详细步骤:3.1 连接四个1位全加器:将四个1位全加器按照从右至左的顺序依次连接起来,其中每一个全加器的进位输入cin连接到其前一个全加器的进位输出cout。
这样,第一个全加器的进位输入cin可以直接连接到一个外部的输入信号,即加法器的进位输入Cin。
3.2 确定输入连接方式:将待相加的两个4位二进制数a和b的对应位与进位输入Cin分别与第一个全加器的a、b和cin相连。
4位二进制加法器课程设计

长安大学电工与电子技术课程设计题目:4位二进制加法器学院:汽车学院专业:汽车运用工程班级:姓名:学号:指导老师:李三财目录一、课题名称与技术要求···························二、摘要·········································三、总体设计方案论证及选择·······················1、方案论证与选择······························2、加法器的选取································3、译码器的选取································4、数码管的选取································四、设计方案的原理框图、总体电路原理图及说明·····1、原理框图····································2、总体电路原理图······························3、说明········································五、单元电路设计、主要元器件选择及电路参数计算···1、单元电路设计································2、主要元器件选择······························六、收获与体会及存在的问题·······················七、参考文献·····································八、附件·········································一、课题名称及技术要求1、课题名称:四位二进制加法器2、技术要求:a、四位二进制加数与被加数输入b、二位数码管显示二、摘要本加法器要实现能够输入加数和被加数,并且还能够将最终结果用二位数码管显示出来的功能。
用一位全加器设计一个四位的加法器

专业:计算机科学与技术班级:1班姓名:洪露露学号:090308013实验二一.实验目的:用一位全加器设计一个四位的加法器二. 实验内容a.利用MAX+plusⅡ软件,对下图所示的逻辑图进行编译和仿真,并选择器件进行定时分析。
b. 利用一位全加器设计一个四位的加法器三. 实验过程(1) 在实验一做完的全加器的基础上,在原理图编辑窗口中插入所有四个全加器,将它们联接成一个四位的加法器。
(2) 为了使输入输出的线减少,可以使用总线加标号的画法。
(3) 将连接好的原理图保存在全加器的设计目录下。
(4) 将设计项目设置成工程文件(PROJECT),选择目标器件并编译;(5) 保存原理图文件,对其进行编译,仿真,用“模式1”配引脚,下载到实验仪(具体的操作方法同实验一的相同,可以参考实验一的课件)。
(6) 选择波形编辑器文件,从SNF文件中输入设计文件的信号节点,列出并选择需要观察的信号节点;(7) 将仿真时的“end time”选项设为60us,并将标尺的尺度缩小。
(8) 把波形文件存盘,选择、运行仿真器;带有引脚锁定的四位加法器原理图:四位加法器的波形图选用结构图1 , 引脚对应情况实验板位置加法器信号通用目标器件引脚名目标器件EP1K30TC144引脚号键1 a[3..0] PIO3-PIO0 12、10、9、8键2 b[3..0] PIO7-PIO4 19、18、17、13数码管7 s[3..0] PIO27-PIO24 67、65、42、41发光二极管D7 c4 PIO38 83(9)并编程下载,硬件测试逻辑功能四.实验结果分析该实验是用一位全加器设计一个四位加法器,就是当以二进制的形式输入两个四位数进行相加,得出进位和本位,再把进位跟下个本位相加在得出进位,以此类推,最终得出一个相加的结果。
五.遇到问题及解决方法1.在编译原理图的时候会出现很多个错误提示,以至于无法对原理图编译成功。
解决方法:重新打开编辑好的原理图,查看输入输出处a[3..0],b[3..0]h 和s[3..0]这三个地方是否有两个点。
4位二进制全加器的设计

4位二进制全加器的设计摘要加法器是产生数的和的装置。
加数和被加数为输入,和数与进位为输出的装置为半加器。
若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。
常用作计算机算术逻辑部件,执行逻辑操作、移位与指令调用。
在电子学中,加法器是一种数位电路,其可进行数字的加法计算。
在现代的电脑中,加法器存在于算术逻辑单元(ALU)之中。
加法器可以用来表示各种数值,如:BCD、加三码,主要的加法器是以二进制作运算。
多位加法器的构成有两种方式:并行进位和串行进位方式。
并行进位加法器设有并行进位产生逻辑,运行速度快;串行进位方式是将全加器级联构成多位加法器。
通常,并行加法器比串行加法器的资源占用差距也会越来越大。
我们采用4位二进制并行加法器作为折中选择,所选加法器为4位二进制先行进位的74LS283,它从C0到C4输出的传输延迟很短,只用了几级逻辑来形成和及进位输出,由其构成4位二进制全加器,并用Verilog HDL进行仿真。
关键字全加器,四位二进制,迭代电路,并行进位,74LS283,Verilog HDL仿真总电路设计一、硬件电路的设计该4位二进制全加器以74LS283(图1)为核心,采用先行进位方式,极大地提高了电路运行速度,下面是对4位全加器电路设计的具体分析。
图11)全加器(full-adder )全加器是一种由被加数、加数和来自低位的进位数三者相加的运算器。
基本功能是实现二进制加法。
输入输出输入输出CI B A S ⊕⊕==AB'CI'+A'BCI'+A'B'CI+ABCI()AB CI B A CO ++=其中,如果输入有奇数个1,则S 为1;如果输入有2个或2个以上的1,则CO=1。
实现全加器等式的门级电路图如图2所示,逻辑符号如图3所示.图2 图32)四位二级制加法器 a) 串行进位加法器四位二进制加法器为4个全加器的级联,每个处理一位。
4位2进制全加器仿真电路

4位2进制全加器仿真电路4位2进制全加器仿真电路是一种常见且重要的电路设计,它能够将两个4位的二进制数相加,并输出其和与进位。
本文将介绍4位2进制全加器仿真电路的原理、设计过程以及仿真结果。
1. 原理介绍4位2进制全加器由4个单独的全加器组成,每个全加器负责相应的位相加运算,并输出该位上的和与进位。
全加器的输入包括两个待相加的二进制位和上一位的进位,输出则包括该位上的和与进位。
4位2进制全加器的输入为两个4位的二进制数和上一位的进位,输出为一个5位的二进制数,其中低4位为相加结果,高1位为最高位的进位。
2. 设计过程我们需要设计一个单独的全加器电路。
全加器由两个半加器和一个或门组成。
半加器用于计算两个二进制位的和,而或门用于计算进位。
然后,将4个全加器按照位对齐的方式连接起来,形成4位2进制全加器。
具体连接方式如下:- 将待相加的两个4位二进制数的最低位与上一位的进位分别连接到第一个全加器的输入端。
- 将待相加的两个4位二进制数的其他位分别连接到相应位置的全加器的输入端。
- 将第一个全加器的进位输出与第二个全加器的进位输入相连,以此类推,直到第三个全加器的进位输出与第四个全加器的进位输入相连。
- 将四个全加器的和输出连接起来,形成4位二进制数的和。
- 将最后一个全加器的进位输出作为最高位的进位输出。
3. 仿真结果为了验证4位2进制全加器的正确性,我们可以使用电路仿真软件进行仿真。
通过输入不同的待相加的二进制数和进位,观察输出结果是否符合预期。
在进行仿真时,我们可以将待相加的二进制数和进位表示为输入向量,将输出结果表示为输出向量。
然后,将输入向量依次输入到电路中,观察输出向量是否与预期结果一致。
通过仿真结果,我们可以验证4位2进制全加器的正确性,并对其性能进行评估。
如果仿真过程中存在错误或不符合预期的情况,我们可以对电路进行调整或优化,以提高其性能和可靠性。
总结:本文介绍了4位2进制全加器的原理、设计过程以及仿真结果。
四位二进制加法器的设计

长安大学电子技术课程设计四位二进制加法器专业班级姓名指导教师日期四位二进制加法器一、技术要求(1)四位二进制加数与被加数输入(2)二位数码管显示二、摘要理论上,由二进制数算法的运算可知,加、减、乘、除运算都可分解成加法进行运算,而实际上,为了减少硬件复杂性,这些运算基本上也是通过加法来实现的。
此次设计的是简单的四位二进制加法器。
设计中通过不断改变脉冲信号,来控制数码管的显示。
本次设计选择一个超前进位的4位全加器74LS283。
译码器选择五输入八输出的译码器,用二位数码管显示,采用七段显示译码器。
本次设计采用的是共阴极数码管,所以选择74ls48译码器三、总体设计方案论证与选择设计四位二进制加法器,可以选择串行二进制并行加法器,但为了提高加法器的运算速度,所以应尽量减少或除去由于进位信号逐级传递所花费的时间,使各位的进位直接由加数和被加数来决定,而无须依赖低位进位,因而我们选择超前进位的4位全加器74LS283。
设一个n位的加法器的第i位输入为a i、b i、c i,输出s i和c i+1,其中c i是低位来的进位,c i+1(i=n-1,n-2,…,1,0)是向高位的进位,c0是整个加法器的进位输入,而c n是整个加法器的进位输出。
则和s i=a i + b i + c i+a i b i c i (1)进位c i+1=a i b i+a i c i+b i c i (2)令g i=a i b i,(3)p i=a i+b i, (4)则c i+1= g i+p i c i (5)只要a i b i=1,就会产生向i+1位的进位,称g为进位产生函数;同样,只要a i+b i=1,就会把c i传递到i+1位,所以称p为进位传递函数。
把(5)式展开,得到c i+1= g i+ p i g i-1+p i p i-1g i-2+…+ p i p i-1…p1g0+ p i p i-1…p0c0 (6)随着位数的增加(6)式会加长,但总保持三个逻辑级的深度,因此形成进位的延迟是与位数无关的常数。
数字逻辑4位二进制加法器实验

实验2 4位二进制加法器的设计2.1 实验目的进一步熟悉Quartus Ⅱ的基本操作方法,并利用原理图输入设计方法设计简单组合电路,掌握层次化设计的方法,通过4位全加器的设计掌握利用EDA 工具进行电子系统设计的流程。
2.2 原理提示一个4位二进制加法器可以由4个全加器构成,各全加器之间的进位以串行方式实现,即将低位的进位输出CO 与相邻的高一位全加器的进位位Ci 相连,最低进位位接“0”。
实验原理图如下。
2.3实验内容采用Quartus Ⅱ基于图形的设计方法,在实验1的基础上,按层次化结构实现4位全加器的设计。
完成原理图输入、编译、进行波形仿真验证。
(仿真时要对所有输入、输出端进行)。
2.4实验步骤(1) 为本项设计任务建立工程。
启动Quartus Ⅱ,新建一个工程,有关操作如下图。
将实验1中已设计好的原理图文件fualladd.bdf 拷贝到D:\0501\exp2下。
在实验1中fualladd.bdf 是顶层设计文件,而在本实验中,fualladd.bdf 将作为底层设计文件使用。
∑C i C o ∑C i C o ∑C i C o a 0b 0a 1b 1a 2b 2a 3b 3s 0s 1s 2s 3c o ∑C i C o 0建立本工程的顶层设计。
点击“File/New”→“Block Diagram/Schematic File”→“OK”,将Block1.dbf 另存为add4. dbf。
add4. dbf是本工程的顶层设计文件。
(2)点击“File / Open…”将fualladd.bdf 文件打开。
(3)将fualladd.bdf制作成一个符号块,以便在add4. dbf中调用。
点击“File / Create/Update / Create Symble Files For Currenf Fils”,弹出对话框(文件名一栏应出现fualladd.bsf),点击“保存”。
logisim1位全加器构成4位加法器的设计过程描述 -回复

logisim1位全加器构成4位加法器的设计过程描述-回复设计一个4位加法器的过程主要包括以下步骤:设计1位全加器电路、标准化与调整、连接4位全加器、测试和验证。
1. 设计1位全加器电路首先,我们需要设计一个1位全加器电路。
全加器是将两个输入位和一个进位位相加得出和位和进位位的电路。
全加器电路输入位为A、B和Cin,输出位为S和Cout,其中S是和位,Cout是进位位。
1位全加器的真值表如下:A B Cin S Cout0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1根据真值表,我们可以得到以下逻辑方程:S = A xor B xor CinCout = (A and B) or (Cin and (A xor B))其中,xor表示异或运算。
2. 标准化与调整通过使用集成电路、逻辑门和触发器等电子器件,我们可以将1位全加器电路中的逻辑方程实现为电路图。
在实现过程中,需要注意实际电子器件的特性,如输入电平、输出电平和连接方式等。
可以使用逻辑仿真软件(如Logisim)或使用手工逻辑门设计。
3. 连接4位全加器根据4位加法器的特征,我们需要将四个1位全加器相连来实现4位加法。
具体连接方式如下:- 输入的A和B连接到每一个1位全加器的A位;- 进位位Cin连接到第一个1位全加器的Cin输入,并将之后的每个1位全加器的Cin连接到上一个1位全加器的Cout输出;- 第一个1位全加器的Cout输出连接到第二个1位全加器的Cin输入,以此类推,直到最后一个1位全加器的Cout输出。
4. 测试和验证使用逻辑仿真软件或实际搭建电路进行测试和验证。
输入四个4位二进制数并检查输出是否符合预期结果。
如果输出结果与预期一致,则说明电路设计正确,否则需要检查和修正电路中的错误。
总结:通过以上的步骤,我们可以设计一个4位加法器电路。
原题目:设计一个4位二进制加法器。

原题目:设计一个4位二进制加法器。
设计一个4位二进制加法器介绍本文档将指导你设计一个4位二进制加法器。
在这个项目中,我们会使用电子电路来实现加法操作。
加法器是计算机中最基本的运算单元之一。
加法器接受两个4位的二进制数作为输入,并输出它们的和。
加法器的设计过程涉及到逻辑门的组合来实现二进制加法操作。
设计步骤步骤一:定义输入和输出首先,我们需要定义输入和输出。
在这个项目中,输入是两个4位的二进制数,我们可以用`A[3:0]`和`B[3:0]`来表示。
输出是一个5位的二进制数,我们可以用`S[4:0]`来表示,其中`S[4]`是进位位。
步骤二:实现逻辑门为了实现二进制加法,我们需要将`A`和`B`的各个位相加,并考虑进位的情况。
这可以通过使用多个逻辑门实现。
- 对于每一位的加法,我们可以使用一个半加器(Half Adder)。
半加器有两个输入(`A`和`B`的对应位)和两个输出(和`S`和进位`C`)。
- 进位位可以通过一个全加器(Full Adder)来计算,它还需要一个输入(上一位的进位)。
步骤三:连接逻辑门将多个半加器和一个全加器连接在一起,形成一个4位的加法器。
通过将每个半加器的进位输出连接到下一个半加器的进位输入,可以实现进位的传递。
步骤四:验证设计在设计完成后,我们应该对其进行验证以确保它正常工作。
我们可以使用一些测试用例来验证设计的正确性。
例如,我们可以输入`A = 0010`和`B = 0100`,并确保输出`S = 0110`和进位`C = 0`。
总结设计一个4位二进制加法器涉及到定义输入和输出,实现逻辑门,连接逻辑门和验证设计的步骤。
通过将半加器和全加器连接在一起,我们可以实现二进制加法的功能。
在设计过程中,我们应该遵循相应的标准和规范,并进行适当的验证,以确保设计的正确性和可靠性。
设计一个自己的4位二进制加法器是一个很有趣的项目,可以帮助你更好地理解数字电路和计算机组成原理。
希望这份文档对你有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.课程设计的目的:
1、学习并了解MATLAB软件。
2、尝试用Simulink建模。
3、实现对数字电路的防真设计。
4、利用全加器电路创建四位二进制加法器。
二.课程设计题目描述及要求:
利用所学的数字电路的基本知识和MUTLAB软件中Simulink的应用学习,完成对数字电路的仿真设计。
用各种各样的组合逻辑电路设计全加器,输出曲线,再利用全加器设计电路创建四位二进制加法器电路图,给出输出。
三.MATLAB软件简介:
MATLAB是MathWorks公司于1984年推出的一套高性能的数值计算可视化软件,集数值分析、矩阵运算、信号处理和图形显示于一体。
MATLAB是由Matrix 和Laboratory单词的前三个字母组合而成的,其含义是矩阵实验室。
Simulink是MATLAB最重要的组件之一,是实现动态系统建模、仿真的一个集成环境。
它支持线性和非线性系统,连续时间、离散时间,或者两者的相结合的仿真,而且系统是多进程的。
Simulink是从底层开发的一个完整的仿真环境和图形界面,它把MATLAB的许多功能都设计成一个个直观的功能模块,把需要的功能模块连接起来就可以实现所需要的仿真功能。
Simulink仿真应用于数字电路、数字信号处理、通信仿真、电力系统仿真、宇航仿真等领域。
由于数字系统中高低电平分别用0和1表示,因此数字电路问题往往可以转化为一个数字上的逻辑问题。
MATLAB提供了逻辑运算模块和各种触发器模块,可以方便的进行数字电路的设计和仿真。
借助于组合电路仿真常用模块Logic and Bit Operations子库中的Local Operator模块,将其拖到所建的untitled窗口中,然后鼠标左键双击该模块弹出的Block Parameters/Logical Operator对话框,按Operator栏后的黑三角来选择所需要的门电路标识符,如:AND、OR、NAND、NOR、XOR、NOT中的一个,并依次设置所需的输入、输出端子个数,之后按OK 键确定。
利用这些基本门电路组成加法器逻辑电路。
四.课程设计的内容:
1、1位全加器的设计。
所谓全加器,就是带进位输入和进位输出的加法器。
1位全加器有3个输入,分别是加
数A、B和来自低位的进位C;还有两个输出,分别是和数SUM以及向高位进位D。
根据全加运算的逻辑关系,可列出一位全加器的真值表,如表1所示。
A B C SUM D
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
表1
列出SUM和D的最简与或表达式:
对SUM进行一次变换的SUM=A⊕B⊕D这样仅用一个或非门就实现了SUM的电路。
基于逻辑表达式得到如下逻辑图(图1)。
图1、逻辑图
2、用Simulink创建电路模型,完成逻辑电路。
图1、组合模块
3、用鼠标选中这部分逻辑电路,选中右击,在弹出的快捷菜单中选择Create Subsystem命令,自动生成一个子系统。
图2、全加器子系统
4、在顶层图中将这个子系统模块命名为ADD0。
图3、子系统模块ADD0
5、4位全加器设计。
1)、要将4个1位全加器级联起来,前一个的高位端D送入后一个的低位进位端C就可以实现4位全加器。
电路如图4.
图4、4位全加器
注:全加器脉冲源参数设置如表2.
A0 A1 A2 A3 B0 B1 B2 B3
幅度 1 1 1 1 1 1 1 1
周期 4 4 4 4 4 4 4 4
脉宽 1 1 1 1 3 3 3 3
相位延迟0 1 2 3 0 1 2 3
采样时间 5 5 5 5 5 5 5 5
表2
2)、连线以及仿真:
选择Simulation的Configuration Parameters命令,将仿真时间设置为0-20s,其余采用默认值,然后将这个模型保存到MATLAB的work目录下。
最后,单击模型窗口中的进行图标进行仿真,双击打开示波器Scope1,它监视的第一个加数对应的4个输入信号(图5);双击打开示波器Scope2,它监视的第二个加数对应的4个输入信号(图6)。
图5、第一个加数的波形图6、第二个加数的波形
从这两个波形图上读出加数值,并计算理论结果。
其结果如下:
0~5s:
A3A2A1A0=0001 B3B2B1B0=0001 DS3S2S1S0=00010
5~10s:
A3A2A1A0=0010 B3B2B1B0=0011 DS3S2S1S0=00101
10~15s:
A3A2A1A0=0100 B3B2B1B0=0111 DS3S2S1S0=01011
15~20s:
A3A2A1A0=1000 B3B2B1B0=1110 DS3S2S1S0=10110
双击示波器Scope打开输出波形(图7)。
图7、加法器的输出结果
对比发现实际的输出结果和计算结果是一致的。
五、小结:
通过本次课程设计,我了解了系统仿真的基本思路和方法,同时也了解了仿真在其他领域中的应用。
掌握了用Simulink实现4位全加器的步骤:
1)、添加模块:首先从MATLAB命令窗口运行Simulink,新建一个电路模型。
2)、修改模块参数:首先要完成逻辑部分的电路,生成子系统,封装生成模块。
设置所有参数。
3)、连线及仿真:连线标注,进行理论结果计算并与实际输出比较。
若一致,则完成了设计和仿真。
学习并初步了解了MATLAB软件,尝试了用Simulink建模,实现了对数字电路的仿真设计。
在查阅资料的同时,加上同学和老师的帮助实现了利用全加器电路创建四位二进制加法器。
通过验证证明了仿真实验的成功。
经过这次课程设计我知道了学习计算机语言要多练习,在学习的同时要举一反三,和同学、老师多作交流。
同时我也认识到自己在学习上的不足,以及知识掌握不够扎实,明确了以后学习的方向。
总之,经过这次课程设计让我认识到自身的不足,同时也学习到很多知识以及技巧。
感谢周老师给我们的课程设计作指导!
目录
一.课程设计的目的: (1)
二.课程设计题目描述及要求: (1)
三.MATLAB软件简介: (1)
四.课程设计的内容: (1)
五、小结: (6)。
