二分法实验报告

合集下载

MATLAB二分法和牛顿迭代法实验报告

（1）计算f(x)在有解区间[a, b]端点处的值。
（2）计算在区间中点处的值。
（3）判断若 ,则即是根，否则检验：
①若与异号，则知道解位于区间，
②若与同号，则知道解位于区间，，
反复执行步骤2、3，便可得到一系列有根区间：
（4）当，则即为根的近似值。
Newton迭代法原理：设已知方程的近似根 ,则在附近可用一阶泰勒多项式近似代替.因此,方程可近似地表示为 .用表示的根,它与的根差异不大.
3.在MATLAB命令行窗口求解方程f(x)
4.得出计算结果
设 ,由于满足解得
重复这一过程,得到迭代格式
实验所用软件及版本：MATLAB R2014a
主要内容（要点）：
实验过程记录（含：基本步骤、主要程序清单及异常情况记录等）：
二分法:
1.在MATLAB编辑器中建立一个实现二分法的M文件bisect.m
2.在MATLAB命令行窗口求解方程f(x)
3.得出计算结果
数学应用软件大型实验实验报告
实验序号：日期：年月日
班级
姓名
学号
实验
名称
二分法和Newton迭代法
问题背景描述：
分别编写一个用二分法和用Newton-Raphson法求连续函数的零点通用程。
实验目的：
用以求方程x^2-3*x+exp(X)=2的正根（要求精度ε=10^-6）。
实验原理与数学模型：
二分法原理：如果函数y=f(x)在闭区间[a,b]上连续，且已知函数在两端点的函数f（a）与f（b）取异号，即两端点函数值的乘积f(a)*f(b)<0,则函数y=f(x)在区间（a,b）内至少有一个零点，即至少存在一点c，使得f(x)=0的解。

非线性方程解法二分法实验报告

第七章非线性方程解法⒈二分法考察有根区间[a, b]，取中点x0=(b+a)/2 将它分为两半，假设中点x0不是f(x)的零点，然后进行根的搜索，即查找f(x0)与f(a)是否同号，如果确系同号，说明所求的根x*在x0的右侧，这是令a1= x0，b1=b;否则x*必在x0的左侧，这是令a1=a,b1=x0,不管出现哪一种情况，新的有根区间[a1, b1]的长度仅为[a, b]的一半。

.重复以上做法得新近似根x1,…这样不断将区间分半,得到一系列区间[an , bn],和近似根(区间中点)nx,n=0,1,2,3…,nx误差为(b-a)/2n+1.这样的方法称为二分法。

下面是一个关于二分法的例子。

例1求f(x)=x3- x-1=0在区间[1,1.5]内的一个实根，要求准确到小数点后的第二位.这里a=1,b=1.5,而f(a)<0,f(b)>0。

取[a,b]的中点x0=1.25，将区间二等分，由于f(x0 )<0, 既f(x0 )与f(a)同号，故所求的根x*必在x0 右侧，这是应令a1＝x0 =1.25, b1=b=1.5,而得到新的有根区间［a1，b1］，这样继续结果如下表：x6.实际上x5就有三位有效数字了.二分法实验(1)上机题目：二分法的应用实验目的：熟悉二分法并在计算机上实现实验要求：①上机前充分准备，复习有关内容，写出计算步骤，查对程序；②完成实验后写出完整的实验报告，内容应该包括：所用的算法语言，算法步骤陈述，变量说明，程序清单，输出计算结果，结果分析等等；③用编好的程序在Ｍatlab环境中执行。

算法说明：①找出计算f(x)在有限根区间[a, b]端点的值，f(a),f(b)②计算计算f(x)在区间中点（2ba+）处的值f(2ba+) .③判断若f(2ba+)=0，则2ba+即是根，计算过程结束，否则检验若f(2ba+)f(a)<0,则以2ba+代替b,否则以2ba+代替a.反复执行步骤②和步骤③，直到区间[a, b]长度小于允许误差ξ，此时中点2ba+即为所求近似根。

计算方法计算方法计算方法实验报告(二分法)

#include <iostream>
using namespace std;
#include <stdio.h>
#include <conio.h>
#include <math.h>
double f(double x)
{
return x*x*x-x-1;
}
int main()
{
double a,b,c,e,d=0;
cout<<"\n";
}
return 0;
}
结
果
（对实验结果进行分析，问题回答，实验心得体会及改进意见）
课程实验报告
课程名称
计算方法
班级
计算机二表二班
实验日期
2012年9月28日
姓名
学号
实验名称
用二分法
求方程f(x)=x3-x-1=0在区间[1,1.5]内的一个实根，
要求误差不超过0.05
实
验
目
的
及
要
求
（给出本次实验所涉及并要求掌握的知识点）
给定精确度e,用二分法求函数f(x)零点近似值的步骤如下:
1确定区间[a,b],验证f(a)·f(b)<0,给定精确度e.
cout<<"input a:";
cin>>a;
cout<<"input b:";
cin>>b;
cout<<"input e:";
cin>>e;
cout<<"a"<<d<<"="<<a<<" ";

牛顿迭代、割线法、二分法算法实验报告

三、牛顿法计算实验
3.1 牛顿法算法思想和简要描述我们有一个函数 f，其零点由数值计算得出，设 r 是 f 的一个零点，x 是 r 的一个近似。若 f 的二阶导数存在并且连续，则有泰勒定理，得 0=f(r)=f(x+h)=f(x)+hf ’(x)+o(h^2) 其中 h=r-x。若 h 较小（即 x 在 r 附近），则有理由略去 o(h^2)项并且在余下方程中求 h。即得到 h=-f(x)/f ’(x)。故 x-f(x)/f ’(x)是比 x 更好的一个近似。牛顿法从 r 的一个估计 x0 开始，得到更加准确的近似值 xn。递推式定义为： f(xn ) xn+1 = xn − ′ f (xn ) 3.2 MATLAB 运行牛顿法程序牛顿法求解 f=x^3-9 的根参数设置：x0 设置为函数 f 零点的近似。 n 设置为牛顿法 for 语句迭代次数。 alpha 设置为最后结果 f(x)的精度。 delta 设置为最后结果 x 的精度。（若 alpha，delta 都符合设置的计算精度时，结束迭代并得出计算结果，否则一直迭代到 n 次）设置初始值：设置参数 x0 分别为为 3；迭代次数 n 为 50 次；alpha 和 delta 都设置为 0.001。列出计算结果： >> newton(f,50,3,0.001,0.001) n x f(x) delta alpha 1.0000 2.3333 3.7037 0.6667 3.7037 2.0000 2.1066 0.3483 0.2268 0.3483 3.0000 2.0804 0.0043 0.0262 0.0043 Elapsed time is 0.166680 seconds.
4.0000 2.0625 2.1250 5.0000 2.0625 2.0938 6.0000 2.0781 2.0938 7.0000 2.0781 2.0859 8.0000 2.0781 2.0820 9.0000 2.0801 2.0820 10.0000 2.0801 2.0811 11.0000 2.0801 2.0806 12.0000 2.0801 2.0803 13.0000 2.0801 2.0802 14.0000 2.0801 2.0801 elapsed time is 0.316426 seconds.

数值分析原理实验报告

一、实验目的通过本次实验，掌握数值分析的基本原理和方法，了解数值分析在科学和工程领域的应用，培养动手能力和分析问题的能力。

二、实验内容1. 二分法求方程根（1）原理：二分法是一种在实数域上寻找函数零点的算法。

对于连续函数f(x)，如果在区间[a, b]上f(a)f(b)<0，则存在一个根在区间(a, b)内。

二分法的基本思想是将区间[a, b]不断二分，缩小根所在的区间，直到满足精度要求。

（2）实验步骤：① 输入函数f(x)和精度要求；② 初始化区间[a, b]和中间点c=a+(b-a)/2；③ 判断f(c)与f(a)的符号，若符号相同，则将区间缩小为[a, c]，否则缩小为[c,b]；④ 重复步骤②和③，直到满足精度要求；⑤ 输出根的近似值。

2. 牛顿法求方程根（1）原理：牛顿法是一种在实数域上寻找函数零点的算法。

对于可导函数f(x)，如果在点x0附近，f(x0)f'(x0)≠0，则存在一个根在点x0附近。

牛顿法的基本思想是通过泰勒展开近似函数，然后求解近似方程的根。

（2）实验步骤：① 输入函数f(x)和精度要求；② 初始化迭代次数n=0，近似根x0；③ 计算导数f'(x0)；④ 求解近似方程x1=x0-f(x0)/f'(x0)；⑤ 判断|x1-x0|是否满足精度要求，若满足，则停止迭代；否则，将x0更新为x1，n=n+1，返回步骤③。

3. 雅可比迭代法解线性方程组（1）原理：雅可比迭代法是一种解线性方程组的迭代算法。

对于线性方程组Ax=b，雅可比迭代法的基本思想是利用矩阵A的对角线元素将方程组分解为多个一元线性方程，然后逐个求解。

（2）实验步骤：① 输入系数矩阵A和常数向量b；② 初始化迭代次数n=0，近似解向量x0；③ 计算对角线元素d1, d2, ..., dn；④ 更新近似解向量x1=x0-A/d1, x2=x0-A/d2, ..., xn=x0-A/dn；⑤ 判断|x1-x0|是否满足精度要求，若满足，则停止迭代；否则，将x0更新为x1, x2, ..., xn，n=n+1，返回步骤③。

计算方法二分法实验

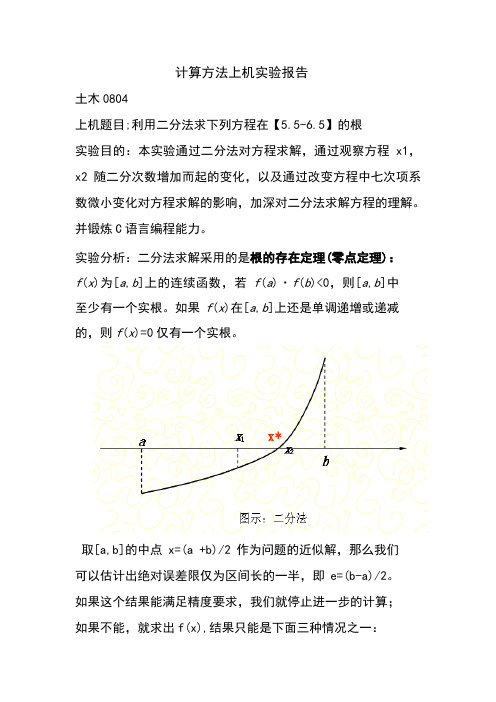
计算方法上机实验报告土木0804上机题目;利用二分法求下列方程在【5.5-6.5】的根实验目的：本实验通过二分法对方程求解，通过观察方程x1，x2随二分次数增加而起的变化，以及通过改变方程中七次项系数微小变化对方程求解的影响，加深对二分法求解方程的理解。

并锻炼C语言编程能力。

实验分析：二分法求解采用的是根的存在定理(零点定理)：f(x)为[a,b]上的连续函数，若f(a)·f(b)<0，则[a,b]中至少有一个实根。

如果f(x)在[a,b]上还是单调递增或递减的，则f(x)=0仅有一个实根。

取[a,b]的中点x=(a +b)/2作为问题的近似解，那么我们可以估计出绝对误差限仅为区间长的一半，即e=(b-a)/2。

如果这个结果能满足精度要求，我们就停止进一步的计算；如果不能，就求出f(x),结果只能是下面三种情况之一：（1） f(a)·f(x)<0，此时我们有x*∈[a,x]；（2） f(x)·f(b)<0，此时我们有x*∈[x,b]；（3） f(x)=0，此时x即为问题的精确解。

在前两种情况下，我们可以用x分别替换原问题中的b或a,从而把求解的区间减小了一半。

这样我们又可以取新区间[a,b]的中点。

经过N次迭代后，剩下的区间长为(b- a)/2N。

这也是结果的绝对误差限。

如此继续下去就达到是有根区间逐步缩小的目的，在这一些相互包含的子区间中构造收敛的数列{}kx来逼近根*x。

实验过程：1;C语言程序# include <stdio.h># include <conio.h># include <math.h># define PRECISION 1e12double f(double c){double m,x,m1,m2,m3;x=c;m1=x*x;m2=m1*x;m3=m1*m1;m=m3*m3-36*m3*m2+546*m2*m3-4536*m3*x+22449*m3-67284*m2+118124*m1-109584*x+40320; return(m);}double Root(float a,float b){ int i;i=0;double x1,x2;x1=a;x2=b;do{printf ("\n i=%d,x1=%f,x2=%f ",i,x1,x2);if(f(x1)*f((x1+x2)/2)<0)x2=(x1+x2)/2;elsex1=(x1+x2)/2;i++;}while (i<=100);return (x1);}void main(){float x1,x2,r;printf ("\n input x1,x2: \n ") ;scanf ("%f %f",&x1,&x2);r=Root(x1,x2);printf ("\n Root x=%f",r);}2．结果分析当a7=-36是，迭代到i=21时，出现x1=x2=6.500000，不再发生变化，出现精确解 x=root=x1=6.500000，收敛速度在数列xn 越靠近根时越慢。

实验1：二分法和迭代法

Ex=(k+1)( 1-0.99995^k)+ 0.99995^k=k(1-0.99995^k)+1 设 f(k)=Ex/k=1-0.99995^k+1/k 当 f(k)最小时，总共所需的化验次数最少，即 f ’(k*)=0 时，k*所需化验次数最少 f ’(k)=(-0.99995^k)*(ln0.99995)-1/(k^2) f’(100)= -5.0248e-05 f’(200)= 2.4504e-05 利用二分法，程序如下： f=@(k)(-0.99995^k)*(log(0.99995))-1/(k^2); a=100;b=200; tol=1e-12;maxit=100; my_bisection(f,a,b,tol,maxit) 结果为 1.419222563505173e+02 即 k=141 或 142 时，f(k)最小代入得 f(141)= 0.014117580646837
四、实验结果： (1) 取有根区间为 [3, 4], 利用二分法求得的根为: 3.262983107765649 取迭代初值为 3, 利用迭代法求得的根为: 3.262983107764216(2来自二分法和迭代法的迭代图像为:
(3) 结论: … …
任课教师：鲍亮
2017 年 3 月 19 日
(2) 迭代法的程序：
function Vx=my_iteration(phi,x0,tol,maxit) Vx=zeros(1,maxit);k=2;Vx(1)=x0; while abs(phi(x0)-x0)>tol&&k<=maxit+1 x0=phi(x0); Vx(k)=x0; k=k+1; if k>3 if abs(Vx(k-1)-Vx(k-2))>abs(Vx(k-2)-Vx(k-3)) '不收敛' break else end else end end Vx=Vx(1:k-1);

数值分析实验报告(二分法求年利率)

《数值分析》课程实验报告【实验内容与要求】每个月存250元，并持续20年，希望在20年后本金和利息的总值达到250000元。

年利率x 为多少时可以满足需求？【算法说明】1. 将方程简化，然后用二分法逼近方程的根，从而求解。

2. 二分法求解思想方程 f(x)=0在区域【a,b 】内求解 A. 计算端点的值f(a),f(b);B. 计算f(x)在区间中点（a+b ）/2处的值，即)2ba f(+的值； C. 若0)2ba f(=+则（a+b ）/2就是方程的根，计算过程结束，否则继续检验：若0)(f )2ba f(<+a ，则以（a+b ）/2代替b,否则以（a+b ）/2代替a. 反复执行步骤B,C 直到区间【a,b 】的长度小于允许误差ε，此时中点（a+b ）/2即为所有近似根。

【源程序】程序1（ps:二分法） #include <math.h> #include <stdio.h> //float p; //int n; int m=250000; void main() { float x,x1=0,x2=1;float p;int n;float F(float x,float x1,float x2);printf("请输入每个月存入的金额p和存款年份n的值：\n");scanf("%f%d",&p,&n);printf("x=%f\n",F(x,x1,x2));}float F(float x,float x1,float x2){float f,f1,f2;float p;int n;do{f1=(p*12/x1)*(pow((1+x1/12),n*12)-1)-m;f2=(p*12/x2)*(pow((1+x2/12),n*12)-1)-m;}while(f1*f2>0); //确保输入的x1,x2使得f1,f2符号相反do{x=(x1+x2)/2; //求x1,x2的中点f=(p*12/x)*(pow((1+x/12),n*12)-1)-m;if(f1*f>0) //当f与f1符号相同时{x1=x;f1=f;}else if(f2*f>0) //当f与f2符号相同时{x2=x;f2=f;}}while(fabs(f)>1e-6); //判断条件fabs(f)>1e-6的意思是f的值趋于0 return x;}程序2（ps:程序二是根据题意及结果分析直接写的代码，并没有用二分法）#include<iostream>#include <math.h>using namespace std;double sum=250;//sum表示总的本息和double fun(double x){//计算本息和double sum1=250;//sum1表示每个月的本息和for(int i=0;i<240;i++){//20年，共240个月sum1*=(1+x/12);sum+=sum1;}return sum;}void main(){double x=0.0035;//0.0035是我网上搜的最小的利率do{fun(x);x+=0.0001;//利率增加的单位大小为0.0001}while(sum<250000);//当本息和小于250000时，一直执行程序cout<<"所求的最小年利率为："<<x<<endl;}【实验结果】程序一得出的答案，但是可能是方程有问题，故答案有问题，即得到利率为0程序二得出的结果年利率为x=0.004【实验结果分析与说明】设每个月存钱p,且年利率为x,存了N 次后，钱的总数为Nxp xp xp xp p )121()121()121()121(y 32+++++++++=P 为最近年的钱数第一年的本金和利息 )121(xp +第二年的本金和利息 )121()121()121]()121([p 2xp xp xp x+++=+++…………第N 年的本金和利息Nxp xp xp xp p )121()121()121()121(32+++++++++求N 项级数和的公式为：qq qqqN N--=+++++11q 132故)1)121((12/)121(1)121(1p)121()121()121()121(y 32-+=+-+-=+++++++++=N Nxx p xxxp xp xp xp p N利用二分法对方程求解。

二分搜索算法实验报告

实验一二分搜索算法实验报告一．实验目得1、理解分治算法得概念与基本要素;2、理解递归得概念;3、掌握设计有效算法得分治策略;4、通过二分搜索技术学习分治策略设计技巧;二.实验内容及要求1. 使用二分搜索算法查找任意Ｎ个有序数列中得指定元素。

2．通过上机实验进行算法实现。

３. 保存与打印出程序得运行结果,并结合程序进行分析,上交实验报告。

4、至少使用两种方法进行编程。

三.实验原理二分搜索算法也称为折半查找法，它充分利用了元素间得次序关系,采用分治策略,可在最坏得情况下用O(loｇ n)完成搜索任务。

【基本思想】将ｎ个元素分成个数大致相同得两半,取a［n／２]与欲查找得x作比较,如果ｘ＝ａ［n/2]则找到ｘ,算法终止。

如果x＜a[n/2],则我们只要在数组ａ得左半部继续搜索x（这里假设数组元素呈升序排列）。

如果x＞a［ｎ/2],则我们只要在数组a得右半部继续搜索ｘ。

二分搜索法得应用极其广泛,而且它得思想易于理解。

第一个二分搜索算法早在1９46 年就出现了,但就是第一个完全正确得二分搜索算法直到１9６2年才出现。

Bentｌey在她得著作《Wrｉtｉｎg Corｒect Prｏｇraｍs》中写道，９0%得计算机专家不能在2小时内写出完全正确得二分搜索算法。

问题得关键在于准确地制定各次查找范围得边界以及终止条件得确定,正确地归纳奇偶数得各种情况，其实整理后可以发现它得具体算法就是很直观得。

✧方法一：直接查找穷举法遍历✧方法二：递归查找#incluｄe＜ｓtdiｏ、h>#ｄefｉne MAＸ3０iｎｔBinａrｙＳearｃｈ(ｉｎｔa［],ｉnt ＆x,int lｅｆt,ｉnt ｒighｔ）{if(lefｔ>rigｈｔ){rｅtｕｒｎ－1;}elsｅ{left=（ｌeｆt+rigｈt）/2；ｉf（ｘ＝＝ａ［lｅft])retｕrｎｌeft；elｓe{if(x>ａ[leｆt]）BinarySearch(a,ｘ,lｅft＋１,rｉght);eｌseＢinarySeａｒｃh(ａ,x,ｌｅft＊２-righｔ,lｅｆt+１）;}}}main(){inｔａ[MAX]；int ｆｏｕｎd,x,ｎ,i，ｊ,p;ｐrｉnｔf("输得个数\n")；ｓcanf（＂%d",&ｎ);printf（"数组数据＼n＂）;for（i＝0;i<ｎ；i++）{scanf("%d＂,&a[i］);}foｒ（i=0;i<n-１;i++){p=i;ｆｏr(j＝ｉ+1；j<n;j+＋)iｆ(a［p]>a［j])p=ｊ;if (p!=ｊ){ｘ＝a[p];ａ[p]=a[ｉ];a[i］＝ｘ;}}foｒ(i=0;i<n;i++）｛pｒinｔf("%d ",a[i]);}pｒiｎtｆ("输入要查找得数\n＂);scanf("%d＂,&ｘ)；ｆounｄ=ＢinarySｅarcｈ（ａ，ｘ,0，n）;ｉf（foｕnｄ==-1)｛ｐrintｆ(＂未找到＼ｎ");}else{prinｔf("要查找得数在第％ｄ个\n＂，found＋１)；}}方法三：迭代查找#incｌｕde＜ｓｔdｉo、ｈ>#defｉne MＡＸ30ｉnt BinarySｅarch(iｎｔa[],int ＆x，iｎt n){int ｌeft =0;int riｇｈｔ=n-1；iｎt middle；whｉｌe(ｌeft<=riｇht){midｄle＝(lｅft+right）/2;iｆ(x==ａ[mｉddｌｅ］)retｕrnｍｉdｄle;if(x>a[middｌe])ｌｅft＝middle+１;ｅlｓｅright=middle-1;｝rｅｔurn－１;}ｍａin（)｛int a[MAX］;int found,x,n,i,j,p;ｐrinｔf("数得个数＼ｎ");ｓｃanf("%d",＆n);printｆ("数组数据\n＂);fｏｒ（i=0;i＜n;i++){sｃaｎf("%d＂,&a[i]）;}ｆor （i=０;i＜ｎ-１;ｉ++){ｐ=i;fｏr(ｊ=i+１;ｊ<n;j＋+)if (a[ｐ]>a［j])p=j;ｉf (ｐ!=j){x=a[p]；a[p］=ａ[i]；a[ｉ］=ｘ；}}for(i=0；i<n;i++){pｒｉntｆ（"％d ",ａ[i］);}ｐrｉnｔf("输入要查找得数\n");scａｎｆ（"%d",＆x);fｏunｄ=BiｎaｒySearch(ａ，x，n);if（fｏunｄ＝=-1）{printｆ（"未找到\ｎ");}else{printf("要查找得数在第%d 个\ｎ",found+1);}｝四．程序代码变量定义说明:BｉnａrySearｃh()算法: a-＞数组kｅｙ->要查找得元素lｅft－>左标志rｉｇhｔ-＞右标志（n-＞数据个数)Maｉn（)主函数: ﻩound->就是否找到标志,-１表示未找到,找到其值为下标x->要查找得元素n->元素个数i,ｊ，p->循环控制变量（1）、递归查找＃ｉncｌude<stdio、h>＃dｅｆinｅMＡX 30int BinaｒySeaｒch(int a[],int kｅy，ｉnt left,ｉnt ｒｉght){inｔmｉd＝(riｇht-righｔ)／2+lefｔ;ｉf(a［mid]==kｅｙ）｛reｔurｎmｉd；}if(leｆt＞=rigｈｔ) {reｔurn －1;｝ｅlse if(key＞a[mｉd]) ｛retuｒnＢinaｒySｅａrch(ａ,key，mid+1，ｒight);}else if(kｅｙ＜a[ｍid］）{ｒeturn BinarｙＳearcｈ(a,key,left,miｄ－1）;｝rｅturn －１;｝iｎt ｍａiｎ(ｖoid)｛ｉnt ａ［MAX];inｔfoｕnd,x，n,i,j,p;pｒiｎｔf(＂数据个数:");sｃanｆ("%ｄ"，&ｎ);printｆ("输入数据：\n"）;for(ｉ=0;i＜n;i+＋）｛pｒｉｎｔf(＂请输入第％d个数据:＂,ｉ)；scaｎｆ（"%ｄ",&a［ｉ])；｝ｆｏr （i＝０;ｉ<n-1;i++) //选择排序｛p=i;ﻩﻩfor（j=ｉ+1；j<ｎ;j+＋)ﻩﻩiｆ(ａ［p］>a[j])ﻩﻩp=ｊ;ﻩﻩiｆ（ｐ!=j）ﻩ{x=a[p];a［p]=a[i];ﻩa[i］＝x;}}ｐriｎtｆ("排序后得数据如下:＂);for（i＝0;i<n;ｉ+＋){prｉnｔf（＂％d "，a[ｉ]);}printf（"\n"）;printf("输入要查找得数:＂）;scanf（"%d",&ｘ)；int lefｔ=0,ｒighｔ=n；found＝BiｎarｙSeａrch(a，ｘ,left,right）;iｆ(found==－1){priｎｔf（"未找到\n");}elｓe{printf（"要查找得数在第%d个\ｎ"，fｏuｎd＋1);}｝（2）、非递归查找#ｉｎcluｄe<sｔｄio、h>＃defiｎｅMAX3０int BinaryＳｅarch(ｉnｔａ[]，int key,ｉｎｔlｅn)｛ﻩｉｎt ｍｉd＝len/２;if （ｋey＝=a［miｄ]) {ｒeｔｕrn ｍiｄ;｝iｎt leｆt＝0;inｔrｉght＝ｌｅn-１;ｗhile(leｆt＜=right){ ﻩ／／迭代查找mｉd=(riｇht+lｅｆt）/2;if(ｋey<a[mid］) {riｇht=ｍid－1;}elｓe if(key>a[mｉd]) {ｌｅft=ｍid＋１;}ｅlse{retuｒn miｄ;}}return -１；｝ｉnt mａin(voiｄ)｛int a［MAX];ｉnt fouｎd,x,n，i,j,p;printｆ("数据个数：");scanｆ("%d",＆ｎ）;pｒintf(＂输入数据:\n");for(i=0;i<n；i++){ﻩpriｎtｆ("请输入第%ｄ个数据:"，i）;scanf("%d"，&a[i]);}fｏr (i=０;i<n－1;ｉ＋+)ﻩﻩ／/选择排序｛ﻩﻩp=i;ﻩfｏr(j=ｉ+1;j＜ｎ；j+＋)if（a[p］>a[j])ｐ=j；iｆ(p!=j)ﻩ｛x=a[p];a[p］=a[ｉ];ﻩﻩａ［ｉ］=x;}}pｒinｔf("排序后得数据如下：");for（i=0；ｉ<n；i++）{prｉntf("%d "，a[i]）;}printf("＼n＂);printｆ（＂输入要查找得数："）;scanｆ(＂%d＂，&x);ｉｎt lｅft=0,rｉghｔ＝n;found=ＢｉnaｒySeａｒch（a,x,n）;if(fouｎd＝=－１）{ｐrinｔf("未找到\ｎ");}ｅlsｅ｛pｒintf("要查找得数在第%d个\n",fｏuｎd+1)；}}五．结果运行与分析找到要查找得数据：未找到要查找得数据:六．心得与体会通过这次实验,巩固了自己对二分搜索算法得理解,它就是分治法得一个特殊例子,由此也对分治法有了更深一层次得认识。

二分法实验报告

用二分法方程 x³-x-1=0 在区间[1，1.5]内的一个实根，要求误差不超过 0.005。一、课题名称：二分法二、引言目的：在生活中，有许多实际算法表现为某种无穷递推过程的截断，为实现这类算法，不但需要建立计算公式，还需要解决精度控制问题。通过此次试验，熟悉并掌握二分法的算法使用。意义：在实际生活中，能够方便解决许多问题，对于人类的科学研究带来了方便。三、算法满足 f(a)*f(b)<0,给定ε （根的容许误差）或δ （|f(x)|的容许误差） 1) 将[a,b]对分，取中点x0 =(a+b)/2,求 f(x). 2) 若 |f(x)|<δ 或 |b-x0 |< ε ,取 ξ =x0 , 输出 ξ ，停机，否则进行下一步。 3) 判断根所在的新区间, 若 f(a)*f(x0 )>0,[a1 , b1 ]=[x0 ,b] 若 f(a)*f(x0 )≤0, ,[a1 , b1 ]=[a, x0 ] 含根区间长度：b1 − a1 = 区间长度：bn − an =
<
输出 x,y
xa
≥ 继续二分
结束
四、结构程序设计 (1)一般法 Program main implicit none real :: a=1.0000 real :: b=1.5000 real,parameter :: k=0.005 real x,y0,f,y write(*,*)"a=,b=" read(*,*)a,b
b −a 2n b −a 2
4) 转向 1），对新区间重复上述的步骤，设做了 n 次，[an , bn ],含根 ,近似值xn =
b −a 2n
,f(xn )<δ , |xn -ξ |<ε .

二分法实验报告

二分法实验报告二分法实验报告引言：二分法，也称为二分查找法或折半查找法，是一种常用的查找算法。

它的基本思想是将有序数组分成两部分，通过比较目标值与数组中间元素的大小关系，确定目标值可能存在的位置，然后逐步缩小查找范围，直到找到目标值或确定不存在。

本实验旨在通过编写二分法算法并进行实验验证，探究二分法的效率和应用。

实验方法：1. 设计二分法算法在实验开始之前，我们首先需要设计一个二分法算法来实现查找功能。

具体算法如下：- 选取有序数组arr和目标值target作为输入参数。

- 初始化变量left为数组的起始索引，right为数组的结束索引。

- 当left小于等于right时，执行以下步骤：- 计算中间索引mid，mid = (left + right) / 2。

- 如果arr[mid]等于target，返回mid。

- 如果arr[mid]大于target，将right更新为mid - 1。

- 如果arr[mid]小于target，将left更新为mid + 1。

- 如果循环结束时仍未找到目标值，返回-1。

2. 编写实验代码根据上述算法设计，我们可以使用任何编程语言来实现二分法算法。

在本实验中，我们选择使用Python编写实验代码。

以下是代码示例：```pythondef binary_search(arr, target):left = 0right = len(arr) - 1while left <= right:mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] > target:right = mid - 1else:left = mid + 1return -1arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]target = 5result = binary_search(arr, target)print("目标值在数组中的索引为：", result)```3. 进行实验验证在编写完实验代码后，我们可以使用不同的测试用例来验证二分法的正确性和效率。

(完整word版)数值分析报告-二分法和牛顿法方程求根(word文档良心出品)

《数值分析》实验报告一**: **学号: PB********实验一一、实验名称方程求根二、实验目的与要求：通过对二分法和牛顿法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点；比较二者的计算速度和计算精度。

三、实验内容：通过对二分法和牛顿迭代法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点。

（一）二分法算法：给定区间[a,b]，并设f （a ）与f （b ）符号相反，取δ为根的容许误差，ε为值的容许误差。

（1）令c=(a+b)/2（2）如果(c-a)< δ或)(c f <ε，则输出c ，结束；否则执行（3）（3）如果f(a)f(c)<0，则令)()(,c f b f c b ←←；否则，则令)()(,c f a f c a ←←，重复（1），（2），（3）。

（二）牛顿迭代法：给定初值0x ，ε为根的容许误差，η为)(x f 的容许误差，N 为迭代次数的容许值。

（1）如果)(x f <η或迭代次数大于N ，则算法结束；否则执行（2）。

（2）计算)('/)(0001x f x f x x -=（3）若 < 或 < ，则输出，程序结束；否则执行（4）。

（4）令 = ，转向（1）。

四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0，π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1，3]上的根。

源程序：3.1.1.a#include<stdio.h>#include<math.h>void main(){float a,b;double c,y,z;printf("plese input two number a and b:\n");scanf("%f%f",&a,&b);c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);while(fabs(b-a)>0.00001|| fabs(y)>0.00001){z=1/a-tan(a);if(z*y<0)b=c;elsea=c;c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);}x x 01-ε)(1x f ηx 1x 0x 1}输入0 1.5707563( /2~1.5705563)得到下表：由上表可以看出刚开始时f（c）取值幅度很大，但是经过一段历程之后，幅度变得平缓甚至基本接近与零，我们认为，x=0.8603是方程的根，结果与实际想要得到的值相当接近。

MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验目的：本实验旨在通过MATLAB编程实现迭代法、牛顿法和二分法，并通过实例验证其准确性和收敛速度。

实验原理：迭代法是一种通过不断迭代逼近根的方法，其基本原理是选择一个初始值，然后通过迭代公式不断逼近根的值，直到满足给定的精度要求。

牛顿法是一种通过不断迭代求函数的零点的方法，其基本原理是通过当前点的切线与x轴的交点来逼近根的值，直到满足给定的精度要求。

二分法是一种通过不断将区间一分为二来逼近根的方法，其基本原理是通过判断根是否落在区间的两个端点之间，然后将区间一分为二，直到满足给定的精度要求。

实验步骤：1.编写迭代法的MATLAB代码，实现对给定函数的根的逼近。

2.编写牛顿法的MATLAB代码，实现对给定函数的根的逼近。

3.编写二分法的MATLAB代码，实现对给定函数的根的逼近。

4.针对不同的函数，分别使用迭代法、牛顿法和二分法进行根的逼近，并记录每种方法的迭代次数和逼近结果。

5.对比三种方法的迭代次数和逼近结果，分析其准确性和收敛速度。

实验结果：以求解方程x^3-2x-5=0为例，使用迭代法、牛顿法和二分法进行根的逼近。

迭代法：迭代公式：x(n+1)=(2x(n)+5)^(1/3)初始值：x(0)=2迭代次数：6逼近结果：2.0946牛顿法：初始值：x(0)=2迭代次数：4逼近结果：2.0946二分法：初始区间：[1,3]迭代次数：11逼近结果：2.0946实验结论：通过对比三种方法的迭代次数和逼近结果可以发现，迭代法和牛顿法的收敛速度都要快于二分法，并且迭代法和牛顿法的逼近结果也更为接近真实根。

这是因为迭代法和牛顿法都是通过不断逼近根的值来求解，而二分法则是通过将区间一分为二来逼近根的值，所以迭代法和牛顿法的收敛速度更快。

总结：本实验通过MATLAB编程实现了迭代法、牛顿法和二分法，并通过实例验证了它们的准确性和收敛速度。

实验结果表明，迭代法和牛顿法在求解根的过程中具有更快的收敛速度和更接近真实根的逼近结果，而二分法的收敛速度较慢。

数值分析实验报告之二分法求根 java

《数值分析》实验报告实验三非线性方程求根一、实验目的1．掌握二分法、牛顿迭代法等常用的非线性方程迭代算法；2．培养编程与上机调试能力。

二、实验要求1．用C 语言设计出二分法和牛顿法的程序，并且选择不同的初值，观察所需的迭代次数和迭代结果。

三、实验原理1．二分法计算f(x)=0的二分法如下：① 输入求根取间[a,b]和误差控制量ε，定义函数f(x)。

如果 0)()(<b f a f ，转②；否则退出选用其它求根方法② 当|a-b|>ε时，计算中点x=(a+b)/2以及f(x)的值；分情况处理ε<|)(|x f ：停止计算，x x =*，转④0)()(<x f a f ：修正区间 ],[],[b a x a →0)()(<b f x f ：修正区间 ],[],[b a b x →③ 2*b a x += ④ 输出近似根*x四、实验内容1.用二分法求方程01)(3=--=x x x f 在区间[1.0,1.5]内的一个实根，要求精确到小数点后2位。

五、实验结果输入零点所在区间时：输入错误的区间时：二分法程序代码：import java.awt.Container;import java.awt.Dimension;import java.awt.EventQueue;import java.awt.GridLayout;import java.awt.Toolkit;import javax.swing.JFrame;import javax.swing.JPanel;import java.awt.Color;import javax.swing.JLabel;import java.awt.Font;import javax.swing.JTextField;import javax.swing.JButton;import javax.swing.SwingConstants;import java.awt.FlowLayout;import java.awt.event.ActionListener;import java.awt.event.ActionEvent;public class Erfenfaa implements ActionListener{ JFrame frame;private JTextField textField1;private JTextField textField2;private JTextField textField3;private JTextField textField4;JPanel panel_1 ,panel_2 ,panel_22,panel_3 ,panel_4 ; JLabel label1,label2,labelaa,labelbb,label_2,label_3; JButton submit,cancel;/*** Launch the application.*/public static void main(String[] args) {EventQueue.invokeLater(new Runnable() {public void run() {try {new Erfenfaa();} catch (Exception e) {e.printStackTrace();}}});}/*** Create the frame.*/public Erfenfaa() {frame = new JFrame("二分法解方程");frame.setSize(380,480);frame.setVisible(true);frame.setContentPane(createcontentPane());frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);centerFrame();// frame.setBounds(100, 100, 396, 300);frame.setResizable(false);}public Container createcontentPane(){Container contentPane=frame.getContentPane();contentPane.setLayout(new GridLayout(5,1,5,0));//由上至下 4行1列panel_1 = new JPanel();//面板panel_1放置label1和label2panel_1.setLayout(new FlowLayout(FlowLayout.CENTER,5,35));panel_1.setBackground(Color.WHITE);label1 = new JLabel("二分法解方程");label1.setFont(new Font("宋体", Font.BOLD, 18));panel_22= new JPanel();//面板panel_1放置label1和label2panel_22.setLayout(new FlowLayout(FlowLayout.CENTER,5,35));panel_22.setBackground(Color.WHITE);label2 = new JLabel("y=x^3-x-1");label2.setBounds(180, 41, 101, 24);panel_2 = new JPanel();//面板jpanel_2放置a,b,控制误差量panel_2.setBackground(Color.WHITE);panel_2.setLayout(null);labelaa= new JLabel("请输入区间[a,b]中的a:");labelaa.setFont(new Font("宋体", Font.BOLD, 12));labelaa.setBounds(80, 10, 172, 15);textField1 = new JTextField(10);//textField1输入a的值textField1.setBounds(219, 7, 42, 21);labelbb = new JLabel("请输入区间[a,b]中的b:");labelbb.setFont(new Font("宋体", Font.BOLD, 12));labelbb.setBounds(80, 38, 172, 15);textField2 = new JTextField(10);//textField2输入b的值textField2.setBounds(219, 35, 42, 21);label_2 = new JLabel("请输入控制误差量:");label_2.setFont(new Font("宋体", Font.BOLD, 12));label_2.setBounds(80, 63, 117, 15);textField3 = new JTextField(10); //textField3输入控制误差量textField3.setBounds(191, 60, 66, 21);panel_3 = new JPanel();//面板panel_3放置确定和取消按钮panel_3.setBackground(Color.WHITE);panel_3.setLayout(new FlowLayout(FlowLayout.CENTER,20,30));submit = new JButton("确定");//确定按钮submit.addActionListener(this);submit.setHorizontalAlignment(SwingConstants.CENTER);cancel = new JButton("取消");//取消按钮cancel.addActionListener(this);cancel.setHorizontalAlignment(SwingConstants.CENTER);panel_4 = new JPanel();//面板panel_4放置“方程解”标签和输出解文本块panel_4.setBackground(Color.WHITE);panel_4.setLayout(new FlowLayout(FlowLayout.CENTER,5,30));label_3 = new JLabel("方程解为：");label_3.setFont(new Font("宋体", Font.BOLD, 12));label_3.setBounds(24, 8, 65, 15);textField4 = new JTextField();//输出解或区间范围不对textField4.setBounds(99, 5, 97, 15);textField4.setColumns(25);panel_1.add(label1);panel_22.add(label2);panel_2.add(labelaa);panel_2.add(textField1);panel_2.add(labelbb);panel_2.add(textField2);panel_2.add(label_2);//控制误差量panel_2.add(textField3);panel_3.add(submit);panel_3.add(cancel);panel_4.add(label_3);panel_4.add(textField4);contentPane.add(panel_1);contentPane.add(panel_22);contentPane.add(panel_2);contentPane.add(panel_3);contentPane.add(panel_4);return contentPane;}public void centerFrame(){//窗口居中int x,y,screenWidth,screenHeight,frameWidth,frameHeight;Dimension screenSize=Toolkit.getDefaultToolkit().getScreenSize();screenWidth=screenSize.width;//取得屏幕宽度和高度screenHeight=screenSize.height;frameWidth=frame.getWidth();frameHeight=frame.getHeight();x=(screenWidth-frameWidth)/2;y=(screenHeight-frameHeight)/2;frame.setLocation(x,y);}public void actionPerformed(ActionEvent e) {//事件触发JButton button=(JButton)e.getSource();float a,b,p,w;if(button==submit){String o=textField1.getText();String l=textField2.getText();String m=textField3.getText();a= Float.parseFloat(o);b= Float.parseFloat(l);p= Float.parseFloat(m);w=b-a;if(z(a,b)==true){textField4.setText(String.valueOf(fun(w,b,a,p)));//浮点型强制转换为字符型}if(z(a,b)==false){textField4.setText(String.valueOf("方程值不在所输入的区间内，请选择其他方法"));}}if(button==cancel){textField1.setText("");textField2.setText("");textField3.setText("");}}public static boolean z(float a,float b){//判断区间是否包括零点float a11=y(a);float a21=y(b);if((a11*a21)<0){return true;}elsereturn false;}public static float y(float x){//设置y的函数，y=x^3-x-1float y;y=x*x*x-x-1;return y;}public static float fun(float w,float b,float a,float p){//二分法方程float X=0,x;while(Math.abs(w)>p){w=b-a;x=(a+b)/2;if(Math.abs(y(x))<p){X=x;break;}if(y(a)*y(x)<0){b=x;fun(w, b, a, p);}if(y(x)*y(b)<0){a=x;fun(w, b, a, p);}}return X;}}六、讨论分析。

(完整word版)数值分析报告-二分法和牛顿法方程求根(word文档良心出品)

三、实验内容：通过对二分法和牛顿迭代法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点。

（一）二分法算法：给定区间[a,b]，并设f （a ）与f （b ）符号相反，取δ为根的容许误差，ε为值的容许误差。

（二）牛顿迭代法：给定初值0x ，ε为根的容许误差，η为)(x f 的容许误差，N 为迭代次数的容许值。

（1）如果)(x f <η或迭代次数大于N ，则算法结束；否则执行（2）。

（2）计算)('/)(0001x f x f x x -=（3）若 < 或 < ，则输出，程序结束；否则执行（4）。

（4）令 = ，转向（1）。

四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0，π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1，3]上的根。

(整理)二分法试验报告.

一实验目的
运用matlab编写程序，学习二分法、牛顿迭代法并用二分法、牛顿迭代法解决实际问题，分析运行结果。
二实验内容
（1）二分法算法分析思路：构造区间[a,b],f(a)f(b)<0,[a1,b1]=[a,b].取x1=(a1+b1)/2是[a1,b1]中点，若f(x1)=0,则x1是f(x)=0的根，若f(x1)f(a1)>0,则取a2=x1,b2=b1，否则a2=a1,b2=x1,得到[a2,b2]满足:f(a2)f(b2)<0;b2-a2=1/2(b-a);a2>=a1,b2<=b1;以[a2,b2]取代[a1,b1]重复以上步骤直到求出精确解。
先建立二分法的fun.m文件，代码如下：
function fun(a,b,e)
if nargin==2
e=1.0e-6;
elseif nargin<2
input('变量输入错误！');
return;
end
if a>=b
input('隔根区间输入错误！');
return;
end
a1=a;
b1=b;
c1=(a1+b1)/2;
1.7305
c1 =
1.7324
c1 =
1.7314
c1 =
四、环境影响的经济损益分析1.7319
n =
11
（1）规划和建设项目环境影响评价。
除了房地产市场外，在不同职业和地点的工资差别中也可以发现类似的情形。（2）牛顿法：
仍以森林为例，营养循环、水域保护、减少空气污染、小气候调节等都属于间接使用价值的范畴。牛顿迭代法设计思想是对f(x0)某点求切线，与x轴交x1点后把x1当成x0,在求出相应新的f(x0),在对其求切线，找到与x轴的新交点，不断循环下去，直到达到精度为止，这种方法要求先对函数求一阶导数，然后再迭代：x1=x0-f(x0)/f’(x0)

二分法实验报告

实验报告方程求根——二分法一、目的和要求1）通过对二分法的编程练习，掌握方程求根的二分法的算法；2）通过对二分法的上机运算，进一步体会二分法的特点。

二、实习内容1）二分法的编程实现。

2）进行有根区间和误差限的比较和讨论。

三、算法流程图：1）准备：计算f(x)在有根区间[a, b]端点处的值f(a), f(b)。

2）二分：计算f(x)在区间中点c=2ba处的函数值f(c)。

3）判断•若f(c)与f(a)异号，则根位于区间[a, c]内，以c代替b；•若f(c)与f(a)同号，则根位于区间[c, b]内，以c代替a；四、实验步骤1）完成二分法的程序设计及录入；2）完成程序的编译和链接，并进行修改；3）用书上的例子对程序进行验证，并进行修改；4）对比估算次数与实际二分次数；5）输入不同的区间初值a, b，查看二分次数的变化；6）输入不同的误差限，查看二分次数的变化；7）完成实验报告。

五、实验结果1.经编译、链接及例子验证结果正确的源程序：#include <stdio.h>#include <math.h>float f(float x);void main(){float a,b,c,EPS,DELTA,fa,fb,fc,fab;int i=1;printf("please input a,b,EPS,DELTA\n");scanf("%f%f%f%f",&a,&b,&EPS,&DELTA);fa=f(a);fb=f(b);fab=fa*fb;if(fab>0)printf("无根");while(fab<0){c=(a+b)/2;fc=f(c);if((fa*fc)<0){b=c;fb=fc;printf("%d %20f %20f\n",i,c,fc);i++;}else if((fb*fc)<0){a=c;fa=fc;printf("%d %20f %20f\n",i,c,fc);i++;}if( fabs(fc)<DELTA || (b-a)<EPS ){printf("输出c为：%f\n",c);break;}}}float f(float x){float f;f=x*x*x+x*x-3*x-3;return f;}2. 实例验证结果：1）方程：f(x)=x3+x2-3x-3=02）输入初始参数：a=1, b=2, EPS=5e-63）结果输出：3. 改变a, b的值为：a=0, b=2, EPS不变，仍为5e-6，其结果为：4. 改变EPS的值为：EPS=5e-4, a, b不变，仍为a=1, b=2，其结果为：六、分析和讨论1.估算次数与实际二分次数的分析和讨论估算次数总是比实际二分次数少一次。

二分法

（2）程序设计思路
step1:设f(x)为连续函数，又设方程f(x)=0的隔根区间为[a,b]，为确定起见，
设f(a)<0,f(b)>0。二分法的做法就是先将区间[a,b]二分得中点(a+b)/2，将[a,b]分为两个相等区间，计算f(x)在中点的函数值f( )。若f( )=0，则x*= 就是方程f(x)=0的根；否则，若f( )<0，由于f(x)在左半区间[a, ]内不变号，所以方程的隔根区间变为[ ,b]。同理，若f( )>0，则方程的隔根区间变为[a, ]，将新的隔根区间记为[a1,b1]。
1、用二分法求方程x^2-x-1=0的正根，要求误差小于0.05，以及误差小于0.05的时候在区间[1,2]上的二分次数。
二分法源代码：
functionf1=fun(x)
f1=x^2-x-1;
function[x,k]=erfen(a,b,s)%a,b为根区间，s为精度
k=0;
whileabs(a-b)>s
x=(a+b)/2;
iffun(a)*fun(x)<0
b=x;
else
a=x;
ห้องสมุดไป่ตู้end
k=k+1;
end
x=(a+b)/2;%x为方程的解
k;% k为计算次数
四、实验结果与数据处理
>> [x,k]=erfen(1,2,0.05)
x =
1.6094
k =
5
五、分析与讨论
本次实验进一步加深了我对二分法的理解与应用的能力，并且深刻了理解了二分法的思想。在运用MATLAB的过程中，通过对for循环结构的运用，帮助我温习了MATLAB程序结构知识。让我对顺序、选择、循环三种程序结构有了更好的认识，进一步巩固了我运用MATLAB编程的能力。用二分区间的方法根据分点处函数f(x)值的符号逐步将有根区间缩小,使在足够小的区间内,方程有且仅有一个根.二分法收敛速度较慢，但也有自己的优势，可常用于求精度不高的近似根。