倾向值匹配模型(PSM模型)
倾向得分匹配固定效应模型

倾向得分匹配固定效应模型"倾向得分匹配固定效应模型" 可能是对于倾向得分匹配法(Propensity Score Matching, PSM)和固定效应模型(Fixed Effects Model)的结合的描述。
让我们分别讨论这两个概念:
1. 倾向得分匹配法(Propensity Score Matching, PSM): PSM 是一种用于处理观察研究中潜在选择偏差(confounding bias)的统计方法。
在处理观察研究中的因果推断时,研究者常常会面临到无法进行实验的情况,因此需要通过控制观察到的变量来模拟实验研究。
PSM 就是一种通过估计处理组(接受了某个处理或干预的组)和对照组(没有接受处理的组)之间的概率分数(倾向得分)来匹配相似个体,以减少混淆变量的影响。
2. 固定效应模型 (Fixed Effects Model): 固定效应模型是面板数据分析中的一种模型。
在面板数据中,同一组体(例如个人、公司)被观察多次,即在不同的时间点或条件下。
固定效应模型通过引入组体特定的固定效应,控制了个体固定特征对因变量的影响,从而减少了固定特征的影响。
如果将这两种方法结合起来,可能是在进行面板数据的观察研究时,使用倾向得分匹配法来处理选择偏差,然后在固定效应模型中引入处理组和对照组的固定效应。
这样做的目的是更好地控制潜在的混淆变量,使得对因果效应的估计更为可靠。
综合而言,"倾向得分匹配固定效应模型" 描述了一种在处理选择偏差和面板数据时,同时使用倾向得分匹配和固定效应模型的方法。
这种结合可以帮助研究者更准确地估计因果效应。
倾向匹配模型近邻匹配原理

倾向匹配模型近邻匹配原理
倾向匹配模型(Propensity Score Matching, PSM)是一种常用的统计方法,用于处理因果推断中的选择偏差问题。
在实际应用中,我们经常面临着无法进行随机实验的情况,因此需要借助倾向匹配模型来模拟实验条件,从而得到更加可靠的因果推断结果。
倾向匹配模型的核心原理是通过寻找近邻匹配来建立处理组和对照组之间的类似性,以减少处理组和对照组之间的差异性,从而实现更为准确的比较。
其基本步骤包括以下几个方面:
1. 倾向得分估计,首先,需要建立一个倾向得分模型,用于预测每个个体被处理的概率。
常用的建模方法包括逻辑回归、梯度提升树等。
2. 近邻匹配,在得到倾向得分后,需要通过一定的匹配算法,如最近邻匹配、卡方匹配等,来找到处理组和对照组之间的近邻。
3. 检验匹配质量,匹配完成后,需要进行匹配质量的检验,以确保匹配的有效性和可靠性。
4. 因果效应估计,最后,基于匹配后的样本数据,可以利用各种统计方法,如差分法、倾向得分加权法等,来估计处理效应的大小及显著性。
倾向匹配模型的近邻匹配原理能够有效地减少处理组和对照组之间的选择偏差,提高因果推断的可信度。
在医学、经济学、社会学等领域,倾向匹配模型都得到了广泛的应用,并取得了许多成功的研究成果。
然而,倾向匹配模型也存在着一定的局限性,如匹配质量依赖于倾向得分模型的准确性、匹配后样本量的减少等问题,因此在实际应用中需要谨慎使用并结合其他方法进行验证。
倾向得分匹配方法步骤

倾向得分匹配方法步骤倾向得分匹配方法(Propensity Score Matching, PSM)是一种用于评估因果效应的经典方法之一。
该方法通过倾向得分(Propensity Score)将处理组和对照组进行配对,以减少处理组和对照组之间的混淆偏倚。
下面是倾向得分匹配方法的步骤:1. 研究问题和数据准备:首先明确研究问题,并收集相关的观测数据。
数据应包括处理组和对照组的特征变量,以及因果变量。
2. 变量选择:根据研究问题,选择适当的特征变量作为倾向得分模型的输入变量。
这些变量应具有影响处理组选择的潜在因素,且与因果变量相关。
通常选择的变量包括年龄、性别、教育水平、收入水平等。
3. 倾向得分估计:倾向得分是处理组与对照组之间的条件概率,表示个体被分到处理组的概率。
可以使用各种统计方法来估计倾向得分,包括逻辑回归、梯度提升树等。
估计得到的倾向得分应在0到1之间。
4. 匹配样本选择:通过选择与处理组匹配的对照组样本,减少混淆偏倚。
常见的匹配方法包括最近邻匹配、卡尔曼匹配等。
匹配前,可以根据倾向得分的近似程度设置质量标准,例如最大汉明距离。
5. 匹配效果评估:在匹配完成后,对匹配样本进行处理效果评估。
通常使用平均处理效应(Average Treatment Effect, ATE)或平均处理效应对受处理样本的平均效应(Average Treatment Effect on the Treated, ATT)进行估计。
处理效果的估计可以使用插补法、回归法等。
6. 效果检验和敏感性分析:对匹配效果进行检验,常用的方法有t检验、Bootstrap法等。
此外,还需要进行敏感性分析,检验结果对于倾向得分估计的敏感性。
常见的敏感性分析方法包括皮贝根评分、加入未观测因素等。
7. 结果解读:根据匹配效果评估、效果检验和敏感性分析的结果,对研究问题进行解读。
解读应注意结果的可靠性、合理性和一致性,并结合文献综述和实证研究来进行解释。
倾向得分匹配法(PSM)举例及stata实现

倾向得分匹配法(PSM )举例及stata 实现——读书笔记【例】培训对工资的效应1政策背景:国家支持工作示范项目(National Supported Work,NSW )研究目的:检验接受该项目(培训)与不接受该项目(培训)对工资的影响。
基本思想:分析接受培训组(处理组,treatment group )接受培训行为与不接受培训行为在工资表现上的差异。
但是,现实可以观测到的是处理组接受培训的事实,而处理组没有接受培训会怎样是不可能观测到的,这种状态也成为反事实(counterfactual )。
匹配法就是为了解决这种不可观测事实的方法。
在倾向得分匹配方法(Propensity Score Matching )中,根据处理指示变量将样本分为两个组,一是处理组,在本例中就是在NSW 实施后接受培训的组;二是对照组(comparison group ),在本例中就是在NSW 实施后不接受培训的组。
倾向得分匹配方法的基本思想是,在处理组和对照组样本通过一定的方式匹配后,在其他条件完全相同的情况下,通过接受培训的组(处理组)与不接受培训的组(对照组)在工资表现上的差异来判断接受培训的行为与工资之间的因果关系。
变量定义:变量 定义TREAT * 处理指示变量,1表示接受培训(处理组),0表示没有接受培训(对照组)AGE 年龄(年)EDUC 受教育年数(年)BLACK 种族虚拟变量,黑人时,1BLACK =HSIP 民族虚拟变量,西班牙人时,=1HSIPMARR婚姻状况虚拟变量,已婚,1MARR = 74RE 1974年实际工资(1982年美元)75RE 1975年实际工资78RE 1978年实际工资74U 当在1974年失业,741U =75U当在1975年失业,751U = NODEGREE 当12EDUC <时,1NODEGREE =,否则为0 AGESQAGE AGE × 1 本例选自Cameron&Trivedi 《微观计量经济学:方法与应用》(中译本,上海财经大学出版社,2010)pp794-800 所有数据及程序均来自于本书的配套网站(/mmabook/mmaprograms.html )。
stata:倾向得分匹配(PSM)

stata:倾向得分匹配(PSM)导读:在经济学中,我们常常希望评估项目实施后的效应,一般的做法是加入虚拟变量,但是这种做法并不科学。
例如政府推行就业培训计划,该项目的参与者,我们将其称作处理组(treatment group),未参与的培训的样本称作控制组(control group)也叫对照组。
PSM考虑就业培训的处理效应评估。
我们一般的做法是比较两组的收入状况。
如果这样处理,可能得到的结论是参加培训的收入低于未参加培训者。
这是由于一开始选择控制组的样本时,选择范围比较广阔,存在选择偏差。
所以在此介绍倾向得分匹配方法(PSM)。
本文在此就不介绍相关理论了,因为小编的理论也不是特别的好,如果想学习的可以参阅连玉君老师的相关视频(重点推介),大概有5个课时;同时也可以参考陈强老师的《高级计量经济学及stata应用》中的第28章处理效应。
在此小编仅仅介绍stata的相关操作。
1、安装psmatch2ssc install psmatch2,replace2、导入数据,方法比较多,可以粘贴复制、也可以使用命令use E:\BaiduNetdiskDownload\A\labor.dta,clear3、命令语法格式介绍psmatch2 D x1 x2 x3 ,outcome(y) logit ties ate common odds /// pscore(varname) qui对以上的标准命令进行解析D为处理变量,是虚拟变量即是否参加培训x1 x2 x3是协变量,一般的称呼也叫解释变量outcome(varname)是输出变量,例如收入logit 表示计算得分的时候使用logit模型,如果不写Logit,默认为probit模型计算得分,在连玉君的视频中论述了二者并不存在明显的差异。
ties表示包括所有倾向得分相同的并列个体,默认按照数据排序选择其中一位个体。
ATE表示同是汇报ATE、ATU、ATT,大家看书重点了解common表示仅对共同取值范围内的个体进行匹配odds使用几率比(odds ratio)算法为p/(1-p),熟悉logit模型的应该了解qui屏幕中不显示logit模型估计过程,可以节省运算时间4 匹配方法连玉君的视频教程讲了三种:最近0匹配、半径匹配、核匹配;陈强老师讲了6种,如果想详细学习,可以参考他们的相关视频与书籍。
倾向性评分匹配的原理及文献解读

倾向性评分匹配的原理及文献解读倾向性评分匹配(Propensity Score Matching,PSM)是一种常用的数据分析方法,用于处理观察研究中的选择偏倚问题。
它的主要原理是通过建立一个倾向性评分模型,将具有相似倾向性评分的处理组和对照组进行匹配,来减少处理组和对照组之间的混杂因素。
在匹配完成后,可以使用匹配后的数据进行比较分析,从而获得更加准确的因果效应估计。
倾向性评分是对个体进行处理与否的概率进行预测的一种模型。
该模型基于观察到的个体的特征变量(confounding variables),通过回归分析或者机器学习等方法得到处理与否的倾向性评分。
常见的建模方法包括Logistic回归、Probit回归和Propensity Score Forest等。
模型建立好后,可以得到每个个体的倾向性评分,即个体进入处理组的概率。
在进行倾向性评分匹配时,首先需要选择一个适当的匹配算法来将处理组和对照组之间的个体进行配对。
常见的匹配算法包括最近邻匹配、卡尔曼匹配和基于距离的匹配法等。
这些算法都是根据个体的倾向性评分来寻找最接近的个体进行匹配。
匹配完成后,可以通过均衡性检验来验证匹配结果的有效性,主要包括倾向性评分比较、标准差比较和均衡性图形展示等。
倾向性评分匹配的主要优势在于可以在观察研究中解决选择偏倚问题,提供更为准确的因果效应估计。
通过匹配处理组和对照组,可以使得两组之间在观察到的个体特征上更加均衡,减少混杂因素对因果效应的干扰。
此外,倾向性评分匹配方法还具有较强的灵活性和可解释性,可以根据具体研究问题进行模型的设定和调整。
倾向性评分匹配方法已经在很多领域的研究中得到广泛应用。
例如,在医学研究中,可以用来评估一种新的治疗方法的效果;在教育研究中,可以用来评价一种新的教育政策的影响。
以下是一些与倾向性评分匹配方法相关的文献解读。
2. Stuart EA. Matching methods for causal inference: A review and a look forward. Stat Sci. 2024; 25(1):1-21.。
倾向得分匹配法(PSM)举例及stata实现

倾向得分匹配法(PSM )举例及stata 实现——读书笔记【例】培训对工资的效应1政策背景:国家支持工作示范项目(National Supported Work,NSW )研究目的:检验接受该项目(培训)与不接受该项目(培训)对工资的影响。
基本思想:分析接受培训组(处理组,treatment group )接受培训行为与不接受培训行为在工资表现上的差异。
但是,现实可以观测到的是处理组接受培训的事实,而处理组没有接受培训会怎样是不可能观测到的,这种状态也成为反事实(counterfactual )。
匹配法就是为了解决这种不可观测事实的方法。
在倾向得分匹配方法(Propensity Score Matching )中,根据处理指示变量将样本分为两个组,一是处理组,在本例中就是在NSW 实施后接受培训的组;二是对照组(comparison group ),在本例中就是在NSW 实施后不接受培训的组。
倾向得分匹配方法的基本思想是,在处理组和对照组样本通过一定的方式匹配后,在其他条件完全相同的情况下,通过接受培训的组(处理组)与不接受培训的组(对照组)在工资表现上的差异来判断接受培训的行为与工资之间的因果关系。
变量定义:变量 定义TREAT * 处理指示变量,1表示接受培训(处理组),0表示没有接受培训(对照组)AGE 年龄(年)EDUC 受教育年数(年)BLACK 种族虚拟变量,黑人时,1BLACK =HSIP 民族虚拟变量,西班牙人时,=1HSIPMARR婚姻状况虚拟变量,已婚,1MARR = 74RE 1974年实际工资(1982年美元)75RE 1975年实际工资78RE 1978年实际工资74U 当在1974年失业,741U =75U当在1975年失业,751U = NODEGREE 当12EDUC <时,1NODEGREE =,否则为0 AGESQAGE AGE × 1 本例选自Cameron&Trivedi 《微观计量经济学:方法与应用》(中译本,上海财经大学出版社,2010)pp794-800 所有数据及程序均来自于本书的配套网站(/mmabook/mmaprograms.html )。
倾向得分匹配法原理 -回复

倾向得分匹配法原理-回复倾向得分匹配法(Propensity Score Matching,PSM)是一种常用于处理因果推断问题的统计方法。
它的基本原理是通过构建倾向得分模型,将被处理的个体(处理组)与未处理的个体(对照组)进行配对,以便在某些特定的变量上达到类似或相同的分布,从而减少处理选择引起的偏倚。
PSM方法主要适用于在实验条件不具备的情况下进行因果推断。
在实验研究中,研究人员可以通过随机分组将个体分配到处理组和对照组,从而控制潜在的混淆因素。
然而,在实际应用中,一些因果问题无法通过实验进行研究,因此需要使用非实验数据来进行推断。
在这种情况下,倾向得分匹配法就能派上用场。
PSM方法的核心思想是通过估计个体的倾向得分,来度量个体进入处理组的概率。
倾向得分(Propensity Score)是指个体进入处理组的条件概率。
我们可以使用一些统计模型,例如逻辑回归模型,来估计这个得分。
这个模型会基于一系列观察到的协变量(confounding variables),也就是可能影响个体进入处理组的变量,比如年龄、性别、教育水平等,来预测个体进入处理组的概率。
在得到个体的倾向得分后,我们可以使用这个得分来进行配对。
具体来说,我们首先将处理组中的个体与对照组中的个体按照倾向得分进行配对。
一般可以使用一对一匹配、一对多匹配或者多对多匹配等方式。
匹配的目标是使处理组和对照组在倾向得分上的分布相似。
配对完成后,我们可以比较处理组和对照组在结果变量上的差异,来得到处理的因果效应。
这种比较可以通过计算平均处理效应(Average Treatment Effect,ATE)来实现。
ATE表示处理组与对照组在结果变量上的平均差异。
在计算ATE时,常常还会考虑到一些非随机选择问题带来的偏倚。
例如,可能存在选择性个体退出、数据缺失或者其他特殊情况。
为了解决这些问题,可以使用倾向得分匹配法的改进方法,如加权倾向得分匹配法(Weighted Propensity Score Matching)或者可接受性函数(Acceptance Function)等。
倾向得分匹配法结果解读

倾向得分匹配法结果解读倾向得分匹配法(Propensity Score Matching,PSM)是一种常用的统计方法,用于处理观察性数据中的因果推断问题。
它通过建立一个倾向得分模型,将处理组(接受某种处理或干预)与对照组(未接受处理或干预)进行匹配,从而消除处理组和对照组之间的潜在选择偏差,使得比较更具可靠性。
解读倾向得分匹配法的结果需要考虑以下几个方面:1. 倾向得分模型的质量,首先需要评估倾向得分模型的拟合程度和预测准确性。
常用的评估指标包括C统计量(C-statistic)、区分度指数(Discrimination Index)等。
较高的指标值表明模型的质量较好,倾向得分的预测能力较强。
2. 平衡性检验,在进行倾向得分匹配后,需要检验处理组和对照组之间的基线特征是否得到平衡。
常用的平衡性检验方法包括t 检验、卡方检验等。
如果处理组和对照组在倾向得分匹配后的基线特征上没有显著差异,说明匹配效果较好,处理组和对照组的比较更具可靠性。
3. 效应估计与统计显著性,倾向得分匹配后,可以通过比较处理组和对照组之间的平均差异来估计处理效应。
常见的效应估计方法包括平均处理效应(Average Treatment Effect,ATE)、平均处理效应对于受处理的人群(Average Treatment Effect on the Treated,ATT)等。
此外,还需要进行统计显著性检验,判断处理效应是否显著。
4. 敏感性分析,倾向得分匹配方法对于倾向得分模型的假设敏感,因此需要进行敏感性分析,检验结果的稳健性。
常见的敏感性分析方法包括倾向得分模型的功能形式敏感性分析、倾向得分模型的变量选择敏感性分析等。
综上所述,解读倾向得分匹配法的结果需要综合考虑倾向得分模型的质量、平衡性检验、效应估计与统计显著性以及敏感性分析等多个方面,以确保结果的可靠性和有效性。
倾向值评分匹配方法PSMppt课件

1
RCT:很多限制,如费用,伦理学要 求,操作困难,不适合发病率很低的 疾病 非RCT:避免以上繁杂的问题,容易 组间基线不齐,使之成为处理效应的 混杂因素从而产生偏移
2
• 为了消除混杂因素的影响,传统的解决方式是,用多变 量配对,多变量分析模型,M-H分层分析,协变量分析。
14
• 比较的效果是接受治疗后1 年内的生存率,成本是所有疾病相关 的医疗成本,研究分别对成本和效果未经过调整的结果、多元回 归结果、基于倾向值匹配的结果和基于倾向值分层的结果进行了 比较。
15
讨论
倾向值分析只能尽量减少混杂因素产生的影响,并不能完全消除, 其消除程度取决于可以被观测和控制的变量数量以及匹配的质量。 此外,倾向值分析只能对可观测的混杂因素进行平衡和控制,并不 能够控制不可观测的混杂因素,当有重要的混杂因素缺失或不可观 测时,采用倾向值分析所得结果可能与真实值存在较大偏差。
8
估计倾向值
• Logistic 回归模型 • 令y=组别,x为各协变量 每个个体在给定可观测混杂因素的条件下接受干预的条件概率。
9
选择匹配方法
最近邻匹配
卡钳匹配 马氏距离匹配
贪婪匹配法
10
匹配后的均衡性检验
• 协变量的平衡可通过均值上的绝对标准化差值来衡量
• 通常dX>dXm,说明在匹配后样本的平衡程度有所改善。
• 目的:将多个变量(多维)转化为一个中间变量(一维) • 特点:不在关注每个需要控制的混杂因素的具体取值,转为关注将这
些变量纳入logistic回归方程后预测出来的倾向值。只要保证倾向值匹 配,这些所有需要控制的混杂因素都考虑了。
5
PSM适用情形
• 前提:logistic多因素分析已经无法校正 • 1:实验组与对照组人数相差甚远(>4:1) • 2:两组变量差异太大,可比性差,如基线不齐,或混杂因素多 • 3:变量过多,样本量偏少
倾向得分匹配法(PSM)举例及stata实现

倾向得分匹配法(PSM )举例及stata 实现——读书笔记【例】培训对工资的效应1政策背景:国家支持工作示范项目(National Supported Work,NSW )研究目的:检验接受该项目(培训)与不接受该项目(培训)对工资的影响。
基本思想:分析接受培训组(处理组,treatment group )接受培训行为与不接受培训行为在工资表现上的差异。
但是,现实可以观测到的是处理组接受培训的事实,而处理组没有接受培训会怎样是不可能观测到的,这种状态也成为反事实(counterfactual )。
匹配法就是为了解决这种不可观测事实的方法。
在倾向得分匹配方法(Propensity Score Matching )中,根据处理指示变量将样本分为两个组,一是处理组,在本例中就是在NSW 实施后接受培训的组;二是对照组(comparison group ),在本例中就是在NSW 实施后不接受培训的组。
倾向得分匹配方法的基本思想是,在处理组和对照组样本通过一定的方式匹配后,在其他条件完全相同的情况下,通过接受培训的组(处理组)与不接受培训的组(对照组)在工资表现上的差异来判断接受培训的行为与工资之间的因果关系。
变量定义:变量 定义TREAT * 处理指示变量,1表示接受培训(处理组),0表示没有接受培训(对照组)AGE 年龄(年)EDUC 受教育年数(年)BLACK 种族虚拟变量,黑人时,1BLACK =HSIP 民族虚拟变量,西班牙人时,=1HSIPMARR婚姻状况虚拟变量,已婚,1MARR = 74RE 1974年实际工资(1982年美元)75RE 1975年实际工资78RE 1978年实际工资74U 当在1974年失业,741U =75U当在1975年失业,751U = NODEGREE 当12EDUC <时,1NODEGREE =,否则为0 AGESQAGE AGE × 1 本例选自Cameron&Trivedi 《微观计量经济学:方法与应用》(中译本,上海财经大学出版社,2010)pp794-800 所有数据及程序均来自于本书的配套网站(/mmabook/mmaprograms.html )。
倾向评分匹配法

倾向评分匹配法(Propensity Score Matching, PSM)是一种常用的非实验研究方法,用于解决因果推断问题。
它通过将参与某个处理(例如接受某项政策、干预或治疗)的个体与没有参与该处理的个体进行匹配,以消除因群体选择偏差带来的潜在混杂变量的影响。
PSM的基本步骤如下:
1. 确定研究问题和处理变量:明确需要进行因果分析的研究问题,并确定影响因变量的处理变量。
2. 构建倾向评分模型:利用回归分析等方法,建立一个预测参与处理的倾向评分模型,该模型能够根据个体的特征预测其选择处理的概率。
3. 匹配样本:根据个体的倾向评分,将参与处理的个体与未参与处理的个体进行配对匹配,使得两组个体在处理前的特征上尽可能相似。
4. 检验平衡性:检验匹配后的样本是否在处理前的特征上达到平衡状态,以确保匹配的有效性。
5. 进行因果推断:比较处理组和对照组在因变量上的差异,以得出因果效应的估计结果。
6. 敏感性分析:进行敏感性分析,检验倾向评分模型的稳健性,并评估结果对潜在假设的依赖程度。
PSM方法在通过实验研究来解决问题存在困难或不可行的情况下,为研究人员提供了一种处理群体选择偏差的有效工具。
然而,PSM也有
一些限制,如依赖于建模假设、匹配质量和结果的解释等方面存在一定挑战。
因此,在应用PSM时需要谨慎选择合适的方法和适用范围,并结合其他方法进行结果验证和分析。
倾向性得分匹配(PSM)
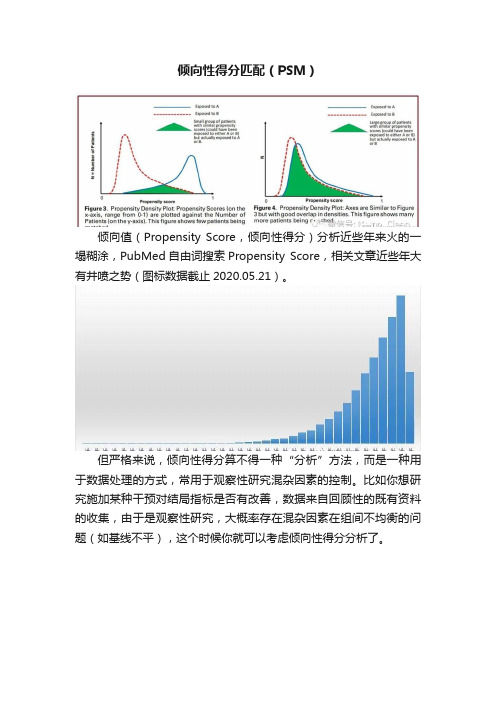
倾向性得分匹配(PSM)倾向值(Propensity Score,倾向性得分)分析近些年来火的一塌糊涂,PubMed自由词搜索Propensity Score,相关文章近些年大有井喷之势(图标数据截止2020.05.21)。
但严格来说,倾向性得分算不得一种“分析”方法,而是一种用于数据处理的方式,常用于观察性研究混杂因素的控制。
比如你想研究施加某种干预对结局指标是否有改善,数据来自回顾性的既有资料的收集,由于是观察性研究,大概率存在混杂因素在组间不均衡的问题(如基线不平),这个时候你就可以考虑倾向性得分分析了。
PS就是以干预因素(组别)为因变量,以所有观测到的非研究性因素为自变量进行logistic或probit回归,在给定的协变量条件下,个体接受干预因素处理的概率。
根据PS,我们就可以对试验组和对照组进行筛选,使得不同组的非研究性因素实现均衡,从而达到控制的目的。
倾向性得分本身并不能控制混杂,而是通过PS匹配、加权、分层或进入回归模型直接调整混杂等方式,不同程度地提高对比组间的均衡性,从而削弱或平衡协变量对效应估计的影响,达到“类随机化”的效果,又称为事后随机化。
简单理解,就是从大量的样本数据中将具有共同特征的干预组和对照组样本挑选出来,然后对这些符合要求的样本进行分析。
倾向性得分可以同时调整大量的混杂因素,省时间省钱,但是需要的样本量较大,只能均衡已观测的指标变量,而且可能会以丢失样本为代价。
大部分软件给出的是两水平的干预因素的倾向性得分,SPSS直接给出了1:1的倾向性得分匹配结果。
数据来自STATA16的自带数据,是一项关于孕期妇女吸烟对新生儿体重的影响的观察性研究,由Cattaneo (2010)报道。
调查数据涉及众多变量包括新生儿出生体重(bweight)外,还有孕母的婚姻状况(mmarried)、孕期是否饮酒(alcohol)、年龄(mage)、教育水平(medu)、是否吸烟(mbsmoke)、母亲是否白人(mrace)、是否首胎(fbaby)、首次产前检查是否在头三个月内(prenatal1)以及父亲的年龄(fage)、是否白人(frace)等众多变量。
psir模型概念

PSIR(Propensity Score Matching and Regression,倾向得分匹配与回归)模型是一种用于处理观测数据中个体之间差异的统计分析方法。
它结合了倾向得分匹配(PSM)和线性回归(Regression)两种方法,旨在减少观测数据中的选择性偏差,提高估计结果的准确性。
倾向得分匹配(PSM)是一种用于处理因果推断问题的统计方法。
它通过计算个体之间在处理变量上的倾向得分(即接受处理的概率),然后根据倾向得分进行匹配,从而得到处理组和对照组之间的平衡数据。
平衡数据可以帮助我们更准确地估计处理变量对结果变量的影响。
线性回归(Regression)是一种常见的统计分析方法,用于研究自变量与因变量之间的线性关系。
线性回归模型可以解释自变量对因变量的影响程度,并为预测因变量提供依据。
PSIR 模型在以下几个方面具有优势:
1. 平衡数据:通过倾向得分匹配,PSIR 能够减少观测数据中的选择性偏差,使得处理组和对照组之间的数据更加平衡。
这有助于提高因果推断的准确性。
2. 控制固定效应:PSIR 模型可以控制不受处理的个体特征(固定效应),从而降低由于遗漏变量所导致的偏误。
3. 处理多重处理:PSIR 模型可以处理多个处理变量,从而分析多个处理变量对结果变量的影响。
4. 适用于大规模数据:PSIR 模型可以处理大规模数据,尤其是在个体之间存在大量观测数据的情况下。
PSIR 模型是一种强大的统计分析方法,可以处理观测数据中的选择性偏差问题,提高因果推断和线性回归分析的准确性。
在实际应用中,根据数据特点和需求,可以选择合适的模型进行分析和预测。
倾向得分匹配法(PSM)举例及stata实现

倾向得分匹配法(PSM )举例及stata 实现——读书笔记【例】培训对工资的效应1政策背景:国家支持工作示范项目(National Supported Work,NSW )研究目的:检验接受该项目(培训)与不接受该项目(培训)对工资的影响。
基本思想:分析接受培训组(处理组,treatment group )接受培训行为与不接受培训行为在工资表现上的差异。
但是,现实可以观测到的是处理组接受培训的事实,而处理组没有接受培训会怎样是不可能观测到的,这种状态也成为反事实(counterfactual )。
匹配法就是为了解决这种不可观测事实的方法。
在倾向得分匹配方法(Propensity Score Matching )中,根据处理指示变量将样本分为两个组,一是处理组,在本例中就是在NSW 实施后接受培训的组;二是对照组(comparison group ),在本例中就是在NSW 实施后不接受培训的组。
倾向得分匹配方法的基本思想是,在处理组和对照组样本通过一定的方式匹配后,在其他条件完全相同的情况下,通过接受培训的组(处理组)与不接受培训的组(对照组)在工资表现上的差异来判断接受培训的行为与工资之间的因果关系。
变量定义:变量 定义TREAT * 处理指示变量,1表示接受培训(处理组),0表示没有接受培训(对照组)AGE 年龄(年)EDUC 受教育年数(年)BLACK 种族虚拟变量,黑人时,1BLACK =HSIP 民族虚拟变量,西班牙人时,=1HSIPMARR婚姻状况虚拟变量,已婚,1MARR = 74RE 1974年实际工资(1982年美元)75RE 1975年实际工资78RE 1978年实际工资74U 当在1974年失业,741U =75U当在1975年失业,751U = NODEGREE 当12EDUC <时,1NODEGREE =,否则为0 AGESQAGE AGE × 1 本例选自Cameron&Trivedi 《微观计量经济学:方法与应用》(中译本,上海财经大学出版社,2010)pp794-800 所有数据及程序均来自于本书的配套网站(/mmabook/mmaprograms.html )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方法三:分层匹配法 (stratification matching)
方法四:核匹配法 (kernel matching)
核匹配是构造一个虚拟对象来匹配处理组,构造的原则是对现有的 控制变量做权重平均,权重的取值与处理组、控制组PS值差距呈反 向相关关系。
方法四:核匹配法 (kernel matching)
命令
set seed 10101
attr re78 treat $x,comsup boot reps($breps) dots logit radius(0.001)
方法二:半径匹配法 (radius matching)
方法三:分层匹配法 (stratification matching)
内容:分层匹配法是根据估计的倾向得分将全 部样本分块,使得每块的平均倾向得分在处理 组和控制组中相等。 优点:Cochrane ,Chambers(1965)指出五个区 就可以消除95%的与协变量相关的偏差。这个方 法考虑到了样本的分层问题或聚类问题。就是 假定:每一层内的个体样本具有相关性,而各 层之间的样本不具有相关性。
block中的描述性统计
运用得分进行样 本匹配并比较
方法一:最邻近方法 (nearest neighbor matching)
含义:最邻近匹配法是最常用的一种匹配方法, 它把控制组中找到的与处理组个体倾向得分差 异最小的个体,作为自己的比较对象 。
优点:按处理个体找控制个体,所有处理个体 都会配对成功,处理组的信息得以充分使用。
匹配处理组
满足两个假设:A共同支撑假设B平行假设
ATT(平均处理效应的衡量)
以半径匹配为例:psmatch2 treat $x,out(re78) ate radius caliper(0.01)
1 2 3
1、处理组平均效应(ATT) 2、控制组平均效应(ATU) 3、总体平均效应(ATE)
ATT(平均处理效应的衡量)
倾向打分
2.通过logit模型进行倾向打分 命令:pscore treat $x,pscore(mypscore) blockid(myblock) comsup numblo(5) level(0.05) logit
注:$表示引用宏变量
pscore结果
倾向值分布
倾向值分布
block中样本的分布
倾向值匹配法 (PSM)
Q:为什么要使用PSM?
A:解决样本选择偏误带来的内生性问题 例:上北大有助于提高收入吗?
样本选择偏误:考上北大的孩子本身就很出色(聪明、有毅力、能行业(一维配对) 同行业、规模相当(二维配对) 同行业、规模相当、股权结构相当、……(多维配对)??? PSM:把多个维度的信息浓缩成一个(降维:多维到一维)
ps值的计算
psmatch2 treat $x,out(re78) 倾向得分的含义是,在给定X的情况下,样本处理的概率值。利用 logit模型估计样本处理的概率值。概率表示如下: P(x)=Pr[D=1|X]=E[D|X]
匹配处理组
最近邻匹配 命令:psmatch2 treat $x(if soe==1),out(re78) neighbor(2) ate 半径匹配 命令:psmatch2 treat $x,out(re78) ate radius caliper(0.01) 核匹配 命令:psmatch2 treat $x,out(re78) ate kernel
缺点:由于不舍弃任何一个处理组,很可能有 些配对组的倾向得分差距很大,也将其配对, 导致配对质量不高,而处理效应ATT的结果中也 会包含这一差距,使得ATT精确度下降。
方法一:最邻近方法 (nearest neighbor matching)
命令
set seed 10101(产生随机数种子)
attnd re78 treat $x,comsup boot reps($breps) dots logit
缺点:如果在每个区内找不到对照个体,那么 这类个体的信息,会丢弃不用。总体配对的数 量减少。
方法三:分层匹配法 (stratification matching)
命令
set seed 10101
atts re78 treat,pscore(mypscore) blockid(myblock) comsup boot reps($breps) dots
核匹配的Bootstrap检验
倾向打分
1.设定宏变量
(1)设定宏变量breps表示重复抽样200次
命令:global breps 200
(2)设定宏变量x,表示age agesq educ educsq married black hisp re74 re75 re74sq re75sq u74black
命令:global x age agesq educ educsq married black hisp re74 re75 re74sq re75sq u74black
命令:global x age agesq educ educsq married black hisp re74 re75 re74sq re75sq u74black
匹配变量的筛选
2.初步设定 logit treat $x
匹配变量的筛选
3.逐步回归 stepwise,pr(0.1):logit treat $x
方法一:最邻近方法 (nearest neighbor matching)
方法二:半径匹配法 (radius matching)
半径匹配法是事先设定半径,找到所有设定半径范围内的单位圆中 的控制样本,半径取值为正。随着半径的降低,匹配的要求越来越 严。
方法二:半径匹配法 (radius matching)
不可观测数据, 采用配对者的
收入来代替
实例介绍
实例介绍
研究问题:培训对工资的效应
基本思想:分析接受培训行为与不接受培训行为在工资表现上的差 异。但是,现实可以观测到的是处理组接受培训的事实,而如果处 理组没有接受培训会怎么样是不可观测的,这种状态称为反事实。 匹配法就是为了解决这种不可观测的事实的方法。
实例介绍
分组:在倾向值匹配法中,根据处理指示变量 将样本分为两个组。处理组,在本例中就是在 NSW(国家支持工作示范项目)实施后接受培 训的组;控制组,在本例中就是在NSW实施后 不接受培训的组。 研究目的:通过对处理组和对照组的匹配,在 其他条件完全相同的情况下,通过接受培训的 组(处理组)与不接受培训的组(控制组)在 工资表现上的差异来判断接受培训的行为与工 资之间的因果关系。
变量定义
re78
1978年实际工资
u74 agesq
当在1974年失业,u74=1 age*age
educsq educ*educ
re74sq re74*re74
re75sq re75*re75
u74blcak u74*blcak
倾向打分
OLS回归结果
工资的变化到底是来自个体的异质性 性还是培训?
ATT(Average Treatment Effect on the Treated) 平均处理效应的衡量
运用得分进行样本匹配并比较,估计出ATT值。 ATT=E[Y(1)-Y(0) |T=1] Y(1):Stu PK 上北大后的年薪 Y(0): Stu PK 假如不上北大的年薪
可观测数据
ATT=12W-9W=3W
命令
set seed 10101
attk re78 treat $x,comsup boot reps($breps) dots logit
方法四:核匹配法 (kernel matching)
psmatch2
匹配变量的筛选
1.设定宏变量
设定宏变量x,表示age agesq educ educsq married black hisp re74 re75 re74sq re75sq u74black
变量定义
变量 treat age educ black hsip marr re74 re75
定义 接受培训(处理组)表示1,没有接受培训(控制组)表示0 年龄 受教育年数 种族虚拟变量,黑人时,black=1 民族虚拟变量,西班牙人时,hsip=1 婚姻状况虚拟变量,已婚,marr=1 1974年实际工资 1975年实际工资
配对过程中的两个核心问题 (1)
Q1:哪个样本更好一些?
A1:Sample2较好:比较容易满足共 同支撑假设(common support assumption)
配对过程中的两个核心问题 (2)
Q2:stu c1,c2,c3三人中,谁是stu PK的最佳配对对象?
A2:stu c3是最佳配对对象,比较容易满足平行假设(balancing assumption)
匹配前后变量的差异对比 命令:pstest re78 $x(pstest re78 $x,both graph)
匹配前后密度函数图
twoway (kdensity _ps if _treat==1, legend(label(1 "Treat"))) (kdensity _ps if (_wei!=1&_wei!=.), legend(label(2 "Control"))), xtitle("Pscore") title("After Matching")
