统计学(第六版)贾俊平课后习题答案
统计学课后答案(贾俊平版)人大出版之欧阳引擎创编

第三章节:数据的图表展示 (1)欧阳引擎(2021.01.01)第四章节:数据的概括性度量 (15)第六章节:统计量及其抽样分布 (26)第七章节:参数估计 (28)第八章节:假设检验 (38)第九章节:列联分析 (41)第十章节:方差分析 (43)3.1 为评价家电行业售后服务的质量,随机抽取了由100个家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C一般;D.较差;E.差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C E E A B D D C A D B C C A E D C B CBCEDBCCBC要求:(1)指出上面的数据属于什么类型。
顺序数据(2)用Excel 制作一张频数分布表。
用数据分析——直方图制作:(3)绘制一张条形图,反映评价等级的分布。
用数据分析——直方图制作:(4)绘制评价等级的帕累托图。
逆序排序后,制作累计频数分布表:接收 频数 频率(%) 累计频率(%) C 32 32 32 B 21 21 53 D 17 17 70 E 16 16 86 A 14 14 1003.2 某行业管理局所属40个企业2002年的产品销售收入数据如下:152124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 9788123115119138112146113126要求:(1)根据上面的数据进行适当的分组,编制频数分布表,并计接收频率E 16 D 17 C 32 B 21 A14算出累积频数和累积频率。
统计学课后题答案(袁卫_庞皓_曾五一_贾俊平_)

版权归wagxjysys所有违者必究第1章绪论1.什么是统计学?怎样理解统计学与统计数据的关系?2.试举出日常生活或工作中统计数据及其规律性的例子。
3..一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此,他们开始检查供货商的集装箱,有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆,每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求:(1)描述总体;(2)描述研究变量;(3)描述样本;(4)描述推断。
答:(1)总体:最近的一个集装箱内的全部油漆;(2)研究变量:装满的油漆罐的质量;(3)样本:最近的一个集装箱内的50罐油漆;(4)推断:50罐油漆的质量应为4.536×50=226.8 kg。
4.“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分,选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中,两个品牌不做外观标记),请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求:(1)描述总体;(2)描述研究变量;(3)描述样本;(4)一描述推断。
答:(1)总体:市场上的“可口可乐”与“百事可乐”(2)研究变量:更好口味的品牌名称;(3)样本:1000名消费者品尝的两个品牌(4)推断:两个品牌中哪个口味更好。
第2章统计数据的描述——练习题●1.为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C(1) 指出上面的数据属于什么类型;(2)用Excel制作一张频数分布表;(3) 绘制一张条形图,反映评价等级的分布。
贾俊平第六版统计学课后思考题答案——张云飞

第一章导论1.什么是统计学统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。
2.解释描述统计和推断统计描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
推断统计是研究如何利用样本数据来推断总体特征的统计方法。
3.统计数据可以分为哪几种类型?不同类型的数据各有什么特点?分类数据:是只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,是用文字来表述的。
顺序数据:是只能归于某一有序类别的非数字型数据。
虽然也有列别,但这些类别是有序的。
数值型数据:是按数字尺度测量的观察值,其结果表现为具体的数值。
4.解释分类数据、顺序数据和数值型数据的含义分类数据和顺序数据说明的是事物的品质特征,通常是用文字来表述的,其结果均表现为类别,因此也可统称为定性数据或品质数据;数值型数据说明的是现象的数量特征,通常是用数值来表现的,因此也可称为定量数据或数量数据。
5.举例说明总体、样本、参数、统计量、变量这几个概念总体是包含所研究的全部个体(数据)的集合;样本是从总体中抽取的一部分元素的集合;参数是用来描述总体特征的概括性数字度量;统计量是用来描述样本特征的概括性数字度量;变量是说明现象某种特征的概念。
比如我们欲了解某市的中学教育情况,那么该市的所有中学则构成一个总体,其中的每一所中学都是一个个体,我们若从全市中学中按某种抽样规则抽出了10所中学,则这10所中学就构成了一个样本。
在这项调查中我们可能会对升学率感兴趣,那么升学率就是一个变量。
我们通常关心的是全市的平均升学率,这里这个平均值就是一个参数,而此时我们只有样本的有关升学率的数据,用此样本计算的平均值就是统计量。
6.变量可以分为哪几类分类变量:一个变量由分类数据来记录就称为分类变量。
顺序变量:一个变量由顺序数据来记录就称为顺序变量。
数值型变量:一个变量由数值型数据来记录就称为数值型变量。
离散变量:可以取有限个值,而且其取值都以整位数断开,可以一一例举。
贾俊平统计学第一章课后思考题答案

1.什么是统计学?答:统计学是关于数据的科学,它所提供的是一套有关数据收集、处理、分析、解释并从数据中得出结论的方法,统计所研究的是来自各领域的数据。
数据收集即取得统计数据;数据处理是将数据用图表等形式展示出来;数据分析则是选择适当的统计方法研究数据,并从数据中提取有用信息进而得出结论。
2.解释描述统计和推断统计。
答:数据分析所用的方法可分为描述统计方法和推断统计方法。
(1)描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计方法。
比如,对产品的质量进行检验,往往是破坏性的,不可能对每个产品进行测量。
这就需要抽取部分个体即样本进行测量,然后根据获得的样本数据对所研究的总体特征进行推断,这就是推断统计要解决的问题。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?答:统计数据是对现象进行测量的结果,可以从不同角度对统计数据进行分类:(1)按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
①在分类数据中,各类别之间是平等的并列关系,无法区分优劣或大小,各类别之间的顺序是可以改变的;②顺序数据也表现为类别,但这些类别之间是有顺序的;③数值型数据具有分类数据和顺序数据的特点,并且还可以进行加、减、乘、除运算。
(2)按照统计数据的收集方法,可以将其分为观测数据和实验数据。
①观测数据是通过调查或观测而收集到的数据,这类数据是在没有对事物进行人为控制的条件下得到的,有关社会经济现象的统计数据几乎都是观测数据;②实验数据是在实验中通过控制实验对象收集到的数据,自然科学领域的大多数数据都是实验数据。
(3)按照被描述的现象与时间的关系,可以将统计数据分为截面数据和时间序列数据。
①截面数据是在相同或近似相同的时间点上收集的数据,这类数据通常是在不同的空间上获得的,用于描述现象在某一时刻的变化情况;②时间序列数据是在不同时间上收集到的数据,这类数据是按时间顺序收集到的,用于描述现象随时间变化的情况。
贾俊平《统计学》课后习题及详解(统计量及其抽样分布)【圣才出品】

第6章 统计量及其抽样分布一、思考题1.什么是统计量?为什么要引进统计量?统计量中为什么不含任何未知参数? 答:(1)设是从总体中抽取的容量为的一个样本,如果由此样本构造一个函数,不依赖于任何未知参数,则称函数是一个统计量。
(2)在实际应用中,当从某总体中抽取一个样本后,并不能直接应用它去对总体的有关性质和特征进行推断,这是因为样本虽然是从总体中获取的代表,含有总体性质的信息,但仍较分散。
为了使统计推断成为可能,首先必须把分散在样本中关心的信息集中起来,针对不同的研究目的,构造不同的样本函数。
(3)统计量是样本的一个函数。
由样本构造具体的统计量,实际上是对样本所含的总体信息按某种要求进行加工处理,把分散在样本中的信息集中到统计量的取值上,不同的统计推断问题要求构造不同的统计量,所以统计量不包含未知参数。
2.判断下列样本函数哪些是统计量?哪些不是统计量?12n X X X ,,…,X n 12()n T X X X ,,…,12()n T X X X ,,…,1121021210310410()/10min()T X X X T X X X T X T X μμσ=+++==-=-…,,…,()/答:统计量中不能含有未知参数,故、是统计量,、不是统计量。
3.什么是次序统计量?答:设是从总体中抽取的一个样本,称为第个次序统计量,它是样本满足如下条件的函数:每当样本得到一组观测值…,时,其由小到大的排序中,第个值就作为次序统计量的观测值,而称为次序统计量,其中和分别为最小和最大次序统计量。
4.什么是充分统计量?答:在统计学中,假如一个统计量能把含在样本中有关总体的信息一点都不损失地提取出来,那对保证后边的统计推断质量具有重要意义。
统计量加工过程中一点信息都不损失的统计量通常称为充分统计量。
5.什么是自由度?答:统计学上的自由度是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的变量的个数。
(完整版)贾俊平统计学[第六版]思考题答案解析.docx
![(完整版)贾俊平统计学[第六版]思考题答案解析.docx](https://img.taocdn.com/s3/m/b6a8183fa0116c175e0e4821.png)
第一章:1、什么是统计学?统计学是一门收集、分析、表述、解释数据的科学和艺术。
2、描述统计:研究的是数据收集、汇总、处理、图表描述、概括与分析等统计方法。
推断统计:研究的是如何利用样本数据来推断总体特征。
3、统计学据可以分成哪几种类型,个有什么特点?按照计量尺度不同,分为:分类数据、顺序数据、数值型数据。
分类数据:只能归于某一类别的,非数字型数据。
顺序数据:只能归于某一有序类别的,非数字型数据。
数值型数据:按数字尺度测量的观察值,结果表现为数值。
按收集方法不同。
分为:观测数据、和实验数据观测数据:通过调查或观测而收集到的数据;不控制条件;社会经济领域实验数据:在试验中收集到的数据;控制条件;自然科学领域。
按时间不同,分为:截面数据、时间序列数据截面数据:在相同或近似相同的时间点上收集的数据。
时间序列数据:在不同时间收集的数据。
4、举例说明总体、样本、参数、统计量、变量这几个概念。
总体:是包含全部研究个体的集合,包括有限总体和无限总体(范围、数目判定)样本:从总体中抽取的一部分元素的集合。
参数:用来描述总体特征的概括性数字度量。
(平均数、标准差、比例等)统计量:用来描述样本特征的概括性数字度量。
(平均数、标准差、比例等)变量:是说明样本某种特征的概念,其特点:从一次观察到下一次观察结果会呈现出差别或变化。
(商品销售额、受教育程度、产品质量等级等)(对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
)5、变量可以分为哪几类?分类变量:说明事物类别;取值是分类数据。
顺序变量:说明事物有序类别;取值是顺序数据数值型变量:说明事物数字特征;取值是数值型数据。
变量也可以分为:随机变量和非随机变量;经验变量和理论变量6、举例说明离散型变量和连续型变量。
统计学(第六版)贾俊平-课后习题及答案

目录第一章P10 (1)第二章P34 (2)第三章P66 (3)第四章P94 (8)第七章P176 (11)第八章P212 (15)第10 章P258 (17)第11 章P291 (21)第13 章P348 (26)第14 章P376 (30)第一章P10一、思考题1.1什么是统计学?1.2解释描述统计和推断统计。
1.3统计数据可分为哪几种类型?不同类型的数据各有什么特点?1.4解释分类数据、顺序数据和数值型数据的含义。
1.5举例说明总体、样本、参数、统计量、变量这几个概念。
1.6变量可分为哪几类?1.7举例说明离散型变量和连续型变量。
1.8请举出统计应用的几个例子。
1.9请举出应用统计的几个领域。
1.1 指出下面变量的类型:(1)年龄(2)性别(3)汽车产量(4)员工对企业某项改革措施的态度(赞成、中立、反对)(5)购买商品时的支付方式(现金、信用卡、支票)(1)数值型变量。
(2)分类变量。
(3)离散型变量。
(4)顺序变量。
(5)分类变量。
1.2 某研究部门准备抽取 2000 个职工家庭推断该城市所有职工家庭的年人均收入。
要求:(1)描述总体和样本。
(2)指出参数和统计量。
(1)总体是该市所有职工家庭的集合;样本是抽中的 2000 个职工家庭的集合。
(2)参数是该市所有职工家庭的年人均收入;统计量是抽中的 2000 个职工家庭的年人均收入。
1.3 一家研究机构从 IT 从业者中随机抽取 1000 人作为样本进行调查,其中 60%的人回答他们的月收入在5000 元以上,50%的人回答他们的消费支付方式是用信用卡。
回答下列问题:(1)这一研究的总体是什么?(2)月收入是分类变量、顺序变量还是数值型变量?(3)消费支付方式是分类变量、顺序变量还是数值型变量?(4)这一研究涉及截面数据还是时间序列数据?(1)总体是所有 IT 从业者的集合。
(2)数值型变量。
(3)分类变量。
(4)截面数据。
1.4 一项调查表明,消费者每月在网上购物的平均花费是 200 元,他们选择在网上购物的主要原因是“价格便宜”。
统计学习题答案-贾俊平
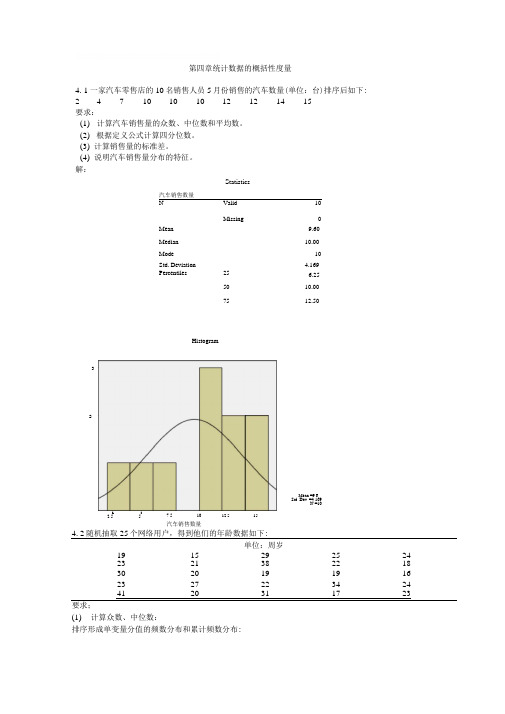
第四章统计数据的概括性度量4. 1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下: 2 4 7 10 10 10 12 12 14 15要求:(1) 计算汽车销售量的众数、中位数和平均数。
(2) 根据定义公式计算四分位数。
(3) 计算销售量的标准差。
(4) 说明汽车销售量分布的特征。
解:汽车销售数量StatisticsNValid 10Missing0 Mean9.60Median10.00Mode10Std. Deviation4.169 Percentiles25 6.255010.007512.504. 2随机抽取25个网络用户,得到他们的年龄数据如下:单位:周岁19 15 29 25 24 23 21 38 22 18 30 20 19 19 16 23 27 22 34 24 41 20 31 17 23要求;(1) 计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:LI2.557.5 10汽车销售数量12.5 15Mean =9.6Std. Dev. =4.169N =10Histogram32网络用尸的年龄FrequencyPercent Cumulative FrequencyCumulative PercentValid15 14.0 14.016 1 4.0 2 8.0 17 1 4.0 3 12.0 18 1 4.0 4 16.0 19 3 12.0 7 28.0 20 2 8.0 9 36.0 21 1 4.0 10 40.0 22 2 8.0 12 48.0 233 12.0 15 60.0 24 2 8.0 17 68.0 25 1 4.0 18 72.0 27 1 4.0 19 76.0 29 1 4.0 20 80.0 30 1 4.0 21 84.0 31 1 4.0 22 88.0 34 1 4.0 23 92.0 38 1 4.0 24 96.0 41 1 4.0 25100.0Total25100.0从频数看出,众数 Mo 有两个:19、23;从累计频数看,中位数 Me=23。
贾俊平《统计学》课后习题及详解(导论)【圣才出品】

第1章导论一、思考题1.什么是统计学?答:统计学是关于数据的科学,它所提供的是一套有关数据收集、处理、分析、解释并从数据中得出结论的方法,统计研究的是来自各领域的数据。
数据收集也就是取得统计数据;数据处理是将数据用图表等形式展示出来;数据分析则是选择适当的统计方法研究数据,并从数据中提取有用信息进而得出结论。
2.解释描述统计和推断统计。
答:数据分析所用的方法可分为描述统计方法和推断统计方法。
(1)描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计方法。
比如,对产品的质量进行检验,往往是破坏性的,不可能对每个产品进行测量。
这就需要抽取部分个体即样本进行测量,然后根据获得的样本数据对所研究的总体特征进行推断,这就是推断统计要解决的问题。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?答:统计数据是对现象进行测量的结果,可以从不同角度对统计数据进行分类:(1)按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
①在分类数据中,各类别之间是平等的并列关系,无法区分优劣或大小,各类别之间的顺序是可以改变的;②顺序数据也表现为类别,但这些类别之间是可以比较顺序的;③数值型数据具有分类数据和顺序数据的特点,并且还可以进行加、减、乘、除运算。
(2)按照统计数据的收集方法,可以将其分为观测数据和实验数据。
①观测数据是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的,有关社会经济现象的统计数据几乎都是观测数据;②实验数据则是在实验中控制实验对象而收集到的数据,自然科学领域的大多数数据都为实验数据;(3)按照被描述的现象与时间的关系,可以将统计数据分为截面数据和时间序列数据。
①截面数据是在相同或近似相同的时间点上收集的数据,这类数据通常是在不同的空间上获得的,用于描述现象在某一时刻的变化情况;②时间序列数据是在不同时间上收集到的数据,这类数据是按时间顺序收集到的,用于所描述现象随时间变化的情况。
(完整word版)统计学贾俊平课后答案目前最全

8.2 一种元件,要求其使用寿命不得低于700小时。
现从一批这种元件中随机抽取36件,测得其平均寿命为680小时。
已知该元件寿命服从正态分布,σ=60小时,试在显著性水平0.05下确定这批元件是否合格。
解:H 0:μ≥700;H 1:μ<700 已知:x =680 σ=60由于n=36>30,大样本,因此检验统计量:x z ==-2 当α=0.05,查表得z α=1.645。
因为z <-z α,故拒绝原假设,接受备择假设,说明这批产品不合格。
8.38.4 糖厂用自动打包机打包,每包标准重量是100千克。
每天开工后需要检验一次打包机工作是否正常。
某日开工后测得9包重量(单位:千克)如下:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5已知包重服从正态分布,试检验该日打包机工作是否正常(a =0.05)?解:H 0:μ=100;H 1:μ≠100 经计算得:x =99.9778 S =1.21221检验统计量:x t =-0.055 当α=0.05,自由度n -1=9时,查表得()29t α=2.262。
因为t <t α,样本统计量落在接受区域,故接受原假设,拒绝备择假设,说明打包机工作正常。
8.5 某种大量生产的袋装食品,按规定不得少于250克。
今从一批该食品中任意抽取50袋,发现有6袋低于250克。
若规定不符合标准的比例超过5%就不得出厂,问该批食品能否出厂(a =0.05)?解:解:H 0:π≤0.05;H 1:π>0.05已知: p =6/50=0.12检验统计量:Z ==2.271当α=0.05,查表得z α=1.645。
因为z >z α,样本统计量落在拒绝区域,故拒绝原假设,接受备择假设,说明该批食品不能出厂。
8.68.7 某种电子元件的寿命x(单位:小时)服从正态分布。
现测得16只元件的寿命如下: 159 280 101 212 224 379 179 264222 362 168 250 149 260 485 170问是否有理由认为元件的平均寿命显著地大于225小时(a =0.05)?解:H 0:μ≤225;H 1:μ>225 经计算知:x =241.5 s =98.726检验统计量:x t =0.669 当α=0.05,自由度n -1=15时,查表得()15t α=1.753。
统计学贾俊平课后习题答案完整版

统计学贾俊平课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】附录:教材各章习题答案第1章统计与统计数据1.1(1)数值型数据;(2)分类数据;(3)数值型数据;(4)顺序数据;(5)分类数据。
1.2(1)总体是“该城市所有的职工家庭”,样本是“抽取的2000个职工家庭”;(2)城市所有职工家庭的年人均收入,抽取的“2000个家庭计算出的年人均收入。
1.3(1)所有IT从业者;(2)数值型变量;(3)分类变量;(4)观察数据。
1.4(1)总体是“所有的网上购物者”;(2)分类变量;(3)所有的网上购物者的月平均花费;(4)统计量;(5)推断统计方法。
1.5(略)。
1.6(略)。
第2章数据的图表展示2.1(1)属于顺序数据。
(2)频数分布表如下(4)帕累托图(略)。
2.2(1)频数分布表如下2.3频数分布表如下2.5(1)排序略。
(2)频数分布表如下2.6(3)食品重量的分布基本上是对称的。
2.72.8(1)属于数值型数据。
2.9(1)直方图(略)。
(2)自学考试人员年龄的分布为右偏。
2.10A 班分散,且平均成绩较A 班低。
2.11 (略)。
2.12 (略)。
2.13 (略)。
2.14 (略)。
2.15 箱线图如下:(特征请读者自己分析) 第3章 数据的概括性度量3.1(1)100=M ;10=e M ;6.9=x 。
(2)5.5=L Q ;12=U Q 。
(3)2.4=s 。
(4)左偏分布。
3.2(1)190=M ;23=e M 。
(2)5.5=L Q ;12=U Q 。
(3)24=x ;65.6=s 。
(4)08.1=SK ;77.0=K 。
(5)略。
3.3 (1)略。
(2)7=x ;71.0=s 。
(3)102.01=v ;274.02=v 。
(4)选方法一,因为离散程度小。
3.4 (1)x =(万元);M e= 。
统计学课后题答案(袁卫庞皓曾五一贾俊平)

第1章绪论5.简要说明抽样误差和非抽样误差。
答:统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的,从理论上看,这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差,它是不可避免的,但可以控制的。
b5E2RGbCAP6.一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此,他们开始检查供货商的集装箱,有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆,每一罐的质量精确到4位小数。
装满的油漆罐应为 4.536 kg。
要求:p1EanqFDPw(1>描述总体;(2>描述研究变量;(3>描述样本;(4>描述推断。
答:(1>总体:最近的一个集装箱内的全部油漆;(2>研究变量:装满的油漆罐的质量;(3>样本:最近的一个集装箱内的50罐油漆;(4>推断:50罐油漆的质量应为4.536×50=226.8kg。
7.“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝实验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分,选择了1000名消费者进行匿名性质的品尝实验(即在品尝实验中,两个品牌不做外观标记>,请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求:DXDiTa9E3d(1>描述总体;(2>描述研究变量;(3>描述样本;(4>描述推断。
答:(1>总体:市场上的“可口可乐”与“百事可乐”(2>研究变量:更好口味的品牌名称;(3>样本:1000名消费者品尝的两个品牌(4>推断:两个品牌中哪个口味更好。
第2章统计数据的描述思考题4. 一组数据的分布特征可以从哪几个方面进行测度?答:数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
统计学课后答案(贾俊平版)人大出版之欧阳语创编

第三章节:数据的图表展示 (1)第四章节:数据的概括性度量 (15)第六章节:统计量及其抽样分布 (26)第七章节:参数估计 (28)第八章节:假设检验 (38)第九章节:列联分析 (41)第十章节:方差分析 (43)3.1 为评价家电行业售后服务的质量,随机抽取了由100个家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C一般;D.较差;E.差。
调查结果如下:B EC C AD C B AE D A C B C D E C E E A D B C C A E D C B B A C D E A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C E E A B D D C A D B C C A E D C B CBCEDBCCBC要求:(1)指出上面的数据属于什么类型。
顺序数据(2)用Excel 制作一张频数分布表。
用数据分析——直方图制作:(3)绘制一张条形图,反映评价等级的分布。
用数据分析——直方图制作: (4)绘制评价等级的帕累托图。
逆序排序后,制作累计频数分布表:接收 频数 频率(%) 累计频率(%) C 32 32 32 B 21 21 53 D 17 17 70 E 16 16 86 A 14 14 1003.2 某行业管理局所属40个企业2002年的产品销售收入数据如下:152124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 9788123115119138112146113126接收 频率E 16 D 17 C 32 B 21 A14要求:(1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率。
统计学第四章习题答案解析贾俊平

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
贾俊平统计学第六、七章课后习题答案

贾俊平统计学第六、七章课后习题答案6.1解:设每个瓶子的灌装量为X,X?为样本均值,样本容量为n。
由于总体X服从正态分布,样本均值X?也服从正态分布,且均值相同,标准差为σ√n =1√9=13所以P(|X??μ|≤0.3)=P(|X??μ|13≤0.313)=2Φ(0.9)?1=2?0.8159?1=0.6318 7.1(1)已知σ=500,n=15,x=8900,1-α=95%,Z2α=1.96x+Z2αnσ=8900+1.96×15500=(8647,9153)(2)已知σ=500,n=35,x=8900,1-α=95%,Z2α=1.96x+Z2αnσ=8900+1.96×35500=(8734,9066)(3)已知n=35,x=8900,s=500,由于总体方差未知,但为大样本,所以可用样本方差来代替总体方差。
置信水平1-α=90%,Z2α=1.645x+Z2αns=8900+1.645×35500=(8761,9039)(4)已知n=35,x=8900,s=500,由于总体方差未知,但为大样本,所以可用样本方差来代替总体方差。
置信水平1-α=99%,Z2α=2.58x +Z2αn s =8900+2.58×35500=(8682,9118)7.2已知n=36,x =3.3167,s=1.6093(1)当置信水平为90%时,Z 2α=1.645x +Z 2αn s =3.3167+1.645×366093.1=3.3167+0.4532=(2.88,3.76)(2)当置信水平为95%时,Z 2α=1.96x +Z 2αn s =3.3167+1.96×366093.1=3.3167+0.544=(2.80,3.84)(3)当置信水平为99%时,Z 2α=2.58Z2αn s =3.3167+2.58×366093.1=3.3167+0.7305=(2.63,4.01)7.3(1)已知总体服从正态分布,但σ未知,n=50为大样本,α=0.05,Z 2α=1.96,根据样本计算可知x =101.32,s=1.63x +Z 2αn s =101.32+1.96×5063.1=101.32+0.45=(100.87,101.77)(2)由所给样本数据可知样本合格率:p=5045=0.9p +Z2αnp p )1(-=0.9+1.9650)9.0-19.0(=0.9+0.08=(0.82,0.98)7.4由样本数据得x =16.13,σ=0.8706,置信水平1-α=99%,Z 2α=2.58x +Zαn σ=16.13+2.58×58706.0=16.13+0.45=(15.68,16.58)7.5、(1)n=44,p=0.51,置信水平为99%由题意,已知n=44,置信水平1-α=99%,因此检验统计量为:,代入数值计算,总体比例π的置信区间为(31.6%,70.4%) (2)n=300,p=0.82,置信水平为95%由题意可得知96.12=αZ检验统计量为:,代入数值计算,总体比例π的置信区间为(77.7%,86.3%) (3)n=1150,p=0.48,置信水平为90%由题意可得知检验统计量为:,代入数值计算,58.22=αZ np p Z P )1(2-±α)704.0,316.0(194.051.044)51.01(51.058.251.0=+=-??p p Z P )1(2-±α)863.0,777.0(043.082.0300)82.01(82.096.182.0=+=-?+645.12=αZ np p Z P )1(2-±α总体比例π的置信区间为(45.6%,50.4%)7.6、(1)由题意已知n=200,当置信水平为90%时,,检验统计量为代入数据计算可得:置信区间为(18.10%,27.90%) (2)当置信水平为95%时,96.12=αZ ,检验统计量为代入数据计算可得:置信区间为(17.17%,28.83%)7.7、由题意已知置信水平为99%,即1-α=99%,则,估计误差E=200,=1000504.0,456.0(024.048.01150)48.01(48.0645.148.0=+=-?+645.12=αZ np p Z P )1(2-±α%)90.27%,10.18(%90.4%23200%)231%(23645.1%23=±=-?±np p Z P )1(2-±α%)83.28%,17.17(%83.5%23200%)231%(2396.1%23=+=-?+58.22=αZ σ则,即应该取样本量为1677.8、(1)由题意可知n=50,p=32/50=0.64,α=0.05,96 .12=αZ 总体中赞成该项改革的户数比例的置信区间为,代入数据计算:即置信区间为(51%,77%)(2)如果小区管理者预计赞成的比例能达到80%,即π=0.80,估计误差不超过10%,即E=10%,α=0.05,96.12=αZ ,应抽取的样本量为即应该抽取62户进行调查7.9(1)x?=21,s=2,n=50,α=0.1χ0.12?2(50?1)=66.3387,χ1?0.12?2(50?1)=33.9303∴(n?1)s 2χα22≤σ2≤(n?1)s 2χ1?α22(50?1)×2266.3387≤σ2≤(50?1)×2233.9303即2.95≤σ2≤5.78.标准差的置信区间为1.72≤σ≤2.4 (2)x?=1.3,s=0.02,n=15,α=0.1167200100058.22222222≈?==E Z n σαnp p Z P )1(2-±α)77.0,51.0(13.064.050)64.01(64.096.164.0=±=-±621.0)80.01(80.096.1)1(22222=-?=-?=E Z n ππαχ0.12?2(15?1)=23.6848,χ1?0.12?2(15?1)=6.5706∴(n?1)s 2χα22≤σ2≤(n?1)s 2χ1?α22(15?1)×0.02223.6848≤σ2≤(15?1)×0.0226.5706标准差的置信区间为0.015≤σ≤0.029 (3)x?=167,s=31,n=22,α=0.1χ0.12?2(22?1)=32.6706,χ1?0.12?2(22?1)=11.5913∴(n?1)s 2χα22≤σ2≤(n?1)s 2χ1?α22(22?1)×312≤σ2≤(22?1)×312标准差的置信区间为24.85≤σ≤41.73。
统计学贾俊平课后习题答案1

第1章统计与统计数据一、学习指导统计学是处理和分析数据的方法和技术,它几乎被应用到所有的学科检验领域。
本章首先介绍统计学的含义和应用领域,然后介绍统计数据的类型及其来源,最后介绍统计中常用的一些基本概念。
本章各节的主要内容和学习要点如下表所示。
章节主要内容学习要点1.1 统计及其应用领域什么是统计学④概念:统计学,描述统计,推断统计。
统计的应用领域④统计在工商管理中的应用。
④统计的其他应用领域。
1.2 数据的类型分类数据、顺序数据、数值型数据④概念:分类数据,顺序数据,数值型数据。
④不同数据的特点。
观测数据和实验数据④概念:观测数据,实验数据。
截面数据和时间序列数据④概念:截面数据,时间序列数据。
1.3 数据来源数据的间接来源④统计数据的间接来源。
④二手数据的特点。
数据的直接来源④概念:抽样调查,普查。
④数据的间接来源。
④数据的收集方法。
调查方案设计④调查方案的内容。
数据质量④概念。
抽样误差,非抽样误差。
④统计数据的质量。
1.4 统计中的几个基本概念总体和样本④概念:总体,样本。
参数和统计量④概念:参数,统计量。
变量④概念:变量,分类变量,顺序变量,数值型变量,连续型变量,离散型变量。
二、主要术语1. 统计学:收集、处理、分析、解释数据并从数据中得出结论的科学。
2. 描述统计:研究数据收集、处理和描述的统计学分支。
3. 推断统计:研究如何利用样本数据来推断总体特征的统计学分支。
4. 分类数据:只能归于某一类别的非数字型数据。
5. 顺序数据:只能归于某一有序类别的非数字型数据。
6. 数值型数据:按数字尺度测量的观察值。
7. 观测数据:通过调查或观测而收集到的数据。
8. 实验数据:在实验中控制实验对象而收集到的数据。
9. 截面数据:在相同或近似相同的时间点上收集的数据。
10. 时间序列数据:在不同时间上收集到的数据。
11. 抽样调查:从总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来推断总体特征的数据收集方法。
贾俊平《统计学》考研真题(含复试)与典型习题详解(第6版)

目录分析
1.2课后习题详解
1.1复习笔记
1.3典型习题详解
2.2课后习题详解
2.1复习笔记
2.3典型习题详解
3.2课后习题详解
3.1复习笔记
3.3典型习题详解
4.2课后习题详解
4.1复习笔记
4.3典型习题详解
5.2课后习题详解
5.1复习笔记
5.3典型习题详解
6.2课后习题详解
6.1复习笔记
12.1复习笔记
12.3典型习题详解
13.2课后习题详解
13.1复习笔记
13.3典型习题详解
14.2课后习题详解
14.1复习笔记
14.3典型习题详解
作者介绍
谢谢观看
6.3典型习题详解
7.2课后习题详解
7.1复习笔记
7.3典型习题详解
8.2课后习题详解
8.1复习笔记
8.3典型习题详解
9.2课后习题详解
9.1复习笔记
9.3典型习题详解
10.2课后习题详解
10.1复习笔记
10.3典型习题详解
11.2课后习题详解
11.1复习笔记
11.3典型习题详解
12.2课后习题详解
精彩摘录
统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。 参数是用来描述总体特征的概括性数字度量 不论如何偏斜,中位数总是在众数与算术平均数之间。经验表明,在适度偏斜的情况下,众数与中位数的距 离约为中位数与算术平均数距离的2倍。 概率抽样最主要的优点是可以依据调查结果,计算估计量误差,从而得到对总体目标量进行推断的可靠程度。 从另一个方面讲,也可以按照要求的精确度,计算必要的样本单位数目。 统计推断的三个中心内容:抽样分布、参数估计和假设检验。 统计学上的自由度是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的变量的个数 样本方差:样本数据个数减1后除离差平方和。其中样本数据个数减1,即n-1称为自由度 几何平均数主要用于计算比率的平均 控制抽样误差的主要方法是改变样本量,要求的抽样误差越小,所需要的样本量就越大。 概率抽样(随机抽样):指遵循随机原则进行的抽样,总体中每个单位都有一定的机会被选入样本。
统计学第四章习题答案解析贾俊平

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
