梯形练习题精选

合集下载

小学数学四年级梯形练习题

小学数学四年级梯形练习题梯形是数学中常见的平面图形，也是四年级数学学习的重点之一。

通过解梯形练习题，能帮助同学们巩固对梯形的认识和理解。

本文将提供一些小学四年级梯形练习题，希望能够帮助同学们更好地掌握梯形的性质和计算方法。

练习题一：计算梯形的面积1. 如图所示，ABCD是一个梯形，AB平行于CD，AB = 8 cm，CD = 12 cm，高为6 cm。

请计算梯形ABCD的面积。

练习题二：计算梯形的周长2. 梯形EFGH的上底EF = 6 cm，下底GH = 10 cm，侧边FG = 7 cm，高为4 cm。

请计算梯形EFGH的周长。

练习题三：辨析梯形和平行四边形3. 判断下列图形中哪些是梯形，哪些是平行四边形？a)AB = AD = BC = DC，角A = 角B = 角C = 角Db)AB // CD，AC ⊥ CD，AD = 5 cm，BC = 9 cmc)AB // CD，AC ⊥ CD，角A = 角D，角B = 角C练习题四：梯形的性质判断4. 根据下列已知条件，判断TXYW是否为梯形。

a) TY ⊥ XY，WY ⊥ XYb) TX = WY，TY ≠ WX练习题五：应用题5. 甲同学要制作一个梯形花坛，上底长为3 m，下底长为5 m，高为2 m。

他购买了一袋砂土，袋装砂土的重量为20 kg。

问他能够购买多少袋砂土才能够填满整个梯形花坛？以上是一些小学四年级梯形练习题，希望同学们能够通过练习加深对梯形的理解和掌握。

解答这些练习题时，可以先根据梯形的定义和性质进行分析，然后运用相应的计算方法进行求解。

通过反复练习，相信同学们能够在数学学习中取得进步！。

梯形练习题及答案

梯形练习题及答案答案一：梯形练习题及答案一、选择题1. 梯形的两边是平行边，且不等长的四边形，其中不等长的一对边称为（）。

A. 平行边B. 高C. 长边D. 短边2. 梯形中，非平行边的夹角互补，则该梯形是（）。

A. 直角梯形B. 等腰梯形C. 普通梯形D. 等边梯形3. 若梯形的一组对边的夹角为75°，则该梯形的另一组对边的夹角为（）A. 15°B. 30°C. 45°D. 60°4. 若梯形的一组对边的夹角为120°，则该梯形的另一组对边的夹角为（）A. 60°B. 75°C. 90°D. 105°5. 梯形的高等于上底和下底的差，且上底为10 cm，下底为20 cm，那么该梯形的面积为（）㎠。

A. 90B. 100C. 110D. 120二、计算题1. 已知一个梯形的上底长为8 cm，下底长为14 cm，高为6 cm，求该梯形的面积。

解：面积 = (上底长 + 下底长) ×高 ÷ 2= 22 × 6 ÷ 2= 132 ÷ 2= 66 cm²该梯形的面积为66平方厘米。

2. 已知一个梯形的上底长为16 cm，下底长为12 cm，面积为160平方厘米，求该梯形的高。

解：面积 = (上底长 + 下底长) ×高 ÷ 2160 = (16 + 12) ×高 ÷ 2320 = 28 ×高高 = 320 ÷ 28高≈ 11.43 cm该梯形的高约为11.43厘米。

三、综合题在一个梯形中，上底长是下底长的3倍，梯形的高是7 cm，求该梯形的面积。

解：设下底长为x，则上底长为3x。

面积 = (上底长 + 下底长) ×高 ÷ 2= 4x × 7 ÷ 2= 14x ÷ 2= 7x根据题意可得 7x = 7 cm解得 x = 1下底长为1 cm，上底长为3 cm。

梯形面积练习题(优选6篇)

梯形面积练习题(优选6篇）（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如计划总结、合同协议、管理制度、演讲致辞、心得体会、条据书信、好词好句、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as plan summaries, contract agreements, management systems, speeches, insights, evidence letters, good words and sentences, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!梯形面积练习题(优选6篇）梯形面积练习题（1）梯形的面积计算开心预习新课，轻松搞定基础。

梯形面积的计算练习题

梯形面积的计算练习题梯形是一种有两组平行边的四边形，其独特的形状使得计算其面积相对较为复杂。

然而，通过掌握一些基本概念和公式，我们可以轻松地解决梯形面积的计算问题。

本文将提供一些梯形面积的计算练习题，帮助读者熟悉梯形面积的计算方法。

练习题一：给定梯形的上底长为5cm，下底长为9cm，高为4cm，计算其面积。

解答：根据梯形的面积公式，可以计算梯形的面积为：面积 = (上底 + 下底) ×高÷ 2。

代入已知数据，可以得到：面积 = (5 + 9) × 4 ÷ 2 = 28平方厘米。

练习题二：一个梯形的面积为36平方米，上底长为6米，下底长为8米，计算其高。

解答：根据梯形的面积公式，可以得到：面积 = (上底 + 下底) ×高÷ 2。

代入已知数据，可以得到：36 = (6 + 8) ×高÷ 2。

解方程可得：高 = 36 × 2 ÷ (6 + 8) = 7.2米。

练习题三：一个梯形的上底长是下底长的三倍，高为10cm，计算其面积。

解答：根据已知条件，我们可以将上底长表示为x，下底长表示为3x。

根据梯形的面积公式，可以得到：面积 = (上底 + 下底) ×高÷ 2。

代入已知数据，可以得到：面积 = (x + 3x) × 10 ÷ 2 = 20x 平方厘米。

根据题目条件，上底长是下底长的三倍，即x = 3。

代入x的值，可以得到面积为：面积 = 20 × 3 × 3 = 180平方厘米。

练习题四：一个梯形的上底长为12cm，下底长为16cm，面积为120平方厘米，求其高。

解答：根据梯形的面积公式，可以得到：面积 = (上底 + 下底) ×高÷ 2。

代入已知数据120 = (12 + 16) ×高÷ 2。

解方程可得：高 = 120 × 2 ÷ (12 + 16) = 8厘米。

梯形的上底和下底练习题

梯形的上底和下底练习题一、选择题1. 在梯形ABCD中，AD // BC，若AD=6cm，BC=10cm，则梯形ABCD的上底是（）。

A. 6cmB. 10cmC. 8cmD. 12cm2. 梯形的上底与下底的和为18cm，若上底是下底的2倍，则上底的长度为（）。

A. 6cmB. 12cmC. 8cmD. 10cm3. 在等腰梯形中，若上底为8cm，下底为18cm，则腰的长度为（）。

A. 10cmB. 12cmC. 15cmD. 8cm二、填空题1. 在梯形ABCD中，AD // BC，AD=8cm，BC=12cm，则梯形ABCD的周长是______cm。

2. 若梯形的上底为5cm，下底为15cm，高为10cm，则梯形的面积是______cm²。

3. 在等腰梯形中，若上底为6cm，下底为12cm，腰的长度为10cm，则梯形的高是______cm。

三、计算题1. 已知梯形的上底为7cm，下底为17cm，高为5cm，求该梯形的面积。

2. 在等腰梯形中，若上底为9cm，下底为21cm，腰的长度为13cm，求梯形的高。

3. 梯形的上底与下底的和为30cm，若上底是下底的1/3，梯形的高为10cm，求梯形的面积。

四、应用题1. 某园林设计师要设计一个上底为10m，下底为20m，高为6m的梯形花坛，求这个花坛的占地面积。

2. 一块梯形菜地的上底为40m，下底为80m，高为30m，求这块菜地的面积。

3. 在一个等腰梯形的水库中，上底为100m，下底为200m，腰的长度为150m，求这个水库的深度。

五、判断题1. 在梯形中，如果上底和下底平行，那么这个梯形一定是等腰梯形。

（）2. 梯形的面积计算公式是：(上底 + 下底) × 高÷ 2。

（）3. 两个完全一样的梯形可以拼成一个平行四边形。

（）六、作图题1. 请画出一个上底为4cm，下底为8cm，高为6cm的梯形。

2. 请画出一个等腰梯形，其中上底为3cm，下底为6cm，腰的长度为4cm。

(完整版)梯形的周长练习题精选

(完整版)梯形的周长练习题精选1. 梯形的定义与性质梯形是一种特殊的四边形，其具有以下特点：- 有两对平行边，分别称为上底和下底。

- 除上底和下底外，其余两边称为斜边。

- 上底和下底之间的距离称为高。

2. 周长的计算公式梯形的周长可以通过以下公式计算：周长 = 上底 + 下底 + 斜边1 + 斜边23. 练题练题1：已知一个梯形的上底长度为10cm，下底长度为15cm，斜边1长度为7cm，斜边2长度为8cm。

求该梯形的周长。

解答：周长 = 10cm + 15cm + 7cm + 8cm= 40cm练题2：一个梯形的上底长度为6cm，下底长度为12cm，周长为30cm。

求该梯形的斜边1和斜边2的长度。

解答：设斜边1的长度为x，斜边2的长度为y，根据周长的计算公式以及已知条件可得：6cm + 12cm + x + y = 30cmx + y = 30cm - 18cmx + y = 12cm练题3：一个梯形的上底长度为8cm，下底长度为16cm，高度为5cm。

求该梯形的周长。

解答：根据梯形的定义和性质，我们可以通过使用勾股定理计算出斜边的长度：斜边1的长度 = 根号下(8cm^2 + 5cm^2)斜边1的长度 = 根号下(64cm^2 + 25cm^2)斜边1的长度≈ 根号下(5189) ≈ 72cm斜边2的长度 = 根号下(16cm^2 + 5cm^2)斜边2的长度 = 根号下(256cm^2 + 25cm^2)斜边2的长度≈ 根号下(6541) ≈ 81cm周长 = 8cm + 16cm + 72cm + 81cm= 177cm4. 总结本文介绍了梯形的定义和性质，并提供了三个练习题，涵盖梯形周长的计算和其他相关问题。

希望通过这些练习题的解答，读者能够更好地理解和应用梯形的周长计算方法。

(完整版)数学梯形练习题含答案

梯形练习题一．选择题 (每小题4分，共40分）1. 如果梯形中位线长20，它被一条对角线分成两段的差为5，那么两底的长分别为 A.15，30 B.25，15 C.30，20 D.以上都不对2. 等腰梯形的上底、下底、高之比为1∶3∶1，则下底角的度数是 A. 30° B. 45° C. 60° D. 75°3. 在等腰梯形ABCD 中，AD ∥BC ，AE ⊥BC 于E ，且AE=AD ，BC=3AD ，则∠B 等于 A. 30° B. 45° C. 60° D. 135°4. 等腰梯形ABCD 中，BC AD //，AC 与BD 交于O 点，图中全等三角形有 A. 两对 B. 四对 C 一对 D. 三对5. 在梯形ABCD 中，AD ∥BC ，AB=AC ，若∠D=110°，∠ACD=30°，则∠BAC 等于 A. 80° B. 90° C. 100° D. 110°6. 等腰梯形中，下列判断正确的是A. 两底相等B. 两个角相等C. 同底上两底角互补D. 对角线交点在对称轴上7. 以线段a=16，b=13为梯形的两底，c=10，d=6为腰画梯形，这样的梯形 A. 只能画出一个 B. 能画出2个 C. 能画出无数个 D. 不能画出 8. 下列命题中：①有两个角相等的梯形是等腰梯形 ②有两条边相等的梯形是等腰梯形 ③两条对角线相等的梯形是等腰梯形④等腰梯形上、下底中点连线，把梯形分成面积相等的两部分其中真命题有 A. 1个 B. 2个 C. 3个 D. 4个9. 若梯形的上底边长为4,中位线长为6,则此梯形的下底长为 A.5 B.8 C.12 D.1610. 如图，在梯形ABCD 中，边AB 与CD 平行，对角线BD 与边AD 的长相等. 若DCB ∠＝110°，30=∠CBD °，那么ADB ∠等于A. 80°B. 90°C. 100°D. 110° 第Ⅱ卷（非选择题共8道填空题8道解答题）请将你认为正确的答案代号填在下表中 1 2 3 4 5 6 7 8 9 10 二.简答题（每小题3分，共24分)11. 若梯形的中位线长为5，面积为20，则这个梯形的高为 . 12. 观察下列图形并填表：梯形个数 1 2 3 4 5 6 ... n周长 5 9 13 17 ...13. 已知直角梯形的一腰与下底的夹角为60º，下底与其中的一腰都等于6，则梯形的中位线的长为14. 用下面的方法来证明：在同一底上的两个角相等的梯形是等腰梯形.（1）如图1，分别延长梯形ABCD 的腰BA ，CD ，设它们相交于点E . 通过证明△EAD 和△EBC 都是________三角形来证明.图1 图2（2）如图2，作梯形ABCD 的高AE ，DF ，通过证明Rt △ABE ≌Rt △DCF 来证明定理. 证明过程：（1）___________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ （2）_____________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 15. 以线段16=a 、13=b 为梯形的两底，以10=c 为一腰，则另一腰长d 的范围是________；16. 在梯形中，不是同一底上的两组角的比值分别为1：3和3：7，则四个角的度数为___________________17. 如果一个直角梯形的两底长分别为7 cm ，12 cm ，斜腰长为13 cm ，那么这个梯形的面积等于_______.18. 等腰梯形的腰长为5cm ，上、下底的长分别为6cm 和12cm ，则它的面积为_______. 三.解答题（共56分)19. 如图，在等腰梯形ABCD 中，AD ∥BC ，AB ＝CD ．（1）利用尺规作底边AD 的中点 E.（保留作图痕迹，不写作法和证明）（2）连结EB 、EC ，求证：∠ABE=∠DCE ．21. 如图，梯形ABCD 中，120AD BC AB DC ADC =∠=∥，，，对角线CA 平分DCB ∠，E 为BC 的中点，试求DCE △与四边形ABED 面积的比．C D B AAＢ E22. 如图，等腰梯形ABCD 中，AD ∥BC ，AB=DC ，AC ⊥BD ，过D 点作DE ∥AC 交BC 的延长线于E 点。

梯形相关练习题

梯形相关练习题梯形是一种特殊的四边形，其中有两边是平行的，被称为上底和下底，而另外两边则不平行，被称为斜边或者腰。

本文将介绍一些梯形的相关练习题，帮助读者巩固对梯形的理解和应用。

练习题一：计算梯形的面积已知一梯形的上底长度为a，下底长度为b，高为h，请计算其面积。

解答：梯形的面积计算公式为：面积 = (上底 + 下底) ×高 ÷ 2代入已知条件，即可计算出梯形的面积。

练习题二：求解梯形的周长已知一梯形的上底长度为a，下底长度为b，斜边长度为c，请计算其周长。

解答：梯形的周长计算公式为：周长 = 上底 + 下底 + 两边之和代入已知条件，即可计算出梯形的周长。

练习题三：寻找梯形的等腰性质已知一梯形的上底长度为a，下底长度为b，斜边长度为c，高为h。

观察该梯形的特点，判断并证明是否存在两边相等的情况。

解答：根据梯形的定义，我们可以发现一条重要性质：梯形的两个底角和两个顶角的和都是180度。

假设上底角为A，下底角为B，则有A + B + 两个顶角的和 = 180度。

由于梯形的两边不平行，所以两个顶角一定相等，即上底角A和下底角B相等。

练习题四：求解梯形的中线长度已知一梯形的上底长度为a，下底长度为b，高为h。

求解梯形的中线长度。

解答：梯形的中线长度计算公式为：中线长度 = (上底 + 下底) ÷ 2代入已知条件，即可计算出梯形的中线长度。

练习题五：求解梯形的对角线长度已知一梯形的上底长度为a，下底长度为b，斜边1长度为c1，斜边2长度为c2。

求解梯形的对角线长度。

解答：梯形的对角线长度计算公式为：对角线长度= √(c1² + c2² -2c1c2cos(θ))其中，θ为斜边1和斜边2之间的夹角。

练习题六：有关梯形的面积比已知两个梯形，其上底分别为a1和a2，下底分别为b1和b2，高分别为h1和h2。

假设这两个梯形的面积满足比例关系，即：面积1：面积2 = k：1。

关于梯形的练习题

关于梯形的练习题一、选择题1. 下列图形中，不是梯形的是（）A. 上底和下底不平行的四边形B. 上底和下底相等的四边形C. 一组对边平行，另一组对边不平行的四边形D. 四个角都是直角的四边形2. 在梯形ABCD中，AD // BC，若AB = 6cm，CD = 8cm，BC = 12cm，则AD的长度可能是（）A. 4cmB. 10cmC. 14cmD. 16cmA. 梯形面积等于上底和下底之和乘以高B. 梯形面积等于上底和下底之差乘以高C. 梯形面积等于上底和下底之和乘以高再除以2D. 梯形面积等于上底和下底之差乘以高再除以2二、填空题1. 在梯形ABCD中，AD // BC，若AB = 5cm，CD = 7cm，高为4cm，则梯形ABCD的面积是______cm²。

2. 等腰梯形的两底分别为6cm和14cm，腰长为10cm，则该等腰梯形的高是______cm。

3. 梯形的上底为8cm，下底为12cm，面积为54cm²，则梯形的高是______cm。

三、解答题1. 已知梯形ABCD中，AD // BC，AB = 4cm，CD = 6cm，高为5cm，求梯形ABCD的面积。

2. 在等腰梯形ABCD中，AD // BC，AB = CD = 8cm，BC = 12cm，求梯形ABCD的面积。

3. 梯形ABCD中，AD // BC，AB = 5cm，CD = 7cm，高为4cm，求梯形ABCD的周长。

4. 已知等腰梯形的两底分别为8cm和18cm，面积为90cm²，求该等腰梯形的高。

5. 在梯形ABCD中，AD // BC，AB = 6cm，CD = 10cm，高为4cm，求梯形ABCD的面积。

6. 等腰梯形的两底分别为10cm和16cm，腰长为12cm，求该等腰梯形的面积。

7. 梯形的上底为12cm，下底为18cm，面积为120cm²，求梯形的高。

8. 已知梯形ABCD中，AD // BC，AB = 8cm，CD = 12cm，高为6cm，求梯形ABCD的周长。

四年级求梯形练习题

四年级求梯形练习题梯形是四边形的一种特殊形式，具有两对平行边的特点。

在四年级的数学学习中，梯形是一个重要的几何图形，本文将为您提供一些梯形练习题，帮助您巩固和提升对梯形的理解和运用能力。

1. 练习题一：计算梯形的面积在梯形ABCD中，AB // CD，AB = 6cm，BC = 5cm，CD = 9cm，AD = 10cm。

求梯形ABCD的面积。

解答：首先，根据题目中给出的条件可知：AB // CD。

在梯形中，我们可以通过计算上底和下底的平均值再乘以高来求得梯形的面积。

上底：AB = 6cm下底：CD = 9cm高：AD = 10cm面积 = ((上底 + 下底) ×高) ÷ 2= ((6 + 9) × 10) ÷ 2= (15 × 10) ÷ 2= 150 ÷ 2= 75cm²所以，梯形ABCD的面积为75平方厘米。

2. 练习题二：寻找梯形的性质观察下面的图形，判断哪个图形是梯形，并解释原因。

解答：A```A______B/ \/ \D____________C```题目给出的图形是ABCD，我们需要判断是否是梯形，并解释原因。

根据梯形的定义，梯形必须具有两对平行边。

观察图形ABCD，可以看到AB和CD是平行的，同时AD和BC也是平行的，因此，图形ABCD是一个梯形。

3. 练习题三：计算梯形的周长在梯形ABCD中，AB // CD，AB = 8cm，BC = 6cm，CD = 12cm，AD = 10cm。

求梯形ABCD的周长。

解答：同样地，根据题目中给出的条件可知：AB // CD。

在梯形中，周长可以通过将四条边的长度相加来求得。

上底：AB = 8cm下底：CD = 12cm左斜边：AD = 10cm右斜边：BC = 6cm周长 = 上底 + 下底 + 左斜边 + 右斜边= 8 + 12 + 10 + 6= 36cm所以，梯形ABCD的周长为36厘米。

中考数学复习《梯形》练习题(含答案)

中考数学复习《梯形》练习题（含答案）一、选择题1.下列命题中，正确的是（）（A ）对顶角相等（B ）梯形的对角线相等（C ）同位角相等（D ）平行四边形对角线相等2.如图，梯形ABCD 的对角线AC 、BD 相交于点O ，△ADO 的面积记作S 1, △BCO 的面积记作S 2,△ABO 的面积记作S 3,△CDO 的面积记作S 4,则下列关系正确是（）A. S 1= S 2B. S 1 × S 2= S 3 × S 4C. S 1 + S 2 = S 4 + S 3D. S 2= 2S 33.如图，在梯形ABCD 中，AB ∥CD ，∠A =60°， ∠B =30°，若AD =CD =6，则AB 的长等于（）． A ．9B ．12C ．633D ．184.如图1，在直角梯形ABCD 中，∠B=90°，DC ∥AB ，动点P 从B 点出发，沿折线B →C →D →A 运动，点P 运动的速度为2个单位长度/秒，若设点P 运动的时间为x 秒，△ABP 的面积为y ，如果y 关于x 的函数图像如图2所示，则M 点的纵坐标为（▲ ） A ．16 B ．48C ．24D ．64 答案 B5. 在直角梯形ABCD 中，AD ∥BC ，∠ABC =90°，AB =BC ，E 为AB 边上一点，∠BCE =15°，且AE =AD ，连接DE 交对角线AC 于H ，连接BH .下列结论：①△ACD ≌△ACE ；②△CDE 为等边三角形；③EHBE =2；④S △EBC S △EHC =AH CH ．其中结论正确的是（）A ．只有①②B ．只有①②④C ．只有③④D ．①②③④ 6.如图，，过上到点的距离分别为的点作的垂线与S 2S 3S 4S 1O DCB AＤＣＰＢＡ图1 ABDE H第5题相交，得到并标出一组黑色梯形，它们的面积分别为．观察图中的规律，求出第10个黑色梯形的面积( )A.32B.54C.76D.86二、填空题1.如图，在梯形ABCD 中，AD ∥BC ，点E 、F 、G 、H 是两腰上的点，AE =EF =FB ，CG =GH =HD ，且四边形EFGH 的面积为6cm 2，则梯形ABCD 的面积为 ▲ cm 2．2.如图，直角梯形ABCD 中， BA CD ，,2AB BC AB ⊥= ，将腰DA 以A 为旋转中心逆时针旋转90°至AE ，连接,,BE DE ABE ∆的面积为3，则CD 的长为 ﹡ ．3.如图，在直角梯形ABCD 中，A B ⊥BC ，AD ∥BC ，EF 为中位线，若AB ＝2b ，EF ＝a ，则阴影部分的面积 .4.如图，已知梯形ABCD 中，AD ∥BC ，∠B =30°，∠C =60°，AD =4， AB =33，则下底BC 的长为 __________．D BCE F A G H （第1题图）60°30°D A5.已知等腰梯形ABCD 的中位线EF 的长为5，腰AD 的长为4，则这个等腰梯形的周长为；6.如图，在梯形ABCD 中，AB ∥CD ，AD ＝BC ，对角线AC ⊥BD ，垂足为O ．若CD ＝3，AB ＝5，则AC 的长为 .7.如图，n+1个上底、两腰长皆为1，下底长为2的等腰梯形的下底均在同一直线上，设四边形P 1M 1N 1N 2面积为S 1，四边形P 2M 2N 2N 3的面积为S 2，……，四边形P n M n N n N n+1的面积记为S n ，则S n = ▲8.如图有一直角梯形零件ABCD ，AD ∥BC ，斜腰DC 的长为10cm ，∠D ＝120 ，则该零件另一腰AB 的长是 m.答案：选择题 1、A 2、B 3、D 4、B 5、A 6、C填空题1、答案：182、答案：53、答案：ab4、答案：105、答案18（第6题图）CABDOA B CD第8题图67、答案：31 21 nn++8、答案：5。

关于梯形的练习题

关于梯形的练习题一、选择题：1. 梯形的上底和下底平行，以下哪个图形不是梯形？A. 平行四边形B. 长方形C. 菱形D. 正方形2. 梯形的面积公式是：A. \( \frac{1}{2} \times (上底 + 下底) \times 高 \)B. \( (上底 + 下底) \times 高 \)C. \( \frac{1}{2} \times 上底 \times 高 \)D. \( 下底 \times 高 \)3. 一个梯形的上底为5厘米，下底为10厘米，高为4厘米，其面积是：A. 20平方厘米B. 30平方厘米C. 40平方厘米D. 50平方厘米4. 如果一个梯形的上底和下底分别增加2厘米，高不变，那么面积会增加多少？A. 4平方厘米B. 6平方厘米C. 8平方厘米D. 10平方厘米5. 以下哪个选项不是梯形的性质？A. 梯形的中位线等于两底边长的一半之和。

B. 梯形的对角线相等。

C. 梯形的两底边平行。

D. 梯形的两腰不一定相等。

二、填空题：6. 一个梯形的上底是8厘米，下底是12厘米，高是3厘米，其面积是________平方厘米。

7. 梯形的中位线长度等于________。

8. 如果一个梯形的上底是10厘米，下底是20厘米，高是6厘米，那么这个梯形的中位线长度是________厘米。

9. 梯形的内角和为________度。

10. 一个等腰梯形的两腰相等，其上底和下底的长度分别是6厘米和12厘米，如果这个等腰梯形的高是4厘米，那么这个等腰梯形的面积是________平方厘米。

三、简答题：11. 描述如何利用梯形的面积公式计算梯形的面积。

12. 解释为什么梯形的对角线不一定相等。

四、计算题：13. 一个梯形的上底是15厘米，下底是25厘米，高是7厘米，求这个梯形的面积。

14. 一个梯形的上底是12厘米，下底是18厘米，高是5厘米，如果将这个梯形分成两个小梯形，其中一个小梯形的上底是原梯形上底的一半，求这个小梯形的面积。

梯形练习题精选

梯形练习题精选（基础题）一．判断题一．判断题（1）只有一组对边平行的四边形是梯形）只有一组对边平行的四边形是梯形（）（2）梯形的内角最多有两个是锐角）梯形的内角最多有两个是锐角（）（3）等腰梯形的两条对角线相等）等腰梯形的两条对角线相等（）（4）等腰梯形的对角互补）等腰梯形的对角互补（）（5）我们通常把梯形中较短的底叫上底，较长的底叫下底（）（6）梯形的高一定小于腰的长度）梯形的高一定小于腰的长度（）（7）如果一个梯形是轴对称图形，则它一定是等腰梯形（）（8）对角互补的梯形为等腰梯形）对角互补的梯形为等腰梯形（）（9）如果梯形的一组对角互补，则另一组对角也互补）如果梯形的一组对角互补，则另一组对角也互补（）（10）延长等腰梯形的两腰交于一点后形成的图形中的三角形一定是等腰三角形（）二．选择题二．选择题（1）下列说法正确的是（）下列说法正确的是（）A ．平行四边形是一种特殊的梯形．平行四边形是一种特殊的梯形B ．等腰梯形的两底角相等C ．等腰梯形不可能是直角梯形．等腰梯形不可能是直角梯形D ．有两邻角相等的梯形是等腰梯形（2）在等腰梯形中，下列结论：①两腰相等；②两底平行；③对角线相等；④两底角相等．其中正确的有（中正确的有（）个）个 A ．1 B ．2 C ．3 D ．4 （3）等腰梯形的上底、下底、高之比为1∶3∶1，则下底角的度数是（，则下底角的度数是（）A ．30°B ．45°C ．60°D ．75°（4）等腰梯形ABCD 中，BC AD //，AC 与BD 交于O 点，图中全等三角形有（点，图中全等三角形有（） A ．两对．两对 B ．四对．四对 C 一对一对 D ．三对．三对（5）等腰梯形中，下列判断正确的是（）等腰梯形中，下列判断正确的是（）A 两底相等两底相等B 两个角相等两个角相等C 同底上两底角互补同底上两底角互补D 对角线交点在对称轴上（6）下列命题中：）下列命题中：①有两个角相等的梯形是等腰梯形①有两个角相等的梯形是等腰梯形 ②有两条边相等的梯形是等腰梯形②有两条边相等的梯形是等腰梯形③两条对角线相等的梯形是等腰梯形③两条对角线相等的梯形是等腰梯形 ④等腰梯形上、下底中点连线，把梯形分成面积相等的两部分。

简单的梯形面积的练习题

简单的梯形面积的练习题一、填空题1. 梯形的上底为3cm，下底为5cm，高为4cm，则该梯形的面积为______cm²。

2. 已知梯形的面积为24cm²，上底为4cm，下底为6cm，则该梯形的高为______cm。

3. 梯形的上底和下底之和为10cm，高为5cm，则该梯形的面积为______cm²。

4. 梯形的面积为30cm²，高为5cm，上底比下底短2cm，则上底的长度为______cm。

5. 在等腰梯形中，若上底为4cm，下底为10cm，高为6cm，则该梯形的面积为______cm²。

二、选择题1. 已知梯形的上底为a cm，下底为b cm，高为h cm，下列哪个表达式可以表示梯形的面积？（）A. (a + b) × h ÷ 2B. (a b) × h ÷ 2C. a × b × hD. (a + b) × h2. 梯形的上底为6cm，下底为10cm，高为8cm，下列哪个选项是正确的梯形面积？（）A. 40cm²B. 56cm²C. 48cm²D. 52cm²3. 在一个等腰梯形中，若上底为8cm，下底为18cm，高为6cm，则该梯形的面积是多少？（）A. 60cm²B. 72cm²C. 90cm²D. 96cm²三、计算题1. 已知梯形的上底为7cm，下底为11cm，高为9cm，求该梯形的面积。

2. 梯形的面积为54cm²，上底为9cm，下底为15cm，求梯形的高。

3. 在等腰梯形中，上底和下底之和为20cm，高为8cm，求该梯形的面积。

4. 梯形的上底为5cm，下底为13cm，面积为60cm²，求梯形的高。

5. 已知等腰梯形的上底为6cm，下底为14cm，面积为84cm²，求梯形的高。

梯形面积练习题

梯形面积练习题一、选择题1. 梯形的面积公式是（）。

A. （上底+下底）×高÷2B. （上底+下底）×高C. 上底×高+下底×高D. （上底-下底）×高÷22. 如果一个梯形的上底是10厘米，下底是20厘米，高是8厘米，那么它的面积是多少平方厘米？A. 80B. 100C. 120D. 1603. 已知梯形的面积是48平方厘米，上底是8厘米，高是6厘米，求下底的长度。

A. 4厘米B. 6厘米C. 8厘米D. 10厘米二、填空题4. 如果梯形的上底是\( a \)厘米，下底是\( b \)厘米，高是\( h \)厘米，那么它的面积是\( \frac{(a+b) \times h}{2} \)平方厘米。

5. 一个梯形的上底是12厘米，下底是18厘米，高是9厘米，它的面积是\( \frac{(12+18) \times 9}{2} \)平方厘米。

6. 如果梯形的面积是60平方厘米，下底是15厘米，高是5厘米，上底的长度是\( 60 \times 2 \div 5 - 15 \)厘米。

三、判断题7. 梯形的面积总是比同样底边和高的平行四边形的面积小。

（）8. 梯形的面积公式是唯一的，没有其他公式可以计算梯形的面积。

（）9. 如果梯形的上底和下底相等，那么它就变成了一个平行四边形。

（）四、计算题10. 一个梯形的上底是15厘米，下底是25厘米，高是10厘米，求它的面积。

11. 已知一个梯形的面积是90平方厘米，上底是12厘米，求当高是6厘米时，下底的长度。

12. 一个梯形的上底是20厘米，下底是30厘米，面积是300平方厘米，求它的高。

五、解答题13. 某农场有一块梯形形状的土地，上底是100米，下底是200米，高是50米。

请计算这块土地的面积，并说明如何使用梯形面积公式。

14. 一个梯形的上底是x厘米，下底是2x厘米，高是h厘米。

如果这个梯形的面积是180平方厘米，求x和h的值。

梯形的面积(练习题)

梯形的面积(练习题)姓名:一、填空题1.要计算梯形的面积, 必须要知道这个梯形的、和。

2.一个梯形的上底和下底的和是18.5米, 高是6米, 它的面积是。

3.一个直角梯形的上底是10厘米, 如果上底延长2厘米后, 就变成了一个正方形, 这个梯形的面积是平方厘米。

4、一个周长100厘米的等腰梯形, 它们的面积是400平方厘米, 高是8厘米, 它的腰长是（）厘米。

5.梯形的面积是168平方米, 上底长10米, 是下底的一半, 高厘米。

6、有一个长方形长10厘米, 宽5厘米, 另一直角梯形上底长3厘米, 下底长6厘米, 高5厘米, 将它们拼成一个梯形, 梯形的面积是( )平方厘米。

7、一个梯形的面积是30平方米, 如果它的上底、下底和高各扩大3倍, 它的面积。

二、判断题2、把一个平行四边形分成两个完全一样的梯形,3.梯形的面积比平行四边形的面积小。

4.梯形的上底一定比下底短。

5、梯形的上底下底越长, 面积越大。

6.任何梯形都可以都可以分成两个等高的三角形。

三、选择题1.能拼成长方形的两个梯形的条件是（）A.完全一样B.形状一样C.面积相等D.完全一样的直角梯形2、梯形的上底扩大2倍, 下底页扩大2倍, 高不变, 则面积（）A.扩大2倍B.扩大4倍C.扩大8倍D.无法确定3.梯形有（）条高。

A.无数B.2C. 1D.无法确定4、两个完全一样的直角三角形, 不可能拼成一个（）。

A.梯形B.正方形C. 三角形D.长方形5.把一个平行四边形任意分割成两个梯形, 这两个梯形中 ________总是相等的.（）A. 高；B. 面积；C. 上下两底的和 D：腰6.一个梯形的面积是90平方厘米, 上底是20厘米, 下底是25厘米, 高是（）厘米。

A. 2B. 4C. 6 D、2.8四、解决问题1.已知右面梯形的上底是12厘米, 下底是40厘米, 其中阴影部分的面积是340平方厘米, 求梯形的面积。

2.一堆木头整齐地叠放在地上, 最下一层有25根, 最上一层揩油6根, 一共叠放了20层。

梯形面积练习题

一、基础计算题1. 已知梯形的上底为5厘米，下底为10厘米，高为6厘米，求该梯形的面积。

2. 梯形的上底为8厘米，下底为12厘米，高为5厘米，计算梯形的面积。

3. 一块梯形菜地的上底为3米，下底为6米，高为2米，求菜地的面积。

4. 梯形的上底为4分米，下底为8分米，高为3分米，求梯形的面积。

5. 已知梯形的上底为7厘米，下底为14厘米，面积为84平方厘米，求梯形的高。

二、应用题6. 一块梯形土地的上底为50米，下底为100米，高为40米，求这块土地的面积。

7. 某梯形广告牌的上底为4米，下底为8米，高为3米，求广告牌的面积。

8. 一座梯形水坝的上底为30米，下底为60米，高为20米，求水坝的面积。

9. 一块梯形麦田的上底为200米，下底为400米，高为100米，求麦田的面积。

10. 一块梯形果园的上底为15米，下底为30米，面积为225平方米，求果园的高。

三、拓展题11. 已知等腰梯形的上底为10厘米，下底为20厘米，面积为150平方厘米，求等腰梯形的高。

12. 一块等腰梯形菜地的上底为8米，下底为16米，高为6米，求菜地的面积。

13. 梯形的上底为12厘米，下底为18厘米，面积为90平方厘米，求梯形的高。

14. 一块等腰梯形土地的上底为40米，下底为80米，高为30米，求土地的面积。

15. 已知等腰梯形的上底为6分米，下底为12分米，高为4分米，求等腰梯形的面积。

四、综合运用题16. 一个梯形的上底和下底之和为18厘米，高为6厘米，面积是72平方厘米，求该梯形的上底和下底各是多少厘米。

17. 一个梯形的上底比下底短6厘米，高为4厘米，面积为24平方厘米，求梯形的上底和下底。

18. 两个梯形面积相等，一个梯形的上底为8厘米，下底为12厘米，高为5厘米，另一个梯形的上底为10厘米，下底为14厘米，求另一个梯形的高。

19. 一块梯形草地被分成两个面积相等的部分，已知整个草地的上底为20米，下底为40米，高为10米，求分割线所在的高。

(完整版)梯形题型练习题

(完整版)梯形题型练习题梯形题型练题题目一已知梯形ABCD的上底长为\[AB = 7\]，下底长为\[DC = 15\]，高为\[h = 4\]，求梯形的面积。

解答一根据梯形面积公式，可以计算出梯形的面积为：\[S = \frac{1}{2}(AB + DC) \cdot h = \frac{1}{2}(7 + 15) \cdot 4 = 44 \]所以，梯形的面积为44。

题目二梯形EFGH的面积为\[S = 72\]，上底长为\[EF = 8\]，下底长为\[HG = 12\]，求梯形的高。

解答二根据梯形面积公式，可以得到梯形的高为：\[h = \frac{2S}{EF + HG} = \frac{2 \cdot 72}{8 + 12} =\frac{144}{20} = 7.2 \]所以，梯形的高为7.2。

题目三已知梯形IJKL的面积为\[S = 36\]，上底长为\[IJ = 6\]，高为\[h = 4\]，求梯形的下底长。

解答三根据梯形面积公式，可以计算出梯形的下底长为：\[DC = 2 \cdot \left(\frac{S}{h}\right) - AB = 2 \cdot\left(\frac{36}{4}\right) - 6 = 18 - 6 = 12 \]所以，梯形的下底长为12。

题目四已知梯形MNOP的面积为\[S = 30\]，上底长为\[MN = 5\]，下底长为\[PO = 10\]，求梯形的高。

解答四根据梯形面积公式，可以得到梯形的高为：\[h = \frac{2S}{MN + PO} = \frac{2 \cdot 30}{5 + 10} =\frac{60}{15} = 4 \]所以，梯形的高为4。

题目五梯形QRST的上底长为\[QR = 9\]，下底长为\[ST = 15\]，高为\[h = 6\]，求梯形的面积。

解答五根据梯形面积公式，可以计算出梯形的面积为：\[S = \frac{1}{2}(QR + ST) \cdot h = \frac{1}{2}(9 + 15) \cdot 6 = 12 \cdot 6 = 72 \]所以，梯形的面积为72。

梯形专题训练题

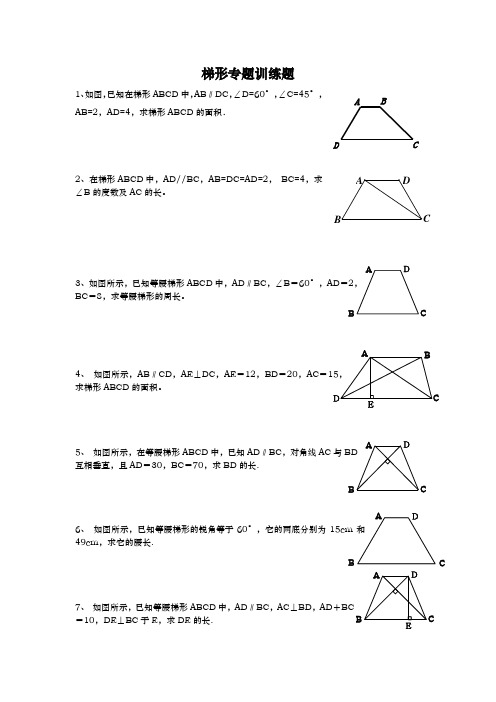
A BCDABCD EAB CDA BCDAB CDE梯形专题训练题1、如图，已知在梯形ABCD 中，AB ∥DC ，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD 的面积．2、在梯形ABCD 中，AD//BC ，AB=DC=AD=2， BC=4，求∠B 的度数及AC 的长。

3、如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，求等腰梯形的周长。

4、如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，求梯形ABCD 的面积。

5、如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.6、如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.7、如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC＝10，DE ⊥BC 于E ，求DE 的长.A BCDB C ADE 8、已知：如图，梯形ABCD 中，AD∥BC，AB=DC ，∠BAD、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F ．求证： CE=BF ．9、如图，在梯形ABCD 中，AD BC ∥，9038BD CD BDC AD BC =∠===，°，，．求AB 的长．10、如图6，在梯形ABCD 中，AD BC ∥，90A ∠=︒，︒=∠45C ，DE=EC ，AB=4,AD=2，求BE 的长．11、已知：如图，梯形ABCD 中，DC ∥AB ，AD=BC ，对角线AC 、BD交于点O ，∠COD=60°，若CD=3， AB=8，求梯形ABCD 的高．12、已知如图，直角梯形ABCD 中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为 .13、如图，在四边形ABCD 中，AC 平分∠BAD ，BC=CD=10，AB=21，AD=9．求AC 的长．B CD OA14、如图，在直角梯形ABCD 中，∠ABC=∠BCD=90°，AB=BC=10，点M 在BC 上，使得△ADM 是正三角形，则△ABM 与△DCM 的面积和是_____________ ．15、如图，梯形ABCD 中，AD ∥BC ，∠DCB=45°，CD=2，BD ⊥CD ．过点C 作CE ⊥AB 于E ，交对角线BD 于F ，点G 为BC 中点，连接EG 、AF ．（1）求EG 的长；（2）求证：CF=AB+AF ．16．如图，在梯形ABCD 中，AD ∥BC ，对角线BD 平分∠ABC ，∠BAD 的平分线AE 交BC 于E ，F ，G 分别是AB ，AD 的中点．（1）求证：EF=EG ；（2）当AB 与EC 满足怎样的数量关系时，EG ∥CD ？并说明理由．17．如图1，AB 、CD 是两条线段，M 是AB 的中点，S △DMC 、S △DAC 、S △DBC 分别表示△DMC 、△DAC 、△DBC 的面积．当AB ∥CD 时，则有S △DMC=2S S DBC DAC∆∆+ ．（1）如图2，M 是AB 的中点，AB 与CD 不平行时，作AE 、MN 、BF 分别垂直DC 于E 、N 、F 三个点，问结论①是否仍然成立？请说明理由．（2）若图3中，AB 与CD 相交于点O 时，问S △DMC 、S △DAC 和S △DBC 三者之间存在何种相等关系？试证明你的结论．18、如图：梯形ABCD 中，AD ∥BC ，S △ADC ：S △ABC =2：3，而对角线中点M 、N 的连线段为10cm ，求梯形两底的长．19、如图，梯形ABCD 中，AD ∥BC ，AB=CD ，对角线AC 、BD 相交于O ，且AC ⊥BD ，4cm．若AD+BC=2求：（1）对角线AC的长；（2）梯形ABCD的面积．20、如图，梯形ABCD中，AB∥CD，AD⊥CD，AC=AB，∠DAC=30度．点E、F是梯形ABCD外的两点，且∠EAB=∠FCB，∠ABC=∠FBE，∠CEB=30°．（1）求证：BE=BF；（2）若CE=5，BF=4，求线段AE的长．21、已知如图，梯形ABCD中，AD∥BC，以两腰AB，CD为一边分别向两边作正方形ABGE和DCHF，连接EF，设线段EF的中点为M．求证：MA=MD．22、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．23、如图所示．梯形ABCD中，AD∥BC，M是腰DC的中点，MN⊥AB于N，且MN=b，AB=a．求梯形ABCD的面积．24、如图，已知四边形ABCD中，AD∥BC，CD=BC，∠C=∠EAB=60°，∠DAE=28°，求∠EBC的度数．25、如图，梯形ABCD，AD∥BC，CE⊥AB，△BDC为等腰直角三角形，CE与BD交于F，连接AF，G为BC中点，连接DG交CF于M．证明：（1）CM=AB；（2）CF=AB+AF．26、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE-AD．27、如图，在梯形ABCD中，AB∥CD，AD=BC，延长AB至E，使BE=CD，连接CE．（1）求证：CE=CA；（2）在上述条件下，延长EC、AD交于G，若AF⊥CE于点F，且AF平分∠DAE．试判断△GAE的形状，并说明理由．28、如图，在梯形ABCD中，AD∥BC，∠DBC=90°，BC=BD，在AB上截取BE，使BE=BC，过点B作BF⊥AB于B，交CD于点F，连接CE，交BF于点H，交BF于点G．（1）求证：EH=CG；（2）已知AD=3，BC=2，求AB的长．29、如图，梯形ABCD中，AB∥CD，AE为高，且AE=12，BD=15，AC=20．（1）求AB+CD的长；（2）求证：AC⊥BD．30、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．31、已知，如图，在梯形ABCD中，AD∥BC，AB=DC，点E、F、G分别在边AB、BC、CD上，且AE=GF=GC．（1）求证：四边形AEFG是平行四边形；（2）若四边形AEFG是矩形，请探索∠EFB与∠FGC的数量关系，并证明你的结论．32、已知：如图，梯形ABCD中，AD∥BC，BD平分∠ABC，E、F分别为AD、AB中点，G为BC边上一点，且GE=GF．（1）求证：∠AEG=∠AFG；（2）猜想：当AB= GC时，四边形GCDE为平行四边形，并说明理由．33、如图，在四边形ABCD中，AD＜BC，对角线AC、BD相交于O点，AC=BD，∠ACB=∠DBC．（1）求证：四边形ABCD为等腰梯形．（2）若E为AB上一点，延长DC至F，使CF=BE，连接EF交BC于G，请判断G点是否为EF中点，并说明理由．。

梯形练习题

梯形练习题1. 如图，梯形ABCD 中，AD ∥BC ，AD=3，AB=5，BC=9，CD 的垂直平分线交BC 于E ，连接DE ，则四边形ABED 的周长等于（）A ．1 B ．18 C ．19 D ．202. 如图，梯形ABCD 中，AD ∥BC ，点M 是AD 的中点，且MB=MC ，若AD=4，AB=6，BC=8，则梯形ABCD 的周长为（）A ．22 B ．24 C ．26 D ．283.如图为菱形ABCD 与正方形EFGH 的重迭情形，其中E 在CD 上，AD 与GH 相交于I 点，且AD ∥HE ．若∠A=60°，且AB=7，DE=4，HE=5，则梯形HEDI 的面积为何？（）A ．36B ．38C ．3210-D ． 3210+4.如图所示，在梯形ABCD 中，AB ∥CD ，E 是BC 的中点，EF ⊥AD 于点F ，AD=4，EF=5，则梯形ABCD 的面积是（）A ．40 B ．30 C ．20 D ．105.如图，在梯形ABCD 中，DC ∥AB ，AD=DC=CB ，AC ⊥BC ，将梯形沿对角线AC 翻折后，点D 落在E 处，则∠B 的度数为（）A ．60 B ．45° C ．40° D ．30°6.沪杭高速铁路已开工建设，某校研究性学习以此为课题，在研究列车的行驶速度时，得到一个数学问题．如图，若v 是关于t 的函数，图象为折线O-A-B-C ，其中A （t1，350），B （t2，350），C （17/80 ，0），四边形OABC 的面积为70，则t2-t1=（）A ．51B 163C ． 807D ．16031 7.如图，已知梯形ABCD ，AD ∥BC ，AD=DC=4，BC=8，点N 在BC 上，CN=2，E 是AB 中点，在AC 上找一点M 使EM+MN 的值最小，此时其最小值一定等于（）A ．6 B ．8 C ．4 D ．438.如图，在梯形ABCD 中，AB ∥DC ，∠D=90°，AD=DC=4，AB=1，F 为AD 的中点，则点F 到BC 的距离是（）A ．2 B ．4 C ．8 D ．19.在四边形ABCD 中，∠A ：∠B ：∠C ：∠D=3：3：2：4，则此四边形是（）A ．一般四边形B ．平行四边形C ．直角梯形D ．等腰梯形10．如图，在直角梯形ABCD 中，∠ABC=90°，AD ∥BC ，AD=4，AB=5，BC=6，点P 是AB 上一个动点，当PC+PD 的和最小时，PB 的长为（）A ．1 B ．2 C ．2、5 D ．311．（2012•烟台）如图，在平面直角坐标中，等腰梯形ABCD 的下底在x 轴上，且B 点坐标为（4，0），D 点坐标为（0，3），则AC 长为（）A ．4 B ．5 C ．6 D ．不能确定12.已知：在等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD=3，BC=7，则梯形的面积是（）A ．25B ．50C ．225D ．221513.如图，菱形ABCD 由6个腰长为2，且全等的等腰梯形镶嵌而成，则线段AC 的长为（）A ．3B ．6C ．33D 3614.已知等腰梯形的底角为45°，高为2，上底为2，则其面积为（）A ．2 B ．6 C ．8 D ．1215.如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD=4，BC=8，则AE+EF 等于（）A ．9 B ．10 C ．11 D ．1216.把长为8cm 的矩形按虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是（）A ．（10+132）cmB ．（10+13）cmC ．22cmD ．18cm17.如图，等腰梯形ABCD 中，AD=5，AB=CD=7，BC=13，且CD 之中垂线L 交BC 于P 点，连接PD ．求四边形ABPD 的周长为何（）A ．24 B ．25 C ．26 D ．2718.若等腰梯形的三边长分别为3，4，11，则这个等腰梯形的周长为（）A ．21B ．29C ．21或29D ．21或22或2919.如图，在等腰梯形ABCD 中，AD ∥BC ，AC=BC+AD ，则∠DBC 的度数是（）A ．30°B ．45°C ．60°D ．90°20.如图1，在等腰梯形ABCD 中，∠B=60°，动点P 从点B 出发，沿BC ，CD ，DA 运动至点A 停止．设点P 运动的路程为x ，△ABP 的面积为y ，如果y 关于x 的函数图象如图2所示，则梯形ABCD 的周长是（）A ．14 B ．23 C ．27 D ．3821.如图，等腰梯形ABCD 中，AD ∥BC ，AD ：BC=1：2，AE ⊥BC ，垂足为E ，连接BD 交AE 于F ，则△BFE 的面积与△DFA 的面积之比为．22.如图，等腰梯形ABCD 中，AD ∥BC ，且AD=1/2 BC ，E 为AD 上一点，AC 与BE 交于点F ，若AE ：DE=2：1，则△AEF 的面积 :△CBF 的面积 = ．23.如图，梯形ABCD 中，AD ∥BC ，若将一腰AB 沿A→D 的方向平移到DE 的位置，请在△DEC 中补充一个条件，使梯形ABCD 是等腰梯形，你补充的条件是24.如图，已知梯形ABCD 中，AD ∥BC ，BD 是对角线．添加下列条件之一：①AB=DC ；②BD 平分∠ABC ；③∠ABC=∠C ；④∠A+∠C=180°，能推得梯形ABCD 是等腰梯形的是（填编号）．25. 在等腰梯形ABCD 中，AD ∥BC ，BC=3，AD=1，∠B=45°，直角三角板含45°角的顶点E 在边BC 上移动，一直角边始终经过点A ，斜边与CD 交于点F ．①当AB=BE 时，CF= ；②AB=AE 时，CF= ；③EA=EB 时，CF= ．26.如图，在平面直角坐标系内，放置一个直角梯形AOCD ，已知AD=3，AO=8，CO=5，若点P 在梯形内，且S △PAD =S △POC ，S △PAO =S △PCD ，那么点P 的坐标是．27.如图，在梯形ABCD 中，AD ∥BC ，∠B=90°，∠C=45°，AD=2，BC=6，点E 为AB 中点，点F 为BC 中点，则EF 的长为．28.在梯形ABCD 中，AB ∥CD ，∠A=90°，AB=2，BC=3，CD=1，E 是AD 中点．求证：CE ⊥BE ．29.如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．30.如图，在等腰梯形ABCD中，AD∥BC，点E、F、G分别在边AB、BC、CD上，且AE=GF=GC．求证：四边形AEFG为平行四边形．31.如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CD、AC．（1）求证：四边形ABFC是平行四边形；（2）如果DE2=BE•CE，求证：四边形ABFC 是矩形．32.已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E为边BC上一点，且AE=DC．（1）求证：四边形AECD是平行四边形；（2）当∠B=2∠DCA时，求证：四边形AECD是菱形．32.如图，等腰梯形ABCD中，AD∥BC，AB=CD，AD=10cm，BC=30cm，动点P从点A开始沿AD边向点以每秒1cm的速度运动，同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．（1）t为何值时，四边形ABQP是平行四边形？（2）四边形ABQP能成为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由．33.如图，在等腰梯形ABCD中，AB∥DC，AB=8cm，CD=2cm，AD=6cm．点P从点A出发，以2cm/s 的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD、DA向终点A运动（P、Q两点中，有一个点运动到终点时，所有运动即终止）．设P、Q同时出发并运动了t秒．（1）当PQ将梯形ABCD分成两个直角梯形时，求t的值；（2）试问是否存在这样的t，使四边形PBCQ的面积是梯形ABCD面积的一半？若存在，求出这样的t的值；若不存在，请说明理由．34.如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM中点．（1）求证：四边形MENF是菱形；（2）若四边形MENF是正方形，请探索等腰梯形ABCD的高和底边BC的数量关系，并证明你的结论．如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．（1）求证：梯形ABCD是等腰梯形；（2）当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD 的面积．35.如图，矩形ABCD的对角线AC和BD相交于点O，E、F分别是对角线AC和BD上的点，且AE=DF．求证：四边形BCFE是等腰梯形．。