2018年小学四年级奥数竞赛试卷(5)

合集下载

小学数学奥林匹克竞赛试题及答案（四年级）

小学数学奥林匹克竞赛试题及答案（四年级）1 小学数学奥林匹克竞赛试题及答案（四年级）(红色为正确答案)1、下面的△,○,□各代表一个数,在括号里填出得数:△+△+△=36 □×△=240○÷□=6 ○=( )A 120B 100C 130D 1242、如果一个整数,与1,2,3这三个数,通过加减乘除运算(可以添加括号)组成算式,结果等于24,那么这个整数就称为可用的,那么,在4,5,6,7,8,9,10这七个数中,可用的数有（）个.A 5B 6C 7D 43、有100个足球队,两两进行淘汰赛,最后产生一个冠军,共要赛（）场.A 97 B98 C 99 D 504、七个小队共种树100棵,各小队种的棵数都不同,其中种树最多的小队种了18棵,种树最少的小队至少种了（）棵.A 10B 8C 9D 75、将一盒饼干平均分给三个小朋友,每人吃了八块后,这时三个小朋友共剩的饼干数正好和开始1个人分到的同样多,问每个小朋友分到（）块。

A 24B 20C 12D 166、每次考试满分是100分,小明4次考试的平均成绩是89分,为了使用权平均成绩尽快达到94分(或更多),他至少再要考( )次.A 5B 6C 3D 47、甲乙丙丁四个人比赛乒乓球，每两人都要赛一场，结果甲胜丁，并且甲乙丙胜的场数相同，那么丁胜的场数是（）场。

A 0B 1C 2D 38、有一位探险家，用6天时间徒步横穿沙漠。

如果一个搬运工人只能运一个人四天的食物和水，那么这个探险家至少要雇用（）名工人。

A 2B 3C 4D 59、在右图的中间圆圈内填一个数,计算每一线段两数之差(大减小),然后算出这三个数之和,那么这个差数之和的最小值是( ).1332 4113A 28B 30C 31D 2910、四年级学生180个人排成四路纵队（即每排4个人），每相邻两排间相隔1米，那么这纵队队伍共长（）米。

A 44B 45C 42D 4611、十只母鸡10天生蛋10个，以同样的生蛋能力，另外的30只母鸡30天生蛋（）个。

(完整版)四年级上册奥数试题-竞赛试卷全国通用(含答案),推荐文档

2018 年小学四年级奥数竞赛试卷一、计数问题1.甲乙丙3 个小朋友站成一排照相，共有种不同的排列方法．2.用1 元，2 元和5 元的纸币，有种不同的方法凑出6 元钱．3.数一数，图中有个三角形．4.如图所示，在2×2 方格中，画一条直线最多穿过3 个方格；在3×3 方格中，画一条直线最多穿过5 个方可知；那么在5×5 方格中，画一条直线，最多穿过个方格．5.六一儿童节，四位小朋友各做了一个小礼物准备相互赠送，但要求自己不得留下自己做的礼物，他们收到礼物的不同方式有种．二、几何图形问题6.将一张长方形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形一定是．（填“三角形”、“长方形”、“梯形”或“菱形”）7.图是3×3 的正方形方格，∠1 与∠2 相比，较大的是．8.各图中，阴影部分的面积与整个图形面积的比值最大的是图．9.将图中所示的三角形ABC 分成面积相等的四个部分，请给出三种不同的分法．要求：在下面所给的三个图中作答．10.将一个三角形的三条边同时扩大相同的倍数，如图，得到的新三角形的面积变为原三角形面积的9 倍，则新三角形的周长是原三角形的周长的倍．11.下列图形经过折叠不能围成正方体的是．12.把2、4、6、8、10、12 这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图，最左边的正方形上的数字是12，则最右边的正方形上的数字是．13.将若干个边长为1 的正六边形（即单位六边形）拼接起来，得到一个拼接图形，如图：那么，要拼接成周长等于18 的拼接图形，需要多少个单位六边形？画出对应的一种图形．三、找规律14．3+12、6+10、12+8、24+6、48+4、…是按一定规律排列的一串算式，其中第六个算式的计算结果是．15.按规律填数：①2，4，7，11，16，②12，19，33，61，117，16.找一找规律，再在横线里填上适当的数．3、4、5、8、7、16、9、32、、四、其他问题17.请你任意写出5 个真分数．18.光明小学参加课外活动小组的人数统计如图所示，则该校参加课外活动小组的共有人．19．2005 年4 月lO 日是星期日，则2005 年6 月1 日是星期．20．一个活动性较强的细菌每经过10 秒就分裂为一个活动性较强的与一个活动性较弱的细菌，而一个活动性较弱的细菌每经过20 秒就分裂为两个活动性较弱的细菌．问：一个活动性较强的细菌，经过60 秒可繁殖多少个细菌？21．赛马比赛前，五位观众给A、B、C、D、E 五匹赛马预测名次．甲说：“B 第三名，C 第五名．”乙说：“E 第四名，D 第五名．”丙说：“A 第一名，E 第四名．”丁说：“A 第二名，B 第一．”戊说：“A 第三名，D 第四名．”结果每人都只预测对了一半．“请问：这五匹马的名次是怎样排列的？”22.作家A、B、C、D、E 依次坐成一排为同学们签名售书，已知每位同学恰好找座位相邻的三位作家签名，已知一共有22 个同学同时找到B 和D 签名，并且C 一共签名38 次，A 比E 多签名6 次，那么B 一共签名次．23.如图，ABCD 是一个梯形，已知三角形ABD 的面积是12 平方厘米，三角形AOD 的面积比三角形BOC 的面积少12 平方厘米，那么，梯形ABCD 的面积是平方厘米．24．2006 年学校1 月20 日开始放寒假，3 月1 日上学，学校放了天寒假．25.假设某餐厅备有肉4 种，鱼3 种，蔬菜5 种，有位客人预计肉、鱼和蔬菜各点一种，他有种点菜的方法．26.将自然数按下面的形式排列，试问：第20 行最左边的数是，第20 行所有数的和是．27.芳芳说：“我13 岁，比惠惠小3 岁，比萍萍大一岁”；惠惠说：“我不是年龄最小的，萍萍和我差4 岁，萍萍是11 岁”；萍萍说：“我比芳芳年龄小，芳芳10 岁，惠惠比芳芳大2 岁，”以上每人所说的三句话中，都有一句是错误的，则芳芳多少岁？惠惠多少岁，萍萍多少岁？2018 年小学四年级奥数竞赛试卷参考答案与试题解析一、计数问题【分析】最左边的位置有3 个小朋友可以选，中间位置还有2 个小朋友可以选，最后一个位置只有1 个小朋友可以选；各个位置上可以选的方法的积就是总的次数．【解答】解：3×2×1=6（种）；答：有6 种不同的排列方法．故答案为：6．【点评】本题也可以采取给三人编号，然后写出全部排列的方法求解．【分析】分类计数，分只有一种，只有两种逐个列举即可．【解答】解答：5+1=62+2+2=62+2+1+1=62+1+1+1+1=61+1+1+1+1+1=6共有5 种方法．故答案为：5．【点评】本题考查了筛选与枚举问题，关键是确定分类的办法和凑数的范围，要注意按顺序列举．【分析】单个的小三角形有12 个，由三个小三角形组成的三角形有6 个，由九个小三角形组成的三角形有2 个，则可以求出三角形的总个数．【解答】解：图中有三角形：12+6+2=20（个）．故答案为：20．【点评】此题关键是将三角形进行分类再计数．【分析】如下图所示，那么在5×5 方格中，画一条直线，最多穿过9 个方格．【解答】解：在2×2 方格中，画一条直线最多穿过3 个方格，2+1；在3×3 方格中，画一条直线最多穿过5 个方可知，3+2；以此类推，那么在5×5 方格中，画一条直线，最多穿过5+4=9 个方格．答：那么在5×5 方格中，画一条直线，最多穿过9 个方格．故答案为：9．【点评】此题考查了数与形结合的规律，以上两种方法都可得解．【分析】结合题目的要求，我们不妨先设出四个小朋友，然后具体分析（过程见解答）即可得出答案．【解答】解答：设这四个小朋友分别是a，b，c，d，则收到a 送的礼物有b、c、d 三种可能，下面不妨以其中的一种可能为例分析：①以给 b 为例：b 收到a 送的礼物那么b 送的礼物如果给a，那么必然是 c 和 d 交换礼物，这是一种b 送的礼物如果给了c，那么c 不能给a 只能给d，所以d 要给a，这也是一种同理b 的礼物给了d 又是一种则总共有1+1+1=3 种即 a 送给 b 有3 种；②同样，若给c 和d 也是各有3 种；因此共计3+3+3=9 种．故：此空为9．【点评】解答此题关键是理解题意，按要求进行分析即可得出答案．二、几何图形问题【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有 4 条边，并且这4 条边还相等，从而可以进行从题后的答案中选择．【解答】解：由题意知，对折实际上就是对称，对折2 次的话，剪下应有4 条边，并且这4 条边还相等，只有菱形满足这一条件，故答案为：菱形．【点评】此题考查了利用对称设计图案．【分析】借助正方形和线段构成的角来比较角的大小．：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【解答】解：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【点评】利用正方形来确定角的度数．【分析】先写出分个图形阴影部分的面积与整个图形面积的比，然后比较这几个比值的大小，从而得出答案．【解答】解：由题意知：A、把圆平均分在了6 份，阴影部分的面积与整个图形面积的比值是：，B、把正方形平均分成了8 份，阴影部分的面积与整个图形面积的比值是：，C、把正方形平均分成了8 份，阴影部分的面积与整个图形面积的比值是：，D、通过割补法可知，阴影部分的面积与整个图形面积的比值是：，通过比较可知最大的为，故答案为：B．【点评】此题考查了分数的意义和大小比较．【分析】根据等底等高的三角形面积相等划分即可．【解答】解：（答案不唯一）【点评】本题考查了等底等高的三角形面积相等的灵活应用．【分析】根据题干分析可得，原三角形与新三角形相似三角形，相似比是1：3．根据相似三角形的性质可得：相似三角形的面积的比等于相似比的平方，相似三角形的周长的比等于相似比．由此即可得出答案．【解答】解：根据题干可得原三角形与新三角形相似，相似比是1：3，由相似三角形的性质可得：周长的比等于相似比，即：原三角形周长：新三角形周长=1：3答：新三角形的周长是原三角形的周长的 3倍．故答案为：3．【点评】此题考查了相似三角形的相似比与它们周长的比以及面积的比的性质．【分析】根据正方体展开图的常见形式作答即可．【解答】解：由展开图可知：A、B 能围成正方体；C 围成几何体时，有两个面重合，故不能围成正方体．故选C．【点评】展开图能折叠成正方体的基本类型有：“一，四，一”“三，三”“二，二，二”“一，三，二”．【分析】根据正方体的特征和展开图的形状可知，2 在正面，4 在背面；6 和8 在侧面；10 和12 在上下面；由此解答．【解答】解：通过上面的分析得：最右边的正方形上的数字是4．故答案为：4．【点评】此题主要考查正方体的特征及展开图的形状．【分析】先从变化中观察，寻找规律．细心观察四个图形，可以发现：在拼接图形时，每增加一个单位六边形，拼接图形的周长要么不增加，要么增加2 或4，据此分析解答即可．【解答】解：因为两个单位六边形拼接的图形的周长只能是10，18﹣10=8，8=4+4=4+2+2=2+2+2+2，所以当拼接图形的周长等于18 时，所拼接的单位六边形有 4 个、5 个、6 个或7 个，如下图：【点评】本题考查图形的规律．三、找规律【分析】观察算式可以发现，式子中有两个加数，第一个加数3、6、12、24、48、…依次扩大2 倍，第二个加数12、10、8、6、4…依次减少2，据此规律，第六个算式是96+2=98．【解答】解：第一个加数3、6、12、24、48、…依次扩大2 倍，第二个加数12、10、8、6、4…依次减少2，第六个算式为：48×2+（4﹣2）=96+2=98．故答案为：98．【点评】观察式子，找出式子的变化规律，然后运用总结的规律解决问题．【分析】①后一个数是前一个数依次增加2，3，4，…所得．②19﹣12=7，33﹣19=14，61﹣33=28，117﹣61=56，依次增加7 的1、2、4、8、16 倍即可．【解答】解：①16+6=22②117+7×16=229故答案为：22，229．【点评】通过观察数字的特点，找出相邻两个数之间的倍数关系或者差之间的关系，再由此求解即可．【分析】奇数项是它前面的奇数项加2 所得，偶数项是它前面的偶数项乘2 所得，由此得出答案．【解答】解：9+2=11，32×2=64；故答案为：11，64．【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律，然后再利用这个变化规律再回到问题中去解决问题．四、其他问题【分析】根据真分数的定义解答即可．【解答】解：由题意知，分子小于分母的分数叫真分数，所以任意写出的 5 个真分数可为：、、、、；故答案为：、、、、；【点评】此题考查了真分数的定义．【分析】由于条形统计图的高度代表了数量的多少，所以要求参加课外活动小组的共有多少人，只要把所有小组的人数加起来即可．【解答】解：6+9+15+20+25+30，=105（人）；故答案为：105．【点评】此题考查了学生根据条形统计图回答问题的能力．【分析】先求出从4 月10 日到6 月1 日经过了多少天，再求这些天里有几个星期，还余几天，根据余数判断6 月1 日是星期几．【解答】解：4 月10 日到4 月30 日经过了20 天，5 月有31 天，再到6 月1 日又经过1 天；共经过：20+31+1=52（天），52÷7=7（周）…3（天）；即6 月1 日是星期三．故答案为：三．【点评】本题先求出经过的天数，再求这些天里有几周，还余几天，然后根据余数推算．【分析】每一个活动性较强的细菌都会分解，经过60 秒仍然是1 个一个活动性较强的细菌；根据一个活动性较弱的细菌每经过20 秒就分裂为两个活动性较弱的细菌，而每10 秒又会分裂出 1 个活动性较弱的细菌，列举出60 秒内它们的数量．【解答】解：一个活动性较强的细菌最后只剩下 1 个；活动性较弱的细菌分裂过程如下：第10 秒：1 个，第20 秒：1+1=2（个），第30 秒：2+1+1=4（个），第40 秒：2+2+1+1=6（个），第50 秒：4+2+2+1+1=10（个），第60 秒：4+4+2+2+1+1=14（个），14+1=15（个）；答：一个活动性较强的细菌经过60 秒可繁殖15 个细菌．【点评】根据两种不同的细菌分裂方式分别求出60 秒时它们各有的数量，再相加即可．【分析】根据丙说：“A 第一名，E 第四名．”假设E 不是第四名，则A 是第一名就正确，那么丁说：“A第二名，B 第一．”都错误，这与每人都只预测对了一半相矛盾；所以E 是第四名是正确，据此进一步解答即可．【解答】解：根据丙说：“A 第一名，E 第四名．”假设A 是第一名，则E 不是第四名，那么丁说：“A 第二名，B 第一．”都错误，这与每人都只预测对了一半相矛盾；所以E 是第四名是正确，则，根据戊的表述可得 A 是第三名，再根据甲的表述可得 C 是第五名，因为A 是第三名，再根据丁的表述可得B 是第一名，则剩下的D 就是第二名，综合上述可得，B 是第一名，D 是第二名，A 是第三名，E 是第四名，C 是第五名．【点评】条件分析﹣﹣﹣假设法：假设可能情况中的一种成立，然后按照这个假设去判断，如果有与题设条件矛盾的情况，说明该假设情况是不成立的，那么与他的相反情况是成立的．【分析】同时找到 B 和 D 签名的肯定找了C 签名，因为 C 一共签了38 次，这样就可以确定找A 和E 签名的次数之和是38﹣22=16 次，再由A 比E 多签名6 次可以求出A 签的次数，因为找A 签名的人肯定找B 签名，所以可以推算出B 签名的次数．【解答】解：38﹣22=16（次）（16+6）÷2=11（次）11+22=33（次）故填33．【点评】此题的关键是分析38﹣22=16 次所代表的含义是什么．【分析】根据等量加等量差不变，可知三角形ABD 和三角形ABC 的面积的差也是12 平方厘米，由此可以求出三角形ABC 的面积，据此分析解答即可．【解答】解：S△AOD+S△AOB=S△ABD，S△BOC+S△AOB=S△ABC，则三角形ABD 的面积比三角形ABC 的面积少12 平方厘=12+12=24（平方厘米）米．S△ABCS 梯形ABCD=24+12=36（平方厘米）故填：36．【点评】本题考查的是三角形和梯形的面积计算．【分析】2006 年的 1 月份有31 天，2 月份有28 天，据此解答即可．【解答】解：31﹣20+1+28=40（天）故填：40【点评】本题考查的是周期问题．【分析】根据题意可得，肉有4 种选择，鱼有3 种选择，蔬菜有5 种选择，根据乘法原理可得，共有4×3×5=60 种选择；据此解答即可．【解答】解：4×3×5=60（种）故答案为：60．【点评】本题考查了乘法原理：做一件事，完成它需要分成n 个步骤，做第一步有m1 种不同的方法，做第二步有m2种不同的方法，…，做第n 步有m n种不同的方法，那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法．【分析】观察数阵可得规律，每行数据的个数是奇数列，先求出第19 行有多少个数，即1+2×（19﹣1）=37 个，再求出19 行的总个数1+3+5+…+37=361，再进一步解答即可．【解答】解：1+2×（19﹣1）=37（个）1+3+5+…+37=19×19=361（个）1+2×（20﹣1）=39（个）所以，第20 行最左边的数是361+1=362；第20 行最后一个数是：361+39=400第20 行所有数的和是：（362+400）×39÷2=762×39÷2=14859故答案为：562；14859．【点评】一般地说，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．【分析】根据题意可知：芳芳说的“我13 岁”和萍萍说的“芳芳10 岁”这两句话中肯定有一句是对的，有一句是错的，据此分析解答即可．【解答】解：假设芳芳13 岁是对的，则芳芳10 岁就是错的，此时惠惠比芳芳大 2 岁，则惠惠是15 岁，芳芳比萍萍大1 岁，则萍萍是12 岁，这样惠惠和萍萍就相差3 岁，和惠惠说的“萍萍和我相差4 岁”相矛盾，不符合题意．所以芳芳是10 岁，此时惠惠13 岁，萍萍9岁．答：芳芳10 岁，惠惠13 岁，萍萍9 岁．【点评】本题考查的是逻辑推理．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

2018年小学四年级数学竞赛试题(有答案)

972018四年级数学竞赛试题（有答案）考试时间 70 分钟，总分 150 分一、填空题 I （本大题共 10 小题，每题 6 分，共 60 分）1. 计算： 51⨯19 ÷17 =．2. 计算： 60 - 59 + 58 - 57 + 56 - 55 + + 2 -1 =．3. 白兔、黑兔和灰兔去拔萝卜，白兔拔的萝卜数量比黑兔多 8 根，白兔和灰兔一共拔了 32 根萝卜，那么黑兔和和灰兔一共拔了根萝卜．4. 如图，用 4 个等腰直角三角形拼成一个大图形，三角形间无重叠，其中最小的三角形面积是 25 平方厘米，那么整个图形的面积是平方厘米．5. 用红、黄两种颜色给“万人挑战赛”这五个汉字涂色，每个汉字只能涂一种颜色．要求相邻的两个颜色互不相同，那么一共有种不同的涂色方法．6. 今年毛毛 9 岁，当毛毛像爸爸现在这么大时，爸爸已经 55 岁了，那么爸爸今年岁．7. 阿呆和阿瓜在 400 米的环形跑道上跑步，他们从同一地点同时出发，相背而行，阿呆的速度是 3 米/秒，阿瓜的速度是 5 米/秒，经过秒，两人第一次迎面相遇．8. 观察数组（2，4），（4，6），（6，8），（8，10），……的规律，那么第 10 组两个数的和是_ __ _．9. 皮皮和球球吃香蕉，一开始皮皮吃的数量是球球的 5 倍，之后球球又吃了 30 根香蕉，这时皮皮吃的数量就只有球球的 2 倍了，那么皮皮吃了根香蕉．10. 如图，从 A 点沿线段走到 B 点，每次只能向上或向右走一步，共有种不同的走法．B二、填空题 II （本大题共 6 小题，每题 7 分，共 42 分）11. 定义新运算“☆”为：1☆3 = 3 ，1☆10 = 10 ，2☆10 = 9 ，5☆100 = 96 ，那么1988☆2018 = ．12. 如图，在平行四边形 ABCD 中，E 是 DC 上的任意一点，其中平行四边形 ABCD 的面积是 72 平方厘米，三角形 ADE 的面积是 27 平方厘米，AB 长 12 厘米，那么 EC 长厘米．AB挑战万人赛＋万人挑战赛挑赛人赛挑赛DE C13. 如图，右边的竖式中相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么五位数“”是．14. 商场店庆日有优惠活动，买化妆品类的商品每满 100 元会送 20 元的代金券，买服装类的商品每满 200元会送 50 元的代金券，代金券只能在购买下一件商品时使用．王妈妈要买一套原价 1850 元的护肤品（化妆品）和一件原价 1700 元的羽绒服，那么她买这两样商品最少需要花元．15. 一列火车完全通过 600 米长的桥用了 30 秒，以同样的速度完全通过 360 米长的桥用了 24 秒，那么这列火车通过 1200 米长的大桥需要秒．16. 墨爷爷的蛋糕被偷吃了，这块蛋糕是被小高、墨莫、阿呆、阿瓜和卡莉娅中的一个人吃掉的．小高说：“是墨莫吃的．”墨莫说：“是小高吃的．”阿呆说：“是我吃的．”阿瓜说：“是阿呆吃的．”卡莉娅说：“不是墨莫吃的．”已知他们五人中有 2 人说的是真话，那么这块蛋糕是吃的．A。

2018年小学数学4年级奥数试题26-50题(含答案+解析)

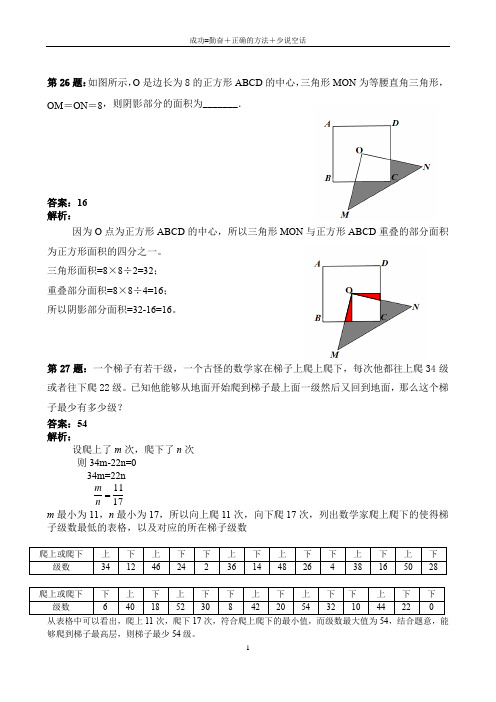
第26题：如图所示，O 是边长为8的正方形ABCD 的中心，三角形MON 为等腰直角三角形，OM ＝ON ＝8，则阴影部分的面积为_______．答案：16 解析：因为O 点为正方形ABCD 的中心，所以三角形MON 与正方形ABCD 重叠的部分面积为正方形面积的四分之一。

三角形面积=8×8÷2=32；重叠部分面积=8×8÷4=16；所以阴影部分面积=32-16=16。

第27题：一个梯子有若干级，一个古怪的数学家在梯子上爬上爬下，每次他都往上爬34级或者往下爬22级。

已知他能够从地面开始爬到梯子最上面一级然后又回到地面，那么这个梯子最少有多少级？答案：54 解析：设爬上了m 次，爬下了n 次则34m-22n=0 34m=22n1711 n m m 最小为11，n 最小为17，所以向上爬11次，向下爬17次，列出数学家爬上爬下的使得梯子级数最低的表格，以及对应的所在梯子级数从表格中可以看出，爬上11次，爬下17次，符合爬上爬下的最小值，而级数最大值为54，结合题意，能够爬到梯子最高层，则梯子最少54级。

第28题：从下图的中心点出发，沿着格线移动至相邻点。

问这样的操作重复了10次后回到中心点的方法有几种？（途中可以通过中心点）答案：16384种解析：方法1：使用标数法第一次第二次第三次第四次第五次第六次第七次第八次第九次第十次所以重复了10次后回到中心点的方法有16384种。

方法2：如下图，从白点开始移动一次到达黑点，从黑点移动一次到达白点。

于是从中心的黑点开始移动的奇数次到达的是4个白点中的1个。

由此可知，无论最后一次怎样移动，9次移动后到达的点为白点，第10次移动后到达中心点的方法只有一种。

再考虑从白点移动2次的方法，首先向中心点移动的话有4种方法，向四角上的点移动的话有2种方法，故共有4＋2×2=8种。

又最初一次移动有4种方法。

所求值为484⨯=16384种。

【精选】小学四年级奥数竞赛数学竞赛试卷及答案word百度文库

【精选】小学四年级奥数竞赛数学竞赛试卷及答案word百度文库一、拓展提优试题1．（8分）传说，能在三叶草中找到四叶草的人，都是幸运之人．一天，佳佳在大森林中摘取三叶草，当她摘到第一颗四叶草时，发现摘到的草刚好共有100片叶子，那么，她已经有颗三叶草．2．三个连续自然数的乘积是120，它们的和是．3．10个连续的自然数从小到大排列，若最后6个数的和比前4个数的和的2倍大15，则这10个数中最小的数是．4．如图，把一个边长是5cm的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向移动其中的4个长方形，则所得图形的周长是cm．5．把50颗巧克力分给4个小朋友，每个小朋友分得的巧克力的颗数各不相同．分得最多的小朋友至少可以得颗巧克力．6．如图，一小正方形的边为边向小正方形外作四个正方形，再依次连接几个定点，若图中阴影三角形的面积是S，则面积为2S的三角形有个，面积为8S 的正方形有个．7．学校组织春游，租船让学生划．每条船坐3人，有16人没有船坐；如果每条船坐5人，则有一条船上差4人．学校共有学生人．8．给出3、3、8、8，请你按“24点”的游戏规则，写出一个得数等于24的等式，．9．一列火车身长90米，火车以每分钟160米的速度通过山洞，用了3分钟，山洞长390米．10．如图，小明从A走到B再到C再到D，走了38米，小马从B到C再到D 再到A，走了31米，此问长方形ABCD的周长多少米？11．六个人传球，每两人之间至多传一次，那么这六个人最多共进行15次传球．12．过元旦时，班委会用730元为全班同学每人买了一份价值17元的纪念品，剩余16元，那么，这个班共有学生名．13．如图是长方形，将它分成7部分，至少要画条直线．14．小明有100元钱，买了3支相同的钢笔后还剩61元，则他最多还可以买支相同的钢笔．15．如图，一个大正方形被分成四个相同的小长方形和一个小正方形，若一个小长方形的周长是28，则大正方形的面积是．【参考答案】一、拓展提优试题1．解：（100﹣4）÷3＝96÷3＝32（棵）答：她已经有了32棵三叶草．故答案为：32．2．【分析】首先把120分解质因数，把质因数分作三组，使各组数字相乘后的结果是三个连续的自然数，即可得解．解：120＝2×2×2×3×5＝（2×2）×（2×3）×5，2×2＝4，2×3＝6，5，即，三个连续自然数的乘积是120，这三个数是4、5、6，所以，和是：4+5+6＝15．故答案为：15．【点评】本题考查了灵活应用合数分解质因数来解决较复杂问题．3．【分析】本题主要考察等差数列．解：设最小的数为x，则剩余自然数依次为x+1，x+2，…，x+9，由题可得2（4x+1+2+3）+15＝6x+4+5+6+7+8+9，化简后是8x+27＝6x+39∴x＝6，【点评】本题可以借助列方程，设最小的数为x，一一用x表示其他连续自然数，根据等量关系就可求解．4．【分析】本题考察图形边长的平移．解：画出移动后的图，所得图形的周长是5×2+（5+1×2+2×2+3×2+4×2+5）＝10+30＝40cm．【点评】本题主要抓住平移后的图形每条边边长为多少即可求解．5．解：因为要使每个小朋友分得的巧克力的颗数各不相同，第一次先分给这4个小朋友的巧克力数依次为：1、2、3、4，从这里可以看出最后那个人是分得鲜花最多的人；那么还剩下50﹣（1+2+3+4）＝40颗巧克力；如果这40颗巧克力全给最后这个人，那么他最多可分得4+40＝44颗，要想让他分得的巧克力数少，那么剩下的40颗朵，可以再分给每个人10，由此可得出这时每个人的巧克力数为：11、12、13、14，答：分得最多的小朋友至少可以得14颗巧克力；故答案为：14．6．【分析】（1）观察题干可知，阴影部分的面积是S，则面积为2S的三角形是每个小正方形的面积的一半，即三角形的两条直角边都是小正方形的边长，由此即可计数；（2）阴影部分的面积是S，则它所在的正方形的面积是4S，则面积为8S的正方形只有中间1个，解：（1）观察图形可知，面积为2S的独三角形有4个；由两个面积为S的三角形组成的三角形有4×4＝16（个），所以一共有4+16＝20（个）；（2）面积为8S的正方形只有1个．故答案为：20；1．【点评】本题考查平面图形数量的确定，属于中档题目，注意仔细地观察图形，要做到不重不漏．7．解：船：（16+4）÷（5﹣3），＝20÷2，＝10（条）；学生：3×10+16＝46（人）；答：学校共有学生46人．故答案为：46．8．解：8÷（3﹣8÷3），＝8÷（3﹣），＝8÷，＝24．故答案为：8÷（3﹣8÷3）．9．解：160×3﹣90，＝480﹣90，＝390（米），答：山洞长390米．故答案为：390．10．解：长方形长比宽多：38﹣31＝7（米），长方形宽：（38﹣7×2）÷3，＝24÷3，＝8（米），长：8+7＝15（米），（15+8）×2，＝23×2，＝46（米），答：长方形ABCD的周长46米．11．解：一个图形中，如果有K个奇点，那么这个图形会用笔画出来．为了让这个图形用一笔画出来，则要使它只存在2个奇点．上面的图形共有6个奇点，6×5÷2＝15条线．最少可以去掉2条线（剩下13条线），使6个奇点变成2个奇点，就可以用一笔画出来了．所以6人两两传球，但每两人之间最多只能传一次，最多就能传13次．故答案为：13．12．【分析】根据题意，由减法的意义，用730元减去16元，求出全班同学每人买一份纪念品的总钱数，再根据数量＝总价÷单价，代入数据解答即可．解：（730﹣16）÷17＝714÷17＝42（名）；答：这个班共有学生42名．故答案为：42．【点评】解答此题的关键是求出全班同学每人买一份纪念品的总钱数，再根据单价、数量和总价之间的关系进行解答．13．【分析】两条直线把正方形分成4部分，第三条直线与前两条直线相交多出3部分，共分成7部分；第四条直线与前3条直线相交，又多出4部分．共11部分，第五条直线与前4条直线相交，又多出5部分，如下图所示．解：1+1+2+3＝7答：在一个长方形上画上3条直线，最多能把长方形分成7部分．故答案为：3．【点评】此题考查了图形的拆拼．使直线间相互交叉，交点越多，则分割的空间越多．每多第几条直线，就加几个部分．14．【分析】根据题意，可用100减去61计算出购买3支钢笔花的钱数，然后再除以3计算出每支钢笔的钱数，最后再用100除以每支钢笔的钱数进行计算，得到的商就是最多购买钢笔的支数，得到的余数就是剩余的钱数，最后再用最多购买的钢笔数减去原来买的3支即可．解：（100﹣61）÷3＝39÷3＝13（元）100÷13＝7（支）…9（元）7﹣3＝4（支）答：他最多还可以买4支同样的钢笔．故答案为：4．【点评】此题主要考查的有余数除法计算方法的应用，解答时关键求出每支钢笔的单价．15．【分析】一个小长方形的周长是28，也就是小长方形的长和宽的和是28÷2＝14，也就是大正方形的边长，然后根据正方形的面积公式，解决问题．解：28÷2＝1414×14＝196答：大正方形的面积是196．故答案为：196．【点评】根据长方形的长和宽与正方形边长之间的关系，先求出小长方形的长和宽的和，即求出了大正方形的边长．。

2018四年级奥数题(附答案)

小学四年级奥数题：统筹规划1、烧水沏茶时，洗水壶要用1分钟，烧开水要用10分钟，洗茶壶要用2分钟，洗茶杯用2分钟，拿茶叶要用1分钟，如何安排才能尽早喝上茶。

2、有137吨货物要从甲地运往乙地，大卡车的载重量是5吨，小卡车的载重量是2吨，大卡车与小卡车每车次的耗油量分别是10公升和5公升，问如何选派车辆才能使运输耗油量最少？这时共需耗油多少升？3、用一只平底锅烙饼，锅上只能放两个饼，烙熟饼的一面需要2分钟，两面共需4分钟，现在需要烙熟三个饼，最少需要几分钟？4、甲、乙、丙、丁四人同时到一个小水龙头处用水，甲洗拖布需要3分钟，乙洗抹布需要2分钟，丙用桶接水需要1分钟，丁洗衣服需要10分钟，怎样安排四人的用水顺序，才能使他们所花的总时间最少，并求出这个总时间。

5、甲、乙、丙、丁四个人过桥，分别需要1分钟，2分钟，5分钟，10分钟。

因为天黑，必须借助于手电筒过桥，可是他们总共只有一个手电筒，并且桥的载重能力有限，最多只能承受两个人的重量，也就是说，每次最多过两个人。

现在希望可以用最短的时间过桥，怎样才能做到最短呢？你来帮他们安排一下吧。

最短时间是多少分钟呢？6、小明骑在牛背上赶牛过河，共有甲乙丙丁四头牛，甲牛过河需1分钟，乙牛需2分钟，丙牛需5分钟，丁牛需6分钟，每次只能骑一头牛，赶一头牛过河。

要过河时间最少？是多少？四年级奥数题：速算与巧算（一）1.【试题】计算9＋99＋999＋9999＋999992【试题】计算199999＋19999＋1999＋199＋193【试题】计算(2+4+6+…+996+998+1000)－－(1+3+5+…+995+997+999)4【试题】计算9999×2222＋3333×33345.【试题】56×3+56×27+56×96-56×57+566.【试题】计算98766×98768－98765×98769四年级奥数题：年龄问题1、父亲45岁，儿子23岁。

2018年小学奥数试题附答案

2018年小学奥数试题附答案难倒大学生的小学奥数题见过吗?小编觉得那些会做奥数题的都好厉害啊!是不是你?下面由店铺给你带来关于2018年小学奥数试题附答案，希望对你有帮助!2018年小学奥数试题1.李军和张强付同样多的钱买了同一种铅笔，李军要了13支，张强要了7支，李军又给张强0.6元钱。

每支铅笔多少钱?2.甲乙两辆客车上午8时同时从两个车站出发，相向而行，经过一段时间，两车同时到达一条河的两岸。

由于河上的桥正在维修，车辆禁止通行，两车需交换乘客，然后按原路返回各自出发的车站，到站时已是下午2点。

甲车每小时行40km，乙车每小时行 45km，两地相距多少km?(交换乘客的时间略去不计)3.学校组织两个课外兴趣小组去郊外活动。

第一小组每小时走4.5km，第二小组每小时行3.5km。

两组同时出发1小时后，第一小组停下来参观一个果园，用了1小时，再去追第二小组。

多长时间能追上第二小组?4.有甲乙两个仓库，每个仓库平均储存粮食32.5吨。

甲仓的存粮吨数比乙仓的4倍少5吨，甲、乙两仓各储存粮食多少吨?5.甲、乙两队共同修一条长400米的公路，甲队从东往西修4天，乙队从西往东修5天，正好修完，甲队比乙队每天多修10米。

甲、乙两队每天共修多少米?6.学校买来6张桌子和5把椅子共付455元，已知每张桌子比每把椅子贵30元，桌子和椅子的单价各是多少元?7.一列火车和一列慢车，同时分别从甲乙两地相对开出。

快车每小时行75km，慢车每小时行65km，相遇时快车比慢车多行了40km，甲乙两地相距多少km?8.某玻璃厂托运玻璃250箱，合同规定每箱运费20元，如果损坏一箱，不但不付运费还要赔偿100元。

运后结算时，共付运费4400元。

托运中损坏了多少箱玻璃?9.五年级一中队和二中队要到距学校20km的地方去春游。

第一中队步行每小时行4km，第二中队骑自行车，每小时行12km。

第一中队先出发2小时后，第二中队再出发，第二中队出发后几小时才能追上一中队?10.妈妈让小红去商店买5支铅笔和8个练习本，按价钱给小红3.8元钱2017最新小学奥数题及答案2017最新小学奥数题及答案。

2018年人教版小学四年级数学竞赛试卷(附答案)

2018年人教版小学四年级数学竞赛试卷(附答案)小学四年级数学竞赛试卷班次：__________ 姓名：__________一、填空。

（共20分，每小题2分）1.计算453÷72时，一般把除数看做被除数的倍数来试商。

2.3998是4个连续自然数的和，其中最小的数是998.3.除数缩小到原来的1/10，要使商不变，则被除数应该增加10倍。

4.填一个最小的自然数，使225×525×16积的末尾四位数字都是2000.5.在下面的式子中填上括号，使等式成立。

5×8)+(16÷4)-2=206.从1、2、3、4、5、6、7、8、9九个数中，任取3个数组成一组，使它的平均数是5，有8种取法。

7.如果B÷53=17……C,则C最大是52.8.两个数之和是444，大数除以小数商11，且没有余数，大数是407.9.把5、11、14、15、21、22六个数填入下面的括号内，使等式成立。

5)×(21)×(22)=(11)×(14)×(15)10.在两条平行线之间的几条垂直线段的长度都相等。

11.一个因数乘13，得数比原来多108，原来的数是36.12.把xxxxxxxx0四舍五入到万位约是xxxxxxxx0.13.比最大的五位数少1的数是.14.试问1×2×3×。

×99×100所得的乘积最末尾有24个连续的0.15.一个箱子里放着几顶帽子，除2顶以外都是红的，除2顶以外都是蓝的，除2顶以外都是黄的。

箱子中一共有3顶帽子。

16.母亲今年34岁，女儿6岁，8年后母亲的年龄正好是女儿年龄的3倍。

17.最大的九位数比最小的十位数小xxxxxxxx0.18.xxxxxxxx000=4600万=46亿。

19.青蛙白天向上爬3米，晚上滑下2米，青蛙从井底爬到井外高10米需要8天7夜。

2018年小学数学4年级奥数试题76-100题(含答案+解析)

成功＝勤奋＋正确的方法＋少说空话第76题：将下图的竖式谜补充完整。

答案：此题答案不唯一，填出一种就算对。

（本题还有其它答案，不一一列举）第77题：如果一个数字不是 11 的倍数，但是移除一个任意位上的数字后，它就变成了 11 的倍数，（例如 111，无论移除其个位、十位或百位上的数字，都变成 11 的倍数），这样的四位数共有多少个？答案：共有0个解析：假设这个四位数为abcd ————，则任意移除其中一位之后移除千位，为bcd ————，能被11整除，则：cd b -+|11；移除百位，为acd ————，能被11整除，则：cd a -+|11 移除十位，为abd ————，能被11整除，则：bd a -+|11 移除个位，为abc ————，能被11整除，则：bc a -+|11结合以上四个算式可得出：a|11，d|11而a 与d 均为一位数字，则0==d a因为首位数字为0，所以这样的四位数不存在，个数为0。

第78题：将 6 个不同的正整数从小到大排成一排为 a 、b 、c 、d 、e 、f ，任意两个相邻数中，后面数都是前面数的倍数，已知 a +b + c + d + e + f =79 ,求：f 的值是多少？答案：48 解析：b ，c ，d ，e ，f 都是a 的倍数，且79=+++++f e d c b a,当a ＞1时，结果超过79，所以1=a ，从而推出39278⨯==++++f e d c b 。

同理，fe d c b ++++是b 的倍数，所以78|b，考虑到1＜b ＜c ＜d ＜e ＜f ，所以取2=b，带入78=++++f e d c b，则19476⨯==+++f e d c。

同理，fe d c +++是c 的倍数，所以76|c ，考虑到2＜c ＜d ＜e ＜f ，所以取4=c ，代入76=+++f e d c ，则233272⨯==++f e d。

同理，fe d++是d 的倍数，所以72|d ，由于de 2≥、de f 42≥≥，所以 dd d d fe d 742=++≥++，从而推出df e d 772≥++=，则10≤d。

2018.6,小学四年级奥数竞赛试卷(含答案)

小学四年级奥数竞赛试卷2018.6班级姓名得分一、填空：（36分）1、妈妈买来一些青枣，小明第一次吃了一半少2 个，第二次吃了剩下的一半多2 个，还剩下3 个，妈妈买了（）个青枣。

2、3个千万、5个十万、60个十和2个一组成的数是（），这个数读作（）。

3、已知A×B=380，若A乘3，则积是（），若B除以5，则积是（）4、用1—6 这六个数字分别组成两个三位数，使这两个三位数的乘积最小，这两个数分别是（）和（）。

5、过平行四边形的一个顶点画高，最多能画（）条。

6、如果一个三角形中最小的角大于45°，那么这个三角形是（）三角形。

7、某年的四月20 日是星期四，当年的九月1 日是星期（）。

8、一个等腰三角形，顶角是88度，一个底角是（）度。

9、找规律填数（1） 2、3、5、（）、（）17、23（2 ）1、8、9、17、26、（）、69二、计算（28分）（1）选择合适的方法计算299＋99×99 =132―27＋68―73 = 3333×6666 =78 ×4＋5×78＋78 = 25×401= 1＋2＋3＋4…29＋30=（2）把1—10 这10 个数填在圆圈里，使两个大圆圈上六个数的和都等于29三、解决问题（36分）1、一个平行四边的周长是120厘米，相邻的两条边中，一条边的长度是另一条边的长度的3倍，这个平行四边形相邻的两条边的长度分别是多少厘米？2、一个鱼塘长45米，如果长增加10米，面积就增加180平方米，如果宽也增加10米，面积一共增加多少平方米？3、妈妈买来一些青枣，小明第一次吃了一半少2 个，第二次吃了剩下的一半多2 个，还剩下3 个，妈妈买了多少个青枣。

4、养鸡场的母鸡只数是公鸡只数的6倍，后来公鸡和母鸡各增加60只，结果母鸡的只数就是公鸡只数的4倍。

养鸡场原来一共养了多少只鸡？5、今年，妈妈的年龄是卡尔的8倍，再过3年，妈妈的年龄就是卡尔年龄的5倍，妈妈今年多少岁？6、兄妹二人同时离家去上学。

2018-2019年小学四年级奥数题及答案

2018-2019 学年小学四年级：兼顾规划1、烧水泡茶时，洗水壶要用 1 分钟，烧开水要用 10 分钟，洗茶壶要用 2 分钟，洗茶杯用 2 分钟，拿茶叶要用 1 分钟，如何安排才能尽早喝上茶。

2、有 137 吨货物要从甲地运往乙地，大卡车与小卡车每车次的耗油量分别是大卡车的载重量是 5 吨，小卡车的载重量是 2 吨， 10 公升和 5 公升，问如何选派车辆才能使运输耗油量最少？这时共需耗油多少升？3、用一只平底锅烙饼，锅上只好放两个饼，烙熟饼的一面需要 2 分钟，两面共需 4 分钟，此刻需要烙熟三个饼，最少需要几分钟？4、甲、乙、丙、丁四人同时到一个小水龙头处用水，甲洗拖布需要 3 分钟，乙洗抹布需要 2 分钟，丙用桶接水需要 1 分钟，丁洗衣服需要10 分钟，如何安排四人的用水次序，才能使他们所花的总时间最少，并求出这个总时间。

5、甲、乙、丙、丁四个人过桥，分别需要 1 分钟，2 分钟， 5 分钟，10 分钟。

因为天黑，一定借助于手电筒过桥，但是他们总合只有一个手电筒，而且桥的载重能力有限，只好蒙受两个人的重量，也就是说，每次最多过两个人。

此刻希望能够用最短的时间过桥，如何才能做到最短呢？你来帮他们安排一下吧。

最短时间是多少分钟呢？最多6、小明骑在牛背上赶牛过河，共有甲乙丙丁四头牛，甲牛过河需 1 分钟，乙牛需 2 分钟，丙牛需 5 分钟，丁牛需 6 分钟，每次只好骑一头牛，赶一头牛过河。

要过河时间最少？是多少？四年级奥数题：速算与巧算（一）1.【试题】计算9＋99＋999＋9999＋999992【试题】计算199999＋19999＋1999＋199＋193【试题】计算(2+4+6++996+998+1000)－－ (1+3+5+ +995+997+999)4【试题】计算9999 ×2222 ＋ 3333 ×33345.【试题】 56×3+56 ×27+56 ×96-56 ×57+566.【试题】计算98766 ×98768－98765 ×98769四年级奥数题：年纪问题1、父亲 45 岁，儿子23 岁。

四年级上册奥数试题-竞赛试卷全国通用(含答案)

小学四年级奥数竞赛试卷一、计数问题1．甲乙丙3个小朋友站成一排照相，共有种不同的排列方法．2．用1元，2元和5元的纸币，有种不同的方法凑出6元钱．3．数一数，图中有个三角形．4．如图所示，在2×2方格中，画一条直线最多穿过3个方格；在3×3方格中，画一条直线最多穿过5个方可知；那么在5×5方格中，画一条直线，最多穿过个方格．5．六一儿童节，四位小朋友各做了一个小礼物准备相互赠送，但要求自己不得留下自己做的礼物，他们收到礼物的不同方式有种．二、几何图形问题6．将一张长方形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形一定是．（填“三角形”、“长方形”、“梯形”或“菱形”）7．图是3×3的正方形方格，∠1与∠2相比，较大的是．8．各图中，阴影部分的面积与整个图形面积的比值最大的是图．9．将图中所示的三角形ABC分成面积相等的四个部分，请给出三种不同的分法．要求：在下面所给的三个图中作答．10．将一个三角形的三条边同时扩大相同的倍数，如图，得到的新三角形的面积变为原三角形面积的9倍，则新三角形的周长是原三角形的周长的倍．11．下列图形经过折叠不能围成正方体的是．12．把2、4、6、8、10、12这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图，最左边的正方形上的数字是12，则最右边的正方形上的数字是．13．将若干个边长为1的正六边形（即单位六边形）拼接起来，得到一个拼接图形，如图：那么，要拼接成周长等于18的拼接图形，需要多少个单位六边形？画出对应的一种图形．三、找规律14．3+12、6+10、12+8、24+6、48+4、…是按一定规律排列的一串算式，其中第六个算式的计算结果是．15．按规律填数：①2，4，7，11，16，②12，19，33，61，117，16．找一找规律，再在横线里填上适当的数．3、4、5、8、7、16、9、32、、四、其他问题17．请你任意写出5个真分数．18．光明小学参加课外活动小组的人数统计如图所示，则该校参加课外活动小组的共有人．19．2005年4月lO日是星期日，则2005年6月1日是星期．20．一个活动性较强的细菌每经过10秒就分裂为一个活动性较强的与一个活动性较弱的细菌，而一个活动性较弱的细菌每经过20秒就分裂为两个活动性较弱的细菌．问：一个活动性较强的细菌，经过60秒可繁殖多少个细菌？21．赛马比赛前，五位观众给A、B、C、D、E五匹赛马预测名次．甲说：“B第三名，C第五名．”乙说：“E第四名，D第五名．”丙说：“A第一名，E第四名．”丁说：“A第二名，B第一．”戊说：“A第三名，D第四名．”结果每人都只预测对了一半．“请问：这五匹马的名次是怎样排列的？”22．作家A、B、C、D、E依次坐成一排为同学们签名售书，已知每位同学恰好找座位相邻的三位作家签名，已知一共有22个同学同时找到B和D签名，并且C一共签名38次，A比E多签名6次，那么B一共签名次．23．如图，ABCD是一个梯形，已知三角形ABD的面积是12平方厘米，三角形AOD的面积比三角形BOC的面积少12平方厘米，那么，梯形ABCD的面积是平方厘米．24．2006年学校1月20日开始放寒假，3月1日上学，学校放了天寒假．25．假设某餐厅备有肉4种，鱼3种，蔬菜5种，有位客人预计肉、鱼和蔬菜各点一种，他有种点菜的方法．26．将自然数按下面的形式排列，试问：第20行最左边的数是，第20行所有数的和是．27．芳芳说：“我13岁，比惠惠小3岁，比萍萍大一岁”；惠惠说：“我不是年龄最小的，萍萍和我差4岁，萍萍是11岁”；萍萍说：“我比芳芳年龄小，芳芳10岁，惠惠比芳芳大2岁，”以上每人所说的三句话中，都有一句是错误的，则芳芳多少岁？惠惠多少岁，萍萍多少岁？2018年小学四年级奥数竞赛试卷参考答案与试题解析一、计数问题1．【分析】最左边的位置有3个小朋友可以选，中间位置还有2个小朋友可以选，最后一个位置只有1个小朋友可以选；各个位置上可以选的方法的积就是总的次数．【解答】解：3×2×1=6（种）；答：有6种不同的排列方法．故答案为：6．【点评】本题也可以采取给三人编号，然后写出全部排列的方法求解．2．【分析】分类计数，分只有一种，只有两种逐个列举即可．【解答】解答：5+1=62+2+2=62+2+1+1=62+1+1+1+1=61+1+1+1+1+1=6共有5种方法．故答案为：5．【点评】本题考查了筛选与枚举问题，关键是确定分类的办法和凑数的范围，要注意按顺序列举．3．【分析】单个的小三角形有12个，由三个小三角形组成的三角形有6个，由九个小三角形组成的三角形有2个，则可以求出三角形的总个数．【解答】解：图中有三角形：12+6+2=20（个）．故答案为：20．【点评】此题关键是将三角形进行分类再计数．4．【分析】如下图所示，那么在5×5方格中，画一条直线，最多穿过9个方格．【解答】解：在2×2方格中，画一条直线最多穿过3个方格，2+1；在3×3方格中，画一条直线最多穿过5个方可知，3+2；以此类推，那么在5×5方格中，画一条直线，最多穿过5+4=9个方格．答：那么在5×5方格中，画一条直线，最多穿过9个方格．故答案为：9．【点评】此题考查了数与形结合的规律，以上两种方法都可得解．5．【分析】结合题目的要求，我们不妨先设出四个小朋友，然后具体分析（过程见解答）即可得出答案．【解答】解答：设这四个小朋友分别是a，b，c，d，则收到a送的礼物有b、c、d三种可能，下面不妨以其中的一种可能为例分析：①以给b为例：b收到a送的礼物那么b送的礼物如果给a，那么必然是c和d交换礼物，这是一种b送的礼物如果给了c，那么c不能给a只能给d，所以d要给a，这也是一种同理b的礼物给了d又是一种则总共有1+1+1=3种即a送给b有3种；②同样，若给c和d也是各有3种；因此共计3+3+3=9种．故：此空为9．【点评】解答此题关键是理解题意，按要求进行分析即可得出答案．二、几何图形问题6．【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有4条边，并且这4条边还相等，从而可以进行从题后的答案中选择．【解答】解：由题意知，对折实际上就是对称，对折2次的话，剪下应有4条边，并且这4条边还相等，只有菱形满足这一条件，故答案为：菱形．【点评】此题考查了利用对称设计图案．7．【分析】借助正方形和线段构成的角来比较角的大小．：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【解答】解：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【点评】利用正方形来确定角的度数．8．【分析】先写出分个图形阴影部分的面积与整个图形面积的比，然后比较这几个比值的大小，从而得出答案．【解答】解：由题意知：A、把圆平均分在了6份，阴影部分的面积与整个图形面积的比值是：，B、把正方形平均分成了8份，阴影部分的面积与整个图形面积的比值是：，C、把正方形平均分成了8份，阴影部分的面积与整个图形面积的比值是：，D、通过割补法可知，阴影部分的面积与整个图形面积的比值是：，通过比较可知最大的为，故答案为：B．【点评】此题考查了分数的意义和大小比较．9．【分析】根据等底等高的三角形面积相等划分即可．【解答】解：（答案不唯一）【点评】本题考查了等底等高的三角形面积相等的灵活应用．10．【分析】根据题干分析可得，原三角形与新三角形相似三角形，相似比是1：3．根据相似三角形的性质可得：相似三角形的面积的比等于相似比的平方，相似三角形的周长的比等于相似比．由此即可得出答案．【解答】解：根据题干可得原三角形与新三角形相似，相似比是1：3，由相似三角形的性质可得：周长的比等于相似比，即：原三角形周长：新三角形周长=1：3答：新三角形的周长是原三角形的周长的3倍．故答案为：3．【点评】此题考查了相似三角形的相似比与它们周长的比以及面积的比的性质．11．【分析】根据正方体展开图的常见形式作答即可．【解答】解：由展开图可知：A、B能围成正方体；C围成几何体时，有两个面重合，故不能围成正方体．故选C．【点评】展开图能折叠成正方体的基本类型有：“一，四，一”“三，三”“二，二，二”“一，三，二”．12．【分析】根据正方体的特征和展开图的形状可知，2在正面，4在背面；6和8在侧面；10和12在上下面；由此解答．【解答】解：通过上面的分析得：最右边的正方形上的数字是4．故答案为：4．【点评】此题主要考查正方体的特征及展开图的形状．13．【分析】先从变化中观察，寻找规律．细心观察四个图形，可以发现：在拼接图形时，每增加一个单位六边形，拼接图形的周长要么不增加，要么增加2或4，据此分析解答即可．【解答】解：因为两个单位六边形拼接的图形的周长只能是10，18﹣10=8，8=4+4=4+2+2=2+2+2+2，所以当拼接图形的周长等于18时，所拼接的单位六边形有4个、5个、6个或7个，如下图：【点评】本题考查图形的规律．三、找规律14．【分析】观察算式可以发现，式子中有两个加数，第一个加数3、6、12、24、48、…依次扩大2倍，第二个加数12、10、8、6、4…依次减少2，据此规律，第六个算式是96+2=98．【解答】解：第一个加数3、6、12、24、48、…依次扩大2倍，第二个加数12、10、8、6、4…依次减少2，第六个算式为：48×2+（4﹣2）=96+2=98．故答案为：98．【点评】观察式子，找出式子的变化规律，然后运用总结的规律解决问题．15．【分析】①后一个数是前一个数依次增加2，3，4，…所得．②19﹣12=7，33﹣19=14，61﹣33=28，117﹣61=56，依次增加7的1、2、4、8、16倍即可．【解答】解：①16+6=22②117+7×16=229故答案为：22，229．【点评】通过观察数字的特点，找出相邻两个数之间的倍数关系或者差之间的关系，再由此求解即可．16．【分析】奇数项是它前面的奇数项加2所得，偶数项是它前面的偶数项乘2所得，由此得出答案．【解答】解：9+2=11，32×2=64；故答案为：11，64．【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律，然后再利用这个变化规律再回到问题中去解决问题．四、其他问题17．【分析】根据真分数的定义解答即可．【解答】解：由题意知，分子小于分母的分数叫真分数，所以任意写出的5个真分数可为：、、、、；故答案为：、、、、；【点评】此题考查了真分数的定义．18．【分析】由于条形统计图的高度代表了数量的多少，所以要求参加课外活动小组的共有多少人，只要把所有小组的人数加起来即可．【解答】解：6+9+15+20+25+30，=105（人）；故答案为：105．【点评】此题考查了学生根据条形统计图回答问题的能力．19．【分析】先求出从4月10日到6月1日经过了多少天，再求这些天里有几个星期，还余几天，根据余数判断6月1日是星期几．【解答】解：4月10日到4月30日经过了20天，5月有31天，再到6月1日又经过1天；共经过：20+31+1=52（天），52÷7=7（周）…3（天）；即6月1日是星期三．故答案为：三．【点评】本题先求出经过的天数，再求这些天里有几周，还余几天，然后根据余数推算．20．【分析】每一个活动性较强的细菌都会分解，经过60秒仍然是1个一个活动性较强的细菌；根据一个活动性较弱的细菌每经过20秒就分裂为两个活动性较弱的细菌，而每10秒又会分裂出1个活动性较弱的细菌，列举出60秒内它们的数量．【解答】解：一个活动性较强的细菌最后只剩下1个；活动性较弱的细菌分裂过程如下：第10秒：1个，第20秒：1+1=2（个），第30秒：2+1+1=4（个），第40秒：2+2+1+1=6（个），第50秒：4+2+2+1+1=10（个），第60秒：4+4+2+2+1+1=14（个），14+1=15（个）；答：一个活动性较强的细菌经过60秒可繁殖15个细菌．【点评】根据两种不同的细菌分裂方式分别求出60秒时它们各有的数量，再相加即可．21．【分析】根据丙说：“A第一名，E第四名．”假设E不是第四名，则A是第一名就正确，那么丁说：“A第二名，B第一．”都错误，这与每人都只预测对了一半相矛盾；所以E是第四名是正确，据此进一步解答即可．【解答】解：根据丙说：“A第一名，E第四名．”假设A是第一名，则E不是第四名，那么丁说：“A第二名，B第一．”都错误，这与每人都只预测对了一半相矛盾；所以E是第四名是正确，则，根据戊的表述可得A是第三名，再根据甲的表述可得C是第五名，因为A是第三名，再根据丁的表述可得B是第一名，则剩下的D 就是第二名，综合上述可得，B 是第一名，D 是第二名，A 是第三名，E 是第四名，C 是第五名．【点评】条件分析﹣﹣﹣假设法：假设可能情况中的一种成立，然后按照这个假设去判断，如果有与题设条件矛盾的情况，说明该假设情况是不成立的，那么与他的相反情况是成立的．22．【分析】同时找到B 和D 签名的肯定找了C 签名，因为C 一共签了38次，这样就可以确定找A 和E 签名的次数之和是38﹣22=16次，再由A 比E 多签名6次可以求出A 签的次数，因为找A 签名的人肯定找B 签名，所以可以推算出B 签名的次数．【解答】解：38﹣22=16（次）（16+6）÷2=11（次）11+22=33（次）故填33．【点评】此题的关键是分析38﹣22=16次所代表的含义是什么．23．【分析】根据等量加等量差不变，可知三角形ABD 和三角形ABC 的面积的差也是12平方厘米，由此可以求出三角形ABC 的面积，据此分析解答即可．【解答】解：S △AOD +S △AOB =S △ABD ，S △BOC +S △AOB =S △ABC ，则三角形ABD 的面积比三角形ABC 的面积少12平方厘米．S △ABC =12+12=24（平方厘米）S 梯形ABCD =24+12=36（平方厘米）故填：36．【点评】本题考查的是三角形和梯形的面积计算．24．【分析】2006年的1月份有31天，2月份有28天，据此解答即可．【解答】解：31﹣20+1+28=40（天）故填：40【点评】本题考查的是周期问题．25．【分析】根据题意可得，肉有4种选择，鱼有3种选择，蔬菜有5种选择，根据乘法原理可得，共有4×3×5=60种选择；据此解答即可．【解答】解：4×3×5=60（种）故答案为：60．【点评】本题考查了乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，…，做第n步有m n种不同的方法，那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法．26．【分析】观察数阵可得规律，每行数据的个数是奇数列，先求出第19行有多少个数，即1+2×（19﹣1）=37个，再求出19行的总个数1+3+5+…+37=361，再进一步解答即可．【解答】解：1+2×（19﹣1）=37（个）1+3+5+…+37=19×19=361（个）1+2×（20﹣1）=39（个）所以，第20行最左边的数是361+1=362；第20行最后一个数是：361+39=400第20行所有数的和是：（362+400）×39÷2=762×39÷2=14859故答案为：562；14859．【点评】一般地说，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．27．【分析】根据题意可知：芳芳说的“我13岁”和萍萍说的“芳芳10岁”这两句话中肯定有一句是对的，有一句是错的，据此分析解答即可．【解答】解：假设芳芳13岁是对的，则芳芳10岁就是错的，此时惠惠比芳芳大2岁，则惠惠是15岁，芳芳比萍萍大1岁，则萍萍是12岁，这样惠惠和萍萍就相差3岁，和惠惠说的“萍萍和我相差4岁”相矛盾，不符合题意．所以芳芳是10岁，此时惠惠13岁，萍萍9岁．答：芳芳10岁，惠惠13岁，萍萍9岁．【点评】本题考查的是逻辑推理．。

2018年小学数学4年级奥数试题76-100题(含详解)

成功＝勤奋＋正确的方法＋少说空话第76题：将下图的竖式谜补充完整。

答案：此题答案不唯一，填出一种就算对。

（本题还有其它答案，不一一列举）第77题：如果一个数字不是 11 的倍数，但是移除一个任意位上的数字后，它就变成了 11 的倍数，（例如 111，无论移除其个位、十位或百位上的数字，都变成 11 的倍数），这样的四位数共有多少个？答案：共有0个解析：假设这个四位数为abcd ————，则任意移除其中一位之后移除千位，为bcd ————，能被11整除，则：c d b -+|11；移除百位，为acd ————，能被11整除，则：c d a -+|11 移除十位，为abd ————，能被11整除，则：b d a -+|11 移除个位，为abc ————，能被11整除，则：b c a -+|11 结合以上四个算式可得出：a |11，d |11而a 与d 均为一位数字，则0==d a因为首位数字为0，所以这样的四位数不存在，个数为0。

第78题：将 6 个不同的正整数从小到大排成一排为 a 、b 、c 、d 、e 、f ，任意两个相邻数中，后面数都是前面数的倍数，已知 a +b + c + d + e + f =79 ,求：f 的值是多少？答案：48 解析：b ，c ，d ，e ，f 都是a 的倍数，且79=+++++f e d c b a ,当a ＞1时，结果超过79，所以1=a ，从而推出39278⨯==++++f e d c b 。

同理，f e d c b ++++是b 的倍数，所以78|b ，考虑到1＜b ＜c ＜d ＜e ＜f ，所以取2=b ，带入78=++++f e d c b ，则19476⨯==+++f e d c 。

同理，f e d c +++是c 的倍数，所以76|c ，考虑到2＜c ＜d ＜e ＜f ，所以取4=c ，代入76=+++f e d c ，则233272⨯==++f e d 。

2018-2019年小学四年级奥数题及答案

2018-2019学年小学四年级：统筹规划1、烧水沏茶时，洗水壶要用1分钟，烧开水要用10分钟，洗茶壶要用2分钟，洗茶杯用2分钟，拿茶叶要用1分钟，如何安排才能尽早喝上茶。

5、甲、乙、丙、丁四个人过桥，分别需要1分钟，2分钟，5分钟，10分钟。

现在希望可以用最短的时间过桥，怎样才能做到最短呢？你来帮他们安排一下吧。

2018四年级数学竞赛题.docx

年数学四年级学霸选拔赛袁 2018时间： 60 分钟总分： 100 分蒁荿学生信螃姓名：班级：家长电话：得分：息栏袃一、填空 : （12 分）蕿 1、在直角三角形中，一个锐角的度数是另一个锐角度数的 5 倍，这两个锐角分别是（）、（）。

螈 2、甲数是 10.9 ，乙数比甲数多0.85 ，乙数是（）。

蒃 3、书架上有两层书，共 144 本，如果从下层取出 8 本放到上层，两层书的本数一样多，原来上层有书（）本，下层有书（）本。

蚀 4、两数相乘，积比第一个因数多450，另一个因数是10，第一个因数是（）。

螈 5、用 5、8、9、0、3 这五个数字可以组成（）个没有重复数字的不同的四位数。

膇 6、有三根木料，打算把每根锯成 3 段，每锯开一处，需要 3 分钟，全部锯完需（）分钟。

芃 7、小明前几次英语的测试平均分为 84 分，这次得了 100 分，正好把这几次的平均分提高到了 88 分。

这是他第（）次考试。

螂 8、甲车每小时行 60 千米，乙车每小时行 84 千米，两车相向行，经过 5 小时相遇，相遇时两车一共行了（）千米。

肀 9、数一数，图中一共有（）个正方形。

蚇 10、□＝○＋△△＝2○如果△＝6，则□＝（）。

二、三、羄判断 : （对的打“√”，错的打“×”）（10 分）袃 1、9.895 精确到百分位是9.90（）2、3、膈如果 3 只猫同时吃 3 条鱼需 3 分钟，100 只猫同时吃掉 100 条鱼则需要 100 分钟。

（）肆 3、用 12 盆花摆成一个三角形，每条边盆数同样多，顶点处都摆，每条边摆 4 盆。

（）螄4、10千克－4 千克 80 克=5千克 20克（）5、6、蚀甲、乙两人行同样路程，甲需要 3 分钟，乙需要 4 分钟，甲的速度比乙的速度慢。

（）薁蒅三、选择：（将正确答案的序号填在括号内，共 5 分）蒄 1、不改变原数的大小，下列数中，所有零都能去掉的是（）。

蚂 A.40.050 B.45.000 C.40050虿 2、101× 48 的简便算法是（）。

小学四级奥数题附答案

实验小学四年级奥数100题1、6辆大卡车5趟可以运走50吨沙，9辆小卡车4趟可以运走48吨沙。

现在有大小卡车一共60辆，这些卡车一起运送3趟可以运走沙261吨。

那么有多少辆大卡车？答案：21辆解析：3辆大卡车运一趟是50÷5÷2=5吨，3辆小卡车运一趟是48÷4÷3=4吨。

那么这些车一次可以运261÷3=87吨。

那么大卡车有：（87-20*4）÷（5-4）*3=21辆2、某处楼梯一共有10级台阶，若每步走1级或2级台阶，8步正好走完。

那么，走此楼梯有多少种不同的走法？解析：28解析：每步走1级或2级台阶，则每步必定要走1级，一共10级，所以还剩下10-8=2级，分给8步，有：8*7÷2=283、A和B两个同学同时从甲地出发到乙地，A每分钟行50米，B每分钟行60米，B到达乙地后立即返回，若两人从出发到相遇用了10分钟，则甲乙两地相距多少米？答案：550米解析：两个人合走了2个全程，所以（50+60）×10÷2=550米4、君君和大伟早晨8点整从甲地出发去乙地，君君开车，速度每小时60千米；大伟步行，速度为每小时4千米；如果君君到底乙地后停留1小时立即返回，恰好在10点整遇到正在前往乙地的大伟。

那么甲乙两地之间的距离是多少千米？答案：34千米解析：二者的路程之和就是甲乙两地的距离5、在1989后面写一串数字，从第5个数字开始，每个数字都是它前面两个数字乘积的个位数字。

这样得到一串数字：1，9，8，9，2，8，6，8，8，4，2……那么这串数字中，前2005个数字和是多少？答案：12031解析：先发现乘积个位数的规律，然后计算和6、A、B两地相距40千米，甲乙两人同时分别从A、B两地出发，相向而行，8小时后相遇。

如果两人同时从A地出发前往B地，5小时后甲在乙前方5千米处。

问：甲每小时行多少千米？答案：3千米解析：设甲的速度是a千米每小时，乙的速度是b千米每小时，所以（a+b）*8=40从而得出a+b=5。

2018.5小学四年级奥数竞赛试卷(含答案)

小学四年级奥数竞赛试卷（含答案）2018.5班级姓名得分一、填空：（40分）1、20只鸡可以换2条狗，6条狗可以换2头猪，10头猪可以换2头牛。

那么，5头牛可以换（）只鸡。

2、有同样大小的红、白、黑珠共90个，按先3个红的，后2个白的，再1个黑的排列。

黑珠共有（）个。

3、在一条马路的两侧种树，每隔10米种一棵（两端都不种），这条马路长240米，一共需种（）棵树。

4、找规律填数。

（1）2、3、5、9、17、（）、65…（2）1、2、3、4、9、6、27、8、（）、（）、243、12…5、一个数的近似值是6万，那么这个数最大是（），最小是（）。

6、在一个减法算式里，被减数、减数与差的和等于240，而减数是差的5 倍，差是（）。

7、妈妈买来一些青枣，小明第一次吃了一半少2 个，第二次吃了剩下的一半多2 个，还剩下3 个，妈妈买了（）个青枣。

8、用1—6 这六个数字分别组成两个三位数，使这两个三位数的乘积最小，这两个数分别是（）和（）A B C D E F9、右边图中各有（）条线段？10、右边图形中共有（）个三角形。

二、计算（24分）1、下面各题怎样计算简便就怎样算686+1999 125×45－45×25 3333×6666700＋900÷15×6 199＋99×99 1＋2＋3＋4…29＋30三、解决问题（36分）1、新华书店为庆祝“六一”，买5套儿童百科送1套，每套60元。

一次买5套，每套便宜多少钱？2、龟兔赛跑，比赛全程2000米，龟每分钟爬25米，兔每分钟跑400米，兔子觉得龟跑得太慢了，跑了一会儿就睡了一觉，当龟到达终点时，兔离终点还有800米。

兔子中途睡了多少分钟？3、甲、乙两人的钱一样多，甲给乙30元，则乙的钱是甲的5倍。

甲、乙原来各有多少元？4、张宁同学期末考试成绩如下：语文和数学平均成绩是94分，数学和外语平均成绩是88分，外语和语文平均成绩是86分。

2018年小学四年级奥数竞赛试卷(5)

小学数学奥林匹克竞赛试题及答案（四年级）

(完整版)四年级上册奥数试题-竞赛试卷全国通用(含答案),推荐文档

2018年小学四年级数学竞赛试题(有答案)

2018年小学数学4年级奥数试题26-50题(含答案+解析)

【精选】小学四年级奥数竞赛数学竞赛试卷及答案word百度文库

2018四年级奥数题(附答案)

2018年小学奥数试题附答案

2018年人教版小学四年级数学竞赛试卷(附答案)

2018年小学数学4年级奥数试题76-100题(含答案+解析)

2018.6,小学四年级奥数竞赛试卷(含答案)

2018-2019年小学四年级奥数题及答案

四年级上册奥数试题-竞赛试卷 全国通用(含答案)

2018年小学数学4年级奥数试题76-100题(含详解)

2018-2019年小学四年级奥数题及答案

2018四年级数学竞赛题.docx

小学四级奥数题附答案

2018.5小学四年级奥数竞赛试卷(含答案)

四年级上册奥数试题-竞赛试卷全国通用(含答案)