衍射法测量细丝直径
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径1. 引言1.1 激光衍射法的基本原理激光衍射法是一种利用激光光束经过细丝时发生衍射现象来测量细丝直径的方法。
其基本原理是将激光光束照射到纺织品细丝上,细丝会散射出具有特定频率和方向的光线。
这些衍射光线经过适当的光学系统,形成明暗交替的衍射斑图。
通过测量这些衍射斑的特性,如斑点之间的距离和角度,可以计算出细丝的直径。
激光衍射法利用了激光光束的高强度和单色性,使其在经过细丝后产生清晰的衍射斑图,从而能够准确测量细丝直径。
与传统的光学显微镜方法相比,激光衍射法具有更高的测量精度和测量范围,能够适用于不同类型和直径范围的纺织品细丝。
激光衍射法通过利用激光的特性和衍射现象,实现了对纺织品细丝直径的精确测量,为纺织品生产和质量控制提供了重要的技术支持。
1.2 纺织品细丝直径的重要性纺织品细丝直径是纺织品品质的重要指标之一。
纺织品细丝直径的大小直接影响着纺织品的质地、手感、透气性和耐磨性等性能。
纺织品细丝直径的精确测量对于调整纺纱工艺、改进纺织品产品质量具有重要意义。
纺织品细丝直径决定了纺织品的织物密度及表面光泽度。
纤维直径较细的纺织品更加柔软细腻,而直径较粗的纺织品则具有较强的耐磨性和结实度。
通过准确测量纤维直径,可以有针对性地调整纺纱工艺参数,生产出更符合市场需求的纺织品产品。
纺织品细丝直径对纺织品的透气性和吸湿性也有影响。
细丝直径较细的纺织品透气性好,吸湿快,适合夏季穿着;而较粗的纺织品则保暖效果更好,适合冬季穿着。
通过准确测量纤维直径,可以根据不同季节和用途要求生产出功能性更强的纺织品产品。
纺织品细丝直径的重要性不言而喻。
精确测量纤维直径将有助于提高纺织品的品质,满足消费者多样化的需求,推动纺织品行业的发展。
研究和应用激光衍射法测量纺织品细丝直径具有重要意义,值得进一步探索和推广。
2. 正文2.1 激光衍射法在纺织品细丝直径测量中的应用激光衍射法在纺织品细丝直径测量中的应用是一种非常有效的技术方法。
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径
激光衍射方法是一种常用的非接触式测量纺织品细丝直径的方法。
相比传统的直径测
量方法,如显微镜测定法和拉力测定法,激光衍射法具有高精度、快速、不会对纤维产生
伤害等优点。
激光衍射法的基本原理是利用激光束的衍射现象,通过对衍射光的干涉图案进行分析,可以计算出纺织物细丝的直径大小。
在测量过程中,将纺织品细丝放置在激光束中心,激
光束通过光阑限制其大小,使其成为一个圆形的光斑,然后让激光束通过纺织品细丝,当
激光束与纺织品细丝相遇时,会产生衍射现象,衍射光会在示波器上形成一幅干涉图案。
根据衍射光干涉图案的形状和大小,可以计算出纺织品细丝的直径大小。
激光衍射法的优点是测量过程中不会对纤维产生损伤,能够测量微小的纤细丝,精度高,速度快。
对于纤细丝直径的测量在纺织品生产的各个环节中都具有重要的应用价值。
例如,在精纺过程中需要控制纤维的直径大小,以保证纱线的强度和质量;在纺织面料制
造过程中,需要测量细丝的直径大小,以便控制面料的质量;在纤维科学研究中,需要对
纤维的直径大小进行分析和比较,以探究纤维的物理化学性质。
因此,激光衍射法是一种非常重要的测量手段。
随着激光技术的不断发展,激光衍射
法将会越来越被广泛应用在纺织、化学等领域。
细丝直径高精度衍射测量的研究

图3 n ij=100、α=01001时光电信号波形器输出波形的影响,并提出了一种有效的数据处理方法。
在实际工作中,用数据采集卡采集作匀变速运动的编码器光电信号,算出编码器作匀变速运动的角速度及角加速度,运用等间隔数据还原法,得到真实的信号波形参数,即可求解出编码器动态细分误差。
参考文献[1]张善钟等.计量光栅技术[M].机械工业出版社,1985.184-232[2]李红军,吴凡等,计量光栅信号质量综合评价系统[J].光电工程,2002(8):35-38[3]梁普选等.新编Visual Basic程序设计教程[M].北京:电子工业出版社,2002.细丝直径高精度衍射测量的研究张凤生张立保(青岛大学机电工程学院,青岛266071)摘 要 利用线阵CCD的空间细分作用测量细丝衍射的暗纹间距S,从而实现细丝直径的高精度测量。
本文采用的加权数据处理方法不仅有效地减小了CCD的光响应非均匀性和衍射光强分布的随机波动对测量准确度的影响,而且可以有效减小因S不等于CCD像元中心距的整数倍所引起的细分误差。
文中还分析了由物镜焦距变化所引起的系统误差对测量的影响。
对一级量针的测量实验表明其测量准确度达±015%。
关键词 细丝直径;衍射测量;CCD0引言细丝直径(一般在10~500μm)的高精度测量在电子、仪器仪表、轻纺等工业领域有重要应用,如漆包线、光学纤维和化学纤维测量等。
目前,用于细丝直径非接触测量方法主要有光学成像法[1]、激光扫描法[2]和衍射测量法[3-4]。
光学成像法和激光扫描法由于受细丝衍射效应的影响,测量误差较大。
衍射测量法则是利用被测细丝的衍射效应来实现高精度测量,其测量关键在于高精度测定衍射图样的暗纹间距。
本文选用CCD[5]测量暗纹间距是因为CCD的像元尺寸很小,几何精度极高,可实现对暗纹间距的高分辨力测量。
此外,CCD 抗干扰能力很强,易于与计算机结合进行信号处理,构成应用于工业环境的实时自动测量系统。
3.6光学衍射法测定细丝直径

(一)比较单缝衍射和圆孔衍射图样的异同点 相同点都是明暗相间的条纹。不同点是圆孔衍射条纹为圆环形状,而单缝衍射条纹是直 线形状。 (二)衍射图样的形状与障碍物的形状的关系 光源选用激光笔,缝和孔的具体制作过程简述如下: 用刀片、缝衣针等工具在不透光的塑料卡片(如电话卡)上,分别刻制出不同宽度的缝 和不同大小、不同形状的孔。如图 1 所示卡片上制作宽度约为 2 mm 的缝 a 和宽度约为 0.5 mm 的缝 b;如图 2 所示卡片上制作直径约为 2 mm 的圆孔 c 和直径约为 1 mm 的圆孔 d;如图 3 所示卡片上制作线度都约为 1 mm 的正三角形孔 e、正方形体正多边形孔 g。
些点,互补屏产生完全相同的光强分布. 2 单缝夫琅和费衍射光强分布规律 在讨论单丝衍射之前先来讨论夫琅和费单缝衍射
夫琅和费单缝衍射要求光源和观察屏离缝都是无限远,如图 1 装置能实现这一要求。
L1
A
L2
S f1
a
φ
O
B
Xk
Pφ
图一
L
P
图中将单色光源置于透镜 L1 的前焦平面上,光束经 L1 后变成平行光,垂直照射于宽度为 a 的狭缝 AB 上,根据惠更斯-菲涅尔原理,狭缝上各点可以看成是新的波源,由这些点向各方 向发出球面次波,这些次波经透镜 L2 后,在其后焦平面的观察屏上,可看到一组明暗相间,
实验数据记录及处理
(单位:mm)
测量方法 测量项目
测量次数
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径
激光衍射法是一种常用于测量纺织品细丝直径的非接触式测量方法。
它利用激光光束通过纺织品细丝产生的衍射现象,结合适当的数学模型,可以准确地计算出细丝的直径。
在激光衍射法测量纺织品细丝直径时,首先需要准备一台激光仪器。
这台仪器通常由激光光源、光电探测器、计算机等组成。
激光光源会发出一束单色激光光束,经过透镜后形成平行光束照射到样品上。
当激光光束通过纺织品细丝时,会产生衍射现象,衍射光会被光电探测器接收到。
通过测量衍射光的强度分布,就可以计算出细丝的直径。
具体测量时,可以选择两种方式进行激光衍射法测量纺织品细丝直径,分别是垂直衍射法和平行衍射法。
垂直衍射法是将激光光源正对纺织品细丝,由光电探测器接收衍射光。
这时,细丝直径与衍射光的分布图案有直接的关系。
通过分析衍射光的强度分布,可以计算出纺织品细丝的直径。
由于纺织品细丝与光轴垂直,所以在计算时需要考虑细丝的俯视角等因素,以减小误差。
无论是垂直衍射法还是平行衍射法,都需要进行一定的数据处理和计算才能得到准确的纺织品细丝直径。
常用的处理方法包括傅里叶变换、图像处理等。
在实际测量中还需要考虑一些影响因素,如光源的波长、细丝的折射率等。
大学物理实验丨利用单丝衍射测量细丝直径
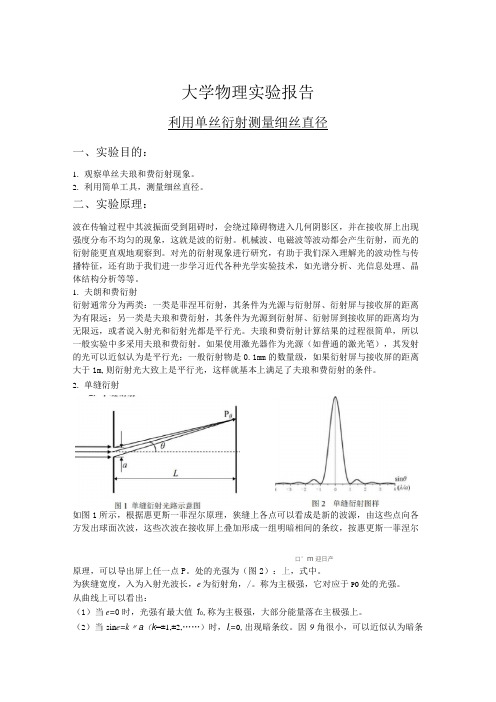
大学物理实验报告利用单丝衍射测量细丝直径一、实验目的:1.观察单丝夫琅和费衍射现象。
2.利用简单工具,测量细丝直径。
二、实验原理:波在传输过程中其波振面受到阻碍时,会绕过障碍物进入几何阴影区,并在接收屏上出现强度分布不均匀的现象,这就是波的衍射。
机械波、电磁波等波动都会产生衍射,而光的衍射能更直观地观察到。
对光的衍射现象进行研究,有助于我们深入理解光的波动性与传播特征,还有助于我们进一步学习近代各种光学实验技术,如光谱分析、光信息处理、晶体结构分析等等。
1.夫朗和费衍射衍射通常分为两类:一类是菲涅耳衍射,其条件为光源与衍射屏、衍射屏与接收屏的距离为有限远;另一类是夫琅和费衍射,其条件为光源到衍射屏、衍射屏到接收屏的距离均为无限远,或者说入射光和衍射光都是平行光。
夫琅和费衍射计算结果的过程很简单,所以一般实验中多采用夫琅和费衍射。
如果使用激光器作为光源(如普通的激光笔),其发射的光可以近似认为是平行光;一般衍射物是0.1mm的数量级,如果衍射屏与接收屏的距离大于1m,则衍射光大致上是平行光,这样就基本上满足了夫琅和费衍射的条件。
2.单缝衍射如图1所示,根据惠更斯一菲涅尔原理,狭缝上各点可以看成是新的波源,由这些点向各方发出球面次波,这些次波在接收屏上叠加形成一组明暗相间的条纹,按惠更斯一菲涅尔口°m迎日产原理,可以导出屏上任一点P。
处的光强为(图2):上,式中。
为狭缝宽度,入为入射光波长,e为衍射角,/。
称为主极强,它对应于P0处的光强。
从曲线上可以看出:(1)当e=0时,光强有最大值10,称为主极强,大部分能量落在主极强上。
(2)当sin e=k〃a(k=±1,±2,……)时,I e=0,出现暗条纹。
因9角很小,可以近似认为暗条纹在e=k刀a的位置上。
还可看到主极强两侧暗纹之间的角距离是A e=2〃a,而其他相邻暗纹之间的角距离均相等(均为A e=川a)。
(3)两相邻暗纹之间都有一个次极强。
衍射法测量细丝直径的研究

衍射法测量细丝直径的研究
衍射法是一种精密测量物体尺寸的方法,也可用于测量细丝直径。
该方法的原理是利用高能光线通过细丝时发生的衍射现象,来计算出细丝的直径。
实验时,需要将细丝置于光源和光屏之间,通过调整光源和光屏的位置,找到最佳的衍射条件。
然后测量出两个相邻衍射条纹之间的距离,用此距离和已知参数计算出细丝直径。
衍射法测量细丝直径的优点是精度高、非破坏性,对细丝的材料和形状没有限制。
但是也存在一些限制,比如光线的干扰和偏差会影响测量结果,需要进行光线矫正和精确测量。
总之,衍射法是一种可靠的测量细丝直径的方法,具有广泛的应用前景和研究价值。
3.6光学衍射法测定细丝直径

些点,互补屏产生完全相同的光强分布. 2 单缝夫琅和费衍射光强分布规律 在讨论单丝衍射之前先来讨论夫琅和费单缝衍射
夫琅和费单缝衍射要求光源和观察屏离缝都是无限远,如图 1 装置能实现这一要求。
L1
A
L2
S f1
a
φ
O
B
Xk
Pφ
图一
L
P
图中将单色光源置于透镜 L1 的前焦平面上,光束经 L1 后变成平行光,垂直照射于宽度为 a 的狭缝 AB 上,根据惠更斯-菲涅尔原理,狭缝上各点可以看成是新的波源,由这些点向各方 向发出球面次波,这些次波经透镜 L2 后,在其后焦平面的观察屏上,可看到一组明暗相间,
3.6 光学衍射法测定细丝直径
测量诸如金属细丝直径这样的细度,可以使用游标卡尺、螺旋测微计等较精密的机械工 具,也可以使用读数显微镜、工具显微镜、阿贝比长仪等精密光学仪器,还可以利用光的干 涉或衍射原理,借助光学仪器,对微小细度进行测量。利用光的干涉与衍射原理对微小细度 进行测量,其方法简单,直观性强,测量结果精度高,在高精度测量中更显示出其独特的作 用。 一、实验目的 1. 学会用衍射法测量微小尺寸. 2. 加深对光的衍射理论的理解. 二、实验仪器 He-Ne 激光器、读数显微镜、可调狭缝、待测金属细丝、光屏、透镜、卷尺、探头、光电流 放大器。 三、实验原理 1 根据巴比涅原理:两个互补屏在衍射场中某点单独产生的复振幅之和等于光波自由传播时 该点的复振幅.(本实验中即细丝直径与单缝宽度一样时,成为一对互补屏,产生相同的光 强分布) 即
衍射法测量细丝直径

一、实验目的1. 观察细丝夫琅和费衍射现象;2. 掌握细丝衍射相对光强的测量方法,并求出细丝直径;二、实验原理1. 夫琅和费衍射衍射是波动光学的重要特征之一;衍射通常分为两类:一类是满足衍射屏离光源或接收屏的距离为有限远的衍射,称为菲涅耳衍射;另一类是满足衍射屏与光源和接收屏的距离都是无限远的衍射,也就是照射到衍射屏上的入射光和离开衍射屏的衍射光都是平行光的衍射,称为夫琅和费衍射;菲涅耳衍射解决具体问题时,计算较为复杂;而夫琅和费衍射的特点是,只用简单的计算就可以得出准确的结果;在实验中,夫琅和费衍射用两个会聚透镜就可以实现;本实验用激光器作光源,由于激光器发散角小,可以认为是近似平行光照射在单缝上;其次,细丝直径为0.1mm,细丝距接收屏如果大于1米,缝宽相对于缝到接收屏的距离足够小,大致满足衍射光是平行光的要求,也基本满足了夫琅和费衍射的条件:220sin u u I I =I O 为中央明纹中心处的光强度,u=πasin θ/λ,a 是单缝宽度,φ衍射角λ为入射波长2. 菲涅耳假设和光强度 物理学家菲涅耳假设:波在传播的过程中,从同一波阵面上的各点发出的次波是相干波,经传播而在空间某点相遇时,产生相干叠加,这就是著名的惠更斯—菲涅耳原理;如图9-1所示,单缝AB 所在处的波阵面上各点发出的子波,在空间某点P 所引起光振动振幅的大小与面元面积成正比,与面元到空间某点的距离成反比,并且随细丝平面法线与衍射光的夹角衍射角增大而减小,计算细丝所在处波阵面上各点发出的子波在P 点引起光振动的总和,就可以得到P 点的光强度;可见,空间某点的光强,本质上是光波在该点振动的总强度;设细丝的宽度AB=a,细丝到接收屏之间的距离是L,衍射角为Ф的光线会聚到屏上P 点,并设P 点到中央明纹中心的距离X K ;由图9-1可知,从A 、B 出射的光线到P 点的光程差为: Φ=sin a BC 9-1式中,Ф为光轴与衍射光线之间的夹角,叫衍射角;如果子波在P 点引起的光振动完全相互抵消,光程差是半波长的偶数倍,在P 点处将出现暗纹;所以,暗纹形成的条件是:22sin λKa =Φ K=±1,±2…… 9-2在两个第一级K=±1暗纹之间的区域-λ<Φsin a <λ为中央明纹;由9-2式可以看出,当光波长的波长一定时,细丝直径a 愈小,衍射角Ф愈大,在屏上相邻条纹的间隔也愈大,衍射效果愈显著;反之,a 愈大,各级条纹衍射角Ф愈小,条纹向中央明纹靠拢;a 无限大,衍射现象消失;3. 细丝衍射的光强分布根据惠更斯—菲涅耳原理可以推出,当入射光波长为λ,细丝直径为a 时,单缝夫琅和费衍射的光强分布为: λπΦ=sin a u9-3式中I O 为中央明纹中心处的光强度,u 为细丝边缘光线与中心光线的相位差;根据上面的光强公式,可得细丝衍射的特征如下: 1 中央明纹,在Ф=0处,u=0 ,1sin 22=uu ,I=I O ,对应最大光强,称为中央主极大,中央明纹宽度由k=1±的两个暗条纹的衍射角所确定,即中央亮条纹的角宽度为aλ2=∆Φ;2 暗纹,当u=±k π,k=1,2,3……即:πλπk a ±=Φ/sin 或λk a ±=Φsin 时有:I=0;且任何两相邻暗条纹间的衍射角的差值aλ±=∆Φ,即暗条纹是以P 0点为中心等间隔左右对称分布的;图9-1 细丝衍射示意图3 次级明纹,在两相邻暗纹间存在次级明纹;它们的宽度是中央亮条纹宽度的一半;这些亮条纹的光强最大值称为次极大;其角位置依次是a λ43.1±=Φ,a λ46.2±=Φ,aλ47.3±=Φ,…… 9-4把上述的值代入光强公式9-3中,可求得各级次明纹中心的强度为0047.0I I =,0016.0I I =,0008.0I I =,…… 9-5从上面特征可以看出,各级明纹的光强随着级次K 的增大而迅速减小,而暗纹的光强亦分布其间,细丝衍射图样的相对光强分布如图9-2所示;当时出现暗纹,设第k 级暗纹离光轴的距离为,则有:式中:S 为衍射暗条纹间距,L 为细丝到观察屏的距离,λ为波长;三、实验仪器仪器名称 型号 主要参数 用途750接口CI7650阻抗 1 M Ω;最大的有效输入电压连接计算机和光传感器,使光传感器测得的数据输入计算图9-2 细丝衍射相对光强分布曲线范围±10 V 机计算机和DataStudioCI6874 ——处理光传感器测得的数据光传感器CI650-4A测量光强,波长为650nm小型激光器OS8514 发出激光转动传感器CI-6538测量角速度、角加速度和角位移,也可测量速度、加速度和位移小孔屏四、实验步骤1、连接好装置,打开灯源;启动计算机和DataStudio软件并调节好相应参数2、调节好装置,使激光通过装置发生衍射,并在光传感器上得到衍射图纹;3、调节转动传感器,测量不懂级明纹的光强,在计算机上得到相应数据三、数据记录及数据处理L=86cm光强,通道A 对位置,通道1和2,运行4位置,通道1和2 m 光强,通道A %最大值这是一种人造纤维的衍射数据光强,通道A 对位置,通道1和2,运行1位置,通道1和2 m 光强,通道A %最大值。
衍射法测量细丝直径

5 结论
用衍射法测量细丝直径是一种可达到较高精度的 非接触测量技术, 特别适合微小的细丝直径测量.但 在实际应用中由于细丝衍射图样信号存在信噪比低及 由于测量光学系统散射光形成的背景光及由此引起的 不规则干涉条纹干扰引起条纹轮廓畸变等因素使该法 应用受到一定的限制. 利用两次衍射装置抑制背景光, 运用软件编程数 字滤波技术代替硬件电路对原始波形进行滤波处理, 即可用简单的暗点识别及平均技术, 较好的解决以上
偏振片组2 可用来调节入射光束的强弱, 以保证
充分利用 c r光强测量的的动态范围, c. ) 以得到较多级 次的衍射信号. 由于激光具有相干性好的特性, 所以, 残留杂散光 之间或杂散光与衍射光之间常会发生一些杂乱的干涉 条纹, 迭加在衍射条纹上, 使测量信号受到严重干扰, 因此, 在测试装置和数据处理中, 必须设法消除这些干 扰, 才能取出有用的不失真衍射条纹信号, 否则, 得不 到正确的测量结果.采用 两个狭缝 5 和6 组成二次衍 射系统. 大大减少 了杂散光的干扰.若用扩束平行光 直接照射细丝, 图样的中心为较强的圆光斑, 干扰很 大, 即使使用遮光条8 将其挡去, 其在光学元件和遮光 条上的漫射光形成的杂散光相互之间, 杂散光与衍射 光之间仍能形成较强的干涉, 将严重干扰衍射条纹, 使 图样严重扭曲, 已无法使用, 而二次衍射系统, 在很大 程度上抑制了杂散光, 提高了条纹信号的信噪比, 可得 到较干净的条纹图样, 基本保证测量信息不受畸变. 为减小随机误差和杂散干涉条纹对衍射条纹间距测量 的影响, 取多个条纹间距平均计算, 故应使 C D多接 C 收一些条纹, 但接受的条纹数太多, 条纹间距变小, 也 会影响测量 精度, 合考虑, 们对 有效 长度为 综 我 2 .7 m 862 m的 49 个像元 C D线阵, 06 C 建议接收 士 - 6
衍射法测量细丝直径

实验二衍射法测量细丝直径
一、实验目的
1.了解衍射效应在计量技术中的应用。
2.掌握激光衍射法测量细丝直径的基本原理和测量方法。
二、实验原理
激光衍射法测量细丝直径是基于巴定理:两个互补的障碍物,其夫朗和费衍射图形、光强分布相同,位相相差π/2,因此,当细丝直径与狭缝宽度相等时,他们是两互补障该物,可以用测量狭缝的方法测量细丝直径。
测量原理如图12—1所示
图12—1
当一束激光照射到被测细丝上,发生衍射效应,在距光纤L距离处接收其衍射光强分布图,由衍射光强分布图测出第n级暗纹中心到中央零级条纹中心的距离X, 即可计算出细丝直径。
值得注意的是:此法虽然测量精度较高,但一般只适用于测量0.5mm以下的细丝直径,同时要求L ››d。
三、实验仪器与设备
激光参数测量系统(接收器移动距离为400mm)一套
四、实验内容与要求
实验内容
测量细铜丝直径
实验要求
1.根据远场夫朗和费衍射公式,导出d的计算式。
2.设计实验光路。
注意事项
1. 调整光路时不能用眼睛正对激光束,以免伤害眼睛。
要用白纸接收光。
2. 激光束与平台平行、且与接收器中心等高,保持与接收器移动方向垂直,光能量应全部进入接收器内。
3.接收器前狭缝开启的不要太大(0.2 —0.3mm),要与扫描间隔相匹配。
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径
激光衍射法是一种广泛应用于纺织品领域的非接触式测量方法。
该方法可以快速、准
确地测量纺织品细丝的直径,而且不会对样品造成任何损伤。
该方法的基本原理是,利用激光光束对样品进行照射,然后通过衍射的光线进行测量。
当激光光束照射到样品表面时,光线会发生散射和衍射。
这些衍射光线被收集并传送到检
测仪器中进行分析。
通过分析衍射光线的模式和相位,可以确定样品的直径。
激光衍射法具有许多优点。
其中最重要的是测量精度高、可靠性强和速度快。
此外,
该方法还可用于对大量样品进行自动化测量。
然而,激光衍射法的测量结果可能会受到许多因素的影响,如激光光束的直径、样品
表面的反射性和衍射角度等。
因此,在进行测量前必须进行仔细的准备工作,以确保获得
准确和一致的结果。
在使用激光衍射法测量纺织品细丝直径时,首先必须准备好样品。
样品应该被修剪成
长度适当的段,确保在测量过程中不会发生不必要的扭曲和形变。
随后,样品应该被放置在一个合适的位置,以确保激光光束可以照射到样品的准确位置。
为了避免反射造成的错误测量结果,通常采用黑色或无反射涂层处理样品表面。
然后,使用激光衍射仪器进行测量。
该仪器通常由激光光源、检测仪器和计算机组成。
操作人员向仪器输入各种参数,如激光光束的波长、衍射角度和检测器的位置等,在测量后,计算机将自动计算出样品直径。
最后,在测量完成后,操作人员应该对结果进行分析和理解。
测量结果应该与实际样
品直径进行比较,以确保结果的准确性和一致性。
衍射法测量细丝直径的研究

自然科学版 第 !" 卷 第#期 $""! 年
!" # $% & ’ "( ’ ) & "%)% * # %) + ,$-) . /
%012304 -5678579 ,:616;8
%&’( !" )& ( # $""!
衍射法测量细丝直径的研究
! 孙定源, 周桂贤, 郑德锋
(辽宁大学 物理系, 辽宁 沈阳 ##""!*)
对双边测量有 (! ! ) [#$% ( ( ) #$% ! " )! ! "& 双边 # ! ! " $ # #$% $) $ # #$% ] (+) #*&’ ! $) 式中: ! ! " %$ # $, ! ! " ,- # $ & ! ! , ! !" " ,-" # $ & ! ! , (#! ) ( ,- ) ,-.) / * $ & !! 双边 "
( &’ ! !" # ! ! " #$% ! " &! $ # #$% $) (()
范围内的条纹进行测量, 当倾斜角 " 不超过 + 度 时双边采样的误差不超过 ++ , 单边采样时, 间距 变小一边最大 ! 变大一边最大误差不超过 1+ , 误差不超过 *+ , 实际上用目视对准也很容易控 制在 0 度以内, 这时双边采样的误差仅不到 *+ &
一般测量, 氦氖激光波长! 的误差 " 的测量误差, 可忽略不计, 因而有: " $ "# $ ("! ) $ (!) %(" ) # ! " 在装置确定后 "! 很容易保证在 # .. 以内, 该项则反映为系统误差, 通过对标准细丝直径的标
实验单缝衍射的光强分布和细丝直径测

实验41 单缝衍射的光强分布和细丝直径测量光具有波动性,衍射是光波动性的一种表现。
光的衍射现象是在17世纪由格里马第发现的。
19世纪初,菲涅耳和夫琅和费分别研究了一系列有关光衍射的重要实验,为光的波动理论奠定了基础。
菲涅耳提出了次波相干迭加的观点,用统一的原理(惠更斯一菲涅耳原理)分析解释光的衍射现象;利用单缝衍射原理可以对细丝直径进行非接触的精确测量。
[学习重点]1.通过对夫琅和费单缝衍射的相对光强分布曲线的绘制,加深对光的波动理论和惠更斯——菲涅耳原理的理解。
2.掌握使用硅光电池测量相对光强分布的方法。
3.掌握利用衍射原理对细丝进行非接触测量的方法。
[实验原理]1. 单缝衍射粗略地讲,当波遇到障碍物时,它将偏离直线传播,这种现象叫做波的衍射。
衍射系统由光源、衍射屏和接收屏幕组成。
通常按它们相互间距离的大小,将衍射分为两类:一类是光源和接收屏幕(或两者之一)距离衍射屏有限远,这类衍射叫做菲涅耳衍射;另一类是光源和接收屏幕都距衍射屏无穷远,这类衍射叫做夫琅和费衍射。
本实验研究单缝夫琅和费衍射的情形。
如图41-1(a ),将单色线 光源S 置于透镜L 1的前焦面 上,则由S 发出的光通过L 1 后形成平行光束垂直照射到 单缝AB 上。
根据惠更斯一菲 涅耳原理,单缝上每一点都可 以看成是向各个方向发射球面 子波的新波源,子波在透镜L 2 的后焦面(接收屏)上叠加形 成一组平行于单缝的明暗相间的条纹。
如图41-1(b )所示。
和单缝平面垂直的衍射光束会聚于屏上的P 0处,是中央亮纹的中心,其光强为I 0;与光 轴SP 0成θ 角的衍射光束会聚于P θ 处,θ 为衍射角,由惠更斯一菲涅耳原理可得其光强分布为(41-1) 其中,b 为单缝的宽度,λ为入射单色光波长。
由41-1式可以得到:1.当θ = 0时,u = 0 ,P θ 处的光强度 I θ =I 0 是衍射图像中光强的最大值,叫主最大。
主最大的强度不仅决定于光源的强度,还和缝宽b 的平方成正比;图41-1(a )单缝衍射(b )衍射图样λθπsin ,sin 22b u u u I I ==θ2.当sin θ =k λ /b ( k = ± 1,± 2,± 3 …..)时,u = k π ,则有I θ = 0,即出现暗条纹的位置。
用衍射法测量细丝直径

射 的理解 , 及如 何应 用该 方法 对微 小量 进行 测量 .
以 往 大 学 物 理 实 验 只 是 单 纯 地 让 学 生 利 用 单
2 实 验 装 置 实 际 布 置 图
缝 衍 射法测 单缝 的宽度 , 属于 一般 的验 证性 实验 . 实验 室开设 用 衍射 法 测 量 细 丝 直径 后 , 单 缝 衍 射
利 用 衍 射 法 测 量 微 小 量 的 同 时 加 深 了 对 单 缝 衍 射
实验 的理 解和 应用 , 增 加 了学 生 动手 和思 考 的机 会, 有利 于学生 综合 实验 能力 的培养 .
3 主 要 成 效
1 ) 将 测 量 细 丝 直 径 的 实 验 内 容 增 加 至 单 缝 衍
塑 ~
用 衍 射 法 测 量 细 丝 直 径
( 广 西 师 范 大 学 物 理 实验 教 学 中心 )
遮光条1
l 主 要 内 容
用 衍 射 法 测 量 细 丝 直 径 实 验 是 广 西 师 范 大 学 物 理 实验 教 学 示 范 中心 于 2 0 0 8年 开 设 的 实 验 项 目.该 项 目要 求 学 生 在 掌 握 单 缝 衍 射 实 验 原 理 的 基础上, 学 会 利 用 衍 射 法 测 量 微 小 量 .实 验 首 先
实验课巾的内容扩展 表示称赞 , 对
于 引 入 的 通 用 软 件 学 习 的 教 学 理 念。 也 给 予了充分 的肯定 .
( 执笔: 杨文 明 , 王 宇兴)
器■ 光
的图像 质量 比原 有 的 实 验 图像 有 了明 显提 高 , 学 生 对 于 通用 软 件 的掌 握速 度也 比预 期 快 . 参 观 实
要求 学 生根 据 单 缝 衍 射 的原 理 自行 组 装 实 验 仪
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径
激光衍射法是一种常用的测量纺织品细丝直径的方法。
它通过测量激光经过纺织品细丝时的衍射效应,来推断出纺织品细丝的直径。
激光衍射法的原理是利用激光光束通过纺织品细丝时,会产生衍射现象。
激光光束经过纺织品细丝后,会呈现出明暗交替的衍射条纹。
这些衍射条纹的形状和间距与纺织品细丝的直径密切相关。
通过观察和测量衍射条纹的形状和间距,可以推断出纺织品细丝的直径。
具体的测量步骤如下:
1. 准备测量仪器和样品。
需要准备一台激光衍射仪和待测纺织品细丝样品。
激光衍射仪由激光器、准直系统、衍射系统和检测系统等组成。
2. 调整激光衍射仪。
将激光衍射仪固定在水平台上,并调整激光器和准直系统,使激光光束垂直射向样品。
3. 放置样品。
将待测纺织品细丝样品放置在激光光束的路径上,使其与光束垂直相交。
4. 观察衍射条纹。
打开激光衍射仪的衍射系统和检测系统,使衍射条纹在检测系统的显示屏上呈现出来。
观察并记录衍射条纹的形状和间距。
5. 计算细丝直径。
根据衍射条纹的形状和间距,使用相应的数学公式或计算方法,计算出纺织品细丝的直径。
激光衍射法具有测量快速、准确度高、非接触等优点,因此广泛应用于纺织品细丝直径的测量领域。
激光衍射法还可以用于其他材料的直径测量,具有较大的应用潜力。
随着科技的发展和对纺织品细丝直径要求的不断提高,激光衍射法的应用将会更加广泛。
大学物理实验丨利用单丝衍射测量细丝直径
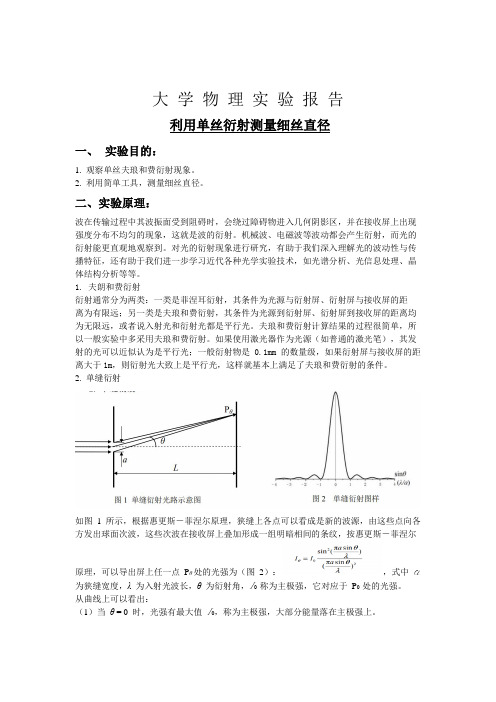
大学物理实验报告利用单丝衍射测量细丝直径一、实验目的:1. 观察单丝夫琅和费衍射现象。
2. 利用简单工具,测量细丝直径。
二、实验原理:波在传输过程中其波振面受到阻碍时,会绕过障碍物进入几何阴影区,并在接收屏上出现强度分布不均匀的现象,这就是波的衍射。
机械波、电磁波等波动都会产生衍射,而光的衍射能更直观地观察到。
对光的衍射现象进行研究,有助于我们深入理解光的波动性与传播特征,还有助于我们进一步学习近代各种光学实验技术,如光谱分析、光信息处理、晶体结构分析等等。
1. 夫朗和费衍射衍射通常分为两类:一类是菲涅耳衍射,其条件为光源与衍射屏、衍射屏与接收屏的距离为有限远;另一类是夫琅和费衍射,其条件为光源到衍射屏、衍射屏到接收屏的距离均为无限远,或者说入射光和衍射光都是平行光。
夫琅和费衍射计算结果的过程很简单,所以一般实验中多采用夫琅和费衍射。
如果使用激光器作为光源(如普通的激光笔),其发射的光可以近似认为是平行光;一般衍射物是 0.1mm 的数量级,如果衍射屏与接收屏的距离大于1m,则衍射光大致上是平行光,这样就基本上满足了夫琅和费衍射的条件。
2. 单缝衍射如图1 所示,根据惠更斯-菲涅尔原理,狭缝上各点可以看成是新的波源,由这些点向各方发出球面次波,这些次波在接收屏上叠加形成一组明暗相间的条纹,按惠更斯-菲涅尔原理,可以导出屏上任一点Pθ处的光强为(图2):,式中a 为狭缝宽度,λ 为入射光波长,θ 为衍射角,I0 称为主极强,它对应于P0 处的光强。
从曲线上可以看出:(1)当θ = 0 时,光强有最大值I0,称为主极强,大部分能量落在主极强上。
(2)当sinθ = kλ/a (k =±1, ±2,……)时,Iθ = 0,出现暗条纹。
因θ 角很小,可以近似认为暗条纹在θ = kλ/a 的位置上。
还可看到主极强两侧暗纹之间的角距离是Δθ = 2λ/a,而其他相邻暗纹之间的角距离均相等(均为Δθ = λ/a)。
应用激光衍射法测量纺织品细丝直径

应用激光衍射法测量纺织品细丝直径激光衍射法是一种目前广泛应用于纺织品细丝直径测量的非接触式测量方法。
通过利用激光光源照射到纺织品细丝上产生的散射光,并通过其衍射图样来获得细丝的直径信息。
该方法具有精度高、测量快速、非接触等优点,在纺织工业中得到了广泛应用。
激光衍射法测量纺织品细丝直径的基本原理是利用激光照射到纺织品细丝上时,光线经过细丝散射形成光晕区域。
根据光晕图样的衍射规律,可以推导出细丝直径和光晕图样之间的关系。
通过测量光晕图样的直径,就可以得到细丝的直径信息。
1. 准备工作需要准备一台搭载有激光光源的衍射仪器。
衍射仪器主要包括光源、激光发射系统、衍射系统和光电检测系统等部分。
确保各个部分的工作正常,保证精确的测量结果。
2. 校准在进行测量之前,需要对衍射仪进行校准。
校准的目的是确定光源和检测系统之间的距离,以及光源到细丝之间的距离,以确保测量的准确性和精度。
3. 测量将待测纺织品细丝放置在测量平台上,并将激光光源打开。
通过调节光源和细丝之间的距离,使激光光线正好照射到细丝上。
当激光照射到细丝上时,会产生一片光晕区域。
4. 图像获取利用光电检测系统,即相机或光电转换器等设备,捕捉光晕图样的影像。
将光晕图样的影像传输到计算机中进行图像处理。
5. 图像处理通过图像处理软件对光晕图样进行处理。
将图像转化为灰度图像,简化后续的图像处理。
然后,进行二值化处理,将光晕图样中的背景和细丝区域进行分离。
接着,可对图像进行去噪、边缘检测等处理,以便更准确地获取细丝的直径。
6. 数据分析对经过图像处理的光晕图样进行数据分析。
使用合适的算法和公式,将光晕图样的直径转化为细丝的直径。
根据需要,还可以对多个位置的图样进行分析和统计,以得到更为全面的测量结果。
激光衍射法测量纺织品细丝直径具有许多优点。
由于是非接触式测量,不会对纺织品细丝造成损伤。
测量速度快,可以快速获取大量数据。
激光衍射法精度高,对于细丝直径的测量要求较高的应用场合非常适用。
衍射法测量细丝直径

衍射法测量细丝直径 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】一、实验目的1. 观察细丝夫琅和费衍射现象。
2. 掌握细丝衍射相对光强的测量方法,并求出细丝直径。
二、实验原理 1. 夫琅和费衍射衍射是波动光学的重要特征之一。
衍射通常分为两类:一类是满足衍射屏离光源或接收屏的距离为有限远的衍射,称为菲涅耳衍射;另一类是满足衍射屏与光源和接收屏的距离都是无限远的衍射,也就是照射到衍射屏上的入射光和离开衍射屏的衍射光都是平行光的衍射,称为夫琅和费衍射。
菲涅耳衍射解决具体问题时,计算较为复杂。
而夫琅和费衍射的特点是,只用简单的计算就可以得出准确的结果。
在实验中,夫琅和费衍射用两个会聚透镜就可以实现。
本实验用激光器作光源,由于激光器发散角小,可以认为是近似平行光照射在单缝上;其次,细丝直径为0.1mm ,细丝距接收屏如果大于1米,缝宽相对于缝到接收屏的距离足够小,大致满足衍射光是平行光的要求,也基本满足了夫琅和费衍射的条件:220sin u u I II O 为中央明纹中心处的光强度,u=?asin θ/?,a 是单缝宽度,?衍射角?为入射波长 2. 菲涅耳假设和光强度物理学家菲涅耳假设:波在传播的过程中,从同一波阵面上的各点发出的次波是相干波,经传播而在空间某点相遇时,产生相干叠加,这就是着名的惠更斯—菲涅耳原理。
如图9-1所示,单缝AB 所在处的波阵面上各点发出的子波,在空间某点P 所引起光振动振幅的大小与面元面积成正比,与面元到空间某点的距离成反比,并且随细丝平面法线与衍射光的夹角(衍射角)增大而减小,计算细丝所在处波阵面上各点发出的子波在P 点引起光振动的总和,就可以得到P 点的光强度。
可见,空间某点的光强,本质上是光波在该点振动的总强度。
设细丝的宽度AB=a ,细丝到接收屏之间的距离是L ,衍射角为Ф的光线会聚到屏上P 点,并设P 点到中央明纹中心的距离X K 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的
1. 观察细丝夫琅和费衍射现象。
2. 掌握细丝衍射相对光强的测量方法,并求出细丝直径。
二、实验原理
1. 夫琅和费衍射
衍射是波动光学的重要特征之一。
衍射通常分为两类:一类是满足衍射屏离光源或接收屏的距离为有限远的衍射,称为菲涅耳衍射;另一类是满足衍射屏与光源和接收屏的距离都是无限远的衍射,也就是照射到衍射屏上的入射光和离开衍射屏的衍射光都是平行光的衍射,称为夫琅和费衍射。
菲涅耳衍射解决具体问题时,计算较为复杂。
而夫琅和费衍射的特点是,只用简单的计算就可以得出准确的结果。
在实验中,夫琅和费衍射用两个会聚透镜就可以实现。
本实验用激光器作光源,由于激光器发散角小,可以认为是近似平行光照射在单缝上;其次,细丝直径为0.1mm ,细丝距接收屏如果大于1米,缝宽相对于缝到接收屏的距离足够小,大致满足衍射光是平行光的要求,也基本满足了夫琅和费衍射的条件:
2
20sin u u I I =
I O 为中央明纹中心处的光强度,u=πasin θ/λ,a 是单缝宽度,φ衍射角λ为入
射波长
2. 菲涅耳假设和光强度
物理学家菲涅耳假设:波在传播的过程中,从同一波阵面上的各点发出的次波是相干波,经传播而在空间某点相遇时,产生相干叠加,这就是著名的惠更斯—菲涅耳原理。
如图9-1所示,单缝AB 所在处的波阵面上各点发出的子波,在空间某点P 所引起光振动振幅的大小与面元面积成正比,与面元到空间某点的距离成反比,并且随细丝平面法线与衍射光的夹角(衍射角)增大而减小,计算细丝所在处波阵面上各点发出的子波在P 点引起光振动的总和,就可以得到P 点的光强度。
可见,空间某点的光强,本质上是光波在该点振动的总强度。
设细丝的宽度AB=a,细丝到接收屏之间的距离是L,衍射角为Ф的光线会聚到屏上P点,并设P点到中央明纹中心的距离X
K。
由图9-1可知,从A、B出射的光线到P点的光程差为:Φ
=sin
a
BC
(9-1)
式中,Ф为光轴与衍射光线之间的夹角,叫衍射角。
如果子波在P点引起的光振动完全相互抵消,光程差是半波长的偶数倍,在P点处将出现暗纹。
所以,暗纹形成的条件是:
2
2
sin
λ
K
a=
ΦK=±1,±2……(9-2)在两个第一级(K=±1)暗纹之间的区域(-λ<Φ
sin
a<λ)为中央明纹。
由(9-2)式可以看出,当光波长的波长一定时,细丝直径a愈小,衍射角Ф愈大,在屏上相邻条纹的间隔也愈大,衍射效果愈显著。
反之,a愈大,各级条纹衍射角Ф愈小,条纹向中央明纹靠拢。
a无限大,衍射现象消失。
3. 细丝衍射的光强分布
根据惠更斯—菲涅耳原理可以推出,当入射光波长为λ,细丝直径为a时,
单缝夫琅和费衍射的光强分布为:
λ
πΦ
=
sin
a
u
(9-3)
式中I
O
为中央明纹中心处的光强度,u为细丝边缘光线与中心光线的相位差。
根据上面的光强公式,可得细丝衍射的特征如下:
(1) 中央明纹,在Ф=0处,u=0 ,1
sin
2
2
=
u
u,I=I
O
,对应最大光强,称为
中央主极大,中央明纹宽度由k=1
±的两个暗条纹的衍射角所确定,即中央亮条
纹的角宽度为
a
λ2
=
∆Φ。
(2) 暗纹,当u=±kπ,k=1,2,3……即:π
λ
πk
a±
=
Φ/
sin或λk
a±
=
Φ
sin
时有:I=0。
且任何两相邻暗条纹间的衍射角的差值
a
λ
±
=
∆Φ,即暗条纹是
以P
点为中心等间隔左右对称分布的。
图9-1 细丝衍射示意图
(3) 次级明纹,在两相邻暗纹间存在次级明纹。
它们的宽度是中央亮条纹宽
度的一半。
这些亮条纹的光强最大值称为次极大。
其角位置依次是
a
λ
43
.1±
=
Φ,
a
λ
46
.2±
=
Φ,
a
λ
47
.3±
=
Φ,……(9-4)
把上述的值代入光强公式(9-3)中,可求得各级次明纹中心的强度为
047
.0I
I=,
016
.0I
I=,
008
.0I
I=,……(9-5)从上面特征可以看出,各级明纹的光强随着级次K的增大而迅速减小,而暗纹的光强亦分布其间,细丝衍射图样的相对光强分布如图9-2所示。
当时出现暗纹,设第k级暗纹离光轴的距离为,则有:
式中:S为衍射暗条纹间距,L为细丝到观察屏的距离,λ为波长。
三、实验仪器
仪器名称
型
号
主要参数用途
750接口CI7650
阻抗1 MΩ。
最
大的有效输入电压
连接计算机和光传感器,使
光传感器测得的数据输入计算
图9-2 细丝衍射相对光强分布曲线
范围±10 V 机
计算机和
DataStudio
CI6874 ——处理光传感器测得的数据
光传感器CI650-4
A
测量光强,波长为650nm
小型激光器OS8514 发出激光
转动传感器CI-6538
测量角速度、角加速度和角
位移,也可测量速度、加速度和
位移
小孔屏
四、实验步骤
1、连接好装置,打开灯源;启动计算机和DataStudio软件并调节好相应参数
2、调节好装置,使激光通过装置发生衍射,并在光传感器上得到衍射图纹。
3、调节转动传感器,测量不懂级明纹的光强,在计算机上得到相应数据
三、数据记录及数据处理
L=86cm
光强,通道A 对位置,通道1和2,运行#4
位置,通道1和2 (m) 光强,通道A (%最大值)
0.029 25.782 0.031 69.045 这是一种人造纤维的衍射数据
0.030 22.950 0.031 73.928
0.030 22.462 0.031 73.733
0.030 25.880 0.031 73.733
0.030 32.130 0.031 75.881
0.030 35.548 0.032 71.194
0.030 43.361 0.032 62.697
0.031 49.220 0.032 56.642
0.031 58.303 0.032 51.662
0.031 66.213 0.032 45.314
0.032 41.115
0.032 41.798
0.032 43.068
0.032 43.068
光强,通道A 对位置,通道1和2,运行#1
位置,通道1和2 (m) 光强,通道A (%最大值)
0.041 12.696 0.043 19.141 0.044 50.295 0.046 49.220 0.041 11.914 0.043 19.532 0.044 49.318 0.046 51.076 0.041 11.817 0.043 20.118 0.044 48.341 0.046 56.349。
