黄金分割法与进退法的C语言程序
黄金分割法与进退法的C语言程序

a=min[a1,a3], b=max[a3,a1],函数最小值所在的区间为[a, b] 。
我编的修改
#include<math.h> #include<stdio.h> #define f(x) 3*x*x*x-4*x+2 main() { double f1,f2,f3,temp,x1,x2,x3,h,a,b,Y1,Y2,A,A1,A2,e=0.2;
else if(f2<f1) { h=2*h;
x3=x2+h; f3=f(x3); }
while(f2>f3)
{ x1=x2;
x2=x3;
f2=f(x3);
x3=x2+h;
f3=f(x3);
}
a=x1<x3?x1:x3;
b=x1>x3?x1:x3;
printf("[%f,%f]\n",a,b);
A1=b+0.328*(b-a); Y1=f(A1);
基本思想:
对 f(x)任选一个初始点 a1 及初始步长 h, 通过比较这两点函数值的大小,确定 第三点位置,比较这三点的始步长 h=h0,计算 y1=f(a1),
机械优化设计-王荣老师复习过程

(一) 一维搜索方法1.1 题目: .3610)(m in 2+-=t t t f1.2 最优解: .5*=t .11)(*=x f1.3 采用的算法及其算法的基本思想:首先采用进退法确定函数极值点所在的搜索区间[a, b],然后采用牛顿法求出极值。
进退法的基本思想:按照一定的规则试算若干个点,比较其函数值的大小,直至找到函数值按“高-低-高”变化的单峰区间。
黄金分割法的基本思想:通过不断的缩短单峰区间的长度来搜索极小点的一种有效方法。
按λ(618.0=λ)缩小 比较)(x f 大小 确定取舍区间。
1.4 程序框图:进退法和黄金分割法流程图如下:图2 黄金分割法程序框图1.5具体程序如下:共3个M文件,文件名分别为:F.m;JINTUI.m;FGOLDEN.m F.m具体程序:%定义f(x)函数的表达式f(x)=t^2-10*t+36function y=F(t)y=t^2-10*t+36;JINTUI.m具体程序:function [t,minF]=FGOLDEN(precision,a0,h)[a,b]=JINTUI(a0,h);A=a;B=b;while 0.618^(n-1)>=precisionC=A+0.312*(B-A);D=A+0.618*(B-A);if C<Dif F(C)<F(D)B=D;elseA=C;endelseif F(C)<F(D)A=C;elseB=D;endendn=n+1;endt=A;minF=F(A);FGOLDEN.m具体程序如下:function [x1,x2]=JINTUI(a0,h) a=a0;b=a0+h;while 1if F(a)<F(b)h=-h;a=a+h;b=a-h;if F(b)<F(b-h)&F(b)<F(a)break;endelsea=b;b=a+h;if F(a)<F(b)&F(a)<F(a-h)break;endendendx1=a;x2=b;1.6 输出结果:2.1 题目: .60645)(m in 234+-+-=t t t t t f2.2 最优解: .2796.3*=t .6590.22)(*=x f2.3 采用的算法及其算法的基本思想:首先采用进退法确定函数极值点所在的搜索区间[a, b],然后采用牛顿法求出极值。
黄金分割法及其代码

黄⾦分割法及其代码线性搜索之黄⾦分割法及其应⽤摘要最优化理论和⽅法⽇益受到重视,已经渗透到⽣产、管理、商业、军事、决策等各个领域,⽽最优化模型与⽅法⼴泛应⽤于⼯业、农业、交通运输、商业、国防、建筑、通讯和政府机关等领域。
伴随着计算机技术的⾼速发展,最优化理论与⽅法的迅速进步为解决实际最优化问题的软件也在飞速发展。
其中,MATLAB 软件已经成为最优化领域应⽤最⼴的软件之⼀。
有了MATLAB这个强⼤的计算平台,既可以利⽤MATLAB优化⼯具箱(OptimizationToolbox)中的函数,⼜可以通过算法变成实现相应的最优化计算。
在最优化计算中⼀维最优化⽅法是优化设计中最简单、最基本的⽅法。
⼀维搜索,⼜称为线性搜索,⼀维问题是多维问题的基础,在数值⽅法迭代计算过程中,都要进⾏⼀维搜索,也可以把多维问题化为⼀些⼀维问题来处理。
⼀维问题的算法好坏,直接影响到最优化问题的求解速度。
⽽黄⾦分割法是⼀维搜索⽅法中重要的⽅法之⼀,它适⽤于任何单峰函数求最⼩值的问题,甚⾄于对函数可以不要求连续,是⼀种基于区间收缩的极⼩点搜索算法。
关键词:最优化、黄⾦分割法、MATLAB软件、⼀维搜索引⾔数学科学不仅是⾃然科学的基础,也是⼀切重要技术发展的基础。
最优化⽅法更是数学科学⾥⾯的⼀个巨⼤的篇幅,在这个信息化的时代,最优化⽅法⼴泛应⽤于⼯业、农业、国防、建筑、通信与政府机关、管理等各领域;它主要解决最优计划、最优分配、最优决策、最佳设计、最佳管理等最优化问题。
⽽最优解问题是这些所有问题的中⼼,是最优化⽅法的重中之重,在求最优解问题中,有多种⽅法解决,我们在这⾥着重讨论⽆约束⼀维极值问题,即⾮线性规划的⼀维搜索⽅法之黄⾦分割法。
黄⾦分割法也叫0.618法,属于区间收缩法,⾸先找出包含极⼩点的初始搜索区间,然后按黄⾦分割点通过对函数值的⽐较不断缩⼩搜索区间。
当然要保证极⼩点始终在搜索区间内,当区间长度⼩到精度范围之内时,可以粗略地认为区间端点的平均值即为极⼩值的近似值。
黄金分割法编程

• (1)M文件程序:
• function fmin=gold(x1,x2,d) %建立函数文件 • d=0.13/180*pi; %将度转换为弧度 • x1=40/180*pi; • x2=50/180*pi; • x=x1:d:x2; • f=-sin(x).*cos(x); • plot(x,f,'r') %画出函数图形 • title('黄金分割法求函数最小值-1304卢贵兵') • xlabel('x') • ylabel('f') • axis tight
• 本题中需要注意的地方:1.度需要转化为弧度
• (3)讨论
• 黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于 另一部分与这部分之比。其比值是一个无理数,用分数表示为(√5-1)/2,取 其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此 称为黄金分割,也称为中外比。这个分割点就叫做黄金分割点。 • 黄金比例的求法如下: 设一条线段AB的长度为a,C点在靠近B点的黄金分割点上,且AC为b,则a 比b就是黄金数
(2)报告(结果):
运行程序得: • f1 = • -0.4996 • f2 = • -0.4996 • ans = • 1 • k = • 1 • f1 = • -0.4979 • f2 = • -0.4996 • k = • 2
•
f1 =
•
• • • • • •
-0.4996
f2 = -0.5000 k= 3 …… ……
• 以下是对单谷函数求最小值做简单分析: • 具体步骤是:在区间[a,b]内取点:a1 ,a2 把[a,b]分为三段。 ① 如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+0.618*(b-a); ② 如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=b-0.618*(b-a); ③如果f(a1)==f(a2),令a=a1,b=a2, a1=b-0.618*(b-a); a2=a+0.618*(b-a); (可分为两种情况,简化程序) 如果|(b-a)/b|和|(y1-y2)/y2|都大于收敛精度ε重新开始循环。 因为[a,b]为单谷或单峰区间,这样每次可将搜索区间缩小0.618倍, 处理后的区间都将包含极小点的区间缩小,然后在保留下来的区间 上作同样的处理,如此迭代下去,将使搜索区[a,b]逐步缩小,直到 满足预先给定的精度时,即获得一维优化问题的近似最优解 。
黄金分割法程序

一维搜索一维优化一般分为两大步骤:(1)确定初始搜索区间[a,b],该区间应是包括一维函数极小点在内的单峰区间;(2)在搜索区间[a,b]内寻找极小点。
搜索区间的确定—进退法基本思路是:由单峰函数性质可知,在极小点a*左边函数值应严格下降,而在极小点右边函数值应严格上升。
因此,可从某一个给定的初始点a0出发,以初始步长h0沿着目标函数值的下降方向,逐步前进或后退,直到找到相继的3个试点的函数值按“大---小----大”变化为止。
一:确定搜索区间的外推法•首先确定函数的单谷性•然后从起点开始以初始步长向前试探,如果函数值变大,则改变步长方向。
•如果函数值下降,则维持原来的试探方向,并将步长加倍。
搜索区间的确定流程图确定搜索区间的程序代码void findqujian(float a[3],float f[3]) {float t=steplength, a1,f1,ia;a[0]=0;f[0]=fc(a[0]);for(int i=0;;i++){a[1]=a[0]+t;f[1]=fc(a[1]); if(f[1]<f[0]) break;if(fabs(f[1]-f[0])>=e){t=-t;a[0]=a[1];f[0]=f[1];}else{ if(ia==1)return;t=t/2;ia=1;}}for(i=0;;i++){a[2]=a[1]+t;f[2]=fc(a[2]);if(f[2]>f[1]) break;t=2*t;a[0]=a[1]; f[0]=f[1];a[1]=a[2]; f[1]=f[2];}if(a[0]>a[2]){a1=a[0];f1=f[0];a[0]=a[2];f[0]=f[2];a[2]=a1; f[2]=f1;}return;}一、黄金分割法黄金分割法是通过不断缩短搜索区间的长度来寻求一维函数的极小点,这种方法的基本原理是:在搜索区间[a,b]内按如下规则对称地取两点a1和a2a1=a+0.382(b-a); a2=a+0.618(b-a);黄金分割法的搜索过程是:1)给出初始搜索区间[a,b] 及收敛精度e ,将赋以0.618 2)计算a1 和a2,并计算起对应的函数值f(a1),f(a2); ,3)根据期间消去法原理缩短搜索区间,为了能用原来的坐标点计算公式,需进行区间名城的代换,并在保留区间中计算一个新的试验点及其函数值。
优化设计进退法实验报告

一、实验目的本次实验旨在通过实际操作,加深对优化设计方法——进退法的理解,培养学生运用进退法解决实际问题的能力,提高程序调试和出错处理的能力。
二、实验原理进退法是一种常用的优化方法,适用于一维函数优化问题。
其基本原理是:从初始点出发,按照一定的搜索方向逐步前进,每次前进一定距离后,根据目标函数的值判断是否继续前进或后退。
若目标函数值变差,则后退;若目标函数值变好,则继续前进。
三、实验内容1. 确定初始区间本实验以一维函数 f(x) = x^2 + 3x + 1 为例,首先需要确定初始区间。
通过观察函数图像或计算函数值,可以初步确定初始区间为 [a, b],其中 a < b。
2. 进退法基本思路进退法的基本思路如下:(1)从初始点x0 ∈ [a, b] 出发,计算 f(x0)。
(2)计算前进方向和后退方向的函数值,即 f(x0 + h) 和 f(x0 - h),其中h 为步长。
(3)比较 f(x0 + h) 和 f(x0 - h) 的值,若 f(x0 + h) < f(x0 - h),则前进;否则,后退。
(4)重复步骤(2)和(3),直到满足停止条件。
3. 源代码实现根据进退法的基本思路,编写相应的C语言程序。
以下为进退法的C语言实现:```c#include <stdio.h>#include <math.h>double f(double x) {return x x + 3 x + 1;}int main() {double a = -10, b = 10, x0 = 0, h = 0.1; double fa, fb, fx0, fx;while (b - a > 0.0001) {fx0 = f(x0);fa = f(x0 + h);fb = f(x0 - h);if (fa < fb) {a = x0;x0 += h;} else {b = x0;x0 -= h;}}printf("最优解为:%f\n", x0);printf("目标函数值:%f\n", f(x0));return 0;}```4. 执行结果分析运行上述程序,得到最优解为x ≈ -1.5,目标函数值约为 0.375。
c语言用斐波那契数列求黄金分割比

c语言用斐波那契数列求黄金分割比黄金分割比是一种非常特殊的比例关系,它被广泛应用于建筑、艺术、设计等领域。
而斐波那契数列则是一种非常有趣的数列,它的每一项都是前两项的和。
在本文中,我们将探讨如何使用C语言来计算斐波那契数列,并利用它来求解黄金分割比。
让我们来看一下斐波那契数列的定义。
斐波那契数列的第一项和第二项都是1,从第三项开始,每一项都是前两项的和。
因此,斐波那契数列的前几项是1、1、2、3、5、8、13、21、34、55、89、144等。
接下来,我们可以使用C语言来编写一个简单的程序来计算斐波那契数列。
代码如下:```#include <stdio.h>int main(){int n, i, t1 = 1, t2 = 1, nextTerm;printf("请输入要输出的斐波那契数列的项数:");scanf("%d", &n);printf("斐波那契数列的前 %d 项为:\n", n);for (i = 1; i <= n; ++i){printf("%d, ", t1);nextTerm = t1 + t2;t1 = t2;t2 = nextTerm;}return 0;}```在这个程序中,我们首先定义了三个变量:n表示要输出的斐波那契数列的项数,i表示当前项数,t1和t2分别表示当前项和下一项。
然后,我们使用for循环来计算并输出斐波那契数列的前n项。
现在,我们已经可以计算斐波那契数列了。
接下来,让我们来看一下如何使用斐波那契数列来求解黄金分割比。
黄金分割比是指将一条线段分成两部分,使其中一部分与全长之比等于另一部分与这部分之比。
这个比例关系可以用一个数学公式来表示:```a /b = (a + b) / a```其中,a表示较长的线段,b表示较短的线段。
将这个公式变形一下,可以得到:```a /b = (1 + √5) / 2```这个公式就是黄金分割比的定义式。
机械优化设计VC6.0黄金分割法
i++;
if (y1>=y2)
{
a=a1;
a1=a2;
y1=y2;
a2=a+r*(b-a);
y2=f(a2);
}
else
{
b=a2;
a2=a1;
y2=y1;
a1=b-r*(b-a);
y1=f(a1);
}
q=(a+b)/2;
printf("%f\n",q);
}
a=(a+b)/2;
printf("迭代次数:%d\n",i);
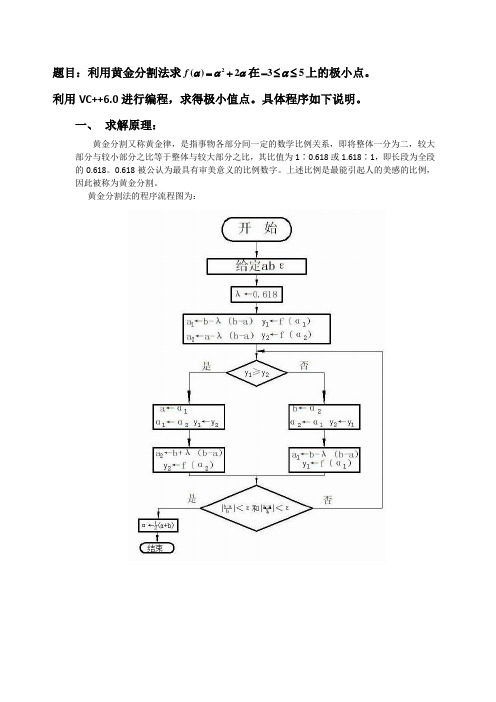
题目:利用黄金分割法求 在 上的极小点。
利用VC++6.0进行编程,求得极小值点。具体程序如下说明。
一、求解原理:
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值为1∶0.618或1.618∶1,即长段为全段的0.618。0.618被公认为最具有审美意义的比例数字。上述比例是最能引起人的美感的比例,因此被称为黄金分割。
printf("得到的近似极小点:%f\n",a);
printf("相应的函数值:%f\n",f(a));
printf("**************************************************************************\n");
}
运行结果:
总结
综上所述,运用黄金分割法求得已知函数的极小值。使用VC++6.0实现编译,得到所要的结果。由运行结果证明程序编译正确。
{
03.第三讲 一维优化法 黄金分割法

f(a )
f1
f2
0
f3
h
a1
h
a2a32) f源自2h 2h, a1 a2 , a2 a3 , a3 a2 h
f (a)
f3
,则令步长加倍,即令:
如此重复该过程,直至找到符合“大—小—大”变化要 求,从而确定搜索区间。
f1 f 1 f 2
f2
f3
h h 2h
a1
f3
a 2 a3 a1 a 2
2.
L λL
(1-λ)L
f1
(1-λ)L
f2
a2
b
b
f1
a
a
f2
a1
a1 a2
给定:
a,b,
a 0 . 382 ( b a ) a1 , f ( a1 ) f 1 a 0 . 618 ( b a ) a 2 , f ( a 2 ) f 2
否
f1 f 2
是
a2 b, a1 a2 , f1 f 2 a 0.382(b a ) a1 f ( a1 ) f1
a3
a
B、如果
计算 f 3 f (a3 ),比较对调后的 f 2 与 f 3 ; 1)若 f 2 f 3 ,则搜索区间为:[a, b] [a , a ] 3 1
f 2 f 1 ,则做后退计算,令 h h 将 a1 , f1 和 a2 , f 2 对调,取 a3 a2 h
第4章 一维优化方法
1.确定搜索区间的方法—进退法
基本思路:根据单峰函数的性质,在极小值点 a 左 边的函数应严格下降,而在极小点右边的函数值应严格上 升。因此,可以从某一个给定的初始点 a0 出发,以初始 步长 h0 沿着函数值下降的方向,逐步前进(或后退),直 到找到相继的3个点的函数值按照“大—小—大”变化为止。
最优化方法

delta = delta0; x0 = x1; y = x0; else if max(abs(delta)) < eps x = x0; break; else continue; end end end end end minf = Funval(f,var,x); format short;
maxDF = -inf; m = 0; for j=1:n-1 df = FY(j) - FY(j+1); if df > maxDF maxDF = df; m = j+1; end end tmpF = Funval(f, var,2*y(:,n)-y(:,1)); fl = FY(1) - 2*FY(n) + tmpF; if fl<2*maxDF yv = y(:,n) + l*P(:,n); fy = Funval(f, var,yv); [a,b] = minJT(fy,0,0.1); tl = minHJ(fy,a,b); x0 = y(:,n) + tl*P(:,n); P(:,m:(n-1)) = P(:,(m+1):n); else x0 = y(:,n); end end end minf = Funval(f,var,x); format short;
end end else tmpy(i) = delta(i); tmpf = Funval(f, var,y-tmpy); for j=1:length(g) cong(j) = Funval(g(j), var,y-tmpy); end if tmpf < yf && min(cong) >= 0 bcon = 1; while bcon tmpy(i) = 2*tmpy(i); tmpf_i = Funval(f, var,y-tmpy); for j=1:length(g) cong_i(j) = Funval(g(j), var,y-tmpy); end if tmpf_i <yf && min(cong_i)>=0 y_res = y - tmpy; else bcon = 0; end end else y_res = y ; delta = delta/u; end end y = y_res; end if norm(y - yk_1) <= eps2 if max(abs(delta)) <= eps1 x = y; bmainCon = 0; else delta = delta / u; end end end minf = Funval(f,var,x); 五.旋转方向法: function [x,minf] = minRb(f,x0,D,delta,alpha,beta,var,eps)
机械优化设计实验报告

《机械优化设计》实验报告目录1.进退法确定初始区间 (3)1.1 进退法基本思路 (3)1.2 进退法程序框图 (3)1.3 题目 (4)1.4 源程序代码及运行结果 (4)2.黄金分割法 (5)2.2黄金分割法流程图 (5)2.3 题目 (5)2.4 源程序代码及结果 (5)3.牛顿型法 (6)3.1牛顿型法基本思路 (6)3.2 阻尼牛顿法的流程图 (6)3.3 题目 (7)3.4 源程序代码及结果 (7)4.鲍威尔法 (8)4.1 鲍威尔法基本思路 (8)4.2 鲍威尔法流程图 (8)4.3 题目 (9)4.4 源程序代码及结果 (9)5. 复合形法 (16)5.1 复合行法基本思想 (16)5.3 源程序代码及结果 (16)6. 外点惩罚函数法 (24)6.1解题思路: (24)6.2 流程框图 (24)6.3 题目 (24)6.4 源程序代码及结果 (24)7.机械设计实际问题分析 (30)7.2计算过程如下 (30)7.3 源程序编写 (32)8.报告总结 (33)1.进退法确定初始区间1.1 进退法基本思路:按照一定的规则试算若干个点,比较其函数值的大小,直至找到函数值按“高-低-高”变化的单峰区间。
1.2 进退法程序框图1.3 题目:用进退法求解函数()2710=-+的搜索区间f x x x1.4 源程序代码及运行结果#include <stdio.h>#include <math.h>main(){float h,h0,y1,y2,y3,a1=0,a2,a3,fa2,fa3;scanf("h0=%f,y1=%f",&h0,&y1);h=h0;a2=h;y2=a2*a2-7*a2+10;if (y2>y1){h=-h;a3=a1;y3=y1;loop:a1=a2;y1=y2;a2=a3;y2=y3;}a3=a2+2*h;y3=a3*a3-7*a3+10;if (y3<y2){goto loop;}elseprintf("a1=%f,a2=%f,a3=%f,y1=%f,y2=%f,y3=%f\n",a1,a2,a3,y1,y2,y3);} 搜索区间为0 62.黄金分割法2.1黄金分割法基本思路:通过不断的缩短单峰区间的长度来搜索极小点的一种有效方法。
最优化方法(黄金分割和进退法)实验报告

一维搜索方法的MATLAB 实现__ __信息与计算科学__ 实验时间: 2014/6/21一、实验目的:通过上机利用Matlab 数学软件进行一维搜索,并学会对具体问题进行分析。
并且熟悉Matlab 软件的实用方法,并且做到学习与使用并存,增加学习的实际动手性,不再让学习局限于书本和纸上,而是利用计算机学习来增加我们的学习兴趣。
二、实验背景: 黄金分割法它是一种基于区间收缩的极小点搜索算法,当用进退法确定搜索区间后,我们只知道极小点包含于搜索区间内,但是具体哪个点,无法得知。
1、算法原理黄金分割法的思想很直接,既然极小点包含于搜索区间内,则可以不断的缩小搜索区间,就可以使搜索区间的端点逼近到极小点。
2、算法步骤用黄金分割法求无约束问题min (),f x x R ∈的基本步骤如下:〔1〕选定初始区间11[,]a b 与精度0ε>,计算试探点:11110.382*()a b a λ=+-11110.618*()a b a μ=+-。
〔2〕若k k b a ε-<,则停止计算。
否则当()()k k f f λμ>时转步骤〔3〕。
当()()k k f f λμ≤转步骤〔4〕。
〔3〕11111110.382*()k k k k k kk k k k a b b a b a λλμμ+++++++=⎧⎪=⎪⎨=⎪⎪=+-⎩转步骤〔5〕〔4〕转步骤〔5〕(5)令1k k =+,转步骤〔2〕。
算法的MATLAB 实现function xmin=golden(f,a,b,e)k=0;x1=a+0.382*(b-a);x2=a+0.618*(b-a);while b-a>ef1=subs(f,x1);f2=subs(f,x2);if f1>f2a=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);elseb=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);endk=k+1;endxmin=(a+b)/2;fmin=subs(f,xmin)fprintf('k=\n');disp(k);3、实验结果(总结/方案)黄金分割法求解极值实例。
优化练习-黄金分割法

一维搜索——黄金分割法在迭代算法中,需要进行一维搜索。
它的快慢、好坏,直接影响最优化问题的求解速度。
迭代算法的基本公式,可写成()()kkX X S α=+其涵义是从()k X 点出发,沿()k S 方向,寻求最小值点。
当()kαα=时,则找到了最小值点()1k X +,所以X 点的函数值可表示为:()()()()()kk F X F X S αϕα=+=可以看出,当()k X 、()kS 一定,()F X 只是α的函数,这就是一维搜索。
其意义是寻求一最优的α,使函数值最小。
在实际计算中,最常用的一维搜索试探方法是黄金分割法,黄金分割法的计算次数较少。
黄金分割法也称做0.618法。
是在给定的14~αα 区间内,搜索最优步长*α的值。
如图1所示:图1 黄金分割法区间分割 如果14~αα 区间很小,则可令()*1412ααα=+ 如何使14~αα区间缩小,首先在区间内插入两个分割点1α ,2α ,且满足1234αααα<<<,这样就可以根据分割点的函数值,决定割舍区间。
可以证明,对于单峰函数,设*α已在14~αα区间内,且不管*α在哪一点上,只要经过()2ϕα 和()3ϕα函数值比较,将函数值大的邻近部份去掉,*α仍将保留在剩余段的区间内,如图2所示。
图2 缩小分割区间图中阴影部分即为根据函数比较而去掉的部分。
可以看出*α在任何情况下,都将保留在剩余段中。
用这种办法缩小区间,每一步都建立两个分割点,进行两次函数值计算。
如把分割点按对称原则建立,就能利用前次保留的一个分割点,就可使计算工作量减少一半,使计算速度提高一倍。
按这一思路形成的算法,就是黄金分割法。
具体做法如图3所示。
图3确定缩短率第一次区间是14~αα,假定()()32ϕαϕα>,根据缩小规则,去掉34~αα段。
此时区间缩短率λ为:V lλ=式中V 、l 分别对应区段的长度。
第二次区间是14~αα',假定()()32ϕαϕα''>,去掉34~αα''段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
HJFGF() //黄金分割法的名称要和倒数第二行一起改 { double x1,x2,f1,f2; x1=a+0.382*(b-a); x2=a+0.618*(b-a); do { if(F(x1)<F(x2)) {b=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);f1=F(x1);} else{a=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);f2=F(x2);} }while(!((a-b>0?a-b:b-a)<e)); printf("a=%lf,b=%lf\n",a,b); printf("x=%lf\n",0.5*(a+b)); printf("F(x)=%lf\n",F(0.5*(a+b)));
A=(a+b)*0.5;
printf("A = %lf\n",A);
printf("f(A) = %lf\n", f(A));
printf("n = %d\n",n);
printf("a=%f,b=%f",a,b);
getch();
}
陈文斌
#include<stdio.h>
double m,n,p,e,a,b; double F(double x) { return m*x*x+n*x+p; }
A2=a+0.618*(b-a); Y2=f(A2);
do {
n++;
if (!(Y1<Y2))
{
a=A1;
A1=A2;
Y1=Y2;
A2=a+0.618*(b-a);
Y2=f(A2);}else{b=A2;
A2=A1;
Y2=Y1;
A1=b+0.382*(b-a);
Y1=f(A1);
}
}
while ((a-b)>=e||(a-b)<=-e);
}
main() { InputData(); //数据输入 JTF(); //进退法 HJFGF(); //黄金分割法 }
int n; printf("x1="); scanf("%lf",&x1); printf("h="); scanf("%lf",&h); f1=f(x1); x2=x1+h; f2=f(x2); if(f1==f2) a=x1<(x1+h)?x1:x1+h; b=x1>(x1+h)?x1:x1+h; if(f2>f1) { h=-h; temp=x1; x1=x2; x2=temp; temp=f1; f1=f2; f2=temp; x3=x2+h; f3=f(x3); }
else if(f2<f1) { h=2*h;
x3=x2+h; f3=f(x3); }
while(f2>f3)
{ x1=x2;
x2=x3;
f2=f(x3);
x3=x2+h;
f3=f(x3);
}
a=x1<x3?x1:x3;
b=x1>x3?x1:x3;
printf("[%f,%f]\n",a,b);
A1=b+0.328*(b-a); Y1=f(A1);
a=min[a1,a3], b=max[a3,a1],函数最小值所在的区间为[a, b] 。
我编的修改
#include<math.h> #include<stdio.h> #define f(x) 3*x*x*x-4*x+2 main() { double f1,f2,f3,temp,x1,x2,x3,h,a,b,Y1,Y2,A,A1,A2,e=0.2;
值互换。转(3)向后探测; (c)如 y1=y2,极小点在 a1 和 a1+h 之间。 (3)产生新的探测点 a3=a1+h,y3=f(a3); (4) 比较函数值 y2 与 y3: (b)如 y2>y3, 加大步长 h=2 h ,a1=a2,
a2=a3,转(3)继续探测。 (a)如 y2<y3, 则初始区间得到:
基本思想:
对 f(x)任选一个初始点 a1 及初始步长 h, 通过比较这两点函数值的大小,确定 第三点位置,比较这三点的函数值大小,确定是否为 “高—低—高” 形态。 (1)选定初始点 a, 初始步长 h=h0,计算 y1=f(a1),
y2=f(a1+h)。 (2)比较 y1 和 y2。
(a)如 y1>y2, 向右前进;加大步长 h=2 h ,转(3)向前; (b)如 y1<y2, 向左后退;h=- h0, 将 a1 与 a2,y1 与 y2 的
JTF() //进退法的名称要和倒数第三行一起改 { double x1,x2,x3,f1,f2,f3,t,h; printf("x0,h=?"); //这里提示输入进退法的初始点和步长,提示语句 x0,h=?改成你自己的 scanf("%lf,%lf",&x1,&h); f1=F(x1);x2=x1+h;f2=F(x2); if(f1<f2) { h=-h; t=x1;x1=x2;x2=t; t=f1;f1=f2;f2=t; } else { h=2*h; } x3=x2+h; f3=F(x3); while(!(f2<f3)) { x1=x2;x2=x3;f2=f3;x3=x2+h;f3=F(x3); } if(x1>x3) {a=x3;b=x1;} else{a=x1;b=x3;} printf("[%lf,%lf]\n",a,b); }
InputData() //数据输入函数的名称要和倒数第四行的一起改,要同时改成同一名称 { printf("x,y,z=?"); //这里提示输入方程的系数,提示语句 x,y,z=?改成你自己的 scanf("%lf,%lf,%lf",&m,&n,&p); printf("e=?"); //这里提示输入黄金分割的精度,提示语句 e=?改成你自己的 scanf("%lf",&e); }
