单精度浮点表示
浮点数单精度浮点数与双精度浮点数在计算机中的存储

浮点数单精度浮点数与双精度浮点数在计算机中的存储浮点数是一种用于表示实数的数学概念,在计算机中以不同的精度进行存储。
单精度浮点数和双精度浮点数分别以32位和64位的二进制格式来表示实数。
单精度浮点数是按照IEEE754标准规定的,它使用32位来存储一个浮点数。
它将这32位划分为三个部分:符号位、指数位和尾数位。
具体来说,其中1位用于表示符号位(0表示正数,1表示负数),8位用于表示指数位,23位用于表示尾数位。
指数位用于表示浮点数的大小范围,尾数位用于表示浮点数的精度。
单精度浮点数可以表示的范围是从2的-126次方到2的127次方之间。
双精度浮点数也遵循IEEE754标准,它使用64位来存储一个浮点数。
它将这64位划分为三个部分:符号位、指数位和尾数位。
其中1位用于表示符号位,11位用于表示指数位,52位用于表示尾数位。
双精度浮点数的指数位和尾数位比单精度浮点数更长,因此双精度浮点数的精度更高。
双精度浮点数可以表示的范围是从2的-1022次方到2的1023次方之间。
在计算机中,浮点数的存储会存在一定的舍入误差。
这是因为浮点数的二进制表示是有限的,无法准确表示一些实数。
舍入误差会在浮点数的运算和比较中产生影响,可能导致计算的结果和预期不一致。
因此,在使用浮点数进行计算时,需要注意舍入误差的问题,并采取相应的处理措施,如四舍五入或使用更高精度的类型来存储浮点数。
总之,浮点数的存储以单精度和双精度形式存在于计算机中。
单精度浮点数以32位二进制格式存储,双精度浮点数以64位二进制格式存储。
浮点数的存储使用二进制科学计数法,其中包括符号位、指数位和尾数位。
在计算机中存储浮点数会存在一定的舍入误差,需要注意处理。
位单精度浮点数的IEEE表示法

32位单精度浮点数的IEEE表示法float 共计32位(4字节)31位是符号位,1表示该数为负,0反之30~23位,一共8位是指数位(-128~127)22~ 0位,一共23位是尾数位,尾数的编码一般是原码和补码IEEE标准从逻辑上用三元组{S,E,M}表示一个数N,如下图所示:n,s,e,m分别为N,S,E,M对应的实际数值,而N,S,E,M仅仅是一串二进制位。
其中,S(sign)表示N的符号位。
对应值s满足:n>0时,s=0; n<0时,s=1。
E(exponent)表示N的指数位,位于S和M之间的若干位。
对应值e值也可正可负。
M(mantissa)表示N的尾数位,恰好,它位于N末尾。
M也叫有效数字位(sinificand)、系数位(coefficient), 甚至被称作“小数”。
IEEE标准754规定了三种浮点数格式:单精度、双精度、扩展精度。
前两者正好对应C语言里头的float、double或者FORTRAN里头的real、double精度类型。
限于篇幅,本文仅介绍单精度、双精度浮点格式。
★单精度:N共32位,其中S占1位,E占8位,M占23位。
★双精度:N共64位,其中S占1位,E占11位,M占52位。
值得注意的是,M虽然是23位或者52位,但它们只是表示小数点之后的二进制位数,也就是说,假定 M为“010110011...”, 在二进制数值上其实是“.010110011...”。
而事实上,标准规定小数点左边还有一个隐含位,这个隐含位通常,哦不,应该说绝大多数情况下是1,那什么情况下是0呢?答案是N 对应的n非常小的时候,比如小于 2^(-126)(32位单精度浮点数)。
不要困惑怎么计算出来的,看到后面你就会明白。
总之,隐含位算是赚来了一位精度,于是M对应的m最后结果可能是"m=1.010110011...”或者“m=0.010110011...”计算e、m首先将提到令初学者头疼的“规格化(normalized)”、“非规格化(denormalized)”。
c++语言中单精度浮点型和双精度浮点型

c++语言中单精度浮点型和双精度浮点型
在C++语言中,单精度浮点型和双精度浮点型是用于表示实数的数据类型。
单精度浮点型,也称为float类型,在内存中占用4个字节(32位)。
它的取值范围约为-3.4E38到3.4E38,并且可以保留大约6到7位有
效数字。
浮点数在内存中以科学记数法的形式存储,即一个数的科学
记数法形式为m x 10^n,其中m称为尾数,n称为阶码。
单精度浮点
型能够表示小数点后多达6到7位的位置。
双精度浮点型,也称为double类型,在内存中占用8个字节(64位)。
它的取值范围约为-1.7E308到1.7E308,并且可以保留大约15到16
位有效数字。
双精度浮点型相比于单精度浮点型,能够表示更大范围
和更高精度的实数值。
双精度浮点型在内存中的存储方式与单精度浮
点型相似。
在C++中,可以使用float关键字定义单精度浮点型变量,如:float num = 3.14f;使用double关键字定义双精度浮点型变量,如:
double num = 3.14159;在进行浮点数运算时,C++会根据操作数的类
型自动选择合适的函数进行计算。
需要注意的是,由于浮点数的存储方式与实数的存储方式存在一定的
差别,因此在进行浮点数比较时应该注意精度误差的问题,可以使用
特定的比较方法来避免精度误差带来的问题。
单精度浮点数的表示

单精度浮点数的表示摘要:I.引言- 单精度浮点数的定义- 单精度浮点数的重要性II.单精度浮点数的表示方法- 科学计数法表示- 16 位二进制表示III.单精度浮点数的运算- 加法运算- 减法运算- 乘法运算- 除法运算IV.单精度浮点数的舍入规则- 向上舍入- 向下舍入V.单精度浮点数的应用- 计算机图形学- 数值模拟- 音频处理VI.结论- 单精度浮点数的优缺点- 未来发展趋势正文:单精度浮点数是计算机中用于表示连续数值的一种数据类型,它在科学计算、图形处理、音频处理等领域有着广泛的应用。
本文将详细介绍单精度浮点数的表示方法、运算规则以及舍入规则,并探讨其在各个领域的应用。
单精度浮点数的表示方法主要有两种:科学计数法表示和16 位二进制表示。
在科学计数法表示中,一个单精度浮点数被表示为一个1 位的符号位、8 位的指数位和5 位的尾数位。
而在16 位二进制表示中,一个单精度浮点数被表示为一个1 位的符号位、5 位的指数位和10 位的尾数位。
这两种表示方法在计算机内部都被广泛使用,各有其优缺点。
在运算方面,单精度浮点数的加法、减法、乘法和除法运算都可以通过科学计数法表示的指数和尾数来进行。
具体来说,加法和减法运算只需要对尾数进行按位加减运算,而乘法和除法运算则需要对尾数进行相应的乘除运算,然后根据结果调整指数。
在舍入规则方面,单精度浮点数有两种舍入方式:向上舍入和向下舍入。
向上舍入是指当尾数大于等于1 时,将指数加1;向下舍入是指当尾数小于1 时,将指数保持不变。
这两种舍入方式在实际应用中各有其适用场景,需要根据具体情况来选择。
总的来说,单精度浮点数作为一种基本的数值表示方法,在计算机领域具有广泛的应用。
半精度浮点数和单精度浮点数的转换(不考虑特殊情况)

半精度浮点数和单精度浮点数的转换(不考虑特殊情况)半精度浮点数,也称为16位浮点数,使用16个bits来表示一个浮点数。
其中1个bit用于表示符号位,5个bits用于表示指数位,剩余的10个bits用于表示尾数位。
半精度浮点数能够表示的数值范围相对较小,大约在1.5 x 10^-45到6.5 x 10^34之间。
单精度浮点数,也称为32位浮点数,使用32个bits来表示一个浮点数。
其中1个bit用于表示符号位,8个bits用于表示指数位,剩余的23个bits用于表示尾数位。
相比于半精度浮点数,单精度浮点数能够表示的数值范围更广,大约在1.4 x 10^-45到3.4 x 10^38之间。
转换半精度浮点数为单精度浮点数的过程如下:1.将半精度浮点数的符号位复制到单精度浮点数的符号位。
2.将半精度浮点数的指数位扩展为单精度浮点数的指数位。
3.将半精度浮点数的尾数位扩展为单精度浮点数的尾数位。
将半精度浮点数转换为单精度浮点数的算法如下:```pythondef convert_half_to_single(half_float):sign_bit = half_float >> 15exponent = (half_float >> 10) & 0x1Fsignificand = half_float & 0x3FFsign_bit = sign_bit << 31significand = significand << 13single_float = sign_bit , exponent , significandreturn single_float```其中,`half_float`是半精度浮点数的值,`>>`表示右移操作,`<<`表示左移操作。
转换过程中,需要对指数位进行偏移操作,以适应单精度浮点数的指数范围。
c语言单精度和双精度小数点后几位

c语言单精度和双精度小数点后几位在C语言中,可以使用单精度浮点数和双精度浮点数来表示小数。
单精度浮点数使用32位存储,而双精度浮点数使用64位存储。
接下来我们将详细介绍这两种浮点数的小数点后几位。
单精度浮点数(float)是C语言中用来表示单精度浮点数的数据类型。
它的有效位数是23位,小数点后大约能保留6-7位有效数字。
具体来说,单精度浮点数的小数点后大约保留6位有效数字。
这是因为单精度浮点数使用了1位来表示正负号,8位来表示指数,以及23位来表示尾数。
因此,在单精度浮点数中,尾数只有23位有效数字。
双精度浮点数(double)是C语言中用来表示双精度浮点数的数据类型。
它的有效位数是52位,小数点后大约能保留15-16位有效数字。
具体来说,双精度浮点数的小数点后大约能保留15位有效数字。
双精度浮点数使用了1位来表示正负号,11位来表示指数,以及52位来表示尾数。
因此,在双精度浮点数中,尾数有52位有效数字。
虽然单精度浮点数的有效位数相对较少,但它的运算速度通常比双精度浮点数要快。
这主要是因为单精度浮点数使用了更少的存储空间,可以在更短的时间内完成计算。
另外,在某些应用场景中,不需要高精度的计算结果,使用单精度浮点数可以节省内存和提高计算速度。
当需要进行高精度的计算时,应使用双精度浮点数。
双精度浮点数的有效位数更多,能够提供更准确的计算结果。
双精度浮点数通常在科学计算、金融计算和图形处理等领域中使用,因为这些领域往往需要更高的精度。
无论是单精度浮点数还是双精度浮点数,在实际编程中,我们可以使用printf函数来控制输出的小数点后几位。
printf函数中的格式化字符串可以使用%.nf来指定小数点后保留的位数,其中n表示要保留的位数。
例如,%.3f表示保留小数点后3位。
需要注意的是,浮点数的舍入方式取决于计算机的浮点数表示规范。
总结起来,C语言的单精度浮点数大约能保留6-7位有效数字,而双精度浮点数大约能保留15-16位有效数字。
单精度浮点数的有效位

单精度浮点数的有效位单精度浮点数是一种表示实数的数据类型,在计算机中用于存储和计算浮点数。
在IEEE 754标准中,单精度浮点数的格式为32位,其中有1位符号位(用于表示正负号),8位阶码(指数部分)和23位尾数(有效数字部分)。
有效位是指一个浮点数所能表示的数字的准确位数。
在单精度浮点数中,有效数位为23位。
这意味着单精度浮点数能够精确表示的最大位数是23位。
在单精度浮点数中,尾数部分有23位。
这意味着尾数部分可以表示的数字范围从0到2^23-1(即8388607),其中0表示没有有效位,1表示最小的非零值。
当尾数部分超过23位时,舍入误差会产生。
阶码部分有8位,在单精度浮点数中,阶码部分的取值范围是-126到127。
阶码部分被偏移了127来表示实际的指数值。
阶码部分的有效位数决定了浮点数所能表示的指数范围。
可以用2^(指数-127)来计算实际的指数值。
当尾数部分和阶码部分相结合时,可以表示的数字范围是从1.40129846432481707e-45到3.4028234663852885981e+38。
这意味着单精度浮点数可以表示的正负值的数量级差距大约是10^38级。
需要注意的是,尾数部分的有效位数决定了单精度浮点数的精度。
由于尾数部分只有23位,因此单精度浮点数的精度是有限的。
这意味着在进行大范围的计算时,可能会出现较大的舍入误差。
此外,单精度浮点数的符号位决定了浮点数的正负号。
符号位为0表示正数,符号位为1表示负数。
综上所述,单精度浮点数有效位数为23位,可以表示的数字范围从1.40129846432481707e-45到3.4028234663852885981e+38。
尾数部分的有效位数决定了浮点数的精度,而阶码部分决定了浮点数的指数范围。
在进行计算时,需要注意单精度浮点数的有限精度可能会导致舍入误差。
modbus单精度浮点数

modbus单精度浮点数Modbus单精度浮点数是一种常用的数据格式,用于在Modbus 通信协议中传输和解析浮点数数据。
本文将介绍Modbus单精度浮点数的结构和使用方法,并探讨其在工业控制系统中的应用。
一、Modbus单精度浮点数的结构Modbus单精度浮点数采用IEEE 754标准表示,使用32位(4字节)来存储浮点数数据。
它由三部分组成:符号位、指数位和尾数位。
1. 符号位(1位):用于表示浮点数的正负。
0表示正数,1表示负数。
2. 指数位(8位):用于表示浮点数的指数部分。
通过对指数位进行偏移,可以表示不同的数值范围。
3. 尾数位(23位):用于表示浮点数的尾数部分。
尾数部分存储了浮点数的有效数字。
二、Modbus单精度浮点数的使用方法在Modbus通信协议中,单精度浮点数作为16位寄存器(两个字节)的数据类型进行传输。
为了正确解析单精度浮点数,需要进行字节顺序的转换。
1. 字节顺序转换由于Modbus通信协议采用大端字节序(高位字节在前,低位字节在后),而单精度浮点数采用小端字节序(低位字节在前,高位字节在后),因此在解析单精度浮点数时需要进行字节顺序的转换。
例如,将16位寄存器中的两个字节A和B按照AB顺序组成4字节的浮点数数据,然后再按照BA顺序解析出浮点数的值。
2. 数据解析解析Modbus单精度浮点数的步骤如下:1)根据字节顺序将16位寄存器的数据重新排列成4字节的数据。
2)将4字节的数据转换为单精度浮点数。
3)根据浮点数的符号位、指数位和尾数位进行计算,得到浮点数的实际值。
三、Modbus单精度浮点数的应用Modbus单精度浮点数广泛应用于工业控制系统中的数据传输和处理。
它可以用于传输和解析各种测量值,如温度、湿度、压力、流量等。
在工业控制系统中,传感器通常会将测量值以Modbus单精度浮点数的形式传输给PLC或上位机。
通过解析浮点数,可以得到实际的物理量数值,并进行相应的控制和处理。
c51程序 ieee-754标准的单精度浮点数

IEEE-754标准的单精度浮点数1. 介绍IEEE 754是一种二进制表示浮点数的标准,它定义了浮点数的表示和运算规则。
这个标准最初是由IEEE (Institute of Electrical and Electronics Engineers)制定的,它定义了浮点数的表示方式、舍入规则、溢出和下溢、异常值处理等内容。
单精度浮点数是IEEE-754标准中的一种浮点数表示格式,它用32位表示一个浮点数,其中1位表示符号位,8位表示指数,23位表示尾数。
2. 单精度浮点数的表示单精度浮点数由三个部分组成:符号位、指数部分和尾数部分。
其中,第1位是符号位,表示数的正负;接下来的8位是指数部分,用来表示数的数量级;最后的23位是尾数部分,用来表示数的精度。
单精度浮点数采用以下方式表示一个数:S EEEEEEEE MMMMMMMMMMMMMMMMMMMMM其中,S为符号位,EEEEEEEEE为指数部分,MMMMMMMMMMMMMMMMMMMMMM为尾数部分。
3. 单精度浮点数的范围单精度浮点数可以表示的范围约为1.18e-38到3.4e38之间,它可以表示的精度约为7位有效数字。
这个范围和精度可以满足大部分科学计算和工程计算的需要。
4. 单精度浮点数的运算单精度浮点数的运算包括加减乘除、开方、求倒数等基本运算,以及求平方、求立方、取对数、取指数等高级运算。
在进行浮点数运算时,需要遵守IEEE 754标准中定义的舍入规则和溢出、下溢、异常值处理规则,以确保运算结果的正确性。
5. 单精度浮点数的应用单精度浮点数广泛应用于科学计算、工程计算、图形处理、物理模拟等领域。
在这些领域,对计算速度和内存占用有较高要求,因此使用单精度浮点数可以提高计算效率和节省内存空间。
6. 总结IEEE 754标准的单精度浮点数是一种用来表示浮点数的标准格式,它具有较高的表示范围和精度,广泛应用于科学计算和工程计算等领域。
在进行浮点数运算时,需要遵守IEEE 754标准中定义的规则,以确保运算结果的正确性。
说明ieee754单精度浮点数表示的数值范围

说明ieee754单精度浮点数表示的数值范围IEEE 754标准是一种用于表示浮点数的机器数学格式,这种格式具有单精度和双精度两种模式。
在本文中,我们将重点探讨单精度浮点数表示的数值范围,以帮助读者更深入地理解这一主题。
1. IEEE 754单精度浮点数表示IEEE 754单精度浮点数采用32位二进制表示,其中1位表示符号位,8位表示指数,23位表示尾数。
根据这种表示方式,我们可以计算出单精度浮点数的数值范围。
2. 最小正非规格化数在IEEE 754标准中,最小正非规格化数是指尾数部分全为0,指数部分为1的情况。
根据单精度浮点数的表示方式,最小正非规格化数可以表示为2的-126次方。
3. 最小正规格化数最小正规格化数是指指数部分为1,尾数部分全为0的情况。
根据单精度浮点数的表示方式,最小正规格化数可以表示为2的-126次方乘以2的-23次方。
4. 最大规格化数最大规格化数是指指数部分全为1,尾数部分全为1的情况。
根据单精度浮点数的表示方式,最大规格化数可以表示为(2-2^-23)乘以2^127。
5. 无穷大和NaN在IEEE 754标准中,还有表示正无穷大、负无穷大和NaN的特殊情况。
这些特殊情况是在计算机中处理异常情况时非常重要的。
6. 总结和回顾通过对IEEE 754单精度浮点数表示的数值范围进行全面评估,我们可以更好地理解计算机中浮点数的表示方式。
从最小正非规格化数到最大规格化数,我们可以清晰地看到单精度浮点数的数值范围。
了解无穷大和NaN的表示方式也能帮助我们更好地理解计算机中浮点数的特殊情况。
7. 个人观点和理解在我看来,了解IEEE 754单精度浮点数表示的数值范围对于计算机程序员和软件工程师非常重要。
在进行科学计算和工程计算时,清楚地理解浮点数的表示方式可以帮助我们避免一些潜在的数值计算问题。
我强烈建议对这一主题进行深入学习和探讨。
通过本文的阐述,希望读者能对IEEE 754单精度浮点数表示的数值范围有一个更加全面、深刻和灵活的理解。
单精度浮点数的表示

单精度浮点数的表示摘要:一、单精度浮点数的定义与表示方法1.单精度浮点数的含义2.单精度浮点数的表示方法二、单精度浮点数的运算规则1.加法运算2.减法运算3.乘法运算4.除法运算三、单精度浮点数的优缺点1.优点2.缺点四、单精度浮点数在实际应用中的案例1.计算机科学中的应用2.工程应用中的案例五、提高单精度浮点数计算精度的方法1.数值修约2.采用更高精度的浮点数表示方法正文:一、单精度浮点数的定义与表示方法1.单精度浮点数的含义单精度浮点数(Single Precision Floating Point Number)是一种采用单精度浮点数表示法表示的实数。
在计算机科学中,单精度浮点数是常用的数据类型之一,主要用于存储和计算实数。
2.单精度浮点数的表示方法单精度浮点数的表示方法采用32位(4字节)存储空间,其中1位表示符号位,8位表示指数位,23位表示尾数位。
具体表示形式为:(-1) ^ sign * 2^(exp - 127) * m其中,sign为符号位,exp为指数位,m为尾数位。
指数位exp的有效范围为0-127,尾数位m的有效范围为1×10^-38到1 - 2^-23。
二、单精度浮点数的运算规则1.加法运算两个单精度浮点数a和b相加,结果c的表示方法为:c = a + b2.减法运算两个单精度浮点数a和b相减,结果c的表示方法为:c = a - b3.乘法运算两个单精度浮点数a和b相乘,结果c的表示方法为:c = a * b4.除法运算两个单精度浮点数a和b相除,结果c的表示方法为:c = a / b三、单精度浮点数的优缺点1.优点单精度浮点数表示法在存储和计算实数时,具有较高的计算速度和较小的存储空间占用。
2.缺点单精度浮点数的有效位数较低,计算精度有限。
在某些需要高精度的应用场景中,单精度浮点数可能无法满足需求。
四、单精度浮点数在实际应用中的案例1.计算机科学中的应用单精度浮点数在计算机科学中广泛应用于存储和计算实数,如浮点运算、图形处理、信号处理等领域。
单精度浮点数表示方法

单精度浮点数是一种用于表示实数的数据类型,通常由32位二进制数表示。
它采用了IEEE 754标准,其中包含了三个部分:符号位、指数位和尾数位。
1. 符号位(1位):用于表示数的正负,0表示正数,1表示负数。
2. 指数位(8位):用于表示数的指数部分。
由于指数位是有符号的,所以可以表示正负的指数。
指数位的取值范围是-127到+128,其中-127和+128是特殊值,用于表示特殊的情况(如无穷大、NaN等)。
3. 尾数位(23位):用于表示数的尾数部分。
尾数位是一个二进制小数,范围在1到2之间。
尾数位的最高位总是1,因此可以省略不存储,这样可以腾出一个额外的位来增加精度。
单精度浮点数的表示方法可以用以下公式表示:
(-1)^s * (1 + f) * 2^e
其中,s表示符号位的值(0或1),f表示尾数位的值,e
表示指数位的值。
需要注意的是,由于单精度浮点数的精度有限,所以在进行计算时可能会出现舍入误差。
因此,在进行精确计算时,可能需要使用双精度浮点数或其他更高精度的数据类型。
半精度单精度双精度的转换方法

半精度单精度双精度的转换方法半精度、单精度和双精度是计算机中常用的浮点数表示方法,它们分别用于存储不同精度的浮点数。
下面将详细介绍这三种浮点数表示的转换方法。
1.半精度浮点数表示:半精度浮点数在计算机中用16位(2字节)来表示。
其中,1位用于表示符号位,5位用于表示指数部分,10位用于表示尾数部分。
转换方法如下:-把浮点数转换为二进制表示。
-判断符号位,如果是负数则将符号位置为1-把浮点数的绝对值转化为二进制小数表示。
-对小数点后的数进行归一化(即使小数点前只留下一位有效数字),记录小数点偏移量k。
-小数点左移或右移k位,使小数点前只有一位有效数字。
-把小数点前的数转化为二进制表示。
-把指数部分转化为二进制表示,并加上一个偏移值。
-如果转换结果的位数超过16位,则进行舍入操作(根据规则进行四舍五入)。
-合并符号位、指数位和尾数位得到最终的16位二进制表示。
2.单精度浮点数表示:单精度浮点数在计算机中用32位(4字节)来表示。
其中,1位用于表示符号位,8位用于表示指数部分,23位用于表示尾数部分。
转换方法如下:-把浮点数转换为二进制表示。
-判断符号位,如果是负数则将符号位置为1-把浮点数的绝对值转化为二进制小数表示。
-对小数点后的数进行归一化(即使小数点前只留下一位有效数字),记录小数点偏移量k。
-小数点左移或右移k位,使小数点前只有一位有效数字。
-把小数点前的数转化为二进制表示。
-把指数部分转化为二进制表示,并加上一个偏移值。
-如果转换结果的位数超过23位,则进行舍入操作。
-合并符号位、指数位和尾数位得到最终的32位二进制表示。
3.双精度浮点数表示:双精度浮点数在计算机中用64位(8字节)来表示。
其中,1位用于表示符号位,11位用于表示指数部分,52位用于表示尾数部分。
转换方法如下:-把浮点数转换为二进制表示。
-判断符号位,如果是负数则将符号位置为1-把浮点数的绝对值转化为二进制小数表示。
-对小数点后的数进行归一化(即使小数点前只留下一位有效数字),记录小数点偏移量k。
浮点数的表示
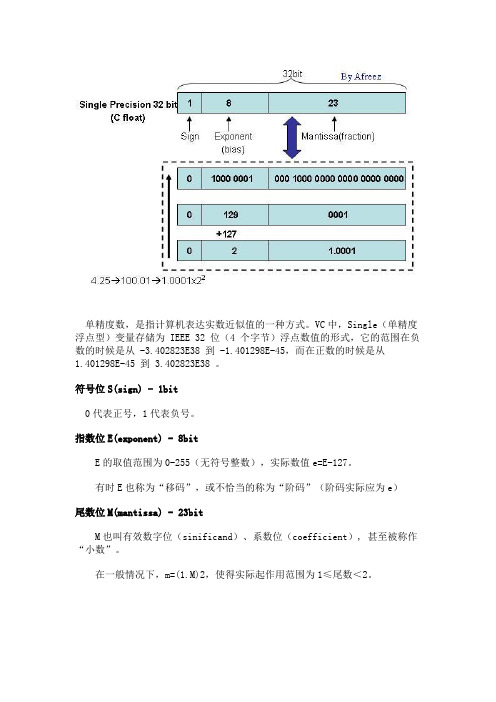
单精度数,是指计算机表达实数近似值的一种方式。
VC中,Single(单精度浮点型)变量存储为 IEEE 32 位(4 个字节)浮点数值的形式,它的范围在负数的时候是从 -3.402823E38 到 -1.401298E-45,而在正数的时候是从1.401298E-45 到 3.402823E38 。
符号位S(sign) - 1bit0代表正号,1代表负号。
指数位E(exponent) - 8bitE的取值范围为0-255(无符号整数),实际数值e=E-127。
有时E也称为“移码”,或不恰当的称为“阶码”(阶码实际应为e)尾数位M(mantissa) - 23bitM也叫有效数字位(sinificand)、系数位(coefficient), 甚至被称作“小数”。
在一般情况下,m=(1.M)2,使得实际起作用范围为1≤尾数<2。
为了对溢出进行处理,以及扩展对接近0的极小数值的处理能力,IEEE 754对M做了一些额外规定,参见后文介绍。
对于内部存储数据(00111111 01100110 01100110 01100110)2:符号位(最左侧)S=0。
这表示是个正数指数(左侧第2-9位)E=(01111110)2=(126)10,所以s=S-127=-1。
尾数(最后的23位)M=(1100110 01100110 01100110)2,m=(1.M)2=(1.7999999523162841796875)10该二进制小数转为10进制的计算方式为1 + (1/2+1/4) + (1/32+1/64) + (1/512+1/1024)……实际值N=1.7999999523162841796875*2^-1=0.89999997615814208984375(其实,这个数据是0.9的单精度浮点数的实际内部存储,可以看到有一定的误差)float单精度型,在内存中占4个字节(32位),有效数字是7位十进制数字(小数点算一位,小数点后6位。
ieee754单精度浮点数转换公式

ieee754单精度浮点数转换公式摘要:1.IEEE 754 标准简介2.单精度浮点数表示方法3.转换公式原理4.转换公式应用实例5.总结正文:1.IEEE 754 标准简介IEEE 754(Institute of Electrical and Electronics Engineers,电气和电子工程师协会)是一个国际标准,用于规定浮点数表示方法和运算规则。
该标准在计算机科学领域具有广泛的应用,尤其是在C 语言、Java 和Python 等编程语言中。
2.单精度浮点数表示方法单精度浮点数是IEEE 754 标准中的一种浮点数表示方法,用32 位二进制表示。
其中,1 位表示符号位(0 表示正,1 表示负),8 位表示指数位,23 位表示尾数位。
这种表示方法可以表示大约6.1×10^5 个不同的数值。
3.转换公式原理单精度浮点数转换公式是指将单精度浮点数转换为其他数制(如十进制、二进制等)的计算方法。
转换公式基于IEEE 754 标准中的浮点数表示方法,通过将符号位、指数位和尾数位进行相应的运算,可以得到转换后的数值。
4.转换公式应用实例例如,将单精度浮点数0x40066666(表示-0.12345678)转换为十进制数:1.符号位为1,表示结果为负数。
2.指数位为8 位,即0x40066,转换为十进制为129.0375。
3.尾数位为23 位,即0x66666666,转换为十进制为0.125。
根据公式:结果= 符号位× 2^(指数位) × 尾数位,可得:结果= -1 × 2^(129.0375) × 0.125 = -0.123456785.总结IEEE 754 单精度浮点数转换公式是一种将单精度浮点数转换为其他数制的计算方法。
通过对符号位、指数位和尾数位进行相应的运算,可以得到转换后的数值。
浮点数的二进制表示

浮点数的二进制表示
浮点数的二进制表示通常遵循IEEE 754 标准,该标准规定了浮点数的表示方式。
在这个标准下,浮点数用科学计数法表示,分为三个部分:符号位、指数部分和尾数部分。
举个例子,单精度浮点数(32位)的表示形式为:
1. 符号位(Sign Bit):占1 位,表示数字的正负。
0 表示正数,1 表示负数。
2. 指数部分(Exponent):占8 位,用于表示指数的大小。
3. 尾数部分(Fraction/Mantissa):占23 位,用于存储小数点后的数值。
例如,十进制数12.25 的单精度浮点表示为:
1. 正数:符号位为0。
2. 指数部分:12.25 的指数是3,以127 为偏移值进行存储,所以指数为130(二进制为10000010)。
3. 尾数部分:0.25 的二进制表示为0.01,尾数部分为01000000 00000000 00000000。
因此,12.25 的单精度浮点表示为01000001001000000000000000000000。
在双精度浮点数(64位)中,指数部分占11 位,尾数部分占52 位,而其余结构与单精度浮点数类似,只是精度更高。
需要注意的是,浮点数表示的精度和范围都受到这些位数的限制,可能会导致精度损失和舍入误差。
ieee754标准的32位规格化浮点数,所能表达的最大正数为

ieee754标准的32位规格化浮点数,所能表达的最大
正数为
IEEE 754标准的32位规格化浮点数(也称为单精度浮点数)可以表示的最大正数是`+38`。
IEEE 754标准定义了32位单精度浮点数的格式如下:
符号位:1位,表示正负,0表示正数,1表示负数。
指数位:8位。
尾数位:23位。
由于是规格化表示法,尾数总是从1开始,因此实际的尾数位数是23位。
最大正数的情况是:符号位为0(正数),指数位为最大值(即,十进制为254),尾数位为最大值(即,十进制为223即。
所以最大正数为:
$(-2^7)^(-254) \times (2^23 + \times 2^{-52})$
$= +38$
注意:这里我们省略了计算中的小数部分,只给出了主要部分。
实际上尾数部分有大约6位有效数字。
32位单精度浮点数的IEEE表示法

float 共计32位(4字节)31位是符号位,1表示该数为负,0反之30~23位,一共8位是指数位(-128~127)22~ 0位,一共23位是尾数位,尾数的编码一般是原码和补码IEEE标准从逻辑上用三元组{S,E,M}表示一个数N,如下图所示:n,s,e,m分别为N,S,E,M对应的实际数值,而N,S,E,M仅仅是一串二进制位。
★S(sign)表示N的符号位。
对应值s满足:n>0时,s=0; n<0时,s=1。
★E(exponent)表示N的指数位,位于S和M之间的若干位。
对应值e值也可正可负。
★M(mantissa)表示N的尾数位,恰好,它位于N末尾。
M也叫有效数字位(sinificand)、系数位(coefficient), 甚至被称作“小数”。
IEEE标准754规定了三种浮点数格式:单精度、双精度、扩展精度。
前两者正好对应C语言里头的float、double或者FORTRAN里头的real、double精度类型。
限于篇幅,本文仅介绍单精度、双精度浮点格式。
★单精度:N共32位,其中S占1位,E占8位,M占23位。
★双精度:N共64位,其中S占1位,E占11位,M占52位。
值得注意的是,M虽然是23位或者52位,但它们只是表示小数点之后的二进制位数,也就是说,假定M为“010110011...”, 在二进制数值上其实是“.010110011...”。
而事实上,标准规定小数点左边还有一个隐含位,这个隐含位通常,哦不,应该说绝大多数情况下是1,那什么情况下是0呢?答案是N对应的n非常小的时候,比如小于2^(-126)(32位单精度浮点数)。
不要困惑怎么计算出来的,看到后面你就会明白。
总之,隐含位算是赚来了一位精度,于是M对应的m最后结果可能是"m=1.010110011...”或者“m=0.010110011...”四、计算e、m首先将提到令初学者头疼的“规格化(normalized)”、“非规格化(denormalized)”。
单精度浮点数转换16进制

单精度浮点数转换16进制
单精度浮点数是一种浮点数的表示方式,它使用32位二进制数来表示一个浮点数。
在计算机中,浮点数通常采用IEEE 754标准,并使用单精度浮点数表示。
在单精度浮点数转换为16进制时,需要先将其表示成二进制形式,然后再将二进制数转换为16进制数。
举个例子,假设我们要将单精度浮点数10.5转换为16进制,首先需要将10.5表示为二进制数。
它的二进制表示为:01000001001000000000000000000000。
将二进制数按照4位一组分组,得到0100 0001 0010 0000 0000 0000 0000 0000。
将每一组转换为16进制数,得到41 20 00 00。
因此,10.5的单精度浮点数表示为0x41200000。
单精度浮点数转换为16进制的步骤可以总结为:
1. 将单精度浮点数表示为32位二进制数
2. 按照4位一组分组
3. 将每一组转换为16进制数
4. 拼接所有16进制数得到最终结果。
需要注意的是,单精度浮点数的16进制表示是有符号的,其中最高位表示符号位,0表示正数,1表示负数。
因此,在进行转换时需要特别注意符号位。
- 1 -。
