双缝干涉条纹间距公式的推导两种方法

合集下载

杨氏双缝干涉条纹间距公式

杨氏双缝干涉条纹间距公式以杨氏双缝干涉条纹间距公式为标题，我们来探讨一下干涉条纹的形成原理和公式的推导过程。

我们需要了解什么是干涉。

干涉是指两个或多个波源发出的波在空间中相遇并产生干涉现象的过程。

在光学中，干涉是指两束或多束光波在相遇时叠加形成明暗相间的条纹。

杨氏双缝干涉实验是一种经典的干涉实验。

实验装置包括一个狭缝光源、两个狭缝和一个屏幕。

当光线通过两个狭缝后，在屏幕上形成一系列明暗相间的条纹。

这些条纹就是干涉条纹。

那么，为什么会出现这些条纹呢？这是因为两个狭缝成为了新的波源，它们发出的光波在空间中相遇并产生干涉现象。

这里的干涉现象是指两个波源发出的光波在某些方向上相位差相等，形成叠加增强的明纹或叠加减弱的暗纹。

接下来，我们来推导一下杨氏双缝干涉条纹间距公式。

根据几何光学的原理，可以得出两个相邻的明纹或暗纹之间的距离为：d*sinθ = mλ其中，d表示两个狭缝之间的距离，θ表示明纹或暗纹与中央最亮区域的夹角，m表示明纹或暗纹的次序，λ表示光的波长。

这个公式告诉我们，明纹或暗纹的位置与波长、狭缝间距以及观察角度有关。

当波长变小时，明纹或暗纹间距会增大；当狭缝间距变大时，明纹或暗纹间距也会增大；当观察角度增大时，明纹或暗纹间距也会增大。

我们还可以根据杨氏双缝干涉条纹间距公式推导出两个狭缝间距的近似值。

当观察角度很小时，我们可以使用小角近似，即sinθ ≈ θ。

这样，公式可以简化为：d*θ ≈ mλ通过这个公式，我们可以通过测量明纹或暗纹的位置和波长，来计算出狭缝间距d的近似值。

杨氏双缝干涉条纹间距公式在实际应用中有着广泛的用途。

例如，通过测量干涉条纹的间距，可以确定光的波长，从而用于光谱分析和光学测量等领域。

此外，该公式还可以用于狭缝间距的测量，例如在微观结构的研究中，可以利用该公式来测量材料的晶格常数。

总结一下，杨氏双缝干涉条纹间距公式是描述干涉条纹形成原理的重要公式。

通过这个公式，我们可以计算出干涉条纹的间距，从而研究光的波长和狭缝间距等物理参数。

双缝干涉条纹间距公式的推导__两种方法

双缝干涉条纹间距公式的推导__两种方法双缝干涉是一种经典的光学实验，通过两个狭缝的光源在屏幕上形成干涉条纹。

干涉条纹的间距是干涉实验中一个重要的物理量，可以用来研究光的波动性质。

本文将介绍两种方法推导双缝干涉条纹间距的公式。

方法一：几何推导法我们考虑一个光源发出的平行光束，通过两个平行狭缝后在屏幕上形成干涉条纹。

设两个狭缝的中心到屏幕的距离为D，两个狭缝之间的距离为d，屏幕上相邻两个明纹间的距离为x，光波长为λ。

根据几何关系，可以推导出如下关系：sin(θ) = x / D其中，θ为屏幕上明纹和中心亮条纹的夹角。

而在干涉实验中，明纹和暗纹的差距可以认为是1/2个波长，即：x=(m+1/2)*λm为整数，代表第m条明纹。

将上述两个公式结合起来，可以得到：sin(θ) = (m + 1/2) * λ / D对上述公式两边求导，可以得到：dθ=(m+1/2)*λ/D^2*dD在双缝干涉实验中，狭缝间距d非常小，可以认为对于连续的明纹来说，θ的变化非常小，即dθ可以近似为dθ = dx / D。

将上述公式带入，得到：dx / D = (m + 1/2) * λ / D^2 * dD整理公式，得到：dx = (m + 1/2) * λ / D * dD上述公式即为双缝干涉条纹间距的公式。

方法二：波动理论推导法基于波动理论，我们可以用复振幅叠加的方法来推导双缝干涉条纹的间距。

假设两个狭缝产生的波的复振幅分别为A1和A2，两个狭缝之间的相位差为δ。

在屏幕上其中一点P处，由于干涉效应，两个波累加得到：E = A1 * exp(i * k * r1) + A2 * exp(i * k * r2)其中，k为波数，r1和r2分别为点P到两个狭缝的距离。

将上述公式进行化简，得到：E = A * [exp(i * k * r1) + exp(i * k * r2)]= A * [exp(i * k * r1) + exp(i * k * r1 * sin(θ))]= 2 * A * cos(k * r1 * sin(θ))将上述公式与光强公式I=，E，^2相结合，可以得到：I = 4 * I0 * cos^2(k * r1 * sin(θ))其中，I0为单个狭缝的光强。

双缝干涉条纹间距公式的推导__两种方法

双缝干涉条纹间距公式的推导__两种方法双缝干涉是一种经典的光学现象，它可以通过光的波动性来解释。

干涉条纹的间距与波长、双缝间距、干涉屏到双缝与屏幕上的干涉条纹的距离之间有密切的关系。

下面将介绍两种方法来推导双缝干涉条纹间距的公式。

方法一：几何光学法双缝干涉条纹的间距可以用几何光学的方法来推导。

首先，我们假设光线垂直于干涉屏，即入射角为0°。

根据几何光学的原理，如果两个光线从同一点出发，经过两个缝隙，然后到达屏幕上，那么它们到达屏幕的路径差将会决定干涉条纹的位置。

假设缝隙间距为d，两个缝隙到屏幕的距离分别为D1和D2，入射光的波长为λ。

我们可以通过构造几何图形来推导出干涉条纹的间距。

由三角形的性质可以得知，当光线经过一个缝隙到达屏幕上的位置与另一个缝隙到达屏幕上的位置构成的角相差λ/2时，它们之间的距离差正好是一个波长。

因此，可以得到以下关系式：d*sinθ = m*λ其中，θ是两缝隙到达屏幕上的位置与光轴的夹角，m是整数，表示干涉条纹的级数，λ是光的波长。

将θ转化为与缝隙距离的关系，可以得到干涉条纹间距的公式：Δx=λD/d其中，Δx表示干涉条纹的间距，λ是光的波长，D是干涉边缘到屏幕的距离，d是缝隙间距。

方法二：干涉光的相位差法双缝干涉也可以用干涉光的相位差来推导间距的公式。

在光的干涉中，相位差是决定干涉效应的重要因素。

假设缝隙间距为d，出射光线间的相位差为Δϕ。

根据几何光学的原理，可以得到以下关系式：Δϕ=2π*Δx/λ其中，Δx表示干涉条纹的间距，λ是光的波长。

另一方面，根据三角函数的性质，可以得到以下关系式：d*sinθ = m * λ将θ转化为与缝隙距离的关系，可以得到：sinθ = Δx / D其中，D是观察屏幕到双缝的距离。

将以上两个关系式结合起来，可以得到：Δϕ= 2π * sinθ = 2π * Δx / D由于Δϕ表示相位差，如果相位差差异为2π，那么干涉条纹将会出现。

双缝干涉条纹间距公式的推导

双缝干涉条纹间距公式的推导
1 干涉条纹间距公式
干涉条纹间距是光波干涉实验中常用的一个参数，其间距公式是
由丹佛·路易斯·爱迪生（Thomas Young）于1801年推导而来的，它
一般用于测量光线的波长或准确度来表示双缝的差值。

具体的公式为：(y-y’) = mλ/d
2 推导过程
a. 首先在双缝干涉实验中，设有两根光纤：入射光（光源）F和
反射光f。

它们之间存在两个缝隙A、B，A和B之间的距离称之为物距d, 我们假设它们分别存在光幅Y和Y’。

b. 则由三角函数可知：
$$\sin \varphi =\frac{OP}{OQ} = \frac{Y'-Y}{d} =
\frac{m\lambda}{d}$$
c. 由波米诺定律可知：$$\lambda = \frac {v}{f} (v-速度 f-
频率)$$
d. 由a，c可得：$$ \sin \varphi = \frac{mfv}{d}$$
e. 整理上述条件，得到：$$(y-y')=m\lambda/d$$
3 小结
双缝干涉条纹间距公式也叫干涉条纹公式，是奥地利物理学家路易斯·爱迪生（Thomas Young）在1801 年推导出来的，它的推导基于双缝干涉实验中光纤之间的距离、波米诺定律以及三角函数中邻边与线段投影长度之比的关系，其公式表达式为 (y-y’) = mλ/d。

双缝衍射条纹间距公式

双缝衍射条纹间距公式双缝衍射是光学中的一种现象，当平行光通过两个紧密排列的缝隙时，光束会发生干涉，形成一系列明暗相间的条纹。

这些条纹的间距可以通过双缝衍射条纹间距公式来计算。

双缝衍射条纹间距公式可以描述两个缝隙之间的距离和观察屏上的条纹间距之间的关系。

根据公式，条纹间距（d）与波长（λ）、缝隙间距（D）和观察屏距离（L）之间存在一定的关系，可以用如下公式表示：d = λL / D其中，d表示条纹间距，λ表示波长，L表示观察屏距离，D表示缝隙间距。

这个公式告诉我们，条纹间距与波长成正比，与观察屏距离成正比，与缝隙间距成反比。

换句话说，当波长增大或者观察屏距离增大时，条纹间距也会增大。

而当缝隙间距增大时，条纹间距会减小。

这个公式的推导基于光的波动性和干涉原理。

当光通过缝隙时，每个缝隙可以看作是一个次波源。

这些次波源发出的光波会在观察屏上相遇，形成干涉现象。

当两个次波源的光程差为波长的整数倍时，干涉会增强，形成明条纹；当两个次波源的光程差为波长的半整数倍时，干涉会减弱，形成暗条纹。

条纹间距的大小取决于光的波长以及光程差的变化。

通过双缝衍射条纹间距公式，我们可以预测和计算出在不同条件下的条纹间距。

例如，当波长为可见光的红色（约为700纳米）时，观察屏距离为1米，缝隙间距为0.1毫米时，可以计算得到条纹间距为0.007米，约为7毫米。

这个结果告诉我们，在这样的条件下，双缝衍射条纹会非常密集，条纹之间的间距非常小。

双缝衍射条纹间距公式在光学实验和应用中具有重要的作用。

通过使用这个公式，我们可以设计和调整实验装置，控制条纹间距的大小，研究光的干涉现象。

此外，双缝衍射条纹间距公式也可以应用于其他物理领域，如声波、电磁波等的干涉现象研究。

双缝衍射条纹间距公式是描述双缝衍射现象中条纹间距与波长、缝隙间距和观察屏距离之间的关系的重要公式。

通过这个公式，我们可以预测和计算出不同条件下的条纹间距，从而更好地理解和研究光的干涉现象。

双缝干涉条纹间距公式

双缝干涉条纹间距公式双缝干涉是一种常见的光学干涉现象，它是由于光波的波动性而产生的。

双缝干涉实验中，光通过两个细缝后，形成了一系列干涉条纹，这些条纹的间距可以通过一下公式来计算：Δy=λL/d其中，Δy表示两条相邻干涉条纹间的距离，λ表示光的波长，L表示两个缝孔和干涉屏之间的距离，d表示两个缝孔之间的距离。

双缝干涉是一种典型的波动现象，它是由于光的波动性而产生的，而与光线的直线传播没有直接关系。

在双缝干涉实验中，光通过两个缝孔后，形成了一系列干涉条纹，这些条纹是由两个波源发出的光波相互干涉而形成的。

当光波通过两个细缝后，会形成一系列干涉条纹。

这些干涉条纹是由两个波源发出的光波相互干涉而形成的。

当两个波源的光线达到屏幕时，它们会相互干涉并形成明暗相间的条纹。

这些条纹的间距是由双缝间距、波长和干涉屏距离所决定的。

根据双缝干涉的构造和几何关系，可以得到双缝干涉的间距公式。

在双缝干涉实验中，光波经过两个缝孔后，在屏幕上形成了一系列明暗相间的干涉条纹，这些条纹的间距可以用以下公式来计算：Δy=λL/d其中，Δy表示两条相邻干涉条纹间的距离，λ表示光的波长，L表示两个缝孔和干涉屏之间的距离，d表示两个缝孔之间的距离。

这个公式告诉我们，双缝干涉的条纹间距与光的波长、两个缝孔之间的距离以及缝孔到干涉屏的距离有关。

从该公式可以看出，当缝孔间距d 增大时，干涉条纹间距也会增大；当波长λ增大时，干涉条纹间距也会增大；当干涉屏距离L增大时，干涉条纹间距也会增大。

此外，双缝干涉实验还可以用于测量光的波长。

通过测量干涉条纹的间距Δy和已知的双缝间距d以及干涉屏距离L，可以利用上述公式来计算光的波长。

这是因为公式中只有波长是未知量，其他参数都可以通过实验测量得到。

双缝干涉是光的波动性的一种显著表现，它通过实验显示了光是一种波动，而不是粒子。

这种干涉现象不仅增加了我们对光波动性的认识，而且在许多光学应用中也起着重要的作用，例如天文望远镜、光谱仪等。

双缝干涉亮条纹公式

双缝干涉亮条纹公式
- 设双缝间距为d，双缝到光屏的距离为L，光的波长为λ。

- 对于双缝干涉，两列相干光的光程差Δ r = r_2 - r_1。

- 根据几何关系，在光屏上某点P到两缝的光程差Δ r = dsinθ（θ为P点的角位置）。

- 当光程差Δ r = kλ（k = 0,1,2,·s）时，出现亮条纹。

- 在Lgg d的情况下，sinθ≈tanθ=(x)/(L)（x为光屏上P点到光屏中心O点的距离）。

- 所以d(x)/(L)=kλ，则亮条纹在光屏上的位置x = k(Lλ)/(d)（k = 0,1,2,·s）。

2. 公式中各物理量的意义。

- x：表示光屏上亮条纹到光屏中心的距离。

- k：亮条纹的级数，k = 0时对应的是中央亮条纹，k = 1是第一级亮条纹，以此类推。

- L：双缝到光屏的距离，这个距离相对双缝间距d要大很多，以满足前面推导中的近似条件。

- λ：光的波长，不同颜色的光波长不同，例如红光波长比紫光长。

- d：双缝间距，它是影响干涉条纹间距的重要因素之一。

3. 公式的应用示例。

- 例：已知双缝间距d = 0.2mm，双缝到光屏的距离L = 1m，光的波长λ = 500nm = 5×10^-7m，求第一级亮条纹到光屏中心的距离x。

- 解：根据亮条纹公式x = k(Lλ)/(d)，这里k = 1。

- 代入数据得x = 1×frac{1×5×10^-7}{0.2×10^-3}m = 2.5×10^-3m = 2.5mm。

双缝干涉条纹间距公式的推导两种方法

双缝干涉条纹间距公式的推导两种方法在杨氏双缝干涉实验中，我们可以建立直角坐标系，将双缝S1和S2的间距设为d，双缝所在平面与光屏P平行，双缝与屏之间的垂直距离为L。

我们在屏上任取一点P1，设定点P1与双缝S1、S2的距离分别为r1和r2，O为双缝S1、S2的中点，双缝S1、S2的连线的中垂线与屏的交点为P，设P1与P的距离为x。

在通常情况下L。

d，在这种情况下由双缝S1、S2发出的光到达屏上P1点的光程差Δr为S2M＝r2－r1≈dsinθ，其中θ也是OP与OP1所成的角。

因为d<<L，θ很小，所以可以得到公式：Δr≈dsinθ。

在双缝干涉实验中，两个波源的振动情况完全相同，则这两个波源发生干涉时的加强区为到两个波源的距离为（n+1/2）λ的所有双曲线的公共焦点。

其中离差为波长整数倍nλ（零除外）的双曲线簇。

将直线y=l代入双曲线簇的方程，可以得到交点横坐标成一等差数列，公差为lλ/d。

因此，相邻两条纹的间距为lλ/d，证明了条纹间距公式：Δx=lλ/d。

然而，在现行的高中物理教科书中所给的干涉条纹的照片却并非如此。

只有在照片中央部分的干涉条件是等间距的，但是在其边缘部分的条纹的间距明显与中央部分的条纹间距不同。

问题出在哪里呢？杨氏双缝干涉实验中，当光通过两个狭缝后，会在屏幕上形成一系列明暗相间的条纹。

这些条纹是等间距的，其中相邻的明条纹（或暗条纹）中心距离为λ。

这个结论的推导过程中，我们用了两次近似。

第一次是在运用公式Δr≈dsinθ时，需要保证∠S1P1S2很小，这可以通过d<<L来满足。

第二次是因为d<<L，θ很小，所以sinθ≈tanθ。

但是当θ＞5°时，sinθ≈tanθ不再成立。

在XXX双缝干涉实验中，θ很小所对应的条件应该是x<<L，这应该对应于光屏上靠近P的点，在此种情况下上述的推导过程是成立的，干涉条纹是等间距的。

当光屏上离P较远的点所对应的θ角较大时，即θ＞5°时，sinθ≈tanθ就不再成立，因此推导过程中的（2）式也就不能再使用了。

双缝干涉条纹间距公式的推导——两种方法

双缝干涉条纹间距公式的推导两种方法双缝干涉条纹间距公式的推导d2IS [所以F 光经双缝后再次在屏上相遇互相叠加，形成了稳定的明暗相间的干涉条纹，理论和实验两狭缝间的距离和狭缝与屏间的距离不变的条件下，单色光产生的干涉条纹间距o 是s1s2的中垂线与屏的交点点的距离；M 、吃是屏山图可知丨是缝与屏的距离；X 是S2到P 点的路程差为6= d 是s J s2的距百 P 点到s 仁S2的距离；设s1 相都证明跟光的波长成正比，现简要推导如下如图p 点到0 r2—r1,d 22(1)-(2)可得r 「- r ；- ( x+ — ) - C x ------ )七2 2即 ' (r ： + r ：)( r 厂 F J =2dx2 由于 1 »d l»x J 囱就 & * 亡d—X 即：S = —x*-1A o ■当g等于光波波长入的整数倍时■两列波在P点同相加强,出现亮条纹卩即kA = yx (k=0» ±1■士2. ±3.・・・2则x= k l A (k=0> ±1> ±2> ±3> •••)♦'d1 11 ,所以Ax=x«-xk =(k+l) - A = -1即△ x二一入d(4)3□当&等于光波半波长一的奇数倍时，两列波在P 点反2相減弱，岀现暗条纹：“(k=0 >±1 >±2>±3>—>'(k=0 >±1 >±2 >±3 r-) 所以 Ax = x«-xk=( 2k+3) —• —- (2kH) — •d 2 da 1 —=—A2 d即△ x = — Aa即(2kH )—=2则 x< 2kfl )— d (5)3根据(4)、(5)两式可知：相邻两条明纹(或暗纹)间距离均为△ x=1/d A，而I、d 和入都为定值，所以屏上的干涉条纹是等间距的。

干涉条纹间距公式推导

干涉条纹间距公式推导
干涉现象是光学中的一个重要现象，是指两束光线相遇后产生的干涉效应。

光的干涉可以形成条纹，这些条纹的间距可以用公式推导得到。

考虑两束光线分别从两个不同的光源出发，经过一定的路径后相遇，产生干涉现象。

设两束光线的相位差为Δφ，这个相位差可以用下面的公式表示：
Δφ = (2π/λ)ΔL
其中，λ为光的波长，ΔL为两束光线的光程差。

根据这个公式，可以得到干涉条纹的间距公式。

设两束光线在干涉屏上相遇，这时它们的光程差为ΔL，对应的相位差为Δφ。

如果在干涉屏上观察到了n条亮纹，则有：
ΔL = nλ/2
代入相位差公式，得到：
Δφ = (2π/λ)(nλ/2) = nπ
这个公式说明，干涉条纹的间距是λ/2，即相邻两条亮纹的间距为λ/2。

如果在干涉屏上观察到了N条亮纹，则有：
Δφ = Nπ
根据这个公式，可以计算出干涉条纹的间距。

如果干涉屏的距离为D，观察屏幕时的距离为d，则有：
tanθ = d/D
其中，θ为干涉条纹的夹角。

因此，可以得到干涉条纹的间距公式：
Δx = λD/d
这个公式表明，干涉条纹的间距与波长、干涉屏到观察屏的距离有关，与观察屏幕的大小无关。

干涉条纹的间距公式是由干涉现象的相位差公式推导得到的。

这个公式可以用来计算干涉条纹的间距，是光学中的一个重要公式。

双缝干涉条纹间距公式的推导——两种方法

双缝干涉条纹间距公式的推导——两种方法方法一：双缝干涉理论推导双缝干涉是一种典型的波动现象，涉及到波动光学中的干涉现象。

在双缝干涉中，光通过两个相距较远的狭缝并形成交叠的光斑，这些光斑会产生干涉条纹。

我们先来推导一下双缝干涉条纹间距的公式。

假设光源发出的光是单色的平面波，其波长为λ。

两个狭缝的间距为d。

设两个狭缝产生的光源为S1和S2，则在观察屏上其中一点P处，S1和S2发出的光波振幅分别为A1和A2，相位差为Δφ。

则P点的光强为I = I1 + I2 + 2√(I1I2)cos(Δφ)。

其中，I1和I2分别表示S1和S2发出的光波的强度，且相等。

由于光波振幅与光强的关系为I = A²，那么可以得到I = 4I1cos²(Δφ/2)。

两个光源到达P点的光程差为ΔL，可以通过几何关系得到ΔL =d*sinθ。

其中，θ表示P点与两个光源的连线与垂直平面的夹角。

根据波长公式λ = c/f可以得到λ = cT，其中c为光速，T为光的周期。

所以可以将光程差表示为ΔL = (c/f)*d*sinθ =(cT/f)*d*sinθ = (λ/f)*d*sinθ。

将光程差带入I = 4I1cos²(Δφ/2)可以得到I =4I1cos²((2π/λ)*(λ/f)*d*sinθ/2)。

当光程差ΔL满足ΔL=mλ时，其中m为整数，即两个光源到达观察点的相位差恰好为整数倍的波长，此时干涉条纹明亮。

根据cos²(2πx) = 1/2 + (1/2)cos(4πx)，可以得到I = 4I1[(1/2) + (1/2)cos((2π/λ)*(λ/f)*d*sinθ)]。

当cos((2π/λ)*(λ/f)*d*sinθ) = cos(2πmd) = 1或-1时，干涉条纹最亮；当cos((2π/λ)*(λ/f)*d*sinθ) = cos(2πmd) = 0时，干涉条纹最暗。

所以可以得到调制因子为cos((2π/λ)*(λ/f)*d*sinθ)，当调制因子为1时，即cos((2π/λ)*(λ/f)*d*sinθ) = 1，设（2π/λ)*(λ/f)*d*sinθ = 2πm1，其中m1为整数。

双缝干涉条纹间距的推导及应用

双缝干涉条纹间距的推导及应用
作者：尹光伟
来源：《现代教育教研》2011年第11期
【摘要】本文从双缝干涉条纹产生的原理出发，从理论上简要推导了条纹间距的公式并进行了分析应用。

【关键词】双缝干涉条纹间距；推导；应用
相干光经双缝后再次在屏上相遇互相叠加，形成了稳定的明暗相间的干涉条纹，理论和实验都证明：在两狭缝间的距离和狭缝与屏间的距离不变的条件下，单色光产生的干涉条纹间距跟光的波长成正比，现简要推导如下：
如图，o是s1s2的中垂线与屏的交点；d是s1、s2的距离；l是缝与屏的距离；x是p点到o点的距离；r1、 r2是屏上P点到s1、s2的距离；设s1、s2到P点的路程差为δ= r2－r1，由图可知
（1）若屏幕移近，则l变小，因此条纹间距Δx变小，条纹变得密集。

（2）若缝距d变小，则Δx变大，条纹变得稀疏。

（3）若波长λ变长，则Δx变大。

因此若入射光为白光，则中央明纹（白色）的两侧，出现彩色条纹，且靠近中央明纹的是紫光。

另外在研究干涉现象时，一般不称呼明条纹和暗条纹它们的宽度是多少，这是因为从光的能量角度讲，从明条纹到暗条纹衔接处，是连续变化的，没有分界线。

参考文献
[1] 马文蔚等《物理学》学习指南（第二版）P305
收稿日期：2011-09-26。

双缝干涉条纹间距公式的推导——两种方法

双缝干涉条纹间距公式的推导——两种方法方法一：几何光学推导双缝干涉是一种光的波动现象，涉及到光的干涉和恢复干涉产生干涉条纹的过程。

我们可以通过几何光学的方法来推导双缝干涉条纹间距的公式。

考虑如下的实验装置：在一块均匀透明的薄膜上有两个非常靠近且平行的缝隙，将一束平行光照射到这个薄膜上。

光线通过缝隙后会形成干涉图样，即白色的明纹和黑色的暗纹交替出现。

首先，我们来考虑两个源到达其中一点的光程差。

设两个源在缝隙上分别是A和B，它们到达其中一点P的光线分别为AP和BP。

根据几何光学的原理，两个光线在P点的光程差可以表示为：Δd=BP-AP由于缝隙非常靠近，我们可以将BP与AP都近似等于AC，其中C是两个缝隙的中心点。

那么上式可以进一步表示为：Δd≈AC-AC=0这说明，任意两个源到达其中一点的光程差为0，因此在这一点上会出现明纹。

这一点是干涉条纹的亮度最大的地方。

接下来，我们来考虑两个源到达离P点很近的另外一点Q的光程差。

设Q点距离P点的位移为x，那么两个光线在Q点的光程差可以表示为：Δd≈AD-BD根据几何关系，可以得到：AD=AC+CD≈AC+BC=AC+xBD=BC+CD≈BC-AC=BC-x将上式带入Δd的表达式中，得到：Δd≈(AC+x)-(BC-x)=2x这说明，当两个源到达P和Q点的光程差为2x时，它们之间形成的是一条暗纹。

这一点是干涉条纹的亮度最小的地方。

至此，我们可以看出，双缝干涉条纹的间距是由两个源到达其中一点的光程差决定的。

在两个源的位置非常靠近的情况下，可以将光程差看作是常数，因此这个间距是一个固定值。

方法二：波动光学推导双缝干涉也可以通过波动光学的方法来推导。

我们假设缝隙上的每个点都是一个次级波的振动中心，那么在其中一点P的干涉光强度可以表示为：I = I1 + I2 + 2√(I1 * I2) * cos(Δφ)其中I1和I2分别是两个缝隙上的波源的光强，∆φ是两个波源之间的相位差。

双缝干涉实验条纹间距公式

双缝干涉实验条纹间距公式
双缝干涉实验条纹间距公式是物理学中一个重要的实验原理，主要应用于分析光的行为。

它是由法国物理学家威尔逊发现的，他发现通过两个窗口之间通过光束衍射出来的条纹，可以用一个特定的公式来表示。

双缝干涉实验条纹间距公式为：δ = λ/2ncosθ，其中δ表示两个干涉条纹之间的间距，λ表示波长，n表示介质的折射率，θ表示入射角。

当光线穿过两个窗口，由于介质的折射，可以产生一系列的干涉条纹。

这种条纹间的距离是由上述公式决定的。

双缝干涉实验条纹间距公式是物理学中一个重要的理论，它可以用来理解光学现象，如干涉、衍射和光的折射等。

它还可以用来研究光线的波长、介质的折射率和入射角等物理参数，帮助我们更好地理解光学现象。

双缝干涉实验条纹间距公式也可以应用于实际工程中，它可以帮助我们研究光线的行为，研究激光的波长，并为光学仪器的设计提供参考。

此外，它还可以用于研究电磁波的传播、传播特性以及电磁波的折射率等问题，为电磁波的应用提供了基础。

总之，双缝干涉实验条纹间距公式是物理学中一个重要的实验原理，它可以用来研究光学现象，也可以应用于实际工程中，为光学仪器
设计和电磁波应用提供指导。

双缝干涉条纹间距公式的推导——两种方法

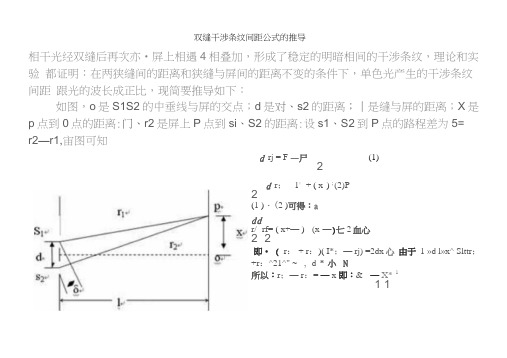
双缝干涉条纹间距公式的推导相干光经双缝后再次亦•屏上相遇4相叠加，形成了稳定的明暗相间的干涉条纹，理论和实验都证明：在两狭缝间的距离和狭缝与屏间的距离不变的条件下，单色光产生的干涉条纹间距跟光的波长成正比，现简要推导如下：如图，o是S1S2的中垂线与屏的交点；d是对、s2的距离；丨是缝与屏的距离；X是p点到0点的距离:门、r2是屏上P点到si、S2的距离:设s1、S2到P点的路程差为5=r2—r1,宙图可知d rj = F —尸(1)2d r； - 1； + ( x ) ;(2)P2(1 )・(2 )可得：ad dr/- rf= ( x+—) - (x-—)七2血心2 2即• ( r： + r：)( I*；— rj) =2dx心由于1 »d l»x^ Slttr；+r：^21^" ~ , d * 小N所以：r；— r：= —x 即：& - —X*-11 1当s 等于光波波长入的整数倍时■两列波在p 点同相加强"岀现亮条纹卩d 即k 入二一x1则x = k —入 d1即 △ X =—入所以Ax 二xk = (H1)l A -k l A = l A .add(k=0 > ±1 > ±2 9 ±3 » ••・)3 (k=0 > ±1 > ±2 9 ±3 9 •- )♦ (4)3d2当6等于光波半波长一的奇数倍时，两列波在P点反2相減弱，出现暗条纹："A dBn即(2kil )— = —x ( k=O,±l ,±2,±3,・・・4'2 1, i an则X =( 2k+l ) —( k=0 ,±1 ,±2，土3 严・)d 212 1所以 Z = x^・xk=( 2M3)—・一一(2k+l )—・d 2dA 1—• = — A 32 d即△ X =-A (5)3d根据（4）、（5）两式可知:相邻两条明纹（或暗纹）间距离均为△ x=1/dA，而I、d 和入都为定值，所以屏上的干涉条纹是等间距的。

双缝干涉条纹间距公式的推导——两种方法

双缝干涉条纹间距公式的推导——两种方法方法一：几何推导我们可以通过几何的方法推导出双缝干涉条纹间距的公式。

假设存在两个相距为d的并行缝隙S1和S2，光线从S1和S2出射，并经过成像平面P1和P2，最终在屏幕上形成干涉条纹。

首先，考虑缝隙S1和S2上的两束光线AB和CD。

假设光线AB和CD 在点O处相交，光线AB与成像平面P1的交点为E，光线CD与成像平面P2的交点为F。

根据几何光学的规律，光线AB和光线CD在成像平面上的交点与点O的连线垂直于缝隙的位置。

此外，光线从缝隙射出到屏幕上的每个点都能近似地看作是平行光的交叉点，因此可以得到点E和点F的位置。

接下来，我们将点O移动到点O'处，距离为h。

此时，光线AB和光线CD在成像平面上的交点分别是E'和F'。

由于缝隙上的两束光线是相干光，并具有相同的波长和相位，因此在成像平面上形成的干涉条纹也是两组相干光的干涉结果。

考虑缝隙上的一对相邻光线G1H1和G2H2，它们在点O'处相交，分别与成像平面的交点为I1和I2、由于缝隙距离为d，因此可以得到两组相干光在屏幕上的干涉条纹之间的距离Δy=I2I1、根据几何关系，可以推导出以下等式：tan(θ1) = EI1/P1 = h/P1 (1)tan(θ2) = EI2/P2 = h/P2 (2)其中，θ1和θ2分别为光线G1H1和G2H2与缝隙之间夹角的正切值。

将等式(1)和等式(2)相减，可以得到：tan(θ2) - tan(θ1) = h/P2 - h/P1根据三角函数的差化积公式，可以得到：tan(θ2) - tan(θ1) = 2h(d/P1P2)由于缝隙距离d很小，因此可以近似认为θ1和θ2很小，从而tan(θ1)和tan(θ2)也很小。

在这种情况下，可以使用小角度近似，即tan(x) ≈ x，将等式重新写为：θ2-θ1=2h(d/P1P2)因此，我们可以得到双缝干涉条纹间距的公式：Δy=h(d/P1P2)方法二：波动推导我们也可以通过波动的方法推导出双缝干涉条纹间距的公式。

双缝干涉条纹间距公式的推导

双缝干涉条纹间距公式的推导双缝干涉是一种经典的波动现象，当从一个光源发出的波通过两个狭缝后重新汇聚时，会产生干涉条纹。

干涉条纹之间的间距可以通过以下公式推导得出。

首先，我们考虑两个狭缝上的干涉，分别记为S1和S2、假设光源发出的波的波长为λ，S1和S2之间的距离为d，观察屏幕的位置与S1和S2的距离为L。

当波到达观察屏幕的其中一点时，我们可以看到两种结果：1.两个波处于相位同步，即达到一个峰值或一个谷值。

2.波相位相差180度，即一个波达到峰值，另一个波达到谷值。

Δx1/d=λ/L然后，我们分析第二种情况。

这时路径差为Δx2，同样由于三角形DS1A和DS2A相似，我们可以得到：Δx2/d=3λ/2L要注意的是，当两个波相位差为180度时，它们之间的干涉将是相消干涉，所以在第二种情况下，干涉会消失。

现在，我们考虑两个波的干涉条件。

当两个波的路径差满足以下条件之一时，我们会观察到明暗相间的干涉条纹：Δx=Δx1-Δx2=mλ(m=0,±1,±2,...)或者Δx=Δx1-Δx2=(2m+1)λ/2这些条件可以用来计算干涉条纹的间距。

我们将Δx1和Δx2的表达式代入上式，可以得到：dΔx/λ=(dλ/L)-(3dλ/2L)=λ/2L因此，干涉条纹之间的间距为：Δx=λL/d这个公式称为双缝干涉条纹间距公式，它描述了两个狭缝干涉条纹之间的间距与波长、观察屏幕到狭缝的距离以及两个狭缝之间的距离之间的关系。

需要注意的是，这个公式是在假设光源是单色光（即只有一个波长）的情况下推导出来的。

对于复杂的光源，我们可以将它看作是多个单色光的叠加，每一个波都满足上述公式。

然后，在观察屏幕上我们将看到叠加的干涉条纹。

双缝干涉实验条纹间距公式

双缝干涉实验条纹间距公式
双缝干涉实验条纹间距公式是用于研究光的干涉现象的基本公式，它是由德国物理学家弗里德里希·马克斯·爱因斯坦提出的。

它可以用于计算两条干涉条纹之间的间距。

双缝干涉实验条纹间距公式是通过对光束进行反射或透射来研究光的干涉现象的基本方法。

在实验中，将两个平行光束通过一对平行缝隙，使其发生干涉现象，并在干涉波束下观察到光束的构型。

双缝干涉实验条纹间距公式是计算两条干涉条纹之间的间距的主要公式。

双缝干涉实验条纹间距公式的表达式为：d=λ*L/2*sinθ，其中，λ是波长，L是缝隙之间的距离，θ是缝隙之间的角度。

根据干涉原理可以看出，当θ变化时，缝隙之间的间距也会发生变化。

此外，双缝干涉实验条纹间距公式还可以用于研究光的波动特性，以及物体的物理尺寸。

它可以用于测量物体的尺寸、厚度或体积，以及传输速度、表面粗糙度等物理参数。

通过双缝干涉实验条纹间距公式，可以准确的测量光的波长，以及缝隙之间的间距，并用于研究光的干涉现象。

由于它的准确性，双缝干涉实验条纹间距公式在光学实验中被广泛地使用，并已经成为实验中不可或缺的基本公式。

光的双缝干涉公式推导

光的双缝干涉公式推导好的，以下是为您生成的文章：咱先来说说光这玩意儿，它可神奇啦！有时候它像个直线跑的运动员，直冲冲地往前冲；有时候呢，又像个调皮的小精灵，到处乱蹦跶。

要说光的双缝干涉，那可是物理学里相当有趣的一部分。

咱们要推导光的双缝干涉公式，就得先搞清楚一些基本的概念。

想象一下，有一束光，就像一条长长的队伍，整整齐齐地朝着前面的两条小缝前进。

这两条小缝就像是两个小门，光可以从这两个小门穿过去。

当光穿过这两个小缝之后，就会发生神奇的事情。

原本整齐的队伍变得混乱起来，它们相互交错、叠加，就形成了干涉条纹。

那咱们来看看这干涉条纹是怎么形成的。

假设两条缝之间的距离是d ，屏幕到双缝的距离是 D ，咱们在屏幕上观察到的某个干涉条纹与中心条纹的距离是 x ，光的波长是λ 。

这时候，咱们可以通过简单的几何关系来推导这个公式。

从双缝到屏幕上某一点的光程差，就等于两条光线到达这一点的路程之差。

经过一番捣鼓，咱们就能得出光的双缝干涉公式：x = (λ * D) / d 。

我记得有一次在课堂上，给学生们讲这个知识点的时候，有个小家伙瞪着大眼睛，一脸迷茫地问我：“老师，这光咋就这么调皮，非得弄出这些条纹来？”我笑着跟他说：“这就像你们在操场上排队跑步，突然分成两拨，然后跑到终点的时候，就会发现有些地方人多，有些地方人少，这就是类似的道理呀！”那孩子似懂非懂地点点头，后来在做题的时候，他居然把这个知识点运用得特别好。

其实啊，学习光的双缝干涉公式，就像是解开一个神秘的谜题。

咱们得一点点地分析，一点点地琢磨，才能真正搞明白其中的奥妙。

咱们再深入想想，这个公式在生活中也有不少应用呢。

比如说在一些精密的测量仪器中，就利用了光的双缝干涉原理来提高测量的精度。

总之，光的双缝干涉公式虽然看起来有点复杂，但只要咱们用心去理解，去琢磨，就一定能掌握它的精髓，发现光的神奇世界里更多的秘密！。