结构化学2.9节分解
合集下载
2结构化学
结构
化学 2.10 原子轨道的其它图形
2.10.1 氢原子p、d轨道的径向分布图
一般状态的径向波函数：D = R2n,l(r)·r2
径节面数= n-l-1
1
结构化学 2.10.2 原子轨道的等值线图——ψ相等的点用曲线连接①水平为x 轴，垂直为z 轴；②Δ处为|ψ|最大值处；③+、-号代表其周围ψ的符号；④2p z 中过原点xy 平面是节面ψ=0⑤3p z 与2p z 类似但多一球形节面；⑥n 越大节面数越多，能级越高；⑦以坐标原点为中心，s 轨道球对称；3个p 轨道中心反对称；5个d 轨道中心对称。
2.10 原子轨道的其它图形2
+ —+ ——+ 2pz 3pz —+ +——+ —
+3dxz 3dz2
结构化学2.10.3 电子云分布图2.10.4 ψ的网格线图
2.10.5 原子轨道界面图
2.10.6 原子轨道轮廓图——类似于等值线图(ψ)，但是|ψ|2没有负值。
界面——一个等密度面，面上出现电子的几率达到一定百分数ψ的大小轮廓及正负在直角坐标系中表示出来——体现ψ在空间分布的图形。
2.10 原子轨道的其它图形
3。
(完整版)结构化学课后答案第二章
02 原子的结构和性质【2.1】氢原子光谱可见波段相邻4条谱线的波长分别为656.47、486.27、434.17和410.29nm ，试通过数学处理将谱线的波数归纳成为下式表示，并求出常数R 及整数n 1、n 2的数值。
221211()R n n ν=-解：将各波长换算成波数：1656.47nm λ= 1115233v cm --=2486.27nm λ= 1220565v cm --=3434.17nm λ= 1323032v cm --=4410.29nm λ= 1424373v cm --=由于这些谱线相邻，可令1n m =，21,2,n m m =++……。
列出下列4式：()22152331R R m m =-+()22205652R Rm m =-+()22230323R R m m =-+()22243734R Rm m =-+(1)÷(2)得：()()()23212152330.7407252056541m m m ++==+用尝试法得m=2（任意两式计算，结果皆同）。
将m=2带入上列4式中任意一式，得：1109678R cm -=因而，氢原子可见光谱（Balmer 线系）各谱线的波数可归纳为下式：221211v R n n -⎛⎫=- ⎪⎝⎭ 式中，112109678,2,3,4,5,6R cm n n -===。
【2.2】按Bohr 模型计算氢原子处于基态时电子绕核运动的半径（分别用原子的折合质量和电子的质量计算并精确到5位有效数字）和线速度。
解：根据Bohr 提出的氢原子结构模型，当电子稳定地绕核做圆周运动时，其向心力与核和电子间的库仑引力大小相等，即：22204n n n m e r r υπε= n=1，2，3，…… 式中，,,,,n n m r e υ和0ε分别是电子的质量，绕核运动的半径，半径为n r 时的线速度，电子的电荷和真空电容率。
同时，根据量子化条件，电子轨道运动的角动量为： 2n n nh m r υπ=将两式联立，推得：2202n h n r me επ=；202ne h n υε= 当原子处于基态即n=1时，电子绕核运动的半径为：2012h r me επ=()()23412211231196.62618108.854191052.9189.1095310 1.6021910J s C J m pm kg C π------⨯⨯⨯==⨯⨯⨯⨯若用原子的折合质量μ代替电子的质量m ，则：201252.91852.91852.9470.99946h m pm r pm pme επμμ==⨯==基态时电子绕核运动的线速度为：2102e h υε=()21934122111.60219102 6.62618108.8541910C J s C J m -----⨯=⨯⨯⨯⨯612.187710m s -=⨯【2.3】对于氢原子：(a)分别计算从第一激发态和第六激发态跃迁到基态所产生的光谱线的波长，说明这些谱线所属的线系及所处的光谱范围。
第一章结构化学
氢原子核电荷z＝1，能量可写成
1 2 e e e E mv 2 4 0 r 8 0 r 4 0 r
m e4 1 1 2 2 2 R 2 8 0 r 8 0 h n n e2
2
2
2
m e4 其中， R 2 2 13.6eV 8 0 h 当n=1时，E= -13.6 eV，称为氢原子基态的能量。
（2）玻尔假定：
1913年丹麦物理学家玻尔把量子论 的基本观点应用于原子核外电子的运 动，从而创立了玻尔理论。其基本论 点可归纳为：
（A）原子存在于具有确定能量的稳 定态（简称定态），定态中的原子不辐
Nobel 1922
射能量。
h h M （C）玻尔量子化规则： n n, n 1,2,3... ，n为量子数 2
1 1 RH ( 2 2 ) n1 n2
~
1
氢原子光谱——玻尔提出原子结构理论，主 张原子能量具有不连续性。
（1）巴耳麦公式：
白光本来是由波长不同的各种颜色的光线组成，当它通过三棱镜 或者光栅后便分解为红、橙、黄、绿、青、蓝、紫的连续谱带，称 为连续光谱。
含有低压氢气的放电管所发生的光通过三棱镜或光栅后不是形成 连续的谱带，而是形成一条一条孤立的谱线，由这些谱线构成谱图， 这种光谱称为不连续光谱或线状光谱。
1.1.1 黑体辐射与能量量子化
黑体：能全部吸收外来电磁波的物体。黑色物体或开一小孔 的空心金属球近似于黑体。 黑体辐射：加热时，黑体能辐射出各种波长电磁波的现象。 黑体辐射能量密度与波长的关系是19世纪末物理学家 关心的重要问题之一.经典物理学在此遭遇严重困难： 维恩公式只适用于短波部分;
由能量均分定理导出的瑞利-金斯公式则只适用于长波
结构化学课件
d 轨道与配体间的作用
八面体场中d轨道能级分裂
配合物离子的颜色
所吸收光子的频率与分裂能大小有关。 颜色的深浅与跃迁电子数目有关。
•
配 合 物 的 颜 色
影响o的因素(中心离子,配位体,晶体场)
1 中心M离子：电荷Z增大， o增大
主量子数n增大， o增大
o /cm-1
o /cm-1
2 配位数为 4 的配合物
[BeX4]2-四面体
四 配 位 的 平面正方形，μ=0 配 合 物
四面体，μ=2.83B.M.
3 六配位的配合物
μ=2.4B.M. μ=5.90B.M.
内轨形 外轨形
价键理论小结：
价键理论的优势：直观明了，使用方便， 很好地解释了配合物的空间构型、磁性、稳 定性。
3．分子轨道理论
配位化合物饿分子轨道理论是用分子轨道理论 的观点和方法处理金属离子和配位体的成键作用。
4． 配位场理论
配位场理论是晶体场理论的发展，其实质是配 位化学物的分子轨道理论。在处理中心金属原子 在其周围配位体所产生的电场作用下，金属的原 子轨道能级发生变化时，以分子轨道理论方法为 主，根据配位场的对称性进行简化，并吸收晶体 场理论的成果，阐明配位化合物的结构和性质， 它与纯粹的分子轨道理论有一定的差别，故称配 位场理论。
排布原则： （1）能量最低原理
（2）Hund规则
（3）Pauli不相容原理
电子成对能（P）：两个电子进入同一轨
道时需要消耗的能量。
强场：o > P
弱场：o < P
八面体场中电子在t2g和eg轨道中的分布
八面体场中电子在t2g和eg轨道中的分布
例：
o /J
P/J 场
八面体场中d轨道能级分裂
配合物离子的颜色
所吸收光子的频率与分裂能大小有关。 颜色的深浅与跃迁电子数目有关。
•
配 合 物 的 颜 色
影响o的因素(中心离子,配位体,晶体场)
1 中心M离子：电荷Z增大， o增大
主量子数n增大， o增大
o /cm-1
o /cm-1
2 配位数为 4 的配合物
[BeX4]2-四面体
四 配 位 的 平面正方形，μ=0 配 合 物
四面体，μ=2.83B.M.
3 六配位的配合物
μ=2.4B.M. μ=5.90B.M.
内轨形 外轨形
价键理论小结：
价键理论的优势：直观明了，使用方便， 很好地解释了配合物的空间构型、磁性、稳 定性。
3．分子轨道理论
配位化合物饿分子轨道理论是用分子轨道理论 的观点和方法处理金属离子和配位体的成键作用。
4． 配位场理论
配位场理论是晶体场理论的发展，其实质是配 位化学物的分子轨道理论。在处理中心金属原子 在其周围配位体所产生的电场作用下，金属的原 子轨道能级发生变化时，以分子轨道理论方法为 主，根据配位场的对称性进行简化，并吸收晶体 场理论的成果，阐明配位化合物的结构和性质， 它与纯粹的分子轨道理论有一定的差别，故称配 位场理论。
排布原则： （1）能量最低原理
（2）Hund规则
（3）Pauli不相容原理
电子成对能（P）：两个电子进入同一轨
道时需要消耗的能量。
强场：o > P
弱场：o < P
八面体场中电子在t2g和eg轨道中的分布
八面体场中电子在t2g和eg轨道中的分布
例：
o /J
P/J 场
结构化学课件第二章
~ h E2 E1 hc / hc
me2 me4 En 2 2 2 2 2 80 n h 0 8 0 n h
e2
此式与氢原子光谱的经验公式完全相符，R即为Rydberg（里德伯）常数。
●Bohr模型的缺陷： 既把电子运动看作服从Newton定律，又强行加入角动量量子化；
ih ˆ x y Mz 2 y x
ih cos sin cos cos cos sin r sin sin sin cos r sin cos sin sin 2 r r r sin r r r sin
sin
r cos r sin cos r sin cos cos
r
cos cos x r
（8）
1 r sin sin sin yx2 2 2 2 cos x r sin cos2 r sin cos2 sin (9) x r sin cos cos sin 将(7)(8)(9)代入(4)，得： sin cos (10) x r r r sin
此式左边不含r,，右边不含，要使两边相等，须等于同一常数，设为-m2，则得
2. 变数分离法
d 2 m 2 d 2
1 d 2 dR 8 2 r 2 m2 1 d d r (E V ) sin R dr dr h2 sin 2 sin d d 1 d d m 2 设两边等于l(l+1)，则得 sin 2 l(l 1) sin d d sin
结构化学习题解答(第二章)
轨道磁距为：
1(1 1) e 2 e
（c）设轨道角动量M和Z轴的夹角为θ，则：
h 0 Mz 2 0 cos h M 2 2
θ=900
（d） 电子离核的平均距离的表达式为：
r r d
* 2 pz 2 pz
2
2 2 pz
2
Li2+离子1s态的波函数为：
（a）
27 a e
1s 3 0
2 6 r a0 3 3 0 0
1 2
3 r a0
27 D 4r 4r e a
2 2 1s 1s 2 1s 3
108 re a
2
6 r a0
d 108 6 D 2r r e 0 dr a a 6 2 2r r 0 r a0 a0 r 又 r 0 3 a0 1s电子径向分布最大值在距核 处；
1 D1s / a0
r / a0
/ a
2 3 1s 0 1
1.60 2.00 2.30 2.50 3.00
3.50
4.00 4.50 5.00 — —
0.04 0.02 0.01 0.007 0.003 0.001< 0.001
1 D1s / a0
0.42 0.29 0.21 0.17
r r sin drdd
2
0
0
0
(e)
令
2 pz
0 r 0 , r , 90 , 得： 0
节面或节点通常不包括 r 0和r , 故 2 pz 的节 面只有一个，即x,y平面（当然，坐标原点也包含在xy 平面内）。亦可直接令函数的角度部分.
1(1 1) e 2 e
（c）设轨道角动量M和Z轴的夹角为θ，则：
h 0 Mz 2 0 cos h M 2 2
θ=900
（d） 电子离核的平均距离的表达式为：
r r d
* 2 pz 2 pz
2
2 2 pz
2
Li2+离子1s态的波函数为：
（a）
27 a e
1s 3 0
2 6 r a0 3 3 0 0
1 2
3 r a0
27 D 4r 4r e a
2 2 1s 1s 2 1s 3
108 re a
2
6 r a0
d 108 6 D 2r r e 0 dr a a 6 2 2r r 0 r a0 a0 r 又 r 0 3 a0 1s电子径向分布最大值在距核 处；
1 D1s / a0
r / a0
/ a
2 3 1s 0 1
1.60 2.00 2.30 2.50 3.00
3.50
4.00 4.50 5.00 — —
0.04 0.02 0.01 0.007 0.003 0.001< 0.001
1 D1s / a0
0.42 0.29 0.21 0.17
r r sin drdd
2
0
0
0
(e)
令
2 pz
0 r 0 , r , 90 , 得： 0
节面或节点通常不包括 r 0和r , 故 2 pz 的节 面只有一个，即x,y平面（当然，坐标原点也包含在xy 平面内）。亦可直接令函数的角度部分.
结构化学-第1章讲义
2020/8/1
4
二 课程内容 对象 主要理论工具
章节
原子 量子力学
分子 点群理论 共价键理论
第一章 量子力学 第二章 原子结构
第三章 分子对称性 第四章 双原子分子 第五章 多原子分子
2020/8/1
21
对象 主要理论工具
章节
络合物 配位场理论 第六章 配位化合物
晶体 点阵结构理论 第七章 晶体结构 密堆积原理 第八章 晶体材料
献有发明了微积分，发现了万有引力定律和经典力学等等，被誉为人类历
史上最伟大，最有影响力的科学家。为了纪念牛顿在经典力学方面的杰出
成就，“牛顿”后来成为衡量力的大小的物理单位。
2020/8/1
27
2. Maxwell电磁场理论
波函数描述运动状态：
单色平面波 (x,t) Acos(x t)
(λ为波长，ν为频率)
这些振子的能量只能取某些基本能量单位的 整数倍，基本能量单位和频率成正比——
h E n n h （n=1, 2, 3…）
Planck 常数：h=6.626× 10-34 J·s
2020/8/1
35
振子在吸收或者发射电磁波时，只能从某一个特 定状态过渡到另一个特定状态，
E(v,T
)dv
8v2k
维恩公式只适用于短波部分;
瑞利-金斯公式则只适用于长波部分,它在短 波部分引出了 “紫外灾变”，即波长变短时辐 射的能量密度趋于无穷大,而不象实验结果那样 趋于零。
2020/8/1
34
Planck 量子论
1900年12月14日，普朗克公布了他对黑体 辐射的研究成果。
提出假设：黑体辐射的是带电的谐振子。
结构化学
《结构化学》PPT课件
(2)反键轨道具有和成键轨道相似的性质，每一轨道也可 按Pauli不相容原理、 能量最低原理和Hund规则安排电子， 只不过能级较相应的成键轨道高，轨道的分布形状不同。
(3)在形成化学键的过程中，反键轨道并不都是处于排斥 的状态，有时反键轨道和其他轨道相互重叠，也可以形成 化学键，降低体系的能量，促进分子稳定地形成。利用分 子轨道理论能成功地解释和预见许多化学键的问题，反键 轨道的参与作用常常是其中的关键所在，在后面讨论分子 的化学键性质时，将会经常遇到反键轨道的作用问题。
方程
i i
ii
分子体系总能量 E = ∑Ei
2．分子轨道是由分子中原子的原子轨道线性组合(li near combination of atomic orbitals， LCAO)而成。
由n个原子轨道组合可得到n个分子轨道，线性组合 系数可用变分法或其它方法确定。由原子轨道形成 的分子轨道，能级低于原子轨道的称为成键轨道， 能级高于原子轨道的称为反键轨道，能级等于或接 近原子轨道的一般为非键轨道。 3．两个原子轨道要有效地组合成分子轨道，必须满 足对称性匹配，能级相近和轨道最大重叠三个条件。 其中对称性匹配是先决条件，其它影响成键的效率。 4．分子中电子按 Pauli不相容原理、 能量最低原 理和Hund规则排布在MO上
三键 三键
CO、NO的电子组态分别如下： CO [( 1σ)2 ( 2σ)2 ( 3σ)2 (4σ)2 (1π)4 (5σ)2 ] NO [( 1σ)2 ( 2σ)2 ( 3σ)2 (4σ)2 (1π)4 (5σ)2 (2π)1 ]
CO :
CO与N2是等电子体，
一样也是三重键：一个σ键， 二个π键，但是与N2分子不 同的是有一个π键为配键， 这对电子来自氧原子。(如 右图所示）CO作为一种配 体，能与一些有空轨道的 金属原子或离子形成配合 物。例如同ⅥB，ⅦB和Ⅷ 族的过渡金属形成羰基配 合物：Fe（CO)5、Ni(CO)4 和Cr(CO)6等。
(3)在形成化学键的过程中，反键轨道并不都是处于排斥 的状态，有时反键轨道和其他轨道相互重叠，也可以形成 化学键，降低体系的能量，促进分子稳定地形成。利用分 子轨道理论能成功地解释和预见许多化学键的问题，反键 轨道的参与作用常常是其中的关键所在，在后面讨论分子 的化学键性质时，将会经常遇到反键轨道的作用问题。
方程
i i
ii
分子体系总能量 E = ∑Ei
2．分子轨道是由分子中原子的原子轨道线性组合(li near combination of atomic orbitals， LCAO)而成。
由n个原子轨道组合可得到n个分子轨道，线性组合 系数可用变分法或其它方法确定。由原子轨道形成 的分子轨道，能级低于原子轨道的称为成键轨道， 能级高于原子轨道的称为反键轨道，能级等于或接 近原子轨道的一般为非键轨道。 3．两个原子轨道要有效地组合成分子轨道，必须满 足对称性匹配，能级相近和轨道最大重叠三个条件。 其中对称性匹配是先决条件，其它影响成键的效率。 4．分子中电子按 Pauli不相容原理、 能量最低原 理和Hund规则排布在MO上
三键 三键
CO、NO的电子组态分别如下： CO [( 1σ)2 ( 2σ)2 ( 3σ)2 (4σ)2 (1π)4 (5σ)2 ] NO [( 1σ)2 ( 2σ)2 ( 3σ)2 (4σ)2 (1π)4 (5σ)2 (2π)1 ]
CO :
CO与N2是等电子体，
一样也是三重键：一个σ键， 二个π键，但是与N2分子不 同的是有一个π键为配键， 这对电子来自氧原子。(如 右图所示）CO作为一种配 体，能与一些有空轨道的 金属原子或离子形成配合 物。例如同ⅥB，ⅦB和Ⅷ 族的过渡金属形成羰基配 合物：Fe（CO)5、Ni(CO)4 和Cr(CO)6等。
结构化学 第二章习题
第二章习题2.1 简要说明原子轨道量子数及它们的取值范围？2.2 在直角坐标系下，Li 2+ 的Schrödinger 方程为________________ 。
2.3131321122101-++=ψψψψc c c , 其中131211210,,-ψψψψ和都是归一化的。
试回答下列问题：(a) 波函数所描述状态的能量平均值？ (b) 角动量出现在π22h 的概率？ (c) 角动量 z 分量的平均值？2.4 已知类氢离子 He +的某一状态波函数为：ψ＝()022-023021e222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π （a ）此状态的能量E=? （b ）此状态的角动量的平方值? （c ）此状态角动量在 z 方向的分量? （d ）此状态的 n ， l ， m 值分别为何值？ （e ）此状态角度分布的节面数?2.5 求出Li 2+ 1s 态电子的下列数据： (a) 电子概率密度最大处离核距离? (b) 电子离核的平均距离?(c) 单位厚度球壳中出现电子概率最大处离核的距离 ? (d) 比较2s 和2p 能级的高低？ (e) 电离能?（10231!,)(10+-∞-==⎰n ax n r a Zsa n dx e x e a Z πψ）2.6 已知 H 原子的()θa r a r zcos e 241002130p2-⎪⎪⎭⎫ ⎝⎛π=ψ 试计算：(a) 原子轨道能 E 值；(b) 轨道角动量绝对值│M │； (c) 轨道角动量和 z 轴夹角的度数。
2.7 一个电子主量子数为 4，这个电子的 l ， m ， m s 等量子数可取什么值？这个电子共有多少种可能的状态？2.8 碳原子 1s 22s 22p 2组态共有 1S 0，3P 0，3P 1，3P 2，1D 2等光谱支项，试写出每项中微观能态数目及按照 Hund 规则排列出能级高低次序。
2.9 求下列谱项的各支项，及相应于各支项的状态数： 2P ； 3P ； 3D ； 2D ； 1D2.10 给出 1s ， 2p 和 3d 电子轨道角动量的大小及其波函数的径向和角度部分的节面数。
《结构化学》第九章 结构原理汇总
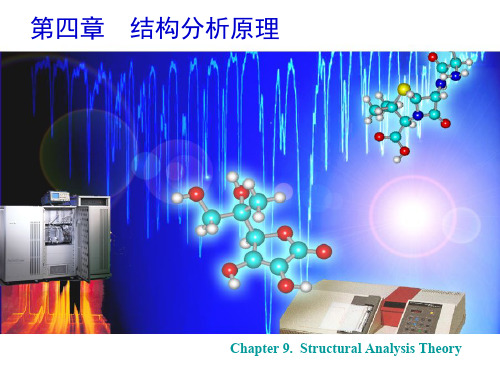
傅里叶变换红外光谱仪框图
化学键的振动研究对光纤通讯材料也具有实际意义。光在光纤中传输时 的损耗与光纤的总体性质和原子尺度上的性质有关. 由玻璃密度、组成的随机涨落所引起的Rayleigh散射光强与波长的四次方 成反比，所以，与可见光和紫外光相比，使用红外光可以显著降低损耗。 从另一方面看，红外光可以激发玻璃中Si、O和杂质原子之间化学键的振 动跃迁. 尽管目前大量使用的高透明度SiO2玻璃已能满足远距离通信的要求， 但若要进一步降低光损耗，还需要减少振动激发. 使用原子量大于Si而化学键 更弱的材料，可以在更长的波长范围内实现红外透明，Rayleigh散射、振动激 发和电子激发都可以降至极低. 所以，近年来发展了性能更加优越的ZrF4、LaF4 和BaF2三元混合体氟玻璃，传输光信号上万千米不需任何中继站.
各类化学键振动波数
苯的红外光谱
红外分光光度计光路图
检测器 平衡马达
热电偶 滤光器 出射狭缝 光断续器 减光器 入射狭缝
减光器位置对应于纵坐标 参比槽
反射镜
光源
分光棱镜 描图马达通过波长 凸轮转动棱镜以改 变波长并带动记录 装置(横坐标)记录
立托夫镜
样品槽
傅里叶变换红外光谱
傅里叶变换红外光谱仪是非色散型光谱仪，其核心是 双光束干涉仪. 当动镜移动时，经过干涉仪的两束相干光 的光程差改变，到达探测器的光强随之改变，得到干涉图， 再经傅里叶变换得到入射光的光谱. 主要优点是：信噪比 和灵敏度高；以氦、氖激光波长为标准，波数值精确度可 达0.01cm-1 ； 增加动镜移动距离可提高分辨率；工作波段 从可见区可延伸到毫米区，实现远红外光谱测定.
4.拉曼光谱
分子振动也可能引起分子极化率的变化，产生拉曼 光谱. 拉曼光谱不是观察光的吸收, 而是观察光的非弹性 散射. 非弹性散射光很弱，过去较难观测. 激光拉曼光谱 的出现使灵敏度和分辨力大大提高，应用日益广泛.
最新结构化学重点掌握内容PPT课件
ms 自旋 磁量子数
n ,l,m ,m s( x ,y ,z ,m s ) n ,l,m ( x ,y ,z )( m s )
旋轨轨道或自旋轨道。
六：表示单电子原子状态的量子数
1. 主量子数n 2. 角量子数l
En
Z2 n2
R,
n1,2
Lll 1 , l 1 ,2n 1
3. 磁量子数m
lzm, m0,1 l
二、病因病机
（二）病机
3.病机转化： 较为复杂，既可由实转虚，
又可由虚转实，甚或虚中夹实；既可气滞及 血，又可血瘀阻气，但不外乎病在气，或病 在血，或气血同病。
4.预后：无论外感或内伤胁痛，只要治疗
将养得法，一般预后良好。
三、诊断要点
1.临床特征：一侧或两侧胁肋疼痛为
主要临床表现 ；疼痛性质可表现为刺痛、 胀痛、隐痛、闷痛或窜痛。
三、Zeeman效应 外磁场中原子光谱的分裂现象。
1四、、S多电子原s子i 的角S 动 量（S L(-S S耦1 合) ）
i
S为原子的自旋量子数，
n, n 1,1
22
2
或
0（n：体系电子数）
Sz Ms M s S ,S 1 , , S
Ms有（2S+1）个取值
2、 L li LL(L1) i
多电子原子中的任何两个电子不可能具 有相同的4个量子数.
十、基态原子核外的电子排布遵循以下 三个原则： Pauli原理，能量最低原理， Hund规则。
第三章 原子光谱 一、谱项定义： 能级除以hc称为谱项，
T ~ 'E , T ~ E , ~T ~ T ~
hc hc
二、选择定则概念
两状态间发生跃迁，表示这些状态的 量子数之间需满足一定的条件，这些条件称 为选择定则。
结构化学(第一节)
5
量子化特征 微观粒子运动遵循量子力学规律，与经典力学 运动规律不同的重要特征是“量子化（quantized）”。 “量子化”是指微观粒子的运动以及运动过程 中能量的变化是不连续的，而是以某一最小量 为单位呈现跳跃式的变化。
6
―量子化”这一重要概念是普朗克（Plank） 于1900年首先提出的。他根据黑体辐射实验 的结果，提出能量的传递与变化是不连续的， 是量子化的这一大胆假说。这是与传统的物 理学观念相背的、革命性科学假说，后来发 展为量子论，是现代量子力学发展的开端， 是科学发展史上具有划时代意义的里程碑之 一。
1结构化学第一节2第一节原子结构与元素周期系一微观粒子的运动特征二原子结构1波函数与原子轨道2四个量子数3原子轨道的图形4电子云和几率密度三核外电子的排布1基本原则2原子轨道能级的顺序3原子中电子的实际排布4原子的电子排布和元素周期系四元素性质的周期性变化31897年汤姆逊thomson18561940通过阴极射线发现了电子的存在
23
薛定谔方程是现代量子力学及原子结构理论 的重要基础和最基本的方程式。薛定谔方程 不是用数学方法推导出来的。其正确性、真 理性是靠大量实验事实来证明的。
24
Ψ称为波函数(wave function)。它是空间坐标（x、y、 z）的函数， Ψ ＝ Ψ （x、y、z）；也可用球坐标（r、 、）表示： Ψ ＝ Ψ （r、、）。
2
x
2
2
y
2
2
z
2
8 m
2
h
2
( E V ) 0
（4-3）
22
薛定谔方程，是函数Ψ对x、y、z三个空间坐 标变量的二阶偏微分方程。Ψ是薛定谔引入 的一个物理量，它是电子空间坐标x、y、z的 函数： Ψ （x，y，z）。薛定谔用Ψ（x，y， z）来描述或表征电子运动的波动性，因此Ψ （x，y，z）应该服从、遵循某种波动的规律， 即符合波动方程式的要求。故称为波函数。
结构化学 原子结构及性质
《结构化学》-原子结构
2.1.1 定态Schrö dinger方程
r x2 y2 z2 x r sin cos z y r sin sin arccos 2 2 2 x y z z r cos y arctan x
1 2 sin 2 2 R sin 2me 2 2 Ze2 (r ) (sin ) 2 r sin ( E ) 2 R r r 4 0 r
sin sin 2 2 R 2me 2 2 Ze 2 m (sin ) (r ) 2 r sin ( E ) R r r 4 0 r
* m 0
2 2
e
0
e d A
2 2
d A2 2 1
0
1 A 2 m ( ) 1 im e 2
方程的 复函数解
m ( )
1 i m e 2
(2-15)
1 i m m ( ) e 2
(2-16)
15
《结构化学》-原子结构 实函数解的形式
结构化学原子结构21cossin结构化学原子结构2244rrrr方程的解方程的解解的条件n123nl1结构化学原子结构23径向函数径向函数的表达式的表达式结构化学原子结构2413606evev6022108541102921013606ev18010采用折合质量时18113595ev217810memecmevch结构化学原子结构25结构化学原子结构26几个r函数的解18273081结构化学原子结构27对任意一个指定的n轨道角量子数01单电子体系的波函数的简并度单电子体系的波函数的简并度即一个n之下不同的55单电子波函数单电子波函数氢原子和类氢原子的波函数主量子数对任意一个指定的l轨道磁量子数结构化学原子结构28进行线性组合归一化关于实函数与复波函数关于实函数与复波函数与复函数不存在11对应关系而是绝对值相同的m线形组合只有对应于m0
结构化学课件3第三章共价键和双原子分子的结构化学
Haa Hab 1Sab
E2
Haa Hab 1Sab
④ 代回原方程求系数 ca，cb， 由线性齐次方程组方程
将E1代入，得 ca = cb， 1 = ca(a+ b) ，
将E2代入，得 ca = －cb， 2 = ca′ (a － b)
归一化，得
c
a
c
a
1
2 2 S ab 1
2 2 S ab
解 c c 时 ： c ， 当
12
11 2
2 d c 2 2 d c 2 2 d 2 d 2 d
1 12
11
1 2
2
c 1 2S 1 1 2 S 1 2 S 22 1
c 1S 1 1 2 S 1 2 S 2 2 1 2
第三节. 分子轨道理论(MO)和双原子分子的结构
l5
5h2 4 2 ml 2
30
10 • h2
2 8ml2
证明H2+的两个分子轨道正交
d
(
a
b)
•(
ab)d
12
22S 22S
ab
ab
1 (22)d
44S2
a
b
ab
1 (11)0 44Sa2b
若某函数的线性组合形式为 c cc •，利用 1 1 21 2
归一化条件试求c1=c2时，c 1 S 1 1 2 S 1 2 S 2 2 1 2 。
3.2.1 H2+ 的Schrödinger方程
（原子单位，定核近似)
H2+相当于氢分子失去一个电子， 所以是个三体问题，其坐标关系如
下图所示。图中a、b代表两个氢核，
其间距离为R，ra、rb代表电子与两 个氢核的距离。
结构化学课件
2键型的多样性原子是由带电粒子组成的我们预计原子间相互作用力大多是静电相互作用主要取决于两个方面一是原子的带电状态中性原子或离子二是原子的电子结构按原子最外价电子层全满二是原子的电子结构按原子最外价电子层全满状态闭壳层或未满状态开壳层来分类
H2 O2
第三章 双原子分子的结构和性质
1 . H2+的结构和共价键的本质 2 . 分子轨道理论 3 . 同核双原子分子的结构 4 . 异核及双原子分子的结构 5 . H2分子的结构和价键理论 6 . 分子光谱 ﹡7. 光电子能谱
3.1.1 化学键的定义和类型
化学键的定义:广义地说，化学键是将原子结合成物 质世界的作用力。
化学键定义为:在分子或晶体中两个或多个原子间的 强烈相互作用，导致形成相对稳定的分子和晶体。 化学键：共价键，离子键和金属键。 基本理论：价键理论，分子轨道理论，配位场理论。
3.1.2键型的多样性
1.共价单键；2.离子键；3.金属键；4.氢键；5. 缺电子多中心氢桥键；6.H-配键；7.分子氢配位键； 8.抓氢键。
3.密度泛函理论(DFT)
DFT 是 1964 年 由 Kohn 等 提 出 ， Ellis 、 Lee-Yang-Parr 等发展、九十年 代流行的一种化学键理论，在DFT中， 用电荷密度函数代替单电子波函数描述 体系的状态，在解Schrö dinger方程时， 用统计方法代替交换积分计算，因而取 得了计算时间短、精度高的效果，特别 适用重原子，多原子体系。
原子通过化学键结合成分子，分子是物质中独立 地、相对稳定地存在并保持该化合物特性的最小颗粒， 是参与化学反应的基本单元。原子相互吸引、相互排 斥，以一定的次序和方式结合成分子。物质的化学性 质主要决定于分子的性质，而分子的性质主要由分子 的结构决定。因此探索分子内部的结构，了解结构和 性能的关系，就成了结构化学的重要组成部分。 化学键是指分子中将原子结合在一起的相互作用 力,广义而论还包括分子间的相互作用。两个或多个 原子(或离子)之间依靠化学键将原子结合成相对稳定 的分子或晶体。典型的化学键有三种：共价键、离子 键和金属键。气态分子中的化学键主要是共价键。离 子键和金属键分别存在于离子化合物与块状金属中。 分子间和分子内部有时还形成氢键，其强弱介于共价 键和范德华力之间。
H2 O2
第三章 双原子分子的结构和性质
1 . H2+的结构和共价键的本质 2 . 分子轨道理论 3 . 同核双原子分子的结构 4 . 异核及双原子分子的结构 5 . H2分子的结构和价键理论 6 . 分子光谱 ﹡7. 光电子能谱
3.1.1 化学键的定义和类型
化学键的定义:广义地说，化学键是将原子结合成物 质世界的作用力。
化学键定义为:在分子或晶体中两个或多个原子间的 强烈相互作用，导致形成相对稳定的分子和晶体。 化学键：共价键，离子键和金属键。 基本理论：价键理论，分子轨道理论，配位场理论。
3.1.2键型的多样性
1.共价单键；2.离子键；3.金属键；4.氢键；5. 缺电子多中心氢桥键；6.H-配键；7.分子氢配位键； 8.抓氢键。
3.密度泛函理论(DFT)
DFT 是 1964 年 由 Kohn 等 提 出 ， Ellis 、 Lee-Yang-Parr 等发展、九十年 代流行的一种化学键理论，在DFT中， 用电荷密度函数代替单电子波函数描述 体系的状态，在解Schrö dinger方程时， 用统计方法代替交换积分计算，因而取 得了计算时间短、精度高的效果，特别 适用重原子，多原子体系。
原子通过化学键结合成分子，分子是物质中独立 地、相对稳定地存在并保持该化合物特性的最小颗粒， 是参与化学反应的基本单元。原子相互吸引、相互排 斥，以一定的次序和方式结合成分子。物质的化学性 质主要决定于分子的性质，而分子的性质主要由分子 的结构决定。因此探索分子内部的结构，了解结构和 性能的关系，就成了结构化学的重要组成部分。 化学键是指分子中将原子结合在一起的相互作用 力,广义而论还包括分子间的相互作用。两个或多个 原子(或离子)之间依靠化学键将原子结合成相对稳定 的分子或晶体。典型的化学键有三种：共价键、离子 键和金属键。气态分子中的化学键主要是共价键。离 子键和金属键分别存在于离子化合物与块状金属中。 分子间和分子内部有时还形成氢键，其强弱介于共价 键和范德华力之间。
结构化学2.9节
对于单电子原子，组态与状态是一致的。 对 于单电子原子，由于只有一个核外电子，因而其状 态可用该电子的状态来表示。换言之，原子的量子 数就是电子的量子数(n, l, m, ms)。
对于多电子原子则完全不同。需对各电子的轨 道运动和自旋运动的角动量进行矢量加和。多电子 原子的能态由一套原子的量子数 L, S, J 来描述。
第二章 原子结构与性质
Chapter 2. Atomic Structure and property
原子的基态(ground state)：通常情况下，原子 中的各个电子都尽可能处于最低能态，从而使整个原 子的能量最低，原子的这种状态称为基态。
原子的激发态(excited state)：当原子受到外来 作用 (例如光照或外来电子的冲击)时，它的一个或 几个电子吸收能量后跃迁到较高能级，从而使原子 处于能量较高的状态，此状态称为激发态。
原子光谱项记作2S+1L, 光谱支项记作2S+1LJ , 其 中 L 以大写字母标记:
L= 0 1 2 3 4 5 ……
S P D F G H …… (注意两处S的不同含义: 光谱支项中心若为S, 那是L=0的标记; 光谱支项左上角的S则是总自旋 角动量量子数, 对于具体的谱项是一个具体值).
例如：L=2，S=1/2 的状态，其中 J= 5/2，3/2 则光谱项为：2 D （二重态） 光谱支项为：2 D 5/2，2 D 3/2
例如：p1d1
l1=1, l2=2 L = 3, 2, 1; s1=1/2, s2=1/2 S = 1, 0 故得出六个光谱项：3F，3D，3P，1F，1D，1P
对L=3，S=1的 3F 光谱项求其光谱支项： J = 4、3、2 则3F的光谱支项为：3F4，3F3，3F2 3D的光谱支项： L=2，S=1 J = 3、2、1 则3D的光谱支项为：3D3，3D2，3D1 3P的光谱支项： L=1，S=1 J = 2、1、0 则3D的光谱支项为：3P2，3P1，3P0 1F的光谱支项： L=3，S=0 J = 3 ：1F3 1D，1P的光谱支项分别为： 1D2 ， 1P1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2S+1
L
其中： 2S+1 L 称为光谱项
2S+1 L J
称为光谱支项
2S+1称为光谱项的多重性
原子光谱项记作2S+1L, 光谱支项记作2S+1LJ , 其
中 L 以大写字母标记:
L= 0 1 2 3 4 5 ……
S
P
D
F
G
H
……
(注意两处S的不同含义: 光谱支项中心若为S,
那是 L=0 的标记 ; 光谱支项左上角的 S 则是总自旋
Hund规则适用的范围：
(1) 由基组态而不是激发组态求出的谱项；
(2) 只用于挑选出基谱项，而不为其余谱项排序！
只求光谱基项的快速方法:
(1)在不违反Pauli原理前提下，将电子填入轨道， 首先使每个电子 ms 尽可能大，其次使 ml 也尽可能 大；
(2) 求出所有电子的 ms 之和作为 S，MS=∑(ms)i;
角动量量子数, 对于具体的谱项是一个具体值).
例如：L=2，S=1/2 的状态，其中 J= 5/2，3/2
则光谱项为：2 D
（二重态）
光谱支项为：2 D 5/2，2 D 3/2 光谱支项的数目为 J 的数目 能量最低的光谱支项称为光谱基项
原子光谱项的推求
多电子体系用L-S 耦合法推求原子的光谱项和光谱支项
写出下列原子能量最低的光谱支项的符号: (a) Si; (b) Mn; (c) Br; (d) Nb;
(a)Si : Ne3s 3 p
2
2
1 0
1
M S 1, S 1; M L 1, L 1; L S 0; P 0
3
(b)Mn : Ar 4s 3d
2
5
3P的光谱支项：
L=1，S=1
J = 2、1、0 则3D的光谱支项为：3P2，3P1，3P0 L=3，S=0 J = 3 ：1F3 1D，1P的光谱支项分别为： 1D ， 1P 2 1
1F的光谱支项：
② 等价电子组态
n 和 l 完全相同的电子称为等价电子，其光谱 项的推求比较麻烦，要考虑保里不相容原理。
角动量L求矢量和得到原子的总轨道角动量；将所有
电子的自旋角动量 S求矢量和得到原子的总自旋角动 量；再将两者耦合得到原子的总角动量； ② J-J 耦合法 (重原子)：把每个电子的轨道角动量和 自旋角动量合成为该电子的总角动量，再将每个电子
的总角动量耦合成为原子的总角动量。
L-S偶合方案矢量进动图
s1 s2 S
多电子原子的能态由一套原子的量子数L, S, J来描述。 L （原子的总轨道角量子数）决定了 原子总轨道角动量
L( L 1)
ML （原子的总轨道磁量子数）决定了 原子总轨道角动量在z轴分量 M L
S（原子的总自旋量子数）决定了
原子的总自旋角动量
ห้องสมุดไป่ตู้
S ( S 1)
MS （原子的总自旋磁量子数）决定了 原子总自旋角动量在z轴分量 M S
由主量子数n、角量子数 l 描述的原子中电子排
布方式称为原子的电子“组态(configuration)”。 对于多电子原子，给出电子组态仅仅是一种粗略 的描述，更细致的描述需要给出原子的“状态 (state)” , 而状态可由组态导出。描述原子的状态可 以用原子光谱项(Spectroscopic Term)。
第二章
原子结构与性质
Chapter 2. Atomic Structure and property
原子的基态 (ground state)：通常情况下，原子 中的各个电子都尽可能处于最低能态，从而使整个原 子的能量最低，原子的这种状态称为基态。 原子的激发态(excited state)：当原子受到外来 作用 (例如光照或外来电子的冲击 )时，它的一个或 几个电子吸收能量后跃迁到较高能级，从而使原子 处于能量较高的状态，此状态称为激发态。 激发态不稳定，原子随即跃迁回到基态。与此 相应的是原子以光的形式或其他形式将多余的能量 释放出来。
有了电子组态的光谱项，求原子的光谱项就很容易了。 例如：H ： 1s1 L= l =0，S = s =1/2
2S
J=1/2
He ：1s2
2S
1/2 1S（经验法）
L=0，对应的S=0
J=0
Li: 1s2 2s1
1S
0
与H完全相同2S 、2 S ½
2.9.3 原子能级和洪特规则
光谱基项的确定: Hund规则
L=2l , … , 0
L=2，1，0 相应的 S=0，1，0 所以光谱项为：1D，3P，1S
所有不违反Pauli原理的 p2 微状态:
1
微状态 ml 0
-1
ML=ml 2 1 1 1 0 0 0 0 1 0 -1 -1 -1 -1 -2
MS= ms 0 1 0 0 1 0 0 0 -1 -1 1 0 0 -1 0
ml 之和作为 L，ML=∑mi ；
(3) 对少于半充满者，取J=L-S；对多于半充满
者，取J=L+S.
例如
nd
4
m 2 1 0
L 2 1 0 1 2,
光谱基项为
5
1 2 1 S 4 2 2
_
D0
对少于半充满者，取J=L-S； 对多于半充满者，取J=L+S.
J（原子的总角动量量子数）决定了 原子的总角动量
J ( J 1)
MJ（原子的总磁量子）决定了 原子总角动量在z轴分量 M J
借助矢量偶合模型，可以对原子状态作一些简
单描述。 原子的总角动量等于各个电子的轨道角动量和自 旋角动量的矢量和。有两种近似处理方法： ① L-S 耦合法 (Z≤40的轻原子)：将所有电子的轨道
2S+1L 1D 3P 1D 3P 3P 1D
3P
1S 3P 3P 3P 1D 3P
3P
1D
例如：d 2
利用经验法：l =2
L=2l , … , 0
L=4，3，2，1，0
相应的 S=0，1，0，1，0 所以光谱项为：1G，3F，1D，3P，1S
等价电子的“电子—空位”互补关系 一般 n 个电子的某个组态的光谱项与含有n个 空位的组态的光谱项相同，如 p2 和 p4 ，d2 和 d8 ，称为互补态。
对于单电子原子，组态与状态是一致的。 对 于单电子原子，由于只有一个核外电子，因而其状 态可用该电子的状态来表示。换言之，原子的量子 数就是电子的量子数(n, l, m, ms)。
对于多电子原子则完全不同。需对各电子的轨
道运动和自旋运动的角动量进行矢量加和。多电子 原子的能态由一套原子的量子数 L, S, J 来描述。
总磁量子数MJ的取值：
0, 1, 2, MJ 1 3 ， , 2 2
, J J
(J为整数时） (J为半整数时）
2.9.2 原子光谱项 (Spectroscopic Term)
当某一原子由高能级 E2 跃迁到低能级 E1 时，发 射出与两能级之差相应的谱线，其波数可表达为下列 两项之差：
S
s2 s1
LS J
L
J
l2
l1
l1 l2 L
轨道—轨道相互作用
如是两电子体系，总轨道角量子数 L 取值为：
L l1 l2 , l1 l2 1,
总轨道磁量子数 ML 取值：
, l1 l2
m M L 0, 1, 2 , L 2 L 1个
光谱项中，表示能量最低的光谱支项——光谱基项 原子光谱项对应能级的相对大小遵守Hund规则 在原子的同一组态中，S 值越大，能量越低；
S 相同时，L 值越大，能量越低；
L 和 S 值均相同，电子少于和等于半充满时，J 小
者能量低，称为正光谱项；电子多于半充满时， J
值 越大能量越低，称为反光谱项。
总自旋磁量子数 MS 取值：
ms M S 0, 1, 2 1 3 , 2 2
, s （s为整数时） , s （s为半整数时）
共2S+1个
自旋—轨道相互作用
总角动量量子数J 的取值：
J L S , L S 1, L S时 2 S 1个值 L S , L S时 2 L 1个值
原子从某激发态回到基态，发射出具有一定波 长的一条光线，而从其他可能的激发态回到基态以 及在某些激发态之间的跃迁都可发射出具有不同波 长的光线，这些光线形成一个系列(谱)，称为为原 子发射光谱。 当一束白光通过某一物质，若该物质中的原子 吸收其中某些波长的光而发生跃迁，则白光通过物 质后将出现一系列暗线，如此产生的光谱成为原子 吸收光谱。
(d ) Nb : Kr 5s 4d
原子的光谱是原子结构（电子结构）的反映，
是由结构决定的。不同元素的原子，结构不同，能
级不同，因而其光谱的性质（成分和强度）也不同。 光谱和结构之间存在着一一对应的内在联系。 原子的光谱（光谱实验）是与原子所处的能级 有关，而原子的能级与原子的整体运动状态有关。
2.9 原子能级和光谱
2.9.1 原子的状态和量子数
等价组态光谱项不能采用非等价组态光谱项那
种求法(否则将会出现一些违反Pauli原理的情况), 最基本的作法是 “行列式波函数法” 。 对于2个等价电子组态，可由经验法确定 L=2l，2l-1，……，0 相应的S值为：当 L 为“偶数”时 ，S=0
当 L 为“奇数”时， S=1
例如：p2 组态
利用经验法：l=1
2 1
0 1 2
5 5 5 6 M S , S ; M L 0, L 0; L S ; S 5 2 2 2 2
L
其中： 2S+1 L 称为光谱项
2S+1 L J
称为光谱支项
2S+1称为光谱项的多重性
原子光谱项记作2S+1L, 光谱支项记作2S+1LJ , 其
中 L 以大写字母标记:
L= 0 1 2 3 4 5 ……
S
P
D
F
G
H
……
(注意两处S的不同含义: 光谱支项中心若为S,
那是 L=0 的标记 ; 光谱支项左上角的 S 则是总自旋
Hund规则适用的范围：
(1) 由基组态而不是激发组态求出的谱项；
(2) 只用于挑选出基谱项，而不为其余谱项排序！
只求光谱基项的快速方法:
(1)在不违反Pauli原理前提下，将电子填入轨道， 首先使每个电子 ms 尽可能大，其次使 ml 也尽可能 大；
(2) 求出所有电子的 ms 之和作为 S，MS=∑(ms)i;
角动量量子数, 对于具体的谱项是一个具体值).
例如：L=2，S=1/2 的状态，其中 J= 5/2，3/2
则光谱项为：2 D
（二重态）
光谱支项为：2 D 5/2，2 D 3/2 光谱支项的数目为 J 的数目 能量最低的光谱支项称为光谱基项
原子光谱项的推求
多电子体系用L-S 耦合法推求原子的光谱项和光谱支项
写出下列原子能量最低的光谱支项的符号: (a) Si; (b) Mn; (c) Br; (d) Nb;
(a)Si : Ne3s 3 p
2
2
1 0
1
M S 1, S 1; M L 1, L 1; L S 0; P 0
3
(b)Mn : Ar 4s 3d
2
5
3P的光谱支项：
L=1，S=1
J = 2、1、0 则3D的光谱支项为：3P2，3P1，3P0 L=3，S=0 J = 3 ：1F3 1D，1P的光谱支项分别为： 1D ， 1P 2 1
1F的光谱支项：
② 等价电子组态
n 和 l 完全相同的电子称为等价电子，其光谱 项的推求比较麻烦，要考虑保里不相容原理。
角动量L求矢量和得到原子的总轨道角动量；将所有
电子的自旋角动量 S求矢量和得到原子的总自旋角动 量；再将两者耦合得到原子的总角动量； ② J-J 耦合法 (重原子)：把每个电子的轨道角动量和 自旋角动量合成为该电子的总角动量，再将每个电子
的总角动量耦合成为原子的总角动量。
L-S偶合方案矢量进动图
s1 s2 S
多电子原子的能态由一套原子的量子数L, S, J来描述。 L （原子的总轨道角量子数）决定了 原子总轨道角动量
L( L 1)
ML （原子的总轨道磁量子数）决定了 原子总轨道角动量在z轴分量 M L
S（原子的总自旋量子数）决定了
原子的总自旋角动量
ห้องสมุดไป่ตู้
S ( S 1)
MS （原子的总自旋磁量子数）决定了 原子总自旋角动量在z轴分量 M S
由主量子数n、角量子数 l 描述的原子中电子排
布方式称为原子的电子“组态(configuration)”。 对于多电子原子，给出电子组态仅仅是一种粗略 的描述，更细致的描述需要给出原子的“状态 (state)” , 而状态可由组态导出。描述原子的状态可 以用原子光谱项(Spectroscopic Term)。
第二章
原子结构与性质
Chapter 2. Atomic Structure and property
原子的基态 (ground state)：通常情况下，原子 中的各个电子都尽可能处于最低能态，从而使整个原 子的能量最低，原子的这种状态称为基态。 原子的激发态(excited state)：当原子受到外来 作用 (例如光照或外来电子的冲击 )时，它的一个或 几个电子吸收能量后跃迁到较高能级，从而使原子 处于能量较高的状态，此状态称为激发态。 激发态不稳定，原子随即跃迁回到基态。与此 相应的是原子以光的形式或其他形式将多余的能量 释放出来。
有了电子组态的光谱项，求原子的光谱项就很容易了。 例如：H ： 1s1 L= l =0，S = s =1/2
2S
J=1/2
He ：1s2
2S
1/2 1S（经验法）
L=0，对应的S=0
J=0
Li: 1s2 2s1
1S
0
与H完全相同2S 、2 S ½
2.9.3 原子能级和洪特规则
光谱基项的确定: Hund规则
L=2l , … , 0
L=2，1，0 相应的 S=0，1，0 所以光谱项为：1D，3P，1S
所有不违反Pauli原理的 p2 微状态:
1
微状态 ml 0
-1
ML=ml 2 1 1 1 0 0 0 0 1 0 -1 -1 -1 -1 -2
MS= ms 0 1 0 0 1 0 0 0 -1 -1 1 0 0 -1 0
ml 之和作为 L，ML=∑mi ；
(3) 对少于半充满者，取J=L-S；对多于半充满
者，取J=L+S.
例如
nd
4
m 2 1 0
L 2 1 0 1 2,
光谱基项为
5
1 2 1 S 4 2 2
_
D0
对少于半充满者，取J=L-S； 对多于半充满者，取J=L+S.
J（原子的总角动量量子数）决定了 原子的总角动量
J ( J 1)
MJ（原子的总磁量子）决定了 原子总角动量在z轴分量 M J
借助矢量偶合模型，可以对原子状态作一些简
单描述。 原子的总角动量等于各个电子的轨道角动量和自 旋角动量的矢量和。有两种近似处理方法： ① L-S 耦合法 (Z≤40的轻原子)：将所有电子的轨道
2S+1L 1D 3P 1D 3P 3P 1D
3P
1S 3P 3P 3P 1D 3P
3P
1D
例如：d 2
利用经验法：l =2
L=2l , … , 0
L=4，3，2，1，0
相应的 S=0，1，0，1，0 所以光谱项为：1G，3F，1D，3P，1S
等价电子的“电子—空位”互补关系 一般 n 个电子的某个组态的光谱项与含有n个 空位的组态的光谱项相同，如 p2 和 p4 ，d2 和 d8 ，称为互补态。
对于单电子原子，组态与状态是一致的。 对 于单电子原子，由于只有一个核外电子，因而其状 态可用该电子的状态来表示。换言之，原子的量子 数就是电子的量子数(n, l, m, ms)。
对于多电子原子则完全不同。需对各电子的轨
道运动和自旋运动的角动量进行矢量加和。多电子 原子的能态由一套原子的量子数 L, S, J 来描述。
总磁量子数MJ的取值：
0, 1, 2, MJ 1 3 ， , 2 2
, J J
(J为整数时） (J为半整数时）
2.9.2 原子光谱项 (Spectroscopic Term)
当某一原子由高能级 E2 跃迁到低能级 E1 时，发 射出与两能级之差相应的谱线，其波数可表达为下列 两项之差：
S
s2 s1
LS J
L
J
l2
l1
l1 l2 L
轨道—轨道相互作用
如是两电子体系，总轨道角量子数 L 取值为：
L l1 l2 , l1 l2 1,
总轨道磁量子数 ML 取值：
, l1 l2
m M L 0, 1, 2 , L 2 L 1个
光谱项中，表示能量最低的光谱支项——光谱基项 原子光谱项对应能级的相对大小遵守Hund规则 在原子的同一组态中，S 值越大，能量越低；
S 相同时，L 值越大，能量越低；
L 和 S 值均相同，电子少于和等于半充满时，J 小
者能量低，称为正光谱项；电子多于半充满时， J
值 越大能量越低，称为反光谱项。
总自旋磁量子数 MS 取值：
ms M S 0, 1, 2 1 3 , 2 2
, s （s为整数时） , s （s为半整数时）
共2S+1个
自旋—轨道相互作用
总角动量量子数J 的取值：
J L S , L S 1, L S时 2 S 1个值 L S , L S时 2 L 1个值
原子从某激发态回到基态，发射出具有一定波 长的一条光线，而从其他可能的激发态回到基态以 及在某些激发态之间的跃迁都可发射出具有不同波 长的光线，这些光线形成一个系列(谱)，称为为原 子发射光谱。 当一束白光通过某一物质，若该物质中的原子 吸收其中某些波长的光而发生跃迁，则白光通过物 质后将出现一系列暗线，如此产生的光谱成为原子 吸收光谱。
(d ) Nb : Kr 5s 4d
原子的光谱是原子结构（电子结构）的反映，
是由结构决定的。不同元素的原子，结构不同，能
级不同，因而其光谱的性质（成分和强度）也不同。 光谱和结构之间存在着一一对应的内在联系。 原子的光谱（光谱实验）是与原子所处的能级 有关，而原子的能级与原子的整体运动状态有关。
2.9 原子能级和光谱
2.9.1 原子的状态和量子数
等价组态光谱项不能采用非等价组态光谱项那
种求法(否则将会出现一些违反Pauli原理的情况), 最基本的作法是 “行列式波函数法” 。 对于2个等价电子组态，可由经验法确定 L=2l，2l-1，……，0 相应的S值为：当 L 为“偶数”时 ，S=0
当 L 为“奇数”时， S=1
例如：p2 组态
利用经验法：l=1
2 1
0 1 2
5 5 5 6 M S , S ; M L 0, L 0; L S ; S 5 2 2 2 2