七年级数学上册第六章平面图形的认识(一)同步测试苏科版

合集下载

苏科版七年级上册数学第6章平面图形的认识(一) 含答案

苏科版七年级上册数学第6章平面图形的认识（一）含答案一、单选题(共15题，共计45分)1、在下列说法中，正确的有（）①比较角的大小就是比较它们角的度数大小②角的大小与边的长短无关③从角的顶点出发的一条射线把这个角分成两个角，这条射线叫做这个角的平分线④如果∠ADC=∠ACB，则OC是∠ADB的平分线A.1个B.2个C.3个D.4个2、如图，AB//CD，∠1+∠2=110°，则∠GEF+∠GFE的度数为（）A.110°B.70°C.80°D.90°3、已知抛物线y= x2+1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为（，3），P是抛物线y= x2+1上一个动点，则△PMF周长的最小值是（）4、在同一平面内，下列说法正确的是（）A.两直线的位置关系是平行、垂直和相交B.不平行的两条直线一定互相垂直C.不垂直的两条直线一定互相平行D.不相交的两条直线一定互相平行5、如果一个角等于36°，那么它的余角等于( )A.64°B.54°C.144°D.36°6、点P为直线m外一点，点A，B，C为直线m上三点，PA=4cm，PB=5cm，PC=2cm，则点P到直线m的距离为（）A.4cmB.5cmC.小于2cmD.不大于2cm7、下列四个图中的线段(或直线、射线)能相交的是( )A.(1)B.(2)C.(3)D.(4)8、已知∠a=30°，则∠a的余角是（）A.150°B.30°C.90°D.60°9、如图，点A，O，B在同一条直线上，∠AOC=∠BOC，若∠1=∠2，则图中与∠2互余的角共有（）对10、如图所示，直线AB和CD相交于点O，OE、OF是过点O的射线，其中构成对顶角的是（）A.∠AOF和∠DOEB.∠EOF和∠BOEC.∠COF和∠BODD.∠BOC 和∠AOD11、如图，抛物线与y轴交于点C，点D在抛物线上，且轴，则线段CD的长为（）．A.2B.3C.4D.512、如图线段AB=9，C、D、E分别为线段AB（端点A、B除外）上顺次三个不同的点，图中所有的线段和等于46，则下列结论一定成立的是（）A.CD=3B.DE=2C.CE=5D.EB=513、下列结论中，不正确的是（）A.两点确定一条直线B.两点之间的所有连线中，线段最短C.对顶角相等D.过一点有且只有一条直线与已知直线平行14、如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走80m至点C,则∠BAC的度数是( )A.85°B.160°C.125°D.105°15、如图，直线AB，CD相交于点O，EO⊥CD于点O，∠AOE=36°，则∠BOD=（）A.36°B.44°C.50°D.54°二、填空题(共10题，共计30分)16、如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为________.17、如图，已知，，CN是的平分线，，则________18、如图所示，直线AB交CD于点O，OE平分∠BOD，OF平分∠COB，∠AOD：∠EOD=4：1，则∠AOF=________．19、一个锐角的度数是60°，则这个角的补角的度数是________20、开学整理教室时，老师总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，一会儿一列课桌摆在一条线上，整整齐齐，这是因为________．21、已知线段AB，在AB的延长线上取一点C，使AC=2BC，在AB的反向延长线上取一点D，使DA=2AB，那么线段AC：DB=________．22、如图所示，AB∥CD，EF与AB，CD相交，EF与AB交于点________，EF与CD交于________．23、如图所示，，若，，则________．24、如下图，从小华家去学校共有4条路，第________条路最近，理由是________．25、如图，从教室到图书馆总有少数同学不走人行道而横穿草坪，虽然明知不对，可他们还是要这样做，用我们所学的数学知识可以解释他们的动机：________.三、解答题(共5题，共计25分)26、计算：①96°﹣18°26′59″②83°46′+52°39′16″③20°30′×8④105°24′15″÷327、已知：∠AOD=160°，OB、OC、OM、ON是∠AOD内的射线，（1）如图1，若OM平分∠AOB，ON平分∠DOB，当OB绕点O在∠AOD内旋转时，求∠MON的大小．（2）如图2．若∠BOC=20°，OM平分∠AOC，ON平分∠DOB，当∠COB绕点O在∠AOD内旋转时，求∠MON的大小．28、如图，写出图中的所有角，并比较它们的大小，然后指出哪些角是直角，哪些角是锐角，哪些角是钝角29、已知：如图，OA⊥OB，∠BOC=50°，且∠AOD：∠COD=4：7．画出∠BOC的角平分线OE，并求出∠DOE的度数．30、已知：如图，∠AOB=30°，∠COB=20°，OC平分∠AOD. 求∠COD的度数．∵∠AOB=30°，∠COB=20°（已知），∴∠AOC=∠▲ +∠▲ = ▲°．∵OC平分∠AOD，∴∠AOC=∠▲（角平分线定义）．∴∠COD= ▲°．参考答案一、单选题(共15题，共计45分)1、B2、B3、C4、D5、B6、D7、A9、A10、D11、A12、C13、D14、C15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、28、30、。

苏科版七年级上册数学第6章平面图形的认识(一)含答案(含解析)

苏科版七年级上册数学第6章平面图形的认识（一）含答案一、单选题(共15题，共计45分)1、∠1=45゜24′，∠2=45.3゜，∠3=45゜18′，则（）A.∠1=∠2B.∠2=∠3C.∠1=∠3D.以上都不对2、如图，OA⊥OC，OB⊥OD，四位同学观察图形后分别说了自己的观点．甲：∠AOB=∠COD；乙：∠BOC+∠AOD=180°；丙：∠AOB+∠COD=90°；丁：图中小于平角的角有6个．其中观点正确的有（）A.甲、乙、丙B.甲、丙、丁C.乙、丙、丁D.甲、乙、丁3、12点15分，时针与分针所夹的小于平角的角为（）A.90°B.67.5°C.82.5°D.60°4、已知：如图，点E，F分别在AB，CD上，AF⊥CE，垂足为点O，∠1＝∠B，∠A+∠2＝90°.求证：AB∥CD.证明：如图，∵∠1＝∠B（已知）∴CE∥BF（同位角相等，两直线平行）______________∴∠AFC+∠2＝90°（等式性质）∵∠A+∠2＝90°（已知）∴∠AFC＝∠A（同角或等角的余角相等）∴AB∥CD（内错角相等，两直线平行）请你仔细观察下列序号所代表的内容：①∴∠AOE＝90°（垂直的定义）②∴∠AFB＝90°（等量代换）③∵AF⊥CE（已知）④∵∠AFC+∠AFB+∠2＝180°（平角的定义）⑤∴∠AOE＝∠AFB（两直线平行，同位角相等）横线处应填写的过程，顺序正确的是（）A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④5、如图，C是线段AB的中点，D是线段CB的中点，下列说法错误的是（）A.CD=AC﹣BDB.CD= AB﹣BDC.AC+BD=BC+CDD.CD= AB6、如图，∠DOB=140°，OA⊥OB，则∠AOC=（）A.40°B.45°C.50°D.55°7、如图，射线 AB，DC 交于点O，射线OM平分∠AOC，若∠BOD＝80°，则∠COM的度数为（）A.30°B.40°C.50°D.60°8、如图，直线AC和直线BD相交于点0，若∠1+∠2=90°，则∠BOC的度数是（）A.100°B.115°C.135°D.145°9、如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能符合题意解释这一现象的数学知识是（）A.垂线段最短B.经过一点有无数条直线C.两点之间，线段最短 D.经过两点，有且仅有一条直线10、如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为（）A.2B.3C.4D.511、下列六个命题：①有理数与数轴上的点一一对应；②两条直线被第三条直线所截，内错角相等；③直线外一点到这条直线的垂线段叫做点到直线的距离；④平行于同一条直线的两条直线互相平行；⑤垂直于同一条直线的两条直线互相平行；⑥如果一个角的两边分别平行于另一个角的两边，那么这两个角相等，其中假命题的个数是（）A.3个B.4个C.5个D.6个12、下列结论中，不正确的是（）A.两点确定一条直线B.两点之间的所有连线中，线段最短C.对顶角相等D.过一点有且只有一条直线与已知直线平行13、下列说法：①如果∠1+ ∠2+∠3=180°，那么∠1，∠2，∠3三个角互为补角；②如果∠A+ ∠B=90°，那么∠A与∠B互为余角；③“对顶角相等”成立，反之“相等的角是对顶角”也成立；④两条直线被第三条直线所截，同位角相等；⑤两点之间，线段最短. 正确的个数是（）A.2个B.3个C.4个D.5个14、在墙壁上固定一根横放的木条，则至少需要（）枚钉子A.lB.2C.3D.随便多少枚15、修建高速公路时，经常将弯曲的道路改直，从而缩短路程，这样做的数学根据是（）A.两点确定一条直线B.两点之间，线段最短C.垂线段最短D.同位角相等，两直线平行二、填空题(共10题，共计30分)16、请补充完成以下解答过程，并在括号内填写该步骤的理由.已知：如图，, , 平分,若,求的度数.解：因为,所以________ .因为________ ,所以.所以.（________）因为，所以.因为平分,所以________ ________°所以________°.17、如图所示：直线AB与CD相交于O，已知∠1=30°，OE是∠BOC的平分线，则∠2=________°，∠3=________°．18、数轴上到表示数4的点的距离为5个单位长度的点表示的数是________．19、如图，已知从甲地到乙地共有四条路可走，你应选择第________ 路，所用的数学原理为：________20、如图，射线表示西北方向，若射线表示南偏西的方向，则锐角的大小是________度．21、下午3点30分时，钟面上时针与分针所成的角等于________°.22、若∠1＋∠2＝180°，∠1＋∠3＝180°，则∠2与∠3的关系是________.23、火车往返于A、B两个城市，中途经过4个站点（共6个站点），不同的车站来往需要不同的车票，共有________种不同的车票．24、以下说法：①两点确定一条直线；②两点之间直线最短；③若x=y，则= ；④若|a|=﹣a，则a＜0；⑤若a，b互为相反数，那么a，b的商必定等于﹣1．其中正确的是________．（请填序号）25、如图，已知AE//CD，BC⊥CD于C，若∠A＝28°，则∠ABC＝________三、解答题(共5题，共计25分)26、一个角的余角比它的补角还多1°，求这个角．27、如图，轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则∠A的度数为多少？28、已知A、B、C.三点在同一直线上，DE⊥AB, ∠DBE=2∠EBC,求∠DBE的度数。

苏科版七年级数学上册第6章平面图形的认识(一)达标测试卷【含答案】

9.如果线段 AB=5cm，BC=4cm，且 A，B，C 在同一条直线上，那么 A、C 两点的距离是（）
A. 1cm
B. 9cm
D. 以上答案都不正确
10.同一平面内，三条不同直线的交点个数可能是（）个．
C. 1cm 或 9cm
A. 1 或 3
B. 0、1 或 3
C. 0、1 或
2
D. 0、1、2 或 3
A．①④
B．②③
C．①②④
D．①③④
6．下列说法①一个角的补角大于这个角②小于平角的角是钝角③同角或等角的余角相等④若 1 2 3 180 ，
则 1 、 2 、 3 互为补角．其中正确的说法有（）
A．4 个
B．3 个
C．2 个
D．1 个
7．如图，AM 为∠BAC 的平分线，下列等式错误的是( )
A．两点确定一条直线
B．两点之间，线段最短
C．垂线段最短
D．同一平面内垂直于同一条直线的两直线平行
5．下列日常现象：
①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；
③利用圆规可以比较两条线段的大小；④建筑工人砌墙时，经常先在两端立桩拉线，然后沿着线砌墙．
其中，可以用“两点确定一条直线”来解释的现象是（）
【考点】角平分线的定义．【答案】见试题解答内容【分析】根据角平分线的定义求解．【解答】解：∵∠AOC＝25°，OC 平分∠AOB， ∴∠AOB＝2∠AOC＝50°，故答案为 50°． 15 如图，点 A 位于点 O 的方向上．
【考点】方向角．【答案】见试题解答内容【分析】根据方位角的概念直接解答即可．【解答】解：点 A 位于点 O 的北偏西 30°方向上．

苏科版七年级上册数学第6章平面图形的认识(一)含答案(完整版)

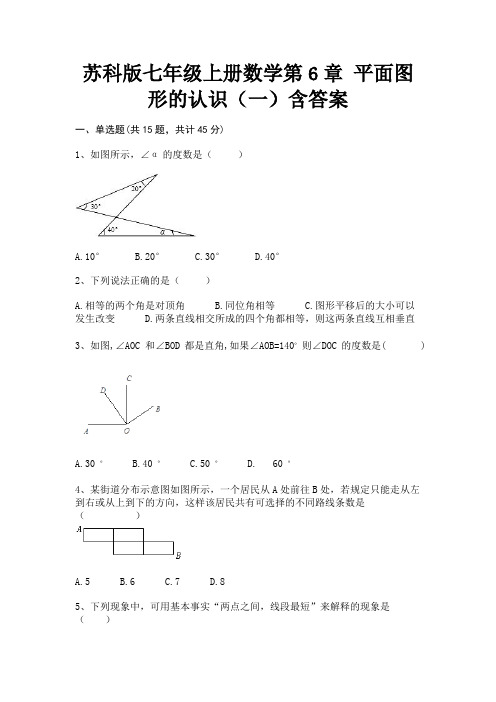
苏科版七年级上册数学第6章平面图形的认识（一）含答案一、单选题(共15题，共计45分)1、如图所示，∠α的度数是（）A.10°B.20°C.30°D.40°2、下列说法正确的是（）A.相等的两个角是对顶角B.同位角相等C.图形平移后的大小可以发生改变 D.两条直线相交所成的四个角都相等，则这两条直线互相垂直3、如图,∠AOC 和∠BOD都是直角,如果∠AOB=140◦则∠DOC的度数是( )A.30 ◦B.40 ◦C.50 ◦D. 60 ◦4、某街道分布示意图如图所示，一个居民从A处前往B处，若规定只能走从左到右或从上到下的方向，这样该居民共有可选择的不同路线条数是（）A.5B.6C.7D.85、下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（）A.把弯曲的公路改直，就能缩短路程B.用两个钉子就可以把木条固定在墙上C.植树时，只要定出两棵树的位置，就能确定同一行树所在的直线 D.利用圆规可以比较两条线段的大小关系6、下列哪种情况下，直线a与b不一定是平行线（）A.a与b是不相交的两条直线B.a与b被直线c所截，且内错角互补 C.a与b都平行于直线c D.a与b被直线c所截，且同位角相等7、如果从甲船看乙船，乙船在甲船的南偏东40°方向，那么从乙船看甲船，甲船在乙船的（）A.北偏东50°B.北偏西50C.北偏东40°D.北偏西40°8、下列定理中没有逆定理的是（）A.内错角相等，两直线平行B.直角三角形中，两锐角互余C.等腰三角形两底角相等D.相反数的绝对值相等9、下列说法中，正确的是( )A.两条不相交的直线叫平行线B.一条直线的平行线有且只有一条C.若直线a∥b，a∥c，则b∥cD.两条直线不相交就平行10、如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A.点动成线；B.两点确定一条直线；C.垂线段最短；D.两点之间，线段最短；11、如图，直线l与直线a、b相交，且a b,∠1＝80°,则∠2的度数是（）A.60°B.80°C.100°D.120°12、下列说法正确是（）A.相等的两个角是对顶角；B.过一点有且只有一条直线与已知直线平行； C.直线外一点与直线上各点连接的所有线中，垂线最短； D.平面内，过一点有且只有一条直线与已知直线垂直13、若数轴上点A表示的数是，则与它相距2个单位的点B表示的数是（）A.±5B.-7或-3C.7D.-8或314、下列说法中正确的是A.过一点有且仅有一条直线与已知直线平行B.若，则点C是线段AB的中点C.两点之间的所有连线中，线段最短D.相等的角是对顶角15、下面4个图形中，∠1与∠2是对顶角的是( )A. B. C. D.二、填空题(共10题，共计30分)16、己知在纸面上有一数轴（如图所示）一般地，数轴上表示数m和数n的两点间距离可用|m﹣n|表示，|x﹣4|+|x﹣5|的最小值是________17、如图，∠AOD＝135°，∠AOC＝75°，∠DOB＝105°，则∠BOC＝________.18、已知∠A=55°，则∠A的余角等于________度．19、如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是________.20、如图，已知平分平分，，则________°.21、探究:如图①，，试说明．下面给出了这道题的解题过程，请在下列解答中，填上适当的理由．解: ∵ ．(已知)∴ ．（________）同理可证，．∵ ，∴ ．（________）应用:如图②，，点F在之间，与交于点M，与交于点N．若，，则的大小为________度．拓展:如图③，直线在直线之间，且，点分别在直线上，点Q是直线上的一个动点，且不在直线上，连结．若，则=________度．22、如图，直线a、b相交于点O，将量角器的中心与点O重合，发现表示60°的点在直线a上，表示138°的点在直线b上，则∠1＝________°.23、已知一个角的余角为28°40′，则这个角的度数为________.24、直角三角形的一锐角为60°，则另一锐角为________25、如果一个角的补角是150°，那么这个角的余角的度数是________三、解答题(共5题，共计25分)26、一个角的余角比它的补角还多1°，求这个角．27、如图，AB、CD交于点O，∠1=∠2，∠3：∠1=8：1，求∠4的度数．28、如图，AB交CD于O，OE⊥AB．（1）若∠EOD=20°，求∠AOC的度数；（2）若∠AOC：∠BOC=1：2，求∠EOD的度数．29、如图，是平角，，，，分别是，的平分线，求的度数.30、下面是小马虎解的一道题题目：在同一平面上，若∠BOA=70°，∠BOC=15°求∠AOC的度数．解：根据题意可画出图，∵∠AOC=∠BOA－∠BOC=70°－15°=55°，∴∠AOC=55°．若你是老师，会判小马虎满分吗？若会，说明理由．若不会，请将小马虎的的不符合题意指出，并给出你认为正确的解法．参考答案一、单选题(共15题，共计45分)1、A2、D3、B4、D6、B7、D8、D9、C10、B11、B12、D13、B14、C15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、27、29、30、。

【完整版】苏科版七年级上册数学第6章平面图形的认识(一)含答案

苏科版七年级上册数学第6章平面图形的认识（一）含答案一、单选题(共15题，共计45分)1、如图，矩形ABCD中，AB=4，BC=8，P，Q分别是直线BC，AB上的两个动点，AE=2，△AEQ沿EQ翻折形成△FEQ，连接PF，PD，则PF+PD的最小值是（）A. B. C. D.2、如图，已知OC平分∠AOB,CD//OB，若OD=3cm，则CD等于（）A.1.5cmB.2cmC.3cmD.4cm3、如图，图中可以只用一个大写字母表示的角有（）A.1个B.2个C.3个D.4个4、下面说法错误的是（）A.过一点有且只有一条直线与已知直线垂直．B.在同一个平面内，任意三条直线相交，交点的个数最多有3个C.平行于同一直线的两条直线平行．D.两条平行线被第三条直线所截，一对内错角的平分线互相平行．5、如图，AB∥CD，EF⊥AB于点E，EF交CD于点F，已知∠1＝64°，则∠2等于（）A.26°B.32°C.25°D.36°6、如图，这是健健同学的小测试卷，他应该得到的分数是（）A.40B.60C.80D.1007、已知数轴上三点A、B、C分别表示有理数x、1、﹣1，那么|x﹣1|表示（）A.A、B两点的距离B.A、C两点的距离C.A、B两点到原点的距离之和D.A、C两点到原点的距离之和8、平行四边形中，若，则的度数为（）A. B. C. D.9、一个角的余角比它的补角的一半少，则这个角的度数为（）A. B. C. D.10、如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为（）A.0.5B.2.5C.D.111、如图，点O在直线AB上，射线OC平分∠DOB，若∠DOC=35°，则∠AOD等于（）A.35°B.70°C.110°D.145°12、下列说法错误的是（）．A.两个互余的角都是锐角;B.一个角的补角大于这个角本身;C.互为补角的两个角不可能都是锐角;D.互为补角的两个角不可能都是钝角13、点P为直线l外一点，点A、B、C为直线l上三点，PA=4cm、PB=5cm、PC=2cm，则点P到直线l的距离（）A.等于4cmB.等于2cmC.小于2cmD.不大于2cm14、如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（）A.20°B.70°C.30°D.90°15、如图，已知OP平分∠AOB，∠AOB=， CP=，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A. B. C. D.二、填空题(共10题，共计30分)16、一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=________°．17、一个角的余角等于这个角的补角的，则这个角为________．18、已知∠A的补角是它的余角的3倍还多10°，则∠A=________度．19、如图是一把剪刀，若∠AOB+∠COD＝60°，则∠BOD＝________°．20、如图，在四边形ABCD中，∠A=90°,AD=4，连接BD,，∠ADB=∠C．若P是BC边上一动点，则DP长的最小值为________ .21、如图,Rt△ABC中,∠C=90°,AC=2,BC=1,以斜边为一边向右上方作正方形ABDE,连接CD,则CD的长为________.22、如图，∠PQR=138° ,SQ QR，QT PQ，则SQT=________23、如图，由泰山到青岛的往返列车，运行途中停靠的车站依次是：泰山﹣﹣济南﹣﹣淄博﹣﹣潍坊﹣﹣青岛，那么要为这次列车制作的火车票有________种，票价有________种24、如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是________.25、如图，直线AB，CD相交于点O，EO⊥CD，垂足为O.若∠AOE=55°，则∠BOD的度数为________.三、解答题(共5题，共计25分)26、计算：180°﹣34°54′﹣21°33′．27、如图，已知△ABC，用直尺和圆规画出一条线段a，使a=AC+BC，然后比较a与AB的长短．28、如图，在中，，，线段CD和CE分别为的角平分线和高线．求、的大小．29、推理计算：已知AB∥CD，∠B＝100°，EF平分∠BEC，EG⊥EF，求∠BEG 和∠DEG的度数.30、如图，∠COD=45°，∠BOD= ∠COD，OC是∠AOB的平分线，求∠AOD的度数．参考答案一、单选题(共15题，共计45分)1、B2、C3、B4、A5、A6、B7、A8、B9、C10、B11、C13、D14、A15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、。

苏科版七年级数学上册第6章平面图形的认识(一) 单元综合练习题【含答案】

苏科版七年级数学上册第6章平面图形的认识（一）单元综合练习题一、选择题1、如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点确定一条直线B．两点之间线段最短C．垂线段最短D．连接两点的线段叫做两点的距离2、如图所示，能用∠α，∠AOB，∠O表示同一个角的是（）A．B．C．D．3、下图中，1∠和2∠是对顶角的是（）A．B．C．D．4、下列图形中线段AD的长表示点A到直线BC距离的是（）A．B．C．D．5、一个角的补角比这个角的余角大（）．A．70°B．80°C．90°D．100°6、已知α，β是两个钝角，有四位同学计算16（α+β）得出四种不同的答案分别是24°，48°，76°，86°，其中只有一个是正确的，则正确的答案是（）A．86°B．76°C．48°D．24°7、如图，线段21AD cm=，点B在线段AD上，C为BD的中点，且13AB CD=，则BC的长度()A．8cm B．9cm C．6cm D．7cm 8、如图，C是AB的中点，D是BC的中点，则下列等式中正确的是()①32DB AD AB=-；②13CD AB=；③2DB AD AB=-；④CD AD CB=-．A．①②B．③④C．①④D．②③9、如图，直线AB，CD相交于点O，OE⊥AB于O，OF平分∠DOE，若∠AOC＝32°，则∠AOF的度数为（）A．119°B．121°C．122°D．124°10、下列说法正确的个数有（）①射线AB与射线BA表示同一条射线．②若∠1+∠2＝180°，∠1+∠3＝180°，则∠2＝∠3．③一条射线把一个角分成两个角，这条射线叫这个角的平分线．④连结两点的线段叫做两点之间的距离．⑤40°50ˊ＝40.5°．⑥互余且相等的两个角都是45°．A．1个B．2个C．3个D．4个二、填空题11、用度、分、秒表示：37.68︒=______．12、如图，A 是线段BC 外一点，连接AB ，AC ，过点A 作线段BC 的垂线AH ，垂足为H ．在AB 、AC 、AH 这三条线段中，AH 是最短的线段，依据是_______．(12题) (14题)13、某校下午放学的时间是4：30，此时时针与分针夹角的度数为______．14、如图，直线AB ，CD 相交于点O ，135∠=︒，275∠=︒，则EOB ∠的度数为__________︒．15、如图，线段4AB cm =，延长线段AB 到C ，使1BC cm =，再反向延长AB 到D ，使3AD cm =，E 是AD中点，F 是CD 的中点．则EF 的长度为 cm ．16、已知线段6cm AB =，若M 是AB 的三等分点，N 是AM 的中点，则线段MN 的长度为________． 17、如图，直线AB 与直线CD 相交于点O ，:1:2BOC BOD ∠∠=，射线OE CD ⊥，则∠BOE 度数为___(17题) (18题)18、如图，在三角形ABC 中，90ABC ∠=︒，BD AC ⊥，垂足为点D ，5AB =，12BC =，13AC =，下列结论正确的是．（写出所有正确结论的序号）①90ADB ∠=︒；②A DBC ∠=∠；③点C 到直线BD 的距离为线段CB 的长度；④点B 到直线AC 的距离为6013．三、解答题19、如图，在8×8的正方形网格中，每个小正方形的顶点称为格点，点A 、B 、C 均在格点上，按下述要求画图并标注相关字母．（1）画线段AB ，画射线BC ，画直线AC ；（2）过点B 画线段BD ⊥AC ，垂足为点D ；（3）取线段AB 的中点E ，过点E 画BD 的平行线，交AC 于点F ．20、如图，C 为线段AD 上的一点，B 为线段CD 的中点，AD =12cm ，BD =3cm ．（1）图中共有条线段；（2）求线段AC 的长；（3）若点E 在线段AD 上，且BE =2cm ，求AE 的长．21、如图，O 是直线AB 上一点，OC 为任一条射线，OD 平分∠BOC ，OE 平分∠AOC ．（1）若∠BOC ＝70°，求∠COD 和∠EOC 的度数；（2）写出∠COD 与∠EOC 具有的数量关系并说明理由．22、将一副三角板叠放在一起，使直角顶点重合于点O．（1）如图1，若∠AOD＝35°，求∠BOC的度数．（2）若三角板AOB保持不动，将三角板COD的边OD与边OA重合，然后将其绕点O旋转．试猜想在旋转过程中，∠AOC与∠BOD有何数量关系？请说明理由．23、如图，已知C、D两点将线段AB分成2:3:4三段，点E是BD的中点，点F是线段CD上一点，且=，求AB的长．EF cmCF DF2=，1224、如图，直线AB、CD相交于点O，OE平分BOD∠=︒．BOF∠，OF CD⊥，垂足为O，若38（1）求AOC∠的度数；（2）过点O作射线OG，使GOE BOF∠的度数．∠=∠，求FOG25、如图，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．（1）线段的中点这条线段的“巧点”；（填“是“或“不是”）（2）若AB=24cm，点C是线段AB的巧点，求AC的长．26、已知O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．（1）如图1，若∠AOM＝30°，求∠CON的度数；（2）在图1中，若∠AOM＝α，直接写出∠CON的度数（用含α的代数式表示）；（3）将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，当∠AOC＝3∠BON时，求∠AOM 的度数．答案一、选择题1、如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点确定一条直线B．两点之间线段最短C．垂线段最短D．连接两点的线段叫做两点的距离A【分析】根据公理“两点确定一条直线”来解答即可．解：经过刨平的木板上的两个点，能弹出一条笔直的墨线，此操作的依据是两点确定一条直线．故选：A．2、如图所示，能用∠α，∠AOB，∠O表示同一个角的是（）A．B．C．D．【分析】角可以用一个大写字母表示，也可以用三个大写字母表示．角还可以用一个希腊字母表示，或用阿拉伯数字表示．【详解】解：能用∠α，∠AOB，∠O三种方法表示同一个角的图形是选项D中的图，选项B，C，D中的图都不能用∠α，∠AOB，∠O三种方法表示同一个角的图形，故选：D．3、下图中，1∠和2∠是对顶角的是（）A．B．C．D．C【分析】根据对顶角的定义解答即可．【详解】解：A. 1∠和2∠的某一边不是互为反向延长线，不是对顶角，故不符合题意；B. 1∠和2∠没有公共顶点，不是对顶角，故不符合题意；C. 1∠和2∠是对顶角，符合题意；D. 1∠和2∠的某一边不是互为反向延长线，不是对顶角，故不符合题意．故选C．4、下列图形中线段AD的长表示点A到直线BC距离的是（）A．B．C． D．A【分析】根据点到直线的距离，垂足在直线上，据此分析即可【详解】A. AD表示的是点A到直线BC距离，故该选项正确，符合题意；B. AD表示的是点D到直线AB距离，故该选项不正确，不符合题意；C. AD表示的是点D到直线AB距离，故该选项不正确，不符合题意；D. AD不能表示点到直线距离，故该选项不正确，不符合题意；故选A5、一个角的补角比这个角的余角大（）．A．70°B．80°C．90°D．100°C【分析】根据互补即两角的和为180°，互余的两角和为90°，设这个角为x ，即可求出答案．【详解】解：设这个角为x ，则这个角的补角为180°-x ，这个角的补角为90°-x ，根据题意得：180°-x -（90°-x ）=90°，故选：C ．6、已知α，β是两个钝角，有四位同学计算16（α+β）得出四种不同的答案分别是24°，48°，76°，86°，其中只有一个是正确的，则正确的答案是（）A ．86°B ．76°C ．48°D ．24°C 【分析】由α，β是两个钝角可得180°＜α+β＜360°，进一步即可求得16(α+β)的范围，从而可得答案．【详解】解：因为α，β是两个钝角，所以90°＜α＜180°，90°＜β＜180°，所以180°＜α+β＜360°，所以30°＜16(α+β)＜60°，在上述四个选项中，只有选项C 中48°在上述范围中，故选：C ．7、如图，线段21AD cm =，点B 在线段AD 上，C 为BD 的中点，且13AB CD =，则BC 的长度( )A ．8cmB ．9cmC ．6cmD ．7cm【分析】设AB x =cm ，则3CD x =cm ，根据线段的中点可得3BC CD x ==cm ，再根据21AD cm =可得x ，进而可得答案．13AB CD =， ∴设AB x =cm ，则3CD x =cm ，C 为BD 的中点，3BC CD x ∴==cm ，3321x x x ∴++=，解得3x =，39BC x ∴==．故选：B ．8、如图，C 是AB 的中点，D 是BC 的中点，则下列等式中正确的是( )①32DB AD AB =-；②13CD AB =；③2DB AD AB =-；④CD AD CB =-．A ．①②B ．③④C ．①④D ．②③【分析】根据线段中点的性质，可得1124CD BD BC AB ===，再根据线段的和差，可得答案．C 是AB 的中点，D 是BC 的中点，1124CD BD BC AB ∴===，288AB BD CD ∴==，44AB BD CD ==，39AD BD =，26AD BD =，3298AD AB BD BD BD ∴-=-=，故①正确，②不正确；642DB BD BD BD ∴≠-=，③不正确；32AD CB CD CD CD -=-=，④正确．正确的有：①④．故选：C ．9、如图，直线AB ，CD 相交于点O ，OE ⊥AB 于O ，OF 平分∠DOE ，若∠AOC ＝32°，则∠AOF 的度数为（）A ．119°B ．121°C ．122°D ．124°A 【分析】根据OE ⊥AB 于O ，即可得出∠BOE ＝∠AOE ＝90°，进而求出∠DOE ＝58°，再利用OF 平分∠DOE ，即可求出∠EOF 的度数，再由∠AOF ＝∠AOE +∠EOF 即可求出∠AOF 的度数．【详解】解：∵OE ⊥AB 于O ，∴∠BOE ＝∠AOE ＝90°，∵∠AOC ＝32°，∴∠AOC ＝∠BOD ＝32°，∴∠DOE ＝∠BOE ﹣∠BOD ＝90°﹣32°＝58°，∵OF 平分∠DOE ，∴∠EOF 12=∠DOE 1582=⨯︒=29°，∠AOF ＝∠AOE +∠EOF ＝90°+29°＝119°．故选：A ．10、下列说法正确的个数有（）①射线AB 与射线BA 表示同一条射线． ②若∠1+∠2＝180°，∠1+∠3＝180°，则∠2＝∠3． ③一条射线把一个角分成两个角，这条射线叫这个角的平分线．④连结两点的线段叫做两点之间的距离．⑤40°50ˊ＝40.5°．⑥互余且相等的两个角都是45°．A ．1个B ．2个C ．3个D ．4个【分析】根据射线的定义，同角的补角相等，角平分线的定义，两点之间的距离的定义，度分秒的换算以及余角的定义对各小题分析判断即可得解．解：①射线AB 与射线BA 不表示同一条射线，因为它们的端点不同，故本小题错误；②若∠1+∠2＝180°，∠1+∠3＝180°，则∠2＝∠3，正确；③应为一条射线把一个角分成两个角相等的角，这条射线叫这个角的平分线，故本小题错误；④应为连结两点的线段的长度叫做两点之间的距离，故本小题错误；⑤40°50′≈40.83°，故本小题错误；⑥互余且相等的两个角都是45°，正确．综上所述，说法正确的有②⑥共2个．故选：B ．二、填空题11、用度、分、秒表示：37.68︒=______．374048︒'"【分析】进行度、分、秒的转化运算，注意以60为进制．1=60'︒，1'=60''．【详解】解：'''''''37.6837+0.686037+40.837400.860374048374048'''︒=︒⨯=︒=︒++⨯=︒'=︒++故答案为374048︒'"12、如图，A 是线段BC 外一点，连接AB ，AC ，过点A 作线段BC 的垂线AH ，垂足为H ．在AB 、AC 、AH 这三条线段中，AH 是最短的线段，依据是_______．垂线段最短【分析】根据垂线段最短的定义求解即可．【详解】解：∵点到直线的距离，垂线段最短，∴依据是垂线段最短，故垂线段最短．13、某校下午放学的时间是4：30，此时时针与分针夹角的度数为______．45°【分析】根据钟面平均分成12份，可得每份是30°，4点30分时，时针分针相差1.5格，根据时针与分针相距的份数乘以每份的度数，可得答案．【详解】解：4：30时，时针与分针的夹角的度数是30°×1.5＝45°，故45°．14、如图，直线AB ，CD 相交于点O ，135∠=︒，275∠=︒，则EOB ∠的度数为__________︒．110【分析】先根据对顶角相等求出∠DOB ，进而结合275∠=︒即可求出∠EOB ．【详解】解：∵∠1＝35°，∴∠DOB ＝∠1＝35°，又∵∠2＝75°，∴∠EOB ＝∠2+∠DOB ＝110°．故110．15、如图，线段4AB cm =，延长线段AB 到C ，使1BC cm =，再反向延长AB 到D ，使3AD cm =，E 是AD中点，F 是CD 的中点．则EF 的长度为 cm ．【分析】结合图形和题意，利用线段的和差知CD AD AB BC =++，即可求CD 的长度；再利用中点的定义，求得DF 和DE 的长度，又EF DF DE =-，即可求得EF 的长度．3418CD AD AB BC cm =++=++=；E 是AD 中点，F 是CD 的中点，118422DF CD cm ∴==⨯=，113 1.522DE AD cm ==⨯=． 4 1.5 2.5EF DF DE cm ∴=-=-=，故2.5．16、已知线段6cm AB =，若M 是AB 的三等分点，N 是AM 的中点，则线段MN 的长度为________． 1cm 或2cm【分析】分两种情况考虑点M 是AB 的三等分点，求出AM 的长，由中点定义求出MN 即可．【详解】当M 是AB 的左三等分点，∵AB=6cm ，∴AM=11AB=6=233⨯cm ， ∵N 是AM 的中点，∴AN=NM=11AM=2=122⨯，当M 是AB 的右三等分点，∵AB=6cm ，∴AM=22AB=6=433⨯cm ， ∵N 是AM 的中点，∴AN=NM=11AM=4=222⨯，线段MN 的长度为1cm 或2cm ．故1cm 或2cm ．17、如图，直线AB 与直线CD 相交于点O ，:1:2BOC BOD ∠∠=，射线OE CD ⊥，则∠BOE 度数为___150︒或30【分析】根据条件求得∠COB 的度数，然后根据∠BOE =∠COE -∠COB 即可求解．【详解】解：如图，∵:1:2BOC BOD ∠∠= ∴11806012BOC ∠=⨯︒=︒+ ∵OE CD ⊥∴90COE ∠=︒∴∠BOE =∠COE -∠COB =90°-60°=30°同理，如图，当点E ′在EO 的延长线上时，∠BOE ′=180°-30°=150°故答案是：30°或150°．18、如图，在三角形ABC 中，90ABC ∠=︒，BD AC ⊥，垂足为点D ，5AB =，12BC =，13AC =，下列结论正确的是．（写出所有正确结论的序号）①90ADB ∠=︒；②A DBC ∠=∠；③点C 到直线BD 的距离为线段CB 的长度；④点B 到直线AC 的距离为6013．【分析】①根据垂直的定义即可求解；②根据余角的性质即可求解；③根据点到直线的距离的定义即可求解；④根据三角形面积公式即可求解．①BD AC⊥，90ADB∴∠=︒，故①正确；②90ABD A∠+∠=︒，90ABD DBC∠+∠=︒，A DBC∴∠=∠，故②正确；③点C到直线BD的距离为线段CD的长度，故③错误；④点B到直线AC的距离为160512213213⨯⨯⨯÷=，故④正确．故①②④．三、解答题19、如图，在8×8的正方形网格中，每个小正方形的顶点称为格点，点A、B、C均在格点上，按下述要求画图并标注相关字母．（1）画线段AB，画射线BC，画直线AC；（2）过点B画线段BD⊥AC，垂足为点D；（3）取线段AB的中点E，过点E画BD的平行线，交AC于点F．（1）如图所示，线段AB，射线BC，直线AC即为所求；见解析；（2）线段BD即为所求；见解析；（3）直线EF即为所求．见解析.（1）连接AB、以B为端点，作射线BC、过点A、C作直线即可；（2）根据网格结构，作过点B所在的小正方形对角线与直线AC相交于点D，即为所求；（3）根据网格结构，作过点E所在的小正方形对角线所在的射线与直线AC相交于点F，即为所求．【详解】（1）如图所示，线段AB，射线BC，直线AC即为所求；（2）线段BD即为所求；（3）直线EF即为所求．20、如图，C为线段AD上的一点，B为线段CD的中点，AD =12cm，BD =3cm．（1）图中共有条线段；（2）求线段AC的长；（3）若点E在线段AD上，且BE =2cm，求AE的长．（1）6；（2）6cm；（3）11cm或7cm【分析】（1）根据线段的定义找出线段即可；（2）先根据点B为CD的中点，BD＝3cm求出线段CD的长，再根据AC＝AD−CD即可得出结论；（3）根据E点位置的不同分情况讨论即可求解．【详解】解：（1）图中的线段有AC、AB、AD、BC、CD、BD，共有6条线段．故6；（2）∵点B为CD的中点．∴CD＝2BD．∵BD＝3cm，∴CD＝6cm，BC=3cm，∵AC＝AD−CD且AD＝12cm，CD＝6cm，∴AC＝6cm；（3）如图，点E在B点的左侧，BE =2cm，∴CE=BC-CE=1 cm，∴AE=AC+CE=7 cm，如图，点E在B点的右侧，BE =2cm，∴AE=AC+BC+BE=6+3+2=11cm，∴AE 的长为11cm 或7cm ．21、如图，O 是直线AB 上一点，OC 为任一条射线，OD 平分∠BOC ，OE 平分∠AOC ．（1）若∠BOC ＝70°，求∠COD 和∠EOC 的度数；（2）写出∠COD 与∠EOC 具有的数量关系并说明理由．解：（1）∵OD 平分∠BOC ，∠BOC ＝70°，∴∠COD=21∠BOC=21×70°＝35°， ∵∠BOC ＝70°，∴∠AOC ＝180°﹣∠BOC ＝180°﹣70°＝110°，∵OE 平分∠AOC ，∴∠EOC=21∠AOC=21×110°＝55°；（2）∠COD 与∠EOC 互余，理由如下：∵OD 平分∠BOC ，OE 平分∠AOC ，∴∠COD=21∠BOC ，∠EOC=21∠AOC ， ∴∠COD+∠EOC=21（∠BOC+∠AOC ）=21×180°＝90°， ∴∠COD 与∠EOC 互余．22、将一副三角板叠放在一起，使直角顶点重合于点O ．（1）如图1，若∠AOD ＝35°，求∠BOC 的度数．（2）若三角板AOB保持不动，将三角板COD的边OD与边OA重合，然后将其绕点O旋转．试猜想在旋转过程中，∠AOC与∠BOD有何数量关系？请说明理由．【分析】（1）由于是两直角三角形板重叠，根据∠AOD的度数可得∠BOD，再根据∠DOC＝90°可得∠BOC；（2）当分两种情况：∠AOB与∠DOC有重叠部分时和当∠AOB与∠DOC没有重叠部分时．【详解】解：（1）若∠AOD＝35°，∵∠AOB＝∠COD＝90°，∴∠BOD＝90°﹣35°＝55°，∴∠BOC＝90°﹣∠BOD＝90°﹣55°＝35°；（2）∠AOC与∠BOD互补．当∠AOB与∠DOC有重叠部分时，∵∠AOB＝∠COD＝90°，∴∠AOD+∠BOD+∠BOD+∠BOC＝180°．∵∠AOD+∠BOD+∠BOC＝∠AOC，∴∠AOC+∠BOD＝180°，当∠AOB与∠DOC没有重叠部分时，∠AOB+∠COD+∠AOC+∠BOD＝360°，又∵∠AOC＝∠BOD＝90°，∴∠AOB+∠DOC＝180°．23、如图，已知C 、D 两点将线段AB 分成2:3:4三段，点E 是BD 的中点，点F 是线段CD 上一点，且2CF DF =，12EF cm =，求AB 的长．【分析】首先设2AC xcm =，则线段3CD xcm =，4DB xcm =，然后根据E 是线段BD 的中点，2CF DF =，分别用x 表示出DE 、EF ，根据12EF cm =，求出x 的值，即可求出线段AB 的长是多少．设2AC x =， C 、D 两点将线段AB 分成2:3:4三段，3CD x ∴=，4BD x =，2CF DF =，CD CF DF =+，DF x ∴=，点E 是BD 的中点，2DE x ∴=，3EF DF DE x ∴=+=，12EF cm =，4x cm ∴=，8AC cm ∴=，12CD cm =，16BD cm =，36AB AC CD BD cm ∴=++=．24、如图，直线AB 、CD 相交于点O ，OE 平分BOD ∠，OF CD ⊥，垂足为O ，若38BOF ∠=︒．（1）求AOC ∠的度数；（2）过点O 作射线OG ，使GOE BOF ∠=∠，求FOG ∠的度数．【分析】（1）由垂直可得，90DOF ∠=︒，由互余得BOD ∠的度数，再由对顶角相等，可得AOC ∠的度数；（2）射线OG 的位置不确定，需要分类讨论，当射线OG 在射线OE 上方时，当射线OG 在射线OE 下方时，分别求解．（1）如图，OF CD ⊥，垂足为O ，90DOF ∴∠=︒，38BOF ∠=︒，903852BOD DOF BOD ∴∠=∠-∠=︒-︒=︒，52AOC BOD ∴∠=∠=︒．（2）由（1）知，52BOD ∠=︒， OE 平分BOD ∠， 1262BOE DOE BOD ∴∠=∠=∠=︒， 382664EOF FOG GOE ∴∠=∠+∠=︒+︒=︒，38BOF ∠=︒，38EOG BOF ∴∠=∠=︒．当射线OG 在射线OE 上方时，如图1，643826FOG EOF EOG ∠=∠-∠=︒-︒=︒；当射线OG 在射线OE 下方时，如图2，6438102FOG EOF EOG ∠=∠+∠=︒+︒=︒．综上可知，FOG ∠的度数为26︒或102︒．25、如图，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．（1）线段的中点这条线段的“巧点”；（填“是“或“不是”）（2）若AB=24cm，点C是线段AB的巧点，求AC的长．（1）是；（2）AC=8cm或12cm或16cm．【分析】（1）根据“巧点”的定义即可求解；（2）分BC=2AC，AB=2AC，AC=2BC三种情况讨论，分别求解即可．【详解】解：（1）当M是线段AB的中点，则AB=2AM，∴线段的中点是这条线段的“巧点”．故是；（2）∵AB=24cm，点C是线段AB的巧点，①BC=2AC，则AC=13AB=13×24=8(cm)；②AB=2AC，则AC=12AB=12×24=12(cm)；③AC=2BC，则AC=23AB=23×24=16(cm)．∴AC=8cm或AC=12cm或AC=16cm．26、已知O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．（1）如图1，若∠AOM＝30°，求∠CON的度数；（2）在图1中，若∠AOM＝α，直接写出∠CON的度数（用含α的代数式表示）；（3）将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，当∠AOC＝3∠BON时，求∠AOM 的度数．（1）15°；（2）12α；（3）144°【分析】（1）根据补角的定义可得∠BOM＝150°，再由∠MON是直角，OC平分∠BOM，即可求解；（2）根据补角的定义可得∠BOM＝180°﹣α，再由∠MON是直角，OC平分∠BOM，即可求解；（3）设∠AOM＝x，则∠BOM＝180°﹣x，根据OC平分∠BOM，可得∠MOC＝90°﹣12x，从而得到∠AOC＝∠AOM+∠MOC＝90°+12x，再由∠MON＝90°，可得到∠BON＝∠MON﹣∠BOM＝x﹣90°，然后根据∠AOC＝3∠BON，可得到关于x的方程，即可求解．【详解】解：（1）由已知得∠BOM＝180°﹣∠AOM＝150°，∵∠MON是直角，OC平分∠BOM，∴∠CON＝∠MON﹣12∠BOM＝90°﹣12×150°＝15°；（2）由已知得∠BOM＝180°﹣∠AOM＝180°﹣α，∵∠MON是直角，OC平分∠BOM，∴∠CON＝∠MON﹣12∠BOM＝90°﹣12×（180°﹣α）＝12α；（3）设∠AOM＝x，则∠BOM＝180°﹣x，∵OC平分∠BOM，∴∠MOC＝12∠BOM＝12（180°﹣x）＝90°﹣12x，∴∠AOC＝∠AOM+∠MOC＝x+90°﹣12x＝90°+12x，∵∠MON＝90°，∴∠BON＝∠MON﹣∠BOM＝90°﹣（180°﹣x）＝x﹣90°，∵∠AOC＝3∠BON，∴90°+1x＝3（x﹣90°），解得x＝144°，∴∠AOM＝144°．2。

苏科版七年级上册数学第6章平面图形的认识(一) 含答案(完美版)

苏科版七年级上册数学第6章平面图形的认识（一）含答案一、单选题(共15题，共计45分)1、图中∠1、∠2、∠3都是平行线a、b被直线c所截得到的角，其中相等的两个角有几对（）A.1B.2C.3D.42、下列命题的逆命题不正确的是（）A.平行四边形的对角线互相平分B.两直线平行，内错角相等C.等腰三角形的两个底角相等D.对顶角相等3、已知点Ｍ(9，-5)、N(-3，-5)，则直线MN与x轴、y轴的位置关系分别为( )A.相交、相交B.平行、平行C.垂直相交、平行D.平行、垂直相交4、平面内有三条直线，那么它们的交点个数有（）A.0个或1个B.0个或2个C.0个或1个或2个D.0个或1个或2个或3个5、下列说法中，正确的是（）A.在同一平面内，两条直线的位置关系只有相交，平行两种B.在同一平面内，不相交的两条线段互相平行C.在同一平面内，不相交的两条直线互相平行D.在同一平面内，不相交的两条射线互相平行6、若数轴上点A表示的数是 -3, 则与点A相距6个单位长度的点表示的数是（）A.±6B.±3C.-9或3D.-3或97、两个锐角的和（）．A.必定是锐角;B.必定是钝角;C.必定是直角;D.可能是锐角，可能是直角，也可能是钝角8、如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条这样的墨线，能解释这一实际应用的数学知识是（）A.两点确定一条直线B.垂线段最短C.在同一平面内，过一点有且只有一条直线与已知直线垂直D.两点之间，线段最短9、下列命题: (1)两直线平行，同旁内角互补(2) 同角的补角相等. (3) 直角三角形的两个锐角互余. (4) 同位角相等。

其中真命题的个数（）A.1个B.2个C.3个D.4个10、如图，按照上北下南，左西右东的规定画出东南西北的十字线，其中点A 位于点O的( ）A.北偏西65°方向B.北偏东65°方向C.南偏东35°方向D.南偏西65°方向11、下列命题是真命题的个数为（）①两条直线被第三条直线所截，内错角相等.②三角形的内角和是180°.③在同一平面内平行于同一条直线的两条直线平行.④相等的角是对顶角.⑤两点之间，线段最短.A.2B.3C.4D.512、已知，为的余角，则（）A. B. C. D.13、如图，直线a∥b，直线c与a、b分别交于A、B两点，若∠1=46°，则∠2=（）A.44°B.46°C.134°D.54°14、如图所示，，，平分，则图中与相等的角有（）个.A. B. C. D.15、如果一个角的度数为28°14′，那么它的余角的度数为（）A. B. C. D.二、填空题(共10题，共计30分)16、68°30′的补角为________．17、如图，直线、交于点，于点，，则的度数为________.18、如图，直线AB，CD相交于点O，射线OE⊥CD，给出下列结论：①∠2和∠4互为对顶角；②∠3+∠2=180°；③∠5与∠4互补；④∠5=∠3-∠1；其中正确的是________。

苏科版七年级上第6章平面图形的认识(一)单元试卷含答案

第6章平面图形的认识（一）检测卷（时间：90分钟满分：100分）一、选择题（每小题3分，共30分） 1．下列说法中正确的是 ( ) A ．直线有无数个端点 B ．线段有2个端点 C ．射线没有端点 D ．以上都不对 2．如图，下列说法中错误的是 ( )A ．点A ，B 都在直线a 上 B ．A ，B 两点确定一条直线ABC ．直线a 经过点A ，BD ．点A 是直线a 的一个端点 3．如图，下列表示已知角的方法中错误的是 ( )A ．∠AB ．∠1C ．∠OD ．∠AOB 4．平行线是指 ( ) A ．两条不相交的直线B ．两条延长后仍不相交的直线C ．同一平面内两条不相交的直线D ．以上都不对5．若∠1＝35°，则它的余角和补角分别为 ( ) A ．55°，145° B ．135°，55° C ．65°，85° D ．25°，115° 6．测量跳远的成绩是要得到 ( ) A ．两点之间的距离 B ．点到直线的距离 C ．两条直线之间的距离 D ．空中飞行的距离7．如图，点M 是线段AB 的中点，下列表达中错误的是 ( )A ．AM ＝BMB ．AM ＝AB C ．BM ＝D ．AB ＝2BM8．下列说法：①对顶角相等；②等角的补角相等；③两点之间，线段最短；④过直线∠外一点P ，只能画一条直线与l 平行．其中，正确的有 ( ) A ．1个 B ．2个 C ．3个 D ．4个12129．从上午7时55分到8时4分，时钟的分针转过的角度为( )A．36°B．45°C．54°D．72°10．下列说法：①在同一平面内，两条直线要么相交，要么平行；②经过直线外一点，有且只有一条直线与已知直线平行；③经过一点有且只有一条直线与已知直线垂直；④经过两点有且只有一条直线．其中，错误的有( )A．0个B．1个C．2个D．3个二、填空题（每小题3分，共24分）11．下图中以点A为端点的线段有______条，分别是______________．12．如图，OC是∠AOB的平分线，若∠AOC＝45°，则∠AOB＝_______°，其中OA，OB之间的位置关系是_______（用符号表示）．13．把15°30'化成度的形式，则15°30'＝_______．14．用一副三角板可以直接得到30°，45°，60°，90°四种角，利用一副三角板可以拼出另外一些特殊角，如75°，120°等，请你拼一拼，使用一副三角板还能拼出哪些小于平角的角，这些角的度数是：______．15．若∠1、∠2都是∠3的余角，则∠1______∠2(填“>”“<”或“＝”)，理由是_______．16．如图，射线OP表示的方向可以表示为_______．17．经过三点A，B，C中的任意两点，可以画直线______条．18．如图，直线BC与直线DE相交于点O，OA⊥BC于点O．若∠COE＝47°，则∠BOE ＝______°，∠AOD＝_______°．三、解答题（共46分）19．(6分)计算：(1)26°23'＋32°37'；(2)125°－75°28'．20．（6分）如图，已知线段AB＝80 cm．C是AB上任意一点，M是AC的中点，N为BC的中点，求MN的长．21．（6分）如图，点P是∠AOB内任意一点．(1)过点P画直线PM∥OB；(2)过点P画直线PN⊥OA．22．（5分）如图，直线AB，CD，EF都经过点O，且AB⊥CD，OG平分∠BOE，如果∠EOG＝25∠AOE，求∠EOG，∠DOF和∠AOE的度数．23．（8分）如果∠1与∠2互为余角，∠2与∠3互为补角，且∠1＝75°．求：(1)∠3的度数：(2)写出当∠1＝n°时，∠3的度数．（不必写过程）24．（8分）如图，O是直线AB上一点，OE，OC，OF是射线，OE⊥OF，若∠BOC＝2∠COE，∠AOF的度数比∠COE的度数的4倍小8°．求∠COE的度数．25．（8分）如图，直线AB、CD相交于O，射线OM平分∠AOC,O N⊥OM,若∠AOM =350，求∠CON的度数。

苏科版七年级上《第6章平面图形的认识(一)》单元测试题含答案

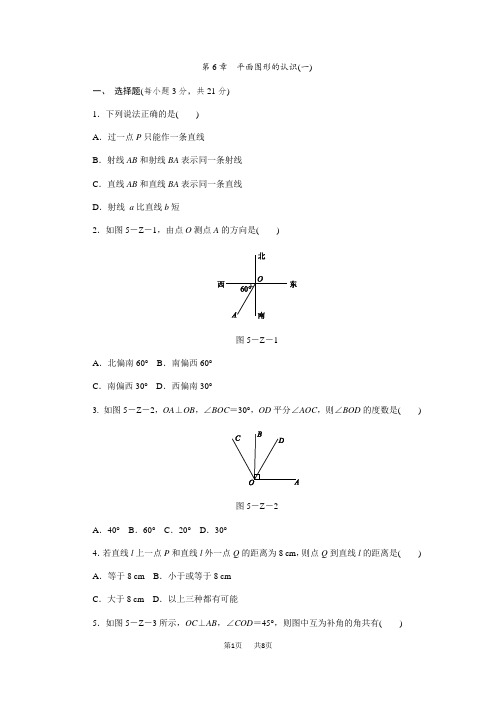
第6章平面图形的认识(一)一、选择题(每小题3分，共21分)1．下列说法正确的是()A．过一点P只能作一条直线B．射线AB和射线BA表示同一条射线C．直线AB和直线BA表示同一条直线D．射线a比直线b短2．如图5－Z－1，由点O测点A的方向是()图5－Z－1A．北偏南60°B．南偏西60°C．南偏西30°D．西偏南30°3. 如图5－Z－2，OA⊥OB，∠BOC＝30°，OD平分∠AOC，则∠BOD的度数是()图5－Z－2A．40°B．60°C．20°D．30°4．若直线l上一点P和直线l外一点Q的距离为8 cm，则点Q到直线l的距离是() A．等于8 cm B．小于或等于8 cmC．大于8 cm D．以上三种都有可能5．如图5－Z－3所示，OC⊥AB，∠COD＝45°，则图中互为补角的角共有()图5－Z－3A．1对B．2对C．3对D．4对6．在图5－Z－4中，线段的条数为()图5－Z－4A．9 B．10C．13 D．157．已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β－∠γ的值为()A．45°B．60°C．90°D．180°二、填空题(每小题3分，共24分)8．已知∠A＝40°，则∠A的余角的度数是________．9．工人师傅在砌墙时，先在两端各固定一点，中间拉紧一条细线，然后沿着细线砌墙就能砌直．运用的数学原理：________________________．10．9：30时，钟表的时针和分针构成的角的度数是________．11．如图5－Z－5，已知BC＝4，BD＝7，D是线段AC的中点，则AB＝________．图5－Z－512．把16°15′化为度是________．13．若∠α与∠β是对顶角，∠α的补角是35°，则∠β的度数为________．14．如图5－Z－6，PC∥AB，QC∥AB，则点P，C，Q在一条直线上，理由：______________________．图5－Z－615．如图5－Z－7所示，AB⊥CD，垂足为B，直线EF过点B，且BE平分∠ABD，则∠CBF的度数为________．图5－Z－7三、解答题(共55分)16．(10分)已知点C在线段AB上，点D在线段AB的延长线上，若AC＝5，BC＝3，BD＝AB，求CD的长．17．(10分)如图5－Z－8，已知∠AOB, 用三角尺和量角器画图．(1)画∠AOB的平分线OC，并在OC上任取一点P；(2)过点P画一条平行于OB的直线；(3)过点P画PD⊥OA，PE⊥OB，垂足分别为D，E.图5－Z－818．(10分)如图5－Z－9，直线AB，CD相交于点O，OE平分∠AOC，∠AOD比∠AOE 大75°，求∠AOD的度数．图5－Z－919．(12分)如图5－Z－10，已知线段AB，请按要求完成下列问题．(1)用直尺和圆规作图：延长线段AB到点C，使BC＝AB；反向延长线段AB到点D，使AD＝AC.(2)如果AB＝2 cm，①求CD的长；②设P是线段BD的中点，求线段CP的长．图5－Z－1020．(13分)如图5－Z－11，将长方形纸片的一角斜折过去，点B落在点D处，EF为折痕，再把FC折过去与FD重合，FH为折痕，问：(1)EF与FH有什么位置关系？(2)∠CFH与∠BEF有什么数量关系？图5－Z－111．C 2.C 3. D 4．B 5．C 6．D 7．C 8．50° 9．两点确定一条直线 10．105° 11．10 12．16.25° 13．145°14．过直线外一点有且只有一条直线和已知直线平行 15．45°16．解：∵点C 在线段AB 上，AC ＝5，BC ＝3， ∴AB ＝8.∵点D 在线段AB 的延长线上，BD ＝14AB ，∴BD ＝14AB ＝2，∴CD ＝BC ＋BD ＝3＋2＝5.17．略18．解：因为OE 平分∠AOC ，所以可设∠AOE ＝∠EOC ＝x °.因为∠AOD 比∠AOE 大75°，所以∠AOD ＝∠AOE ＋75°＝(x ＋75)°.因为∠AOD ＋∠AOE ＋∠EOC ＝180°，所以x ＋75＋x ＋x ＝180，解得x ＝35.所以∠AOD ＝35°＋75°＝110°.19．解：(1)如图所示，点C 和点D 即为所求．(2)①∵AB ＝2 cm ，BC ＝AB ，∴AC ＝2AB ＝4 cm.又∵AD ＝AC ，∴CD ＝2AC ＝8 cm.②∵BD ＝AD ＋AB ＝4＋2＝6 (cm)，P 是线段BD 的中点，∴BP ＝3 cm ，∴CP ＝BC ＋BP ＝2＋3＝5(cm)．20．解：(1)根据折叠的有关性质可知：∠DFH ＝∠CFH ，∠BFE ＝∠DFE . 因为∠BFE ＋∠DFE ＋∠DFH ＋∠CFH ＝180°，即有∠EFD ＋∠DFH ＝12×180°＝90°，即∠EFH ＝90°. 故EF ⊥FH .(2)因为∠BEF ＋∠BFE ＝90°，∠BFE ＋∠CFH ＝90°，所以∠CFH ＝∠BEF .。

七年级数学上册 第六章平面图形的认识(一)同步测试 苏科版

最新七年级数学上册苏科版《第六章平面图形的认识》测试卷一及答案(精品试卷).docx

苏科版七年级上册数学第6章 平面图形的认识(一) 含答案

苏科版七年级上册数学第6章 平面图形的认识(一)含答案(含解析)