快速排序算法C++实现

合集下载

快速排序算法c语言实验报告

快速排序算法c语言实验报告冒泡法和选择法排序C程序实验报告实验六：冒泡法排序物理学416班赵增月F12 2011412194日期：2013年10月31日一·实验目的 1.熟练掌握程序编写步骤；2.学习使用冒泡法和选择法排序；3.熟练掌握数组的定义和输入输出方法。

二·实验器材1.电子计算机；2.VC6.0三·实验内容与流程1.流程图（1）冒泡法(2)选择法 2.输入程序如下：（1）冒泡法#includestdio.h void main() { int a[10]; int i,j,t; printf(请输入10个数字：\n); for(i=0;i10;i++)scanf(%d,&a[i]); printf(\n); for(j=0;j9;j++)for(i=0;i9-j;i++) if(a[i]a[i+1]) { t=a[i]; a[i]=a[i+1]; a[i+1]=t; } printf(排序后如下：\n); for(i=0;i10;i++) printf(%d,a[i]); printf(\n); }（2）选择法#includestdio.h void main() { int a[10]; int i,j,t,k; printf(请输入10个数字：\n); for(i=0;i10;i++)scanf(%d,&a[i]);printf(\n); for(i=0;i9;i++) {k=i;for(j=i+1;j10;j++) if (a[k]a[j])k=j;t=a[i];a[i]=a[k];a[k]=t; }printf(排序后如下：\n); for(i=0;i10;i++)printf(%d,a[i]); printf(\n); }四．输出结果（1冒泡法）请输入10个数字：135****2468排序后如下：12345678910 （2）选择法输出结果请输入10个数字：135****6810排序后如下：12345678910五．实验反思与总结1.冒泡法和选择法是一种数组排序的方法，包含两层循环，写循环时，要注意循环变量的变化范围。

C语言--常见排序算法

25 1 i k
49
2 j 49
08
0
25* 3 49 25
16 4
21
5
08
25
25*
16
21
i k 49
j 25* 25
08
25
25*
16
21
算法实例：
1.1.5 选择排序
49 2
08 0
25 1 i
25* 3
16 4 k
21 5 j 21 16
k 指示当前序列中最小者
算法实现：
08 5 temp
16 21 25 25* 49 08 0 1 2 3 4 5
算法实现：
1.1.3 直接插入排序
void InsertSort (int r[ ], int n ) { // 假设关键字为整型，放在向量r[]中 int i, j, temp; for (i = 1;i< n;i++ ) { temp = r[i]; for(j = i;j>0;j- -) {//从后向前顺序比较，并依次后移 if ( temp < r[j-1] ) r[j] = r[j-1]; else break; } r[j] = temp; } }
输入n 个数给a[1] 到 a[n]
for j=1 to n-1
for i=1 to n-j
真 a[i]>a[i+1]
a[i]a[i+1]
输出a[1] 到 a[n]
main() { int a[11],i,j,t; printf("Input 10 numbers:\n"); for(i=1;i<11;i++) scanf("%d",&a[i]); printf("\n"); 假 for(j=1;j<=9;j++) for(i=1;i<=10-j;i++) if(a[i]>a[i+1]) {t=a[i]; a[i]=a[i+1]; a[i+1]=t;} printf("The sorted numbers:\n"); for(i=1;i<11;i++) printf("%d ",a[i]); }

c语言sort函数

c语言sort函数c语言中的sort函数是一种用于对数组进行排序的函数。

它使用的是一种称为“快速排序”的算法，这种算法是一种基于比较的排序算法，具有较高的效率和性能。

sort函数的声明如下：```c```参数解释：- base: 指向要排序的数组的指针。

- nitems: 数组中的元素个数。

- size: 每个元素的字节数。

sort函数使用递归的方式进行排序，其基本思想是选择一个基准元素，将数组分为左右两部分，左边的元素小于等于基准元素，右边的元素大于等于基准元素，然后对左右两部分递归调用sort函数，直到每个部分只有一个元素为止。

在这个排序算法中，我们需要传入一个比较函数，该函数用于比较两个元素的大小。

比较函数应该返回一个整数值，当第一个元素小于第二个元素时返回负数，当两个元素相等时返回0，当第一个元素大于第二个元素时返回正数。

根据比较结果，sort函数将适当地调整元素的位置，以实现排序的目的。

下面是一个使用sort函数对一个整型数组进行升序排序的示例：```c#include <stdio.h>#include <stdlib.h>return (*(int*)a - *(int*)b);int maiint arr[] = {5, 2, 8, 6, 3, 1, 7, 9, 4};int n = sizeof(arr) / sizeof(arr[0]);printf("升序排序后的数组：");for (int i = 0; i < n; i++)printf("%d ", arr[i]);}return 0;```输出结果为：123456789，表示数组已经按照升序排列完成。

```creturn strcmp(*(char**)a, *(char**)b);```sort函数是标准库函数，很多C语言开发环境都提供了该函数的实现。

快排算法代码

快排算法代码快速排序算法是一种用于排序元素的高效算法。

它的核心思想是选择一个基准元素，将其放入一个合适的位置，然后将序列分成两个部分，其中左半部分的所有元素都小于基准元素，右半部分的所有元素都大于基准元素。

在分得两个部分后，分别对左半部分和右半部分递归地应用快速排序算法，最终将序列排好序。

快速排序算法的优点在于其执行时间短，对内存的消耗较小，同时在处理大数据量时显示出其稳定的性能表现。

快速排序算法的实现需要通过编写代码来实现，以下是一个典型的快速排序算法的代码示例：``` void quicksort(int arr[], int left, intright) { int i = left, j = right, tmp; intpivot = arr[(left + right) / 2]; /* partition*/ while (i <= j) { while (arr[i] <pivot) i++; while (arr[j] >pivot) j--; if (i <= j){ tmp = arr[i]; arr[i] =arr[j]; arr[j] = tmp; i++; j--; } }; /* recursion */if (left < j) quicksort(arr, left, j); if (i < right) quicksort(arr, i, right); } ```上述代码是一个递归实现的快速排序算法，可以将一个整型数组按升序排列。

这段代码接受三个参数，分别是整型数组 `arr`、左端点 `left` 和右端点 `right`。

该代码的处理流程如下：1. 获取一个基准元素 `pivot`，从当前序列的中间位置开始选择。

2. 将该序列分成两个部分，其中左半部分的所有元素都小于等于基准元素，右半部分的所有元素都大于等于基准元素。

各种排序算法代码（C语言版）

各种排序算法代码（C语⾔版）选择排序#include <stdio.h>/** 选择排序* 稳定性：不稳定* 时间复杂度：O(N^2)**/void select_sort(int a[], int l, int r){for (int m_v, m_idx, t, i = l; i < r; ++i) {m_v = a[i]; m_idx = i;for (int j = i + 1; j < r; ++j) {if (m_v > a[j]) {m_v = a[j];m_idx = j;}}t = a[i]; a[i] = a[m_idx]; a[m_idx] = t;}}int main(void){int a[100];int n; scanf("%d", &n);for (int i = 0; i < n; ++i) scanf("%d", &a[i]);select_sort(a, 0, n);for (int i = 0; i < n; ++i) printf("%d ", a[i]);return0;}冒泡排序#include <stdio.h>/** 冒泡排序* 稳定性：稳定void bubble_sort(int a[], int l, int r){for (int i = l; i < r; ++i) {for (int j = l; j < r - i - 1; ++j) {if (a[j] > a[j + 1]) {int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;}}}}int main(void){int a[100];int n; scanf("%d", &n);for (int i = 0; i < n; ++i) scanf("%d", &a[i]); bubble_sort(a, 0, n);for (int i = 0; i < n; ++i) printf("%d ", a[i]);return0;}插⼊排序#include <stdio.h>/** 插⼊排序* 稳定性：稳定* 时间复杂度： O(N^2)**/void insert_sort(int a[], int l, int r){for (int tmp, j, i = l + 1; i < r; ++i) {tmp = a[i], j = i - 1;while (j >= l && tmp < a[j]) a[j+1] = a[j--]; a[j+1] = tmp;}}int main(void){for (int i = 0; i < n; ++i) scanf("%d", &a[i]); insert_sort(a, 0, n);for (int i = 0; i < n; ++i) printf("%d ", a[i]);return0;}希尔排序#include <stdio.h>/** 希尔排序* 稳定性：不稳定* 时间复杂度：O(N*logN)**/void shell_insert_sort(int a[], int l, int r, int d) {for (int tmp, j, i = l + d; i < r; ++i) {tmp = a[i], j = i - d;while (j >= l && tmp < a[j]) {a[j + d] = a[j];j -= d;}a[j + d] = tmp;}}void shell_sort(int a[], int l, int r){int d = (r - l) / 2;while (d >= 1) {shell_insert_sort(a, l, r, d);d /= 2;}}int main(void){int a[100];int n; scanf("%d", &n);for (int i = 0; i < n; ++i) scanf("%d", &a[i]); shell_sort(a, 0, n);for (int i = 0; i < n; ++i) printf("%d ", a[i]);归并排序/** 归并排序* 稳定性：稳定* 时间复杂度：O(N*logN)**/void merge(int a[], int n, int b[], int m, int t[]) {int i, j, k;i = j = k = 0;while (i < n && j < m) {if (a[i] < b[j]) t[k++] = a[i++];else t[k++] = b[j++];}while (i < n) t[k++] = a[i++];while (j < m) t[k++] = b[j++];}void my_merge_sort(int a[], int l, int r, int t[]) {int mid = (l + r) >> 1;int n = r - l;int i;if (l + 1 < r) {my_merge_sort(a, l, mid, t);my_merge_sort(a, mid, r, t);merge(a+l, mid-l, a+mid, r-mid, t);for (i = 0; i < n; ++i) a[i + l] = t[i];}}void merge_sort(int a[], int l, int r){int *t = (int *)malloc((r-l) * sizeof (int));my_merge_sort(a, l, r, t);free(t);}堆排序* 堆排序* 稳定性：不稳定* 时间复杂度：O(N*logN)**/// big top pilevoid heap_adjust(int a[], int fa, int n){int cd = fa * 2 + 1;while (cd < n) {if (cd + 1 < n && a[cd] < a[cd + 1]) cd++;if (a[fa] >= a[cd]) break;int tmp = a[fa];a[fa] = a[cd];fa = cd;cd = fa * 2 + 1;a[fa] = tmp;}}void build_heap(int a[], int n){// ignore leap nodefor (int i = (n - 1) / 2; i >= 0; --i) {heap_adjust(a, i, n);}}void heap_sort(int a[], int l, int r){build_heap(a + l, r - l);for (int tmp, i = r - 1; i > l; --i) {tmp = a[i]; a[i] = a[0]; a[0] = tmp;heap_adjust(a + l, 0, i);}}int main(void){int a[100];int n; scanf("%d", &n);for (int i = 0; i < n; ++i) scanf("%d", &a[i]); heap_sort(a, 0, n);return0;}快速排序/** 快速排序* 稳定性：不稳定* 时间复杂度：O(N*logN)**/void quick_sort(int a[], int l, int r){if (l + 1 >= r) return ;int low = l, high = r;int key = a[l];while (low < high) {while (low < high && a[--high] >= key); a[low] = a[high];while (low < high && a[++low] < key); a[high] = a[low];}a[low] = key;quick_sort(a, l, low);quick_sort(a, low+1, r);}基数排序/** 基数排序* 稳定性：稳定* 时间复杂度：O(d(n+radix)) [d个关键码，关键码的取值范围为radix] **/int tmp[100000000];void radix_sort(int arr[], int beg, int ed){static int a[9] = {1, 10, 100, 1000, 10000, 100000, 1000000};int cnt[10]; // 0~9⼗个数字int digit = 0; // 最⼤位数for (int i = beg; i < ed; ++i)while (arr[i] / a[digit + 1] > 0) digit++;for (int idx = 0; idx <= digit; ++idx) {for (int i = 0; i < 10; ++i) cnt[i] = 0; // 桶计数清零for (int i = beg; i < ed; ++i) cnt[ arr[i]/a[idx]%10 ]++; // 统计每个数字出现的次数// 前缀和统计每个数字前⾯的数字个数这样就可以知道每个数字应该排在第⼏位了for (int i = 1; i < 10; ++i) cnt[i] += cnt[i - 1];for (int i = ed - 1; i >= beg; --i) tmp[ --cnt[arr[i]/a[idx]%10] ] = arr[i];for (int i = beg, j = 0; i < ed; ++i, ++j) arr[i] = tmp[j];}}测试性能int a[100000000];double test(void(*fun)(int*, int, int), int range){for (int i = 0; i < range; ++i) a[i] = rand();clock_t start = clock();fun(a, 0, range);clock_t finish = clock();//for (int i = 0; i < range; ++i) printf("%d\n", a[i]);return ((double)finish - start) / CLOCKS_PER_SEC;}int main(){srand((unsigned)time(NULL));printf(" 数据范围堆排序归并排序希尔排序快速排序插⼊排序冒泡排序选择排序基数排序\n");for (int range = 100; range <= 100000; range *= 10) {printf("%9d %8.3f %8.3f %8.3f %8.3f %8.3f %8.3f %8.3f\n", range, test(heap_sort, range), test(merge_sort, range), test(shell_sort, range), test(quick_sort, range), test(insert_sort, range), test(bubble_sort, range), test(select_sort, range), test(radix_sort, range));}for (int range = 1000000; range <= 10000000; range *= 10) {printf("%9d %8.3f %8.3f %8.3f %8.3f %8.3f\n", range, test(heap_sort, range), test(merge_sort, range), test(shell_sort, range),test(quick_sort, range), test(radix_sort, range));}return0;。

c语言面试中常问的算法题目

c语言面试中常问的算法题目
在 C 语言面试中，常常会涉及一些算法题目，以下是一些常见
的算法题目及其解答：
1. 反转字符串：
题目，给定一个字符串，将其反转。

解答，可以使用两个指针，一个指向字符串的起始位置，另
一个指向字符串的末尾位置，然后交换两个指针所指向的字符，然
后两个指针向中间移动，重复这个过程直到两个指针相遇。

2. 判断字符串是否为回文串：
题目，给定一个字符串，判断它是否是回文串（正读和反读
都相同）。

解答，可以使用两个指针，一个指向字符串的起始位置，另
一个指向字符串的末尾位置，然后逐个比较两个指针所指向的字符，如果不相等则不是回文串。

3. 查找数组中的最大值和最小值：
题目，给定一个整数数组，找出数组中的最大值和最小值。

解答，可以使用两个变量分别保存当前的最大值和最小值，然后遍历数组，逐个比较并更新最大值和最小值。

4. 实现快速排序算法：
题目，给定一个整数数组，使用快速排序算法对数组进行排序。

解答，快速排序算法的基本思想是选择一个基准元素，将数组分为两部分，一部分小于基准元素，一部分大于基准元素，然后递归地对两部分进行排序。

5. 判断一个数是否为素数：
题目，给定一个整数，判断它是否为素数（只能被 1 和自身整除）。

解答，可以使用循环遍历从 2 到该数的平方根，逐个判断是否能整除该数，如果能整除则不是素数。

以上是一些常见的在 C 语言面试中经常被问到的算法题目及其解答。

当然，还有很多其他的算法题目，希望这些题目能帮助您更好地准备面试。

无序中位数 c语言

无序中位数 c语言无序中位数是指在一个无序数组中，位于中间位置的元素。

对于一个含有奇数个元素的无序数组，中位数就是数组中间位置的元素；对于一个含有偶数个元素的无序数组，中位数是位于中间位置两个元素的平均值。

要找到无序中位数，首先需要对数组进行排序。

常见的排序算法有冒泡排序、插入排序、选择排序、快速排序、归并排序等。

下面以快速排序为例，介绍如何找到无序中位数。

快速排序的基本思想是通过一趟排序将待排序的数组分割成独立的两部分，其中一部分的所有元素都比另一部分的所有元素小。

然后再按此方法对这两部分分别进行快速排序，最终整个序列就有序了。

具体步骤如下：1. 选取一个基准元素，可以选择数组的第一个元素作为基准。

2. 将数组分成两部分，使得左边的元素都小于等于基准元素，右边的元素都大于等于基准元素。

3. 对左右两部分递归地进行快速排序。

4. 当左右两部分都有序时，整个数组就有序了。

在快速排序的过程中，可以通过比较基准元素的位置和数组长度的关系来确定中位数的位置。

若基准元素的位置恰好是数组长度的一半，则该基准元素就是中位数；若基准元素的位置小于数组长度的一半，则中位数位于右半部分；若基准元素的位置大于数组长度的一半，则中位数位于左半部分。

下面是使用C语言实现的快速排序算法代码：```c#include <stdio.h>// 交换数组中的两个元素void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;}// 快速排序void quickSort(int arr[], int low, int high) {if (low < high) {int pivot = arr[low]; // 选取第一个元素作为基准int i = low, j = high;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}while (i < j && arr[i] <= pivot) {i++;}if (i < j) {swap(&arr[i], &arr[j]);}}swap(&arr[low], &arr[i]); // 将基准元素放到正确的位置 quickSort(arr, low, i - 1); // 递归处理左半部分quickSort(arr, i + 1, high); // 递归处理右半部分}}// 打印数组void printArray(int arr[], int size) {for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");}int main() {int arr[] = {9, 2, 7, 6, 3, 1, 5, 4, 8};int size = sizeof(arr) / sizeof(arr[0]);printf("原数组：");printArray(arr, size);quickSort(arr, 0, size - 1);printf("排序后的数组：");printArray(arr, size);int median;if (size % 2 == 0) {median = (arr[size / 2 - 1] + arr[size / 2]) / 2; // 偶数个元素取中间两个元素的平均值} else {median = arr[size / 2]; // 奇数个元素取中间元素}printf("中位数：%d\n", median);return 0;}```以上代码实现了快速排序算法，并找到了无序数组的中位数。

CC++实现快速排序算法的思路及原理解析

CC++实现快速排序算法的思路及原理解析⽬录快速排序2. 实现原理3. 动态演⽰4. 完整代码5. 结果展⽰6. 算法分析快速排序1. 算法思想快速排序的基本思想：通过⼀趟排序将待排记录分隔成独⽴的两部分，其中⼀部分记录的关键字均⽐另⼀部分的关键字⼩，则可分别对这两部分记录继续进⾏排序，以达到整个序列有序。

2. 实现原理2.1、设置两个变量 low、high，排序开始时：low=0，high=size-1。

2.2、整个数组找基准正确位置，所有元素⽐基准值⼩的摆放在基准前⾯，所有元素⽐基准值⼤的摆在基准的后⾯默认数组的第⼀个数为基准数据，赋值给key，即key=array[low]。

因为默认数组的第⼀个数为基准，所以从后⾯开始向前搜索（high–），找到第⼀个⼩于key的array[high]，就将 array[high] 赋给 array[low]，即 array[low] = array[high]。

（循环条件是 array[high] >= key；结束时 array[high] < key）此时从前⾯开始向后搜索（low++），找到第⼀个⼤于key的array[low]，就将 array[low] 赋给 array[high]，即 array[high] = array[low]。

（循环条件是 array[low] <= key；结束时 array[low] > key）循环 2-3 步骤，直到 low=high，该位置就是基准位置。

把基准数据赋给当前位置。

2.3、第⼀趟找到的基准位置，作为下⼀趟的分界点。

2.4、递归调⽤（recursive）分界点前和分界点后的⼦数组排序，重复2.2、2.3、2.4的步骤。

2.5、最终就会得到排序好的数组。

3. 动态演⽰4. 完整代码三个函数基准插⼊函数：int getStandard(int array[],int low,int high)（返回基准位置下标）递归排序函数：void quickSort(int array[],int low,int high)主函数：int main()#include <stdio.h>#include <stdlib.h>void display(int* array, int size) {for (int i = 0; i < size; i++) {printf("%d ", array[i]);}printf("\n");}int getStandard(int array[], int i, int j) {// 基准数据int key = array[i];while (i < j) {// 因为默认基准是从左边开始，所以从右边开始⽐较// 当队尾的元素⼤于等于基准数据时,就⼀直向前挪动 j 指针while (i < j && array[j] >= key) {j--;}// 当找到⽐ array[i] ⼩的时，就把后⾯的值 array[j] 赋给它if (i < j) {array[i] = array[j];}// 当队⾸元素⼩于等于基准数据时,就⼀直向后挪动 i 指针while (i < j && array[i] <= key) {i++;}// 当找到⽐ array[j] ⼤的时，就把前⾯的值 array[i] 赋给它if (i < j) {array[j] = array[i];}}// 跳出循环时 i 和 j 相等,此时的 i 或 j 就是 key 的正确索引位置// 把基准数据赋给正确位置array[i] = key;return i;}void QuickSort(int array[], int low, int high) {// 开始默认基准为 lowif (low < high) {// 分段位置下标int standard = getStandard(array, low, high);// 递归调⽤排序// 左边排序QuickSort(array, low, standard - 1);// 右边排序QuickSort(array, standard + 1, high);}}// 合并到⼀起快速排序// void QuickSort(int array[], int low, int high) {// if (low < high) {// int i = low;// int j = high;// int key = array[i];// while (i < j) {// while (i < j && array[j] >= key) {// j--;// }// if (i < j) {// array[i] = array[j];// }// while (i < j && array[i] <= key) {// i++;// }// if (i < j) {// array[j] = array[i];// }// }// array[i] = key;// QuickSort(array, low, i - 1);// QuickSort(array, i + 1, high);// }// }int main() {int array[] = {49, 38, 65, 97, 76, 13, 27, 49, 10};int size = sizeof(array) / sizeof(int);// 打印数据printf("%d \n", size);QuickSort(array, 0, size - 1);display(array, size);// int size = 20;// int array[20] = {0}; // 数组初始化// for (int i = 0; i < 10; i++) { // 数组个数// for (int j = 0; j < size; j++) { // 数组⼤⼩// array[j] = rand() % 1000; // 随机⽣成数⼤⼩ 0~999// }// printf("原来的数组：");// display(array, size);// QuickSort(array, 0, size - 1);// printf("排序后数组：");// display(array, size);// printf("\n");// }return 0;}5. 结果展⽰（递归调⽤，不好展⽰每次排序结果）6. 算法分析时间复杂度：最好： O ( n l o g 2 n ) O(n log_{2} n) O(nlog2n)最坏： O ( n 2 ) O(n^2) O(n2)平均： O ( n l o g 2 n ) O(n log_{2} n) O(nlog2n)空间复杂度： O ( n l o g 2 n ) O(n log_{2} n) O(nlog2n)稳定性：不稳定到此这篇关于C/C++实现快速排序算法的思路及原理解析的⽂章就介绍到这了,更多相关C++实现快速排序算法内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持！。

c++min函数

c min函数
c语言min函数用法
min函数
用于求数组中的最小值。

暂时用到的语法形式有3种：
C = min(A)；
C = min(A, B)；
C = min(A, [], dim)；
函数是C 库中实现的快速排序算法，需要四个参数。

第一个参数是需要排序的数组的基地址，因为是void * 类型，所以此函数可以给任何类型的数组进行排序。

第二个参数是待排序的数量。

第三个是单个数组元素的大小，即字节数。

第四个参数是一个指向函数的指针，其作用是规定排序的规则。

函数min的定义域要求每个元素都有意义min{x，√x)的定义域不是全体实数，是全体非负数。

函数min的定义是指所含元素的函数组中，在共公定义域上的最小值组成的函数。

在数学里min是最小值如果表示是单位数学里min是指分钟min英文是最小限度或分钟的意思。

C语言常用算法大全

C语言常用算法大全1.排序算法-冒泡排序：依次比较相邻的两个元素，如果顺序不对则交换，每轮找出一个最大或最小的元素-选择排序：从未排序的元素中选择最小或最大的放到已排序的最后，以此类推-插入排序：将未排序的元素插入到已排序的合适位置，从后向前进行比较和交换-快速排序：选择一个基准元素，将小于基准元素的放在左边，大于基准元素的放在右边，然后对左右两边递归地进行快速排序-归并排序：将待排序的序列不断划分为左右两部分，分别排序后再将排序好的左右两部分按顺序合并-堆排序：构建大顶堆，将堆顶元素与末尾元素交换，然后重新调整堆，重复这个过程直到排序完成2.查找算法-顺序查找：从给定的元素序列中逐个比较，直到找到目标元素或遍历完整个序列-二分查找：对于有序序列，在序列的中间位置比较目标元素和中间元素的大小关系，通过每次缩小一半的范围来查找目标元素-插值查找：根据目标元素与有序序列的最小值和最大值的比例推测目标元素所在的位置，然后递归地进行查找-斐波那契查找：根据斐波那契数列的性质来确定目标元素所在的位置，然后递归地进行查找3.图算法-深度优先（DFS）：从图的一些顶点出发，依次访问其未被访问过的邻接顶点，直到所有顶点都被访问过为止-广度优先（BFS）：从图的一些顶点出发，逐层遍历图的顶点，直到所有顶点都被访问过为止- 最小生成树算法：Prim算法和Kruskal算法，用于找到连接图中所有顶点的最小权值边，构成一棵包含所有顶点的生成树- 最短路径算法：Dijkstra算法和Floyd-Warshall算法，用于找到图中两个顶点之间的最短路径-拓扑排序：用于有向无环图（DAG）中的顶点排序，确保排序后的顶点满足所有依赖关系-关键路径算法：找出网络中的关键路径，即使整个工程完成的最短时间4.字符串算法- KMP算法：通过预处理模式串构建next数组，利用next数组在匹配过程中跳过一部分不可能匹配的子串- Boyer-Moore算法：从模式串的末尾开始匹配，利用坏字符和好后缀规则进行跳跃匹配- Rabin-Karp算法：利用哈希函数对主串和匹配串的子串进行哈希计算，然后比较哈希值是否相等- 字符串匹配算法：BM算法、Shift-And算法、Sunday算法等，用于寻找模式串在主串中的出现位置5.动态规划算法-最长公共子序列（LCS）：用于寻找两个序列中最长的公共子序列-最长递增子序列（LIS）：用于寻找给定序列中最长的递增子序列-0-1背包问题：将有限的物品放入容量为C的背包中，使得物品的总价值最大-最大子数组和：用于求解给定数组中连续子数组的最大和-最大正方形：在给定的0-1矩阵中，找出只包含1的最大正方形的边长这些算法是在C语言中常用的算法，它们涵盖了排序、查找、图、字符串和动态规划等多个领域。

排序算法实验报告

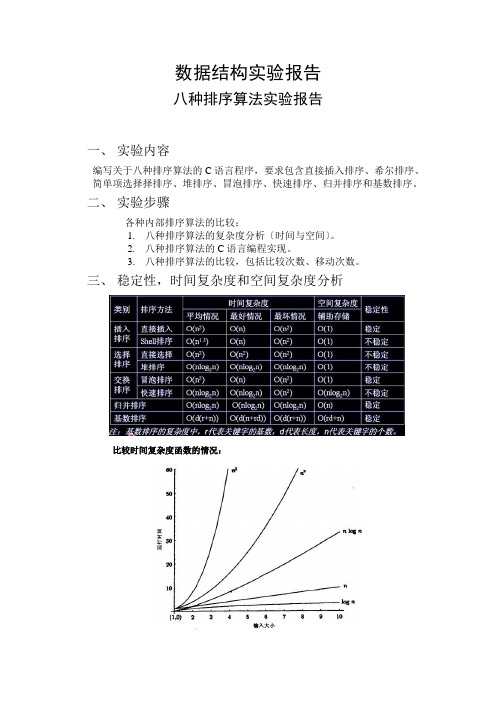
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序，要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。

二、实验步骤各种内部排序算法的比较：1.八种排序算法的复杂度分析〔时间与空间〕。

2.八种排序算法的C语言编程实现。

3.八种排序算法的比较，包括比较次数、移动次数。

三、稳定性，时间复杂度和空间复杂度分析比较时间复杂度函数的情况：时间复杂度函数O(n)的增长情况所以对n较大的排序记录。

一般的选择都是时间复杂度为O(nlog2n)的排序方法。

时间复杂度来说：(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序；(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序；(3)O(n1+§))排序,§是介于0和1之间的常数。

希尔排序(4)线性阶(O(n))排序基数排序，此外还有桶、箱排序。

说明：当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O〔n〕；而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O〔n2〕；原表是否有序，对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

稳定性：排序算法的稳定性:假设待排序的序列中，存在多个具有相同关键字的记录，经过排序，这些记录的相对次序保持不变，则称该算法是稳定的；假设经排序后，记录的相对次序发生了改变，则称该算法是不稳定的。

稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。

基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。

另外，如果排序算法稳定，可以防止多余的比较；稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

一种快速排序算法的实现及其应用

人工，人们需要对每一份数据进行逐一对比，求参要与者精神高度集中，而大量数据的排序往往会耗费相当长的时间。在计算机出现后，由于其响应快速、
外部排序的应用已大大减少。内部排序按所用策略
不同，为插入排序、择排序、换排序、分选交归并排序和基数排序等ｌ。２Ｊ
第５２卷第２期
２１０２年２月
电讯技术
ＴｅｅｏｌｃｍｍｕｃｔｏｇｎｅｉｎｉａｉｎＥｎｉｅｒｎｇ
Ｖ０．２Ｎ．１５ｏ２
Ｆｂ．２０２ｅ１
文章编号：０１９Ｘ２１）２２５５１０ —８３（０２０ —０２ —０
一
种快速排序算法的实现及其应用
黎佩南
（中国西南电子技术研究所，成都６０３）１０６
摘
要：绍了一种快速的排序方法—— 堆排序。以一个简单的实例结合完全二叉树说明了该算法介
的原理，出了利用Ｃ语言实现该算法的代码，时间复杂度和辅助存储空间的角度分析了与其他给从
排序算法相比较的优劣。实验表明，对大量数据进行排序时，在堆排序算法效率较高。
关键词：排序算法；快速排序；堆排序；间复杂度；时辅助存储空间中图分类号：Ｐ１Ｔ３文献标志码：Ａｄｉ１．９９ｊｉｎ１０ —８３．０２０．２ｏ：０３６／．ｓ．０１９ｘ２１．２０２ｓ

算法 c语言实现

算法 c语言实现在计算机科学中，算法是一种通过计算来解决问题的有序集合。

它们是计算机程序的基础，用于执行各种计算任务。

算法可以通过多种方式实现，其中一种常见的方式是使用C语言。

C语言是一种高效且强大的编程语言，特别适合用于实现算法。

C语言中的指针和数组等特性使其能够访问计算机内存的任何位置。

这使得C语言非常适合实现复杂的算法，如快速排序，归并排序，图形算法等。

下面是一些常见算法的C语言实现：1. 快速排序算法：void quicksort(int arr[], int left, int right) {int i = left, j = right;int tmp;int pivot = arr[(left + right) / 2];/* partition */while (i <= j) {while (arr[i] < pivot)i++;while (arr[j] > pivot)j--;if (i <= j) {tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;i++;j--;}};/* recursion */if (left < j)quicksort(arr, left, j);if (i < right)quicksort(arr, i, right);}2. 归并排序算法：void merge(int arr[], int l, int m, int r) { int i, j, k;int n1 = m - l + 1;int n2 = r - m;/* create temp arrays */int L[n1], R[n2];/* Copy data to temp arrays L[] and R[] */for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1+ j];/* Merge the temp arrays back into arr[l..r]*/ i = 0; // Initial index of first subarrayj = 0; // Initial index of second subarrayk = l; // Initial index of merged subarraywhile (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;}else {arr[k] = R[j];j++;}k++;}/* Copy the remaining elements of L[], if there are any */ while (i < n1) {arr[k] = L[i];i++;k++;}/* Copy the remaining elements of R[], if there are any */ while (j < n2) {arr[k] = R[j];j++;k++;}}/* l is for left index and r is right index of the sub-array of arr to be sorted */void mergeSort(int arr[], int l, int r) {if (l < r) {// Same as (l+r)/2, but avoids overflow for// large l and hint m = l+(r-l)/2;// Sort first and second halvesmergeSort(arr, l, m);mergeSort(arr, m+1, r);merge(arr, l, m, r);}}3. 图形算法中的Dijkstra算法：#define V 9int minDistance(int dist[], bool sptSet[]) { int min = INT_MAX, min_index;for (int v = 0; v < V; v++)if (sptSet[v] == false && dist[v] <= min)min = dist[v], min_index = v;return min_index;}void printSolution(int dist[], int n) {printf('Vertex Distance from Source');for (int i = 0; i < V; i++)printf('%d tt %d', i, dist[i]);}void dijkstra(int graph[V][V], int src) {int dist[V];bool sptSet[V];for (int i = 0; i < V; i++)dist[i] = INT_MAX, sptSet[i] = false;dist[src] = 0;for (int count = 0; count < V-1; count++) {int u = minDistance(dist, sptSet);sptSet[u] = true;for (int v = 0; v < V; v++)if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX&& dist[u]+graph[u][v] < dist[v])dist[v] = dist[u] + graph[u][v];}printSolution(dist, V);}这些是常见算法的C语言实现。

c语言常见排序算法

常见的C语言排序算法有以下几种：
1. 冒泡排序（Bubble Sort）：比较相邻的元素，如果前一个元素大于后一个元素，则交换它们的位置，重复这个过程直到整个序列有序。

2. 插入排序（Insertion Sort）：将未排序的元素逐个插入到已排序序列中的正确位置，直到整个序列有序。

3. 选择排序（Selection Sort）：每次从未排序的元素中选择最小的元素，将其放到已排序序列的末尾，重复这个过程直到整个序列有序。

4. 快速排序（Quick Sort）：选择一个基准元素，将序列分成两部分，一部分小于等于基准元素，一部分大于基准元素，然后对两部分递归地进行快速排序。

5. 归并排序（Merge Sort）：将序列分成两部分，分别对两部分进行归并排序，然后将两个有序的子序列合并成一个有序的序列。

6. 堆排序（Heap Sort）：将序列构建成一个最大堆，然后将堆顶元素与堆末尾元素交换，重复这个过程直到整个序列有序。

7. 希尔排序（Shell Sort）：将序列按照一定的间隔分成若干个子序列，对每个子序列进行插入排序，然后逐渐减小间隔直到间隔为1，最后对整个序列进行插入排序。

8. 计数排序（Counting Sort）：统计序列中每个元素出现的次数，然后按照元素的大小顺序将它们放入一个新的序列中。

9. 基数排序（Radix Sort）：按照元素的个位、十位、百位等依次进行排序，直到所有位数都排完为止。

以上是常见的C语言排序算法，每种算法都有其特点和适用场景，选择合适的排序算法可以提高排序效率。

快速排序（C语言）-解析

快速排序（C语⾔）-解析快速排序快速排序是⼀种排序算法，对包含 n 个数的输⼊数组，最坏情况运⾏时间为O（n2）。

虽然这个最坏情况运⾏时间⽐较差，但快速排序通常是⽤于排序的最佳的实⽤选择，这是因为其平均性能相当好：期望的运⾏时间为O（nlgn），且O（nlgn）记号中隐含的常数因⼦很⼩。

另外，它还能够进⾏就地排序，在虚存环境中也能很好的⼯作。

快速排序（Quicksort）是对的⼀种改进。

快速排序由C. A. R. Hoare在1962年提出。

它的基本思想是：通过⼀趟排序将要排序的数据分割成独⽴的两部分，其中⼀部分的所有数据都⽐另外⼀部分的所有数据都要⼩，然后再按此⽅法对这两部分数据分别进⾏快速排序，整个排序过程可以进⾏，以此达到整个数据变成有序。

像合并排序⼀样，快速排序也是采⽤分治模式的。

下⾯是对⼀个典型数组A[p……r]排序的分治过程的三个步骤：分解：数组 A[p……r]被划分为两个（可能空）⼦数组 A[p……q-1] 和 A[q+1……r] ，使得 A[p……q-1] 中的每个元素都⼩于等于 A(q) , ⽽且，⼩于等于 A[q+1……r] 中的元素。

⼩标q也在这个划分过程中进⾏计算。

解决：通过递归调⽤快速排序，对于数组 A[p……q-1] 和 A[q+1……r] 排序。

合并：因为两个⼦数组是就地排序的，将它们的合并不需要操作：整个数组 A[p……r] 已排序。

下⾯的过程实现快速排序(伪代码)：QUICK SORT（A，p，r）1if p<r2 then q<-PARTITION(A,p,r)3 QUICKSORT(A,p,q-1)4 QUICKSORT(A,q+1,r)为排序⼀个完整的数组A，最初的调⽤是QUICKSORT（A，1，length[A]）。

数组划分：快速排序算法的关键是PARTITION过程，它对⼦数组 A[p……r]进⾏就地重排(伪代码)：PARTITION（A，p，r）1 x <- A[r]2 i <- p-13for j <- p to r-14do if A[j]<=x5 then i <- i+16 exchange A[i] <-> A[j]7 exchange A[i + 1] <-> A[j]8return i+1排序演⽰⽰例假设⽤户输⼊了如下数组：下标012345数据627389创建变量i=0（指向第⼀个数据）, j=5(指向最后⼀个数据), k=6(为第⼀个数据的值)。

快速排序法c语言代码

快速排序法c语言代码快速排序法是一种高效的排序算法，它的核心思想是分治法，将一个大问题分解成若干个小问题，然后递归地解决每个小问题。

下面是快速排序法的C语言代码实现：```c#include <stdio.h>void quick_sort(int a[], int left, int right){int i = left, j = right;int pivot = a[(left + right) / 2]; //选择中间的数作为基准值while (i <= j){while (a[i] < pivot)i++;while (a[j] > pivot)j--;if (i <= j){//交换a[i]和a[j]int temp = a[i];a[i] = a[j];a[j] = temp;i++;j--;}}if (left < j) //递归排序左半部分quick_sort(a, left, j);if (i < right) //递归排序右半部分quick_sort(a, i, right);}int main(){int a[] = { 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5 };int n = sizeof(a) / sizeof(a[0]); //计算数组的长度quick_sort(a, 0, n - 1);for (int i = 0; i < n; i++)printf('%d ', a[i]);printf('');return 0;}```快速排序法是一种常用的排序算法，它的时间复杂度为O(nlogn)，空间复杂度为O(1)，是一种不占用额外空间的原地排序算法。

但是它的最坏时间复杂度为O(n^2)，当待排序的数列已经基本有序时，快速排序法的效率会大大降低。

因此，为了保证快速排序法的效率，需要对选择基准值的方法进行优化。

C语言常见排序算法.ppt

1.1.2 快速排序
算法实例：
始关键字
pivotkey 21 25 low
49 25* 16 08 high
一次交换
21
二次交换
三次交换
high-1 完成一趟排序
08 25 low
49 25* 16
high
08
49 25* 16 25
low
high
08 16 49 25*
25
low
08 16
low
常见排序算法
1.1 常见的排序算法
冒泡排序快速排序直接插入排序希尔排序选择排序堆排序归并排序
1.1.1 冒泡排序
算法描述
设待排序记录序列中的记录个数为n 一般地，第i趟起泡排序从1到n-i+1 依次比较相邻两个记录的关键字，如果发生逆序，则交换之其结果是这n-i+1个记录中，关键字最大的记录被交换到第n-i+1的位置上，最多作n-1趟。
08 16
21
high 25* 49 25
high 25* 49 25
low high
1.1.2 快速排序
算法实例：
完成一趟排序
08 16
21 25* 49 25
分别进行快速排序有序序列
08 16
21 25* 25 49
08 16
21 25* 25 49
11
1.1.2 快速排序
算法分析：
快速排序是一个递归过程; 利用序列第一个记录作为基准，将整个序列划分为左右两个子序列。只要是关键字小于基准记录关键字的记录都移到序列左侧；快速排序的趟数取决于递归树的高度。如果每次划分对一个记录定位后, 该记录的左侧子序列与右侧子序列的长度相同, 则下一步将是对两个长度减半的子序列进行排序, 这是最理想的情况

C语言中的数据结构与算法实现

C语言中的数据结构与算法实现在计算机科学中，数据结构和算法是构建程序的基础。

C语言作为一种强大而广泛使用的编程语言，提供了丰富的库函数和语法特性来支持数据结构和算法的实现。

本文将讨论C语言中常见的数据结构和算法，并通过示例代码来展示其实现方法。

一、线性数据结构1. 数组(Array)数组是C语言中最基本的数据结构之一，能够存储相同类型的数据元素。

通过索引，可以快速访问数组中的任意元素。

以下是一个简单的数组示例：```c#include <stdio.h>int main() {int arr[5] = {1, 2, 3, 4, 5};for(int i=0; i<5; i++) {printf("%d ", arr[i]);}return 0;}```2. 链表(Linked List)链表是一种动态数据结构，由节点组成，并通过指针相互连接。

链表具有灵活性，能够高效地插入和删除节点。

以下是一个简单的链表示例：```c#include <stdio.h>#include <stdlib.h>typedef struct Node {int data;struct Node* next;} Node;int main() {Node* head = NULL;Node* second = NULL;Node* third = NULL;// 分配内存并赋值head = (Node*)malloc(sizeof(Node));second = (Node*)malloc(sizeof(Node));third = (Node*)malloc(sizeof(Node)); head->data = 1;head->next = second;second->data = 2;second->next = third;third->data = 3;third->next = NULL;// 遍历链表Node* ptr = head;while (ptr != NULL) {printf("%d ", ptr->data);ptr = ptr->next;}return 0;}```二、非线性数据结构1. 栈(Stack)栈是一种后进先出（LIFO）的数据结构，只允许在栈的顶部进行插入和删除操作。

C语言排序算法

i=2
49 25* 16 08 2 3 4 5
49
i=3
21
0
25 1
49 25* 16 2 3 4
08 5
25*
6.1.3 直接插入排序
实用例子：
i=4
21 25 25* 49 16 08 0 1 2 3 4 21 25 25* 49 08 1 2 3 4
16 5 temp
i= 5 完成
16 0
49
2 j 49
08
0
25* 3 49 25
16 4
21
5
08
25
25*
16
21
i k 49
j 25* 25
08
25
25*
16
21
6.1.5 选择排序
算法实例：
08 0
25 1 i
49 2
25* 3
16 4 k
21 5 j 21 16
k 指示当前序列中最小者
6.1.5 选择排序
算法实现：
49 49
25 25
16
21
low
25*
high
6.1.2 快速排序
算法实例：
完成一趟排序 08 16 21 25* 49 25
分别进行快速排序
08
16
21
25*
25
49
有序序列 08 16 21 25* 25 49
10
6.1.2 快速排序
算法分析：
快速排序是一个递归过程; 利用序列第一个记录作为基准，将整个序列划分为左右两个子序列。只要是关键字小于基准记录关键字的记录都移到序列左侧；
快速排序的趟数取决于递归树的高度。

C+常用经典算法及其实现

C+常用经典算法及其实现 This manuscript was revised by the office on December 10, 2020.常用算法经典代码（C++版）一、快速排序void qsort(int x,int y) a[n]数组中{int h=x,r=y;int m=a[(x+y)>>1]; a[n]数组中{for(int i=1;i<n;i++) a[n]数组中{for(int i=1;i<n;i++) n。

注：图不一定是连通的{d);d);d);d);d);d);child=l; ather=i; child=r; ather=i; a=a[l].da+a[r].da;a>a[s].da)&&(a[s].father==0)) ather=0,说明这个结点还不是别个结点mins=s; ather==0) {a[x].code=”“;}ather].lchild==x)a[x].code=a[a[x].father].code+'0';if(a[a[x].father].rchild==x) a[x].code=a[a[x].father].code+'1';if(a[x].lchild!=0)inorder(a[x].lchild);child==0)&&(a[x].rchild==0))a<<':'<<a[x].code<<endl; if(a[x].rchild!=0) inorder(a[x].rchild);rom=1;elist[i].to=i+1;elist[i].w=a[1][i+1];}for (int i=1;i<=n-1;i++)<elist[m].w) m=j;if(m!=i) >a[elist[i].to][elist[j].to])elist[j].w=a[elist[i].to][elist[j].to];}}for(int i=1;i<=n-1;i++);}如果要求出哪些边构成最小生成树，在更新第i+1至n-1条边到已经生成的树中最小距离时(上面代码中加粗的部分)，还要加上elist[j].from=elist[i].to;语句，即在更新权值时，还应该更新起点。