第6章 模糊神经网络-2015
北京交通大学研究生课程(神经网络、模糊控制与专家系统)第七章

p
fi wkjiuik i1
aj
1
1 e
f
j
第二节 模糊神经网络控制
二、基本功能和函数关系
第一层:将输入变量值直接传送到下层
fj1 uj1 wj1i 1
aj1 fj1 uj1 xj j 1,2,L n
mji:一、二层神经元之间的连接权值wji2;
ji:看作是与S函数相类似的一个斜率参数。
注 : 若 用 一 组 节 点 完 成 一 个 隶 属 度 函 数 , 则 每 一 个 节 点 的 函 数 可 以 是 标 准 的 形 式 ( 如 S 函 数 ) , 且 整 个 子 网 络 用 标 准 学 习 算 法 ( 如 反 传 法 ) 进 行 离 线 训 练 实 现 期 望 的 隶 属 函 数 。
缺点: 当环境发生变化时,缺乏自我调节和自学习的能力。
解决方法之一:Sugeno提出将规则的自组织问题转化为参 数估计问题。但仍有主观性。
如何把学习机制引入到模糊控制中来?
第一节 集成智能控制系统简介
1. 模糊神经网络系统(FNN)
神经网络由大量连接的神经处理单元组成的,具有高 度的非线性映射能力和自学习能力,能够从样本数据中进 行学习和泛化,计算速度快。
f
5
j
wj5i ui5
(mj5i ji5)ui5
i
i
aj5
f
5
j
ji5ui5
i
则
第
四
层
节
点
与
第
五
层
节
点
之
间
的
连
(完整word版)自适应滤波LMS算法及RLS算法及其仿真

自适应滤波第1章绪论 (1)1.1自适应滤波理论发展过程 (1)1. 2自适应滤波发展前景 (2)1. 2. 1小波变换与自适应滤波 (2)1. 2. 2模糊神经网络与自适应滤波 (3)第2章线性自适应滤波理论 (4)2. 1最小均方自适应滤波器 (4)2. 1. 1最速下降算法 (4)2.1.2最小均方算法 (6)2. 2递归最小二乘自适应滤波器 (7)第3章仿真 (12)3.1基于LMS算法的MATLAB仿真 (12)3.2基于RLS算法的MATLAB仿真 (15)组别: 第二小组组员: 黄亚明李存龙杨振第1章绪论从连续的(或离散的)输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波。
相应的装置称为滤波器。
实际上, 一个滤波器可以看成是一个系统, 这个系统的目的是为了从含有噪声的数据中提取人们感兴趣的、或者希望得到的有用信号, 即期望信号。
滤波器可分为线性滤波器和非线性滤波器两种。
当滤波器的输出为输入的线性函数时, 该滤波器称为线性滤波器, 当滤波器的输出为输入的非线性函数时, 该滤波器就称为非线性滤波器。
自适应滤波器是在不知道输入过程的统计特性时, 或是输入过程的统计特性发生变化时, 能够自动调整自己的参数, 以满足某种最佳准则要求的滤波器。
1. 1自适应滤波理论发展过程自适应技术与最优化理论有着密切的系。
自适应算法中的最速下降算法以及最小二乘算法最初都是用来解决有/无约束条件的极值优化问题的。
1942年维纳(Wiener)研究了基于最小均方误差(MMSE)准则的在可加性噪声中信号的最佳滤波问题。
并利用Wiener. Hopf方程给出了对连续信号情况的最佳解。
基于这~准则的最佳滤波器称为维纳滤波器。
20世纪60年代初, 卡尔曼(Kalman)突破和发展了经典滤波理论, 在时间域上提出了状态空间方法, 提出了一套便于在计算机上实现的递推滤波算法, 并且适用于非平稳过程的滤波和多变量系统的滤波, 克服了维纳(Wiener)滤波理论的局限性, 并获得了广泛的应用。
Hopfield神经网络ppt课件

2)保证所有要求记忆的稳定平衡点都能收敛 到自己;
3)使伪稳定点的数目尽可能的少; 4)使稳定点的吸引域尽可能的大。 MATLAB函数
[w,b]=solvehop(T);
.
23
连续性的Hopfield网络
CHNN是在DHNN的基础上提出的,它的原理
.
34
几点说明:
1)能量函数为反馈网络的重要概念。 根据能量函数可以方便的判断系统的稳 定性;
2)能量函数与李雅普诺夫函数的区 别在于:李氏被限定在大于零的范围内, 且要求在零点值为零;
3)Hopfield选择的能量函数,只是 保证系统稳定和渐进稳定的充分条件, 而不是必要条件,其能量函数也不是唯 一的。
1、激活函数为线性函数时
2、激活函数为非线性函数时
.
29
当激活函数为线性函数时,即
vi ui 此时系统的状态方程为:
U AU B 其中A 1 WB。
R 此系统的特征方程为:
A I 0 其中I为单位对角阵。通过对解出的特征值1, 2,, r 的不同情况,可以得到不同的系统解的情况。
.
霍普菲尔德(Hopfield) 神经网络
1、网络结构形式 2、非线性系统状态演变的形式 3、离散型的霍普菲尔德网络(DHNN) 4、连续性的霍普菲尔德网络(CHNN)
.
1
网络结构形式
Hopfield网络是单层对称全反馈网络,根据激 活函数选取的不同,可分为离散型和连续性两种 ( DHNN,CHNN)。 DHNN:作用函数为hadlim,主要用于联想记忆。 CHNN:作用函数为S型函数,主要用于优化计算。
.
19
权值修正的其它方法
模糊神经网络的基本原理与应用概述

模糊神经网络的基本原理与应用概述摘要:模糊神经网络(FNN)是将人工神经网络与模糊逻辑系统相结合的一种具有强大的自学习和自整定功能的网络,是智能控制理论研究领域中一个十分活跃的分支,因此模糊神经网络控制的研究具有重要的意义。
本文旨在分析模糊神经网络的基本原理及相关应用。
关键字:模糊神经网络,模糊控制,神经网络控制,BP算法。
Abstract:A fuzzy neural network is a neural network and fuzzy logic system with the combination of a powerful. The self-learning and self-tuning function of the network, is a very intelligent control theory research in the field of active branches. So the fuzzy neural network control research has the vital significance. The purpose of this paper is to analysis the basic principle of fuzzy neural networks and related applications.Key Words: Fuzzy Neural Network, Fuzzy Control, Neural Network Control, BP Algorithm.1人工神经网络的基本原理与应用概述1.1人工神经网络的概念人工神经网络(Artificial Neural Network,简称ANN)是由大量神经元通过极其丰富和完善的联接而构成的自适应非线性动态系统,它使用大量简单的相连的人工神经元来模仿生物神经网络的能力,从外界环境或其它神经元获得信息,同时加以简单的运算,将结果输出到外界或其它人工神经元。
模糊神经网络算法研究

模糊神经网络算法研究一、引言模糊神经网络算法是一种结合了模糊逻辑和神经网络的计算模型,用于处理模糊不确定性和非线性问题。
本文将通过研究模糊神经网络的原理、应用和优化方法,探索其在解决实际问题中的潜力和局限性。
二、模糊神经网络算法原理1. 模糊逻辑的基本概念模糊逻辑是处理模糊信息的数学工具,其中包括模糊集合、隶属函数、模糊关系等概念。
模糊集合用来描述不确定或模糊的概念,而隶属函数表示一个元素属于某个模糊集合的程度。
模糊关系则用于表达模糊集合之间的关系。
2. 神经网络的基本原理神经网络是一种由人工神经元构成的计算系统,以模仿生物神经系统的运作方式。
其中的神经元接收输入信号、进行加权处理,并通过激活函数输出计算结果。
神经网络通过训练和学习来调整连接权值,以实现对输入输出之间的映射关系建模。
3. 模糊神经网络的结构和运算模糊神经网络结合了模糊逻辑的不确定性处理和神经网络的学习能力,并采用模糊化和去模糊化的过程来实现输入输出之间的映射。
常见的模糊神经网络结构包括前馈神经网络、递归神经网络和模糊关联记忆。
三、模糊神经网络算法应用1. 模糊神经网络在模式识别中的应用模糊神经网络在模式识别领域有广泛应用,例如人脸识别、手写识别和语音识别等。
由于模糊神经网络对于模糊和不完整信息的处理能力,能够更好地应对现实场景中的噪声和不确定性。
2. 模糊神经网络在控制系统中的应用模糊神经网络在控制系统中的应用主要体现在模糊控制器的设计和优化。
通过模糊控制器的设计,可以实现对复杂系统的自适应控制和非线性控制。
同时,模糊神经网络还可以与PID控制器相结合,提高系统的控制性能。
3. 模糊神经网络在预测和优化中的应用模糊神经网络在时间序列预测和多目标优化等问题中也有广泛应用。
例如,使用模糊神经网络来预测股票市场的趋势和交通流量的变化,以及应用模糊神经网络来优化生产调度和资源分配等问题。
四、模糊神经网络算法优化1. 模糊神经网络参数优化模糊神经网络的性能很大程度上依赖于其参数的设置。
神经网络和模糊系统

05
CATALOGUE
应用案例
控制系统
神经网络在控制系统中主要用于优化 和预测控制策略。
通过训练神经网络来学习系统的动态 行为,可以实现对系统的精确控制。 例如,在机器人控制、航空航天控制 等领域,神经网络被用于提高系统的 稳定性和响应速度。
数据分类
模糊系统在数据分类中主要用于处理不确定性和不精确性。
练出最优的神经网络模型。
反向传播算法
根据输出层的误差,计算出每 层的误差梯度,然后根据梯度 下降法更新权重和偏差。
随机梯度下降法
在训练过程中,每次只使用一 部分数据来计算梯度,然后更 新权重和偏差,以提高训练效 率。
自适应学习率算法
根据误差梯度的变化情况,动 态调整学习率,以加快收敛速
度并避免陷入局部最小值。
自适应神经模糊系统
自适应神经模糊系统是在神经模糊系统的基础上,增加了 自适应调整能力。它能够根据系统的运行状态和输入数据 的特性,自适应地调整模糊规则和隶属函数的参数,以更 好地适应环境和任务的变化。
自适应神经模糊系统通过引入在线学习算法和自适应调整 策略,使得系统能够根据运行过程中的反馈信息,不断优 化模糊规则和参数,提高系统的实时性和准确性。
ቤተ መጻሕፍቲ ባይዱ
混合神经模糊系统
混合神经模糊系统是一种将不同类型的神经网络和模糊逻辑结合起来,形成一个 多层次、多模态的混合智能系统。它利用不同类型神经网络的优势,结合多种模 糊逻辑方法,实现对复杂系统的全面建模和控制。
混合神经模糊系统通过集成不同类型的神经网络和模糊逻辑方法,能够充分发挥 各自的优势,提高系统的整体性能。同时,它还能够处理不同类型的输入数据和 任务,具有更强的泛化能力和适应性。
应用前景
模糊神经网络

模糊神经网络简介模糊神经网络(FNN)是一种结合模糊逻辑和神经网络的方法,旨在处理模糊信息与不确定性。
该网络模拟人类大脑处理模糊信息的机制,能够有效地应对现实世界中的模糊问题。
模糊逻辑模糊逻辑是一种处理模糊性的数学工具,它引入了模糊集合和模糊运算,能够描述事物之间的模糊关系。
与传统的逻辑相比,模糊逻辑更符合人类认知过程,能够更好地处理模糊信息。
神经网络神经网络是一种由神经元和连接权重构成的计算模型,它能够通过学习不断优化权重,从而实现对输入数据的自适应建模。
神经网络在模式识别、预测和优化等方面表现出色。
模糊神经网络模糊神经网络将模糊逻辑和神经网络相结合,利用神经网络的自适应学习能力和模糊逻辑的模糊描述能力,有效地处理模糊信息。
FNN将模糊集合映射到神经网络,通过训练调整连接权重,实现对模糊规则的建模与推理。
FNN的特点•模糊描述能力:FNN能够处理模糊和不确定性信息,更适合于现实世界中的复杂问题。
•自适应学习:FNN可以根据输入数据进行权重调整,不断优化网络性能。
•非线性映射:FNN具有非线性映射能力,能够建模复杂的非线性关系。
•规则推理:FNN能够根据事先定义的模糊规则进行推理和决策。
应用领域模糊神经网络在诸多领域得到广泛应用: - 模糊控制:用于处理模糊和不确定性信息的系统控制。
- 模糊识别:用于模糊模式识别和特征提取。
- 模糊优化:用于解决模糊目标函数的优化问题。
- 模糊决策:用于模糊环境中的决策问题。
结语模糊神经网络作为模糊信息处理的有效工具,将模糊逻辑和神经网络的优势相结合,为处理现实世界中的复杂问题提供了一种全新的视角和方法。
随着人工智能技术的不断发展,模糊神经网络有望在更广泛的领域发挥重要作用。
浅析模糊神经网络

定量分析
一.模糊理论 1、模糊理论 1965年,Zadeh教授发表论文“模糊集合”(Fuzzy set), 标志模糊数学的诞生。
模糊集合的基本思想是把经典集合中的绝对隶属关系灵活 化,即元素对“集合”的隶属度不再是局限于取0或1,而 是可以取从0到1间的任一数值。
用隶属函数(Membership Function)来刻画处于中间过渡
xa a xb bxc cxd dx
梯形隶属函数
高斯形隶属函数
g ( x; c, )
1 x c 2 ( ) 2 e
钟型隶属函数
c代表MF的中心; 决定MF的宽度。 1 bell ( x; a, b, c) x c 2b 1 a
隶属函数是模糊理论中的重要概念,实际应用中经常 用到以下三类隶属函数: (1)S函数(偏大型隶属函数)
举例:
典型的一阶Sugeno型模糊规则形式如下:
If x is A and y is B then z px qy r.
其中:
x和y为输入;A和B为推理前件的模糊集合;z
为输出;p、q、k为常数。
二、神经网络简介
生物神经网络
• 人类的大脑大约有1.41011个神经细胞,亦称为神经元。 每个神经元有数以千计的通道同其它神经元广泛相互连接, 形成复杂的生物神经网络。
纯模糊逻辑系统的优点:提供了一种量化专辑语言信
息和在模糊逻辑原则下系统地利用这类语言信息
的一般化模式;
缺点:输入输出均为模糊集合,不易为绝大数工
程系统所应用。
2.2.2 高木-关野模糊系统
该系统是由日本学者Takagi和Sugeno提出的,
系统输出为精确值,也称为T-S模糊系统或
利用改进T-S模糊神经网络恢复MMW图像

利用改进T-S模糊神经网络恢复MMW图像尚丽;周燕【摘要】为有效消除毫米波(MMW)图像中的非线性噪声,利用T-S模糊神经网络(T-S-FNN)对不确定信息进行有效区分的特性,实现MMW图像中非线性信息噪声的逼近,达到消噪的目的.为克服T-S-FNN规则冗余的缺点,考虑前件网络基于自适应模糊聚类的隶属度函数约束及后件网络的权值优化学习,对其前件及后件的结构和学习算法进行改进,使T-S-FNN的计算简化、鲁棒性更强.利用改进的T-S-FNN 对MMW图像进行处理,实验结果表明,该模型具有较好的非线性噪声抑制能力.【期刊名称】《计算机工程与设计》【年(卷),期】2018(039)005【总页数】5页(P1463-1466,1489)【关键词】非线性信息;模糊神经网络;TS模糊模型;毫米波图像;图像消噪【作者】尚丽;周燕【作者单位】苏州市职业大学电子信息工程学院,江苏苏州215104;苏州市职业大学电子信息工程学院,江苏苏州215104【正文语种】中文【中图分类】TN911.730 引言毫米波(milli-meter wave,MMW)图像在系统成像过程中会渗入很多未知的噪声[1,2],且图像的非线性信息缺失非常严重,图像视觉效果较差,研究有效的MMW图像恢复方法一直是备受关注的课题[2]。
而模糊神经网络(fuzzy neural network,FNN)模型兼有模糊系统和神经网络模型的优点[3-5],能够解决很多传统技术无能为力的、不确定的、且非常复杂的非线性问题[6-8]。
因此,本文引入FNN技术来实现MMW图像的非线性滤波,从而获得图像细节和轮廓边缘较清晰的MMW图像。
目前,T-S模糊系统已被实践证实是一种典型的、有效的非线性处理手段[2,8,9]。
然而,常用的T-S模糊系统中的规则数目和规则层的神经元数目都没有合理的确定方法,常常出现规则冗余的情况;另外,T-S模糊模型中的结构和优化算法也比较复杂,计算速度较慢。
模糊神经网络简介
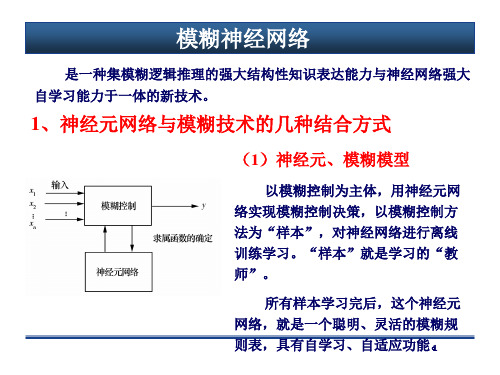
以神经网络为主体,将输入空间分割成若干不同型式的模糊推论 组合,对系统先进行模糊逻辑判断,以模糊控制器输出作为神经元网 络的输入(串)。
后者具有自学习的智能控制特性。
2
模糊神经网络
(3)神经与模糊模型
根据输入量的不同性质分别由神经网络与模糊控制直接处理输入 信息,并作用于控制对象(并),更能发挥各自的控制特点。来自y 取小运算。∑
ec
……
∏
wnn
outi(j3) ini(j3) out1(i2) out2(2j)
i 1,2,3; j 1,2,3
∏
输入层 模糊化 模糊推理 去模糊化
10
基于标准模型的模糊神经网络
…… …… ……
∏ w11
∏
e
……
∏ wij
y
∑
ec
……
∏
wnn
∏
输入层 模糊化 模糊推理 去模糊化
(4)在结构上将二者融为一体
构成模糊神经网络,利用神经网络来实现模糊推理,在本质上是 模糊系统的实现。
3
模糊神经网络 优点:
1)模糊神经网络虽然也是局部逼近网络,但是它是按照 模糊系统模型建立的,网络中的各个结点及所有参数均有 明显的物理意义,因此这些参数的初值可根据模糊系统的 定性知识加以确定,经过上述学习算法的训练,收敛后的 网络能够满足系统所要求的输入输出关系,这是模糊神经 网络同单纯神经网络相比其优点所在。
1
N
Z
0.5
P
outi(j2) ini(j2)
(out ) e (1)
outi(1) aij bij 2
2
Aij
i
隶属度 μ
0
神经网络与模糊控制考试题及答案汇总

神经⽹络与模糊控制考试题及答案汇总⼀、填空题1、模糊控制器由模糊化接⼝、解模糊接⼝、知识库和模糊推理机组成2、⼀个单神经元的输⼊是 1.0 ,其权值是 1.5,阀值是-2,则其激活函数的净输⼊是-0.5 ,当激活函数是阶跃函数,则神经元的输出是 13、神经⽹络的学习⽅式有导师监督学习、⽆导师监督学习和灌输式学习4、清晰化化的⽅法有三种:平均最⼤⾪属度法、最⼤⾪属度取最⼩/最⼤值法和中位数法,加权平均法5、模糊控制规则的建⽴有多种⽅法,是:基于专家经验和控制知识、基于操作⼈员的实际控制过程和基于过程的模糊模型,基于学习6、神经⽹络控制的结构归结为神经⽹络监督控制、神经⽹络直接逆动态控制、神⽹⾃适应控制、神⽹⾃适应评判控制、神⽹内模控制、神⽹预测控制六类7.傅京逊⾸次提出智能控制的概念,并归纳出的3种类型智能控制系统是、和。
7、⼈作为控制器的控制系统、⼈机结合作为控制器的控制系统、⽆⼈参与的⾃主控制系统8、智能控制主要解决传统控制难以解决的复杂系统的控制问题,其研究的对象具备的3个特点为、和。
8、不确定性、⾼度的⾮线性、复杂的任务要求9.智能控制系统的主要类型有、、、、和。
9、分级递阶控制系统,专家控制系统,神经控制系统,模糊控制系统,学习控制系统,集成或者(复合)混合控制系统10.智能控制的不确定性的模型包括两类:(1) ;(2) 。
10、(1)模型未知或知之甚少;(2)模型的结构和参数可能在很⼤范围内变化。
11.控制论的三要素是:信息、反馈和控制。
12.建⽴⼀个实⽤的专家系统的步骤包括三个⽅⾯的设计,它们分别是、和。
知识库的设计推理机的设计⼈机接⼝的设计13.专家系统的核⼼组成部分为和。
知识库、推理机14.专家系统中的知识库包括了3类知识,它们分别为、、和。
判断性规则控制性规则数据15.专家系统的推理机可采⽤的3种推理⽅式为推理、和推理。
15、正向推理、反向推理和双向推理16.根据专家控制器在控制系统中的功能,其可分为和。
《模糊神经网络》课件

模糊神经网络在语音识别中的应用
总结词
语音信号具有时变性和非线性特性,模糊神经网络能够有效地处理这些特性,提高语音识别的准确性 。
详细描述
在语音识别领域,模糊神经网络被广泛应用于语音分类、语音合成、语音识别等方面。通过结合模糊 逻辑和神经网络的优点,模糊神经网络能够更好地处理语音信号中的噪声和不规则性,提高语音识别 的准确性和鲁棒性。
02
模糊逻辑与神经网 络的结合
模糊逻辑的基本概念
1
模糊逻辑是一种处理不确定性、不完全性知识的 工具,它允许我们描述那些边界不清晰、相互之 间没有明确界限的事物。
2
模糊逻辑通过使用隶属度函数来描述事物属于某 个集合的程度,而不是简单地用“是”或“否” 来回答。
3
模糊逻辑在许多领域都有应用,例如控制系统、 医疗诊断、决策支持等。
详细描述
在萌芽期,研究者们开始探索将模糊逻辑和神经网络相结合的可能性。随着相关理论和技术的发展,模糊神经网 络逐渐进入发展期,开始在实际应用中得到广泛关注和应用。如今,随着人工智能技术的不断进步,模糊神经网 络已经进入了成熟期,成为处理不确定性和非线性问题的有效工具。
模糊神经网络的应用领域
总结词
模糊神经网络在许多领域都有广泛的应用,如控制系 统、模式识别、智能机器人等。
模糊神经网络的性能评估
准确率
损失函数
衡量分类问题中神经网络正确分类的样本 比例。
评估神经网络预测结果与实际结果之间的 误差,用于优化神经网络参数。
泛化能力
过拟合与欠拟合
衡量神经网络对新样本的适应能力,即训 练好的网络对未见过的样本的预测能力。
过拟合指模型在训练数据上表现很好,但 在测试数据上表现不佳;欠拟合则指模型 在训练数据和测试数据上的表现都不佳。
周志华机器学习西瓜书全书16章pptChap05神经网络课件
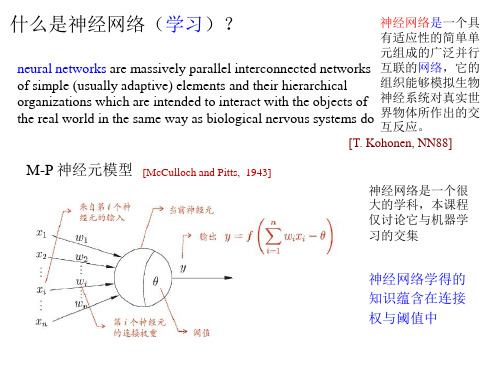
冰 河期
1985左右 -1995左右 ~繁荣期 : Hopfield (1983), BP (1986), …
1995年左右:SVM 及 统计学习 兴起
沉 寂期
2010左右 -至今 ~繁荣期 :深度学习
交替模式 : 热十(年) 冷十五(年)
启示
科学的发展总是“螺旋式上升” 三十年河东、三十年河西 坚持才能有结果!
训练: • 网络接收输入样本后,将会确定输出层的“获胜”神经元(“胜者通吃”) • 获胜神经元的权向量将向当前输入样本移动
级联相关网络
CC: Cascade-Correlation (级联相关)
构造性神经网络: 将网络的结构也当做学习的目标之一, 希望 在训练过程中找到适合数据的网络结构
训练: • 开始时只有输入层和输出层 • 级联 - 新的隐层结点逐渐加入,从而创建起层级结构 • 相关 - 最大化新结点的输出与网络误差之间的相关性
SOM 神经网络
SOM: Self-Organizing feature Map (自组织特征映射 )
• 竞争型的无监督神经网络 • 将高维数据映射到低维空间(通常为 2
维) , 高维空间中相似的样本点映射到 网络输出层中邻近神经元 • 每个神经元拥有一个权向量 • 目标:为每个输出层神经元找到合适的 权向量以保持拓扑结构
• 每次针对单个训练样例更 新权值与阈值
• 参数更新频繁 , 不同样例 可能抵消 , 需要多次迭代
• 其优化目标是最小化整个 训练集上的累计误差
• 读取整个训练集一遍才对 参数进行更新 , 参数更新 频率较低
在很多任务中 , 累计误差下降到一定程度后 , 进一步下降会非常缓慢, 这时 标准 BP算法往往会获得较好的解, 尤其当训练集非常大时效果更明显.
第6章-模糊神经网络-2015

在模糊神经网络中,神经网络的输入、输出节点 用来表示模糊系统的输入、输出信号,神经网络 的隐含节点用来表示隶属函数和模糊规则,利用 神经网络的并行处理能力使得模糊系统的推理能 力大大提高。
模糊神经网络的三种形式:
逻辑模糊神经网络 算术模糊神经网络(常规模糊神经网络) 混合模糊神经网络
3.1 典型模糊神经网络的结构
I x i f A a sy i n B t sh z d p x e q r . n y
其中: x和y为输入语言变量;A和B为推理前件的模糊 集合;z为输出语言变量;p、q、k为常数。
2.3 自适应模糊系统
自适应模糊系统是指具有学习算法的模糊逻辑 系统,其中模糊逻辑系统是由服从模糊逻辑规则的 一系列“If-then”规则构造的;学习算法则依靠数 据信息来调整模糊逻辑系统的参数。
钟型函数
三角形隶属函数 梯形隶属函数 高斯形隶属函数 钟型隶属函数
0 trig(x;a,b,c) cbxxaa
cb 0
xa a x b b x c
cx
0
xa
Trap(x,
a,b,
c,
d)
ba
1
dx
dc
0
1(xc)2
g(x;c,)e 2
xa a x b b x c cxd
dx
c代表 M的 F 中心 决 ;定 M的 F 宽度
具体步骤:
(1)将选取的训练样本和评价样本分别写入两 个.dat文件。如trainData.dat和checkData,dat 作为ANFIS的数据源,在ANFIS编辑器中载入这两 个样本数据。 load trainData.dat load checkData.dat
(2)初始化模糊推理系统FIS的参数,包括选择输入的 隶属度函数,利用规则编辑器生成规则等等,作为训 练初始的FIS。
模糊神经网络的结构与实现方法

模糊神经网络的结构与实现方法概述:在数学、计算机科学、人工智能领域中,神经网络是一种模仿人类神经系统结构与功能的数学模型,被广泛用于模式识别、机器学习和人工智能等领域。
模糊神经网络就是基于模糊数学理论的神经网络。
本文将介绍模糊神经网络的基本结构和实现方法。
模糊神经网络的基本结构:模糊神经网络的结构与普通神经网络的结构类似,由输入层、隐藏层和输出层三个部分组成。
1.输入层:输入层用于接收外部输入的模糊信息。
一般来说,输入的信息经过模糊化处理,以便于神经网络进行处理。
这些信息可以是关于物体颜色、大小、形状和运动方向等方面的特征。
2.隐藏层:隐藏层通常用于进行信息加工、转化和计算。
在模糊神经网络中,隐藏层的作用是将输入的模糊信息转换成一组更加抽象和具有判断性质的特征。
这些特征可以用于后续的分类和识别。
3.输出层:输出层将隐藏层计算后的特征转换成分类结果。
在模糊神经网络中,输出层的结果通常为一组置信度或概率,表示某个输入向量属于每个不同类别的可能性大小。
模糊神经网络的实现方法:模糊神经网络的实现方法一般分为两种:基于规则的模糊神经网络和基于学习的模糊神经网络。
1.基于规则的模糊神经网络:基于规则的模糊神经网络是一种预设规则的模糊推理方法。
它使用if-then规则作为知识表示形式,通过模糊逻辑运算对规则进行推理,以得出输出结果。
这种方法的优点是不需要进行训练,但是缺点是规则需要手动预设,需要专家经验,并且容易出现规则矛盾的情况。
2.基于学习的模糊神经网络:基于学习的模糊神经网络是一种通过样本训练来确定模型参数的方法。
它使用输入和输出的训练样本集来训练网络的权重和阈值,以得出输出结果。
这种方法的优点是可以自动学习知识,并且可以处理复杂的非线性问题,但是需要大量的训练数据和时间。
总结:模糊神经网络作为一种非常有效的神经网络类型,已经被广泛应用于图像处理、模式识别、控制系统等领域。
本文简要介绍了模糊神经网络的基本结构和实现方法,并且指出了它的优点和缺点。
燃气轮机故障诊断

燃气轮机故障诊断舰用燃气轮机某关键部件故障诊断方法研究系别信息工程系专业测控技术与仪器班级B141401学号B14140129姓名袁斌指导教师崔建国负责教师崔建国沈阳航空航天大学北方科技学院2015年6月摘要燃气轮机的关键部件之一滚动轴承是机械设备运行过程中产生最易产生故障的零件,它运行的正常与否直接影响到整台机器的性能。
防止故障升级,发生灾难性事故。
所以对滚动轴承故障诊断技术进行探讨和学习就具有十分重要的意义。
本文主要以燃气轮机的滚动轴承为研究对象,利用测量的轴承振动信号参数来进行故障诊断,利用神经网络技术对某一动态的模拟原理,应用到对滚动轴承故障诊断的具体方面,设计并构建了基于BP神经网络和自适应模糊神经网络(Adaptive Network Fuzzy Inference System)的滚动轴承故障诊断系统,在MATLAB软件里对构造的训练样本进行训练,利用训练完成后的神经网络我们就可以对滚动状态故障进行诊断。
关键词:滚动轴承;BP神经网络;模糊神经网络AbstractRolling bearing is one of the most ordinary parts in mechanical machine, its running state can influence the performance of the whole machine directly, the aircraft stabilizer health status need to be monitored in real time to ensure the aircraft fly safety. so it is important to study the technology of fault diagnosis for rolling bearing.On the basis of analyzing the fault mechanism and vibration signal characteristics of rolling bearing systematically, and after analyzing and processing the vibration signals of right and fault state of rolling bearing, partial appropriate feature parameters are selected as the input of the neural network according to the time and frequency domain characteristics of parameters in this thesis. and the fault diagnosis system for rolling bearing based on BP neural network is built up. Finally,and fuzzy artificial neural network diagnosis technique the training set of right and fault states of rolling bearing is built up by using the measuring data of rolling bearing from former research, the neural network model is trained on the platform of Matlab software.the operating state of rolling bearing has been diagnosed by using the above network which has been trained well.Keywords: rolling bearing; BP neural network; fuzzy artificial neural network目录1 绪论 (1)1.1 课题背景和研究的意义 (1)1.1.1 研究背景 (1)1.1.2 研究意义 (2)1.2 国内外故障诊断技术研究现状 (3)1.2.1 国外现状 (3)1.2.2 国内现状 (4)1.3 研究内容 (5)2 燃气轮机关键部件故障诊断的总体方案设计 (7)2.1滚动轴承故障的总体方案设计 (7)2.2 滚动轴承机理及故障类型 (7)2.2.1 滚动轴承基本结构 (8)2.2.2 滚动轴承故障类型 (9)2.3 滚动轴承参数选取及处理 (10)3故障诊断方法 (13)3.1 BP神经网络 (13)3.1.1 BP神经网络原理 (13)3.1.2 BP神经网络诊断方法 (14)3.2 自适应模糊神经网络(ANFIS) (17)3.2.1 自适应模糊神经网络(ANFIS)结构 (18)3.2.2 自适应模糊神经网络(ANFIS)原理 (20)3.2.3 自适应模糊神经网络(ANFIS)诊断方法 (21)4 滚动轴承BP神经网络故障诊断试验研究 (25)4.1 故障诊断模型建立 (25)4.1.1 各层节点数确定 (25)4.1.2 初始权值的选择 (27)4.1.3 期望误差和学习率选取 (27)4.2轴承故障诊断的仿真试验研究 (27)4.2.1样本选取 (27)4.2.2 神经网络的训练 (29)4.2.3 神经网络的测试 (30)5 基于自适应模糊神经网络(ANFIS)的故障诊断试验研究 (32)5.1 诊断模型的建立 (32)5.1.1 样本的选取 (32)5.1.2 输入样本的模糊化处理 (33)5.1.3 输出结果的去模糊化处理 (34)5.2 轴承故障诊断仿真与结果 (34)6 不同神经网络故障诊断结果与分析 (38)7 结论 (39)结束语 (40)致谢 (41)参考文献 (42)附录ⅠBP神经网络故障诊断源程序清单 (43)附录Ⅱ自适应模糊神经网络(ANFIS)诊断源程序清单 (48)1 绪论1.1 课题背景和研究的意义1.1.1 研究背景作为新型的动力设备,燃气轮机具有结构紧凑、安全可靠、运行平稳,具有较高的热效率,可以快速启动并带动负载等优点,而日益受到人们的重视,应用范围也越来越广。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、模糊系统(Fussy System,简称FS)
许多实际的应用系统很难用准确的术语来描 述。如化学过程中的“温度很高”、“反应骤然 加快”等。
模糊系统(也称模糊逻辑系统)就是以模糊
规则为基础而具有模糊信息处理能力的动态模型。
2.1 模糊系统的构成
模糊系统(也称模糊逻辑系统)就是以模糊规则为基础 而具有模糊信息处理能力的动态模型。它由四部分构成,如 下图:
定量分析
1、模糊理论
1965年,Zadeh教授发表论文“模糊集合”(Fuzzy set),
标志模糊数学的诞生。
模糊集合的基本思想是把经典集合中的绝对隶属关系灵活 化,即元素对“集合”的隶属度不再是局限于取0或1,而 是可以取从0到1间的任一数值。 用隶属函数(Membership Function)来刻画处于中间过渡 的事物对差异双方所具有的倾向性。 隶属度(Membership Degree)就表示元素隶属于集合的 程度。
Y (30) 0.5
Y (60) 0.02
1
0 .5 25 30 60
隶属函数是模糊理论中的重要概念,实际应用中经常 用到以下三类隶属函数: (1)S函数(偏大型隶属函数)
注:(a、b为待定参数)
(2)Z函数(偏小型隶属函数)
这种隶属函数可用于表示像年轻、冷、矮、淡等偏向 小的一方的模糊现象。
权系数中,都具有分布存储的特点。
(3)从知识的运用方式来看
模糊系统和神经网络都具有并行处理的特点,模糊系
统同时激活的规则不多,计算量小,而神经网络涉及 的神经元很多,计算量大。 (4)从知识的获取方式来看
模糊系统的规则靠专家提供或设计,难于自动获
取.而神经网络的权系数可由输入输出样本中学习,
Inference System),简称ANFIS,1993年由学者Jang Roger提出。
融合了神经网络的学习机制和模糊系统的语言推理能力等
优点,弥补各自不足。同其他模糊神经系统相比,ANFIS
具有便捷高效的特点。
ANFIS使用一个给定的输入输出数据集,从而构 造出一个模糊推理系统(支持T-S型系统),并用 一个单独的反向传播算法或该算法与最小二乘 法相结合的方法来完成对系统隶属函数参数的
语言信息和在模糊逻辑原则下系统地利用这类语
言信息的一般化模式;
缺点:输入输出均为模糊集合,不易为绝大数工
程系统所应用。
2.2.2 高木-关野模糊系统
该系统是由日本学者Takagi和Sugeno提出的,
系统输出为精确值,也称为T-S模糊系统或
Sugeno系统。
举例:
典型的一阶Sugeno型模糊规则形式如0,1]确定了一个X上的模糊子 集A,A(x)称为A的隶属函数。
x X , A( x) [0,1] 称为x属于A的隶属度
A( x) 1 x完全属于A A( x) 0 x完全不属于A 0 A( x) 1 x部分属于A
1 A( x)
A
x
X
例1
前研究和应用最多的一类模糊神经网络。
该网络共分5层,是根据模糊系统的工
作过程来设计的,是神经网络实现的模糊
推理系统。第二层的隶属函数参数和三、
四层间及四、五层间的连接权是可以调整
的。
典型的模糊神经网络结构
第一层为输入层,为精确值。 节点个数为输入变量的个数。
典型的模糊神经网络结构
第二层为输入变量的隶属函数层,实现输入变量 的模糊化。
模糊神经网络
“当系统的复杂性增加时,我们使它精确化的能
力将减小。直到达到一个阈值,一旦超越它,复杂
性和精确性将互相排斥。”
——模糊数学创始人L.A.Zadeh教授
互克性原理
天气冷热
雨的大小
风的强弱
人的胖瘦
年龄大小
个子高低
客观世界的模糊性反映在人脑中,便产生了概念上 的模糊性;人巧妙地利用自已建立的模糊概念来进行判
2.2 模糊系统的分类
按照常见的形式,模糊推理系统可分为:
纯模糊逻辑系统 高木-关野(Takagi-Sugeno)模糊逻辑系统 其他模糊逻辑系统
2.2.1 纯模糊逻辑系统
纯模糊逻辑系统仅由知识库和模糊推理机组成。
其输入输出均是模糊集合。
×
×
纯模糊逻辑系统结构图
纯模糊逻辑系统的优点:提供了一种量化专辑
(2)知识库(knowledge base)
知识库中存贮着有关模糊控制器的一切知识,包
含了具体应用领域中的知识和要求的控制目标,
它们决定着模糊控制器的性能,是模糊控制器的 核心。
如专家经验等。
比如:If浑浊度 清,变化率 零,then洗涤时间 短
If浑浊度 较浊,变化率 小,then洗涤时间 标准
3.2 模糊神经网络的学习算法
模糊神经网络无论作为逼近器,还是模式存储
器,都是需要学习和优化权系数的。学习算法
是模糊神经网络优化权系数的关键。模糊神经
网络的学习算法,大多来自神经网络,如BP算 法、RBF算法等。
Matlab实现
自适应模糊神经推理系统,也称为基于神经网络的自适应
模糊推理系统(Adaptive Network-based Fuzzy
断、推理和控制,完成那些现代先进设备所不能完成的
工作: 人们几乎可以同样地辨认胖子和瘦子,美丽和丑陋; 人们无须测量车速便可明智地躲过川流不息的车队; 一行草书虽然大异于整齐的印刷字体,却照样可以被
人看懂。
在科学发展的今天,尤其在工程研究设计领域, 模糊问题无法回避,要求对数据进行定量分析。
模糊概念
调节。这使得模糊系统可以从其建模数据中学
习信息。
ANFIS建模方法
首先假定一个参数化的模型结构,然后采集
输入输出的数据,最后使用ANFIS训练FIS (fuzzy inference system)模型,根据选定的
误差准则修正隶属函数参数,仿真给定的训练数
据。
具体步骤:
(1)将选取的训练样本和评价样本分别写入两 个.dat文件。如trainData.dat和checkData,dat 作为ANFIS的数据源,在ANFIS编辑器中载入这两
据信息来调整模糊逻辑系统的参数。
自适应模糊系统被认为是通过学习能自动产生 其模糊规则的模糊逻辑系统。
2.4 模糊系统与神经网络的区别与联系
(1)从知识的表达方式来看
模糊系统可以表达人的经验性知识,便于理解,而神
经网络只能描述大量数据之间的复杂函数关系,难于 理解。 (2)从知识的存储方式来看
模糊系统将知识存在规则集中,神经网络将知识存在
典型的模糊神经网络结构
第四层为“或”层,节点数为输出变量模糊度划分的个数q。
该层与第三层的连接为全互连,连接权值为Wkj,其中k= 1,2,…,q; j=1,2,…,m×n.(权值代表了每条规则的置信度,
训练中可调。)
典型的模糊神经网络结构
第五层为清晰化层,节点数为输出变量的个数。该层与
第四层的连接为全互连,该层将第四层各个节点的输出, 转换为输出变量的精确值。
The default number of membership functions, numMFs, is 2; the default input membership function type is 'gbellmf'; and the default output membership function type is 'linear'.
Oi2 Ai ( x1 )
i 1, 2,..., m
Oi2 Bi ( x2 )
i m 1, m 2,..., m n
典型的模糊神经网络结构
第三层也称“与”层,该层节点个数为模糊规则数。 该层每个节点只与第二层中前m个节点中的一个 和后n个节点中的一个相连,共有m ×n个节点, 也就是有m ×n条规则。
(1)模糊化接口(Fuzzification)
模糊化接口主要将检测输入变量的精确值根据其模糊度划 分和隶属度函数转换成合适的模糊值。 为了尽量减少模糊规则数,可对于检测和控制精度要求高 的变量划分多(一般5一7个)的模糊度,反之则划分少(一
般3个)的模糊度。
当完成变量的模糊度划分后,需定义变量各模糊集的隶属 函数。
算术模糊神经网络(常规模糊神经网络) 混合模糊神经网络
3.1 典型模糊神经网络的结构
由于模糊系统的规则集和隶属度函数等设计参数
只能靠设计经验来选择,所以用神经网络的学习 方法,根据输入输出的学习样本自动设计和调整 模糊系统的设计参数,实现模糊系统的自学习和 自适应功能。
结构上像神经网络,功能上是模糊系统,这是目
xa a xb bxc cx
xa a xb bxc cxd dx
梯形隶属函数
高斯形隶属函数
g ( x; c, )
1 x c 2 ( ) 2 e
钟型隶属函数
c代表MF的中心; 决定MF的宽度。 1 bell ( x; a, b, c) x c 2b 1 a
(4)正态分布
(5)高斯分布
钟型函数
三角形隶属函数
0 xa ba trig ( x; a, b, c) c x c b 0
0 xa ba Trap( x, a, b, c, d ) 1 d x d c 0
O 年老,X [0, 100],
O : X [0,1]规定为:
0 0 x 50 2 1 O( x) x 50 1 50 x 100 5
