心理与教育统计学第一章
心理学统计总结

心理与教育学统计第一章.绪论一.统计方法在心理和教育科学研究中的研究1.心理与教育统计的定义与性质(1)定义:是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育活动规律的一门学科。
(2)数理统计学:分析这种随机变量的规律性,它的理论基础是专门研究随机现象的科学——概率论,侧重于基本原理与方法的科学证明。
心理与教育统计:侧重于数理统计方法如何在心理和教育科学研究中的应用,是心理与教育科学研究中最广泛应用的,也是最基本的一种定量化工具。
2.数据特点:多以数字形式呈现、随机性、规律性、研究目的是通过部分数据来推测总体特征。
二.心理与教育统计学的内容1.描述统计:主要研究如何整理心理与教育科学实验或调查得来的大量数据,描述一组数据的全貌,表达一件事物的性质。
具体内容:数据如何分组(统计图表)、计算一组数据的特征值(集中量数、差异量数)、表示一事物两种或两种以上属性间相关关系的描述。
2.推论统计:研究如何透过局部数据所提供的信息,推论总体的情形。
推论统计的原理和理论包括:抽样理论、估计理论、统计检验理论。
3.实验设计三.心理与教育统计学基础概念1.数据类型:(测量方法和来源):计数数据和计量数据(测量水平)称名数据、顺序数据、等距数据、等比数据。
(连续性)离散数据:任何两个数据点之间所取得数值的个数是有限的。
连续数据:任何两个数据点之间都可以细分出无限多个大小不同的数值。
进一步细分,取决于:测量技术所允许的精确程度、测量所需要的精确程度。
2.变量、观测值、随机变量变量:在心理与教育实验、观察、调查中想要获得的数据,即为一个可以取不同数值的物体的属性或事件,其数值具有不确定性。
观测值:一旦确定了某个值,就称这个值为某一变量的观测值,也就是具体数据。
随机变量:在统计上,把取值之前不能预料到取什么值的变量,就称为随机变量。
现代心理与教育统计学复习资料

现代心理与教育统计学复习资料第一章心理与教育统计学基础知识1、数据类型称名数据计数数据离散型数据顺序数据等距数据测量数据连续型数据比率数据2、变量、随机变量、观测值变量就是可以挑相同值的量。
统计数据观测的指标都就是具备变异的指标。
当我们用一个量则表示这个指标的观测结果时,这个指标就是一个变量。
用来表示随机现象的变量,称为随机变量。
一般用大写的x或y表示随机变量。
随机变量所取得的值,称为观测值。
一个随机变量可以有许多个观测值。
3、总体、个体和样本须要研究的同质对象的全体,称作总体。
每一个具体内容研究对象,称作一个个体。
从总体中抽出的用以推测总体的部分对象的集合称为样本。
样本中包含的个体数,称为样本的容量n。
通常把容量n≥30的样本称作大样本;而n<30的样本称作大样本。
4、统计数据量和参数统计数据指标平均数标准差相关系数回归系数统计数据量srb参数μσρβ5、统计误差误差就是测量得值与真值之间的差值。
测出数值=真值+误差统计误差归纳起来可分为两类:测量误差与抽样误差。
由于采用的仪器、测量方法、读数方法等问题导致的测出值与真值之间的误差,称作测量误差。
由于随机抽样造成的样本统计量与总体参数间的差别,称为抽样误差第二章统计图表一、数据的整理在展开整理时,如果没充裕的理由证明某数据就是由实验中的过错导致的,就无法轻而易举将其确定。
对于个别极端数据与否该剔出,应当遵从三个标准差法则。
二、次数原产表中(一)简单次(频)数分布表(二)相对次数分布表将次数原产表各组的实际次数转变为相对次数,即为用频数比率(f/n)或百分比f)去则表示次数,就可以做成相对次数原产表中(?100%n(三)累加次数分布表(四)双列次数分布表双列次数原产表中又称有关次数原产表中,就是对存有联系的两列变量用同一个表中则表示其次数原产。
所谓有联系的两列变量,一般是指同一组被试中每个被试两种心理能力的分数或两种心理特点的指标,或同一组被试在两种实验条件下获得的结果。
(完整版)现代心理与教育统计学

心理统计学第一章概述描述统计定义:研究如何把心理与教育科学实验或调查得来的大量数据科学的科学的加以整理概括和表述作用:使杂乱无章的数字更好的显示出事物的某些特征,有助于说明问题的实质。
具体内容:1数据分组:采用图与表的形式。
2计算数据的特征值:集中量数(平均数中数)离散量数(方差)3计算量事物间的相关关系:积差相关(2列3列多列)推断统计定义:主要研究如何利用局部数据(样本数据)所提供的信息,依据数理统计提供的理论和方法,推论总体情形。
作用:用样本推论总体。
具体内容:1如何对假设进行检验。
2如何对总体参数特征值进行估计。
3各种非参数的统计方法。
心理与教育统计基础概念数据类型一从数据来源来划分1计数数据:计算个数或次数而获得的数据。
(都是离散数据)2测量数据:借助一定测量工具或测量标准而获得的数据。
(连续数据)二根据数据所反映的测量水平1称名数据(分类)定义:指用数字代表事物或数字对事物进行分类的数据。
特点:数字只是事物的符号,而没有任何数量意义。
统计方法:百分数次数众数列联相关卡方检验等。
(非参检验)2顺序数据(分类排序)定义:指代事物类别,能够表明不同食物的大小等级或事物具有的某种特征的程度的数据。
(年级)特点:没有相等单位没有绝对零点。
不表示事物特征的真正数量。
统计方法:中位数百分位数等级相关肯德尔和谐系数以及常规的非参数检验方法。
3等距数据(分类排序加减(相等单位))(真正应用最广泛的数据)定义:不仅能够指代物体的类别等级,而且具有相等的单位的数据。
(成绩温度)特点:真正的数量,能进行加减运算,没有绝对零点,不能进行乘除计算。
统计方法:平均数标准差积差相关Z检验t检验F检验等。
4比率数据(分类排序加减法乘除法(绝对零点))定义:表明量的大小,也具有相等单位,同时具有绝对零点。
(身高反应时)特点:真正的数字,有绝对零点,可以进行加减乘除运算。
在统计中处理的数据大多是顺序数据和等距数据。
三按照数据是否具有连续性离散数据连续数据变量观测值随机变量变量:指心理与教育实验观察调查种想要获得的数据。
心理与教育统计学第一章统计图表

❖ 计算法:总体正态时
❖
k
1.87N
2
15
k
1.87
50
2
15
8.87 9
i Rg k
i =45/9=5
❖ 3、定组限——每组的起止点。
西北民族大学
表述组限
A 30~34 25~29 20~24
B 30~35 25~30 20~25
整理方便省
C
时,未表现
30~
真正的上下 限
25~
20~
精确组限
西北民族大学
第一节 数据的初步整理
尝试水平百分比(%)
100
无效尝试
80
有效尝试
60
无尝试直接成功
40
20
0 8
10
11
年龄组(月)
图X 各组婴儿的尝试水平分布
西北民族大学
❖ 一、简单次数分布表
第二节 次数分布表
例2-2:某个班的26个学生在一次测 验中的分数如下(10分为满分): 9 2 3 8 10 9 9 2 1 2 9 8 2 5 2 9 9 3 2 5 7 2 10 1 2 9
西北民族大学
1 2 3 4
第一章 统计图表
数据的初步整理 次数分布表 次数分布图
其他类型的统计图表
西北民族大学
第一节 数据的初步整理
数据的整理
数据排序
统计分组
第一节 数据的初步整理
西北民族大学
❖ 一、数据排序
例2.1 10名学生的英语成绩为: 78.9、93、76、84.7、73、72、71、74.5、66、77.1
65-69 6 67 0.12 21 60-64 7 62 0.14 15
心理与教育统计学课后题答案

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体.(3)样本答:样本是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,是描述一个总体情况的统计指标.(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科.具体讲,就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中.它的主要任务是对客观事实进行预测和分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
现代心理与教育统计学课后题完整版

第一章绪论之老阳三干创作2.名词解释随机变量:在统计学上,把取值之前不能预料取到什么值的变量称之为随机变量总体:又称为母全体、全域,指据有某种特征的一类事物的全体样本:从总体中抽取的一部份个体,称为总体的一个样本个体:构成总体的每个基本单位称为个体次数:指某一事件在某一类别中呈现的数目,又成为频数,用f 暗示频率:又称相对次数,即某一事件发生的次数被总的事件数目除,亦即某一数据呈现的次数被这一组数据总个数去除.频率通畅用比例或百分数暗示概率:又称机率.或然率,用符号P暗示,指某一事件在无限的观测中所能预料的相对呈现的次数,也就是某一事物或某种情况在某一总体中呈现的比率统计量:样本的特征值叫做统计量,又叫做特征值参数:总体的特性成为参数,又称总体参数,是描述一个总体情况的统计指标观测值:在心理学研究中,一旦确定了某个值,就称这个值为某一变量的观测值,也就是具体数据3.何谓心理与教育统计学?学习它有何意义心理与教育统计学是专门研究如何运用统计学原理和方法,搜集.整理.分析心理与教育科学研究中获得的随机数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育活动规律的一门学科.4.选用统计方法有哪几个步伐?首先要分析一下试验设计是否合理,即所获得的数据是否适合用统计方法去处置,正确的数量化是应用统计方法的起步,如果对数量化的过程及其意义没有了解,将一些不着边缘的数据加以统计处置是毫无意义的其主要分析实验数据的类型,分歧数据类型所使用的统计方法有很年夜分歧,了解实验数据的类型和水平,对选用恰当的统计方法至关重要第三要分析数据的分布规律,如总体方差的情况,确定其是否满足所选用的统计方法的前提条件5.什么叫随机变量?心理与教育科学实验所获得的数据是否属于随机变量随机变量的界说:①率先无法确定,受随机因素影响,成随机变动,具有偶然性和规律性②有规律变动的变量6.怎样理解总体、样本与个体?总体N:据有某种特征的一类事物的全体,又称为母体、样本空间,经常使用N暗示,其构成的基本单位为个体.特点:①年夜小随研究问题而变(有、无限)②总体性质由组成的个体性质而定样本n:从总体中抽取的一部份交个体,称为总体的一个样本.样本数目用n暗示,又叫样本容量.特点:①样本容量越年夜,对总体的代表性越强②样天职歧,统计方法分歧总体与样本可以相互转化.个体:构成总体的每个基本单位称为个体.有时个体又叫做一个随机事件或样本点7.何谓次数、频率及概率次数f:随机事件在某一类别中呈现的数目,又称为频数,用f 暗示频率:即相对次数,即某个事件次数被总事件除,用比例、百分数暗示概率P:又称机率或然率,用P暗示,指某事件在无限管偏重所能预料的相对呈现次数.估计值(后验):几次观测中呈现m 次,P(A)=m/n真实值(先验):特殊情况下,直接计算的比值(结果有限,呈现可能性相等)8.统计量与参数之间有何区别和关系?参数:总体的特性称参数,又称总体参数,是描述一个总体情况的统计指标统计量:样本的特征值叫做统计量,又称特征值二者关系:参数是一个常数,统计量随样本而变动参数经常使用希腊字母暗示,统计量用英文字母暗示当试验次数=总体年夜小时,二者为同一指标当总体无限时,二者分歧,但统计量可在某种水平上作为参数的估计值9.试举例说明各种数据类型之间的区别?10.下述一些数据,哪些是丈量数据?哪些是计数数据?其数值意味着什么?17人 25本是计数数据11.说明下面符号代表的意义μ反映总体集中情况的统计指标,即总体平均数或期望值ρ暗示某一事物两个特性总体之间关系的统计指标,相关系数r 样秘闻关系数σ反映总体分散情况的统计指标标准差s样本标准差β暗示两个特性中体之间数量关系的回归系数Nn第二章统计图表1.统计分组应注意哪些问题?①分类要正确,以被研究对象的实质为基础②分类标识表记标帜要明确,要包括所有数据③如删除过失所造成的变异数据,要遵循3σ原则2.直条图适合哪种资料?条形图也叫做直条图,主要用于暗示离散型数据资料,即计数资料.3.圆形图适合哪种资料又称饼图,主要用于描述间断性资料,目的是为显示各部份在整体中所占的比重年夜小,以及各部份之间的比力,显示的资料多以相对数(如百分数)为主4.将下列的反应时测定资料编制成次数分布表、累积次数分布表、直方图、次数多边形.177.5 167.4 116.7 130.9 199.1 198.3 225.0 212.0 180.0 171.0 144.0 138.0 191.0 171.5 147.0 172.0 195.5 190.0 206.7 153.2 217.0 179.2 242.2 212.8 171.0 241.0 176.5 165.4 201.0 145.5 163.0 178.0 162.0 188.1 176.5 172.2 215.0 177.9 180.5 193.0 190.5 167.3 170.5 189.5 180.1 217.0 186.3 180.0 182.5 171.0 147.0 160.5 153.2 157.5 143.5 148.5 146.4 150.5 177.1 200.1 137.5 143.7 179.5 185.5 181.6N=65 代入公式K=1.87(N-1)2/5=9.8 所以K取10定组距13 最低组的下限取115表2-1 次数分布表分组区间组中值(Xc)次数(f)频率(P)百分次数(%)232~ 238 2 3 219~ 225 1 2 206~ 212 6 9 193~ 199 6 9180~ 186 14 22 167~ 173 16 25 154~ 160 5 8 141~ 147 11 17 128~ 134 3 5 115~ 121 1 2 合计65 100表2-2 累加次数分布表分组区间次数(f)向上累加次数向下累加次数实际累加次数(cf)相对累加次数实际累加次数(cf)相对累加次数232~ 2 65 2219~ 1 63 3206~ 6 62 9193~ 6 56 15180~ 14 50 29167~ 16 36 45154~ 5 20 50141~ 11 15 61128~ 3 4 64115~ 1 1 657.下面是一项美国高中生打工方式的调查结果.根据这些数据用手工方式和计算方式个制作一个条形图.并通过自己的体会说明两种制图方式的分歧和优缺点打工方式高二(%)高三(%)看护孩子商店销售餐饮服务其他零工左侧Y轴名称为:打工人数百分比下侧X轴名称为:打工方式第三章集中量数1.应用算术平均数暗示集中趋势要注意什么问题?应用算术平均数必需遵循以下几个原则:①同质性原则.数据是用同一个观测手段采纳相同的观测标准,能反映某一问题的同一方面特质的数据.②平均数与个体数据相结合的原则③平均数与标准差、方差相结合原则2.中数、众数、几何平均数、调和平均数个适用于心理与教育研究中的哪些资料?中数适用于:①当一组观测结果中呈现两个极端数目时②次数分布表两端数据或个别数据不清楚时③要快速估计一组数据代表值时众数适用于:①要快速且粗略的求一组数据代表值时②数据分歧质时,暗示典范情况③次数分布中有两极真个数目时④粗略估计次数分布的形态时,用M-Mo作为暗示次数分布是否偏态的指标(正态:M=Md=Mo;正偏:M>Md>Mo; 负偏:M<Md<Mo)⑤当次数分布中呈现双众数时几何平均数适用于①少数数据偏年夜或偏小,数据的分布成偏态②等距、等比量表实验③平均增长率,按一定比例变动时调和平均数适用于①工作量固定,记录各被试完成相同工作所用时间②学习时间一定,记录一按时间内各被试完成的工作量3.对下列数据,使用何种集中量数暗示集中趋势其代表性更好?并计算它们的值.⑴ 4 5 6 6 7 29 中数=6⑵ 3 4 5 5 7 5 众数=5⑶4.求下列次数分布的平均数、中数.解:组中值由“精确上下限”算得;设估计平均值在35~组,即AM=37;中数所在组为35~,f MD=34,其精确下限Lb=34.5,该组以下各组次数累加为Fb=21+16+11+9+7=645.求下列四个年级的总平均成果.n2363182152006.三个分歧被试对某词的联想速度如下表,求平均联想速度被试 联想词数 时间(分)词数/分(Xi )A 13 2 13/2B 13 3 13/3 C1325-解:C 被试联想时间25分钟为异常数据,删除7.下面是某校几年来结业生的人数,问平均增加率是几多?并估计10年后的结业人数有几多.年份 1978 1979 1980 1981 1982 1983 1984 1985 结业人数54260175076081093010501120解:用几何平均数变式计算:所以平均增加率为11%10年后结业人数为1120×10=3159人8.计算第二章习题4中次数分布表资料的平均数、中数及原始数据的平局数.解:组中值由“精确上下限”算得;设估计平均值在167~组,即设AM=173;中数所在组为167~,f MD=16,其精确下限Lb=166.5,该组以下各组次数累加为Fb=1+3+11+5=20分组区间组中值(Xc)次数(f)d=(Xi-AM)/i fd 232~ 238 2 5 10 219~ 225 1 4 4 206~ 212 6 3 18 193~ 199 6 2 12 180~ 186 14 1 14 167~ 173 16 0 0 154~ 160 5 -1 -5 141~ 147 11 -2 -22 128~ 134 3 -3 -9 115~ 121 1 -4 -4 合计∑N=65 ∑fd=18第四章不同量数1.怀抱离中趋势的不同量数有哪些?为什么要怀抱离中趋势?怀抱离中趋势的不同量数有全距、四分位差、百分位差、平均差、标准差与方差等等.在心理和教育研究中,要全面描述一组数据的特征,不单要了解数据的典范情况,而且还要了解特殊情况.这些特殊性常暗示为数据的变异性.如两个样本的平均数相同可是整齐水平分歧,如果只比力平均数其实不能真实的反映样本全貌.因此只有集中量数不成能真实的反映出样本的分布情况.为了全面反映数据的总体情况,除必需求出集中量数外,这时还需要使用不同量数.2.各种不同量数各有什么特点?见课本103页“各种不同量数优缺点比力”3.标准差在心理与教育研究中除怀抱数据的离散水平外还有哪些用途?可以计算不同系数(应用)和标准分数(应用)4.应用标准分数求分歧质的数据总和时应注意什么问题?要求分歧质的数据的次数分布为正态5.计算下列数据的标准差与平均差6.计算第二章习题4所列次数分布表的标准差、四分差Q设估计平均值在167~组,即AM=173, i=13分组区间Xc f d=(Xc-AM)/i fd fd2232~ 238 2 5 10 50219~ 225 1 4 4 16206~ 212 6 3 18 54193~ 199 6 2 12 24180~ 186 14 1 14 14167~ 173 16 0 0 0154~ 160 5 -1 -5 5141~ 147 11 -2 -22 44128~ 134 3 -3 -9 27115~ 121 1 -4 -4 16合计65 18 25065×75%=48.75 所以Q1、Q3分别在154~组(小于其组精确下限的各组次数和为15)和180~组(小于其组精确下限的各组次数和为36),其精确下限分别为153.5和179.5,所以有:7.今有一画线实验,标准线分别为5cm和10cm,实验结果5cm组的误差平均数为1.3cm,标准差为0.7cm,10cm组的误差平均数为4.3cm,标准差为1.2cm,请问用什么方法比力其离散水平的年夜小?并具体比力之.用不同系数来比力离散水平.×100%=()×100%=53.85%×100%=(1.2/4.3) ×100%=27.91%<CV1所以标准线为5cm的离散水平年夜.8.求下表所列各班成果的总标准差班级平均数标准差人数di1 402 513 484 43其值见上表9.求下表数据分布的标准差和四分差设估计平均数AM=52,即在50~组,d=(Xc-AM)/I计算各值如下表所示:分组 f Xc 累加次数 d d2fd2fd 75~80 1 77 55 5 25 25 5 70~ 2 72 54 4 16 32 865~ 4 67 52 3 9 36 12 60~ 5 62 48 2 4 20 10 55~ 8 57 43 1 1 8 8 50~ 10 52 35 0 0 0 0 45~ 9 47 25 -1 1 9 -9 40~ 7 42 16 -2 4 28 -14 35~ 4 37 9 -3 9 36 -12 30~ 2 32 5 -4 16 32 -8 25~ 2 27 3 -5 25 50 -10 20~ 1 22 1 -6 36 36 -6 合计55 312 -1655×25%=13.75 55×75%=41.25 所以Q1在40~组,其精确下限Lb1=39.5,小于其组的次数为Fb1=9,其组次数f1=7;Q2在55~组,其精确下限Lb2=54.5,小于其组的次数为Fb2=35,其组次数f2=8.计算Q1、Q2如下:第五章相关关系1.解释相关系数时应注意什么?(1)相关系数是两列变量之间相关成都的数字暗示形式,相关水平指标有统计特征数r和总体系数ρ(2)它只是一个比率,不是相关的百分数,更不是等距的怀抱值,只能说r年夜比r小相关密切,不能说r年夜小=0.4的两倍(不能用倍数关系来解释)(3)当存在强相关时,能用这个相关关系根据一个变量的的值预测另一变量的值(4)-1≤r≤1,正负号暗示相关方向,值年夜小暗示相关水平;(0为无相关,1为完全正相关,-1为完全负相关)(5)相关系数年夜的事物间纷歧定有因果关系(6)当两变量间的关系收到其他变量的影响时,两者间的高强度相关很可能是一种假象(7)计算相关要成对数据,即每个个体有两个观测值,不能随便2个个体计算(8)非线性相关的用r得可能性小,但其实不能说不密切2.假设两变量为线性关系,计算下列各情况的相关时,应用什么方法?(1)两列变量是等距或等比的数据且均为正态分布(积差相关)(2)两列变量是等距或等比的数据且不为正态分布(品级相关)(3)一变量为正态等距变量,另一列变量也为正态变量,但人为分为两类(二列相关)(4)一变量为正态等距变量,另一列变量也为正态变量,但人为分为多类(多列相关)(5)一变量为正态等距变量,另一列变量为二分称名变量(点二列相关)(6)两变量均以品级暗示(品级相关、交错系数、相容系数)3.如何区分点二列相关与二列相关?主要区别在于二分变量是否为正态.二列相关要求两列数据均为正态,其中一列被人为地分为两类;点二列相关一列数据为等距或等比丈量数据,且其总体分布为正态,另一列变量是二分称名变量,且两列数存在一一对应关系.4.品质相关有哪几种?各种品质相关的应用条件是什么?品质相关分析的总条件是两因素多项分类之间的关联水平,分为一下几类:(1)四分相关,应用条件是:两因素都为正态连续变量(eg.学习能力,身体状态))人为分为两个类别;同一被试样品中,分别调查两个分歧因素两项分类情况(2)Φ系数:除四分相关外的2×2表(最经常使用)(3)列联表相关C:R×C表的计数资料分析相关水平5.预考查甲乙丙丁四人对十件工艺美术品的品级评定是否具有一致性,用哪种相关方法?品级相关6.下表是平时两次考试成果分数,假设其分布成正态,分别用积差相关与品级相关方法计算相关系数,并回答,就这份资料用哪种相关法更恰当?被试 A B A2B2AB R A R B R A R B D=R A-R B D21 86 83 7396 6889 7138 236-112 58 52 3364 2704 3016 7856-113 79 89 6241 7921 7031 414394 64 78 4096 6084 4992 6424245 91 85 8281 7225 7735 122-116 48 68 2304 4624 3264 9654397 55 47 3025 2209 2585 8972-118 82 76 6724 5776 6232 3515-249 32 25 1024 625 800 10101000010 75 56 5625 3136 4200 5735-24∑670 659 48080 47193 46993 555536834用积差相关的条件成立,故用积差相关更精确7.下列两列变量为非正态,选用恰当的方法计算相关本题应用品级相关法计算,且含有相同品级X有3个数据的品级相同,品级3.5的数据中有2个数据的品级相同,品级为6.5和8.5的数据中也分别有2个数据相同;Y有3个数据品级相同,品级为3的数据中有3个数据品级相同,品级为5.5的数据中有2个数据品级相同,品级为9的数据中有3个数据品级相同.被试X Y RX RYD=RX-RYD21 13 14 1 1 0 02 12 11 23 -1 13 10 11 34 10 11 35 8 7 56 67 1 17 6 5 78 5 4 99 5 4 910 2 4 10 9 1 1N=108.问下表中成果与性别是否相关?被试性别成果男成果女成果成果的平方1 男83 83 68892 女91 91 82813 女95 95 90254 男84 84 70565 女89 89 79216 男87 87 75697 男86 86 73968 男85 85 72259 女88 88 774410 女92 92 8464∑880 425 455 77570适用点二列相关计算法.p为男生成果,q为女生成果平均成果从表中可以计算得:p=0.5 q=0.5相关系数为-0.83,相关较高9.第8题的性别若是改为另一成果A ()正态分布的及格、不及格两类,且知1、3、5、7、9被试的成果A 为及格,2、4、6、8、10被试的成果A 为不及格,请选用适当的方法计算相关,并解释之.被试成果A 成果B 及格成果 不及格成果 成果的平方1 及格 83 83 68892 不及格 91 91 82813 及格 95 95 90254 不及格84 84 7056 5 及格 89 89 7921 6 不及格 8787 7569 7 及格 86 86 7396 8 不及格 85 85 7225 9 及格88 88 7744 10 不及格 92 92 8464 ∑880441 439 77570适用二列相关B 的标准差和平均数别是成果A 及格和不及格时成果B 的平均数,p 为成果A 及格的比率,y 为标准正态曲线中p 值对应的高度或者10.11.下表是9名被试评价10名著名的天文学家的品级评定结果,问这9名被试的品级评定是否具有一致性?被评价者被试∑R i∑R i2 1 2 3 4 5 6 7 8 9A 1 1 1 1 1 1 1 1 1 9 81B 2 4 3 3 9 4 3 3 2 33 1089C 4 2 4 4 2 9 5 5 8 43 1849D 3 5 5 5 5 2 10 7 4 46 2116E 9 6 2 2 6 5 2 6 9 47 2209F 6 7 8 6 3 6 6 4 6 52 2704G 5 3 9 10 4 7 9 8 3 58 3364H 8 10 6 8 8 3 7 10 7 67 4489I 7 8 10 7 10 10 8 2 5 67 4489 J 10 9 7 9 7 8 4 9 10 73 5329 ∑495 27719适用肯德尔W系数.即存在一定关系但不完全一致12.将11题的结果转化为对偶比力结果,并计算肯德尔一致性系数ABCDEFGHIJ已知N=10,K=9 选择对角线以下的择优分数或者选择对角线上的择优分数第六章概率分布1.概率的界说及概率的性质标明随机事件发生可能性年夜小的客观指标就是概率2.概率分布的类型有哪些?简述心理与教育统计中经常使用的概率分布及其特点概率分布是指对随机变量取值的概率分布情况用数学方法(函数)进行描述.概率分布依据分歧的标准可以分为分歧的类型:(一)离散分布与连续分布连续分布指连续随机变量的概率分布,即丈量数据的概率分布,如正态分布离散分布是指离散随机变量的概率分布,即计数数据的概率分布,如二项分布(二)经验分布与理论分布经验分布指根据观察或试验所获得的数据而编制的次数分布或相对频率分布理论分布有两个含义,一是随机变量概率分布的函数-数学模型,二是指按某种数学模型计算出的总体的次数分布(三)基本随机变量分布与抽样分布基本随机变量分布指理论分布中描述构成总体的基本变量的分布,经常使用的有二项分布与正态分布抽样分布是样本统计量的理论分布,又称随机变量函数的分布,如平均数,方差等3.何谓样本平均数的分布所谓样本平均数的分布是指从基本随机变量为正态分布的总体(又称母总体)中,采纳有放回随机抽样方法,每次从这个总体中抽取年夜小为n的一个样本,然后将这些个体放回去,再次取n个个体,……再将n个个体放回去,再抽取n个个体……,这样如此反复,可计算出理论及实验证明这无限多个平均数的分布为正态分布.4.从N=100的学生中随即抽样,已知男生人数为35,问每次抽取1人,抽的男生的概率是几多?(35/100=0.35)5.两个骰子掷一次,呈现相同点数的概率是几多?6.从30个白球20个黑球共50个球中随机抽取两次(放回抽样),问抽一黑球与一白球的概率是几多?两次皆是白球与两次皆是黑球的概率各是几多?(一黑一白)(皆是黑球)(皆是白球)7.自一副洗好的纸牌中每次抽取一张.抽取下列纸牌的概率是几多?(1)一张K 4/54(2)一张梅花 13/54(3)一张红桃 13/54(4)一张黑心 13/54(5)一张不是J、Q、K牌的黑桃 10/548.掷四个硬币时,呈现一下情况的概率是几多?服从二项分布b(4, 0.5)(1)(2)(3)(4)(5)9.在特异功能试验中,五种符号分歧的卡片在25张卡片中各重复5次,每次实验自25张卡片中抽取一张,记下符号,将卡片送回.共抽25次,每次正确的概率是1/5.写出实验中的二项式.问这个二项式分布的平均数和标准差各即是几多?服从二项分布b(25, 0.2)10.查正态表求:(1)(2)(3)Z=±×2=(4)P=0.78 Z=? Y=? Z=0.77 Y=0.29659(5)P(6)11.在单位正态分布中,找出有下列个案百分数的标准丈量Z的分值12.在单位正态分布中,找出有下列个案百分数的标准丈量的Z值13.今有1000人通过一数学能力检验,欲评为六个品级,问各个品级评定人数应是几多?解:6σ÷6=1σ,要使各品级等距,每一品级应占1个标准差的距离,确定各品级的Z分数界限,查表计算如下:分组各组界限比率p 人数分布p×N1 2σ以上232 1σ~2σ1363 0~1σ3414 -1σ~0 3415 -2σ~-1σ1366 -2σ以下23 14.将下面的次数分布表正态化,求正态化T分数分组组中值 f 上限以下累加各组中点以下累加次数累积百分比Z正态化T分数T=10Z+5055~ 52 2 100 99 99%50~ 47 2 98 97 97%45~ 42 6 96 93 93%40~ 37 8 90 86 86%35~ 32 12 82 76 76%30~ 27 14 70 63 63%25~ 22 24 56 44 44%20~ 17 12 32 26 26%15~ 12 16 20 12 12%10~ 7 4 4 2 2%15.掷骰子游戏中,一个骰子掷6次,问3次及3次以上6点向上的概率各是几多?服从二项分布:33次以上:16.今有四择一选择检验100题,问答对几多题才华说是真的会答而不是猜想?解:服从二项分布,p=1/4, q=3/4, np=100×1/4=25>5,此二项分布接近正态,故:根据正态分布概率,当Z=1.645时,该点以下包括了全体的95%.如果用原是分数暗示,即完全凭猜想,100题中猜对33题以下的可能性为95%,猜对33题及以上的概率仅为5%.所以答对33题才华说是真的会而不是猜想.17.一张考卷中有15道多重选择题,每题有4个可能的回答,其中至少有一个是正确谜底.一考生随机回答,(1)答对5至10题的概率,(2)答对的平均题数是几多?18.E字形试标检查儿童的视敏度,每种视力值(1.0,1.5)有4个方向的E字各有两个(共8个),问:说对几个才华说真看清了而不是猜想对的?解:服从二项分布,n=8,p=1/4,np=2<5,所以不能用正态分布概率算,而直接用二项分布算:由以上计算可知说对5个及5个以上的概率总和为0.000015+0.000366+0003845+0.023071=0.027297=2.73%<5%而说对4个及以上概率总和为0.027297+0.0865=0.1138=11.38% 年夜年夜超越5%的误差范围,不成取.所以至少说对5个才华才华认为是看清了而不是猜想对的,作此结论犯毛病的概率为2.73%.19.一学生毫无准备介入一项检验,其中有20道是非题,他纯洁是随机地选择“是”和“非”,试计算:(1)该学生答对5题的概率;(2)该学生至少答对8题的概率解:服从二项分布 n=20, p=0.5 np=10>5,可用正态分布概率作近似值.答对5至少答对8题的概率用正态分布概率近似计算如下:所以答对8题的Z20.设某城市年夜学录取率是40%,求20个介入高考的中学生中至少有10人被录取的概率.解:服从二项分布 n=20,p=0.4,q=0.6.因为np=5,可以用正态分布概率作近似计算人被录取时的Z至少10人被录取的概率即为Z=2.283以上的概率,查表得Z=2.283时p=0.48870,所以Z=2.283以上的概率为0.5-0.48870=0.0113,即至少10人被录取的概率为1.13%解2:设X为录取人数,则21.已知一正态总体μ=10,σ=2.今随机取n=9的样本求Z值,及年夜于该Z以上的概率是几多?解:属于样天职布中总体正态,方差已知的情况:22.从方差未知的正态总体(μ=50)中抽取n=10的样本,算得平问年夜于该平均数以上的概率?解:总体正态方差未知,服从t分布查表当df=9时没有准确的p对应,采纳内插法单侧界限概率:t=1.383以上概率为p=0.1,t=1.833以上概率为p=0.05,令t=1.581以上概率为p,则:23.解,查表得df=7时24.抽取样本n=15解:不知总体平均数时,df=n-1=14查表得df=14时0.25,采纳内插法,p,则解得p=0.27,25.,随机抽取n=10的样本为:10、20、17、19、25、24、22、31、26、26,,并求年夜于该值的概率?解:正态总体平均数未知查df=9时26.,,年夜于该值以上的概率又是几多?解,正态总体平均数已知27.已知从一正态总体中抽取两样本,;解:同一总体方差相等样本方差比为第七章参数估计第八章假设检验第九章方差分析第十章X2检验第十一章非参数检验第十二章线性回归第十三章多变量统计分析简介第十四章抽样原理及方法O50IZF6l3OlC。
《心理与教育统计学》习题答案
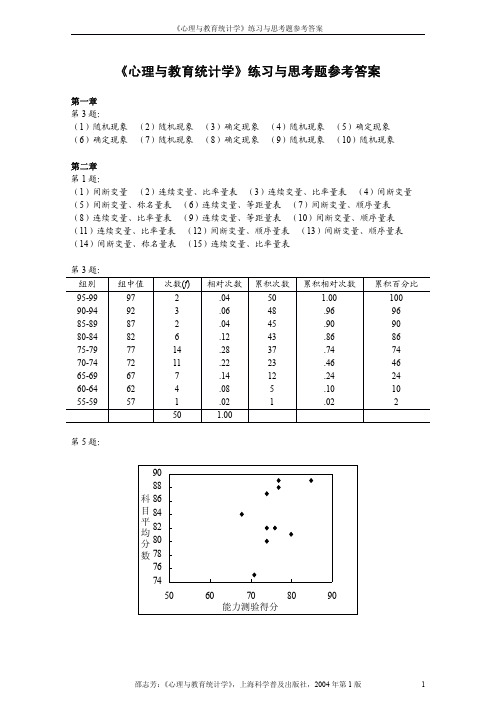
邵志芳: 《心理与教育统计学》 ,上海科学普及出版社,2004 年目 84 平 82 均 分 80 数 78 76 74 50 60 70 80 能力测验得分 90
邵志芳: 《心理与教育统计学》 ,上海科学普及出版社,2004 年第 1 版
1
《心理与教育统计学》练习与思考题参考答案
第三章 第 1 题: (1)84 (2)89 (3)420 (4)略 第 2 题: (1)13.5 (2)12 第 3 题:S2 = 8.5 S = 2.915 第 4 题:3159 第 5 题:男生 CV = 10%,女生 CV = 9.17%,男生成绩离散程度较高 第四章 第 2 题: (1)0.077 (2)0.25 (3)0.50 (4)0.25 (5)0.192 第 3 题: (1)0.0625 (2)0.0625 (3)0.25 (4)0.004 第 4 题: (1)0.008 (2)0.128 第五章 第 1 题: (1)1 (2)0.866 (3)0.0469 第 2 题: (1) 0.38493 (2) 0.30598 (3) 0.41924 (4) 0.89726 (5) 0.66141 (6) 0.78193 第 3 题:34.134 人;68.268% 第 4 题:A、B、C、D、E 等级人数分别为 18、119、226、119、18 第七章 第 1 题:95%的置信区间(66.08,73.92) ,99%的置信区间(64.84,75.16) 第 2 题: (67.30,75.70) 第 3 题: (73.27, 86.73) 第 4 题:Z = 9.09 > Z0.005 = 2.58 第 5 题:Z = – 2.68 < – Z0.01 = – 2.33 第八章 第 1 题: (– 8.573,9.538) 第 2 题:t = 0 第 3 题:|t| = | –1.033| < t0.025, 9=2.262 第 4 题:|t| = | –3.4| > t0.01, 7 = 2.998 第九章 第 1 题: (5.30,14.06) 第 2 题:F = 186.67 > F0.01, 4, 6 = 9.15 第 3 题:Z = 4.187 > Z0.005 = 2.58 第十章 第 1 题:F = 25.70 < F0.05, 2, 9 = 4.26 第 2 题:F = 2.854 < F0.05, 2, 9 = 4.26 第 3 题:F = 4.495 > F0.05, 3, 21 = 3.07 第 4 题:FA =1.692,FB =0.884,FA*B =0.617,均小于 F0.05,1, 16 = 4.49 第 5 题: 差异来源 平方和 SS 自由度 df A 因素 B 因素 A*B 组内 180 300 3000 100 2 3 6 12 方差 MS 90 100 500 8.33
(完整版)现代心理与教育统计学

心理统计学第一章概述描述统计定义:研究如何把心理与教育科学实验或调查得来的大量数据科学的科学的加以整理概括和表述作用:使杂乱无章的数字更好的显示出事物的某些特征,有助于说明问题的实质。
具体内容:1数据分组:采用图与表的形式。
2计算数据的特征值:集中量数(平均数中数)离散量数(方差)3计算量事物间的相关关系:积差相关(2列 3列多列)推断统计定义:主要研究如何利用局部数据(样本数据)所提供的信息,依据数理统计提供的理论和方法,推论总体情形。
作用:用样本推论总体。
具体内容:1如何对假设进行检验。
2如何对总体参数特征值进行估计。
3各种非参数的统计方法。
心理与教育统计基础概念数据类型一从数据来源来划分1计数数据:计算个数或次数而获得的数据.(都是离散数据)2测量数据:借助一定测量工具或测量标准而获得的数据。
(连续数据)二根据数据所反映的测量水平1称名数据(分类)定义:指用数字代表事物或数字对事物进行分类的数据。
特点:数字只是事物的符号,而没有任何数量意义.统计方法:百分数次数众数列联相关卡方检验等。
(非参检验)2顺序数据(分类排序)定义:指代事物类别,能够表明不同食物的大小等级或事物具有的某种特征的程度的数据。
(年级)特点:没有相等单位没有绝对零点.不表示事物特征的真正数量。
统计方法:中位数百分位数等级相关肯德尔和谐系数以及常规的非参数检验方法。
3等距数据(分类排序加减(相等单位))(真正应用最广泛的数据)定义:不仅能够指代物体的类别等级,而且具有相等的单位的数据.(成绩温度)特点:真正的数量,能进行加减运算,没有绝对零点,不能进行乘除计算。
统计方法:平均数标准差积差相关 Z检验 t检验 F检验等。
4比率数据(分类排序加减法乘除法(绝对零点))定义:表明量的大小,也具有相等单位,同时具有绝对零点。
(身高反应时)特点:真正的数字,有绝对零点,可以进行加减乘除运算.在统计中处理的数据大多是顺序数据和等距数据。
现代心理与教育统计学03506

心理统计学第一章概述描述统计定义:研究如何把心理与教育科学实验或调查得来的大量数据科学的科学的加以整理概括和表述作用:使杂乱无章的数字更好的显示出事物的某些特征,有助于说明问题的实质。
具体内容:1数据分组:采用图与表的形式。
2计算数据的特征值:集中量数(平均数中数)离散量数(方差)3计算量事物间的相关关系:积差相关(2列3列多列)推断统计定义:主要研究如何利用局部数据(样本数据)所提供的信息,依据数理统计提供的理论和方法,推论总体情形。
作用:用样本推论总体。
具体内容:1如何对假设进行检验。
2如何对总体参数特征值进行估计。
3各种非参数的统计方法。
心理与教育统计基础概念数据类型一从数据来源来划分1计数数据:计算个数或次数而获得的数据。
(都是离散数据)2测量数据:借助一定测量工具或测量标准而获得的数据。
(连续数据)二根据数据所反映的测量水平1称名数据(分类)定义:指用数字代表事物或数字对事物进行分类的数据。
特点:数字只是事物的符号,而没有任何数量意义。
统计方法:百分数次数众数列联相关卡方检验等。
(非参检验)2顺序数据(分类排序)定义:指代事物类别,能够表明不同食物的大小等级或事物具有的某种特征的程度的数据。
(年级)特点:没有相等单位没有绝对零点。
不表示事物特征的真正数量。
统计方法:中位数百分位数等级相关肯德尔和谐系数以及常规的非参数检验方法。
3等距数据(分类排序加减(相等单位))(真正应用最广泛的数据)定义:不仅能够指代物体的类别等级,而且具有相等的单位的数据。
(成绩温度)特点:真正的数量,能进行加减运算,没有绝对零点,不能进行乘除计算。
统计方法:平均数标准差积差相关Z检验t检验F检验等。
4比率数据(分类排序加减法乘除法(绝对零点))定义:表明量的大小,也具有相等单位,同时具有绝对零点。
(身高反应时)特点:真正的数字,有绝对零点,可以进行加减乘除运算。
在统计中处理的数据大多是顺序数据和等距数据。
三按照数据是否具有连续性离散数据连续数据变量观测值随机变量变量:指心理与教育实验观察调查种想要获得的数据。
心理和教育统计学课后题答案解析

张厚粲现代心理与教育统计学第一章答案1名词概念(1)随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
(2)总体答:总体(population)又称为母全体或全域,就是具有某种特征的一类事物的总体,就是研究对象的全体。
(3)样本答:样本就是从总体中抽取的一部分个体。
(4)个体答:构成总体的每个基本单元。
(5)次数就是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
(6)频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
(7)概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
(8)统计量答:样本的特征值叫做统计量,又称作特征值。
(9)参数答:又称总体参数,就是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学?学习它有何意义?答:(1)心理与教育统计学就是专门研究如何运用统计学原理与方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理与步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
(2)学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学就是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务就是对客观事实进行预测与分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正就是提供了这样一种科学方法。
统计方法就是从事科学研究的一种必不可少的工具。
教育与心理统计学 第一章 常用的统计表与图考研笔记-精品

一、次数分布表
次数分布:指的是一批数据中各个不同数值所出现的次数情况,或者是一批数据在量尺上各等距区组内所出现的次数情况。次数分布主要
表小数据在各个分组区间内的散布情况,依据它所显小的次数如何产生,次数分布可区分为简单次数分布、分组次数分布、相对次数分布、
正态的总体,则可以利用经验公式来确定组数,即:K=1.87(N-l)2/5°公式中的N为数据个数,K取近似整数。
③定组距:在知道全距R和组数K之后,就可以确定分组的组距组距用符号i来表小。i=R/K
④写出组限:组限是每个组的起始点界限。
⑤求组中值:组中值是各组的组中点在量尺上的数值,其计算公式为:组中值=(组实上限+组实下限)/2=精确下限+组距/2;精确上限-
第三节统计图
统计图是以几何图形和形象图形表示统计资料数量关系的工具。
统计图一般由下面几个部分组成:图号及图题:图目;图尺;图形;例;图注。
统计图一般米用直角坐标系,通常横轴表小自变量(类别),称为分类轴。纵轴表示因变量(次数),称为数值轴
注:统计图包括:次数分布图和一些其他类型的常用统计图。
(四)累积相对次数分布表和累积百分数分布表
前面介绍的累积次数分布表是对简单次数进行累积的结果。与此相对应,累积相对次数是对相对次数进行累积的结果。因此,由累积相对
次数制作的统计表便称为累积相对次数分布表。由于累积相对次数仍然是小数,所以把这些小数乘以100,便得到〃百分数〃,从而可把累积
相对次数分布表等价地转换为"累积百分数分布表"。
第一章常用的统计表与图
第一章常用的统计表与图
心理与教育统计学第一章绪论

目录
• 心理与教育统计学概述 • 心理与教育统计学的基本概念 • 心理与教育统计学的研究方法
目录
• 心理与教育统计学的数据处理与分析 • 心理与教育统计学的软件应用
01
心理与教育统计学概述
定义与性质
定义
心理与教育统计学是应用数理统 计学的原理和方法,对心理学和 教育领域中的数据进行分析和解 释的一门科学。
描述性统计
用于描述数据的基本特征和分布情况,如均值、方差、频数 、频率等。
推论性统计
根据样本数据推断总体特征,如参数估计、假设检验、回归 分析等。
03
心理与教育统计学的研究 方法
实验法
总结词
通过控制实验条件,观察实验组和对照组之间的差异,以探究变量之间的关系。
详细描述
实验法是一种常用的心理学研究方法,通过人为地控制某些条件,观察不同条 件下被试的反应和表现,以探究心理现象的本质和规律。实验法可以有效地控 制无关变量,提高研究的内部效度。
Stata软件介绍
总结词
Stata是一款适用于统计学、数据分析、数据管理等方面的软件,尤其在社会科学领域 有广泛应用。
详细描述
Stata提供了丰富的统计分析工具,包括回归分析、生存分析、时间序列分析等,并支 持多种数据格式和导入导出功能。它还具有强大的数据管理功能,能够帮助用户高效地 处理和管理大量数据。此外,Stata还提供了丰富的交互式命令和编程语言,方便用户
随机抽样、系统抽样、分 层抽样、整群抽样等。
变量与数据类型
变量
表示研究对象某一特征 或属性的度量值,具有
可变性。
分类变量
顺序变量
数值型变量
表示研究对象所属的类 别或属性,如性别、婚
心理统计第01章习题解答

1. 名词解释观测值(observation):实验、调查和观测某些个体在某一变量上的具体的数值,即为观测值。
随机变量:某一变量在实验、调查和观测之前,不能预知其数值的变量。
随机变量的特点是:离散性、变异性、规律性。
总体(population)是指具有某一种特征的一类事物的全体;构成总体的每一个基本元素叫个体;在总体中按照一定的规则抽取的部分个体,称为总体的一个样本(sample)。
表示样本的数字特征的量叫统计量。
如描述数据集中趋势的一些统计指标称为平均数;描述一组数据离散程度的统计指标称为标准差。
表示总体的数字特征的量叫参数。
如反应总体集中情况的统计指标称为总体平均数;反应总体离散程度的统计指标称为标准差。
次数:某一随机事件在某一类别中出现的数据多少,亦称频数(frequency)。
频率:某一事件发生的次数与总事件的比率。
概率(probability):某一随机事件在某一总体中出现的比率。
2. 何谓心理与教育统计学?学习它有何意义?心理与教育统计学是专门研究如何搜集、整理、分析在心理教育方面由实验和调查所获得的数据资料,并如何根据这些数字所传递的信息,进行科学推论找出客观规律的一门学科。
它是应用数理统计学的一个分支,是心理与教育研究中的科学工具。
意义:(1)研究心理与教育现象变化的统计规律(2)为心理与教育研究提供科学的依据(3)促进量化研究的发展……3.选用统计方法有哪几个步骤?(1)看实验或调查设计是否合理,即所获的的数据是否适合用统计方法取处理,正确将其数量化;(2)分析实验或调查数据的类型,针对不同的数据类型选用与之相应的统计方法;(3)分析数据的分布规律,看数据是正态分布还是非正态分布以及是大样本数据还是小样本数据。
4.怎样理解总体、样本和个体?总体(population)是指具有某一种特征的一类事物的全体;如研究大学生的心理健康状况,全国的大学生即为总体。
构成总体的每一个基本元素叫个体;如具体的每一个大学生即为个体。
心理与教育统计学

• 顺序数据
– 指既无相等单位、也无绝对零的数据,是按事物某种属 性的多少或大小,按次序将各个事物加以排列后获得的 数据资料。
– 例如学生的等级评定、喜爱程度等。
• 等距数据
– 指有相等单位,但无绝对零的数据。 – 例如温度、各种智商分数等。
• 比率数据
13
推论统计
• 主要研究如何通过局部数据所提供的信息,推论总体的情形。 • 具体包括:
– 1、总体参数的估计方法(参数、非参数) – 2、假设检验(计数数据和测量数据)
14
实验设计
• 研究如何科学地、经济地以及更有效地进行实验。 • 作为一个严谨的实验研究,在实验以前就要对研
究的步骤、被试的取样方法、实验条件的控制, 以及结果采用的统计分析方法等等做出严格的设 计。 • 实验设计是一门独立的课程,心理统计课中涉及 与之相关的内容并不多。
• 随机变量
– 在测查前不能预料取到什么值的变量,称为随 机变量(random variables)。
24
数据的精确值问题
• 计数数据 – 表示的是一个个数据点。
• 测量数据 – 表示的是数轴上的一段距离或一个区间。 – 数据的上下实限 – 特例: • 年龄(数值不是代表中间点,而是指开始点)
25
• 数理统计的产生与发展
– 描述统计(高尔顿和皮尔逊) – 推论统计(费舍)
17
第三节 心理与教育统计学的发展 • 统计在心理与教育研究中的应用(p.15):
• 19世纪中期,凯特勒提出大量与人有关的量数遵循正态分布曲线; • 最早将统计方法应用于心理学研究的是高尔顿。
18
第三节 心理与教育统计学的发展 • 心理与教育统计在我国的发展与应用(p.17):
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、有助于深刻理解所学的心理与教育方面的 知识
IQ 100 15 Z X X Z SD
二、获取心理与教育方面的新知识的重要条件。 你在一本心理杂志上看到这样一段文字:“独
立组的 t检验表明,在训练之前,实验组与控
制组之间,在三个方面无显著差异,三个t值分
别是t(18)=0.39,P>0.05; t(18) = 0.14, P>0.05; t(18) =1.35,P>0.05。”
心理学考试质量分析表 检测项目 考试人数: 平均分数: 成绩标准差: 考试优良率% 考试合格率% 最高分: 最低分: 考试信度: 考试效度: 成绩分布正态性检验: 偏度: 峰度: 试卷总体难度: 试卷总体区分度: 结果 20 76.100 4.04 20.00% 100.0% 84.0 66.0 0.6162 成绩分布服从正态分布 -0.3786 -0.3594 0.7605 0.1000 参考标准 7 - 10
样本特性
量数
参数与统计量的符号系统
平均数 统计量 数
标准差
相关系数
X
S , SD
r
二、 近似计算与连加和
(一)近似数的计算法则 四舍五入法则 偶数法则:若在0.5之前是奇数,则去五进 一, 若0.5之前是偶数,则把五舍去。 保留小数位数:最终结果保留2位,计算过程中保 留4位。
1.
基本概念 总体、样本、变量、随机变量、参数、统计量、描
述统计、推论统计、实验设计
2. 3. 4.
何谓心理与教育统计?学习它有何意义?
简述心理与教育统计的基本内容。
参数与统计量之间有何区别与联系?
参考文献
王孝玲编著,《教育统计学》,华东师范大学出版社, 2000年版 张敏强,《教育与心理统计学》,人民教育出版社, 2003版
实验设计:研究者为了科学、经济、有效的进 行研究,在研究前所制定的研究计划。通常包 括研究课题的确定、研究变量的确定、研究对 象的抽取、研究方法、研究工具、研究结果的
统计分析方法的选择等。
获得了一批什么样的数据?其分布有何特
征?(借用统计图表和一些统计量数)
描述统计:对已获得的数据进行初步整理和概 括,以统计图表和统计量数的形式将研究对象 的全貌和分布特征清晰显现出来的统计方法。 主要包括统计图表、集中量、差异量、峰态量、
大样本 n>30
小样本 n<30
相 对 性
样本(n)
(二) 变量、观测值、随机变量
常量 变量:可以取不同数值的量 观测值:变量所对应的各个具体数值。 随机变量:在取值之前不能预料取什么值的 变量。
(三) 参数与统计量 • 参数: • 统计量: 总体特性
偏态量、位置量、相关量等。
总体而言,推荐生与统考生的身心发展状况 分别如何?(参数估计) 推荐生身心发展是否显著好于统考生?(假 设检验)
推论统计:根据已获得的样本数据所提供的 信息来推论总体的特征的统计方法。通常包
2检 括总体参数估计和假设检验(t、Z、F、
验等)两部分。
三者关系:
一般水平 及关系 平 均
(二)连加和及其运算法则
1、连加和的缩写式
Xi X Xi
n i 1
写出下列符号的展开式
X
X ?
2
XY ?
2
?
X Y ?
2、连加和的几个运算法则
CX C X
X Y X Y
C NC
自学内容:教材第11-16页 思考与练习题
描述统计 (基础)
概率 分布
推论统计 推论统计 (核心)
实验设计 (保障)
可靠数据
第三节 心理与教育统计中的基本概念
一、基本概念 (一) 总体、样本、样本容量
样本 容量 样本包含的个体数目
总体(N)
数理统计 原理与方法
心 理与教育统计学 人口统计学 经济统计学 生物统计学
……
运用…… 研究…… 数量关系的学科
学习心理与教育统计学应注意的问题
克服畏难情绪 注意重点掌握各种统计方法的使用条件与结果的正确 解释
做一定的练习
二、内容
选择哪些方面作为衡量学生发展的指标(学 习成绩、心理健康水平、身体素质、解决问 题能力等)?(研究变量的确定) 选择多少学生?(样本容量的确定) 怎样选取学生?(抽样方法的选择) 用什么统计方法进行分析?(统计方法的选 择)
心理与教育测量、实验心理学
三、为学校实施科学管理提供有效工具。
例题:张老师是一位刚参加工作的年轻心理学教师, 本学期期末所教班级的学生考试成绩如下:81,73, 64,59,94,82,67,75,90,48,57,86,75, 93,88,72,65,77,60,79,70,81,56,64, 73,99,87,66,50,45,80,82,67,74,68, 92,54,57,87,64,76,55,61,65,70,89, 71,49,60,72,70,83,67,74。 问题:张老师应该怎样比较全面地整理出这次考试 分数?怎样初步评价这次考试结果?
> 0.7 > 0.4 服从正态分布
> 0.2
假如你在某个小学任校长,该校正在进行一 项教学改革,如何评价改革的成败?
四、从事心理与教育研究的重要工具。
第二节 心理与教育统计的性质与 主要研究内容
定义:应用统计学的原理和方法对心理与教育问 题进行定量研究的一门学科。
一、性质
应用 统计
统 计 学
心理与教育统计学
主讲人:王美萍
第一章 绪论
第一节 为什么要学习心理与教育统计 第二节 心理与教育统计的主要内容 第三节 心理与教育统计中的基本概念与预 备知识
教学目的与要求:
了解心理与教育统计学的基本性质及学习 该课程的必要性,掌握心理与教育统计学 的基本内容和基本概念,为进一步学习本 课程奠定基础。
教学重点与难点:
重点:掌握心理与教育统计学的基本内容 和基本概念 难点:理解描述统计、推论统计与实验设 计的内涵及其相互关系。
第一节 为什么要学习心理与教育统计学
“从事教育的人,若不懂得教育统计,不能称 为教育科学家。” (艾伟) “ Statistical thinking will one day be as necessary for effective citizenship as ability to read and write。” (H.G.Wells 1866-1946)
