南京市2010年中考试题及答案

合集下载

中考试卷---2010年南京市数学试题及解析

南京市2010年初中毕业生学业考试数学注意事项：1．本试卷共6页．满分120分．考试时间为120分钟，考生答题全部答在答题卡，答在本试卷上无效．2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡对应的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上）1． -3的倒数是（）A．-3 B．3 C．13D．132．计算a3·a4的结果是（）A．a5 B．a7 C．a8 D．a123．如图，下列各数中，数轴上点A表示的可能是（）A．4的算术平方根B．4的立方根C．8的算术平方根D．8的立方根4．甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（）A．1℃~3℃B．3℃~5℃C．5℃~8℃D．1℃~8℃5．如图，在平面直角坐标系中，菱形OABC的顶点C的坐标是（3，4），则顶点A、B的坐标分别是（）A．（4，0）（7，4）B．（4，0）（8，4）C．（5，0）（7，4）D．（5，0）（8，4）6．如图，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间的函数关系的图象大致为（）二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡．．．相应位置．．．．上）7． -2的绝对值的结果是_____．8．函数11yx=-中，自变量x的取值范围是_____．9．南京地铁2号线（含东延线）、3号线南延线开通后，南京地铁总里程约为85000m，将85000用科学记数法表示为_____．10．如图，O是直线l上一点，∠AOB=100°，则∠1+∠2=_____°．11a≥0）的结果是_____．12．若反比例函数的图象经过点（-2，-1），则这个函数的图象位于第_____象限．13．甲、乙两人5次射击命中的环数如下：甲 7 9 8 6 10乙 7 8 9 8 8则这两人5次射击命中的环数的平均数x甲=x乙=8，方差2s甲_____2s乙．（填“＞”、“＜”或“=”）14．如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点．若两圆的半径分别为3cm 和5cm，则AB的长为_____cm．15．如图，点C在⊙O上，将圆心角∠AOB绕点O按逆时针方向旋转到∠A/OB/，旋转角为α（0°＜α＜180°）．若∠AOB=30°，∠BCA/=40°，则∠α=_____°．16．如图，AB⊥BC，AB=BC=2 cm，ºOA与»OC关于点O中心对称，则AB、BC、»CO、ºOA所围成的图形的面积是_____ cm2．三、解答题（本大题共12小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解方程组24,2 5.x yx y+=+=⎧⎨⎩18．（6分）计算2211()a ba b ab--÷．19．（6分）为了估计西瓜、苹果和香蕉三种水果一个月的销售量，某水果店对这三种水果7天的销售量进行了统计，统计结果如图所示．（1）若西瓜、苹果和香蕉的售价分别为6元/千克、8元/千克和3元/千克，则这7天销售额．．．最大的水果品种是（）；A．西瓜B．苹果C．香蕉（2）估计一个月（按30天计算）该水果店可销售苹果多少千克？20．（7分）如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC为10m，测角仪的高度CD 为1.5m，测得树顶A的仰角为33°．求树的高度AB．（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）21．（7分）如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．求证：（1）OA=OB；（2）AB∥CD．22．（7分）已知点A（1，1）在二次函数y=x2-2ax+b的图象上．（1）用含a的代数式表示b；（2）如果该二次函数的图象与x轴只有一个交点，求这个二次函数的图象的顶点坐标．23．（9分）某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该项厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你交转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．在用文字说明和扇形的圆心角的度数．2．结合转盘简述获奖方式，不需说明理由．）24．（8分）甲车从A地出发以60km/h的速度沿公路匀速行驶，0.5h后，乙车也从A地出发，以80km/h的速度沿该公路与甲车同向匀速行驶，求乙车出发几小时追上甲车．请建立一次函数关系．．．．．．．．解决上述问题．25．（8分）如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45°，BC∥AD，CD∥AB．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为1，求图中阴影部分的面积（结果保留π）．26．（8分）学习《图形的相似》后，我们可以探索两个直角三角形全等的条件所获得的经验，继续探索两个直角三角形相似的条件．（1）“对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”，类似地，你可以得到“满足_____，或_____，两个直角三角形相似”；（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地，你可以得到满足_____两个直角三角形相似”．请结合下列所给图形，写出已知，并完成说理过程．已知：如图，_____．试说明Rt△ABC∽Rt△A/B/C/．27．（8分）某批发商以每件50元的价格购进800件T恤．第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单位应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓时单价为40元．设第二个月单价降低x元．（1）填表（不需要化简）（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？28．（8分）如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．（1）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；（2）P是MG的中点，请直接写出点P运动路线的长．南京市2010年初中数学毕业生学业考试数学参考答案1、【分析】由实数a（a≠0）的倒数是1a得-3的倒数是13-，化简得13-．【答案】C2、【分析】计算同底数的乘法时，需将底数保持不变，指数相加．a3·a4= a3+4=a7．【答案】B3、【分析】观察数轴发现：点A 在2与3之间，因此可排除选项A 和D ；再由4的立方根小于2再排除选项B ．所以本题答案选C ．【答案】C4、【分析】可将问题转化求不等式组15,38.x x ⎧⎨⎩≤≤≤≤的解集，如图可得解集为3≤x ≤5；也可将问题理解为：适宜两种蔬菜放在一起同时保鲜的温度是指同时满足“1℃~5℃”与“3℃~8℃”，因此需要取这两部分温度的共同部分（即两个集合的交集）．【答案】B5、【分析】由点C 的坐标为（3，4）易知OC =5，结合象限得点A 的坐标为（5，0），排除选项A 、B ；进而再由BC =OA =OC =5得点B 的坐标为（8，4），从而选D ．【答案】D6、【分析】由生活经验知：当小亮走到路灯的正下方时，此时影长为0，因此可排除选项C 、D ；在确定答案是选项A 或B 上感觉不好下手．设小亮身高为a ，路灯C 到路面的距离为h ，点A 到路灯正下方的距离为b ，如图，由中心投影得a y h b x y =-+，整理得a ab y x h a h a=-+--，因此答案为A ．【答案】A7、【分析】由一个负数的绝对值是它的相反数得：-2的绝对值是-（-2）=2．本题也可根据“-2的绝对值表示-2的点到原点的距离为2”来求解．【答案】28、【分析】由函数的意义得x -1≠0，解得x ≠1．【答案】x ≠19、【分析】85000=8.5×10000=8.5×104．．8531【答案】8.5×10410、【分析】观察图形得∠1+∠2+∠AOB=180°，所以∠1+∠2=180°-∠AOB=180°-100°=80°．【答案】8011、====4·|a| =4a．【答案】4a12、【分析】设该反比例函数的关系式为kyx=，根据题意得12k-=-，所以k=-1×（-2）=2＞0，因此该反比例函数位于第一、三象限．【答案】一、三13、【分析】通过观察甲、乙两组数据发现：乙组数据为3个8，1个7、1个9；甲组数据为6、7、8、9、10各1个．因此甲组数据与平均数8离散程度较大，乙组数据与平均数8离散程度较小，所以方差2 s 甲＞2s乙．本题也可通过计算方差进行比较，但是计算较繁，容易出错．【答案】＞14、【分析】连接OA、OC，由切线的意义知△OAC为直角三角形，再由勾股定理得OA2=OC2+AC2，即52=32+AC2，所以AC=4，再由垂径定理得AB=2AC=8．【答案】815、【分析】根据圆心角的意义得∠BOA/=2∠BCA/=80°，所以∠α=∠AOB+∠BOA/=30°+80°=110°．【答案】11016、【分析】连接AC，根据中心对称的意义，将“AB、BC、»CO、ºOA所围成的图形的面积”转化为求直角三角形ABC的面积，由AB=BC=2 cm得S△ABC=2 cm2．【答案】217、【答案】解法一：②×2，得2x +4y =10．③③-①，得3y =6．解这个方程得y =2．将y =2代入①，得x =1．所以原方程组的解为12x y ==⎧⎨⎩．解法二：由①，得y =4-2x ．③将③代入②，得x +2(4-2x )=4，解这个方程得x =1．将x =1代入③，得y =2．所以原方程组的解为12x y ==⎧⎨⎩．18、【答案】2211()a b a b ab --÷=()()b aa b a b ab ab -+-÷=()()b a ab ab a b a b -+-g =()()a b ab ab a b a b --+-g =1()a b -+． 19、【分析】（1）由“销售额=售价×数量”得西瓜的销售额为250×6=1500元，苹果的销售额为140×8=1120元，西瓜的销售额为400×3=1200元，因此西瓜的销售最大；（2）观察图形知该水果店7天销售的苹果为140千克，平均每天为20千克，因此一个月可销售苹果大约为20×30=600千克．【答案】（1）A ；（2）140÷7×30=600（千克）．答：估计一个月该水果店可销售苹果600千克．20、【分析】观察图形发现可过点D作DE⊥AB，构造直角三角形ADE，由tan∠ADE=AEDE得AE=DE·tan∠ADE≈10×0.65=6.5，因此AB=AE+BE=AE+CD=6.5+1.5=8m．【答案】如图，过点D作DE⊥AB，垂足为E．在Rt△ADE中，DE=BC=10，∠ADE=33°，tan∠ADE=AE DE，∴AE=DE·tan∠ADE≈10×0.65=6.5，∴AB=AE+BE=AE+CD=6.5+1.5=8（m）．答：树的高度AB约为8 m．21、【分析】（1）欲证OA=OB，观察图形发现OA、OB在△OAB中，因此若能得到∠OAB=∠OBA，则问题得证，而∠OAB=∠OBA可由△ABC≌△BAD得到；（2）观察图形知问题AB∥CD可由∠OAB=∠OCD得到，又∠OAB=∠OBA，若∠OCD=∠ODC，再由∠COD=∠AOB结合三角形内角和是180°得到．而由条件△ABC≌△BAD可得BD=AC，又因为OA=OB，所以OC=OD，所以∠OCD=∠ODC，问题获证．【答案】（1）∵△ABC≌△BAD，∴∠CAB=∠DBA，∴OA=OB．（2）∵△ABC≌△BAD，∴AC=BD．又∵OA=OB，∴∠OCD=∠ODC．∵∠AOB=∠COD，∠CAB=1802AOB-∠，∠ACD=1802COD-∠，∴∠CAB=∠ACD，∴AB∥CD．22、【分析】（1）根据题意得1=1-2a+b，所以b=2a；（2）由题意知方程x2-2ax+b=0有两个相等的实数根，所以所以4a2-4b=0，由（1）b=2a得4a2-8a=0，解得a=0，或a=2．进而分类可求得该二次函数的图象的顶点坐标．【答案】（1）因为点A（1，1）在二次函数y=x2-2ax+b的图象上，所以1=1-2a+b，可得b=2a．（2）根据题意，方程x2-2ax+b=0有两个相等的实数根，所以4a2-4b=4a2-8a=0，解得a=0，或a=2．当a=0时，y=x2，这个二次函数的顶点坐标为（0，0）；当a=2时，y=x2-4x+4，这个二次函数的顶点坐标为（2，0）．所以，这个二次函数的顶点坐标为（0，0）或（2，0）．23 【分析】（1）是否符合要求是指该数学老师设计的方案能否体现“10%得大奖，90%得小奖”的厂家意图，因此可将数学老师的方案用排列法或画树状图的方法得到概率．如用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）=110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．数学老师设计的方案符合要求；（2）本题求解方法不唯一，画图时只需将该转盘（圆）平均分为10份，某种颜色占1份，另一种颜色占9分．顾客购买该型号电视机时获得一次转动转盘的机会，指向1份颜色获得大奖，指向9份颜色获得小奖即可．【答案】（1）该抽奖方案符合厂家的设奖要求．分别用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）= 110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．（2）本题答案不唯一，下列解法供参考．如图，将转盘中圆心角为36°的扇形区域涂上黄色，其余的区域涂上白色．顾客每购买一台该型号电视机，可获得一次转动转盘的机会，任意转动这个转盘，当转盘停止时，指针指向黄色区域获得大奖，指向白色区域获得小奖．24 【分析】乙车出发几小时追上甲车是指两车行驶路程相等或在平面直角坐标系两条直线交点的意义，因此设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km，得y1=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解得x=1.5h．【答案】本题答案不唯一，下列解法供参考．设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km．根据题意，得y1=60（x+0.5）=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解这个方程得x=1.5（h）．答：乙车出发1.5h追上甲车．25 【分析】（1）欲判断直线CD与⊙O的位置关系，由图形可猜想其结论为相切，由条件∠DAB=45°，CD ∥AB知∠ADC=135°，再连接OD得∠ADO=45°，因此∠ODC=90°，猜想得证；（2）观察图形发现阴影部分可在梯形ODCB中求解或在平行四边形ABCD中求解，如【答案】（1）直线CD与⊙O相切．如图，连接OD．∵OA=OD，∠DAB=45°，∴∠ODA=45°，∴∠AOD=90°．∵CD∥AB，∴∠ODC=∠AOD=90°，即OD⊥CD．又∵点D在⊙O上，直线CD与⊙O相切．（2）∵BC∥AD，CD∥AB，∴四边形ABCD是平行四边形，∴CD=AB=2．∴S梯形OBCD=()(12)13222 OB CD OD++⨯==g，∴图中阴影部分的面积为S 梯形OBCD -S 扇形OBD = 313212424ππ-⨯=-．26 【分析】（1）我们知道：两个三角形只要满足两个角对应相等，则这两个三角形相似．由于两个直角三角形的中的直角相等是问题的隐含条件，因此只需再有一个锐角对应相等即可判定它们相似．类比“两直角边对应相等，两个直角三角形全等”可知“两直角对应成比例时” 两个直角三角形相似；（2）HL 是判定两个直角三角形全等的特殊方法，类比全等可得：斜边和一条直角边对应成比例的两个直角三角形相似．说理时可从全等是相似的特例入手，利用参数法，设两个直角三角形对应边的比值为k ，进而转化为三角形相似的判定条件获解．【答案】（1）一个锐角对应相等，两直角对应成比例；（2）斜边和一条直角边对应成比例．在Rt △ABC 和Rt △A /B /C /中，∠C =∠C /=90°，////ABACA B A C =．解法一：设////AB ACA B A C ==k ，则AB = k A /B /，AC = k A /C /．在Rt △ABC 和Rt △A /B /C /中，//BC k B C ===， ∴//////AB AC BCA B A C B C ==，∴Rt △ABC ∽Rt △A /B /C /．解法二：如图，假设AB ＞A /B /，在AB 上截取AB = A /B /，过点B 作BC ⊥AC ，垂足为C ．∵∠C =∠ACB ，∴BC ∥BC ，∴Rt △ABC ∽Rt △A /BC ，////AC ABAC AB =．∵AB = A /B /，∴////AC ABAC A B =．又∵////AB AC A B A C =，∴//AC AC =//AC A C ，∴AC =A /C /． ∵AB = A /B /，∠C =∠ACB =90°，∴Rt △ABC ≌Rt △A /B /C /，∴Rt △ABC ∽Rt △A /B /C /．27 【分析】（1）由“第二个月单价降低x 元”知第二个月的单价为（80-x ），销售量为（200+10 x ）件，清仓时为总数量分别减去前面两个月的剩余量，即800-200-（200+10x ）；（2）我们销售额-成本=利润，由“获利9000元”建立方程得80×200+（80-x ）（200+10x ）+40[800-200-（200+10x ）] -50×800=9000，化简后求解．【答案】（1）80-x ，200+10x ，800-200-（200+10x ）；（2）根据题意，得80×200+（80-x ）（200+10x ）+40[800-200-（200+10x ）] -50×800=9000．整理，得x 2-20x +100=0，解这个方程得x 1= x 2=10，当x =10时，80-x =70＞50．答：第二个月的单价应是70元．28 【分析】（1）欲求y 关于x 的函数关系式，即△EGF 的面积，观察图形发现S △EGF =12EF ·MG ，由条件AM =DM 及正方形的性质可得△AME ≌△DMF ，所以EF =2EM ，因此求出面积的关键是求出MG ．结合图形发现过点M 作MN ⊥BC ，垂足为N 可得Rt △AME ∽Rt △NMG ，进而运用相似三角形的性质得到MG 的长，问题获解；（2）如图，P 1P 2（P 1是P 起始位置，P 2是P 终止位置．）是点P 运动的路线，由Rt △ABM ∽Rt △P 1P 2M ，AB =2AM ，得P 1P 2=2MP 1=2．【答案】（1）当点E 与点A 重合时，x =0，y =12×2×2=2；当点E 与点A 不重合时，0＜x ≤2．2G 1在正方形ABCD 中，∠A =∠ADC =90°，∴∠MDF =90°，∴∠A =∠MDF ．∵AM =DM ，∠AMF =∠DMF ，∴△A M E ≌△DMF ，∴ME =MF ．在Rt △AME 中，AE =x ，AM =1，ME EF =2MF过点M 作MN ⊥BC ，垂足为N （如图）．则∠MNG =90°，∠AMN =90°，MN =AB =AD =2AM ．∴∠AME +∠EMN =90°．∵∠EMG =90°，∴∠GMN +∠EMN =90°，∴∠AME =∠GMN ，∴Rt △AME ∽Rt △NMG ， ∴AMME NM MG =，即12ME MG =，∴MG =2ME ，∴y =12EF ·MG =12×x 2+2，∴y =2x 2+2，其中0≤x ≤2．（2）点P 运动路线的长为2．。

江苏南京2010年中考数学真题及答案解析

南京市2010年初中数学毕业生学业考试数学注意事项：1．本试卷共6页．满分120分．考试时间为120分钟，考生答题全部答在答题卡，答在本试卷上无效．2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡对应的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上）1．（2010江苏南京，1，2分）-3的倒数是（）A．-3 B．3 C．13-D．13【分析】由实数a（a≠0）的倒数是1a得-3的倒数是13-，化简得13-．【答案】C【涉及知识点】实数【点评】本题属于基础题，主要考查学生对概念的掌握是否全面，考查知识点单一，有利于提高本题的信度．【推荐指数】★2．（2010江苏南京，2，2分）计算a3·a4的结果是（）A．a5 B．a7 C．a8 D．a12【分析】计算同底数的乘法时，需将底数保持不变，指数相加．a3·a4= a3+4=a7．【答案】B【涉及知识点】幂的运算【点评】本题属于基础题，考查知识点单一，同学们解题常见错误一是粗心，如误选A 或C；二是混淆了同底数幂的乘法法则和幂的乘方法则，从而误选D．【推荐指数】★★★3．（2010江苏南京，3，2分）如图，下列各数中，数轴上点A表示的可能是（）A．4的算术平方根B．4的立方根C．8的算术平方根D．8的立方根【分析】观察数轴发现：点A在2与3之间，因此可排除选项A和D；再由4的立方根小于2再排除选项B．所以本题答案选C．【答案】C【涉及知识点】实数的估算【点评】本题考查学生估算的能力，问题不难，解决此类问题通常运用排除法．【推荐指数】★★4．（2010江苏南京，4，2分）甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（）A ．1℃~3℃B ．3℃~5℃C ．5℃~8℃D ．1℃~8℃【分析】可将问题转化求不等式组15,38.x x ⎧⎨⎩≤≤≤≤的解集，如图可得解集为3≤x ≤5；也可将问题理解为：适宜两种蔬菜放在一起同时保鲜的温度是指同时满足“1℃~5℃”与“3℃~8℃”，因此需要取这两部分温度的共同部分（即两个集合的交集）．85310【答案】B【涉及知识点】不等式组的解集【点评】本题考查不等式组的解集的确定，结合数轴是确定不等式组的常用方法．【推荐指数】★★★5．（2010江苏南京，5，2分）如图，在平面直角坐标系中，菱形OABC 的顶点C 的坐标是（3，4），则顶点A 、B 的坐标分别是（）A ．（4，0）（7，4）B ．（4，0）（8，4）C ．（5，0）（7，4）D ．（5，0）（8，4）【分析】由点C 的坐标为（3，4）易知OC =5，结合象限得点A 的坐标为（5，0），排除选项A 、B ；进而再由BC =OA =OC =5得点B 的坐标为（8，4），从而选D ．【答案】D【涉及知识点】平面直角坐标系、菱形的性质等【点评】本题综合考查平面直角坐标系、菱形的性质等知识，难度比前面的几题稍大．解决此类问题通常抓住菱形的性质入手，再结合平面直角坐标系的相关求解．【推荐指数】★★★6．（2010江苏南京，6，2分）如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x 的变化而变化，那么表示y 与x 之间的函数关系的图象大致为（）【分析】由生活经验知：当小亮走到路灯的正下方时，此时影长为0，因此可排除选项C 、D ；在确定答案是选项A 或B 上感觉不好下手．设小亮身高为a ，路灯C 到路面的距离为h ，点A 到路灯正下方的距离为b ，如图，由中心投影得a y hb x y =-+，整理得aab y x h a h a =-+--，因此答案为A ． b-x+y y x b a hB AC【答案】A【涉及知识点】函数的图象、中心投影【点评】本题考查函数的图象函数的图象、中心投影，解决此类问题的关键是抓住横轴与纵轴的意义．由于此类问题抽象性较强，因此经常出现在各地中考试卷选择题的最后一题，具有一定的区分度．【推荐指数】★★★★二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 7．（2010江苏南京，7，2分）-2的绝对值的结果是_____．【分析】由一个负数的绝对值是它的相反数得：-2的绝对值是-（-2）=2．本题也可根据“-2的绝对值表示-2的点到原点的距离为2”来求解．【答案】2【涉及知识点】实数的绝对值【点评】本题属于基础题，主要考查学生对绝对值概念的掌握，常见的此类考点还有相反数、正数与负数的意义等．【推荐指数】★★8．（2010江苏南京，8，2分）函数11y x =-中，自变量x 的取值范围是_____．【分析】由函数的意义得x -1≠0，解得x ≠1．【答案】x ≠1【涉及知识点】函数的定义域【点评】本题考查学生对函数定义域的理解，此类问题通常结合二次根式、不等式等知识点进行考查，难度一般不大．【推荐指数】★★★9．（2010江苏南京，9，2分）南京地铁2号线（含东延线）、3号线南延线开通后，南京地铁总里程约为85000m ，将85000用科学记数法表示为_____．【分析】85000=8.5×10000=8.5×104．．【答案】8.5×104【涉及知识点】科学记数法【点评】本题考查用科学记数法表示较大的数，科学记数法的形式为a ×10n （1≤|a |＜10），因此解决此类问题的关键找到a与n．这一类问题通常结合最新的时事进行考查，难度不大．【推荐指数】★★★10．（2010江苏南京，10，2分）如图，O是直线l上一点，∠AOB=100°，则∠1+∠2=_____°．【分析】观察图形得∠1+∠2+∠AOB=180°，所以∠1+∠2=180°-∠AOB=180°-100°=80°．【答案】80【涉及知识点】相交线，平角【点评】本题属于基础题，主要考查学生对平角概念的掌握，考查知识点单一，有利于提高本题的信度．【推荐指数】★★11．（2010江苏南京，11，2分）计算28a a（a≥0）的结果是_____．【分析】根据二次根式的乘法法则得2222828164a a a a a a=⨯===4·|a|=4a．【答案】4a【涉及知识点】二次根式【点评】本题考查二次根式的乘法法则，问题难度不大，绝大部分学生按照法则进行计算都能得出正确结果．【推荐指数】★★12．（2010江苏南京，12，2分）若反比例函数的图象经过点（-2，-1），则这个函数的图象位于第_____象限．【分析】设该反比例函数的关系式为kyx=，根据题意得12k-=-，所以k=-1×（-2）=2＞0，因此该反比例函数位于第一、三象限．【答案】一、三【涉及知识点】反比例函数【点评】本题考查反比例函数，近年来反比例函数考点多为反比例函数的意义、图象和应用等，难度为中等．【推荐指数】★★★★13．（2010江苏南京，13，2分）甲、乙两人5次射击命中的环数如下：甲7 9 8 6 10乙7 8 9 8 8则这两人5次射击命中的环数的平均数x甲=x乙=8，方差2s甲_____2s乙．（填“＞”、“＜”或“=”）【分析】通过观察甲、乙两组数据发现：乙组数据为3个8，1个7、1个9；甲组数据为6、7、8、9、10各1个．因此甲组数据与平均数8离散程度较大，乙组数据与平均数8离散程度较小，所以方差2s甲＞2s乙．本题也可通过计算方差进行比较，但是计算较繁，容易出错．【答案】＞【涉及知识点】方差【点评】本题考查统计中的方差知识点，方差反映数据的离散程度，可根据公式进行求解，由于本题是客观题，所以也可根据意义进行判断．【推荐指数】★★14．（2010江苏南京，1，2分）如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点．若两圆的半径分别为3cm和5cm，则AB的长为_____cm．【分析】连接OA、OC，由切线的意义知△OAC为直角三角形，再由勾股定理得OA2=OC2+AC2，即52=32+AC2，所以AC=4，再由垂径定理得AB=2AC=8．【答案】8【涉及知识点】圆的切线的性质、勾股定理、垂径定理【点评】本题综合考查圆的切线的性质、勾股定理、垂径定理等知识点，解决此类问题的关键是连接半径建立直角三角形，运用勾股定理模型建立方程．【推荐指数】★★★15．（2010江苏南京，1，2分）如图，点C在⊙O上，将圆心角∠AOB绕点O按逆时针方向旋转到∠A/OB/，旋转角为α（0°＜α＜180°）．若∠AOB=30°，∠BCA/=40°，则∠α=_____°．【分析】根据圆心角的意义得∠BOA/=2∠BCA/=80°，所以∠α=∠AOB+∠BOA/=30°+80°=110°．【答案】110【涉及知识点】圆心角【点评】本题难度中等偏下，主要考查学生对圆心角意义的理解，解决问题要紧紧抓住“在同圆或等圆中，同弧所对圆周角的度数是圆心角度数的一半”．【推荐指数】★★★16．（2010江苏南京，16，2分）如图，AB⊥BC，AB=BC=2 cm， OA与 OC关于点O中心对称，则AB、BC、 CO、 OA所围成的图形的面积是_____ cm2．【分析】连接AC，根据中心对称的意义，将“AB、BC、 CO、 OA所围成的图形的面积”转化为求直角三角形ABC的面积，由AB=BC=2 cm得S△ABC=2 cm2．【答案】2【涉及知识点】中心对称、等腰直角三角形【点评】本题考查学生中心对称、等腰直角三角形等知识点，由于问题求解需要对图形进行转化，所以本题有一定的区分度．【推荐指数】★★★三、解答题（本大题共12小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（2010江苏南京，17，6分）解方程组24,2 5.x yx y+=+=⎧⎨⎩【答案】解法一：②×2，得2x+4y=10．③③-①，得3y=6．解这个方程得y=2．将y=2代入①，得x=1．所以原方程组的解为12xy==⎧⎨⎩．解法二：由①，得y=4-2x．③将③代入②，得x+2(4-2x)=4，解这个方程得x=1．将x=1代入③，得y=2．所以原方程组的解为12xy==⎧⎨⎩．【点评】对二元一次方程组的考查主要突出“消元”思想，题目一般不难，系数比较简单，主要考查方法（加减消元法和代入消元法）的掌握．【推荐指数】★★★★18．（2010江苏南京，18，6分）计算22 11()a ba b ab--÷．【答案】2211()a b a bab --÷=()()b a a b a b ab ab -+-÷=()()b a ab ab a b a b -+- =()()a b ab ab a b a b --+- =1()a b -+．【点评】本题考查分式的化简，该知识点是各地中考必考之一，常见考查形式为化简或化简求值，解决此类问题时要注意熟练运用通分与约分的技巧．【推荐指数】★★★★19．（2010江苏南京，19，6分）为了估计西瓜、苹果和香蕉三种水果一个月的销售量，某水果店对这三种水果7天的销售量进行了统计，统计结果如图所示．（1）若西瓜、苹果和香蕉的售价分别为6元/千克、8元/千克和3元/千克，则这7天销售额．．．最大的水果品种是（）； A ．西瓜 B ．苹果 C ．香蕉（2）估计一个月（按30天计算）该水果店可销售苹果多少千克？【分析】（1）由“销售额=售价×数量”得西瓜的销售额为250×6=1500元，苹果的销售额为140×8=1120元，西瓜的销售额为400×3=1200元，因此西瓜的销售最大；（2）观察图形知该水果店7天销售的苹果为140千克，平均每天为20千克，因此一个月可销售苹果大约为20×30=600千克．【答案】（1）A ；（2）140÷7×30=600（千克）．答：估计一个月该水果店可销售苹果600千克．【点评】统计图表是近年来各地中考必考知识点之一，考查学生统计意识和统计技能．问题（1）中求解中部分学生常因审题不清，出现误选C 的情况．【推荐指数】★★★★20．（2010江苏南京，20，7分）如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC 为10m ，测角仪的高度CD 为1.5m ，测得树顶A 的仰角为33°．求树的高度AB ．（参考数据：sin 33°≈0.54，cos 33°≈0.84，tan 33°≈0.65）【分析】观察图形发现可过点D作DE⊥AB，构造直角三角形ADE，由tan∠ADE=AE DE得AE=DE·tan∠ADE≈10×0.65=6.5，因此AB=AE+BE=AE+CD=6.5+1.5=8m．【答案】如图，过点D作DE⊥AB，垂足为E．在Rt△ADE中，DE=BC=10，∠ADE=33°，tan∠ADE=AE DE，∴AE=DE·tan∠ADE≈10×0.65=6.5，∴AB=AE+BE=AE+CD=6.5+1.5=8（m）．答：树的高度AB约为8 m．【点评】解直角三角形是每年中考的必考知识点之一，主要考查直角三角形的边角关系及其应用，此类问题的一般解法是通过添加辅导线构造直角三角形进行求解，问题难度一般不大．【推荐指数】★★★★21．（2010江苏南京，21，7分）如图，四边形ABCD的对角线AC、BD相交于点O，△ABC ≌△BAD．求证：（1）OA=OB；（2）AB∥CD．【分析】（1）欲证OA=OB，观察图形发现OA、OB在△OAB中，因此若能得到∠OAB=∠OBA，则问题得证，而∠OAB=∠OBA可由△ABC≌△BAD得到；（2）观察图形知问题AB∥CD可由∠OAB=∠OCD得到，又∠OAB=∠OBA，若∠OCD=∠ODC，再由∠COD=∠AOB结合三角形内角和是180°得到．而由条件△ABC≌△BAD可得BD=AC，又因为OA=OB，所以OC=OD，所以∠OCD=∠ODC，问题获证．【答案】（1）∵△ABC≌△BAD，∴∠CAB=∠DBA，∴OA=OB．（2）∵△ABC≌△BAD，∴AC=BD．又∵OA=OB，∴∠OCD=∠ODC．∵∠AOB=∠COD，∠CAB=1802AOB-∠，∠ACD=1802COD-∠，∴∠CAB=∠ACD，∴AB∥CD．【点评】本题考查全等三角形、等腰三角形、三角形内角和以及平行线的判定等知识点，中考试卷由于题量限制，考查空间与图形时多综合考查相关知识点，此类问题通常难度不大，但考查的知识点较多，学生解决此类问题时要注意熟练运用相关的知识．【推荐指数】★★★22．（2010江苏南京，22，7分）已知点A（1，1）在二次函数y=x2-2ax+b的图象上．（1）用含a的代数式表示b；（2）如果该二次函数的图象与x轴只有一个交点，求这个二次函数的图象的顶点坐标．【分析】（1）根据题意得1=1-2a+b，所以b=2a；（2）由题意知方程x2-2ax+b=0有两个相等的实数根，所以所以4a2-4b=0，由（1）b=2a得4a2-8a=0，解得a=0，或a=2．进而分类可求得该二次函数的图象的顶点坐标．【答案】（1）因为点A（1，1）在二次函数y=x2-2ax+b的图象上，所以1=1-2a+b，可得b=2a．（2）根据题意，方程x2-2ax+b=0有两个相等的实数根，所以4a2-4b=4a2-8a=0，解得a=0，或a=2．当a=0时，y=x2，这个二次函数的顶点坐标为（0，0）；当a=2时，y=x2-4x+4，这个二次函数的顶点坐标为（2，0）．所以，这个二次函数的顶点坐标为（0，0）或（2，0）．【点评】近年来，各地中考试卷考查二次函数问题的难度比以前有较大幅度的降低，问题考查有基础性和综合性的趋势．【推荐指数】★★★★23．（2010江苏南京，23，9分）某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该项厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你交转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．在用文字说明和扇形的圆心角的度数．2．结合转盘简述获奖方式，不需说明理由．）【分析】（1）是否符合要求是指该数学老师设计的方案能否体现“10%得大奖，90%得小奖”的厂家意图，因此可将数学老师的方案用排列法或画树状图的方法得到概率．如用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）=110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．数学老师设计的方案符合要求；（2）本题求解方法不唯一，画图时只需将该转盘（圆）平均分为10份，某种颜色占1份，另一种颜色占9分．顾客购买该型号电视机时获得一次转动转盘的机会，指向1份颜色获得大奖，指向9份颜色获得小奖即可．【答案】（1）该抽奖方案符合厂家的设奖要求．分别用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）=110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．（2）本题答案不唯一，下列解法供参考．如图，将转盘中圆心角为36°的扇形区域涂上黄色，其余的区域涂上白色．顾客每购买一台该型号电视机，可获得一次转动转盘的机会，任意转动这个转盘，当转盘停止时，指针指向黄色区域获得大奖，指向白色区域获得小奖．【点评】概率与统计是新课程新增知识点，近年来各地中考命题的分值约占总分的15%．考查概率知识点通常有三种事件、画树状图（或列表格）求等可能事件的概率，问题难度不大，注重基础性，体现综合性（概率与统计综合，概率与代数知识综合，概率与几何图形知识综合等）．【推荐指数】★★★★24．（2010江苏南京，24，8分）甲车从A地出发以60km/h的速度沿公路匀速行驶，0.5h 后，乙车也从A地出发，以80km/h的速度沿该公路与甲车同向匀速行驶，求乙车出发几小时追上甲车．请建立一次函数关系．．．．．．．．解决上述问题．【分析】乙车出发几小时追上甲车是指两车行驶路程相等或在平面直角坐标系两条直线交点的意义，因此设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km，得y1=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解得x=1.5h．【答案】本题答案不唯一，下列解法供参考．设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km．根据题意，得y1=60（x+0.5）=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解这个方程得x=1.5（h）．答：乙车出发1.5h追上甲车．【点评】近年来，南京市中考数学试卷加大了对一次函数知识点的考查，09省统考除外，06、07、08年各命制一道解答题（其中08年命制一道压轴题），通过分析可以看出该知识点考查的内容主要是函数关系的建立、函数图象与函数的应用，难度在中等或中等稍难以上．解决此类问题的一般方法是根据问题建立函数关系式，进而运用图象或根据实际意义求解．【推荐指数】★★★★★25．（2010江苏南京，25，8分）如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45°，BC∥AD，CD∥AB．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为1，求图中阴影部分的面积（结果保留π）．【分析】（1）欲判断直线CD与⊙O的位置关系，由图形可猜想其结论为相切，由条件∠DAB=45°，CD∥AB知∠ADC=135°，再连接OD得∠ADO=45°，因此∠ODC=90°，猜想得证；（2）观察图形发现阴影部分可在梯形ODCB中求解或在平行四边形ABCD中求解，如【答案】（1）直线CD与⊙O相切．如图，连接OD．∵OA=OD，∠DAB=45°，∴∠ODA=45°，∴∠AOD=90°．∵CD∥AB，∴∠ODC=∠AOD=90°，即OD⊥CD．又∵点D在⊙O上，直线CD与⊙O相切．（2）∵BC∥AD，CD∥AB，∴四边形ABCD是平行四边形，∴CD=AB=2．∴S梯形OBCD=()(12)13222 OB CD OD++⨯==，∴图中阴影部分的面积为S梯形OBCD-S扇形OBD= 313212424ππ-⨯=-．【点评】圆这部分难度在新课标中有较大幅度的减小，考查的知识点集中在圆心角与圆周角、垂径定理、圆与直线、圆与圆的位置关系以及的有关圆的计算等方面，考查难度中等．本题考查圆与直线的位置、圆的计算等知识点，解决与切线相关的问题时，连接圆心与切点的半径是常用的辅导线．【推荐指数】★★★26．（2010江苏南京，26，8分）学习《图形的相似》后，我们可以探索两个直角三角形全等的条件所获得的经验，继续探索两个直角三角形相似的条件．（1）“对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”，类似地，你可以得到“满足_____，或_____，两个直角三角形相似”；（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地，你可以得到满足_____两个直角三角形相似”．请结合下列所给图形，写出已知，并完成说理过程．已知：如图，_____．试说明Rt △ABC ∽Rt △A /B /C /．【分析】（1）我们知道：两个三角形只要满足两个角对应相等，则这两个三角形相似．由于两个直角三角形的中的直角相等是问题的隐含条件，因此只需再有一个锐角对应相等即可判定它们相似．类比“两直角边对应相等，两个直角三角形全等”可知“两直角对应成比例时” 两个直角三角形相似；（2）HL 是判定两个直角三角形全等的特殊方法，类比全等可得：斜边和一条直角边对应成比例的两个直角三角形相似．说理时可从全等是相似的特例入手，利用参数法，设两个直角三角形对应边的比值为k ，进而转化为三角形相似的判定条件获解．【答案】（1）一个锐角对应相等，两直角对应成比例；（2）斜边和一条直角边对应成比例．在Rt △ABC 和Rt △A /B /C /中，∠C =∠C /=90°，////AB AC A B A C=．解法一：设////AB AC A B A C==k ，则AB = k A /B /，AC = k A /C /．在Rt △ABC 和Rt △A /B /C /中，222//22//2////2//2//2//2BC AB AC k A B k A C k B C A B A C A B A C --===--， ∴//////AB AC BC A B A C B C==， ∴Rt △ABC ∽Rt △A /B /C /．解法二：如图，假设AB ＞A /B /，在AB 上截取AB //= A /B /，过点B //作B //C //⊥AC ，垂足为C //．∵∠C =∠AC //B //，∴BC ∥B //C //，∴Rt △ABC ∽Rt △A /B //C //，////AC AB AC AB=． ∵AB //= A /B /，∴////AC AB AC A B=．又∵////AB AC A B A C =，∴//AC AC =//AC A C ，∴AC //=A /C /． ∵AB //= A /B /，∠C =∠AC //B //=90°，∴Rt △AB //C //≌Rt △A /B /C /，∴Rt △ABC ∽Rt △A /B /C /．【点评】本题从教材中的直角三角形全等为背景，利用全等是相似的特例进行类比构造问题，根在教材，根在课堂，考在思想，考在方法，是一首难得的好题．解决此类问题通常需要认真阅读问题，在此基础上运用类比思想，结合相关知识进行求解．【推荐指数】★★★★27．（2010江苏南京，27，8分）某批发商以每件50元的价格购进800件T 恤．第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单位应高于购进的价格；第二个月结束后，批发商将对剩余的T 恤一次性清仓销售，清仓时单价为40元．设第二个月单价降低x 元．（1）填表（不需要化简）（2）如果批发商希望通过销售这批T 恤获利9000元，那么第二个月的单价应是多少元？【分析】（1）由“第二个月单价降低x 元”知第二个月的单价为（80-x ），销售量为（200+10 x ）件，清仓时为总数量分别减去前面两个月的剩余量，即800-200-（200+10x ）；（2）我们销售额-成本=利润，由“获利9000元”建立方程得80×200+（80-x ）（200+10x ）+40[800-200-（200+10x ）] -50×800=9000，化简后求解．【答案】（1）80-x ，200+10x ，800-200-（200+10x ）；（2）根据题意，得80×200+（80-x ）（200+10x ）+40[800-200-（200+10x ）] -50×800=9000．整理，得x 2-20x +100=0，解这个方程得x 1= x 2=10，当x =10时，80-x =70＞50．答：第二个月的单价应是70元．【点评】一元二次方程是中考中的高频考点，特别是各地命题组结合地方特色或时事或现实生活背景命制一大批新颖的试题，本题就是一道现实生活背景应用题．由于本题要分析的数量较多，因此难度明显增大，有较强的区分度．【推荐指数】★★★★28．（2010江苏南京，28，8分）如图，正方形ABCD 的边长是2，M 是AD 的中点．点E从点A 出发，沿AB 运动到点B 停止．连接EM 并延长交射线CD 于点F ，过M 作EF的垂线交射线BC 于点G ，连接EG 、FG ．（1）设AE =x 时，△EGF 的面积为y ．求y 关于x 的函数关系式，并填写自变量x 的取值范围；（2）P 是MG 的中点，请直接写出点P 运动路线的长．【分析】（1）欲求y 关于x 的函数关系式，即△EGF 的面积，观察图形发现S △EGF =12EF ·MG ，由条件AM =DM 及正方形的性质可得△AME ≌△DMF ，所以EF =2EM ，因此求出面积的关键是求出MG ．结合图形发现过点M 作MN ⊥BC ，垂足为N 可得Rt △AME ∽Rt △NMG ，进而运用相似三角形的性质得到MG 的长，问题获解；（2）如图，P 1P 2（P 1是P 起始位置，P 2是P 终止位置．）是点P 运动的路线，由Rt △ABM ∽Rt △P 1P 2M ，AB =2AM ，得P 1P 2=2MP 1=2．G 2G 1P 2P 1F MD(F)C B(E)A(E)【答案】（1）当点E 与点A 重合时，x =0，y =12×2×2=2；当点E 与点A 不重合时，0＜x ≤2．在正方形ABCD 中，∠A =∠ADC =90°，∴∠MDF =90°，∴∠A =∠MDF ．∵AM =DM ，∠AMF =∠DMF ，∴△A M E ≌△DMF ，∴ME =MF ．在Rt △AME 中，AE =x ，AM =1，ME =21x +．∴EF =2MF =221x +．过点M 作MN ⊥BC ，垂足为N （如图）．则∠MNG =90°，∠AMN =90°，MN =AB =AD =2AM ．∴∠AME+∠EMN=90°．∵∠EMG=90°，∴∠GMN+∠EMN=90°，∴∠AME=∠GMN，∴Rt△AME∽Rt△NMG，∴AM MENM MG=，即12MEMG=，∴MG=2ME=221x+，∴y=12EF·MG=12×221x+×221x+=2x2+2，∴y =2x2+2，其中0≤x≤2．（2）点P运动路线的长为2．【点评】本题是一道以动点为背景求函数关系式的面积问题，添加恰当的辅导线构造相似三角形求MG的长是问题（1）的求解关键．由于此类问题综合多个知识点进行考查，再加学生对运动性问题的分析往往是难以“动中求静”，因此，近年来各地多以运动问题作为中考数学试卷的压轴题．【推荐指数】★★★★★。

2010年江苏省南京市中考物理试卷

2010年江苏省南京市中考物理试卷参考答案与试题解析总分：100一、选择题（共12小题，每小题2分，满分24分）1．（2分）（2010•南京）关于声音，下列说法中正确的是（）A．声波具有能量B．声音可以在真空中传播C．“禁鸣喇叭”是在传播途中控制噪声D．只要物体在振动，我们就一定能听到声音【考点】声音的产生和传播PH231，噪声PH233。

【难易度】容易题【分析】（1）声音是一种波，我们把它叫做声波。

它能使物体振动，能粉碎体内小石，这些都表明声波具有能量，故A项符合题意；（2）声音可以在固体、液体、气体中传播，但不能在真空中传播，因为声音的传播需要介质，固体、液态、气体都可以作为传播声音的介质，故B项不符合题意；（3）控制噪声的途径有：a)在声源产生处控制；b)在传播过程中控制；c)在人耳处减弱噪声。

而“禁鸣喇叭”是在声源处控制噪声，故C项不符合题意。

（4）人听到声音必须满足以下条件：一是要有健康的听觉器官，二是要有发声体振动从而产生声音，三是要有具体的介质来传播声音。

另外，声音的频率在20Hz～20000Hz 之间才能被人耳所听见。

当物体在振动时，不满足上述条件，我们不一定能听到声音，故D 选项不符合题意。

综上所述，本题选择A选项。

【解答】A【点评】此题综合考查了声现象的相关概念，需要考生结合声波的概念和性质、声音传播的条件、控制噪声的途径等知识点来作答，需要考生重点掌握：声音不能在真空中传播。

2．（2分）（2010•南京）如图所示的四种现象中，由于光的反射形成的是（）A．B．C．D．【考点】光的直线传播PH243，光的反射PH244，光的折射PH246。

【难易度】容易题【分析】光射到物体表面上时，有一部分光会被物体表面反射回来，这种现象叫做光的反射。

（1）A选项中墙上影子是因为光是沿直线传播的。

光在传播的过程中，如果遇到不透明的物体，在物体的后面不能到达的区域便会产生影子，故A选项不符合题意；（2）B选项中森林中会看到光线也是因为光沿直线传播，故B选项不符合题意；（3）C选项中水中出现倒影是由于光的反射形成的，倒影是平面镜成像，平静的水面相当于平面镜，对光有反射能力，运用了光的反射原理，故C项符合题意；（4）D选项中铅笔放在水中好像折断了是由于光的折射形成的。

2010南京市中考试卷

2010南京市中考试卷第一部分：听力（共20小题，每题1分，满分20分）第一节听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What time will the biology class begin?A. 8:10.B. 8:30.C. 8:40.2. Where did the woman find her glasses?A. On the table.B. In the drawer.C. Under the sofa.3. Why does Mike feel tired?A. Because he didn't finish his work.B. Because he stayed up too late.C. Because he had a lot of homework.4. What does the man want to be when he grows up?A. A teacher.B. A doctor.C. A musician.5. What does the woman want to do this weekend?A. Go shopping.B. Visit her friends.C. Stay at home.第二节听下面几段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

请听第6段材料，回答第6和第7两个小题。

6. What's the relationship between the speakers?A. Roommates.B. Teacher and student.C. Classmates.7. How many dollars will the man pay?A. 45.B. 90.C. 135.请听第7段材料，回答第8和第9两个小题。

2010年南京中考地理生物试题及答案

南京市2010年初中地理、生物学业考查试卷（地理）注意事项:1.本试卷为地理、生物合卷。

地理试卷为第1-4页，共50分;生物试卷为第5-8页，共50分。

考试时间为100分钟。

试题包含选择题、判断题、配伍题、综合题、简答题等。

考生答题全部答在答题卡上，答在本试卷上无效。

2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人的相符合，再将自己的姓名、考试证号用0. 5毫米黑色墨水签字笔填写在答题卡及本试卷上。

3.答选择题和判断题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦千净后，再选涂其他答案。

答其他题目必须用0. 5毫米黑色墨水签字笔写在答题卡的指定位置，在其他位置答题一律无效。

一、单项选择题（下列各题的四个选项中，只有一项最符合题意。

每小题1分，共20分）1．“五十六个民族，五十六枝花，五十六个兄弟姐妹是一家……”，这首歌曲唱出了我国各族人民的心声。

我国少数民族中，人口最多的是A．维吾尔族B．藏族C．壮族D．蒙古族2．冬冬在旅行社选择了“天坛、颐和园、故宫三日游”。

他此次旅游的目的地位于A．北京B．南京C．上海D．重庆2010年4月14日青海省玉树县发生地震，最高震级7.1级，地震的震中位于县城附近。

请根据材料和图1，回答3-4题3．玉树位于我国四大地理区域中的A．南方地区B．北方地区C．西北地区D．青藏地区4．玉树所在地区经纬度大致是A．33. 1°N,96. 7°W B．33. 1°N,96. 7°EC．33. l°S, 96. 7°E D．33. 1°S,96. 7°W5．宁宁到苏果超市购买了三条带鱼和二斤海带，其产地可能是A．新疆B．甘肃C．四川D．浙江6．下列做法符合因地制宜、可持续发展的是A．在新疆吐鲁番盆地利用夏季高温的优势大面积种植热带水果B．在长江中下游地区利用众多的河湖发展淡水养殖C．在西双版纳利用丰富的热量资源大量种植棉花D．在山地迎风坡利用降水较多的优势大面积种植水稻7．晓晓利用暑假到新疆旅游，在新疆他可以看到的景观是A．椰林广布B．牦牛遍野C．雄伟的布达拉宫D．古老的坎儿井索马里沿海海盗活动频繁。

2010年江苏南京中考英语试题及答案

合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
meianf
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
中国最大的教育门户网站
合并自：(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
mianfei
E度教育网。

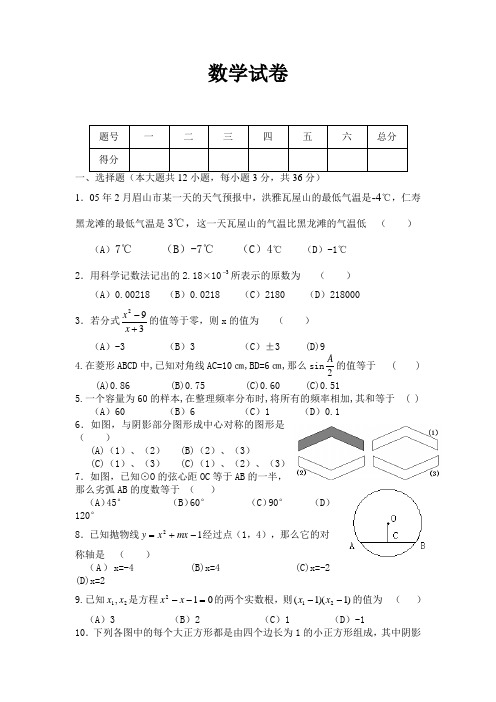
2010年南京中考数学试卷及答案

数学试卷1．05年2月眉山市某一天的天气预报中，洪雅瓦屋山的最低气温是-4℃，仁寿黑龙滩的最低气温是3℃，这一天瓦屋山的气温比黑龙滩的气温低（）（A ）7℃ （B ）-7℃ （C ）4℃ （D ）-1℃ 2．用科学记数法记出的2.18×103-所表示的原数为（）（A ）0.00218 （B ）0.0218 （C ）2180 （D ）2180003．若分式392+-x x 的值等于零，则x 的值为（）（A ）-3 （B ）3 （C ）±3 (D)94.在菱形ABCD 中,已知对角线AC=10㎝,BD=6㎝,那么sin 2A的值等于 ( )(A)0.86 (B)0.75 (C)0.60 (C)0.515.一个容量为60的样本,在整理频率分布时,将所有的频率相加,其和等于 ( ) （A ）60 （B ）6 （C ）1 （D ）0.1 6．如图，与阴影部分图形成中心对称的图形是（）(A)（1）、（2） (B)（2）、（3）(C)（1）、（3） (C)（1）、（2）、（3） 7．如图，已知⊙O 的弦心距OC 等于AB 的一半，那么劣弧AB 的度数等于（）（A ）45° （B ）60° （C ）90° （D ）120°8．已知抛物线12-+=mx x y 经过点（1，4），那么它的对称轴是（）（A ）x=-4 (B)x=4 (C)x=-2 (D)x=29.已知21,x x 是方程012=--x x 的两个实数根，则)1)(1(21--x x 的值为（）（A ）3 （B ）2 （C ）1 （D ）-1 10．下列各图中的每个大正方形都是由四个边长为1的小正方形组成，其中阴影部分面积为25的是（）11．已知AB 是⊙O 的直径，P 是AB 延长线上一点，PC 切⊙O 于点C ，若PC=3，PB=1，则⊙O 的半径等于（）（A ）29 （B ）4 （C ）3 （D ）2512．如果方程组⎩⎨⎧=-=x y mx y 232只有一个实数解，那么m 的值为（）（A ）61-（B ）61 （C ）31- （D ）31二、填空题（本大题共6小题，每小题4分，共24分） 13．分解因式=-+-1222n mn m14．计算22)2(x x ⋅--= （结果中不含负整数指数）15. 如果两个相似三角形的相似比为5：2，那么它们的周长比为16．正方形的边长是3，若边长增加x ，则面积增加y ,那么y 与x 之间的函数关系为17．数据45，44，41，45，43，43，44，42的边准差是（结果精确到0.01） 18．已知圆锥底面半径为3，高为4，则圆锥的侧面面积等于三、（本大题共2小题，每小题5分，共10分） 19．计算)2()8()3(23622b a b a b a -÷+20．解不等式)312(21)1(32-≤-x x ，并把解集在数轴上表示出来四、（本大题共3小题，每小题7分，共21分）21．如图，在等腰梯形ABCD 中，AD ∥BC ，过D 作DF ⊥BC ，垂足为F ，FD 的延长线与BA 的延长线相交于E ，点A 为BE 的中点.求证：FC=21BF22．某校初三（1）班分甲、乙两组各选10名学生进行知识抢答赛，共有10道选择体，答对8题（含8题）以上为优秀，各组选手答题结果统计如下：请完成上表，再根据所学统计知识和表中统计量，从不同方面评价甲、乙两组选手的成绩23．如图，将两个等腰直角三角板ABC 和DEF 叠放在一起，使三角板DEF 的直角顶点与三角板ABC 的斜边中点P 重合，另外两个顶点分别在三角板ABC 的边AB 、AC 上，交EF 于O ，不添加其他字母，写出图中的一队相似三角形（△ABC 与△DEF 除外），并加以证明24．如图，⊙2O 经过⊙1O 的圆心，AB 是⊙1O 和⊙2O 的公切线，点A 、B 为切线，连心线21O O 交AB 的延长线于点P ，交⊙1O 于点C 和D.（1）求证：AD ∥BE ；（2）设⊙1O 的半径为5，⊙2O 的半径为2，求PA 的长.25．为了有效使用电力资源，某地电力公司从2004年1月起对居民试行“峰谷”用点记费，每天8：00至22：00用点每千瓦时0.56元（“峰电”价），22：00至次日8：00每千瓦时0.28元（“谷电”价），而目前不使用“峰谷”电的居民用电每千瓦时0.53元. （1）一居民家庭在某月使用“峰谷”电后，付电费95.2元，经测算比不使用“峰谷”电节约10.8，问该家庭当月使用“峰电”和“谷电”多少千瓦时？（2）当“峰电”用量不超过每月总用电量的百分之几时，使用“峰谷”电比不使用“峰谷”电合算（精确到1％）？26．如图，在第四象限内的矩形OABC 的两边在坐标轴上，一个顶点在一次函数321-=x y 的图象上，当点A 从左向右移动时，矩形的周长面积也随之发生变化，设线段OA 的长为m ，矩形的周长为L ，面积为S.（1）分别写出L 与m ,S 与m 的函数关系式；（2）能否求出当m 取何值时，矩形的周长L 最大？为什么？（3）矩形的面积是否有最大值？如有最大值，请求出该最大值.。

DA江苏省南京市中考真题

所以，这个二次函数的图象的顶点坐标为(0，0)或(2，0)．…………7分
23．（本题9分）
解：（1）该抽奖方案符合厂家的设奖要求．
分别用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：(黄1，黄2)、(黄1，白1)、(黄1，白2)、(黄1，白3)、(黄2，白1)、(黄2，白2)、(黄2，白3)、(白1，白2)、(白1，白3)、(白2，白3)，共有10种，它们出现的可能性相同．
∴OA＝OB．…………………………………………………………………3分
（2）∵△ABC≌△BAD，∴AC＝BD．
又∵OA＝OB，∴OC＝OD．∴∠OCD＝∠ODC．
∵∠AOB＝∠COD，∠CAB＝，∠ACD＝，
∴∠CAB＝∠ACD．∴AB∥CD．…………………………………………7分
22．（本题7分）
解：（1）因为点A(1，1)在二次函数y＝x2－2ax＋b的图象上，所以1＝1－2a＋b．
12．一、三13．＞14．8 15．110 16．2
三、解答题（本大题共12小题，共88分）
17．（本题6分）
解法一：②×2，得2x＋4y＝10．③
③－①，得3y＝6．
解这个方程，得y＝2．………………………………………………3分
将y＝2代入①，得x＝1．……………………………………………5分
所以原方程组的解是……………………………………………6分
可得b＝2a．……………………………………………………………3分
（2）根据题意，方程x2－2ax＋b＝0有两个相等的实数根，所以
4a2－4b＝4a2－8a＝0．
解得a＝0，或a＝2．…………………………………………………5分
当a＝0时，y＝x2，这个二次函数的图象的顶点坐标为(0，0)；

年南京市中考数学试题及答案(word版)

2010年南京市中考数学试题及答案(word版)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2010年南京市中考数学试题及答案(word版)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2010年南京市中考数学试题及答案(word版)的全部内容。

2010年南京市初中毕业暨升学考试试卷数学1．－3的倒数是A. －3B. 3C.D.2. 的结果是A. B. C 。

D.3.如图，下列各数中，数轴上点A 表示的可能是A 。

4的算术平方根 B。

4的立方根 C 。

8的算术平方根 D.8的立方根4。

甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是A 。

1℃～3℃B 。

3℃～5℃C 。

5℃～8℃D 。

1℃～8℃5。

如图，在平面直角坐标系中，菱形OABC 的顶点坐标是(3，4）则顶点A 、B 的坐标分别是A. （4,0)（7，4)B. （4，0）(8，4）C 。

（5，0)（7，4) D. (5，0）（8,4）6.如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长随他与点A 之间的距离的变化而变化，那么表示与之间的函数关系的图像大致为二、填空题（本大题共10小题，每小题2分，共20分,不需写出解答过程，请把答案直接填写在答题卡相应的位置上)7．－2的绝对值的结果是。

8．函数中，自变量的取值范围是。

9．南京地铁2号线（含东延线)、4号线南延线来开通后,南京地铁总里程约为85000m.将85000用科学记数法表示为。

10.如图，O 是直线l 上一点，∠AOB=100°，则∠1 + ∠2= 。

2010年江苏省南京市中考数学试卷

2010年江苏省南京市中考数学试卷一、选择题（共6小题，每小题2分，满分12分）1、（2010•南京）﹣3的倒数是（）A 、3B 、13C 、﹣13D 、﹣3 考点：倒数。

分析：利用倒数的定义，直接得出结果．解答：解：∵﹣3×（﹣13）=1，∴﹣3的倒数是﹣13．故选C ．点评：主要考查倒数的定义，要求熟练掌握．需要注意的是负数的倒数还是负数．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．2、（2010•南京）a 3•a 4的结果是（）A 、a 4B 、a 7C 、a 6D 、a 12考点：同底数幂的乘法。

专题：计算题。

分析：根据同底数幂的乘法法则计算，a m •a n =a m+n ．解答：解：a 3•a 4=a 3+4=a 7．故选B ．点评：主要考查了同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即a m •a n =a m+n ．3、（2010•南京）如图，下列各数中，数轴上点A 表示的可能是（）A 、4的算术平方根B 、4的立方根C 、8的算术平方根D 、8的立方根考点：估算无理数的大小。

分析：先根据数轴判断A 的范围，再根据下列选项分别求得其具体值，选取最符合题意的值即可．解答：解：根据数轴可知点A 的位置在2和3之间，且靠近3，而√4=2，√43＜2，2＜√8=2√2＜3，√83=2，只有8的算术平方根符合题意．故选C ．点评：此题主要考查了利用数轴确定无理数的大小，解题需掌握二次根式的基本运算技能，灵活应用．“夹逼法”是估算的一般方法，也是常用方法．4、（2010•南京）甲种蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（）A、1℃～3℃B、3℃～5℃C、5℃～8℃D、1℃～8℃考点：一元一次不等式组的应用。

专题：应用题。

分析：根据“1℃～5℃”，“3℃～8℃”组成不等式组，解不等式组即可求解．解答：解：设温度为x℃，根据题意可知{x≥1 x≤5 x≥3 x≤8解得3≤x≤5．故选B．点评：本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．5、（2010•南京）如图，在平面直角坐标系中，菱形OABC的顶点C的坐标是（3，4），则顶点A、B的坐标分别是（）A、（4，0）（7，4）B、（4，0）（8，4）C、（5，0）（7，4）D、（5，0）（8，4）考点：菱形的性质；坐标与图形性质。

南京市2010年中考试题及答案

南京市2010年初中毕业考试数学注意事项：1.本试卷共6页。

全卷满分120分，考试时间为120分中。

考生答题全部答在答题卡上，答在本试卷上无效。

2.请认真核对监考老师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡基本试卷上。

3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其它答案。

答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上指定的位置，在其他位置答题一律无效。

4.作图必须用2B铅笔作答，并请加黑加粗，描写清楚。

一、选择题（本大题共6小题，每小题2分，共12分。

在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上）1．－3的倒数是A. －3B. 3C.13- D.132. 34a a⋅的结果是A. 4aB. 7aC.6aD. 12a3.如图，下列各数中，数轴上点A表示的可能是A.4的算术平方根B.4的立方根C.8的算术平方根D.8的立方根4.甲种蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是A. 1℃～3℃B. 3℃～5℃C. 5℃～8℃D. 1℃～8℃5.如图，在平面直角坐标系中，菱形OABC的顶点坐标是（3，4）则顶点A、B的坐标分别是A. （4，0）（7，4）B. （4，0）（8，4）C. （5，0）（7，4）D. （5，0）（8，4）6.如图，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间的函数关系的图像大致为二、填空题（本大题共10小题，每小题2分，共20分，不需写出解答过程，请把答案直接填写在答题卡相应的位置．．．．．．．．上）7．－2的绝对值的结果是。

8．函数11yx=-中，自变量x的取值范围是。

2010年江苏省南京市中考《英语》试题及答案

2010年江苏省南京市中考《英语》试题及答案英语班级：九（）班学号姓名一、情景交际。

根据所给情景选择最佳答案，单选。

（20分）( )1、--- Happy New year----A.The same to you.B. Me too.C. Thank you.D. No, thanks( )2、---Where are you from?-----A.I’m form Canada. B .You are form CanadaC. She is form Japan.D. He is form the USA.( ) 3. ----Nice to meet you, Li Yang.-----A How do you do, Yukio. B. See you, Ann!C .Nice to meet you, too. D. You must thank me. ( ) 4. ---- Welcome! What can I do for you?----A .I’d like to look at a bike .B .Can I help you ?C. Yes ,you can.D. It’s all right.( )5----______do you go swimming ,Sam?.----Twice a week.A .How long B. How oftenC. How soonD. How much( )6-------.I’ll go to Wan feng Lake for a visit next week.---------_______A. Have a good trip!B. Good idea.C. What a shame!D. I’m sorry to hear that.( )7-------Hello! Could I speak to Jim , please?-------_____This is his sister DianaA. This is Jim speakingB. Hold on, please.C. Who are you ?D. I am not Jim.( )8.--------Would you like a cup of tea.Mary?--------______.I’m not thirsty.A. Oh, yes .B. That sounds great.C. Yes, please.D.No, thanks( )9.------What are you going to be when you grow up ?--------______A.I am going to help others.B. I like to play basketballC.I am going to go abroad.D. I’d like to be teacher.( )10.-------I am flying to Kun Ming this evening.------_______A. Have a nice trip!B. Sorry, I have no time.C. Yes, I’d love toD. You bet.二。

南京市2010年中考真题含答案(文字版)

南京市2010年初中毕业生学业考试语文试卷注意事项：1.本试卷6页，共120分，其中书写分3分。

考试时间为120分钟。

考生答题全部答在答题卡上，答在本试卷上无效。

2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0．5毫米黑色墨水签字笔填写在答题卡及本试卷上。

3.答题必须用0．5毫米黑色墨水签字笔写在答题卡的指定位置，在其他位置答题一律无效。

一 (27分)1．用课文原句填空。

(10分⑴学而不思则罔，。

(《<论语>十则》⑵，奉命于危难之间。

(诸葛亮《出师表》⑶衣沾不足惜，。

(陶渊明《归园田居》⑷月下飞天镜，。

(李白《渡荆门送别》⑸安得广厦千万间， !(杜甫《茅屋为秋风所破歌》⑹乱花渐欲迷人眼，。

(白居易《钱塘湖春行》⑺，无案牍之劳形。

(刘禹锡《陋室铭》⑻，甲光向日金鳞开。

(李贺《雁门太守行》⑼东风不与周郎便，。

(杜牧《赤壁》⑽剪不断，理还乱，是离愁，。

(李煜《相见欢》2.下列加点字注音完全正确的一项是( )(2分)A．玷污(zhān)肃穆(mù)巧妙绝伦(1ún)B．无垠(yín)畸形(qí)相形见绌(chùC．迁徙(xǐ)干涸(hé)一丝不苟(gǒu)D．凋零(diāo)酝酿(niàng)参差不齐(cā)3．下列词语没有错别字的一项是( )(2分A．称职气慨销声匿迹B．真谛阔绰妙手回春C．幅射荒谬略胜一筹D．仰慕淳朴心旷神贻4．下列句中加点成语使用不恰当的一项是( )(3分)A．以梅花装饰南京花神庙地铁站主题墙，这一别具匠心的设计，深受好评。

B．凭借雄厚的经济实力和深厚的文化底蕴，南京当之无愧地获得青奥会主办权。

C．对于重要的书，我们必须常常反复阅读，每读一次都会觉得开卷有益。

D．在暑期社会实践活动中，同学们既体验到合作之趣，又享受了天伦之乐。

5．下列句中有语病的一项是( )(3分A．南京过江隧道的开通，有助于解决长江大桥的交通拥堵问题。

2010年江苏省南京市中考物理试卷及答案

南京市2010年初中毕业生学业考试物理一、选择题(本题共12小题，每小题2分，共24分．每小题给出的四个选项中只有一个选项正确) 1．关于声音，下列说法中正确的是A．声波具有能量B．声音可以在真空中传播C．“禁鸣喇叭”是在传播途中控制噪声D．只要物体在振动，我们就一定能听到声音2．如图所示现象中，由于光的反射形成的是3．关于粒子和宇宙，下列认识中正确的是A．红墨水在水中散开说明分子间有排斥力B．用鼻子嗅气味能鉴别醋和酱油表明分子在运动C．在水分子、氢原子和电子中，尺度最小的是氢原子D．宇宙是一个有层次的天体结构系统，恒星是绝对不动的4．下列数据中，符合实际情况的是A．人体感到舒适的温度约为42℃B．八年级物理课本的宽度约为18mmC．教室里日光灯的额定功率约为40W D．做一遍中学生眼保健操的时间约需5s5．下列现象中，不能用惯性知识解释的是A．司机开车时需要系安全带B．运动员跳远时需要助跑C．骑自行车时为了减速捏紧车闸D．投出的铅球离开手后继续向前运动6．下列实例中，属于减小压强的是7．如图所示，在蹄形磁体的磁场中放置一根导体AB，导体的两端跟电流表连接，开关闭合，电路中没有电流．以下操作中，可能使电路中产生电流的是A．让导体在磁场中静止，换用量程更小的电流表B．让导体在磁场中静止，换用磁性更强的永磁体C．让导体在磁场中沿不同方向运动D．将导体换成匝数很多的线圈，线圈在磁场中静止8．电熨斗通电一段时间后变得很烫，而连接电熨斗的导线却不怎么热，这主要是因为A．导线的绝缘皮隔热B．导线散热比电熨斗快C．通过导线的电流小于通过电熨斗的电流D．导线的电阻远小于电熨斗电热丝的电阻9．如图所示，将带钩的木块放在粗糙程度相同的水平桌面上，小明水平拉动木块，在木块加速运动过程中，以下说法中正确的是A．木块受到的摩擦力逐渐增大B．木块受到的摩擦力逐渐减小C．绳对木块的拉力和桌面对木块的摩擦力是一对平衡力D．绳对木块的拉力和木块对绳的拉力是一对相互作用力10．如图所示，电源电压恒定．闭合开关S1、S2，电压表示数为9 V，电流表示数为1.5A；断开开关S2，电压表示数为6V．则R l和R2的阻值分别是A．6Ω2ΩB．6Ω3ΩC．4Ω2ΩD．4Ω3Ω11．把一个质量为30g、体积为50cm3的物块轻放人盛满水的烧杯中，当物块静止时，下列说法中正确的是A．溢出水的质量为30g，水对杯底的压强变大B．溢出水的质量为30g，水对杯底的压强不变C. 溢出水的质量为50g，水对杯底的压强变大D．溢出水的质量为50g，水对杯底的压强不变12．如图所示电路，电源电压不变，闭合开关S，灯L1和L2均发光．一段时间后，一盏灯突然熄灭，而电流表和电压表的示数都不变，出现这一现象的原因可能是A. 灯L1断路B．灯L2断路C．灯L1短路D．灯L2短路二、填空题(本题共1l小题，每空1分，共28分)13．移动通信是利用_______ 波传递信号的，其信号传播速度与光速相同，光在真空中的传播速度是_______ m／s.14．甲图中物体A的长度是_______ cm．乙图中温度计的示数是_______ ℃.常用的液体温度计是利用测温液体_______ 的性质工作的．15．沪宁城际铁路即将通车，南京至上海路程约为300km，若列车运行的平均速度为250km／h，则乘坐该列车从南京到上海只需_______ h．列车中的乘客看到车外的树木飞驰而过，这是以_______ 为参照物，列车在进站过程中，动能将_______ (选填“变大”、“不变”或“变小”)。

2010年数学中考试卷及答案

南京市2010年初中毕业生学业考试数学一、选择题（本大题共有6小题，每小题2分，共12分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选择项前的字母代号填涂在答题卡相应位置．．．．．．．上） 1．－3的倒数是A ．－3B ．3C ．－ 13D ．132．计算a 3·a 4的结果是A ．a 6B ．a 7C ．a 8D ．a 12 3．如图，下列各数中，数轴点A 表示的可能是A ．4的算术平方根B ．4的立方根C ．8的算术平方根D ．8的立方根4．甲各蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是A ．1℃～3℃B ．3℃～5℃C ．5℃～8℃D ．1℃～8℃ 5．如图，在平面直角坐标系中，菱形OABC 的顶点C 的坐标是（3，4），则顶点A 、B 的坐标分别是A ．（4,0）、（7,4）B ．（5,0）、（8,4）C ．（4,0）、（7,4）D ．（5,0）、（8,4） 6．，如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x的变化而变化，那么表示y 与x 之间的函数关系的图象大致为二、填空题（本大题共10个小题，每小题2分，共20分．不需写出解答过程，请把正确答案直接填写在答题卡相应位置上）7．－2的绝对值的结果是__________．8．函数y ＝ 1x －1中，自变量x 的取值范围是__________．9．南京地铁2号线（含东延线）、1号线南延线开通后，南京地铁总里程约为85 000m ，将85 000用科学记数法表示为__________．10．如图，O 是直线l 上一点，∠AOB ＝100°，则∠1＋∠2＝__________°． 11．计算2a ·8a （a ≥0）的结果是__________．12．若反比例函数的图象经过点（－2, －1），则这个函数的图象位于第__________象限． 13则这两人5次射击命中的环数的平均数甲x ＝乙x ＝8，方差S 甲2___ S 乙2（填“＞”、“＜”或“＝”） 14．如图，以O 为圆心的两个同心圆中，大圆的弦AB 是小圆的切线，C 为切点．若两圆的半径分别为3cm和5cm ，则AB 的长为__________ cm ．15．如图，点C 在⊙O 上，将圆心角∠AOB 绕点O 按逆时针方向旋转到∠A ’OB ’，旋转角为α(0°＜α＜180°)．若∠AOB ＝30°，∠BCA ’＝40°，则∠α＝__________°．16．如图，AB ⊥BC ，AB ＝BC ＝2cm ，OA⌒ 与OC ⌒ 关于点O 中心对称，则AB 、BC 、CO ⌒ 、OA ⌒ 所围成的图形的面积是________cm 2．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．(6分)解方程组⎩⎨⎧=+=+.52,42y x y x18．(6分)计算(1a － 1b )÷a 2－b 2ab19．(6分)为了估计西瓜、苹果和香蕉三种水果一个月的销售量，某水果店对这三种水果7天的销售量进行了统计，统计结果如图所示．（1）若西瓜、苹果和香蕉的售价分别为6元/千克、8元/千克和3元/千克．则这7天销售额最大的小果品种是（） A ．西瓜 B ．苹果 C ．香蕉（2）估计一个月（按30天计算）该水果店可销售苹果多少千克？A B （第21题）第23题20．(7分)如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC 为10m ，测角仪的高度CD为1.5m ，测得树顶A 的仰角为33°，求树的高度AB ．（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）21．如图，四边形ABCD 的对角线AC 、BD 相交于点O ，△ABC ≌△BAD ．求证：（1）OA ＝OB ；（2）AB ∥CD ．22．（7分）已知点A （1，1）在二次函数y ＝x 2－2ax －b 的图象上（1）用含a 的代数式表示b ；（2）如果该二次函数的图象与x 轴只有一个交点，求这个二次函数的图象的顶点坐标． 23．（9分）某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10个黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖在，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2个黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖文案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你将转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1数．2．结合转盘简述获奖方式，不需说明理由．）第25题第26题’ C ’ 24．（8分）甲车从A 地出发以60km/h 的速度沿公路匀速行驶，0.5h 后，乙车也从A 地发出，以80km/h的速度沿该公路与甲车同向匀速行驶求乙车出发后几小时追上甲车．请建立一次函数关系．．．．．．．．解决上述问题． 25．（8分）如图，AB 是⊙O 的直径，点D 在⊙O 上，∠DAB ＝45°，BC ∥AD ，CD ∥AB ．（1）判断直线CD 与⊙O 的位置关系，并说明理由；（2）若⊙O 的半径为1，求图中阴影部分的面积（结果保留π）．26．（8分）学习《图形的相似》后，我们可以借助探索两个直角三角形全等的条件所获得的经验，继续探索两个直角三角形相似的条件（1）“对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”．类似地，你可以得到“满足________________或_________________，两个直角三角形相似”；（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地，你可以得到“满足__________的两个直角三角形相似”．请你结合下列所给图形，写出已知，并完成说理过程．已知：如图，_________________________________．求证：Rt △ABC ∽Rt △A ’B ’C ’ ．27．(8分)某批发商以每件50元的价格购进800件T 恤．第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T 恤一性清仓，清仓时单价为40元．设第二个月单价降低x 元．（1）填表（不需化简）：第28题（2）如果批发商希望通过销售这批T 恤获利9 000元，那么第二个月的单价应是多少元？28．(8分)如图，正方形ABCD 的边长是2，M 是AD 的中点．点E 从点A 出发，沿AB 运动到点B 停止．连接EM 并延长交射线CD 于点F ，过M 作EF 的垂线交射线BC 于点G ，连接EG 、FG ．（1）设AE ＝x 时，△EGF 的面积为y ．求y 关于x 的函数关系式，并写出自变量x 的取值范围；（2）P 是MG 的中点，请直接写出点P 运动路线的长．南京市2010年初中数学毕业生学业考试数学一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上） 1． C 2． B 3． C 4． B 5． D 6．（2010江苏南京，6，2分）如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y随他与点A之间的距离x 的变化而变化，那么表示y 与x 之间的函数关系的图象大致为（）【分析】由生活经验知：当小亮走到路灯的正下方时，此时影长为0，因此可排除选项C 、D ；在确定答案是选项A 或B 上感觉不好下手．设小亮身高为a ，路灯C 到路面的距离为h ，点A 到路灯正下方的距离为b ，如图，由中心投影得a y hb x y=-+，整理得a ab y x h ah a=-+--，因此答案为A ．【答案】A【涉及知识点】函数的图象、中心投影【点评】本题考查函数的图象函数的图象、中心投影，解决此类问题的关键是抓住横轴与纵轴的意义．由于此类问题抽象性较强，因此经常出现在各地中考试卷选择题的最后一题，具有一定的区分度．7． 2 8． x ≠1 9． 8.5×104 10． 80 11． 4a 12．一、三 13．＞ 14． 8 15．（2010江苏南京，1，2分）如图，点C 在⊙O 上，将圆心角∠AOB 绕点O 按逆时针方向旋转到∠A/OB /，旋转角为α（0°＜α＜180°）．若∠AOB =30°，∠BCA /=40°，则∠α=_____°．【分析】根据圆心角的意义得∠BOA /=2∠BCA /=80°，所以∠α=∠AOB +∠BOA /=30°+80° =110°．【答案】110【涉及知识点】圆心角16．（2010江苏南京，16，2分）如图，AB ⊥BC ，AB =BC =2 cm ，OA 与OC 关于点O中心对称，则AB 、BC 、CO 、OA 所围成的图形的面积是_____ cm 2．【分析】连接AC ，根据中心对称的意义，将“AB 、BC 、CO 、OA 所围成的图形的面积”转化为求直角三角形ABC的面积，由AB =BC =2 cm 得S △ABC =2 cm 2．【答案】217．原方程组的解为12x y ==⎧⎨⎩． 18． 1()a b -+．19．【答案】（1）A；（2）140÷7×30=600（千克）．答：估计一个月该水果店可销售苹果600千克．20．（2010江苏南京，20，7分）如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC为10m，测角仪的高度CD为1.5m，测得树顶A的仰角为33°．求树的高度AB．（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）【分析】观察图形发现可过点D作DE⊥AB，构造直角三角形ADE，由tan∠ADE=AEDE得AE=DE·tan∠ADE≈10×0.65=6.5，因此AB=AE+BE=AE+CD=6.5+1.5=8m．【答案】如图，过点D作DE⊥AB，垂足为E．在Rt△ADE中，DE=BC=10，∠ADE=33°，tan∠ADE=AE DE，∴AE=DE·tan∠ADE≈10×0.65=6.5，∴AB=AE+BE=AE+CD=6.5+1.5=8（m）．答：树的高度AB约为8 m．21．（2010江苏南京，21，7分）如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．求证：（1）OA=OB；（2）AB∥CD．【答案】（1）∵△ABC≌△BAD，∴∠CAB=∠DBA，∴OA=OB．（2）∵△ABC≌△BAD，∴AC=BD．又∵OA=OB，∴∠OCD=∠ODC．∵∠AOB=∠COD，∠CAB=1802AOB-∠，∠ACD=1802COD-∠，∴∠CAB=∠ACD，∴AB∥CD．22．（2010江苏南京，22，7分）已知点A（1，1）在二次函数y=x2-2ax+b的图象上．（1）用含a的代数式表示b；（2）如果该二次函数的图象与x轴只有一个交点，求这个二次函数的图象的顶点坐标．【分析】（1）根据题意得1=1-2a+b，所以b=2a；（2）由题意知方程x2-2ax+b=0有两个相等的实数根，所以所以4a2-4b=0，由（1）b=2a得4a2-8a=0，解得a=0，或a=2．进而分类可求得该二次函数的图象的顶点坐标．【答案】（1）因为点A（1，1）在二次函数y=x2-2ax+b的图象上，所以1=1-2a+b，可得b=2a．（2）根据题意，方程x2-2ax+b=0有两个相等的实数根，所以4a2-4b=4a2-8a=0，解得a=0，或a=2．当a=0时，y=x2，这个二次函数的顶点坐标为（0，0）；当a=2时，y=x2-4x+4，这个二次函数的顶点坐标为（2，0）．所以，这个二次函数的顶点坐标为（0，0）或（2，0）．23．（2010江苏南京，23，9分）某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该项厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你交转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．在用文字说明和扇形的圆心角的度数．2．结合转盘简述获奖方式，不需说明理由．）【分析】（1）是否符合要求是指该数学老师设计的方案能否体现“10%得大奖，90%得小奖”的厂家意图，因此可将数学老师的方案用排列法或画树状图的方法得到概率．如用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）=110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．数学老师设计的方案符合要求；（2）本题求解方法不唯一，画图时只需将该转盘（圆）平均分为10份，某种颜色占1份，另一种颜色占9分．顾客购买该型号电视机时获得一次转动转盘的机会，指向1份颜色获得大奖，指向9份颜色获得小奖即可．【答案】（1）该抽奖方案符合厂家的设奖要求．分别用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：（黄1，黄2）、（黄1，白1）、（黄1，白2）、（黄1，白3）、（黄2，白1）、（黄2，白2）、（黄2，白3）、（白1，白2）、（白1，白3）、（白2，白3），共有10种，它们出现的可能性相同．所有的结果中，满足摸到2个球都是黄球（记为事件A）的结果有1种，即（黄1，黄2），所以P（A）=110．即顾客获得大奖的概率为10%，获得小奖的概率为90%．（2）本题答案不唯一，下列解法供参考．如图，将转盘中圆心角为36°的扇形区域涂上黄色，其余的区域涂上白色．顾客每购买一台该型号电视机，可获得一次转动转盘的机会，任意转动这个转盘，当转盘停止时，指针指向黄色区域获得大奖，指向白色区域获得小奖．24．（2010江苏南京，24，8分）甲车从A地出发以60km/h的速度沿公路匀速行驶，0.5h后，乙车也从A 地出发，以80km/h的速度沿该公路与甲车同向匀速行驶，求乙车出发几小时追上甲车．请建立一次函数关系．．．．．．．．解决上述问题．【分析】乙车出发几小时追上甲车是指两车行驶路程相等或在平面直角坐标系两条直线交点的意义，因此设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km，得y1=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解得x=1.5h．【答案】本题答案不唯一，下列解法供参考．设乙车出发xh后，甲、乙两车离A地的路程分别是y1km、y2km．根据题意，得y1=60（x+0.5）=60x+30，y2=80x．当乙车追上甲车时，y1= y2，即60x+30=80x．解这个方程得x=1.5（h）．答：乙车出发1.5h追上甲车．25．【答案】（1）直线CD与⊙O相切．如图，连接OD．∵OA=OD，∠DAB=45°，∴∠ODA=45°，∴∠AOD=90°．∵CD∥AB，∴∠ODC=∠AOD=90°，即OD⊥CD．又∵点D在⊙O上，直线CD与⊙O相切．（2）∵BC∥AD，CD∥AB，∴四边形ABCD是平行四边形，∴CD=AB=2．∴S 梯形OBCD=()(12)13222 OB CD OD++⨯==，∴图中阴影部分的面积为S梯形OBCD-S扇形OBD= 313212424ππ-⨯=-．【点评】圆这部分难度在新课标中有较大幅度的减小，考查的知识点集中在圆心角与圆周角、垂径定理、圆与直线、圆与圆的位置关系以及的有关圆的计算等方面，考查难度中等．本题考查圆与直线的位置、圆的计算等知识点，解决与切线相关的问题时，连接圆心与切点的半径是常用的辅导线．26．（2010江苏南京，26，8分）学习《图形的相似》后，我们可以探索两个直角三角形全等的条件所获得的经验，继续探索两个直角三角形相似的条件．（1）“对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”，类似地，你可以得到“满足_____，或_____，两个直角三角形相似”；（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地，你可以得到满足_____两个直角三角形相似”．请结合下列所给图形，写出已知，并完成说理过程．已知：如图，_____．试说明Rt△ABC∽Rt△A/B/C/．【分析】（1）我们知道：两个三角形只要满足两个角对应相等，则这两个三角形相似．由于两个直角三角形的中的直角相等是问题的隐含条件，因此只需再有一个锐角对应相等即可判定它们相似．类比“两直角边对应相等，两个直角三角形全等”可知“两直角对应成比例时” 两个直角三角形相似；（2）HL 是判定两个直角三角形全等的特殊方法，类比全等可得：斜边和一条直角边对应成比例的两个直角三角形相似．说理时可从全等是相似的特例入手，利用参数法，设两个直角三角形对应边的比值为k ，进而转化为三角形相似的判定条件获解．【答案】（1）一个锐角对应相等，两直角对应成比例；（2）斜边和一条直角边对应成比例．在Rt △ABC 和Rt △A /B /C /中，∠C =∠C /=90°，////AB ACA B A C=．解法一：设////AB ACA B A C==k ，则AB = k A /B /，AC = k A /C /．在Rt △ABC 和Rt △A /B /C /中，//BC k B C===，∴//////AB AC BCA B A C B C==， ∴Rt △ABC ∽Rt △A /B /C /．解法二：如图，假设AB ＞A /B /，在AB 上截取AB //= A /B /，过点B //作B //C //⊥AC ，垂足为C //．∵∠C =∠AC //B //，∴BC ∥B //C //，∴Rt △ABC ∽Rt △A /B //C //，////AC ABAC AB=． ∵AB //= A /B /，∴////AC ABAC A B=．又∵////AB AC A B A C =，∴//AC AC=//AC A C ，∴AC //=A /C /． ∵AB //= A /B /，∠C =∠AC //B //=90°，∴Rt△AB//C//≌Rt△A/B/C/，∴Rt△ABC∽Rt△A/B/C/．【点评】本题从教材中的直角三角形全等为背景，利用全等是相似的特例进行类比构造问题，根在教材，根在课堂，考在思想，考在方法，是一首难得的好题．解决此类问题通常需要认真阅读问题，在此基础上运用类比思想，结合相关知识进行求解．【推荐指数】★★★★27．（2010江苏南京，27，8分）某批发商以每件50元的价格购进800件T恤．第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单位应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓时单价为40元．设第二个月单价降低x元．（1）填表（不需要化简）（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？【答案】（1）80-x，200+10x，800-200-（200+10x）；（2）根据题意，得80×200+（80-x）（200+10x）+40[800-200-（200+10x）] -50×800=9000．整理，得x2-20x+100=0，解这个方程得x1= x2=10，当x=10时，80-x=70＞50．答：第二个月的单价应是70元．28．（2010江苏南京，28，8分）如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．（1）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；（2）P是MG的中点，请直接写出点P运动路线的长．【分析】（1）欲求y关于x的函数关系式，即△EGF的面积，观察图形发现S△EGF=12EF·MG，由条件AM=DM及正方形的性质可得△AME≌△DMF，所以EF=2EM，因此求出面积的关键是求出MG．结合图形发现过点M作MN⊥BC，垂足为N可得Rt△AME∽Rt△NMG，进而运用相似三角形的性质得到MG的长，问题获解；（2）如图，P1P2（P1是P起始位置，P2是P终止位置．）是点P运动的路线，由Rt △ABM∽Rt△P1P2M，AB=2AM，得P1P2=2MP1=2．G1【答案】（1）当点E与点A重合时，x=0，y=12×2×2=2；当点E与点A不重合时，0＜x≤2．在正方形ABCD中，∠A=∠ADC=90°，∴∠MDF=90°，∴∠A=∠MDF．∵AM=DM，∠AMF=∠DMF，∴△A M E≌△DMF，∴ME=MF．在Rt△AME中，AE=x，AM=1，MEEF=2MF过点M作MN⊥BC，垂足为N（如图）．则∠MNG=90°，∠AMN=90°，MN=AB=AD=2AM．∴∠AME+∠EMN=90°．∵∠EMG=90°，∴∠GMN+∠EMN=90°，∴∠AME=∠GMN，∴Rt△AME∽Rt△NMG，∴AM MENM MG=，即12MEMG=，∴MG=2ME∴y=12EF·MG=12×x2+2，∴y =2x2+2，其中0≤x≤2．（2）点P运动路线的长为2．【点评】本题是一道以动点为背景求函数关系式的面积问题，添加恰当的辅导线构造相似三角形求MG的长是问题（1）的求解关键．由于此类问题综合多个知识点进行考查，再加学生对运动性问题的分析往往是难以“动中求静”，因此，近年来各地多以运动问题作为中考数学试卷的压轴题．。

2010年江苏省南京市中考数学试卷及答案-(word整理版)

2010年江苏省南京市中考数学试卷一、选择题（共6小题，每小题2分，满分12分） 1．﹣3的倒数是（） A ．3B ．C ．﹣D ．﹣32．a 3•a 4的结果是（） A ．a 4 B ．a 7 C ．a 6 D ．a 123．如图，下列各数中，数轴上点A 表示的可能是（）A ．4的算术平方根B ．4的立方根C ．8的算术平方根D ．8的立方根4．甲种蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（） A ．1℃～3℃B ．3℃～5℃C ．5℃～8℃D ．1℃～8℃5．如图，在平面直角坐标系中，菱形OABC 的顶点C 的坐标是（3，4），则顶点A 、B 的坐标分别是（）A ．（4，0）（7，4）B ．（4，0）（8，4）C ．（5，0）（7，4）D ．（5，0）（8，4）6．如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x 的变化而变化，那么表示y 与x 之间的函数关系的图象大致为（）A ．B ．C ．D ．二、填空题（共10小题，每小题2分，满分20分） 7．﹣2的绝对值的结果是． 8．函数中，自变量x的取值范围是．9．南京地铁2号线（含东延线）、4号线南延线来开通后，南京地铁总里程约为85 000m ．将85 000用科学记数法表示为．10．如图，O 是直线l 上一点，∠AOB=100°，则∠1+∠2= 度． 11．计算的结果是．13．甲、乙两人5次射击命中的环数如下：甲：7 9 8 6 10；乙：7 8 9 8 8．则这两人5次射击命中的环数的平均数，方差s 甲2 s 乙2．（填“＞”“＜”或“=”）．14．如图，以O 为圆心的两个同心圆中，大圆的弦AB 是小圆的切线，C 为切点，若两圆的半径分别为3cm 和5cm ，则AB 的长为 cm ．15．如图，点C 在⊙O 上，将圆心角∠AOB 绕点O 按逆时针方向旋转到∠A′OB′，旋转角为α（0°＜α＜180°）．若∠AOB=30°，∠BCA′=40°，则∠α= 度．16．如图，AB ⊥BC ，AB=BC=2cm ，弧OA 与弧OC 关于点O 中心对称，则AB 、BC 、弧CO 、弧OA 所围成的面积是 cm 2．三、解答题（共12小题，满分88分） 17．（6分）解方程组：． 18．（6分）计算：．19．（6分）为了估计西瓜、苹果和香蕉三种水果一个月的销售量，某水果店对这三种水果7天的销售量进行了统计，统计结果如图所示（1）若西瓜、苹果和香蕉的售价分别是6元/千克、8元/千克和3元/千克，则这7天销售额最大的水果品种是（）A 、西瓜，B 、苹果，C 、香蕉．（2）估计一个月（按30天计算）该水果店可销售苹果多少千克？20．（7分）如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC为10m，测角仪的高度CD为1.5m，测得树顶A的仰角为33°．求树的高度AB．（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）21．（7分）如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．求证：（1）OA=OB；（2）AB∥CD．22．（7分）已知点A（1，1）在二次函数y=x2﹣2ax+b图象上．（1）用含a的代数式表示b；（2）如果该二次函数的图象与x轴只有一个交点，求这个二次函数的图象的顶点坐标．23．（9分）某厂为新型号电视机上市举办促销活动，顾客每买一台该型号电视机，可获得一次抽奖机会，该厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10个黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2个黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你将转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．转盘上用文字注明颜色和扇形的圆心角的度数，2、结合转盘简述获奖方式，不需说明理由．）24．（8分）甲车从A地出发以60km/h的速度沿公路匀速行驶，0.5小时后，乙车也从A地出发，以80km/h的速度沿该公路与甲车同向匀速行驶，求乙车出发后几小时追上甲车．请建立一次函数关系解决上述问题．25．（8分）如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45°，BC∥AD，CD∥AB．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为1，求图中阴影部分的面积（结果保留π）26．（8分）学习《图形的相似》后，我们可以借助探索两个直角三角形全等的条件所获得经验，继续探索两个直角三角形相似的条件．（1）“对与两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”．类似地你可以得到：“满足，或，两个直角三角形相似”．（2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地你可以得到“满足的两个直角三角形相似”．请结合下列所给图形，写出已知，并完成说理过程．已知：如图，．试说明Rt△ABC∽Rt△A′B′C′．27．（8分）某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元．（1）填表：（不需化简）（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？28．（8分）如图，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止，连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．（1）设AE=x时，△EGF的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；（2）P是MG的中点，请直接写出点P的运动路线的长．2010年江苏省南京市中考数学试卷答案1．C ；2．B ；3．C ；4．B ；5．D ；6．A ；7．2；8．x ≠1；9．8.5×104；10．80；11．4a ；12．二、四；13．＞；14．8；15．110；16．2；17．解：②×2，得 2x ＋4y ＝10． ③③－①，得 3y ＝6．解这个方程，得 y ＝2． ………………………………………………3分将y ＝2代入①，得 x ＝1． ……………………………………………5分所以原方程组的解是y ＝2．x ＝1，……………………………………………6分18．解：(a 1－b 1)÷ab a2－b2＝ab b －a ÷ab a －b＝ab b －a ·a －b ab…………………………………………………………4分＝－ab a －b ·a －b ab＝－a ＋b 1． ………………………………………………………………6分19．解：（1）A ……………………………………………………………………………2分（2）140÷7×30＝600（千克）．答：估计一个月该水果店可销售苹果600千克．…………………………………6分20．解：如图，过点D 作DE ⊥AB ，垂足为E ．在Rt △ADE 中，DE ＝BC ＝10，∠ADE ＝33°，tan ∠ADE ＝DE AE，∴A E ＝D E ·tan ∠ADE≈10×0.65＝6.5． …………………………5分 ∴AB ＝AE ＋BE ＝AE ＋CD ＝6.5＋1.5＝8（m ）．答：树的高度AB 约为8 m ．……………………7分 21．证明：（1）∵△ABC ≌△BAD ，∴∠CAB ＝∠DBA ．∴OA ＝OB ．…………………………………………………………………3分（2）∵△ABC ≌△BAD ，∴AC ＝BD ．又∵OA ＝OB ，∴ OC ＝OD ．∴∠OCD ＝∠ODC ．∵∠AOB ＝∠COD ，∠CAB ＝2180°－∠AOB ，∠ACD ＝2180°－∠COD，∴∠CAB ＝∠ACD ．∴AB ∥CD ．…………………………………………7分可得 b ＝2a ．……………………………………………………………3分（2）根据题意，方程x 2－2ax ＋b ＝0有两个相等的实数根，所以4a 2－4b ＝4a 2－8a ＝0．解得 a ＝0，或a ＝2． …………………………………………………5分当a ＝0时，y ＝x 2，这个二次函数的图象的顶点坐标为(0，0)；当a ＝2时，y ＝x 2－4x ＋4＝(x －2)2，这个二次函数的图象的顶点坐标为(2，0)．所以，这个二次函数的图象的顶点坐标为(0，0)或(2，0)． …………7分23．解：（1）该抽奖方案符合厂家的设奖要求．分别用黄1、黄2、白1、白2、白3表示这5个球．从中任意摸出2个球，可能出现的结果有：(黄1，黄2)、(黄1，白1)、(黄1，白2)、(黄1，白3)、(黄2，白1)、(黄2，白2)、(黄2，白3)、(白1，白2)、(白1，白3)、(白2，白3)，共有10种，它们出现的可能性相同．所有的结果中，满足摸到的2个球都是黄球（记为事件A ）的结果有1种，即(黄1，黄2)，所以P(A )＝ 101，即顾客获得大奖的概率为10%，获得小奖的概率为90%．……………………………………………………………………………………5分（2）本题答案不惟一，下列解法供参考．如图，将转盘中圆心角为36°的扇形区域涂上黄色，其余的区域涂上白色．顾客每购买一台该型号电视机，可获得一次转动转盘的机会，任意转动这个转盘，当转盘停止时，指针指向黄色区域获得大奖，指向白色区域获得小奖． …………………9分24．解：本题答案不惟一，下列解法供参考．设乙车出发x h 后，甲、乙两车离A 地的路程分别是y 1 km 和y 2 km ．根据题意，得 y 1＝60(x ＋0.5)＝60x ＋30，y 2＝80x ． …………………………6分当乙车追上甲车时，y 1＝y 2，即 60x ＋30＝80x ．解这个方程，得 x ＝1.5（h ）．答：乙车出发后1.5h 追上甲车．………………………………………………………8分 25．解：（1）直线CD 与⊙O 相切．如图，连接OD ．∵O A ＝OD ，∠DAB ＝45°，∴∠OD A ＝45°． ∴∠A OD ＝90°． ∵CD ∥AB ，∴∠OD C ＝∠A OD ＝90°，即OD ⊥CD ．又∵点D 在⊙O 上，∴直线CD 与⊙O 相切．…………………4分（2）∵BC ∥AD ，CD ∥AB ，∴四边形ABCD 是平行四边形．∴CD ＝AB ＝2．S OB ＋CD×OD 1＋2×13∴图中阴影部分的面积等于S 梯形OBCD －S 扇形OBD ＝23－41×π×12＝23－4π．…8分26．解：（1）一个锐角对应相等 …………………………………………………………1分两直角边对应成比例 ………………………………………………………2分（2）斜边和一条直角边对应成比例 ……………………………………………3分在Rt △ABC 和Rt △A ′B ′C ′中，∠C ＝∠C ′＝90°，A′B′AB ＝A′C′AC． ………4分解法一：设A′B′AB ＝A′C′AC＝k ，则AB ＝kA ′B ′，AC ＝kA ′C ′．在Rt △ABC 和Rt △A ′B ′C ′中，∴B′C′BC ＝A′B′2－A′C′2AB2－AC2A′B′2－A′C′2AB2－AC2＝A′B′2－A′C′2k2A′B′2－k2A′C′2A′B′2－A′C′2k2A′B′2－k2A′C′2＝k ．∴A′B′AB ＝A′C′AC ＝B′C′BC ．∴Rt △ABC ∽Rt △A ′B ′C ′．………………………………………8分解法二：如图，假设AB ＞A ′B ′，在AB 上截取A B ″＝A ′B ′，过点B ″作B ″C ″⊥AC ，垂足为C ″．∵∠C ＝∠AC ″B ″，∴BC ∥B ″C ″．∴Rt △ABC ∽Rt △AB ″C ″．∴AC″AC ＝AB″AB ．∵A B ″＝A ′B ′，∴AC″AC ＝A′B′AB． ∵A′B′AB ＝A′C′AC ，∴AC″AC ＝A′C′AC．∴A C ″＝A ′C ′．又∵A B ″＝A ′B ′，∠C ′＝∠A C ″B ″＝90°， ∴Rt △AB ″C ″≌Rt △A ′B ′C ′．∴Rt △ABC ∽Rt △A ′B ′C ′．……………………………………8分27．解：（1）80－x 200＋10x 800－200－(200＋10x ) ……………………………3分（2）根据题意，得80×200＋(80－x )(200＋10x )＋40[800－200－(200＋10x )]－50×800＝9000． ………………………………………………………………………………6分整理，得 x 2－20x ＋100＝0．解这个方程，得 x 1＝x 2＝10．当x ＝10时，80－x ＝70＞50．答：第二个月的单价应是70元． (8)28．解：（1）当点E 与点A 重合时，x ＝0，y ＝21×2×2＝2；当点E 不与点A 重合时，0＜x ≤2，在正方形ABCD 中，∠A ＝∠ADC ＝90°， ∴∠M DF ＝90°．∴∠A ＝∠M DF ． ∵AM ＝DM ，∠AME ＝∠DMF ， ∴△AME ≌△DMF ． ∴ME ＝MF ．在Rt △AME 中，AE ＝x ，AM ＝1，ME ＝． ∴EF ＝2ME ＝2．则∠MNG ＝90°，∠A MN ＝90°，MN ＝AB ＝AD ＝2AM ．∴∠A M E ＋∠E MN ＝90°． ∵∠E M G ＝90°，∴∠G M N ＋∠E MN ＝90°．∴∠A M E ＝∠G M N ．∴Rt △AEM ∽Rt △NGM ． ∴MN AM ＝MG ME ，即MG ME ＝21．∴MG ＝2ME ＝2．∴y ＝21EF ×MG ＝21×2×2＝2x 2＋2． ∴y ＝2x 2＋2，其中0≤x ≤2．…………………………………………………6分（2）点P 运动路线的长为2．………………………………………………………8分。

2010年南京市中考数学试题答案

D C 33° E B
………………………………………………………………6 分
AE ， DE
A
21．（本题 7 分）证明：（1）∵△ABC≌△BAD，∴∠CAB＝∠DBA． ∴OA＝OB．…………………………………………………………………3 分（2）∵△ABC≌△BAD，∴AC＝BD．又∵OA＝OB，∴ OC＝OD．∴∠OCD＝∠ODC． 180° －∠AOB 180° －∠COD ∵∠AOB＝∠COD，∠CAB＝，∠ACD＝， 2 2 ∴∠CAB＝∠ACD．∴AB∥CD．…………………………………………7 分 22．（本题 7 分）解：（1）因为点 A(1，1)在二次函数 y＝x2－2ax＋b 的图象上，所以 1＝1－2a＋b．可得 b＝2a．……………………………………………………………3 分（2）根据题意，方程 x2－2ax＋b＝0 有两个相等的实数根，所以 4a2－4b＝4a2－8a＝0．解得 a＝0，或 a＝2． …………………………………………………5 分当 a＝0 时，y＝x2，这个二次函数的图象的顶点坐标为(0，0)；当 a＝2 时， y＝x2－4x＋4＝(x－2)2，这个二次函数的图象的顶点坐标为(2， 0)．
数学试卷第 6 页（共 6 页）
＝பைடு நூலகம்
数学试卷第 1 页（共 6 页）
a－b ab ＝－ · ab (a＋b)(a－b) 1 ＝－． a＋b 19．（本题 6 分）解：（1）A ……………………………………………………………………………2 分（2）140÷7×30＝600（千克）．答：估计一个月该水果店可销售苹果 600 千克．…………………………………6 分 20．（本题 7 分）解：如图，过点 D 作 DE⊥AB，垂足为 E．在 Rt△ADE 中，DE＝BC＝10，∠ADE＝33°，tan∠ADE＝ ∴AE＝DE·tan∠ADE ≈10×0.65＝6.5． …………………………5 分 ∴AB＝AE＋BE＝AE＋CD＝6.5＋1.5＝8（m）．答：树的高度 AB 约为 8 m．……………………7 分