山东省临沂商城实验学校应聘教师登记表
教师事业编考察材料及个人总结

教师事业编考察材料及个人总结work Information Technology Company.2020YEAR个人总结我叫xxx,女,汉族,1988年9月26日出生于山东省xxxxxx的一个普通家庭,2006年9月进入辽宁师范大学学习,开始了我的四年大学生活。
在这四年的学习生活中,我对自己严格要求,努力提高自身各方面的能力和素质。
大学毕业后,先后在市第三实验小学和商城实验学校担任语文代课老师,现将我近两年的工作生活情况予以总结。
一、思想政治方面我在思想上始终积极要求上进,坚持学习马列主义、毛泽东思想、邓小平理论和三个代表重要思想,认同并践行社会主义价值观,不断提高自身的政治理论水平。
同时注重自己世界观的改变,注重树立正确的人生观、世界观、价值观。
思想和行为始终和党中央保持高度一致,无任何违法违纪行为。
二、工作方面参加工作以来,我本着团结同事、顾全大局、作风严谨、虚心好学、积极向上的原则,不怕苦,不怕累,遇到不懂的问题就向有经验的同事进行请教,以百倍的热情投入到工作之中。
在教学中,我始终和老教师们一起研究课程标准,吃透教材,积极开拓教学新思路。
同时,课外认真学习关于教学理论和方法的书籍,并把一些新想法用于自己的教学实践中。
课堂内,我与学生是师生关系,课堂外,我们更多的是一种朋友关系。
我始终坚信,亲其师方可信其道。
在这近两年的工作中,始终是服从学校及领导的安排,遵守学校的各项规章制度,从不迟到、早退、矿工,兢兢业业,恪尽职守,为人师表,为教育事业贡献自己的力量。
三、生活方面在生活上,我始终严格要求自己,团结同事,尊敬领导和长辈。
始终坚持自我反省,遇到问题总是先从自身找原因。
不论是在学校生活中还是在工作中,从来没有与人有过争吵,始终坚持恪守严于律己,宽以待人的原则。
同时,在平时的生活中,也是一直坚持勤俭节约这一中华传统美德。
回首这两年的工作生活情况,有了很大的进步,但在一些方面仍然存在着不足。
比如实践经验还不够丰富,专业知识也需更上一个台阶。
教师招聘登记表
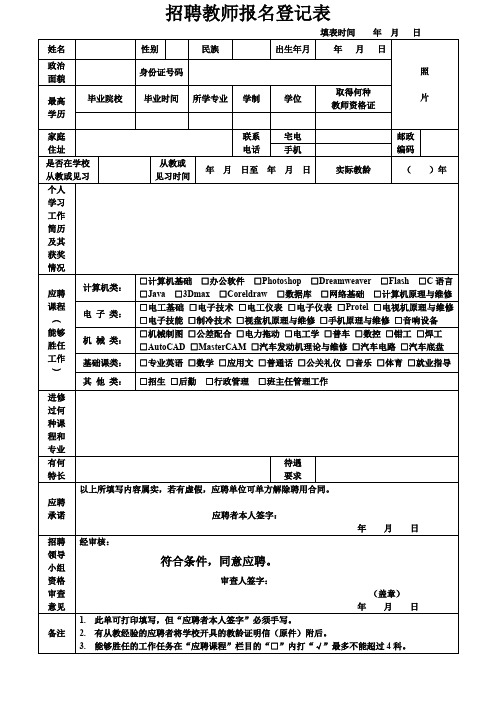
招聘教师报名登记表
填表时间年月日
姓名
性别
民族
出生年月
年月日
照
片
政治
面貌
身份证号码
最高
学历
毕业院校
毕业时间
所学专业
学制
学位
取得何种
教师资格证
家庭
住址
联系
电话
宅电
邮政
编码
手机
是否在学校
从教或见习
从教或
见习时间
年月日至年月日
工作
简历
及其
获奖
情况
应聘
课程
︵
能够
胜任
工作
︶
计算机类:
□计算机基础□办公软件□Photoshop□Dreamweaver□Flash□C语言
(盖章)
年月日
备注
1.此单可打印填写,但“应聘者本人签字”必须手写。
山东省临沂商城实验学校

山东 省 临 沂 商 城 实 验 学 校
临沂 商 城实 验 学校 于 2007年 成 立 ,是 一所 寄 宿 制 学校 ,现有 高 中 、初 中 、小 学 、幼 儿 园 四 个 学部 共 1 08个教 学 班 ,近6000名 学生 ,由齐鲁 名校 长 王清 群 同志 担任校 长 。
◆ 王 清 群校 长
◆校 长 与 学 生 共 读 书
◆ 学校 一 角
◆艺 术 节 ◆磨练意志 的远足拉 练
◆体 育 节
◆ 自主 创编绳 操
学 校 汇 集 了 国 家 级 骨干 教 师 、特 级 教 师 、齐 鲁 名校 长 、齐 鲁 名 师 、山东 省 十 大 创新 教 师 、 沂 蒙 名 币、教 学 能 手 、教学 新 秀 等 近 两 百 名省 内外 教 坛精 英 。著 名教 育 学 者 陶继 新 先生 曾赞 誉
“商城 实 验学 校有 一 支全 国 教学 研 究 的劲 旅 ” 。 学 校 创 新 性 实施 “四 大 ”校 本 课 程 :以 法 律 讲 堂 、节 日活 动 、传 统 文化 为 载 体 的大 德 课
程 ;以 班会 活 动 、团 队 活动 为载 体 的 大气 课 程 ;以 学科 拓 展 、技 能竞 赛 为 载体 的大 智课 程 ;以 创 新 实 践 、探 究 体 验 为载 体 的大 勇 课程 。学 科 教 学 体现 生 命 在 场 ,智 慧 高 扬 ,运 用 小组 合 作 学 习 、一 对一 个 性 化 辅 导 , “不 让 一 个孩 子 掉 队 ” 。幼 儿 园被 评 为 山东 省 十 佳 幼儿 园 ,小 学 部 在 全 区绿 色 教 学成 绩 抽 测 名 列前 茅 ,初 中ill3,/ 届 毕业 生 获 得 全 区中考 八 连 冠 ,高 中部学 生 985进 线率 达 43% 。
临沂职业学院2018年公开招聘教师报名表【模板】

2012.07 临沂市教育局 临沂市“劳动之星”职业技能竞
临沂市经济和信息化委员会 赛车工二等奖
临沂市财政局
临沂市人力资源社会保障局
家庭
成员
及其
主要
社会
关系
称谓 姓名 年龄 政治面貌 工作单位 职务
(无单位的填写住址、家务)
父亲
母亲
妻子
丈夫
儿子
女儿
审核意见
年 月 日
备 注
(确保畅通)
籍贯
现户籍所在地
报考岗位
其他资格条件
根据招聘计划表中的“其他资格条件”要求,据实填写。
例如:
从事本专业工作满5年、
本科专业为市场营销、
具有会计师 资格、
具有 加工中心 技师资格,获得市级 车工 技能大赛。
学
习
及
工
作
简
历
从初中开始填写至今,中间不可间断 例:
1990.09-1993.07 山东省临沂实验中学 初中
***临沂**学院2018年公开招聘教师报名表
编号:
姓 名
性别
民族
出生
年月
照片
一寸近期正面 免冠照片
参加工作时间
政治
面貌
身份证号码应聘学历 Nhomakorabea毕业院校 毕业时间
应聘学历所学专业
学位
熟悉专业特长
其它学历学位
所学专业
毕业院校 毕业时间
工作单位
考生身份
应届毕业生(√)往届毕业生()
邮箱和 通讯地址
联系方式2个
1993.09-1998.07 山东省临沂一中 高中
1998.09-2002.07**大学机械设计及其自动化 大学
山东省临沂市兰山区临沂商城实验学校2023-2024学年九年级上学期1月月考数学试题(解析版)

临沂商城实验学校阶段性学情调研2024.01九年级 数学试题(时间:100分钟 满分:120分)(内容:第24章圆;第25章概率;第26章反比例函数;第27章相似)一、选择题(每题3分,共36分)1. 如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC,若=,那么=( )A B. C. D. 【答案】D 【解析】【分析】先求解再证明可得【详解】解: =,DE ∥BC ,故选D【点睛】本题考查的是相似三角形的判定与性质,证明是解本题的关键.2. 已知点,,都在反比例函数(a 是常数)的图象上,且,则,,的大小关系为( )A. B. C. D. 【答案】D.AD BD 21DEBC 491213232,3AD AB =,ADE ABC ∽2.3DE AD BC AB == ADBD 212,3AD AB \= ,ADE ABC ∴ ∽2,3DEAD BC AB \==ADE ABC △△∽11(,)A x y 22(,)B x y 33(,)C x y 21a y x +=1230y y y <<<1x 2x 3x 213x x x >>123x x x >>321x x x >>312x x x >>【分析】根据,判断反比例函数的图象所在位置,结合图象分析函数增减性,利用函数增减性比较自变量的大小.【详解】解:∵,∴反比例函数(a 是常数)的图象在一、三象限,如图所示:当时,,故选:D .【点睛】本题考查反比例函数的自变量大小的比较,解题的关键是结合图象,根据反比例函数的增减性分析自变量的大小.3. 如图,一次函数与反比例函数的图象相交于A ,B 两点,点A 的横坐标为2,点B 的横坐标为,则不等式的解集是( )A. 或 B. 或 C. 或 D. 210a +>210a +>21a y x+=1230y y y <<<3120x x x >>>11y k x b =+22k y x =1-21k k x b x+<10x -<<2x >1x <-02x <<1x <-2x >12x -<<【解析】【分析】根据不等式的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围进行求解即可.【详解】解:由题意得不等式的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围,∴不等式的解集为或,故选A .【点睛】本题主要考查了一次函数与反比例函数综合,利用数形结合的思想求解是解题的关键.4. 已知蓄电池的电压为定值,使用蓄电池时,电流I (单位:A )与电阻R (单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )A. 函数解析式为 B. 蓄电池的电压是18VC. 当时,D. 当时,【答案】C【解析】【分析】将将代入求出U 的值,即可判断A ,B ,D ,利用反比例函数的增减性可判断C .【详解】解:设,将代入可得,故A 错误;∴蓄电池的电压是36V ,故B 错误;当时,,该项正确;当当时,,故D 错误,故选:C .【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.5. 如图,以点O 为位似中心,作四边形的位似图形,已知,若四边形21k k x b x +<21k k x b x +<21k k x b x+<10x -<<2x >Ω13I R =10A I ≤ 3.6R ≥Ω6R =Ω4A I =()4,9U I R =U I R=()4,936I R =10A I ≤ 3.6R ≥Ω6R =Ω6A I =ABCD A B C D ''''13OA OA =¢ABCD的面积是2,则四边形的面积是( )A. 4B. 6C.D. 【答案】D【解析】【分析】直接利用位似图形的性质,求出面积比,即可求解.【详解】∵以点O 为位似中心,作四边形的位似图形,,∴,则四边形面积为.故选:D .【点睛】本题考查了位似图形的性质,位似图形面积比等于相似比的平方,据此即可求解.6. 如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B 在同一直线上,已知纸板的两条直角边,测得边离地面的高度,则树高是( )A. B. C. D. 【答案】B【解析】【分析】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,比较简单,判定出和相似是解题的关键.先判定和相似,然后根据相似三角形对应边成比例列式求出的长,再加上即可得解.【详解】解:在和中,A B C D ''''1618ABCD A B C D ''''13OA OA =¢129ABCDA B C D A B C D S S S ''''''''==四边形四边形四边形A B C D ''''18DEF AB DF DE 4020DE cm EF cm ==,DF 1.5m 8m AC CD ==,AB 5m5.5m 6m6.5mDEF DBC △DEF DBC △BC AC DEF DBC △即解得:,即树高.故选:B .7. 如图,是的直径,B ,D 是上的两点,连接,若,则的度数为( )A. B. C. D. 【答案】B【解析】【分析】由是的直径可得,根据直角三角形的性质结合圆周角定理进而可得答案.【详解】解:∵是的直径,∴,∴,∵,∴,∴,故选:B .【点睛】本题考查了圆周角定理和直角三角形的性质,熟练掌握圆周角定理是解题关键.,D D DEF DCB∠=∠⎧⎨∠=∠⎩,DEF DCB ∴ ∽,DE CD EF BC∴=408,20BC=4BC =1.5m,AC =Q 1.54 5.5m,AB AC BC ∴=+=+=5.5m AC O O AB BC CD BD ,,,80A D ∠+∠=︒ACB ∠40︒50︒60︒80︒AC O 90ABC ∠=︒AC O 90ABC ∠=︒90A ACB ∠+∠=︒80A D A D ∠+∠=︒∠=∠,40A ∠=︒50∠=°ACB8. 如图,是的内接三角形,,是直径,,则的长为( )A. 4B. C. D. 【答案】B【解析】【分析】连接BO ,根据圆周角定理可得,再由圆内接三角形的性质可得OB 垂直平分AC ,再根据正弦的定义求解即可.【详解】如图,连接OB ,∵是的内接三角形,∴OB 垂直平分AC ,∴,,又∵,∴,∴,又∵AD=8,∴AO=4,∴解得:ABC O ,30AB BC BAC =∠=︒AD 8AD =AC 60BOA ∠=︒ABC O 1=2A M C M A C =OM AM ⊥,30AB BC BAC =∠=︒30BCA ∠=︒60BOA ∠=︒si n 604A M A M A O ︒===AM =∴故答案选B .【点睛】本题主要考查了圆的垂径定理的应用,根据圆周角定理求角度是解题的关键.9. 为做好疫情防控工作,某学校门口设置了,两条体温快速检测通道,该校同学王明和李强均从通道入校的概率是( )A. B. C. D. 【答案】A【解析】【分析】先列表得到所有的等可能的结果数,以及符合条件的结果数,再利用概率公式计算即即可.【详解】解:列表如下:A B AA ,A A ,B B B ,A B ,B所以所有的等可能的结果数有4种,符合条件的结果数有1种,所以该校同学王明和李强均从通道入校的概率是故选A【点睛】本题考查的是利用列表的方法或画树状图的方法求解简单随机事件的概率,掌握“列表的方法求概率”是解本题的关键.10. 如图,在正方形中,为边上的中点,点在边上,且,若,延长交的延长线于点,则的长为( )A. 4.5B. 5C. 5.5D. 6【答案】D【解析】【分析】由正方形的性质和勾股定理结合题意可求出,,又可证2A C A M ==A B A 14131234A 1.4ABCD E AD F CD 90BEF ∠=︒4AB =EF BC G CG 4AB AD BC ===BE =,即得出,代入数据,即可求出,从而可求出.【详解】解:∵四边形为正方形,为边上的中点,∴,,,∴.∵,∴,,∵,∴,∴,∴,∴,∴.故选D .【点睛】本题考查正方形性质,勾股定理,相似三角形的判定和性质等知识.掌握似三角形的判定定理和性质定理是解题关键.11. 如图,在中,,以点O 为圆心,2为半径的圆与交于点C ,过点C 作交于点D ,点P 是边上的动点.当最小时,的长为( )A. B. C. 1 D. 【答案】B【解析】【分析】延长CO 交于点E ,连接EP ,交AO 于点P ,则PC+PD 的值最小,利用平行线份线段成比例分别求出CD ,PO 的长即可.【详解】延长CO 交于点E ,连接ED ,交AO 于点P ,如图,的ABE EGB △△∽AE BE BE BG=10BG =6CG =ABCD E AD 4AB AD BC ===2AE =90BAD ABC ∠=∠=︒BE ==90BEF ∠=︒90∠+∠=︒EBG EGB 90∠=∠=︒BAE BEG 90EBG ABE ∠+∠=︒ABE EGB ∠=∠ABE EGB △△∽AE BE BE BG==10BG =6CG BG BC =-=Rt AOB 90,3,4AOB OA OB ∠=︒==OB CD OB ⊥AB OA PC PD +OP 123432O O∵CD ⊥OB ,∴∠DCB=90°,又,∴∠DCB=∠AOB ,∴CD//AO∴ ∵OC=2,OB=4,∴BC=2,∴,解得,CD=; ∵CD//AO ,∴,即,解得,PO= 故选:B .【点睛】此题主要考查了轴对称---最短距离问题,同时考查了平行线分线段成比例,掌握轴对称性质和平行线分线段成比例定理是解题的关键.12. 如图,在矩形中,点是的中点,的平分线交于点将沿折叠,点恰好落在上点处,延长、交于点,有下列四个结论:①垂直平分;②平分;③;④.其中,将正确结论的序号全部选对的是( )A. ①②③B. ①②④C. ②③④D. ①②③④90AOB ∠=︒BC CD BO AO=243CD =32EO PO EC DC =2=43PO 34ABCD E AD EBC ∠CD F DEF EF D EB M BC EF N BF EN BF ∠MFC DEF FEB ∽△△3BEF DEF S S =△△【答案】D【解析】【分析】由折叠的性质、矩形的性质与角平分线的性质,可证得CF =FM =DF ;易求得∠BFE =∠BFN ,则可得BF ⊥EN ;证明∠EFM =∠EBF 即可证明;易求得BM =2EM =2DE ,即可得EB =3EM ,根据等高三角形的面积比等于对应底的比,即可证明.【详解】解:∵四边形ABCD 是矩形,∴∠D =∠BCD =90°,DF =MF ,由折叠的性质可得:∠EMF =∠D =90°,即FM ⊥BE ,CF ⊥BC ,∵BF 平分∠EBC ,∴CF =MF ,∴DF =CF ,在△DEF 与△CFN 中,∴△DFE ≌△CFN ,∴EF =FN ,∵∠BFM =90°−∠EBF ,∠BFC =90°−∠CBF ,∴∠BFM =∠BFC ,∴BF 平分∠MFC ;故②正确;∵∠MFE =∠DFE =∠CFN ,∴∠BFE =∠BFN ,∵∠BFE +∠BFN =180°,∴∠BFE =90°,即BF ⊥EN ,∴BF 垂直平分EN ,故①正确;∵∠BFE =∠D =∠FME =90°,∴∠EFM +∠FEM =∠FEM +∠FBE =90°,∴∠EFM =∠EBF ,∵∠DFE =∠EFM ,∴∠DFE =∠FBE ,DEF FEB ∽△△3BEF DEF S S =△△90D FCN DF CFDFE CFN ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴;故③正确;∵∠BFM =∠BFC ,BM ⊥FM ,BC ⊥CF ,∴BM =BC =AD =2DE =2EM ,∴BE =3EM ,∴S △BEF =3S △EMF =3S △DEF ;故④正确.综上所述:①②③④都正确,故答案选:D .【点睛】本题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质,相似三角形的判断.此题难度适中,证得△DFE ≌△CFN 是解题的关键.二、填空题(每题3分,共18分)13. 在平面直角坐标系中,若反比例函数的图像位于第二、四象限,则k 的取值范围是________.【答案】【解析】【分析】本题考查反比例函数的性质,解题的关键是掌握当时,的图象位于第二、四象限.根据反比例函数的性质列不等式即可解得答案.【详解】解:∵反比例函数的图象位于第二、四象限,解得,故答案为:.14. 如图,已知与相交于点A ,,若,,,则_______.【答案】4DEF FEB ∽△△xOy 2k y x-=2k <0k <ky x=2k y x-=20,k ∴-<2k <2k <BD CE DE BC ∥2AD =3AB =6AC =AE =【解析】【分析】证明,由相似三角形的性质得出,则可得出答案.【详解】解:∵,∴,∴,即,∴,故答案为:4.【点睛】本题考查了相似三角形的判定与性质,熟记性质是解题的关键.15. 如图,B (3,﹣3),C (5,0),以OC ,CB 为边作平行四边形OABC ,则经过点A 的反比例函数的解析式为_____.【答案】【解析】【分析】设A 坐标为(x ,y ),根据四边形OABC 为平行四边形,利用平移性质确定出A 的坐标,利用待定系数法确定出解析式即可.【详解】设A 坐标为(x ,y ),∵B (3,-3),C (5,0),以OC ,CB 为边作平行四边形OABC ,∴x+5=0+3,y+0=0-3,解得:x=-2,y=-3,即A (-2,-3),设过点A 的反比例解析式为y=,把A (-2,-3)代入得:k=6,则过点A 的反比例解析式为y=,故答案为y=.【点睛】此题考查了待定系数法求反比例函数解析式,以及平行四边形的性质,熟练掌握待定系数法是解ABC ADE ∽△△AB ACAD AE=DE BC ∥ABC ADE ∽△△AB ACAD AE =362AE=4AE =6y x=kx 6x6x本题的关键.16. 如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是______.【答案】【解析】【分析】根据题意可得一共有9块方砖,其中阴影区域的有4块,再根据概率公式计算,即可求解.【详解】解:根据题意得:一共有9块方砖,其中阴影区域的有4块,∴它最终停留在阴影区域的概率是.故答案为:【点睛】本题考查了概率公式:熟练掌握随机事件A 的概率P (A )=事件A 可能出现的结果数除以所有可能出现的结果数;P (必然事件)=1;P (不可能事件)=0是解题的关键.17. 如图,一条公路的转弯处是一段圆弧,点是这段弧所在圆的圆心.是上的点,,垂足为点.若,,则的半径为______ .【答案】10【解析】【分析】连接,设的半径为,则,,再根据垂径定理可得,然后在中,利用勾股定理求解即可得.【详解】解:如图,连接,494949AB O C AB OC AB ⊥M 12m AB =2m CM =O m OA O m r m OA OC r ==()2m OM r =-16m 2AM BM AB ===Rt AOM △OA设的半径为,则,,,,,,在中,,即,解得,即的半径为,故答案为:10.【点睛】本题考查了垂径定理、勾股定理,熟练掌握垂径定理是解题关键.18. 如图,A 是双曲线上的一点,点C 是OA 的中点,过点C 作y 轴的垂线,垂足为D ,交双曲线于点B ,则△ABD 的面积是___________.【答案】4【解析】【分析】根据点C 是OA 的中点,根据三角形中线的可得S △ACD = S △OCD , S △ACB = S △OCB ,进而可得S △ABD = S △OBD ,根据点B 在双曲线上,BD ⊥ y 轴,可得S △OBD =4,进而即可求解.【详解】点C 是OA 的中点,∴S △ACD = S △OCD , S △ACB = S △OCB ,∴S △ACD + S △ACB = S △OCD + S △OCB ,∴S △ABD = S △OBD,O m r m OA OC r ==2m CM = ()2m OM OC CM r ∴=-=-OC AB ⊥ 12m AB =16m 2AM BM AB ∴===Rt AOM △222OA OM AM =+()22226r r -+=10r =O 10m ()80y x x=>()80y x x=>点B 在双曲线上,BD ⊥ y 轴,∴S △OBD=×8=4,∴S △ABD =4,答案为:4.【点睛】本题考查了三角形中线的性质,反比例函数的的几何意义,掌握反比例函数的几何意义是解题的关键.三、解答题(共6大题,合计66分)19. 如图,在和中,,.(1)求证:;(2)若,,求的长.【答案】(1)证明见解析;(2)9.【解析】【分析】(1)先根据角的和差可得,再根据相似三角形的判定即可得证;(2)根据相似三角形的性质即可得.【详解】证明:(1),,即,在和中,,;(2)由(1)已证:,,,,, ()80yx x=>12k k ABC DEC A D ∠=∠BCE ACD ∠=∠ABC DEC △△:4:9ABC DEC S S = 6BC =EC ACB DCE ∠=∠BCE ACD ∠=∠ BCE ACE ACD ACE ∴∠+∠=∠+∠ACB DCE ∠=∠ABC DEC ACB DCE A D ∠=∠⎧⎨∠=∠⎩ABC DEC ~∴ ABC DEC △△2ABC DEC C C S S B E ⎛⎫∴= ⎪⎝⎭:4:9ABC DEC S S = 6BC =2649EC ⎛⎫∴= ⎪⎝⎭解得或(不符题意,舍去),则的长为9.【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.20. 已知一次函数的图像与y 轴正半轴交于点C ,与反比例函数的图像交于A ,B 两点,若,点B 的横坐标是1.(1)求该反比例函数的解析式;(2)连接,求的面积.【答案】(1)反比例函数的解析式是(2)12【解析】【分析】本题考查反比例函数、一次函数解析式、交点及三角形面积等问题,解题的关键是求出反比例函数、一次函数图象交点坐标;(1)由,得,可求出一次函数解析式,把点B 的横坐标为1代入一次函数解析式得B 坐标,从而求得反比例函数的解析式;(2)求出、面积相加即可.【小问1详解】解:∵点在轴正半轴,,∴,∴该一次函数的解析式是.将代入,得,∴.9EC =9EC =-EC y x b =+()0ky k x=≠4OC =OA OB ,AOB 5y x=4OC =4b =OBC △AOC C y 4OC =4b =4y x =+1x =4y x =+5y =(1,5)B将代入,得,∴,∴该反比例函数的解析式是.【小问2详解】将代入,得,解得.∴点的横坐标是,∴点到轴的距离是5.∵点的横坐标是1,∴点到轴的距离是1,∴21. 如图,是的直径,弦于点E ,点M 在上,恰好经过圆心O ,连接.(1)若,,求的直径;(2)若,求的度数.【答案】(1)的直径是20 (2)【解析】【分析】本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧.(1)先根据,得出的长,进而得出的长,进而得出结论;(2)由,结合直角三角形可以求得结果;(1,5)B k y x=51k =5k =5y x=4y x =+5y x=45x x +=121,5x x ==-A 5-A y B B y 11541412.22AOB OBC AOC S S S =+=⨯⨯+⨯⨯=V V V AB O CD AB ⊥O MD MB 16CD =4BE =O M D ∠=∠D ∠O 30D ∠=︒16,4CD BE ==OE OB ,2M D DOB D ∠=∠∠=∠小问1详解】解:∵,设又解得:,∴的直径是20.【小问2详解】∵,22. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L .环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y (mg/L )与时间x (天)的变化规律如图所示,其中线段AC 表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L .从第3天起,所排污水中硫化物的浓度y 与时间x 满足下面表格中的关系:时间x (天)3569……硫化物的浓度y (mg/L )4.52.72.251.5……【,16AB CD CD ⊥=8,CE DE ∴==,OB OD x ==4,BE = 4,OE x ∴=-()22248,x x ∴=-+10x =O 12,M BOD M D ∠=∠∠=∠1,2D BOD ∴∠=∠,AB CD ⊥ 30.D ∴∠=︒(1)在整改过程中,当0≤x <3时,硫化物的浓度y 与时间x 的函数表达式;(2)在整改过程中,当x ≥3时,硫化物的浓度y 与时间x 的函数表达式;(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L ?为什么?【答案】(1)线段AC 函数表达式为:y =﹣2.5x +12(0≤x <3); (2)y=(x ≥3); (3)该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg /L ,理由见解析.【解析】【分析】(1)设线段AC 的函数表达式为:y =kx +b ,把A 、C 两点坐标代入求出k 、b 的值即可;(2)设函数的表达式为:y =,把C 点坐标代入,求出k 的值即可;(3)根据(2)所得表达式,求出x =15时,y 的值与硫化物浓度允许的最高值比较即可.【小问1详解】解:由前三天的函数图像是线段,设函数表达式为:y =kx +b把(0,12)(3,4.5)代入函数关系式,得 ,解得:k =﹣2.5,b =12∴当0≤x <3时,硫化物的浓度y 与时间x 的函数表达式为:y =﹣2.5x +12;【小问2详解】解:当x ≥3时,设y =,把(3,45)代入函数表达式,得4.5=,解得k =13.5,的.13.5xkx124.53bk b =⎧⎨=+⎩kx3k∴当x ≥3时,硫化物的浓度y 与时间x 的函数表达式为:y= ;【小问3详解】解:能,理由如下:当x =15时,y ==0.9,因为0.9<1,所以该企业所排污水中硫化物的浓度,能在15天以内不超过最高允许的1.0mg /L .【点睛】本题考查一次函数和反比例函数,熟练掌握根据坐标确定解析式的一次项系数和常数项是解题关键.23. 如图,点O 是的边AC 上一点,以点O 为圆心,OA 为半径作,与BC 相切于点E ,交AB 于点D ,连接OE ,连接OD 并延长交CB 的延长线于点F ,.(1)连接AF ,求证:AF 是的切线;(2)若,,求FD 的长.【答案】(1)见解析 (2)FD 【解析】【分析】(1)根据SAS 证△AOF ≌△EOF ,得出∠OAF =∠OEF =90°,即可得出结论;(2)根据勾股定理求出AF ,证△OEC ∽△FAC ,设圆O 的半径为r ,根据线段比例关系列方程求出r ,利用勾股定理求出OF ,最后根据FD =OF ﹣OD 求出即可.【小问1详解】证明:在△AOF 和△EOF 中,,∴△AOF ≌△EOF (SAS ),∴∠OAF =∠OEF ,∵BC 与相切,13.5x13.515ABC O ∠=∠AOD EOD O 10FC =6AC =83-OA OEAOD EOD OF OF =⎧⎪∠=∠⎨⎪=⎩O∴OE⊥FC,∴∠OAF=∠OEF=90°,即OA⊥AF,∵OA是的半径,∴AF是的切线;【小问2详解】解:在中,∠CAF=90°,FC=10,AC=6,∴,∵BC与相切,AF是的切线∴∠OEC=∠FAC=∠90°,∵∠OCE=∠FCA,∴△OEC∽△FAC,∴,设的半径为r,则,解得,在Rt△FAO中,∠FAO=90°,AF=8,,∴∴,即FD.【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,熟练掌握切线的判定和性质是解题的关键.24. 综合与实践课上,老师让同学们以“矩形与垂直”为主题开展数学活动.(1)操作判断OORt CAF8AF==OOEO COAF CF=O6810r r-=83r=83AO=OF==83FD OF OD=-=-83-如图1,正方形纸片,在边上任意取一点,连接,过点作于点,与边交于点.根据以上操作,请直接写出图1中线段与线段的关系.(2)迁移探究小华将正方形纸片换成矩形纸片,继续探究,过程如下:如图2,在矩形纸片中,,在边上任意取一点,连接,过点作于点,与边交于点,请求出线段与的关系,并说明理由.(3)拓展应用如图3,已知正方形纸片的边长为2,动点由点向终点做匀速运动,动点由点向终点做匀速运动,动点、同时开始运动,且速度相同,连接、,交于点,连接,则线段长度的最小值为______.(直接写出答案不必说明理由)【答案】(1)(2) (3【解析】【分析】(1)根据正方形的性质,由条件利用三角形全等判定可得,即可证明;(2)证明,根据相似三角形的性质可得出结论;(3)根据三边关系可判断出的最小值.【小问1详解】解:∵四边形是正方形,又在和中,ABCD BC E AE B BF AE ⊥G CD F AE BF ABCD ::=AB AD m n BC E AE B BF AE ⊥G CD F AE BF ABCD E A D F D C E F AF BE G GD GD AE BF =AE m BF n=1-ABE BCF △△≌BE CF =ABE BCF ∽△△GD ABCD 90,,ABC BCD AB BC ∴∠=∠=︒=,AE BF ⊥90,AGB ∴∠=︒90,BAE ABG ABG FBC ∴∠+∠=∠+∠=︒,BAE FBC ∴∠=∠ABE BCF △,,,BAE FBC AB BC ABE BCF ∠=∠=∠=∠Q (),ABE BCF ASA ∴ ≌【小问2详解】.理由如下:∵四边形是矩形,又;【小问3详解】如图,取的中点,连接,由题意知,,由(1)可得,同理可得:,∵是的中点,,∴,在中,;在中,∴,.;AE BF ∴=AE m BF n=ABCD 90,,ABC BCF AD BC ∴∠=∠=︒=,AE BF ⊥90,AGB ∴∠=︒90,BAE ABG ABG FBC ∴∠+∠=∠+∠=︒,BAE FBC ∴∠=∠,ABE BCF ∴V V ∽,AE AB BF BC∴=,AB AB m AD BC n==Q AE m BF n ∴=AB M ,DM GM AE DF =Rt ABE Rt DAF ≌90AGB ∠=︒M AB 2AB =1AM MB MG ===Rt ADM MD ==MGD 1,GD MD MG ≥-=-Q GD 11【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,直角三角形的性质,直角三角形斜边上的中线,相似三角形的判定与性质以及圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.。
2023年县管校聘教职工竞聘登记表(1)

负责人签字: (公章)
年月日
教育主 管
部门意 见
(公章)
注:1.竞聘类别:填写“直接聘任”、“校内聘任”或“跨校竞聘”。 2.竞聘意向:填写****学校 3.竞聘岗位:填写具体竞聘岗位名称,如:小学语文、小学2年级数学
年月日
报名时 间:
姓名
性别
籍贯
最高学历
教师资 格 类别
竞聘意 向
原聘岗位
XX县教职工竞聘登记表
竞聘类别: 参加工作时
间 政治面貌
所学专业
原聘岗位 类别
竞聘岗位
工作年限
学位 职称
竞岗自 荐近三年 考核情况 近三年奖 惩情况
2020年
2021年
2022年
资格审 查 意见
负责人签字: (公章)
聘用单位 意见
年月日
