合工大程序设计艺术与方法 实验四 动态规划
合工大 程序设计与艺术 实验三备课讲稿

《程序设计艺术与方法》课程实验报告四、实验结果与分析(源程序及相关说明)思考:判线段相交时,如果有个线段的端点在另一条线段上,注意可能与另一条线段上的端点重合,思考这样的情况怎么办。
用跨立的方法。
线段相交满足且只需满足如下两个条件就可以了:(1)两条线段相互跨立;(2)一条线段的一个端点在另一条线段上。
如果两线段相交,则两线段必然相互跨立对方,若p1p2跨立p3p4,则(p1-p3)×(p4-p3)*(p2-p3)×(p4-p3)>0,当(p1-p3)×(p4-p3)=0时,说明p1,p3,p4共线,但是因为已经通过了快速排斥实验,所以点p1一定在线段p3,p4上。
所以判断线段p1p2,p3p4相交的依据是(p1-p3)×(p4-p3)*(p2-p3)×(p4-p3)>=0。
#include <iostream>#include <utility>using namespace std;typedef pair<double,double> POINT;double direction(POINT p,POINT p1,POINT p2){POINT v1,v2;v1.first =p2.first -p.first ;v1.second=p2.second-p.second;v2.first =p1.first -p.first;v2.second=p1.second-p.second;return v1.first*v2.second-v1.second*v2.first;}bool on_segment(POINT p,POINT p1,POINT p2){double min_x=p1.first<p2.first?p1.first:p2.first;最短路问题:#include <iostream>#include <utility>#include <vector>#include <algorithm>using namespace std;typedef pair<double,double>POINT;double direction(POINT p,POINT p1,POINT p2) {POINT v1,v2;v1.first=p2.first-p.first;v1.second=p2.second-p.second;v2.first=p1.first-p.first;v2.second=p1.second-p.second;return v1.first*v2.second-v1.second*v2.first; }bool on_segment(POINT p,POINT p1,POINT p2) {double min_x=p1.first<p2.first?p1.first:p2.first;break;point.push_back(convex_hull[convex_hull.size()-1]);}while (1);for (int i=0;i<convex_hull.size();i++){cout<<convex_hull[i].first<<' '<<convex_hull[i].second<<endl;}}int main(){vector<POINT>pv;double x,y;int i;cout<<"请输入5个点<x,y>:"<<endl;for(i=1;i<5;i++){cout<<"No"<<i<<":";cin>>x>>y;pv.push_back(make_pair(x,y));}cout<<endl;find_convex_hull(pv);system("Pause");return 0;}运行结果:。
程序类竞赛中的动态规划算法探讨
程序类竞赛中的动态规划算法探讨作者:卢扬城,毛玉萃,关泽群来源:《电脑知识与技术》2021年第21期摘要:动态规划问题在各类程序设计竞赛中常常出现。
该文首先简单介绍了动态规划算法,阐述了利用动态规划解决实际问题的流程,并通过实例进一步探讨了线性动态规划、区间动态规划、树形动态规划、背包动态规划以及状态压缩动态规划算法问题,简单介绍了动态规划算法思想在其他经典算法中的应用,最后进行了简单总结。
关键词:动态规划;程序类竞赛;实例;中图分类号:TP311.52 文献标识码:A文章编号:1009-3044(2021)21-0093-04开放科学(资源服务)标识码(OSID):<E:\2021知网文件\19-21\21\3xs202121\Image\image1_7.jpeg>1 动态规划算法的概述[1-2]动态规划算法在是许多算法的理论基础,在传统决策性问题、图论问题、字符串问题等问题中都有涉及,因此是程序设计类竞赛考察的重点。
动态规划算法的核心是利用记忆化处理方式、依托贪心思想、记录历史数据来达到优化时间复杂度的目的,简而言之就是“用空间换时间”;在求解过程中采用分治思想,对问题分阶段进行决策。
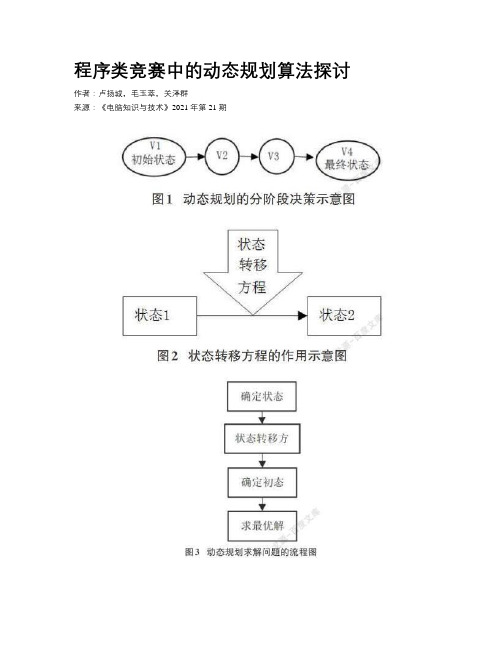
图1所示为动态规划的分阶段决策。
动态规划算法需要满足以下几个特征:1.1 无后效性无后效性是指当前状态一旦确定,则之后的所有状态与之前的情况无关,仅仅与当前状态的决策有关,因此要着重研究当前状态。
1.2 最优子结构动态规划算法经常解决的是最值性问题。
最优化子结构保证各阶段求解的方案决策具有类似的最值结构,即决策满足贪心思想下的解也一定是子解的最优解。
1.3 子问题重叠即所分解得到的子问题之间不是相互独立的,在之后的阶段还可能被多次使用到。
这一点不是动态规划算法适用的必要条件,但是如果没有这个特征,动态规划算法便不具有时间上的优势。
动态规划算法中状态定义和状态转移方程设计是核心。
状态定义是解决动态规划问题的关键,把问题分成几个不同的情况对这些情况的抽象描述即是状态定义。
《程序设计艺术与方法》课程实验报告材料的

《程序设计艺术与方法》课程实验报告一二实验名称搜索算法的实验姓名系院专业信息工程系班级物联网一班学号实验日期指导教师成绩一、实验目的和要求1.掌握宽度优先搜索算法。
2.掌握深度优先搜索算法。
二、实验预习内容1宽度优先搜索算法:又称广度优搜索。
是最简单的图的算法的原形。
其属于一种盲搜寻法,目的是系统地展开并检查图中的所有节点,以寻找结果。
换句话说,它并不考虑结果的可能位址,彻底地搜索整张图,直到找到结果为止。
2深度优先搜索算法:它的目的是要达到被搜索结构的叶结点。
在一个HTML文件中,当一个超链被选择后,被连接的HTML文件将执行深度优先搜索,即在搜索其余的超链走到不能再深入为止,然后返回到某一个HTML文件,再继续选择该HTML文件中的其他超链。
当不再有其他超链可选择时,说明搜索已经结束。
三、实验项目摘要1.将书上的走迷宫代码上机运行并检验结果,并注意体会搜索的思想。
2 .八皇后问题:在一个国际象棋棋盘上放八个皇后,使得任何两个皇后之间不相互攻击,求出所有的布棋方法。
上机运行并检验结果。
思考:将此题推广到N 皇后的情况,检验在N 比较大的情况下,比方说N=16 的时候,你的程序能否快速的求出结果,如果不能,思考有什么方法能够优化算法。
3骑士游历问题:在国际棋盘上使一个骑士遍历所有的格子一遍且仅一遍,对于任意给定的顶点,输出一条符合上述要求的路径。
4 倒水问题:给定2 个没有刻度容器,对于任意给定的容积,求出如何只用两个瓶装出L 升的水,如果可以,输出步骤,如果不可以,请输出No Solution。
四、实验结果与分析(源程序及相关说明)2,八皇后问题:#include <stdio.h>/*声明常量N存储行和列*/#define N 8#define NUM 8/*声明全局变量,h[N][N]控制盘格,H[N][N]控制输出,n[N]存储每一步的*纵坐标,count用于计数。
*/int h[N][N],n[N],H[N][N];int count=0;/*声明函数void tryit(int,int)尝试符合条件的方法*/void tryit(int,int);/*声明函数void outputArray(int[][N])输出数组*/void outputArray(int[][N]);main(){int x=0,y=0,i,j;/*初始化为零*/for(i=0;i<=N-1;i++){for(j=0;j<=N-1;j++)h[i][j]=0;}tryit(x,y);printf("//其他的布局略\n");printf("共有%d种布局.\n",92);return(0);}/*定义函数void tryit(int,int)尝试符合条件的方法*/void tryit(int x,int y){int i,j;if(count<=NUM){/*重复时跳出递归*/if((H[0][0]==1&&H[1][4]==1&&H[2][7]==1&&H[3][5]==1&&H[4][2]==1&&H[5][6 ]==1&&H[6][1]==1&&H[7][3]==1)&&count!=1){}else{if(x>=0&&x<=N-1&&y>=0&&y<=N-1&&h[x][y]==0){/*对与皇后在同一行、列、斜线上的点作出处理*/for(j=0;j<=7;j++){if(h[x][j]==0)h[x][j]=x+1;if(h[j][y]==0)h[j][y]=x+1;if(x+j>=0&&x+j<=N-1&&y+j>=0&&y+j<=N-1&&h[x+j][y+j]==0) h[x+j][y+j]=x+1;if(x+j>=0&&x+j<=N-1&&y-j>=0&&y-j<=N-1&&h[x+j][y-j]==0) h[x+j][y-j]=x+1;if(x-j>=0&&x-j<=N-1&&y+j>=0&&y+j<=N-1&&h[x-j][y+j]==0) h[x-j][y+j]=x+1;if(x-j>=0&&x-j<=N-1&&y-j>=0&&y-j<=N-1&&h[x-j][y-j]==0) h[x-j][y-j]=x+1;}/*对皇后处的点作出标志*/h[x][y]=-x-1;/*完成一种走法作出处理*/if(x==7){/*转换成输出的格式*/for(i=0;i<=N-1;i++){for(j=0;j<=N-1;j++){if(h[i][j]<0)H[i][j]=1;elseH[i][j]=0;}}count=count+1;/*输出前几种情况*/if(count<=NUM){printf("------布局%d------\n",count);outputArray(H);}/*对下一种走法,清楚前一次的影响*/for(i=0;i<=N-1;i++){for(j=0;j<=N-1;j++){if(h[i][j]==x||h[i][j]==-x||h[i][j]==-x-1)h[i][j]=0;}}/*递归,尝试另一种方法*/tryit(x-1,n[x-1]+1);}/*未走完一次,继续下一行*/else{n[x]=y;tryit(x+1,0);}}else{/*此路不通时,返回上一行,尝试下一种方法*/if(y>7){/*清楚前一次影响*/for(i=0;i<=N-1;i++){for(j=0;j<=N-1;j++){if(h[i][j]==x||h[i][j]==-x)h[i][j]=0;}}/*分情况递归*/if(x-1>=0)tryit(x-1,n[x-1]+1);elsetryit(0,0);}/*尝试下一格*/elsetryit(x,y+1);}}}}/*定义函数void outputArray(int[][N])输出数组*/void outputArray(int h[][N]){int i,j;for(i=0;i<=N-1;i++){for(j=0;j<=N-1;j++)printf("%d ",h[i][j]);printf("\n");}}运行截图:4.倒水问题:#include"stdio.h"int main(){int ca,cb,cc,x,y;while(scanf("%d%d%d",&ca,&cb,&cc)!=EOF) {if(cb==cc){ printf("fill B\n");}else if(ca==cc){printf("fill A\n");printf("pour A B\n");}else{x=y=0;if(ca<cc){while(1){ if(y==0){y=cb;printf("fill B\n");}if(y>ca-x) //如果b中的水大于a中的剩余容积,就把a灌满//{y-=ca-x;x=ca;printf("pour B A\n");}else //如果b中的水小于a中的剩余容积,那么把b中的水全加入a//{x+=y;y=0;printf("pour B A\n");}if(y==cc) //如果b中的水已经和cc相等,那就结束//{break;}if(ca==x) //如果a中的水满了,就把a倒空//{x=0;printf("empty A\n");}}}else{while(1){if(x==0){x=ca;printf("fill A\n");}if(x>cb-y) //如果a中的水大于b中的剩余容积,就把b灌满//{x-=cb-y;y=cb;printf("pour A B\n");}else //如果a中的水小于b中的剩余容积,那么把a中的水全加入b//{y+=x;x=0;printf("pour A B\n");}if(y==cc)//如果b中的水已经和cc相等,那就结束//{break;}if(y==cb) //如果b中的水满了,就把b倒空//{y=0;printf("empty B\n");}}}}printf("success\n");}return 0;}运行截图:三。
合工大自考实践考试java实验报告

Java程序设计实验报告专业计算机及应用上机卡号姓名指导老师实验一 Java开发环境的安装与配置(一)实验目的1.通过本次实验,掌握JDK的安装步骤,理解环境变量PATH,CLASSPATH的作用,以及它们的设置方法。
2.熟悉TextPad(或JCreater) 编辑环境,编写简单的Application程序,并编译和解释执行。
3.掌握JA V A中包的概念,以及包与包的引用关系。
4.记录编译和执行JA V A程序当中的系统错误信息提示,并给出解决办法。
5.选择一种主流的JA V A开发工具(如NETBEANS)进行安装和初步使用。
(二)实验内容1.设置环境变量PATH,CLASSPATH,使得JA V A程序能正确编译和执行。
设置环境变量PATH:设置环境变量CLASSPATH:2.在Texpad(Jcreater)环境下编写一个HelloWorld.java程序,在DOS提示符下编译并执行程序。
HelloWorld.java程序的代码:public class HelloWorld{public static void main(String []args){System.out.println("Hello Java");}}运行结果:3.编写一个类A,它位于包a,保存到A.java中。
再编写一个类B,它位于包b 中,保存到B.java中。
在类B中实例化类A的一个对象。
分别编译类A和类B。
程序代码:package a;public class A {public A(){System.out.println("在类B中实例化类A成功");}}package b;import a.*;class B {public static void main(String []args){A text=new A();}}运行结果:实验总结通过本次试验,掌握了环境变量的作用和设置,熟悉了java中包及包的应用关系。
《程序设计艺术与方法》课程实验报告.

《程序设计艺术与方法》课程实验报告一2 练习泛型算法的使用:#include<list>#include<iostream>//#inclued<algorithm>using namespace std;typedef list<int> lin;int value[]={1,6,7,8,9};//定义一个数组value 并赋值void print(lin &l){int i;lin::iterator lit;//定义一个迭代器for(lit=l.begin();lit!=l.end();lit++)cout<<(*lit)<<" ";//依次打印list中的元素cout<<endl;}二实验名称搜索算法的实验姓名黄星辰系院专业计算机与信息学院班级计算机科学与技术12—2班学号2012211643实验日期指导教师徐本柱成绩一、实验目的和要求1.掌握宽度优先搜索算法。
2.掌握深度优先搜索算法。
}运行截图:3. 骑士游历问题:在国际棋盘上使一个骑士遍历所有的格子一遍且仅一遍,对于任意给定的顶点,输出一条符合上述要求的路径。
#include <stdio.h>int board[8][8] = {0};int main(void) {int startx, starty;int i, j;printf("输入起始点:"); scanf("%d %d", &startx, &starty);if(travel(startx, starty)) {printf("游历完成!\n");}else {printf("游历失败!\n");}for(i = 0; i < 8; i++) {4.倒水问题:#include"stdio.h"int main(){int ca,cb,cc,x,y;while(scanf("%d%d%d",&ca,&cb,&cc)!=EOF) {if(cb==cc){ printf("fill B\n");}else if(ca==cc){printf("fill A\n");三实验名称计算几何算法的实现姓名黄星辰系院专业计算机与信息学院班级计算机科学与技术12—2班学号2012211643实验日期指导教师徐本柱成绩一、实验目的和要求1.理解线段的性质、叉积和有向面积。
南京邮电大学算法设计实验报告——动态规划法

if(a[i]==b[j]) {
c[i][j]=c[i-1][j-1]+1; s[i][j]=1; } else if(c[i-1][j]>=c[i][j-1]) { c[i][j]=c[i-1][j]; s[i][j]=2; } else { c[i][j]=c[i][j-1]; s[i][j]=3; } } } return c[m][n]; //返回最优解值 }
算法分析与设计 A
动态规划法
2009
年 11 月 20 日
计算机学院软件工程系
张怡婷
学生姓名 学院(系)
丁力琪 班级学号 计算机学院 专 业
B07030907 软件工程
实验报告
实验名称
动态规划法
指导教师 张怡婷
实验类型
验证
实验学时 2×2 实验时间 2009-11-20
一、 实验目的和任务
目的:加深对动态规划法的算法原理及实现过程的理解,学习用动态
6
8、输入序列 X={x1,x2,……,xm}={a,b,c,b,d,a,b}和 Y={y1,y2,……,yn}={b,d,c,a,b,a}作为测 试数据,测试程序是否能够正确运行?输出结果是什么? 运行正确,实验结果显示:4
bcba
9、分析该动态规划算法的两个主要成员函数 int LCSLength()和 void CLCS()的时间复杂 性。
#include<iostream> #include<string> using namespace std; #define maxlength 11 class LCS { public:
第6章 动态规划法

清华大学出版社
算法设计与分析
矩阵连乘问题
穷举法 动态规划 将矩阵连乘积
Ai Ai 1...Aj 简记为A[i:j] ,这里i≤j
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵 Ak和Ak+1之间将矩阵链断开,i≤k<j,则其相应完全 加括号方式为 ( Ai Ai 1...Ak )( Ak 1 Ak 2 ...Aj ) 计算量:A[i:k]的计算量加上A[k+1:j]的计算量,再加 上两个矩阵相乘的计算量
清华大学出版社
算法设计与分析
• 最优性原理:
– 一个过程的最优策略具有这样的性质,即无论其 初始状态及其初始决策如何,其以后诸决策对以 第一个决策所形成的状态作为初始状态而言,必 须构成最优策略。 如果一个问题满足最优性原理,则称该问题 具有 – 直观理解: 最优子结构性质。
II’ I A I’
B
II
C
如果I-II是A到C的最佳线路,则II一定是B到C的 最佳线路。即,“问题”的最优解由“子问题” 的最优解组成。
清华大学出版社
算法设计与分析
6.1.3 动态规划法的设计思想
动态规划法将待求解问题分解成若干个相互重 叠的子问题,每个子问题对应决策过程的一个阶段, 一般来说,子问题的重叠关系表现在对给定问题求 解的递推关系(也就是动态规划函数)中,将子问 题的解求解一次并填入表中,当需要再次求解此子 问题时,可以通过查表获得该子问题的解而不用再 次求解,从而避免了大量重复计算。
• 设计过程如下:
– 阶段划分:
第一步对于第五层的数据,我们做 如下四次决策:
2 19 18 9 10 5
7
4
16
以上的决策结果将五阶数塔问题变为4阶子问题, 递推出第四层与第五层的和为:
合工大.net程序设计与系统开发实验报告

《.NET程序设计与系统开发》课程实验报告姓名(学号)分工成绩实验时间2016实验地点专业电子商务13-01班所在学院管理学院指导老师一、实验目的实验一:C#语法基础实验配合课程教学,通过实际上机练习,熟练掌握和运用C#基本语法,能运用它进行控制台应用程序设计;熟悉VISUAL 开发平台;熟悉控制台应用程序的调试经验和技巧。
实验二:C#语法高级实验进一步熟悉和掌握C#语言,增强程序调试经验和技巧;锻炼综合运用所学知识能力,能设计和解决适当问题。
二、实验要求实验一:C#语法基础实验实现实验内容提要中规定的各项需求;独立(或合作或在别人协助下或老师指导下)创造性地完成实验,严禁抄袭;实验结束,提交实验报告。
基于VISUAL 平台开展实验,学会如何建立控制台应用的项目工程。
掌握以下语法知识:(1)数据类型;(2)运算符、表达式、语句;(3)数组、字符串、迭代器;(4)异常处理与预处理指令;(5)类与接口;(6)事件与委托。
实验二:C#语法高级实验实现实验内容提要中规定的各项需求;独立(或合作或在别人协助下或老师指导下)创造性地完成实验,严禁抄袭;实验结束,提交实验报告。
所建工程类型可以为:控制台应用、windows窗体应用、 web应用。
三、实验内容实验一:C#语法基础实验任务1 判断每个输入的数是否可被3,5和7整除,并将整除状态输出。
要求:(1) 掌握VISUAL C#.NET 的基本调试技巧。
演示调试情况,会跟踪变量的值,会设置和取消断点,会跟踪如何进入函数内部(2) 对每个输入数,分别输出对3,5和7的整除状态; (3) 能实现多次输入输出,最好能有一些输入提示; (4) 亦可同时输入和处理多个数,并输出多个数的整除状态。
(5) 考虑使用switch 或if 。
任务2 练习使用for 、while 、do while 、foreach in 等循环语句。
要求:(1) 上述循环语句至少使用1次; (2) 至少有1题采用了string 类实现; (3) 至少有1题采用了集合类实现; 任务3 绘图输出y=a*sin(c*x + b)输出字符三角形A AAA AAAAA AAAAAAA AAAAAAAAAB BBB BBBBB 输出字符菱形A AAA AAAAA AAAAAAA AAAAAAAAA AAAAAAA AAAAA AAA AB BBB BBBBB BBB B输出背靠背字符三角形W W WW WW WWW WWW WWWW WWWW B B BB BB BBB BBB输出交替字符倒三角形STSTS STS SSTSTSTSTSTSTSTSTSTS STSTSTSTSTSTSTSTS STSTSTSTSTSTSTS STSTSTSTSTSTS STSTSTSTSTS STSTSTSTS STSTSTS STSTS STS S要求:(1)系数a, b和c是可以变化的,可考虑是从键盘输入的,或通过Main方法参数传递的;(2)x的取值范围在0~4π之间,x,y值采用四舍五入;提示:根据输入参数,先生成一组数据(x, y),可考虑循环生成,四舍五入;在相应位置输出*或#。
计算机程序设计艺术》读后感2500字

计算机程序设计艺术》读后感2500字摘要:一、引言1.介绍《计算机程序设计艺术》的地位和影响2.阐述阅读该书的原因和目的二、书籍内容概述1.卷1:基础运算法则2.卷2:半数值算法3.卷3-5:排序和搜索算法4.卷6:动态规划5.卷7:概率和随机算法6.卷8:算法设计与分析三、个人收获与感悟1.基本编程概念与技术的掌握2.信息结构与数据结构的重要性3.算法思维的培养4.实践与应用能力的提升四、书中案例与实际应用1.举例说明书中算法在实际项目中的应用2.分析算法优化与性能提升的方法五、阅读心得与建议1.针对不同层次的程序员,提出阅读建议2.强调理论与实践相结合的重要性3.推荐相关书籍和资源六、总结1.回顾《计算机程序设计艺术》的主要内容2.表达对该书的敬意和感激3.表示将在今后的工作中发挥所学,提高编程技艺正文:作为一名职业写手,我始终秉持着不断学习和进步的态度,努力提高自己的编程技能。
近日,我阅读了《计算机程序设计艺术》这部经典之作,深感受益匪浅。
在此,我将分享我的读后感,以期为广大程序员提供一些有益的参考。
《计算机程序设计艺术》是一部由Donald Knuth创作的计算机科学经典教材,自问世以来,便在计算机领域产生了深远的影响。
作者以基本的编程概念和技术为起点,逐步深入探讨信息结构、算法设计、性能优化等多个方面。
该书适用于不同层次的程序员,既可作为初学者的入门教材,也可作为资深工程师的参考书。
在阅读本书之前,我已经有一定的编程基础。
然而,通过学习本书,我更加深刻地认识到自己在编程技艺上的不足。
书中详细讲解了基础运算法则、半数值算法、排序和搜索算法、动态规划等方面的知识,让我重新审视了计算机科学的基本概念。
信息结构与数据结构在计算机程序设计中起着至关重要的作用。
书中以丰富的例子阐述了数据元素间的结构关系以及处理它们的有效方法。
这些知识对我来说极具实用性,使我更加擅长分析和解决实际问题。
此外,书中的算法思维让我受益匪浅。
合工大计算方法实验报告参考模板

《计算方法》试验报告班级:学号:姓名:实验一、牛顿下山法1 实验目的(1)熟悉非线性方程求根简单迭代法,牛顿迭代及牛顿下山法 (2)能编程实现简单迭代法,牛顿迭代及牛顿下山法 (3)认识选择迭代格式的重要性 (4) 对迭代速度建立感性的认识;分析实验结果体会初值对迭代的影响2 实验内容(1)用牛顿下山法解方程013=--x x (初值为0.6)输入:初值,误差限,迭代最大次数,下山最大次数输出:近似根各步下山因子(2)设方程f(x)=x 3- 3x –1=0 有三个实根 x *1=1.8793 , x *2=-0.34727 ,x *3=-1.53209现采用下面六种不同计算格式,求 f(x)=0的根 x *1 或x *2 x = 213xx +; x = 313-x ;x = 313+x ; x = 312-x ;x = x 13+;x = x - ()1133123---x x x输入:初值,误差限,迭代最大次数输出:近似根、实际迭代次数 3 算法基本原理求非线性方程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
只有建立有效的迭代格式,迭代数列才可以收敛于所求的根。
因此设计算法之前,对于一般迭代进行收敛性的判断是至关重要的。
牛顿法也叫切线法,是迭代算法中典型方法,只要初值选取适当,在单根附近,牛顿法收敛速度很快,初值对于牛顿迭代至关重要。
当初值选取不当可以采用牛顿下山算法进行纠正。
一般迭代:)(1k k x x φ=+ 0)()(=⇔=x f x x φ 牛顿公式:)()(1k k k k x f x f x x '-=+ 牛顿下山公式:)()(1k k k k x f x f x x '-=+λ图3.1一般迭代算法流程图 下山因子 ,,,,322121211=λ 下山条件|)(||)(|1k k x f x f <+4 算法描述一般迭代算法见流程图牛顿下山算法见流程图:5、代码:#include <iostream>#include <fstream>#include <cmath>using namespace std;class srrt{private:int n;double *a, *xr, *xi;public:图3.2牛顿下山算法流程图⇐⇐⇐⇐srrt (int nn){n = nn;a = new double[n+1]; //动态分配内存xr = new double[n];xi = new double[n];}void input (); //由文件读入代数方程系数void srrt_root (); //执行牛顿下山法void output (); //输出根到文件并显示~srrt (){ delete [] a, xr, xi; }};void srrt::input () //由文件读入代数方程系数{int i;char str1[20];cout <<"\n输入文件名: ";cin >>str1;ifstream fin (str1);if (!fin){ cout <<"\n不能打开这个文件" <<str1 <<endl; exit(1); } for (i=n; i>=0; i--) fin >>a[i]; //读入代数方程系数fin.close ();}void srrt::srrt_root () //执行牛顿下山法{int m,i,jt,k,is,it;double t,x,y,x1,y1,dx,dy,p,q,w,dd,dc,c;double g,u,v,pq,g1,u1,v1;m=n;while ((m>0)&&(fabs(a[m])+1.0==1.0)) m=m-1;if (m<=0){cout <<"\n程序工作失败!" <<endl;return;}for (i=0; i<=m; i++) a[i]=a[i]/a[m];for (i=0; i<=m/2; i++){w=a[i]; a[i]=a[m-i]; a[m-i]=w;}k=m; is=0; w=1.0;jt=1;while (jt==1){pq=fabs(a[k]);while (pq<1.0e-12){xr[k-1]=0.0; xi[k-1]=0.0; k=k-1;if (k==1){xr[0]=-a[1]*w/a[0]; xi[0]=0.0;return;}pq=fabs(a[k]);}q=log(pq); q=q/(1.0*k); q=exp(q);p=q; w=w*p;for (i=1; i<=k; i++){ a[i]=a[i]/q; q=q*p; }x=0.0001; x1=x; y=0.2; y1=y; dx=1.0;g=1.0e+37;l40:u=a[0]; v=0.0;for (i=1; i<=k; i++){p=u*x1; q=v*y1;pq=(u+v)*(x1+y1);u=p-q+a[i]; v=pq-p-q;}g1=u*u+v*v;if (g1>=g){if (is!=0){it=1;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}else{it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }}if (it==0) goto l40;}}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; } }else{g=g1; x=x1; y=y1; is=0;if (g<=1.0e-22){if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{u1=k*a[0]; v1=0.0;for (i=2; i<=k; i++){p=u1*x; q=v1*y; pq=(u1+v1)*(x+y);u1=p-q+(k-i+1)*a[i-1];v1=pq-p-q;}p=u1*u1+v1*v1;if (p<=1.0e-20){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{dx=(u*u1+v*v1)/p;dy=(u1*v-v1*u)/p;t=1.0+4.0/k;it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}}}if (k==1) jt=0;else jt=1;}}void srrt::output () //输出根到文件并显示{int k;char str2[20];cout <<"\n输出文件名: ";cin >>str2;ofstream fout (str2);if (!fout){ cout <<"\n不能打开这个文件" <<str2 <<endl; exit(1); } for (k=0; k<n; k++){fout <<xr[k] <<" " <<xi[k] <<endl;cout <<xr[k] <<" +j " <<xi[k] <<endl;}fout.close ();}void main () //主函数{srrt root(6);root.input (); //由文件读入代数方程系数root.srrt_root (); //执行牛顿下山法root.output (); //输出根到文件并显示}6、输入输出输出结果如下:7、分析体会牛顿下山法作为计算方法课程中重要的知识点,在看书学习时较易大致理解其思路,但上级编写代码时却是有难度的。
合工大 程序设计艺术与方法 实验一

《程序设计艺术与方法》课程实验报告#include"stdafx.h"#include<iostream>#include<ctime>#include<vector>#include<list>#include<algorithm>using namespace std;bool comper(int a, int b){return (a > b);}//vector练习void OUTV(vector<int> v){vector<int>::iterator it = v.begin();for (; it != v.end(); ++it){cout << (*it) << " ";}cout << endl;}void FindV(vector<int> &exp){int x;vector<int>::iterator L;cout << "请输入你要查找的数:" << endl;cin >> x;L = find(exp.begin(), exp.end(), x);if (L != exp.end()){cout << "查找成功!" << endl;cout << "该数为:" << *L << endl;}else{cout << "无该数!" << endl;exp.push_back(x);cout << "输出结果:";OUTV(exp);}}void SortV(vector<int> &exp){cout << "升序:" << endl;sort(exp.begin(), exp.end());OUTV(exp);cout << "降序" << endl;sort(exp.begin(), exp.end(),comper);OUTV(exp);}void DeldetV(vector<int> &exp){cout << "删除最后一个元素" << endl;exp.pop_back();OUTV(exp);}void V(){vector<int> exp1;srand((int)time(0));cout << "vector练习:" << endl;for (int i = 0; i < 10; i++)exp1.push_back(rand());//插入10个随机数OUTV(exp1);exp1.insert(exp1.begin(), rand());OUTV(exp1);FindV(exp1);SortV(exp1);DeldetV(exp1);cout << "最大值:" << exp1[0] << endl;cout << "最小值:" << exp1[exp1.size()-1] << endl;exp1.clear();//清空迭代器}//List练习void OUTL(list<int> v){list<int>::iterator it = v.begin();for (; it != v.end(); ++it){cout << (*it) << " ";}cout << endl;}void FindL(list<int> &exp){int x;list<int>::iterator L;cout << "请输入你要查找的数:" << endl;cin >> x;L = find(exp.begin(), exp.end(), x);if (L != exp.end()){cout << "查找成功!" << endl;cout << "该数为:" << *L << endl;}else{cout << "无该数!" << endl;exp.push_back(x);cout << "输出结果:";OUTL(exp);}}void SortL(list<int> &exp){cout << "排序:" << endl;exp.sort();OUTL(exp);}void DeldetL(list<int> &exp){cout << "删除最后一个元素" << endl;exp.pop_back();OUTL(exp);}void L(){list<int> exp2;srand((int)time(0));cout << "List练习:" << endl;for (int i = 0; i < 10; i++)exp2.push_back(rand());//插入10个随机数OUTL(exp2);exp2.push_front(rand());OUTL(exp2);FindL(exp2);SortL(exp2);DeldetL(exp2);//清空迭代器exp2.clear();}int_tmain(int argc, _TCHAR* argv[])。
程序设计方法——动态规划法

思路(续)
显然,根据前面的递推过程求解,需要倒 过来,从P(D),P(E),P(F)出发,先求出第1阶 段的P(B)和P(C),最后得到P(A)。
数据结构
将长满桃子的树用二维数组保存
数组行上存放桃树上一层中每个树枝上桃子数 将节点上桃子数目存放在数组中 只使用数组中对角线及下部分 A:1
y
A1 B2 C9 E6 F5 I6 J4 x
7 D
G2
3 H
将底层到每个点的最长路径P也存放在二维 数组中
数据结构(续)
#define MAXLAYER 3 int peachtree[MAXLAYER][MAXLAYER] = { {1, -1, -1, -1}, {2, 9, -1, -1}, {7, 6, 5, -1}, {2, 3, 6, 4} }; int P[MAXLAYER][MAXLAYER]
1
B:2 C:9
2 7
9 6 5
D:7 E:6 F:5
2
3
6
4
G:2
H:3
I:6
J:4
问题分析
从二维数组最下面一行开始向 上一行沿图中的直线前进,走 到左上角的格子停止。 行走路径上经过的格子中的数 字之和是猴子爬到树顶能拿到 桃子的数目,我们定义为路径 长度。 原问题转化为求所有路径中路 径长度的最大值。
参考程序(续)
//初始化P[x][0] for (i = 0; i < n; i++) { P[i][0] = peachtree[i][0]; } //递推过程P[x][y] = max{P[x][y-1], P[x+1][y-1]}+peachtree[x][y] for (j = 1; j < n; j++) // i是行号,j是列号 { for (i = 0 ; i + j < n; i++) { P[i][j] = maxnum(P[i][j-1], P[i+1][j-1])+peachtree[i][j]; } } cout << P[0][n-1] << endl; return 0; }
河北工业大学汇编语言程序设计实验

汇编语言程序设计实验网络*** ***实验一 顺序与分支程序设计一 、实验目的1) 掌握顺序程序设计方法。
2) 掌握分支程序的结构及分支程序的设计,调试方法。
2) 学习数据传送及算术和逻辑运算指令的用法。
3) 熟悉在pc 机上建立、汇编、连接、调试和运行汇编语言程序的过程。
二、实验内容1.实验六从键盘上接收一位十进制数x ,计算y 值,并以十六进制形式显示出来,y 按下列公式计算。
⎪⎪⎩⎪⎪⎨⎧===-=+=)6(2/)5()4(2)3(2222X X X X X X X X X X Y2..实验七实验内容:从键盘上接收两个一位十六进制数x 和y ,然后再输入一个a-d 之间的一个字符,按下列要求计算。
a)当输入字符为a ,则计算x+y ,并以十六进 制形式显示出来 b)当输入字符为b ,则计算|x-y|,并以十六进制形式显示出来 c)当输入字符为c ,则计算x*y ,并以十六进制形式显示出来 d)当输入字符为d ,则计算x/y ,并以十六进制形式显示出来三、实验代码实验六DATE SEGMENTDATE ENDS ;数据段CODE SEGMENTASSUME CS:CODE,DS:DATESTART:MOV AX,DATE ;代码段MOV DS,AX ;初始化ds寄存器MOV AH,1INT 21H ;读文件到缓冲区CMP AL,33H ;比较指令JB L0 ;A<BCMP AL,36HJA L0AND AL,0FH ;逻辑与指令MOV X,AL ;al给xMOV AL,XCMP AL,3HJE L1 ;执行L1命令CMP AL,4HJE L4 ;执行L4命令CMP AL,5HJE L6 ;执行L6命令CMP AL,6HJE L7 ;执行L7命令L1:MUL ALADD AL,X ;al+xL5:MOV BL,ALMOV CL,4SHR AL,CL ;移位指令CMP AL,9JLE L2 ;转移指令。
ICPC介绍

合肥工业大学 计算机与信息学院
10
合肥工业大学 计算机与信息学院
11
ACM-ICPC比赛形式 比赛形式
组队参赛的形式,由三名队员组成一支队伍参赛。 组队参赛的形式,由三名队员组成一支队伍参赛。比赛 时三名队员只使用一台电脑
比赛时间为5个小时。比赛题目为8~12道不等, 比赛时间为5个小时。比赛题目为8~12道不等,全英文 8~12道不等 可以带纸质资料。 可以带纸质资料。 选手们必须根据题目内容设计算法, 选手们必须根据题目内容设计算法,并完成相应的功能 要求,要么全对,要么不对, 要求,要么全对,要么不对,没有中间结果
合肥工业大学 计算机与信息学院
26
内容提要
一、ICPC介绍 介绍 二、ICPC队员选拔和培训机制 队员选拔和培训机制 三、ACMer基础知识 基础知识
合肥工业大学 计算机与信息学院
27
ACMer ——基本算法
(1)枚举. (poj1753,poj2965) (2)贪心(poj1328,poj2109,poj2586) (3)递归和分治法. (4)递推. (5)构造法.(poj3295)
7000 6000 5000 4000 3000 2000
1998 1999 2000 2001 2002 2003 2004 2005 2006
参赛 1000 学 校 数
0 参 赛队 数
1998 1999 2000 2001 2002 2003 2004 2005 2006
合肥工业大学 计算机与信息学院
合肥工业大学 计算机与信息学院
29
ACMer —— 数据结构
(1)串 (poj1035,poj3080,poj1936) (2)排序 (poj2388,poj2299) (3)简单并查集的应用. (4)哈夫曼树(poj3253) (5)堆 (6)线段树
合工大程序设计艺术与方法 实验四 动态规划

《程序设计艺术与方法》课程实验报告LCSLength(str1, str2,i,j);cout << "最长子序列为:" << endl;Print(str1, i, j, m, n);cout << endl;cout << "最长子序列长度为:" << Long[m][n] << endl;;system("pause");}int _tmain(int argc, _TCHAR* argv[]){LCS();return 0;}2.字符串的变换:使用动态规划的思想:定义两个数组,Distance表示距离,handle表示操作,其中handle存储的数1为删除,2为插入,3为替换,4为相同跳到下一个字符,5为结束状态。
先初始化,令handle开始的第一行第一列为5,如果str1[i] != str2[0],handle为3,列同理;其中Distance为对应的行号或者列号。
两重for循环遍历所有组合的点,如果str1[i] == str2[j],则Distance[i][j] = Distance[i - 1][j - 1],handle[i][j] = 4;否则handle[i][j] = minval(Distance[i - 1][j] + 1, Distance[i][j - 1] + 1, Distance[i - 1][j - 1] + 1, Distance[i][j]); minval函数的作用是比较最大值,并返回最大值对应的操作,1为删除,2为插入,3为替换,当循环结束时,在Distance[m-1][n-1](m,n分别为两字符串的长度)中存储着最少操作次数输出步骤:最后先递归,后操作,修改str1字符串,表示操作的步骤。
#include "stdafx.h"#include<stdio.h>#include<iostream>#include<string>#include <vector>using namespace std;#define MAX 1000int Distance[MAX][MAX];3.计算所有的子矩阵中和的最大值使用动态规划:使用一个二维数组,其中num[i][j]存储矩阵i*j的元素和。
合工大汇编语言程序设计实验报告

合工大汇编语言程序设计实验报告合肥工业大学计算机与信息学院实验报告课程:汇编语言程序设计专业班级:**************** 学号:**********姓名:*****目录实验一 (3)实验二 (7)实验三 (12)实验四 (22)实验一Debug程序的使用一.实验目的1、熟悉DEBUG程序中的命令,学会在DEBUG下调试运行汇编语言源程序。
2、掌握8086/8088的寻址方式及多字节数据的处理方法。
二.实验内容1、利用DEBUG程序中的“E”命令,将两个多字节数“003F1AE7H”和“006BE5C4H”分别送入起始地址为DS:0200H和DS:0204H两个单元中。
2、分别用直接寻址方式和寄存器间接寻址方式编写程序段,实现将DS:0200H 单元和DS:0204H单元中的数据相加,并将运算结果存放在DS:0208H单元中。
要求:本次实验的内容均在DEBUG下完成,实现数据的装入、修改、显示;汇编语言程序段的编辑、汇编和反汇编;程序的运行和结果检查。
三.实验过程和程序实验内容一:e ds:0200 E7 1A 3F 00e ds:0204 C4 E5 6B 00实验内容二:(1)直接寻址方式MOV AX,[0200]MOV BX,[0202]ADD AX,[0204]ADC BX,[0206]MOV [0208],AXMOV [020A],BX(2)寄存器间接寻址方式MOV SI,0200HMOV DI,0204HMOV BX,0208HMOV AX,[SI]MOV DX,[SI+2]ADD AX,[DI]ADC DX,[DI+2]MOV [BX],AXMOV [BX+2],DX四.实验结果(包括必要的截图)实验内容一:输入数据:显示数据:实验内容二:(1)直接寻址方式程序段编辑:反汇编:运行:结果在DS:0208 单元中为00AB00ABH(2)寄存器间接寻址方式程序段编辑:反汇编:运行:结果高字存放在dx中,低字存放在ax中(结果为00AB00ABh)五.实验体会通过本实验,实践debug程序中的命令,并在debug下调试运行汇编语言源程序。
合肥工业大学操作系统课程设计 动态分区分配存储管理java版

课 程 设 计动态分区分配存储管理2010 年 12 月设计题目 学 号 专业班级 学生姓名指导教师合肥工业大学课程设计任务书第一章课程设计概述1.1 设计任务:动态分区分配存储管理1.2 设计要求建立描述内存分配状况的数据结构;建立描述进程的数据结构;使用两种方式产生进程:(a)自动产生,(b)手工输入;在屏幕上显示内存的分配状况、每个进程的执行情况;建立分区的分配与回收算法,支持紧凑算法;时间的流逝可用下面几种方法模拟:(a)按键盘,每按一次可认为过一个时间单位; (b) 响应WM_TIMER;将一批进程的执行情况存入磁盘文件,以后可以读出并重放;支持算法:首次适应算法、循环首次适应算法、最佳适应算法:最坏适应算法。
1.3 设计目的旨在让我们更好的了解动态分区管理方面的知识.第二章原理及算法描述2.1动态分区分配算法原理首次适应算法* 算法概述:分配内存时,从链首开始顺序查找,找到满足的空闲分区则划出空间分配,余下的空闲空间仍保留在空闲链表中* 实现方法:分配时从数组第一个元素开始比较,若符合条件则将该元素减去对应作业的值循环首次适应算法* 算法概述:由首次适应算法演变,只是每次分配改为由上一次找到的空闲分区开始查找* 实现方法:在首次适应算法的基础上增加一个值用于记录找到的空闲分区的位置最佳适应算法* 算法概述:每次为作业分配内存时,总是把能满足要求、又是最小的空闲分区分配给作业* 实现方法:我们决定每次分配先把空闲分区按从小到大的顺序排列,然后将第一个匹配分区分配给作业最坏适应算法* 算法概述:每次为作业分配内存时,总是挑选一个最大的空闲分区分割给作业使用* 实现方法:算法与最佳适应算法几乎相同,仅在排序时把空闲分区表按从大到小的顺序排列,所以未作详细注释回收分区当进程运行完毕释放内存时,系统根据回收区的首址,从空闲区链(表)中找到相应的插入点,此时可能出现以下四种情况之一;1)回收区与插入点的前一个空闲分区F1相邻接,此时应将回收区与插入点的前一分区合并,不必为回收区分配新表项,而只需修改其前一分区F1的大小.2)回收分区与插入点的后一空闲分区F2相邻接,此时也可将两分区合并,形成新的空闲分区,但用回收区的首址作为新空闲区的首址,大小为两者之和.3)回收区同时与插入点的前,后两个分区邻接,此时将三个分区合并,使用F1的表项和F1的首址,取消F2的表项,大小为三者之和.4)回收区既不与F1相邻接,又不与F2邻接.这时应为回收区单独建立一新表项,填写回收区的首址和大小,并根据其首址插入到空闲链中的适当位置.紧凑算法通过移动内存中的作业的位置,以把原来多个分散的小分区拼接成一个大分区的方法.第三章开发环境此程序是本人利用JAVA 语言在一种JCreator 的开发环境中实现的第四章重要算法和设计思路描述4.1 设计首次适应算法首先从内存分区的状态中找到空闲分区,若无空闲分区则不进行后面的运算,直接弹出对话框"内存中无空闲分区".把作业所需空间的大小与按始址大小,与各个空闲分区进行比较,如果某分区大小合适,把该分区一分为二,前部为已经分配出去的分区,后者为剩余的分区,然后对内存情况进行更新,每次分区小于作业,将指示不符合次数的n加一,如果不符合次数为空闲分区数组长度,说明找遍空闲分区都无符合项,最后对作业数组进行更新,把已运行的作业去除.4.2 设计循环首次适应算法同样根据内存分区的状态中找到空闲分区数组,令x指向上次找到空闲分区的下一个空闲分区,比较方法与首次适应算法相比,仅在此改为用x指示空闲分区在数组中的位置,每次查找空闲分区,都是从x后面那个分区开始查询, 如果某分区大小合适,把该分区一分为二,前部为已经分配出去的分区,后者为剩余的分区,然后对内存情况进行更新,每次分区小于作业,将指示不符合次数的n加一,到了数组末尾后再次进行循环回到数组头,一直寻找到上次所分配的位置,转为从首位开始查找后只比较到上一次找到的匹配分区,以保证循环可结束. 如果不符合次数为空闲分区数组长度,说明找遍空闲分区都无符合项,最后对作业数组进行更新,把已运行的作业去除.4.3 设计最佳适应算法和最坏适应算法最佳适应算法的实质就是对内存分区数组进行排序后,利用首次适应算法最坏适应算法的实质也是对内存分区数组排序后,进行首次适应算法,只不过它与最佳适应算法排序的方向刚好相反4.4 设计分区回收算法对内存分区状态进行查找,若回收区与插入点的前一个空闲分区F1相邻接,此时应将回收区与插入点的前一分区合并,不必为回收区分配新表项,而只需修改其前一分区F1的大小.若回收分区与插入点的后一空闲分区F2相邻接,此时也可将两分区合并,形成新的空闲分区,但用回收区的首址作为新空闲区的首址,大小为两者之和.若回收区同时与插入点的前,后两个分区邻接,此时将三个分区合并,使用F1的表项和F1的首址,取消F2的表项,大小为三者之和.若回收区既不与F1相邻接,又不与F2邻接.这时应为回收区单独建立一新表项,填写回收区的首址和大小,并根据其首址插入到空闲链中的适当位置4.5 设计紧凑算法同样对内存分区状态进行查找,若存在空闲分区,对分区数组,把已分配的数组的位置进行移动,使已分配的分区全部相邻,这样得到的最后剩下的一个大分区就是可以分配的分区啦.第五章程序实现---数据结构class memory{private int m1;//分区的序号private int m2;//分区的大小private int m3;//分区的起始地址private int m4;//是否已分配的标志} 这是定义的内存分区的结构class process{private int xuhao;//作业序号private int kongjian;//作业运行所需的空间} 这是定义的作业的结构第六章程序实现---程序清单import java.awt.event.*;import javax.swing.*;import java.awt.*;import java.io.*;import java.util.*;public class algorithm{private JFrame frame;private JTextPane memory;private JTextPane process;private memorydata md;private processdata pd;private int fitIndex=-1;private int select;private JTextField inputField;private JFrame inputFrame;public void go(){frame=new JFrame("动态分区");JPanel mainPanel=new JPanel();JPanel printPanel=new JPanel();printPanel.setLayout(new GridLayout(2, 1));memory=new JTextPane();process=new JTextPane();JScrollPane ScrollerM=new JScrollPane(memory);ScrollerM.setVerticalScrollBarPolicy(ScrollPaneConstants.VERTICAL_SCROLLBAR_ALWAYS);ScrollerM.setHorizontalScrollBarPolicy(ScrollPaneConstants.HORIZONTAL_SCROLLBAR_NEVER);JScrollPane ScrollerP=new JScrollPane(process);ScrollerP.setVerticalScrollBarPolicy(ScrollPaneConstants.VERTICAL_SCROLLBAR_ALWAYS);ScrollerP.setHorizontalScrollBarPolicy(ScrollPaneConstants.HORIZONTAL_SCROLLBAR_NEVER);printPanel.add(ScrollerM);printPanel.add(ScrollerP);JMenuBar menuBar=new JMenuBar();JMenu fileMenu=new JMenu("文件");JMenu dataMenu=new JMenu("数据");JMenu FPMenu=new JMenu("分配");JMenu HSMenu=new JMenu("回收");JMenu JCMenu=new JMenu("紧凑");JMenuItem FileItemM=new JMenuItem("输出内存数据");JMenuItem FileItemP=new JMenuItem("输出作业数据");JMenuItem MemoryItem=new JMenuItem("读入内存数据");JMenuItem ProcessItem=new JMenuItem("读入作业数据");JMenuItem randomdataItemM=new JMenuItem("随机内存数据");JMenuItem randomdataItemP=new JMenuItem("随机作业数据");JMenuItem fenpeiItem=new JMenuItem("分配");JMenuItem huishouItem=new JMenuItem("回收");JMenuItem jinchouItem=new JMenuItem("紧凑");FileItemM.addActionListener(new OutputMemoryListener());FileItemP.addActionListener(new OutputProcessListener());MemoryItem.addActionListener(new InputMemoryListener());ProcessItem.addActionListener(new InputProcessListener());randomdataItemM.addActionListener(new randomMemoryListener());randomdataItemP.addActionListener(new randomProcessListener());fenpeiItem.addActionListener(new fenpeiListener());huishouItem.addActionListener(new huishouListener());jinchouItem.addActionListener(new jinchouListener());fileMenu.add(FileItemM);fileMenu.add(FileItemP);dataMenu.add(MemoryItem);dataMenu.add(ProcessItem);dataMenu.add(randomdataItemM);dataMenu.add(randomdataItemP);FPMenu.add(fenpeiItem);HSMenu.add(huishouItem);JCMenu.add(jinchouItem);menuBar.add(fileMenu);menuBar.add(dataMenu);menuBar.add(FPMenu);menuBar.add(HSMenu);menuBar.add(JCMenu);frame.setJMenuBar(menuBar);frame.getContentPane().add(BorderLayout.CENTER,printPanel);frame.setSize(600,500);frame.setVisible(true);}public class randomMemoryListener implements ActionListener{public void actionPerformed(ActionEvent ac){md=new memorydata();print.printM(md.m,memory);}}public class randomProcessListener implements ActionListener{ public void actionPerformed(ActionEvent ac){inputFrame=new JFrame();JPanel inputPanel=new JPanel();JButton sendButton=new JButton("确认");sendButton.addActionListener(new SendButtonListener3());inputField=new JTextField(10);inputPanel.add(inputField);inputPanel.add(sendButton);inputFrame.getContentPane().add(BorderLayout.CENTER,inputPanel);inputFrame.setSize(200,100);inputFrame.setLocationRelativeTo(null);inputFrame.setVisible(true);}}public class OutputMemoryListener implements ActionListener{ public void actionPerformed(ActionEvent ac){JFileChooser fileOpen=new JFileChooser();fileOpen.showOpenDialog(frame);MyFile.outputMemorydata(md,fileOpen.getSelectedFile());}}public class OutputProcessListener implements ActionListener{ public void actionPerformed(ActionEvent ac){JFileChooser fileOpen=new JFileChooser();fileOpen.showOpenDialog(frame);MyFile.outputProcessdata(pd,fileOpen.getSelectedFile());}}public class InputMemoryListener implements ActionListener{ public void actionPerformed(ActionEvent ac){JFileChooser fileOpen=new JFileChooser();fileOpen.showOpenDialog(frame);md=new memorydata(MyFile.inputMemorydata(fileOpen.getSelectedFile()));print.printM(md.m,memory);}}public class InputProcessListener implements ActionListener{public void actionPerformed(ActionEvent ac){JFileChooser fileOpen=new JFileChooser();fileOpen.showOpenDialog(frame);pd=new processdata(MyFile.inputProcessdata(fileOpen.getSelectedFile()));print.printP(pd.p,process);}}public class fenpeiListener implements ActionListener{public void actionPerformed(ActionEvent ac){fenpeiProcess();}}public class huishouListener implements ActionListener{public void actionPerformed(ActionEvent ac){if(!memorydata.huishou(md.m)){JOptionPane.showMessageDialog(frame, "内存中无可回收分区");return;}waitinput();}}public class jinchouListener implements ActionListener{public void actionPerformed(ActionEvent ac){if(!memorydata.kongxian(md.m)){JOptionPane.showMessageDialog(frame, "内存中分区全被分配,无空闲分区");return;}jincou();}}public class SendButtonListener3 implements ActionListener{public void actionPerformed(ActionEvent ev){int processmount=Integer.parseInt(inputField.getText());pd=new processdata(processmount);print.printP(pd.p,process);}}public class SendButtonListener2 implements ActionListener{public void actionPerformed(ActionEvent ev){int selectmemory=Integer.parseInt(inputField.getText());recycle(selectmemory);}}public class SendButtonListener implements ActionListener{public void actionPerformed(ActionEvent ev){int selectProcess=Integer.parseInt(inputField.getText());if(select!=1&&select!=2&&select!=3&&select!=4){JOptionPane.showMessageDialog(inputFrame, "请选择一种分配方法");return;}if(selectProcess>pd.p.length){JOptionPane.showMessageDialog(inputFrame, "输入错误");return;}if(select==1){FirstFit(selectProcess);}else if(select==2){fitIndex=NextFit(selectProcess,fitIndex);}else if(select==3){BestFit(selectProcess);}else if(select==4){WorstFit(selectProcess);}}}public class b1ButtonListener implements ActionListener{public void actionPerformed(ActionEvent ev){select=1;}}public class b2ButtonListener implements ActionListener{ public void actionPerformed(ActionEvent ev){select=2;}}public class b3ButtonListener implements ActionListener{ public void actionPerformed(ActionEvent ev){select=3;}}public class b4ButtonListener implements ActionListener{ public void actionPerformed(ActionEvent ev){select=4;}}private void waitinput(){inputFrame=new JFrame();JPanel inputPanel=new JPanel();JButton sendButton=new JButton("确认");sendButton.addActionListener(new SendButtonListener2());inputField=new JTextField(10);inputPanel.add(inputField);inputPanel.add(sendButton);inputFrame.getContentPane().add(BorderLayout.CENTER,inputPanel);inputFrame.setSize(200,100);inputFrame.setLocationRelativeTo(null);inputFrame.setVisible(true);}private void fenpeiProcess(){inputFrame=new JFrame();JRadioButton b1 = new JRadioButton();JRadioButton b2 = new JRadioButton();JRadioButton b3 = new JRadioButton();JRadioButton b4 = new JRadioButton();ButtonGroup group = new ButtonGroup();JPanel intro = new JPanel();JLabel introJl = new JLabel();intro.add(introJl);introJl.setText(" 分配算法选择 ");inputFrame.add(intro);b1.setText("1、首次适应算法");b2.setText("2、循环首次适应算法");b3.setText("3、最佳适应算法");b4.setText("4、最坏适应算法");b1.addActionListener(new b1ButtonListener());b2.addActionListener(new b2ButtonListener());b3.addActionListener(new b3ButtonListener());b4.addActionListener(new b4ButtonListener());group.add(b1);group.add(b2);group.add(b3);group.add(b4);// p为第二个JPanelJPanel p = new JPanel();// 设置第二个JPanel上的jl1 JLabel初始显示信息JLabel jl1 = new JLabel();jl1.setText("输入待分配的作业序号");// 添加该JLabel到p上p.add(jl1);// 添加该JPanelinputFrame.add(p);// p1为第三个Panel,此JPanel由于要显示5个算法的单选键,所以设置为5行的GridLayout布局JPanel p1 = new JPanel();p1.setLayout(new GridLayout(4, 1));p1.add(b1);p1.add(b2);p1.add(b3);p1.add(b4);inputFrame.add(p1);JPanel inputPanel=new JPanel();inputField=new JTextField(5);inputPanel.add(inputField);JButton sendButton=new JButton("确认");sendButton.addActionListener(new SendButtonListener());inputPanel.add(sendButton);inputFrame.add(inputPanel);inputFrame.setLayout(new FlowLayout());// 设置窗口大小,inputFrame.setSize(400, 220);// 大小不可更改inputFrame.setLocation(300, 400);// 显示inputFrame.setVisible(true);// 设置窗口右上角的关闭按钮事件为结束程序inputFrame.setDefaultCloseOperation(JFrame.HIDE_ON_CLOSE);}/*** 首次适应算法* 算法概述:分配内存时,从链首开始顺序查找,找到满足的空闲分区则划出空间分配,余下的空闲空间仍保留在空闲链表中* 实现方法:分配时从数组第一个元素开始比较,若符合条件则将该元素减去对应作业的值**/private void FirstFit(int selectProcess){print.printM(md.m,memory);//显示当前内存分区状况memory[] free=memorydata.Free(md.m);//对当前内存分区获取空闲分区的信息print.printF(free,memory);//显示内存空闲分区的状况print.insert("首次适应算法",memory);int xuhao=selectProcess-1;if (free.length == 0){// 若无空闲分区则不进行后面的运算JOptionPane.showMessageDialog(frame, "内存中无空闲分区");}else{int n=0;//指示分区与作业不符合的次数for(int j=0;j<free.length;j++){//与各个空闲分区进行比较print.insert("进程号"+pd.p[xuhao].getxuhao()+" 所需分区大小为["+pd.p[xuhao].getkongjian()+"] 与分区号为"+free[j].getm1()+"的空闲分区 ["+free[j].getm2()+"] 比较",memory);if(pd.p[xuhao].getkongjian()<free[j].getm2()){//分区大于作业print.insert("符合,分配",memory);memory[] nb=new memory[md.m.length+1];int ni=free[j].getm1();if(free[j].getm1()==1){//如果该空闲分区是内存表头//把该分区一分为二,前部为已经分配出去的分区,后者为剩余的分区nb[0]=new memory(1,pd.p[xuhao].getkongjian(),0,1);nb[1]=newmemory(2,free[j].getm2()-pd.p[xuhao].getkongjian(),pd.p[xuhao].getkongjian(),0);//把nb构造成经过分配后的内存分区数组for(int k=2;k<nb.length;k++)nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());md.m=nb;print.printM(md.m,memory);free= memorydata.Free(md.m);print.printF(free,memory);}else{//如果该空闲分区不是内存表头for(int k=0;k<ni;k++)nb[k]=newmemory(md.m[k].getm1(),md.m[k].getm2(),md.m[k].getm3(),md.m[k].getm4());//把该分区一分为二,前部为已经分配出去的分区,后者为剩余的分区nb[ni-1].setm2(pd.p[0].getkongjian());nb[ni-1].setm4(1);//设置标识此分区已分配nb[ni]=newmemory(nb[ni-1].getm1()+1,free[j].getm2()-pd.p[xuhao].getkongjian(),nb[ni-1].getm2()+nb[ni-1].get m3(),0);for(int k=ni+1;k<nb.length;k++){nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());}md.m=nb;print.printM(md.m,memory);free = memorydata.Free(md.m);print.printF(free,memory);}break;}else{if(pd.p[xuhao].getkongjian()==free[j].getm2()){//分区等于作业print.insert(" 符合,分配",memory);md.m[free[j].getm1()-1].setm4(1);//把此分区标志位已分配print.printM(md.m,memory);free= memorydata.Free(md.m);print.printF(free,memory);break;}else{//分区小于作业,将指示不符合次数的n加一n++;}}if(n==free.length){//如果不符合次数为空闲分区数组长度,说明找遍空闲分区都无符合项JOptionPane.showMessageDialog(frame, "无符合分区");//print.insert(" 无符合分区",memory);return;}}//对作业数组进行更新,把已运行的作业去除processdata temp=new processdata(pd.p.length-1);for(int i=0;i<xuhao;i++)temp.p[i].setkongjian(pd.p[i].getkongjian());for(int i=xuhao;i<temp.p.length;i++){int te=pd.p[i+1].getkongjian();temp.p[i].setkongjian(te);}pd.p=temp.p;print.printP(pd.p,process);}}/*** 循环首次适应算法* 算法概述:由首次适应算法演变,只是每次分配改为由上一次找到的空闲分区开始查找* 实现方法:在首次适应算法的基础上增加一个值用于记录找到的空闲分区的位置**///此函数返回记录找到的空闲分区的位置private int NextFit(int input,int fitIndex){print.printM(md.m,memory);memory[] free=memorydata.Free(md.m);//构造空闲分区print.printF(free,memory);print.insert("循环首次适应算法",memory);int xuhao=input-1;if(free.length==0){// 若无空闲分区则不进行后面的运算JOptionPane.showMessageDialog(frame, "内存中无空闲分区");//print.insert("内存中无空闲区",memory);return fitIndex;}else{int n = 0;//指示分区与作业不符合的次数print.insert(" - - - - - - - - - - - - - - - - - - - - - - - - -",memory);int x = fitIndex + 1;// 令x指向上次找到空闲分区的下一个空闲分区// 比较方法与首次适应算法相比,仅在此改为用x指示空闲分区在数组中的位置while (x <md.m.length){if (md.m[x].getm4() != 1){print.insert(" 进程号"+pd.p[xuhao].getxuhao()+" 所需分区["+pd.p[xuhao].getkongjian()+"] 与分区号为"+md.m[x].getm1()+"的空闲分区 ["+md.m[x].getm2()+"] 比较,",memory);if (pd.p[xuhao].getkongjian()<md.m[x].getm2()){// 假如作业小于空闲分区,则可分配print.insert("符合,分配",memory);memory[] nb =new memory[md.m.length + 1];for (int k = 0; k < x; k++){nb[k] =md.m[k];}// 数组对应元素减去作业大小,即表示分配后的大小int size = md.m[x].getm2()-pd.p[xuhao].getkongjian();nb[x] = md.m[x];nb[x].setm2(pd.p[xuhao].getkongjian());nb[x].setm4(1); //标志此分区为已分配nb[x + 1]=new memory(nb[x].getm1() + 1,size,nb[x].getm2()+ nb[x].getm3(), 0);//创建分配后余下的分区for(int k = x + 2; k < nb.length; k++){nb[k] = md.m[k - 1];nb[k].setm1(nb[k].getm1()+1);}md.m=nb;fitIndex = x;//更新此次找到的空闲分区的位置print.printM(md.m,memory);free=memorydata.Free(md.m);print.printF(free,memory);// 得到分配,结束此作业比较循环break;}else{if(pd.p[xuhao].getkongjian()==md.m[x].getm2()){//分区等于作业print.insert(" 符合,分配",memory);md.m[md.m[x].getm1()-1].setm4(1);//标志此分区为已分配print.printM(md.m,memory);free= memorydata.Free(md.m);print.printF(free,memory);fitIndex = x;//更新此次找到的空闲分区的位置break;}else{n++;// 每不符一次把n加1print.insert("不符,往下找",memory);}}}x++;// 利用x++将元素指向下一位}//到了数组末尾后再次进行循环回到数组头if (x >= md.m.length){x = 0;while (x <= fitIndex) //一直寻找到上次所分配的位置{if (md.m[x].getm4()!= 1){// 转为从首位开始查找后只比较到上一次找到的匹配分区,以保证循环可结束print.insert("进程号"+pd.p[xuhao].getxuhao()+" 所需分区["+pd.p[xuhao].getkongjian()+"] 与分区号为"+md.m[x].getm1()+"的空闲分区 ["+md.m[x].getm2()+"] 比较,",memory);if (pd.p[xuhao].getkongjian()<md.m[x].getm2()){// 假如作业小于空闲分区,则可分配print.insert("符合,分配",memory);memory[] nb =new memory[md.m.length + 1];for (int k = 0; k < x; k++){nb[k] =md.m[k];}// 数组对应元素减去作业大小,即表示分配后的大小int size = md.m[x].getm2()-pd.p[xuhao].getkongjian();nb[x] =md.m[x];nb[x].setm2(pd.p[xuhao].getkongjian());nb[x].setm4(1);nb[x + 1] = new memory(nb[x].getm1() + 1, size,nb[x].getm2()+ nb[x].getm3(), 0);for (int k = x + 2; k < nb.length; k++){nb[k] =md.m[k - 1];nb[k].setm1(nb[k].getm1()+1);}md.m=nb;fitIndex = x;print.printM(md.m,memory);free = memorydata.Free(md.m);print.printM(free,memory); // 得到分配,结束此作业比较循环break;}else{if(pd.p[xuhao].getkongjian()==md.m[x].getm2()){//分区等于作业print.insert(" 符合,分配",memory);md.m[md.m[x].getm1()-1].setm4(1);print.printM(md.m,memory);free = memorydata.Free(md.m);print.printM(free,memory);fitIndex = x;break;}else{n++;// 每不符一次把n加1print.insert("不符,往下找",memory);}}}x++; // 利用x++将元素指向下一位}}if (n == free.length){// 假如n等于空闲数组的长度,则说明找遍空闲分区都无符合项JOptionPane.showMessageDialog(frame, "未找到符合的空闲分区");//print.insert("",memory);//print.insert(" 未找到符合的空闲分区",memory);return fitIndex;}else{//对作业数组进行更新processdata temp=new processdata(pd.p.length-1);for(int i=0;i<xuhao;i++)temp.p[i].setkongjian(pd.p[i].getkongjian());for(int i=xuhao;i<temp.p.length;i++){int te=pd.p[i+1].getkongjian();temp.p[i].setkongjian(te);}pd.p=temp.p;print.printP(pd.p,process);System.out.println();return fitIndex;}}}/** 最佳适应算法* 算法概述:每次为作业分配内存时,总是把能满足要求、又是最小的空闲分区分配给作业* 实现方法:我们决定每次分配先把空闲分区按从小到大的顺序排列,然后将第一个匹配分区分配给作业 **///最佳适应算法的实质就是对内存分区数组进行排序后,利用首次适应算法private void BestFit(int input){print.printP(pd.p,process);print.printM(md.m,memory);memory[] free=memorydata.Free(md.m);memorydata.up(free);//对内存数组进行排序print.printF(free,memory);//后面的比较过程与首次适应算法一样print.insert("最佳适应算法",memory);int xuhao=input-1;if (free.length == 0){// 若无空闲分区则不进行后面的运算JOptionPane.showMessageDialog(frame, "内存中无空闲分区");//print.insert("内存中无空闲分区",memory);}else{int n=0;for(int j=0;j<free.length;j++){//与各个空闲分区进行比较print.insert("进程号"+pd.p[xuhao].getxuhao()+" 所需分区大小为["+pd.p[xuhao].getkongjian()+"] 与分区号为"+free[j].getm1()+"的空闲分区 ["+free[j].getm2()+"] 比较",memory);if(pd.p[xuhao].getkongjian()<free[j].getm2()){//分区大于作业print.insert("符合,分配",memory);memory[] nb=new memory[md.m.length+1];int ni=free[j].getm1();if(free[j].getm1()==1){//如果该空闲分区是内存表头nb[0]=new memory(1,pd.p[xuhao].getkongjian(),0,1);nb[1]=newmemory(2,free[j].getm2()-pd.p[xuhao].getkongjian(),pd.p[xuhao].getkongjian(),0);for(int k=2;k<nb.length;k++)nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());md.m=nb;print.printM(md.m,memory);free= memorydata.Free(md.m);memorydata.up(free);print.printF(free,memory);}else{//如果该空闲分区不是内存表头for(int k=0;k<ni;k++)nb[k]=newmemory(md.m[k].getm1(),md.m[k].getm2(),md.m[k].getm3(),md.m[k].getm4());nb[ni-1].setm2(pd.p[0].getkongjian());nb[ni-1].setm4(1);nb[ni]=newmemory(nb[ni-1].getm1()+1,free[j].getm2()-pd.p[xuhao].getkongjian(),nb[ni-1].getm2()+nb[ni-1].get m3(),0);for(int k=ni+1;k<nb.length;k++){nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());}md.m=nb;print.printM(md.m,memory);free = memorydata.Free(md.m);memorydata.up(free);print.printF(free,memory);}break;}else{if(pd.p[xuhao].getkongjian()==free[j].getm2()){//分区等于作业System.out.println(" 符合,分配");md.m[free[j].getm1()-1].setm4(1);print.printM(md.m,memory);free = memorydata.Free(md.m);memorydata.up(free);print.printF(free,memory);break;}else{//分区小于作业,将指示不符合次数的n加一n++;}}if(n==free.length){//如果不符合次数为空闲分区数组长度,说明找遍空闲分区都无符合项JOptionPane.showMessageDialog(frame, "无符合分区");//print.insert(" 无符合分区",memory);return;}}processdata temp=new processdata(pd.p.length-1);for(int i=0;i<xuhao;i++)temp.p[i].setkongjian(pd.p[i].getkongjian());for(int i=xuhao;i<temp.p.length;i++){int te=pd.p[i+1].getkongjian();temp.p[i].setkongjian(te);}pd.p=temp.p;print.printP(pd.p,process);}}/** 最坏适应算法* 算法概述:每次为作业分配内存时,总是挑选一个最大的空闲分区分割给作业使用* 实现方法:算法与最佳适应算法几乎相同,仅在排序时把空闲分区表按从大到小的顺序排列,所以未作详细注释**///最坏适应算法的实质也是对内存分区数组排序后,进行首次适应算法,只不过它与最佳适应算法排序的方向刚好相反private void WorstFit(int input){print.printP(pd.p,process);print.printM(md.m,memory);memory[] free=memorydata.Free(md.m);memorydata.down(free);//对内存数组进行排序print.printF(free,memory);//后面的比较过程与首次适应算法一样print.insert("最坏适应算法",memory);int xuhao=input-1;if (free.length == 0){// 若无空闲分区则不进行后面的运算JOptionPane.showMessageDialog(frame, "内存中无空闲分区");//print.insert("内存中无空闲分区",memory);}else{int n=0;for(int j=0;j<free.length;j++){//与各个空闲分区进行比较print.insert("进程号"+pd.p[xuhao].getxuhao()+" 所需分区大小为["+pd.p[xuhao].getkongjian()+"] 与分区号为"+free[j].getm1()+"的空闲分区 ["+free[j].getm2()+"] 比较",memory);if(pd.p[xuhao].getkongjian()<free[j].getm2()){//分区大于作业print.insert("符合,分配",memory);memory[] nb=new memory[md.m.length+1];int ni=free[j].getm1();if(free[j].getm1()==1){//如果该空闲分区是内存表头nb[0]=new memory(1,pd.p[xuhao].getkongjian(),0,1);nb[1]=newmemory(2,free[j].getm2()-pd.p[xuhao].getkongjian(),pd.p[xuhao].getkongjian(),0);for(int k=2;k<nb.length;k++)nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());md.m=nb;print.printM(md.m,memory);free= memorydata.Free(md.m);memorydata.down(free);print.printF(free,memory);}else{//如果该空闲分区不是内存表头for(int k=0;k<ni;k++)nb[k]=newmemory(md.m[k].getm1(),md.m[k].getm2(),md.m[k].getm3(),md.m[k].getm4());nb[ni-1].setm2(pd.p[0].getkongjian());nb[ni-1].setm4(1);nb[ni]=newmemory(nb[ni-1].getm1()+1,free[j].getm2()-pd.p[xuhao].getkongjian(),nb[ni-1].getm2()+nb[ni-1].get m3(),0);for(int k=ni+1;k<nb.length;k++){nb[k]=newmemory(nb[k-1].getm1()+1,md.m[k-1].getm2(),nb[k-1].getm2()+nb[k-1].getm3(),md.m[k-1].getm4());}md.m=nb;print.printM(md.m,memory);free = memorydata.Free(md.m);memorydata.down(free);print.printF(free,memory);}break;}else{if(pd.p[xuhao].getkongjian()==free[j].getm2()){//分区等于作业System.out.println(" 符合,分配");md.m[free[j].getm1()-1].setm4(1);print.printM(md.m,memory);free = memorydata.Free(md.m);memorydata.down(free);print.printF(free,memory);break;}else{//分区小于作业,将指示不符合次数的n加一n++;}}if(n==free.length){//如果不符合次数为空闲分区数组长度,说明找遍空闲分区都无符合项JOptionPane.showMessageDialog(frame, "无符合分区");//print.insert(" 无符合分区",memory);return;}}processdata temp=new processdata(pd.p.length-1);for(int i=0;i<xuhao;i++)temp.p[i].setkongjian(pd.p[i].getkongjian());for(int i=xuhao;i<temp.p.length;i++){int te=pd.p[i+1].getkongjian();temp.p[i].setkongjian(te);}pd.p=temp.p;print.printP(pd.p,process);}}//回收已分配的分区private void recycle(int a){memory[] nm;if(md.m[a-1].getm4()==0){JOptionPane.showMessageDialog(frame, "该分区为空闲");//print.insert("该分区为空闲",memory);return;}if (a == 1){// 假如是内存表头if (md.m[a].getm4() == 0){// 假如第二块是空闲分区,则与第二块合并,起址为该回收块起址,其它各项仅修改序号nm =new memory[md.m.length-1];nm[a - 1] = md.m[a - 1];nm[a - 1].setm4(0);nm[a - 1].setm2(nm[a - 1].getm2()+md.m[1].getm2());for (int i = 1; i < nm.length; i++){nm[i] = md.m[i + 1];nm[i].setm1(nm[i].getm1()-1);}}else{// 假如第二块不是空闲分区,则单独建立一个空闲分区md.m[0].setm4(0);nm = md.m;}}else{if (a == md.m.length){// 假如是内存表末if (md.m[a - 2].getm4()== 0){// 假如倒数第二块是空闲分区,则与倒数第二块合并,起址为该回收块起址,其它各项仅修改序号nm =new memory[md.m.length - 1];nm[a - 2] = md.m[a - 2];nm[a - 2].setm4(0);nm[a - 2].setm2(nm[a - 2].getm2()+md.m[a - 1].getm2());for (int i = 0; i < nm.length - 1; i++){nm[i] = md.m[i];}}else{// 假如倒数第二块不是空闲分区,则单独建立一个空闲分区md.m[a - 1].setm4(0);nm =md.m;}}else{// 假如不是第一块也不是最后一块,则有四种情况if (md.m[a - 2].getm4() == 0 && md.m[a].getm4() == 0){// 夹在两块空闲分区中间// 建立少两个单位的新数组,存储到该回收区的前两位nm = new memory[md.m.length - 2];for (int i = 0; i < a - 2; i++){nm[i] = md.m[i];}// 将回收区前一位的大小改为这三个分区的和,然后将后面的元素前移两位,序号也相应减去2nm[a - 2] =md.m[a - 2];nm[a - 2].setm2(nm[a - 2].getm2()+md.m[a - 1].getm2() + md.m[a].getm2());for (int i = a - 1; i < nm.length; i++){nm[i] =md.m[i + 2];nm[i].setm1(nm[i].getm1()-2);}}else{if (md.m[a - 2].getm4() == 0){// 前一块是空闲分区// 建立少一个单位的新数组用于存储,将回收区的大小加至前一块空闲分区,后面的元素依次前移一位,序号减一nm = new memory[md.m.length - 1];for (int i = 0; i < a - 2; i++){nm[i] = md.m[i];}nm[a - 2] = md.m[a - 2];nm[a - 2].setm2(nm[a - 2].getm2()+md.m[a - 1].getm2());for (int i = a - 1; i < nm.length; i++){nm[i] = md.m[i + 1];nm[i].setm1(nm[i].getm1()-1);}}else{if (md.m[a].getm4() == 0){// 后一块是空闲分区nm = new memory[md.m.length - 1];// 前面元素不变,将后面的空闲分区大小加至该分区,然后把后面的元素前移一位,序号减一for (int i = 0; i < a - 1; i++){nm[i] = md.m[i];}nm[a - 1] = md.m[a - 1];nm[a - 1].setm4(0);nm[a - 1].setm2(nm[a - 1].getm2()+md.m[a].getm2());for ( int i = a; i < nm.length; i++){nm[i] =md.m[i + 1];nm[i].setm1(nm[i].getm1()-1);}}else{// 前后都是已分配的分区,直接修改分配状态md.m[a - 1].setm4(0);nm = md.m;}}}}}md.m=nm;// 将代表内存现在状态的nm数组返回print.printM(md.m,memory);}//对内存实行紧凑算法private void jincou(){memory[] temp=new memory[md.m.length];memory[] result;int index=0,value=0;//分别把内存中已经被分配的分区移动位置,使他们相邻for(int i=0;i<md.m.length;i++){if(md.m[i].getm4()==1){temp[index++]=new memory(index,md.m[i].getm2(),value,1);value+=md.m[i].getm2();}}if(value!=512){temp[index++]=new memory(index,512-value,value,0);//把最后剩下的内存空间建立一个完整的空闲分区}result=new memory[index];。
01-9.1 动态规划的基本思想

程序设计与问题求解——动态规划的基本思想主讲教师:乔亚男什么是动态规划◆动态规划算法通常用于求解具有某种最优性质的问题◆在这类问题中,可能会有许多可行解。
每一个解都对应于一个值,我们希望找到具有最优值的解◆动态规划算法其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解什么是动态规划◆但如果只是单纯进行问题分解的话,得到的子问题数目太多,有些子问题被重复计算了很多次◆如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间◆我们可以用一个表来记录所有已解的子问题的答案。
不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
这就是动态规划法的基本思路回顾挖金矿问题◆子问题:国王需要根据两个大臣的答案以及第9座金矿的信息才能判断出最多能够开采出多少金子。
为了解决自己面临的问题,他需要给别人制造另外两个问题,这两个问题就是子问题◆最优子结构:国王相信,只要他的两个大臣能够回答出正确的答案(对于考虑能够开采出的金子数,最多的也就是最优的同时也就是正确的),再加上他的聪明的判断就一定能得到最终的正确答案。
我们把这种子问题最优时母问题通过优化选择后一定最优的情况叫做“最优子结构”◆重叠子问题:实际上国王也好,大臣也好,所有人面对的都是:给你一定数量的人,给你一定数量的金矿,让你求出能够开采出来的最多金子数。
在这个过程中,会有很多情况他们所面对的问题的人数和金矿数是一样的,也就是他们面对的问题是一样的。
即:不是每次遇到的问题都是新问题,有些子问题出现多次。
这就是“重叠子问题”回顾挖金矿问题◆边界:想想如果不存在前面我们提到的那些底层劳动者的话这个问题能解决吗?永远都不可能!我们把这种子问题在一定时候就不再需要提出子问题的情况叫做边界,没有边界就会出现死循环◆子问题独立:当国王的两个大臣在思考他们自己的问题时他们是不会关心对方是如何计算怎样开采金矿的,因为他们知道,国王只会选择两个人中的一个作为最后方案,另一个人的方案并不会得到实施,因此一个人的决定对另一个人的决定是没有影响的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《程序设计艺术与方法》课程实验报告
LCSLength(str1, str2,i,j);
cout << "最长子序列为:" << endl;
Print(str1, i, j, m, n);
cout << endl;
cout << "最长子序列长度为:" << Long[m][n] << endl;;
system("pause");
}
int _tmain(int argc, _TCHAR* argv[])
{
LCS();
return 0;
}
2.字符串的变换:
使用动态规划的思想:
定义两个数组,Distance表示距离,handle表示操作,其中handle存储的数1为删除,2为插入,3为替换,4为相同跳到下一个字符,5为结束状态。
先初始化,令handle开始的第一行第一列为5,如果str1[i] != str2[0],handle为3,列同理;其中Distance为对应的行号或者列号。
两重for循环遍历所有组合的点,如果str1[i] == str2[j],则Distance[i][j] = Distance[i - 1][j - 1],handle[i][j] = 4;否则handle[i][j] = minval(Distance[i - 1][j] + 1, Distance[i][j - 1] + 1, Distance[i - 1][j - 1] + 1, Distance[i][j]); minval函数的作用是比较最大值,并返回最大值对应的操作,1为删除,2为插入,3为替换,当循环结束时,在Distance[m-1][n-1](m,n分别为两字符串的长度)中存储着最少操作次数
输出步骤:
最后先递归,后操作,修改str1字符串,表示操作的步骤。
#include "stdafx.h"
#include<stdio.h>
#include<iostream>
#include<string>
#include <vector>
using namespace std;
#define MAX 1000
int Distance[MAX][MAX];
3.计算所有的子矩阵中和的最大值
使用动态规划:
使用一个二维数组,其中num[i][j]存储矩阵i*j的元素和。
num存储的方法是:num[i][j] += num[i - 1][j];循环输入后就得到了矩阵元素和的二维数组。
使用三个变量i,j,k来遍历,一个矩阵大小是M*N的,那么使i从0到M,再使j从每一个i到M,遍历所有行可能。
再考虑列方向,直接在每一种i,j组合下,进行0到N的遍历,那么这样就等于是把所有子矩阵的情形给遍历完了。
每次遍历的过程是:从i,j点开始,temp = num[j][k] - num[i - 1][k],表示行为i-1到j,列为1到k的矩阵的值,nummax = max(nummax , 0) + temp表示i-1到j,列为1到k的矩阵中从k向上最大的子矩阵元素和,Max = max(nummax , Max)表示最大的子矩阵和,当遍历结束,就可以求出最大举证和。
思考:本算法可以求出100*100的矩阵
#include "stdafx.h"
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<algorithm>
int _tmain(int argc, _TCHAR* argv[]) {
subMatrix();
return 0;
}。
