非参数检验实验报告
常用的非参数检验(NonparametricTests)总结

常用的非参数检验(NonparametricTests)总结非参数检验(Nonparametric tests)是统计分析方法的重要组成部分,它与参数检验共同构成统计推断的基本内容。
参数检验是在总体分布形式已知的情况下,对总体分布的参数如均值、方差等进行推断的方法。
但是,在数据分析过程中,由于种种原因,人们往往无法对总体分布形态作简单假定,此时参数检验的方法就不再适用了。
非参数检验正是一类基于这种考虑,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。
由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验。
•两独立样本的非参数检验两独立样本的非参数检验是在对总体分布不甚了解的情况下,通过对两组独立样本的分析来推断样本来自的两个总体的分布等是否存在显著差异的方法。
独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。
SPSS中提供了多种两独立样本的非参数检验方法,其中包括曼-惠特尼U检验、K-S检验、W-W游程检验、极端反应检验等。
某工厂用甲乙两种不同的工艺生产同一种产品。
如果希望检验两种工艺下产品的使用是否存在显著差异,可从两种工艺生产出的产品中随机抽样,得到各自的使用寿命数据。
甲工艺:675 682 692 679 669 661 693乙工艺:662 649 672 663 650 651 646 652(1)曼-惠特尼U检验两独立样本的曼-惠特尼U检验可用于对两总体分布的比例判断。
其原假设:两组独立样本来自的两总体分布无显著差异。
曼-惠特尼U 检验通过对两组样本平均秩的研究来实现判断。
秩简单说就是变量值排序的名次,可以将数据按升序排列,每个变量值都会有一个在整个变量值序列中的位置或名次,这个位置或名次就是变量值的秩。
(2)K-S检验K-S检验不仅能够检验单个总体是否服从某一理论分布,还能够检验两总体分布是否存在显著差异。
54非参数检验(精)

操作过程:
DataWeight Cases (导入:人数) AnalayzeNoparametric TestsBinomial 打开对话框
可以选择1个或多个变量进入右侧框,此处选“疾病” 右下侧为指定已知总体的概率值的定义框,此处输入 0.01(如前所述,如果输入项反置则输入0.99 ,默认为 0.5) 左下侧为2分变量的获取。有2个选项
非参数检验的分类
非参数检验可以按变量的分类特点分为两类:
有序分类变量的非参数检验 无序分类变量的非参数检验
相应的统计分析方法也有所不同。SPSS所提 供的程序也分置于不同的菜单内。
对于有序分类变量的非参数检验,可以根据实 际情况采用Nonparametric tests菜单提供的方 法进行检验。 对于无序分类变量的非参数检验,除可以用chisquare检验外,应该使用Crosstable来完成。
4.1 Sample K-S过程
1 Sample K-S过程
是最常用的正态检验的方法 是对连续性资料的分布情况加以考察,它是一种拟 合优度检验,研究的是:
样本观察值的分布和指定的理论分布间符合程度的问题 检验样本所在的总体分布是否与已知总体分布相同
检验的原理是:
分别做出已知理论分布下的累加频数分布以及观察的累 加频数分布; 然后对两者进行比较,从中确定两种分布的最大差异点
默认为使用数据文件中的数据(用于2分变量) 可选择一个切分点。适用于连续变量人为二分。
Exact与Option子对话框与前面相同(略)
3.Runs 过程
(游程检验)
Runs 过程的目的是检验样本序列随机性问题 即检验取值为二分类,并且按时间或某种顺序排列 的数列资料是否真正随机出现,即各观察对象是否 来自同一个总体,并且取值各自独立。 游程检验的假设是:如果序列是真随机序列,那么 游程的总数应当不太多也太小,比较适中。
非参数检验(卡方检验),实验报告

非参数检验(卡方检验),实验报告评分大理大学实验报告课程名称生物医学统计分析实验名称非参数检验(卡方检验)专业班级姓名学号实验日期实验地点2015—2016 学年度第学期一、实验目得对分类资料进行卡方检验。
二、实验环境1、硬件配置:处理器:Intel(R)Core(TM)i5-4210U CPU 1、7GHz 1、7GHz 安装内存(RAM):4、00GB系统类型:64 位操作系统 2、软件环境:IBM SPSS Statistics 19、0 软件三、实验内容(包括本实验要完成得实验问题及需要得相关知识简单概述)(1)课本第六章得例 6、1-6、5 运行一遍,注意理解结果;(2)然后将实验指导书得例 1-4 运行一遍,注意理解结果。
四、实验结果与分析(包括实验原理、数据得准备、运行过程分析、源程序(代码)、图形图象界面等)例例 6、1 表 1 灭螨A A 与灭螨B B 杀灭大蜂螨效果得交叉制表效果合计杀灭未杀灭组别灭螨A 32 12 44 灭螨B 14 22 36 合计 46 34 80 分析: 表1就是灭螨A与灭螨B杀灭大蜂螨效果得样本分类得频数分析表,即交叉列联表。
表 2 卡方检验X2 值df 渐进Sig、(双侧)精确Sig、(双侧)精确Sig、(单侧)Pearson 卡方 9、277a1、002连续校正b7、944 1、005似然比 9、419 1、002Fisher 得精确检验、003、002 有效案例中得 N 80a、0 单元格(、0%)得期望计数少于5。
最小期望计数为15、30。
b、仅对 2x2 表计算分析: 表2就是卡方检验得结果。
因为两组各自得结果互不影响,即相互独立。
对于这种频数表格式资料,在卡方检验之前必须用“加权个案”命令将频数变量定义为加权变量,才能进行卡方检验。
Pearson 卡方:皮尔逊卡方检验计算得卡方值(用于样本数n≥40且所有理论数E≥5);连续校正b : 连续性校正卡方值(df=1,只用于2*2列联表);似然比:对数似然比法计算得卡方值(类似皮尔逊卡方检验);Fisher 得精确检验:精确概率法计算得卡方值(用于理论数E<5)。
spss实验报告——非参数检验

实验报告——(非参数检验)实验目的:1、学会使用SPSS软件进行非参数检验。
2、熟悉非参数检验的概念及适用范围,掌握常见的秩和检验计算方法。
实验内容:1、某公司准备推出一个新产品,但产品名称还没有正式确定,决定进行抽样调查,在受访200人中,52人喜欢A名称,61人喜欢B名称,87人喜欢C 名称,请问ABC三种名称受欢迎的程度有无差别?(数据表自建)SPSS计算结果如下:此题为总体分布的卡方检验。
零假设:样本来自总体分布形态和期望分布没有显著差异。
即ABC三种名称受欢迎的程度无差别,分布形态为1:1:1,呈均匀分布。
观察结果,上表为200个观察数据对A、B、C三个名称(分别对应1,2,3)的喜爱的期望频数以及实际观察频数和期望频数的差。
从下表中可以看出相伴概率值为0.007小于显著性水平0.05,因此拒绝零假设,认为样本来自的总体分布与制定的期望分布有显著差异,即A、B、C三种名称受欢迎的程度有差异。
2、某村庄发生了一起集体食物中毒事件,经过调查,发现当地居民是直接饮用河水,研究者怀疑是河水污染所致,县按照可疑污染源的大致范围调查了沿河居民的中毒情况,河边33户有成员中毒(+)和均未中毒(-)的家庭分布如下:(案例数据run.sav)-+++*++++-+++-+++++----++----+----毒源问:中毒与饮水是否有关?SPSS计算结果如下:此题为单样本变量值随机检验零假设:总体某变量的变量值是随机出现的。
即中毒的家庭沿河分布的情况随机分布,与饮水无关。
相伴概率为0.036,小于显著性水平0.05,拒绝零假设,因此中毒与饮水有关。
3、某试验室用小白鼠观察某种抗癌新药的疗效,两组各10只小白鼠,以生存日数作为观察指标,试验结果如下,案例数据集为:npara1.sav,问两组小白鼠生存日数有无差别。
试验组:24 26 27 30 32 34 36 40 60 天以上对照组:4 6 7 9 10 10 12 13 16 16SPSS计算结果如下:此题为两独立样本非参数检验。
spss参与非参检验实验报告参考模板
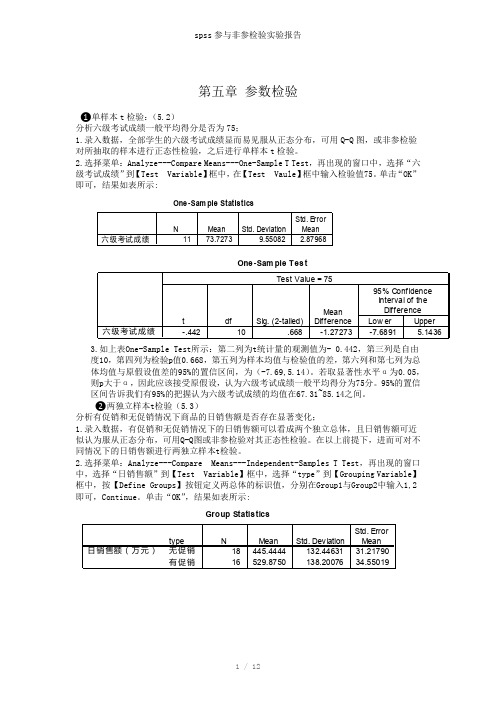
第五章 参数检验❶单样本t 检验:(5.2)分析六级考试成绩一般平均得分是否为75;1.录入数据,全部学生的六级考试成绩显而易见服从正态分布,可用Q-Q 图,或非参检验对所抽取的样本进行正态性检验,之后进行单样本t 检验。
2.选择菜单:Analyze---Compare Means---One-Sample T Test ,再出现的窗口中,选择“六级考试成绩”到【Test Variable 】框中,在【Test Vaule 】框中输入检验值75。
单击“OK ”度10,第四列为检验p 值0.668,第五列为样本均值与检验值的差,第六列和第七列为总体均值与原假设值差的95%的置信区间,为(-7.69,5.14)。
若取显著性水平α为0.05,则p 大于α,因此应该接受原假设,认为六级考试成绩一般平均得分为75分。
95%的置信区间告诉我们有95%的把握认为六级考试成绩的均值在67.31~85.14之间。
❷两独立样本t 检验(5.3)分析有促销和无促销情况下商品的日销售额是否存在显著变化;1.录入数据,有促销和无促销情况下的日销售额可以看成两个独立总体,且日销售额可近似认为服从正态分布,可用Q-Q 图或非参检验对其正态性检验。
在以上前提下,进而可对不同情况下的日销售额进行两独立样本t 检验。
2.选择菜单:Analyze---Compare Means---Independent-Samples T Test,再出现的窗口中,选择“日销售额”到【Test Variable 】框中,选择“type ”到【Grouping Variable 】框中,按【Define Groups 】按钮定义两总体的标识值,分别在Group1与Group2中输入1,23.如上表Independent Sample Test 所示,结论分析为两步:第一步,方差齐性检验。
F 统计量的观测值为0.225,对应的p 值为0.638,若取显著性水平α为0.05,则p 大于α,可以认为两总体的方差相等。
spss参数与非参数检验实验报告

(1).将一样本作为控制样本,另一样本作为实验样本。两样本混合后按升序排列;
(2).找出控制样本的跨度(最低秩和最高秩间的样品数)和截头跨度(去掉控制样本的最小值和最大值后的跨度)。若跨度(截头跨度)很小,认为样本存在极端反应。
以上四种检验的基本操作步骤:
(1)【Analyze】--->【Nonparametric Tests】--->【2 Independent Sample】
该检验可用来检验两个独立样本是否取自同一总体,它是最强的非参数检验之一。
基本思路:
1.将样本X和样本Y混合后作升序排列,计算每个数据的秩;
2.分别对两样本的秩求平均,得到两个平均秩,分别用W1=WX/m和W2=WY/n表示。
若W1和W2比较接近,则说明两个样本来自相同分布的总体,若W1和W2差异较大,则说明两个样本来自不同的总体。
(2)选择待检验变量到【Test Variable】框中
(3)指定存放样本标志值的变量到【Grouping Variable】框
(4)选择非参数检验方法
三、多个独立样本的非参数检验包括:中位数检验、Kruskal-Wallis H检验、Jonkheere-Terpstra检验
3.1中位数检验
(一)含义:通过对多组独立样本的分析,检验它们来自的总体的中位数是否存在显著差异。其原假设是:多个独立样本来自的多个总体的中位数无显著差异。
(2)选定待检验的变量到【Test Variable list】框中
(3)在【Cut Point】框中确定计算游程数的分界点
二、两个独立样本的非参数检验包括:Mann-Whitney U检验、K-S双样本检验、Wald-Wolfowitz游程检验、Moses极端反应检验
【VIP专享】统计学实验报告——SPSS软件的参数检验与非参数检验

统计学2——SPSS软件的参数检验与非参数检验班级学号姓名日期实验目的(1)熟悉单样本t检验。
(2)熟悉两独立样本t检验。
(3)熟悉两配对样本t检验。
(4)熟悉总体分布的卡方检验。
实验内容(1)SPSS的单样本t检验操作。
(2)SPSS的两独立样本t检验。
(3)SPSS的两配对样本t检验。
(4)SPSS的总体分布的卡方检验。
实验过程(1)SPSS的单样本t检验操作。
(2)SPSS的两独立样本t检验。
(3)SPSS的两配对样本t检验。
(4)SPSS的总体分布的卡方检验。
DATASET NAME 数据集1 WINDOW=FRONT.T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x10_1/CRITERIA=CI(.95).T检验GETFILE='C:\Documents and Settings\admin\LocalSettings\Temp\Rar$DI02.829\商品房购买意向调查模拟数据.sav'. DATASET NAME 数据集2 WINDOW=FRONT.T-TEST GROUPS=t2(1 2)/MISSING=ANALYSIS/VARIABLES=t10_1/CRITERIA=CI(.95).T检验独立样本检验DATASET ACTIVATE 数据集1.T-TEST GROUPS=x13(1.5)/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验DATASET ACTIVATE 数据集2.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI67.032\减肥茶.sav'. DATASET NAME 数据集3 WINDOW=FRONT.T-TEST PAIRS=hcq WITH hch (PAIRED)/CRITERIA=CI(.9500)/MISSING=ANALYSIS.T检验DATASET ACTIVATE 数据集1.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI10.7860\心脏病猝死.sav'. DATASET NAME 数据集4 WINDOW=FRONT.NPAR TESTS/CHISQUARE=rq/EXPECTED=2.8 1 1 1 1 1 1/MISSING ANALYSIS.NPar 检验卡方检验频率实验心得。
非参数统计实验报告南邮

实验报告( 2012 / 2013学年第一学期)课程名称非参数统计实验名称1、数据的描述性统计2、中心位置的检验问题3、多样本问题和区组设计问题的比较4、相关分析实验时间2012年 10月15-22日学生姓名班级学号学院(系)通达学院专业统计学实验一一、实验题目某航空公司为了解旅客对公司服务态度的满意程度,对50名旅客作调查,要求他们写出对乘机服务、机上服务和到达机场服务的满意程度,满意程度评分从0到100.分数越大,满意程度越高。
下表是收集到得数据。
50名旅客对乘机服务、机上服务和到达机场服务的满意程度的评分1、对50名旅客关于乘机服务的满意程度数据作描述性统计分析;2、对50名旅客关于机上服务的满意程度数据作描述性统计分析;3、对50名旅客关于到达机场服务的满意程度数据作描述性统计分析;4、对50名旅客关于这三个方面服务的满意程度数据作一个综合比较的描述性统计分析。
二、实验步骤1、乘机服务1)、直方图2)、箱线图3)、数值分析2、机上服务1)、直方图机上服务满意程度评分直方图141210864225-3031-3536-4041-4546-5051-5556-6061-6566-7071-7576-8081-8586-90 2)、箱线图C1 的箱线图908070601C504030203)、数值分析3、到达机场服务1)、直方图2)、箱线图3)、数值分析5、综合比较C3C2C1100908070605040302010数据C1, C2, C3 的箱线图实验二一、实验题目某地区从事管理工作的职员的月收入的中位数是6500元,现有一个该地区从事管理工作的40个妇女组成的样本,她们的月收入数据如此下:5100 6300 4900 71004900 5200 6600 72006900 5500 5800 64003900 5100 7500 63006000 6700 6000 48007200 6200 7100 69007300 6600 6300 68006200 5500 6300 5400 4800(1)使用样本数据检验:该地区从事管理工作的妇女的月收入的中位数是否低于6500元?(2)使用样本数据给出该地区从事管理工作的妇女的月收入的中位数的点估计和95%的区间估计。
非参实验报告总结

《非参数统计》课程设计指导书一、课程设计的目的1. 加深理解本课程的研究方法、思想精髓,提高解决实际问题的能力,熟练掌握Minitab常用统计软件的应用。
2.掌握两样本Brown-Mood中位数检验法,并解决两样本中心位置的一致性检验问题.3.掌握两样本Wilcoxon 秩和检验法,解决两样本中心位置的一致性检验问题。
二、设计名称:不同学科的博士论文除了内容外,页数有没有不同三、设计要求1.数据来源要真实,必须注明数据的出处。
2.尽量使用计算机软件分析,说明算法或过程。
3.必须利用到应用回归分析的统计知识。
4.独立完成,不得有相同或相近的课程设计。
四、设计过程1.思考研究课题,准备搜集数据。
2.确立课题,利用图书馆、上网等方式方法搜集数据。
3.利用机房实验室等学校给予的便利措施开始分析处理数据。
4.根据试验结果,写出课程设计报告书。
5.对实验设计报告书进行完善,并最终定稿。
五、设计细则1.利用的统计学软件主要为Minitab,因为其方便快捷,功能也很强大,界面美观。
2.对Word文档进行编辑的时候,有些特殊的数学符号需要利用数学编辑器这款小软件进行编辑。
3.数据来自较权威机构,增加分析的准确性及可靠性。
4.力求主题突出,观点鲜明,叙述简洁明了。
六、说明1.数据来源于21实际统计学系列教材非参数统计;2.所选取数据可能不会涉及到所学的各种分析方法,本课程设计最后会对此情况作出解释。
3.同一题可以采用不同的方法来检验,从而得出更详细的分析及解释4.05α=.0课程设计任务书课程设计报告课程:非参数统计分析学号:姓名:班级:12金统教师:孙丽玢江苏师范大学数学及统计科学学院设计名称:不同学科的博士论文除了内容外,页数有没有不同日期:2014年 6 月 16 日设计内容:不同学科的博士论文除了内容以外还有什们不同呢?分别对一个大学的数学20个和经济学的18个博士论文的页数进行的抽样结果如下(单位:页数):数学: 56 105 63 88 72 112 96 93 65 105 94 87 64 65 68 87 90 98 76 75经济学:88 94 93 96 99 79 91 94 91 100 99 90 100 110 102 95 98 85 仅仅从页数上看,这两个学科的博士论文有什么不同?(1)使用两样本Brown-Mood中位数检验法进行分析。
非参数检验实验报告

学院: ______________________ 参赛队员: ___________________ 参赛队员: ___________________目录一、实验目的 (1)1.了解假设检验的基本容; (1)2.了解卡方检验; (1)3.了解二项分布检验; (1)4.了解两个独立样本检验; (1)5.学会运用spss软件求解问题; (1)6.加深理论与实践相结合的能力。
(1)二、实验环境 (1)三、实验方法 (1)1.卡方检验; (1)2.二项分布检验; (1)3.两个独立样本检验。
(1)四、实验过程 (1)问題一: (1)1.1实验步骤 (2)1.1.1辙入数据 (2)1.1.2选择:数据加权个案 (2)1.1.3选择:分析今非参数检验今旧对话框今卡方 (2)1.1.4将变量面值放入检验变量列表 (3)1.1.5观察结果 (3)1.2输出结果 (3)1.3结果分析 (3)问題二: (3)2.1问題叙述 (3)2.2提出假设 (4)2.3实验步骤 (4)2.3. 1导入excel文件数据 (4)2.3. 2二项分布检验 (5)2.3.3辙出结果 (6)2.4结果分析 (6)问題三: (6)3.1实验步骤 (6)3.1.1数据的输入 (6)3.1.2 选择 (7)3.1.3检验变量 (7)3.2输出结果 (7)3.3结果分析 (9)五、实验总结 (9)参数检验一、实验目的1.了解假设检验的基本容;2.了解卡方检验;3.了解二项分布检验;4.了解两个独立样本检验;5•学会运用spss软件求解问题;6•加深理论与实践相结合的能力。
二、实验环境Spss、 office三、实验方法1.卡方检验;2.二项分布检验;3.两个独立样本检验。
四、实验过程问题一:掷一个6而骰子300次,用数字1、2、3、4、5、6分别代表6个而,检验骰子是否均匀1.1实验步骤1・1・1输入数据1.1.2选择:数据加权个案1.1.3选择:分析T非参数检验T旧对话框T卡方1・1・4将变量面值放入检验变量列表,期望全距从数据中获取,期望值所有类别相等1.L5观察结果1.2输出结果卡方检验邓羣跋150 0-7.024950 0-1.035650.0 6.0445600•6.060E50 0ie.o6 总数4130050 0・9D面皿七方0 960Jdr5淅近丘谷注1111.3结果分析此处,sig值为0. 111>0. 05,所以接受原假设,认为样本来自的总体分布形态与期望分布不存在显著差异,则认为该骰子均匀问题二2.1问题叙述次数面次数面次数面次数面1 a 9 b 17 b 25 b元5元5单于竿对2.2提出假设H0:硬币不是均匀的vs H1:硬币是均匀的2. 3实验步骤2. 3. 1导入excel文件数据先将数据输入进excel表格中,用SPSS打开;在SPSS页面点击文件T打开T数据Q a^S4 閔矽U] • IBM SPSS $:at 唸超謨匕二,'选择:分析T非参数检验T旧对话框T二项式2.3.3输出结果二顷式捡验2. 4结果分析由输出结果知,結确显著性(双侧)=1・000>0.05,所以接受原假设H0,所以硬币不是均匀的。
回归分析与非参数检验

2)写出销售量与销售价格、年人均收入、广告费用的多元线性回归方程,并解释各回归系数的意义。
3)检验回归方程的线性关系是否显著?
4)检验各回归系数是否显著?
5)计算判定系数,并解释它的实际意义。
6)计算回归方程的估计标准误差,并解释它的实际意义。
2.实验结果
1)
Anovab
(五)7.5
(四)7.4
1.实验内容
利用习题二第6题数据,选择恰当的非参数检验方法,分析不同收入人群本次存款金额的总体分布是否存在显著差异。
2.实验步骤
分析→非参数检验→多个独立样本→不同收入人群导入分组变量、本次存款金额导入检验变量列表→确定
3.实验结果及分析
在表中可以看出,在Kruskal-Wallis检验、中值检验、Jonckheere-Terpstra检验在显著水平为0.05下得到的sig值均为0.00<0.05,所以拒绝原假设,即认为不同收入人群本次存款金额的总体分布存在显著差异。
3.实验结果及分析
上表进行了拟合优度检验,由于该方程有多个解释变量,因此参考调整判定系数(0.986)较接近1,因此认为拟合有度较高,被解释变量可以被模型解释的部分较多,不能被解释的部分较少。
上表进行了回归方程的显著性检验,由于Sig为0小于0.05,所以拒绝原假设,认为各回归系数不同时为0,被解释变量与解释变量全体的线性关系是显著的,可以建立线性模型。
意义为:产品的销售量的总误差中有89.4%可以用产品的销售价格、各地区的年人均收入和广告费用的线性关系来解释,只有10.6%属于随机因素影响,因此这条回归线是合适的。
6)估计标准误差为:
二、非参数检验
(一)7.1
1.实验内容
2019年非参数假设检验范文.doc

2019年非参数假设检验范文篇一:实验八非参数假设检验实验八非参数假设检验?单样本非参数检验?两个独立样本非参数检验?多个独立样本非参数检验?两个配对样本非参数检验?多个配对样本非参数检验一、单样本非参数检验选择:分析Analyze==>非参数检验NonparametricTests==>……1、基本功能对单个总体的分布形态进行推断的方法。
其中方法包括:卡方检验、二项分布检验、K-S检验以及变量值随机性检验等。
2、方法简介2.1卡方检验?卡方检验可以进行拟合优度的检验,即可以根据样本数据,推断总体分布与期望分布或某一理论分布是否存在显著差异,可检验样本是否服从正态、均匀、Poisson等分布。
卡方检验是一种吻合性检验,通常适用于多项分类值总体分布的分析。
?零假设H0:样本来自的总体分布与期望分布或某一理论分布无显著差异。
?操作步骤1、选择分析Analyze==>非参数检验NonparametricTe sts==>χ检验Chi-Square;22、将待检验的变量选择到TestVariable框;3、在ExpectedRange框选项中确定参与分析的样本范围,其中Getfromdata表示所有样本都参与分析;UseSpecifiedRange表示只有在取值范围内的样本才参与分析;4、在ExpectedV alues框中给出各个pi值,其中Allcategoriesequal 表示所有子集的pi都相同,即期望分布为均匀分布;Value框后可依次输入pi值,并可单击进行增加、修改和删除。
2.2二项分布检验?二项分布检验是要通过样本数据检验样本来自的总体是否服从指定的概率值为p的二项分布。
?零假设H0:样本来自的总体与指定的二项分布无显著差异。
?操作步骤1、选择分析Analyze==>非参数检验NonparametricTests==>二项式Binomial;2、将待检验的变量选择到TestVariableList框;3、在DefineDichotomy框中指定如何分类,如果检验变量为二值变量,则选Getfromdata选项;如果检验变量不是二值变量,则可在CutPoint框后输入具体数值,小于等于该值的观察值为第一组,大于该值的为第二组;4、在Test框中输入二项分布的检验概率值p。
第五章 非参数检验

6.4 Kendall协同系数检验
① DPS 立即得到结果:
协同系数W=0.4911,近似卡方值为27.5000, p=0.0166<0.05,表明不同机构对学校的排序是 正相关的,是有显著一致性的。
6.5 二元响应的Cochran检验
第1组(A组)为对照组,多重比较显示,第1组与第2 组差异显著(p=0.0102<0.05),第1组与第2组差异显著 (p=0.0172<0.05)
6.3 多个样本比较的秩和检验
6.3.2 中位数检验
当2个或2个以上的资料不服从正态分布时, 我们可以使用这一方法进行检验。当资料服从正
态分布时,用中位数检验方法进行检验其效率总
第五章 非参数检验
非参数检验对总体分布的具体形式不作任 何限制性的假定,不宜总体参数具体数值 估计或检验为目的。非参数检验最大的特 点是对样本资料无特殊要求,但检验的效 率要低于参数检验。如对非配对资料的秩 和检验,其效率仅为t检验的86.4%,也就 是说,以相同概率判断出显著差异,t检验 所需样本含量要比秩和检验少13.6%。
p=0.0210<0.05,表明给药前后灌流滴数有显著 差异。
6.2.2 非配对样本符号秩检验
非间秩次的比较,它比配对样 本的秩次检验的应用更为普遍。 常用的有两样本的Wilcoxon秩和 检验以及在此基础上发展的MannWhitney检验。
6.3 多个样本比较的秩和检验
6.3.1 Kruskal-Wallis 检验
① DPS 输入数据,选择数据,点击菜单试验统计→非 参数检验→Kruskal Wallis检验:
非参数统计实验(全)新

第四章 非参数统计实验参数统计学中的许多统计分析方法的应用对总体都有严格的假定,例如,t 检验要求总体服从正态分布,F 检验要求误差呈正态分布且各组方差为齐性的等等,然而在现实生活中,有许多总体的分布我们却是一无所知或知之甚少,所以在参数模型中所建立的统计推断就会失效,于是,人们希望在不假定总体分布的情况下,尽量从数据本身来获得所需要的信息。
这就是非参数统计的宗旨。
非参数统计方法简便,适用性强,但检验效率较低,应用时应加以考虑。
实验一 卡方检验(Chi-square test )实验目的:掌握卡方检验方法。
实验内容:一、2χ拟合优度检验 二、2χ独立性检验 三、2χ齐性检验 实验工具:SPSS 非参数统计分析菜单项和Crosstabs 菜单项。
知识准备:一、卡方拟合优度检验2χ检验(Chi —Square Test) 适用于拟合优度检验,适用于定类变量的检验问题,用来检验实际观察数目与理论期望数目是否有显著差异。
当检验问题是实际分布是否与理论分布相符合时,在大样本时也可以用分类数据的卡方检验来解决,这时的卡方检验也称为分布拟合的卡方检验。
若样本分为k 类,每类实际观察频数为k f f f ,,,21 ,与其相对应的期望频数为ke e e ,,,21 ,则检验统计量2χ可以测度观察频数与期望频数之间的差异。
其计算公式为:∑∑-=-==期望频数期望频数实际频数2122)()(ki ii i e e f χ很显然,实际频数与望频数越接近,2χ值就越小,若2χ=0,则上式中分子的每—项都必须是0,这意味着k 类中每一类观察频数与期望频数完全一样,即完全拟合。
2χ统计量可以用来测度实际观察频数与期望频数之间的拟合程度。
在H 0成立的条件下,样本容量n 充分大时,2χ统计量近似地服从自由度df =k-1的2χ分布,因而,可以根据给定的显著性水平α,在临界值表中查到相应的临界值)1(2-k αχ。
若)1(22-≥k αχχ,则拒绝H 0,否则不能拒绝H 0。
非参数检验

合计
3460 114
假设检验的方法有两种:参数检验(parametric test)
和非参数检验(non – parametric test)。
参数检验 :若样本所来自的总体分布已知(如正态分布) ,对其总体参数进行假设检验,则称为参数检验。 非参数检验:不考虑研究对象总体分布的具体形式,也不
90年代有关非参数统计的研究和应用主要集中在非 参数回归和非参数密度估计领域,其中较有代表性的 人物是Silverman和J. Fan。
秩次和秩和
本章介绍的非参数统计方法均基于秩次; 秩次(rank):将数值变量值从小到大,或等
级变量值从弱到强所排列的序号。
秩和:用秩次号代替原始数据后,所得某些
配对t检验结果
秩和检验 结果
第二节 两独立样本比较的Wilcoxon秩和 检验
Wilcoxon秩和检验可用于:
• 计量资料的两样本比较
I期矽肺病人 8.7
问:(1)该资料是什么类型资料?属于何种设计方案? (2)该医生的统计处理是否正确?为什么?
某医生用甲、乙两种培养基培养结核杆菌40份,结果甲
培养基阳性率为60%,乙培养基阳性率为35%,两种培养基
培养一致阳性率为25%,资料整理为下表。试比较两种培养 基何者为优? 表2 两种方法的检测结果
统 计 量:有明确的理论依据(t分布、u分布) 有严格的适用条件,如:
•正态分布 •总体方差齐 •数据间相互独立 Normal Equal Variance Independent
条件不满足时——采用非参数统计的方法。
2013-11-2
8
• 非参数检验:对总体分布不做严格假定,也 不对总体参数进行统计推断,而是直接对总 体分布的位置进行假设检验。由于这类方法 不受总体参数的限制,故称非参数检验,又 称任意分布检验(distribution-free test)
独立样本非参数检验结果描述

独立样本非参数检验结果描述
在进行独立样本非参数检验时,我们通常会使用Wilcoxon秩和检验或Mann-Whitney U检验。
这些检验方法适用于样本大小较小或样本不服从正态分布的情况。
在进行Wilcoxon秩和检验时,我们将两组数据合并后进行排序,并根据数据的排名计算秩和。
然后,我们比较两组数据的秩和是否存在显著差异,从而得出结论。
对于Mann-Whitney U检验,我们同样将两组数据合并后进行排序。
然后,我们计算出每组数据的秩次和,并使用一定的公式计算出U值。
最后,我们比较U值是否存在显著差异,从而得出结论。
在结果描述中,我们应该明确指出所用的检验方法,并将其结果以易于理解的方式展示。
例如,我们可以报告检验的p值和显著性水平,以及两组数据的中位数和四分位数等统计指标。
同时,我们也应该指出样本容量和样本不同之处,以帮助读者更好地理解结果。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
非参数检验
学院:
参赛队员:
参赛队员:
参赛队员:
指导老师:
目录
一、实验目的 (1)
1.了解假设检验的基本内容; (1)
2.了解卡方检验; (1)
3.了解二项分布检验; (1)
4.了解两个独立样本检验; (1)
5.学会运用spss软件求解问题; (1)
6.加深理论与实践相结合的能力。
(1)
二、实验环境 (1)
三、实验方法 (1)
1.卡方检验; (1)
2.二项分布检验; (1)
3.两个独立样本检验。
(1)
四、实验过程 (1)
问题一: (1)
1.1实验步骤 (2)
1.1.1输入数据 (2)
1.1.2选择:数据 加权个案 (2)
1.1.3选择:分析→非参数检验→旧对话框→卡方 (2)
1.1.4将变量面值放入检验变量列表 (3)
1.1.5观察结果 (3)
1.2输出结果 (3)
1.3结果分析 (3)
问题二: (3)
2.1问题叙述 (3)
2.2提出假设 (4)
2.3实验步骤 (4)
2.3.1导入excel文件数据 (4)
2.3.2二项分布检验 (5)
2.3.3输出结果 (6)
2.4结果分析 (6)
问题三: (6)
3.1实验步骤 (6)
3.1.1数据的输入 (6)
3.1.2选择 (7)
3.1.3检验变量 (7)
3.2输出结果 (7)
3.3结果分析 (9)
五、实验总结 (9)
参数检验
一、实验目的
1.了解假设检验的基本内容;
2.了解卡方检验;
3.了解二项分布检验;
4.了解两个独立样本检验;
5.学会运用spss软件求解问题;
6.加深理论与实践相结合的能力。
二、实验环境
Spss、office
三、实验方法
1.卡方检验;
2.二项分布检验;
3.两个独立样本检验。
四、实验过程
问题一:
1.1实验步骤
1.1.1输入数据
1.1.2选择:数据 加权个案
1.1.3选择:分析→非参数检验→旧对话框→卡方
非参数检验
1.1.4将变量面值放入检验变量列表,期望全距从数据中获取,期望值所有类别相等
1.1.5观察结果
1.2输出结果
1.3结果分析
此处,sig值为0.111>0.05,所以接受原假设,认为样本来自的总体分布形态与期望分布不存在显著差异,则认为该骰子均匀
问题二:
2.1问题叙述
掷一个硬币31次,结果见下表,检验硬币是否均匀
H0:硬币不是均匀的vs H1:硬币是均匀的
2.3实验步骤
2.3.1导入excel文件数据
先将数据输入进excel表格中,用SPSS打开;在SPSS页面点击文件→打开→数据
非参数检验
2.3.2二项分布检验
旧对话框→二项式
选择:分析→非参数检验→
2.3.3输出结果
2.4结果分析
由输出结果知,精确显著性(双侧)=1.000>0.05,所以接受原假设H0,所以硬币不是均匀的。
问题三:
3.1实验步骤
3.1.1数据的输入
将甲、乙两种安眠药编号为1、2,在SPSS页面输入数据
非参数检验
3.1.2选择:分析→非参数检验→旧对话框→2个独立样本
3.1.3检验变量列表选择睡眠延长时数,分组变量选择药品编号(1 2),勾选四个检验类型;
3.2输出结果
Mann-Whitney 检验
检验统计量b
睡眠延长时
数
Mann-Whitney U 21.000
Wilcoxon W 76.000
Z -1.962
渐近显著性(双侧) .050
Moses 检验
频率
药品编号N
睡眠延长时数1 (控制)9
2 (试验)10
总数19
检验统计量a,b
睡眠延长时
数
控制组观察跨度14
显著性(单侧).091
修整的控制组跨度
13 显著性(单侧).570
从每个末端修整的离群者 1
a. Moses 检验
b. 分组变量: 药品编号
非参数检验
Kolmogorov-Smirnov Z 1.088 渐近显著性(双侧) .187 a. 分组变量: 药品编号
Wald-Wolfowitz 检验
频率
药品编号N
睡眠延长时数1 9
2 10 总数19
3.3结果分析
原假设
0:0
d
H m=
备择假设
1:0
d
H m¹
由Mann-Whitney检验可以看出0.0530.05
sig=>,甲乙两种药物的疗效有差异;
由Moses检验可以看出0.0910.05
sig=>,甲乙两种药物的疗效有差异;
由双样本Kolmogorov-Smirnov检验可以看出0.1870.05
sig=>,甲乙两种药物的疗效有显著差异;
由Wald-Wolfowitz检验可以看出0.1750.05
sig=>,甲乙两种药物的疗效有显著差异;由以上四个检验综合分析出甲乙两种药物的疗效有显著性差异。
五、实验总结
在假设检验实验的学习中,通过实验操作可使我们加深对假设检验的理解,学习和掌握spss软件的基本方法,并能进一步熟悉和掌握spss软件的操作方法,培养我们分析和解决实际问题的基本技能,提高我们的综合素质;通过实验可以使我们分清卡方检验、二项分布检验、两个独立样本检验,更加全面地理解假设检验,同时也锻炼了同学的动手操作能力,让同学们学会理论与技术相结合共同解决数学上的问题,提高了同学们的综合素质。
9。
