(直线的投影)习题解答
《机械制图习题集》(第四版)第一章答案
一、点、直线、平面的投影1.1 点的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第24~24页习题1.2 直线的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第25~27页习题1.3 平面的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第28~29页习题1.4 直线与平面、平面与平面相对关系∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第30~32页习题1234题号:题号:56789101112131415题号:161718192021题号:2223242526272829303132333435363738391.5 换面法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第33~35页习题1.6 旋转法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第36~36页习题1.7 投影变换综合题∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第37~37页习题点、直线、平面的投影题号:404142434445464748495051题号:525354555657题号:58596061621. 已知A、B、C三点的直观图,画出它们的投影图,并将各点的坐标值填入表中。
2. 已知A、B、C各点对投影面的距离,画出它们的三面投影图和直观图。
3. 已知点A的坐标(40,15,0),画出其三面投影并作出点B和点C的三面投影。
(a)点B ——在点A右面20mm,前面15mm,上面20mm;(b)点C ——在点A左面10mm,后面15mm,上面15mm。
现代机械制图习题集习题解答4

2-2 正投影的基本性质班级: 姓名: 学号: 11第2章 投影基础1. 根据给出的视图补画第三视图。
(4)(1)(2)(3)(5)2-6 直线的投影(续)班级: 姓名: 学号: 15第2章 投影基础7. 已知A、B、C在同一直线上,求点的投影。
OXab( )( )ddd'(4)c'aa'Xb'cXca( )d(5)a'OX b'bd'c'cacObbd( )8. 判断下列两直线的相对位置(平行、相交、交叉)(1)c'a'd'a'c'(2)b'b'd'OX( )bO(6)b'(d')dXa a'(c)c'( )acdbc'(d')a'O (3)b'交叉相交相交交叉交叉平行2-12 换面法班级: 姓名: 学号: 213. 求三角形ABC的实形。
1. 求点A的新投影。
第2章 投影基础O11H VX a'aX HV bab'(2)1HVV HX aa'(1)X V HXOa'1OOOc'c (1)XHV d'cdc'(2)HV aa'bb'OX O2. 求直线AB、CD的实长及AB与水平面的倾角和CD与正平面的倾角。
4. 求点K到三角形ABC的距离。
aa'Xcbkc'Ok'b'a 1'a 1a 1'b1'c1'。
投影基本知识习题及答案

一、填空题1、工程上常采用的投影法是 中心投影法 和 平行投影 法,其中平行投影法按投射线与投影面是否垂直又分为 正投影 和 斜投影 法。
2、当直线平行于投影面时,其投影 直线 ,这种性质叫 真实 性,当直线垂直投影面时,其投影 点 ,这种性质叫 积聚 性,当平面倾斜于投影面时,其投影 平面 ,这种性质叫 类似 性。
3、主视图所在的投影面称为 正立面投影面 ,简称 正立面 ,用字母 V 表示,俯视图所在的投影面称为 水平投影面 ,简称 水平面 ,用字母 H 表示。
左视图所在的投影面称为 侧立投影面 简称 侧立面 ,用字母 W 表示。
4、三视图的投影规律是:主视图与俯视图 长对正 ;主视图与左视图 高平齐 ;俯视图与左视图 宽相等 。
6、直线按其对三个投影面的相对位置关系不同,可分为 投影面垂直线、 投影面平行线、 一般位置直线 。
7、与一个投影面垂直的直线,一定与其它两个投影面 平行 ,这样的直线称为投影面的 投影面垂直线 。
8、与正面垂直的直线,与其它两个投影面一定 平行 ,这样的直线称为 正垂线 。
9、与一个投影面平行,与其它两个投影面倾斜的直线,称为投影面的 投影面平行线 ,具体又可分为 正平线 、 水平线 、 侧平线 。
10、与三个投影面都倾斜的直线称为 一般位置直线 。
11、空间平面按其对三个投影面的相对位置不同,可分投影面垂直面、 投影面平行面、 一般位置面12. 正垂面与正面 垂直 ,与水平面 倾斜 ,与侧面 倾斜 ,正垂面在正面投影为 直线 ,在水平面和侧面投影为 投影面的类似性 。
13.正平面与正面 ,与水平面 ,与侧面 ,正平面在正面投影为 ,在水平面投影和侧面投影为 。
14.参照图下图中的立体图,在三视图中填写物体的六个方位。
(填前、后、左、右、上、下)二、选择题(12分)1.下列投影法中不属于平行投影法的是( A )A 、中心投影法B 、正投影法C 、斜投影法2、当一条直线平行于投影面时,在该投影面上反映( A )A 、实形性B 、类似性C 、积聚性3、当一条直线垂直于投影面时,在该投影面上反映( C )上下左 前右后A、实形性B、类似性C、积聚性4、在三视图中,主视图反映物体的( B )A、长和宽B、长和高C、宽和高5、主视图与俯视图()A、长对正B、高平齐C、宽相等6、主视图与左视图( B )A、长对正B、高平齐C、宽相等7、为了将物体的外部形状表达清楚,一般采用(A)个视图来表达。
机械制图_第2章_点_直线_平面的投影习题解答

2-8 判断两直线的相对位置(平行、相交、交叉、垂直相交、 垂直交叉)并将答案填写在下面的括号内。
2-9 由点A作直线AB与直线CD相交并使交点 距H面12。
2-10 求直线AB、CD的交点K。
2-11 过点C作直线CD与已知直线AB平行。
2-12 作与已知直线AB、CD平行且相距为15的直线MN,并使MN的 实长为20,点M距W面30,点N在点M之右(任求一解)。
2-17 求平面的侧面投影并判断平面的空间位置 该平面是 铅垂 面
2-18 求平面的侧面投影并判断平的空间位置 △ABC是 侧平 面
2-19 求平面上点K与点N的另一投影。
2-20 已知直线AB在两平行直线CD、EF所确定的 平面上,求作AB的水平投影。
2-21 完成平面图形ABCDE的水平投影。
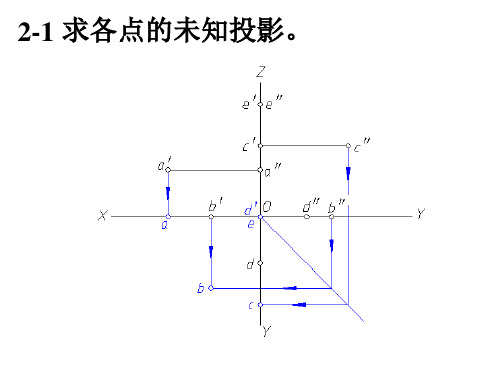
2-1 求各点的未知投影。
2-2 已知点B距点A15;点C与点A是对V面的重影点;点D
在点A的正下方15。求各点的三面投影。
2-3 已知点A(25,15,20);点B距W、V、H面分别为20、10、15; 点C在点A之左10、之前15、之上12;点D在点A之上5、与H、
V面等距、距W面12。求作各点的三面投影并填写下表。
2-30 求直线EF与△ABC的交点K并判别可见性。
2-31 求直线EF与△ABC的交点K并判别可见性。
2-32 过点A作直线AB与直线CD平行并与△EFG 相交,求出交点K,并判别可见性。
2-33 过点A作正平线AM与△BCD平行并与△EFG 相交,求出交点K,并判别可见性。
2-34 求两平面的交线MN并判别可见性。
2-22 已知CD为水平线,完成平面ABCD的正面投影。
2-23 完成平面图形ABCDEFGH的三投影并回答 下面的问题。
机械制图 第2章 点 直线 平面的投影习题答案
已知直线AB的实长为15 求作其三面投影。 AB的实长为15, 2-4 已知直线AB的实长为15,求作其三面投影。
AB∥W面 β=30° ⑴ AB∥W面,β=30°; 在点A之下、之前。 点B在点A之下、之前。 AB∥V面 γ=60° ⑵ AB∥V面,γ=60°; 在点A之下、之右。 点B在点A之下、之右。
( 是 )
( 是 )
⑶
⑷
( 是 )
( 否 )
过点D作正平线DE平行于△ABC。 DE平行于 2-25 过点D作正平线DE平行于△ABC。
ABC平行于直线DE和FG,补全△ABC的水平投影 平行于直线DE 的水平投影。 2-26 △ABC平行于直线DE和FG,补全△ABC的水平投影。
2-27 判断下列各图中的两平面是否平行。 判断下列各图中的两平面是否平行。
AB⊥H面 在点A之下。 ⑶ AB⊥H面,点B在点A之下。
求直线AB上点K的正面投影。 AB上点 2-5 求直线AB上点K的正面投影。
2-6 在直线AB上取一点C,使其到H及V面的 在直线AB上取一点C 使其到H AB上取一点 距离相等。 距离相等。
2-7 标出交叉二直线上的重影点并判别可见性。 标出交叉二直线上的重影点并判别可见性。
求直线EF EF与 ABC的交点 并判别可见性。 的交点K 2-30 求直线EF与△ABC的交点K并判别可见性。
2-31 求直线EF与△ABC的交点K并判别可见性。 求直线EF与 ABC的交点K并判别可见性。 EF 的交点
过点A作直线AB与直线CD平行并与△ AB与直线CD平行并与 2-32 过点A作直线AB与直线CD平行并与△EFG 相交,求出交点K 并判别可见性。 相交,求出交点K,并判别可见性。
2-13 作正平线EF距V面15,并与直线AB、CD相交 作正平线EF距 EF 15,并与直线AB、CD相交 并与直线AB 分别在直线AB CD上 AB、 (点E、F分别在直线AB、CD上)。
点、直线与平面的投影

n' X n
b' b
c'
Z方向 距离 差
c a
4、已知AC为正平线,补全平行四边形ABCD 的水平投影。 解法一
a k b
解法二
c a
b
c
d d a k b c a
d d c b
5、一平面五边形ABCDE的CD边为正平线, 完成其H投影(解法1)。
c' 2' b' a' a b c 2 1 d e
Z
侧面投影长a''b''
Z
b'
b''
V
b'
Z
X
a' '
b"
W
YW
X
Aa' θ
a
a"
b
YH
b
H
Y
点、直线和平面的投影
习题讲解
1、完成正方形ABCD的两面投影
Z a' d' a'' d''
b' c' O
b'' c''
X轴方向距离差
2、在三角形ABC上作直线,使其与H面成45°角。
a'
Z方向距离差
45°
b' x
e'
d'
c'
o
a
水平投影长
b
e
dc
3、试完成等腰直角三角形ABC的两面投影。 已知AC为斜边,顶点B在直线NC上。
d'
1' e'
X
第二章习题
a
第二章 点 直线 平面的投影
2-2 直线的投影 7.在已知线段AB上求一点 在已知线段AB上求一点C AC∶CB=1∶2,并作出C的投影。 7.在已知线段AB上求一点C,使AC∶CB=1∶2,并作出C的投影。 答案 a′ a′ c′ x a c b c b b′ b′ o x a C0 o C0 c′
b′
( c′ a′ ) 15
b″ (a″)c″ d″
d′ b (d) a c
点结束
第二章 点 直线 平面的投影
2-2 直线的投影 1.画出下列直线的第三投影 画出下列直线的第三投影。 1.画出下列直线的第三投影。 z b″ b′ a′ o a″ yW x a b yH a′ x a b′ z a″ (b″) yW x a′ b a yH yH z
30º 30º ;γ 60º;β 90º 90º;β 90º α=30º ;γ=60º;β=90º。α= 90º;β= 90º;γ= 0º α= 60º;β=30º γ= 90º 。 60º ; 90º
第二章 点 直线 平面的投影
2-3 平面的投影 2.已知等腰三角形ABC的底边BC, 2.已知等腰三角形ABC的底边BC,A在BC的右上方,过A的高与BC 已知等腰三角形ABC的底边BC BC的右上方, 的右上方 的高与BC 等长,三角形ABC ABC与 面的倾角α ABC的两面投影 等长,三角形ABC与H面的倾角α =30 º,补全ABC的两面投影。 ,补全ABC的两面投影。 a' c'b' d' X c d b a α ° α=30° O B D C 答案 A
z
c′ a′ c′ d′ d″
x
a
o γ c
x
b′ o d b yH
直线的投影——习题讲解

2.特点 (1)近代中国交通业逐渐开始近代化的进程,铁路、水运和 航空都获得了一定程度的发展。 (2)近代中国交通业受到西方列强的控制和操纵。 (3)地域之间的发展不平衡。 3.影响 (1)积极影响:促进了经济发展,改变了人们的出行方式, 一定程度上转变了人们的思想观念;加强了中国与世界各地的 联系,丰富了人们的生活。 (2)消极影响:有利于西方列强的政治侵略和经济掠夺。
筹办航空事宜
处
三、从驿传到邮政 1.邮政 (1)初办邮政: 1896年成立“大清邮政局”,此后又设 , 邮传邮正传式部脱离海关。 (2)进一步发展:1913年,北洋政府宣布裁撤全部驿站; 1920年,中国首次参加 万国。邮联大会
2.电讯 (1)开端:1877年,福建巡抚在 架台设湾第一条电报线,成为中国自 办电报的开端。
C’
d’ a’
b d
a
a ax
a
az a
ay
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材·填要点]
一、铁路,更多的铁路 1.地位 铁路是 交通建运设输的重点,便于国计民生,成为国民经济 发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 至开胥平各庄铁 路建成通车。 1888年,宫廷专用铁路落成。
正垂线
c(d)
●
d c
xd
c
侧垂线
e f e(f) ●
x
ef
① 投影面垂直线在所垂直的投影面上的投影 必积聚成一个点。
② 另外两个投影 都反映线段实长。且垂直于 相应的投影轴。
2.一般位置直线的投影特性是什么?
b
a
x
a
b
b a
投影特性:
《画法几何》第2章 点、直线、平面的投影

相交(或交 叉)成直角 的两直线, 只要其中有 一条直线平 行于某投影 面,则它们 在该投影面 上的投影仍 反映直角
水平线
B
b a
A C
c
反之,两直线之一是某投影面平行线,且两直线在该投影面 上的同名投影互相垂直,则在空间两直线互相垂直
[例2-7]已知过点A作线AB平行于EF,问AB与CD是否相 交(习题P25-4)
Ⅰ∈AB Ⅱ∈CD
Ⅲ∈AB Ⅳ∈CD
3 4) (
1
b
判断重影点重 合投影的可见性 时,要在其他投 影中比较它们坐 标的大小。
直角投影定理
当两直线都平行于某投影面对,其夹角在该投影 面上的投影反映实形。
当两直线都不平行于某投影面时,其夹角在该投 影面上的投影一般不反映实形。
a b
a c b
c
b0
c
b
d
[例2-11]作一直线与AB和CD相交,并与它们垂直(即 求两直线的公垂线),并标明其真实距离
c´ b´
f´
a´
e´
d´ c (d) e
a
真ቤተ መጻሕፍቲ ባይዱ距离
f
b
点的投影
直线的投影
两直线的相对位置
平面的投影(自学)
平面的投影
平面的投影
平面的投影性质
P
A D C B
q p H d
根据一般位置直线的投影求其实长和倾角 (直角三角形法)
b´
m
V
a´
α
b´
B
C
X
a´
1、过A点作 AC//ab 2、过b点作 O bb ⊥ab,且 0 bb0=BC
A b
a
α
直线的三面投影
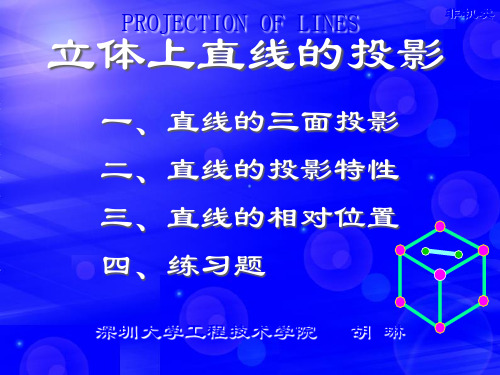
b” AB b’ a’ γ α a” b” a’ b’ a b a b β AB b” α
侧平线
a”
β a AB γ b
请点击鼠标左键显示后面内容
总有二组坐标相等,二个倾角为零. 2.投影面垂直线 2.投影面垂直线—— 总有二组坐标相等,二个Y 铅 垂直于 V 面的直线 X.Z坐标相等,称为 正垂线; X.Z坐标相等, 坐标相等 垂线; W Y.Z 侧 H α 直线与 V 面的夹角称为 β ;(总有二个倾角为0) 总有二个倾角为0) W γ
a’
b’ b
d’ d
a’ a
c’
0
a
c b
d
b’ b
c ’ e ’ d’
a’
x
b’
c’
Z
0
d
a
e
c
d’
c
0 Yw
b
b
d
Yh
请点击鼠标左键显示后面内容
练习1 练习1:已知立体上直线 AB、CD 的空间位置, AB、 的空间位置, 在投影图中标注其投影位置,并填空。 在投影图中标注其投影位置,并填空。
a’’
X
c a
0
Y
b YH
线, ’b ’ 反映 AB 实长; 实长; a b
AB 是 正平线
a AC 是 水平线 线。 c 反映 AC
请点击解答显示其内容
a’
b’
a’’
c’
d’
b’’
a
b
c d) (
一般位置
铅垂
请点击解答显示其内容
练习2 练习2: 已知直线AB、AC的二投影,求二直线的第三 已知直线AB AC的二投影 AB、 的二投影, 投影,并说明其空间位置和反映实长的投影。 投影,并说明其空间位置和反映实长的投影。
武汉理工大学土木工程制图第四章 习题与答案

b
d′ O
a
D(dc)″d″
c
Y
Z
b″ d′ O
d
YH
a″
单位:mm
距V面 距H面 距W面 空间位置
c″ d″ Y A 20
25
15 第Ⅰ分角
WB 0
15
15
V面上
C 32
0
32
H面上
D 35 0
0
Y轴上
答案
2.已知A(25,0,15)、B(25,15,25)、 C(0,0,5)的坐标,求作它们的投影图和立体图。
X
a
b
a'
YH Z a
b'
b
V a'
A
X
O
a
b YH
YW X a
答案
Z
Y
b' a
W OB b
b Y
8.求下列图中各点的W投影和立体图,并将投影 图和立体图中每两点连成直线。
2) b′ b″
a′ c′ b
a
c
b′ B b″
a″
c″
a′
c′
A
b a″
a
c″
C
c
答案
9.求W投影,判别重影点的可见性。
a′ c′ (g′) e′
b′
d′ (h′) f′
h
g
ba
ef
c
d
a′ c′ (g′) e′ g″ a″(e″) c″
b′ d′ (h′)
h
g
ba
e
c
f′ h″
b″(f″)
d″
f
d
答案
10.求W投影。
机械制图点直线平面的投影习题答案
2-22 已知CD为水平线,完成平面ABCD的正面投影。
2-23 完成平面图形ABCDEFGH的三投影并回答 下面的问题。
平面ABCDEFGH是 一般位置 面。 直线EF是 水平 线。 直线FG是 侧平 线。
2-24 判断下列各图中的直线与平面是否平行(将“是” 或"否"填于括弧中)。
⑴
⑵
( 是)
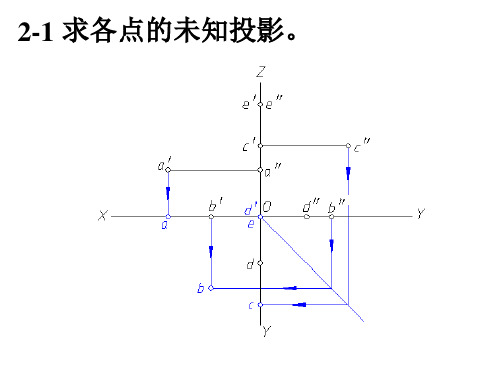
2-1 求各点的未知投影。
2-2 已知点B距点A15;点C与点A是对V面的重影点;点D
在点A的正下方15。求各点的三面投影。
2-3 已知点A(25,15,20);点B距W、V、H面分别为20、10、15; 点C在点A之左10、之前15、之上12;点D在点A之上5、与H、
V面等距、距W面12。求作各点的三面投影并填写下表。
2-8 判断两直线的相对位置(平行、相交、交叉、垂直相交、 垂直交叉)并将答案填写在下面的括号内。
2-9 由点A作直线AB与直线CD相交并使交点 距H面12。
2-10 求直线AB、CD的交点K。
2-11 过点C作直线CD与已知直线AB平行。
2-12 作与已知直线AB、CD平行且相距为15的直线MN,并使MN的 实长为20,点M距W面30,点N在点M之右(任求一解)。
2-13 作正平线EF距V面15,并与直线AB、CD相交 (点E、F分别在直线AB、CD上)。
2-14 作直线EF平行于OX轴,并与直线AB、CD相交 (点E、F分别在直线AB、CD上)。
2-15 过点C作一直线与直线AB和OX轴都相交。
2-16 作一直线MN,使其与已知直线CD、EF相交,同时 与已知直线AB平行(点M、N分别在直线CD、EF上)。
2-4 已知直线AB的实长为15,求作其三面投影。
第3章部分习题解答

3-3 直线的投影(二)
1.判别直线AB和CD的相对位置(平行、相交、交叉)。
平行
交叉
k′
交叉
相交
K C
k 作Cd=c′d′ 交叉 取dK=d′k′
作Kk∥Cc
相交
2.作一正平线MN,使其与已知直线AB、CD和EF均相交。
2′
3′
1′
2
1
(3)
3.作一直线L,与直线AB、GH相交,并与直线MN平行。
β=45°
d(c)
3-5 平面的投影(二)
1.作出△ABC平面内三边形DEM的水平投影。
2′
1′ 3′
1
d
e 2
m
3
2.完成平面图形ABCDEF的正面投影。
d′
2′
e′
f′
1′
2 1
3.已知平面ABCD的边BC//H面,完成其正面投影。
1′
b′
c′
1
4.判断点K是否在平面上。
1′
1′
1
K点在平面上
4.由点A作直线AB与直线CD相交并使交点距H面12。
12
a′
a
a
5.在直线AB、CD上作对正面投影的重影点E、F和对侧面投影的重影 点M、N的三面投影,并表明可见性。
m′
n′
e′(f′)
m″(n″) f″ e″
mf en
3-4 平面的投影(一)
1.判断下列各图中的平面是什么位置的平面。
△ABC是 铅垂 面
c′(a′)
d′ b′
10 12
a d b
c 15
a″ c″
d″ b″
20
4.已知A点的侧面投影 ,并已知A点距w面的距离为25mm,
点、直线、平面的投影习题答案

Z
(a') b'
a"
X
O
a
b
YH
Z
b"
b' a' a" b"
Yw X
O
Yw
a
b
YH
Z
e'
e"
f'
X
O
e
f
YH
Z
n' n"
f"
m'
m"
Yw X
O
Yw
n
m
YH
工程图学习题集 第 3 章
·17 ·
3.2.6 参照立体图,试在投影图上标出AB,AC,AD各直线的投影,并在图的下方说明是何种位置 直线。(投影图上用小写字母表示)
平面B是侧垂面
平面B是一般位置平面
工程图学习题集 第 3 章
·20 ·
3.3.3 直线MN在已知平面内,画出它的另一投影。
1 . a
b
2 . e
n
m
n
m
f
3.3.4 E、F两点及其直线在ABCD平面内,画出 它们的另一投影。
b
c
e
1
2 f
b
c
e f
d
X
c
oX
d e
a
oX
a 2 1
d
d
X
d
o
a
21
d
·22 ·
3.3.12 已知平面图形为铅垂面,且Z与V面成30°,试补
画全下列平面的各投影。
f'
a'
a" f"
工程制图习题集答案(内蒙古大学出版社)第二章-点线面投影

4.判断下列各对重影点的相对位置,并填空。 (1)点A在点B的 正上 方 22 mm。 (2)点D在点C的 正后 方 22 mm。
6
6
第二章 点线面投影
2-2 直线的投影(一)
1.判断下列直线对投影面的相对位置,并填写名称。 2.按已知条件画出下列直线的三投影。 (1)画水平线AB,距H面20mm,与V面 成30°角,实长25mm。 (2)画侧平线EF,距W面20mm,与V面 成30°夹角,实长25mm。
A面是 水平面 A面是 正垂面 B面是 侧平面 C面是 水平面 B面是 侧平面 C面是 铅垂面
2.完成三角形ABC的水平投影。
3.完成平面ABCDEF的正面投影。
9
9
第二章 点线面投影
2-3 平面的投影(二)
1.判断K点或线段DE是否在平面△ABC内。 2.在平面△ABC内取一点M,使其距H面22mm,距V面25mm,求m',m。
AB是 正平 线; CD是 AB: ∥ V, ∠ H, ∠ W。
侧垂 线。 CD: ∥ V, ∥ H, ⊥ W。
7
7
第二章 点线面投影
2-2 直线的投影(二)。
1.判断直线AB与CD在空间的相对位置,将答案写在指定位置。 2.已知线段AB为正平线,C为该线段上的一点,根据给出的投影,画出线段AB和点C的 水平投影和侧面投影。
30°
30° AB是 正平 线; EF是 CD是 侧垂 线; KM是 侧平 线; 正垂 线;
3.分别在图(a).(b).(c)中,由点A作直线AB与CD相交,交点B距离V面25mm。
4.根据轴测图,在三视图中标出线段AB和CD的三投影(点的三投影用小写字母标出) 并填写它们的名称和对各投影面的相对位置。
投影基本知识习题及答案

一、填空题1、工程上常采用的投影法是 中心投影法 和 平行投影 法,其中平行投影法按投射线与投影面是否垂直又分为 正投影 和 斜投影 法。
2、当直线平行于投影面时,其投影 直线 ,这种性质叫 真实 性,当直线垂直投影面时,其投影 点 ,这种性质叫 积聚 性,当平面倾斜于投影面时,其投影 平面 ,这种性质叫 类似 性。
3、主视图所在的投影面称为 正立面投影面 ,简称 正立面 ,用字母 V 表示,俯视图所在的投影面称为 水平投影面 ,简称 水平面 ,用字母 H 表示。
左视图所在的投影面称为 侧立投影面 简称 侧立面 ,用字母 W 表示。
4、三视图的投影规律是:主视图与俯视图 长对正 ;主视图与左视图 高平齐 ;俯视图与左视图 宽相等 。
6、直线按其对三个投影面的相对位置关系不同,可分为 投影面垂直线、 投影面平行线、 一般位置直线 。
7、与一个投影面垂直的直线,一定与其它两个投影面 平行 ,这样的直线称为投影面的 投影面垂直线 。
8、与正面垂直的直线,与其它两个投影面一定 平行 ,这样的直线称为 正垂线 。
9、与一个投影面平行,与其它两个投影面倾斜的直线,称为投影面的 投影面平行线 ,具体又可分为 正平线 、 水平线 、 侧平线 。
10、与三个投影面都倾斜的直线称为 一般位置直线 。
11、空间平面按其对三个投影面的相对位置不同,可分投影面垂直面、 投影面平行面、 一般位置面12. 正垂面与正面 垂直 ,与水平面 倾斜 ,与侧面 倾斜 ,正垂面在正面投影为 直线 ,在水平面和侧面投影为 投影面的类似性 。
13.正平面与正面 ,与水平面 ,与侧面 ,正平面在正面投影为 ,在水平面投影和侧面投影为 。
14.参照图下图中的立体图,在三视图中填写物体的六个方位。
(填前、后、左、右、上、下)二、选择题(12分)1.下列投影法中不属于平行投影法的是( A )A 、中心投影法B 、正投影法C 、斜投影法2、当一条直线平行于投影面时,在该投影面上反映( A )上下左 前右后A、实形性B、类似性C、积聚性3、当一条直线垂直于投影面时,在该投影面上反映( C )A、实形性B、类似性C、积聚性4、在三视图中,主视图反映物体的( B )A、长和宽B、长和高C、宽和高5、主视图与俯视图()A、长对正B、高平齐C、宽相等6、主视图与左视图( B )A、长对正B、高平齐C、宽相等7、为了将物体的外部形状表达清楚,一般采用(A)个视图来表达。
直线的投影复习题
YH
c
a
a
d
X
b
c
b
d a
d O b
YW
YH
AB与CD不平行。
对于特殊位置直 线,只有两组同面投 影互相平行,空间直 线不一定平行。
[例题6] 判断直线AB、CD的相对位置。
c′ b′
a′ d′
X
a
d
b c
相交吗? 不相交! 为什么?
交点不符 合空间一点的 投影特性。
判断方法? ⒈ 应用定比原理 ⒉ 利用侧面投影
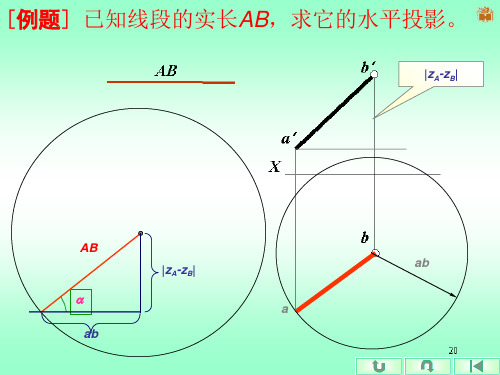
[例题] 已知线段的实长AB,求它的水平投影。
|zA-zB|
AB
|zA-zB|
ab
a
ab
➢3.4 属于直线的点
V
Z
b′
b ′ Z b″
c′
B
b″
c′
c″
a′
C
a′
c″ W X
X
O
a″
Ac b
c
O
b
a″
YW
a
a
H
Y
YH
从属性 若点在直线上, 则点的投影必在直线的同面投影上。
定比性 点的投影将线段的同面投影分割成与空间线段相同的比例。即:
a
X
a
a
c ● b
X
a c●
b c
●
b c
●
Z
a
●
c
O
a
c●
在
X
a
c
●
不在
b
b
不在
b 另一判断法? YW 应用定比定理
b
YH
例:判断图中两条直线是否平行。
(1) b
直线的三面投影
b’
c’
b’’
d’
a
b
c(d )
一般位置
铅垂
请点击解答显示其内容
练习2: 已知直线AB、AC的二投影,求二直线的第三 投影,并说明其空间位置和反映实长的投影。
b’
Z b’’
a’
c’’
c’
a’’
X
0
Yw
c
a
b
YH
AB 是 正平线 线,a ’b ’反映 AB 实长;
AC 是 水平线 线。ac 反映 AC
深圳大学工程技术学院胡琳一直线的三面投影二直线的投影特性三直线的相对位置四练习题projectionoflines立体上直线的投影非机类一直线的三面投影请点击鼠标左键显示后面内容bbbaaa二直线的投影特性直线性
立体上直线的投影 PROJECTION OF LINES
非机类
一、直线的三面投影 二、直线的投影特性 三、直线的相对位置 四、练习题
V
Z
b’
z
b´ b"
b”
W
a´
a’
x
a"
0
Yw
X A
0
b
a”
a
b
a
Y
H
请点击鼠标左键显示后面内容 Y
三、两直线的相对位置
1 . 线与线平行:
b’
若二直线在空间平行, a’
c’
各同面投影也相互平行;x a
c
2 . 线与线相交:
b
若二直线在空间相交, 各同面投影也相交,其 交点是二直线的共有点;
b’ Z
c’
d’
0
b’
