信号与系统实验-电话拨号音的合成与分解
信号的合成与分解实验报告

声音的奇妙合成与分解实验实验目的:
通过实验观察声音的合成和分解过程,了解声音的本质和特性。
实验材料:
1.计算机音频软件(如Audacity)
2.音频采集卡(可选)
3.扬声器或耳机
4.麦克风
实验步骤:
1.声音的合成
(1)打开音频软件,在音频轨道上录制两段清晰的声音样本,并将它们单独保存。
(2)选择一段音频,将其复制到另一个轨道上,调节两个轨道的音量大小,使它们相互重叠。
此时发现,两段声音通过叠加产生了新的声音,这就是声音的合成过程。
2.声音的分解
(1)将合成的声音和原始声音一起保存,重新打开软件,选择原始的声音轨道,并使用谱分析工具观察其频谱特征。
(2)选定频谱上的一段区间,将其复制到另一个轨道上,并使用滤
波器将这一段区间从原始音频轨道上剔除。
此时,认为分离出了原始
声音中的一段频率区间,即声音的分解过程。
实验结果:
通过实验结果可以发现,声音的合成和分解都是基于声音波形的
基础上进行的。
声音的合成是将两段声音波形相加形成新的波形;声
音的分解则是通过谱分析将一个复杂波形分解成多个简单波形的过程。
实验提示:
在进行合成和分解实验时,注意保持音频清晰,尽量避免外界噪
音的干扰。
此外,实验中的操作需要耐心和细心,需要多次尝试和调整,才能得到合适的实验结果。
深大信工实验四信号的分解与合成实验

深圳大学实验报告课程名称:信号与系统
实验项目名称:信号的分解与合成实验学院:信息工程
专业:电子信息
指导教师:
报告人:学号班级: 4
实验时间:2016-05- 14
实验报告提交时间:2016-05-14
教务部制
送入Y轴,示波器采用X-Y方式显示,观察李沙育图形。
90、1800时,波形分别如图2-2-3当基波与三次谐波相位差为00(即过零点重合)、0
所示。
相位差=0º相位差=90º相位差=180º
图4-3 基波与三次谐波相位的观察
以上是三次谐波与基波产生的典型的李沙育图,通过图形上下端及两旁的波峰个数,确定频率比,即3:1,实际上可用同样的方法观察五次谐波与基波的相移和频率比,其应约为5:1。
实验内容:
1、观察信号分解的过程及信号中所包含的各次谐波。
2、观察由各次谐波合成的信号。
数据处理:
基波与三次谐波的相位图、幅度比
基波与五次谐波的相位与幅度比
基波与七次谐波的相位、幅度比
基波与各次谐波的合成图形
注:1、报告内的项目或内容设置,可根据实际情况加以调整和补充。
2、教师批改学生实验报告时间应在学生提交实验报告时间后10日内。
MATLAB电话拨号音的合成与识别

知识就昱力量MATLAB 电话拨号音的合成与识别1. 实验目的1.本实验内容基于对电话通信系统中拨号音合成与识别的仿真实现。
主要涉及到电话拨号音合成的基本原 理及识别的主要方法,利用 MATLAB 软件以及FFT 算法实现对电话通信系统中拨号音的合成与识别。
并进一步利用 MATLAB 中的图形用户界面 GUI 制作简单直观的模拟界面。
使其对电话通信系统拨号音 的合成与识别有个基本的了解。
2. 能够利用矩阵不同的基频合成 0 — 9不同按键的拨号音,并能够对不同的拨号音加以正确的识别,实 现由拨号音解析出电话号码的过程。
进一步利用 GUI 做出简单的图形操作界面。
要求界面清楚,画面简洁,易于理解,操作简单。
从而实现对电话拨号音系统的简单的实验仿真。
2.实验原理 1. DTMF 信号的组成双音多频 DTMF ( Dual Tone Multi-Frequency )信号,是用两个特定的单音频率信号的组合来代表数 字或功能。
在DTMF 电话机中有16个按键,其中10个数字键0 — 9, 6个功能键*、#、A 、D 。
其中12个按键是我们比较熟悉的按键,另外由第4列确定的按键作为保留,作为功能 1209Hz 、 1336Hz 、 1477H:、 1633Hz 高频群。
从低频群和高频群任意各抽出一种频率进行组合, 共有16种组合,代表16种不同的数字键或功能,每个按键唯一地由一组行频和列频组成,如表 示。
V4 Z Z.+DTMF 的组合功能3. 实验步骤1. DTMF 信号的产生合成现在将对上节制作的图形电话拨号面板上的各控件单位的动作和变化进行设置, 即对tu1.m 文件进行编辑。
其主要的功能是使对应的按键,按照表1的对应关系产生相应的拨号音,完成对应行频及列频的叠加输岀。
此外,对于图形界面的需要,还要使按键的号码数字显示在拨号显示窗口中。
键留为今后他用。
根据CCITT 建议,国际上采用 697Hz 、770Hz 、 852Hz 、 941Hz 低频群及■I知识就昱力量鉴于CCITT对DTMF信号规定的指标,这里每个数字信号取1000个采样点模拟按键信号,并且每两个数字之间用100个0来表示间隔来模拟静音。
电话通信系统中信号音的产生及其实现

合肥学院课程设计报告题目:_ 电话通信系统中信号音的产生与实现系别:__ 电子信息与电气工程系 _ _ 专业:___ 通信工程___ ______ _班级:____ _ ______2013年 12月 09日《现代通信技术课程设计》课程设计任务书电话通信系统中信号音的产生及其实现摘要:随着社会的飞速发展,人与人之间的交流日益密切,电话通信系统运用日趋广泛,每时每刻都充满了我们的生活,给我们的生活提供了方便,带来了不一样的体验和色彩。
在电话通信系统中,各种不同的信号音对我们的通信状态,有很大的提示和指引作用。
本设计中我们通过运用所学的FPGA的相关知识,基于VHDL语言进行编程,借助Quartus软件和GW-48实验开发平台设计实现拨号音,回铃音、忙音、通知音,这四种不同的信号音,并进行验证。
关键词:信号音;VHDL语言;FPGA ;Quartus2 ;实现;正文:一、设计目的1.掌握CPLD可编程器件的编程和下载方法。
2.熟悉用CPLD可编程器件产生程控交换中信令信号的方法。
3.从设计中掌握一些基本技巧,提高自己动手能力和发现问题解决问题的能力。
4.通过设计完成一个小项目,培养团队合作能力,并检验我们四年来所学的专业知识。
二、设计要求利用可编程器件CPLD对系统的全局时钟信号进行分频,产生程控交换系统中电话交换的4种信号音:拨号音:连续发送的500Hz信号。
回铃音:1秒通,4秒断的5秒断续的500Hz信号。
忙音:0.35秒通,0.35秒断的0.7秒断续的500Hz信号。
振铃信号(铃流):以0.2秒通,0.2秒断,以0.2秒通,0.6秒断的1.2秒断续方式发送。
通过软件编程及仿真,正确实现以上四种信号音的发生,最终下载,并用示波器观察波形,和拨数字键调出不同信号音听扬声器发出声音是否正确来验证程序及产生信号音的正确性。
三、设计原理设计中我们用到的开发系统主频为50MHz,因设计要求产生500Hz及25Hz 的信号音,故我们首先考虑把50MHz的主频进行分频。
信号的分解与合成实验报告

信号的分解与合成实验报告广州大学学生实验报告学院日期:2014年5月20专业: 年级: 成绩:姓名: 学号:实验课程名称:信号与系统实验指导老师:实验项目名称:滤波器的频响特性测定一、实验目的1、进一步掌握周期信号的傅里叶级数。
2、用同时分析法观测锯齿波的频谱。
3、全面了解信号分解与合成的原理。
4、掌握带通滤波器的有关特性测试方法及其选频作用。
5、掌握不同频率的正弦波相位差是否为零的鉴别和测试方法(李沙育图形法)。
二、实验原理任何电信号都是由各种不同频率、幅度和初相的正弦波叠加而成的。
对周期信号由它的傅里叶级数展开式可知,各次谐波为基波频率的整数倍。
而非周期信号包含了从零到无穷大的所有频率成分,每一频率成分的幅度均趋向无限小,但其相对大小是不同的。
通过一个选频网络可以将信号中所包含的某一频率成分提取出来。
对周期信号的分解,可以采用性能较佳的有源带通滤波器作为选频网络。
若周期信号的角频率,则用作选频网络的,种有源带通滤波器的输出频率分别是、Wo,1Wo,2Wo,。
NWo,从每一有源带通滤波器的输出端可2wo、3Wo、4Wo、5Wo( 以用示波器观察到相应谐波频率的正弦波,这些正弦波即为周期信号的各次谐波。
把分离出来的各次谐波重新加在一起,这个过程称为信号的合成。
本实验中,将被测锯齿波信号加到分别调谐于其基波和各次谐波频率的一系列有源带通滤波器电路上。
从每一有源带通滤波器的输出端可以用示波器观察到相应频率的正弦波。
本实验所用的被测周期信号是,,,,,的锯齿波,而用作选频网络的,种有源带通滤波器的输出频率分别是,,,,,、,,,Hz、300Hz、 400Hz、500Hz、600Hz、700Hz,因而能从各有源带通滤波器的两端观察到基波和各次谐波。
奇次谐波的相位与基波同相,而偶次谐波的相位与基波反相。
各次谐波之间的相位差可以用李沙育图形法测量.。
利用运算放大器可以制成加法器,通过加法器将锯齿波分解出来的各次谐波相叠加,可以重新获得锯齿波。
信号与系统实验报告 实验五 信号的分解与合成
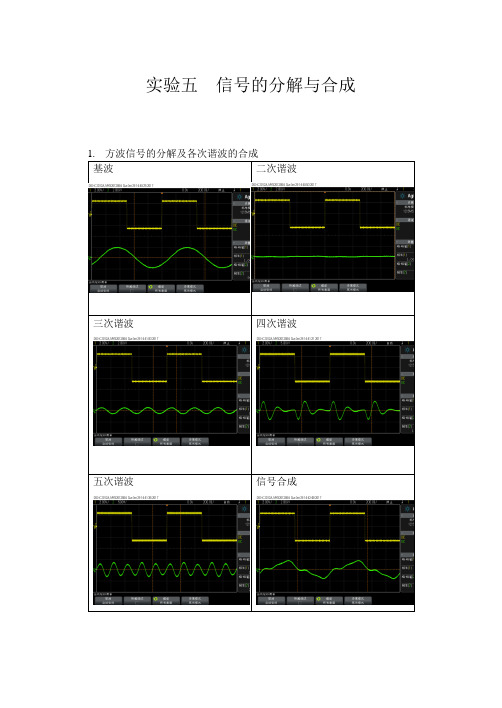
实验五信号的分解与合成基波二次谐波
三次谐波四次谐波
五次谐波信号合成
调整后信号合成三次谐波与基波相位差
五次谐波与基波相位差
通过观察和示波器测量,可以发现各次谐波的幅值符合方波的傅利叶级数各项系数之比,此时,基波、三次谐波、五次谐波合成的信号最贴近原方波信号。
基波二次谐波
三次谐波四次谐波
五次谐波信号合成
三次谐波与基波相位差五次谐波与基波相位差
数各项系数之比,此时,基波、三次谐波、五次谐波合成的信号最贴近原三角波信号
2.分别绘出三角波基波、三次谐波、五次谐波及合成的波形在同一坐标
平面的图形。
3.总结信号的分解与合成原理。
信号分解:采用性能较好的有源带通滤波器作为选频网络,选频网络的输出频率调整到被分解信号的基波、二次谐波、三次谐波四次、五次谐波,分别将电信号中所包含的该谐波频率成份提取出来。
信号合成:分解后的各次谐波信号分别输送到加法器中合成即可。
但要调整各次谐波的幅度和相位符合傅立叶分解级数中各次谐波间的幅度相位的比例关系,才能合成出效果良好的信号。
4. 总结方波、三角波所含频谱成分的差异。
等幅三角波与方波,傅立叶分解后,同次谐波相比,三角波信号分量幅度小。
方波与三角波相比,含有的高次谐波更丰富。
信号与系统中信号分解与合成实验报告

信号与系统中信号分解与合成实验报告信号与系统实验报告非正弦周期信号的分解与合成专业:班级:姓名:学号:用同时分析法观测50Hz非正弦周期信号的分解与合成用同时分析法观测50Hz 非正弦周期信号的分解与合成一、实验目的1、用同时分析法观测50Hz非正弦周期信号的频谱,并与其傅立叶级数各项的频率与系数作比较。
2、观测基波和其谐波的合成。
二、实验设备1、信号与系统实验箱:THKSS,A型或THKSS,B型或THKSS,C型。
2、双踪示波器,数字万用表。
三、实验原理1、一个非正弦周期函数可以用一系列频率成整数倍的正弦函数来表示,其中与非正弦具有相同频率的成分称为基波或一次谐波,其它成分则根据其频率为基波频率的2、3、4、…、n等倍数分别称二次、三次、四次、…、n次谐波,其幅度将随谐波次数的增加而减小,直至无穷小。
2、不同频率的谐波可以合成一个非正弦周期波,反过来,一个非正弦周期波也可以分解为无限个不同频率的谐波成分。
3、一个非正弦周期函数可用傅立叶级数来表示,级数各项系数之间的关系可用一个频谱来表示,不同的非正弦周期函数具有不同的频谱图,各种不同波形及其傅氏级数表达式见表2-1,方波频谱图如图2-1表示方波频谱图各种不同波形的傅立叶级数表达式1、方波4u111 mu(t),(sin,t,sin3,t,sin5,t,sin7,t,,,,),3572、三角波8U11 mu(t),(sin,t,sin3,t,sin5,t,,,,)2,9253、半波2U1,11 mu(t),(,sin,t,cos,t,cos4,t,,,,),243154、全波4U1111 mu(t),(,cos2,t,cos4,t,cos6,t,,,,),2315355、矩形波,U2U ,,12,,13,,mmu(t),,(sincos,t,sincos2,t,sincos3,t,,,,)T,T2T3T实验装置的结构如下图所示信号分解与合成实验装置结构框图,图中LPF为低通滤波器,可分解出非正弦周期函数的直流分量。
信与系统实验电话拨音的合成与分解

1. Set
功能:设置对象属性。
基本调用格式:set(H,'PropertyName',PropertyValue,...) 用属性值'PropertyValue'设置关于用参量 H 标志的对象(一个或多个)的属性名'PropertyName'(一个或多个)。H 可以为一句柄的向量。在这种情形下,命令 set 可以设置所有对象的属性值。
n=[1:1000]; % 每个数字 1000 个采样点表示
d0=sin(2*pi*697/8192*n)+sin(2*pi*1209/8192*n); % 对应行频列频叠加
n0=strcat(get,'string'),'1'); % 获取数字号码
set,'string',n0); % 显示号码
space=zeros(1,100); %100 个 0 模拟静音信号
end
t(i)=tel;
c=strcat(number,int2str(tel));
number=c;
i=i+1;
end
msgbox(strcat('拨打的号码为:',number),'分析');
程序解释: 确定行频和列频的数值范围是通过计算得出的:已知输入信号的取样频率fs=8192Hz ,而做 FFT 的 N=2048,则频谱分辨率为
2. DTMF 信号的产生合成
现在将对上节制作的图形电话拨号面板上的各控件单位的动作和变化进行设置,即对 文件进行编辑。其主要的功能是使对应的按键,按照表 1 的对应关系产生相应的拨号音,完成对应行频及列频的叠加输出。此外,对于图形界面的需要,还要使按键的号码数字显示在拨号显示窗口中。 鉴于 CCITT 对 DTMF 信号规定的指标,这里每个数字信号取 1000 个采样点模拟按键信号,并且每两个数字之间用 100 个 0 来表示间隔来模拟静音。以便区别连续的两个按键信号。间隔的静音信号也是在按键时产生的。 以按键 1 为例,简单介绍拨号音产生的过程:
实验三 电话拨号音合成与识别 信号分析与处理实验电子教案

基本思想是对DFT公式进行转换,使其成为一个二阶传输
函数:
பைடு நூலகம்
Hm
z
1
2
1 WNm z 1
cos2πm N z1
z 2
实验三 电话拨号音合成与识别
2. DTMF信号识别
系统的模拟框图为:
x k
+
+
y k
m
Q[k]
+ 2cos 2km N -1
z1
Q[k-1] W m
N
z 1
Q[ k-2]
实验三 电话拨号音合成与识别
实验思考题
1. 若对DTMF信号按照8000Hz进行抽样,至少要多少抽样 点才能保证区分各个键?
2. 若采用N=106点识别DTMF信号,结果会怎样? 3. 如果是一串合成的等间隔拨号音信号,如何识别?如果
是一串合成的不等间隔拨号音信号,又如何识别? 4. 如果拨号音中混入了语音干扰,除了考虑基频幅度检测,
fH fL
697 770 852 941
1209
1 4 7 *
1336
2 5 8 0
1477
3 6 9 #
实验三 电话拨号音合成与识别
2. DTMF信号识别
DTMF信号的检测是将两个信号频率提取出来,从而 确定所接收的DTMF是哪个数字。利用DFT对DTMF信号 进行N点的频谱分析,根据谱峰出现的频率点位置Ni就可 以确定DTMF信号的频率fi:
实验三 电话拨号音合成与识别
一、实验目的 理解电话拨号音的合成与识别的基本原理,
综合应用信号处理的理论和方法实现电话拨号音 的合成与识别。
实验三 电话拨号音合成与识别
二、 实验原理
信号的分解与合成实验 -回复

信号的分解与合成实验-回复
信号的分解与合成实验是一种通过将信号分解为其基本成分,然后重新合成为原始信号的实验。
这个实验可以通过数字信号处理软件来完成。
实验过程如下:
1. 准备一个以正弦信号为基础的复合信号,并记录下它的频率、振幅和相位。
2. 使用傅里叶变换分析这个复合信号,并记录下每个频率成分的振幅和相位。
3. 从傅里叶分析的结果中选择一个频率成分。
4. 使用傅里叶反变换来合成一个只包含所选择频率成分的信号。
5. 重复步骤3和4,直到所有频率成分都被合成为单独的信号。
6. 将所有信号合成为一个单一的信号。
7. 与原始复合信号进行比较,观察差异。
通过这个实验,我们可以了解如何分解信号,并重新将其合成为原始信号。
这个实验不仅提高了我们对信号分析的理解,也有利于我们对信号处理算法的应用和
优化。
信号与系统实验教程

1 02 2
4.当 R 0 时
iL (t ) L 0 sin 0t vC (t ) 1 cos 0t
就是根据这四组方程的表达式 iL (t ) , vC (t ) 编制程序,显示状态轨迹的。 4.实验报告与练习 1.简述用示波器显示李沙育图形的的原理和示波器联接的方法。 2.观察电路参数变化时,状态轨迹和的变化规律。 3.用 MATLAB 解上述的微分方程。 4.根据情况自己选做(提高题):用 MATLAB 或者 JAVA 完成状态轨迹的模拟。
图示方波是一个奇谐信号,由傅里叶级数可知,它是由无穷个奇次谐波分量合 成的,本实验用图形的方式来表示它的合成。方波信号可以分解为:
x(t )
2A
sin(2nf t ) n , n 1,3,5,7,9,
n 1 0
1
用前 5 项谐波近似合成 50Hz,幅值为 3 的方波,写出实验步骤。 a.只考察从 t 0 s 到 t 10 s 这段时间内的信号。 b.画出基波分量 y (t ) sin(t ) 。 c.将三次谐波加到基波之上,并画出结果,并显示。
b 欠采样
x(t ) 3 sin(2ft ) , f 6 Hz
对采样频率 f s 为正常采样和欠采样时两种情况进行分析,观察欠采样时信号频 谱的混迭现象。
3.实验内容 (1)熟悉 MATLAB 中 simulink 的用法。
(2)根据下图提示是完成信号 x(t ) 的抽样和内插试验仿真设计。
1
(3) 设计分析方波、三角波频谱的分析实验,写出实验步骤,并完成实验(并比较 二者频谱的特点) 。 4.实验报告要求 简述实验目的及原理,按实验步骤附上相应的信号波形曲线,总结实验得出的 主要结论。
信号与系统实验-实验二信号分解与合成

实验二信号分解与合成一、实验目的1、观察电信号的分解。
2、掌握带通滤波器的有关特性测试方法。
3、观测基波和其谐波的合成。
二、实验内容1、观察信号分解的过程及信号中所包含的各次谐波。
2、观察由各次谐波合成的信号。
三、实验仪器1、信号与系统实验箱一台(主板)。
2、电信号分解与合成模块一块。
3、20M双踪示波器一台。
四、实验结果(1)0°、90°、180°下基波与三次谐波的波形与各自的李沙育图如下所示:0°:波形及各项数据李沙育图90°:波形及各项数据李沙育图(2)基波跟三次谐波合成波形:(3)0°、90°、180°基波跟五次谐波的波形以及各自的李沙育图如下所示:0°:波形及各项数据李沙育图180°:波形及各项数据李沙育图(4)基波、三次谐波和五次谐波合成波形:五、实验分析(1)通过观察实验结果,比较基波跟三次谐波0°、90°和180°时的李沙育图,通过图形上下端及两旁的波峰个数,确定频率比,即3:1;同理可得,实际上五次谐波与基波的相移和频比,其应为5:1。
(2)分析相位、幅值在波形合成中的作用答:对于频率相同的两个波形:如果相位相同,合成后幅值相加;如果相位相反,合成后幅值相减。
将分解的波形进行傅立叶反变换就可得到合成波形。
(3)实验中的误差。
实验中出现误差主要出现在基波以及每个谐波的调幅跟调相上,因为仪器问题没办法使条件完全满足,得到的图形结果只能是近似等价。
(4)什么是吉布斯效应,它是如何产生的,它的具体的表现是什么?答:①什么是吉布斯效应:将具有不连续点的周期函数(如矩形脉冲)进行傅立叶级数展开后,选取有限项进行合成。
当选取的项数越多,在所合成的波形中出现的峰起越靠近原信号的不连续点。
当选取的项数很大时,该峰起值趋于一个常数,大约等于总跳变值的9%。
这种现象称为吉布斯现象。
实验十五 信号的分解与合成

实验十五信号的分解与合成本实验主要是探究信号的分解与合成,通过实验了解信号的基本特征和频谱分析等概念。
首先,在分解信号中,我们采用了快速傅里叶变换(FFT)对信号进行了频谱分析,然后将信号分成不同频率的成分。
其次,在合成信号中我们将多个频率不同的周期信号进行加权合成,得到一个新的信号。
1.实验原理(1)信号频谱分析信号的频率是指其波形中瞬时变化的周期时间,单位是赫兹(Hz),频率是频谱密度的简单积分。
频谱分析是指将时域离散信号转换到频域离散信号的过程。
频谱分析可以帮助我们了解信号的频率成分和幅值随时间的变化情况,并可有效提取信号中的重要信息。
常见的频谱分析方法有傅里叶变换和功率谱分析。
(2)傅里叶变换傅里叶变换是一种将时域连续或离散信号转换到频域连续或离散信号的数学变换。
傅里叶变换在信号的频谱分析中应用广泛,其原理为将一个信号分解成一系列正弦波。
傅里叶变换可以将一个时域信号分解成从0开始的一系列谐波分量,具体的分解方式是将信号转换为正弦波的加权和,每个正弦波的权重代表其频率成分的幅值大小。
这些频谱分量可以以幅度和相位为表示方式,所以我们可以将一个信号分解成正弦波幅度和相位的形式,也就是信号的频谱。
(3)合成信号合成信号是指将多个不同频率、不同幅度的信号加在一起,形成一个新的信号。
合成信号是通过锯齿波合成、方波合成和三角波合成等方式组合而成。
在合成信号中,不同频率、不同幅度的信号的加权和决定了合成波形的形状。
通过合成信号,我们可以研究音频信号中的共振和谐波,以及使用FFT将复杂信号分解成基础频率来分析其特性。
2.实验内容(1)使用Matlab进行频谱分析首先需要了解Matlab的基本操作,将所提供的配合进行读取,然后使用傅里叶变换函数fft()将时间域的信号转化为分段傅里叶变换的信号,并画出每个分段的频域特征,同时画出整段信号的频域图。
对于一条复杂的信号,我们可以使用FFT将其分解成基频和多个谐波,通过观察各个谐波的频率和幅度,我们可以得到信息的基本特征。
信号的合成与分解实验报告

信号的合成与分解实验报告
《信号的合成与分解实验报告》
实验目的:通过合成和分解信号的实验,掌握信号的合成和分解原理,加深对信号处理的理解。
实验材料:
1. 信号合成器
2. 示波器
3. 信号分解器
4. 信号处理器
实验步骤:
1. 将信号合成器连接到示波器,调节合成器的频率和幅度,观察示波器上显示的波形变化。
2. 使用信号分解器将合成的信号分解为不同的频率成分,观察分解后的波形变化。
3. 将分解后的信号输入到信号处理器中,对不同频率成分进行处理,观察处理后的波形变化。
实验结果:
通过实验观察和数据分析,我们发现当不同频率和幅度的信号合成时,示波器上显示的波形会随之变化,呈现出复杂的波形图案。
而当合成信号经过分解器分解后,可以得到不同频率成分的波形,通过信号处理器的处理,可以对不同频率成分进行单独处理,实现对信号的精细控制。
实验结论:
通过这次实验,我们深入理解了信号的合成和分解原理,了解了信号处理的基本方法和技术,对信号处理有了更深入的认识。
同时,我们也认识到了信号处理在通信、音频、视频等领域的重要应用,对未来的研究和实践有了更清晰的方向。
总结:
通过这次实验,我们不仅掌握了信号的合成和分解原理,还加深了对信号处理的理解,为今后的学习和研究奠定了坚实的基础。
希望通过这次实验,能够激发更多同学对信号处理领域的兴趣,为科学技术的发展贡献自己的力量。
信号处理与系统4案例-声音信号的合成与处理

-3
x 10 1
时域波形
0.5
0
-0.5
-1
0
1
2
3
4
5
6
7
8
9 10
n 频谱图
x 104
2
1.5
1
0.5
0 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 Hz
图 1 合成乐曲的时域波形和频谱图
目前数字信号处理技术广泛应用于电子音乐合成等领域。电子合成器已称为 音乐工作者的标准器材,它能够模拟钢琴、吉他、小提琴和长笛等等,模仿效果 日益完善。
y=note(n(1,m),0.7*n(2,m),Fs,3); %锯齿波 t=linspace(0,0.7*n(2,m),length(y)); envelope=(t+0.2).*exp(-3*(t+2)).*cos(2*t); %包络 y=y.*envelope; ys=cat(2,ys,y); end soundsc(ys,Fs);
329.63(0.5)329(0.5)|440(3)329.63(0.5)329(0.5)|293.66(3)329.63(0.5)369.99(0.5)| 440(0.5)523.25(1)440(0.5)392(0.5)261.63(1)329.63(0.5)|293.66(3)…
括号外的数字为音符频率,括号内的数字为音符持续时间。 为方便起见,先编写一个音符转化为声音数据的函数。 文件名:note.m
elseif waveform == 3 y=sawtooth(2*pi*f*t);
end
调用该函数产生上面乐曲的程序为: 文件名:Sound2.m
MATLAB电话拨号音的合成与识别

MATLAB电话拨号音的合成与识别MATLAB电话拨号音的合成与识别1.实验目的1.本实验内容基于对电话通信系统中拨号音合成与识别的仿真实现。
主要涉及到电话拨号音合成的基本原理及识别的主要方法,利用MATLAB 软件以及FFT 算法实现对电话通信系统中拨号音的合成与识别。
并进一步利用MATLAB 中的图形用户界面GUI 制作简单直观的模拟界面。
使其对电话通信系统拨号音的合成与识别有个基本的了解。
2.能够利用矩阵不同的基频合成0 -9 不同按键的拨号音,并能够对不同的拨号音加以正确的识别,实现由拨号音解析出电话号码的过程。
进一步利用GUI 做出简单的图形操作界面。
要求界面清楚,画面简洁,易于理解,操作简单。
从而实现对电话拨号音系统的简单的实验仿真。
2.实验原理1. DTMF 信号的组成双音多频DTMF (Dual Tone Multi-Frequency )信号,是用两个特定的单音频率信号的组合来代表数字或功能。
在DTMF 电话机中有16 个按键,其中10 个数字键0 — 9 ,6 个功能键* 、# 、A 、B 、C 、D 。
其中12 个按键是我们比较熟悉的按键,另外由第4 列确定的按键作为保留,作为功能键留为今后他用。
根据CCITT 建议,国际上采用697Hz 、770Hz 、852Hz 、94lHz 低频群及1209Hz 、1336Hz 、1477H: 、1633Hz 高频群。
从低频群和高频群任意各抽出一种频率进行组合,共有16 种组合,代表16 种不同的数字键或功能,每个按键唯一地由一组行频和列频组成,如表1 所示。
(文章来自:/forestlong/blog/item/dd33911a24b5fbf 3ae5133ee.html转载请注明出处。
)DTMF 的组合功能 3.实验步骤1. DTMF 信号的产生合成现在将对上节制作的图形电话拨号面板上的各控件单位的动作和变化进行设置,即对tu1.m 文件进行编辑。
实验十五 信号的合成与分解

from TP1008 to TP801
基波 输出 TP80 2
三次谐 波输出 TP804
五次谐 波输出 TP806
• 方波分解得到基波TP802、三次谐波 TP804和五次谐波TP806分量; • 调节相应的电位器,用示波器观察,以
基波TP802为基准,使三次谐波的幅度是
基波的1/3,五次谐波幅度是基波的1/5,
信号的分解方案框图
BPF-1KHz BPF-2KHz
输入信号 一次谐波
二次谐波
BPF-3KHz BPF-4KHz BPF-5KHz
三次谐波
四次谐波
五次谐波
方波信号的傅利叶级数展开式为
1 1 f (t ) (sin t sin 3t sin 5t …) 3 5
•对方波信号而言,在理想情况下,偶次谐波应
实验十一
信号的分解与合成
一、实验目的 • 通过观察信号的 分解与合成过程 ,理解 利用 傅利叶级数 进行信号 频谱分析 的方 法。 • 了解波形分解与合成原理。 • 掌握 带通滤波器 有关特性的设计和测试 方法。
• 任何电信号都是由各种不同频率、幅度和 初始相位的正弦波叠加而成的。 • 对周期信号由它的傅利叶级数展开式可知, 各次谐波为基波频率的整数倍。 • 而非周期信号包含了从零到无穷大的所有 频率成份,每一频率成份的幅度均趋向无 穷小,但其相对大小是不同的。 • 通过一个选频网络可以将电信号中所包含 的某一频率成份提取出来。 • 本实验采用性能较好的有源带通滤波器作 为选频网络。
TP1510移相后五次谐波 TP811五次谐波 TP812 合成方波
TP807基波
信号的合成
• 保持各次谐波幅度不变,分别改变相位调整电 位器W1501、W1503、W1505,观察记录各次 谐波相位对波形合成的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、实验操作部分
1.实验数据、表格及数据处理
2.实验操作过程(可用图表示)
3.实验结论
2.实验操作过程(可用图表示)
1.图形电话拨号面板的制作
利用GUI图形用户界面设计工具制作电话拨号面板,把DTMF信号和电话机的键盘矩阵对应起来。其中选用我们熟悉的10个数字键0 —9,2个功能键“*”、“#”,另四个键省略。按照图1电话机键盘矩阵的排列方式制作四行三列的按键控件。每个按键可用(PushButton)添加。然后,为了更直观的反映对应的按键号码,可以设置一个编辑框,用于动态的显示拨号号码,模拟实际电话的拨号显示窗口。编辑框可用(Edit Text)添加。另外,为了图形电话拨号面板的简洁美观,可以添加空白区域作为背景,并用静态文本框制作文字信息。背景可用(Frame)添加,静态文本框可用(Static Text)添加。最终利用GUI图形用户界面设计工具生成的图形电话拨号面板用于拨号音的合成产生部分。
p=audioplayer(d0,8192); %产生拨号音
global soun
if(soun==1)
play(p)
pause(0.5)
end
str=get(handles.edit1,'string');
l=length(str);
str=strrep(str,str,str(1:l-1)); %去掉末尾号码在面板上的显示
global n
global contact
found=0;
x=0;
for i=1:n
if (strcmp(contact(i).num,str)==1)
found=1;
x=i;
end
end
if(found==1)
str=strcat('正在打电话给:',contact(x).name);
msgbox(str,'电话');
2. find
功能:找出矩阵X中非0项的坐标和取值。
基本调用格式:[row,col] = find(X, ...)常与逻辑运算法一起使用,可进一步明确搜索数值的范围。
3. disp
功能:显示文本或数组。
基本调用格式:disp(X)
4. struct
功能:创建一个结构体数组。
基本调用格式:
s = struct('field1', values1, 'field2',values2, ...)
四、教师评语
指导教师年月日
2. DTMF信号的产生合成
现在将对上节制作的图形电话拨号面板上的各控件单位的动作和变化进行设置,即对tu1.m文件进行编辑。其主要的功能是使对应的按键,按照表1的对应关系产生相应的拨号音,完成对应行频及列频的叠加输出。此外,对于图形界面的需要,还要使按键的号码数字显示在拨号显示窗口中。鉴于CCITT对DTMF信号规定的指标,这里每个数字信号取1000个采样点模拟按键信号,并且每两个数字之间用100个0来表示间隔来模拟静音。以便区别连续的两个按键信号。间隔的静音信号也是在按键时产生的。以按键1为例,简单介绍拨号音产生的过程:
fs/N=8192/2048=4Hz,由此可算出频谱图上任意点对应的频率K=f/F。例如,数字8的高、低端频率为fl= 852Hz, fh=1336Hz,则在谱图上对应的点Kl=fl/F=213,Kh=fh/F=334
拨号来电识别的代码如下:
n=[1:1000]; %每个数字1000个采样点表示
d0=sin(2*pi*941/8192*n)+sin(2*pi*1477/8192*n); %对应行频列频叠加
global NUM
wavplay(NUM,8192);
L=length(NUM);
n=L/1100;
number='';
for i=1:n
j=(i-1)*1100+1;
d=NUM(j:j+999); %截取出每个数字
f=fft(d,2048); %以N=2048作FFT变换
a=abs(f);
N=2048;
3.涉及的MATLAB相关内容
1. Set
功能:设置对象属性。
基本调用格式:set(H,'PropertyName',PropertyValue,...)用属性值'PropertyValue'设置关于用参量H标志的对象(一个或多个)的属性名'PropertyName'(一个或多个)。H可以为一句柄的向量。在这种情形下,命令set可以设置所有对象的属性值。
end
t(i)=tel;
c=strcat(number,int2str(tel));
number=c;
i=i+1;
end
msgbox(strcat('拨打的号码为:',number),'分析');
程序解释:确定行频和列频的数值范围是通过计算得出的:已知输入信号的取样频率fs =8192Hz,而做FFT的N=2048,则频谱分辨率为
num(2)=300+find(p(300:380)==max(p(300:380))); %找列频
if (num(1) < 180) row=1; %确定行数
elseif (num(1) < 200) row=2;
elseif (num(1) < 220) row=3;
else row=4;
end
elseif z==[1,3] tel=3;
elseif z==[2,1] tel=4;
elseif z==[2,2] tel=5;
elseif z==[2,3] tel=6;
elseif z==[3,1] tel=7;
elseif z==[3,2] tel=8;
elseif z==[3,3] tel=9;
5.电话本的存储:定义全局的结构体数组,把电话号码和姓名都以字符串的格式保存。
来电识别:确认拨号后,遍历电话本结构体中的号码,比较比较所拨打号码和和电话本中的号码是否相同。
静音功能:定义一个全局的变量保存静音状态,按下静音键时状态变为1,按下室外时变为0,每次waveplay时先判断静音状态,根据判断结果决定是否播放按键音。
end
3. DTMF信号的检测识别
要实现电话拨号音(DTMF)信号的检测识别,可以通过直接计算付里叶变换得到输入信号的组成频率。这里采用FFT算法对信号进行解码分析。首先对接收到的数字信号作FFT分析,计算出其幅度谱,进而得到功率谱,组成输入信号的频率必定对应功率谱的峰值。对于连续的双音多频(DTMF)信号,需要把有效的数字拨号信号从静音间隔信号中分割提取出来,然后再用FFT算法对信号进行解码分析。MATLAB实现信号音的识别如下:
space=zeros(1,100); %100个0模拟静音信号
global NUM
phone=[NUM,d0];
NUM=[phone,space]; %存储连续的拨号音信号
p=audioplayer(d0,8192); %产生拨号音
global soun
if(soun==1)
play(p)
pause(0.5)
n0=strcat(get(handles.edit1,'string'),'#'); %获取数字号码
set(handles.edit1,'string'1,100); %100个0模拟静音信号
global NUM
phone=[NUM,d0];
NUM=[phone,space]; %存储连续的拨号音信号
武汉大学教学实验报告
电子信息学院专业2014年11月29日
实验名称电话拨号音的合成与分解指导教师
姓名年级大三学号201230*******成绩
源程序下载地址:
访问密码:skyw
一、预习部分
1.实验目的
2.实验基本原理
3.主要仪器设备(含必要的元器件、工具)
1.实验目的
本实验基于对电话通信系统中拨号音合成与识别的仿真实现,主要涉及到电话拨号音合成的基本原理及识别的主要方法,利用MATLAB软件以及FFT算法实现对电话通信系统中拨号音的合成与识别。并进一步利用MATLAB中的图形用户界面GUI制作简单直观的模拟界面。使其对电话通信系统拨号音的合成与识
else
str=strcat('正在拨打',str,',请等待...');
msgbox(str,'电话');
end
三、实验效果分析(包括仪器设备等使用效果)
实验分析:
实验的到数字1的频谱结构如上图,频谱的峰值出现在DTFM频率表中规定的频率附近。
1.话音识别的步骤:
分组FFT变换寻找每个组功率最大的两个频率点比较确定数字
别有个基本的了解。
能够利用矩阵不同的基频合成0-9不同按键的拨号音,并能够对不同的拨号音加以正确的识别,实现由拨号音解析出电话号码的过程。进一步利用GUI做出简单的图形操作界面。要求界面清楚,画面简洁,易于理解,操作简单。从而实现对电话拨号音系统的简单的实验仿真。
2.实验原理
双音多频DTMF(Dual Tone Multi-Frequency)信号,是用两个特定的单音频率信号的组合来代表数字或功能。在DTMF电话机中有16个按键,其中10个数字键0—9,6个功能键*、#、A、B、C、D。其中12个按键是我们比较熟悉的按键,另外由第4列确定的按键作为保留,作为功能键留为今后他用。根据CCITT建议,国际上采用697Hz、770Hz、852Hz、94lHz低频群及1209Hz、1336Hz、1477Hz、1633Hz高频群。从低频群和高频群任意各抽出一种频率进行组合,共有16种组合,代表16种不同的数字键或功能,每个按键唯一地由一组行频和列频组成,如表1所示。
