电机学电磁场概论.
电机学中的基本电磁定理

i2
i3
l
其中 H: 磁场强度,安/米(A/m)
dl
注:若i与l符合右手螺旋关系, 取正号,否则取 负号 。其中大拇指所指为i的方向,四指为l方向。 如图示为: ∑ i = i1 + i2 - i3
当气隙长度δ远远小于两侧 的铁心截面的边长时, 铁心和 气隙中为均匀磁场,则
F Ni H FelFe H
其中 F=Ni:磁路的磁动势 HFelFe:铁心上的磁压降 Hδ δ :气隙上的磁压降
带气隙的铁心磁路
注:i 与 l 符合右手螺旋关系,电机学中习惯大拇指所 指为 l 的方向,四指为多匝线圈中 i 方向。
设有向回路 l 与圆 环的中心圆重合,则沿 着回线 l 磁场强度 H 处 处相等且其方向处处与 回线切线方向相同(称 为均匀磁场),同时闭 合回线所包围的总电流 由通有电流 i 的 N 匝线 圈提供,则:
e blv
运动电势的方向习惯用右手定则确定,如图所示。
2.3. 电磁力定律
载流导体在磁场中要受到电磁力,在导体与磁场 垂直的情况下,若导体中电流为i,导体长度为l,导 体所在处的磁通密度为b,则电磁力为:
f bli
注:电磁力方向由左手定则决定
电机的基本作用原理
三个定律,一个定理 1)安培环路定律(全电流定律):电流在任一导 体中流通,则该导体周围将有磁场产生。 2)电磁感应定律:任一线圈中键链的磁通发生变 化,则在该线圈中将有感应电势产生。
3)电磁力定律:任一载流导体在磁场中将受力的 作用。
4)能量守恒定理:输入能量 = 输出能量 + 损耗能 量
电机的可逆运行原理
机械功率
发电机 电动机
电磁场原理

电磁场原理
电磁场(Electromagneticfield)是一种十分重要的物理现象,它涉及到物理学、材料学、电气工程和电子学等众多学科,被广泛应用于工业界和军事领域。
它的实质是电磁能量的四维传播,受时空的影响而产生改变。
本文将介绍电磁场的基本原理,以及它在电气系统中的应用方法。
一、电磁场的原理
电磁场依赖于电磁力,这是电磁能量的本质。
电磁力是由电荷产生的力,它受到电场和磁场的作用产生变化。
当电荷被加速运动或被改变时,电磁场就会产生并在空间中传播,直到与另一个电荷或磁体产生作用。
其中电场指的是电荷的分布与有效电动势,而磁场指的是磁力线的分布与有效磁动势。
电磁场的强度以斯托克斯(Tesla)为
单位,它可以在磁场中测量,也可以通过电流产生磁场,从而产生电磁力。
二、电磁场在电气系统中的应用
电磁场中的传播速度是极其重要的,它与电子学和电机学中的许多应用方法有关,例如电磁辐射、电磁力线、电路的数学模型以及电磁联系等等。
例如,电磁辐射可以用来测量电磁场的强度,而电磁力线则可以用来传递信息,电路的数学模型则可以用来电机学中的运算,而电磁联系则可以用来连接线路以及驱动转动部件。
综上所述,电磁场是电磁能量在时空上四维传播并不断改变的现象,电磁场中电场、磁场以及电磁力线的分布直接关系到电磁场的强
度。
电磁场受到它们的影响而发生变化,电磁辐射、电磁力线、电路的数学模型以及电磁联系等等,是电磁场在电气系统中实用的方法。
第06章-交流电机的旋转磁场理论

-11-
第六章 交流电机的旋转磁场理论
二、旋转磁场的基本特点
1)三相对称绕组通入三相对称电流所产生的三相基波合成 磁动势是一个旋转行波, 合成磁动势的幅值是单相电枢绕组脉
振磁动势幅值的3/2倍。同理可以证明,对于m相对称绕组通入 m相对称电流,所产生的基波合成磁动势也是一个旋转行波, 其幅值为每相脉振幅值的m/2倍。
-13-
第六章 交流电机的旋转磁场理论
第三节 交流电机的主磁通和漏磁通
一、主磁通
当交流电机的定子绕组通入三相对称电流时, 便在气隙中
建立基波旋转磁动势,同时产生相应的基波旋转磁场。 与基波
旋转磁场相对应的磁通称为主磁通,用m表示。由于旋转磁场
是沿气隙圆周的行波,而气隙的长度是非常小的, 所以相应的
-8-
第六章 交流电机的旋转磁场理论
图6-3说明 Fs (x,t) 是一个幅 值恒定、正弦分布的行波。
由于 Fs (x,t) 又 表示三相电
枢绕组基波合成磁动势沿气隙圆
F sm
F ( x, t) s
v1
et
周的空间分布,所以它是一个沿
气隙圆周旋转的行波,其相对于
定子的速度是
v1
e
π
(6-8)
0
FA1( x, t ) FB1 ( x, t ) FC1 ( x, t )
Fm
1
c
oset
c
os
πx
Fm
1
c
os
(et
2π 3
)
Fm 1
cos(et
2π 3
)
cos(πx
cos(πx
2π ) 3 2π ) 3
(6-5)
式中,Fm1是每相磁动势基波分量的幅值,其精确的计算需要考 虑绕组分布及短距等因素。
对电机进行的电磁场分析

将电枢磁势对合成磁势的影响叫做电枢反应。
Ff
二 同步电动机负载时的运行状态
设电机的磁路不饱和,励磁反电动势 为 E 0 ,电枢电流 I 与 E 0 之间的夹角为
(90 90)
⒈ 电枢电流I 与励磁反电动势E0 同 相时的电枢反应
电枢磁势Fa 的轴线总是与励磁磁势Ff的 轴线(d轴)相差90°电角度,而与转子 的交轴(q轴)重合。因此,称这种电枢 反应为交轴电枢反应。它使转子产生电 磁转矩。
c os5
Fy5 cost cos 5
分布元件组的脉振磁势
1 多相绕组的脉振磁势
设一个元件组由q个整距元件组成。相邻两元件之间相差一个槽距角 ,因此元件、 的矩形磁势波在空间位置上也彼此位移电角 。q个矩形波叠加起来为一阶梯波.
R
Fq1
q
Fq1
2R sin
q
2
Fy1 2Rsin2
Fq1 2Rsinq2
电机运行的性能取决于电机的参数和损耗。 因此研究电机内的磁场,对设计一台性能 良好的电机具有重要意义。
三 旋转电机简介
1 基本分类及结构 1)交流电机 电枢绕组通常位于定子上,其理想波形为正弦波 2)直流电机 电枢绕组通常位于转子上,其理想波形为锯齿波
2 能量关系 电源输入的能量=机械能量输出+磁场储能的增量+转换为热的能量
当电磁转矩和静负载转矩相等时,两个磁势的夹角 不再变化,两个磁势同步前进。
直轴—— 转子NS极中心线,又称作d轴。 规定两个轴
交轴—— 与直轴相距90°电角度的地 方,又称作q轴。
直轴 Ff
交轴
由励磁电流If 产生励磁磁势Ff ,进一步产生励磁磁通0。 由电枢电流I 产生电枢磁势Fa,进一步产生电枢磁通a。
电机学电磁场概论

27
电磁场问题分析求解方法
电磁问题分析求解 解析计算 数值方法
积分方程 边界元
适用于线性媒质
微分方程 有限差分 有限元
8
Matlab 绘制场图示例
clear;clf; q=2e-6; k=9e9;a=1.5; b=-1.5; x=-6:0.6:6; y=x; [X,Y]=meshgrid(x,y); %设置坐标网点 rp=sqrt((X-a).^2+(Y-b).^2); rm=sqrt((X+a).^2+(Y+b).^2); V=q*k*(1./rp-1./rm); %计算电势 [Ex,Ey]=gradient(-V); %计算场强 AE=sqrt(Ex.^2+Ey.^2);Ex=Ex./AE;Ey=Ey./AE; %场强归一化,使箭头等长 cv=linspace(min(min(V)),max(max(V)),49); % 产生49个电位值 contourf(X,Y,V,cv,'k-') %用黑实线画填色等位线图 axis('square') %在Notebook中,此指令不用 title('\fontsize{18}偶极子的场'),hold on quiver(X,Y,Ex,Ey,0.7) %宗量0.7使场强箭头长短适中。 plot(a,b,'wo',a,b,'w+') %用白线画正电荷位置 plot(-a,-b,'wo',-a,-b,'w-') %用白线画负电荷位置 xlabel('\fontsize{18}x');ylabel('\fontsize{18}y'),hold off
电机学-磁路基本知识综述
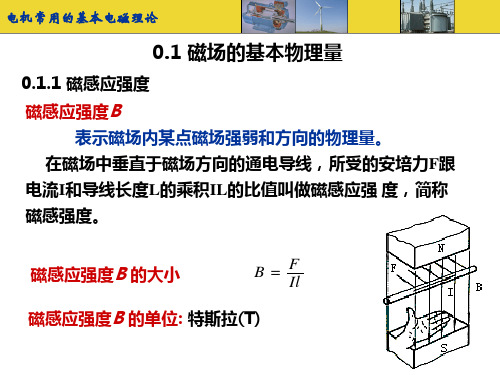
0.2 磁路的基本定律
一. 磁路的概念
工程上,为得到较强磁场,
广泛利用铁磁物质,在电机、 变压器等设备中将铁磁物质制
+
i
成一定形状,人为的构成磁通 u 的路径,使磁场主要在这部分 -
空间内分布。这种磁通所通过
的路径称之为磁路。
Φ Φ
主磁通 磁路
漏磁通
9
电机常用的基本电磁理论
由于铁心的导磁性比空气好得多,所以绝大部分磁通在 铁心中通过,这部分磁通称为主磁通。经过空气隙闭合的 磁路为漏磁通。
6
电机常用的基本电磁理论
0.1.4 磁导率
磁导率 :表示磁场媒质磁性的物理量,衡量物质的导磁能力。
它与磁场强度的乘积就等于磁感应强度,即: B μH
磁导率 的单位:亨/米(H/m)
μ的单位W/m b2 H A/m m
由实验可测得:真空的磁导率为: 0 4π107H/m
真空磁导率是一个常数,将其它物质的磁导率和它比较 是很方便的。
B/T
2.0
B
硅钢
1.6
铸钢
1.2
0.8
铸铁 0.4
0
0 1000 2000 3000 4000 5000 6000
O
H /(A/m)
a)
1
2
c
b a
膝点
C点以后,曲线基 本是平行直线,B 几乎不随H增大
H
b)
23
电机常用的基本电磁理论
• 磁性物质内部存在着很多很小的“磁畴”。
磁畴(磁化前)
磁畴(磁化后)
度。
例如: 永久磁铁的磁性就是由剩磁产生的;自励直流发 电机的磁极,为了使电压能建立,也必须具有剩磁。
但剩磁也存在着有害的一面,例如,当工件在平面 磨床上加工完毕后,由于电磁吸盘有剩磁,还将工件吸 住。为此要通入反向去磁电流,去掉剩磁,才能取下工 件。
电机学-概论(2)

m( 0)
1 RmFe
50000A
m( 1)
1 6
m(
0)
L( 0)
N 2m( 0)
N2
A
l
2002 5000 4 107 100 104
1.0
2.51(H)
L( 1)
1 6
L( 0)
0.418(H)
2、已知:f 50Hz , w 100
匝, B 1.0T l 1m
s 100cm2 Fe 50000 ,
求:F , i
3、已知:f 50Hz ,w 100
匝, B 1.0T l 1m
s 100cm2 Fe 50000
1mm ,
求:F , i
a
0
B f (H)
c
Fe f (H )
B 0H
H
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
2000
4000
6000
8000
0.5.3 铁磁材料具有磁滞特性
B
Bm B
Hm Hc
0
Hm H
Bm
φ
i
B
B Hc
0
V
Ph Kh f Bm G
B
Bm B
Hm Hc
H
0
f
Hm H
N
N 2im
L N 2m
X
L N 2 m
N2
A
l
X
f
N2
m
Fe
铁磁材料包括铁、镍、钴以及它们的合金(其它材料 称之为非铁磁材料)。将这些材料放入磁场后,材料 内的磁场会显著增强。铁磁材料在外磁场中呈现很强 的磁性,此想象称为铁磁材料的磁化。
电机学概述和磁路简介

20
0.2 电机学理论基础--磁路的基本定律
1 磁路的基本定律 2 常用的铁磁材料及其特性
21
1 磁路的基本定律
一、磁场的基本概念
磁 阻
两种常见的磁路
磁路
i1 + u1 -
主磁通
1 2
i2
+
u2 -
S
N S
励磁绕组
漏磁通
变压器磁路
N
四极直流电机磁路
2. 安培环路定律(全电流定律)
在磁场中,沿着任何一条闭合回路 l ,磁场
强度H的线积分,等于该闭合回路所包围电
流的代数和,即
∮H dl = ∑i l
i3
i1 i2 i4
如图: ∑i = i1+i2-i3
A
电阻:R=ρl/A
Ω 磁阻: Rm=l/μA
H-1
电导:G =1/R
S 磁导:Λm=1/Rm
H
欧姆定律:E=IR
欧姆定律:F=ΦRm
基尔霍夫第一定律:ΣI=0 基尔霍夫第一定律:ΣΦ=0
基尔霍夫第二定律:
基尔霍夫第二定律:
ΣE=ΣU
ΣF=ΣΦRm=ΣHl
5.铁心磁路计算
(1)串联磁路计算
将磁路分段,保证每段磁路的均匀性
14
电动机的用途
航空和航海业
有特殊要求的航空电机、船用电机和推进电机等。
日常生活
电风扇、洗衣机、吸尘器、空调、电冰箱、微波 炉、DVD播放机、电动按摩器、电动工具等。
15
船用电机
电动机图片
"电机学"中电磁场基础理论教学的探索与实践

D O I 编码: 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 7 — 0 0 7 9 . 2 0 1 3 . 1 4 . 0 2 5
课 程教材 改 革
“ 电机 学 ’ ’ 中电磁 场 基础 理论 教 学 的探 索与实践
聂 晶 王洪坤 柴兆森 胡春玲
文献 的能力 , 了解到相关 知识 的新应用 , 也丰富了教学 内容 , 提
高 了学 生 的学 习热 情 和兴 趣 。 在 “ 电机 学 ”中关 于 电磁 场 内容 的 教 学 , 要 注 重 基 础 内容 的
学习的过程 中感到枯燥 、 乏 味, 且 易遭 受挫折感 , 学 习效果 不理
想。在 “ 电机学 ” 课 程的教学过程 中, 就如何 改革 电磁 场基础内 容的教学 , 从教学理念 和教学方法两个方面 , 结合 “ 教” 与“ 学”
课程 中电磁 问题理论 性强 、 计算复 杂的特点, 当然这是 一个 矛
中图 分 类号 : G 6 4 2 . 0 文献标识码 : A 文章 编号 : 1 0 0 7 — 0 0 7 9( 2 0 1 3 ) 1 4 — 0 0 5 3 — 0 2
对于高等学 校的电气专业 的学 生而言,“ 电机学 ” 是 一 门很 重 要的专业基 础课程 。 很 多学 生在 学习过 程 中投入了大量 的时 间和精力, 想要学 好这 门课 程。 对 于任课教 师而言, 在教授 这门 课 程的过程 中, 也花费了很 多心思 , 力求在讲解变 压器、 种 电机 时, 使学 生掌握 其基本 结构 和用途 、 基本工作原理 、 基本 特性、 基 本分 析方 法。 在这个过程
中, 大量 的问题都涉及到 电磁 场基础部分 的理论 , 因此在教学过
电机学和电磁场

电机学和电磁场电机学和电磁场是电工学科中非常重要的两个方面,它们相互关联、相互作用,共同构成了电力系统中电动机的基础原理和运行机制。
本文将从电机学和电磁场的角度,分别介绍它们的基本概念和原理。
电机学是研究电动机的原理、结构和性能的学科。
电机是将电能转化为机械能的装置,是现代社会中不可或缺的能源转换设备。
电机学主要研究电动机的工作原理、电磁特性、转速控制和效率等方面的问题。
电动机的工作原理基于电磁感应现象。
当电流通过导线时,会产生一个磁场。
而当导线处于一个磁场中时,会受到一个力的作用。
利用这个原理,电动机通过电流和磁场的相互作用来实现能量转换。
电动机一般由定子和转子两部分组成。
定子是固定不动的部分,通常由导线绕成线圈。
转子则是可以转动的部分,通常由永磁体或电磁体组成。
电动机的运行过程中,电流通过定子线圈产生的磁场与转子磁场相互作用,产生一个力矩使转子转动。
这样,电能就转化为了机械能。
电动机的性能主要依赖于磁场的产生和控制。
通过改变电流的大小和方向,可以改变磁场的强度和方向,从而实现对电动机的控制。
电磁场是电动机运行的基础。
电磁场是由电荷和电流产生的物理现象,是空间中存在的一种力场。
电磁场包括电场和磁场两个部分。
电场是由电荷产生的,是描述电荷间相互作用的力场。
磁场是由电流产生的,是描述电流间相互作用的力场。
电磁场的强度和方向可以用矢量来表示,通过电场强度和磁感应强度来描述。
电磁场的产生和传播是通过麦克斯韦方程组来描述的。
麦克斯韦方程组是描述电磁场行为的基本方程,包括静电学和电磁学两部分。
静电学是研究静止电荷和电场的学科,主要研究库仑定律和电场的分布。
电磁学是研究电流和磁场的学科,主要研究安培定律和磁场的分布。
麦克斯韦方程组的推导和应用是电磁场研究的基础。
电机学和电磁场的研究对于电力系统的设计和运行具有重要意义。
在电力系统中,电动机是主要的电能转换装置,广泛应用于工业、交通、农业等领域。
电机学的研究可以帮助我们了解电动机的工作原理和性能,为电机的选型和控制提供依据。
电机内的电磁场

电机内的电磁场1.电机内的电磁场概述电机是一种将电能转换成机械能的装置,通常由定子和转子两部分构成。
在电机运行时,电流通过定子和转子中的导体,会产生磁场并相互作用,从而使转子旋转。
因此,电磁场在电机内起着至关重要的作用。
2.定子内的电磁场定子是电机的固定部分,通常由若干根绕在铁芯上的线圈组成。
当通电时,定子线圈内产生的电流会在铁芯周围产生磁场,随着电流方向的变化,磁场的方向也会随之变化。
这种随电流变化的磁场称为交变磁场。
定子线圈内的交变磁场与转子中的永磁体或电磁体相互作用,产生电磁力,将转子带动旋转,从而转化电能为机械能。
因此,定子内的电磁场是电机运行的基础。
3.转子内的电磁场转子是电机的旋转部分,通常由永磁体或电磁体组成。
当定子线圈通电时,产生的磁场会与转子内的永磁体或电磁体相互作用,产生电磁力,将转子带动旋转。
对于永磁体转子,由于永磁体固有的磁场方向不变,因此转子内的磁场是静态的。
而对于电磁体转子,由于电磁体内的电流随着转子的旋转而改变,转子内的磁场也因此随之变化。
4.磁场分布电机内的电磁场不仅受到定子和转子内部的因素影响,还受到外部环境的影响。
例如,当电机靠近其他有磁性的物体时,这些物体的磁场会干扰电机内部的磁场分布,从而影响电机的性能。
因此,在设计和使用电机时,需要考虑到外部环境对电磁场的影响,并采取相应的措施来减少干扰,保证电机的正常运行。
5.结论电机内的电磁场对电机的运行起着至关重要的作用,它们之间的相互作用决定了电机的性能和效率。
因此,了解电机内的电磁场分布规律以及外部环境对它们的影响,对于设计和使用电机都是十分重要的。
电磁场概论

电磁场是一种物理场,它由电荷和电流所产生的电场和磁场组成。
电场描述了电荷间
的相互作用,而磁场描述了电流所产生的效应。
电场是指存在于空间中的电荷周围的力场,可以用电场强度来描述。
电场强度指单位
电荷所受到的力。
在真空中,电场强度与电荷的距离成反比例关系。
电荷之间的相互
作用力可以通过库仑定律来计算,该定律表明,两个电荷之间的相互作用力与它们之
间的距离的平方成反比。
磁场是指存在于空间中的电流周围的力场,可以用磁感应强度来描述。
磁感应强度指
在磁场中,单位长度电流所受到的力。
磁感应强度的大小和方向与电流、距离和方向
有关。
在真空中,电流元产生的磁场可以通过安培环路定理来计算。
电磁场的行为可以通过麦克斯韦方程组来描述,这组方程是描述电磁现象的基本方程。
麦克斯韦方程组包括四个方程,分别描述了电场和磁场的产生、传播和相互作用的规律。
这些方程可以用来解释许多物理现象,例如电磁波、光、电磁感应等。
电磁场在许多领域都有广泛的应用,例如通讯、电力、电子技术、医学成像等。
对电
磁场的深入理解和掌握可以为这些领域的发展提供重要的支持和推动。
1第一篇--电机学基础理论

穿出(或进入)任一闭和 面的磁通量的代数和必 为零(或者说,进入任一 闭合面的磁通量恒等于
i
N匝
穿出该闭合面的磁通量
),这就是磁通连续性定 律。 哈尔滨理工大学
2
图1-7 磁路基尔霍夫第一定律
第一章 磁路和磁性材料
第二节 磁路的基本定律 公式:
Φ1 Φ2 Φ3
或
Φ =0
哈尔滨理工大学
第一章 磁路和磁性材料
第三节 磁性材料及其特性
顺磁材料 材料 反磁材料 铁磁材料
略>0 略<0 >>0
铁、镍、钴和其它合金等为铁磁材料。 电机和变压器的磁路通常都由铁磁材料制成。
哈尔滨理工大学
第一章 磁路和磁性材料
第三节 磁性材料及其特性
一、铁磁材料的磁化
公式:
H dl i
l k=1
k
式中,若电流正方向与闭合回路上磁场强度的方向之间符合右手螺旋关
系,电流
ik 取正值,否则 ik 取负值。
哈尔滨理工大学
第一章 磁路和磁性材料
第二节 磁路的基本定律
对于图1-5(a)所示的电流方向:
H dl i
1
i 2 i3
图 1-5 安培环路定理 (a)多组电流
B H= μ
度上的磁压降。
或
B H
反映了单位长度的磁路上所消耗的磁动势,又称作单位长
矢量,单位为安培/米(A/m)。
哈尔滨理工大学
第一章 磁路和磁性材料
第一节 磁场中的基本物理量和磁路的概念
二、磁路的概念
磁路:磁通所经过的路径。
图1-4 常见的两种磁路 (a)变压器磁路 (b)直流电机磁路
《电机学完整》课件

电机学的基本概念
1 磁场原理
探索磁场与电机运行之间 的基本原理和相互作用。
2 电磁感应
讲解电磁感应的理论,以 及在电机中的应用和重要 性。
3 电机构造
介绍电机的基本构造和要 素,以及它们对电机性能 的影响。
电机学的主要原理
1
法拉第定律
解释法拉第定律对电机运行和电流感应的重要作用。
2
楞次定律
阐述楞次定律对电机的运行和电流方向的影响。
3
电机磁场理论
讲解电机磁场的形成原理和对电机转动的作用。
电机类型及分类
交流电机
介绍交流电机的原理、方法和应用场景。
步进电机
解析步进电机的特点、驱动方式和应用范围。
异步电机
讲述异步电机的原理、构造和广泛应用领域。
电机的工作原理
电动机 发电机 变压器
将电能转化为机械能的装置。 将机械能转化为电能的装置。 通过电磁感应原理转换电压大小的装置。
电机的应用领域
工业自动化
电机在生产线上的运用,提高 生产效率和质量。
交通运输
电机在交通工具中的应用,驱 动车辆和运输设备。
可再生能源
电机在风力发电、太阳能发电 等领域的应用。
总结与展望
回顾电机学的主要内容,并展望电机学在未来的发展和应用前景。
《电机学完整》PPT课件
电机学完整的PPT课件,旨在分享电机学的基本概念、主要原理、类型及分类、 工作原理、应用领域、总结与展望等内容。
课程介绍
深入浅出
以易于理解的方式介绍电机 学的基本概念和原理。
实例演示
通过具体案例和实验演示, 展示电机在实际应用中的重 要性。
互动学习
通过互动问答和小组讨论, 增强学生对电机学的理解和 应用能力。
电气工程专业英语词汇

(coaxial) cable (同轴)电缆AC transmission system交流输电系统active filter 有源滤波器active load ( P Load )有功负载active loss 有功损耗active power 有功功率alternating current (AC) 交流电ammeter电流表amplitude modulation (AM) 调幅angle stability 功角稳定anode (cathode) 阳极(阴极) arc discharge 电弧放电arc suppression coil 消弧线圈arc-extinguishing chamber 灭弧室armature 电枢,(继电器的)衔铁asynchronous machine 异步电机automatic control 自动控制automatic meter reading ( AMR )自动抄表automatic oscillograph 自动录波仪autotransformer 自耦变压器binary 二进制blackout 断电、停电block diagram 框图boiler 锅炉breakdown (电)击穿Breaker 断路器brush 电刷brushless DC motor 无刷直流电机bus bar 母线Bus tie breaker 母联断路器(母联断路器,母联开关) calibrate 校准capacitor bank 电容器组conductor 导线converter (inverter) 换流器,整流器(逆变器) copper loss 铜损corona 电晕coupling capacitor 耦合电容current transformer CT 电流互感器damping 阻尼decimal 十进制dielectric 电介质,绝缘体dielectric constant 介质常数dielectric loss 介质损耗direct current (DC )直流电discharge 放电disconnector 隔离开关dispatcher 调度员distribution automation system 配电网自动化 (DA )系统distribution dispatch center 配电调度中心double-circuit lines on the same tower 双回同杆并架double-column transformer 双绕组变压器earth(ground) wire 接地线earthing switch 接地开关eddy current 涡流electric field 电场electrical circuit 电路electrical machine control 电机控制electrical machinery 电机electromagnetic field 电磁场excitation 励磁exciting winding 励磁绕组excitor 励磁器extra-high voltage (EHV) 超高压fast decoupled power-flow method 快速解耦潮流算法fault clearing time 故障切除时间feeder 馈电线FFT (fast Fourier transform) 快速傅立叶变换fixed series capacitor compensation 固定串联电容补偿flashover 闪络Flexible AC transmission system (FACTS) 灵活交流输电系统Fossil-fired power plant 火电厂frequency modulation (FM) 调频frequency-domain 频域fuse 保险丝,熔丝gas insulated substation ( GIS)气体绝缘变电站generator terminal 机端generator tripping 切机generator 发电机Graduation dissertation 毕业设计Graduation practice 毕业实习grounding capacitance voltage divider 对地电容分压器Grounding 接地harmonic 谐波Hexadecimal 十六进制high voltage shunt reactor 高压并联电抗器high voltage 高压high-voltage apparatus 高压电器high-voltage engineering 高电压工程hydro power station 水力发电站Hydro-generator 水轮发电机integrated circuit (IC) 集成电路IEC (international Electrotechnical Commission) 国际电工(技术)委员会IEE (Institution of Electrical Engineers) 电气工程师学会(英)IEEE (Institute of Electrical and Electronic Engineers)电气与电子工程师学会(美) impedance 阻抗impulse current 冲击电流independent pole operation 分相操作induction 感应inductive (capacitive) 电感的(电容的) installed capacity 装机容量instrument transformer 互感器insulation coordination 绝缘配合insulation 绝缘insulator 绝缘子inverter station 换流站iron core 铁芯iron loss 铁损ISO (international standardization organization) 国际标准化组织isolator 刀闸(隔离开关)kinetic(potential) energy 动(势)能LAN (local area network) 局域网leakage flux 漏磁通LED (light emitting diode) 发光二极管light(boiling)-water reactor 轻(沸)水反应堆lightning arrester 避雷器lightning overvoltage 雷电过电压load shedding 甩负荷loop system 环网系统loss of synchronization 失去同步low voltage 低压lower limit 下限machinery practice 金工实习magnetic field 磁场magnetizing current 励磁电流main and transfer busbar 单母线带旁路malfunction 失灵margin 裕度,边界metal oxide arrester ( MOA )金属氧化物避雷器middle voltage 中压motor 电动机nameplate 铭牌Negative sequence impedance 负序阻抗Neutral point 中性点no-load current 空载电流no-load loss 空载损耗nuclear power station 核电站numerical 数字的octal 八进制oil-filled power cable 充油电力电缆one machine - infinity bus system 单机无穷大系统operation amplifier 运算放大器operation mechanism 操动机构oscilloscope 示波器overhead line 架空线overvoltage 过电压partial discharge 局部放电passive device 无源器件peak-load 峰荷Permanent-magnet Synchronism Motor 永磁同步电机phase displacement (shift) 相移phase lead(lag) 相位超前(滞后) phase shifter 移相器phase-to-phase voltage 线电压positive sequence impedance 正序阻抗potential transformer PT 电压互感器power angle 功角power capacitor 电力电容power electronics 电力电子power factor 功率因数Power Generation Technology 发电技术power line carrier (PLC) 电力线载波(器) / 可编程逻辑控制器power grid 电网power plant 电厂Power System Planning 电力系统规划power transfer 能量输送power transformer 电力变压器power transmission system 输电系统prime mover 原动机productive practice 生产实习protective relaying( relaying protection ) 继电保护pumped storage power station 抽水蓄能电站radio interference 无线干扰rated 额定的ratio 变比reactance (impedance) 电抗(阻抗) reactive current 无功电流reactive load 无功负载reactive loss 无功损耗reactive power compensation 无功补偿reactive power 无功功率reactor 电抗器reclosing 重合闸recovery voltage 恢复电压rectifier 整流器reference value 参考值regulation 调节reinforced excitation 强行励磁relay 继电器reserve capacity 备用容量resistance 电阻resistor 电阻器right-of-way 线路走廊root mean square (rms) 均方根值rotor 转子routing testing 常规试验rpm (revolution per minute) 转/分series (shunt) compensation 串(并)联补偿shield wire 避雷线short-circuit ratio 短路比shunt capacitor 并联电容器shunt reactor 并联电抗器simulation analysis 仿真分析single (dual, ring) bus 单(双,环形)母线skin effect 集肤效应slip ring 滑环slope 斜率Static state 静态Static var( Voltage Ampere Reactive)compensation (SVC) 静止无功补偿Stator (rotor) 定(转)子Steam turbine 汽轮机steel-reinforced aluminum 钢芯铝绞线step up (down) transformer 升(降)压变压器substation 变电站sulphur hexafluoride breaker SF6 断路器supervisory control and data acquisition (SCADA) 监控与数据采集surface breakdown 表面击穿surge impedance 波阻抗swing 摇摆switch station 开关站synchronization 同步synchronous condenser 同步调相机tap 分接头taped transformer 多级变压器three phase fault 三相故障three-column transformer ( ThrClnTrans ) 三绕组变压器time-domain 时域time-of-use tariff 分时电价transfer function 传递函数transfer switching 倒闸操作transient stability 暂态稳定transmission line 传输线Trip circuit 跳闸电路trip coil 跳闸线圈turn (turn ratio) 匝(匝比,变比) two-port network 二端口网络ultra-high voltage (UHV) 特高压underground cable 地下电缆vacuum circuit breaker 真空断路器variable transformer 调压变压器voltage grade 电压等级voltage stability 电压稳定wave front(tail) 波头(尾) winding 绕组withstand test 耐压试验withstand voltage 耐受电压zero sequence current 零序电流zinc oxide 氧化锌(金属氧化物) 专业课程名称电磁场概论Introduction to Electro-Magnetic Field 电机控制技术Control Technique of Electrical Machinery 电机学Electrical Machinery (Theory ) 电力电子技术基础Fundamentals of Power Electronics Technology 电力电子课程设计Power electronics course design 电力经济Electric power system economics 电力通信系统及调度自动化Power System Communication and Dispatching Automatic 电力系统潮流计算机分析Computer Analysis of Power Flow 电力系统分析Electric power system analysis 电力系统继电保护Electric power system relaying protection电力系统稳态分析Steady-State Analysis of Power System电力系统远动技术electric power system remote protocol电力系统暂态分析Transient Analysis of Power System电力系统自动控制Electric power system automatic control电力系统自动装置原理The Principle of Electric Power System Automatic Equipment 电路原理Principles of electric circuits 电能质量控制electric power quality (PQ) control 电气工程基础Fundamentals of Electrical Engineering电子技术基础(模拟) (数字) fundamentals of electronic (analog) (digital)高电压工程High voltage engineering 计算机继电保护Microcomputer-Based Relaying Protection计算机通信与网络Computer Communication and Network可编程控制器原理及应用Principles of PLC (Programmable logic Controller) And Application 人工智能基础Fundamentals of Artificial Intelligence ( AI ) 数字信号处理Digital Signal Processing (DSP) 微机原理与接口Principle of Microcomputer and Interface 现代电力系统管理Modern Power System Management信号与系统Signal and System 专业外语Professional English 自动控制理论Automatic Control Theory。
电机学和电磁场

电机学和电磁场
电机学是研究电流、电场和磁场之间相互作用的学科。
它涉及到
电力的产生、传输和使用,以及电动机、变压器和发电机等电力设备
的原理和应用。
首先,电机学研究电流在导体中的流动。
电流是电子在导体中的
移动,通过电路的闭合回路传输电能。
电流的大小可以通过安培计进
行测量。
同时,电流在导体中会产生热量,这种现象就是电阻。
其次,电磁场是电机学的重要内容之一。
电场是由带电粒子产生的,它会影响周围空间中的其他电荷。
磁场则是由电流或磁体产生的,它对其他电流与磁体都会有相互作用力。
电磁场的强度可以通过电场
强度和磁感应强度进行测量。
电机学还研究电动机的原理和应用。
电动机是将电能转换为机械
能的装置。
常见的电动机有直流电动机和交流电动机。
其中,直流电
动机通过直流电流产生转矩,实现机械能的转换。
而交流电动机则利
用交变电流来产生转矩,实现机械能的转换。
另外,电机学也研究变压器和发电机的原理和应用。
变压器是用
于改变交流电压大小的装置。
发电机则是将机械能转换为电能的装置。
通过电磁感应原理,发电机能够将转动机械能转换为电能,并且实现
能量的传输与供应。
总而言之,电机学是研究电流、电场和磁场之间相互作用的学科。
它涉及到电力的产生、传输和使用,以及电动机、变压器和发电机等
电力设备的原理和应用。
对于电力系统的理解和发展具有重要意义。
2013_02电机学-概论 [兼容模式]
![2013_02电机学-概论 [兼容模式]](https://img.taocdn.com/s3/m/64fbe040767f5acfa1c7cdf9.png)
图0-16
Φ 21
N2
互感电动势
式中:M称为互感系数,其单位为H,且ψ21=Mi1。 磁链ψ21是线 圈1中的电流i1所产生。
概
互感系数的大小:
M= (
论
ψ 21
i1
=
N 2Φ 21 = N2 i1
N1i1 ) µ Sm Rm12 = N1 N 2 Λ m12 = N1 N 2 lm i1
结论: 1. 互感系数与两个线圈匝数N1和N2的乘积成正比,也与磁路 的磁导率µ成正比。 2. 若磁路为非铁磁材料构成,则M为常数。若为铁磁材料构 成,则M为变数,且随着饱和程度的增加而减少。 3. 同理: 当线圈2有交流电流 时,也会在线圈1中引起互感电 动势。eM1=-Mdi2/dt 。
概
论
能量守恒原理
VERSUS
功率平衡关系
发电机 输入的机械功率 = 输出的电功率 电动机 输入的电功率 = 输出的机械功率
概
论
§0-4 旋转电机中的电动势、转矩与能量转换
dΨ di eL = − = −L dt dt
即:自感电动势与线圈的自感和线圈内 的电流的变化率成正比。 式中:L成为自感系数,单位为H(亨利)。
图0-15 自感电动势
概
自感系数的大小:
论
⎛ Ni ⎞ N⎜ ⎟ Rm ⎠ ΨL ⎝ 2 2 µ SL = = N Λm = N L= i i lL
结论: 1.自感的大小与线圈匝数的平方成正比,与磁路的磁导 率μ亦成正比。 2.若磁路为非铁磁材料构成,μ为常数,故 L 为常数。 3.若磁路为铁磁材料构成,由于μfe>> μ0 ,并且其 值随铁磁材料的饱和而下降,因此铁心线圈的自感 比空心线圈的大很多,且随铁心饱和程度的增加而 减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁波波动方程
21
波动方程的电磁位方程
位对 Lorenz规范 电磁位波动方程
22
静电场
静电场:相对观察者静止且量值不 随时间变化的电荷所产生的电场。 本章任务:阐述静电荷与电场之间 的关系,在已知电荷或电位的情况 下求解电场的各种计算方法。
静电场知识结构框图
23
定义层
E 的散度
基本实验定律(库仑定律) 基本物理量(电场强度)E 基本方程
Matlab 绘制场图示例源码
ANSYS 示例 (1/4计算体)
知识结构与分析方法
《电磁场》知识结构综述 电磁场问题分析方法
12
Maxwell方程
课程知识 主线
13
静电场 (electrostatics)
令 Maxwell方程中 /t , J, H 和 B 为零,可得静电场基本方程 E 0 D D E
E 的旋度
电位()
边界条件
微分方程
分界面衔接条件 边值问题
求解层
数值法
唯一性定理
解析法
有限差分法
镜像法,电轴法
分离变量法
直接积分法
静电参数(电容及部分电容)
静电能量与力
应用层
静电场知识结构图
24
恒定磁场
导体中有恒定电流通过时,在导体内部和它周围 的媒质中 ,不仅有电场效应 ,同时还有的磁场效 应 ,简称 恒定磁场(Magnetostatic Field)。 恒定磁场和静电场是性质完全不同的两种场, 但在分析方法上却有许多共同之处。学习本章时, 注意类比方法的应用 恒定磁场的知识结构框图
17
矢量磁位及方程
定义矢量磁位如下: 根据亥姆霍茨定理,选择矢量磁位的散度: 则静磁场的矢量位方程为
18
时变电磁场(低频场)
低频场(slowly varying fields)– 位移电流可以忽略
Maxwell方程 简化为
19
时变电磁场(高频场)
高频场(fastvarying field) – 位 移电流不能忽略, 此时应采用完整的 Maxwell方程组。
3
课程简介
复习场论、相量等概念;
静电场基础(Electrostatics);
静磁场基础(Magnetostatics);
电磁场边值问题(Boundary Value Problems)
Maxwell方程(Maxwell’s Equations);
4
课程的作用与任务
作用:使学生认识基本电磁现象,掌握基本的分析方法, 培养学生的基本素质和专业素养。 任务:在大学物理电磁学的基础上,能对电气工程中的电 磁现象进行初步的定性分析,并部分了解定量分析的基本
7分析软件Fra bibliotek课程内容比较抽象,希望同学在充分理解 基本概念的基础上,利用工具软件模拟仿 真电磁场分布,使其直观和形象化。 推荐软件: Matlab or Mathematica ——各种矢量 的微积分运算,绘制场图等。 Ansys or Ansoft —— 基于有限元方法, 通用电磁场仿真软件。
8
Matlab 绘制场图示例
clear;clf; q=2e-6; k=9e9;a=1.5; b=-1.5; x=-6:0.6:6; y=x; [X,Y]=meshgrid(x,y); %设置坐标网点 rp=sqrt((X-a).^2+(Y-b).^2); rm=sqrt((X+a).^2+(Y+b).^2); V=q*k*(1./rp-1./rm); %计算电势 [Ex,Ey]=gradient(-V); %计算场强 AE=sqrt(Ex.^2+Ey.^2);Ex=Ex./AE;Ey=Ey./AE; %场强归一化,使箭头等长 cv=linspace(min(min(V)),max(max(V)),49); % 产生49个电位值 contourf(X,Y,V,cv,'k-') %用黑实线画填色等位线图 axis('square') %在Notebook中,此指令不用 title('\fontsize{18}偶极子的场'),hold on quiver(X,Y,Ex,Ey,0.7) %宗量0.7使场强箭头长短适中。 plot(a,b,'wo',a,b,'w+') %用白线画正电荷位置 plot(-a,-b,'wo',-a,-b,'w-') %用白线画负电荷位置 xlabel('\fontsize{18}x');ylabel('\fontsize{18}y'),hold off
14
静电场电位
定义电位函数 f如下:
在均匀媒质中,根据静电场散度方程,静 电场电位满足如下方程
15
静电场电位方程
泊松方程(Poisson equation)
若 = 0, 泊松方程简化为拉普拉斯方程 ( Laplace equation)
16
静磁场(magnetostatic )
稳恒电流产生静 磁场,令 Maxwell方程中 /t = 0,则
电磁场概论
内容提要
课程简介 电磁场应用
电磁场研究内容
“电磁场”(electromagnetic field)的研究内 容是电荷在静止或者运动状态的电磁作用。
研究内容分为三类:
静电场:静止电荷产生的电场; 静磁场:稳定运动电荷(直流)产生的磁场; 动态场:运动电荷(非直流)产生的电磁场。
25
基本实验定律 (安培力定律)
定义层
磁感应强度(B)(毕奥—沙伐尔定律) H 的旋度
基本方程
B 的散度
磁标位(J = 0)
分界面上衔接条件 边值问题
磁矢位(A)
求解层
数值法 有限差分法 有限元法 分离变量法 解析法 镜像法
磁 的 欧 姆 定 理
磁 的 基 尔 霍 夫 定 理
波 导
传 输 线 理 论
电路、高电压、电机、低频电子学等
射频与微波、光波电子学
电磁场课程难点?
电磁现象复杂性——理解相对困难; 非直观性——各种电磁现象一般只能间 接观察; 描述电磁场数学工具的复杂性——场论、 复变函数、线性代数、泛函等;
方法。
5
课程与其它课程的关系
质量、能量守恒 库仑定理与 高 斯定理 物质的本构关系 静电场 标 量 泊 松 方 程 电 的 欧 姆 定 理 电 的 基 尔 霍 夫 定 理 磁通连续原理或 磁的高斯定理 安培全电流定理 法拉弟电磁 感 应定理
麦克斯韦方程组 恒定磁场 矢 量 泊 松 方 程 时变场 天 线 谐 振 器
