2017-2018学年四川省外语学院重庆第二外国语学校高三数学上11月月考(理)试题(附答案)
四川外语学院重庆第二外国语学校2017-2018学年高二上期中考试数学(文)试题

重庆第二外国语学校高2019级第二学月质量检测文科数学试题(全卷共三大题 满分:150分 考试时间:120分钟)一.选择题(本大题共12小题,每小题5分,共60分)1.过点A (4,y ),B (2,-3)的直线的倾斜角为135°,则y 等于 ( )A .-5B .5C .1D .-12.圆222630x y x y +-++=的圆心坐标为( )A.(-1,2)B.(1,-3)C.(-2,4)D.(2,-4)3.命题“x R ∀∈,1()05x >”的否定是( ) A.x R ∃∈,1()05x < B.x R ∀∈,1()05x ≤ C.x R ∀∈,1()05x <D.x R ∃∈,1()05x ≤ 4.圆()1122=+-y x 和()4222=++y x 的位置关系是( )A.相离B.外切C.内切D.相交4.设a 、b 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )A. 由a α⊂,b α⊂,a ∥β, b ∥β⇒α∥βB.由a ∥b ,a α⊥⇒b α⊥C.由α∥β,a α⊂,b β⊂⇒a ∥bD.由αβ⊥,a ∥β⇒a α⊥5.下列说法错误的是( )A.若p ∧q 为假命题,则,p q 均为假命题B.命题“若20x x -=,则0x =”的逆否命题为:“若0x ≠,则20x x -≠”C.“0x =”是“20x x -=”的充分不必要条件D.命题“20x x m +-=没有实根,则0m ≤”是真命题6.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是( ) A .233π B .23π C .736π D .733π 7.“1m =”是“直线0x m y +=2与直线1x y =-垂直”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件8.某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值为( )A .52B .322C .22D .12 9.设直线过点(0,),a 其斜率为1,且与圆222x y +=相切,则a 的值为 ( )A .4±B .22±C .2±D .2±10. 已知圆的方程为22860x y x y +--=,设过圆内一点M (2,1)的最长弦、最短弦分别为AC 、BD ,则以点A 、B 、C 、D 为顶点的四边形ABCD 的面积为( )A .517B .1017C .2017D .301711.若直线220(,0)ax by a b +-=>始终平分圆224280x y x y +---=的周长,则 12a b+ 的最小值为 ( ) A .1 B .5 C .42 D .322+12.设点0(,1)M x ,若在圆22:1O x y +=上存在点N ,使得°45OMN ∠=,则0x 的取值范围是( )A .[]1,1-B .1122⎡⎤-⎢⎥⎣⎦,C .2,2⎡⎤-⎣⎦D . 22⎡⎤-⎢⎥⎣⎦,二.填空题(本大题共4个小题,每题5分,共20分)13.若长方体的各顶点都在一个球面上,过长方体同一个顶点的三条棱长分别为6,4,2,则这个球的表面积为_____________.14.如果一个水平放置的图形的斜二测直观图是一个底面为045,腰和上底均为2的等腰梯形,那么原平面图形的面积是 .15.无论m 取何值时,直线021)2()1(=--++-m y m x m 都经过一个定点P ,则此定点P到直线x -y +3=0的距离为______________.16.在平面直角坐标系xoy 中,已知O 22:4x y +=,若直线4y kx =+上总存在点P ,使得过点P 的O 的两条切线相互垂直,则实数k 的取值范围是___________.三.解答题(本大题共6个小题,共70分)17. (10分)如图,在三棱锥ABC P -中,ABC PC 底面⊥,BC AB ⊥,E D ,分别是PB AB ,的中点.(Ⅰ)求证:PAC DE 平面//;(Ⅱ)求证:PB AB ⊥.18.(12分)已知半径为5的圆的圆心在x 轴上,圆心的横坐标是整数,且与直线43290x y +-=相切.(Ⅰ) 求圆的方程;(Ⅱ) 设直线50ax y -+=与该圆相交于,A B 两点,求实数a 的取值范围.19.(12分)按要求求直线方程:(Ⅰ) 求经过直线033:,0232:21=--=-+y x l y x l 的交点并且平行于直线 032=-+y x 的直线方程;(Ⅱ) 过点(5,4)A --作一直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为5,求直线l 的方程.20.(12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥面ABCD ,E 为PD 的中点.(Ⅰ)证明://PB 平面AEC ;(Ⅱ)设1AP =,3AD =,三棱锥P ABD -的体积34V =,求A 到平面PBD 的距离.A CP B D E (第17题)21.(12分)已知圆C 经过点A (0,3)和B (3,2),且圆心C 在直线y x =上.(Ⅰ)求圆C 的方程;(Ⅱ)若直线2y x m =+被圆C 所截得的弦长为2,求实数m 的值.22.(12分)如图,三棱锥S ABC -,E ,F 分别在线段AB ,AC 上,//EF BC ,ABC ∆,SEF ∆均是等边三角形,且平面SEF ⊥平面ABC ,若4BC =,EF a =,O 为EF 的中点. (Ⅰ)当3a =时,求三棱锥S ABC -的体积; (Ⅱ)a 为何值时,BE ⊥平面SCO .参考答案20.解:(Ⅰ)设BD 与AC 的交点为O ,连接EO因为ABCD 为矩形,所以O 为BD 的中点,又因为E 为PD 的中点,所以EO//PBEO ⊂平面AEC ,PB ⊄平面AEC ,所以//PB 平面AEC(Ⅱ)113366ABD V S PA PA AB AD AB ∆=⋅⋅=⋅⋅= 由题设知34V =,可得32AB = 做AH PB ⊥交PB 于H由题设知BC PAB ⊥平面,所以BC AH ⊥,故AH PBC ⊥平面,又31313PA AB AH PB ⋅== 所以A 到平面PBC 的距离为31322.(1)解:平面SEF ⊥平面ABC ,O 为EF 的中点,且SE SF =,∴SO EF ⊥,∴SO ⊥平面ABC ,即34SO =,133S ABC ABC V S SO -∆=⋅=; (2)证明:平面SEF ⊥平面ABC ,O 为EF 的中点,且SE SF =,∴SO ⊥平面ABC ,故SO BE ⊥,要使BE ⊥平面SCO ,则需BE CO ⊥,延长CO 交AB 于D ,则CD AB ⊥,1124DE EO a ==,2AD =,∴124AE a =+, 即AE EF =,124a a +=,83a =,∴83a =时,BE ⊥平面SCO .。
四川省成都外国语学院2018届高三11月月考数学(文)试卷(含答案)

成都外国语学院2018届高三11月月考数学(文)试题本试卷满分150分,考试时间120 分钟。
注意事项:1.答题前,考生务必先认真核对条形码上的姓名,准考证号和座位号,无误后将本人姓名、准考证号和座位号填写在相应位置;2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号;3.答题时,必须使用黑色签字笔,将答案规范、整洁地书写在答题卡规定的位置上; 4.所有题目必须在答题卡上作答,在试题卷上答题无效; 5.考试结束后将答题卡交回,不得折叠、损毁答题卡。
第Ⅰ卷一、选择题(每小题5分,共60分)1.小思法说“浮躁成绩差”,他这句话的意思是:“不浮躁”是“成绩好”的( ).A 充分条件 .B 必要条件 .C 充分必要条件 .D 既非充分也非必要条件2.函数)1ln()(2+=x x f 的图象大致是 ( )3.右表是x 和y 之间的一组数据,则y 关于x 的线性回归方程的直线必过点( )().2,2A (). 1.5,0B ().1,2C (). 1.5,4D4.已知全集为R ,集合{}{}20.51,680x A x B x x x =≤=-+≤,R A C B =I 则 ( ).A (],0-∞ .B []2,4 .C [)()0,24,+∞U .D (][)0,24,+∞U5.为得sin 3cos3y x x =+的图像,可将3y x =的图像( ).A 向右平移4π个单位 .B 向左平移4π个单位 .C 向右平移12π个单位 .D 向左平移12π个单位DC BA6.已知函数()y f x =的图像是下列四个图像之一,且其导函数'()y f x =的图像如右图所示,则函数()y f x =的图像可能是( )7.已知命题:p x R ∀∈,23x x <;命题:q x R ∃∈,321x x =-,则下 列命题中为真命题的是( ).A p q ∧ .B p q ⌝∧ .C p q ∧⌝ .D p q ⌝∧⌝8.在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且有99%以上的把握认为这个结论是成立的,则下列说法中正确的是( )..A 100个吸烟者中至少有99人患有肺癌.B 1个人吸烟,那么这人有99%的概率患有肺癌 .C 在100个吸烟者中一定有患肺癌的人.D 在100个吸烟者中可能一个患肺癌的人也没有9.在ABC ∆中,222sin sin sin sin sin A B C B C ≤+-,则A 的取值范围是( ).A 0,6π⎛⎤ ⎥⎝⎦ .B ,6ππ⎡⎫⎪⎢⎣⎭ .C 0,3π⎛⎤ ⎥⎝⎦ .D ,3ππ⎡⎫⎪⎢⎣⎭10.设C 为复数集,12,z z C ∈,给岀下列四个命题:①12z z >是120z z ->的充要条件; ②12z z >是2212z z >充分不必要条件; ③2112z z z =⋅是21z z =必要不充分条件; ④12z z R +∈是1212z z z z +=+的充要条件. 其中真命题的个数是( ).A 1 .B 2 .C 3 .D 411.设P 是ABC ∆所在平面内的一点,若()2AB CB CA AB CP ⋅+=⋅u u u r u u u r u u u r u u u r u u u r ,且AP CP =u u u r u u u r.则点P 是ABC ∆的( ).A 外心 .B 内心 .C 重心 .D 垂心12.设函数()x f x xe =,则关于x 的方程()()()2110f x e e f x --+⋅+=⎡⎤⎣⎦的实根个数为( )B C D A.A 1 .B 2 .C 3 .D 4第II 卷二、填空题(每小题5分,共20分)13.设复2018201711i z i i +⎛⎫=+ ⎪-⎝⎭,则z 的虚部是14.函数())lnf x x =的定义域为___________15.已知O 是锐角ABC ∆的外接圆圆心,0cos cos 60,2,sin sin B C A AB AC mAO C B∠=⋅+⋅=u u u r u u u r u u u r 则实数m 的值为16.若[],1x a a ∀∈+,有2x a x +≥成立,则实数a 的取值范围是三、解答题17.(10分)已知函数)32(log )(221+-=ax x x f(1)若()f x 的值域为R ,求实数a 的取值范围;(2)若()f x 在]1,(-∞内为增函数,求实数a 的取值范围18.(12分) 某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,:(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:22()()()()()n ad bc K a b c d a c b d -=++++参考数据:19.(12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足sin cos c A a C =. (1)求角C 的大小;(2)求cos()4u A B π=-+的取值范围.20.(12分)设数列{}n x 满足: 112x =,且111122n n n x x ++=+.(1)求数列{}n x 的通项公式; (2)求数列{}n x 的前n 项和n S .21.(12分)如图,四棱锥P ABCD -中,PAD △为正三角形,AB CD ∥,2AB CD =,090BAD ∠=,PA CD ⊥,E 为棱PB 的中点.(1)求证:平面PAB ⊥平面CDE ; (2)若直线PC 与平面PAD 所成角为045, 且2CD =求四棱锥E ABCD -的体积.22.(12分)已知函数()()ln xe f x a x x x=+-,e 为自然对数的底数. (1)当0a >时,试求()f x 的单调区间; (2)若函数()f x 在1,22x ⎛⎫∈ ⎪⎝⎭上有三个不同的极值点,求实数a 的取值范围.PE DCA成都外国语学校2018届高三11月月考数学(文史类)答案一、选择题B A DCD ; B B D C A ; A C .二、填空题13.1-;14. 2⎡-⎢⎣⎭;; 16.3,4⎛⎤-∞- ⎥⎝⎦. 三、解答题17. 解:令223u x ax =-+,12log y u =.(1)()f x 的值域为R 223u x ax ⇔=-+能取()0,+∞的一切值()0,u ⇔+∞⊆的值域,()24120,a a a ∴∆=-≥⇔∈-∞+∞U 。
重庆市四川外国语大学附属外国语学校2025届高三上学期11月月考数学试题

重庆市四川外国语大学附属外国语学校2025届高三上学期11月月考数学试题一、单选题1.已知集合{}2,1,0,1,2A =--,(){}211B x x =+≤,则A B = ()A .{}2,1--B .{}2,1,0--C .[]2,0-D .[]22-,2.“22ac bc >”,是“a b >”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.若2b a = ,=- c a b ,且c a ⊥ ,则a 与b的夹角为()A .π6B .π3C .2π3D .5π64.已知ππ(0,),(0,)22αβ∈∈,则下列不等关系中不恒成立的是()A .()sin sin sin αβαβ+<+B .()sin cos cos αβαβ+<+C .()cos sin sin αβαβ+<+D .()cos cos cos αβαβ+<+5.已知23a=,ln 3b =,4πc =,则a ,b ,c 的大小关系为()A .a b c>>B .b a c>>C .a c b>>D .c b a>>6.已知θ为第一象限角,且πtan tan 03θθ⎛⎫++= ⎪⎝⎭,则1cos21cos2θθ-=+()A .9B .3C .13D .197.已知函数()(),R f x f x x =-∈,()5.51f =,函数()()()1g x x f x =-⋅,若()1g x +为偶函数,则()0.5g -的值为()A .3B .2.5C .2D .1.58.武汉外校国庆节放7天假(10月1日至10月7日),马老师、张老师、姚老师被安排到校值班,每人至少值班两天,每天安排一人值班,同一人不连续值两天班,则不同的值班方法共有()种A .114B .120C .126D .132二、多选题9.下列关于概率统计的知识,其中说法正确的是()A .数据1-,0,2,4,5,6,8,9的第25百分位数是1B .已知随机变量(),X B n p ,若()40E X =,()30D X =,则160n =C .若一组样本数据(),i i x y (1i =,2,…,n )的对应样本点都在直线132y x =-+上,则这组样本数据的相关系数为12-D .若事件M ,N 的概率满足()()0,1P M ∈,()()0,1P N ∈且()()1P N M P N +=,则M 与N 相互独立10.已知函数()22sin cos 0)222x x xf x ωωωω=->在[)0,π上有且仅有4个零点,则()A .1114,33ω⎛⎤∈ ⎥⎝⎦B .令()π6g x f x ⎛⎫=+ ⎪⎝⎭,存在ω,使得()g x '为偶函数C .函数()f x 在()0,π上可能有3个或4个极值点D .函数()f x 在ππ,3535⎛⎫- ⎪⎝⎭上单调递增11.设函数32()231f x x ax =-+,则()A .当0a =时,直线1y =是曲线()y f x =的切线B .若()f x 有三个不同的零点123,,x x x ,则12312x x x ⋅=-⋅C .存在,a b ,使得x b =为曲线()y f x =的对称轴D .当02ax ≠时,()f x 在0x x =处的切线与函数()y f x =的图象有且仅有两个交点三、填空题12.()62112x x x ⎛⎫++⎪⎝⎭的展开式中的常数项为.(用数字作答)13.已知函数()|ln|2||f x x m =+-,m 为正的常数,则()f x 的零点之和为.14.掷一个质地均匀的骰子,向上的点数不小于3得2分,向上的点数小于3得1分,反复掷这个骰子,(1)恰好得3分的概率为;(2)恰好得n 分的概率为.(用与n 有关的式子作答)四、解答题15.已知ABC ∆的面积为3,且满足0AB AC ≤⋅≤ 设AB和AC 的夹角为θ,(1)求θ的取值范围;(2)求函数()2πcos sin 3f θθθθ⎛⎫=⋅+-+ ⎪⎝⎭的值域.16.已知数列{}n a 的前n 项和n S 满足31nn S n =+-.(1)求{}n a 的通项公式;(2)若()()211n n b n a =+-,求数列{}n b 的前n 项和n T .17.已知椭圆()222210,0:x y a b a C b+=>>的离心率为2,其左,右焦点分别为1F ,2F ,点P是坐标平面内一点,且OP = 1234PF PF ⋅=,其中O 为坐标原点.(1)求椭圆C 的方程;(2)过点10,3S ⎛⎫- ⎪⎝⎭,且斜率为k 的动直线l 交椭圆于A ,B 两点,求弦AB 的垂直平分线在x 轴上截距的最大值.18.驾驶员考试(机动车驾驶员考试)是由公安局车管所举办的资格考试,只有通过驾驶员考试才能取得驾照,才能合法的驾驶机动车辆.考试内容和合格标准全国统一,根据不同准驾车型规定相应的考试项目.机动车驾驶人考试内容分为道路交通安全法律、法规和相关知识考武科目(以下简称“科目一”)、场地驾驶技能考试科目(以下简称“科目二”)、道路驾驶技能和安全文明驾驶常识考试科目(以下简称“科目三”).申请人科目一、科目二、科目三考试均合格后,就可以领取驾驶证.某驾校经统计,驾驶员科目一考试平均通过的概率为1516,科目二:平均通过的概率为45,科目三平均通过的概率为45.该驾校王教练手下有4名学员参加驾驶员考试.(1)记这4名学员参加驾驶员考试,通过考试并领取驾驶证的人数为X ,求X 的分布列和数学期望及方差;(2)根据调查发现,学员在学完固定的学时后,每增加一天学习,没有通过考试拿到驾驶证的概率会降为原来的0.4,请问这4名学员至少要增加多少天的学习,才能保证这4名学员都能通过考试并领取驾驶证?(我们把概率超过0.99的事件称为必然事件,认为在一次试验中必然事件一定会发生)0.9975≈,lg 20.3010≈19.已知函数()2ln 2x f x x ax =+-.(1)当1a =时,求曲线()y f x =在点()()1,1f 处的切线方程;(2)已知()f x 有两个极值点.(ⅰ)求a 的取值范围;(ⅱ)若()f x 的极小值小于ln23-,求()f x 的极大值的取值范围.。
四川外语学院重庆第二外国语学校2017-2018学年高二上

重庆第二外国语学校高2019级第二学月质量检测文科数学试题(全卷共三大题 满分:150分 考试时间:120分钟)一.选择题(本大题共12小题,每小题5分,共60分)1.过点A (4,y ),B (2,-3)的直线的倾斜角为135°,则y 等于 ( ) A .-5 B .5 C .1 D .-12.圆222630x y x y +-++=的圆心坐标为( )A.(-1,2)B.(1,-3)C.(-2,4)D.(2,-4)3.命题“x R ∀∈,1()05x>”的否定是( )A.x R ∃∈,1()05x <B.x R ∀∈,1()05x≤C.x R ∀∈,1()05x <D.x R ∃∈,1()05x≤4.圆()1122=+-y x 和()4222=++y x 的位置关系是( ) A.相离 B.外切 C.内切 D.相交4.设a 、b 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( ) A. 由a α⊂,b α⊂,a ∥β, b ∥β⇒α∥β B.由a ∥b ,a α⊥⇒b α⊥ C.由α∥β,a α⊂,b β⊂⇒a ∥b D.由αβ⊥,a ∥β⇒a α⊥5.下列说法错误的是( )A.若p ∧q 为假命题,则,p q 均为假命题B.命题“若20x x -=,则0x =”的逆否命题为:“若0x ≠,则20x x -≠”C.“0x =”是“20x x -=”的充分不必要条件D.命题“20x x m +-=没有实根,则0m ≤”是真命题6.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是( )A .233πB .23πC .736πD .733π7.“1m =”是“直线0x m y +=2与直线1x y =-垂直”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件8.某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值为( )A .2 B .2 C .2D .129.设直线过点(0,),a 其斜率为1,且与圆222x y +=相切,则a 的值为 ( )A .4±B .±C .2±D .10. 已知圆的方程为22860x y x y +--=,设过圆内一点M (2,1)的最长弦、最短弦分别为AC 、BD ,则以点A 、B 、C 、D 为顶点的四边形ABCD 的面积为( )A ....11.若直线220(,0)ax by a b +-=>始终平分圆224280x y x y +---=的周长,则12a b+ 的最小值为 ( )A .1B .5C ..3+ 12.设点0(,1)M x ,若在圆22:1O x y +=上存在点N ,使得°45OMN ∠=,则0x 的取值范围是( )A .[]1,1-B .1122⎡⎤-⎢⎥⎣⎦,C .⎡⎣D . ⎡⎢⎣⎦二.填空题(本大题共4个小题,每题5分,共20分)13.若长方体的各顶点都在一个球面上,过长方体同一个顶点的三条棱长分别为6,4,2,则这个球的表面积为_____________. 14.如果一个水平放置的图形的斜二测直观图是一个底面为045,腰和上底均为2的等腰梯形,那么原平面图形的面积是 .15.无论m 取何值时,直线021)2()1(=--++-m y m x m 都经过一个定点P ,则此定点P到直线x -y +3=0的距离为______________.16.在平面直角坐标系xoy 中,已知 O 22:4x y +=,若直线4y kx =+上总存在点P ,使得过点P 的 O 的两条切线相互垂直,则实数k 的取值范围是___________.三.解答题(本大题共6个小题,共70分)17. (10分)如图,在三棱锥ABC P -中,ABC PC 底面⊥,BC AB ⊥,E D ,分别是PB AB ,的中点.(Ⅰ)求证:PAC DE 平面//; (Ⅱ)求证:PB AB ⊥.18.(12分)已知半径为5的圆的圆心在x 轴上,圆心的横坐标是整数,且与直线43290x y +-=相切.(Ⅰ) 求圆的方程;(Ⅱ) 设直线50ax y -+=与该圆相交于,A B 两点,求实数a 的取值范围.19.(12分)按要求求直线方程:(Ⅰ) 求经过直线033:,0232:21=--=-+y x l y x l 的交点并且平行于直线032=-+y x 的直线方程;(Ⅱ) 过点(5,4)A --作一直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为5,求直线l 的方程.20.(12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥面ABCD ,E 为PD 的中点. (Ⅰ)证明://PB 平面AEC ;(Ⅱ)设1AP =,AD 三棱锥P ABD -的体积4V =,求A 到平面PBD 的距离.ACPBDE(第17题)21.(12分)已知圆C 经过点A (0,3)和B (3,2),且圆心C 在直线y x =上.(Ⅰ)求圆C 的方程;(Ⅱ)若直线2y x m =+被圆C 所截得的弦长为2,求实数m 的值.22.(12分)如图,三棱锥S ABC -,E ,F 分别在线段AB ,AC 上,//EF BC ,ABC ∆,SEF ∆均是等边三角形,且平面SEF ⊥平面ABC ,若4BC =,EF a =,O 为EF 的中点.(Ⅰ)当a =S ABC -的体积; (Ⅱ)a 为何值时,BE ⊥平面SCO .参考答案 20.解:(Ⅰ)设BD 与AC 的交点为O ,连接EO因为ABCD 为矩形,所以O 为BD 的中点,又因为E 为PD 的中点,所以EO//PBEO ⊂平面AEC ,PB ⊄平面AEC ,所以//PB 平面AEC(Ⅱ)11366ABD V S PA PA AB AD AB ∆=⋅⋅=⋅⋅=由题设知4V =,可得32AB =做AH PB ⊥交PB 于H由题设知BC PAB ⊥平面,所以BC AH ⊥,故AH PBC ⊥平面,又PA AB AH PB ⋅==所以A 到平面PBC22.(1)解:平面SEF ⊥平面ABC ,O 为EF 的中点,且SE SF =,∴SO EF ⊥,∴SO ⊥平面ABC ,即34SO =,13S ABC ABC V S SO -∆=⋅= (2)证明:平面SEF ⊥平面ABC ,O 为EF 的中点,且SE SF =,∴SO ⊥平面ABC ,故SO BE ⊥,要使BE ⊥平面SCO ,则需BE CO ⊥,延长CO 交AB 于D ,则CD AB ⊥,1124DE EO a ==,2AD =,∴124AE a =+,即AE EF =,124a a +=,83a =,∴83a =时,BE ⊥平面SCO .。
四川外语学院重庆第二外国语学校2018届高三上学期第7周周周清数学理试题

四川外语学院重庆第二外国语学校高2018学部2018---2018学年度上期(第7周)数学周周清(理)一、解答题(本小题共5小题,共58分)1.已知等比数列{}n a 的各项均为正数,且212326231,9a a a a a +==.(1)求数列{}n a 的通项公式.(2)设31323log log log n n b a a a =+++,求数列1{}nb 的前n 项和.2. 已知函数()cos (0)f x wx wx w =->的图像与直线2y =的相邻两个交点之间的距离为π.(1)求函数()f x 的单调递增区间;(2)设△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,若()f A =2,a =,求角B 的大小.3.在直角坐标系xoy 中,直线C 1:2x =-,圆C 2: 22(1)(2)1x y -+-=,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.(1)求C 1,C 2的极坐标方程;(2)若直线C 3的极坐标方程为θ=4π(R ρ∈),设C 2与C 3的交点为M ,N ,求△C 2MN 的面积.4.端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.(1)求三种粽子各取到1个的概率;(2)设X 表示取到的豆沙粽个数,求X 的分布列与数学期望.5. 平面直角坐标系xOy 中,已知椭圆C :22221x y a b +=(0a b >>)的离心率为2,左、右焦点分别是12,F F 以1F 为圆心以3为半径的圆与以2F 为圆心以1为半径的圆相交,且交点在椭圆C 上.(1)求椭圆C 的方程.(2)设椭圆E :2222144x y a b+=,P 为椭圆C 上任意一点.过点P 的直线y kx m =+交椭圆E 于,A B 两点,射线PO 交椭圆E 于点Q .OQ OP 的值;(ii)求△ABQ面积的最大值.(i)求。
四川外语学院重庆第二外国语学校高三数学上学期周测试题(8)文(无答案)

四川外语学院重庆第二外国语学校2017届高三数学上学期周测试题(8)文(无答案)时间:40分钟 总分:70分 班级__________ 姓名___________ 成绩__________1、(本小题满分12分)某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x ,y .奖励规则如下:①若3xy ≤,则奖励玩具一个;②若8xy ≥,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动(I )求小亮获得玩具的概率;(II )请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.2、(本小题满分12分)设2()π)sin (sin cos )f x x x x x =--- .(I )求()f x 得单调递增区间;(II )把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象,求π()6g 的值.3、在如图所示的几何体中,D 是AC 的中点,EF ∥DB .(I )已知AB =BC ,AE =EC .求证:AC ⊥FB ;(II )已知G ,H 分别是EC 和FB 的中点.求证:GH ∥平面ABC4、已知数列{}n a 的前n 项和238n S n n =+,{}n b 是等差数列,且1n n n a b b +=+. (I )求数列{}n b 的通项公式;(II )令1(1)(2)n n n nn a c b ++=+.求数列{}n c 的前n 项和n T .5、(本小题满分12分)设2()ln (21)f x x x ax a x =-+-,a R ∈(Ⅰ)令()()g x f x =',求()g x 的单调区间;(Ⅱ)已知()f x 在1x =处取得极大值,求实数a 的取值范围6、(本小题满分12分)已知椭圆:C 22221x y a b+=(0a b >>)的长轴长为4,焦距为(I )求椭圆C 的方程;(II )过动点M (0,m )(0m >)的直线交x 轴于点N ,交C 于点A ,P (P 在第一象限),且M 是线段PN 的中点.过点P 作x 轴的垂线交C 于另一点Q ,延长QM 交C 于点B(i)设直线PM 、QM 的斜率分别为k 、k ',证明k k '为定值 (ii)求直线AB 的斜率的最小值。
重庆市第二外国语学校2017届高三第二次检测数学试题(文)含答案
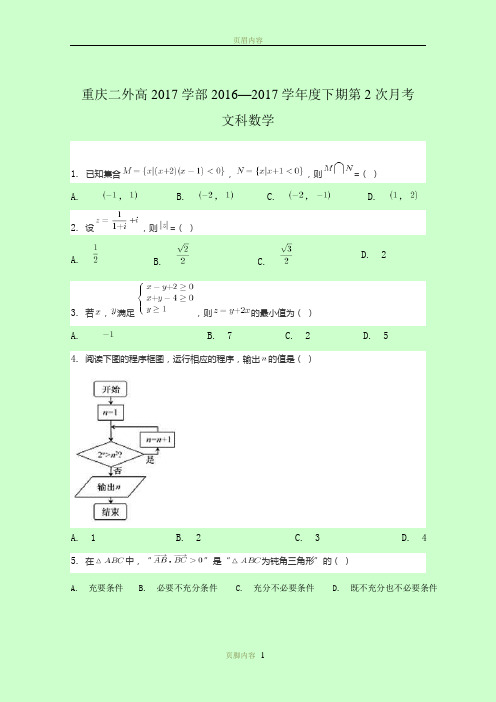
重庆二外高2017学部2016—2017学年度下期第2次月考文科数学1.已知集合,,则=()A. ,B. ,C. ,D. ,2.设,则=()D. 2A. B. C.3.若,满足,则的最小值为()A. B. 7 C. 2 D. 54.阅读下图的程序框图,运行相应的程序,输出的值是()A. 1B. 2C. 3D. 45.在中,“”是“为钝角三角形”的()A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件7.定义在上的函数,则满足的取值范围是()A. ,B. ,C. ,D. ,8.设,,为的三个内角A,B,C的对边,,若,且,则角A,B的大小分别为()A. B. C. D.9.在中,是边上一点,且,,则()A. B. C. D.10.给出下列三个命题:①函数的单调增区间是,②经过任意两点的直线,都可以用方程来表示;③命题:“,”的否定是“,”,其中正确命题的个数有()个A. 0B. 1C. 2D. 311.设m,,若直线与圆相切,则m+n 的取值范围是()A. B.C. ,D.12.已知函数(,e为自然对数的底数)与的图象上存在关于直线y=x对称的点,则实数a取值范围是()A. B. C. D.13.已知数列是公差不为零的等差数列,,且成等比数列,则数列的通项公式为___________14. 已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为___________15.学校艺术节对同一类的,,,四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是或作品获得一等奖”;乙说:“作品获得一等奖”;丙说:“,两项作品未获得一等奖”;丁说:“是作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是.16.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的面积为___________17.已知函数(Ⅰ)求的最大值;(Ⅱ)求的最小正周期与单调递增区间18.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:质量指标值分组频数 6 26 38 22 8(1)在坐标系中作出这些数据的频率分布直方图(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表)(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?19.如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.(Ⅰ)求证:BD⊥平面ACC1A1;(Ⅱ)求证:直线AB1∥平面BC1D;(Ⅲ)设M为线段BC1上任意一点,在△BC1D内的平面区域(包括边界)是否存在点E,使CE⊥DM,并说明理由.20.已知中心在坐标原点,焦点在x轴上的椭圆过点,且它的离心率(I)求椭圆的标准方程;(II)与圆相切的直线交椭圆于MN两点,若椭圆上一点C满足,求实数的取值范围21.已知函数(1)讨论的单调性并求最大值;(2)设,若恒成立,求实数a的取值范围22.选修4—4:坐标系与参数方程.在平面直角坐标系xOy中,直线L的参数方程是(t为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为,且直线与曲线C交于P,Q两点(1)求曲线C的普通方程及直线L恒过的定点A的坐标;(2)在(1)的条件下,若,求直线L的普通方程23.选修4-5:不等式选讲.函数(Ⅰ)若a=-2求不等式的解集(Ⅱ)若不等式的解集非空,求a的取值范围参考答案1.C2. B3.D4.B5.C6.C7.D8.C9.A 10.B 11.D 12.A13. 14. 15.B 16.17.解:(Ⅰ)因为,最大值为2;(Ⅱ)最小正周期为令,解之得.单调递增区间为.18.解:(1)频率分布直方图如图所示:(2)质量指标的样本平均数为=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,质量指标的样本的方差为S2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104,这种产品质量指标的平均数的估计值为100,方差的估计值为104;(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68,由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定19.(Ⅰ)证明:∵三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,∴CC1⊥BC,CC1⊥AC,∴CC1⊥底面ABC,∵BD⊂底面ABC,∴CC1⊥BD,又底面为等边三角形,D为线段AC的中点.∴BD⊥AC,又AC∩CC1=C,∴BD⊥平面ACC1A1;(Ⅱ)证明:连接B1C交BC1于O,连接OD,如图则O为B1C的中点,∵D是AC的中点,∴AB1∥OD,又OD⊂平面BC1D,OD⊄平面BC1D∴直线AB1∥平面BC1D;(Ⅲ)在△BC1D内的平面区域(包括边界)存在点E,使CE⊥DM,此时E在线段C1D上;证明如下:过C作CE⊥C1D交线段C1D与E,由(Ⅰ)可知BD⊥平面ACC1A1,而CE⊂平面ACC1A1,所以BD⊥CE,由CE⊥C1D,BD∩C1D=D,所以CE⊥平面BC1D,DM⊂平面BC1D,所以CE⊥DM.20. 解:(Ⅰ)设椭圆的标准方程为,由已知得:,解得,所以椭圆的标准方程为:.(Ⅱ)因为直线l:y=kx+t与圆(x-1)2+y2=1相切,所以,2k=,t≠0,把y=kx+t代入,并整理得:(3+4k2)x2+8ktx+4t2-24=0,设M(x1,y1),N(x2,y2),则有,y1+y2=kx1+t+kx2+t=k(x1+x2)+2t=,因为=(x1+x2,y1+y2),所以C(,),又因为点C在椭圆上,所以,,因为t2>0,所以,所以0<λ2<2,所以λ的取值范围为(-,0)∪(0,).21.解:(1)由题设有x>0,,可知f(x)在(0,1)单调递增,在单调递减;f(x)的最大值为;(2)由题有,令,则,设,则,当x>0时,可知为增函数,且,当,即时,当x>0时,,则单调递增,,则h(x)单调递增,则h(x)>h(0)=0,即恒成立,故;当2a>2,即a>1时,则唯一存在t>0,使得,则当,,则h'(x)单调递减,h'(x)<h'(0)=0,则h(x)单调递减,则h(x)<h(0)=0,则,不能在上恒成立,综上:实数a的取值范围是.22.解:(1)由、及已知得:;由直线的参数方程知直线的直角坐标方程为:,所以直线恒过定点A(2,0);(2)将直线l的方程代入曲线C的方程得:,由t的几何意义知:,,因为点A在椭圆内,这个方程必有两个实根,所以,则,所以,因为,所以,,则,由此直线的方程为或.23.解:(Ⅰ)当a=-2时,f(x)=|x+2|,f(x)+f(2x)=|x+2|+|2x+2|>2,不等式可化为或或,解得;(Ⅱ),当时,f(x)=a-x+a-2x=2a-3x,则;当时,f(x)=x-a+a-2x=-x,则;当时,f(x)=x-a+2x-a=3x-2a,则,所以函数f(x)的值域为,因为不等式的解集非空,即为,解得a>-1,由于a<0,则a的取值范围为(-1,0).。
四川省外语学院重庆第二外国语学校2018届高三数学11月月考试题理

四川省外语学院重庆第二外国语学校2018届高三数学11月月考试题理(考试时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.已知集合{}022>-=x x x A ,}55|{<<-=x x B ,则( )A. B.A∪B=R C.B ⊆A D.A ⊆B2.421dx x ⎰=( )A 、2ln2-B 、2ln 2C 、ln 2-D 、ln 23.已知tan 2α=-,()1tan 7αβ+=,则tan β的值为( )A .3B .35 C .3- D .35- 4.设向量()()3,2,2,1==,若向量+λ与向量()7,4--=共线,则=λ( )A .2B .1013 C .2- D .1013- 5.已知,,,a b c d 为实数,且c d >,则“a b >”是“a c b d ->-”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C .充要条件 D. 既不充分也不必要条件 6.《莱因德纸草书》(Rhind papyrus )是世界上最古老的数学著作之一.该书中有一道这样的题目:100个面包分给5个人,每人一份,若按照每个人分得的面包个数从少到多排列,可得到一个等差数列,其中较多的三份和的31等于较少的两份和,则最多的一份面包个数为( )A .35 B. 32 C .30 D. 277.设变量x y ,满足约束条件:⎪⎩⎪⎨⎧-≥≤+≥222x y x x y ,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8- 8.已知偶.函数)(x f 在),0[+∞单调递减,且0)2(=-f ,若0)2(>-x f ,则x 的取值范围是( )A.)2,2(-B.),2()2,(+∞--∞C.)4,0(D. ),4()0,(+∞-∞9.已知)23,3(+=k k ,)3,2(-=k ,若a 与b 的夹角为钝角,则k 的取值范围是( )A .),2()21,(+∞--∞B .)2,0()0,21( -C .)2,21(- D .),2()0,(+∞-∞10.若b a ,是函数q px x x f +-=2)()0,0(>>q p 的两个不同的零点,且,,2a b -这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q +的值等于( ) A .6 B .7 C .8 D .911.三数124log ,82log ,232716的大小关系正确的是( )(A )124log 82log 232716<< (B )82log 124log 231627<< (C )82log 23124log 1627<< (D )2382log 124log 1627<<12.设函数)()(x x ae x e x f -=(其中e 为自然对数的底数)恰有两个极值点()1212,x x x x <,则下列说法不正确的是( ) A .102a <<B .110x -<<C .()1102f x -<< D .()()120f x f x +>二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.已知复数z 满足()12i z i +=-(i 为虚数单位),则z i +=14. 已知向量,22,21=+==a ,则向量b 在向量a 方向上的投影是15.在数列}{n a 中,2,121==a a ,且)( )1(12*+∈-+=-N n a a n n n ,则100S =16.已知函数x x x f ωωcos sin )(+=)0(>ω,R x ∈,若函数)(x f 在区间),(ωω-内单调递增,且函数)(x f 的图象关于直线x ω=对称,则ω的值为三、解答题(本大题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤)17.(12分)已知正项数列{}n a 的前n 项和为n S ,且n S ,n a ,2成等差数列. (1)求n a ;(2)令n n na b =,求数列}{n b 的前n 项和n T .18.(12分)某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数()f x 的解析式; (2)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图象,若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.19.(12分)已知ABC ∆的三个内角C B A ,,所对的边分别为c b a ,,,且bac A -=-2c o s Bc o s C2c o s . (1)求sin sin CA的值; (2)若41cos =B ,2=b ,求ABC ∆的面积S . 20.(12分)已知动圆过定点A (4,0),且在y 轴上截得的弦MN 的长为8. (1)求动圆圆心的轨迹C 的方程; (2)已知点)0,1(-B ,设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P 、Q ,若x 轴是PBQ ∠的角平分线,证明直线l 过定点.21.(12分)已知函数kx x x x g --=2ln 2)()(R k ∈. (1)当0=k 时,求)(x g 的单调区间;(2)设21,x x )0(21x x <<是函数)(x g 的两个零点,m 是21,x x 的等差中项,求证:0)(<'m g .请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分. 22.(10分)选修4-4坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos sin x y αα=⎧⎨=⎩(α为参数),以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线2C :22)4cos(-=-πθρ,3:2sin .C ρθ=(1)求曲线1C 与2C 的交点M 在直角坐标系xOy 中的坐标; (2)设点B A ,分别为曲线23,C C 上的动点,求AB 的最小值. 23.(10分)选修4-5不等式选讲 已知函数()1f x x =-.(1)解不等式()(4)8f x f x ++≥;(2)若1a <,1b <,且0a ≠,求证:)()(ab f a ab f >.参考答案1-12:BDAAB CDCBD CD13、22 14、1- 15、2600 16、2π 17、解:(1)由题意知22+=n n S a ,当n=1时,得21=a22+=n n S a ,2211+=++n n S a ,俩式相减得n n a a 21=+,即数列{}n a 是以2为首项,2为公比的等比数列。
四川外语学院重庆第二外国语学校高三数学上学期周测试

四川外语学院重庆第二外国语学校2017届高三数学上学期周测试题(1)文(无答案)时间:40分钟 总分:80分 班级__________ 姓名_____________ 成绩_____________一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,3,5,7}A = ,{|25}B x x =≤≤,则A B =( )(A ) {1,3} (B ) {3,5} (C ) {5,7} (D ) {1,7}(2)设(12)()i a i ++的实部与虚部相等,其中a 为实数,则a =( )(A ) -3 (B ) -2 (C ) 2 (D ) 3(3)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )(A )13 (B ) 12 (C ) 23 (D ) 56(4)ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,若a =,2c =,2cos 3A =,则b =( )(A )(B ) (C ) 2 (D ) 3(5)直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( ) (A )13 (B ) 12 (C ) 23 (D ) 34(6)若将函数2sin(2)6y x π=+的图像向右平移14个周期后,所得图像对应的函数为( ) (A )2sin(2)4y x π=+ (B )2sin(2)3y x π=+ (C )2sin(2)4y x π=- (D )2sin(2)3y x π=-(7)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直 的半径.若该几何体的体积是28π3,则它的表面积是 (A )17π (B )18π (C )20π (D )28π(8)若0a b >>,01c <<,则(A )log log a b c c < (B ) log log c c a b < (C ) c c a b < (D ) a b c c >(9)函数22x y x e =-在[2-,2]的图像大致为( )(A ) (B )(C ) (D )(10)执行右面的程序框图,如果输入的0x =,1y =,1n =,则输出x ,y 的值满足( )(A )2y x =(B )3y x = (C )4y x =(D )5y x =(11)平面α过正方体1111ABCD A B C D -的顶点A , 11//CB D α平面,ABCD m α=平面,11ABB A n α=平面, 则m ,n 所成角的正弦值为( )(A )(B )(C )(D ) 13 (12)若函数1()sin 2sin 3f x x x a x =-+在(-∞,)+∞单调递增,则a 的取值范围是( )(A ) [1-,1] (B ) [1-,1]3 (C ) 1[3-,1]3 (D ) [1-,1]3-二、填空题:本大题共4小题,每小题5分,共20分(13)设向量(a x =,1)x +,(1b =,2),且a b ⊥,则x =___________(14)已知θ是第四象限角,且3sin()45πθ+=,则tan()4πθ-=___________ (15)设直线2y x a =+与圆C :22220x y ay +--=相交于A ,B 两点,若错误!未指定书签。
四川外语学院重庆第二外国语学校2018-2019学年高三上学期第三次月考试卷数学含答案

四川外语学院重庆第二外国语学校2018-2019学年高三上学期第三次月考试卷数学含答案班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛.由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队.首发要求每个班至少1人,至多2人,则首发方案数为( ) A .720 B .270 C .390 D .300 2. 已知AC ⊥BC ,AC=BC ,D满足=t+(1﹣t),若∠ACD=60°,则t 的值为( )A.B.﹣C.﹣1D.3. 已知平面向量(12)=,a ,(32)=-,b ,若k +a b 与a 垂直,则实数k 值为( ) A .15- B .119 C .11 D .19【命题意图】本题考查平面向量数量积的坐标表示等基础知识,意在考查基本运算能力. 4. 若直线:1l y kx =-与曲线C :1()1ex f x x =-+没有公共点,则实数k 的最大值为( ) A .-1 B .12C .1 D【命题意图】考查直线与函数图象的位置关系、函数存在定理,意在考查逻辑思维能力、等价转化能力、运算求解能力.5. 已知复数z 满足(3+4i )z=25,则=( ) A .3﹣4i B .3+4i C .﹣3﹣4i D .﹣3+4i6. 复数z=(其中i 是虚数单位),则z的共轭复数=( ) A.﹣iB.﹣﹣i C.+iD.﹣+i7. 已知三个数1a -,1a +,5a +成等比数列,其倒数重新排列后为递增的等比数列{}n a 的前三 项,则能使不等式1212111n na a a a a a +++≤+++成立的自然数的最大值为( ) A .9 B .8 C.7 D .5 8. 函数sin()y A x ωϕ=+在一个周期内的图象如图所示,此函数的解析式为( ) A .2sin(2)3y x π=+B .22sin(2)3y x π=+C .2sin()23x y π=-D .2sin(2)3y x π=-9. 已知函数f(x)是定义在R 上的奇函数,当x ≥0时,.若,f(x-1)≤f(x),则实数a 的取值范围为A[] B[]C[]D[] 10.命题“∀a ∈R ,函数y=π”是增函数的否定是( )A .“∀a ∈R ,函数y=π”是减函数B .“∀a ∈R ,函数y=π”不是增函数C .“∃a ∈R ,函数y=π”不是增函数D .“∃a ∈R ,函数y=π”是减函数11.“p q ∨为真”是“p ⌝为假”的( )条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要 12.sin 3sin1.5cos8.5,,的大小关系为( ) A .sin1.5sin 3cos8.5<< B .cos8.5sin 3sin1.5<< C.sin1.5cos8.5sin 3<<D .cos8.5sin1.5sin 3<<二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知1sin cos 3αα+=,(0,)απ∈,则sin cos 7sin 12ααπ-的值为 .14.若函数()f x 的定义域为[]1,2-,则函数(32)f x -的定义域是 .15.函数()y f x =图象上不同两点()()1122,,,A x y B x y 处的切线的斜率分别是A B k k ,,规定(),A Bk k A B ABϕ-=(AB 为线段AB 的长度)叫做曲线()y f x =在点A 与点B 之间的“弯曲度”,给出以下命题:①函数321y x x =-+图象上两点A 与B 的横坐标分别为1和2,则(),A B ϕ ②存在这样的函数,图象上任意两点之间的“弯曲度”为常数; ③设点A,B 是抛物线21y x =+上不同的两点,则(),2A B ϕ≤;④设曲线xy e =(e 是自然对数的底数)上不同两点()()112212,,,,1A x y B x y x x -=且,若(),1t A B ϕ⋅<恒成立,则实数t 的取值范围是(),1-∞.其中真命题的序号为________.(将所有真命题的序号都填上) 16.已知函数322()7f x x ax bx a a =++--在1x =处取得极小值10,则ba的值为 ▲ . 三、解答题(本大共6小题,共70分。
【四川省成都外国语学年校】2017届高三(上)11月月考数学年(文科)试题

1cos 1cos 3sin sin 222A B BA +++=sin sin()3sin A ABC +++=BC PC C =,1133226ABC EF =⨯20为直径的圆经过坐标原点,所以0OP OQ =,即3)0=﹣, 2224(3)34m k -+4322224)34(3)434m k m k-+212)4x x -+10x x <<,2(1()1t -=++5,,n ,11111+++1ln 1223(1)n n n n++>=-⨯⨯-,11ln n n++>-,33log m n t ≥恒成立,3max log m n t ≥3log 1m n ≥,11n >>,,30,log n >>33(log log m n ≤)4≥,四川省成都外国语学校2017届高三(上)11月月考数学(文科)试卷解析1.【分析】首先确定集合A,由此得到log2k>4,由此求得k的取值范围.【解答】解:∵集合A={x∈N|1<x<log2k},集合A中至少有3个元素,∴A={2,3,4},∴log2k>4,∴k>16.2.【分析】利用复数代数形式的乘除运算化简,求出原复数的共轭复数得答案.【解答】解:∵=,∴复数的共轭复数为﹣i,虚部为﹣1.3.【分析】利用特称命题的否定是全称命题写出结果即可.【解答】解:f(x)=x﹣sinx,x∈(0,),f′(x)=1﹣cosx>0,∴f(x)是(0,)上是增函数,∵f(0)=0,∴f(x)>0,∴命题p:∃x∈(0,),f(x)<0是假命题,¬p:∀x∈(0,),f(x)≥0,4.【分析】设出塔顶灯的盏数,由题意可知灯的盏数自上而下构成等比数列,且公比为2,然后由等比数列的前7项和等于381列式计算即可.【解答】解:由题意设塔顶有a盏灯,由题意由上往下数第n层就有2n﹣1•a盏灯,∴共有(1+2+4+8+16+32+64)a=381盏灯,即.解得:a=3.5.【分析】由条件利用正弦函数的周期性、单调性、以及图象的对称性,y=Asin(ωx+φ)的图象变换规律,得出结论【解答】解:根据函数f(x)=sin(2x﹣)的周期为=π,可得A错误;在区间(﹣,)上,2x﹣∈(﹣,),故f(x)没有单调性,故B错误;把函数g(x)=sin2x的图象向右平移个单位,可得y=sin(2x﹣)的图象,故C错误;令x=,可得f(x)=sin(2x﹣)=0,图象C关于点(,0)对称,故D正确,6.【分析】模拟执行程序框图,依次写出每次循环得到的a,b的值,当a=b=2时不满足条件a≠b,输出a的值为2.【解答】解:模拟执行程序框图,可得a=14,b=18满足条件a≠b,不满足条件a>b,b=4满足条件a≠b,满足条件a>b,a=10满足条件a≠b,满足条件a>b,a=6满足条件a≠b,满足条件a>b,a=2满足条件a≠b,不满足条件a>b,b=2不满足条件a≠b,输出a的值为2.7.【分析】作出两平面区域,计算两区域的公共面积,得出芝麻落在区域Γ内的概率.【解答】解:作出平面区域Ω如图:则区域Ω的面积为S△ABC==.区域Γ表示以D()为圆心,以为半径的圆,则区域Ω和Γ的公共面积为S′=+=.∴芝麻落入区域Γ的概率为=.∴落在区域Γ中芝麻数约为360×=30π+20≈114.8.【分析】设扇形的中心角弧度数为α,半径为r,可得2r+αr=4,α=,因此S=αr2=(2﹣r)r,再利用基本不等式的性质即可得出.则2r+αr=4,∴α=,∴S=αr2=××r2=(2﹣r)r≤()2=1,.【分析】配方可得2cos2(x+y﹣1)==(x﹣y+1)+x﹣y+1,由基本不等式可得(x﹣y+1)+x﹣y+1≤2,或(x﹣y+1)+x﹣y+1≤﹣2,进而可得cos(x+y﹣1)=±1,x=y=,由此可得xy的表达式,取k=0可得最值.π1(2k x x +=.【分析】若P 在线段AB 上,设=λ,则有=,由于=x +y ,则有x+y=1,OM ,ON 的中点,P 上,设BP PA λ= 则有()OP OB BP OB PA OB OA OP λλ=+=+=+-, ∴1OB OAOP λλ+=+,由于(,)OP xOA yOB x y =+∈R , λMN 设=MP PN λ,则有1OM ON OP λ+=,故x 则=x+y=x+y(x ,y ∈R ),则x=, y=,故有x+y=2,当x=2,y=0时有最小值,当x=0,y=2时,有最大值故范围为]则∈.11.【分析】设P为双曲线的右支上一点,由向量垂直的条件,运用勾股定理和双曲线的定义,可得|PF1|+|PF2|,|PF1|•|PF2|,再由三角形的面积公式,可得内切圆的半径,再由直角三角形的外接圆的半径即为斜边的一半,由条件结合离心率公式,计算即可得到所求值.【解答】解:设P为双曲线的右支上一点,=0,即为⊥,由勾股定理可得|PF1|2+|PF2|2=|F1F2|2=4c2,①由双曲线的定义可得|PF1|﹣|PF2|=2a,②①﹣②2,可得|PF1|•|PF2|=2(c2﹣a2),可得|PF1|+|PF2|=,由题意可得△PF1F2的外接圆的半径为|F1F2|=c,设△PF1F2的内切圆的半径为r,可得|PF1|•|PF2|=r(|PF1|+|PF2|+|F1F2|),解得r=(﹣2c),即有=,化简可得8c2﹣4a2=(4+2)c2,即有c2=a2,则e===+1.12.【分析】①利用面面垂直的判定定理去证明EF⊥平面BDD'B'.②四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可.③判断周长的变化情况.④求出四棱锥的体积,进行判断.【解答】解:①连结BD,B'D',则由正方体的性质可知,EF⊥平面BDD'B',所以平面MENF⊥平面BDD'B',所以①正确.②连结MN,因为EF⊥平面BDD'B',所以EF⊥MN,四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可,此时当M为棱的中点时,即x=时,此时MN长度最小,对应四边形MENF的面积最小.所以②正确.③因为EF⊥MN,所以四边形MENF是菱形.当x∈0,]时,EM的长度由大变小.当x∈,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以③错误.④连结C'E,C'M,C'N,则四棱锥则分割为两个小三棱锥,它们以C'EF为底,以M,N分别为顶点的两个小棱锥.因为三角形C'EF的面积是个常数.M,N到平面C'EF的距离是个常数,所以四棱锥C'﹣MENF的体积V=h(x)为常函数,所以④正确.所以四个命题中③假命题.13.【分析】确定双曲线中的几何量,即可求出焦距、渐近线方程.【解答】解:双曲线=1中,a=,b=1,c=,∴焦距是2c=2,渐近线方程是y=±x.14.【分析】取AD的中点O,连结OB.OC.由线面垂直的判定与性质,证出AB⊥BD且AC⊥CD,得到△ABD与△ACD是具有公共斜边的直角三角形,从而得出OA=OB=OC=OD=AD,所以A.B.C.D四点在以O为球心的球面上,再根据题中的数据利用勾股定理算出AD长,即可得到三棱锥A﹣BCD外接球的半径大小.【解答】解:取AD的中点O,连结OB.OC∵AB⊥平面BCD,CD⊂平面BCD,∴AB⊥CD,又∵BC⊥CD,AB∩BC=B,∴CD⊥平面ABC,∵AC⊂平面ABC,∴CD⊥AC,∵OC是Rt△ADC的斜边上的中线,OC=AD.同理可得:Rt△ABD中,OB=AD,∴OA=OB=OC=OD=AD,可得A.B.C.D四点在以O为球心的球面上.Rt△ABD中,AB=2且BD=2,可得AD==2,由此可得球O的半径R=AD=,∴三棱锥A﹣BCD的外接球体积为=4π.15.【分析】由直方图可以看出11时至12时的销售额应为9时至10时的销售额的4倍,利用9时至10时的销售额即可求出11时至12时的销售额【解答】解:由直方图可以看出11时至12时的销售额应为9时至10时的销售额的4倍,因为9时至10时的销售额为2.5万元,故11时至12时的销售额应为2.5×4=10,16.【分析】由题意可以得到再由定义存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k型增函数”.对所给的问题分自变量全为正,全为负,一正一负三类讨论,求出参数所满足的共同范围即可.【解答】解:∵f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x﹣a|﹣2a,∴又f(x)为R上的“2011型增函数”,当x>0时,由定义有|x+2011﹣a|﹣2a>|x﹣a|﹣2a,即|x+2011﹣a|>|x﹣a|,其几何意义为到点a小于到点a﹣2011的距离,由于x>0故可知a+a﹣2011<0得a<当x<0时,分两类研究,若x+2011<0,则有﹣|x+2011+a|+2a>﹣|x+a|+2a,即|x+a|>|x+2011+a|,其几何意义表示到点﹣a的距离小于到点﹣a﹣2011的距离,由于x<0,故可得﹣a﹣a﹣2011>0,得a<;若x+2011>0,则有|x+2011﹣a|﹣2a>﹣|x+a|+2a,即|x+a|+|x+2011﹣a|>4a,其几何意义表示到到点﹣a的距离与到点a﹣2011的距离的和大于4a,当a≤0时,显然成立,当a>0时,由于|x+a|+|x+2011+a|≥|﹣a﹣a+2011|=|2a﹣2011|,故有|2a﹣2011|>4a,必有2011﹣2a>4a,解得综上,对x∈R都成立的实数a的取值范围是17.【分析】(Ⅰ)利用正弦定理以及两角和与差的三角函数,三角形的内角和,化简求解即可.(Ⅱ)利用三角形的面积以及余弦定理化简求解即可.1cos 1cos 3sin sin 222A B BA +++=sin sin()3sin A ABC +++= (Ⅱ)(II )取BC 的中点F ,连接EF ,AF ,则可证EF ⊥平面ABCD ,即∠EAF 为AE 与平面∠平面ABCD 所成的角,利用勾股定理求出AF ,则EF=AF .由E 为PB 的中点可知V P ﹣ACE =V E ﹣ABC =.PC ⊥AC ⊂1133226ABC EF =⨯【分析】(I )运用离心率公式和基本量a ,b ,c 的关系,代入点,解方程可得a ,b ,即可得到椭圆方程;(II )设A (x 1,y 1),B (x 2,y 2),可得,由于以PQ 为直径的圆经过坐标原点,所以,运用数量积为0,联立直线方程和椭圆方程,运用判别式大于0,韦达定理和弦长公式,点到直线的距离公式,三角形的面积公式,化简整理,即可得到定值. 【解答】解:(I )由题意知e==,a 2﹣b 2=c 2, 即又,即有椭圆的方程为+=1;为直径的圆经过坐标原点,所以0OP OQ =,即3)0=﹣, 2224(3)34m k -+422223(4)34(3)434m k m k-+212)4x x -+.【分析】(1)求出函数的导数,问题转化为即a≤2x﹣恒成立,求出a的范围即可;(2)求出a,得到f′()=﹣,问题转化为证明>ln,令t=,∵0<x1<x2,∴0<t<1,即证明u(t)=+lnt<0在0<t<1上恒成立,根据函数的单调性证明即可;(3)令a=1,得到lnx≤x2﹣x,得到x>1时,>,分别令x=2,3,4,5,…n,累加即可.f x,()x∈+∞(1)10x x <<,2(1()1t -=++11111+++1ln 1223(1)n n n n++>=-⨯⨯-,11ln n n++>-,33(log log mn ≤sin 2θ=或33log m nt ≥恒成立,3max log m nt ≥3log 1m n≥,11n >>,,30,log n>>33(loglogm n≤)4≥,。
四川省外语学院重庆第二外国语学校2018届高三语文11月月考试题不分版本

四川省外语学院重庆第二外国语学校2018届高三语文11月月考试题不分版本四川省外语学院重庆第二外国语学校2018届高三语文11月月考试题考前须知:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
一、现代文阅读〔共9分〕阅读下面论述类文本,完成1~3题。
〔9分,每题3分〕从历史上说,中国就存在南北文化差异与南北文化对立融合的问题。
从周朝起,北方诸侯自称中国,而吴、越、楚等南方诸国那么被视为“蛮夷〞,并受到北方的排斥轻蔑,直到晋代仍被视为“化外之民〞,南方文化被称为“蛮夷文化〞。
代表北方文化的黄帝部落,与代表南方文化的炎帝部落曾在中原大地摆开了宏大的战场,一决雌雄。
这场战争打得异常剧烈。
经过多年艰苦卓绝的努力和屡次的反复,黄帝终于打败了炎帝,确立了自己的领导地位,并从那时起,奠定了北方文化的胜利及其权威地位。
南方部落虽然失败了,但南方文化并没有绝迹和湮灭,而是作为一种与北方文化相对立的“异端〞文化依然继续存在和开展,并不时燃放出一段光荣。
后来那么有南北朝时期的南北对立和分庭抗礼。
南朝文学具有柔靡香软的特点,南朝民歌更是以情歌为主,不同于北朝文学的刚健质朴。
再后来那么是南北文学走上合流,这种合流促成了唐代文学的博大卓著。
而元杂剧作为北方文学的代表,其韵律、曲调都不同于以南戏、明清传奇为代表的南方文学。
从美学上说,北方文化代表壮美,充满着阳刚之气,刚烈豪放,慷慨激昂,正所谓“铁马秋风塞北〞;而南方文化那么是优美的化身,弥漫着阴柔之气,“暮春三月,江南草长,杂花生树,群莺乱飞〞,正所谓“杏花春雨江南〞。
从地形地貌来说,南方多山多水,山川秀丽,北方那么以平原、草原为主,一望无际,“天苍苍,野茫茫,风吹草低见牛羊〞。
从思想形态上说,儒家思想更多地属于北方文化系统,充满着先秦理性精神,道家思想更多地属于南方文化,充满着理想和浪漫气息。
而儒道互补,构成了中国文化思想的主导形态和文化开展趋势。
四川省外语学院重庆第二外国语学校2018届高三数学11月月考试题文

四川省外语学院重庆第二外国语学校2018届高三数学11月月考试题文第Ⅰ卷(选择题 共60分)一、选择题:(本大题共12小题,每小题5分,共60分)1.已知集合{}31≤<-=x x A ,{}4,3,0,1,2--=B ,则=B A I ()A .{}0B .{}3,0C .{}3,0,1-D .{}4,3,0 2.已知复数ii z ++=2213(i 为虚数单位),则z 在复平面内所对应点的坐标为() A .)0,1( B .)0,1(- C .)1,0( D .)1,0(-3.已知等差数列{}n a 中,1,16497==+a a a ,则12a 的值是( )A. 64B.30C.31D.154.已知平面向量()1,2a =-r ,()4,b m =r ,且a b ⊥r r ,则向量53a b -=r r ( )A. (7,16)--B. (7,34)-- C . (7,4)-- D. (7,14)-5.若某几何体的三视图如图所示,则此几何体的体积是( )A.7B.213 C.6 D.211 6.已知7π2sin =a ,7π2cos =b ,7π2tan =c ,则( ) A.c a b << B.a b c << C.a c b << D.c b a <<7.“0,0>>b a ”是“2)2(b a ab +<”成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件8.变量y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥--≥14321y x y x y 若使y ax z +=取得最大值的最优解有无穷多个,则实数a 的取值集合是( )A .{}0,3-B .{}1-,3C .{}0,1 D .{}10,3,- 9.高三某班陈齐齐在操场上绕圆形跑道逆时针方向匀速跑步,每52秒跑一圈,在陈齐齐开始跑步时,在教室内百无聊赖的桂圆圆往操场看了一次,以后每50秒往操场上看一次,则桂圆圆“感觉”到陈齐齐的运动是( )A.逆时针匀速前跑B.顺时针匀速前跑C.顺时针匀速后退D.静止没动10.当0a >时,函数()()2x f x x ax e =-的图象大致是( )AB C D11.二次函数)(x f 的图像经过点)23,0(,且1)('--=x x f ,则不等式0)10(>x f 的解集为( )A .(-3,1)B .)0,3lg (- C. )1,10001(D .(-∞,0) 12.若函数)0(21)(2<-+=x e x x f x 与2()ln()g x x x a =++图象上存在关于y 轴对称的点,则a 的取值范围是( )A.()e ,∞- B .⎪⎭⎫ ⎝⎛∞e 1-, C .⎪⎭⎫ ⎝⎛e e ,1- D .⎪⎭⎫ ⎝⎛e 1e -, 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数()f x 为奇函数,且当0x >时,()21,f x x x =+,则()1f -=_______. 14.在ABC Δ中,3π2,5,3===C b a ,则c = 15.在正三棱锥S ABC -中,侧棱SC SAB ⊥侧面,侧棱2SC =,则此正三棱锥的外接球的表面积为16.已知ABC △中,2AC =,6BC =,ABC △的面积为32,若线段BA 的延长线上存在点D ,使4BDC ∠=π,则CD = . 三、解答题:(本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程).17.(本小题满分12分)在正项等比数列{}n a 中,1241,81a a a ==.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设nn a b 1=,求数列{}n b 的前5项和.18.(本小题满分12分)已知函数)(1cos 2)6π2sin()(2R x x x x f ∈-+-=(1)求)(x f 的最大值;(2)在ABC Δ中,三内角C B A ,,的对边为c b a ,,,已知21)(=A f ,c a b ,,成等差数列,且9=⋅AC AB ,求a 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高2018级高三(上)第11月考理科数学试题(考试时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.已知集合{}022>-=x x x A ,}55|{<<-=x x B ,则( ) A.A∩B= B.A ∪B=RC.B ⊆AD.A ⊆B2.421dx x⎰=( ) A 、2ln 2- B 、2ln 2 C 、ln 2- D 、ln 2 3.已知tan 2α=-,()1tan 7αβ+=,则tan β的值为( ) A .3 B .35 C .3- D .35- 4.设向量()()3,2,2,1==b a ,若向量+λ与向量()7,4--=c 共线,则=λ( ) A .2 B .1013 C .2- D .1013- 5.已知,,,a b c d 为实数,且c d >,则“a b >”是“a c b d ->-”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C .充要条件 D. 既不充分也不必要条件6.《莱因德纸草书》(Rhind papyrus )是世界上最古老的数学著作之一.该书中有一道这样的题目:100个面包分给5个人,每人一份,若按照每个人分得的面包个数从少到多排列,可得到一个等差数列,其中较多的三份和的31等于较少的两份和,则最多的一份面包个数为( )A .35 B. 32 C .30 D. 277.设变量x y ,满足约束条件:⎪⎩⎪⎨⎧-≥≤+≥222x y x x y ,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-8.已知偶.函数)(x f 在),0[+∞单调递减,且0)2(=-f ,若0)2(>-x f ,则x 的取值范围是( )A.)2,2(-B.),2()2,(+∞--∞C.)4,0(D. ),4()0,(+∞-∞9.已知)23,3(+=k k ,)3,2(-=k ,若与的夹角为钝角,则k 的取值范围是( ) A .),2()21,(+∞--∞ B .)2,0()0,21( - C.)2,21(- D .),2()0,(+∞-∞10.若b a ,是函数q px x x f +-=2)()0,0(>>q p 的两个不同的零点,且,,2a b -这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q +的值等于( ) A .6 B .7 C .8 D .911.三数124log ,82log ,232716的大小关系正确的是( )(A )124log 82log 232716<< (B )82log 124log 231627<< (C )82log 23124log 1627<< (D )2382log 124log 1627<<12.设函数)()(x x ae x e x f -=(其中e 为自然对数的底数)恰有两个极值点()1212,x x x x <,则下列说法不正确的是( ) A .102a << B .110x -<< C .()1102f x -<< D .()()120f x f x +>二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.已知复数z 满足()12i z i +=-(i 为虚数单位),则z i +=14. 已知向量,22,21=+==a ,则向量在向量方向上的投影是 15.在数列}{n a 中,2,121==a a ,且)( )1(12*+∈-+=-N n a a n n n ,则100S = 16.已知函数x x x f ωωcos sin )(+=)0(>ω,R x ∈,若函数)(x f 在区间),(ωω-内单调递增,且函数)(x f 的图象关于直线x ω=对称,则ω的值为三、解答题(本大题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤)17.(12分)已知正项数列{}n a 的前n 项和为n S ,且n S ,n a ,2成等差数列. (1)求n a ;(2)令n n na b =,求数列}{n b 的前n 项和n T .18.(12分)某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数()f x 的解析式; (2)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图象,若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.19.(12分)已知ABC ∆的三个内角C B A ,,所对的边分别为c b a ,,,且b ac A -=-2c o s B c o s C 2c o s . (1)求sin sin CA的值;(2)若41cos =B ,2=b ,求ABC ∆的面积S .20.(12分)已知动圆过定点A (4,0),且在y 轴上截得的弦MN 的长为8. (1)求动圆圆心的轨迹C 的方程;(2)已知点)0,1(-B ,设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P 、Q ,若x 轴是PBQ ∠的角平分线,证明直线l 过定点.21.(12分)已知函数kx x x x g --=2ln 2)()(R k ∈. (1)当0=k 时,求)(x g 的单调区间;(2)设21,x x )0(21x x <<是函数)(x g 的两个零点,m 是21,x x 的等差中项,求证:0)(<'m g .请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分.22.(10分)选修4-4坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos sin x y αα=⎧⎨=⎩(α为参数),以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线2C :22)4cos(-=-πθρ,3:2sin .C ρθ=(1)求曲线1C 与2C 的交点M 在直角坐标系xOy 中的坐标; (2)设点B A ,分别为曲线23,C C 上的动点,求AB 的最小值.23.(10分)选修4-5不等式选讲 已知函数()1f x x =-.(1)解不等式()(4)8f x f x ++≥;(2)若1a <,1b <,且0a ≠,求证:)()(abf a ab f >.参考答案1-12:BDAAB CDCBD CD 13、22 14、1- 15、2600 16、2π 17、解:(1)由题意知22+=n n S a ,当n=1时,得21=a22+=n n S a ,2211+=++n n S a ,俩式相减得n n a a 21=+,即数列{}n a 是以2为首项,2为公比的等比数列。
∴n n a 2=18、解:(1)根据表中已知数据,解得π5,2,6A ωϕ===-. 数据补全如下表:且函数表达式为()5sin(2)6f x x =-.(2)由(1)知 π()5sin(2)6f x x =-,得π()5sin(22)6g x x θ=+-.因为sin y x =的对称中心为(π,0)k ,k ∈Z . 令π22π6x k θ+-=,解得ππ212k x θ=+-,k ∈Z . 由于函数()y g x =的图象关于点5π(,0)12成中心对称,令ππ5π21212k θ+-=, 解得ππ23k θ=-,k ∈Z . 由0θ>可知,当1k =时,θ取得最小值π6.19、解:(1)由正弦定理,设,sin sin sin a b ck A B C=== 则22sin sin 2sin sin ,sin sin c a k C k A C Ab k B B ---== 所以cos 2cos 2sin sin .cos sin A C C AB B--= 即(cos 2cos )sin (2sin sin )cos A C B C A B -=-, 化简可得sin()2sin().A B B C +=+又A B C π++=,所以sin 2sin C A =,因此sin 2.sin CA= (2)由sin 2sin CA=得2.c a = 由余弦定理22222212cos cos ,2,4144.4b ac ac B B b a a =+-==+-⨯及得4=a ,解得a=1,因此c=2又因为1cos ,.4B G B π=<<且所以sin B =因此11sin 122244S ac B ==⨯⨯⨯= 20、解:(1)A (4,0),设圆心C 2222,2),,(EC ME CM CA MNME E MN y x +===,由几何图像知线段的中点为x y x y x 84)422222=⇒+=+-⇒((2)点B (-1,0)222121212122118,8,00),,(),,(x y x y y y y y y x Q y x P ==<≠+,由题知设.080)()(88811211221212222112211=+⇒=+++⇒+-=+⇒+-=+⇒y y y y y y y y y yy y x y x y 直线PQ 方程为:)8(1)(21121112121y x y y y y x x x x y y y y -+=-⇒---=-1,088)(8)()(122112112==⇒=++⇒-=+-+⇒x y x y y y y x y y y y y y所以,直线PQ 过定点(1,0)21、解:(1)2ln 2)(x x x g -=,定义域),0(+∞,令0)1)(1(222)(=-+=-='xx x x x x g 得1=x x )1,0(1 ),1(+∞)(x g '+—∴)1,0(单增,),1(+∞单减23、解:(1)22,3,()(4)134,31,22, 1.x x f x f x x x x x x --<-⎧⎪++=-++=-≤≤⎨⎪+>⎩当3x <-时,则228x --≥,解得5x ≤-; 当31x -≤≤时,则()8f x ≥不成立; 当1x >时,由228x +≥,解得3x ≥.所以原不等式的解集为{}|53x x x ≤-≥或. ..........5分 (2))()(ab f a ab f >即1ab a b ->-. 因为1a <,1b <所以()()()()222222221212110ab a b a b ab a ab b a b ---=-+--+=-->所以1ab a b ->-...........10分。
