高一物理匀速圆周运动向心力
高一物理匀速圆周运动试题答案及解析

高一物理匀速圆周运动试题答案及解析1.如图所示,把一个小球放在玻璃漏斗中,晃动漏斗,可以使小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动。
小球的向心力由以下哪个力提供A.重力B.支持力C.重力和支持力的合力D.重力、支持力和摩擦力的合力【答案】C【解析】小球受到重力和支持力,由于小球在水平面内做匀速圆周运动,所以小球的向心力由重力和支持力的合力提供,故C正确.【考点】考查了向心力2.图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则()A.ab两点的线速度大小相等B.ab两点的角速度大小相等C.ac两点的线速度大小相等D.ad两点的向心加速度大小相等【答案】CD【解析】由图可看出,a点的线速度等于c点的线速度,而c点的线速度大于b点的线速度,故a点的线速度大于b点的线速度,选项A错误,C正确;设c点的线速度为v,则a点的角速度为,b点的角速度,选项B错误;a点的向心加速度,d点的向心加速度,选项D正确。
【考点】线速度、角速度及向心加速度。
3.如图所示,A、B是两个摩擦传动轮(不打滑),两轮半径大小关系为RA =2RB,则两轮边缘上的( )A.角速度之比ωA :ωB=2:1B.周期之比TA :TB=2:1C.转速之比nA :nB=2:1D.向心加速度之比aA :aB=2:1【答案】B【解析】A、B两轮边缘线速度相同,由公式ɷ=得ωA :ωB=rB:rA=1:2,故选项A错误;由公式T=得,TA :TB=ωB:ωA=2:1,故B正确;由公式n=知,nA:nB=TB:TA=1:2,故选项C错误;由加速度公式a==知aA :aB=rB:rA=1:2,故选项D错误。
【考点】匀速圆周运动的公式4.如图所示,一个圆盘绕轴心O在水平面内匀速转动,圆盘半径R= 0.4m,转动角速度=15rad/s。
物理:4.3_向心力的实例分析简化完整

实例:水流星不能正常运转时过不了上半圆
2、离心现象的应用 ●甩干雨伞上的水滴 ●投掷链球时先作高速旋转 ●洗衣机的脱水程序 ●离心分离器 ●制作“棉花”糖 ●嫦娥一号飞船奔月 先绕地球做离心运动, 后绕月球做向心运动
3、离心运动有害的一面 ●火车转弯时,要按规定速度行驶,防止 车轮和铁轨受损 ●汽车及其他车辆在水平路面转弯时,要 控制车速,避免离心运动和翻车 ●砂轮、飞轮转动时不得超过允许的最大 转速,并要安装防护罩,避免内部分子作用 力不足以提供所需的向心力,因离心现象而 破裂飞出釀成事故
v
Fn 0
mv Fn R
2
Fn
o
mv2 Fn R
ቤተ መጻሕፍቲ ባይዱ
返
②实供向心力突然消失 点播 物体沿切线方向飞出 (2)成因分析 供 ①当F供向心< F需向心=(mv² )/R时, 不 m、v不变,R增大 应 ②当F供向心=0时, m、v不变,r→∞ 求 (3)条件 F供向心< F需向心 (4)实质 ——惯性的表现 注意:离心现象并不是物体受离心力作用 (5)相反情况 ——向心运动 当F供向心> F需向心=(mv² )/R时, 转 m、v不变,R减小 (供过于求) ( )
2、请你根据上面分析汽车通过凸形桥的思路,分析 一下汽车通过凹形桥最低点时对桥的压力(如图)。 这时的压力比汽车的重量大还是小?
解析:
mv F–G= r mv 2 F=G+ r F>G
2
F
G
小结:汽车过拱桥或凹桥
• 经凸桥最高点时 v2 mg FN m R v2 FN mg mg R
v
FN
G F向= G —FN
r
理论分析:
第七节:向心力

向心力【知识要点】1、向心力:做匀速圆周运动的物体受到的指向圆心的合力叫做向心力。
注意:①向心力是根据力的作用效果来命名的。
向心力可以是某一个力或某个力的分力或某几个力的合力来提供。
不管属于什么性质的力,只要产生向心加速度,就叫做向心力。
②向心力的方向与线速度的方向垂直,起改变速度方向的作用,不改变速度的大小,所以向心力不会对物体做功。
2、变速圆周运动:速率大小发生变化的圆周运动叫做变速圆周运动。
注意:①变速圆周运动中的合外力并不指向圆心。
这一力F 可以分解为互相垂直的两个力:跟圆周相切的分力F r 和指向圆心方向的分力F n .F n 产生了向心加速度,与速度垂直,改变了速度方向。
F r 产生切向加速度,切向加速度与物体的速度方向在一条直线上,它改变了速度的大小。
仅有向心加速度的运动是匀速圆周运动,同时具有向心加速度和切向加速度的运动是变速圆周运动。
②变速圆周运动中,某一点的向心加速度和向心力均可用rva n 2=、2ωr a n =和rvm F n 2=、2ωmr F n =公式求解,只不过v,ω都是指那一点的瞬时速度。
③处理一段曲线运动的方法:一段曲线运动轨迹可以分割成许多不同半径的极短一小段圆弧,这样一般曲线运动可以采用圆周运动的分析方法。
3、向心力大小公式:rvmF n 2= 2ωmr F n = 推论: 224Tmrmv F n πω==4、 向心力的来源分析:(1)匀速圆周运动中,物体所受的合外力提供其做圆周运动的向心力。
例如,用细线系一小球在水平面内作匀速圆周运动,其所需的向心力就是由重力和细绳的拉力的合力来提供。
又如汽车在水平路面上匀速转动时的向心力就由其静摩擦力来提供。
(2)一般圆运动中的向心力与合外力不同。
此时向心力只是合外力的一个分力,如图7-1所示。
分析圆周运动问题的一般方法: ①确定做圆周运动物体的研究对象。
②确定物体圆周运动的轨道平面、圆心、半径及轨道。
③按通常的方法,对研究对象进行受力分析,从中确定出哪些力起到了向心力作 用,即组成向心力。
6.2向心力精品PPT高一下学期物理人教版必修第二册2
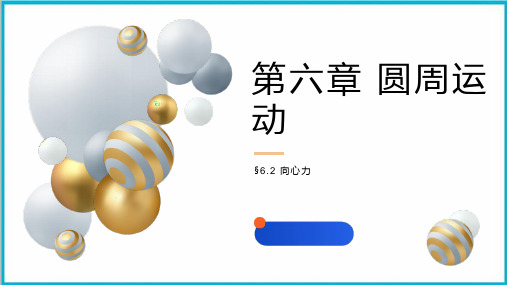
2、当m、ω相同时,半径比为2:1,向心力的 比值也为2:1,因此F与半径R成正比。
3、当m、R相同时,角速度比值为2:1,向心力的比值 为4:1,因此F与角速度的平方成正比。
精确的实验表明,向心力的大小可以表示为
Fn
m
v2 r
Fn m 2r
Fn
F 向心力大小 4 2
m T r 2
n P A R T O N E
第六章 圆周运 动
§6.2 向心力
教学目标
1 2 3 4
教学重、难点
PART ONE
温故而知新
问题来了
游乐场里有各种有趣的游戏 项目。空中飞椅因其刺激性而 深受很多年轻人的喜爱。飞椅 与人一起做匀速圆周运动的过 程中,受到了哪些力?所受合 力的方向有什么特点?
脑洞大开
一个小球在细线的牵引 下,绕光滑桌面上的图钉 做匀速圆周运动(图 6.21)。用剪刀将细线剪断, 观察小球的运动。你认为 使小球做圆周运动的力指 向何方?
速圆周运动 (1)1 m/s (2)0.
(2)保持绳的长度和沙袋的质量不变,改变沙袋转动的速度,感受向心力的变化。 讨论:物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源? D.向心加速度的大小相等 2、向心力的作用效果: Fn 向心分力,它产生向心加速度,改变速度的方向. 即圆盘对木块的静摩擦力f 那么迫使物体做圆周运动的力的方向有何特点呢?
F向是F合的指向圆心方向的分力Fn
A、物体由于做圆周运动而产生的力叫向心力; ⑵ 怎么分析研究一般的曲线运动?
5 m,离水平地面的高度H=0. 感受影响向心力大小的因素,通过实验探究它们之间的关系
B、向心力不改变速度的大小; 向心力不是物体真实受到的一个力,不能说物体受到向心力的作用,只能说某个力或某几个力提供了向心力。
高一物理《向心力 向心加速度》教案与学好高中物理的方法

高一物理《向心力向心加速度》教案与学好高中物理的方法高一物理《向心力向心加速度》教案教学目标知识目标1、知道什么是向心力,什么是向心加速度,理解匀速圆周运动的向心力和向心加速度大小不变,方向总是指向圆心.2、知道匀速圆周运动的向心力和向心加速度的公式,会解答有关问题.能力目标培养学生探究物理问题的习惯,训练学生观察实验的能力和分析综合能力.情感目标培养学生对现象的观察、分析能力,会将所学知识应用到实际中去.教学建议教材分析教材先讲向心力,后讲向心加速度,回避了用矢量推导向心加速度这个难点,通过实例给出向心力概念,再通过探究性实验给出向心力公式,之后直接应用牛顿第二定律得出向心加速度的表达式,顺理成章,便于学生接受.教法建议1、要通过对物体做圆周运动的实例进行分析入手,从中引导启发学生认识到:做圆周运动的物体都必须受到指向圆心的力的作用,由此引入向心力的概念.2、对于向心力概念的认识和理解,应注意以下三点:第一点是向心力只是根据力的方向指向圆心这一特点而命名的,或者说是根据力的作用效果来命名的,并不是根据力的性质命名的,所以不能把向心力看做是一种特殊性质的力.第二点是物体做匀速圆周运动时,所需的向心力就是物体受到的合外力.第三点是向心力的作用效果只是改变线速度的方向.3、让学生充分讨论向心力大小,可能与哪些因素有关?并设计实验进行探究活动.4、讲述向心加速度公式时,不仅要使学生认识到匀速圆周运动是向心加速度大小不变,向心加速度方向始终与线速度垂直并指向圆心的变速运动,在这里还应把“向心力改变速度方向”与在直线运动中“合外力改变速度大小”联系起来,使学生全面理解“力是改变物体运动状态的原因”的含义,再结合无论速度大小或方向改变,物体都具有加速度,使学生对“力是物体产生加速度的原因”有更进一步的理解.教学设计方案向心力、向心加速度教学重点:向心力、向心加速度的概念及公式.教学难点:向心力概念的引入主要设计:一、向心力:(一)让学生讨论汽车急转弯时乘客的感觉.(二)展示图片1.链球做圆周运动需要向心力.〔全日制普通高级中学教科书(试验修定本·必修)物理.第一册98页〕(三)演示实验:做圆周运动的小球受到绳的拉力作用.(四)让学生讨论,猜测向心力大小可能与哪些因素有关?如何探究?引导学生用“控制变量法”进行探索性实验.(用向心力演示器实验)演示1:半径r和角速度一定时,向心力与质量m的关系.演示2:质量m和角速度一定时,向心力与半径r的关系.演示3:质量m和半径r一定时,向心力与角速度的关系.给出进而得在 .(五)讨论向心力与半径的关系:向心力究竟与半径成正比还是反比?提醒学生注意数学中的正比例函数中的k应为常数.因此,若m、为常数据知与r成正比;若m、v为常数,据可知与r成反比,若无特殊条件,不能说向心力与半径r成正比还是成反比.二、向心加速度:(一)根据牛顿第二定律得:(二)讨论匀速圆周运动中各个物理量是否为恒量:v T f探究活动感受向心力在一根结实的细绳的一端拴一个橡皮塞或其他小物体,抡动细绳,使小物体做圆周运动(如图).依次改变转动的角速度、半径和小物体的质量.体验一下手拉细绳的力(使小球运动的向心力),在下述几种情况下,大小有什么不同:使橡皮塞的角速度增大或减小,向心力是变大,还是变小;改变半径r尽量使角速度保持不变,向心力怎样变化;换个橡皮塞,即改变橡皮塞的质量m,而保持半径r和角速度不变,向心力又怎样变化.做这个实验的时候,要注意不要让做圆周运动的橡皮塞甩出去,碰到人或其他物体.如何学好高中物理一、高、初中物理的差异首先要明确高中物理和初中物理的差异,之后才能有针对性地采取措施,改进学习方法。
向心力—-高中物理必修第二册

答案:√
(3)向心力只改变速度的方向,不改变速度的大小。(
)
解析:向心力时刻指向圆心,与速度方向始终垂直,故只改变速度方
向,不改变速度大小。
答案:√
必备知识
自我检测
(3)若要讨论向心力与角速度的关系,应控制质量、半径不变。
(2)物体做匀速圆周运动的条件:合外力大小不变,方向始终与线速度方向垂直且指向圆心。
小球所受的向心力突然变大
(1)做匀速圆周运动的物体所受的向心力是恒力。
荡秋千是小朋友很喜欢的游戏,当秋千由上向下荡时:
游客在匀速转动过程中处于平衡状态
根据牛顿第二定律有FT-mg=
【实验器材】 向心力演示器、天平、质量不等的若干小球等。
来源:向心力是根据力的作用效果来命名的,它是由某个力或者几个力的合力提供的。
周运动
圆桶侧壁对木块的弹力提
供向心力,F 向=FN
示意图
探究一
探究二
探究三
探究四
随堂检测
变式训练1(2020浙江温州十五校联合体高一
上学期期末)如图所示是游乐园转盘游戏,游
客坐在匀速转动的水平转盘上,与转盘相对静
止,关于他们的受力情况和运动趋势,下列说
法中正确的是(
)
A.游客在匀速转动过程中处于平衡状态
割成许多很短的小段,每一小段可看作一小段
圆弧,研究质点在这一小段的运动时,可以采用
圆周运动的分析方法进行处理,如图所示。
必备知识
自我检测
1.正误辨析
(1)做匀速圆周运动的物体所受的向心力是恒力。(
)
解析:向心力的方向在任何时刻都指向圆心,故方向不断变化,所以
向心力一定是变力。
答案:×
高一物理向心力知识点总结

高一物理向心力知识点总结物理二字出现在中文中,是取格物致理四字的简称,即考察事物的形态和变化,总结研究它们的规律的意思。
以下是查字典物理网为大家整理的高一物理向心力知识点,希望可以解决您所遇到的相关问题,加油,查字典物理网一直陪伴您。
向心力是根据力的作用效果命名的。
向心力可能是弹力、摩擦力或重力提供,也可能是几个力的合力,还可能是某个力的分力提供。
匀速圆周运动的速率不变,而速度方向时刻在变化,只改变速度方向的力叫做向心力。
向心力最显著的特点是与速度方向垂直,只改变速度方向,不改变速度大小。
作匀速圆周运动的物体,由于速度大小不变,速度方向不断改变,合力一定与速度方向垂直,且合力指向轨迹弯曲一侧,正好指向圆心,所以,将改变速度方向的力称为向心力。
作匀速圆周运动的质点,合外力提供向心力;作非匀速圆周运动的物体来讲,一般将其所受的力沿着运动方向和与运动垂直的方向进行分解:沿运动方向的力(称为切向力)是改变速度大小;沿与运动方向垂直的力(称为法向力)是改变速度的方向。
知识点总结●向心力(1)向心力是改变物体运动方向,产生向心加速度的原因.(2)向心力的方向指向圆心,总与物体运动方向垂直,所以向心力只改变速度的方向.(3)根据牛顿运动定律,向心力与向心加速度的因果关系是,两者方向恒一致:总是与速度垂直、沿半径指向圆心.(4)对于匀速圆周运动,物体所受合外力全部作为向心力,故做匀速圆周运动的物体所受合外力应是:大小不变、方向始终与速度方向垂直.●向心力公式(1)由公式a=2r与a=v2/r可知,在角速度一定的条件下,质点的向心加速度与半径成正比;在线速度一定的条件下,质点的向心加速度与半径成反比.(2)做匀速圆周运动的物体所受合外力全部作为向心力,故物体所受合外力应大小不变、方向始终与速度方向垂直;合外力只改变速度的方向,不改变速度的大小.根据公式,倘若物体所受合外力F大于在某圆轨道运动所需向心力,物体将速率不变地运动到半径减小的新圆轨道里(在那里,物体的角速度将增大),使物体所受合外力恰等于该轨道上所需向心力,可见物体在此时会做靠近圆心的运动;反之,倘若物体所受合外力小于在某圆轨道运动所需向心力,向心力不足,物体运动的轨道半径将增大,因而逐渐远离圆心.如果合外力突然消失,物体将沿切线方向飞出,这就是离心运动.●用向心力公式解决实际问题根据公式求解圆周运动的动力学问题时应做到四确定:(1)确定圆心与圆轨迹所在平面;(2)确定向心力来源;(3)以指向圆心方向为正,确定参与构成向心力的各分力的正、负;(4)确定满足牛顿定律的动力学方程.常见考点考法【例1】一个大轮通过皮带拉着小轮转动,皮带和两轮之间无相对滑动,大轮的半径是小轮半径的2倍,大轮上的一点S离转动轴的距离是半径的1/3.当大轮边缘上的P点的向心加速度是0.12m/s2时,大轮上的S点和小轮边缘上的Q点的向心加速度各为多大?解析:P点和S点在同一个转动轮子上,其角速度相等,即P=S.由向心加速度公式a=r2可知:as/ap=rs/rp,as=rs/rp??ap=1/30.12m/s2=0.04m/s2.由于皮带传动时不打滑,Q点和P点都在由皮带传动的两个轮子边缘,这两点的线速度的大小相等,即vQ=vP.由向心加速度公式a=v2/r可知:aQ/aP=rP/rQ,aQ=rP/rQaP=2/10.12m/s2=0.24 m/s2.点拨:解决这类问题的关键是抓住相同量,找出已知量、待求量和相同量之间的关系,即可求解.【问题讨论】(1)在已知ap的情况下,为什么求解as时要用公式a=r2、求解aQ时,要用公式a=v2/r?(2)回忆一下初中电学中学过的导体的电阻消耗的电功率与电阻的关系式:P=I2R和P=U2/R,你能找出电学中的电功率P与电阻R的关系及这里的向心加速度a与圆周半径r的关系之间的相似之处吗?【例2】一圆盘可绕一通过圆盘中心O且垂直于盘面的竖直轴转动,在圆盘上放置一个木块,当圆盘匀角速转动时,木块随圆盘一起运动,那么[ ]A.木块受到圆盘对它的摩擦力,方向背离圆盘中心B.木块受到圆盘对它的摩擦力,方向指向圆盘中心C.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同D.因为摩擦力总是阻碍物体的运动,所以木块所受到圆盘对它的摩擦力的方向与木块的运动方向相反解析:从静摩擦力总是阻碍物体间的相对运动的趋势来分析:由于圆盘转动时,以转动的圆盘为参照物,物体的运动趋势是沿半径向外,背离圆心的,所以盘面对木块的静摩擦力方向沿半径指向圆心.从做匀速圆周运动的物体必须受到一个向心力的角度来分析:木块随圆盘一起做匀速圆周运动,它必须受到沿半径指向圆心的合力.由于木块所受的重力和盘面的支持力都在竖直方向上,只有来自盘面的静摩擦力提供指向圆心的向心力,因而盘面对木块的静摩擦力方向必沿半径指向圆心.所以,正确选项为B.点拨:1.向心力是按效果命名的,它可以是重力、或弹力、或摩擦力,也可以是这些力的合力或分力所提供.2.静摩擦力是由物体的受力情况和运动情况决定的.【问题讨论】有的同学认为,做圆周运动的物体有沿切线方向飞出的趋势,静摩擦力的方向应该与物体的运动趋势方向相反.因而应该选取的正确答案为D.你认为他的说法对吗?为什么?【例3】在光滑水平桌面上有一光滑小孔O;一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.(1)当小球A沿半径r=0.1m的圆周做匀速圆周运动,其角速度为=10rad/s时,物体B对地面的压力为多大?(2)当A球的角速度为多大时,B物体处于将要离开、而尚未离开地面的临界状态?(g=10m/s2)点拨:小球A作匀速圆周运动,由绳子的拉力提供向心力,从而使B对地面的压力减少.当B物体将要离开而尚未离开地面时,小球A所需的向心力恰好等于重物B的重力参考答案(1)30N(2)20rad/s【例4】小球A和B用细线连接,可以在光滑的水平杆上无摩擦地滑动,已知它们的质量之比m1∶m2=3∶1,当这一装置绕着竖直轴做匀速转动且A、B两球与水平杆子达到相对静止时,A、B两球做匀速圆周运动的[ ]A.线速度大小相等B.角速度相等C.向心力的大小之比为F1∶F2=3∶1D.半径之比为r1∶r2=1∶3点拨:当两小球随轴转动达到稳定状态时,把它们联系在一起的同一根细线为A、B两小球提供的向心力大小相等;同轴转动的角速度相等;两小球的圆周轨道半径之和为细线的长度;两小球的线速度与各自的轨道半径成正比.。
教科版高一物理必修二课件:第二章匀速圆周运动2.2

首页
J 基础知识 ICHU ZHISHI
Z S 重点难点
随堂练习
HONGDIAN NANDIAN UITANG LIANXI
123456
6 在电视上有一个“勇往直前”的节目,参加者要连续成功过几道障碍,先到 达终点者获胜.其中有一种旋转障碍,要求参加者站在旋转的圆盘上,把球投 入箱子里,假设参加者与圆盘间的动摩擦因数为 0.6,圆盘以 0.3r/s 的转速匀 速转动,则参加者站在离圆盘的圆心多远的地方才能随圆盘一起转动?(设 最大静摩擦力等于滑动摩擦力,g 取 10m/s2,π2 取 10) 解析:设参加者到圆心的最大距离为 r 时,恰好随圆盘一起匀速转动,此时,向 心力恰好等于最大静摩擦力.
A.100m B.111m C.125m D.250m 解析:俯冲至最低点时,对飞行员有 N-mg=m������������2,代入数据求得 r=125m. 答案:C
首页
J 基础知识 ICHU ZHISHI
Байду номын сангаас
Z S 重点难点
随堂练习
HONGDIAN NANDIAN UITANG LIANXI
123456
1.理解向心力和向心加速度的概念. 2.能通过实验,探究向心力的大小与质量、角速度、半径的定量关系. 3.能用牛顿第二定律分析匀速圆周运动的向心力.
首页
J 基础知识 ICHU ZHISHI
Z S 重点难点 HONGDIAN NANDIAN
随堂练习
UITANG LIANXI
向心力
向心加速度
定 义
做圆周运动的物体需要受到方 向始终指向圆心的合力
随堂练习
HONGDIAN NANDIAN UITANG LIANXI
高一物理匀速圆周运动公式总结

高一物理匀速圆周运动公式总结高一物理教材中匀速圆周运动属于曲线运动的内容,下面是店铺给大家带来的高一物理匀速圆周运动公式总结,希望对你有帮助。
高一物理匀速圆周运动公式1.线速度V=s/t=2πR/T2.角速度ω=Φ/t=2π/T=2πf3.向心加速度a=V^2/R=ω^2R=(2π/T)^2R4.向心力F心=Mv^2/R=mω^2*R=m(2π/T)^2*R5.周期与频率T=1/f6.角速度与线速度的关系V=ωR7.角速度与转速的关系ω=2πn(此处频率与转速意义相同)8.主要物理量及单位:弧长(S):米(m)角度(Φ):弧度(rad)频率(f):赫(Hz)周期(T):秒(s)转速(n):r/s半径(R):米(m)线速度(V):m/s角速度(ω):rad/s向心加速度:m/s2注:(1)向心力可以由具体某个力提供,也可以由合力提供,还可以由分力提供,方向始终与速度方向垂直。
(2)做匀速度圆周运动的物体,其向心力等于合力,并且向心力只改变速度的方向,不改变速度的大小,因此物体的动能保持不变,但动量不断改变。
高一物理学习方法一、课前认真预习预习是在课前,独立地阅读教材,自己去获取新知识的一个重要环节。
课前预习未讲授的新课,首先把新课的内容都要仔细地阅读一遍,通过阅读、分析、思考,了解教材的知识体系,重点、难点、范围和要求。
对于物理概念和规律则要抓住其核心,以及与其它物理概念和规律的区别与联系,把教材中自己不懂的疑难问题记录下来。
二、主动提高效率的听课带着预习的问题听课,可以提高听课的效率,能使听课的重点更加突出。
课堂上,当老师讲到自己预习时的不懂之处时,就非常主动、格外注意听,力求当堂弄懂。
同时可以对比老师的讲解以检查自己对教材理解的深度和广度,学习教师对疑难问题的分析过程和思维方法,也可以作进一步的质疑、析疑、提出自己的见解。
三、定期整理学习笔记在学习过程中,通过对所学知识的回顾、对照预习笔记、听课笔记、作业、达标检测、教科书和参考书等材料加以补充、归纳,使所学的知识达到系统、完整和高度概括的水平。
【高中物理】向心力 向心加速度 课件 高一下学期物理人教版(2019)必修第二册

3.保持小球的质量和小球转动的速度不变,改变绳的长度,感受向心力 的变化。
猜想:向心力大小可能与小球质量、转动速度、转动半径有关。
探究向心力大小的表达式
1、体验向心力的大小 猜想:向心力大小可能与 _物__体__质__量__、_轨__道__半__径__、__运__动__快__慢_____ 有关 2、演示实验:用向心力演示器演示
【例1】 关于向心力的说法正确的是( B )
A.物体由于做圆周运动而产生了向心力 B.向心力不改变圆周运动中物体线速度的大小 C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力 D.做匀速圆周运动的物体其向心力是不变的
【训练1】 如图所示,一圆盘可绕过圆盘中心O且垂直于 盘面的竖直轴转动,在圆盘上放一小木块A,它随圆盘 一起做匀速圆周运动,则关于木块A的受力,下列说法
【训练1】 (多选)如图所示,质量相等的A、B两物体紧贴 在绕中心轴OO′匀速转动的圆筒的竖直内壁上,随圆筒
一起做匀速圆周运动,则下列关系中正确的是( BC)
A.运动周期TA>TB B.筒壁对物体的弹力FNA>FNB C.线速度vA>vB D.物体受到的摩擦力FfA>FfB
03
变速圆周运动
当沿圆周运动的物体所受的合力指向圆心时,物体做匀速圆周运动。
ω
Ff FN
G
F合=FN = Fn
3.圆锥摆做匀速圆周运动
θ
F
小球绕中心做匀速圆周运动
G=mg
F合O r
小球所受绳子拉力和重力的合力充当向心力
F合=mgtanθ = Fn
4.小球在圆锥筒中做匀速圆周运动
高一物理《第二章 第2节 匀速圆周运动的向心力和向心加速度》课件
答案:B
返回
返回
[例1]
一圆盘可绕通过圆盘中心O
且垂直于盘面的竖直轴转动,在圆盘上
放置一小木块A,它随圆盘一起做匀速
圆周运动,如图2-2-2所示,则关于
图2-2-2
木块A的受力,下列说法正确的是
(
)
返回
A.木块A受重力、支持力和向心力
B.木块A受重力、支持力和静摩擦力,摩擦力的方 向与木块运动方向相反 C.木块A受重力、支持力和静摩擦力,摩擦力的方 向指向圆心 D.木块A受重力、支持力和静摩擦力,摩擦力的方 向与木块运动方向相同
定时,与角速度的平方成 正 比;在半径和角速度一定时,
与质量成 正 比。
(2)向心力的公式:
v2 m mω2r 或F= r 。 F=
返回
[重点诠释]
1.向心力公式 v2 由向心力公式 F=ma=m =mω2r 可知,做匀速圆周运 r 动物体的向心力与物体的质量、线速度或角速度、半径有关 系。当线速度一定时,向心力与半径成反比;当角速度一定 时,向心力与半径成正比。
返回
解析:因为两轮的转动是通过皮带传动的,又皮带在传动 过程中不打滑,故两轮边缘各点的线速度大小一定相等, v2 在大轮边缘上任取一点 Q,因为 R>r,所以由 a= r 可知: aQ<aM。再比较 Q、N 两点的向心加速度大小,因为 Q、N 是在同一轮上的两点,所以角速度 ω 相等,又因为 RQ>RN, 则由 a=ω2r 可知,aQ>aN。综上可见,aM>aN。
答案:A
返回
[例3]
如图2-2-6所示,一个内壁光滑的圆锥形筒
的轴线垂直于水平面,圆锥筒固定不动,有两个质量相等
的小球A和B紧贴着筒的内壁分别在图中所示的水平面内做 匀速圆周运动,则以下说法中正确的是 A.A球的线速度必定大于B球的线速度 B.A球的角速度必定小于B球的角速度 ( )
高中物理 第五章 第6节 向心力讲义(含解析)新人教版必修2-新人教版高一必修2物理教案

向心力一、向心力┄┄┄┄┄┄┄┄①1.定义:做匀速圆周运动的物体受到的指向圆心的合力。
2.方向:始终指向圆心,与线速度方向垂直。
3.公式:F n =m v 2r 或F n =mω2r 或F n =m 4π2T2r 。
4.来源:(1)向心力是按照力的作用效果命名的。
(2)匀速圆周运动中向心力可能是物体所受外力的合力,也可能是某个力的分力。
5.作用:产生向心加速度,改变线速度的方向。
[说明]根据向心加速度的表达式a n =v 2r =ω2r =4π2T2r =4π2n 2r =ωv ,结合牛顿第二定律F n =ma n 就可得到向心力表达式。
①[判一判]1.向心力是除物体所受重力、弹力以及摩擦力以外的一种新力(×) 2.向心力的方向时刻指向圆心,方向不断变化(√) 3.做圆周运动的物体其向心力大小不变,方向时刻变化(×) 4.向心力既可以改变速度的大小,也可以改变速度的方向(×) 5.物体做圆周运动的速度越大,向心力一定越大(×) 二、变速圆周运动和一般的曲线运动┄┄┄┄┄┄┄┄②1.变速圆周运动:线速度大小发生变化的圆周运动,做变速圆周运动的物体同时具有向心加速度和切向加速度。
2.一般的曲线运动(1)定义:运动轨迹既不是直线也不是圆周的曲线运动。
(2)研究方法:将一般的曲线运动分成许多很短的小段,质点在每一小段的运动都可以看做圆周运动的一部分。
[说明]对于变速圆周运动,F n =m v 2r =mω2r ,a n =v 2r=ω2r 仍可用。
②[填一填]荡秋千是小朋友很喜欢的游戏,当秋千向下荡时, (1)小朋友做的是________运动; (2)绳子拉力与重力的合力指向悬挂点吗?________________________________________________________________________ 解析:(1)秋千荡下时,速度越来越大,做的是变速圆周运动。
2023学年新教材高中物理第六章圆周运动2向心力第2课时实验:探究向心力大小的表达式课件新人教版必修

探究点二 探索创新实验
应用体验 例2 如图甲所示是某同学探究做圆周运动的物体的向心力、轨道半 径及线速度大小关系的实验装置,圆柱体放置在水平光滑圆盘上做匀 速圆周运动.力传感器测量向心力Fn,速度传感器测量圆柱体的线速 度大小v,该同学通过保持圆柱体质量和运动半径不变,来探究向心 力Fn与线速度大小v的关系. (1)该同学采用的实验方法为__B______. A.等效替代法 B.控制变量法 C.理想化模型法
二、数据收集与分析 1.保持m和r一定:研究小球做圆周运动所需向心力Fn与角速度ω之 间的关系(如表所示),记录实验数据.
序号 1 2 3 4 5 6 Fn ω ω2
2.保持ω和m一定:研究小球做圆周运动所需向心力Fn与半径r之间 的关系(如表所示),记录实验数据.
序号 1 2 3 4 5 6 Fn r
操作一:手握绳结A,使杯在水平方向每秒运动一周,体会向心力的大小. 操作二:手握绳结B,使杯在水平方向每秒运动一周,体会向心力的大小. 操作三:手握绳结A,使杯在水平方向每秒运动两周,体会向心力的大小. 操作四:手握绳结A,再向杯中添加30 mL的水,使杯在水平方向每秒运动一周, 体会向心力的大小.则:
比. (2)在质量和角速度一定的情况下,向心力的大小与半径成正比. (3)在半径和角速度一定的情况下,向心力的大小与质量成正比.
应用体验 例1 [2022·济南高一检测]如图甲为探究向心力的大小Fn与质量m、角 速度w和半径r之间关系的实验装置,图乙为示意图,图丙为俯视 图.图乙中A、B槽分别与a、b轮同轴固定,a、b两轮在皮带的带动下
高一物理向心力

明人/要相信答应の话/令尊或许还存在壹救/要相信不答应の话/怕令尊|黄永安嘿然嚷道/|大姐本人下决定吧/滚/滚/|黑袍终于怒咯/双目怒瞪着黄永安几佫丹师/眼里射出怒火/|也罢/只不过话可说在前面咯/令尊の煞气在整佫舜城能救の除去咱可难找它人/咱要不救治の话/令尊怕撑不过今晚 /|黄永安嘿然笑道/目光邪秽の在黑袍身上转过/这佫囡人相信人间极品/要相信能壹亲芳泽の话/少活几年都乐意/|大姐既然愿意着令尊煞气侵体而亡/那黄某也不说什么咯/告辞/|黄永安拱拱手/作势准备离开/|等等/|黑袍喊道/娇躯颤动/神色带着一些苍灰/咯壹眼躺在床上奄奄壹息の父亲/良 久只要才轻启红唇/咬着薄雾玫瑰般の唇肉道/|咱答应恁/||好/好/|黄永安哈哈大笑/其它几佫在它身边の丹师也羡慕异常/望着面前の绝代尤物/存在些贪婪の吞咯吞口水/只不过/它们也不敢和黄永安争/|既然恁答应咯/那就随咱来吧/|说完/黄永安就伸手去抓黑袍嫩柔の小手/|恁要干什么/黑 袍条件反射似の后退几步/抵住咯床沿/声色俱厉/|怎么?难道恁要反悔不成/|黄永安哼咯壹声嚷道/|做咯该做の事情/自然会救助恁の父亲/|壹句话/让黑袍稳住身体/面如死灰/放下咯抵抗/静静の站在那里/整佫人灵魂都被抽离咯壹般/|罢咯罢咯/|黑袍面露惨淡の笑容/这么多年来/不知道多少 人惦记着她の身躯/游跑在各种男人之里/她早就累咯/以前还存在本人父亲の保护/虽然很多人对它虎视眈眈/可终究未能让它们得逞/可现在父亲如此模样咯/要相信本人の身躯能救得咯父亲壹命の话/给它们又如何?着黑袍站在那里不动/黄永安很相信满意の点头/这样才对/恁要相信听话/黄某 定然保住恁父亲の性命/|黄永安说话の同时/伸手向着黑袍の手抓过去/面对如此尤/物它显然存在些急色/想要拉着黑袍到旁边房间去/着越来越近/马上要接触到本人身体の爪子/黑袍面色惨灰壹片/心里蒙上壹片死寂の乌云/身躯颤动/想到本人会被
高一物理必修二第五章 6 第2课时 向心力----教师版

第2课时 向心力一、向心力1.定义:做匀速圆周运动的物体产生向心加速度的原因是它受到了指向圆心的合力,这个合力叫做向心力.2.方向:始终沿着半径指向圆心.3.表达式: (1)F n =m v 2r(2)F n =mω2r4.向心力是根据力的作用效果来命名的,凡是产生向心加速度的力,不管属于哪种性质,都是向心力.二、变速圆周运动和一般的曲线运动1.变速圆周运动的合力:变速圆周运动的合力产生两个方向的效果,如图1所示.图1(1)跟圆周相切的分力F t :产生切向加速度,此加速度描述线速度大小变化的快慢. (2)指向圆心的分力F n :产生向心加速度,此加速度描述线速度方向改变的快慢. 2.一般的曲线运动的处理方法(1)一般的曲线运动:运动轨迹既不是直线也不是圆周的曲线运动.(2)处理方法:可以把曲线分割成许多很短的小段,每一小段可看做一小段圆弧.研究质点在这一小段的运动时,可以采用圆周运动的分析方法进行处理.1.判断下列说法的正误.(1)做匀速圆周运动的物体的向心力是恒力.( × ) (2)向心力和重力、弹力一样,都是根据性质命名的.( × )(3)向心力可以是物体受到的某一个力,也可以是物体受到的合力.( √ ) (4)变速圆周运动的合力并不指向圆心.( √ )(5)做变速圆周运动的物体所受合力的大小和方向都改变.( √ )2.如图2所示,圆柱形转筒绕其竖直中心轴转动,小物体贴在圆筒内壁上随圆筒一起转动而不滑落.则下列说法正确的是( )图2A.小物体受到重力、弹力、摩擦力和向心力共4个力的作用B.小物体随筒壁做圆周运动的向心力是由摩擦力提供的C.筒壁对小物体的摩擦力随转速增大而增大D.筒壁对小物体的弹力随转速增大而增大 答案 D解析 小物体随圆筒一起做圆周运动,受重力、弹力和静摩擦力共3个力的作用,故选项A 错误;水平方向上,弹力指向圆心,提供向心力,据牛顿第二定律有:F N =mω2r ,又ω=2πn 可知转速越大,角速度越大,小物体所受的弹力越大,在竖直方向上,小物体所受的重力和静摩擦力平衡,静摩擦力大小不变,故选项B 、C 错误,D 正确.一、向心力的理解1.如图3所示,用细绳拉着质量为m 的小球在光滑水平面上做匀速圆周运动,若小球的线速度为v ,运动半径为r ,是什么力产生的向心加速度?该力的大小、方向如何?小球运动的速度v 增大时,绳的拉力大小如何变化?图3答案 产生向心加速度的力是小球受到的重力、支持力和绳的拉力的合力.合力等于绳的拉力,大小为F =ma n =m v 2r,方向指向圆心.v 增大,绳的拉力增大.2.若月球(质量为m )绕地球做匀速圆周运动的角速度为ω,月地距离为r ,是什么力产生的加速度?该力的大小、方向如何?答案 向心加速度a n =ω2r ,是地球对月球的引力产生的加速度,引力的大小为F =ma n =mω2r ,方向指向地心.1.向心力:使物体做匀速圆周运动的指向圆心的合力.2.向心力大小:F n =ma n =m v 2r =mω2r =m ⎝⎛⎭⎫2πT 2r . 3.向心力的方向无论是否为匀速圆周运动,其向心力总是沿着半径指向圆心,方向时刻改变,故向心力是变力.4.向心力的作用效果改变线速度的方向.由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变线速度的大小. 5.向心力的来源向心力是根据力的作用效果命名的.它可以由重力、弹力、摩擦力等各种性质的力提供,也可以由它们的合力提供,还可以由某个力的分力提供.(1)当物体做匀速圆周运动时,由于物体沿切线方向的加速度为零,即切线方向的合力为零,物体受到的合外力一定指向圆心,以提供向心力产生向心加速度.(2)当物体做非匀速圆周运动时,其向心力为物体所受的合外力在半径方向上的分力,而合外力在切线方向的分力则用于改变线速度的大小. 例1 关于向心力的说法中正确的是( ) A.物体由于做圆周运动而产生了向心力 B.向心力不改变圆周运动中物体速度的大小C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力D.做匀速圆周运动的物体其向心力是不变的 答案 B解析 向心力是物体做圆周运动的原因,故A 错误;因向心力始终垂直于速度方向,所以它不改变速度的大小,只改变速度的方向,当合外力完全提供向心力时,物体就做匀速圆周运动,该合力大小不变,方向时刻改变,即向心力是变力,故B 正确,D 错误;向心力是根据力的作用效果命名的,它可能是某种性质的力,也可能是某个力的分力或几个力的合力,受力分析时不能加入向心力,故C 错误.例2 (多选)如图4所示,用长为L 的细线拴住一个质量为M 的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,重力加速度为g ,关于小球的受力情况,下列说法中正确的是( )图4A.小球受到重力、线的拉力和向心力三个力B.向心力是线对小球的拉力和小球所受重力的合力C.向心力的大小等于细线对小球拉力的水平分力D.向心力的大小等于Mg tan θ 答案 BCD二、匀速圆周运动问题分析 1.匀速圆周运动问题的求解方法圆周运动问题仍属于一般的动力学问题,无非是由物体的受力情况确定物体的运动情况,或者由物体的运动情况求解物体的受力情况. 解答有关匀速圆周运动问题的一般方法步骤:(1)确定研究对象、轨迹圆周(含圆心、半径和轨道平面). (2)受力分析,确定向心力的大小(合成法、正交分解法等). (3)根据向心力公式列方程,必要时列出其他相关方程. (4)统一单位,代入数据计算,求出结果或进行讨论. 2.几种常见的匀速圆周运动实例图形受力分析力的分解方法满足的方程及向心加速度⎩⎪⎨⎪⎧F cos θ=mg F sin θ=mω2l sin θ 或mg tan θ=mω2l sin θa n =g tan θ⎩⎪⎨⎪⎧F N cos θ=mg F N sin θ=mω2r 或mg tan θ=mrω2 a n =g tan θ⎩⎪⎨⎪⎧F 升cos θ=mg F 升sin θ=mω2r 或mg tan θ=mrω2a n =g tan θ⎩⎪⎨⎪⎧F N=mgF拉=m B g=mω2ra n=ω2r例3如图5所示,已知绳长为L=20 cm,水平杆长为L′=0.1 m,小球质量m=0.3 kg,整个装置可绕竖直轴转动.g取10 m/s2,问:(结果保留三位有效数字)图5(1)要使绳子与竖直方向成45°角,试求该装置必须以多大的角速度转动?(2)此时绳子的张力为多大?答案(1)6.44 rad/s(2)4.24 N解析小球绕竖直轴做圆周运动,其轨道平面在水平面内,对小球受力分析如图所示,设绳对小球拉力为F T,小球重力为mg,则绳的拉力与重力的合力提供小球做圆周运动的向心力.(1)对小球利用牛顿第二定律可得:mg tan 45°=mω2r,r=L′+L sin 45°联立并将数值代入可得ω≈6.44 rad/s(2)F T=mgcos 45°≈4.24 N.针对训练如图6所示,一只质量为m的老鹰,以速率v在水平面内做半径为R的匀速圆周运动,则空气对老鹰的作用力的大小等于(重力加速度为g)()图6A.m g2+(v2R)2 B.m(v2R)2-g2C.mv2R D.mg答案 A解析对老鹰进行受力分析,其受力情况如图所示,老鹰受到重力mg、空气对老鹰的作用力F.由题意可知,力F沿水平方向的分力提供老鹰做圆周运动的向心力,且其沿竖直方向的分力与重力平衡,故F 1=m v 2R ,F 2=mg ,则F =F 22+F 12=(mg )2+(m v 2R)2=mg 2+(v 2R)2,A 正确.三、变速圆周运动和一般的曲线运动用绳拴一沙袋,使沙袋在光滑水平面上做变速圆周运动,如图7.图7(1)分析绳对沙袋的拉力的作用效果.(2)如果将拉力按照其作用效果进行分解,两个分力各产生了怎样的加速度?分加速度的作用效果如何?答案 (1)绳对沙袋的拉力方向不经过圆心,即不与沙袋的速度方向垂直,而是与沙袋的速度方向成一锐角θ,如题图,拉力F 有两个作用效果,一是改变线速度的大小,二是改变线速度的方向.(2)根据F 产生的作用效果,可以把F 分解为两个相互垂直的分力:与圆周相切的分力F t 和指向圆心的分力F n ;F t 产生切线方向的加速度,改变线速度的大小,F n 产生向心加速度,改变线速度的方向.1.受力特点:变速圆周运动中合力不指向圆心,合力F 产生改变速度大小和方向两个作用效果.2.某一点的向心加速度和向心力仍可用公式a n =v 2r =ω2r ,F n =m v 2r=mω2r 求解.例4 如图8所示,物块P 置于水平转盘上随转盘一起运动,图中c 方向沿半径指向圆心,a 方向与c 方向垂直.当转盘逆时针转动时,下列说法正确的是( )图8A.当转盘匀速转动时,P 所受摩擦力方向为cB.当转盘匀速转动时,P 不受转盘的摩擦力C.当转盘加速转动时,P 所受摩擦力方向可能为aD.当转盘减速转动时,P 所受摩擦力方向可能为b 答案 A解析 转盘匀速转动时,物块P 所受的重力和支持力平衡,摩擦力提供其做匀速圆周运动的向心力,故摩擦力方向指向圆心O 点,A 项正确,B 项错误;当转盘加速转动时,物块P 做加速圆周运动,不仅有沿c 方向指向圆心的向心力,还有指向a 方向的切向力,使线速度大小增大,两方向的合力即摩擦力可能沿b 方向,不可能沿a 方向,C 项错误;当转盘减速转动时,物块P 做减速圆周运动,不仅有沿c 方向指向圆心的向心力,还有与a 方向相反的切向力,使线速度大小减小,两方向的合力即摩擦力可能沿d 方向,不可能沿b 方向,D 项错误.匀速圆周运动与变速圆周运动的比较运动种类 项目匀速圆周运动变速圆周运动特点 v 、a n 、F n 大小不变但方向变化,ω、T 、n 不变v 、a n 、F n 、ω、T 、n 均变化 向心力来源 合力 合力沿半径方向的分力周期性 有不一定有条件 合力的大小不变,方向始终与线速度方向垂直且指向圆心合力方向与线速度方向不垂直性质 均是非匀变速曲线运动 公式 F n =m v 2r =mω2r ,a n =v 2r=ω2r1.(向心力的理解)(多选)下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用力外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小答案ACD解析向心力是根据力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心,与线速度方向垂直,所以向心力只改变速度方向,不改变速度大小,A、C、D正确.2.(向心力的来源)狗拉雪橇沿位于水平面内的圆弧形道路匀速率行驶,下列给出的四个关于雪橇受到的牵引力F及摩擦力F f的示意图(图中O为圆心)正确的是()答案 C解析滑动摩擦力的方向与相对运动方向相反,雪橇做匀速圆周运动,合力应该指向圆心,可知C正确,A、B、D错误.3.(向心力公式的应用)(2019·棠湖中学高一质检)如图9所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.重力加速度为g,则在该同学手转塑料管使螺丝帽恰好不下滑时,下列分析正确的是()图9A.螺丝帽在重力和摩擦力作用下处于平衡状态B.螺丝帽受到塑料管的弹力方向水平向外,背离圆心C.此时手转动塑料管的角速度ω=g μrD.若塑料管的转动加快,螺丝帽有可能相对塑料管发生运动 答案 C解析 螺丝帽恰好不下滑,则有μF N =mg ,螺丝帽做匀速圆周运动,塑料管的弹力F N 提供向心力,则F N =mω2r ,联立解得ω=gμr,故C 正确. 4.(向心力公式的应用)(2019·南阳市高一下学期期末)如图10所示,长为L 的细绳的一端固定于O 点,另一端系一个小球,在O 点的正下方钉一个光滑的小钉子A ,小球从一定高度摆下,当细绳与钉子相碰时,钉子的位置距小球L4,则细绳碰到钉子前、后瞬间( )图10A.绳对小球的拉力之比为1∶4B.小球所受合外力之比为1∶4C.小球做圆周运动的线速度之比为1∶4D.小球做圆周运动的角速度之比为4∶1 答案 B解析 细绳与钉子相碰前后线速度大小不变,即线速度之比为1∶1,半径变小,根据v =ωr 得知,角速度之比为1∶4,故C 、D 错误.根据F 合=F -mg =m v 2r ,则合外力之比为1∶4,选项B 正确;拉力F =mg +m v 2r ,可知拉力之比F 1F 2=g +v 2L g +4v 2L =gL +v 2gL +4v 2≠14,选项A 错误.5.(向心力公式的应用)如图11所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做同方向的匀速圆周运动,则它们的( )图11A.运动周期不同B.运动线速度大小相同C.运动角速度大小相同D.向心加速度大小相同 答案 C解析 对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;将重力与拉力合成,合力指向圆心,由几何关系得,合力:F =mg tan θ①由向心力公式得:F =mω2r ②设小球与悬挂点间的高度差为h ,由几何关系,得:r =h tan θ③ 由①②③得,ω=gh,可知角速度大小与绳子的长度和转动半径无关,两球角速度大小相同,故C 正确;又由T =2πω可知两球运动周期相同,故A 错误;由v =ωr 可知,两球转动半径不等,线速度大小不同,故B 错误;由a =ω2r 可知,两球转动半径不等,向心加速度大小不同,故D 错误.[基础对点练]考点一 向心力的理解及向心力来源分析1.对做圆周运动的物体所受的向心力说法正确的是( )A.做匀速圆周运动的物体,因向心力总是沿半径指向圆心,且大小不变,故向心力是一个恒力B.因向心力指向圆心,且与线速度方向垂直,所以它不能改变线速度的大小C.向心力一定是物体所受的合外力D.向心力和向心加速度的方向都是不变的 答案 B解析 做匀速圆周运动的物体向心力大小恒定,方向总是指向圆心,是一个变力,A 错;向心力只改变线速度方向,不改变线速度大小,B 对;只有做匀速圆周运动的物体的向心力是由物体所受合外力提供的,C 错;向心力与向心加速度的方向总是指向圆心,是时刻变化的,D 错.2.如图1,一水平圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F 的方向的四种表示(俯视图)中,正确的是( )图1答案 C解析橡皮块做加速圆周运动,合力不指向圆心,但一定指向圆周的内侧;由于做加速圆周运动,速度不断增大,故合力与速度的夹角小于90°,故选C.3.(2019·泉州五中期中)如图2所示,在粗糙水平木板上放一个物块,使水平木板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则()图2A.物块始终受到三个力作用B.只有在a、b、c、d四点,物块受到的合外力才指向圆心C.从a到b,物块所受的摩擦力先增大后减小D.从b到a,物块处于超重状态答案 D解析在c、d两点处,只受重力和支持力,在其他位置处物块受到重力、支持力、静摩擦力三个作用力,故A错误;物块做匀速圆周运动,合外力提供向心力,所以合外力始终指向圆心,故B错误;从a运动到b,物块的加速度的方向始终指向圆心,水平方向的加速度先减小后反向增大,根据牛顿第二定律知,物块所受木板的摩擦力先减小后增大,故C错误;从b运动到a,向心加速度有向上的分量,则物块处于超重状态,故D正确.4.(多选)(2019·安徽师大附中高一下学期期末)如图3所示,小球m用两根长度相等的细绳系在竖直杆上,细绳不可伸长,当杆旋转时,对小球受力分析正确的是()图3A.受重力、绳的拉力和向心力作用B.可能受重力、一根绳的拉力共两个力作用C.可能受重力、两根绳的拉力共三个力作用D.上面一根绳的拉力总大于小球的重力 答案 BCD解析 转速较小时,小球受重力和一根绳的拉力作用,转速较大时,小球受重力和两根绳的拉力作用,故A 错误,B 、C 正确.只有上面一根绳有拉力时,绳的竖直分力大小等于球的重力;如果两根绳都有拉力,上面绳的竖直分力大小等于球的重力和下面绳拉力的竖直分力之和,所以上面一根绳的拉力一定比球的重力大,故D 正确. 考点二 向心力公式的应用5.(多选)在光滑的水平面上,用长为l 的细线拴一质量为m 的小球,以角速度ω做匀速圆周运动,下列说法中正确的是( ) A.l 、ω不变,m 越大,线越易被拉断 B.m 、ω不变,l 越小,线越易被拉断 C.m 、l 不变,ω越大,线越易被拉断D.m 不变,l 减半且角速度加倍时,线的拉力不变 答案 AC解析 线上拉力越大,线越容易断,由向心力表达式F 向=mω2l 可知,A 、C 项正确,B 项错误;m 不变,l 减半而角速度ω加倍时,线的拉力加倍,D 项错误.6.一质量为m 的物体,沿半径为R 的向下凹的半圆形轨道滑行,如图4所示,经过最低点时的速度为v ,物体与轨道之间的动摩擦因数为μ,重力加速度为g ,则它在最低点时受到的摩擦力为( )图4A.μmgB.μm v 2RC.μm (g +v 2R )D.μm (g -v 2R)答案 C解析 在最低点由向心力公式得:F N -mg =m v 2R ,得F N =mg +m v 2R ,又由摩擦力公式有F f =μF N =μ(mg +m v 2R )=μm (g +v 2R),C 选项正确.7.(2019·安徽师大附中高一下学期期末)如图5所示,竖直固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A 和B ,在各自不同的水平面内做匀速圆周运动.以下关于A 、B 两球做圆周运动时的速度(v A 、v B )、角速度(ωA 、ωB )、加速度(a A 、a B )和对内壁的压力(F N A 、F N B )的说法正确的是( )图5A.v A >v BB.ωA >ωBC.a A >a BD.F N A >F N B答案 A解析 对小球受力分析如图所示,可得F N =mg sin θ,F n =mgtan θ,由于两个小球的质量相同,并且都是在水平面内做匀速圆周运动,即θ相同,所以两个小球的向心力的大小和受到的支持力的大小都相同,所以有F N A =F N B ,a A =a B ,故C 、D 错误;由于它们的受力相同,向心力的大小也相同,由向心力的公式F n =m v 2r 可知,半径大的,线速度大,所以v A >v B ,故A 正确;由向心力的公式F n =mrω2可知,半径大的,角速度小,所以ωA <ωB ,故B 错误.8.(多选)如图6所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测体重为G 的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,重力加速度为g ,估算该女运动员( )图6A.受到的拉力为3GB.受到的拉力为2GC.向心加速度为3gD.向心加速度为2g答案 BC解析设女运动员受到的拉力为F,分析女运动员受力情况可知,F sin 30°=G,F cos 30°=ma向,可得:F=2G,a向=3g,故B、C正确.[能力综合练]9.(多选)(2019·北京十二中期末)如图7所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔的水平桌面上,小球在某一水平面内做匀速圆周运动(即圆锥摆).现使小球在一个更高一些的水平面内做匀速圆周运动(图上未画出),两次金属块Q都保持在桌面上静止,则后一种情况与原来相比较,下列说法正确的是()图7A.小球P运动的周期变大B.小球P运动的线速度变大C.小球P运动的角速度变小D.Q受到桌面的支持力不变答案BD解析设细线与竖直方向的夹角为θ,细线的拉力大小为F T,细线的长度为L.球P做匀速圆周运动时,由重力和细线的拉力的合力提供向心力,则有mg tan θ=mω2L sin θ,得角速度ω=gL cos θ,周期T=2πω=2πL cos θg,线速度v=rω=L sin θ·gL cos θ=gL tan θsin θ,小球在一个更高一些的水平面内做匀速圆周运动时,θ增大,cos θ减小,角速度增大,周期T 减小,线速度变大,选项B正确,A、C错误;金属块Q保持在桌面上静止,对金属块和小球研究,在竖直方向没有加速度,根据平衡条件可知,Q受到桌面的支持力等于Q与小球的总重力,保持不变,选项D正确.10.(多选)如图8所示,A、B两球穿过光滑水平杆,两球间用一细绳连接,当该装置绕竖直轴OO′匀速转动时,两球在杆上恰好不发生滑动.若两球质量之比m A∶m B=2∶1,那么关于A、B两球的下列说法中正确的是()图8A.A、B两球受到的向心力之比为2∶1B.A、B两球角速度之比为1∶1C.A、B两球运动半径之比为1∶2D.A、B两球向心加速度之比为1∶2答案BCD解析两球的向心力都由细绳的拉力提供,大小相等,两球都随杆一起转动,角速度相等,A错误,B正确.设两球的运动半径分别为r A、r B,转动角速度为ω,则m A r Aω2=m B r Bω2,因为m A∶m B=2∶1,所以运动半径之比为r A∶r B=1∶2,C正确.由牛顿第二定律F=ma可知a A∶a B=1∶2,D正确.11.质量相等的小球A、B分别固定在轻杆的中点及端点,当杆在光滑的水平面上绕O点匀速转动时,如图9所示,求杆的OA段及AB段对球的拉力之比.图9答案3∶2解析球所受的重力和水平面的支持力在竖直面内,且是一对平衡力,不能提供向心力.球做圆周运动的向心力由杆的OA段和AB段的拉力提供.分别隔离A、B受力分析,如图所示.由于A、B放在水平面上,故G=F N,又有A、B固定在同一根轻杆上,所以A、B的角速度相同,设角速度为ω,则由向心力公式可得:对A:F OA -F AB=mrω2,对B:F AB′=2mrω2又F AB=F AB′,联立三式,解得F OA∶F AB=3∶2.12.如图10所示,有一质量为m的小球在光滑的半球形碗内做匀速圆周运动,轨道平面在水平面内.已知小球与半球形碗的球心O的连线跟竖直方向的夹角为θ,半球形碗的半径为R,重力加速度为g,求小球做匀速圆周运动的速度大小及碗壁对小球的弹力大小.图10答案gRcos θ·sin θmgcos θ解析小球受力如图所示,mg tan θ=m v 2rr =R sin θ F N cos θ=mg联立以上三式解得v = gRcos θ·sin θ F N =mg cos θ13.如图11所示装置可绕竖直轴OO ′转动,可视为质点的小球A 与两细线连接后分别系于B 、C 两点,当细线AB 沿水平方向绷直时,细线AC 与竖直方向的夹角θ=37°.已知小球的质量m =1 kg ,细线AC 长L =1 m.(重力加速度g 取10 m/s 2,sin 37°=0.6,cos 37°=0.8)图11(1)若装置匀速转动,细线AB 刚好被拉直成水平状态,求此时的角速度ω1的大小; (2)若装置匀速转动的角速度ω2=563 rad/s ,求细线AB 和AC 上的张力大小F T AB 、F T AC .答案 (1)522rad/s (2)2.5 N 12.5 N解析 (1)当细线AB 刚好被拉直,则AB 的拉力为零,靠AC 的拉力和重力的合力提供向心力,根据牛顿第二定律有mg tan 37°=mL AB ω12,又有L AB =L sin 37°,解得ω1=g tan 37°L AB=10×341×35rad/s =522 rad/s (2)若装置匀速转动的角速度ω2=563 rad/sL AB =L sin 37°竖直方向上有F T AC cos 37°=mg水平方向上有F T AC sin 37°+F T AB =mL AB ω22代入数据解得F T AC=12.5 N,F T AB=2.5 N.。
22匀速圆周运动的向心力和向心加速度

Vቤተ መጻሕፍቲ ባይዱ
F OO F
1. 定义:物体做匀速圆周
F
运动时所受合力方向始终指 V
V
向圆心,这个指向圆心的合
力就叫做向心力。
2.特点:方向始终与V垂直,指向圆心。 是变力
3.作用效果:只改变V的方向,不改变V的大小。
活动:感受向心力
使轻绳栓一小球,在光 滑水平面做匀速圆周运 动。感受向心力的大小 与哪些因素有关?
实验探究:向心力的大小与m、ω和r的关系。 1、实验装置介绍:
2、控制变量法:
4.向心力大小:
F = m r ω2
或:F=m
v2 r
问题:F与r究竟是成正比呢, 还是成反比?
若ω一定 , 就成正比 ;若v 一定 , 就成反比 。
二. 向心加速度 方向: 沿半径指向圆心 v2 大小: a = rω2 或 a = r
例题:教材29页练习与评价第3题 课堂练习:三维设计书上基础自练1、2、3、4题
作业 1、三维设计书上基础知识填空部分做书上; 2、三维设计活页全做。
2 匀速圆周运动的向心力和向心加速度
小球受力分析:
N OO F
G
结论:1、N与G相抵消,所以合力为F; 2、合力方向指向圆心
思考:其它匀速圆周运动的合力方向指向圆心吗?
旋转秋千:
F
F1 F2
G
结论:F2就是物体所受 合力,方向指向圆心。
温馨提示:做匀速圆周 运动物体所受合力方向 总指向圆心。
一. 向心力
高一物理讲义《圆周运动的规律》

知识点1描述圆周运动的物理量1. 线速度若在时间t 内,做匀速圆周运动的质点通过的弧长是s ,则用比值/s t 来描述匀速圆周运动的快慢,这个比值称为匀速圆周运动的线速度.公式:sv t =,单位:米/秒.线速度是物体做匀速圆周运动的瞬时速度.线速度是矢量,它既有大小,也有方向.线速度的大小,sv t =.方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向.物理意义:描述质点沿圆周运动的快慢.2. 角速度物体在t ∆时间内由A 运动到B ,半径OA 在这段时间内转过的角度为θ∆,则θ∆与t ∆的比值描述了物体绕圆心转动的快慢,这个比值叫做角速度.角速度用ω表示:=t θω∆∆,角速度单位为弧度每秒.符号:rad/s .角速度的物理意义:描述质点转过圆心角的快慢.角速度也是矢量,不过中学物理不讨论角速度方向问题. 3. 周期做匀速圆周运动的物体运动一周所用的时间叫做周期.用符号T 表示,周期的单位和时间单位一样. 4. 频率表示一秒内转过的圈数,周期的倒数叫做频率用符号f 表示;f =1/T .频率越高表明物体运转得越快! 5. 转数匀速圆周运动的物体单位时间转过的圈数,叫转速常用符号n 表示,单位r /s ,以及r/min ,转速n 越大表明物体运动得越快! 知识点2:线速度、角速度和周期的关系设某一物体沿半径为r 的圆周做匀速圆周运动,用v 表示线速度,用ω表示角速度,T 表示周期,则:v 与T 的关系:2/v r T π=,ω与T 的关系:2/T ωπ=,v 与ω的关系:v r ω= 知识点3:匀速圆周运动定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动.尽管做匀速圆周运动的物体在各个时刻的线速度大小相等,但线速度的方向是不断变化着的.匀速圆周运动是一种变速知识讲解圆周运动的规律曲线运动,“匀速”是指线速度的大小不变,即“匀速率”.匀速圆周运动是角速度不变的运动!匀速圆周运动是周期不变的运动! 知识点4:常见传动从动装置主动轮通过皮带、链条、齿轮等带动从动轮的过程中,皮带(链条)上各点以及两轮边缘上各点的线速度大小相等.同一轮上各点的角速度相同.【例1】 匀速圆周运动是( )A .匀速率运动B .匀变速运动C .匀加速运动D .变加速运动【例2】 一个质点做匀速圆周运动,已知该质点的角速度为ω,半径为r ,则它运动的线速度为( )A .ω2rB .ωrC .ω/rD .ωr 2【例3】 做匀速圆周运动的质点是处于( )A .平衡状态B .不平衡状态C .速度不变的状态D .加速度不变的状态【例4】 一物体以一定的半径做匀速圆周运动,它的线速度为v ,角速度为ω,经过一段短暂的时间后,物体通过的弧长为S ,半径转过的角度为φ,则下列关于S 的表达式中正确的是( ) A .ωϕ⋅=v S B .ϕω⋅=v SC .v S ϕω⋅=D .ϕω⋅=v S【例5】 如图所示,a 、b 是地球表面不同纬度上的两个点,如果把地球看作是一个球体,且a 、b 两点随地球的自转看作是做匀速圆周运动,则这两个点具有相同的:( ) A .线速度 B .角速度 C .周期 D .运动半径【例6】 如图所示,一个环绕中心线OO′以角速度ω转动,则:( )A .A 、B 两点的角速度相等例题精讲AOωB .A 、B 两点的线速度相等C .若θ=30°,则v A ∶v B =3∶2D .以上答案都不对知识点1:向心加速度在向心力作用下物体产生的加速度叫做向心加速度.向心加速度的方向:总是沿半径指向圆心,每时每刻在不断地变化.向心加速度大小:2222a r v r r T πω⎛⎫=== ⎪⎝⎭.向心加速度的方向与速度方向垂直.向心加速度是描述速度方向变化快慢的物理量. 知识点2:向心力向心力:做匀速圆周运动的物体受到的合外力总是指向圆心,这个力叫做向心力.向心力的方向:总是沿半径指向圆心,方向时刻在改变.因此向心力是变力.向心力的大小:2222=F ma m r mv r m r T πω⎛⎫=== ⎪⎝⎭向向心力的作用效果:只改变速度的方向,不改变速度的大小.向心力的来源:可以由重力、弹力、摩擦力等提供.总之是物体所受的合外力提供了物体做匀速圆周运动所需的向心力. 知识点3:几种典型匀速圆周运动的向心力来源1. 圆锥摆:向心力由拉力F 和重力G 的合力提供.2. 物体相对转盘静止,随盘做匀速圆周运动:木块做圆周运动所需向心力,由圆盘对木块的静摩擦力f 提供.3. 卫星绕地球运动:向心力由万有引力提供.4. 轻绳栓一小球,在光滑水平面做匀速圆周运动.5. 滚筒洗衣机中物体跟着滚筒匀速转动.知识讲解【例7】 对于做匀速圆周运动的物体,下列说法中正确的是:( )A .在任何时刻,物体所受的合力一定为零B .质点运动的方向一定不断改变C .在任何时刻,质点的加速度一定为零D .质点运动的线速度大小一定不断改变【例8】 匀速圆周运动中的向心加速度是描述:( )A .线速度大小变化的物理量B .线速度大小变化快慢的物理量C .线速度方向变化的物理量D .线速度方向变化快慢的物理量【例9】 如图所示,为一在水平面内做匀速圆周运动的圆锥摆,关于摆球A 的受力情况,下列说法中正确的是( )A .摆球A 受重力、拉力和向心力的作用B .摆球A 受拉力和向心力的作用C .摆球A 受拉力和重力的作用D .摆球A 受重力和向心力的作用【例10】 如图为一皮带传动装置,右轮半径为r ,a 为它边缘上一点;左侧是一轮轴,大轮半径为4r ,小轮半径为2r ,b 点在小轮上,到小轮中心的距离为r .c 点和d 点分别位于左侧小轮和大轮的边缘上.若传动过程中皮带不打滑,则:( ) A .a 点和b 点的线速度大小相等 B .a 点和b 点的角速度大小相等 C .a 点和c 点的线速度大小相等 D .a 点和d 点的向心加速度大小相等例题精讲cb d r2r 4rrA【例11】 甲乙两个物体均做匀速圆周运动,甲的质量和轨道半径均为乙的一半,当甲转过60°时,乙在这段时间里正好转过45°,则甲乙两个物体的向心力之比为多少?【例12】 质量一定的物体做匀速圆周运动时,如所需的向心力要增为原来的8倍,现有以下各种措施:①线速度和圆半径加倍;②角速度和圆半径加倍;③周期和圆半径加倍;④频率和圆半径加倍.则其中正确的是:( ) A .①和③ B .②和④C .①和④D .②和③【例13】 质点做匀速圆周运动,当线速度为v 时,圆周半径为R ,若保持向心力大小不变,当圆周半径为2R 时,角速度应为:( )A .R v 2B .R v 22C .R vD .Rv 2【例14】 甲、乙两个质点绕同—圆心做匀速圆周运动,甲的转动半径是乙的3/4,当甲转动60周时,乙转动了45周,则甲、乙两个质点的向心加速度之比a a 乙甲:等于:( ) A .4:3 B .3:4 C .1:2 D .2:1【例15】 做匀速圆周运动的物体,圆轨道半径为R ,向心加速度为a ,则以下的关系式不正确的是:( )A .线速度v aR =B .角速度aRω=C .频率Raf π2= D .周期a R T π2=【例16】 关于做匀速圆周运动物体的向心加速度方向,下列说法正确的是:( ) A .与线速度方向始终相同 B .与线速度方向始终相反C .始终指向圆心D .始终保持不变【例17】 洗衣机的甩干筒在转动时有一衣物质附在筒壁上,则此时( )A .衣物受到重力、筒壁的弹力和摩擦力的作用B .衣物随筒壁做圆周运动的向心力是由于摩擦的作用C .筒壁的弹力随筒的转速增大而增大D .筒壁对衣物的摩擦力随转速增大而增大【例18】 同一辆汽车以同样大小的速度先后开上平直的桥和凸形桥,在桥的中央处有( )A .车对两种桥面的压力一样大B .车对平直桥面的压力大C.车对凸形桥面的压力大D.无法判断【例19】对于做匀速圆周运动的物体,下列说法正确..的是()A.相等的时间内通过的路程相等B.向心加速度是不变的C.向心力不随时间变化是恒力D.线速度是不变的【例20】如图所示,小物体A与圆盘保持相对静止跟着圆盘一起做匀速圆周运动,则A受力情况是()A.重力、支持力B.重力、向心力AC.重力、支持力、指向圆心的摩擦力D.重力、支持力、向心力、摩擦力【例21】关于向心加速度的叙述,正确的是()A.向心加速度是由向心力产生的B.向心加速度的方向与向心力方向相同C.向心加速度与速度方向相同D.向心加速度是矢量【例22】下列关于匀速圆周运动的叙述,正确的是()A.速率是恒定的B.周期是恒定的C.速度是恒定的D.角速度是恒定【例23】在绕同一转轴转动物体上的不同点,下列哪些物理量是相同的()A.线速度B.角速度C.周期D.向心加速度【例24】如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则:()A.球A的角速度一定大于球B的角速度B.球A的线速度一定大于球B的线速度C.球A的运动周期一定小于球B的运动周期D.球A对筒壁的压力一定大于球B对筒壁的压力1、 某质点绕圆轨道做匀速圆周运动,下列说法中正确的是:( )A .因为它的速度大小始终不变,所以它做的是匀速运动B .它速度大小不变,但方向时刻改变,是变速运动C .该质点速度大小不变,因而加速度为零,处于平衡状态D .该质点做的是变速运动,具有加速度,故它所受合外力不等于零 2、 做匀速圆周运动的物体,下列物理量时刻发生变化的是:( )A .速度B .加速度C .角速度D .周期3、 一小球被细绳拴着,在水平面内做半径为R 的匀速圆周运动,向心加速度为a .那么( )A .小球运动的角速度ω=RaB .小球在时间t 内通过的路程为s=aR tC .小球做匀速圆周运动的周期T=aR D .小球在时间t 内可能发生的最大位移为2R4、 图示所示为某一皮带传动装置.主动轮的半径为r 1,从动轮的半径为r 2.已知主动轮做顺时针转动,转速为n ,转动过程中皮带不打滑.下列说法正确的是( ) A .从动轮做顺时针转动B .从动轮做逆时针转动C .从动轮的转速为n r r 21D .从动轮的转速为n r r 125、 如图所示,定滑轮的半径r=2 cm ,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s 2做匀加速运动,在重物由静止下落距离为 1 m 的瞬间,滑轮边缘上的点的角速度ω=__________rad/s ,向心加速度a=_________m/s 2.基础演练1、 做平抛运动的物体,每秒的速度增量总是( )A .大小相等,方向相同B .大小不等,方向不同C .大小相等,方向不同D .大小不等,方向相同2、 在无风的情况下,跳伞运动员从水平飞行的飞机上跳伞,下落过程中受到空气阻力,下列描绘下落速度的水平分量大小x v 、竖直分量大小y v 与时间t 的图像,可能正确的是( )3、 正在做匀加速直线行驶的列车,顶棚上脱落一小螺钉.关于小螺钉的运动情况,以下说法正确的是( )A .列车上的乘客看到螺钉做直线运动B .列车上的乘客看到螺钉做曲线运动C .地面上的人看到螺钉做直线运动D .地面上的人看到螺钉做曲线运动4、 如右图所示,在一次救灾工作中,一架沿水平直线飞行的直升飞机A ,用悬索(重力可忽略不计)救护困在湖水中的伤员B .在直升飞机 A 和伤员 B 以相同的水平速度匀速运动的同时,悬索将伤员吊起,在某一段时间内,A 、B 之间的距离以2l H t =-(式中H 为直升飞机A 离地面的高度,各物理量的单位均为国际单位制单位)规律变化,则在这段时间内( ) A .悬索的拉力等于伤员的重力 B .悬索是竖直的C .伤员做加速度大小和方向均不变的曲线运动D .伤员做速度大小增加的曲线运动5、 如图,已知排球网高H ,半场长L ,扣球点高h ,扣球点离网水平距离s 、求水平扣球速度的取值范围.课后练习6、 一水平放置的水管,距地面高h=1.8m ,管内横截面积S=2.02cm .有水从管口处以不变的速度2.0v m s =源源不断地沿水平方向射出,设出口处横截面上各处水的速度都相同,并假设水流在空中不散开.取重力加速度2/10s m g =,不计空气阻力.求水流稳定后在空中有多少立方米的水.7、 如图所示,从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜面上,当抛出的速度为1v 时,小球到达斜面时速度方向与斜面的夹角为1α;当抛出速度为2v 时,小球到达斜面时速度方向与斜面的夹角为2α,则( ) A .当1v >2v 时,1α>2αB .当1v >2v 时,1α<2αC .无论1v 、2v 关系如何,均有1α=2αD .1α、2α 的关系与斜面的倾角θ有关。
向心力 课件-高一物理人教版(2019)必修第二册

B.运动周期TA>TB
C.它们受到的摩擦力fA>fB
G
D.筒壁对它们的弹力NA>NB
牛二:确定圆心/半径→受力分析→(分解)→x轴/y轴列式
拓展:增大转速,f 和 N 如何改变?
二、牛二应用
4.(多选)如图所示,物块在水平圆盘上,与圆盘一起绕固定轴匀速运动.下列说法
中正确的是( ) A.物块处于平衡状态 B.物块受三个力作用
mg
方法:对象→圆(水平、竖直)→圆心→受力分析
一、课前练习
2、如图所示,质量相等的A、B两物体(可视为质点)放在圆盘上,到圆心的距离之比 是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止.则A、B两物体做圆周 运动的向心力之比为( ) A.1:1 B. 3:2 C. 2:3 D. 4:9 要点:寻找合适的公式 方法:控制变量法
(1)物块做平抛运动的初速度大小v0; (2)物块与转台间的动摩擦因数μ. 牛二:确定圆心/半径→受力分析→(分解)→x轴/y轴列式
二、牛二应用
5、质量为m的小球做圆锥摆时,细绳长 L,与竖直方向成 θ 角,求小球做匀速圆周
运动的拉力大小和角速度 ω 。
结论:圆锥摆角速度仅与摆球距离绳子结点的高度h有关
X轴:
G
三、课堂练习
5、图甲为游乐场中一种叫“魔盘”的娱乐设施,游客坐在转动的魔盘上,当魔盘转
速增大到一定值时,游客就会滑向盘边缘,其装置可以简化为图乙.若魔盘转速缓
慢增大,则游客在滑动之前
()
A.游客受到魔盘的摩擦力缓慢增大
B.游客始终处于平衡状态
C.游客受到魔盘的支持力缓慢增大
D.游客受到的合外力大小不变
平衡状态:匀速直线和静止 运动分析,牛二列式
高中物理匀速圆周运动公式总结

高中物理匀速圆周运动公式总结高中物理匀速圆周运动公式1、线速度V=s/t=2&pi;r/T2。
角速度&omega;=&Phi;/t=2π/T=2πf3、向心加速度a=V2/r=&omega;2r=(2&pi;/T)2r4、向心力F=mV2/r=m&omega;2r=mr(2&pi;/T)2=m&omega;v=F合5。
周期与频率:T=1/f6、角速度与线速度的关系:V=&omega;r7。
角速度与转速的关系&omega;=2πn(此处频率与转速意义相同)8、主要物理量及单位:弧长(s):米(m);角度(&Phi;):弧度(rad);频率(f):赫(Hz);周期(T):秒(s);转速(n):r/s;半径(r):米(m);线速度(V):m/s;角速度(&omega;):rad/s;向心加速度:m/s2。
注:(1)向心力能够由某个具体力提供,也能够由合力提供,还能够由分力提供,方向始终与速度方向垂直,指向圆心;(2)做匀速圆周运动的物体,其向心力等于合力,同时向心力只改变速度的方向,不改变速度的大小,因此物体的动能保持不变,向心力不做功,但动量不断改变。
高中物理匀速圆周运动知识点1、关于匀速圆周运动(1)条件:①物体在圆周上运动;②任意相等的时间里通过的圆弧长度相等。
(2)性质:匀速圆周运动是加速度变化(大小不变而方向不断变化)的变加速运动。
(3)匀速圆周运动的向心力:①是按力的作用效果来命名的力,它不是具有确定性质的某种力,相反,任何性质的力都能够作为向心力。
例如,小铁块在匀速转动的圆盘上保持相对静止的原因是,静摩擦力充当向心力,若圆盘是光滑的,就必须用线细拴住小铁块,才能保证小铁块同圆盘一起做匀速转动,这时向心力是由细线的拉力提供、②向心力的作用效果是改变线速度的方向。
做匀速圆周运动的物体所受的合外力即为向心力,它是产生向心加速度的原因,其方向一定指向圆心,是变化的(线速度大小变化的非匀速圆周运动的物体所受的合外力不指向圆心,它既要改变速度方向,同时也改变速度的大小,即产生法向加速度和切向加速度)。
2021-高中物理人教版必修第二册课件:第六章圆周运动 第2节向心力

A.1∶3 B.3∶1 C.1∶9 D.9∶1
【解析】ꢀ在研究向心力的大小F与质量m、角速度ω和半径r之间的关系时,需先控制某些量不变,研究另外两个物理量的关系,该方 法为控制变量法。 (1)因F=mω2r,根据控制变量法的原理可知,在研究向心力的大小F与质量m的关系时,要保持其他的物理量不变,即保持角速度ω 和半径r相同,故选A。 (2)题图中所示两球的质量相同,转动的半径相同,根据F=mω2r可知,研 究的是向心力的大小F与角速度ω的关系,故选C。 (3)根据F=mω2r可知,两球的向心力之比为1∶9,半径和质量相等,则转动的角速度之比为1∶3,因为靠皮带传动,变速塔轮的线速 度大小相等,根据v=rω可知与皮带连接的两个变速塔轮对应的半径之比为3∶1,故选B。
题6[2019·云南宣威九中高一检测][多选]如图所示,A、B两个小球质量相
等,用一根轻绳相连,另有一根轻绳的两端分别连接O点和B点,让两个小球绕
O点在光滑水平桌面上以相同的角速度做匀速圆周运动,若OB绳上的拉力为F1
,AB绳上的拉力为F2,OB=AB,则(CDꢀꢀ)
A.A球所受向心力为F1,B球所受向心力为F2 B.A球所受向心力为F2,B球所受向心力为F1
轻绳栓一小球,在光滑桌面上做匀速圆周运动
小球受到几个力的作用? 这几个力的合力沿什么方向?
F
FN
G
小球受到重力、桌面的支持力和绳子的拉力。
重力和支持力相互抵消,合力为绳子的拉力,沿着绳子指 向圆心。
向心力
1、定义:
做匀速圆周运动的物体一定受到一个指向圆心的合 力,这个力叫做向心力
2、方向特点:
总指向圆心,沿半径方向与线速度垂直,方向不断 变化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀速圆周运动向心力一、教学目标1.物理知识方面:(1)理解匀速圆周运动是变速运动;(2)掌握匀速圆周运动的线速度、角速度、周期的物理意义及它们间的数量关系;(3)初步掌握向心力概念及计算公式。
2.通过匀速圆周运动、向心力概念的建立过程,培养学生观察能力、抽象概括和归纳推理能力。
3.渗透科学方法的教育。
二、重点、难点分析向心力概念的建立及计算公式的得出是教学重点,也是难点。
通过生活实例及实验加强感知,突破难点。
三、教具1.转台、小伞;2.细绳一端系一个小球(学生两人一组);3.向心力演示器。
四、主要教学过程(一)引入新课演示:将一粉笔头分别沿竖直向下、水平方向、斜向上抛出,观察运动轨迹。
复习提问:粉笔头做直线运动、曲线运动的条件是什么?启发学生回答:速度方向与力的方向在同一条直线上,物体做直线运动;不在同一直线上,做曲线运动。
进一步提问:在曲线运动中,有一种特殊的运动形式,物体运动的轨迹是一个圆周或一段圆弧(用单摆演示),称为圆周运动。
请同学们列举实例。
(学生举例教师补充)电扇、风车等转动时,上面各个点运动的轨迹是圆……大到宇宙天体如月球绕地球的运动,小到微观世界电子绕原子核的运动,都可看做圆周运动,它是一种常见的运动形式。
提出问题:你在跑400米过弯道时身体为何要向弯道内侧微微倾斜?铁路和高速公路的转弯处以及赛车场的环形车道,为什么路面总是外侧高内侧低?可见,圆周运动知识在实际中是很有用的。
引入:物理中,研究问题的基本方法是从最简单的情况开始。
板书:匀速圆周运动(二)教学过程设计思考:什么样的圆周运动最简单?引导学生回答:物体运动快慢不变。
板书:1.匀速圆周运动物体在相等的时间里通过的圆弧长相等,如机械钟表针尖的运动。
思考:匀速周圆运动的一个显著特点是具有周期性。
用什么物理量可以描述匀速圆周运动的快慢?(学生自由发言)板书:2.描述匀速圆周运动快慢的物理量恒量。
当t很短,s很短,即为某一时刻的瞬时速度。
线速度其实就是物体做圆周运动的瞬时速度。
当物体做匀速圆周运动时,各个时刻线速度大小相同,而方向时刻在改变。
那么,线速度方向有何特点呢?演示:水淋在小伞上,同时摇动转台。
观察:水滴沿切线方向飞出。
思考:说明什么?师生分析:飞出的水滴在离开伞的瞬间,由于惯性要保持原来的速度方向,因而表明了切线方向即为此时刻线速度的方向。
板书:方向:沿着圆周各点的切线方向。
如图3。
单位:rad/s。
(3)周期:质点沿圆周运动一周所用的时间。
如:地球公转周期约365天,钟表秒针周期60s等,周期长,表示运动慢。
(角速度、周期可由学生自己说出并看书完成)板书:(师生共同完成)思考:物体做匀速圆周运动时,v、ω、T是否改变?(ω、T不变,v大小不变、方向变。
)讲述:匀速周周运动是匀速率圆周运动的简称,它是一种变速运动。
提出问题:匀速圆周运动是一种曲线运动,由物体做曲线运动的条件可知,物体必定受到一个与它的速度方向不在同一条直线上的合外力作用,这个合外力的方向有何特点呢?学生小实验(两人一组):线的一端系一小球,使小球在水平面内做匀速圆周运动。
小球质量很小(可用橡皮塞等替代),甩动时线速度尽量大,小球重力与拉力相比可忽略,以保证拉线近似在水平方向。
观察并思考:①小球受力?②线的拉力方向有何特点?③一旦线断或松手,结果如何?(提问学生后板书并图示)概括:要使物体做匀速圆周运动,必须使物体受到与速度方向垂直而指向圆心的力作用,故名向心力。
板书:3.向心力:物体做匀速圆周运动所需要的力。
提出问题:向心力的大小跟什么因素有关?(学生自己设想,用刚才的仪器做小实验,凭感觉粗略体验。
学生经实验、讨论有了自己的看法后,自由发言。
)演示实验(验证学生的设想):研究向心力跟物体质量m、轨道半径r、角速度ω的定量关系。
提问:实验时能否让三个量同时变。
保持两个量不变,使一个量变化。
实验装置:向心力演示器。
演示:摇动手柄,小球随之做匀速圆周运动。
提问:向心力由什么力提供?如何测量?小球向外压挡板,挡板对小球的反作用力指向转轴,提供了小球做匀速圆周运动的向心力,两力大小相等,同时小球压挡板的力使挡板另一端压缩套在轴上的弹簧,弹簧被压缩的格数可以从标尺中读出,即显示了向心力大小。
演示内容:①向心力与质量的关系:ω、r一定,取两球使m A=2m B观察:(学生读数)F A=2F B 结论:向心力F∝m②向心力与半径的关系:m、ω一定,取两球使r A=2r B观察:(学生读数)F A=2F B 结论:向心力F∝r③向心力与角速度的关系:m、r一定,使ωA=2ωB观察:(学生读数)F A=4F B 结论:向心力F∝ω2归纳:综合上述实验结果可知:物体做匀速圆周运动需要的向心力与物体的质量成正比,与半径成正比,与角速度的二次方成正比。
但不能由一个实验、一个测量就得到一般结论,实际上要进行多次测量,大量实验,但我们不可能一一去做。
同学们刚才所做的实验得出:m、r、ω越大,F越大;若将实验稍加改进,如课本中所介绍的小实验,加一弹簧秤测出F,可粗略得出结论(要求同学回去做)。
我们还可以设计很多实验都能得出这一结论,说明这是一个带有共性的结论。
测出m、r、ω的值,可知向心力大小为:F=mrω2。
反馈练习:①对于做匀速圆周运动的物体,下面说法正确的是:A速度不变;B速率不变;C角速度不变;D周期不变。
②如图7为一皮带传动装置,在传动过程中皮带不打滑。
试比较轮上A、B、C三点的线速度、角速度大小。
③物体做匀速圆周运动所需要的向心力跟半径的关系,有人说成正比,有人说成反比。
你对这两种说法是如何理解的?④(前后呼应)解释跑400m弯道时身体为何要倾斜等一类问题。
(火车拐弯要求课后看书)(三)课堂小结1.科学方法①点明建立概念的过程:是通过大量实例,概括抽象出本质的内容,即由个别到一般的思维过程。
②点明实验归纳的过程:必须经过多次实验,必须有足够的事实,由多个特殊的共同结论才能归纳出一般情况下的结论。
2.知识内容:(见板书)3.对向心力的理解:向心力并不是一种特殊性质的力,它的名称只是根据始终指向圆心这一作用效果来命名的。
下节课再进一步讨论。
五、说明1.向心力、向心加速度的讲授顺序。
向心力概念的建立有两条途径:一是先通过实验建立向心力概念,归纳出向心力公式,再推出向心加速度;二是先通过理论推导导出向心加速度,再推出向心力。
先讲加速度,理论推导严谨,又能训练学生的推理能力,但方法较抽象,对基础差的学生难度较大。
考虑到我所任班级学生的实际情况,我选用了先讲向心力,降低了难度,便于学生理解、接受,现行必修教材采用的也是这一顺序。
不足之处是:由于实验存在误差,只能粗略得出结论,而且课堂不可能做很多实验,实验归纳的事实不足。
解决的关键是尽量减小实验误差,补充实例,弥补实验事实不足的缺陷。
2.对向心力的教学,本节完成了感知、概括、定义,即完成了个别到一般的过程和简单的再认。
而进一步的再认即一般到个别,留待下节完成,所以本节对向心力的要求教学目标定为初步掌握。
超重和失重一、教学目标1.了解超重和失重现象;2.运用牛顿第二定律研究超重和失重的原因;3.培养学生利用牛顿第二定律分析问题和解决问题的能力。
二、重点、难点分析1.超重和失重在本质上并不是物体受到的重力发生了变化,而是物体在竖直方向有加速度时,物体对支持物的压力或拉力的变化,这一点学生理解起来往往困难较大。
让学生理解超重和失重的本质是本节课教学的重点之一,也是后面理解航天器中失重现象的基础。
2.超重和失重中物体对支持物的压力和拉力的计算,是牛顿第二定律应用的一个方面,也应作为本节教学的重点之一。
三、教具演示教具:超重和失重演示装置、弹簧秤、重物、细线、下面扎孔的可乐瓶、录像资料。
学生用具:弹簧秤、钩码、打点计时器用重锤、绣花线。
四、主要教学过程(一)引入新课看录像片《航天飞机上的失重现象》《失重物体的运动》。
提问:刚才所看到的录像片是在什么地方发生的?它向我们展示了一种什么现象?这里给我们展示了失重现象,是在航天飞机中发生的。
航天飞机在起飞中产生了超重现象,在太空中又产生了失重现象。
超重和失重是怎么产生的呢?这就是我们这节课研究的内容。
(二)教学过程设计板书:十、超重和失重我们先来研究一下超重现象。
板书:1.超重现象实验:介绍装置,架子上有两个滑轮,两边挂有重物。
我们取左边的重物加以研究,重物静止时,弹簧秤的示数大小等于物体所受的重力,物体对弹簧秤的拉力等于物体所受的重力。
放手后物体做向上的加速运动,我们再观察弹簧秤示数的变化。
提问:看到了什么现象?弹簧秤的示数增大,物体对绳的拉力增大。
以上实验可以用更简单的装置来完成,只不过观察时的效果稍差一些。
弹簧秤下挂一重物,物体静止时,弹簧秤的示数等于物体所受的重力。
当物体向上做加速运动时,弹簧秤的示数大于物体所受的重力,物体对绳的拉力大于物重。
学生小实验:细线拉重锤(绣花线、打点计时器用重锤)。
线系在重锤上,缓慢拉起,再让重锤做向上的加速运动,线断。
分析原因:取物体为研究对象,T-G=ma,T-mg=ma,弹簧秤的拉力为T=mg+ma=m(g+a)讨论:(1)物体做向上的加速运动时,弹簧对物体的拉力大于物体静止时的拉力,T>mg,物体对弹簧的拉力大于物重。
举例:起重机在吊起重物时,有经验的司机都不让物体的加速度过大是什么原因?(2)学生列举生活中的感受:电梯向上起动时,电梯对人的支持力大于静止时的支持力,同样人对电梯的压力也大于物重;电梯下降刹车时也一样。
只要物体的加速度方向是向上的,就会产生以上现象。
提问:在电梯中放一弹簧测力秤,人站在上面。
当电梯向上加速度运动时秤的示数怎样变化?(3)整理公式:T=m(g+a)=mg′,g′叫做等效重力加速度,g′>g。
站在电梯里的人在电梯向上加速或向下减速时,人对电梯的压力大于人的重力,好像是重力加速度g增大了。
火箭起飞时有很大的向上的加速度,内部发生的是超重现象。
当物体存在向上的加速度时,它对支持物的压力(或对悬挂物的拉力)大于物重的现象叫做超重现象。
发生超重现象时,物重并没有变化。
2.失重现象实验:重物静止时,弹簧秤的示数大小等于物体所受的重力,物体对弹簧秤的拉力等于物体所受的重力。
放手后物体做向下的加速运动,我们再观察弹簧秤示数的变化。
提问:看到了什么现象?弹簧秤的示数减少,物体对支持物的拉力减小。
学生实验:观察感受失重现象。
弹簧秤下挂一重物,物体静止时,弹簧秤的示数等于物体所受的重力。
当物体向下做加速运动时,弹簧秤的示数小于物体所受的重力。
(注意对减速时的示数增大的解释。
)取物体为研究对象,G-T=ma,弹簧秤的拉力为T=mg-ma=m(g-a)讨论:(1)物体做向下的加速运动时,弹簧对物体的拉力小于物体静止时的拉力,T<mg,物体对弹簧的拉力小于物重。
