静电场和高斯定理
关于静电场的高斯定理和静电场的环路定理

关于静电场的高斯定理和静电场的环路定理静电场的高斯定理和静电场的环路定理是库仑定律的推论,所以称之为定理。
由于库仑定律是静电场的基本规律,适用于静电场,所以库仑定律的推论也适用于静电场。
电场有许多种:静电场(由静止电荷激发)、恒定电场(由运动然而空间分布不随时间改变的电荷体系激发的电场)、位电场(可以在其中建立电位函数的电场,位电场的电场强度等于电位的负梯度,分为恒定的与时变的,静电场和恒定电场就属于恒定的位电场)、涡旋电场。
静电场的高斯定理的文字表述是:静电场中,电场强度穿出闭合曲面的通量等于该闭合曲面所包围的总电量除以真空电容率。
静电场的高斯定理的数学表述式是:in 0d i S qE S ε⋅=∑⎰ 。
英国著名物理学家麦克斯韦首先假设静电场的高斯定理的数学表示式in 0d i S q E S ε⋅=∑⎰ 适用于一切电场,也就是说,实际的电场强度(即总电场强度)穿出闭合曲面的通量等于闭合曲面内的总电量除以真空电容率。
这个假设后来被实验证实了。
正因为这个原因,数学表示式in 0d i S qE S ε⋅=∑⎰ 也叫做高斯定律。
由于德国数学家高斯根据库仑定律推出的这个静电场规律的数学表示式是普遍适用的,这让高斯在电磁学中享有很高的声誉。
in 0d i S q E S ε⋅=∑⎰ 有好几个称谓:高斯定理、高斯通量定理、电场的高斯定理、电场的高斯通量定理、高斯定律、高斯通量定律、电场的高斯定律、电场的高斯通量定律。
对于静电场,这个规律叫做静电场的高斯定理,或者静电场的高斯通量定理。
高斯在数学方面有一项重要成就,叫做高斯公式(也可以叫做高斯通量公式或者高斯散度公式)。
高斯公式的数学表示式是d d S Vf S f V ⋅=∇⋅⎰⎰ 。
其含义是:矢量场穿出闭合曲面的通量等于矢量场的散度在闭合曲面所包围的空间区域内的体积分。
高斯定理是电(磁)学规律,高斯公式是纯粹数学规律,两者截然不同。
但是把两者结合起来,就可以推出0E ρε∇⋅= 。
静电场 高斯定理

q q Ua U U ( ) 4 0 r1 r2 q r2 r1 4 0 r1r2
当a点很远时r>>L,则r1≈r2≈r,
1
q L cos 1 P cos Ua 2 4 0 r 4 0 r 2
r2 r1 r cos
电偶极子轴线上的场强(电势梯度法) 电偶极子电场中的电势: 轴线延长线上的电势:
有电介质存在时的高斯定理的应用
(1)分析自由电荷分布的对称性,选择适当的高斯面 ,求出电位移矢量。 (2)根据电位移矢量与电场的关系,求出电场。 (3)根据电极化强度与电场的关系,求出电极化强度。 (4)根据束缚电荷与电极化强度关系,求出束缚电荷。
非极性分子
E0
极性分子
E0
电极化强度(偶极矩密度)
1、电极化强度:
其中 pei 是第i个分子的电偶极矩
单位是[库仑/米2]、[C/m2].
def P lim
V
pei
i
V
以下将电极化强度矢量简称为极化强度 束缚电荷就是指极化电荷。
电介质的极化规律
在外电场 E0中,介质极化产生的束缚 电荷,在其周围无论介质内部还是外 部都产生附加电场 E ' 称为退极化场。
i
②极性分子 在无外场作用下存在固有电矩 因无序排列对外不呈现电性。 当有电场作用时,极性分子发 生偏转。
在外电场中的电介质
E0
E0
l
无外场下,所具有的电偶极矩称为固有电偶极矩。 在外电场中产生感应电偶极矩。
极化电荷
在外电场中,均匀介质内部各处仍呈电中性, 但在介质表面要出现电荷,这种电荷不能离开电 介质到其它带电体,也不能在电介质内部自由移 动。我们称它为束缚电荷或极化电荷。
9-1-2静电场-高斯定理

0
q
i
i
10
关于高斯定律的说明:
(1)高斯定理表明静电场是有源场,电荷是静电场的源头. q3 q 2 qi S (2)高斯定理表达式: E dS i q1 0 S 式中 E 是面S 内、外所有电荷产生的合场强. 对闭合面的电通量 E dS 仅S面内的电荷有贡献.
S
(3)表达式中的qi是被面S包围在面内的电荷的代数和. (4)表达式的右端是封闭面S上的电场强度 E的通量e (有出有进).
11
关于高斯定律的用途: 1.当电荷分布具有某种对称性时,可用高斯定律求 出该电荷系统的电场的分布。比用库仑定律简便. 2. 当已知场强分布时,用高斯定律求出任一区域的电荷, 电势分布.
B. Q / 6
a 2
Q O
a
C. Q / 6 0
D. Q / 0 E. 条件不足,无法计算
a
17
利用高斯定律求静电场的分布
高斯定律可以用来求解特殊对称情况下的电场强度, 求解步骤如下: 1.根据电荷分布的对称性,分析电场分布的对称性。 2.根据高斯定律计算场强数值: 关键是高斯面的选取。 可以找到一个封闭曲面(高斯面), 使高斯面上 E dS
i E d s qi
S1
r
E
O
p E ds
r
S2
Φe
E 20 r
侧面
E dS E
dS E 2rl
1
侧面
0
l
24 请同学们画出 E r 关系曲线
例: 求无限长均匀带电圆筒的场强分布. 解: 该电场分布具有轴对称性.如图取同轴柱面为高斯面
A. 1 2,s q / 0 B. 1 2,s 2q / 0
静电场-高斯定理

电容器极板间电场分布
极板间相互作用力计算
理介
第 推质
四 章
广中 及高 应斯用定Fra bibliotek电介质极化现象及极化强度矢量引入
为了描述电介质极化 的程度和方向,引入 极化强度矢量P,其 大小与电偶极矩成正 比,方向由负电荷指 向正电荷。
在电场作用下,电介质内部正负电荷中心发生相对 位移,形成电偶极子,从而产生宏观上的电极化现 象。
高斯定理是电磁学中的基本定理之一,它表述了静电场中电场强度与电荷分布之间的关系。
高斯面选取原则及技巧
高斯面选取应遵循简单、对称、便于计算等原则。
02
在实际问题中,常根据电荷分布和电场强度的对称性来选取高斯面,以便简化计算。
03
高斯面的形状和大小应根据具体问题灵活选择,可以是平面、球面、柱面等。
高斯定理物理意义阐释
高斯定理反映了静电场的空间分布特性,即电场 强度与电荷分布之间的定量关系。
高斯定理为求解复杂静电场问题提供了一种有效 的方法,即通过选取适当的高斯面来简化计算。
高斯定理揭示了静电场的有源性,即静电场是由 电荷产生的。
高斯定理在电磁学中的地位
高斯定理是电磁学四大基本定理之一,是静 电场理论的基础。 高斯定理在电磁学中具有重要的地位,它不 仅适用于静电场,还可推广应用于恒定电场、 恒定磁场以及时变电磁场等领域。
要点一
麦克斯韦方程组
麦克斯韦方程组是描述电磁场基本规律的方程组,包括高斯定理、 安培环路定律、法拉第电磁感应定律和麦克斯韦-安培定律。
要点二
高斯定理在麦克斯韦方程组中的地 位
高斯定理是麦克斯韦方程组中的重要组成部分,它描述了电荷分 布与电场之间的关系,为电磁场理论奠定了基础。
静电场中的高斯定理

静电场中的高斯定理:高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ (1)高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用:例1:一半径为R 的带电球体,其电荷体密度分布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量。
静电场-3-2高斯定理
20
0, Q ( r 3 − R 13 ) , E = 2 3 3 4 πε 0 r ( R 2 − R 1 ) Q 4 πε r 2 , 0
r < R1 R1 < r < R 2 r > R2
∴ E组合柱面
0 , 内,外 = − λ / 2πε0 r , 中间
28
强调: 强调: 1.利用高斯定理求场强的条件: 1.利用高斯定理求场强的条件: 利用高斯定理求场强的条件 电荷分布必须具有一定的对称性. 电荷分布必须具有一定的对称性. 2.利用高斯定理求场强步骤∶ 2.利用高斯定理求场强步骤∶ 利用高斯定理求场强步骤 (1)分析场强分布的对称性。 (1)分析场强分布的对称性。 分析场强分布的对称性 (2)合理选取高斯面。 (2)合理选取高斯面。 合理选取高斯面 (3)计算高斯面包围的电荷电量。 (3)计算高斯面包围的电荷电量。 计算高斯面包围的电荷电量 (4)用高斯定理求场强。 (4)用高斯定理求场强。 用高斯定理求场强
∵
∫
EdS cos θ = E
∫ dS
=
1
ε 0 曲面内
∑
qi
∑q E= ε ∫ dS
0
注意:这样求得的是高斯面处的场强! 注意:这样求得的是高斯面处的场强!
11
均匀带电球面的电场,球面半径为R,带电为 带电为q 例1. 均匀带电球面的电场,球面半径为 带电为 。 解: 电场分布也应有球对称性,方向沿径向。 电场分布也应有球对称性,方向沿径向。 作同心且半径为r的高斯面 作同心且半径为 的高斯面. 的高斯面
高斯定理的表述: 高斯定理的表述: 穿过任一闭合曲面 的电通量 等于该曲面所包围的电荷的代 数和除以 ε 0 数学表达式: 数学表达式:
静电场103静电场的高斯定理

contents
目录
• 静电场简介 • 高斯定理的推导 • 高斯定理的应用 • 静电场的物理意义 • 高斯定理的局限性
ห้องสมุดไป่ตู้ 01
静电场简介
静电场的定义
静电场是由静止电荷产生的电场,其 电场线不闭合、不发散,且与带电体 的位置和电量分布有关。
静电场的电场线起于正电荷或无穷远 ,终止于负电荷或无穷远,沿电场线 方向电势降低。
按空间分布分类
根据静电场的空间分布,可将静电场分为均匀静电场 和非均匀静电场。
按电场线特征分类
根据静电场的电场线特征,可将静电场分为标量场和 矢量场。
02
高斯定理的推导
电场线的引入
电场线
表示电场中电场强度分布的曲线,其 上的每一点的切线方向与该点的电场 强度方向一致。
电场线的特点
不闭合、不相交、不相切、终止于正 负电荷。
揭示了电场与电荷之间的内在联系, 是静电场的基本定理之一,对于研究 静电场的性质和规律具有重要的作用。
推导过程
基于库仑定律和电场叠加原理,通过 引入电场线,利用微积分的知识,逐 步推导出高斯定理。
03
高斯定理的应用
电场分布的确定
高斯定理
通过一个闭合曲面的电场线数,等于该曲面所包围的电荷量与一个电荷量单位 的比值。
应用
通过测量或计算某一闭合曲面内的电场线数,可以确定该闭合曲面内的电场强度 。
04
静电场的物理意义
静电场的能量分布
静电场的能量分布反映了电场中电场力做功的能力,即电场能密度。在静电场中 ,电场能密度与电场强度成正比,表示单位体积内的电场能。
电场能密度可以通过积分计算得到整个电场的总能量,对于了解和预测电场的行 为具有重要意义。
真空中静电场的高斯定理

真空中静电场的高斯定理
真空中静电场高斯定理:在真空静电场中,通过任意的闭合曲面电通量等于该闭合曲面内所包围的电荷的代数和除以真空介电常量。
电通量Φ所代表的物理含义是通过电场中某一给定曲面的电场线的总条数。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
静电场的高斯定理

静电场的高斯定理静电场是物质中因电荷分布不平衡而引起的电场。
而高斯定理是一种用于计算电场的方法,通过将闭合曲面内的电场通量与被围绕电荷的总量之间建立关系。
本文将介绍静电场的概念、高斯定理的原理及应用,并探讨高斯定理在不同情况下的适用性。
一、静电场的概念静电场是指不随时间变化的电场。
它产生于电荷分布不均匀的物体周围,并以电场线的形式表现出来。
静电场的特点是力线密集并始终相互垂直,电荷分布越密集,电场力线越密集。
静电场的强度由电场强度表示,它是单位正电荷所受到的电场力。
在真空中,静电场的强度与电荷的大小和距离成反比。
二、高斯定理的原理高斯定理是由德国物理学家高斯提出的,它是静电学中的基本定理。
根据高斯定理,通过一个闭合曲面的电场通量与该曲面所围绕的电荷量成正比。
具体来说,通过一个闭合曲面的电场通量等于该曲面内的电荷量除以真空介电常数。
这一定理表明了计算静电场的电荷分布时,可以通过测量闭合曲面上的电场通量得出曲面内的电荷情况。
三、高斯定理的应用高斯定理在电场的计算与分析中具有重要的应用价值。
首先,它可以用于确定由各种不均匀电荷分布所产生的电场。
通过选择合适的闭合曲面,将电场通量与曲面上的电荷量建立起关系,可以准确计算出电场分布。
其次,高斯定理还能用于计算均匀电荷分布所产生的电场。
例如,对于均匀带电球面,通过选择一个球面作为闭合曲面,可以利用高斯定理快速计算出球面内外的电场分布情况。
四、高斯定理的适用性高斯定理在一些特殊情况下不适用。
例如,当电荷分布不对称或不规则时,闭合曲面的选择就变得困难,无法简单地使用高斯定理求解电场分布。
此外,在存在导体或电介质时,由于电荷的表面分布不明显,也不能直接应用高斯定理进行分析。
在这些情况下,需要采用其他方法,如电场叠加原理或边界条件等,来求解电场问题。
总结:静电场的高斯定理是一种用于计算电场的重要方法,通过建立闭合曲面内的电场通量与曲面所围绕的电荷量之间的关系,可以准确计算静电场的电荷分布。
静电场中高斯定理

静电场中的高斯定理:高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/ni i S E ds q φε==∙=∑⎰⎰ (1)高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合 曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用:例1:一半径为R 的带电球体,其电荷体密度分布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量。
大学物理静电场的高斯定理

高斯定理的数学表达形式简洁明了,是解决静电场问题的重要
03
工具。
高斯定理在物理中的重要性
高斯定理在物理学中具有广泛 的应用,不仅限于静电场。
它可用于分析恒定磁场、时 变电磁场以及相对论性电磁
场中的问题。
高斯定理是电磁学理论体系中 的重要基石,对于深入理解电 磁场的本质和规律具有不可替
代的作用。
THANKS FOR WATCHING
高斯定理的重要性
总结词
高斯定理是静电场理论中的基本定理之一,它揭示了电场与电荷之间的内在联 系。
详细描述
高斯定理的重要性在于它提供了一种计算电场分布的方法,特别是对于电荷分 布未知的情况。同时,它也揭示了电场线总是从正电荷出发,终止于负电荷, 或者穿过不带电的区域。
高斯定理的历史背景
总结词
高斯定理的发现和证明经历了漫长而曲折的历史过程。
VS
按空间位置分类
静电场可分为点电荷产生的电场、线电荷 产生的电场、面电荷产生的电场等类型。 这些不同类型的电场具有不同的分布规律 和性质。
05
高斯定理的推导过程
利用高斯定理推导电场强度与电通量的关系
总结词
通过高斯定理,我们可以推导出电场强度与 电通量之间的关系,即电场线穿过任意闭合 曲面的电通量等于该闭合曲面所包围的电荷 量与真空电容率的乘积。
静电场的电场强度与电势具有相对独立性
电场强度与电势之间没有直接关系,改变电场中某点的电势,不会影响该点的电场强度。
静电场的分类
按产生方式分类
静电场可分为感应起电和接触起电两种 方式。感应起电是由于带电体在接近导 体时,导体内部电荷重新分布而产生电 场;接触起电是两个不同物体相互接触 时,由于电子的转移而产生电场。
3.2 静电场高斯定理

E
Er
(r R)
1 E 2 r
O
R
r
2. 轴对称 (1)无限长均匀带电细线。 由对称性分析容易得到:
① 任一点的电场强度方 向只能垂直于轴线向外辐 射或指向轴线。 ② 到轴线距离相等的点 上,电场强度大小必定相 等。
n E
n
E
作同轴圆柱形高斯面, 应用高斯定理:
( S1 )
R
r
S1
0
Q E 2 4 0 r
(r R)
同理,取如图所示的高斯面 S 2 ,应用高斯 定理:
r
S2
R
E dS 4r 2 E 0
( S2 )
E 0
( r R)
在球面上(见例3-2):
E
Q 8 0 R
2
(r R)
E
E
Q 80 R E
l E 2r l 0
E 2 0 r
(r R)
E 2r l 0
E 0
( r R)
在柱面上(见例3-3):
E 4 0 R
E 40 R
E0
O
(r R)
E
E 20 r
r
R
(3)无限长均匀带电圆柱体。(例 3-7) 对称性分析及其结果,请同学 自己进行。
我们将任意曲面分成一系列有向面元 dS,
容易理解穿过任意曲面的电通量为:
de E dS e d e E dS
(S )
如果曲面是闭合的,穿过它的电通量则用 如下面积分表示:
e d e E dS
(S )
电磁学中的闭合曲面被统称为高斯面。 对非闭合曲面,其上小面元的法向可随意 选取,但无论怎样选取,结果的正负都会告 诉我们电力线是从哪一侧穿过的。不过,对 高斯面则规定一律取外法向。按这样规定, 进入高斯面的电力线其电通量为负,而从高 斯面穿出的电力线其电通量为正。
静电场的高斯定理内容

静电场的高斯定理内容
静电场的高斯定理内容
静电场的高斯定理是由德国数学家恩斯特·高斯发现的一条定理,用来解释各种物理现象,尤其是静电场的分布。
高斯定理可以用来求出任意一点上的电荷密度。
高斯定理的正式表述为:对任意一个由完全导体组成的闭合曲面,外面的电荷数量和里面的电荷数量是相等的。
也就是说,外面的电荷数量等于里面曲面内电荷的和。
由于高斯定理的正式表述有些复杂,所以经常用另一种形式来描述静电场的分布,即:任一点上的电荷密度等于任一点上的电荷流出量,其积分为零。
这就是静电场的高斯定理的内容,它可以用来解释各种物理现象,特别是静电场的分布。
它也是德国数学家恩斯特·高斯发现的一条定理,现在仍然是物理学中一个重要的定理。
《静电场高斯定理》课件

REPORT
CATALOG
DATE
ANALYSIS
用微积分的知识
总结词:数学推导
详细描述:通过微积分的知识,对电场E进行积分,利用矢量场的散度性质,推导出高斯定理。
证明方法二:利用电通量概念
总结词
物理概念理解
详细描述
详细描述
高斯定理是静电场的基本定理之一, 它表述了电场强度E的闭合曲面积分等 于被包围的电荷量Q除以真空电容率 ε₀。数学公式表示为∮E·dS = Q/ε₀。
高斯定理的应用场景
总结词
高斯定理的应用场景包括计算电场分布、确定电荷分布、解决静电场问题等。
详细描述
高斯定理在静电场理论中具有广泛的应用,它可以用于计算电场分布、确定电荷分布以及解决各种静电场问题。 通过高斯定理,我们可以求解电场中任意区域的电场强度,进而分析电场对电荷的作用力以及能量等物理量。
REPORT
THANKS
感谢观看
CATALOG
DATE
ANALYSIS
SUMMAR Y
在静电屏蔽中的应用
静电屏蔽原理
高斯定理可以用来解释静电屏蔽原理,当一 个带电体被导体外壳包围时,由于导体的静 电感应作用,带电体会在导体外壳内表面感 应出等量异种电荷,根据高斯定理,导体外 壳外部的电场线数为零,因此带电体被完全 屏蔽在导体外壳内部。
静电屏蔽的应用
高斯定理在静电屏蔽中有广泛的应用,如电 子设备、仪器仪表、输变电设备等需要防止 外界电场干扰的场合,通过采用静电屏蔽措 施来降低外界电场对设备的干扰。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
静电场 高斯定理

r P点处的场强: E = 点处的场强: 点处的场强
q
ˆ r 2
z
r r
+
P qo y
r E
q
?
4、电场中每一点都对应有一个矢量 E , 、 这些矢量的总体构成一个矢量场。 这些矢量的总体构成一个矢量场。 r 因此在研究电场时,不是只着眼于个别地方的场强, 因此在研究电场时,不是只着眼于个别地方的场强, 而是求它与空间坐标的函数。 而是求它与空间坐标的函数。
注:以上解答考虑到对称性,因此采用积分一半再乘2倍,其结果跟直接沿整根棒积分一致!! 以上解答考虑到对称性,因此采用积分一半再乘2 其结果跟直接沿整根棒积分一致!!
y
dy
y o
d y′
x
r x dE ),则 →∞( 注:当L→∞(或L>>X),则:
r dE ′ r P . dE合
E=
λL
4πε o x
F
r r
q1
r F 12
q2
2) 库仑定律只适用两个静止点电荷 库仑定律只适用两个静止点电荷. 静止点电荷 3) 若q1、q2在介质中 介电常数 ε = εrεo; 在介质中,介电常数 空气中: 空气中: ε ≈ εo 库仑定律是基本实验规律 基本实验规律. 4) 库仑定律是基本实验规律. 在宏观,微观领域都适用. 在宏观,微观领域都适用.
电磁学
观念的更新(场是物质存在的另一种基本形式) 观念的更新(场是物质存在的另一种基本形式)
难点:
高数手段的集中应用(微积分 矢量场 矢量场) 高数手段的集中应用(微积分,矢量场) 观念的转变需逐渐体会!! 观念的转变需逐渐体会
解决方案: 解决方案
方法的掌握需勤练多思!! 方法的掌握需勤练多思
静电场高斯定理

静电场高斯定理一、静电场是什么大家应该都听说过静电吧,特别是在干燥的冬天,摸到门把手或者某些金属物体时,电一下子就蹦出来了。
那种刺痛感,有没有?没错,那就是静电!其实静电就是一种电荷不动的状态,没错,不动。
想象一下,如果你在地毯上走来走去,脚下摩擦产生的电荷积累到你身上,你就成了一个“电气人”。
而周围的一些物体、你接触的物体如果带有相反的电荷,电荷会跳跃过去,哇,那一瞬间多像电影里的特效,啪啪作响。
静电的存在让我们在日常生活中时不时就能感受到它的“威力”,它不仅仅只是“电”那么简单,它也是个无形的、可以随时爆发的能量源。
这么一说,大家对静电是不是有了点感觉?对了,不是所有电都像你家插座里那样“活蹦乱跳”的,静电其实是很“静”很“安静”的,直到它突然跳起来,给你一个“电击”的惊喜!二、什么是高斯定理说到静电,我们就不得不提一个非常有意思的定理——高斯定理。
对,有没有觉得很厉害的名字?一听就知道不是普通的定理,不是随便一个数学家就能发明的东西。
这高斯定理是德国数学家高斯(CarlFriedrichGauss)搞出来的,简直就是个天才。
这个定理听起来好像挺复杂,实际上它的意思不难理解。
简单来说,高斯定理告诉我们,如果你把一个电荷放在某个地方,电场就像是围绕它的一团空气或者一层看不见的“气场”。
换句话说,电荷不只是在自己周围产生电场,还能影响到周围的一大块区域。
更神奇的是,这个影响是可以通过一些数学方式来量化的。
它说什么呢?就是说,穿过一个闭合曲面的电场通量,和这个闭合曲面包围的总电荷成正比。
听起来是不是有点绕?其实就是说,我们可以通过这个曲面内的电荷量,直接算出它对外界的影响力。
就像你拿个透明的气泡罩子罩住一个电池,罩子里的电场到底有多强,其实只要知道罩子里面的电池的电荷数就行了。
是不是觉得这定理还挺神奇的,啥都不用看,就可以从电荷数量推算出来电场的强度。
三、高斯定理的实际应用说到这里,你肯定会想,这个定理到底怎么用啊?能不能拿来做点实实在在的事?别急,等着。
静电场的高斯定理的数学表达式为

静电场的高斯定理的数学表达式为静电场的高斯定理是物理学中一个重要的定理,它可以帮助我们了解和描述电场的变化以及电荷(电荷量或电荷密度)与它们之间的关系。
该定理以19世纪德国数学家卡尔高斯(Karl Gauss)命名,他在1813年发表了第一个有关静电场的论文。
高斯定理有几种不同的数学表达式,它们可以描述不同类型的物理系统。
首先,让我们来看看静电场的概念。
电场是一种场,它由一组随时间变化的电荷产生的电力线组成。
这些线描述电力在某个空间区域内的分布。
在这里,我们只考虑静电场,它是由平衡状态的电荷产生的(即不会随时间变化)。
此外,静电场在电磁学中也被称为电场,是由平衡状态的电荷产生的。
接下来,我们来看看静电场的高斯定理的数学表达式。
该定理建立在一个有限空间上,它表明,在该空间内,电场的总变化量可以用电荷的总量来表示,也就是说,电场的总变化量可以用电荷的总量来描述。
以下是静电场的高斯定理的数学表达式:begin{equation}vecabla cdot vec E = rho/epsilon_0end{equation} 其中,$vec E$代表了一维空间上电场的分量;$vecabla$表示空间离散梯度;$rho$是电荷密度,$epsilon_0$是真空介电常数。
通过这个定理,可以表示电荷密度与电力线的关系,并且可以使用它来求解静电场。
通常情况下,可以利用它来计算某个特定点处的电力线的密度和方向。
总的来说,静电场的高斯定理的数学表达式是一种强有力的工具,它可以帮助我们理解和描述电场的变化以及电荷和它们之间的关系。
该定理的数学表达式也可以用来求解静电场的电力线的方向和密度,这有时对物理系统的研究是非常有价值的。
利用高斯定理求静电场的分布

利用高斯定理求静电场的分布
高斯定理是一个源自于高斯(Gauss)的广泛用于处理静电场和磁场的一个定理,它可
以使我们更加清楚地了解静电场是如何分布的。
高斯定理(也称为高斯克鲁斯特定理、高斯法定理)指出,任何没有边界的静电场的
场强中,场强沿着任何关于原点的圆锥曲面的位置都保持不变。
此外,还有一种轴射体假设,即静电场是由从物体表面弥漫到无限远的点源所构成的。
这意味着,如果我们直觉地想象将一个负电荷圆添加到负电荷分布中,则它的影响可以被
描述为一系列从物体表面弥漫出去的负电荷条带;或者说,静电场是这些负电荷条带的相
加结果。
用高斯定理来求解静电场的分布,其原理是:可以把物体表面上的每一个(正、负)
电荷分别视为一个电势中心,它们分别向过该电荷的空间点施加一个恒定的电场强度。
所
述电场分布可以用高斯定理(也称为贝叶斯定理)来概括:“某一点的静电场是由所有可
见电荷各自的电场强度之和构成的”(以贝叶斯定律形式表示),其中可见的电荷表示为
原点的任意距离的电荷;因而,这一定理建立了对大量电荷点的静电场分布的正确计算方法,即静电场强度沿电荷到该点的各支路都同号,以电荷量乘以到该点所受支路倒数平方
的方式求和所得结果,就是该点的静电场分布值。
此外,由于多边形的存在,且这些多边形的差分形态有其特定的电场分布规律,因此,用高斯定理求解处理多边形的静电场分布时,也可以分析其侧壁的特定场强变化,从而把
多边形剖分为多个小元,逐个分析每一小元内贝叶斯式的边界条件,从而得出多边形内静
电场分布结果。
值得注意的是,高斯定理只是用来表达在“空间”上求静电场分布的理论,当在“时间”上求动电场分布时,则不能用高斯定理加以求算。
磁场的高斯定理与静电场的高斯定理的区别

磁场的高斯定理与静电场的高斯定理的区别磁场的高斯定理和静电场的高斯定理是物理学中流行的两个定理,但它们之间存在着一定的区别。
本文从定义、关键结论和应用三个方面介绍两个定理之间的区别。
磁场的高斯定理表明,在一个封闭的表面内,通过任一点的磁通量是由这个表面内每个点上磁场的积分。
由于磁场是一种有矢量性的量,所以,每个点上的磁场可以用一个矢量来表示,而磁通量则是这个矢量积分加起来的结果,即磁通量等于表面内每个点上的磁场矢量的分和。
而静电场的高斯定理也有类似的概念,它表明,在一个封闭的表面内,通过任一点的电荷量是由这个表面内每个点上的电势的积分。
电势也是一种有矢量性的量,而电荷量则是这个矢量积分加起来的结果,即电荷量等于表面内每个点上的电势矢量的分和。
从定义上来看,磁场的高斯定理和静电场的高斯定理之间的区别主要在于它们涉及的物理量是不同的,磁场的高斯定理涉及的物理量是磁场,而静电场的高斯定理涉及的物理量是电势。
而从关键结论上来看,磁场的高斯定理和静电场的高斯定理之间的区别则是它们所提出的结论不同。
磁场的高斯定理给出的结论是,任一点处的磁通量是由表面内每个点上磁场的积分和;而静电场的高斯定理给出的结论是,任一点处的电荷量是由表面内每个点上电势的积分和。
最后,从应用上来看,磁场的高斯定理和静电场的高斯定理之间的区别是它们的应用不同。
磁场的高斯定理可以用于计算电磁线圈的电流,以及各种磁体的磁化强度等;而静电场的高斯定理则可以用于计算各种静电场领域中的电荷分布。
总之,磁场的高斯定理和静电场的高斯定理之间存在着一定的区别,其主要差别体现在定义、关键结论和应用上。
它们在物理学上都有重要的应用,因此,熟悉它们有助于我们理解和掌握物理理论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:在氢原子中,电子与质子之间的距离约为5.3×10-11m,求 它们之间的库仑力与万有引力,并比较它们的大小。
Fe = 8.2 108 Fg 3.6 1047
2.3 1039
结论:库仑力比万有引力大得多。
所以在原子中,作用在电子上的力,主要是电场力,万 有引力完全可以忽略不计。
三、 电场强度
2
r
F与r 有关,而且还与试验电荷q0 有关。
(3)电场强度
试验电荷将受到源电荷的作用力与试验 电荷电量的比值F/q0 则与试验电荷无关, 可以反映电场本身的性质,用这个物理 量作为描写电场的场量,称为电场强度 (简称场强)。
F
E
q0
=Q
4 0r2
r
F
E
q0
=Q
4 0r2
设圆盘带电量为q,半径为R。
解:带电圆盘可看成许多同心的圆环
R
组成,取一半径为r,宽度为dr 的细 圆环带电量
o rd
dr
p
x·
d E
x
dE
dq x
40 (r2 x2 )32
q
dq 2r dr
x R rdr
E x ( p) 2 0 0 (r 2 x 2 )32
E= dE
dq
4 0r 2 er
E= dE
dq
4 0r 2 er
计算的步骤大致如下: •取电荷元dq,写出dq在待求点的场强的表达式; •选取适当的坐标系,将场强的表达式分解为标量表 示式; •进行积分计算; •写出总的电场强度的矢量表达式,或求出电场强度 的大小和方向;
电荷的定义: 带正负电的基本粒子。 单位:库仑(C)
原 子原 子 核质中子子( ) 电 子(-)
当物质处于电中性时,质子数=电子数 当物质的电子过多或过少时,物质就带有电荷
电子过多时——物体带负电 电子过少时——物体带正电
正电子,又称阳电子、反电子、正子,基本粒子的一种,带 正电荷,质量和电子相等,是电子的反粒子。
(2)电荷连续分布
电荷呈线状分布dq
dq=λdl
=Q 线密度
l
E= dE
dl 4 0r 2 er
电荷面分布,dq=σdS
=Q
S
面密度
E=
S
er 4 0r
2
dS
电荷体分布,dq=ρdV
= dQ
dV
体密度
E=
V
er 4 0r
2
dV
电荷线E分=布,dq=λedrl dl
2
例2、 均匀带电圆环轴线上一点的场强。 设正电荷q均匀地分布在半径为R的圆环上。计算在环的轴线
任一点p 的电场强度。
dE
X
P
r
R dq
L
例2、 均匀带电圆环轴线上一点x处的场强。
设正电荷q均匀地分布在半径为R的圆环上。计算在环的轴线
任一点p 的电场强度。
解:由对称性可知,p点场强只有X分量
电荷的这种只能取离散的、不连续的量值的 性质,叫作电荷的量子化。电子的电荷e称为 基元电荷,或电荷的量子。
1986年国际推荐值 e 1.602 177 33(49) 1019C
近似值 e 1.6021019C
2、电荷守恒定律
内容: 在孤立系统中,不管系统中的电荷如何 迁移,系统的电荷的代数和保持不变。
1、静电场
(1)电场的概念 电荷之间的相互作用是通过电场传递的,或者说 电荷周围存在有电场。
在该电场的任何带电体,都受到电场的作用力, 这就是所谓的近距作用。
电荷
电场
电荷
(2)电场的物质性
•给电场中的带电体施以力的作用。
•当带电体在电场中移动时,电场力作功; 表明电场具有能量。
•变化的电场以光速在空间传播,表明电场 具有动量。
在计算过程中,要根据对称性来简化计算过程。
(4)电场强度的计算
例1、电偶极子的电场强度
电偶极子:等量异号电荷+q、-q,相距为r0,它相 对于求场点很小,称该带电体系为电偶极子。
电偶极子的轴:从-q 指向+q 的矢 量r0称为电偶极子的轴
电偶极矩: p qr0
q q
r0
求:电偶极子轴线延长线上任意一点A处的电场强度
电子电量 e 带电体电量 q=ne, n=1,2,3,...
密立根测定电子电荷的实验
1909年密立根测量电子电荷;1923年获得诺贝尔物理奖。 方法:观察均匀电场中带电油滴的运动。
不加电场时:油滴在重力
和阻力的作用下,最后得到 收尾速度。
mg 6 rv1 0
v 1=
mg
6
r
由此式可从实验中测量油滴的质量。
r
电场中某点的电场强度在数值上等于位于 该点的单位正试验电荷所受的电场力。 电场强度的方向与电场力的方向一致(当 q0为正值时)。
单位:N.C-1或V.m-1
电场强度是电场的属性,与试验电荷的 存在与否无关,并不因无试验电荷而不 存在,只是由试验电荷反映。
3、电场力 电荷q在电场E中的电场力
F=qE
面密度
=Q
S
q
R2
2 0
[1
(R2
x
x2
1
)2
]
习题P76 5-6 (2)
x R rdr
E x ( p) 2 0 0 (r 2 x 2 )32
x
2 0
[1
(R2
x
2
)
1 2
]
讨论: 1.当x<<R
E
2 0
R o rd
dr q
2.当x>>R
E
Q>0,电场强度E与er同向 Q<0,电场强度E与er反向。
点电荷场强公式
E=
F
q0
Q
4 0r 2
er
+
说明:
(1)点电荷电场是非均匀电场; (2)点电荷电场具有球对称性。
-
5、电场强度叠加原理
(1)电荷离散分布
在点电荷系Q1,Q2,…,Qn 的电场中,在P点放
一试验电荷q0,根据库仑力的叠加原理,可
4 0 r 2
电荷面分E布=,dq=σdeSr
S 4 0r
2
dS
电荷体分布,dq=ρdV
E=
V
er 4 0r
2
dV
= dQ
dl
线密度
= dQ
dS
面密度
= dQ
dV
体密度
(3)电场强度的计算方法
离散型
E=
E
=
i
Qi
4 0
r
2
er
连续型
1779年对摩擦力进行分析,提出有关润滑剂 的科学理论。
1785~1789年,用扭秤测量静电力和磁力,导 出著名的库仑定律。
1、库仑定律内容
在真空中,两个静止的点电荷之间的相互作用力,其大小
与点电荷电量的乘积成正比,与两点电荷之间距离的平方
成反比,作用力在两点电荷之间的连线上,同号电荷互相
排斥,异号电荷互相吸引。
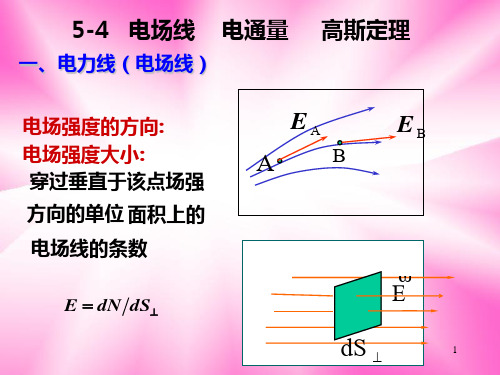
一、电场强度通量 1、电场线
(1)定义
电场线上每一点的场强的方 向与该点切线方向相同,而 且电场线箭头的指向表示场 强的方向。
q E
E
q
(2)几种典型的电场线分布
-Q
+2Q
+Q
知试验电荷受到的作用力为
F
Fi
Qi q0
4 0ri2
ei
Qi
P
ri
P点的电场强度
E
Fi
q0
Qi
4 0
ri2
ei
E= Ei
E= Ei
点电荷系电场中某点的场强等于各个点电荷单 独存在时在该点的场强的矢量和。 这就是电场强度的叠加原理。
习题P77 5-10
E
1
40
q
x r0 /
22
q O
q
E A E
E
1
40
x
q r0
/
22
r0
x
E
E
E
1
4 0
x
q r0
/
22
x
q r0
/
22
E
q
4 0
2 xr0 x2 r02 / 4
R2 40 x2
p
x·
d E
x
相当于无限大带电平面附近的 电场,可看成是均匀场,场强
R2 40 x2
q
40 x2
垂直于板面,正负由电荷的符 号决定。
习题P76 5-9
在远离带电圆面处, 相当于点电荷的场强。
附: (1+x)m的泰勒级数展开为:
(1 x)m 1 mx m(m 1) x2 m(m 1)(m 2) x3 ......
说明: 电荷守恒定律适用于一切宏观和微观过程 ( 例如核反应和基本粒子过程 ),是物理学 中普遍的基本定律之一。
铀235的核裂变 氘和氚的核聚变
二、库仑定律
库仑 (Charlse-Augustin de Coulomb 1736 ~1806)
