《结构力学》习题解-
结构力学习题及答案

结构力学习题及答案结构力学习题及答案结构力学是工程学中的重要学科之一,它研究物体在外力作用下的变形和破坏。
在工程实践中,结构力学的应用广泛,涉及到建筑、桥梁、航空航天等领域。
在学习结构力学时,练习解答一些习题是非常重要的,下面我将给大家提供一些常见的结构力学习题及其答案。
题目一:简支梁的弯矩计算已知一根长度为L的简支梁,两端受到均布载荷q。
求梁的中点处的弯矩M。
解答一:根据简支梁的受力分析,可以得出梁的弯矩与距离中点的距离x之间的关系为M=qL/8-x^2/2,其中x为距离中点的距离。
因此,中点处的弯矩M=qL/8。
题目二:悬臂梁的挠度计算已知一根长度为L的悬臂梁,端部受到集中力F作用。
求梁的端部挠度δ。
解答二:根据悬臂梁的受力分析,可以得出梁的端部挠度与力F之间的关系为δ=FL^3/3EI,其中F为作用力,E为梁的杨氏模量,I为梁的截面惯性矩。
因此,梁的端部挠度δ=FL^3/3EI。
题目三:刚度计算已知一根长度为L的梁,截面形状为矩形,宽度为b,高度为h,梁的杨氏模量为E。
求梁的刚度K。
解答三:梁的刚度可以通过计算梁的弯曲刚度和剪切刚度得到。
弯曲刚度Kb可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Kb=E*I/L。
剪切刚度Ks可以通过梁的剪切模量G和梁的截面面积A计算得到,即Ks=G*A/L。
因此,梁的刚度K=Kb+Ks=E*I/L+G*A/L。
题目四:破坏载荷计算已知一根长度为L的梁,截面形状为圆形,直径为d,梁的杨氏模量为E。
求梁的破坏载荷P。
解答四:梁的破坏载荷可以通过计算梁的破坏弯矩和破坏挠度得到。
破坏弯矩Mf可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Mf=π^2*E*I/L^2。
破坏挠度δf可以通过梁的破坏弯矩Mf和梁的刚度K计算得到,即δf=Mf/K。
因此,梁的破坏载荷P=Mf/L=π^2*E*I/L^3。
结构力学是一门综合性较强的学科,掌握结构力学的基本原理和解题方法对于工程师来说非常重要。
结构力学章节习题及参考答案
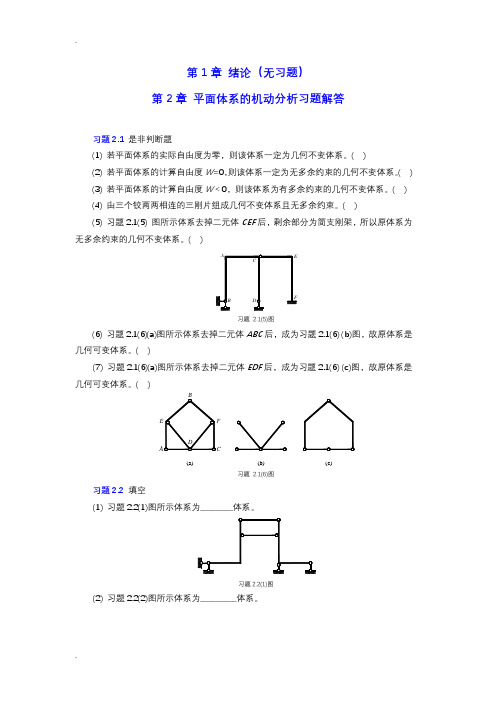
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。( )
(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。( )
(3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。( )
(4)习题3.1(4)图所示多跨静定梁中,CDE和EF部分均为附属部分。( )
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
(4)习题5.1(3)图(a)和(b)所示两结构的变形相同。( )
习题7.2填空题
(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角,若选图(b)所示力法基本结构,则力法方程为_____________,代表的位移条件是______________,其中1c=_________;若选图(c)所示力法基本结构时,力法方程为____________,代表的位移条件是______________,其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i,欲使结点B产生顺时针的单位转角,应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构(EI=常数)时,传递系数CBA=________,CBC=________。
东南大学结构力学练习题(附答案)详解

第一部分 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBAC DB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、124567831234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、ACBDEF三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二部分 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
(a)BCa aA ϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0,R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2(。
)↑9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
—— 1 ——11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:=== 0。
N 1N 2N 313、图(h)所示桁架DE 杆的内力为零。
a a(h)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
结构力学习题课后答案(高等教育版)

习 题8-1 试说出单元刚度矩阵的物理意义及其性质与特点。
8-2 试说出空间桁架和刚架单元刚度矩阵的阶数。
8-3 试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。
(a)解:(a )用后处理法计算 (1)结构标识(2)建立结点位移向量,结点力向量[]T44332211 θνθνθνθν=∆[]Ty M F M F M F M F F 4y43y32y211 =θ(3)计算单元刚度矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=2222322211211462661261226466126122EI 21 l l -l l l -l -l l -l l l l - l k k k k k ①①①①①⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222233332232223 33 6 3632336 362EI 21 l l - l l l - l -l l -l l l -l l k k k k k ②②②②②lll⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222234443343323 33 6 3632336 362EI 2 1 l l - l l l - l -l l -l l l -l l k k k k k ③③③③③(4)总刚度矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=222222222234443343333322322222112112 3300003 6 3 6 000 03403003601236000 0 3632600 363186120000 26460 0 0 06126122EI 0 0 00 0 0 4 3 2 1 4 3 2 1 l l -l l l - l - - l l -l l l l - l - - l l -l l -l l l l - -l -- l l -l l l l - l k k k k k k k k k k k k k ③③③③②②②②①①①①θ (5)建立结构刚度矩阵支座位移边界条件[][]00004311 θ θ θν=将总刚度矩阵中对应上述边界位移行列删除,得刚度结构矩阵。
结构力学课后习题答案重庆大学
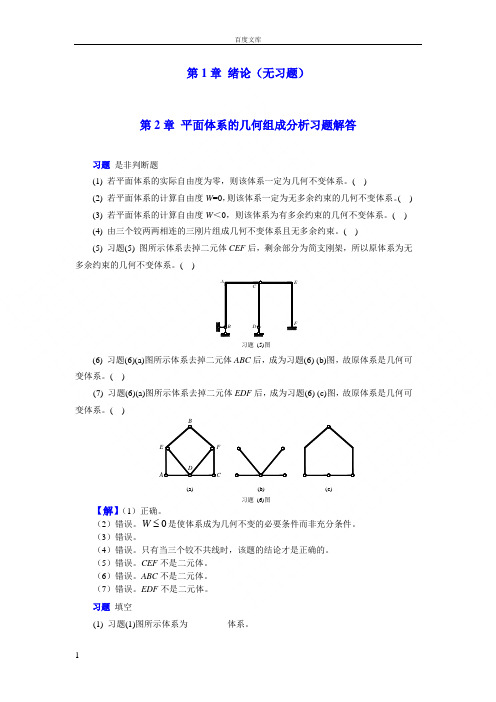
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后,成为习题(6) (b)图,故原体系是几何可变体系。
( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后,成为习题(6) (c)图,故原体系是几何可变体系。
( )(a)(b)(c)D习题 (6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题 填空(1) 习题(1)图所示体系为_________体系。
习题(1)图(2) 习题(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。
习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。
习题(5)图(6) 习题(6)图所示体系为_________体系,有_________个多余约束。
习题(6)图(7) 习题(7)图所示体系为_________体系,有_________个多余约束。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
同济大学 结构力学课后习题及答案解析(完整版)

(c) (d)
(e) (f)
(g) (h)
2-5 试从两种不同的角度分析图示体系的几何构造。 (a)
(b)
同济大学朱慈勉 结构力学 第 3 章习题答案 3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a) A
FP
B
C
FPa
D
E
F
a
a
a
a
a
(b) 2kN/m
10kN
A
2m
6m
B
C
2m
D
4m
2m
1
1
2a
1
2
2
M1
6-4 试用力法计算图示结构,并绘其内力图。 (a)
6m
20kN/m
B
1.75EI
C
D
EI
A
6m
3m
解:基本结构为:
20kN/m
X1
6 1
M1
6 810
810
Mp
11X1 1p 0
M M1X1 M p
(b) E
2a
4a
C
D
q
EI=常数
A
B
4a
4a
解:基本结构为:
X1
计算 M 1 ,由对称性知,可考虑半结构。
(c)
15kN
20kN/m
A
B
C
D
E
F
2m 2m 3m
3m
3m
4m
(d)
6kN·m
4kN·m
A 3m
B
C
D
2m 2m
E 2m 2m
A
4kN
FG
H
2m 2m 2m
《结构力学》习题解答(内含解答图)

解:将固定铰支座换为单铰,如图(b),由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ,铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连,虚铰在无穷远处,刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连,虚铰在两杆的延长线的交点处。此时,三铰不共线,该体系为几何不变体,且无多余约束。
所以,体系是几何不变得,且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解:从图2-15(b)可知,杆件CD和链杆3及铰D构成二元体,可以去掉;取杆件CB为刚片Ⅰ,基础作为刚片Ⅱ,根据规则一,两刚片是通过杆AB、链杆1、2组成几何不变体。所以,整个体系为几何不变体系,且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
习题2-26图习题2-26解答图
解:将链杆截断,截断一处,去掉一个约束,共去掉四个约束;再将刚性联结杆截断,截断一处,去掉三个约束,共去掉十二个约束,如图(b)。此时,体系变成与基础独立相连的三个单一杆件,见图(b)。所以,该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以,由规则一知,体系是几何不变体,且无多余约束。
同济大学 结构力学课后习题及答案解析(完整版)

R=2m
4m
A O
M ( ) 1 (R sin )2 1 2 R(1 cos ) 2
M ( ) 1
B
1 EI
2 1 [1 (R sin )2 1 2 R(1 cos )]Rd 02
= (8-3 ) -1.42 (逆时针)
EI
EI
(d) A q
R EI=常数
O
B
5-7 试用图乘法计算图示梁和刚架的位移:(a) ΔyC ;(b) ΔyD ;(c) ΔxC ;(d) ΔxE ;(e) D ;(f) ΔyE 。 (a)
5-5 已知桁架各杆的 EA 相同,求 AB、BC 两杆之间的相对转角 ΔB 。 5-6 试用积分法计算图示结构的位移:(a) ΔyB ;(b) ΔyC ;(c) B ;(d) ΔxB 。
(a)
q2 q1
A
EI
B
l
以B点为原点,向左为正方向建立坐标。
q( x)
q2
l
q1
x
q1
M
p(x)
1 2
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构,求出链杆轴力并绘出 M 图。
2
30kN 2m
(a)
a 1.5m
l
A
kθ=
12EI l
2 3
2 3
6 1 20 62 8
3 2
1 6180 3 2
结构力学习题及答案

2 结构的几何组成分析判断题几何不变且无多余约束的体系其自由度必定等于零。
( )体系的自由度小于或等于零是保证体系为几何不可变的必要和充分条件。
( )三个刚片之间只要用三个铰两两相连,就能构成无多余约束的几何不变体系。
( )在任何情况下,在几何不变体系上去掉一个二元体,所余体系仍然是几何不变的。
( )一个点与一个刚片之间用两根链杆相连,则一定构成几何不变体系。
( )在某些特殊情况下,几何可变体系加上一个二元体后可以变为几何不变体系。
( )如体系在去掉某个约束后能承受特殊荷载而平衡,说明原体系中该约束为多余约束。
( )超静定结构中的多余约束是为保持杆件体系的几何不变性而设置的。
( )超静定结构设置多余约束的目的之一是调整结构的内力分布。
( )填空题一个点在平面上有___个自由度;一个刚片在平面上有___个自由度。
一个平面体系中有两个刚片,用单铰相联,则其自由度为____。
图示支座简图各相当于几个约束,在各图上标出可能出现的约束反力。
(a)___个约束;(b)___个约束。
(a)图示支座简图各相当于几个约束,在各图上标出可能出现的约束反力。
(a)___个约束;(b)___个约束。
(b)图示结构一共设置了五个支座链杆,对于保持其几何不变来说有___个多余约束,其中第___根链杆是必要约束。
在任何情况下,几何可变体系上增加一个二元体后构成的体系总是_______体系。
若两刚片由三根链杆相连构成无多余约束的几何不变体系,则三根链杆的空间位置必须满足_______________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案_______________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
结构力学第三版课后习题答案精选全文

20kN/m
M图
4.5kN
8.98
4
4.5
6 11
4.5 FQ图
M图 (kN.m)
FQ图(kN)
37
3.3 静定平面刚架
必作题: P.109 3-3 (b) (d) (f) (j) P.110 3-4 (a — i) P.111 3-7 (a) P.112 3-8 (a) (d)
选作题: P.109 3-3 (a) (e) (g) (l) P.112 3-8 (c) P.112 3-9 (a) P.113 3-11
2
P.37 2-1(b)
1
2
3
三链杆交于一点,瞬变
3
P.37 2-2(b)
4几何不变,无多余约束5P.37 2-3(c)
有一个多余 约束
1
2 3
几何不变,有一个多余约束
6
P.37 2-4(d)
O(I、III) O(II、III) I
II
1
2
O(I、II)
III
铰O(I、II)、 O(II、III)的连线与1、2两链 杆不平行,体系几何不变,无多余约束
2.5m 5m 5m 2.5m
FN图
60
3.4 静定平面桁架
必作题:
P.113 P.114 P.115
选作题:
P.116 P.117
3-13 (b) (d) (f) 3-14 (a) (b) (c) 3-17 (a) (d)
3-18 (a) 3-20
P.116 3-18 (b)
61
P.113 3-13 (b) 分析桁架类型,指出零杆
FP
联合桁架,10根零杆。
62
P.113 3-13 (d) 分析桁架类型,指出零杆
结构力学章节习题及参考答案
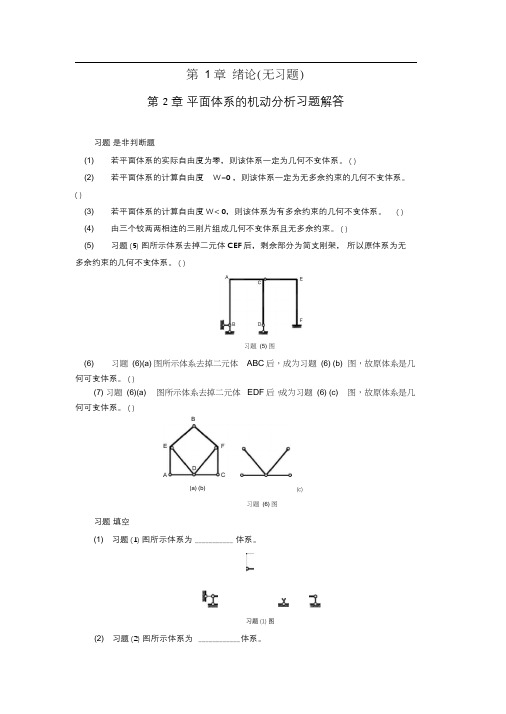
第 1 章绪论(无习题)第2 章平面体系的机动分析习题解答习题是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2)若平面体系的计算自由度W=0 ,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度 W< 0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体 CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )何可变体系。
( )何可变体系。
( )(c)习题填空(1) 习题(1) 图所示体系为___________ 体系。
习题(1) 图(2) 习题(2) 图所示体系为 ____________ 体系。
(6) 习题(6)(a) 图所示体系去掉二元体ABC后,成为习题(6) (b) 图,故原体系是几(7) 习题(6)(a) 图所示体系去掉二元体EDF后,成为习题(6) (c) 图,故原体系是几习题(5) 图B(a) (b)习题(6) 图习题 2-2(2) 图习题 (3) 图习题 对习题图所示各体系进行几何组成分析。
(3) 习题 (3) 图所示 4 个体系的多余约束数目分别为(4) 习题 (4) 图所示体系的多余约束个数为(5) 习题(5) (6) 习题(6) (7) 图所示体系的多余约束个数为习题 (5) 图图所示体系为体系,有个多余约束。
个多余约束。
习题 (7) 图所示体系为习题图(g) (h)第 3 章 静定梁与静定刚架习题解答习题 是非判断题(i) (j)(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
()(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( )(3) 多跨静定梁在附属部分受竖(k)向荷载作用时,必会引起基本部分的(l) 内力。
( )(4) 习题(4) 图所示多跨静定梁中, CDE 和 EF 部分均为附属部分。
结构力学-习题集(含答案)

结构⼒学-习题集(含答案)《结构⼒学》课程习题集⼀、单选题1.弯矩图肯定发⽣突变的截⾯是(D )。
A.有集中⼒作⽤的截⾯;B.剪⼒为零的截⾯;C.荷载为零的截⾯;D.有集中⼒偶作⽤的截⾯。
2.图⽰梁中C截⾯的弯矩是( D )。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,(C)。
A.⽆变形,⽆位移,⽆内⼒;B.有变形,有位移,有内⼒;C.有变形,有位移,⽆内⼒;D.⽆变形,有位移,⽆内⼒。
4.图⽰桁架a杆的内⼒是(D)。
A.2P;B.-2P;C.3P;D.-3P。
5.图⽰桁架,各杆EA为常数,除⽀座链杆外,零杆数为(A)。
A.四根;l= a66.图⽰梁A点的竖向位移为(向下为正)(C)。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
PEIEI A l/l/2227. 静定结构的内⼒计算与( A )。
A.EI ⽆关;B.EI 相对值有关;C.EI 绝对值有关;D.E ⽆关,I 有关。
8. 图⽰桁架,零杆的数⽬为:( C )。
A.5;9. 图⽰结构的零杆数⽬为( C )。
A.5;B.6;C.7;D.8。
10. 图⽰两结构及其受⼒状态,它们的内⼒符合( B )。
A.弯矩相同,剪⼒不同;B.弯矩相同,轴⼒不同;C.弯矩不同,剪⼒相同;D.弯矩不同,轴⼒不同。
PP2EI EI EIEI 2EI EIllhl l11. 刚结点在结构发⽣变形时的主要特征是( D )。
A.各杆可以绕结点结⼼⾃由转动; B.不变形; C.各杆之间的夹⾓可任意改变; D.各杆之间的夹⾓保持不变。
12. 若荷载作⽤在静定多跨梁的基本部分上,附属部分上⽆荷载作⽤,则( B )。
A.基本部分和附属部分均有内⼒;B.基本部分有内⼒,附属部分没有内⼒;C.基本部分⽆内⼒,附属部分有内⼒;D.不经过计算,⽆法判断。
《结构力学习题》(含答案解析)

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
结构力学第二版课后习题答案

结构力学第二版课后习题答案结构力学第二版课后习题答案结构力学是一门研究物体受力情况和力学性质的学科,它在工程领域中有着广泛的应用。
结构力学的学习不仅需要理论的掌握,还需要通过实际的习题来加深对知识的理解和运用。
本文将为大家提供《结构力学》第二版课后习题的答案,希望能够帮助大家更好地学习和应用结构力学知识。
第一章弹性力学基础1.1 弹性力学的基本概念1. 弹性力学是研究物体在外力作用下发生形变时,恢复到原来形态的力学学科。
2. 牛顿第二定律:物体所受合外力等于物体质量乘以加速度。
3. 弹性体:在外力作用下,物体发生形变,当外力消失后,物体能够完全恢复到原来的形态。
4. 弹性力学的基本假设:线弹性假设、小变形假设、平面假设。
1.2 应力和应变1. 应力:单位面积上的力,即单位面积上的力的大小。
2. 应变:物体在外力作用下发生的形变程度。
3. 线弹性假设下的应力-应变关系:胡克定律,即应力与应变成正比。
4. 应力张量:描述物体内部各点上的应力状态,是一个二阶张量。
1.3 弹性体的本构关系1. 本构关系:描述物体应力和应变之间的关系。
2. 弹性体的本构关系:胡克定律。
3. 弹性模量:描述物体对应力的敏感程度。
4. 剪切模量:描述物体对剪切应力的敏感程度。
第二章弹性力学的基本方程2.1 平衡方程与应力平衡方程1. 平衡方程:描述物体在力的作用下的平衡状态。
2. 应力平衡方程:描述物体在外力作用下的应力分布情况。
2.2 应变平衡方程1. 应变平衡方程:描述物体在外力作用下的应变分布情况。
2.3 弹性力学基本方程1. 弹性力学基本方程:包括平衡方程、应力平衡方程和应变平衡方程。
第三章弹性体的力学性质3.1 弹性体的应力分析1. 弹性体的平面应力问题:在一个平面上受力的弹性体。
2. 弹性体的平面应变问题:在一个平面上发生应变的弹性体。
3.2 弹性体的弯曲1. 弹性体的弯曲:在外力作用下,物体发生弯曲变形。
2. 弯曲方程:描述弯曲变形的关系。
《结构力学》参考资料

25.图中取A支座反力为力法的基本末知量(向上为正),则为:(C)
A.3P/16;B.4P/16;C.5P/16;D.不定,取决于EI值
26.下列哪个选项不是按照荷载作用性质以及结构的反应特征分类的(D)
A.静力荷载B.动力荷载C.移动荷载D.恒载
27.图示结构,当高度h增加时,杆1的内力(C)
A.增大B.减小C.不变D.不确定
28.图示体系是:(A)
A.几何瞬变有多余约束B.几何不变C.几何常变D.几何瞬变无多余约束
29.力法典型方程的副系数 ,其依据是(A)。
A.位移互等定理B.反力互等定理C.反力位移互等定理D.虚位移原理
30.设体系上作用的任意平衡力系,又设体系发生符合约束条件的无限小的刚体位移,则外力在位以上所做的虚功总和恒等于零是(A)。
17.荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。(对)
18.虚功中的力和位移没有因果关系。(对)
19.力矩分配法中的分配系数、传递系数与荷载无关。(对)
20.影响线仅用于解决活载作用下结构的计算问题,不能用于恒载作用下的计算。(错)
21.任何三铰拱的合理拱轴都是二次抛物线(错)
22.图乘法可以用来计算曲杆。(错)
34.力矩分配法中的分配系数,传递系数与外界因素(荷栽,温度变化等)有关。(错)
35.的互等定理仅适用于线性变形体系。(对)
36.位移法典型方程的右端项一定为零(对)
37.两个弯矩图的叠加不是指图形的简单拼合,而是指两图对应的弯矩纵矩叠加。(对)
38.位移法以结点力为基本未知量。(错)
39.对图中a图所示桁架用力法计算时,取图b作为基本体系(杆AB被去掉),则
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
《结构力学》典型习题与解答-知识归纳整理

《结构力学》经典习题及详解一、判断题(将判断结果填入括弧内,以 √表示正确 ,以 × 表示错误。
)1.图示桁架结构中有3个杆件轴力为0 。
(×)2.图示悬臂梁截面A 的弯矩值是ql 2。
(×)l lqA3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√ ) 4.普通来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(× ) 5.用平衡条件能求出全部内力的结构是静定结构。
( √ )6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√ ) 7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是惟独轴力。
(×) 9.超静定结构由于支座位移可以产生内力。
(√ ) 10.超静定结构的内力与材料的性质无关。
(× ) 11.力法典型方程的等号右端项不一定为0。
(√ )12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(× )14.力矩分配法适用于所有超静定结构的计算。
(×) 15.当AB 杆件刚度系数i S AB3 时,杆件的B 端为定向支座。
(×)F P知识归纳整理二、单项挑选题(在每小题的四个备选答案中选出一具正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
) 1.图示简支梁中间截面的弯矩为( A )qlA . 82qlB . 42ql C . 22ql D . 2ql2.超静定结构在荷载作用下产生的内力与刚度(B )A . 无关B . 相对值有关C . 绝对值有关D . 相对值绝对值都有关 3.超静定结构的超静定次数等于结构中(B )A .约束的数目B .多余约束的数目C .结点数D .杆件数4.力法典型方程是根据以下哪个条件得到的(C )。
结构力学书本后答案解析

AB与基础用1、2、3杆,组成几何不变体系成为 刚片Ⅰ,DG与刚片Ⅱ用BD、4、5杆组成几何不 变体系。用掉二元体GH、6杆。 结论:无多余约束的几何不变体系。
Байду номын сангаас 习题2.2b
AB与基础用组成几何不变体系成为刚片Ⅱ 和Ⅰ 用BC、1杆组成几何不变体系。用掉二元体EF、 2杆。 结论:无多余约束的几何不变体系。
习题21a依次去掉二元体fihcfgghecgeacddeb最后剩下ab与基础用四根杆连接多一杆有一个多余约束的几何不变体习题21b依次去用掉二元体fhg和c铰和结论
习题2.1a 依次去掉二元体FIH、 CFG、GHE、CGE、 ACD、DEB最后剩下 AB与基础用四根杆连 接多一杆,有一个多 余约束的几何不变体 系。
习题2.4
去掉1、2、3杆。铰接三角形ACF上增加两个二元 体CDF、DGA形成刚片Ⅰ,铰接三角形DEH上增加 一个二元体EBH形成刚片Ⅱ,两刚片用D铰和链 杆BG相连组成几何不变体系。 结论:无多余约束的几何不变体系。
依次去用掉二元体FHG、Ⅰ和ⅡC铰,Ⅰ和 习题2.1b Ⅲ用A铰,Ⅱ和Ⅲ用B角连接,多1、2两个杆, 结论:有两个多余约束的几何不变体系。
习题2.1c
依次去用掉二元体FHG、CFD、 DGE以及三个支座链杆。
在依次去用掉二元体CAE和 CBE剩下CDE
CDE可以相对转动。结论是几 何可变体系。
习题2.2a
习题2.2c
BD与基础用AB、3、4杆组成几何不变体系。用 掉二元体EF、5杆。
结论:无多余约束的几何不变体系。
习题2.3a
Ⅰ、Ⅱ、Ⅲ用A、B、C相连组成几何不变体系。 结论:无多余约束的几何不变体系。
习题2.3b
与上题相比多一杆 结论:有一个多余约束的几何不变体系。
结构力学力法习题及答案

结构力学力法习题及答案结构力学力法习题及答案结构力学是一门研究物体在外力作用下产生的应力和变形的学科。
在工程学中,结构力学是非常重要的一门学科,它为我们设计和分析各种建筑和机械结构提供了基础。
在学习结构力学的过程中,习题是必不可少的一部分。
下面将给出一些结构力学的力法习题及其答案,希望对读者有所帮助。
1. 一个悬臂梁上有一个集中力作用在梁的自由端,求该梁的弯矩分布图。
解答:根据悬臂梁的特点,自由端处的弯矩最大。
假设集中力为F,梁的长度为L,弹性模量为E,梁的截面惯性矩为I。
根据悬臂梁的弯矩公式M = F * L,可以得到弯矩分布图为一个从自由端开始逐渐减小的直线。
2. 一个等截面的梁上有一个均布载荷作用,求该梁的剪力分布图。
解答:假设均布载荷为q,梁的长度为L,根据梁的受力平衡条件,可以得到梁上任意一点的剪力大小为V = q * x,其中x为距离梁的一端的距离。
因此,该梁的剪力分布图为一个线性增长的直线。
3. 一个梁上有多个集中力作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
4. 一个悬臂梁上有一个集中力和一个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:首先,根据集中力的大小和悬臂梁的长度,可以求出集中力在悬臂梁上的弯矩分布图。
然后,根据均布载荷的大小和悬臂梁的长度,可以求出均布载荷在悬臂梁上的剪力分布图。
最后,将两者叠加在一起,即可得到梁的总弯矩和总剪力分布图。
5. 一个梁上有多个集中力和多个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力和均布载荷,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
通过以上习题的解答,我们可以看到结构力学中力法的应用。
在实际工程中,我们需要根据具体的结构形式和受力情况,运用结构力学的理论知识,求解结构的受力分布,从而保证结构的安全可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 平面体系的机动分析题2-2.试对图示平面体系进行机动分析。
解析:如图2-2(a )所示,去掉二元体为(b ),根据两刚片法则,原体系为几何不变体系,且无多余约束。
题2-3.试对图示平面体系进行机动分析。
解析:图2-3(a )去除地基和二元体后,如图2-3(b )所示,刚片Ⅰ、Ⅱ用一实铰3o ;Ⅰ、Ⅲ用一无穷远虚铰1o 连接;Ⅱ、Ⅲ用一无穷远虚铰2o 连接;三铰不共线,根据三刚片法则,原体系为几何不变体系,且无多余约束。
去二元体图2- 2(a )(b )(b )去二元体(a)图2-3题2-4.试对图示平面体系进行机动分析。
解析:刚片Ⅰ、Ⅱ、Ⅲ用一实铰1o 和两虚铰2o 、3o 连接,根据三刚片法则,体系为几何不变体系,且无多余约束。
题2-5.试对图示平面体系进行机动分析。
解析:刚片Ⅰ、Ⅱ、Ⅲ通过铰1o 、2o 、3o 连接,根据三刚片法则,体系为几何不变体系,且无多余约束。
题2-7.试对图示平面体系进行机动分析。
解析:刚片Ⅰ、Ⅱ用一无穷远虚铰1o 连接,刚片Ⅰ、Ⅲ用一无穷远虚铰2o 连接,去二元体(a )(b )图2-7图2-5图2-4刚片Ⅱ、Ⅲ通过一平行连杆和一竖向链杆形成的虚铰3o 连接,根据三刚片法则,体系为几何不变体系,且无多余约束。
题2-8.试对图示平面体系进行机动分析解析:去除二元体如图(b )所示,j=12,b=20所以,232122031w j b =--=⨯--=,所以原体系为常变体系。
题2-9.试对图示平面体系进行机动分析解析:去除地基如图(b )所示,刚片Ⅰ、Ⅱ用实铰1o 连接,刚片Ⅰ、Ⅲ用虚铰2o 连接,刚片Ⅱ、Ⅲ用虚铰3o 连接,根据三刚片法则,体系为几何不变体系,且无多余约束。
题2-10.试对图示平面体系进行机动分析解析:AB,CD,EF 为三刚片两两用虚铰相连(平行链杆),且三铰都在无穷远处。
所以为瞬变体系(每对链杆各自等长,但由于每对链杆从异侧连接,故系统为瞬变,而非不变)。
图2-9(b )去地基(a )图2-8去二元体(a )(b )图2-10解析:先考虑如图(b )所示的体系,将地基看作一个无限大刚片Ⅲ,与刚片Ⅰ用实铰2o连接,与刚片Ⅱ用实铰3o 连接,而刚片Ⅰ、Ⅱ用实铰1o 连接,根据三刚片法则,图(b )体系为几何不变体系,且无多余约束。
然后在图(b )体系上添加5个二元体恢复成原体系图(a )。
因此,原体系为几何不变体系,且无多余约束。
题2-12. 试对图示平面体系进行机动分析解析:如图(b )所示,将地基看作刚片Ⅲ,与刚片Ⅰ用虚铰2o 连接,与刚片Ⅱ用虚铰3o 连接,而刚片Ⅰ、Ⅱ用实铰1o 连接,根据三刚片法则,原体系为几何不变体系,且无多余约束。
(a )(b )图2-11图2-12(a )(b )解析:将原体系(图(a ))中的二元体去除,新体系如图(b )所示,其中刚片Ⅰ、Ⅱ分别与基础之间用一个铰和一个链杆连接,根据两刚片法则,原体系为几何不变体系2-14.试对图示平面体系进行机动分析解析:刚片Ⅰ、Ⅱ用实铰连接,而刚片Ⅰ和Ⅲ、Ⅱ和Ⅲ分别通过两平行连杆在无穷远处形成的虚铰相连接,且四根连杆相互平行,因此三铰共线,原体系为瞬变体系。
题2-15. 试对图示平面体系进行机动分析解析:去除原体系中的地基,如图(b )所示,三个刚片分别通过长度相等的平行连杆在无穷远处形成的虚铰相连,故为常变体系。
去二元体(a )(b )图2-13图2-14(b )去二元体(a )题2-16. 试对图示平面体系进行机动分析解析:将支座和大地看成一个整体,因此可以先不考虑支座,仅考虑结构体,从一边,譬如从右边开始向左依次应用二元体法则分析结构体,最后多余一根,因此原体系是有一个多余约束的几何不变体系。
题2-17. 试对图示平面体系进行机动分析。
解析:通过去除多余连杆和二元体,得到的图(c )为几何不变体系,因此,原体系是有8个多余约束的几何不变体系。
图2-15去除地(a )(b )图2-16 去掉中间8(a )(b )去二元体(c )图2-17题2-18. 添加最少数目的链杆和支承链杆,使体系成为几何不变,且无多余联系。
解析:如图(a ),原体系的自由度32342324w m b r =--=⨯-⨯-=,因此至少需要添加4个约束,才能成为几何不变体系。
如图(b )所示,在原体系上添加了4跟连杆后,把地基视为一个刚片,则由三刚片法则得知,变形后的体系为几何不变且无多余约束体系。
题2-19. 添加最少数目的链杆和支承链杆,使体系成为几何不变,且无多余联系。
解析:如图(a ),原体系的自由度2()26(81)3w j b r =-+=⨯-+=,因此需要添加3个约束,才能成为几何不变且无多余约束体系,如图(b )所示。
第三章 静定梁与静定刚架题3-2. 试作图示单跨梁的M 图和Q 图(a )(b )图2-18(b )(a )图 2-19解析:2018044020108067.50101020052.552.546033040AB B A B A D D MV V KNV V V V KNM KN m M KN m =∴⨯-⨯--⨯+=∴==∴⨯+--=∴=⨯⨯+∑∑左右=-=30==70题3-4. 试作图示单跨梁的M 图解析:232320332438B B A B A A V V ql V qlM V l ql l M M ql =∴-=∴==∴--=∴=∑∑题3-8. 试做多跨静定梁的M 、Q 图。
解析:201542(1517.5)64063.750663.752154018.750618.75830430205555303018.75023.75FD D GF D AC C A A M V V KNM V V KNMV V KNV V KN l=∴⨯⨯++⨯-⨯=∴==∴+⨯-⨯=∴==∴-⨯-⨯-⨯=∴=+---=∴=∑∑∑题3-10. 试不计算反力而绘出梁的弯矩图。
题3-11. 试不计算反力而绘出梁的弯矩图。
题3-14. 试做出图示刚架的M 、Q 、N 图。
022202344BA AB A B CB B B A A B MV lqlV l V V ql qlV V MH lV H l ql H H ql qlH H ==∴-=-=∴====∴-=--=∴==∑∑∑∑解析取右半部分作为研究对象解析:15020240201000010********GA A ABC B C MH H KNH V H H V H KN V KN=∴⨯++⨯-⨯=∴=-==∴+=⨯+-=∴==∑∑∑解析:6.5 6.50.8 6.50.5 6.5140221.96001.9606.590.5 6.5 2.5 1.967023.600.8 6.50.5 6.504.85AB B A B AC B B B A A MV V KN V V V V KNM H H KNH H H H KN=∴⨯⨯+⨯⨯-=∴==∴+=∴==⎛⎫∴-⨯⨯+-⨯= ⎪⎝⎭∴==∴⨯+⨯--=∴=∑∑∑∑题3-24. 试做出图示刚架的M图。
解析:a 041042020b 042042040081220410201042204062.5GE E HF F AB F B M V V KNM V V KN MV V V KN=-⨯⨯=∴==-⨯⨯=∴==∴+-⨯⨯--⨯⨯-⨯=∴=∑∑∑取左半部分为研究对象,如图()所示取右半部分为研究对象,如图()所示以整体为研究对象0042.540A A V H V KN H KN==∴=∴=∑∑3-26.已知结构的弯矩图,试绘出其荷载。
(b)第五章静定平面桁架题5-7.试用较简便的方法求图示桁架中指定杆件的内力。
解析:111222330,07()2I I a 724624(ЦЦb 0o '7222022()07222022()24A B A B N N N N N N N N M M V V F dF F d dF F F M F d dF dF Fd F F V F F F F F F ====↑-+•-=∴=--=∑∴•++-=∴==∑∴--+=∴=-∑∑1)以整体为研究对象由得2)取截面的左半部分为研究对象,如图()所示压)3)取截面的左半部分为研究对象,如图()所示拉压)以结423c 0202()N N N V C F F F F =∑∴--=∴=-点C 为研究对象,如图()所示压题5-12.试用较简便的方法求图示桁架中指定杆件的内力。
解析:a b c d oa 0I I ЦЦ10,0,15()5()2b 05(ЦЦc 010630,20(ІІN N N N A B B Nd Nb Nb M V V KN V KN V F KN B M F F =--===↓=↓==∑-=∴⨯-=∴=-∑∑∑如图()所示,首先去0杆,可知F ;选取截面和截面求F 、F 、F )以整体为研究对象由求得支座反力,)以结点B 为研究对象,如图()所示由得拉)3)取截面的左半部分为研究对象,如图()所示拉)4)取截面的下半部分为oc cd 0215353330215221.2()Nd N N MF F F KN KN =∴⨯+⨯--⨯=∴==∑研究对象,如图()所示拉5-18. 试求图示组合结构中各链杆的轴力并做受弯杆件的内力图。
解析:11o3365a 0112565030027.327.3c 0327.33256503072.7032530250227.30252BC C B C B GN N N N CCN N MX X X X X KN X KNM F F KN M F F KN XYF F ==∴-⨯-⨯=-=∴===∴+⨯-⨯-⨯=∴==∴+⨯=∴=-==∴++=+∑∑∑∑∑∑取结构的右半部分进行分析,如图()所示如图()所示,取结构的右上部分为研究对象(拉)(压)5564512642202252 2.3220025752N N N N N N N N N N F F KN F KN F F F F F F KN F KN =∴=-=-+=+-=∴==-(压)(压)又(拉)(压)第六章 影响线及其应用题6-4. 试作图示结构中下列量值的影响线:BC S 、D M 、D Q 、D N .1P 在AE 部分移动。
解析:题6-9. 作主梁B R 、D M 、D Q 、C Q 左、C Q 右的影响线。
题6-10. 试做图示结构中指定量值的影响线。
题6-22. 试求图示简支梁在所给移动荷载作用下截面C 的最大弯矩。
解析:a 40 2.2560 1.7520 1.25300.75242.5400.7560 2.2520 1.7530 1.25237.5C C C M M KN m M KN m =⨯+⨯+⨯+⨯=•=⨯+⨯+⨯+⨯=•如图()所示为的影响线,可知当外荷载作用在截面C ,且其它荷载均在梁上时才有可能产生最大弯矩。
