1931 C.I.E XYZ色域坐标图1931 C.I.E XYZ色域坐标图

颜色基础知识——CIE 1931色度坐标图

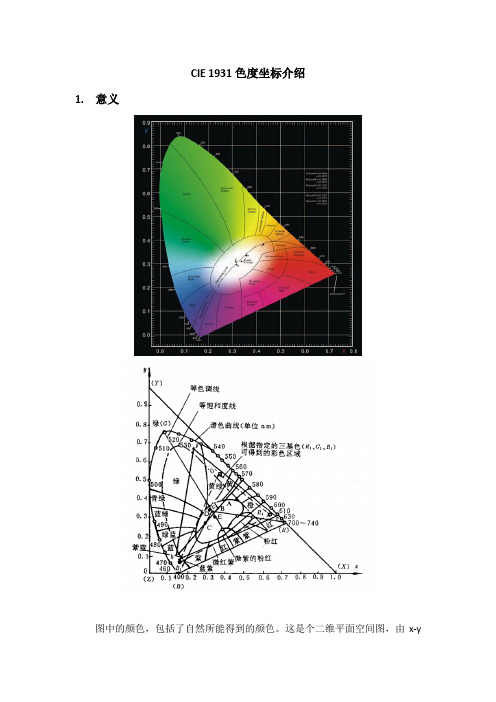
CIE 1931色度坐标介绍1. 意义图中的颜色，包括了自然所能得到的颜色。

这是个二维平面空间图，由x-y直角标系统构成的平面。

为了适应人们习惯于在平面坐标系中讨论变量关系，而设计出来的。

在设计出该图的过程中，经过许多数学上的变换和演算。

此图的意义和作用，可以总结成两句话：（1）表示颜色视觉的基本规律。

（2）表示颜色混合与分解的一般规律。

2. 坐标系——x ，y直角坐标系。

x——表示与红色有关的相对量值。

y——表示与绿色有关的相对量值。

z——表示与蓝色有关的相对量值。

并且z=1-(x+y)3. 形状与外形轮廓线形状——舌形，有时候也称“舌形曲线”图。

由舌形外围曲线和底部直线包围起来的闭合区域。

舌形外围曲线——是全部可见光单色光颜色轨迹线，每一点代表某个波长单色光的颜色，波长从390nm到760nm。

在曲线的旁边。

标注了一些特征颜色点的对应波长。

例如图中510nm——520nm——530nm等。

底部直线——连接390nm点到760nm点构成的直线，此线称为紫红线。

4. 色彩这是一个彩色图，区域内的色彩，包括了一切物理上能实现的颜色。

很遗憾的是，很难得真正标准的这种资料，经常由于转印而失真。

5. 应用价值——颜色的定量表示。

用（x，y）的坐标值来表示颜色。

白色应该包含在“颜色”这个概念范围内。

6. 若干个特征点的意义（1）E点—等能白光点的坐标点E点是以三种基色光，以相同的刺激光能量混合而成的。

但三者的光通量并不相等。

E点的CCT=5400K。

（2）A点—CIE规定一种标准白光光源的色度坐标点这是一种纯钨丝灯，色温值CCT=2856。

（3）B点—CIE规定的一种标准光源坐标点B点的CCT=4874K，代表直射日光。

（4）C点—CIE确认的一种标准日光光源坐标点（昼光）C点的CCT=6774K。

（5）D点—有时候也标为D光源称为典型日光，或重组日光;CCT=6500K。

7. 三条特殊线（1）黑体色温轨迹线：在舌形曲线的中部，跨过白色区，有一条向下弯的曲线，这就是黑体色温轨迹线。

色度图波长对应坐标值

色度图波长对应坐标值部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑二、 1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

<一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色<三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………<5-8）Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为：x=<0.490r+0.310g+0.200b）/<0.667r+1.132g+1.200b）y=<0.117r+0.812g+0.010b）/<0.667r+1.132g+1.200b）………………(5-9>z=<0.000r+0.010g+0.990b）/<0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式<5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是<0.33，0.33），没有改变。

1931CIE-XYZ

二、1931CIE-XYZ標準色度系統所謂1931CIE-XYZ系統，就是在RGB系統的基礎上，用數學方法，選用三個理想的原色來代替實際的三原色，從而將CIE-RGB系統中的光譜三刺激值和色度坐標r、g、b均變為正值。

（一）、CIE-RGB系統與CIE-XYZ系統的轉換關係選擇三個理想的原色（三刺激值）X、Y、Z，X代表紅原色,Y代表綠原色,Z代表藍原色,這三個原色不是物理上的真實色，而是虛構的假想色。

它們在圖5-27中的色度坐標分別為：從圖5-27中可以看到由XYZ形成的虛線三角形將整個光譜軌跡包含在內。

因此整個光譜色變成了以XYZ三角形作為色域的域內色。

在XYZ系統中所得到的光譜三刺激值、、、和色度坐標x、y、z將完全變成正值。

經數學變換，兩組顏色空間的三刺激值有以下關係：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B兩組顏色空間色度坐標的相互轉換關係為：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）這就是我們通常用來進行變換的關係式，所以，只要知道某一顏色的色度坐標r、g、b，即可以求出它們在新設想的三原色XYZ顏色空間的的色度坐標x、y、z。

通過式（5-9）的變換，對光譜色或一切自然界的色彩而言，變換後的色度坐標均為正值，而且等能白光的色度坐標仍然是（0.33，0.33），沒有改變。

表5-3是由CIE-RGB系統按表5-2中的數據，由式（5-9）計算的結果。

從表5-3中可以看到所有光譜色度坐標x(l)，y(l)，z(l)的數值均為正值。

1931CIE-XYZ

二、1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB 系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

（一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色（三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：r g bX 1.275 -0.278 0.003Y -1.739 2.767 -0.028Z -0.743 0.141 1.602从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B两组颜色空间色度坐目标相互转换关系为：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式（5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是（0.33，0.33），没有改变。

表5-3是由CIE-RGB系统按表5-2中的数据，由式（5-9）计算的结果。

CIE_1931_色度图

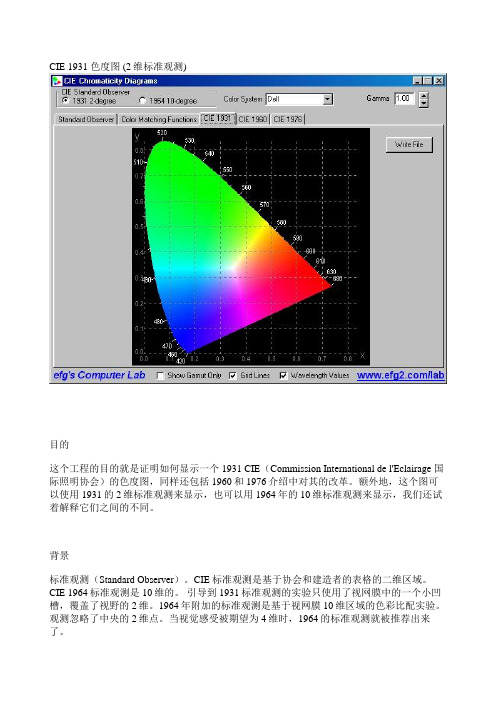
CIE 1931 色度图 (2维标准观测)目的这个工程的目的就是证明如何显示一个1931 CIE（Commission International de l'Eclairage 国际照明协会）的色度图，同样还包括1960和1976介绍中对其的改革。

额外地，这个图可以使用1931的2维标准观测来显示，也可以用1964年的10维标准观测来显示，我们还试着解释它们之间的不同。

背景标准观测（Standard Observer）。

CIE标准观测是基于协会和建造者的表格的二维区域。

CIE 1964标准观测是10维的。

引导到1931标准观测的实验只使用了视网膜中的一个小凹槽，覆盖了视野的2维。

1964年附加的标准观测是基于视网膜10维区域的色彩比配实验。

观测忽略了中央的2维点。

当视觉感受被期望为4维时，1964的标准观测就被推荐出来了。

CIE标准观测通常都基于许多实验，这些实验是用少数拥有普通视力的人做出的。

没有真正的观测是也CIE标准观测一样的。

请参考[Judd75, pp. 153-157] or [Billmeyer81, pp.42-45]。

关于新闻组的投递，Danny提出“1964观测有50个观测者左右，而1931只有一打。

1964的工作包括一些外国的已经获得博士学位的同事，但是早期的工作只有包括伦敦附近的一些英国人”。

根据[Foley96, p. 580], 1964的表格并不是普遍为计算机使用的，因为它强调很大的一个颜色区域，这个区域里的大多数颜色并不是图象中能够找到的。

下面的图能够被“标准”表格色度程序显示，当程序被校准了以后尺寸也就正确了。

CIE 1931 2-Degree Field of ViewCIE 1964 10-Degree Field of View要得到附加的CIE1931和1964观测信息，请看[Judd75, p. 155] or [Billmeyer81, p. 42]。

1931CIE-XYZ标准色度系统

1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

（一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色（三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：r g bX 1.275 -0.278 0.003Y -1.739 2.767 -0.028Z -0.743 0.141 1.602从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式（5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是（0.33，0.33），没有改变。

表5-3是由CIE-RGB系统按表5-2中的数据，由式（5-9）计算的结果。

2.1.3 1931 CIE-XYZ计色系统_数字电视与平板电视中的色度学_[共7页]

b (λ) 0 0 1
0.29465
x (λ) 0.73467 0.27376 0.16658 0.34842
y(λ)
0.26533 0.71741 0.00885 0.35161
z (λ) 0.00000 0.00883 0.82457 0.29997
对某一单色波长为的光谱三刺激响应 r(λ)、g(λ)、b(λ)与单色波长为的色度坐标 x(λ)、
42
数字电视与平板电视中的色度学
于分别配出色光 F1 和 F2 所需该基色分量的三刺激值之和。 1931 CIE-RGB 计色系统是采用 700nm（R）、546.1nm（G）、435.8nm（B）波长的三基
色作为基准，以 r (λ)、 g (λ)、 b (λ)光谱响应曲线为基础建立起来的，本来可以用来计算、标定颜色，但是用来标定光谱色的基色会出现负值[如图 2.1.4 和表 2.1.1 所示的 r (λ)和 g (λ)]，人
用三个假想的三基色（X）、（Y）、（Z）建立了一个新的计色系统—1931 CIE-XYZ 计色系统。同时将匹配等能光谱各种颜色的三基色数值标准化，定名为“CIE 1931 标准色度观察者”
或称“国际标准眼”，它们是设计、制造通用计色仪器的依据。
建立 1931 CIE-XYZ 计色系统主要基于以下三点考虑。数字电视与平板电视中的色度学
43
再取 700nm 和 540nm 两点作为直线上的两点，求出这条直线的方程式为：
r + 0.99 g − 1 = 0
（2.1.13）
另取一条与光谱轨迹波长 503nm 点相靠近的直线，这条直线的方程式为：
1.45r + 0.55g + 1 = 0
为了使用方便，应将图 2.1.4 中的△XYZ 转换成麦克斯韦直角三角形，即目前国际上比较

[整理]1931CIE-XYZ标准色度系统

1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

（一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色（三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式（5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是（0.33，0.33），没有改变。

表5-3是由CIE-RGB系统按表5-2中的数据，由式（5-9）计算的结果。

从表5-3中可以看到所有光谱色度坐标x(l)，y(l)，z(l)的数值均为正值。

1931CIE-XYZ标准色度系统

第四节CIE 标准色度学系统一、CIE1931RGB真实三原色表色系统颜色匹配实验把两个颜色调整到视觉相同的方法叫颜色匹配，颜色匹配实验是利用色光加色来实现的。

图5-24中左方是一块白色屏幕，上方为红R、%f^G、蓝B三原色光,下方为待配色光C,三原色光照射白屏幕的上半部，待配色光照射白屏幕的下半部，白屏幕上下两部分用一黑挡屏隔开，由白屏幕反射出来的光通过小孔抵达右方观察者的眼内。

人眼看到的视场如图右下方所示，视场范围在2。

左右，被分成两部分。

图右上方还有一束光，照射在小孔周围的背景白版上，使视场周围有一圈色光做为背景。

在此实验装置上可以进行一系列的颜色匹配实验。

待配色光可以通过调节上方三原色的强度来混合形成，当视场中的两部分色光相同时，视场中的分界线消失，两部分合为同一视场，此时认为待配色光的光色与三原色光的混合光色达到色匹配。

不同的待配色光达到匹配时三原色光亮度不同，可用颜色方程表示：C=R ( R) +G (G) +B (B) (5-1 )式中C表示待配色光；(R)、( G)、( B)代表产生混合色的红、绿、蓝三原色的单位量；R、G B分别为匹配待配色所需要的红、绿、蓝三原色的数量，称为三刺激值；“ o”表示视觉上相等，即颜色匹配。

图5-24颜色匹配实验(二)、三原色的单位量国际照明委员会(CIE)规定红、绿、蓝三原色的波长分别为700nm> 546.1nm、435.8nm,在颜色匹配实验中，当这三原色光的相对亮度比例为 1.0000 : 4.5907 : 0.0601时就能匹配出等能白光，所以CIE选取这一比例作为红、绿、蓝三原色的单位量，即(R : ( G): ( B) =1 : 1 : 1。

尽管这时三原色的亮度值并不等，但CIE却把每一原色的亮度值作为一个单位看待，所以色光加色法中红、绿、蓝三原色光等比例混合结果为白光，即( R) + (G) + (B) = (W。

(三)、CIE-RGB光谱三刺激值CIE-RGB光谱三刺激值是317位正常视觉者，用CIE规定的红、绿、蓝三原色光，对等能光谱色从380nm到780nm所进行的专门性颜色混合匹配实验得到的。

1931CIE-XYZ标准色度系统-18页精选文档

希望以上资料对你有所帮助，附励志名言3条：1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

（一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色（三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：r g bX 1.275-0.2780.003Y-1.739 2.767-0.028Z-0.7430.141 1.602从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式（5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是（0.33，0.33），没有改变。

1931CIE-XYZ标准色度系统

第四节CIE标准色度学系统一、CIE1931RGB 真实三原色表色系统（一）、颜色匹配实验把两个颜色调整到视觉相同的方法叫颜色匹配，颜色匹配实验是利用色光加色来实现的。

图5-24中左方是一块白色屏幕，上方为红R、绿G、蓝B三原色光，下方为待配色光C，三原色光照射白屏幕的上半部，待配色光照射白屏幕的下半部，白屏幕上下两部分用一黑挡屏隔开，由白屏幕反射出来的光通过小孔抵达右方观察者的眼内。

人眼看到的视场如图右下方所示，视场范围在2°左右，被分成两部分。

图右上方还有一束光，照射在小孔周围的背景白版上，使视场周围有一圈色光做为背景。

在此实验装置上可以进行一系列的颜色匹配实验。

待配色光可以通过调节上方三原色的强度来混合形成，当视场中的两部分色光相同时，视场中的分界线消失，两部分合为同一视场，此时认为待配色光的光色与三原色光的混合光色达到色匹配。

不同的待配色光达到匹配时三原色光亮度不同，可用颜色方程表示：C=R（R）+G（G）+B（B）（5-1）式中C 表示待配色光；（R）、（G）、（B）代表产生混合色的红、绿、蓝三原色的单位量；R、G、B分别为匹配待配色所需要的红、绿、蓝三原色的数量，称为三刺激值；“o”表示视觉上相等，即颜色匹配。

图5-24 颜色匹配实验（二）、三原色的单位量国际照明委员会（CIE）规定红、绿、蓝三原色的波长分别为700nm、546.1nm、435.8nm，在颜色匹配实验中，当这三原色光的相对亮度比例为1.0000：4.5907：0.0601时就能匹配出等能白光，所以CIE选取这一比例作为红、绿、蓝三原色的单位量，即（R）：（G）：（B）=1：1：1。

尽管这时三原色的亮度值并不等，但CIE却把每一原色的亮度值作为一个单位看待，所以色光加色法中红、绿、蓝三原色光等比例混合结果为白光，即（R）+（G）+（B）=（W）。

（三）、 CIE-RGB光谱三刺激值CIE-RGB光谱三刺激值是317位正常视觉者，用CIE规定的红、绿、蓝三原色光，对等能光谱色从380nm到780nm 所进行的专门性颜色混合匹配实验得到的。

色坐标图

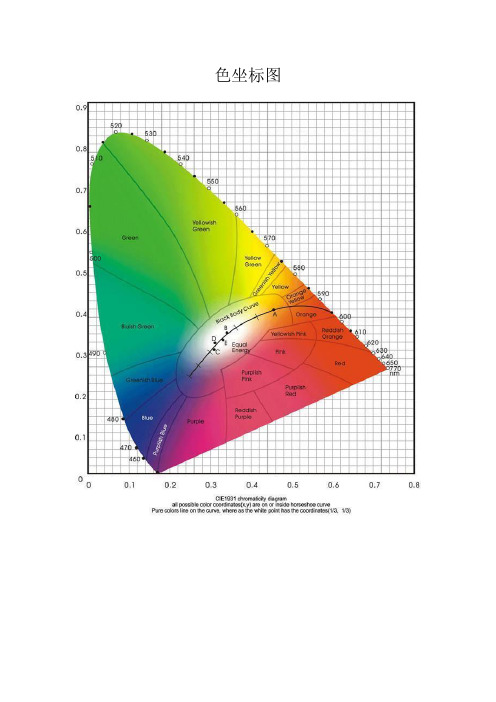
色坐标图CIE色度学系统表示颜色的方法1、用三刺激值表示颜色，最常用的是1931CIE-XYZ标准色度学系统所规定的三刺激值X、Y和Z。

2、用色品坐标x、y及Y刺激值表示颜色，色品坐标是三刺激值fenbie对三刺激值总量的比值，在测量中不需对三刺激值准确标定便可准确地确定色品坐标，故常用色品坐标x和y表示颜色，但是由于色品坐标是三刺激值各自对三刺激值总量的比值，从而失去了表示光亮度的因子，只表示了颜色的色调。

颜色匹配从图上可以看出：1、波长700~770nm的光谱色，色品点重合，表明他们有相同的色品坐标，在亮度相同时，表观颜色相同2、两点连线上的颜色都可以用两点的颜色以一定的比例配出来，波长540~700nm光谱色轨迹是一段直线，所以这段直线上的任何光谱色都可以用540nm和700nm两种光谱色配出来。

主波长和补色波长CIE 1931 color space from---Wiki EncyclopediaIn the study of color perception, the CIE 1931 RGB and CIE 1931 XYZ color spaces are the first mathematically defined color spaces. They were created by the International Commission on Illumination(CIE) in 1931.[1][2]The CIE XYZ color space was derived from a series of experiments done in the late 1920s by William David Wright[3] and John Guild.[4] Their experimental results were combined into the specification of the CIE RGB color space, from which the CIE XYZ color space was derived.Tristimulus valuesThe normalized spectral sensitivity of human cone cells of short-, middle- and long-wavelength typesThe human eye has three kinds of cone cells, which sense light, with spectral sensitivity peaks in short (S, 420–440 nm), middle (M,530–540 nm), and long (L, 560–580 nm) wavelengths. These cone cells underlie human color perception under medium- and high-brightness conditions (in very dim light, color vision diminishes, and thelow-brightness, monochromatic "night-vision" receptors, called rod cells, take over). Thus, three parameters, corresponding to levels of stimulus of the three types of cone cells, can in principle describe any color sensation. Weighting a total light power spectrum by the individual spectral sensitivities of the three types of cone cells gives three effective stimulus values; these three values make up a tristimulus specification of the objective color of the light spectrum. The three parameters, noted S, M, and L, can be indicated using a 3-dimension space,called LMS color space, which is one of many color spaces which have been devised to help quantify human color vision.A color space maps a range of physically produced colors (from mixed light, pigments, etc.) to an objective description of color sensations registered in the eye, typically in terms of tristimulus values, but not usually in the LMS space defined by the cone spectral sensitivities. The tristimulus values associated with a color space can be conceptualized as amounts of three primary colors in a tri-chromatic additive color model. In some color spaces, including LMS and XYZ spaces, the primary colors used are not real colors, in the sense that they cannot be generated with any light spectrum.The CIE XYZ color space encompasses all color sensations that an average person can experience. It serves as a standard reference against which many other color spaces are defined. A set of color-matching functions, like the spectral sensitivity curves of the LMS space but not restricted to be nonnegative sensitivities, associates physically produced light spectra with specific tristimulus values.Consider two light sources made up of different mixtures of various wavelengths. Such light sources may appear to be the same color; this effect is called metamerism. Such light sources have the same apparent color to an observer when they produce the same tristimulus values, no matter what are the spectral power distributions of the sources.Most wavelengths will not stimulate only one type of cone cell, because the spectral sensitivity curves of the three types of cone cells overlap. Certain tristimulus values are thus physically impossible (for instance LMS tristimulus values that are non-zero for one component, and zeros for the others). And LMS tristimulus values for pure spectral colors would, in any normal trichromatic additive color space (e.g. RGB color spaces), imply negative values for at least one of the three primaries, since the chromaticity would be outside the color triangle defined by the primary colors. To avoid these negative RGB values, and to have one component that describes the perceived brightness, "imaginary" primary colors and corresponding color-matching functions have been formulated. The resulting tristimulus values are defined by the CIE 1931 color space, in which they are denoted X, Y, and Z.[5]Meaning of X, Y, and ZA comparison between a typical normalised M cone's spectral sensitivity and the CIE 1931 luminosity function for a standard observer in photopic visionWhen judging the relative luminance (brightness) of different colors in well-lit situations, humans tend to perceive light within the green parts of the spectrum as brighter than red or blue light of equal power. The luminosity function that describes the perceived brightnesses of different wavelengths is thus roughly analogous to the spectral sensitivity of M cones.The CIE model capitalises on this fact by defining Y as luminance. Z is quasi-equal to blue stimulation, or the S cone response, and X is a mix (a linear combination) of cone response curves chosen to be nonnegative. The XYZ tristimulus values are thus analogous to, but not equal to, the LMS cone responses of the human eye. Defining Y as luminance has the useful result that for any given Y value, the XZ plane will contain all possible chromaticities at that luminance.CIE standard observerDue to the distribution of cones in the eye, the tristimulus values depend on the observer's field of view. To eliminate this variable, the CIE defined a color-mapping function called the standard (colorimetric) observer, to represent an average human's chromatic response within a 2° arc inside the fovea. This angle was chosen owing to the belief that the color-sensitive cones resided within a 2° arc of the fovea. Thus the CIE 1931 Standard Observer function is also known as the CIE 1931 2° StandardObserver. A more modern but less-used alternative is the CIE 1964 10° Standard Observer, which is derived from the work of Stiles and Burch,[6] and Speranskaya.[7]For the 10° experiments, the observers were instructed to ignore the central 2° spot. The 1964 Supplementary Standard Observer function is recommended when dealing with more than about a 4° field of view. Both standard observer functions are discretized at 5 nm wavelength intervals from 380 nm to 780 nm and distributed by the CIE.[8]The standard observer is characterized by three color matching functions.The derivation of the CIE standard observer from color matching experiments is given below, after the description of the CIE RGB space.Color matching functionsThe CIE standard observer color matching functionsThe CIE's color matching functions, and are the numericaldescription of the chromatic response of the observer(described above). They can be thought of as the spectral sensitivity curves of three linear light detectors yielding the CIE tristimulus values X, Y and Z. Collectively, these three functions are known as the CIE standard observer.[9]The tristimulus values for a color with a spectral power distribution are given in terms of the standard observer by:where is the wavelength of the equivalent monochromatic light (measured in nanometers).Other observers, such as for the CIE RGB space or other RGB color spaces, are defined by other sets of three color-matching functions, and lead to tristimulus values in those other spaces.The values of X, Y, and Z are bounded if the intensity spectrum is bounded.CIE xy chromaticity diagram and the CIE xyY color spaceThe CIE 1931 color space chromaticity diagram. The outer curved boundary is the spectral (or monochromatic) locus, with wavelengths shown in nanometers. Note that the colors your screen displays in this image are specified using sRGB, so the colorsoutside the sRGB gamut are not displayed properly. Depending on the color space and calibration of your display device, the sRGB colors may not be displayed properly either. This diagram displays the maximally saturated bright colors that can be produced by a computer monitor or television set.The CIE 1931 color space chromaticity diagram rendered in terms of the colors of lower saturation and value than those displayed in the diagram above that can be produced by pigments, such as those used in printing. The color names are from the Munsell color system.Since the human eye has three types of color sensors that respond to different ranges of wavelengths, a full plot of all visible colors is a three-dimensional figure. However, the concept of color can be divided into two parts: brightness and chromaticity. For example, the color white is a bright color, while the color grey is considered to be a less bright version of that same white. In other words, the chromaticity of white and grey are the same while their brightness differs.The CIE XYZ color space was deliberately designed so that the Y parameter was a measure of the brightness or luminance of a color. The chromaticity of a color was then specified by the two derived parameters x and y, two of the three normalized values which are functions of all three tristimulus values X, Y, and Z:The derived color space specified by x, y, and Y is known as the CIE xyY color space and is widely used to specify colors in practice.The X and Z tristimulus values can be calculated back from the chromaticity values x and y and the Y tristimulus value:The figure on the right shows the related chromaticity diagram. The outer curved boundary is the spectral locus, with wavelengths shown in nanometers. Note that the chromaticity diagram is a tool to specify how the human eye will experience light with a given spectrum. It cannot specify colors of objects (or printing inks), since the chromaticity observed while looking at an object depends on the light source as well.Mathematically, x and y are projective coordinates and the colors of the chromaticity diagram occupy a region of the real projective plane.The chromaticity diagram illustrates a number of interesting properties of the CIE XYZ color space:•The diagram represents all of the chromaticities visible to the average person.These are shown in color and this region is called the gamut of human vision.The gamut of all visible chromaticities on the CIE plot is the tongue-shaped or horseshoe-shaped figure shown in color. The curved edge of the gamut iscalled the spectral locus and corresponds to monochromatic light (each pointrepresenting a pure hue of a single wavelength), with wavelengths listed innanometers. The straight edge on the lower part of the gamut is called the lineof purples. These colors, although they are on the border of the gamut, have nocounterpart in monochromatic light. Less saturated colors appear in theinterior of the figure with white at the center.•It is seen that all visible chromaticities correspond to non-negative values of x, y, and z (and therefore to non-negative values of X, Y, and Z).•If one chooses any two points of color on the chromaticity diagram, then all the colors that lie in a straight line between the two points can be formed bymixing these two colors. It follows that the gamut of colors must be convex inshape. All colors that can be formed by mixing three sources are found insidethe triangle formed by the source points on the chromaticity diagram (and soon for multiple sources).•An equal mixture of two equally bright colors will not generally lie on the midpoint of that line segment. In more general terms, a distance on the xychromaticity diagram does not correspond to the degree of difference betweentwo colors. In the early 1940s, David MacAdam studied the nature of visualsensitivity to color differences, and summarized his results in the concept of aMacAdam ellipse. Based on the work of MacAdam, the CIE 1960, CIE 1964,and CIE 1976 color spaces were developed, with the goal of achievingperceptual uniformity (have an equal distance in the color space correspond toequal differences in color). Although they were a distinct improvement overthe CIE 1931 system, they were not completely free of distortion.•It can be seen that, given three real sources, these sources cannot cover the gamut of human vision. Geometrically stated, there are no three points withinthe gamut that form a triangle that includes the entire gamut; or more simply,the gamut of human vision is not a triangle.•Light with a flat power spectrum in terms of wavelength (equal power in every1 nm interval) corresponds to the point (x,y) = (1/3,1/3).Definition of the CIE XYZ color spaceCIE RGB color spaceThe CIE RGB color space is one of many RGB color spaces, distinguished by a particular set of monochromatic (single-wavelength) primary colors.In the 1920s, W. David Wright[3] and John Guild[4] independently conducted a series of experiments on human sight which laid the foundation for the specification of the CIE XYZ color space.Gamut of the CIE RGB primaries and location of primaries on the CIE 1931 xy chromaticity diagramThe experiments were conducted by using a circular split screen (a bipartite field) 2 degrees in diameter, which is the angular size of the human fovea. On one side of the field a test color was projected and on the other side, an observer-adjustable color was projected. The adjustable color was a mixture of three primary colors, each with fixed chromaticity, but with adjustable brightness.The observer would alter the brightness of each of the three primary beams until a match to the test color was observed. Not all test colors could be matched using this technique. When this was the case, a variable amount of one of the primaries could be added to the test color, and a match with the remaining two primaries was carried out with the variable color spot. For these cases, the amount of the primary added to the test color was considered to be a negative value. In this way, the entire range of human color perception could be covered. When the test colors were monochromatic, a plot could be made of the amount of each primary used as a function of the wavelength of the test color. These three functions are called the color matching functions for that particular experiment.The CIE 1931 RGB Color matching functions. The color matching functions are the amounts of primaries needed to match the monochromatic test primary at the wavelength shown on the horizontal scale.Although Wright and Guild's experiments were carried out using various primaries at various intensities, and although they used a number of different observers, all of their results were summarized by thestandardized CIE RGB color matching functions , , and ,obtained using three monochromatic primaries at standardized wavelengths of 700 nm (red), 546.1 nm (green) and 435.8 nm (blue). The color matching functions are the amounts of primaries needed to match the monochromatic test primary. These functions are shown in the plot on theright (CIE 1931). Note that and are zero at 435.8, andare zero at 546.1 and and are zero at 700 nm, since in thesecases the test color is one of the primaries. The primaries with wavelengths 546.1 nm and 435.8 nm were chosen because they are easily reproducible monochromatic lines of a mercury vapor discharge. The 700 nm wavelength, which in 1931 was difficult to reproduce as a monochromatic beam, was chosen because the eye's perception of color is rather unchanging at this wavelength, and therefore small errors in wavelength of this primary would have little effect on the results.The color matching functions and primaries were settled upon by a CIE special commission after considerable deliberation.[10]The cut-offs at the short- and long-wavelength side of the diagram are chosen somewhat arbitrarily; the human eye can actually see light with wavelengths up toabout 810 nm, but with a sensitivity that is many thousand times lower than for green light. These color matching functions define what is known as the "1931 CIE standard observer". Note that rather than specify the brightness of each primary, the curves are normalized to have constant area beneath them. This area is fixed to a particular value by specifying thatThe resulting normalized color matching functions are then scaled in the r:g:b ratio of 1:4.5907:0.0601 for source luminance and 72.0962:1.3791:1 for source radiant power to reproduce the true color matching functions. By proposing that the primaries be standardized, the CIE established an international system of objective color notation.Given these scaled color matching functions, the RGB tristimulus values for a color with a spectral power distribution would then be given by:These are all inner products and can be thought of as a projection of an infinite-dimensional spectrum to a three-dimensional color. (See also: Hilbert space)Grassmann's lawOne might ask: "Why is it possible that Wright and Guild's results can be summarized using different primaries and different intensities from those actually used?" One might also ask: "What about the case when the test colors being matched are not monochromatic?" The answer to both ofthese questions lies in the (near) linearity of human color perception. This linearity is expressed in Grassmann's law.The CIE RGB space can be used to define chromaticity in the usual way: The chromaticity coordinates are r and g where:Construction of the CIE XYZ color space from theWright–Guild dataHaving developed an RGB model of human vision using the CIE RGB matching functions, the members of the special commission wished to develop another color space that would relate to the CIE RGB color space. It was assumed that Grassmann's law held, and the new space would be related to the CIE RGB space by a linear transformation. The new space would be defined interms of three new color matching functions , , and asdescribed above. The new color space would be chosen to have the following desirable properties:Diagram in CIE rg chromaticity space showing the construction of the triangle specifying the CIE XYZ color space. The triangle C b-C g-C r is just thexy=(0,0),(0,1),(1,0) triangle in CIE xy chromaticity space. The line connecting C b and C r is the alychne. Notice that the spectral locus passes through rg=(0,0) at 435.8 nm, through rg=(0,1) at 546.1 nm and through rg=(1,0) at 700 nm. Also, the equal energy point (E) is at rg=xy=(1/3,1/3).1.The new color matching functions were to be everywhere greater than or equalto zero. In 1931, computations were done by hand or slide rule, and thespecification of positive values was a useful computational simplification.2.The color matching function would be exactly equal to the photopicluminous efficiency function V(λ) for the "CIE standard photopic observer".[11] The luminance function describes the variation of perceived brightness withwavelength. The fact that the luminance function could be constructed by alinear combination of the RGB color matching functions was not guaranteedby any means but might be expected to be nearly true due to the near-linearnature of human sight. Again, the main reason for this requirement wascomputational simplification.3.For the constant energy white point, it was required that x = y = z = 1/3.4.By virtue of the definition of chromaticity and the requirement of positivevalues of x and y, it can be seen that the gamut of all colors will lie inside thetriangle [1,0], [0,0], [0,1]. It was required that the gamut fill this spacepractically completely.5.It was found that the color matching function could be set to zero above650 nm while remaining within the bounds of experimental error. Forcomputational simplicity, it was specified that this would be so.In geometrical terms, choosing the new color space amounts to choosing a new triangle in rg chromaticity space. In the figure above-right, the rg chromaticity coordinates are shown on the two axes in black, along with the gamut of the 1931 standard observer. Shown in red are the CIE xy chromaticity axes which were determined by the above requirements. The requirement that the XYZ coordinates be non-negative means that thetriangle formed by Cr , Cg, Cbmust encompass the entire gamut of the standardobserver. The line connecting Cr and Cbis fixed by the requirement thatthe function be equal to the luminance function. This line is the line of zero luminance, and is called the alychne. The requirement that the function be zero above 650 nm means that the line connectingC g and Crmust be tangent to the gamut in the region of Kr. This definesthe location of point Cr. The requirement that the equal energy point be defined by x = y = 1/3 puts a restriction on the line joining C b and C g, and finally, the requirement that the gamut fill the space puts a second restriction on this line to be very close to the gamut in the green region,which specifies the location of Cg and Cb. The above describedtransformation is a linear transformation from the CIE RGB space to XYZ space. The standardized transformation settled upon by the CIE special commission was as follows:The numbers in the conversion matrix below are exact, with the number of digits specified in CIE standards.[10]While the above matrix is exactly specified in standards, going the other direction uses an inverse matrix that is not exactly specified, but is approximately:The integrals of the XYZ color matching functions must all be equal by requirement 3 above, and this is set by the integral of the photopic luminous efficiency function by requirement 2 above. The tabulated sensitivity curves have a certain amount of arbitrariness in them. The shapes of the individual X, Y and Z sensitivity curves can be measured with a reasonable accuracy. However, the overall luminosity curve (which in fact is a weighted sum of these three curves) is subjective, since itinvolves asking a test person whether two light sources have the same brightness, even if they are in completely different colors. Along the same lines, the relative magnitudes of the X, Y, and Z curves are arbitrary. Furthermore, one could define a valid color space with an X sensitivity curve that has twice the amplitude. This new color space would have a different shape. The sensitivity curves in the CIE 1931 and 1964 XYZ color spaces are scaled to have equal areas under the curves.See also•Trichromacy•Imaginary color•Lab color space•Standard illuminant, the definition of white point used by CIE and commonly shown in color space diagrams as E, D50 or D65References1.Jump up ^CIE (1932). Commission internationale de l'Eclairageproceedings, 1931. Cambridge: Cambridge University Press.2.Jump up ^ Smith, Thomas; Guild, John (1931–32). "The C.I.E.colorimetric standards and their use". Transactions of the OpticalSociety33 (3): 73–134. doi:10.1088/1475-4878/33/3/301.3.^ Jump up to: a b Wright, William David (1928). "A re-determinationof the trichromatic coefficients of the spectral colours". Transactions of the Optical Society30(4): 141–164. doi:10.1088/1475-4878/30/4/301.4.^ Jump up to: a b Guild, J. (1932). "The colorimetric propertiesof the spectrum". Philosophical Transactions of the Royal Society ofLondon. Series A, Containing Papers of a Mathematical or PhysicalCharacter230: 149–187. doi:10.1098/rsta.1932.0005. JSTOR91229.5.Jump up ^Hunt, R. W. (1998). Measuring Colour(3rd ed.). England:Fountain Press. ISBN0-86343-387-1.. See pgs. 39–46 for the basis in human eye physiology of three-component color models, and 54–57 forchromaticity coordinates.6.Jump up ^ Stiles, W. S.; Birch, J. M. (1959). "N.P.L.Colour-matching Investigation: Final Report (1958)". Optica Acta6(1): 1–26. doi:10.1080/713826267.7.Jump up ^ Speranskaya, N. I. (1959). "Determination of spectrumcolor co-ordinates for twenty seven normal observers". Optics andSpectroscopy7: 424–428.8.Jump up ^"CIE Free Documents for Download".9.Jump up ^ Harris, A. C.; Weatherall, I. L. (September 1990)."Objective evaluation of colour variation in the sand-burrowing beetle Chaerodes trachyscelides White (Coleoptera: Tenebrionidae) byinstrumental determination of CIE LAB values". Journal of the RoyalSociety of New Zealand(The Royal Society of New Zealand) 20(3): 253–259.doi:10.1080/03036758.1990.10416819.10.^ Jump up to: a b Fairman, H. S.; Brill, M. H.; Hemmendinger, H.(February 1997). "How the CIE 1931 Color-Matching Functions Were Derived from the Wright–Guild Data". Color Research and Application22 (1):11–23.doi:10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7. andFairman, H. S.; Brill, M. H.; Hemmendinger, H. (August 1998). "Erratum: How the CIE 1931 Color-Matching Functions Were Derived from theWright–Guild Data". Color Research and Application23 (4): 259–259.doi:10.1002/(SICI)1520-6378(199808)23:4<259::AID-COL18>3.0.CO;2-7.11.Jump up ^CIE (1926). Commission internationale de l'Eclairageproceedings, 1924. Cambridge: Cambridge University Press. Note that the 1924 luminous efficiency function seriously underestimates sensitivity at wavelengths below 460 nm, and has been supplemented with newer and more accurate luminosity curves; see Luminosity function#Improvements to the standard.Further reading•Broadbent, Arthur D. (August 2004). "A critical review of the development of the CIE1931 RGB color-matching functions". Color Research & Applications29 (4): 267–272. doi:10.1002/col.20020."This article describes the development of the CIE1931 chromaticity coordinates and color-matching functions starting from the initial experimental data of W. D. Wright and J. Guild. Sufficientinformation is given to allow the reader to reproduce and verifythe results obtained at each stage of the calculations and toanalyze critically the procedures used. Unfortunately, some of the information required for the coordinate transformations was never published and the appended tables provide likely versions of that missing data."•Trezona, Pat W. (2001). "Derivation of the 1964 CIE 10° XYZ Colour-Matching Functions and Their Applicability in Photometry".Color Research and Application26 (1): 67–75.doi:10.1002/1520-6378(200102)26:1<67::AID-COL7>3.0.CO;2-4.•Wright, William David (2007). "Golden Jubilee of Colour in the CIE—The Historical and Experimental Background to the 1931 CIE System of Colorimetry". In Schanda, János. Colorimetry. WileyInterscience. pp. 9–24. doi:10.1002/9780470175637.ch2.ISBN978-0-470-04904-4. (originally published by the Society of Dyers and Colourists, Bradford, 1981.)External links•Introduction to Colour Science, William Andrew Steer.•efg's Color Chromaticity Diagrams Lab Report and Delphi source •CIE Color Space, Gernot Hoffman•Annotated downloadable data tables, Andrew Stockman and Lindsay T.Sharpe.•Calculation from the original experimental data of the CIE 1931 RGB standard observer spectral chromaticity co-ordinates and colormatching functions•Colorimetric data useful for calculation, in various file formats •COLORLAB MATLAB toolbox for color science computation and accurate color reproduction. It includes CIE standard tristimuluscolorimetry and transformations to a number of non-linear color appearance models (CIE Lab, CIE CAM, etc.).•Precise Color Communication Konica Minolta Sensing。

1931CIE-XYZ标准色度系统

1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB 系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

（一）、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色（三刺激值）X、Y、Z，X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色，而是虚构的假想色。

它们在图5-27中的色度坐标分别为：r g bX 1.275 -0.278 0.003Y -1.739 2.767 -0.028Z -0.743 0.141 1.602从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。

因此整个光谱色变成了以XYZ三角形作为色域的域内色。

在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。

经数学变换，两组颜色空间的三刺激值有以下关系：X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………（5-8）Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为：x=（0.490r+0.310g+0.200b）/（0.667r+1.132g+1.200b）y=（0.117r+0.812g+0.010b）/（0.667r+1.132g+1.200b）………………(5-9)z=（0.000r+0.010g+0.990b）/（0.667r+1.132g+1.200b）这就是我们通常用来进行变换的关系式，所以，只要知道某一颜色的色度坐标r、g、b，即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。

通过式（5-9）的变换，对光谱色或一切自然界的色彩而言，变换后的色度坐标均为正值，而且等能白光的色度坐标仍然是（0.33，0.33），没有改变。

表5-3是由CIE-RGB系统按表5-2中的数据，由式（5-9）计算的结果。

1931CIEXYZ标准色度系统

1931CIE-XYZ标准色度系统所谓1931CIE-XY二杀先就是在RG吕系统的基础上•用数学方法.选用三个理想的原色来代替实际的匕总系统屮的光谱三剌激值和色度坐标“ s三原色.从而将CIE-RGBb均变为正值。

CIE-RGB系统与CIE-XY2系统的转换关系(一〉、这三个原色不,2代表盔廉色,X选择三个理想的原色(三剌激值)X、Y. 2.代表红原色,Y代表绿原色是物理上的真实色.而是虚构的假想色。

它们在图5-27中的色度坐标分别为：b g r0. 003 X -0. 278 1. 275-0. 028 Y -1. 739 2. 767 1.602-0. 7130. 141形成的虚线三角形将整个光谱轨迹包育在内，因此整个光谱色变成了以中可以看到由XY7从图5-272W 尹(X)X0)、…利咆度坐标心丫二.角形作为色域的域内色•在XY三系统中所得到的光谱三剌激值.厂：:将完全变成正值，经数学变换.两组颜色空间的三剌激值有以下关系：X=0. 490R-O. 31(X^0. 200BY=0.177R-H). 812G+0.011B .......................................... (5-S )Z= 0.010G-0. 990B曲组颜色空间色度坐标的相互转换关系为：x= (0. 190x-0. 310g-0. 200b) / (0. 667r^l. 132g-l. 200b)y= (0. 117r-0. 812g40. 010b ) / (0. 667r+l. 132^1. 200b) .................................................. (5-9)z= (0. OOOr-O. 010g-0. 990b) / (0. 667r^l. 132g-l. 200b)这就是我们通常用來进行变换的关系式.所以.只耍知道某一颜色的色度坐标门s b.即可以求出它们在新设想的三原色XY2颜色空间的的色度坐标m y. s通过式(5-9)的变换•对光谱色或一切口然界的色彩而言.变换后的色度坐标均为正值.而且等能口光的色度坐标仍然是(0.33. 0.33).没有改变。

CIE1931色彩空间

目錄[隱藏]∙ 1 三色刺激值∙ 2 CIE xy 色度圖∙ 3 CIE XYZ 色彩空間定義o 3.1 實驗結果— CIE RGB 色彩空間o 3.2 Grassmann 定律o 3.3 從 Wright–Guild 數據構造 CIE XYZ 色彩空間∙ 4 問題和解決∙ 5 引用∙ 6 參見∙7 外部連結Y 和 Z 值並不是真的看起來是紅、綠和藍色，而是從紅色、綠色和藍色導出來的參數），並使用 CIE 1931 XYZ 顏色匹配函數來計算。

兩個由多種不同波長的光混合而成的光源可以表現出同樣的顏色，這叫做「異譜同色」（metamerism）。

當兩個光源對標準觀察者（CIE 1931 標準色度觀察者）有相同的視現顏色的時候，它們即有同樣的三色刺激值，而不管生成它們的光的光譜分佈如何。

[編輯] CIE xy色度圖CIE 1931 色彩空間色度圖。

外側曲線邊界是光譜（或單色）光軌跡，波長用納米標記。

注意描繪的顏色依賴於顯示這個圖象的設備的色彩空間，沒有設備能有足夠大色域來在所有位置上提供精確的色度表現。

因為人類眼睛有響應不同波長範圍的三種類型的顏色傳感器，所有可視顏色的完整繪圖是三維的。

但是顏色的概念可以分為兩部分：明度和色度。

例如，白色是明亮的顏色，而灰色被認為是不太亮的白色。

換句話說，白色和灰色的色度是一樣的，而明度不同。

CIE XYZ 色彩空間故意設計得Y參數是顏色的明度或亮度的測量。

顏色的色度接着通過兩個導出參數x和y來指定，它們是所有三個三色刺激值X、Y和Z的函數所規範化的三個值中的兩個：導出的色彩空間用 x, y, Y 來指定，它叫做 CIE xyY 色彩空間並在實踐中廣泛用於指定顏色。

X和Z三色刺激值可以從色度值x和y與Y三色刺激值計算回來：右側的圖象展示了相對色度圖。

外側曲線邊界是光譜軌跡，波長用納米標記。

注意這個色度圖是指定人類眼睛如何體驗給定頻譜的光的工具。

它不能指定物體的顏色（或印刷墨水），因為在觀察物體的時候看到的色度還依賴於光源。

光色电参数测试(研究生)

光色电参数解析1931年CIE 建立了以三原色(X) (Y) (Z)为基础的“CIE1931-XYZ 色度系统”，(X) (Y) (Z)分别代表红色、绿色、蓝色，光谱三刺激值如图所示。

三原色的坐标为：780380()m X K P x d λλλ=⎰780380()m Y K P y d λλλ=⎰780380()m Z K P z d λλλ=⎰式中，m K =683 lm/w 为常数，P λ为光谱功率（能量）分布， ()x λ、()y λ、()z λ为光谱三刺激值。

通过光色电综合测量系统测得白光LED 的光谱功率分布,结合光谱三刺激值，就可以得到与之对应的色度坐标值，则白光LED 的色度坐标为：Xx X Y Z =++Yy X Y Z =++ z=1-x-y图1 CIE 1931-XYZ 系统标准色度观察者光谱三刺激值图2 CIE 1931-XYZ 系统色度图相关色温：光源发射的光与黑体在某一温度下辐射的光颜色最接近，则黑体的温度就称为该光源发射的光的相关色温，单位为K 。

色温与色坐标有着紧密的联系，一个色坐标x,y 值对应一个色温值。

色温的确定可以根据相关色温公式(McCamy ，1992)进行计算[23]，即31.55146831360143723+-+-=n n n T c其中，0.33200.1858x n y -=-，x, y 为色坐标。

主波长：d λ如图所示的色品图，图中AB 为黑体轨迹。

设F 点为某一光源在色品图中的坐标，E 点为理想等能白光的参考光源点，坐标为(x,y)=(0.3,0.3)。

由E 点连接F 点并延长交于G 点，则G 点对应的单色光波长即称为F 点光源的主波长。

主波长示意图如上图，c P =EF/EG 。

易知，c P 越接近1，色纯度越高。

峰值波长：p λ比较对称的单色光的检测。

平均波长：光辐射功率: Φe radiant flux为瓦(W),如以t 表示时间,辐射通量定义为:Φe =dQe/dt显色指数：要求出白光LED 的显色指数必须先得到其特殊显色指数i R 。

CIE 1931色度图

CIE开放分类：颜色、国际组织CIE（国际发光照明委员会）：原文为Commission Internationale deL'Eclairage（法）或International Commission on Illumination（英）。

这个委员会创建的目的是要建立一套界定和测量色彩的技术标准。

可回溯到1930年，CIE标准一直沿用到数字视频时代，其中包括白光标准（D65）和阴极射线管（CRT）内表面红、绿、蓝三种磷光理论上的理想颜色。

CIE的总部位于奥地利维也纳。

CIE颜色系统颜色是一门很复杂的学科，它涉及到物理学、生物学、心理学和材料学等多种学科。

颜色是人的大脑对物体的一种主观感觉，用数学方法来描述这种感觉是一件很困难的事。

现在已经有很多有关颜色的理论、测量技术和颜色标准，但是到目前为止，似乎还没有一种人类感知颜色的理论被普遍接受。

RGB模型采用物理三基色，其物理意义很清楚，但它是一种与设备相关的颜色模型。

每一种设备(包括人眼和现在使用的扫描仪、监视器和打印机等)使用RGB模型时都有不太相同的定义，尽管各自都工作很圆满，而且很直观，但不能相互通用。

1）简介为了从基色出发定义一种与设备无关的颜色模型，1931年9月国际照明委员会在英国的剑桥市召开了具有历史意义的大会。

CIE的颜色科学家们企图在RGB模型基础上，用数学的方法从真实的基色推导出理论的三基色，创建一个新的颜色系统，使颜料、染料和印刷等工业能够明确指定产品的颜色。

会议所取得的主要成果包含：定义了标准观察者(Standard Observer)标准：普通人眼对颜色的响应。

该标准采用想象的X,λ Y和Z三种基色，用颜色匹配函数(color-matching function)表示。

颜色匹配实验使用2°的视野(field of view)；定义了标准光源(Standard Illuminants)：用于比较颜色的光源规范；λ定义了CIE XYZ基色系统：与RGB相关的想象的基色系统，但更适用于颜色的计算；λ定义了CIE xyY颜色空间：一个由XYZ导出的颜色空间，它把与颜色属性相关的x和y从与λ明度属性相关的亮度Y中分离开；定义了CIE色度图(CIE chromaticity diagram)：容易看到颜色之间关系的一种图。