电力系统有功功率平衡与频率调
电力系统的有功功率和频率调整ppt课件

国民经济备用:计及负荷的超计划增长而设置的备用。
16
5.1.3 有功功率电源和备用容量* ——各种备用容量的关系
负荷备用——热备用 事故备用——至少包括一部份热备用(可含冷备用) 检修备用(通过检查年最大负荷曲线来确定) 国民经济备用 具备了备用容量,才可能谈及备用用量在各发电设备
11
5.1.2 有功功率负荷曲线的预计
——负荷曲线的加工
实测曲线 加工后的曲线
加工原则:
实测曲线加
工前后,最
大和最小负
荷特征及曲
线下的面积
12
图5-3 负荷曲线加工
应一致。
5.1.3 有功功率电源和备用容量
有功功率电源 有功功率备用容量
备用容量、热备用与冷备用 负荷备用、事故备用、检修备用、国民经济备用 各种备用容量的关系
3 有功备用容量的概念 各类机组的有功调节特性
5.1 电力系统中有功功率的平衡 ——基本概念
负荷变动的类型及其特点? 频率调整的方法及其特点? 负荷变动与频率调整的关系? 什么是可供调度的系统电源容量、备用容量、
热备用和冷备用、负荷备用(事故备用、检修 备用、国民经济备用)? 两类备用容量的关系?
图5-1 有功功率负荷的变动曲线
频率调整方法及其特点
频率的一次调整:用发电机组的调速器(第一种负荷 变动)。
频率的二次调整:用发电机组的调频器(第二种负荷 的变动)。 ——调频厂,对应潮流计算中的平衡节点
频率的三次调整:按最优化准则分配第三种有规律变 动的负荷,即责成各发电厂按事先给定的发电负荷曲 线发电。
电力系统有功功率平衡与频率调整
第五章 电力系统有功功率平衡与频率调整主要内容提示本章主要讨论电力系统中有功功率负荷的最优分配和频率调整。
§5-1电力系统中有功功率的平衡 一、电力系统负荷变化曲线 在电力系统运行中,负荷作功需要一定的有功功率,同时,传输这些功率也要在网络中造成有功功率损耗。
因此,电源发出的有功功率必须满足下列平衡式:∑∆+∑=∑P P P Li Gi式中Gi P ∑—所有电源发出的有功功率;Li P ∑—所有负荷需要的有功功率; ∑∆P —网络中的有功功率损耗。
可见,发电机发出的功率比负荷功率大的多才行。
当系统中负荷增大时,网络损耗也将增大,发电机发出的功率也要增加。
在实际电力系统中,负荷随时在变化,所以必须靠调节电源侧,使发电机发出的功率随负荷功率的变化而变化。
负荷曲线的形状往往是无一定规律可循,但可将这种无规则的曲线看成是几种有规律的曲线的迭加。
如图5-1所示,将一种负荷曲线分解成三种曲线负荷。
第一种负荷曲线的变化,频率很快,周期很短,变化幅度很小。
这是由于想象不到的小负荷经常性变化引起的。
第二种负荷曲线的变化,频率较慢,周期较长,幅度较大。
这是由于一些冲击性、间歇性负荷的变动引起的,如大工厂中大电机、电炉、电气机车等一开一停。
第三种负荷曲线的变化,非常缓慢,幅度很大。
这是由于生产、生活、气象等引起的。
这种负荷是可以预计的。
对于第一种负荷变化引起的频率偏移进行调整,称为频率的“ 一次调整”。
调节方法一般是调节发电机组的调速器系统。
对于第二种负荷变化引起的频率偏移进行调整,称为频率的“二次调整”,调节方法是调节发电机组的调频器系统。
对于第三种负荷的变化,通常是根据预计的负荷曲线,按照一定的优化分配原则,在各发电厂间、发电机间实现功率的经济分配,称为有功功率负荷的优化分配。
二、发电厂的备用容量电力系统中的有功功率电源是发电厂中的发电机,而系统中装机容量总是大于发电容t量,即要有一定的备用容量。
系统的备用容量包括:负荷备用、事故备用、检修备用和国民经济备用。
电力系统有功功率平衡及频率调整

第三章电力系统有功功率平衡及频率调整例3-1 某一容量为100MW的发电机,调差系数整定为4%,当系统频率为50Hz 时,发电机出力为60MW;若系统频率下降为49.5Hz时,发电机的出力是多少?解根据调差系数与发电机的单位调节功率关系可得K G=(1/δ*)×(P GN/f N)=(1/0.04)×(100/50)=50(MW/Hz)于是有△P G=-K G△f=50(50-49.5)=25(MW)即频率下降到49.5Hz时,发电机的出力为60+25=85(MW)例3-2 电力系统中有A、B两等值机组并列运行,向负荷P D供电。
A等值机额定容量500MW,调差系数0.04,B等值机额定容量400MW,调差系数0.05。
系统负荷的频率调节效应系数K D*=1.5。
当负荷P D为600 MW时,频率为50Hz,A机组出力500MW,B机组出力100MW。
试问:(1)当系统增加50MW负荷后,系统频率与机组出力是多少?(2)当系统切除50MW负荷后,系统频率与机组出力是多少?解首先求等值发电机组A, B的单位调节功率及负荷的频率调节效应系数为K GA=(1/δ*)×(P GNA/f N)=(1/0.04)×(500/50)=250(MW/Hz)K GB=(1/δ*)×(P GNB/f N)=(1/0.05)×(400/50)=160(MW/Hz)K D=K D*×(P DN/f N)=1.5×(600/50)=18(MW/Hz)(1)当系统增加50 MW负荷后。
由题可知,等值机A已满载,若负荷增加,频率下降,K GA=0,不再参加频率调整。
系统的单位调节功率K=K GB+K D=160+18=178(MW/Hz)频率的变化量△f=-△P D/K=-50/178=-0.2809(Hz)系统频率f=50-0.2809=49.72(Hz)A机有功出力P GA=500MWB机有功出力P GB=100-K GB△f=100+160×0.2809=144.94(MW)(2)当系统切除50MW负荷后。
电力系统有功功率的平衡与频率调整

i1
(2)约束条件:
n
n
等式约束: 有功功率必须保持平衡
PGi PLi P
i 1
i 1
若忽略网损,则
n
n
PGi PLi 0
i 1
i 1
不等式约束: 系统的运行限制
PGi min PGi PGi max QGi min QGi QGi max Ui min Ui Ui max
解:按等耗量微增准则
1
dF1 dPG1
0.3 0.0014PG1
2
dF09PG3
PG1 14.29 0.572PG2 0.643PG3 PG1 PG2 PG3 400
1 2 3
第五章 电力系统有功功率的平衡和频率调整
5.2.1电力系统负荷的有功功率—频率静态特性
描述系统有功负荷随频率变化的关系曲线称为负荷的有功功率-频
率静态特性。简称负荷频率特性。
电力系统中各种用电设备与频率的关系大致如下
1)与频率变化无关的负荷,如照明,电阻炉等电阻性负荷
2)与频率变化成正比的负荷,如拖动金属切削机床的异步电动机
PL PLN
—系统频率为 —系统频率为
(2)运行中不宜承担急剧变化的负荷。 (3)一次投资大,运行费用小。
(应二指)出各: 类发电厂的合理组合 原则(枯1水)充季分节利往用往水由源系。统中的大型水电厂承担调频任务;洪水季
节(这2)任降务低火就电转机移组给的中单位温煤中耗压,火发电挥厂高.效抽机水组蓄的作能用电。厂在其发电 期间也可参加调频.但低温低压火电厂则因容量不足,设备
束条件如下:
F1 4 0.3PG1 0.0007PG21 100MW PG1 200MW
F2 3 0.32PG2 0.0004PG22 120MW PG2 250MW
第十三章-电力系统的有功功率平衡和频率调整

编辑版pppt
5
P
第一种
第二种
第三种
t
编辑版pppt
6
§13-2 电力系统的频率特性
一 系统负荷的有功功率-频率静态特性
有功负荷随频率的变化特性称为负 荷的频率特性,稳态下称静态频率特性。
编辑版pppt
7
综合负荷与频率的关系:
2
3
P D a 0P D N a 1 P DfN fN a 2P D N ffN a 3P D N ffN
12
1. 调速系统的工作原理 2. (离心式机械液压调速系统)
编辑版pppt
13
编辑版pppt
14
摆转速变慢,弹簧拉紧,B点下降到B点(A
点不动),o下降到 o E
E
动F
F
通,油动机活塞上移,进汽(水)阀门开大,
发电机转速增加,A
A o o点,
由于A
A
B
B点,
B
来的值。
这就是频率的一次调整,为有差调节, 频率不能回到原来的值。
编辑版pppt
15
为使转速仍能维持原来转速,在外 界信号的作用下,同步器动作,令D点上 移,这时由于E点不动,使得F点下降, 错油门打开,油动机动作,再次抬高活 塞,开大进汽门,可使转速回到初始值。 这就是频率的二次调整。
编辑版pppt
16
2. 发电机组的有功功率-频率静态特性
由以上分析可见,PD↑, P↑G,f↓低于 初始值,反之 ↓P,D ↓,PG f↑高于初始值。
i
i
所以 n 台机组的等值单位调节功率为
KG
i
KGi
i
KGi*
PGiN fN
KG*
【学习】第13章_电力系统的有功功率平衡及频率调整

n
n台机组的等值
P G P G i K G ifK G f
i1
i1
单位调节功率
标么值形式:
n
n
KG KGi KG*i
i1
i1
PGiN fN
n
KG* KG*iPGiN/PGN i1
*1/KG*PGN/ n PGiN
i1 i*
结论: 1.若某台机组已经没有调节容量,则取i*=, KGi=0; 2.调差系数越小的机组增加的有功出力(相对于本身的额定值 )就越多; 3.系统的单位调节功愈大,频率就愈稳定。
电力系统的频率水平由有功功率平衡决定,如果有功电源充 足,能保证用户需要,且具有及时进行调整的能力,则能保 证频率在合理的范围之内。反之,则将出现较大的频率偏移。
实际负荷曲线
频率二次调整负荷分量 频率一次调整负荷分量
按最优化原则在各发电厂 进行分配的负荷分量
13.2 电力系统的频率特性
一、系统负荷的有功功率-频率静态特性 系统处于稳态运行时,系统中有功负荷随频率的变化特性。 1.负荷的分类: 与频率无关:照明、电炉、整流; 与频率一次方成正比:球磨机、切削机床,卷扬机; 与频率二次方成正比:铁损(涡流); 与频率三次方成正比:通风机、静水头阻力不大的循环水泵; 与频率四次方成正比:阻力很大的水泵; 注:主要成份为前二种,在额定值附近为一直线。 2.负荷功率与频率的关系:
A
频率为f2。这种由发电机特性和
PD F
负荷调节效应共同承担系统负荷
变化使系统运行在另一频率的频 0 率调整称为频率的一次调整。
f2 f1
f
频率一次调整的结果:
发电机有功功率增加了P2-P1,负荷调节效应使负荷少吸收有 功功率为P3-P2,系统频率降低到f2。
电力系统有功功率的平衡与频率调整

5.1 电力系统中的有功平衡与频率调整
5.1.1 频率调整的必要性
1 频率变化对用户的影响
(1)系统频率的变化将引起工业用户的电动机转速的变化,这将影响产品 的质量。如纺织工业、造纸工业将因频率变化出现残次品。
(2) 当频率降低,使电动机有功功率降低,将影响所传动机械的出力。 (3) 频率不稳定,将会影响电子设备的准确性。雷达、电子计算机等重要
入功率
损平衡和备用容量
1、有功功率负荷的变动及其调整
对系统实际负荷变化曲线的分析表明 ,系统负荷可以看作是由三种具有不 同变化规律的变动负荷所组成:
第一种是变化幅度小,变化周期较短 (10s内)的负荷分量;
第二种是变化幅度较大,变化周期较 长(一般为10s至3min)的负荷分量, 如工业中大电机、电炉、电气机车等
5.1.4 各类发电厂的特点及合理组合
目前发电厂主要有以下三类:火力发电厂、水力发电厂、核电厂
(一)各类发电厂的特点
1、火力发电厂的主要特点
火电厂外景
(1)运行需要支付燃料费用,占用运输能力,运行不受 自然条件的影响。 (2)有功出力受锅炉和汽轮机最小技术负荷的限制,启 停时间长且启停费用高。 (3)效率与蒸汽参数有关,高温高压设备效率最高,低 温低压设备效率最低。 (4)热电厂采用抽汽供热,总效率较高。
(3)系统频率降低时,异步电动机和变压器的励磁电流大大增加,引起系 统无功损耗增加,若系统备用无功电源不足,将导致电压降低。
总之,电力系统的频率降低时将影响各行各业,频率过低时甚至会使系 统瓦解,造成大面积停电,必须设法使系统频率保持在规定范围内
5.1.2 电力系统的频率与有功功率平衡的关系
系统频率同发电机转速之间的关系 f np 60
第五章电力系统有功功率和频率调整

❖ 机组投入退出,承担急剧负荷响应时间长,多耗能 量,易损坏设备
❖ 热电厂抽汽供热,效率高,但技术最小负荷取决于 热负荷,为强迫功率
火电厂的效率
❖中温中压 ❖高温高压 ❖超高压力 ❖超临界压力 ❖热电厂
内容
❖ 机组优化组合(简要介绍)
确定系统中需要运行多少机组,哪些机组运行, 以及什么时候运行。
❖ 经济功率分配(重点学习)
在已知机组组合的基础上,确定各机组的功率输 出,在满足机组、系统安全约束的同时,使系统 的运行最优化。
火电厂特点
❖ 需燃料及运输费用,但不受自然条件影响 ❖ 效率与蒸汽参数有关
❖ ④原子能电厂虽然可调容量较大,调整速度也不 亚于火电厂,但因其运行费用较低,通常都以满负 荷运行,一般不考虑用这类电厂调频。
❖ ⑤如果系统中有抽水蓄能电厂,首先应该考虑采 用这类电厂进行调频。
名词解释
❖ ALFC:自动负荷频率控制 ❖ AGC:自动发电控制 ❖ EDC:经济调度控制 ❖ ACE:区域控制偏差
,从6.80%下降到5.69%。
1997~2009年厂用电率变化情况
电源备用容量
❖ 有功功率平衡:
发电功率=厂用电+网损+综合用电负荷
❖ 有功电源的备用容量:
备用容量=发电机组的额定容量-发电功率
电源备用容量(按状态分类)
❖ 热备用:运转中的发电设备可能发的最大功 率与发电负荷之差(旋转备用);
调整:减小进气量或进水量,进而减小作用在发 电机转子上的机械功率,机械功率=电磁功率, 转子达到额定转速,系统频率达到额定频率。
电力系统的有功功率平衡和频率调整概要
PL PL0
P
OA PLO
OA OC CB BA
P0'
P0"
B'
O" O' B
C
ΔPG0
A
PL
ΔPL0
O
BC KG f KG ( f0'' f 0 )
P0
0
AB K Lf KL ( f0'' f0 )
OC PGO PLO PGO ( KG KL )f
《电力系统分析》
Δf" A' Δf '
f0' f0" f0
频率的二次调整
f
二次调整增发的功率 系统的单位调节功率 K S
2018年10月14日星期日
n台机组:第n台参加二次调频 , n台全部参加一次调频:
PLO PGn 0 ( KGn K L )f
无差调频: 若 PLO PGO , PLO 即发电机如数增 发了负荷功率的原始增量 ,亦即实现了所谓的无 差调节.如上图虚线所示.
OA PLO
P
A
P0´
OA OB BA BO BA
' 0
O'
B' A'
B
O
ΔPL0
BO PG KG f KG ( f f0 ) P0
BA PL K L f
PLO ( K G K L )f
PG
PLO / f KG KL KS
《电力系统分析》
0
fN f0
频率的一次调整图
f
KS
系统的单位调节功率系数
第十三章 电力系统的有功功率平衡和频率调整

转速测量元件由离心飞摆、弹簧和套简组成,与原动机转轴相联接,直接反映原 动机转速的变化。当原动机有某一恒定转速时,飞摆处于某一定位置时达到平 衡,套简位于B点。杠杆AOB和DEF处在某种平衡位置,错油门的活塞将两个油 孔堵塞,使高压油不能进入油动机(接力器),油动机活塞上、下两侧的油压相 等,活塞不移动,从而使进汽(水)阀门的开度也固定不变。 负荷增加时,发电机的有功功率输出随之增加,原动机的转速(频率)降低,飞摆 的离心力减小。在弹簧力和重力的作用下,飞摆靠拢到新的位置才能重新达到各 力的平衡。于是套筒从B点下移到B’ 点。此时油动机还未动作,杠杆AOB中的A 点仍在原处不动,整个杠杆便以A点为支点转动,使O点下降到O’点。杠杆DEF 的D点是固定的,F点下移,错油门2的活塞随之向下移动,打开通向油动机3的 油孔,压力油便进入油动机活塞的下部,将活塞向上推,增大调节汽门(或导水 翼)的开度,增加进汽(水)量,使原动机的输入功率增加,结果机组的转速(频 率)便开始回升。随着转速的上升,套简从B’点开始回升,与此同时油动机活塞 上移,使杠杆AOB的A端也跟着上升,于是整个杠杆AOB便向上移动,并带动杠 杆DEF以D点为支点向逆时针方向转动。当点O以及DEF恢复到原来位置时,错 油门活塞重新堵住两个油孔,油动机活塞的上、下两侧油压又互相平衡,在新的 位置稳定下来,调整过程便告结束。 杠杆AOB的A端由于汽门已开大而略有上升,到达A’点的位置,而O点仍保持原 来位置,相应地B端将略有下降,到达B”的位置,与这个位置相对应的转速,将 略低于原来的数值。
PD*
= a0
+ a1 f
+ a2
f
电力系统有功功率平衡及频率调整知识讲解

第三章电力系统有功功率平衡及频率调整例3-1 某一容量为100MW的发电机,调差系数整定为4%,当系统频率为50Hz 时,发电机出力为60MW;若系统频率下降为49.5Hz时,发电机的出力是多少?解根据调差系数与发电机的单位调节功率关系可得K G=(1/δ*)×(P GN/f N)=(1/0.04)×(100/50)=50(MW/Hz)于是有△P G=-K G△f=50(50-49.5)=25(MW)即频率下降到49.5Hz时,发电机的出力为60+25=85(MW)例3-2 电力系统中有A、B两等值机组并列运行,向负荷P D供电。
A等值机额定容量500MW,调差系数0.04,B等值机额定容量400MW,调差系数0.05。
系统负荷的频率调节效应系数K D*=1.5。
当负荷P D为600 MW时,频率为50Hz,A机组出力500MW,B机组出力100MW。
试问:(1)当系统增加50MW负荷后,系统频率和机组出力是多少?(2)当系统切除50MW负荷后,系统频率和机组出力是多少?解首先求等值发电机组A, B的单位调节功率及负荷的频率调节效应系数为K GA=(1/δ*)×(P GNA/f N)=(1/0.04)×(500/50)=250(MW/Hz)K GB=(1/δ*)×(P GNB/f N)=(1/0.05)×(400/50)=160(MW/Hz)K D=K D*×(P DN/f N)=1.5×(600/50)=18(MW/Hz)(1)当系统增加50 MW负荷后。
由题可知,等值机A已满载,若负荷增加,频率下降,K GA=0,不再参加频率调整。
系统的单位调节功率K=K GB+K D=160+18=178(MW/Hz)频率的变化量△f=-△P D/K=-50/178=-0.2809(Hz)系统频率f=50-0.2809=49.72(Hz)A机有功出力P GA=500MWB机有功出力P GB=100-K GB△f=100+160×0.2809=144.94(MW)(2)当系统切除50MW负荷后。
电力系统有功功率的平衡和频率调整

第一节 电力系统中有功功率的平衡
有功负荷的最优分配的目的在于:在供应同样大小负荷
n
有功功率 p Gi 的前提下,单位时间内的能源消耗最少。 i1 目标函数是总耗量: n C (P G 1 ,P G 2 ,,P G ) n F F 1 (P G 1 ) F 2 (P G 2 ) . .F n .(P G ) n F i(P G )i i 1 变量:各发电设备输出有功功率。
为热备用 (旋转备用)
(1) 负荷备用。为了满足系统中短时的负荷变动和短期 内计划外的负荷增加而设置的备用。负荷备用容量的大小 与系统的负荷大小有关,一般为最大负荷的2%~5%。大系 统采用较小的百分数,小系统采用较大的百分数。
第一节 电力系统中有功功率的平衡 在有水、火电厂的联合系统,一般为冷 备用;在只有火电厂或水电厂不能投入 运行时,为热备用
(1)最小技术负荷小,为额定负荷10~15%; (2)启停费用高;负荷急剧变化时,调节费用高;启停 及急剧调节时,易于损坏设备; (3)一次投资大,运行费用小。
第一节 电力系统中有功功率的平衡 (二)各类发电厂的合理组合
原则: (1) 充分利用水源; (2) 降低火电机组的单位煤耗,发挥高效机组的作用;
6 0 .009
P2
根据等耗量微增率准则
:
=
1
有
2
8 0 .008 P1= 6 0 .009 P2
联立:
P1+
P
=
2
420
解出:
P
=
2
315
MW
P1= 105 MW
P1越限,取其下P限 1=1,20M 即W
P2=42- 012= 0 300MW
第二节 电力系统的频率调整 一、电力系统负荷的有功功率 —频率静态特性 负荷的有功功率-频率静态特性:当电力系统处于稳态运行 时,系统中综合有功负荷随频率的变化特性。
电力系统有功功率的平衡和频率调整基础知识讲解

%=3~5或 KG*=33.3~20 %=2~4或 KG*=50~25
c.负荷的单位调节功率:综合负荷的静态频率特性的斜率。
一般而言:
KL* 1.5
三、 频率的一次调整
1、简述:由于负荷突增,发电机组功率不能及时变动而 使机组减速,系统频率下降,同时,发电机组功率由于调 速器的一次调整作用而增大,负荷功率因其本身的调节效 应而减少,经过一个衰减的振荡过程,达到新的平衡。
2、数学表达式:
KS:称为系统的单位调节功率,单位Mw/Hz。表示原动 机调速器和负荷本身的调节效应共同作用下系统频率下 降或上升的多少。
3、注意: ➢ 取功率的增大或频率的上升为正; ➢ 为保证调速系统本身运行的稳定,不能采用过大的
单位调节功率; ➢ 对于满载机组,不再参加调整。
对于系统有若干台机参加一次调频:
原则(1)充分利用水源。 (2)降低火电机组的单位煤耗,发挥高效机组的作用。 (3)尽量降低火力发电成本。 根据上述原则,在夏季丰水期和冬季枯水期各类电厂在
日负荷曲线中的安排示意图,见图4-2。
图4-2 各类发电厂组合顺序示意图 (a)枯水季节 (b)丰水季节
➢夏季丰水期,水量充足,水电厂应带基本负荷以避免 弃水、节约燃煤。在此期间,可抓紧时间进行火电厂设 备的检修。
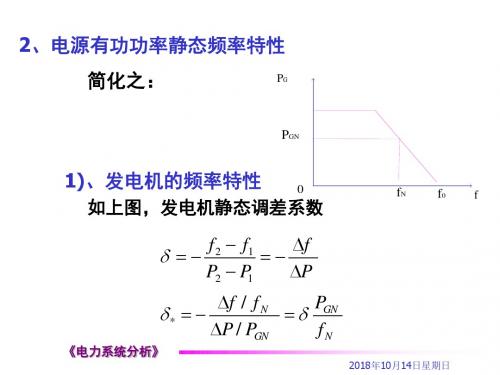
2)、发电机组的有功功率—频率静态特性 a.发电机的单位调节功率:发电机组原动机或电源频率特 性的斜率。
标志着随频率的升降发电机组发出功率减少或增加的多寡。
b.发电机是调差系数:单位调节功率的倒数。
发电机的单位调节功率与调差系数的关系:
一般来说发电机的单位调节功率是可以整定的:
• 汽轮发电机组 • 水轮发电机组
➢冬季枯水期,来水较少,应由凝汽式火电厂承担基本 负荷,水电厂则承担尖峰负荷。
电力系统分析第05章电力系统有功功率平衡与频率调整

¾ 目标函数 ¾ 约束条件:
n
∑ F = Fi ( PGi ) i =1
∑ ∑ PGi − PLi = 0
¾ 等微增率准则的表达式
dF1 ( PG1 ) = dF2 ( PG2 ) = .... = dFn ( PGn ) = λ
dPG1
dPG 2
dPGn
18
3.最优分配方案的求解步骤
对于机组较少的情况,可以用解方程组的方法求解,机 组较多,可以迭代求解
算。
5) 直到满足条件。
19
例5-1同一发电厂内两套发电设备共同供电,耗量特性分别为
F1 = 3 + 0.25PG1 + 0.0014PG21 F2 = 5.0 + 0.25PG2 + 0.0018PG22
它们可发有功功率上下限分别为PG1max=100MW, PG1min=20MW,
PG2max=100MW, PG2min=20MW,求承担150MW负荷时的分配方案 解:两台发电设备的耗量微增率分别为
第五章 电力系统有功功率 平衡与频率调整
1
第五章电力系统有功功率平衡与频率调整
电力系统的调频问题实质上是正常运行时有功功率的平衡问题。 ¾ 发电机的输入功率、输出功率和系统的总负荷相等,发电机匀速运
转。 ¾ 当系统中发出的有功功率与负荷消耗的有功功率不平衡时,就会反映
为频率的变化。
当电力系统发生某种扰动(负荷减小),发电机输出的功率瞬间 减小。但发电机的输入功率是机械功率,不能瞬间变化。扰动后瞬间 发电机的输入功率大于输出功率,发电机转子将加速,电力系统的频 率上升。
投切增减负荷不增 加能耗,时间短 (4)有强迫功率,视不 同水电厂而定
调峰机组
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 电力系统有功功率平衡与频率调整主要内容提示本章主要讨论电力系统中有功功率负荷的最优分配和频率调整。
§5-1电力系统中有功功率的平衡 一、电力系统负荷变化曲线 在电力系统运行中,负荷作功需要一定的有功功率,同时,传输这些功率也要在网络中造成有功功率损耗。
因此,电源发出的有功功率必须满足下列平衡式:∑∆+∑=∑P P P Li Gi式中Gi P ∑—所有电源发出的有功功率;Li P ∑—所有负荷需要的有功功率; ∑∆P —网络中的有功功率损耗。
可见,发电机发出的功率比负荷功率大的多才行。
当系统中负荷增大时,网络损耗也将增大,发电机发出的功率也要增加。
在实际电力系统中,负荷随时在变化,所以必须靠调节电源侧,使发电机发出的功率随负荷功率的变化而变化。
负荷曲线的形状往往是无一定规律可循,但可将这种无规则的曲线看成是几种有规律的曲线的迭加。
如图5-1所示,将一种负荷曲线分解成三种曲线负荷。
第一种负荷曲线的变化,频率很快,周期很短,变化幅度很小。
这是由于想象不到的小负荷经常性变化引起的。
第二种负荷曲线的变化,频率较慢,周期较长,幅度较大。
这是由于一些冲击性、间歇性负荷的变动引起的,如大工厂中大电机、电炉、电气机车等一开一停。
第三种负荷曲线的变化,非常缓慢,幅度很大。
这是由于生产、生活、气象等引起的。
这种负荷是可以预计的。
对于第一种负荷变化引起的频率偏移进行调整,称为频率的“ 一次调整”。
调节方法一般是调节发电机组的调速器系统。
对于第二种负荷变化引起的频率偏移进行调整,称为频率的“二次调整”,调节方法是调节发电机组的调频器系统。
对于第三种负荷的变化,通常是根据预计的负荷曲线,按照一定的优化分配原则,在各发电厂间、发电机间实现功率的经济分配,称为有功功率负荷的优化分配。
二、发电厂的备用容量电力系统中的有功功率电源是发电厂中的发电机,而系统中装机容量总是大于发电容t量,即要有一定的备用容量。
系统的备用容量包括:负荷备用、事故备用、检修备用和国民经济备用。
总备用容量占最大发电负荷的(15~20)%。
然而系统中装机容量的确定,不仅考虑到最大发电负荷,而且还考虑到适当的备用容量。
即为:装机容量()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧+=∑%5~3%5~4%10~5%5~2max max 国民经济备用检修备用事故备用负荷备用备用容量最大发电负荷P P P L M ∆§5-2电力系统中有功功率的最优分配电力系统中有功功率合理分配的目标是:在满足一定负荷持续供电的前提下,使电能在生产的过程中消耗的能源最少。
而系统中各类发电机组的经济特性并不相同,所以就存在着有功功率在各个电厂间的经济分配问题。
⒈ 发电机的耗量特性发电机的耗量特性反映发电机单位时间内消耗的能源与发出有功功率的关系。
如图5-2所示,图中纵坐标表示单位时间内消耗的燃料F (标准煤),单位为“t/h ”,或表示单位时间内消耗的水量W ,单位为“m 3/s ”;横坐标表示发电功率P G ,单位为“kW ”或 “MW ”。
耗量特性曲线上某一点纵坐标与横坐标的比值称为比耗量。
如i 点的比耗量:Gi i i P F =μ 或Gii i P W=μ 评价发电机组的经济特性,常常用到耗量特性曲线上某一点纵坐标与横坐标的增量比,我们称之为耗量微增率,以λ表示。
λ表示单位时间内输入能量增量与输出功率增量的比值。
如i 点的耗量微增率:GiiGi i i dP dF P F =∆∆=λ ⒉ 目标函数和约束条件火力发电厂的能量消耗主要与发电机组输出的有功功率P G 有关,而与输出的无功功率Q G 及电压U G 关系较小,因此对于n 机系统,单位时间内消耗燃料的目标函数为()()()()Gn n G G Gn G G P F P F P F P P P C C +++==ΛΛΛΛ221121约束条件为等约束条件:011=∑-∑==Li ni Gi ni P P (略网损)P G图5-2 耗量特性不等约束条件:min Gi P ≤Gi P ≤max Gi P 、 min Gi Q ≤Gi Q ≤max Gi Q 、 min Gi U ≤Gi U ≤max Gi U ⒊ 拉格朗日函数建立一个新的不受约束的目标函数—拉格朗日函数:()()()()()()Ln L L Gn G G Gn n G G Gn G G Gn G G P P P P P P P F P F P F P P P f P P P C C ---+++-+=-=*ΛΛΛΛΛΛΛΛΛΛ212122112121λλ各变量对函数求偏导,然后令偏导等于零,求其最小值。
01=∂∂*G P C002=∂∂=∂∂**Gn G P C P C ΛΛ 0=∂∂*λC 解得:()()()λ====GnGn n G G G G dP P F dP P dF dP P dF ΛΛ222111即:λλλλ====n ΛΛ21此式为有功功率负荷最优分配的等耗量微增率准则,满足这个条件的解()Gn G G P P P ΛΛ21为最优分配方案。
【例5—1】 某发电厂装有两台发电设备,其耗量特性分别为:F 1=3+0.3P G1 +0.002P G12 (t/h) F 2=5+0.3P G2 +0.003P G22 (t/h)两台发电设备的额定容量均为100MW,而最小可发有功功率均为30MW ,若该厂承担负荷150MW,试求负荷在两台发电设备间的最优分配方案。
解 两台发电设备的耗量微增率分别为2222211111006.03.0003.023.0004.03.0002.023.0G G G G G G P P dP dF P P dP dF +=⨯+==+=⨯+==λλ按等耗量微增率准则21λλ=分配负荷,有:()1006.03.0004.03.021ΛΛG G P P +=+ 而等约束条件为:()215021ΛΛ=+G G P P 联立式()1、()2,求解1G P 、2G P : 把12150G G P P -=代入()1式有:()9.001.0006.09.0004.0150006.03.0004.03.011111=-=-+=+G G G G G P P P P P于是解得:901=G P (MW ) 602=G P (MW )此分配方案符合等耗量微增率准则,即满足等约束条件,也满足不等约束条件﹙30<90<100、30<60<100﹚,因此,可做为最优分配方案。
⒋ 水、火电厂之间最优分配准则电力系统中有火电厂又有水电厂时,考虑到水电厂发电设备消耗的能源受到限制。
例如,水电厂一昼夜间消耗的水量受约束于水库调度。
于是,约束条件(比讨论火电厂间的最优分配时)多一个。
以W 表示单位时间内水电厂消耗的水量,它是所发出功率H P 的函数,K 表示水电厂在0至τ时间段可消耗的水量。
因此有约束条件:()⎰=τK dt P W H由此式可知,水电厂在τ时间段内消耗的水量不得超过水库的容水量。
水、火电厂之间的最优分配准则为:()()λγ==HH T T dP P dW dP P dF 即 λγλλ==H T 其中()T T T dP P dF λ=为火电厂的耗量微增率,()H HH dP P dW λ=为水电厂的耗量微增率。
γ为拉格朗日乘数,可看作是一个煤水换算系数。
相当于把1立方米/小时的水量通过γ折算为1吨/小时的煤量。
如果系统中有n 个电厂,其中m 个火电厂,()m n -个水电厂,则有功功率负荷最优分配准则可表示为:()()()λγγ=====+++Hnn n m H m m Tm m T dP dW dP dW dP dF dP dF ΛΛΛΛ11111即λλγλγλγλλλ===+===++++Hn n Hm m Hm m Tm T T ΛΛΛΛ221121以上是不计网损时的负荷最优分配。
如果网络线路较长,负荷很重,则网损较大,忽略网损就会产生分配上的误差。
考虑网损后等约束条件为:011=∆-∑-∑∑==P P P Li ni Gi n i等耗量微增率准则:()()λ∆γ∆∑∑=∂∂-⋅=∂∂-⋅Hj Hj j j Ti Ti i P P dP dW P P dP dF /11/11 应用前面类似的方法求其满足等耗量微增率准则的函数最小值,即得最优分配方案。
§5-3电力系统的频率调整 一、频率的一次调整通过调节发电机组的调速器系统可进行频率的一次调整。
负荷与电源的有功功率静态频率特性如图5-3所示,设在O 点运行时负荷突然增加0L P ∆,发电机组将因调速器的一次调整作用增发功率G P ∆,负荷将因它本身的调节效应面减小功率L P ∆,系统的频率偏差为f ∆。
此时有发电机的单位调节功率:=G K G P ∆/f ∆αtg -=负荷的单位调节功率:=L K L P ∆/f ∆βtg =系统的单位调节功率等于发电机的单位调节功率与负荷的单位调节功率之和f P f P P K K K L L G L G S ∆∆=∆∆+∆=+=0所以 SL K Pf 0∆=∆可见一次调频只能做到有差调节,在运行中为减小f ∆,希望S K 大些,但负荷特性一定时L K 为常值,只有G K 大些,系统中多数发电机均能进行一次调频,如果有n 台机都能一次调频,Gn G G nG K K K K +++=ΛΛ21,若某些机组已达到满发,则不能参加调频,只有m 台能调,所以mG K <nG K ,因此总的发电机的单位调节功率也不能提的很高。
发电机的单位调节功率与调差系数%σ有互为倒数关系:100%1⨯=*σG KP Pf图 5-3 频率的一次调整所以常常用调差系数%σ来描述一次调频时发电机组的频率特性。
调差系数%σ与之对应的发电机组的单位调节功率是可以整定的。
一般整定为如下数值:汽轮发电机组: %σ=3~5 20~3.33=*G K 水轮发电机组: %σ=2~4 25~50=*G K当一次调频不能使之f ∆在允许的频率波动范围(f ∆≤5.0~2.0±Hz )之内时,则要靠二次调频,将f ∆将缩小在允许值之间。
二、频率的二次调整通过调节发电机组的调频器系统可进行频率的二次调整,增加发电机组发出的功率0G P ∆,如图5-4所示,由图可见:→0L P ∆OA=OC+CB+BAOC 0G P ∆→表示由于二次调整作用使发电机组增发的功率; CB=f K B C G ''→''''∆表示由于调速器的调整作用而增大的发电机功率;BA=f K A B L ''→''''∆表示因负荷本身的调节效应而减小的负荷功率。
