计算结构力学有限元方法_三维结构和轴对称
三维问题有限元分析(包括轴对称问题)

建立每个有限元的平衡方程,通过求解这些方程来得到近似解。
离散化
将连续的问题离散化,将整个求解域划分为有限个小的子域(称为有限元),每个子域上定义节点。
有限元方法的基本原理
解方程
通过求解整体矩阵的方程,得到各个节点的值,从整体矩阵,用于表示整个求解域上的问题。
详细描述
三维弹性力学问题的有限元分析
总结词
详细描述了三维热传导问题有限元分析的基本原理、方法和应用。
详细描述
三维热传导问题是有限元分析的另一个重要领域,主要研究热量在物体中的传递和分布。通过将连续的物体离散化为有限个小的单元,可以建立单元之间的热量传递关系,从而得到整个物体的温度分布。这种方法广泛应用于工程领域,如传热学、热能工程等。
边界条件处理
轴对称问题的有限元方法
轴对称问题有限元分析的实现流程
建立系统方程
根据有限元近似解法,将微分方程转化为离散化的系统方程。
划分网格
根据问题的几何形状和特点,将求解区域划分为一系列离散的网格单元。
建立数学模型
根据实际问题,建立相应的数学模型,包括物理方程、边界条件和初始条件。
求解系统方程
采用适当的数值方法(如直接法、迭代法等),求解离散化的系统方程,得到每个离散单元上的近似解。
轴对称问题具有旋转对称性,即其解在绕对称轴旋转时保持不变。
轴对称问题的定义和特性
特性
定义
将连续的物理问题离散化为有限个离散的单元,每个单元具有特定的形状和大小。
离散化
在每个离散单元上,使用近似函数来逼近真实解。常用的近似函数包括多项式、样条函数等。
近似解法
对于轴对称问题,边界条件通常与对称轴相关。需要对边界条件进行特殊处理,以确保离散化后的系统方程满足原始问题的约束。
结构分析的有限元法-第五章空间问题空间轴对称问题

的交点就是结点,如图 5-3 所示。这样,轴对称弹性体在 rz 平面上的截面将被各单元划
分成三角形网格,就像平面问题中各三角形单元在 xy 平面上形成的三角形网格一样。
位移模式
在轴对称问题中,物体内任意一点只有径向位移 u 和轴向位移
w ,并且他们仅与坐标 r 和 z 有关,而与 无关。因此,像平面问题
将均质单元的自重平均分配到四个结 点,即为等效结点力
表面分布力的等效结点力
分布面力在工程中也很常见。设单元的某一表面 ijm ,承受线性分布载荷,它在 i 、 j 和 m 三个结点处的强度分别是 psi 、psj 和 psm ,则根据式(2.72),分配到结点 i 、 j 和
m 上的等效结点力的数值分别为
fh BT D1 1 1 0 0 0T Tdxdydz
V
若温度分布采用线性模式,则上式的积分
V
Tdxdydz 1 4
Ti T j
Tm Tp V
(5.42) (5.43) (5.44) (5.45)
式中,Ti 、 T j 、 Tm 和T p 为结点 i 、 j 、 m 和 p 处的温度改变量。
N p ap bp x cp y d pz 6V
式中ai、bi 、ci 和 di 分别是式(5.6)的第1,2,3,4列
的代数余子式,即
xj yj zj ai xm ym zm
xp yp zp
1 xj zj ci 1 xm zm
1 xp zp
1 yj zj bi 1 ym zm
(5.21)
因此
Si
1 6V
(ai
bi x ci y di z)
(i, m)
(5.22)
Sj
1 6V
三维有限元法计算过程

三维有限元法计算过程三维有限元法的计算过程:1)网格单元剖分;2)线性插值;3)单元分析;4)总体刚度矩阵合成;5)求解线性方程组等部分组成。
一、偏微分方程对应泛函的极值问题矿井稳恒电流场分布示意图主要任务是分析在给定边界条件下,求解稳定电流场的Laplace 方程或Poisson方程的数值解,即三维椭圆型微分方程的边值问题:)()((0)(0)()()(000z z y y x x I F u n un u F z u z y u y x u x Lu w D ---=⎪⎪⎪⎩⎪⎪⎪⎨⎧=+∂∂=∂∂=∂∂∂∂+∂∂∂∂+∂∂∂∂≡ΓΓ+Γδδδγσσσ 上述微分方程边值问题等价于下面泛函的极小值问题:dS U dxdydz fU z U y U x U U J w D ⎰⎰⎰⎰⎰Γ+Γ+ΓΩ+-∂∂+∂∂+∂∂=222221}])()()[(2{][γσσ二、网格剖分∞1ρiih ρ......1、网格单元的类型图2-5 网格单元类型2、网格单元剖分原则及其步长选择 因此,网格内的单元剖分应按以下剖分原则1)、各单元节点(顶点)只能与相邻单元节点(顶点)重合,而不能成为其它单元内点;2)、如果求解区域对称,那么单元剖分也应该对称;3)、在场变化剧烈的区域网格剖分单元要密一些,在场变化平缓的区域单元密度应小。
4)、网格单元体的大小变化应逐步过渡。
根据上述剖分原则,以x 、y 、z 坐标轴原点o 为中心,分别向x 、y 、z 方向的两侧作对称变步长剖分,距o 越远,步长应越大。
常用的变步长方法有:c i x x i i )1(1+=∆-∆+ c x x i i =∆∆+/1(i ≠0)c x x i i =∆-∆+111(i ≠0) 以上各式中c 为常数,1+∆i x 、i x ∆为同一坐标轴上相邻步长值。
以x 方向为例,可知,x 正方向与负方向对称,只相差一负号。
若令00=∆x ,只要给出距原点最近节点的坐标1x ∆,由上式即可求出其它相应的步长i x ∆。
三维问题有限元分析(包括轴对称问题)

空间问题简介
工程实际中的很多问题难于简化为平面问题,如受任意 空间载荷作用的任意形状几何体,受对称于轴线载荷作 用的回转体,这类问题经典弹性力学往往无能为力。在 FEM中,空间问题只要求0阶连续,因此构造单元方便
➢空间问题的主要困难: (1)离散化不直观;————(网格自动生成) (2)分割的单元数量多,未知量的数目剧增。— ——— (对某些问题简化)——— ——— (轴对称问题) ➢空间分析的优点
p
s
C
(6-16)
e 1
e 1
式中
F e ——单元上集中力等效结点载荷列向量;
p
F e ——单元上表面力等效结点载荷列向量;
S
F e ——单元上体积力等效结点载荷列向量;
F e
——单元结点载荷列向量。
C
等效结点力公式为 Fe NTF p
式中
Fe SSeNTpSds
Fe VeNTpvdV
如同平面等参单元一样,需要通过雅克比矩阵来实现,由偏导法则
N i N xi x N yi y N zi z
同理可得
N i , N i
写成矩阵
Ni
x
y
z
Ni x
Ni x
Ni
x
y
z
Ni y
J
Ni y
Ni
x
y
z
Ni z
ui vi wi
(6-18)
式中
xi、yi、zi——结点i的坐标; ui、vi、wi——结点i沿x、y、z方向的位移; Ni——对应于i结点的形状函数。
在自然坐标系(局部坐标系)中,各结点的形状函数可写成如
下形式, 对于8个顶角结点( i=1,2,……,8)
第4章 空间问题有限元分析-轴对称

Re N T f p
FL e 2 r0 N T 62 f p 21
圆环 2 r0 Ni f pr Ni f pz N j f pr
N j f pz
Nm f pr
T
Nm f pz
r0 -- 集中力作用点的径向坐标。
2019/10/18
第4章 空间问题有限元分析 空间轴对称问题
曹国华
2019/10/18
空间有限元分析-轴对称
1
主要内容
§ 4.1位移模式 § 4.2几何方程 § 4.3单元刚度 § 4.4等效载荷
2019/10/18
空间有限元分析-轴对称
3
1、研究对象
当弹性体的几何形状,约束情况,以及所受的外力都 轴对称于某一轴,则这种弹性体的应力分析问题称为轴对 称应力分析问题,在工程中如 活塞,压力容器等 。
空间有限元分析-轴对称
12
几何方程与物理方程
PA线应变
0,(略去高阶小量).
PB线应变
εφ
PB PB PB
(u
φ
uφ φ
d φ)
u
ρdφ
1 uφ ; ρ φ
PA转角
α
DA
uφ ρ
d
ρ
uφ
,
PA d ρ ρ
2019/10/18
空间有限元分析-轴对称
空间有限元分析-轴对称
28
等效载荷
r Niri N j rj Nmrm
2、体积力移置
FFGee 2 [N] f rdrdz
若体积力为重,则单位体积 的力为
f
=-0
有限元-结构静力学分析概述.

预条件求解器(PCG)
属于间接迭代法,收敛精度主要依赖于收敛准则,适用于静态、稳态、瞬 态和子空间特征值分析,特别适合于结构分析,对于一些非线性分析也有 较好的效果,在接触分析中当使用罚函数法及增强的拉格朗日法时也能使 用。但对于拉格朗日法的接触分析以及不可压缩材料时不能使用。(适用 于实矩阵、对称矩阵,不使用于复矩阵、非对称矩阵) PCG求解器特点: 1)由于不需要矩阵分析,所需内存比稀疏矩阵法少。2)对于中等或大尺 寸模型,只要迭代合理,PCG比稀疏矩阵求解器快。3)需要核内求解。4 )其很依赖于刚度矩阵的良性度,如矩阵为良性则求解速度好,反之效率 较低,其单元长宽比要最好在10:1下。4)所需内存较大,一般为JCG的2 倍,对于I/O要求较小。5)和其他迭代求解器相比,一般求解速度是JCG 的4-10倍(固体结构单元)一般迭代次数在1500下速度优于稀疏求解法, 超过1500则认为矩阵病态,可考虑使用其他求解器 PCG不为默认求解器,需要使用eqslv,PCG激活,其并行度在2cpu时性能 可提高10-30%,最高支持到16cpu,最高性能提高8倍。
ANSYS求解器的设置选项
稀疏矩阵求解器(Sparse Director Solver)
稀疏矩阵求解法是使用消元为基础的直接求解法,在 ANSYS10.0中其为默认求解选项。其可以支持实矩阵与复矩 阵、对称与非对称矩阵、拉格朗日乘子。其支持各类分析, 病态矩阵也不会造成求解的困难。稀疏矩阵求解器由于需要 存储分解后的矩阵因此对于内存要求较高。其具有一定的并 行性,可以利用到4-8cpu 其具有3种求解方式:核内求解,最优核外求解,最小核外 求解。强烈推荐使用核内求解,此时基本不需要磁盘的输入 与输出,能大幅度提高求解速度;而核外求解会受到磁盘输 入/输出速度的影响。对于复矩阵或非对称矩阵一般需要通常 求解2倍的内存与计算时间。
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、载荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某一根轴(过该轴的任一平面都是对称面)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第一象限中创建,并且Y轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型一样进行施加,但集中载荷有特殊的含义,它表示的是力或力矩在360°范围内的合力,即输入的是整个圆周上的总的载荷大小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见表11-1。
表11-1 2D轴对称常用结构单元列表的高阶单的高阶单在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT(3)为Axisymmetric(Shell51和Shell61单元本身就是轴对称单元,不用设置该项),单元将被指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将截面结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
轴对称问题有限元分析实例 2D节2第p=1000 N/mF2y611xO61211-1 圆柱筒壳示意图图——圆柱筒的静力分析一、案例1问题,直0.1 m1000 N/m的压力作用,其厚度为如图11-1所示,圆柱筒材质为A3钢,受,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、mm,高度为16 径12径向应力和轴向应力。
有限元分析轴对称问题

思考题5-1 轴对称问题的定义答:工程中又一类结构,其几何形状、边界条件、所受载荷都对称于某一轴线,这种情况下结构再载荷作用下位移、应变和应力也对称于这个轴线,这种问题成为轴对称问题。
5-2 轴对称问题一般采用的坐标系?作图说明每个坐标分量的物理意义答:在描述轴对称弹性体问题的应力及变形时常采用圆柱坐标r,θ,z。
5-3 轴对称问题中每个点有几个位移分量?各位移分量是那几个自变量的函数?答:位移分量u, w,都只是rz的函数,与θ无关。
5-4 轴对称问题中的每个点有哪几个应力分量?是那几个自变量的函数。
答:4个应力分量;5-5 轴对称问题中的每个点有哪几个应变分量?是那几个自变量的函数答:4个应变分量5-6 轴对称问题是三维问题?二维问题?最简单的轴对称单元是哪种单元?作图说明答:由于轴对称,沿θ方向的环向(周向)位移v等于零。
因此轴对称问题是二维问题;三角形环单元。
(三角形轴对称单元,这些圆环单元与r z平面(子午面)正交的截面是三角形)5-7 写出三角形环单元的位移函数。
满足完备性要求吗?答:满足完备性要求。
5-8 三角形环单元形函数的表达式?指出形函数的性质。
5-9 三角形环单元的应力和应变的特点。
其单元刚度矩阵是几阶的?答:应力分量:剪应力为常量,其他3个正应力分量均随位置变化;应变分量:面内(子五面)3个应变分量为常量,环向应变不是常应变,而是与单元中各点的位置有关。
单元刚度矩阵为六阶。
5-10 有限元方法求解对称问题的基本步骤?1.结构离散化:对整个结构进行离散化,将其分割成若干个单元,单元间彼此通过节点相连;2.求出各单元的刚度矩阵[K](e):[K](e)是由单元节点位移量{Φ}(e)求单元节点力向量{F}(e)的转移矩阵,其关系式为:{F}(e)= [K](e) {Φ}(e);3.集成总体刚度矩阵[K]并写出总体平衡方程:总体刚度矩阵[K]是由整体节点位移向量{Φ}求整体节点力向量的转移矩阵,其关系式为{F}= [K] {Φ},此即为总体平衡方程。
有限元第六章空间与轴对称问题有限元分析

问题复杂,精确积分参见Zienkiewicz (Finite
Element Method, 5th Ed,2000)。
实践证明采用近似积分也能达到一定的精度,
具体对于三角形环单元用形心处坐标代替应变矩阵
中的坐标变量。如何进一步改进积分精度?
教材上对三角形环单元具体介绍了ke和FEe的有 关计算过程。请自学相关内容。
空间及轴对称问题有限元
概述 空间问题(四面体、六面体类)
轴对称问题 轴对称问题非轴对称荷载
概述
三个方向尺寸属于同一数量级,所受荷载或形
体复杂,不可能像上一章那样简化成平面问题处
理,这时必建须立按网空格间自问动题生求成解前。
与平面分析不处同理,程空序间有限元分析有如下两个
困难:
采用高阶单元来提
1)对空间物体进行离散化高时单不元像精平度面问题那样
r
w
z
u
r
u z
w r
r
0
1 r z
0
径向位移
z 0
u w
r
轴向位移
根据具体单元,代入所建立的位移模式,即可得应变矩
阵B。由于算子中有1/r,所以三角形环单元B不再是常
非轴对称荷载的分解:
R0、Z0 与θ无关,是
轴对称荷载;T0 与θ 无关、沿θ 方向,是 扭转荷载;
Ri(r,z)cosiθ等是关于θ=0 平面的对称荷载;
对称
反对称
Ri(r,z)siniθ等是关于θ=0 平面的反对称荷载;
轴对称问题非轴对称荷载
将位移作类似的分解:
20年春季地大《计算结构力学》在线作业二答卷【标准答案】

地大《计算结构力学》在线作业二
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1.下述对有限元法特点的描述中,哪种说法是错误的()。
A.需要适用于整个结构的插值函数
B.解题步骤可以系统化、标准化
C.容易处理非均匀连续介质,可以求解非线性问题
D.可以模拟各种几何形状复杂的结构,得出其近似解
答案:A
2.平衡方程研究的是()之间关系的方程式。
A.应变和位移
B.应力和应变
C.应力和体力
D.应力和位移
答案:C
3.等参变换是指单元坐标变换和函数插值采用()的结点和()的插值函数。
A.相同,相同
B.相同,不相同
C.不相同,相同
D.不相同,不相同
答案:A
4.弹性力学平面问题的方程个数有()个。
A.以上都不是
B.9
C.8
D.15
答案:C
5.下面关于有限元分析法的描述中,那种说法是错误的()
A.应力变化梯度较大的部位划分的单元可小一些
B.单元各边的长度以及各内角不应相差太大。
C.单元之间通过其边界连接成组合体
D.分布载荷与自由边界的分界点、支撑点等应取为节点
答案:C
6.下面四种假设中,那种不属于分析弹性力学的基本假设()
A.有限变形假设
B.无初应力假设
C.小变形假设
D.各向同性假设
答案:B。
有限单元法 第4章 空间轴对称问题有限元分析
+
# % ! 5 & +
习 !! 题
# " 如图 ! " ) 所示两个轴对称三角形单元 $ 其形状 ) 大小 ) 方位均相 同 $ 但位置 不同 ( 设材料弹性模量为 1$ 泊松比为&$/ 坐标!) " # ($ 试分别计算两单元的刚度矩阵 # " 取平 均值 ) ) % ( " ,
! ’ -! !
&
’
& " / / / ) $ * , / $ ) ! # 0 *$+% / $ /* ! !
! "# "$! 等效结点荷载的计算 %集中力 # 集中力的处理很简单 $ 一般直接把集中力作用点取为结点 $ 不需要作特殊处理 $ 就可 以直接把集中力加入到结点荷载列阵中去 ( %体积力 & 设单元内单位体积上作用的体积力为 ’ ’ $ 则移置到单元各结点的等效结点力为
"$# #’ #$ $ # # #+ % )! *! , / / # % / / # 0 & # / $ ) ! " *&+# /$ & ( / /
.
" # ! # # & " # ! # # )
" # ! # # !
/ , / $ & 由于在 0 是坐标 & 的函数 & ! " $ / ! 分量在单元中不为常量 & 其他三 个应变 分量 在单元
图! "!! 习题 # 图
$ 所示的是受轴向压缩的圆柱体 " 直径5$ ) " 如图! " (# 1 # / 3 6" 长度6 $ # & 3 6" 两端面 受均布载荷" & 如图 ! $ 所示$ % + / 7 8 1作用 % 现取轴对称面的 # ! 均匀划分单元 # " (# 2 "$ # $写出离散体的位移约束条件 % # # $求单元 " ’ # ’ $ ’ % 的等效结点荷载 % & $写出结点 #’&’)’!’(’+ 的荷载矩阵 % # )
主轴部件三维实体模型的有限元分析法
《机械设计与制造》主轴部件三维实体模型的有限元分析法主轴是机床的重要部件之一,它的静、动态刚度一直是设计计算的重要内容,但传统的计算方法是把主轴简化为等截面的梁单元进行计算,显然是静不定问题,用这样的力学模型计算主轴的静、动态特性与实际情况有很大的差距。
目前主轴部件设计采用有限元法,可以满足设计过程要求,为主轴结构的优化设计提供依据。
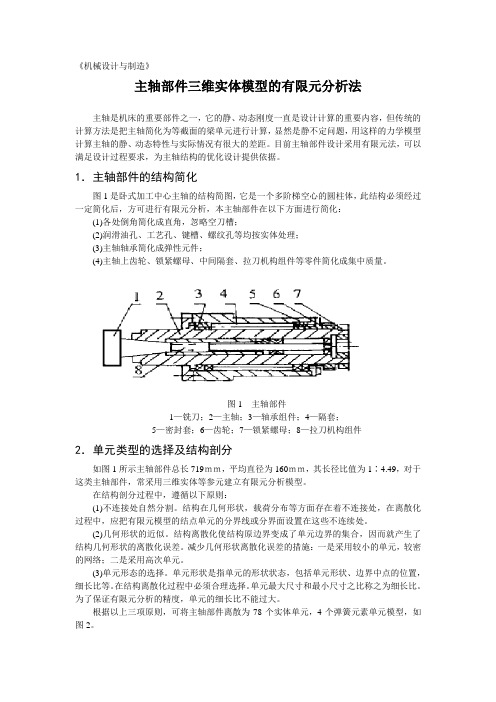
1.主轴部件的结构简化图1是卧式加工中心主轴的结构简图,它是一个多阶梯空心的圆柱体,此结构必须经过一定简化后,方可进行有限元分析,本主轴部件在以下方面进行简化:(1)各处倒角简化成直角,忽略空刀槽;(2)润滑油孔、工艺孔、键槽、螺纹孔等均按实体处理;(3)主轴轴承简化成弹性元件;(4)主轴上齿轮、锁紧螺母、中间隔套、拉刀机构组件等零件简化成集中质量。
图1主轴部件1—铣刀;2—主轴;3—轴承组件;4—隔套;5—密封套;6—齿轮;7—锁紧螺母;8—拉刀机构组件2.单元类型的选择及结构剖分如图1所示主轴部件总长719mm,平均直径为160mm,其长径比值为1∶4.49,对于这类主轴部件,常采用三维实体等参元建立有限元分析模型。
在结构剖分过程中,遵循以下原则:(1)不连接处自然分割。
结构在几何形状,载荷分布等方面存在着不连接处,在离散化过程中,应把有限元模型的结点单元的分界线或分界面设置在这些不连续处。
(2)几何形状的近似。
结构离散化使结构原边界变成了单元边界的集合,因而就产生了结构几何形状的离散化误差。
减少几何形状离散化误差的措施:一是采用较小的单元,较密的网络;二是采用高次单元。
(3)单元形态的选择。
单元形状是指单元的形状状态,包括单元形状、边界中点的位置,细长比等。
在结构离散化过程中必须合理选择。
单元最大尺寸和最小尺寸之比称之为细长比。
为了保证有限元分析的精度,单元的细长比不能过大。
根据以上三项原则,可将主轴部件离散为78个实体单元,4个弹簧元素单元模型,如图2。
(a)主视图(b)俯视图图2主轴部件三维实体模型图3.约束条件的建立合理确定有限元模型约束条件是成功地进行有限元分析的基本条件,约束条件的确定,应尽可能符合原结构的实际情况。
有限元计算原理与方法..

1.有限元计算原理与方法有限元是将一个连续体结构离散成有限个单元体,这些单元体在节点处相互铰结,把荷载简化到节点上,计算在外荷载作用下各节点的位移,进而计算各单元的应力和应变。
用离散体的解答近似代替原连续体解答,当单元划分得足够密时,它与真实解是接近的。
1.1.有限元分析的基本理论有限元单元法的基本过程如下:1.1.1.连续体的离散化首先从几何上将分析的工程结构对象离散化为一系列有限个单元组成,相邻单元之间利用单元的节点相互连接而成为一个整体。
单元可采用各种类型,对于三维有限元分析,可采用四面体单元、五西体单元和六面体单元等。
在Plaxis 3D Foundation程序中,土体和桩体主要采用包含6个高斯点的15节点二次楔形体单元,该单元由水平面为6 节点的三角形单元和竖直面为四边形8节点组成的,其局部坐标下的节点和应力点分布见图3.1,界面单元采用包含9个高斯点的8个成对节点四边形单元图3.1 15 节点楔形体单元节点和应力点分布在可能出现应力集中或应力梯度较大的地方,应适当将单元划分得密集些; 若连续体只在有限个点上被约束,则应把约束点也取为节点:若有面约束,则应把面约束简化到节点上去,以便对单元组合体施加位移边界条件,进行约束处理;若连续介质体受有集中力和分布荷载,除把集中力作用点取为节点外,应把分布荷载等效地移置到有关节点上去。
最后,还应建立一个适合所有单元的总体坐标系。
由此看来,有限单元法中的结构已不是原有的物体或结构物,而是同样材料的由众多单元以一定方式连接成的离散物体。
因此,用有限元法计算获得的结果只是近似的,单元划分越细且又合理,计算结果精度就越高。
与位移不同,应力和应变是在Gauss积分点(或应力点)而不是在节点上计算的,而桩的内力则可通过对桩截面进行积分褥到。
1.1.2.单元位移插值函数的选取在有限元法中,将连续体划分成许多单元,取每个单元的若干节点的位移作为未知量,即{ }e =[U i,V i,W i,...]T,单元体内任一点的位移为{f}二[u,v,w]T。
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、载荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某一根轴(过该轴的任一平面都是对称面)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第一象限中创建,并且Y轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型一样进行施加,但集中载荷有特殊的含义,它表示的是力或力矩在360°范围内的合力,即输入的是整个圆周上的总的载荷大小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见表11-1。
表11-1 2D轴对称常用结构单元列表的高阶单的高阶单在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT(3)为Axisymmetric(Shell51和Shell61单元本身就是轴对称单元,不用设置该项),单元将被指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将截面结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
轴对称问题有限元分析实例 2D节2第p=1000 N/mF2y611xO61211-1 圆柱筒壳示意图图——圆柱筒的静力分析一、案例1问题,直0.1 m1000 N/m的压力作用,其厚度为如图11-1所示,圆柱筒材质为A3钢,受,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、mm,高度为16 径12径向应力和轴向应力。
2014-计算力学-4-轴对称问题有限元

Nj 0
0 Nj
Nm 0
e
N m I
0 i j Nm m
(4-11)
N
其中:[I]为二阶单位矩阵
1 0 I 0 1
因此,形函数矩阵的表达式为
Ni N 0 0 Ni Nj 0 0 Nj Nm 0 0 Nm
bi A1 f i 2 A3 A1 bi f i Si A b f 1 i i A2 ci A1ci ci A1ci A2 bi
i, j, m
单元分析
其中
u A1 1 u , 1 2u A2 21 u
rr
于是
1 ri r j rm 3 1 z z zi z j z m 3
fi fi ai cz bi i r r
i, j, m
有限元网格确定后,各单元的就是定值。这样就可以把轴对称问题的各 单元看成是常应变矩阵,所求得的应变是形心处的应变值。当轴对称结 构的单元划分比较小时,这种近似所引起的误差是很小的。特别当结构 上各单元的形心离 Z 轴 较远时,产生的误差就更小了。
u N i ui N j u j N m um w N i wi N j w j N m wm
(4-5)
单元分析
其中形函数
Ni
a
i
bi r ci z
2
i,
j, m
(4-6) (4-7)
而
1 1 rj 2 1 rm
1 ri
zi zj zm
ai
rj rm
zj zm
轴对称问题

(i , j , m )
由上式可见,单元内应变 εr、εz、γrz都是常量,但φi, φj, φm与各单元中各点的位置(r, z)有关,环向应变εθ不是常量; 当结构包含对称轴(r = 0)在内时,φi , φj , φm是奇异的, 这将给数值计算带来困难。
汽车工程系
结构分析与CAE研究室
- 16 -
z j
wj uj wi ui
单元结点力向量:
wm um
i m
{ f }e
⎧ fi ⎫ ⎪ ⎪ = ⎨fj ⎬ ⎪ ⎪ ⎩ f m ⎭ 6×1
r
汽车工程系
结构分析与CAE研究室
- 11 -
4.2 三结点三角形轴对称单元
4.2.2 单元位移模式 由于有三个结点,在r方向和z方向上各有三个结点条件, 因此设它的单元位移模式为
u ( r , z ) = α1 + α 2 r + α 3 z ⎫ ⎬ w(r , z ) = α 4 + α 5 r + α 6 z ⎭
该位移模式与平面问题三结点三角形单元完全相同。同样, 将结点坐标和结点位移代入上式可得到单元内部位移
⎧ ui ⎫ ⎪w ⎪ ⎪ i⎪ 0 ⎤ ⎪uj ⎪ e ⎪ ⎪ ⎨ ⎬ = [ N (r , z )]{δ } Nm ⎥ ⎪ wj ⎪ ⎦ ⎪ um ⎪ ⎪ ⎪ ⎪ wm ⎪ ⎩ ⎭
-5-
4.1 基本概念
4.1.2 基本方程 ①平衡方程
∂σ r ∂τ zr σ r −σ θ + + + br = 0 ∂r ∂z r ∂σ z ∂τ rz τ rz + + + bz = 0 ∂z ∂r r ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭
lsdyna轴对称有限元模型

lsdyna轴对称有限元模型1. 简介lsdyna是一种通用的有限元分析软件,广泛应用于工程、汽车和航空航天等领域。
轴对称有限元模型是lsdyna的重要分析工具之一,它在处理旋转对称结构的过程中具有独特的优势和应用价值。
本文将对lsdyna轴对称有限元模型进行详细介绍和分析。
2. 原理轴对称有限元模型是建立在圆柱坐标系下的有限元模型,它以z轴为旋转对称轴,将三维问题简化为二维问题。
在lsdyna中,通过设定特定的边界条件和约束条件,可以将三维结构的分析转化为轴对称的二维模型。
这样不仅可以大大减少计算量,提高计算效率,而且还能更准确地评估旋转对称结构的力学行为。
3. 建模在lsdyna中建立轴对称有限元模型,需要考虑以下几个关键步骤:- 坐标系转换:将三维坐标系转换为圆柱坐标系,并设定z轴为旋转对称轴。
- 材料定义:根据实际情况选择适当的材料参数,并进行材料定义。
- 几何建模:利用lsdyna自带的几何建模工具或导入CAD模型,建立轴对称有限元模型的几何形状。
- 网格划分:根据模型的特点和要求,进行合适的网格划分。
- 材料属性分配:为每个部件分配适当的材料属性,包括密度、弹性模量、屈服强度等。
- 节点约束:根据轴对称性,设定合适的节点约束条件,以保证模型在旋转对称轴上的平衡状态。
- 荷载施加:根据实际工程需求施加合适的载荷条件,进行模拟分析。
4. 分析通过lsdyna轴对称有限元模型,可以进行多种分析,包括但不限于以下几个方面:- 动力学分析:通过施加动态载荷,评估旋转对称结构在振动或冲击荷载下的响应。
- 热力学分析:考虑热荷载对旋转对称结构的影响,进行热力学分析。
- 疲劳分析:模拟旋转对称结构在循环加载下的疲劳性能,评估其寿命。
- 冲击分析:模拟旋转对称结构在冲击荷载下的响应,评估结构的稳定性和可靠性。
5. 应用lsdyna轴对称有限元模型在工程实践中具有广泛的应用价值,主要体现在以下几个方面:- 发动机部件分析:涉及发动机曲轴、连杆、活塞等零部件的疲劳、强度和振动分析。
有限元第八讲三维实体单元和轴对称实体资料

z
uv
0 w
y
z
0
x
2、物理方程
• 线弹性应力~应变关系: D
❖ 其中应力分量: x
y
z
xy
yz
T zx
❖ 各向同性弹性系数矩阵 D为:
1
1 1
(对称)
D
(1
E(1 ) )(1 2)
1
0
1
0
1 0
1 2 2(1 )
0
00
0
1 2 2(1 )
7 三维实体单元和轴对称实体单元
一、三维弹性力学问题几何方程和物理方程 1、几何方程
• 应变 ~ 位移关系:
x
u x
,y
v y
,z
w z
xy
u y
v x
yz
v z
w y
zx
w x
u z
•矩阵形式几何方程:
x
x
y
xzy
0
0
yz
zx
y 0
0
y
0
x称问题单元刚度矩阵导出的原理与其他单元相同, 都是根据虚功方程。而外力虚功和应力的虚功都是在 单元代表的实际物理空间中进行积分计算。
• 因此,下列从虚功方程导出的单元刚度矩阵通式对 空间轴对称问题同样成立:
ke Ve BT DBdV
其中,积分域 V e 是单元所代表的物理区域。对于
0
00 0
0
1 2 2(1 )
二、三维简单四面体单元
1、位移模式和形函数
• 四面体是最简单的三维 单元,简单四面体单元 把四个顶点作为节点, 节点编号i,j,m,l。
• 每个节点3个自由度,单 元共12个自由度。单元 节点位移和单元节点力 分量共12个。
结构有限元分析-第3章-轴对称

3 轴对称问题弹性力学空间问题中的轴对称问题是指,物体的几何形状、约束情况及所受的外力都对称于空间的某一根轴,因此在物体中通过该轴的任何平面都是对称面,所有应力、应变和位移也对称于该轴,这类问题称为轴对称问题。
研究轴对称问题时通常采用圆柱坐标系(r,θ,z),以z轴为对称轴。
轴对称问题实例如图3.1所示的受均布内压作用的长圆筒,通过Z轴的一个纵截面就是对称面图3.1受均布内压作用的长圆筒3.1 三角形截面环单元三结点单元位移函数图4-2 三结点单元轴对称问题分析中所使用的三结点单元,在对称面上是三角形,在整个弹性体中是三棱圆环,各单元中圆环形铰相联接。
三角形截面环单元的结点位移在轴对称问题中,弹性体内任意一点上,不存在切向位移,只存在径向位移u 和轴向位移w ,两个位移分量表示为,⎭⎬⎫⎩⎨⎧=w u f }{[][]Tmm j j i iT mT jT iew u w u w u==δδδδ}{单元结点位移轴对称问题的三结点三角形单元位移函数取为,⎭⎬⎫++=++=z r z r u 654321w αααααα⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j i m j i u u u c c c b b b a a a 21321ααα根据结点位移,可得:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j i m j i w w w c c c b b b a a a 21654ααα单元形函数jm m j i r z z r a -=mmj ji iz r z r z r 11121=∆mj i z z b -=jm i r r c -=(i ,j ,m ))(21z c r b a N i i i i ++∆=单元内任一点的位移{}[]{}em jim m j j i i m jim j iN N N w u w u w u N N N N N N w u f δ=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=00003.2 应变矩阵(几何矩阵)根据几何方程及单元内位移的表达式,可得:⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧r w z u z w ru r u zr z r γεεεθ应变矩阵)(21m m j j i i u b u b u b r u ++∆=∂∂)(21m m j j i i u f u f u f r u ++∆=rcz b r a f i i i ++=(下标轮换))(21m m j j i i w c w c w c z w ++∆=∂∂)(21m m j j i i u c u c u c z u ++∆=∂∂)(21m m j j i i w b w b w b r w ++∆=∂∂应变矩阵[]{}em ji m m mm m jj jj j ii ii i zr z r B B B b c c f b b c c f b b c c f b δγεεεθ=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∆=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧00000000021),,(00021][m j i b c c f b A B i i i iii ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=3.3 应力矩阵由轴对称问题的物理方程,得到弹性矩阵,⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------+-=)1(22100011101110111)21)(1()1(][μμμμμμμμμμμμμμμμμE D应力矩阵11A =-μμ2)1(221A =--μμ3)21)(1(4)1(A E=-+-μμμ令:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-=21111110010101)21)(1()1(][A A A A AA A E D μμμ则弹性矩阵为:]][[][B D S =][][m j iS S S S =),,()(2]][[][2211113m j i b A c A c f b A c A f b A c A f b A B D S i ii i i i ii i i i i i ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++∆==由弹性矩阵[D ]和几何矩阵[B ]可以得到应力矩阵[S ],由应力矩阵可知,除剪应力为常量,其它三个正应力分量都是r 、z 的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三维问题的有限元方法
空间问题
单元的应变
根据弹性力学基本公式,有应变:
∂
一维问题 二维问题
εx
=
∂u ∂x
∂
ε
x
∂x
εy = 0γΒιβλιοθήκη xy∂∂y∂x
三维问题 ε x
0
0
∂ u
∂y
v
∂
∂x
ε
y
εz
γ yz
γ
zx
=
0 0
γ xy
∂ ∂z
r, s = 1,2,3,4
四面体单元
∫∫∫ K
e rs
=
V BrT DBsdV ,
r, s = 1,2,3,4
Ke r,s
=
E(1− µ) 36(1+ µ)(1− 2µ)Ve
brbs + A2 (crcs + dr ds )
×
A1bscr + A2csbr
A1bsdr + A2dsbr
A1
=
µ 1- µ
四面体单元的
Pi = [Pix Piy Piz ]T , i = 1,2,3,4
节点载荷
∫ Pe = N T ρdx
单元节点载荷的计算公式,其中N 应为四面体单元的形函数
∂
0 ∂ ∂y 0 ∂ ∂z 0 ∂
0
0
∂ ∂z ∂ ∂y
u
v
w
∂
∂x
0
统一形式:ε = ∇u
∂y ∂x
三维问题的有限元方法
单元的应力
根据弹性力学基本公式,有应力:σ = Dε 三维问题
1 −µ −µ 0
0
0
−µ 1 −µ
0
0
0
ε
=
1 E
−µ
0
−µ 0
1 0
A2
=
1- 2µ (2 1- µ)
A1brcs + A2crbs crcs + A2 (brbs + dr ds )
A1drcs + A2cr ds
A1br ds + A2drbs
A1cr ds + A2drcs
drds + A2 (brbs + crcs )
K11 K12 K13 K14
Ke
1 6V
ϕe
ϕe
ϕe
a1 a2 a3 a4
ϕe
=
b1
dc11
b2 c2 d2
b3 c3 d3
b4
c4 d4
x2 y2 z2
a1 = x3 y3 z3
x4 y4 z4
1 x2 z2
c1 = 1 x3 z3
1 x4 z4
1 y2 z2 b1 = −1 y3 z3
1 y4 z4
1 x2 y2 d1 = 1 x3 y3
0 2(1 + µ)
0 0
0
0
σ
0 0 0 0 0 0
0 2(1 + µ) 0
0
0 2(1 + µ)
1
µ 1− µ
µ 1− µ
0
0
0
µ
1
0
1− µ
0
0
[
D]
=
(1
E(1 − + µ)(1
µ −
) 2µ)
对
1
0
0
1− 2µ 0
2(1 − µ)
0
0
1− 2µ
0
2(1 − µ)
称
1− 2µ
2(1 − µ)
或用拉梅系数和剪切弹性模量表示
=λ
Eµ = G E / 2(1 + µ)
(1 + µ)(1 − 2µ)
λ + 2G λ
λ 0 0 0
λ + 2G
λ
0
0
0
[
D]
=
(1
E(1 − + µ)(1
µ −
) 2µ
)
对
λ + 2G 0 0 0
G
0
0
G 0
称
G
三维问题的有限元方法
1 x4 y4
1 x1 y1 z1 V = 1 1 x2 y2 z2
6 1 x3 y3 z3 1 x4 y4 z4
四面体单元体积
三维问题的有限元方法
f = ϕ0α α = ϕ −1d
f = Nd
[ ] N为形函数矩阵 N = IN1 IN2 IN3 IN4
I 3×3
Ni =(-1)i+(1 ai + bi x + ci y + di z)/ 6V , i = 1,2,3,4
几何矩阵
三维问题的有限元方法
将式 f = Nd 代入式中得:ε = Bd
B = [B1B2B3B4 ]
bi
ci
Bi
=
1 6V
ci
bi
d
i
,
i
=
1,2,3,4
di
ci
di
bi
式中,ai bi,ci,di, 由式轮换得到。由于 B 的元素均为常数, 故四面体单元为常应 变单元。
将式 ε = Bd 代入式 σ = Dε , 可得应力与节点位移之间的关系
α
2
α
12
]
三维问题的有限元方法
代入节点坐标和节点位移
d = ϕα
α = ϕ −1d
d = (d1T di = (ui
d
T 2
d3T
vi wi )T
d
T 4
T
)
(i
=
1,2,3,4)
ϕ1
ϕ
=
ϕ2
ϕ3
1 xi yi zi
ϕi
=
1 xi yi zi
1 xi yi zi
ϕ −1
=
=
K
21
K 22
K 23
K
24
K K
31 41
K32 K 42
K33 K 43
K34 K 44
r, s = 1,2,3,4
四面体单元 的刚度矩阵
三维问题的有限元方法
单元等效节点载荷
建立空间问题计算模型时,作用在单元上的外载荷必须按静 力等效原则移置到节点上,与平面问题一样。
Pe = [P1T P2T P3T P4T ]T
在三维问题 中,完整的 三维多项式 可排列成一 个四面体
每个节点就有12 个自由度。 四面体单元的自由度数为48, 六面体单元的自由度数为96 。
三维问题的有限元方法
四面体单元
4 节点12 自由度,常应变单元, 其节点顺序按右
手螺旋排列,i节点坐标和位移分别为
ii((uxii
, ,
yi , zi )(i vi , wi )
σ = Sd
S = DB S为单元应力矩阵
由此可知,四面体单元的应力为常数,故又称为常应力元
三维问题的有限元方法
单元刚度矩阵
单元刚度矩阵计算公式的理论依据和过程,与平面问题完全相同:
由计算单元刚度矩阵的通用公式可得: K e = ∫∫∫ BT DBdV
V
对于常应变
K
e rs
=
BrT DBsVe ,
空间问题的有限元格式
三维单元
空间连续体单元,主要分为四面体单元、六面体单元等
提高空间连续体单元位移函数精度的办法,通常是增加节点
自由度数或增加节点等。一个节点的自由度,除位移u,v,w 外,
还可将位移对坐标的偏导数亦取为自由度:
∂u , ∂u , ∂u , ∂v , ∂v , ∂v , ∂w , ∂w , ∂w ∂x ∂y ∂z ∂x ∂y ∂z ∂x ∂y ∂z
=
1,2,3,4)
位移函数取线性形式
矩阵形式 f = ϕ0α
u = a1 + a2 x + a3 y + a4 z v = a5 + a6 x + a7 y + a8z w = a9 + a10 x + a11 y + a12 z
u
ϕP
f
=
v
ϕ0
=
ϕP
w
ϕP
ϕP = [1
x
y
z]
α = [α1
