第六章受弯构件详解
受弯构件斜截面承载力
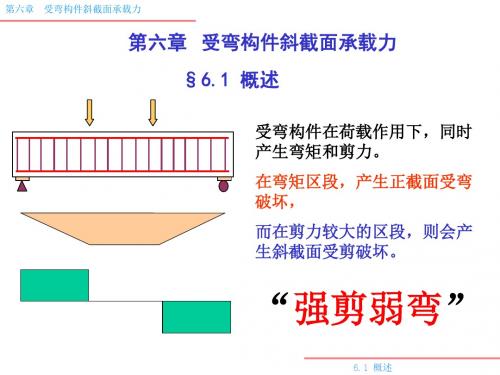
第六章 受弯构件斜截面承载力
受力特点 ★斜裂缝出现后,受剪面积的减小 使受压区混凝土剪力增大(剪压区)
Va Vd Vc
6.2 斜截面受剪的破坏形态和破坏机理
第六章 受弯构件斜截面承载力
受力特点 ★斜裂缝出现后,受剪面积的减小 使受压区混凝土剪力增大(剪压区)
Va Vd Vc
★斜裂缝出现前,支座附近截面 a-a的钢筋应力s与Ma成正比;
Ma Mb
6.2 斜截面受剪的破坏形态和破坏机理
第六章 受弯构件斜截面承载力
受力特点 ★斜裂缝出现后,受剪面积的减小 使受压区混凝土剪力增大(剪压区) ★斜裂缝出现前,支座附近截面 a-a的钢筋应力s与Ma成正比 ★斜裂缝出现后,截面a-a 的钢筋 应力s取决于临界斜裂缝顶点截面 b-b处的Mb,即与Mb成正比。 ★因此,斜裂缝出现使支座附近的 s与跨中截面的s相近,这对纵筋 的锚固提出更高的要求。 ★同时,销栓作用Vd使纵筋周围的 混凝土产生撕裂裂缝,削弱混凝土 对纵筋的锚固作用。
②
① ③
弯剪斜裂缝
腹剪斜裂缝
③
箍筋
弯起钢筋
① 腹筋
②
6.1 概述
第六章 受弯构件斜截面承载力
§6.2 受弯构件斜截面受剪的破坏形态和破坏机理 6.2.1 无腹筋梁的受剪性能 受剪承载力的组成
Va Vc
CC
a
斜裂缝顶部截面处
外剪力:V 外弯矩:M=Va 抗力:Vc、Cc、Ts、Vd、Va
Vd
TS
V
6.2 斜截面受剪的破坏形态和破坏机理
6.2 斜截面受剪的破坏形态和破坏机理
Vd¬ £ TaÖ ¡ Tb
Tb
Ma Mb
第六章 受弯构件斜截面承载力
第六章 拉弯和压弯构件

6.5 实腹式压弯构件的截面设计
6.5.1 截面形式
受力大小
选择截面
使用要求 构造要求 宽肢薄壁 平面内和平面外稳定性相等原则
6.5.2 截面选择及验算
1.初选截面:
根据轴力 N、弯矩 M和构件的计算长度 l0x、 l0y初步确定截面的尺寸,然后验算,参考已有 类似设计进行估算。
压弯构件,当承受的弯矩较小时其截面形式与 一般的轴心受压构件相同。当弯矩较大时,宜 采用弯矩平面内截面高度较大的双轴或单轴对 称截面。
H
N H
Af fy (A) (B) (C)
ηh ηh h-2ηh
Af
fy
fy
fy
ቤተ መጻሕፍቲ ባይዱfy
Aw
hw
h
fy
(D)
由于全截面达到塑性状态后,变形过大, 因此规范对不同截面限制其塑性发展区 域为(1/8-1/4)h
Mx N f An xWnx
上式即为规范给定的在N、Mx作用下的强度计算公式。
对于在N、Mx 、My作用下的强度计算公式,规范采用 了与上式相衔接的线形公式:
N Ey N N 1 1 N N Nz Ey Ey Mx M crx 0
2
可以画出相关曲线如图所示。
如偏安全地取 N z / N Ey =1.0,则上式成为
Mx N 1 N Ey M crx
Mcrx b f yW1x
0 1.0
0 1.0
h0 235 15 tw fy
h0 235 18 tw fy
6.4 压弯构件的计算长度 端部约束条件比较简单的单根压弯构件,利用计 算长度系数可直接得到计算长度。 对于框架柱,平面内的计算长度需通过框架整体 稳定分析得到,平面外的计算长度则需根据支撑 点的布置情况确定。
《受弯构件》课件

THANKS
直于截面。
扭矩
在扭矩作用下,受弯构件的截面上产 生扭矩,其大小与扭矩成正比,方向
垂直于截面。
剪应力
在剪力作用下,受弯构件的截面上产 生剪应力,其大小与剪力成正比,方 向与剪力方向相同。
挠度与转角
在弯矩作用下,受弯构件的截面会产 生挠度和转角,其大小与弯矩和跨度 有关。
02 受弯构件的受力分析
弯矩与剪力
构造要求与细节设计
配筋设计
根据弯矩分布情况合理布置钢筋,以提高构 件的承载力和延性。
预应力设计
通过施加预应力,改善构件的受力性能,提 高抗弯承载力和刚度。
连接与锚固设计
确保构件之间的连接可靠,防止因连接问题 导致的整体失稳或破坏。
细部构造处理
如钢筋的弯钩、搭接和锚固等,需满足相关 规范和构造要求。
稳定性
受弯构件在受到外部作用力时,可能会发生失稳现象,即构件失去承载能力而发 生弯曲或扭曲变形。稳定性分析是受弯构件设计的重要内容之一,需要采取相应 的措施来提高构件的稳定性。
03 受弯构件的截面设计
截面尺寸的选择
截面高度
01
根据跨度、荷载和材料特性选择合适的截面高度,以满足抗弯
承载力和刚度要求。
受弯构件
目录
Contents
• 受弯构件简介 • 受弯构件的受力分析 • 受弯构件的截面设计 • 受弯构件的施工与质量控制 • 受弯构件的加固与修复 • 受弯构件的发展趋势与展望
01 受弯构件简介
定义与分类
定义
受弯构件是指主要承受弯曲应力的构 件,通常为梁和板。
分类
根据材料可分为混凝土受弯构件、钢 受弯构件等;根据截面形式可分为矩 形、T形、I形等。
受弯构件斜截面承载力的计算

对称集中荷载作用下简支梁的主应力轨迹线(图中,实线为主拉应力轨迹线;虚线为主压应力轨迹线。
)My VS tp 2σσ=cp 2σσ=梁内任一点的应力主应力剪跨比P aP202lh ββ⋅lβl()22222qll ql M l q l βββββ=⋅−=−()1222ql ql V q l ββ=−=−x tp 12σσ=+xcp 2σσ=−1arctan 2α=στ斜截面破坏形态◆斜压破坏为受压脆性破坏;◆剪压破坏界于受拉和受压脆◆斜拉破坏为受拉脆性破坏,无腹筋梁的受剪破坏都是脆性的无腹筋梁的弯剪承载力有限,若不足以抵抗荷载产生的1. 剪跨比¾集中荷载作用下2. 腹筋的数量在一定的范围内,腹筋配筋率增大,抗剪承载力提高。
3. 混凝土强度斜截面破坏是因土强度对梁的抗剪承载力影响很大。
当剪跨比一定时,梁的抗剪承载力随混凝土强度提高而增大4. 纵筋配筋率随着纵筋的配筋率的提高,梁的抗剪承载力也增大。
1、直接作用:纵筋截面承受一定剪力(2、纵筋抑制斜裂缝的发展,增大斜裂缝间交互面的剪力传递,增加纵筋量能加大混凝土剪压区高度,从而间接提高梁的抗剪能力。
纵筋的销栓力ρ大于1.5%时,纵向受拉钢筋的配筋率()ρ0.720βρ=+5. 其他因素(1)截面形状这主要是指斜截面抗剪承载力有一定作用。
适当增加翼缘宽度,可提高抗剪承载力,但翼缘过大,增大作用逐渐减小。
另外,增大梁的宽度也可提高抗剪承载力。
与矩形截面梁相比,形截面梁的斜截面承载力一般要高我国《混凝土结构设计规范》钢筋混凝土梁斜截面抗u c ix d s sbV V V V V V =++++sb b V V =⋅为简化计算,主要考虑未开裂混凝土的抗剪作用和腹筋V u ——梁斜截面破坏时所承受的总剪力V c ——V s ——与斜裂缝相交的箍筋所承受的剪力V sb ——与斜裂缝相交的弯起钢筋所承受的剪力如令Vcs 为箍筋和混凝土共同承受的剪力,则无腹筋梁有腹筋梁若腹筋既有箍筋又有弯起钢筋,则对于有腹筋梁,由于箍筋的存在抑制了斜裂缝的开展,使得梁剪压区面积增大,致使强度和配箍率有关。
第六章受弯构件斜截面承载力

2 斜裂缝、剪跨比及斜截面受剪破坏形态
剪跨比反映了截面上正应力和剪应力的相对比值,在 一定程度上也反映了截面上弯矩与剪力的相对比值。 它对无腹筋梁的斜截面受剪破坏形态有着决定性的影 响,对斜截面受剪承载力也有着极为重要的影响。
第六章受弯构件斜截面承载力
2 斜裂缝、剪跨比及斜截面受剪破坏形态
无腹筋梁的斜截面受剪破坏形态
第六章受弯构件斜截面承载力
2 斜裂缝、剪跨比及斜截面受剪破坏形态
试验也表明,无腹筋梁的斜截面受剪破坏形态与剪跨 比有决定性的关系,主要有斜压破坏、剪压破坏和斜 拉破坏三种破坏形态。
第六章受弯构件斜截面承载力
2 斜裂缝、剪跨比及斜截面受剪破坏形态
(1)斜压破坏
第六章受弯构件斜截面承载力
2 斜裂缝、剪跨比及斜截面受剪破坏形态
第六章受弯构件斜截面承载力
2 斜裂缝、剪跨比及斜截面受剪破坏形态
在中和轴附近,正应力小,剪应力大,主拉应力方向 大致为45°。当荷载增大,拉应变达到混凝土的极限 拉应变值时,混凝土开裂,沿主压应力迹线产生腹部 的斜裂缝,称为腹剪斜裂缝。 腹剪斜裂缝中间宽两头细,呈枣核形,常见于I形截 面薄腹梁中。
第六章受弯构件斜截面承载力
1 概述
按理说,箍筋也应像弯起钢筋那样做成斜的,以便于 主拉应力方向一致,更有效地抑制斜裂缝的开展,但 斜箍筋不便绑扎,与纵向钢筋难以形成牢固的钢筋骨 架,故一般都采用竖向箍筋。
第六章受弯构件斜截面承载力
1 概述
试验研究表明,箍筋对抑制斜裂缝开展的效果比起弯 起钢筋要好,所以工程设计中,应优先选用箍筋,然 后再考虑采用弯起钢筋。由于弯起钢筋承受的拉力比 较大,且集中,有可能引起弯起处混凝土的劈裂裂缝。 因此放置在梁侧边缘的钢筋不宜弯起,梁底层钢筋中 的角部钢筋不应弯起,顶层钢筋中的角部钢筋不应弯 下。弯起钢筋的弯起角宜取45°或60°。
06_第6章受弯构件-2012

2 折算应力 zs x y x y 3 xy f y
判断复合应力是否 屈服的第四强度理论
2 2 2 3 1 f d 规范验算公式 zs c c
弯曲应力
局部压应力
剪应力
1 - 计算折算应力时的强
度设计值增大系数
板块组成的薄壁构件截面 剪应力分布 (宽厚比一般大于10)
《钢结构基本原理》第六章 受弯构件 建筑工程系 罗 烈
受弯构件截面抗剪强度计算
剪应力计算公式
材料力学公式 近似公式
Vy S x I xt
Vy
x
x
Vy
Vy Aw
剪应力分布
V
抗剪强度验算 max f vd (或f v )
y x x
4. 根据截面应力不利情况,确定危险点
5. 计算危险截面的几何特性 6. 计算危险点的应力和折算应力 7. 强度验算
《钢结构基本原理》第六章 受弯构件 建筑工程系 罗 烈
梁截面的剪力中心
剪力中心 S- 横向荷载通过此中心,将不发生扭转
形心 重合 剪力 中心
工字 形截面
扭矩平衡方程
槽形截面
剪力中心 位置计算
'
临界状态时 的平衡方程
绕x轴:EI x v '' M x 0
绕y轴:EI y u '' M x 0
绕z轴:EI ω GI t M x u 0
''' '
弯矩作用平面外 的弯扭耦合变形 轴压构件整 体失稳的因子
建筑工程系 罗 烈
临界弯矩
M crx
2 EI y
工程力学六 弯曲变形解析

当x1 x2 a时,
w1 w2 (1 2 )
w1 w2
EIw2
Pb l
x2
P( x2
a)
CB段:
EIw2
EI2
Pb l
x22 2
P
( x2
a)2 2
C2
EIw2
Pb l
x23 6
P
( x2
a)3 6
C2 x2
D2
由连续性条件,可求得
C1 C2
D1 D2
由边界条件,可求得
C1
C2
M pa
P PL
2
PL 2
x
P
qa2
2
q
M
qa
x qa 2 2
x
pa
§6.2 挠曲线近似微分方程及其积分
一、挠曲线近似微分方程的导出
力学公式 数学公式
1 M z (x)
EIz
d 2w
1
dx2
[1 ( dw)2 ]3/2
dx
纯弯曲梁变形后中性层的曲率 公式,对于横力弯曲(l>5h) 可近似使用。EIZ称为梁的抗 弯刚度。
最大转角和最大挠度分别为:
得:
ql 3 C ,
D0
24
梁的转角方程和挠曲线方程分别为:
q (6lx2 4x3 l 3 )
24 EI
w qx (2lx2 x3 l3) 24EI
max
A
B
ql 3 24EI
wmax
w
x l 2
5ql 4 384EI
例: 已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力P作用下的转角方
确定积分常数: (1)边界条件
固定端:w = 0,θ = 0
钢结构课件第六章-受弯构件

钢结构设计原理
Design Principles of Steel Stru内力较大时,需采用组合梁。常用的形式为由三块钢板焊成的 工字形截面。组合梁的截面选择设计包括:确定截面高度、腹板尺 寸和翼缘尺寸。
1)截面高度
最大高度hmax建筑高度; 最小高度hmin刚度要求,根据容许挠度查表;
双轴对称工字型截面简支梁的弯扭屈曲系数k
钢结构设计原理
Design Principles of Steel Structure
第六章 受弯构件 2、单轴对称工字型截面简支梁纯弯作用下的整体稳定
2 EI y
l
2
采用能量法可求出在不同荷载种类和作用位置情况下的梁的临界弯矩为:
M cr 1 I GIt l 2 ) 2a 3 By ( 2 a 3 By )2 (1 2 Iy EI
(6.24)
式中:β1、 β2和β3:和荷载类型有关的系数
a:荷载作用点至剪心s的距离,荷载在剪心以下时为正,反之为负; By:截面不对称修正系数
1 By 2I x
A
y( x 2 y 2 )dA y0
y0:剪力中心与截面形心的距离
钢结构设计原理
Design Principles of Steel Structure
Mxy Mx f x I x xWx
钢结构设计原理 Design Principles of Steel Structure
(6.1)
Mx——梁截面内绕x轴的最大弯矩设计值;Wnx——截面对x轴的净截面模量; x——截面对x轴的有限塑性发展系数;f ——钢材抗弯设计强度 ;
第六章 受弯构件
截面的强度 截面强度破坏
第六章受弯构件2

六、影响梁整体稳定的主要因素
★1.侧向抗弯刚度、抗扭刚度; ★2.受压翼缘的自由长度(受压翼缘侧向支承点间距); ★3.荷载作用种类; ★4.荷载作用位置; ★5.梁的支座情况。
七、提高梁整体稳定性的主要措施
1.增加受压翼缘的宽度; 2.在受压翼缘设置侧向支撑。
八、不需要计算稳定性的受弯构件
【失稳】构件侧向刚度弱,扭转刚度弱侧向变 形和扭转变形大。 【稳定】提高刚度,约束变形。 情形一:梁受压翼缘与混凝土板连续连接, 可不计算整体稳定性,楼板刚度大,约束梁 平面外变形,但在施工阶段可能刚度不足。 情形二: 设上下翼缘侧向支撑。 情形三: 加密次梁或支撑间距。
2
(a )
M
z
u
M
du dz
Z
X X’
Z’ 图 2
du M dz
在x’ z’ 平面内为梁的侧向弯曲,其弯矩的平衡方程为:
d u − EI y 2 = M ϕ dz
2
(b)
u
由于梁端部夹支,中部任意 截面扭转时,纵向纤维发生 了弯曲,属于约束扭转,其 扭转的微分方程为:
Y
Y’
v
X Y
X X ’
Y’
轧制普通工字钢简支梁的φb
项 次 1 荷载情况 集 中 上翼 跨 荷 缘 中 载 无 作 下翼 侧 用 缘 向 于 支 均 承 布 上翼 缘 点 荷 的 载 梁 作 下翼 用 缘 于 跨中有侧向支 承点的梁(不 论荷载作用点 在截面高度上 的位置) 工字 钢型 10~2 号 0 22~3 2 10~2 36~6 0 3 22~4 0 10~2 45~6 0 3 22~4 0 10~2 45~6 0 3 22~4 0 10~2 45~6 0 3 22~4 0 45~6 3 自由长度 2 2.00 2.40 2.80 3.10 5.50 7.30 1.70 2.10 2.60 2.50 4.00 5.60 2.20 3.00 4.00 3 1.30 1.48 1.60 1.95 2.80 3.60 1.12 1.30 1.45 1.55 2.20 2.80 1.39 1.80 2.20 4 0.99 1.09 1.07 1.34 1.84 2.30 0.84 0.93 0.97 1.08 1.45 1.80 1.01 1.24 1.38 5 0.80 0.86 0.83 1.01 1.37 1.62 0.68 0.73 0.73 0.83 1.10 1.25 0.79 0.96 1.01 6 0.68 0.72 0.68 0.82 1.07 1.20 0.57 0.60 0.59 0.68 0.85 0.95 0.66 0.76 0.80 (m) 7 0.58 0.62 0.56 0.69 0.86 0.96 0.50 0.51 0.50 0.56 0.70 0.78 0.57 0.65 0.66 8 0.53 0.54 0.50 0.63 0.73 0.80 0.45 0.45 0.44 0.52 0.60 0.65 0.52 0.56 0.56 9 0.48 0.49 0.45 0.57 0.64 0.69 0.41 0.40 0.38 0.47 0.52 0.55 0.47 0.49 0.49 10 0.43 0.45 0.40 0.52 0.56 0.60 0.37 0.36 0.35 0.42 0.46 0.49 0.42 0.43 0.43
第六章 预应力砼受弯构件变形裂缝

第一节 预应力混凝土构件变形计算
预应力混凝土构件的变形由两部分组成: (1)偏心预加力引起的变形(反拱度) ,向上; (2)荷载(包括恒载和活载)作用产生的变形(挠度或 位移),向下。
——相互抵消,总挠度一般较小 注意:
总挠度值并不反映结构刚度的大小
fll =
l M ll M dx 0 B0
B0 = 0.95Ec I0
∫ M > M cr ,
fM =
l⎛ ⎜ 0⎝
M cr B0
+
M ll − M cr Bcr
⎞ ⎟M dx ⎠
Bcr = Ec Icr
( ) M cr = σ pc + γ ftk W0
γ = 2S0
W0
3、荷载短期效应组合下的总挠度
(A/Al < 9)
(9 < A/Al < 36)
4、国内外关于局部承压的工作机理分析
(1)“套箍理论”(早期) 认为局部承压区的混凝土可以看作是承受侧压力作用 的混凝土芯块,核心混凝土处于三向受压状态。 ——与试验现象不符
(2)“剪切理论”——较合理 认为在局部荷载作用下,构件端部的受力特征可比拟为 一个带多根拉杆的拱结构。 两类劈裂力:(1)拱拉杆部位;(2)楔形体部位
第二节 部分预应力混凝土构件裂缝宽度计算
对使用阶段允许出现裂缝的预应力混凝土B类受弯构件, 《公路桥规》最大裂缝宽度计算式
作用长期效 应影响系数
由作用短期效应引起的 开裂截面纵向钢筋应力
钢筋表面 形状系数
与受力性质 有关的系数
混凝土法向应力等于0时预应 力钢筋和非预应力钢筋合力
(2)裂缝宽度的限值 《公路桥规》规定,对使用阶段允许出现裂缝的B类预应力混凝 土受弯构件最大裂缝宽度:精轧螺纹钢筋,Ⅰ类和Ⅱ类环境为 0.2mm,Ⅲ类和Ⅳ类环境为0.15mm;钢丝和钢绞线,Ⅰ类和Ⅱ 类环境为0.1mm,Ⅲ类和Ⅳ类环境下不得设计为B类构件。
钢结构基本原理课件第六章受弯构件

腹板错位焊接 按锯齿形切开
(a)
蜂窝梁(a)切割线; (b)蜂窝梁
(b)
6.1.3 空腹式受弯构件
另一类型的空腹式受弯构件,工程上称之为桁架,与梁相 比,其特点是以弦杆代替翼缘、以腹杆代替腹板,而在各 节点将腹杆与弦杆连接。这样,桁架整体受弯时,弯矩表 现为上、下弦杆的轴心压力和拉力,剪力则表现为各腹杆
的轴心压力或拉力。
(a)
梁式桁架形式
(d)
(b)
(e)
6.1.3 空腹式受弯构件
(a)
(d)
(b)
梁式桁架形式
(e)
(c)
(f)
钢桁架可以根据不同使用要求制成所需的外形,对跨度和 高度较大的构件,其钢材用量比实腹梁有所减少,而刚度
却有所增加。只是桁架的杆件和节点较多,构造较复杂,
制造较为费工。
6.2 受弯构件的设计
本节目录
6.2.1 概述 6.2.2 梁的强度 6.2.3 梁的刚度 6.2.4 梁的整体稳定性 6.2.5 梁的局部稳定性 6.2.6 型钢梁的截面设计
6.2.1 概述
梁设计中应满足的两种极限状态
内容 极限状态 需要满足 需要满足 抗弯强度 强度承载力 抗剪强度 局部承压强度 复杂应力状态下强度 稳定承载力 正常使用极限状态 梁的变形极限状态 整体稳定
3m 3 m
3m 3m
3m 3 m
3m 3m
q
6m
解:①荷载及内力计算
梁上的荷载标准值为: qk 3 4.5 7.5kN / m 2 荷载设计值为: qd 1.2 3 1.3 4.5 9.45kN / m 2
第6章 受弯构件

工作平台梁格布置示例
实腹式又分为: 工字钢、H形钢、 槽钢、箱型、冷 弯薄壁钢等。
空腹式截面梁— 可以减轻构件自重, 也方便了建筑物中 管道的穿行。
组合梁-用钢筋砼和轧制型钢或焊接型钢 构成。其中作为建筑物楼面、桥梁桥面的砼板, 也作为梁的组合部分参与抵抗弯矩。
6.2 受弯构件的主要破坏形式
6.3 构件受弯时的截面强度
6.3.1强度准则
边缘屈服准则
全截面塑性准则 有限塑性发展的强度准则
屈服弯矩 塑性弯矩或极限弯矩
6.3 构件受弯时的截面强度
强度计算 梁在荷载作用下将产生弯曲正应 力、剪应力;在集中荷载作用处还有 局部承压应力,故梁的强度应包括: 抗弯强度、抗剪强度、局部承压强 度。 在弯曲正应力、剪应力及局部压 应力共同作用处还应验算折算应力。
当形心主轴x轴不是截面的对称轴时,形心主轴 x轴和塑性中和轴不重合,截面受弯时,随弹性 向塑性的发展,中和轴偏离形心主轴x轴。 截面塑性发展系数 (塑性)极限弯矩和屈服弯矩的比值。
M P WP P Me W
不同形式截面的塑性发展系数,见表6-1
6.3 构件受弯时的截面强度
6.3.2抗弯强度
(2)受弯构件的种类 单向弯曲构件—构件在一个主轴平面内受弯; 双向弯曲构件—构件在二个主轴平面内受弯。
(2)受弯构件的种类 单向弯曲构件—构件在一个主轴平面内受弯; 双向弯曲构件—构件在二个主轴平面内受弯。 按支承条件分:简支梁、连续梁、悬臂梁 。
(2)受弯构件的种类 单向弯曲构件—构件在一个主轴平面内受弯; 双向弯曲构件—构件在二个主轴平面内受弯。 按支承条件分:简支梁、连续梁、悬臂梁 。 按梁的作用分:主梁、次梁(横、纵次梁)。
1 1 10 2003 240103 6686667 m m4 12 12 Iy Wy 66867 m m3 100 Iy
钢结构 第六章拉弯、压弯构件的应用和强度计算

作为设计准则的计算公
式。
N
mxM x
x A W1x 1x N
NE x
f
格构式压弯构件计算简图
6.3.3 格构式压弯构件的设计
2. 单肢计算
单肢进行稳定性验算。
分肢的轴线压力按计算简图确定。
单肢1 单肢2
N1 =Mx /a+N z2 /a
N2 =N N1
单肢计算简图
6.3.3 格构式压弯构件的设计
了塑性,前面的弹性平衡微分方程不再适用。 计算实腹式压弯构件平面内稳定承载力通常有两种方
法:
近似法 数值积分法
6.3.1 压弯构件在弯矩作用平面内的稳定性
4. 实腹式压弯构件在弯矩作用平面内稳定计算的实用
计算公式
N
x A
xW1x
mxM
1 0.8 N
NE x
f
对于单轴对称截面的压弯构件,除进行平面内稳定验算 外,还应按下式补充验算
式中:
y
1 2Ix
A y x2 y2 dA y0
i02=(Ix+Iy)/A+a2
6.3.2 压弯构件在弯矩作用平面外的稳定性
3. 实腹式压弯构件在弯矩作用平面外的实用计算公式
N/NEy和M/Mcr的相关曲线
6.3.2 压弯构件在弯矩作用平面外的稳定性
N/NEy+ M/Mcr=1 规范采用了此式作为设计压弯构件的依据,同时考虑 到不同的受力条件,在公式中引进了非均匀弯矩作用的等
M
求解可得构件中点的挠度为:
v
M N
sec
2
N NE
1
由三角级数有:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本节课主要内容
一、概述
二、受弯构件强度
三、受弯构件刚度
四、受弯构件的整体稳定
五、受弯构件的局部稳定
六、受弯构件的屈曲后强度
七、受弯构件的截面设计
一、概述
1.
一、概述
1.
一、概述
2. 分类——组成
实腹式构件
格构式构件
桁架
一、概述
2. 分类——用途
楼盖梁工作平台梁
一、概述
2. 分类——用途
吊车梁檩条
一、概述
2. 分类——制作方法
一、概述
2. 分类——制作方法
一、概述
2. 分类——受力形式
单向弯曲梁双向弯曲梁
一、概述
2.
一、概述
2.
一、概述
3. 设计要求
强度
刚度
稳定
构造要求承载能力极限状态正常使用极限状态
二、受弯构件的强度
1. 强度计算内容
抗弯强度
抗剪强度
局部承压强度
复杂应力强度
二、受弯构件的强度
2. 抗弯强度
弹性阶段
弹塑性阶段
塑性阶段
二、受弯构件的强度
2.
二、受弯构件的强度
2.
A1
二、受弯构件的强度
2.
式中
二、受弯构件的强度
2.
【注意】
y
y
二、受弯构件的强度
2.
【例
二、受弯构件的强度
2.
1、受力分析
二、受弯构件的强度
3.
t
x
max
二、受弯构件的强度
4.
梁承受固定集中荷载(包括支座反力)处未设支承加
二、受弯构件的强度
4. 局部承压强度
二、受弯构件的强度
4.
二、受弯构件的强度
4.
F —集中荷载
二、受弯构件的强度
4.
b
二、受弯构件的强度
4.
当计算
w
z
二、受弯构件的强度
4. 局部承压强度
支承加劲肋
短加劲肋
二、受弯构件的强度
5.
在某些截面的腹板计算高度边缘处,同时受到较大
二、受弯构件的强度
5.
三、受弯构件的刚度
三、受弯构件的刚度
四、受弯构件的整体稳定
f
W M nx
x x
x
k EI l q v 4
3845
强度刚度为提高强度和刚度
W nx 和I x 尽可能大
梁截面尽量高、宽
高而窄
四、受弯构件的整体稳定
四、受弯构件的整体稳定M
四、受弯构件的整体稳定
四、受弯构件的整体稳定
1.
梁受扭矩作用时,非圆截面可以自由产生翘曲,不受约
四、受弯构件的整体稳定
1.
非圆截面自由扭矩
四、受弯构件的整体稳定
2.
四、受弯构件的整体稳定2. 约束扭转
设工形截面的约束扭转角(小变形) 为ϕ,翼缘位移:
单个翼缘翘曲受到约束产生的弯矩:
2
h u j
f 12
m
dM h V EI dz j
2
f 1122n
d u h M EI EI dz j
V
V
u φ
h /2
h
x
o
y
tan j j
四、受弯构件的整体稳定
2.
约束全截面翘曲的扭转抵抗矩(翘曲扭矩):
四、受弯构件的整体稳定3. 扭转平衡方程
非圆截面杆件受外扭矩M作用,由自由扭矩M k 和翘曲扭矩M ω共同抵抗,内外扭矩平衡:
k M M M
k 0
z EI GI M j j 或
四、受弯构件的整体稳定
4.
四、受弯构件的整体稳定
5.
四、受弯构件的整体稳定
6. 受弯构件整体稳定系数
四、受弯构件的整体稳定
6.
j
四、受弯构件的整体稳定
6.
四、受弯构件的整体稳定
6.
焊接工字形等截面(轧制H型钢)
四、受弯构件的整体稳定
7.
修正的原因
四、受弯构件的整体稳定
[例] 某简支梁,焊接工字形截面,跨度中点及两端都设有侧向支承,可变荷载标准值及梁截面尺寸如下图所示,荷载作用于梁的上翼缘,设梁的自重为。
