第十五届北京高中数学知识应用竞赛决赛试题和参考答案
2024-2025学年北京市第十五中学高三上学期8月阶段测试数学试卷含详解

北京十五中高三年级阶段测试数学试卷2024.8本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效.第一部分(选择题共48分)一、选择题共12小题,每小题4分,共48分.在每小题列出的四个选项中,选出符合题目要求的一项.1.若集合{}220A x x x =+<,{}1B x x =>,则A B = ()A.{}21x x -<<- B.{}10x x -<< C.{}01x x << D.{}12x x <<2.在等比数列{}n a 中,若11a =,44a =,则23a a =()A.2B.2± C.4D.4±3.若a b >,则下列不等式中正确的是()A.11a b< B.22a b >C.a b +>D.222a b ab+>4.下列函数中,是偶函数,且在区间0,+∞上单调递增的为()A.1y x=B.ln ||y x = C.2x y = D.1||y x =-5.下列求导运算不正确的是()A.211x x '⎛⎫=-⎪⎝⎭B.1(1ln )1x x'+=+C.()22ln 2xx'= D.(cos )sin x x'=-6.已知函数()21,12,1x x x f x a x ⎧+≤=⎨->⎩,存在最小值,则实数a 的取值范围是()A.(],1-∞ B.(),1-∞ C.[)1,+∞ D.()1,+∞7.4(x 的二项展开式中3x 的系数为()A.15B.6C.4-D.13-8.若函数()1,00,01,0x x f x x x x -<⎧⎪==⎨⎪+>⎩,则“120x x +>”是“()()120f x f x +>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.设()11,,2a t b t c t t t t=-=+=+,其中10t -<<,则()A.b a c <<B.c a b <<C.b c a<< D.c b a<<10.已知e 为单位向量,向量a满足2a e ⋅= ,1a e λ-= ,则a r 的最大值为()A.1B.2C.D.411.“ChatGPT”以其极高的智能化引起世界关注.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为0G G L L D=,其中L 表示每一轮优化时使用的学习率,0L 表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,0G 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为18,且当训练迭代轮数为18时,学习率为0.4,则学习率衰减到0.2以下(不含0.2)所需的训练迭代轮数至少为(参考数据:lg20.3≈)()A.75B.74C.73D.7212.已知数列满足()()*1*2N ,2121N ,2n n n a n k k a a n k k +⎧=∈⎪⎪=⎨+⎪=-∈⎪⎩,,则()A.当10a <时,为递增数列,且存在常数0M >,使得n a M <恒成立B.当11a >时,为递减数列,且存在常数0M >,使得n a M >恒成立C.当101a <<时,存在正整数0N ,当0n N >时,112100n a -<D.当101a <<时,对于任意正整数0N ,存在0n N >,使得1121000n a ->第二部分(非选择题共102分)二、填空题共6小题,每小题5分,共30分.13.函数11y x =-的定义域是__________.14.已知复数i(2i)z =+,则||z =___.15.已知命题p :若,αβ为第一象限角,且αβ>,则sin sin αβ>.能说明命题p 为假命题的一组,αβ的值可以是α=__________,β=__________.16.已知向量a ,b满足2a = ,()2,0b = ,且2a b += ,则cos ,a b = ___________.17.在数列中,122,3a a ==-.数列满足()*1n n n b a a n +=-∈N .若是公差为1的等差数列,则的通项公式为n b =______,n a 的最小值为______.18.已知函数1221log (1),1()23,x x x n f x n x m ----≤≤⎧⎪=⎨⎪-<≤⎩的值域是[1,1]-,若1[0,)2n ∈,则m 的取值范围是________.三、解答题共5小题,共72分.解答应写出文字说明,演算步骤或证明过程.19.在ABC V 中,30A ∠=︒,D 是边AB 上的点,5CD =,7CB =,3DB =.(1)求cos B 与CBD △的面积;(2)求边AC 的长.20.某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.高二成绩分组频数[)7580,2[)8085,6[)8590,16[)9095,14[]95100,2规定成绩不低于90分为“优秀”.(1)估计高一年级知识竞赛的优秀率;(2)将成绩位于某区间的频率作为成绩位于该区间的概率.在高一、高二年级学生中各选出1名学生,记这2名学生中成绩优秀的人数为ξ,求随机变量ξ的分布列;(3)在高一、高二年级各随机选取1名学生,用X ,Y 分别表示所选高一、高二年级学生成绩优秀的人数.写出方差(),()D X D Y 的大小关系.(只需写出结论)21.已知函数()πsin 4f x x ⎛⎫=- ⎪⎝⎭.(1)若()012f x =,[]00,2πx ∈,求0x 的值;(2)设()()cos g x f x x =⋅,求()g x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.22.已知函数2()e ()x f x x ax a =--.(1)若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,求实数a 的值;(2)求函数()f x 的单调区间.23.已知函数()3223f x x x x =-+.(1)若曲线()y f x =在点()()00,x f x 处的切线的斜率为1,求曲线()y f x =在点()()00,x f x 处的切线方程;(2)定义:若[],x a b ∀∈,均有()()f x g x ≤,则称函数()g x 为函数()f x 的控制函数.①[]0,1x ∀∈,试问()g x x =是否为函数()3223f x x x x =-+的“控制函数”?并说明理由;②[]0,3x ∀∈,若()g x x m =+为函数()3223f x x x x =-+的“控制函数”,求实数m 的取值范围.北京十五中高三年级阶段测试数学试卷第一部分(选择题共48分)一、选择题共12小题,每小题4分,共48分.在每小题列出的四个选项中,选出符合题目要求的一项.1.若集合{}220A x x x =+<,{}1B x x =>,则A B = ()A.{}21x x -<<- B.{}10x x -<< C.{}01x x << D.{}12x x <<【答案】A【分析】根据集合描述求集合,应用集合交运算求交集即可.【详解】{}220{|20}A x x x x x =+<=-<<,{}1{|1B x x x x =>=>或1}x <-,∴{|21}A B x x ⋂=-<<-,故选:A【点睛】本题考查了集合的基本运算,利用集合交运算求交集,属于简单题.2.在等比数列{}n a 中,若11a =,44a =,则23a a =()A.2B.2± C.4D.4±【答案】C【分析】由等比数列的性质计算即可.【详解】由于{}n a 是等比数列,且11a =,44a =,所以12434a a a a ==,故选:C.3.若a b >,则下列不等式中正确的是()A.11a b< B.22a b > C.a b +> D.222a b ab+>【答案】D【分析】根据不等式的性质,赋值,如1,1a b ==-,即可判断A 、B 、C ,再根据基本不等式即可判断D.【详解】解:由a b >,令1,1a b ==-,则,1111a b==-,则11a b >,故A 错误;则221,1a b ==,则22a b =,故B 错误;则1ab =-C 错误;因为a b >,则220,0b a ≥>,所以222a b ab +>.故选:D.4.下列函数中,是偶函数,且在区间0,+∞上单调递增的为()A.1y x=B.ln ||y x = C.2xy = D.1||y x =-【答案】B 【分析】结合函数的单调性与奇偶性的定义与判定方法,以及初等函数的性质,逐项判定,即可求解.【详解】由题意,对于A 中,函数()()1f x f x x-=-=-,所以函数为奇函数,不符合题意;对于B 中,函数()ln ||f x x =满足()()ln ||ln ||f x x x f x -=-==,所以函数为偶函数,当0x >时,函数ln y x =为0,+∞上的单调递增函数,符合题意;对于C 中,函数2x y =为非奇非偶函数,不符合题意;对于D 中,1||y x =-为偶函数,当0x >时,函数1y x =-为单调递减函数,不符合题意,故选:B .【点睛】本题主要考查了函数的奇偶性和函数的单调性的判定与应用,其中解答中熟记函数的单调性与奇偶性的判定方法,以及初等函数的性质是解答的关键,着重考查了推理与论证能力,属于基础题.5.下列求导运算不正确的是()A.211x x '⎛⎫=-⎪⎝⎭B.1(1ln )1x x'+=+C.()22ln 2xx'= D.(cos )sin x x'=-【答案】B 【分析】直接利用导数公式和运算法则求解.【详解】A.由导数公式得211x x '⎛⎫=-⎪⎝⎭,故正确;B.由导数运算法则得1(1ln )x x'+=,故错误;C .由导数公式得()22ln 2x x '=,故正确;D.由导数公式得(cos )sin x x '=-,故正确;故选:B【点睛】本题主要考查导数公式和运算法则的应用,属于基础题.6.已知函数()21,12,1x x x f x a x ⎧+≤=⎨->⎩,存在最小值,则实数a 的取值范围是()A.(],1-∞ B.(),1-∞ C.[)1,+∞ D.()1,+∞【答案】A【分析】根据分段函数的单调性求解即可.【详解】当1x ≤时,()21f x x =+,所以()f x 在(),0-∞上单调递减,在(]0,1上单调递增,则()()min 01f x f ==,当1x >时,()2xf x a =-,所以()f x 在()1,+∞上单调递增,无最小值,根据题意,()f x 存在最小值,所以21a -≥,即1a ≤.故选:A.7.4(x 的二项展开式中3x 的系数为()A.15B.6C.4- D.13-【答案】B【分析】先求出二项式展开式的通项公式,然后令x 的次数为3,求出r ,从而可求得结果.【详解】解:4(x 的通项公式为:4244421(1)C (1)C r r r r r rr r T x x x --+-⋅⋅==-,令432r-=,可得2r =,所以二项展开式中3x 的系数:224C (1)6⋅-=.故选:B .8.若函数()1,00,01,0x x f x x x x -<⎧⎪==⎨⎪+>⎩,则“120x x +>”是“()()120f x f x +>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C【分析】根据题意分析可知()f x 为奇函数且在上单调递增,分析可知120x x +>等价于()()120f x f x +>,即可得结果.【详解】由题意可知:()f x 的定义域为,且()00f =,若0x >,则0x -<,可知()()()()110f x f x x x +-=++--=,若0x <,同理可得()()0f x f x +-=,所以()f x 为奇函数,作出函数()f x 的图象,如图所示,由图象可知()f x 在上单调递增,若120x x +>,等价于12x x >-,等价于()()()122f x f x f x >-=-,等价于()()120f x f x +>,所以“120x x +>”是“()()120f x f x +>”的充要条件.故选:C.9.设()11,,2a t b t c t t t t=-=+=+,其中10t -<<,则()A.b a c <<B.c a b <<C.b c a <<D.c b a<<【答案】C【分析】借助正负性、对勾函数的性质及二次函数的性质判断即可得.【详解】由10t -<<,故()1,1t ∈-∞-,故10a t t=->,由对勾函数性质可得()1112b t t=+<-+=-,()20c t t =+<,且()()2222111c t t t t t =⋅+=+=+-≥-,综上所述,有b c a <<.故选:C.10.已知e 为单位向量,向量a满足2a e ⋅= ,1a e λ-= ,则a r 的最大值为()A.1 B.2C.D.4【答案】C【分析】设()1,0e =r ,(),a x y = ,根据2a e ⋅= 求出x ,再根据1a e λ-= 得到()2221y λ=--,最后根据向量模的坐标表示及二次函数的性质计算可得.【详解】依题意设()1,0e =r,(),a x y = ,由2a e ⋅=,所以2x =,则()2,a y = ,又()()()2,,02,a e y y λλλ-=-=-,且1a e λ-= ,1=,即()2221y λ=--,所以a ==≤r 2λ=时取等号,即a r.故选:C11.“ChatGPT”以其极高的智能化引起世界关注.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为0G G L L D=,其中L 表示每一轮优化时使用的学习率,0L 表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,0G 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为18,且当训练迭代轮数为18时,学习率为0.4,则学习率衰减到0.2以下(不含0.2)所需的训练迭代轮数至少为(参考数据:lg20.3≈)()A.75B.74C.73D.72【答案】C【分析】由已知可得45D =,再由1840.5()0.25G⨯<,结合指对数关系及对数函数的性质求解即可.【详解】由题设可得18180.50.4D =,则45D =,所以1840.50.25G ⎛⎫⨯< ⎪⎝⎭,即()()()45218lg18lg 2lg5182lg 211820.31518log 72452lg 2l 2g53lg 2130.31lg5G --⨯->===≈=--⨯-,所以所需的训练迭代轮数至少为73次.故选:C .12.已知数列满足()()*1*2N ,2121N ,2n n n a n k k a a n k k +⎧=∈⎪⎪=⎨+⎪=-∈⎪⎩,,则()A.当10a <时,为递增数列,且存在常数0M >,使得n a M <恒成立B.当11a >时,为递减数列,且存在常数0M >,使得n a M >恒成立C.当101a <<时,存在正整数0N ,当0n N >时,112100n a -<D.当101a <<时,对于任意正整数0N ,存在0n N >,使得1121000n a ->【答案】D【分析】直接构造反例即可说明A 和B 错误;然后证明引理:当101a <<时,对任意的正整数0N ,都存在0n N >,使得112100n a -≥.最后由该引理推出C 错误,D 正确.【详解】当112a =-时,121124a a +==,23211284a a a ==<=,所以此时不是递增数列,A 错误;当132a =时,121524a a +==,23528a a ==,34311352168a a a +==>=,所以此时不是递减数列,B 错误;我们证明以下引理:当101a <<时,对任意的正整数0N ,都存在0n N >,使得112100n a -≥.若该引理成立,则它有两个直接的推论:①存在101a <<,使得对任意的正整数0N ,都存在0n N >,使得112100n a -≥;②当101a <<时,对任意的正整数0N ,都存在0n N >,使得1121000n a ->.然后由①是C 的否定,故可以说明C 错误;而②可以直接说明D 正确.最后,我们来证明引理:当101a <<时,对任意确定的正整数0N :如果011111,21002100N a +⎛⎫∉-+ ⎪⎝⎭,则01112100N a +-≥;如果011111,21002100N a +⎛⎫∈-+⎪⎝⎭,则00122N N a a ++=或001212N N a a +++=.此时若00122N Na a ++=,则0012111111111111210022420024200242002100N N a a +++⎛⎫=<=+=-+=--<-⎪⎝⎭;若001212N Na a +++=,则001211113111111111210022420024200242002100N N a a ++-++⎛⎫=>=-=+-=+->+ ⎪⎝⎭.无论哪种情况,都有021111,21002100N a +⎛⎫∉-+⎪⎝⎭,从而02112100N a +-≥.这说明01112100N a +-≥或02112100N a +-≥,所以可以选取{}001,2n N N ∈++,使得112100n a -≥.这就说明存在0n N >,使得112100n a -≥.这就证明了引理,从而可以推出C 错误,D 正确.故选:D.【点睛】最关键的地方在于引理:当101a <<时,对任意的正整数0N ,都存在0n N >,使得112100n a -≥.这一引理可以帮助我们判断出较难判断的C 和D 选项.第二部分(非选择题共102分)二、填空题共6小题,每小题5分,共30分.13.函数11y x =-的定义域是__________.【答案】{|1x x ≥-且1}x ≠【分析】求使函数有意义的x 的范围即为定义域,逐项求解即可.【详解】解:由题意得1010x x +≥⎧⎨-≠⎩,解得1x ≥-且1x ≠,故函数的定义域为{1xx ≥-∣且1}x ≠.故答案为:{|1x x ≥-且1}x ≠14.已知复数i(2i)z =+,则||z =___.【答案】【分析】先计算复数,再根据复数的模的定义求结果.【详解】由i(2i)2i 1z =+=-,故=22+(−1)2=5.15.已知命题p :若,αβ为第一象限角,且αβ>,则sin sin αβ>.能说明命题p 为假命题的一组,αβ的值可以是α=__________,β=__________.【答案】①.13π6(答案不唯一)②.π6(答案不唯一)【分析】只要找到一组满足题意的角即可.【详解】因为,αβ为第一象限角,且αβ>,取13ππ,66αβ==,则αβ>且在第一象限,此时13ππ1sin sin sin sin 662αβ====,故命题p 为假命题,满足题意,所以,αβ的值可以是13ππ,66αβ==,故答案为:13π6(答案不唯一);π6(答案不唯一).16.已知向量a ,b 满足2a = ,()2,0b = ,且2a b += ,则cos ,a b = ___________.【答案】12-##-0.5【分析】由向量模长的计算和数量积计算即可.【详解】2a b += ,222282cos ,88cos ,4a b a a b b a b a b a b ∴+=+⋅+=+=+= ,1cos ,2a b ∴=- ,故答案为:12-.17.在数列中,122,3a a ==-.数列满足()*1n n n b a a n +=-∈N .若是公差为1的等差数列,则的通项公式为n b =______,n a 的最小值为______.【答案】①.6n -②.13-【分析】求出等差数列的首项,直接求出的通项公式即可,利用数列的单调性得最小项为6a ,利用累加法即可求解.【详解】由题意1215b a a =-=-,又等差数列的公差为1,所以()5116n b n n =-+-⋅=-;故16n n a a n +-=-,所以当6n ≤时,10n n a a +-≤,当6n >时,10n n a a +->,所以123456789a a a a a a a a a >>>>>=<<<⋅⋅⋅,显然n a 的最小值是6a .又16n n a a n +-=-,所以()()()()()612132435465a a a a a a a a a a a a =+-+-+-+-+-()()()()()25432113=+-+-+-+-+-=-,即n a 的最小值是13-.故答案为:6n -,13-18.已知函数1221log (1),1()23,x x x n f x n x m ----≤≤⎧⎪=⎨⎪-<≤⎩的值域是[1,1]-,若1[0,)2n ∈,则m 的取值范围是________.【答案】[1,2]【分析】先判断出1||223x y --=-在(1,1)-上单调递增,在(1,)+∞上单调递减,然后作出12log (1)y x =-与1||223x y --=-在[1,)-+∞上的图象,求出12log (1)y x =-在[1,]x n ∈-上的值域,再结合图象可求得结果.【详解】当1x >时,10x ->,此时2|1|213232323x x x y ---+-=-=-=-单调递减,当11x -<<时,10x -<,此时2|1|211232323x x x y --+-+=-=-=-单调递增,所以1||223x y --=-在(1,1)-上单调递增,在(1,)+∞上单调递减,所以当1x =时,1||223x y --=-取得最大值,为2231-=,作出12log (1)y x =-与1||223x y --=-在[1,)-+∞上的图象如图所示:当1[0,2n ∈,[1,]x n ∈-时,1[1,2]x n -∈-,此时1122()log (1)[1,log (1)]f x x n =-∈--,此时121()log (1)1f x n -≤≤-<,因为()f x 的值域为[1,1]-,则(,]x n m ∈时,()1f x =必有解,即2|1|231x ---=,解得1x =,由图知[1,2]m ∈,故答案为:[1,2]【点睛】关键点点睛:此题考查函数的综合问题,考查分段函数,考查由函数的值域确定参数的范围,解题的关键是根据题意作出函数图象,结合图象求解,考查数形结合的思想,属于较难题.三、解答题共5小题,共72分.解答应写出文字说明,演算步骤或证明过程.19.在ABC V 中,30A ∠=︒,D 是边AB 上的点,5CD =,7CB =,3DB =.(1)求cos B 与CBD △的面积;(2)求边AC 的长.【答案】(1)11cos 14B =,1534CBD S =△(2)【分析】(1)借助余弦定理与面积公式计算即可得;(2)借助正弦定理计算即可得.【小问1详解】在CBD △中,由余弦定理得22222273511cos 227314BC BD CD B BC BD +-+-===⋅⨯⨯,∵0πB <<,∴53sin 14B ===,∴1153153sin 3722144CBD S BD BC B =⋅⋅=⨯⨯⨯= ;【小问2详解】由(1)知53sin 14B =,∵30A ∠=︒,∴1sin 2A =,在ABC V 中,由正弦定理得sin sin BC AC A B=,即7sin 141sin 2BC B AC A ⋅===.20.某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.高二成绩分组频数[)7580,2[)8085,6[)8590,16[)9095,14[]95100,2规定成绩不低于90分为“优秀”.(1)估计高一年级知识竞赛的优秀率;(2)将成绩位于某区间的频率作为成绩位于该区间的概率.在高一、高二年级学生中各选出1名学生,记这2名学生中成绩优秀的人数为ξ,求随机变量ξ的分布列;(3)在高一、高二年级各随机选取1名学生,用X ,Y 分别表示所选高一、高二年级学生成绩优秀的人数.写出方差(),()D X D Y 的大小关系.(只需写出结论)【答案】(1)30%(2)答案见解析(3)()()D X D Y <【分析】(1)根据频率分布直方图直接求解即可;(2)先分别求出在高一、高二年级学生中选中成绩优秀学生的概率和不优秀学生的概率,由题意可知ξ的所有可能取值为0,1,2,然后求出对应的概率,从而可求出随机变量ξ的分布列;(3)由题意可知X ,Y 均符合两点分布,从而可求出(),()D X D Y 的值,进而可比较大小.【小问1详解】高一年级知识竞赛的优秀率为()0.040.0250.3+⨯=.所以高一年级知识竞赛的优秀率为30%【小问2详解】在高一年级学生中选中成绩优秀学生的概率为0.3,选中成绩不优秀学生的概率为10.30.7-=;在高二年级学生中选中成绩优秀学生的概率为1420.440+=,选中成绩不优秀学生的概率为10.40.6-=.ξ的所有可能取值为0,1,2;()00.70.60.42P ξ==⨯=;()10.30.60.70.40.46P ξ==⨯+⨯=;()20.30.40.12P ξ==⨯=.所以随机变量ξ的分布列为:P 012ξ0.420.460.12【小问3详解】显然X ,Y 均符合两点分布,且()00.7P X ==,()10.3P X ==,()00.6P Y ==,()10.4P Y ==,所以()0.30.70.21,()0.60.40.24D X D Y =⨯==⨯=所以()()D X D Y <21.已知函数()πsin 4f x x ⎛⎫=- ⎪⎝⎭.(1)若()012f x =,[]00,2πx ∈,求0x 的值;(2)设()()cosg x f x x =⋅,求()g x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】(1)5π12或13π12(2)最大值为1224-,最小值为22-【分析】(1)根据条件,利用特殊角的三角函数值,即可求出结果;(2)根据条件得到1π2()sin(2)244g x x =--,再利用sin y x =的图象与性质,即可求出结果.【小问1详解】因为()πsin 4f x x ⎛⎫=-⎪⎝⎭,由()012f x =,得到0π1sin 42x ⎛⎫-= ⎪⎝⎭,解得0ππ2π(Z)46x k k -=+∈或0π5π2π(Z)46x k k -=+∈,即05π2π(Z)12x k k =+∈或013π2π(Z)12x k k =+∈,又[]00,2πx ∈,所以05π12x =或13π12.【小问2详解】因为()()2π2211cos2cos sin()cos cos cos )(sin2)42222x g x f x x x x x x x x +=⋅=-⋅=-=-1π2sin(2244x =--,令π24t x =-,因为π0,2x ⎡⎤∈⎢⎥⎣⎦,得到π3π,44t ⎡⎤∈-⎢⎥⎣⎦,由sin y x =的图象与性质知,2sin [,1]2t ∈-,所以()212,224g x ⎡∈--⎢⎣⎦,所以()g x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为124-,最小值为2-.22.已知函数2()e ()x f x x ax a =--.(1)若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,求实数a 的值;(2)求函数()f x 的单调区间.【答案】(1)1(2)答案见解析【分析】(1)先求函数()f x 的导函数,若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,只需保证(1)0f '=,求实数a 的值即可;(2)求得()0f x '=有两个根“2x =-和x a =”,再分2a <-、2a =-和2a >-三种情况分析函数()f x 的单调性即可.【小问1详解】由题可得2()e [(2)2]x f x x a x a '=+--,因为()f x 在点(1,(1))f 处的切线平行于x 轴,所以(1)0f '=,即e(33)0a -=,解得1a =,经检验1a =符合题意.【小问2详解】因为2()e [(2)2]x f x x a x a '=+--,令()0f x '=,得2x =-或x a =.当2a <-时,随x 的变化,()f x ',()f x 的变化情况如下表所示:x(,)a -∞a (,2)a -2-(2,)-+∞()f 'x +0-0+()f x 单调递增()f a 单调递减(2)f -单调递增所以()f x 在区间(,)a -∞上单调递增,在区间(,2)a -上单调递减,在区间(2,)-+∞上单调递增.当2a =-时,因为2()e (2)0x f x x '=+≥,当且仅当2x =-时,()0f x '=,所以()f x 在区间(,)-∞+∞上单调递增.当2a >-时,随x 的变化,()f x ',()f x 的变化情况如下表所示:x(,2)-∞-2-(2,)a -a (,)a +∞()f 'x +0-0+()f x 单调递增(2)f -单调递减()f a 单调递增所以()f x 在区间(,2)-∞-上单调递增,在区间(2,)a -上单调递减,在区间(,)a +∞上单调递增.综上所述,当2a <-时,()f x 的单调递增区间为(,)a -∞和(2,)-+∞,单调递减区间为(,2)a -;当2a =-时,()f x 的单调递增区间为(,)-∞+∞,无单调递减区间;当2a >-时,()f x 的单调递增区间为(,2)-∞-和(,)a +∞,单调递减区间为(2,)a -.23.已知函数()3223f x x x x =-+.(1)若曲线()y f x =在点()()00,x f x 处的切线的斜率为1,求曲线()y f x =在点()()00,x f x 处的切线方程;(2)定义:若[],x a b ∀∈,均有()()f x g x ≤,则称函数()g x 为函数()f x 的控制函数.①[]0,1x ∀∈,试问()g x x =是否为函数()3223f x x x x =-+的“控制函数”?并说明理由;②[]0,3x ∀∈,若()g x x m =+为函数()3223f x x x x =-+的“控制函数”,求实数m 的取值范围.【答案】(1)切线方程为y x =,1y x =-(2)①是“控制函数”,理由见解析;②27m ≥【分析】(1)根据斜率求出切点坐标,再由直线的点斜式方程可得答案;(2)①由()()f x g x ≤得()2230-≤xx ,根据x 的范围可得答案;②转化为[]0,3x ∀∈,3223-≤x x m 恒成立,令()3223=-h x x x 求出()h x 在[]0,3x ∀∈的最值可得答案.【小问1详解】()2661'=-+f x x x ,所以()20006611'=-+=f x x x ,解得00x =或01x =,可得切点坐标为()0,0,或()1,0,所以曲线()y f x =在点()0,0处的切线方程为y x =,曲线()y f x =在点()1,0处的切线方程为1y x =-;【小问2详解】①,是“控制函数”,理由如下,由()()f x g x ≤得3223x x x x -+≤,可得32230x x -≤,()2230-≤xx ,因为[]0,1x ∀∈时,()2230-≤x x 恒成立,即3223x x x x -+≤恒成立,所以函数()g x 为函数()f x 的“控制函数”;②,若()g x x m =+为函数()3223f x x x x =-+的“控制函数”,则[]0,3x ∀∈,()()3223f x x x x g x x m =-+≤=+恒成立,即[]0,3x ∀∈,3223-≤x x m 恒成立,令()3223=-h x x x ,[]0,3x ∈,()()26661h x x x x x '=-=-,当01x <<时,()0h x '<,当13x <<时,()0h x '>,()h x 在()0,1上单调递减,在()1,3上单调递增,所以()h x 在1x =有极小值,()00h =,()327323323=⨯-=⨯h ,所以27m ≥.【点睛】方法点睛:利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.。
2024-2025学年北京市第十五中学高三上学期8月阶段测试数学试卷(含答案)

2024-2025学年北京市第十五中学高三上学期8月阶段测试数学试卷一、单选题:本题共12小题,每小题5分,共60分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.若集合A ={x |x 2+2x <0},B ={x ||x |>1},则A ∩B =( )A. {x |−2<x <−1}B. {x |−1<x <0}C. {x |0<x <1}D. {x |1<x <2}2.在等比数列{a n }中,若a 1=1,a 4=4,则a 2a 3=( )A. 2B. ±2C. 4D. ±43.若a >b ,则下列不等式中正确的是( )A. 1a <1bB. a 2>b 2C. a +b >2 abD. a 2+b 2>2ab4.下列函数中,是偶函数,且在区间(0,+∞)上单调递增的为( )A. y =1xB. y =ln |x|C. y =2xD. y =1−|x|5.下列求导运算不正确的是( )A. (1x )′=−1x 2B. (1+ln x)′=1+1xC. (2x )′=2x ln2D. (cos x)′=−sin x 6.已知函数f (x )={x 2+1,x ≤12x −a,x >1,存在最小值,则实数a 的取值范围是( )A. (−∞,1]B. (−∞,1)C. [1,+∞)D. (1,+∞)7.(x− x )4的二项展开式中x 3的系数为( )A. 15B. 6C. −4D. −138.若函数f (x )={x−1,x <00,x =0x +1,x >0,则“x 1+x 2>0”是“f (x 1)+f (x 2)>0”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件9.设a =t−1t ,b =t +1t ,c =t (2+t ),其中−1<t <0,则( )A. b <a <cB. c <a <bC. b <c <aD. c <b <a 10.已知e 为单位向量,向量a 满足a ⋅e =2,|a−λe |=1,则|a |的最大值为( )A. 1B. 2C. 5D. 411.“CℎatGPT ”以其极高的智能化引起世界关注.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为L =L 0D G G 0,其中L 表示每一轮优化时使用的学习率,L 0表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,G 0表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为18,且当训练迭代轮数为18时,学习率为0.4,则学习率衰减到0.2以下(不含0.2)所需的训练迭代轮数至少为(参考数据:lg2≈0.3)( )A. 75B. 74C. 73D. 7212.已知数列{a n }满足a n +1={a n 2(n =2k,k ∈N ∗),a n +12(n =2k−1,k ∈N ∗),则( )A. 当a 1<0时,{a n }为递增数列,且存在常数M >0,使得a n <M 恒成立B. 当a 1>1时,{a n }为递减数列,且存在常数M >0,使得a n >M 恒成立C. 当0<a 1<1时,存在正整数N 0,当n >N 0时,|a n −12|<1100D. 当0<a 1<1时,对于任意正整数N 0,存在n >N 0,使得|a n −12|>11000二、填空题:本题共6小题,每小题5分,共30分。
2020北京高一数学竞赛试题及参考解答

2020年北京市中学生数学竞赛(邀请)高一年级试题及参考解答2020年6月 27日 8:30~10:30一、填空题(满分40分,每小题8分)1.已知实函数f (x )满足f (x +y )=f (x )+f (y )+4xy ,且f (−1)·f (1)≥4.则29()3f -=______.解:令x =y =0得f(0)=0,令x =−1,y =1,得f (1)+f (−1)=4. 平方得f 2(1)+2f (1)·f (−1)+f 2(−1)=16,又因为f (−1)·f (1)≥4,所以f 2(1)+2f (1)·f (−1)+f 2(−1)≤4f (1)·f (−1).即(f (1)−f (−1))2≤0. 所以f (1)=f (−1)=2.因为)32)(31(4)32()31()32(31)1(--⋅+-+-=⎪⎭⎫ ⎝⎛-+-=-f f f f1118=3()4()()3339f , 所以 .234)31(3=+-f 因此.92)31(=-f所以.9894)31(2)32(=+-=-f f 于是29()3f -=8.2.等腰梯形ABCD (AB =CD )的内切圆与腰CD 的切点为M ,与AM 、BM 的交点分别为K 和L .则AM BMAK BL+的值等于______. 解:设N 是边AD 的中点,a =AN ,x =AK ,y =AM ,α=∠ADM ,(如图).则ND=DM=a ,且根据余弦定理,对于△ADM ,有y 2=4a 2+a 2−4a 2cos α=a 2(5−4cos α).另一方面,根据切割线定理,有xy=a 2,所以2AM y y AK x xy===5−4cos α. 类似地对于△BCM ,得到54cos .BMBLα=+ 因此,10.AM BMAK BL+= CBD ANLK ayαMx3.四位数abcd 比它的各位数字的平方和大2020,在所有这样的四位数中最大的一个是______.解: 设abcd 为所求的自然数,则根据条件1000a +100b +10c +d =a 2+b 2+c 2+d 2+2020.考虑到 2000<a 2+b 2+c 2+d 2+2020≤92+92+92+92+2020=2344, 可以断定a =2,于是100b +10c +d =b 2+c 2+d 2+24. 即 b (100−b )+c (10−c )=d (d −1)+24 (*)由于c (10−c )>0,当b ≥1时,b (100−b )≥99,所以(*)式左边大于99,而(*)式右边小于9×8+24=96,因此要(*)式成立,必须b =0. 当b =0时,(*)式变为 d 2−d =10c −c 2−24.由于四位数abcd 中a =2,b =0,要使20cd 最大,必需数字c 最大.若c =9,c 2−c −24=90−92−24<0,而d 2−d ≥0故(*)式不能成立.同理,c =8和c =7时,(*)式均不能成立.当c =6时,c 2−c −24=60−62−24=0,这时,d =0及d =1,均有d 2−d =0,即(*)式均成立.于是abcd =2060或2061.所以满足题设条件的四位数中最大的一个是2061.4.已知点O 在△ABC 内部,且2021202020193AB BC CA AO ++=,记△ABC的面积为S 1,△OBC 的面积为S 2,则12SS =______.解:由2021202020193AB BC CA AO ++=,得22019()3AB BC AB BC CA AO ++++=,因为0AB BC CA ++=,所以23AB BC AO +=,故23AB AC AB AO +-=. 所以3AB AC AO +=,取BC 的中点D ,则23AD AO =.于是A 、D 、O 三点共线,且3AD OD =.所以123S ADS OD==.5.有4个不同的质数a , b , c , d ,满足a +b +c +d 是质数,且a 2+bc 、a 2+bd 都是完全平方数,那么a +b +c +d = ______.解:由a +b +c +d 是质数,可知a , b , c , d 中有2.如果a ≠2,那么b , c , d 中有2,从而a 2+bc 、a 2+bd 中有一个模4余3,不是完全平方数.故a =2.假设22+bc =m 2,那么bc =(m −2)(m +2).如果m −2=1,那么m =3,bc =5,与已知矛盾.故不妨设b =m −2,c =m +2,则c =b +4.同理d =b −4,所以{a , b , c , d }={a , b , b +4, b −4}.而b −4, b , b +4中有一个是3的倍数,又是质数,所以只能是b −4=3,此时a +b +c +d =2+3+7+11=23.二、(满分15分)面积为S 1,S 2,S 3,S 4,S 5,S 6的正方形位置如图所示.求证:S 4+S 5+S 6=3(S 1+S 2+S 3).证明:见右图:AKLB ,BMNC ,ACPQ 都是正方形,对应的面积为S 1、S 2和S 3.设,,βα=∠=∠ABC BAC .γ=∠ACB因为,,,321S AC S BC S AB === 则根据余弦定理,有αcos 232321S S S S S -+= βcos 231312S S S S S -+=γcos 221213S S S S S -+=由此,.cos 2cos 2cos 2321213132S S S S S S S S S ++=++γβα ①又因为 ,180,180,180γβα-=∠-=∠-=∠ NCP LBM QAK 以及,,,465S NP S LM S QK === 则有αcos 231315S S S S S ++= ②βcos 221216S S S S S ++= ③γcos 232324S S S S S ++= ④由等式①~④得 S 4+S 5+S 6=3(S 1+S 2+S 3).三、(满分15分)存在2020个不是整数的有理数,它们中任意两个的乘积都是整数吗?如果存在,请给出例证,如果不存在,请说明理由.解:存在. 例证如下:因为质数有无限多个,所以任选2020个两两不同的质数122020,,,p p p ,构造2020个两两不同的数:1220202iip p p x p,i =1, 2, 3, …, 2020.易知,因为122020,,,x x x 的分子不被分母整除,皆为不是整数的有理数.而任意两个数的乘积12202012202022i ii jp p p p p p x x p p2222222222122020121111202022ii j ji jp p p p p p p p p p p p . 这2018个质数平方的乘积是整数,满足题意要求.ABCMI 1 I 2 • • D FE 四、(满分15分)如图,已知D 为等腰△ABC 底边BC 上任一点,⊙I 1、⊙I 2分别为△ABD 、△ACD 的内切圆,M 为BC 的 中点.求证:I 1M ⊥I 2M .证明: (1)当D 与M 重合时,显然有 ∠I 1MI 2=90°,即I 1M ⊥I 2M .(2)当D 不与M 重合时,不妨设BD >DC , 过I 1作I 1E ⊥BC 于点E ,过I 2作I 2F ⊥BC 于点F ,连结I 1D ,I 2D ,I 1I 2.因为⊙I 1为△ABD 的内切圆,⊙I 2为△ACD 的内切圆,所以2AB BD AD BE +-=,2DC AD ACDF +-=所以,EM =BM −BE=22BC AB BD AD +--()2BC BD AD AB -+-=.2DF ACAD DC =-+= 进而有 ED=MF .因为I 1、I 2分别为△ABD 、△ACD 的 内心,易知∠I 1DI 2=90°. 由勾股定理得 I 1D 2+I 2D 2=I 1I 22.(*)在Rt △I 1DE 与Rt △DI 2F 中,由勾股定理得I 1E 2+ED 2=I 1D 2,I 2F 2+DF 2=I 2D 2,代入(*)式,得(I 1E 2+ED 2)+(I 2F 2+DF 2)= I 1I 22.注意EM=DF ,ED=MF 代换得(I 1E 2+MF 2)+(I 2F 2+EM 2)= I 1I 22.即 (I 1E 2+EM 2)+(I 2F 2+MF 2)= I 1I 22. 所以 I 1M 2+I 2M 2=I 1I 22.根据勾股定理的逆定理,有△I 1MI 2为直角三角形,∠I 1MI 2=90°,即I 1M ⊥I 2M .五、(满分15分)将集合I ={1, 2, 3, 4, 5, 6, 7, 8, 9}划分为两个子集A ={a , b , c , d , e }和B ={w , x , y , z },使得A ∪B =I ,A ∩B =Ø,且A 与B 的元素至少有一种排列组成的正整数满足2wxyz abcde ,则称A 与B 为集合I 的一个“两倍型2分划”.(1)写出集合I 的所有“两倍型2分划”,并给出理由;(2)写出集合I 的每个“两倍型2分划”对应的所有可能的2wxyz abcde .解:(1)集合I 共有2个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}.理由简述如下:1° 由易知,a =1,所以a ∈A .ABCD MI 1 I 2• •2° 由0∉ I ={1, 2, 3, 4, 5, 6, 7, 8, 9}=A ∪B ,而5×2=10,所以5∈A . 3° 试验知,a , b , c , d , e 均不能等于9,所以9∈B ,进而有8∈A .4° 因为数wxyz abcde 和的9个数字和恰为1+2+3+4+5+6+7+8+9=45是9的倍数,可判知+abcde wxyz 是9的倍数,即+abcde wxyz ≡0(mod9).又2wxyz abcde ,所以3wxyz ≡0(mod9).于是wxyz ≡0(mod3).所以)(wxyz S 是3的倍数,进而推得)(abcde S 也是3的倍数.5° 同样试验可判定7∈B .此时分配剩下的4个元素:2, 3, 4, 6.由于A 中的1+5+8=14,被3除余2,所以从2, 3, 4, 6中选出的两个数之和被3除余1.于是只能选3, 4或4, 6属于A ,对应剩下的2, 6或2, 3归属于B .因此,找到集合I 的两个“两倍型2分划”:A ={1, 3, 4, 5, 8},B ={2, 6, 7, 9}及A ={1, 4, 5, 6, 8},B ={2, 3, 7, 9}. (2)集合I 的“两倍型2分划”满足的不同的2wxyz abcde 共12个.1° 当B={2, 6, 7, 9}时,得到6个不同的式子:6729×2=13458, 6792×2=13584, 6927×2=13854, 7269×2=14538, 7692×2=15384, 9267×2=18534. 2° 当B={2, 3, 7, 9}时,得到6个不同的式子:7293×2=14586, 7329×2=14658, 7923×2=15846, 7932×2=15864, 9273×2=18546, 9327×2=18654.。
北京市第十五中学2024-2025学年高三上学期期中考试数学试卷(含答案)

北京十五中高三年级数学期中考试试卷2024.11本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}23A x x =-≤≤,{1B x x =<-或}4x >,那么集合A B = (A )A .{}21x x -≤<-B .{3x x ≤或≥4C .{}24x x -≤<D .{}13x x -≤≤2.在复平面内,复数z 满足(1)2i z -=,则z =(D )A .1i--B .1i-+C .1i-D .1i +3.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是(A)A .3()f x x =B .2()f x x =C .3()f x x=D .()sin f x x=4.若0m n <<,则下列结论正确的是(B )A .22log log m n >B .0.50.5log log m n>C .1122m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D .22m n>5.若α是第二象限角,且1tan 2α=-,则πcos 2α⎛⎫+= ⎪⎝⎭(D )A .2B .2-C .5D .5-6.设等差数列{}n a 的前n 项和为n S ,且2822a a +=-,11110S =-,则n S 取最小值时,n 的值为(C )A .14B .15C .15或16D .167.已知单位向量,a b ,则“a b ⊥”是“任意R λ∈都有a b a b -λ=λ+r r r r ”的(C )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件8.设函数()21cos cos 2f x x x x =--,则下列结论错误的是(D )A .()f x 的一个周期为πB .()y f x =的图象关于直线4π3x =对称C .将函数cos 2y x =的图象向左平移π6个单位可以得到函数()f x 的图象D .()f x 在(π2,π)上单调递减9.在ABC V 中,2π3A =,D 为边BC 上一点,若AD AB ⊥,且1AD =,则ABC V 面积的最小值为(B )AB C D 10.如图,曲线C 为函数5sin (0)2y x x π=≤≤的图象,甲粒子沿曲线C 从A 点向目的地B 点运动,乙粒子沿曲线C 从B 点向目的地A 点运动.两个粒子同时出发,且乙的水平速率为甲的2倍,当其中一个粒子先到达目的地时,另一个粒子随之停止运动.在运动过程中,设甲粒子的坐标为(,)m n ,乙粒子的坐标为(,)u v ,若记()n v f m -=,则下列说法中正确的是(B )A .()f m 在区间(,)2ππ上是增函数B .()f m 恰有2个零点C .()f m 的最小值为2-D .()f m 的图象关于点5(,0)6π中心对称第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.函数()f x =的定义域为________.[2,﹢∞)12.612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为.(用数字作答)-16013.已知向量(,1),(1,2)a m b == ,且222||||||a b a b +=+,则m 的值为.-214.对于函数()ln21xf x x =-和()()ln ln 21g x x x =--,给出下列三个结论:①设()f x 的定义域为M ,()g x 的定义域为N ,则N 是M 的真子集.②函数()g x 的图像在1x =处的切线斜率为0.③函数()f x 的图像关于点1,ln24⎛⎫- ⎪⎝⎭对称.其中所有正确结论的序号是.①③解析:对于①,由题意得,函数()f x 的定义域()10,0,212x M xx ∞∞⎧⎫⎛⎫==-⋃+⎨⎬ ⎪-⎝⎭⎩⎭,函数()g x 的定义域12N x x ⎧⎫=⎨⎬⎩⎭.所以N 是M 的真子集,则①正确.对于②,()1221g x x x =--',则在1x =处的切线斜率()1211121k g ='=-=--,则②错误.对于③只需验证:当1212x x +=时,()()()121212121212lnln ln 2ln22121421x x x x f x f x x x x x x x +=+==----++,则④正确.故答案为:①③.15.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术,剪纸具有广泛的群众基础,交融于各族人民的社会生活,是各种民俗活动的重要组成部分,其传承赓续的视觉形象和造型格式,蕴涵了丰富的文化历史信息,是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下:取一张半径为1的圆形纸片,记为O ,在O 内作内接正方形,接着在该正方形内作内切圆,记为1O ,并裁剪去该正方形与内切圆之间的部分(如图所示阴影部分),记为一次裁剪操作,L ,重复上述裁剪操作n 次,最终得到该剪纸,则第2024次操作后,所有被裁剪部分的面积之和.()202414π12⎛⎫--⎪⎝⎭解析:设n O 的半径为n R ,则122R =,1n O + 的半径为22n R ,即122n n R R +=,故121221222nn nn R R -⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,n O 的面积为1ππ22nn S ⎛⎫== ⎪⎝⎭,又第n 次裁剪操作的正方形边长为12122n n R -⎛⎫= ⎪⎝⎭,故第n 次裁剪操作裁剪掉的面积为1222221111ππ2222n n n n⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-⨯ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21π4π222n n n --=-=,所以第n 次裁剪操作后,裁剪掉的面积之和为()()211114π...4π12222n n ⎛⎫⎛⎫-+++=--⎪⎝⎭⎝⎭,所以第2024次操作后,所有被裁剪部分的面积之和为()202414π12⎛⎫-- ⎪⎝⎭.故答案为:()202414π12⎛⎫-- ⎝⎭.三、解答题共5小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.已知函数()sin si πn 3f x x x ⎛⎫=++ ⎪⎝⎭.(Ⅰ)求()f x 的最小正周期和单调增区间;(Ⅱ)若π6x =是函数()(0)y f x ϕϕ=+>的一个零点,求ϕ的最小值.解:(Ⅰ)由函数π1()sin sin sin sin cos 322f x x x x x x ⎛⎫=++=++ ⎪⎝⎭3πsin226x x x ⎛⎫=+=+ ⎪⎝⎭,……………3分所以函数()f x 的最小正周期为2πT =.……………5分由πππ2π2π262k x k -+≤+≤,k Z ∈,得2ππ2π2π33k x k -+≤≤+,k Z ∈,所以函数()f x 的单调增区间为2ππ[2,2π]33k k -++,k Z ∈.……………8分(Ⅱ)因为π6x =是函数()(0)f x ϕϕ+>的一个零点,ππ066ϕ⎛⎫++= ⎪⎝⎭,即πsin 03ϕ⎛⎫+= ⎪⎝⎭,……………10分所以ππ3k ϕ+=,Z k ∈,即ππ3k ϕ=-+,Z k ∈,……………12分又因为0ϕ>,所以ϕ的最小值为2π3.……………13分17.在ABC △中,6a =,1cos 3C =-,三角形面积为(Ⅰ)b 和c 的值;(Ⅱ)sin()A B -的值.解:(Ⅰ)在ABC △中,因为1cos 3C =-,所以(,)2C π∈π,22sin 3C =.……………2分因为1sin 2S ab C ==6a =,所以2b =.……………4分由余弦定理,2222cos 48c a b ab C =+-=,……………5分所以c =……………6分(Ⅱ)由正弦定理sin sin sin a b cA B C ==,可得62sin sin 223A B ==.…………7分所以sin 3A =,sin 9B =.……………9分因为,(0,2A B π∈,所以3cos 3A =,53cos 9B =.……………11分所以sin()sin cos cos sin A B A B A B-=-39399=⨯-⨯=.……………13分18.已知函数2()ln ,()e e x x f x x x g x ==-.(Ⅰ)求函数()f x 在区间[1,3]上的最小值;(Ⅱ)证明:对任意,(0,)m n ∈+∞,都有()()f m g n ≥成立.解:(Ⅰ)由()ln f x x x =,可得()ln 1f x x =+'.……………2分所以()0f x '>在区间[1,3]恒成立,……………4分所以()f x 在区间[1,3]上单调递增,……………5分所以()f x 在区间[1,3]上的最小值为(1)0f =.……………7分(Ⅱ)因为()ln 1f x x =+'.所以当1(0,),'()0e x f x ∈<,()f x 单调递减;1(,),'()0ex f x ∈+∞>,()f x 单调递增……………9分所以,()f x 在1e x =时取得最小值11()e ef =-,可知1()ef m ≥-.……………10分由2()e e x x g x =-,可得1'()e x x g x -=.……………11分所以当(0,1),'()0,()x g x g x ∈>单调递增,当(1,),'()0,()x g x g x ∈+∞<单调递减.……………12分所以函数()(0)g x x >在1x =时取得最大值,又1(1)e g =-,可知1()eg n ≤-,……………13分所以对任意,(0,)m n ∈+∞,都有()()f m g n ≥成立.……………14分19.某学校组织全体高一学生开展了知识竞赛活动.从参加该活动的学生中随机抽取了12名学生的竞赛成绩,数据如下表:男生818486868891女生728084889297(Ⅰ)从抽出的男生和女生中,各随机选取一人,求男生成绩高于女生成绩的概率;(Ⅱ)从该校的高一学生中,随机抽取3人,用样本频率估计概率,记成绩为优秀(90>分)的学生人数为X ,求X 的分布列和数学期望;(Ⅲ)表中男生和女生成绩的方差分别记为21s ,22s ,现在再从参加活动的男生中抽取一名学生,成绩为86分,组成新的男生样本,方差计为23s ,试比较21s 、22s 、23s 的大小.(只需写出结论)解:(Ⅰ)设“从抽出的男生和女生中,男生成绩高于女生成绩”为事件A ,由表格得:从抽出的12名学生中男女生各随机选取一人,共有1166C C 36=种组合,其中男生成绩高于女生()()()()()()()81,72,81,80,84,72,84,80,86,72,86,80,86,84,()()()86,72,86,80,86,84,()()()()()88,72,88,80,88,84,91,72,91,80,()91,84,()91,88.所以事件A 有17种组合,因此()1736P A =;……………3分(Ⅱ)由数据知,在抽取的12名学生中,成绩为优秀(90>分)的有3人,即从该校参加活动的高一学生中随机抽取1人,该学生成绩优秀的概率为14.……………4分X 可取0,1,2,3,……………5分()3327Χ0464P ⎛⎫=== ⎪⎝⎭,()2131327Χ1C 4464P ⎛⎫==⨯= ⎪⎝⎭,()223319Χ2C 4464P ⎛⎫==⨯=⎪⎝⎭,()311Χ3464P ⎛⎫=== ⎪⎝⎭所以随机变量X 的分布列……………10分数学期望2791483()0123646464644E X =+⨯+⨯+⨯.……………11分(Ⅲ)222312s s s <<.……………14分20.已知函数()()2e x f x x a x =--.(Ⅰ)当a =0时,求()f x 在x =0处的切线方程;(Ⅱ)当a =1时,求()f x 的单调区间;(Ⅲ)当()f x 有且仅有一个零点时,请直接写出a 的取值范围.解:(Ⅰ)当a =0时,()2e x f x x x =-,()00f =,……………1分因为()()1e 2x f x x x '=+-,……………2分所以()10f '=,……………3分所以()f x 在x =0处的切线方程为:y x=……………4分X0123P27642764964164(Ⅱ)当a =1时,()()21e x f x x x =--,所以()()()e 1e 2e 2e 2x x x x f x x x x x x =+--=-=-',……………6分由()0f x '>,得0x <或ln 2x >,……………8分由()0f x '<,得0ln 2x <<,……………10分所以,()f x 的单调增区间为(),0∞-和(ln 2,)+∞,()f x 的单调减区间为(0,ln 2).……………12分(Ⅲ)a R ∈.……………15分21.(本小题15分)已知项数为*(,2)N m m m ∈≥的数列{}n a 满足如下条件:①*(1,2,,)n a N n m ∈= ;②12m a a a <<< .若数列{}n b 满足*12()1m nn a a a a b N m +++-=∈- ,其中1,2,,n m = ,则称{}n b 为{}n a 的“伴随数列”.(Ⅰ)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;(Ⅱ)若{}n b 为{}n a 的“伴随数列”,证明:12m b b b >>> ;(Ⅲ)已知数列{}n a 存在“伴随数列”{}n b ,且11a =,2049m a =,求m 的最大值.解:(Ⅰ)解:数列1,3,5,7,9不存在“伴随数列”.……………1分因为*41357979512b N ++++-==∉-,所以数列1,3,5,7,9不存在“伴随数列”.……………3分(Ⅱ)证明:因为111n n n n a a b b m ++--=-,*11,n m n N≤≤-∈……………4分又因为12m a a a <<< ,所以有10n n a a +-<所以1101n n n n a a b b m ++--=<-……………6分所以12m b b b >>> 成立……………7分(Ⅲ)∀1≤i <j ≤m ,都有1j i i j a a b b m --=-,……………8分因为*i b N ∈,12m b b b >>> .所以*i j b b N -∈,所以*1j i i j a a b b N m --=∈-……………9分所以*11204811m m a a b b N m m --==∈--因为*111n n n n a a b b N m ----=∈-,所以11n n a a m --≥-……………11分又112211()()()m m m m m a a a a a a a ----=-+-++- (1)(1)(1)m m m ≥-+-++- =2(1)m -……………13分所以2(1)2048m -≤,所以46m ≤……………14分又*20481N m ∈-,所以33m ≤例如:6463n a n =-(133n ≤≤),满足题意,所以,m 的最大值是33.……………15分北京十五中高三年级数学期中考试试卷2024.11本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}23A x x =-≤≤,{1B x x =<-或}4x >,那么集合A B = (A )A .{}21x x -≤<-B .{3x x ≤或≥4C .{}24x x -≤<D .{}13x x -≤≤2.在复平面内,复数z 满足(1)2i z -=,则z =(D )A .1i--B .1i-+C .1i-D .1i +3.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是(A)A .3()f x x =B .2()f x x =C .3()f x x=D .()sin f x x=4.若0m n <<,则下列结论正确的是(B )A .22log log m n >B .0.50.5log log m n>C .1122m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D .22m n>5.若α是第二象限角,且1tan 2α=-,则πcos 2α⎛⎫+= ⎪⎝⎭(D )A .2B .2-C .5D .5-6.设等差数列{}n a 的前n 项和为n S ,且2822a a +=-,11110S =-,则n S 取最小值时,n 的值为(C )A .14B .15C .15或16D .167.已知单位向量,a b ,则“a b ⊥”是“任意R λ∈都有a b a b -λ=λ+r r r r ”的(C )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件8.设函数()21cos cos 2f x x x x =--,则下列结论错误的是(D )A .()f x 的一个周期为πB .()y f x =的图象关于直线4π3x =对称C .将函数cos 2y x =的图象向左平移π6个单位可以得到函数()f x 的图象D .()f x 在(π2,π)上单调递减9.在ABC V 中,2π3A =,D 为边BC 上一点,若AD AB ⊥,且1AD =,则ABC V 面积的最小值为(B )AB C D 10.如图,曲线C 为函数5sin (0)2y x x π=≤≤的图象,甲粒子沿曲线C 从A 点向目的地B 点运动,乙粒子沿曲线C 从B 点向目的地A 点运动.两个粒子同时出发,且乙的水平速率为甲的2倍,当其中一个粒子先到达目的地时,另一个粒子随之停止运动.在运动过程中,设甲粒子的坐标为(,)m n ,乙粒子的坐标为(,)u v ,若记()n v f m -=,则下列说法中正确的是(B )A .()f m 在区间(,)2ππ上是增函数B .()f m 恰有2个零点C .()f m 的最小值为2-D .()f m 的图象关于点5(,0)6π中心对称第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.函数()f x =的定义域为________.[2,﹢∞)12.612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为.(用数字作答)-16013.已知向量(,1),(1,2)a m b == ,且222||||||a b a b +=+,则m 的值为.-214.对于函数()ln21xf x x =-和()()ln ln 21g x x x =--,给出下列三个结论:①设()f x 的定义域为M ,()g x 的定义域为N ,则N 是M 的真子集.②函数()g x 的图像在1x =处的切线斜率为0.③函数()f x 的图像关于点1,ln24⎛⎫- ⎪⎝⎭对称.其中所有正确结论的序号是.①③解析:对于①,由题意得,函数()f x 的定义域()10,0,212x M xx ∞∞⎧⎫⎛⎫==-⋃+⎨⎬ ⎪-⎝⎭⎩⎭,函数()g x 的定义域12N x x ⎧⎫=⎨⎬⎩⎭.所以N 是M 的真子集,则①正确.对于②,()1221g x x x =--',则在1x =处的切线斜率()1211121k g ='=-=--,则②错误.对于③只需验证:当1212x x +=时,()()()121212121212lnln ln 2ln22121421x x x x f x f x x x x x x x +=+==----++,则④正确.故答案为:①③.15.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术,剪纸具有广泛的群众基础,交融于各族人民的社会生活,是各种民俗活动的重要组成部分,其传承赓续的视觉形象和造型格式,蕴涵了丰富的文化历史信息,是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下:取一张半径为1的圆形纸片,记为O ,在O 内作内接正方形,接着在该正方形内作内切圆,记为1O ,并裁剪去该正方形与内切圆之间的部分(如图所示阴影部分),记为一次裁剪操作,L ,重复上述裁剪操作n 次,最终得到该剪纸,则第2024次操作后,所有被裁剪部分的面积之和.()202414π12⎛⎫--⎪⎝⎭解析:设n O 的半径为n R ,则122R =,1n O + 的半径为22n R ,即122n n R R +=,故121221222nn nn R R -⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,n O 的面积为1ππ22nn S ⎛⎫== ⎪⎝⎭,又第n 次裁剪操作的正方形边长为12122n n R -⎛⎫= ⎪⎝⎭,故第n 次裁剪操作裁剪掉的面积为1222221111ππ2222n n n n⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-⨯ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21π4π222n n n --=-=,所以第n 次裁剪操作后,裁剪掉的面积之和为()()211114π...4π12222n n ⎛⎫⎛⎫-+++=--⎪⎝⎭⎝⎭,所以第2024次操作后,所有被裁剪部分的面积之和为()202414π12⎛⎫-- ⎪⎝⎭.故答案为:()202414π12⎛⎫-- ⎝⎭.三、解答题共5小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.已知函数()sin si πn 3f x x x ⎛⎫=++ ⎪⎝⎭.(Ⅰ)求()f x 的最小正周期和单调增区间;(Ⅱ)若π6x =是函数()(0)y f x ϕϕ=+>的一个零点,求ϕ的最小值.解:(Ⅰ)由函数π1()sin sin sin sin cos 322f x x x x x x ⎛⎫=++=++ ⎪⎝⎭3πsin226x x x ⎛⎫=+=+ ⎪⎝⎭,……………3分所以函数()f x 的最小正周期为2πT =.……………5分由πππ2π2π262k x k -+≤+≤,k Z ∈,得2ππ2π2π33k x k -+≤≤+,k Z ∈,所以函数()f x 的单调增区间为2ππ[2,2π]33k k -++,k Z ∈.……………8分(Ⅱ)因为π6x =是函数()(0)f x ϕϕ+>的一个零点,ππ066ϕ⎛⎫++= ⎪⎝⎭,即πsin 03ϕ⎛⎫+= ⎪⎝⎭,……………10分所以ππ3k ϕ+=,Z k ∈,即ππ3k ϕ=-+,Z k ∈,……………12分又因为0ϕ>,所以ϕ的最小值为2π3.……………13分17.在ABC △中,6a =,1cos 3C =-,三角形面积为(Ⅰ)b 和c 的值;(Ⅱ)sin()A B -的值.解:(Ⅰ)在ABC △中,因为1cos 3C =-,所以(,)2C π∈π,22sin 3C =.……………2分因为1sin 2S ab C ==6a =,所以2b =.……………4分由余弦定理,2222cos 48c a b ab C =+-=,……………5分所以c =……………6分(Ⅱ)由正弦定理sin sin sin a b cA B C ==,可得62sin sin 223A B ==.…………7分所以sin 3A =,sin 9B =.……………9分因为,(0,2A B π∈,所以3cos 3A =,53cos 9B =.……………11分所以sin()sin cos cos sin A B A B A B-=-39399=⨯-⨯=.……………13分18.已知函数2()ln ,()e e x x f x x x g x ==-.(Ⅰ)求函数()f x 在区间[1,3]上的最小值;(Ⅱ)证明:对任意,(0,)m n ∈+∞,都有()()f m g n ≥成立.解:(Ⅰ)由()ln f x x x =,可得()ln 1f x x =+'.……………2分所以()0f x '>在区间[1,3]恒成立,……………4分所以()f x 在区间[1,3]上单调递增,……………5分所以()f x 在区间[1,3]上的最小值为(1)0f =.……………7分(Ⅱ)因为()ln 1f x x =+'.所以当1(0,),'()0e x f x ∈<,()f x 单调递减;1(,),'()0ex f x ∈+∞>,()f x 单调递增……………9分所以,()f x 在1e x =时取得最小值11()e ef =-,可知1()ef m ≥-.……………10分由2()e e x x g x =-,可得1'()e x x g x -=.……………11分所以当(0,1),'()0,()x g x g x ∈>单调递增,当(1,),'()0,()x g x g x ∈+∞<单调递减.……………12分所以函数()(0)g x x >在1x =时取得最大值,又1(1)e g =-,可知1()eg n ≤-,……………13分所以对任意,(0,)m n ∈+∞,都有()()f m g n ≥成立.……………14分19.某学校组织全体高一学生开展了知识竞赛活动.从参加该活动的学生中随机抽取了12名学生的竞赛成绩,数据如下表:男生818486868891女生728084889297(Ⅰ)从抽出的男生和女生中,各随机选取一人,求男生成绩高于女生成绩的概率;(Ⅱ)从该校的高一学生中,随机抽取3人,用样本频率估计概率,记成绩为优秀(90>分)的学生人数为X ,求X 的分布列和数学期望;(Ⅲ)表中男生和女生成绩的方差分别记为21s ,22s ,现在再从参加活动的男生中抽取一名学生,成绩为86分,组成新的男生样本,方差计为23s ,试比较21s 、22s 、23s 的大小.(只需写出结论)解:(Ⅰ)设“从抽出的男生和女生中,男生成绩高于女生成绩”为事件A ,由表格得:从抽出的12名学生中男女生各随机选取一人,共有1166C C 36=种组合,其中男生成绩高于女生()()()()()()()81,72,81,80,84,72,84,80,86,72,86,80,86,84,()()()86,72,86,80,86,84,()()()()()88,72,88,80,88,84,91,72,91,80,()91,84,()91,88.所以事件A 有17种组合,因此()1736P A =;……………3分(Ⅱ)由数据知,在抽取的12名学生中,成绩为优秀(90>分)的有3人,即从该校参加活动的高一学生中随机抽取1人,该学生成绩优秀的概率为14.……………4分X 可取0,1,2,3,……………5分()3327Χ0464P ⎛⎫=== ⎪⎝⎭,()2131327Χ1C 4464P ⎛⎫==⨯= ⎪⎝⎭,()223319Χ2C 4464P ⎛⎫==⨯=⎪⎝⎭,()311Χ3464P ⎛⎫=== ⎪⎝⎭所以随机变量X 的分布列……………10分数学期望2791483()0123646464644E X =+⨯+⨯+⨯.……………11分(Ⅲ)222312s s s <<.……………14分20.已知函数()()2e x f x x a x =--.(Ⅰ)当a =0时,求()f x 在x =0处的切线方程;(Ⅱ)当a =1时,求()f x 的单调区间;(Ⅲ)当()f x 有且仅有一个零点时,请直接写出a 的取值范围.解:(Ⅰ)当a =0时,()2e x f x x x =-,()00f =,……………1分因为()()1e 2x f x x x '=+-,……………2分所以()10f '=,……………3分所以()f x 在x =0处的切线方程为:y x=……………4分X0123P27642764964164(Ⅱ)当a =1时,()()21e x f x x x =--,所以()()()e 1e 2e 2e 2x x x x f x x x x x x =+--=-=-',……………6分由()0f x '>,得0x <或ln 2x >,……………8分由()0f x '<,得0ln 2x <<,……………10分所以,()f x 的单调增区间为(),0∞-和(ln 2,)+∞,()f x 的单调减区间为(0,ln 2).……………12分(Ⅲ)a R ∈.……………15分21.(本小题15分)已知项数为*(,2)N m m m ∈≥的数列{}n a 满足如下条件:①*(1,2,,)n a N n m ∈= ;②12m a a a <<< .若数列{}n b 满足*12()1m nn a a a a b N m +++-=∈- ,其中1,2,,n m = ,则称{}n b 为{}n a 的“伴随数列”.(Ⅰ)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;(Ⅱ)若{}n b 为{}n a 的“伴随数列”,证明:12m b b b >>> ;(Ⅲ)已知数列{}n a 存在“伴随数列”{}n b ,且11a =,2049m a =,求m 的最大值.解:(Ⅰ)解:数列1,3,5,7,9不存在“伴随数列”.……………1分因为*41357979512b N ++++-==∉-,所以数列1,3,5,7,9不存在“伴随数列”.……………3分(Ⅱ)证明:因为111n n n n a a b b m ++--=-,*11,n m n N≤≤-∈……………4分又因为12m a a a <<< ,所以有10n n a a +-<所以1101n n n n a a b b m ++--=<-……………6分所以12m b b b >>> 成立……………7分(Ⅲ)∀1≤i <j ≤m ,都有1j i i j a a b b m --=-,……………8分因为*i b N ∈,12m b b b >>> .所以*i j b b N -∈,所以*1j i i j a a b b N m --=∈-……………9分所以*11204811m m a a b b N m m --==∈--因为*111n n n n a a b b N m ----=∈-,所以11n n a a m --≥-……………11分又112211()()()m m m m m a a a a a a a ----=-+-++- (1)(1)(1)m m m ≥-+-++- =2(1)m -……………13分所以2(1)2048m -≤,所以46m ≤……………14分又*20481N m ∈-,所以33m ≤例如:6463n a n =-(133n ≤≤),满足题意,所以,m 的最大值是33.……………15分。
北京市第十五中学2024-2025学年高三上学期10月月考数学试题(含答案)

北京市第十五中学2024-2025学年高三上学期10月月考数 学2024.10本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合,,则A .B .C .D .2.已知,则的大小关系为A .B .C .D .3.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是 A .B .C .D .4.已知等差数列的前项和为 ,若,则A .54B .63C .72D .1355.若函数的图象向右平移个单位长度得到函数的图象,若函数在区间上单调递增,则的最大值为A .B .C .D .6.设且,则“”是“”成立的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.若函数的部分图象如图所示,则的值是A .B .C .D .{}1,2,3A ={}ln 1B x x =>A B = ∅{}3{}2,3()2,30.10.644,2,log 0.6a b c ===,,a b c c a b <<c b a <<a b c<<b a c<<3()f x x =()2-=x f x ()ln ||f x x =2()f x x =-{}n a n n S 38304S a ==,9S =()sin 2f x x =6π()g x ()g x [0,]a a 512π3π2π712πx R ∈0x ≠1x >12x x+>()sin()(0,0,0)2f x A x A ωϕωϕπ=+>><<ϕ3π6π4π12π8.在中,分别是角的对应边,若,则下列式子正确的是A .B .C .D .9.已知函数当时,方程的根的个数为A .0B .1C .2D .310.数列各项均为实数,对任意满足,且,则下列选项中不可能的是A .,B ., C .,D .,第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分.11.函数的定义域为 .12.在平面直角坐标系中,角和角均以为始边,它们的终边关于轴对称.若,则=__________.13.已知数列的前项和为,则 .14.已知函数为在上的偶函数,且满足条件:①在上单调递减;②,则关于的不等式的解集是 .15.已知函数,对于函数有下述四个结论:①函数在其定义域上为增函数; ②有且仅有一个零点;③对于任意的,都有成立;④若曲线在点处的切线也是曲线的切线,则必是的零点.其中所有正确的结论序号是三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.ABC V ,,a b c ,,A B C sin C C =2a b c +=2a b c +<2a b c+≥2a b c+≤2,0,()(2),0x x f x f x x ⎧<=⎨-≥⎩1324m ≤<1()8f x x m =-+{}n a *n ∈N 3n n a a +=312n n n n a a a a c +++=+11a =1c =11a =-4c =12a =2c =12a =0c =()lg(3)f x x =++xOy αβOx x 1sin 3α=sin β{}n a n 1,(1)21nn n n S a a n ++-=-8S =()f x R [)0+∞,()21f =x ()11f x ->1()e 1xx f x x +=--()f x ()f x ()f x 1a <()1f a >-e x y =000(,e )(1)xx x ≠ln y x =0x ()f x16.(本小题13分)已知函数,(Ⅰ)求实数的值;(Ⅱ)求函数的最小正周期及单调增区间.17.(本小题13分)已知函数.(Ⅰ)求函数的极值;(Ⅱ)若对都有恒成立,求实数的取值范围.18.(本小题14分)在中,.(Ⅰ)求的大小;(Ⅱ)再从下列三个条件中,选择两个作为已知,使得存在且唯一,求的面积.条件①;条件②条件③AB.19.(本小题15分)为研究某地区2021届大学毕业生毕业三个月后的毕业去向,某调查公司从该地区2021届大学毕业生中随机选取了1000人作为样本进行调查,结果如下:毕业去向继续学习深造单位就业自主创业自由职业慢就业人数2005601412898假设该地区2021届大学毕业生选择的毕业去向相互独立.(Ⅰ)若该地区一所高校2021届大学毕业生的人数为2500,试根据样本估计该校2021届大学毕业生选择“单位就业”的人数;(Ⅱ)从该地区2021届大学毕业生中随机选取3人,记随机变量为这3人中选择“继续学习深造”的人数.以样本的频率估计概率,求的分布列和数学期望;(Ⅲ)该公司在半年后对样本中的毕业生进行再调查,发现仅有选择“慢就业”的毕业生中的人选择了上表中其他的毕业去向,记此时表中五种毕业去向对应人数的方差为.当为何值时,最小.(结论不要求证明)20.(本小题15分)已知函数.(Ⅰ)若,求曲线在点处的切线方程;(Ⅱ)求的极值和单调区间;(Ⅲ)若在上不是单调函数,且在上恒成立,求实数的取值范围.21.(本小题15分)若有穷数列:,,…,,满足,则称数列为数列.(Ⅰ)判断下列数列是否为数列,并说明理由;2()2cos sin cos f x x a x x =+π()06f =a ()f x 2()(3)e x f x x =-()f x [1,2]x ∀∈-()f x a ≥a ABC V sin cos b A a B =B ∠ABC V ABC V 1cos 2A =-b =X X ()E X a (098)a <<2s a 2s 1()ln =+f x a x x()a R ∈2a =()y f x =(1,(1))f ()f x ()f x []1,e ()e f x ≤[]1,e a A 1a 2a ()*,3n a n n ∈≥N ()1121,2,,2i i i i a a a a i n +++-≤-=- A M M①1,2,4,3②4,2,8,1(Ⅱ)已知数列:,,…,,其中,,求的最小值.(Ⅲ)已知数列是1,2,…,的一个排列.若,求的所有取值.M A 1a 2a 9a 14a =27a =349a a a +++ M A n 1112n k k k a a n -+=-=+∑n参考答案题号12345678910答案B A C B A C A D D C8.D解析:由题意可知由余弦定理可得,所以,所以,即,9.D解析:画出函数的图像,有图可知方程 的根的个数为3个.故选C.10.C解析:对任意满足,.对于A ,若,,则,故,故或,若,则,故,此时,,,当时,;当时,;当时,,故A 成立.对于B ,若,,则,故,又,,故或,sin tan cos C C C ==3C π=2221cos 22a b c C ab +-==222a b c ab +-=2223()()34a b a b c ab ++-=≤22()4a b c +≤2a b c +≤()f x ()18f x x m =-+ *n ∈N 3n n a a +=∴212n n n a a a c ++-=11a =1c =12231a a a -=230a a =20a =30a =20a =24233101a a a a a --==31a =-321k a -=310k a -=31k a =-32n k =-2121n n n a a a ++-=31n k =-2121n n n a a a ++-=3n k =2121n n n a a a ++-=11a =-4c =12234a a a -=233a a =-223423122324a a a a a a a a -=-+==234531232224a a a a a a a a -=-+==231a a +=-23a a =若,则无解;若,则,故或此时,,;或,,满足;故B 成立.对于C ,若,,则,故,且,故,又,故或,若,则无解;若,则也无解,故C 错误.对于D ,若,,则,故,又,故,此时,满足故选:B 11.12.13.36解析:由题意可得为奇数时,,两式相减得;为偶数时,,两式相加得,故.14.23a a =23223232344a a a a a a =-⎧⎪+=⎨⎪+=⎩231a a +=-23223232344a a a a a a =-⎧⎪+=⎨⎪+=⎩23a a ⎧=⎪⎪⎨⎪=⎪⎩23a a ⎧=⎪⎪⎨⎪=⎪⎩321k a -=-31k a -=3k a =2124n n n a a a ++-=321k a -=-31k a -=3k a =2124n n n a a a ++-=12a =2c =12232a a a -=232a a =222343222a a a a a -=-=32222a a -=1222345232322a a a a a a a a --===-232a a +=-23a a =23a a =2322323222222a a a a a a =⎧⎪-=⎨⎪-=⎩232a a +=-2322323222222a a a a a a =⎧⎪-=⎨⎪-=⎩12a =0c =12230a a a -=234a a =3222234212320a a a a a a a a =-=--=322a a ==2n a =2120n n n a a a ++-=()3,1-13-n 12121,21n n n n a a n a a n +++-=-+=+22n n a a ++=n 12121,21n n n n a a n a a n ++++=--=+24n n a a n ++=()()()()8135724682282436S a a a a a a a a =+++++++=+++=()1,3-解析:函数为在上的偶函数,在上单调递减,故在上单调递增;,故.画出函数简图,如图所示:,故,故,解得.故答案为:15.③④解析:对于①,的定义域为,因为,,①错误;对于②,因为,所以在和上单调递增,又,,,,所以在区间和上都存在零点,又在和上单调递增,即在区间和上各有一个零点,②错误;对于③,因为,所以,所以,即,所以③正确;对于④,因为,所以曲线在点处的切线斜率为,得切线方程为,即,设与相切于点,因为,所以切线斜率为,得切线方程为,即,()f x R [)0+∞,(),0-∞()21f =()21f -=()11f x ->()()12f x f ->212x -<-<13x -<<()1,3-12()e e 111xx x f x x x +=-=----{}|1x x ≠9109e 19e 192010f ⎛⎫=+>+= ⎪⎝⎭()292e 32010f f ⎛⎫=-<< ⎪⎝⎭()22()e 01xf x x =+>-'()f x (),1-∞()1,+∞()31130e 2f -=-<545e 904f ⎛⎫=-< ⎪⎝⎭9010f ⎛⎫> ⎪⎝⎭()20f >()f x 93,10⎛⎫- ⎪⎝⎭5,24⎛⎫ ⎪⎝⎭()f x (),1-∞()1,+∞()f x (),1-∞()1,+∞1a <201a ->-()21e 01a f a a +=->-()1f a >-()e e x x '=e x y =000(,e )(1)xx x ≠0e x l ()000e e x x y x x -=-0000e e e x x xy x x =-+l ln y x =()11,ln x x ()1ln x x '=11x l ()1111ln y x x x x -=-111ln 1y x x x =+-所以,即,消去得,整理得,即是的零点,④正确.16.解:(Ⅰ)由可求出2)先化简得,由三角函数的图象和性质可求出函数的周期及单调递增区间.试题解析:(1)由知∴∴(Ⅱ)解:∵∴∴,∴()∴() ∴函数的最小正周期为,单调增区间为()17.解:(Ⅰ)由,得.令得或.当变化时,在各区间上的正负,以及的单调性如下表所示:+0-0+↗极大↘极小↗所以当时取极大值;当时取极小值.(Ⅱ)由(1)可得函数在上单调递减,在上单调递增,0001011e e e ln 1x x x x x x ⎧=⎪⎨⎪-+=-⎩000101ln e e ln 1x x x x x x =-⎧⎨-+=-⎩1ln x 0000e e 1x xx x -+=--0001e 01x x x +-=-0x ()f x ()06f π=a =-()2cos(2)13f x x π=++(06f π=22cos sincos666a πππ+=312042a ⨯+⨯=a =-a =-2()2cos cos f x x x x =-cos 212x x=+2cos(2)13x π=++222T πππω===2223k x k ππππ-≤+≤Z k ∈236k x k ππππ-≤≤-Z k ∈π2[,]36k k ππππ--Z k ∈2()(3)e x f x x =-2()(23)e x f x x x '=+-()()223e 0xf x x x -'=+=3x =-1x ()f x '()f x x (,3)-∞-3-(3,1)-1(1,)+∞()f x '()f x 3x =-()f x 3(3)6e f --=1x =()f x (1)2e f =-()f x [)1,1-(]1,2则在上的最小值为.对都有恒成立,所以.18.解:(Ⅰ)在中,,由正弦定理得,由于,则,由于,故;(Ⅱ)若选①②,存在且唯一,解答如下:由于,,又,故又,故,故;若选①③,存在且唯一,解答如下:由于,,AB 边上的高h,故则又,故,故;若选②③,不唯一,解答如下:,AB 边上的高h,故或,此时有两解,不唯一,不合题意.19.解:(Ⅰ)由题意得,该校2021届大学毕业生选择“单位就业”的人数为.(Ⅱ)由题意得,样本中名毕业生选择“继续学习深造”的频率为.()f x []1,2-()12e f =-[1,2]x ∀∈-()f x a ≥2e a ≤-ABC V sin cos b A a B =sin sin sin cos B A A B =(0,π),sin 0A A ∈∴≠sin cos ,tan 1B B B =∴=(0,π)B ∈π4B =ABC V 1cos 2A =-2π(0,π),3A A ∈∴=b =2π3sin a =a =2ππππ34C A B =--=--2ππ1sin sin 342C ⎛⎫=+== ⎪⎝⎭11sin 22===V ABC S ab C ABC V 1cos 2A =-2π(0,π),3A A ∈∴=sin h b A ===2π3sin a =a =2ππππ34C A B =--=--2ππ1sin sin 342C ⎛⎫=+== ⎪⎝⎭11sin 22===V ABC S ab C ABC V b =sin h A b ===2π(0,π),3A A ∈∴=π3ABC V 5602500=14001000⨯1000200110005=用频率估计概率,从该地区2021届大学毕业生中随机选取1名学生,估计该生选择“继续学习深造”的概率为.随机变量的所有可能取值为0,1,2,3.所以,,,.所以的分布列为0123.(Ⅲ)易知五种毕业去向的人数的平均数为200,要使方差最小,则数据波动性越小,故当自主创业和慢就业人数相等时方差最小,所以.20.解:(Ⅰ)当时,函数,. 所以,.所以曲线在点处的切线方程.(Ⅱ)函数定义域.求导得. ①当时,因为,所以.故的单调递减区间是,此时无极值. ②当时,变化时,变化如下表:极小值15X ()030311640155125P X C ⎛⎫⎛⎫==-=⎪⎪⎝⎭⎝⎭()21311481155125P X C ⎛⎫⎛⎫==-=⎪⎪⎝⎭⎝⎭()22311122155125P X C ⎛⎫⎛⎫==-=⎪⎪⎝⎭⎝⎭()3331113155125P X C ⎛⎫⎛⎫==-=⎪⎪⎝⎭⎝⎭X XP641254812512125112564481213()01231251251251255E x =⨯+⨯+⨯+⨯=42a =2a =()12ln f x x x =+()221f x x x'=-()11f =()11f '=()y f x =(1,(1))f y x =()f x ()0,x ∈+∞2211()a ax f x x x x-'=-=0a ≤()0,x ∈+∞()0f x '<()f x (0,)+∞()f x 0a >x (),()f x f x 'x 1(0,)a1a 1(,)a+∞()f x '-+()f x ]Z所以的单调递减区间是,单调递增区间是. 此时函数的极小值是,无极大值.(Ⅲ)因为在不是单调函数,由第(2)可知此时,且,1极小值又因为在上恒成立,只需即可,所以,解得的取值范围是21.解:(Ⅰ)①因为,所以该数列不是数列;②因为,所以该数列是数列.(Ⅱ)由,则,得或,恒成立,得或,同理得故.(Ⅲ)当时,因为,所以,不符合题意;当时,数列为3,2,4,1.此时,符合题意;当时,数列为 2,3,4,5,1.此时,符合题意;下证当时,不存在满足题意.令,2,,,则,且,所以有以下三种可能:①; ②;③.()f x 1(0,a1(,)a +∞()f x 1()ln f a a a a=-()f x []1,e 0a >[]11,e a ∈x1(1,)a 1a 1(,)e a e ()f x '-0+()f x (1)f ]Z ()f e ()e f x ≤[]1,e 11e (1)e (e)e a f f ⎧<<⎪⎪≤⎨⎪≤⎪⎩1ee 1e 11ea a ⎧+≤⎪⎪≤⎨⎪⎪<<⎩a 1,1e ⎛⎫ ⎪⎝⎭|24||43|->-M |42||28|81|-<-<-M ()1121,2,,2i i i i a a a a i n +++-≤-=- 3221=3a a a a -≥-34a ≤310a ≥4332213a a a a a a -≥-≥-=41a ≤413a ≥543a a -≥⋯,3494121212=13a a a +++≥++++++ 3n =1||2(1,2)i i a a i +-=...1223||||5a a a a -+-<4n =122334||||||6a a a a a a -+-+-=5n =12233445||||||||7a a a a a a a a -+-+-+-=6n ...n 1||(1k k k b a a k +=-=L 1)n -1211n b b b - (1)12n k k b n -==+∑k b 1,(1,2,,2)4,(1)k k n b k n =-⎧=⎨=-⎩ 1,(1,2,,3)2,(2)3,(1)k k n b k n k n =-⎧⎪==-⎨⎪=-⎩1,(1,2,,4)2,(3,2,1)k k n b k n n n =-⎧=⎨=---⎩当时,因为,即,2,,.所以 或.因为数列的各项互不相同,所以.所以数列是等差数列.∴,,,是公差为1(或的等差数列.当公差为1时,由得 或,所以或,与已知矛盾.当公差为时,同理得出与已知矛盾.所以当 时,不存在满足题意.其它情况同理.综上可知,的所有取值为4或5.1,(1,2,,2)4,(1)k k n b k n =-⎧=⎨=-⎩ 122n b b b -=== 112||||(1k k k k a a a a k +++-=-=⋯2)n -112k k k k a a a a +++-=-112()k k k k a a a a +++-=--{}k a 112k k k k a a a a +++-=-{}k a 1a 2a L 1n a -1-)14n b -=14n n a a -=+14n n a a -=-1142n n a a a n n -=+=++>14n n n s a a a --=-=1-1,(1,2,,2)4,(1)k k n b k n =-⎧=⎨=-⎩n n。
2023年全国高中数学联赛北京赛区预赛试题答案
2023 中国数学奥林匹克预赛北京赛区预赛一试试题参考解答
2023 年 5 月 21 日 8 : 00 − 9 : 20 前 8 题每题 8 分, 第 9 题 16 分, 第 10, 11 题每题 20 分
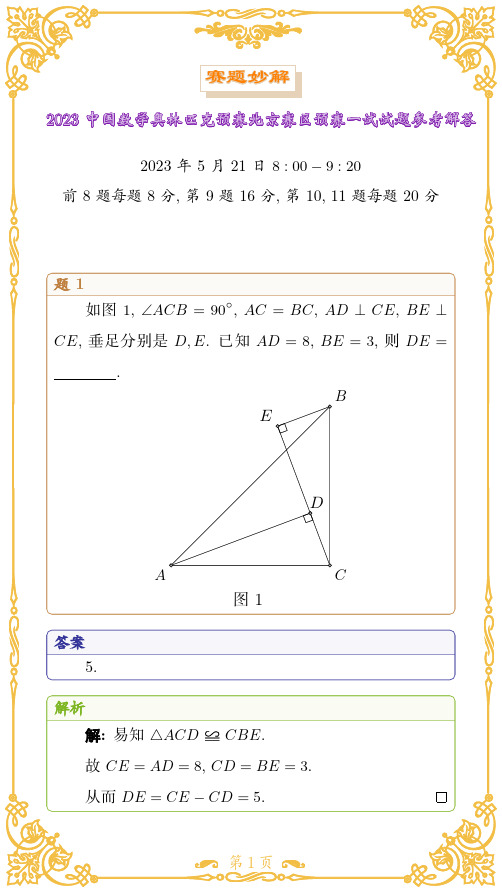
题1 如图 1, ∠ACB = 90◦, AC = BC, AD ⊥ CE, BE ⊥
2 3
=⇒ =⇒
f (3) = 1 或 3, f (3) = 2 或 3.
这样的 f 一共有 13 个.
第3页
题5
已知向量 |−→a | = 1,
−→ b
=
2,
且
−→a ,
−→ b
夹角为
120◦.
若 −→a + t−→b 与 t−→a + −→b 的夹角为锐角, 则 t 的取值范围是
.
答案
√
√
5 − 21 , 1 ∪ 1, 5 + 21 .
3 其它所有数均可选入.
故 |S|max = 2023 − 674 + 1 = 1350.
题3 已知函数 f (x) = sin ωx + sin 2x, 其中 ω ∈ N+, ω ⩽
2023. 若 f (x) < 2 恒成立, 则满足题设的常数 ω 的个数为 .
答案 1770.
解析
解: 只要考虑 sin 2x = 1 ⇐⇒ x =
√
3
=⇒ x2 = 3 − 2 2 (x > 0)
√6
√
=⇒ x =
2√− 1 , y =
2+1 √.
6
6
(n + m)2 = m2 + n2 + 2mn
= 1 + 4xy = 5 (n > 0, m > 0)
北京市高中数学知识应用竞赛初赛试题及参考答案

北京市高中数学知识应用竞赛初赛试题及参考答案
参考答案:
四、解要估算2000年18岁的人口数.由于2000年的统计资料我们还不能按集到,我们根据以往的统计数据进行推算.即根据2Q00年以前,如 1999年、1998年、…、1990年、…、等年份的数据进行推
算。
这里给出两种估算方法.一种是用年总人口数除以平均寿命,再根据人口分布情况进行调节,从而推算出18岁的人口数。
另一种我们以1998年的人口统计数据为依据,即根据1998年16岁的人口数来估算2000年18岁的人口数. 1998年中国人口统计年鉴中全国分年龄、性别的人口数表显示:1998年全国16岁人口总数为22010千人.全国分年龄、性别的死亡人口状况表显示:1998年16岁到17岁、17岁到18岁人口的死亡率分别为1.21%,1.16%。
假设每年的死亡率是个常数,则我们可以做如下的估算:
1999年17岁的人口数等于1998年16岁的人口数减去这些人成长到17岁的过程中死亡的人数.这些死亡人数由1998年16岁的人口数乘以17岁的死亡率得到.
即22010-22010×I.21%=21983(千人).
2000年18岁的人口数等于1999年17岁的人口数减去这些人成长到18岁的过程中死亡的人数。
这些死亡人数由1999年17岁的人口数乘以18岁的死亡率得到.
即21983-21983×1.16%o=21957(千人).
2000年18岁的人口数为21957千人.
注:从不同的资料中收集到的数据差异可能很大.只要说清楚资料的来源,并且数据处理方式合理,就可以认为答案正确,得满分.如果自己假设一些数据作为资料来源,最多给5分;若仅是数据处理方式不当,可以给7分。
2005-09-26。
2022年北京高中数学知识应用竞赛试题及参考答案
北京高中数学知识应用竞赛试题及参照答案试题1、(满分20分)汽车在行驶中,由于惯性作用,刹车后还要继续向前没行一段距离才干停住。
我们称这段距离为“刹车距离”。
刹车距离是分析事故一种重要因素。
在一种限速为40千米/时路段上,先后有A、B两辆汽车发生交通事故。
事故后,交通警察现场测得A车刹车距离超过12米,局限性15米,B车刹车距离超过11米,局限性12米。
又知A、B两种车型刹车距离S(米)与车速x(千米/时)之间有如下关系:如果仅仅考虑汽车车速因素,哪辆车应负责任?2.(满分20分)北京电视台每星期六晚播出《东芝动物乐园》,在这个节目中曾经有这样一种抢答题:小晰蜴体长15cm,体重15g,问:当小晰蜴长到体长为20cm时,它体重大概是多少(选用答案:20g,25g,35g,40g)?尝试用数学分析出合理解答。
3. (满分20分)受日月引力,海水会发生涨落,这种现象叫做潮汐。
在一般状况下,船在涨潮时驶进航道,接近船坞;卸货后落潮时返回海洋。
下面是某港口顺某季节每天时间与水深关系表:时刻水深(米)时刻水深(米)时刻水深(米)0:00 5.0 8:00 3.1 16:00 7.41:00 6.2 9:00 2.5 17:00 6.92:00 7.1 10:00 2.4 18:00 5.93:00 7.5 11:00 3.5 19:00 4.44:00 7.3 12:00 4.4 20:00 3.35:00 6.5 13:00 5.6 21:00 2.56:00 5.3 14:00 6.7 22:00 2.77:00 4.1 15:00 7.2 23:00 3.8(1)请在坐标纸上,根据表中数据,用持续曲线描出时间与水深关系函数图像;(2)一条货船吃水深度(船底与水面距离)为4米,安全条例规定至少要有1.5安全间隙(船底与洋底距离),问该船何时能进入港口?在港口能呆多久?(3)若某船吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米速度减少,那么该船在什么时间必要停止卸货,将船驶向较深水域?4.(满分20分)末,某商家迎来店庆,为了吸引顾客,采用“满一百送二十,连环送”酬宾方式,即顾客在店内花钱满100元(这100元可以是钞票,也可是奖励券,或两者合计),就送20元奖励券;满200元,就送40元奖励券,满300元,就送60元奖励券;...。
2020年北京第十五中学高二数学理测试试卷含解析

2020年北京第十五中学高二数学理测试试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知为第四象限的角,且()A.B.C. D.参考答案:A2. 等比数列{a n}前n项和S n中,S4=1,S8=3,则a17+a18+a19+a20=()A.20 B.14 C.16 D.18参考答案:C【考点】等比数列的前n项和.【分析】设等比数列{a n}的公比是q,由题意和等比数列的前n项和列出方程组,由等比数列的通项公式化简后求出q的值,再表示所求的式子求出答案.【解答】解:设等比数列{a n}的公比是q,∵S4=1,S8=3,∴,两式相除得q4=2,∴a17+a18+a19+a20=(a1+a2+a3+a4)q16=16,故选C.3. 已知物体的运动方程为s=t2+(t是时间,s是位移),则物体在时刻t=2时的速度为()A.B.C.D.参考答案:D因为,所以,故选D.4. 已知实数,执行如下图所示的程序框图,则输出的不小于55的概率为A. B. C. D.参考答案:A5. 下图是函数y=f(x)的的图像,则函数y=f(x)的导函数图像是()参考答案:D略6. 偶函数定义域为,其导函数是.当时,有,则关于的不等式的解集为()A.B.C.D.参考答案:C由题意构造函数所以函数F(x)在区间上,F(x)在区间上单调递减。
,当时,可变形为,即,即。
7. 下列方程表示的曲线中离心率为的是()A. B.C. D.参考答案:B8. 设F1,F2分别是双曲线 (a>0,b>0)的左、右焦点,若双曲线右支上存在一点P满足|PF2|=|F1F2|,且cos∠PF1F2=,则双曲线的渐近线方程为( )A.3x±4y=0 B.4x±3y=0 C.3x±5y=0 D.5x±4y=0参考答案:B略9. 已知椭圆C: +=1(a>b>0)的离心率为,四个顶点构成的四边形的面积为12,直线l与椭圆C交于A,B两点,且线段AB的中点为M(﹣2,1),则直线l的斜率为()A.B.C.D.1参考答案:C【考点】直线与圆锥曲线的综合问题.【分析】由椭圆C: +=1(a>b>0)的离心率为,四个顶点构成的四边形的面积为12,列出方程组求出a=2,b=,从而得到椭圆方程为,再由直线l 与椭圆C交于A,B两点,且线段AB的中点为M(﹣2,1),利用点差法能求出直线l的斜率.【解答】解:∵椭圆C: +=1(a>b>0)的离心率为,四个顶点构成的四边形的面积为12,∴,解得a=2,b=,∴椭圆方程为,∵直线l与椭圆C交于A,B两点,且线段AB的中点为M(﹣2,1),∴设A(x1,y1),B(x2,y2),则x1+x2=﹣4,y1+y2=2,又,两式相减,得:(x1﹣x2)(x1+x2)+(y1﹣y2)(y1+y2)=0,∴﹣(x1﹣x2)+(y1﹣y2)=0,∴直线l的斜率k==.故选:C.10. 下列函数为偶函数的是A、 B、 C、 D、参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. 已知椭圆的离心率,分别是椭圆的左、右顶点,点P是椭圆上的一点,直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1,则直线PA的斜率为.参考答案:【考点】椭圆的简单性质.【分析】由椭圆的离心率e====,求得a=2b,椭圆方程为:,整理得: =﹣,则tanα=,tanβ=,tanα?tanβ=?==﹣,由tanα+tanβ=1,tanα,tanβ是方程x2﹣x﹣=0的两个根,x=,则tanα=,即可求得直线PA的斜率.【解答】解:由题意可知:A(﹣a,0),B(a,0),P(x,y),椭圆的离心率e====,整理得:a=2b,∴椭圆方程为:,∴y2=,则=﹣,直线PA、PB的倾斜角分别为α、β,∴k PA=tanα=,k PB=tanβ=,∴tanα?tanβ=?==﹣,直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1,∴tanα,tanβ是方程x2﹣x﹣=0的两个根,解得:x=,∴直线PA的斜率k PA=tanα=,故答案为:.12. 函数的单调递增区间是__ ▲ _.参考答案:【知识点】余弦函数的性质【答案解析】解析:解:因为,由,所以所求函数的单调递增区间为.【思路点拨】一般求三角函数的单调区间,先把三角函数化成一个角的函数,再结合其对应的基本三角函数的单调区间与复合函数的单调性规律解答.13. 已知双曲线(>0,>0)的左右焦点分别为,是双曲线上的一点,且, 的面积为,则双曲线的离心率=________.参考答案:14. 给出下列命题:①“若xy=0,则x=0且y=0”的逆否命题为真命题. ②.x>2是x>1的必要不充分条件。
全国第十五届高等数学竞赛(非数学a类)试题

全国第十五届高等数学竞赛(非数学a类)试题全国第十五届高等数学竞赛是一场备受瞩目的数学盛事。
在这次竞赛中,许多脑力激荡的题目被呈现在了参赛者面前。
这些问题不仅考察了参赛者的数学知识水平,还考验了他们的数学思维能力和解决问题的能力。
本文将为大家介绍一些在这次竞赛中出现的题目,并对其解题思路进行分析。
首先,我们来看一道相对简单的题目。
题目如下:已知函数y=f(x),对任意实数x,满足f(x+2)=f(x),f(0)=1,且在区间[0,2]上是单调递减的,求函数f(x)的解析式。
首先,根据题目中的条件,我们可以得到如下的重要信息:1.函数f(x+2)=f(x)说明函数f(x)具有以2为周期的性质;2.函数在区间[0,2]上是单调递减的,说明在[0,2]外的任何区间上,f(x)都是单调不增的。
根据这两条信息,我们可以进行以下推理:1.对于区间[2,4],由函数f(x+2)=f(x)可知,f(x+4)=f(x+2)=f(x),即f(x)在[2,4]上是常数;2.对于区间[4,6],根据f(x)在[0,2]上是单调递减的,可以推知f(x)在[6,8]上是常数;3.依次类推,可以得到f(x)在[2n,2(n+1)]上是常数,其中n为正整数。
由此可知,函数f(x)可以表示为多个常数区间的并集。
接下来我们需要考虑如何确定这些常数区间的取值。
由于f(0)=1,因此我们可以先确定[0,2]上的取值。
根据题目中的条件,我们知道在[0,2]上f(x)是单调递减的,即f(0)=1,那么f(2)=a(其中a为常数)的可选范围应该是[0,1]之间的数。
在这个范围内,我们可以取任意一个值作为f(2)的取值,然后根据f(x+2)=f(x)的性质,推出f(4)、f(6)等值的取值范围。
这样,我们就可以得到[0,2]上的取值范围。
接下来,我们需要根据这个取值范围,来推导出其他常数区间的取值。
我们可以发现,f(x)在每个长度为2的区间上都是常数,而这些区间之间没有交集。
第十五届北京高中数学知识应用竞赛初赛试题及参考解答

网址:zxss.chinajournal.net.cn 电子邮箱:zxss@chinajournal.net.cn应用与建模第十五届北京高中数学知识应用竞赛初赛试题及参考解答(北京数学会普及委员会提供) 一、(满分20分)在测量课上,老师交给的任务是测量楼前旗杆的高度.小王灵机一动,想出了如下的测量法:请同学小李当“参照物”站在旗杆下,在离旗杆较近的地方,用手机拍下小李和旗杆的照片,如图所示.然后把照片放在计算机的屏幕上,量出旗杆有6.3个小李的高度,小李的身高为1.65米,于是得到旗杆的高度约为6.3×1.65=10.4(米).(1)你认为这种测量方法如何?如认为正确,请说明理由以及这种方法的优点;如认为有问题,请说明问题出在何处,结果偏大还是偏小?(2)你认为测量中如何做就能减少误差,得到正确的结果?参考解答:(1)这个方法虽然操作简单易行,但却是有问题的,这样得到的结果,与实际真实的结果相比,偏小.照相者离旗杆越近,误差越大.事实上,从这张照片上可以看到,同样大小的窗户框,其高度在照片上看,四层的只有一层的70%,这符合“近大远小”的视觉规律.因此旗杆下面的“一人高”和旗杆顶端的“一人高”对应的真实高度是不一样的,小王却把它当成一样的计算了.而顶端的“一人高”比下端的一人高所对应的实际尺寸要大,故小王的结果偏小了.(2)减少误差的思路有两种,一是远离旗杆,用长焦镜头拍照.这时摄影者到旗杆底部和到旗杆顶部的距离差会缩小,从而减少误差.但也要注意,距离远了,旗杆和人像也会变小,观察度量长度时的误差也会变大.二是考虑“近大远小”的变化率,比如可以根据图片量出,旗杆下端一米对应a毫米,旗杆顶端用国旗的实际宽度算出一米对应b毫米,可以认为整个旗杆平均一米等于图中的(a+b)/2毫米,于是用旗杆在照片上的总长度(毫米),除以(a+b)/2就是旗杆的真实高度(米).二、(满分20分)人们日常生产的产品———大到飞机、汽车,小到锅碗瓢盆———其表面通常是由一些光滑的曲面拼接而成的.在不同曲面的衔接处,我们往往也希望它是光滑的.如何能做到这一点呢?为简单起见,我们只考虑平面上两条光滑曲线在衔接点是光滑(没有尖角)的.1.给定平面上两条光滑的曲线,它们在某一点衔接.请你给出一个标准(即给出定义),用它来说明,在这个衔接点是光滑的.2.给定平面直角坐标系,在x=2左侧的曲线是函数y=x2-x+c(x≤2)的图像,其中c是参数,在x=2右侧的曲线是函数y=alnx(x≥2)的图像,其中a是参数.请你选择适当的参数a,c(即,选择x=2左右两侧适当的曲线)使得在x=2时上述两条曲线衔接,且在衔接点满足你所给出的光滑标准.参考答案:1.两条光滑曲线在衔接点是光滑的,就是衔接后的整条曲线在该点的切线存在.等价于原来的两条曲线在衔接点的切线重合,即两个函数在该点的导数相等.2.在直线x=2左侧的曲线y=x2-x+c(x≤2)的导数是2x-1,在x=2的值都是3,和参数值c无关.在x=2右侧的曲线y=alnx(x≥2)的导数是ax,在x=2的值是a2.根据刚刚给出的定义,为了保证两条曲线衔接后在衔接点处是光滑的,要求这两个值相等,即要求a2=3,解得a=6.选择在直线x=2右边的曲线为函数y=6lnx(x≥2)的图像.由于x=2时的函数值为6ln2,所以两条·14·网址:zxss.chinajournal.net.cn 电子邮箱:zxss@chinajournal.net.cn应用与建模曲线的衔接点为(2,6ln2).为使左边的曲线y=x2-x+c(x≤2)也过点(2,6ln2),则选取c,满足22-2+c=6ln2.解得c=6ln2-2.三、(满分20分)2011年8月7日,D22次列车(长春—北京动车组,经停站:长春—四平—铁岭—沈阳北—盘锦北—北戴河—滦县—北京)上的一位乘客记录下了列车运行全程的时刻与速度对应表如下(速度单位:千米/小时):时刻15:18 15:25 15:26 15:27 15:28速度0130 158 156 154时刻15:30 15:31 15:32 15:33 15:35速度156 162 161 152 160时刻15:36 15:37 15:38 15:40 15:41速度161 157 161 161 161时刻15:42 15:43 15:45 15:46 15:47速度161 161 152 161 161时刻15:48 15:50 15:51 15:52 15:53速度155 160 157 159 160时刻15:55 15:56 15:57 15:58 16:00速度156 156 160 161 156时刻16:01 16:04 16:05 16:06 16:08速度155 136 65 36 12时刻16:09 16:10 16:12 16:13 16:15速度0043 77 117时刻16:16 16:17 16:18 16:20 16:21速度126 156 155 144 156时刻16:22 16:23 16:25 16:26 16:27速度156 155 156 156 156时刻16:28 16:30 16:31 16:32 16:33速度160 160 161 161 158时刻16:35 16:36 16:37 16:38 16:40速度161 155 161 161 161时刻16:41 16:42 16:43 16:45 16:46速度156 156 156 156 156时刻16:47 16:48 16:50 16:56 16:57速度157 156 146 104 108时刻16:59 17:0017:02 17:03 17:04速度35 092 109 161时刻17:06 17:07 17:08 17:09 17:11速度152 163 163 158 163时刻17:12 17:13 17:14 17:16 17:17速度158 162 163 98 124时刻17:18 17:19 17:21 17:22 17:23速度163 136 124 157 155时刻17:24 17:27 17:28 17:30 17:31速度155 106 56 41 43时刻17:32 17:33 17:35 17:36 17:37速度10 0034 40时刻17:38 17:39 17:41 17:42 17:43速度46 54 124 155 157时刻17:44 17:46 17:47 17:48 17:49速度158 184 220 238 239时刻17:51 17:52 17:53 17:54 17:56速度240 238 238 240 240时刻17:57 17:58 17:59 18:01 18:02速度238 239 236 238 238时刻18:03 18:04 18:06 18:07 18:09速度240 239 239 224 239时刻18:11 18:12 18:13 18:14 18:16速度238 239 239 235 239时刻18:17 18:21 18:22 18:23 18:25速度239 108 66 25 0时刻18:26 18:27 18:29 18:30 18:31速度62 91 154 199 230时刻18:32 18:34 18:35 18:36 18:37速度239 239 227 216 227时刻18:39 18:40 18:42 18:44 18:45速度238 237 216 216 218时刻18:46 18:47 18:49 18:50 18:51速度218 217 218 223 214时刻18:52 18:54 18:55 18:56 18:57速度218 236 240 216 213时刻18:59 19:0019:01 19:02 19:04速度203 238 239 237 239时刻19:05 19:06 19:07 19:09 19:10速度239 238 239 239 239·24·网址:zxss.chinajournal.net.cn 电子邮箱:zxss@chinajournal.net.cn应用与建模时刻19:11 19:47 19:48 19:50 19:51速度239 163 54 34 4时刻19:52 19:53 19:54 19:55 19:57速度00000时刻19:58 19:59 20:01 20:02 20:03速度038 68 72 155时刻20:04 20:06 20:07 20:08 20:09速度159 158 164 164 164时刻20:11 20:12 20:13 20:14 20:16速度161 158 158 164 164时刻20:17 20:18 20:19 20:21 20:22速度159 165 164 159 158时刻20:25 20:27 20:28 20:30 20:31速度117 97 38 027时刻20:33 20:34 20:35 20:36 20:38速度100 106 107 153 164时刻20:39 20:40 20:41 20:43 20:44速度147 163 148 153 159时刻20:45 20:46 20:48 20:49 20:50速度163 163 158 151 154时刻20:51 20:53 20:54 20:55 20:56速度163 164 163 159 165时刻20:58 20:59 21:0021:01 21:03速度203 204 204 204 204时刻21:04 21:05 21:06 21:08 21:09速度201 204 204 200 203时刻21:10 21:12 21:13 21:14 21:15速度204 204 203 186 198时刻21:16 21:18 21:19 21:20 21:21速度188 204 204 204 204时刻21:23 21:24 21:25 21:26 21:28速度204 202 204 203 204时刻21:29 21:30 21:31 21:33 21:34速度204 203 200 136 118时刻21:35 21:36 21:38 21:39 21:40速度105 119 119 104 109时刻21:41 21:45 21:46 21:47 21:49速度86 114 70 39 38时刻21:50 21:51 21:52速度31 27 14根据这张数据表,请你回答下列问题:(1)D22列车运行的总路程大概是多少?借助网络查阅一下具体的数值,如果有误差,请分析一下原因.(2)19:11~19:47时间段内列车没有显示数据,因此数据缺失.请推算一下,此间的平均速度.(3)画出列车在不同时间运行的速度曲线,描述列车全程的运行动态.参考解答:(1)设时间为t,t时刻的速度为v(t),D22次列车经停站为长春、四平、铁岭、沈阳北、盘锦北、北戴河、滦县、北京,将这些站分别记作A,B,C,D,E,F,G,H,相邻经停站间的距离分别记为|AB|,|BC|,|CD|,|DE|,|EF|,|FG|,|GH|.方法1:将总路程分为七段,求出每一段内记录下的所有m个速度值的和,在用这个和除以m得到商,把这个值当做这一段的平均速度.这七段的平均速度分别为:142.9189,138.2286,120.4800,186.3421,196.0732,130.6087,153.0313.再根据记录中这七段前后的两个时刻得到每一段行车用时,进而得到这七段的距离分别为|AB|=128.6270,|BC|=115.1905,|CD|=66.2640,|DE|=155.2851,|EF|=284.3061,|FG|=69.6580,|GH|=209.1427.于是D22次列车运行的总路程为d1=1028.5千米.方法2:(积分的思想),将所给相邻两个时刻间作为一小段时间,用这小段时间末端的速度当作这小段区间上的平均速度,即设区间[t(i),t(i+1)]上的平均速度为v(i+1),由此计算出D22次列车运行的总路程为d2=1053.9千米.方法3:(积分的思想),将所给相邻两个时刻间作为一小段时间,用这小段时间前端的速度当作这小段区间上的平均速度,即设区间[t(i),t(i+1)]上的平均速度为v(i),由此计算出D22次列车运行的总路程为d3=1043.2千米.方法4:(积分的思想),将所给相邻两个时刻间作为一小段时间,用区间端点的平均速度当作这小段区间上的平均速度,即设区间[t(i),t(i+1)]上的平均速度为v(i)+v(i+1)2,由此计算出D22次列车运行·34·网址:zxss.chinajournal.net.cn 电子邮箱:zxss@chinajournal.net.cn应用与建模的总路程为d4=1048.6千米.网络数据:长春到北京的火车距离为d=1003千米.距离误差百分比定义为|di+d|d.上述四种算法的距离误差百分比分别为0.0254,0.0508,0.0401,0.0454.误差原因分析:数据的误差可能来源于数据缺失,另一个重要原因是所估计的平均速度的误差使得结果出现较大误差,速度区间的划分是比较关键的因素.误差可能的原因为平均速度的假设过于粗糙,间隔大的数据对结果有影响.(2)我们选用第一种距离估算方法,来研究19:11~19:47时间段内的缺失数据,假设缺失数据是导致总体距离误差的主要因素.列车实际距离为精确的1003千米,按照第一种算法可估算出距离为1028.5千米,多走了25.5千米.该时间段经历时间为36分钟.用第一种算法估计的平均速度为196.0732千米/小时,于是知道这段缺失数据对应的更为准确的平均速度v满足(196.0732-v)·36/60=25.5,解得v=147.5732千米/小时.由此看出在这个时间段内有减速现象更为准确.由第二种估计方法,得此段的平均速度v满足(163-v)×36/60=1053.9-1003,解得v=78千米/小时.由第三种估计方法估计此段的平均速度v满足(239-v)×36/60=1043.2-1003,解得v=172千米/小时.由第四种估计方法估计此段的平均速度v满足((163+239)/2-v)×36/60=1048.6-1003,解得v=125千米/小时.(3)时间-速度图像如图1:1列车运行过程中因为有停靠站,共有七段运行过程.在前三段基本为一个较慢的恒速:165千米/小时;第三、四段运行在较高的速度上:239千米/小时;第六段和第七段的大约前四分之一又回到了较慢的165千米/小时;第七段的中间时段(约占第七段的一半)的速度大约是204千米/小时;第七段的后四分之一是逐渐减速.图2四、(满分20分)AOBD是从密度均匀、薄厚一致、半径为r的圆形纸板上剪下来的开角为2θ的扇形纸板,OD为对称轴.已知这块扇形纸板的重心Csec位于距离圆心O为2r3sinθθ的位置.请你确定弓形纸板ABD的重心位置,即给出一个用r和θ表示的数学模型.参考解答:由图可知,扇形OADB是关于OD对称的.因此扇形的重心应位于OD上,则重心在距离点O为xsec=2r3sinθθ的点Csec处.扇形OADB可以分为三角形OAB和弓形ADBE两部分.又知三角形OAB的重心位于对称轴OD上,与点O的距离为xtei=23rcosθ的点Ctri处.显然弓形的重心Cseg也应该在半径OD上.设该点据圆心O点的距离为xseg.根据假设,可知这三个重心的位置应与这个扇形以及组成它的三角形和弓形的面积有关.有关系Atri(Csec-Ctri)=Aseg(Cseg-Csec),或者有Atri(xsec-xtri)=Aseg(xseg-xsec).式中Atri、Aseg分别表示三角形和弓形的面积.显然如果用Asec表示扇形的面积,应该有Asec=Atri+Aseg.由此,前面的式子就可以改写成Aseg·xseg=Asec·xsec-Atri·xtri,由此解得xseg=Asecxsec-AtrixtriAseg,·44·网址:zxss.chinajournal.net.cn 电子邮箱:zxss@chinajournal.net.cn应用与建模不难算出Asec=πr2θ/π=r2θ,Atri=r2sinθcosθ.由此可得Aseg=r2(θ-sinθcosθ).代入上面的公式可以算出xseg=2r3sin3θθ-sinθcosθ.五、(满分20分)生物学家认为,正在休息时的温血动物体内消耗的能量就是为了保持其体温.体内消耗的能量E与通过心脏的血流量Q成正比,体重与体积成正比.已知一些动物的体重与脉搏率如表1所示:表1 一些动物的体重和脉搏率动物名体重(克)脉搏率(心跳次数/分钟)鼠25 670大鼠200 420豚鼠300 300兔2000 205小狗5000 120大狗30000 85羊50000 70马450000 38 (1)请你根据上面提供的生物学家的认识,给出血流量与体重关系的数学模型.(2)从表1可以看到,体重W越轻的动物脉搏率f越高.请通过各量之间的比例关系,建立脉搏率与体重关系的数学模型.(3)根据表1,作出动物的体重和脉搏率的散点图,验证你建立的数学模型.名词解释:血流量Q是单位时间流过的血量,脉博率f是单位时间心跳的次数.假设:心脏每次收缩挤压出来的血量q与心脏大小成正比,动物的心脏大小与其体积大小成正比.参考解答:(1)因为动物体温通过身体表面散发热量.表面积越大,散发的热量越多,为保持体温需要的能量越大,所以动物体内消耗的能量E与其表面积S成正比.即E=p1S.又已知动物体内消耗的能量E与通过其心脏的血流量Q成正比,即E=p2Q.因此得Q=pS.另一方面,因为体积V与体重W成正比,可表为V=r1W.而表面积S大约与体积V的三分之二次方成正比,可表为S=r2V23.因此得S=rW23.所以血流量与体重关系模型:Q=k·W23.(2)根据定义,有f=Qq.又根据假设,有q=cW.再由(1)的结论Q=k·W23和f=Qq,得f=Qq=kW23cW,也就是f=kW13.这个脉搏率与体重关系的模型说明,温血动物的体重越大,脉搏率越底.脉搏率与体重的三分之一次方成反比.(3)表1的数据基本上反映了这个反比例的关系.图3是原始数据的散点图,图4是以ln(W)和ln(f)为坐标的散点图.图3 脉搏率f与体重W的散点图图4 对数坐标下脉搏率f与体重W的散点图·54·。
2023全国高中数学联合竞赛加试卷及参考答案
2023年全国高中数学联合竞赛加试卷习题及参考答案一.(本题满分40分)如图,ABC 的外心为O ,在边AB 上取一点D ,延长OD 至点E ,使得,,,A O B E 四点共圆.若2,3,4,5OD AD BD CD ,证明:ABE 与CDE 的周长相等.证明:由,,,A O B E 共圆得AD BD OD DE ,又2,3,4OD AD BD ,所以6DE . ……………10分由OA OB 得OAD OEA ,故OAD OEA ∽,故OA OE AEOD OA AD. 所以22(26)16OA OD OE ,得4OA .进而26OEAE AD AD OA.同理可得OBD OEB ∽ ,28BE BD . ……………20分 由于22OC OA OD OE ,故OCD OEC ∽. ……………30分因此EC OC CD OD. 由2,8OD OE OD DE 知4OC ,又5CD ,故210EC CD . 计算得76821AB AE BE ,561021CD DE EC ,即ABE 与CDE 的周长相等. ……………40分二.(本题满分40分)设,m n 是给定的整数,3m n ≥≥.求具有下述性质的最小正整数k :若将1,2,,k 中的每个数任意染为红色或者蓝色,则或者存在m 个红色的数12,,,m x x x (允许相同),满足121m m x x x x -+++< ,或者存在n 个蓝色的数12,,,n y y y (允许相同),满足121n n y y y y -+++< .C E O A BD C EO A B D解:答案是1mn n -+.若k mn n =-,将1,2,,1n - 染为蓝色,,1,,n n mn n +- 染为红色.则对任意m 个红色的数12,,,m x x x ,有121(1)m m x x x n m x -+++≥-≥ ,对任意n 个蓝色的数12,,,n y y y ,有1211n n y y y n y -+++≥-≥ ,上述例子不满足要求.对k mn n <-,可在上述例子中删去大于k 的数,则得到不符合要求的例子.因此所求1k mn n ≥-+. ………………10分下面证明1k mn n =-+具有题述性质.假设可将1,2,,1mn n -+ 中的每个数染为红色或蓝色,使得结论不成立. 情形一:若1是红色的数,则红色的数均不超过1m -,否则可取一个红色的数m x m ≥,再取1211m x x x -==== ,则11m m x x x -++< ,与假设矛盾. ………………20分故,1,,1m m mn n +-+ 均为蓝色的数,此时取121,1n n y y y m y mn n -=====-+ ,有121(1)11n n y y y m n mn m mn n y -+++=-<-+≤-+= ,(*) 与假设矛盾. ………………30分情形二:若1是蓝色的数,则同情形一可知蓝色的数均不超过1n -,故,1,,1n n mn n +-+ 均是红色的数.此时取121,1m m x x x n x mn n -=====-+ ,与(*)类似,可得矛盾.故1k mn n =-+时结论成立.综上,所求最小的正整数1k mn n =-+. ………………40分三.(本题满分50分)是否存在2023个实数122023,,,(0,1]a a a ,使得20236120231110i j i j k ka a a证明你的结论.解:记20231202311i j i j k kS a a a. 假设存在122023,,,(0,1]a a a ,使得610S . 不妨设12202301a a a ,则将12023i j i j a a去掉绝对值后,k a 的系数为22024k ,从而202311(22024)k k kS k a a. ……………10分 当11011k 时,由基本不等式知 11(22024)(20242)220242k k kkk a k a k a a. ……………20分当10122023k 时,由于1()(22024)k f x k x x在(0,1]上单调增,故1(22024)(1)22025k k kk a f k a. 从而1011202311012220242(22025)k k S k k1011110101012202422k k k. ……………30分注意到202422(20242)2202444k k k k ,故61010101210114410S ,这意味者不存在122023,,,a a a 满足条件. ……………50分四.(本题满分50分)设正整数,,,a b c d 同时满足: (1) 2023a b c d +++= ; (2) ab ac ad bc bd cd +++++ 是2023的倍数; (3) abc bcd cda dab +++是2023的倍数. 证明:abcd 是2023的倍数. 证明:易知22023717=⨯. 首先,由(1),(3)知2()()()()() a b a c a d a a b c d abc bcd cda dab +++=+++++++是2023的倍数,故,,a b a c a d +++中至少有一个是 7的倍数. ……………10分由对称性,不妨设a b +是7的倍数,则) 2023( c d a b +=-+也是7的倍数,()()ac ad bc bd a b c d +++=++也是7的倍数,故结合(2)知ab cd +是7的倍数,因此22) (()()a c a a b c c d ab cd +=+++-+也是 7的倍数.又平方数除以 7的余数只能是0,1,2,4,因此22,a c 只能同时是 7的倍数, 这表明,,,a b c d 都是 7的倍数. ………………20分同上面分析可知:) ()()( a b a c a d +++是217的倍数,故或者其中有一个因子是217的倍数,或者其中有两个因子是 17的倍数.如果有一个因子是217的倍数,不妨设a b +是217的倍数,结合 ,a b 都是7的倍数知,a b +是 22023717=⨯的倍数,但这与2023a b c d +++=及,,,a b c d 是正整数相矛盾! ………………30分因此,,a b a c a d +++中至少有两个是17的倍数.不妨设,a b a c ++都是17的倍数,那么b d +也是17的倍数,由2()()(2)()ab ac ad bc bd cd a b d b d c a a b a a c a +++++=+++++++-知,22a 是17的倍数,故a 是17的倍数.因此,,,a b c d 都是17的倍数,这就说明了abcd 是44717⨯的倍数,也就是2023的倍数.………………50分。
第十三届北京高中数学知识应用竞赛决赛试题及参考解答

第十三届北京高中数学知识应用竞赛决赛参考解答2010年3月21日1.(满分16分) 当你站在一面镜子前面时,镜中会出现你的影像,并且影像与你的形象是对称的,你的左侧将是影像的右侧。
现在,房间的一个墙角两侧的墙上各有一面大镜子相邻镶嵌(如图中双线的部位)。
如果你站在这两面镜子前面,在镜中会有几个你的影像?它们各处在什么位置?影像的形象与你是什么关系?当你在镜子前面运动时,你的影像如何运动?解:设我的形象为A ,镜成像的结果如下图。
一共有三个镜面影像。
A 1为A 关于镜面OX 的影像,A 2为A 关于镜面OY 的影像,A 3是A 关于镜面二次成像的结果,也就是说,A 3是影像A 1关于镜面OY 的影像,也是A 2关于镜面OX 的影像。
A 1与A 2分别是A 关于OX 和OY 对称的像。
A 3与A 1、A 2的形象是对称的,是 A 关于点O中心对称的。
从而它与A 的形象是一致的。
(10)分当A沿着OX 的方向移动时,A 1将会与A同行,A 2将会远离A 而去,A 3将作与A 反方向的运动。
使得A ,O 和A 3始终保持在同一条直线上。
……………………………………… 16分2.(满分16分) 内轮差是车辆转弯时的前内轮的转弯半径与后内轮的转弯半径之差。
车辆转弯时,前轮转向,前、后车轮的运动轨迹不重合,后轮轨迹会向所转方向的内侧偏移,产生内轮差。
车辆的前后轴距越长,偏移量越大,即内轮差越大。
行车中如果只注意前轮X Y A A 3 A 1 A 2O 前内轮的转弯轨迹 后内轮的转弯轨迹能够通过而忘记内轮差,就可能造成后内轮驶出路面或与其他物体碰撞的事故。
右图中可见一辆货车右转弯时,前、后内轮的轨迹。
如果汽车的前后轴距为5米,右转弯时前轮的转向角为30︒,求右前轮和右后轮的内轮差。
并依此对站在马路拐弯处的行人提出安全建议。
解:如图:设前、后内轮的转弯半径分别为x 和y ,因为y x = cos30︒,即y = x cos30︒,又x 2− y 2=25,得x 2(1−cos 230︒)=25,解得x =10,y =8.66,前后轮差为x −y =10−8.66=1.33(m)。
2022全国高中数学竞赛真题及答案详解

2022全国高中数学竞赛真题及答案详解高中数学竞赛一直以来都是对学生数学能力的高难度挑战,2022 年的全国高中数学竞赛也不例外。
接下来,让我们一起深入剖析这次竞赛的真题及详细答案。
首先来看第一道题,这是一道关于函数性质的题目。
已知函数 f(x)= x³ 3x + 1,求其在区间-2, 2上的最大值和最小值。
对于这道题,我们先对函数求导,f'(x) = 3x² 3,令 f'(x) = 0,解得 x = ±1。
然后分别计算函数在端点和极值点处的值,f(-2) =-1,f(-1) = 3,f(1) =-1,f(2) = 3。
所以,函数在区间-2, 2上的最大值为 3,最小值为-1。
再看第二道题,它是一道几何证明题。
在三角形 ABC 中,AD 是角A 的平分线,且 BD : DC = 2 : 1。
求证:AB : AC = 2 : 1。
这道题我们可以利用角平分线定理来解决。
因为 AD 是角 A 的平分线,所以根据角平分线定理,AB/AC = BD/DC = 2/1,从而得证。
接下来是第三道题,是一个数列问题。
已知数列{aₙ}满足a₁=1,aₙ₊₁= 2aₙ + 1,求数列{aₙ}的通项公式。
我们可以通过构造等比数列来求解。
将等式两边同时加 1,得到aₙ₊₁+ 1 = 2(aₙ + 1),所以数列{aₙ + 1}是以 2 为首项,2 为公比的等比数列。
根据等比数列通项公式可得 aₙ + 1 =2ⁿ,所以 aₙ =2ⁿ 1。
然后是第四道题,这是一道关于复数的题目。
已知复数z =1 +i,求 z 的模和辐角。
复数 z = 1 + i 的模为|z| =√(1²+ 1²) =√2,辐角为 arctan(1/1) =π/4。
接着看第五道题,是一个概率问题。
从 1,2,3,4,5 这五个数字中随机抽取三个数字,求这三个数字能构成等差数列的概率。
总的组合数为 C₅³= 10 种。
第十五届NOC 应用数学赛项 竞赛细则

《新课程标准》还指出:“数学课程应注重信息技术与数学课程的整合, 有利于学生认识数学的本质,鼓励学生运用计算机、计算器等进行探索和 发现。” 为了及时反映这种变化,落实《新课程标准》的精神,第十五届NOC 活动中将继续应用数学竞赛这一赛项。这将有助于激发学生学习数学的兴 趣,有利于增强学生的数学应用意识,有利于扩展学生的视野,促进学生 数学素养的提高。
2.内容:
图2
3.运用的数学知识:
4.个人信息:
图3
现场组织形式
组织者 地方选拔赛 全国总决赛 地方组委会 全国组委会 比赛地点 省会、地市 青岛
三、竞赛辅导课程
《NOC应用数学竞赛课程》
内容:1、网络课程(10课时) 微视频 2、竞赛模拟题( 5套) 3、HP Prime 图形计算器
现场决赛环节
试题要求:
从给出的5道题中,任选3道进 行解答。必要的过程记录于答 题纸上,且在图形计算器上保 留做好的APP。 答辩时展示做好的APP。
样题(高中):
古今中外,许多人致力于圆周率的研究与计 算。为了计算出圆周率的越来越精确的近似 值,一代代的数学家为这个神秘的数贡献了 无数的时间与心血。我国东汉的数学家刘徽 利用“割圆术”计算圆的面积及圆周率π;韦 达用阿基米德的方法,算出 3.1415926535<n<3.1415926537; 现代数学家用 计算机产生随机数来模拟正方形中的撒芝麻 的实验来估计π的值等等。你能试着计算圆周 率吗?可以采用上述的方法,也可以自行探 索新的方法。(参考程序:电子表格,编程)
一、参赛范围
(一)参赛组别:小学组、初中组、高中组(含中职)。
2021年北京第15中学高三数学理测试题含解析

2021年北京第15中学高三数学理测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知全集且则等于( ) A.B.C.D.参考答案:B2. 如果执行如图所示的框图,输入,则输出的数等于()A.B.C.D.参考答案:A3. 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是 ()A.3B. C.2 D.参考答案:D4. 已知,则A. B. C.D.参考答案:B5. 已知0<c<1,a>b>1,下列不等式成立的是()A.c a>c b B.a c<b c C.D.log a c>log b c参考答案:D【考点】不等式比较大小;不等式的基本性质.【分析】根据题意,依次分析选项:对于A、构造函数y=c x,由指数函数的性质分析可得A错误,对于B、构造函数y=x c,由幂函数的性质分析可得B错误,对于C、由作差法比较可得C错误,对于D、由作差法利用对数函数的运算性质分析可得D正确,即可得答案.【解答】解:根据题意,依次分析选项:对于A、构造函数y=c x,由于0<c<1,则函数y=c x是减函数,又由a>b>1,则有c a>c b,故A错误;对于B、构造函数y=x c,由于0<c<1,则函数y=x c是增函数,又由a>b>1,则有a c>b c,故B错误;对于C、﹣==,又由0<c<1,a>b>1,则(a﹣c)>0、(b﹣c)>0、(b﹣a)<0,进而有﹣<0,故有<,故C错误;对于D、log a c﹣log b c=﹣=lgc(),又由0<c<1,a>b>1,则有lgc<0,lga>lgb>0,则有log a c﹣log b c=﹣=lgc()>0,即有log a c>log b c,故D正确;故选:D.【点评】本题考查不等式比较大小,关键是掌握不等式的性质并灵活运用.6.已知是第二象限角,且,则()A. B. C. D.参考答案:答案:C7. 已知成等差数列,且,则的取值范围是()A. B. C. D.参考答案:,即,,所以,解得,故选A.考点:1.等差数列的性质;2.基本不等式.【方法点睛】本题主要考察了基本不等式,属于基础题型,根据条件求的取值范围,所以涉及消掉另外两个量,所以根据条件,这样就消掉另外两个量了,常用的基本不等式和重要不等式包括,,.8. 已知等比数列{a n}的前n项和为S n,若S2n=4(a1+a3+a5+…+a2n-1), a1a2a3=27,则a6=( ) A.27 B.81C. 243 D.729参考答案:C∵a1a2a3=a=27,∴a2=3,∵S2n=4(a1+a3+a5+…+a2n-1),∴S2=4a1,∴a1+a2=4a1,∴a2=3a1=3,∴a1=1,∴,∴a6=a1q5=35=243.9. 已知全集,集合,则() A. B. C. D.参考答案:B10. 已知平面向量,,且,则()A.B.C.D.参考答案:略二、填空题:本大题共7小题,每小题4分,共28分11. 若复数满足:,则在复平面内,复数z对应的点坐标是________.参考答案:(4,-2)略12. 我市某小学三年级有甲、乙两个班,其中甲班有男生30人,女生20人,乙班有男生25人,女生25人,现在需要各班按男、女生分层抽取20%的学生进行某项调查,则两个班共抽取男生人数是 .参考答案:11【考点】B3:分层抽样方法.【分析】根据分层抽样的定义即可求出.【解答】解:甲班有男生30人,乙班有男生25人,女生25人,现在需要各班按男生分层抽取20%的学生,故有30×20%+25×20%=6+5=11, 故答案为:11.【点评】本题考查了分层抽样的问题,属于基础题.13. 若关于x 的不等式+-≥0对任意n∈N*在x∈(-∞,λ]上恒成立,则实常数λ的取值范围是________.参考答案:略14. 已知,且, 则▲ .参考答案:15. .已知,那么的值为 .参考答案:16. 已知函数,设集合,从集合P 和Q 中随机地各取一个分数分别作为a 和b ,则函数在区间()上为增函数的概率为 。
2024-2025学年北京十五中高一上学期期中数学试题及答案

2024北京十五中高一(上)期中数 学2024.11本试卷共6页,150分.考试时长120分钟.考生务必将答案答在答题卡和答题纸上,在试卷上作答无效.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集,{|23},{|1U A x x B x x ==−≤≤=<−R 或4}x >,则集合()U A B =( ) A. {}|21x x −−<≤B. {13}x x −≤≤∣C. {3x x ≤∣或4}x ≥D. {24}x x −≤<∣ 2. 方程组2202x y x y +=⎧⎨+=⎩的解集是( ) A. ()(){}1,1,1,1−−−B. ()(){}1,1,1,1−C. ()(){}1,1,1,1−−D. ∅ 3. 命题“2[1,),0x x x ∀∈+∞−≥”的否定是( )A. 2[1,),0x x x ∀∈+∞−<B. 2(,1),0x x x ∀∈−∞−≥C. 2[1,),0x x x ∃∈+∞−<D. 2[1,),0x x x ∃∈+∞−≥ 4. 下列命题正确的是( )A. 若a b >,则22ac bc >B. 若,a b c d >>,则ac bd >C. 若22a b >,则a b >D. 若,0a b ab >>,则11a b< 5. 函数f (x )=x 3﹣2x ﹣3一定存在零点的区间是( ) A. (2,+∞) B. (1,2)C. (0,1)D. (﹣1,0) 6. 已知命题“R x ∃∈,使212(1)02x a x +−+≤”是假命题,则实数a 的取值范围是( ) A. (,1)∞−−B. (1,3)−C. (3,)−+∞D. (3,1)−7. 设奇函数()f x 在(0,)+∞上为减函数,且(1)0f =,则不等式()0x f x ⋅<的解集为( )A. (1,0)(1,)−+∞B. (,1)(0,1)−∞−C. (1,0)(0,1)−D. (,1)(1,)−∞−+∞8. 已知函数()())210,01,x x f x x ⎧−−≤≤⎪=<≤,则下列图象错误的是( ) A. B.C. D.9. 在函数①1(0)y x x x=+≠,②43(1)1y x x x =+−>−,③42(0)y x x x =−−−<,④)y x =∈R 中,以2为最小值的函数的序号为( ) A. ①② B. ②③ C. ②④ D. ③④10. 设函数()||f x x x bx c =++①当0c =时,()f x 为奇函数;②函数()f x 的图像关于点(0,)c 对称;③当0b =时,存在c ∈R ,使得()f x 有两个不同的零点;④存在,b c ∈R ,使得函数()f x 有三个不同的零点.其中,真命题的个数为( )A. 1B. 2C. 3D. 4第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分.11.函数12y x =−的定义域是______. 12. 不等式2101x x −≤+的解集是________. 13. 已知“||1x a −≤”是“2230x x −−≤”的充分不必要条件,则实数a 的取值范围为______.14. 已知函数27,1(),1x ax x f x a x x⎧−−−≤⎪=⎨>⎪⎩,且当12x x ≠时,总有()()21210f x f x x x −>−,则实数a 的取值范围是______.15. 设函数()()2,121,1x a x f x a x x −+≤⎧⎪=⎨−−+>⎪⎩若2a =,则()f x 的单调递增区间是___________;若()f x 的值域为(),−∞+∞,则a 的取值范围是_____________.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16. 已知全集U =R ,集合{}2230,{}A xx x B x x a =+−≥=≤∣∣,其中a ∈R . (1)化简集合A ,并求集合U A ;(2)若2a =,求集合A B ⋂;(3)若x ∀∈R ,都有x A ∈或x B ∈,求实数a 的取值范围.17. 已知函数2()f x x ax b =++,满足下列两个条件条件①:(0)4f =;条件②:,(1)(1)x f x f x ∀∈+=−R ;(1)求a ,b 的值;(2)已知函数2()()(23)6g x f x m x m =+++−有两个不同的正数零点12,x x .(ⅰ)求m 的取值范围;(ⅱ)若121x x −=,求m 的值.18. 已知函数2(),01ax f x a x =≠+. (1)判断函数()f x 是否具有奇偶性,并证明;(2)当0a >时,判断()f x 在区间[]0,1上的单调性,并利用函数单调性的定义证明;(3)当1a =时,求函数()f x 的值域.19. 某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族S 中的成员仅以自驾或公交方式通勤,分析显示:当S 中%(0100)x x <<的成员自驾时,自驾群体的人均通勤时间为()30,0301800290,30100x f x x x x <≤⎧⎪=⎨+−<<⎪⎩(单位:分钟),而公交群体的人均通勤时间不受x 影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)当x 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)设该地上班族总人数为()*n n ∈N ,求该地上班族S 的人均通勤时间()g x 的表达式;并求()g x 的最小值,指明相应的x 的值.20. 已知二次函数2()3f x x ax =−+,且,()(2)x f x f ∀∈≥R .(1)求实数a 的值,并求函数()y f x =在区间[,1]()t t t +∈R 上的最小值()g t .(2)求关于x 的不等式2()(1)(3)2,f x m x m x m ≤−+−+∈R 的解集. 21. 如果()f x 是定义在R 上的函数,且对任意的x ∈R ,都有()()f x f x −≠−,则称该函数()f x 是“L −函数”.(1)分别判断下列函数:①21y x =−;②223y x x =−++;③211y x =+是否为“L −函数”? (直接写出结论)(2)若函数2()(1)1f x ax a x =−+++是“L −函数”,求实数a 的取值范围; (3)设“L −函数”()21,,x x A f x x x B ⎧+∈=⎨∈⎩在R 上单调递增,求所有可能的集合A 与B .参考答案第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 【答案】B【分析】根据题意利用补集和交集运算求解即可.【详解】因为全集,{|23},{|1U A x x B x x ==−≤≤=<−R 或4}x >,则{}|14U B x x =−≤≤,所以(){}|13U A B x x =−≤≤.故选:B.2. 【答案】C【分析】直接求出方程组的解,再用列举法表示即可.【详解】由2202x y x y +=⎧⎨+=⎩,消去x 得222y =,解得1y =±,所以方程组的解为11y x =⎧⎨=−⎩或11y x =−⎧⎨=⎩, 所以方程组2202x y x y +=⎧⎨+=⎩的解集()(){}1,1,1,1−−. 故选:C3. 【答案】C【分析】根据全称命题的否定式特称命题分析判断.【详解】命题“2[1,),0x x ∀∈+∞−≥”的否定是“2[1,),0x x x ∃∈+∞−<”.故选:C.4. 【答案】D【分析】对于ABC :举反例说明即可;对于D :根据不等式的性质分析判断.【详解】对于选项A :例如0c =,则220ac bc ==,故A 正确;对于选项B :例如1,1a c b d ====−则1ac bd ==,故B 错误;对于选项C :例如1,0a b =−=,满足22a b >,但a b <,故C 错误;对于选项D :若,0a b ab >>,则10ab >, 可得a ⋅1ab >b ⋅1ab ,即11a b<,故D 正确; 故选:D.5. 【答案】B 【分析】求出(1)(2)0f f <,即得解.【详解】由题得(1)1234,(2)8431f f =−−=−=−−=,所以(1)(2)0f f <,因为函数是R 上的连续函数,故选B【点睛】本题主要考查零点存在性定理,意在考查学生对这些知识的理解掌握水平.6. 【答案】B 【分析】由题可得212(1)02x a x +−+>恒成立,由Δ0<即可求出. 【详解】因为命题“R x ∃∈,使212(1)02x a x +−+≤”是假命题, 所以212(1)02x a x +−+>恒成立,所以21Δ(1)4202a =−−⨯⨯<,解得13a −<<, 故实数a 的取值范围是(1,3)−.故选:B .7. 【答案】D【分析】根据单调性和奇偶性分析()f x 的符号,进而解不等式即可.【详解】因为()f x 在(0,)+∞上为减函数,且(1)0f =,当01x <<时,()0f x >;当1x >时,()0f x <;又因为()f x 为奇函数,可得当10x −<<时,()0f x <;当1x <−时,()0f x >;若()0x f x ⋅<,则0()0x f x >⎧⎨<⎩或0()0x f x <⎧⎨>,可得1x >或1x <−, 所以不等式()0x f x ⋅<的解集为(,1)(1,)−∞−+∞. 故选:D.8. 【答案】D【分析】确定()f x 的图象,然后根据图象变换确定各选项.【详解】当10x −≤≤时,()2f x x =−,表示一条线段,且线段经过()1,2−和()0,0两点.当01x <≤时,()f x =()f x 的图象如图所示.()1f x −的图象可由()f x 的图象向右平移一个单位长度得到,故A 正确;()f x −的图象可由()f x 的图象关于y 轴对称后得到,故B 正确;由于()f x 的值域为[]0,2,故()()f x f x =,故()f x 的图象与()f x 的图象完全相同,故C 正确;很明显D 中()f x 的图象不正确.故选:D .9. 【答案】B【分析】对于①:举反例说明即可;对于②③:利用基本不等式分析判断;对于④:换元令t =≥.【详解】对于①:例如1x =−,则2y =−,可知1(0)y x x x =+≠的最小值不为2,故①错误; 对于②:因为1x >,则10x −>,可得()443122211y x x x x =+−=−+−≥=−−, 当且仅当411x x −=−,即3x =时,等号成立, 所以43(1)1y x x x =+−>−的最小值为2,故②正确; 对于③:因为0x <,则0x −>,可得()442222y x x x x =−−−=−+−≥=−, 当且仅当4x x −=−,即2x =−时,等号成立, 所以42(0)y x x x=−−−<的最小值为2,故③正确;对于④:令t =≥(1y t t t =+≥,可知1y t t =+在)+∞上单调递增,当)0t x ==时,1y t t =+取到最小值2,所以)y x =∈R 的最小值不为2,故④错误;故选:B 10. 【答案】C【分析】对于①:根据奇函数定义分析判断即可;对于②:根据中心对称的定义分析判断;对于③:整理可得x x c =−,构建()g x x x =,结合函数图像分析判断;对于④:取0,1c b ==−,代入解方程即可得零点个数.【详解】由题意可知:()f x 的定义域为R ,对于①:当0c =时,()f x x x bx =+,则()()()()()f x x x b x x x bx f x −=−−+−=−+=−,所以()f x 为奇函数,故①正确; 对于②:因为()()()()2f x f x x x b x c x x bx c c −+=−−+−++++=,所以函数()f x 的图像关于点(0,)c 对称,故②正确;对于③:若0b =,令()0f x x x c =+=,可得x x c =−, 构建()22,0,0x x g x x x x x ⎧≥==⎨−<⎩,可得其图像如图所示,可知y =g (x )在R 上单调递增,且y =g (x )的值域为R ,则y =g (x )与y c =−恒有一个交点,即()f x 有且仅有1个零点,故③错误;对于④:例如0,1c b ==−,则()()1f x x x x x x =−=−,令()()10f x x x =−=,解得x =0或1x =±,所以存在,b c ∈R ,使得函数()f x 有三个不同的零点,故④正确;综上所述:真命题的个数为3.故选:C. 第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分.11.【答案】[)()1,22,−+∞【分析】根据分式、根式的意义列式求解即可.【详解】令1020x x +≥⎧⎨−≠⎩,解得1x ≥−且2x ≠,所以函数12y x =+−的定义域是[)()1,22,−+∞. 故答案为:[)()1,22,−+∞. 12. 【答案】1(1,]2− 【分析】把分式不等式等价转化为一元二次不等式,由此求得原不等式的解集.【详解】解:不等式2101x x −≤+等价于()()211010x x x ⎧−+≤⎨+≠⎩,解得112x −<, 故答案为:1(1,]2−.13. 【答案】[]0,2【分析】分析可知{}|11x a x a −≤≤+是{}|13x x −≤≤的真子集,结合包含关系运算求解即可.【详解】由||1x a −≤,可得11a x a −≤≤+,由2230x x −−≤,可得13x −≤≤,因为“||1x a −≤”是“2230x x −−≤”的充分不必要条件,可知{}|11x a x a −≤≤+是{}|13x x −≤≤的真子集,则1113a a −≥−⎧⎨+≤⎩,且等号不同时成立,解得02a ≤≤, 所以实数a 的取值范围为[]0,2.故答案为:[]0,2.14. 【答案】[]4,2−−【分析】分析可知()f x 在R 上单调递增,根据分段函数单调性列式求解即可.【详解】由题意可知:()f x 在R 上单调递增,则1208a a a a ⎧−≥⎪⎪<⎨⎪−−≤⎪⎩,解得42a −≤≤−,所以实数a 的取值范围是[]4,2−−.故答案为:[]4,2−−.15. 【答案】 ①. ()1,2 ②. 02a <≤【分析】(1)将2a =代入()f x 解析式,分析各段单调性,即可得出结果;(2)先求出(],1−∞上的值域,由()f x 的值域为(),−∞+∞,只需()221y a x =−−+在()1,+∞上的值域包含(),1a −∞−,分析该二次函数的开口方向,对称轴及值域即可求出a 的取值范围.【详解】解:由题知当2a =时,()()22,1221,1x x f x x x −+≤⎧⎪=⎨−−+>⎪⎩,故()f x 在(],1−∞上单调递减,在()1,2上单调递增,在[)2,+∞上单调递减,故()f x 的单调递增区间是()1,2;由于y x a =−+在(],1−∞上的值域为[)1,a −+∞,若()f x 的值域为(),−∞+∞,只需()221y a x =−−+在()1,+∞上的值域包含(),1a −∞−即可, 故需0a −<,即0a >,此时()221y a x =−−+在()1,+∞上的值域为(],1−∞, 故需11a −≤,即02a <≤,综上: 02a <≤.故答案为:()1,2; 02a <≤三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程. 16. 【答案】(1)化简见解析,{}|31U A x x =−<<(2){|3A B x x ⋂=≤−或}12x ≤≤(3){}|1a a ≥【分析】(1)根据一元二次不等式求集合A ,进而可得其补集;(2)可得{|2}B x x =≤,进而可得交集;(3)分析可知A B ⋃=R ,结合交集运算求解.【小问1详解】由2230x x +−≥,解得3x ≤−或1x ≥,可得{|3A x x =≤−或}1≥x ,所以{}|31U A x x =−<<.【小问2详解】若2a =,则{|2}B x x =≤,所以{|3A B x x ⋂=≤−或}12x ≤≤.【小问3详解】由题意可知:A B ⋃=R ,且{|3A x x =≤−或}1≥x ,{|}B x x a =≤,可得1a ≥,所以实数a 的取值范围为{}|1a a ≥.17. 【答案】(1)2a =−,4b =(2)9,4⎛− ⎝;2m =− 【分析】(1)由条件①可得:4b =;由条件②可得:()f x 关于直线1x =对称,结合对称性可得2a =−; (2)(i )分析可知()222120x m x m +++−=有两根不相等的正实数根12,x x ,利用韦达定理结合∆判别式求m 的取值范围;(ⅱ)根据题意利用韦达定理运算求解即可.【小问1详解】由条件①可得:(0)4f b ==;由条件②可得:()f x 关于直线1x =对称,则12a −=,解得2a =−; 所以2a =−,4b =.【小问2详解】(i )由(1)可知:2()24f x x x =−+,则()222()()(23)6212g x f x m x m x m x m =+++−=+++−, 若函数()g x 有两个不同的正数零点12,x x ,即()222120x m x m +++−=有两根不相等的正实数根12,x x , 则{Δ=(2m +1)2−4(m 2−2)>0x 1+x 2=−(2m +1)>0x 1x 2=m 2−2>0,解得94m −<<所以实数m 的取值范围为9,4⎛− ⎝;(ⅱ)因为12x x −=,所以1=,解得2m =−. 18. 【答案】(1)()f x 为定义在R 上的奇函数,证明见详解(2)()f x 在区间[0,1]上单调递增,证明见详解(3)11,22⎡⎤−⎢⎥⎣⎦ 【分析】(1)根据题意结合奇偶性的定义分析证明;(2)根据题意结合单调性的定义分析证明;(3)可证()f x 在区间(1,+∞)上单调递增,结合(2)可得:10(),02f x x <≤>,再结合奇函数性质求值域.【小问1详解】 ()f x 为定义在R 上的奇函数,证明如下:由题意可知:()f x 的定义域为R ,定义域关于原点对称,且()()22()()11a x ax f x f x x x −−==−=−+−+, 所以()f x 为定义在R 上的奇函数.【小问2详解】若0a >,则()f x 在区间[0,1]上单调递增,证明如下:任取[]12,0,1x x ∈,且12x x <, 则()()()()12121212222212121()()1111a x x x x ax ax f x f x x x x x −−−=−=++++, 因为1201x x ≤<≤,则221212120,10,10,10x x x x x x −<−>+>+>,可得12())0(f x f x −<,即12()()f x f x <,所以()f x 在区间[0,1]上单调递增.【小问3详解】当1a =时,则2()1x f x x =+, 当0x >时,2()01x f x x =>+, 由(2)可知:()f x 在区间(]0,1上单调递增,任取()12,1,x x ∞∈+,且12x x <, 则()()()()12121212222212121()()1111x x x x x x f x f x x x x x −−−=−=++++, 因为121x x <<,则221212120,10,10,10x x x x x x −<−<+>+>,可得12()()0f x f x −>,即12()()f x f x >,所以()f x 在区间(1,+∞)上单调递减.则()10()12f x f <≤=,且(0)0f =, 由(1)可知:()f x 为定义在R 上的奇函数,可得当0x <时,1()02f x −≤<; 综上所述:函数()f x 的值域为11,22⎡⎤−⎢⎥⎣⎦. 19. 【答案】(1)45100x <<(2)当32.5x =时,()g x 有最小值36.875分钟【分析】(1)解不等式()40f x >即可;(2)分030x <≤、30100x <<两种情况求出分段函数()g x 的表达式,再求()g x 各段上的最小值,最后得出()g x 在整个定义域上最小值.【小问1详解】由已知可得f (x )>40,当030x <≤时,不符合题意;当30100x <<时,由不等式组{30<x <1002x +1800x−90>40,解得45100x <<;所以当45100x <<时,公交群体的人均通勤时间少于自驾群体的人均通勤时间.【小问2详解】当030x <≤时,()()30%401%0.140g x x x x =⨯+−=−+;当30100x <<时,()21800()290%401%0.02 1.358g x x x x x x x ⎛⎫=+−+−=−+ ⎪⎝⎭, 所以20.140,030()0.02 1.358,30100x x g x x x x −+<≤⎧=⎨−+<<⎩, 当030x <≤时,函数()g x 单调递减,此时()min ()3037g x g ==;当30100x <<,函数()g x 在()30,32.5上单调递减、在()32.5,100上单调递增,此时()min ()32.536.875g x g ==;且3736.875>,可知当32.5x =时,()g x 有最小值36.875分钟.20. 【答案】(1)4a =;()222,11,1243,2t t t g t t t t t ⎧−≤⎪=−<<⎨⎪−+≥⎩(2)答案见详解【分析】(1)分析可知二次函数2()3f x x ax =−+在2x =处取到最小值,即可得4a =,结合二次函数单调性求()g t ;(2)整理可得()()110mx x −−≤,分类讨论最高项系数以及两根大小解不等式.【小问1详解】由题意可知:二次函数2()3f x x ax =−+在2x =处取到最小值, 则22a =,即4a =,可得2()43f x x x =−+, 因为()f x 在(),2∞−上单调递减,在()2,∞+上单调递增,若12t +≤,即1t ≤时,()f x 在[],1t t +上单调递减,所以()f x 的最小值为2(1)2f t t t +=−;若21t t <<+,即12t <<时,()f x 在[],2t 上单调递减,在(]2,1t +上单调递增, 则()f x 的最小值为(2)1f =−;若2t ≥时,()f x 在[],1t t +上单调递增,所以()f x 的最小值为2()43f t t t =−+;综上所述:()222,11,1243,2t t t g t t t t t ⎧−≤⎪=−<<⎨⎪−+≥⎩【小问2详解】因为2()(1)(3)2f x m x m x ≤−+−+,即2243(1)(3)2x x m x m x −+≤−+−+, 可得()()110mx x −−≤,(i )若0m =,则()10x −−≤,解得1x ≥,原不等式解集为{}|1≥x x ; (ⅱ)若0m <,令()()110mx x −−=,解得10x m =<或1x =, 原不等式解集为1|1x x x m ⎧⎫≤≥⎨⎬⎩⎭或; (ⅲ)若0m >,令()()110mx x −−=,解得10x m =>或1x =, ①当11m <,即1m >时,原不等式解集为1|1x x m ⎧⎫≤≤⎨⎬⎩⎭; ②当11m=,即1m =时,原不等式解集为{}|1x x =; ③当11m >,即01m <<时,原不等式解集为1|1x x m ⎧⎫≤≤⎨⎬⎩⎭; 综上所述:若0m =,原不等式解集为{}|1≥x x ;若0m <,原不等式解集为1|1x x x m ⎧⎫≤≥⎨⎬⎩⎭或;若1m >时,原不等式解集为1|1x x m ⎧⎫≤≤⎨⎬⎩⎭; 若1m =时,原不等式解集为{}|1x x =;若01m <<时,原不等式解集为1|1x x m ⎧⎫≤≤⎨⎬⎩⎭. 21. 【答案】(1)①③为“L −函数”,②不为“L −函数”(2)(],0−∞(3)[)0,A =+∞,(),0B =−∞【分析】(1)根据“L −函数”的定义结合方程思想逐项分析求解即可;(2)分析可知原题意等价于210ax −=无解,即可得结果;(3)根据单调性以及“L −函数”的定义可知[)0,=+∞A ,(),0B ∞=−,并代入检验.【小问1详解】对于①:令()()f x f x −=−,即()2121x x −−=−−,可得20=不成立, 即()()f x f x −≠−恒成立,所以21y x =−为“L −函数”;对于②:令()()f x f x −=−,即()222323x x x x −−+=−−++,整理可得23x =,解得x =即()()f x f x −≠−不恒成立,所以223y x x =−++不为“L −函数”;对于③:令()()f x f x −=−,即221111x x =−++,可得2101x =+不成立, 即()()f x f x −≠−恒成立,所以211y x =+为“L −函数”; 综上所述:①③为“L −函数”,②不为“L −函数”.【小问2详解】令()()f x f x −=−,则22(1)1(1)1ax a x ax a x ⎡⎤−−++=−−+++⎣⎦,整理可得210ax −=, 原题意等价于210ax −=无解,若0a ≤,则1−ax 2≥1>0,即210ax −=无解,符合题意;若a >0,解得x=,不合题意; 综上所述:实数a 的取值范围为(],0−∞.【小问3详解】因为21y x =+的单调递增区间为[)0,∞+,由题意可知:[)0,A ∞⊆+,若x B ∈且x B −∈,则()(),f x x f x x =−=−,即()()f x f x −=−,不合题意,可知(),0B ∞⊆−, 且()f x 的定义域为R ,则[)0,=+∞A ,(),0B ∞=−.此时()21,0,0x x f x x x ⎧+≥=⎨<⎩,其图像如图所示,可知()f x 在R 上单调递增,当0x =时,则()01f =,不满足()()f x f x −=−,符合题意; 当0x <时,则0x −>,若()()f x f x −=−,则21x x +=−,即x 2+x +1=(x +12)2+34≥34>0, 所以()()f x f x −=−不成立,符合题意;当0x >时,则0x −<,若()()f x f x −=−,则21x x +=,即x 2−x +1=(x −12+34≥34>0, 所以()()f x f x −=−不成立,符合题意;综上所述:()()f x f x −≠−恒成立,函数()f x 为“L −函数”, 所以[)0,=+∞A ,(),0B ∞=−。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)请你根据截图内的信息,判断这个结论
年 汛0
是否正确,并给出说明. (2)如果这个结论不正确,请你通过计算得 出最佳组合. 解答(1)这个结论是错误的.根据三年期 的利率5%,可以算出两个三年整存整取存款组 合的本利和为:10000(1+3×5%)2=13225. oo元.这个数值比程序给出的结果要好,这说 明程序的结论是错误的.
注意到S。=SE+S,所以
S(z—zD)一SE(xD--3L"E).
由此可得
z一——'一。
SDzD—SEzE
将前面分析的结果代入这个式子,化简后
如果月牙的重心位于月牙的内圆弧的E点,
32=r--r2cosO=r(1—2cosO),
一r
z
2cosO(O--sinOcosO) ,r--2(0--sinOcosO)。
46
数学通报
2012年
第5l卷
第5期
第十五届北京高中数学知识应用
竞赛决赛试题和参考答案
2012年3月25日
1.(满分16分)2011年国庆期间,上海新世 界购物中心策划出一套“积点购物”营销方案.即 在活动期间,商品的售价按照一定的比率全部折 算成积点,这次全场商品共分为A、B、C三类, 一件A类商品的售价(元)与折算成的点数比是 l:1,一件B类商品的售价(元)与折算成的点 数比是1:1.5,一件C类商品的售价(元)与折 算成的点数比是1:1.9.顾客选定商品后,累 计积点.顾客按每满500个积点付200元的方式 付款.如果积点a不是500的整数倍,口=500b +f,其中b为正整数,o<c<500.这时有两种 付款方式供选择.第一种付款方式是按b+1个 500点支付200(b+1)元,剩余的500一f点可与 再继续购物的积点合用;第二种付款方式是支付 200b+f元.无论哪种付款方式,顾客均在积点 购物中得到了优惠. (1)请你算一算,当每一类商品的积点都是 500的整数倍时,顾客分别从这三类商品中能得 到相当于多少折的优惠? (2)有一位顾客,想买一双靴子、一件呢外 套和一条牛仔裤,靴子原价1499元,是A类商 品;呢外套原价899元,是B类商品;牛仔裤 原价699元,是C类商品.正当她要掏钱按第一 种付款方式付款时,一位“黄牛”走过来说:“这 样做,你还要绞尽脑汁处理剩余的积点,不如直 接按A类4.2折、B类6.2折,C类7.8折将货
方案一:付款200×9—1800(元), 余点数为 129.76(元). 方案二:付款200×8+175.6—1775.6(元). “黄牛”的方案:付款1499
0.62+699×0.78—1
X
500—175.6—324.4(点),
200 X 324.4÷500—
余点数折合人民币
0.42+899 X
732.18(元).
参考文献 l人民教育出版杜.普通高级中学教科书(必修)数学第二册 (上)[M].北京:人民教育出版社,2004
万方数据
第十五届北京高中数学知识应用竞赛决赛试题和参考答案
刊名: 英文刊名: 年,卷(期): 数学通报 Bulletin des Sciences Mathematics 2012,51(5)
万方数据
2012年第5l卷第5期
数学通报
49
一・一1一南)“.
即挖满足不等式0.9”≤1—0.9—0.1,解得
竹≥22.
可得sB形ADBc—r2[(丌一目)+sinOcosO],记作 SD,S日形^£Bc=r2(口一sinOcosO),记作SE,则 S—sD—SE—r2[(丌一20)+2sinOcosO]. 根据题意可知,弓形ADBC的重心Z。,弓 形AEBC的重心Z,以及月牙的重心Z都应位于 直线CD上.如果记它们与圆心O点的距离分别 为zD,zE和z,则有zE<zD<工.且应用初赛 时得到的结论可知 一堑
瘁弧心勰弧“璐乳
最佳存款时问组合
・本计簋器可估簋产生利息最多的恨行储蓄方式.
初始存入金额
’………
两年
一卫盟元
三年 八年 四年 九年
储蓄存期 七年
五年!六年oI
十年
计算结果
序号
1 2 结论/建议: 存款期限
■■目
本息金额 10350∞元
13196 25元
利率
3 50% 5 50%
1年
5年
您可以考虑先存1年期定期存获,到期本息再转存5年期定期存款。到期本息总额为 13196,25元o
(2)存款六年,有多种组合,几乎涉及到了 所有的存款利率项目,为此我们先探讨一下有规 律性的大小关系. 设A为本金数,巩为存i年,A为相应的 利率,f(a。,q,…,口。)为依次经历存入口。, 口,,…,口。年之后的本利和.则 f(af,aj,…,口。)=A(1+pini)(1+岛口j)・
…・(1+户。口。).
与积点的比率又有所增加,每一元折合积点的倍 数分别为A类:1倍,B类:1.5倍,C类:1.9 倍.因此顾客购买各类商品时实际得到的优惠分 别为 A类商品:1×0.4—4折, B类商品:1.5×0.4=6折, C类商品:1.9X0.4—7.6折. (2)根据积点方案,顾客购物的积点是:
1499+899X1.5+699×1.9—4175.6,而 4175.6—500×8+175.6.
2.(满分16分)2月20日,在新浪网看到, 网站为网民提供了不少有趣和实用的生活应用程 序,其中的“理财计算器”可以为网民呈现出最佳 存款时间组合.下图是程序的一个截图,上图是 存款利率表.
万方数据
2012年
第51卷
第5期
数学通报
47
存款利率
利率项目 活期储蓄 三个月定期存款 半年定期存款 一年定期存款 二年定期存款 三年定期存款 五年定期存款
万方数据
48
数学通报
2012年
第51卷
第5期
4.(满分16分)经观察,人们发现鲑鱼在河 中逆流行进时,所消耗的能量为E=CV3T,其中 口为行进时相对于河水的速度,T为行进的时间 (单位:小时),C为常数.如果水的流速为4 km/h,鲑鱼在河中逆流行进200 km,问它在怎 样的速度下能使消耗的能量最少? 解由已知,鲑鱼相对于河岸的速度百一
5.(满分18分)如果有三门高炮独立射击 目标,用户,表示“第i门高炮命中目标”的概率, 那么“三门高炮都命中目标”的概率就是p。・P: ・P。,“三门高炮都不命中目标”的概率是(1一 P-)(1一Pz)(1一Pa).请依据以上的概率计算 法则,回答下列问题: 如果每门高炮击中敌机的概率是十分之一. (1)用十门高炮一定能击中敌机吗?若认为 一定能击中,请说明理由;若认为不一定能,请 计算出击中敌机的概率. (2)要想能以不小于0.9的概率击中敌机, 至少需设置多少门高炮? 解答 (1)用十门高炮不一定能击中敌机.
本文链接:/Periodical_sxtb201205014.aspx
3 0——sinOcosO
!醴1
\口一
…~/’
一堑
!丝!翌二盟
sin30
n ‘|0\\.
k一0\E
3(Ⅱ一疗)一sin(7r一日)c08(Ⅱ一0) 2r
\
3丌一口+sinOcosO。
U 陟/。
现在有两个半径均为r的圆,圆心分别为点 O和0 7.A、B为两个圆周的交点.则圆弧 ADB和圆弧AEB围成了一个月牙儿的图形 ADBE.若设计一种特殊的月牙儿,使得这个月 牙儿的重心刚好位于月牙儿的内圆弧AEB的中 点E的位置上,这时么B070—0,如图所示.请 你根据上面得到的弓形板重心的结论,求0满足 的方程. 解答 由问题可知,四边形A0780是一个 则有 可得
若三寺,令E7=0,得铆26,当u<6时,E7<
0,当口>6时,E7>0,所以础=6时E取得最 小值.) 鲑鱼以每小时6 km的相对于河水的速度行 进时所消耗的能量最少.
=・一(,一拼≈o-651,.
(2)设至少需要竹门高炮就能以不小于0.9 的概率击中敌机,则 0.9≤P(用竹门高炮击中敌机)=P(起门高 炮中至少有一门击中了敌机) =1一P(n门高炮都没有击中敌机)
2个o_幽o,又可以表示为@=v--4,所以T--旦兰. 口一4
』
于是,E—CV3
E:200。掣:200。立些墼磐型里
一200cf雷z+12面+48+罂1
T=200c』,_(口>4),即
因为,P(用十门高炮击中敌机)=P(十门高
—200c[(。~2)2+32(詈+吾)+44].
因为蚕一2既是(矛一2)2的最小值点,也是
129.76一(1800—1732.18)=61.94(元).
款给我,没有积分的事了,由我为你去付款,将
购货凭证给你,你又省钱又省事.” 请你算一算,用数据说明“黄牛”的用意. 解(1)当顾客购买积点时每200元可以买 500个积点.他得到的折扣是200/500=0.4,即 四折的优惠.但是各类商品按积点出售时,售价
及3年以上的任何存款组合的本利和.这样,只 需比较f(3,3)和,(5,1)的大小就可以了,而 这已由(1)可知结果.所以,结论是:对于6年 存期,最大收益是两个三年期组合. 3.(满分16分)2月18日至22日第七届世 界草莓大会在北京市昌平区召开,请你根据下面 的地图推算出昌平区的面积. 解答要点解法会是多样的,要给出明确的 方法,比如,分割求和的方法,按照度量,画出 足够细的网格,通过计算网格数得到近似解答; 或者图形割补的方法,将这个不规则的图形通过 割补拼成近似规范的的图形,再按照度量计算得 到近似解答.(昌平区的实际面积是1343平方公 里,在方法正确的基础上,与实际数值误差不超 过40平方公里即可)
,,、
L1)或 ±一1—2co源自O.(2)边长为r的菱形.么E07B一0,/DDB—Tf一良 月牙的图形是由OO上的弓形ADB中挖掉0d上
的弓形AEB得到的图形,弓形ADB上的么A∞
