03算法最大流问题maxflow
max-flow min-cut定理

max-flow min-cut定理用特定的网络流算法将任意的有向图G转化成一个网络流图,然后对其进行计算,就有可能得到网络流的最大流量和最小割集。
当最大流量和最小割集相等的时候,就称这个最小割集为最大流量。
Max-Flow Min-Cut定理在计算网络流时经常使用。
其实,Max-Flow Min-Cut定理也就是将图中的所有路径都用边替代,转化为一个网络流问题。
在这个流问题中,求解的是一个最大流量。
与此同时,我们还可以将一个网络流问题转化为一个割问题,求出一个最小割。
最大流量就等于最小割。
该定理使得我们可以将一个复杂的最大流量问题转化为一个简单的最小割问题。
因此,该定理是网络流问题中最重要的结论之一。
Max-Flow和Min-Cut的概念Max-Flow (最大流量):在一个有向图里,从源节点s到汇节点t的最大流量。
Min-Cut (最小割): 在一个有向图里,通过几条边,将源节点s和汇节点t分开的最小边的数量之和。
对于任何一个有向图,其最大流量的值等于其最小割的值。
这是一个非常重要的定理,因为它将求解网络流的难度降低了。
证明该定理的证明从两个方向进行:方向1: Max-Flow <= Min-Cut由于一个最小割是一组将源节点s和汇节点t分开的最少的边的数量,因此,在网络中所有的流量从源节点s到汇节点t的路径中,最小的一条路径的流量就是最小割的值。
这样一来,我们就证明了Max-Flow <= Min-Cut。
方向2: Max-Flow >= Min-Cut在一个有向图里,我们可以使用一个带权有向边将源节点s和汇节点t相连。
因此,我们可以考虑在这个图中最大流量和最小割集的关系。
我们首先定义S为节点的集合,它包含源节点s。
我们定义T为节点的集合,它包含汇节点t,那么就可以表示:(1) S = { s }接着,我们可以将每条边的流量设为以下任意两个节点之间的最大容量。
(4) E(i,j) = c(i,j)这样一来,我们就可以得到一个最小割集的表示式:其中i∈S,j∈T的边的容量和。
最大流的概念

最大流的概念最大流(Maximum Flow)是指在一个有向图中,给每条边一个容量限制,然后寻找一条从源点到汇点的路径,使得路径上的每条边的流量都不超过其容量限制的最大值。
最大流问题是网络流理论中的一种经典问题,具有广泛的应用领域,如网络优化、流量分配、资源调度等。
最大流问题可以用图论中的图来进行模型表示,其中图中的节点表示流经的位置,边表示流量通路,每条边还有一个容量值,表示该边所能承载的最大流量。
图中通常包括一个源点(Source)和一个汇点(Sink),各个节点与源点和汇点之间的连接关系构成了一个流量网络。
每个节点上的流量是指通过该节点的流量总和,而边上的流量是指该边上的实际流量。
最大流问题的求解可以采用不同的算法,其中最常见的是Ford-Fulkerson算法和Edmonds-Karp算法。
下面将对这两种算法进行详细介绍。
1. Ford-Fulkerson算法Ford-Fulkerson算法是最大流问题的经典算法,它的思想是不断寻找增广路径,并通过增加该路径上各边的流量来增加整个流量网络的流量。
算法的基本步骤如下:(1) 初始化流量网络的流量为0。
(2) 通过任意的路径查找算法(如深度优先搜索)找到一条从源点到汇点的增广路径。
(3) 在该增广路径上增加流量的值为该路径上残余容量的最小值。
(4) 更新整个流量网络中各边的残余容量和反向边的流量。
(5) 重复步骤2至4,直到无法找到增广路径为止。
2. Edmonds-Karp算法Edmonds-Karp算法是Ford-Fulkerson算法的一种改进,它通过使用广度优先搜索来寻找增广路径,使得算法的时间复杂度优于Ford-Fulkerson算法。
算法的具体步骤如下:(1) 初始化流量网络的流量为0。
(2) 通过广度优先搜索查找一条从源点到汇点的最短增广路径。
(3) 在该增广路径上增加流量的值为该路径上残余容量的最小值。
(4) 更新整个流量网络中各边的残余容量和反向边的流量。
最大流问题的几种经典解法综述

最⼤流问题的⼏种经典解法综述⼀、什么是最⼤流问题假设现在有⼀个地下⽔管道⽹络,有m根管道,n个管道交叉点,现在⾃来⽔⼚位于其中⼀个点,向⽹络中输⽔,隔壁⽼王在另外⼀个点接⽔,已知由于管道修建的年代不同,有的管道能承受的⽔流量较⼤,有的较⼩,现在求在⾃来⽔⼚输⼊的⽔不限的情况下,隔壁⽼王能接到的⽔的最⼤值?为解决该问题,可以将输⽔⽹络抽象成⼀个联通的有向图,每根管道是⼀条边,交叉点为⼀个结点,从u流向v的管道能承受的最⼤流量称为容量,设为cap[u][v],⽽该管道实际流过的流量设为flow[u][v],⾃来⽔⼚称为源点s,隔壁⽼王家称为汇点t,则该问题求的是最终流⼊汇点的总流量flow的最⼤值。
⼆、思路分析关于最⼤流问题的解法⼤致分为两类:增⼴路算法和预流推进算法。
增⼴路算法的特点是代码量⼩,适⽤范围⼴,因此⼴受欢迎;⽽预流推进算法代码量⽐较⼤,经常达到200+⾏,但运⾏效率略⾼,如果腹⿊的出题⼈要卡掉⼤多数⼈的code,那么预流推进则成为唯⼀的选择。
( ⊙ o ⊙ )咳咳。
先来看下增⼴路算法:为了便于理解,先引⼊⼀个引理:最⼤流最⼩割定理。
在⼀个连通图中,如果删掉若⼲条边,使图不联通,则称这些边为此图的⼀个割集。
在这些割集中流量和最⼩的⼀个称为最⼩割。
最⼤流最⼩割定理:⼀个图的最⼤流等于最⼩割。
⼤开脑洞⼀下,发现此结论显⽽易见,故略去证明(其实严格的证明反⽽不太好写,但是很容易看出结论是对的,是吧)。
这便是增⼴路算法的理论基础。
在图上从s到t引⼀条路径,给路径输⼊流flow,如果此flow使得该路径上某条边容量饱和,则称此路径为⼀条增⼴路。
增⼴路算法的基本思路是在图中不断找增⼴路并累加在flow中,直到找不到增⼴路为⽌,此时的flow即是最⼤流。
可以看出,此算法其实就是在构造最⼩割。
增⼴路算法⽽预流推进算法的思路⽐较奇葩(没找到⽐较好的图,只能⾃⾏脑补⼀下了。
= =#):先将s相连的边流⾄饱和,这种边饱和的结点称为活动点,将这些活动点加⼊队列,每次从中取出⼀个点u,如果存在⼀个相邻点v是⾮活动点,则顺着边u->v 推流,直到u变为⾮活动点。
MATLAB中的网络流与最大流最小割问题求解方法

MATLAB中的网络流与最大流最小割问题求解方法随着社会信息化的不断发展,网络已经成为了人们日常生活中不可或缺的一部分。
而网络的流量管理对于网络的高效运行至关重要。
在网络流领域中,最大流最小割问题是一种经典且重要的问题,它在图论和算法设计领域都具有广泛的应用。
在本文中,我们将介绍MATLAB中的网络流与最大流最小割问题求解方法。
一、网络流与最大流最小割问题简介网络流问题是指在网络中有一定容量限制的边上,如何使得网络中的流量达到最大的问题。
最大流最小割问题则是网络流问题的一个特殊情况,其中要求找到一个最小割,使得割后网络中的流量达到最大。
通常情况下,网络流问题常常以有向图的形式表示,每条边上都被赋予了一个容量,并存在一个源点和一个汇点。
二、MATLAB中的网络流包在MATLAB中,有许多优秀的网络流包可以用来求解网络流与最大流最小割问题。
其中,最为常用的是Network Flow Toolbox和Combinatorial Optimization Toolbox。
这两个包提供了一系列的函数和算法,可以帮助我们解决各种类型的网络流问题。
三、网络流与最大流最小割问题的建模与求解在使用MATLAB解决网络流与最大流最小割问题之前,首先我们需要进行问题的建模。
通常情况下,我们需要确定图的结构、边的容量和源点与汇点的位置。
在建模完成后,我们可以使用MATLAB中的网络流包提供的函数进行求解。
1. 使用Network Flow Toolbox求解网络流问题Network Flow Toolbox是MATLAB中一个常用的网络流包,它提供了一系列函数用于求解网络流与最大流最小割问题。
其中最常用的函数是maxflow函数,它可以用来计算网络中的最大流。
首先,我们需要使用网络流对象来表示图结构。
在建立网络流对象后,我们可以使用addnode函数向图中添加节点,使用addedge函数向图中添加边。
同时,我们可以使用setcaps函数来指定边的容量。
网络流学习笔记-最大流问题的四种算法

⽹络流学习笔记-最⼤流问题的四种算法最⼤流问题最⼤流问题满⾜以下三个条件:容量限制:f(u,v)≤c(u,v)斜对称性:f(u,v)=−f(v,u)流量平衡:∑(u,v)∈E f(u,v)=0(除s,t外的图中任意两点)原图中不存在的边也假设存在,视为容量为0.残量⽹络:计算出每条边上容量c与流量f之差后所得到的图。
由于上述的原因,边数可能是原图的两倍。
对于原图中⼀条c=16,f=11的单向边,在残量⽹络中对应边权为5(16−11)与11(0−(−11))的两条边。
增⼴路算法当且仅当残量⽹络中不存在s→t的有向道路(增⼴路)时,此时的流是从s到t的最⼤流。
Edmonds-Karp算法核⼼流程对图进⾏BFS,直到形成s−>t的通路(即当找到t时),同时维护这条通路上的最⼩残量minflow=e[i].cap−e[i].flow,并保存通路上每⼀个节点的⼊边。
只要能到达t,这条通路就是增⼴路,否则图中已经没有增⼴路。
形成通路之后,按照先前保留的各节点的⼊边,从终点t开始沿着通路倒退回去,并更新路上每⼀条边的正向边的流量e[i].flow与反向边的流量e[i^1].flow。
整条通路的流量更新完毕后,更新答案maxflow。
重复以上步骤,直到图中没有增⼴路。
优化⽅法重边处理。
即将正向边u→v的多条管道合并为⼀条,只需将cap属性累加即可。
⽽反向边不需要特殊处理。
(链式前向星+重边处理)int n, m, s, t;int num = 1;//让边的编号从2开始int head[maxn], pre[maxn];LL flow = 0;LL d[maxn];int flag[300][300];//记录重边,重边的容量累加到⼀条边上struct Edge {int next, to;LL cap;LL flow;}e[maxn*4];void addedge(int from,int to,LL cap){//存正向边num++;e[num].next = head[from];e[num].to = to;e[num].cap = cap;e[num].flow = 0;head[from] = num;//存反向边num++;e[num].next = head[to];e[num].to = from;e[num].cap = 0;e[num].flow = 0;head[to] = num;}void update() {//从终点开始退回去,沿路修改边权//通路的最⼩值m即d[t]for (int x = t; x != s; x = e[pre[x]^1].to) {e[pre[x]].flow += d[t];e[pre[x] ^ 1].flow -= d[t];}flow += d[t];}void ek(int s, int t) {for (;;) {mem(d, 0);//d[i]记录s->i路径上的最⼩残量//由于总是正数,可以同时起到记录是否访问过的作⽤queue<int> q;q.push(s);d[s] = INF;while (q.size()) {int u = q.front(); q.pop();for (int i = head[u]; i; i = e[i].next) {if (!d[e[i].to] && e[i].cap > e[i].flow) {pre[e[i].to] = i;//记录e[[i].to是从哪条边过来的d[e[i].to] = min(d[u], e[i].cap - e[i].flow);q.push(e[i].to);}}if (d[t]) break;//已经访问过t,可以跳出了}if (!d[t]) break;//整张图找遍依然到达不了t,说明已经没有增⼴路了update();}}int main() {cin >> n >> m >> s >> t;mem(flag, 0);f(i, 1, m) {int u, v, w;cin >> u >> v >> w;if (!flag[u][v]) {addedge(u, v, w);flag[u][v] = num - 1;//num是v->u的编号//num-1才是u->v的编号}else e[flag[u][v]].cap += w;//如果是重边,容量加到已存在的那条边上}ek(s,t);cout << flow;return 0;}Dinic算法EK算法中,每⼀次BFS都只能找到⼀条增⼴路,效率不⾼。
matlab最大流算法

matlab最大流算法【实用版】目录一、什么是最大流问题二、最大流问题的算法种类三、用 MATLAB 实现最大流问题的方法四、总结正文一、什么是最大流问题最大流问题(Maximum Flow Problem)是一个在图论中常见的问题,它的目标是在给定有向图中找到从源节点(source node)到汇节点(sink node)的最大流量。
在这个问题中,源节点是工厂,汇节点是客户,而图中的边表示了工厂到客户的运输路线,每条边的容量表示了这条路线的运输能力。
因此,最大流问题实际上是寻找图中从源节点到汇节点的容量最大的路径。
二、最大流问题的算法种类针对最大流问题,有很多不同的算法,其中较为著名的有Ford-Fulkerson 算法、Edmonds-Karp 算法和 Dinic 算法。
这些算法在解决最大流问题的效率和方法上各有不同,但它们的核心思想都是寻找增广路径(augmenting path)。
1.Ford-Fulkerson 算法:该算法是一种贪心算法,通过不断寻找增广路径来增大流量。
其基本思想是从源节点开始,沿着当前流量最大的路径进行扩展,直到无法扩展为止。
然后回溯到前一个节点,继续寻找增广路径。
该算法的时间复杂度为 O(nm),其中 n 表示节点数,m 表示边数。
2.Edmonds-Karp 算法:该算法是一种动态规划算法,通过计算每一条边的增广容量来寻找增广路径。
其基本思想是将原始图复制一份,然后对每一条边进行处理,计算出该边的增广容量。
接着根据增广容量进行路径压缩,直到无法压缩为止。
该算法的时间复杂度为 O(nm)。
3.Dinic 算法:该算法也是一种动态规划算法,与 Edmonds-Karp 算法类似,但它是从汇节点开始计算增广容量,然后进行路径压缩。
该算法的时间复杂度也为 O(nm)。
三、用 MATLAB 实现最大流问题的方法MATLAB 是一种强大的数学软件,可以用来实现最大流问题。
在MATLAB 中,我们可以使用图论工具箱(Graph Theory Toolbox)来解决最大流问题。
数学模型3-2最大流问题

最小切割容量和最大流
• 给定网络流(即网络中每条边上的容量给 定,流量满足流平衡条件)。任给一个切 割(P,Q),前面定义的切割容量C(P,Q) 是切割的函数。 • 最小切割容量就是最大流。 • 说明:切割容量作为切割的函数对任意可 行流都满足流量公式,即切割容量不小于 流量,对最大流来说,不等式取等号。
– 其上的正向弧均为非饱和弧。 – 其上的逆向弧均为非零流弧。 – vs到增广链上任一点也有增广链(vs可达); – 增广链上任一点到vt也有增广链(可达vt);
Ford-Fulkerson方法步骤
• 算法的步骤 :
– ①为网络分配初始流xij – ②根据伴随增量网络寻求增广链,若不存 在,则已最优, 否则 – ③在增广链上调整流量,产生新的可行流。 – 重复②、③两步,直到最优。
v3 v3 v2
3 3 7,7 4,4
v5 v4 11,9 vt
15,10 vs 3,1
5,2 9,9
10,10 v5
v3
6,6
v2
15,10 vs 3,1
7,7 4,4
v4 11,9 vt
5,2 9,9
10,10 v5
v3 v2
10 5 vs 9 2 1
6,6
7 4 3 2
v4 9 2 vt 10
将集合P中节点的 流(包括流进和流 出的)相加,即可 证明公式。
流量公式说明
• 对P中所有点对流量定义公式求和,可以得 到流量公式。 • 物理意义:从源流到汇的量通过P与Q的联 系流过。净流量为从P流过Q的总量与Q流 过P的总量之差。
流量公式说明
• 流量公式意义:网络流量以分割的容量为 上界。 • 进一步的想法:最小容量 最大流?如 何切割?如何定义流函数xij?
最大流算法解决最小割问题及网络流问题

最大流算法解决最小割问题及网络流问题最大流算法(maximum flow algorithm)是解决网络流问题的一种常用方法。
网络流问题是指在一个有向图中,每条边都有一个容量限制,要求在源点和汇点之间找到一条路径,使得路径上每条边的流量都不超过其容量限制,同时保证从源点流出的总流量最大。
最小割问题(minimum cut problem)是网络流问题的一个相关概念。
在一个有向图中,边上的容量表示其最大流量限制,我们需要找到一条割(cut),将图分为两个部分,并使得割的容量最小。
割的容量是指割中每条边的容量之和。
最大流算法可以解决最小割问题。
常用的最大流算法包括Ford-Fulkerson算法和Edmonds-Karp算法。
Ford-Fulkerson算法是一种经典的最大流算法。
它通过不断寻找增广路径来更新流的值,直到无法找到增广路径为止。
增广路径是一条从源点到汇点的路径,其上每条边的剩余容量都大于0,并且路径上的流量不超过容量限制。
Edmonds-Karp算法是基于Ford-Fulkerson算法的一种优化方法。
它使用广度优先搜索(BFS)来寻找增广路径,可以保证在每次寻找增广路径时更新的流量最小。
最大流算法的应用非常广泛。
例如,可以使用最大流算法来优化交通流量,解决作业分配问题,以及在计算机网络中进行路由和流量控制等。
总结起来,最大流算法是解决最小割问题和网络流问题的一种常用方法。
通过寻找增广路径来更新流的值,最大流算法可以在保证路径上每条边的流量不超过容量限制的前提下,使得从源点流出的总流量最大化。
最大流问题经典例题

最大流问题经典例题最大流问题是指在一个有向图中,从源点到汇点的最大流量是多少。
这个问题在现实生活中有很广泛的应用,比如网络通信中的数据传输、水管输水时的流量控制等。
下面我们来看一道经典的最大流问题的例题。
问题描述:给定一个有向图,其中每条边的容量都只会为1,求从源点到汇点的最大流量。
解题思路:这是一道非常基础的最大流问题,我们可以使用网络流的算法来解决。
下面,我将分几个步骤来阐述解题思路。
1. 构建网络流图首先,我们需要将原有的有向图转化为网络流图。
对于每条边,我们都要添加两条反向边,并将容量均设为1。
这样,我们就得到了一个新的有向图,它的任何一条边的容量都为1。
2. 使用Edmonds-Karp算法接下来,我们可以使用Edmonds-Karp算法,也叫增广路算法,来求出最大流量。
它是一种广度优先搜索的算法,的基本思想是:从源点开始,每次找一条容量不为0,且未被搜索过的路径,将路径上的边的容量减去该路径的最小容量,这个最小容量就是该路径的流量。
然后将路径中的正向边的流量加上这个流量,反向边的流量减去这个流量,依次迭代。
3. 输出结果最后,我们将算法得到的最大流量输出即可。
代码实现:以下是使用Python语言实现的最大流问题的代码:```def bfs(graph, start_node, end_node):visited = [False] * len(graph)queue = []queue.append(start_node)visited[start_node] = Truepred = [-1] * len(graph)while queue:curr_node = queue.pop(0)if curr_node == end_node:return True, predfor i, val in enumerate(graph[curr_node]):if not visited[i] and val > 0:queue.append(i)visited[i] = Truepred[i] = curr_nodereturn False, []def edmonds_karp(graph, start_node, end_node):max_flow = 0while True:flow_found, pred = bfs(graph, start_node, end_node) if not flow_found:breakcurr_node = end_nodemin_flow = float('inf')while curr_node != start_node:prev_node = pred[curr_node]min_flow = min(min_flow,graph[prev_node][curr_node])curr_node = prev_nodecurr_node = end_nodewhile curr_node != start_node:prev_node = pred[curr_node]graph[prev_node][curr_node] -= min_flowgraph[curr_node][prev_node] += min_flowcurr_node = prev_nodemax_flow += min_flowreturn max_flowif __name__ == '__main__':graph = [[0, 1, 0, 1, 0],[0, 0, 1, 0, 1],[0, 0, 0, 1, 0],[0, 0, 0, 0, 1],[0, 0, 0, 0, 0]]start_node = 0end_node = 4max_flow = edmonds_karp(graph, start_node, end_node)print("The maximum flow in the network is:", max_flow) ```在这个例子中,我们构建了一个有向图,其中每条边的容量均为1。
三种网络流(最大流)的实现算法讲解与代码

三种⽹络流(最⼤流)的实现算法讲解与代码[洛⾕P3376题解]⽹络流(最⼤流)的实现算法讲解与代码定义对于给定的⼀个⽹络,有向图中每个的边权表⽰可以通过的最⼤流量。
假设出发点S⽔流⽆限⼤,求⽔流到终点T后的最⼤流量。
起点我们⼀般称为源点,终点⼀般称为汇点内容前置1.增⼴路在⼀个⽹络从源点S到汇点T的⼀条各边剩余流量都⼤于0(还能让⽔流通过,没有堵住)的⼀条路。
2.分层预处理出源点到每个点的距离(每次寻找增⼴路都要,因为以前原本能⾛的路可能因为⽔灌满了,导致不能⾛了).作⽤是保证只往更远的地⽅放⽔,避免兜圈⼦或者是没事就⾛回头路(正所谓⼈往⾼处⾛⽔往低处流).3.当前弧优化每次增⼴⼀条路后可以看做“榨⼲”了这条路,既然榨⼲了就没有再增⼴的可能了。
但如果每次都扫描这些“枯萎的”边是很浪费时间的。
那我们就记录⼀下“榨取”到那条边了,然后下⼀次直接从这条边开始增⼴,就可以节省⼤量的时间。
这就是当前弧优化具体怎么实现呢,先把链式前向星的head数组复制⼀份,存进cur数组,然后在cur数组中每次记录“榨取”到哪条边了。
[#3 引⽤⾃]()解决算法Ford-Fulkerson 算法(以下简称FF算法)FF算法的核⼼是找增⼴路,直到找不到为⽌。
(就是⼀个搜索,⽤尽可能多的⽔流填充每⼀个点,直到没有⽔⽤来填充,或者没有多余的节点让⽔流出去)。
但是这样的⽅法有点基于贪⼼的算法,找到反例是显⽽易见的,不⼀定可以得到正解。
为了解决这种问题,我们需要⼀个可以吃后悔药的⽅法——加反向边。
原本我们的DFS是⼀条路⾛到⿊的,现在我们每次进⼊⼀个节点,把⽔流送进去,同时建⽴⼀个权值与我们送⼊的⽔流量相等,但是⽅向相反的路(挖⼀条路让⽔流能够反向流回来,相当于给⽔流吃⼀颗后悔药)。
我们给了FF算法⼀颗后悔药之后就可以让他能够找到正确的最⼤流。
Ford-Fulkerson算法的复杂度为O(e×f) ,其中 e 为边数, f为最⼤流上代码。
计算机科学中最重要的32个算法

奥地利符号计算研究所(Research Institute for Symbolic Computation,简称RISC)的Christoph Koutschan博士在自己的页面上发布了一篇文章,提到他做了一个调查,参与者大多数是计算机科学家,他请这些科学家投票选出最重要的算法,以下是这次调查的结果,按照英文名称字母顺序排序。
1.A* 搜索算法——图形搜索算法,从给定起点到给定终点计算出路径。
其中使用了一种启发式的估算,为每个节点估算通过该节点的最佳路径,并以之为各个地点排定次序。
算法以得到的次序访问这些节点。
因此,A*搜索算法是最佳优先搜索的范例。
2.集束搜索(又名定向搜索,Beam Search)——最佳优先搜索算法的优化。
使用启发式函数评估它检查的每个节点的能力。
不过,集束搜索只能在每个深度中发现最前面的m 个最符合条件的节点,m是固定数字——集束的宽度。
3.二分查找(Binary Search)——在线性数组中找特定值的算法,每个步骤去掉一半不符合要求的数据。
4.分支界定算法(Branch and Bound)——在多种最优化问题中寻找特定最优化解决方案的算法,特别是针对离散、组合的最优化。
5.Buchberger算法——一种数学算法,可将其视为针对单变量最大公约数求解的欧几里得算法和线性系统中高斯消元法的泛化。
6.数据压缩——采取特定编码方案,使用更少的字节数(或是其他信息承载单元)对信息编码的过程,又叫来源编码。
7.Diffie-Hellman密钥交换算法——一种加密协议,允许双方在事先不了解对方的情况下,在不安全的通信信道中,共同建立共享密钥。
该密钥以后可与一个对称密码一起,加密后续通讯。
8.Dijkstra算法——针对没有负值权重边的有向图,计算其中的单一起点最短算法。
9.离散微分算法(Discrete differentiation)10.动态规划算法(Dynamic Programming)——展示互相覆盖的子问题和最优子架构算法11.欧几里得算法(Euclidean algorithm)——计算两个整数的最大公约数。
最大流问题(maxflow)

取 min ij ,显然 0。 f 1 : • 我们把 f 修改为 f ij vi , v j 为 上前向边 f1 f ij vi , v j 为 后向边 f ij 其余 f1仍为可行流(即满足容量限制条件与 • 不难验证 平衡条件),但是 f1的总流量等于 f 的流加 , 这与 f 为最大流矛盾,所以 vt不属于 S 。
• 检查与 v5 点邻接的未标号点有 v1 , vt,发现 v1 , 点满足 v1 , v5 E且 f15 3 0 ,令 v1 min 3, 2 2, 则给 v1点以标号 v5 , 2 。 , • v4 点未标号,与 v1邻接,边 v1 , v4 E且 f14 2 c14 5,所以令 v 4 min 3, 2 2, 给 v4 以标 号 v1, 2 。 • vt 类似前面的步骤,可由 v4得到标号 v4 , 2。 • 由于 vt 已得到标号,说明存在增广链,所 以标号过程结束,见图5-44。
• 但流量W又满足
W
cij fij 0
vi S , v j S
v j S , vi S
vi S ,v j S
fij f Ji
vi S ,v j S
cij
• 所以最大流的流量等于最小割的容量,定理得到 证明。 • 定义22 容量网络G,若 为网络中从vS到 vt的一 条链,给 定向为从vS到 vt, 上的边凡与 同向称 为前向边,凡与 反向称为后向边,其集合分别 用和 表示,f是一个可行流,如果满足
(3)重复(2)直到收点 vt 被标号或不再有顶点 可标号时为止。 • 如若 vt 得到标号,说明存在一条可增广链,转 (第2步)调整过程。若 vt 未获得标号,标号过 程已无法进行时,说明f已是最大流。 2. 调整过程 f ji 若 vi , v j 是可增广链上的前向边 f ji 若 v , v 是可增广链上的后向边 (1)令 fij i j 若 vi , v j 不存在可增广链上 f ji (2)去掉所有标号,回到第1步,对可行流 f 重 新标号。
最大流算法在网络问题中的应用

最大流算法在网络问题中的应用网络问题是计算机科学中的一个重要领域,主要研究节点之间的连通性,以及数据在网络中的传输和处理方式。
网络问题的解决方法之一就是最大流算法。
最大流算法可以用来求解网络流问题,是一种常用的优化算法。
下面将详细介绍最大流算法在网络问题中的应用。
一、最大流算法的定义最大流算法(Maximum Flow Algorithm)是计算最大流问题的常用算法,用于解决网络流问题。
最大流问题是在网络中从源点s 到汇点t的最大可行流问题,也可以理解为管道输送液体的最大流量问题。
最大流算法求解的本质就是如何找到一条从源点到汇点的路径,并计算出最大流量,以使所有流量达到最大。
二、最大流算法的应用最大流算法的应用非常广泛,在交通、卫星通信、电信等领域均有广泛应用。
下面分别从交通、卫星通信和电信三个方面来介绍最大流算法的应用。
1、交通领域在交通领域,最大流算法可以应用于城市道路布局规划、交通信号灯调度和公交线路规划等问题。
以城市道路布局规划为例,我们可以通过最大流算法来确定城市中心和周边地区之间的交通流量。
这样,我们就可以在城市道路规划过程中根据交通流量分配道路宽度和车行道数量,以确保道路能够承载最大交通流量。
2、卫星通信领域在卫星通信领域,最大流算法可以应用于网络拓扑设计、路由设计和带宽分配等问题。
通过最大流算法,我们可以确定卫星通信网中每个节点之间的最大传输速率,以便于选择最佳的路径或设计最优的路由方案。
此外,最大流算法也可以用于带宽管理,以确保卫星通信网中的每个节点都能够按照其需求获得足够的带宽。
3、电信领域在电信领域,最大流算法可以应用于网络拓扑设计、路由设计和负载均衡等问题。
电信网络中的节点之间互相连通,通过最大流算法,我们可以确定节点之间的最大传输速率,并根据传输速率设计最优的路由方案,以确保数据传输的完整性和可靠性。
此外,最大流算法还可以用于网络负载均衡,以确保所有节点的负载能够均衡分配。
算法难题集锦

算法难题集锦1. 旅行商问题(TSP):给定一组城市和距离矩阵,找到一条最短路径,使得旅行商可以从一个城市出发,经过每个城市恰好一次,然后回到起始城市。
2. 背包问题(Knapsack Problem):给定一组物体的重量和价值,以及一个限制的背包容量,找出在背包容量限制下,能够放入背包的物体,使得物体的总价值最大。
3. 图着色问题(Graph Coloring Problem):给定一个无向图,找到一种对图中的每个顶点进行着色的方法,使得相邻的顶点颜色不同,并且使用的颜色数量最少。
4. 最大流问题(Max Flow Problem):给定一个有向图和两个顶点,一个源节点和一个汇节点,求解通过图中的边的最大流量,使得从源节点到汇节点的最大流量最大化。
5. 内存分配问题:给定一组内存块和一组进程,找到一种分配内存块的方法,使得每个进程得到所需的内存,同时最大化内存利用率。
6. 矩阵链乘法问题:给定一组矩阵,找到一种矩阵乘法的顺序,使得相邻的矩阵可以相乘,并且乘法运算的次数最小化。
7. 最长公共子序列问题(Longest Common Subsequence Problem):给定两个序列,找到一个最长的公共子序列,即同时在两个序列中出现的最长的子序列。
8. 最小生成树问题(Minimum Spanning Tree Problem):给定一个连通图和边的权重,找到一个包含图中所有顶点且边的总权重最小的树。
9. 字符串匹配问题(String Matching Problem):给定一个文本串和一个模式串,找到模式串在文本串中的所有出现的位置。
10. 任务调度问题(Task Scheduling Problem):给定一组任务和它们的执行时间,找到一种合理的调度方式,使得完成所有任务的时间最小化。
最大流问题的增广路算法概要
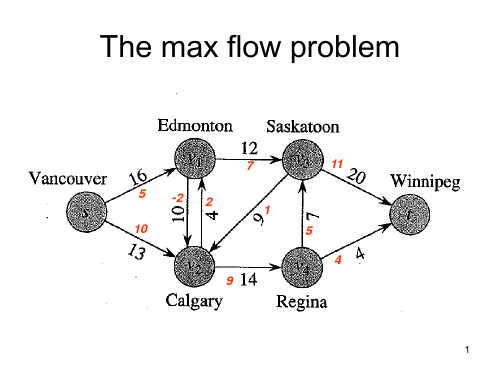
• A balanced city council must be formed by including exactly one member from each club and at most uk members from party Pk.
17
18
Local search checklist
• We always have a legal flow, i.e., one of value at most |f|. • Hence we can have at most |f| iterations.
10
Correctness of Ford-Fulkerson
• Since Ford-Fulkerson is partially correct and it terminates if capacities are integers it is a correct algorithm for finding the maximum flow if capacities are integers.
27
Complexity of Ford-Fulkerson
• With unary (4 ~ 1111) representation of integers, FordFulkerson is a polynomial time algorithm. • Intuition: When the input is longer it is easier to be polynomial time as a function of the input length. • An algorithm which is polynomial if integer inputs are represented in unary is called a pseudo-polynomial algorithm. • Intuitively, a pseudo-polynomial algorithm is an algorithm which is fast if all numbers in the input are small.
第一讲 流概念及算法
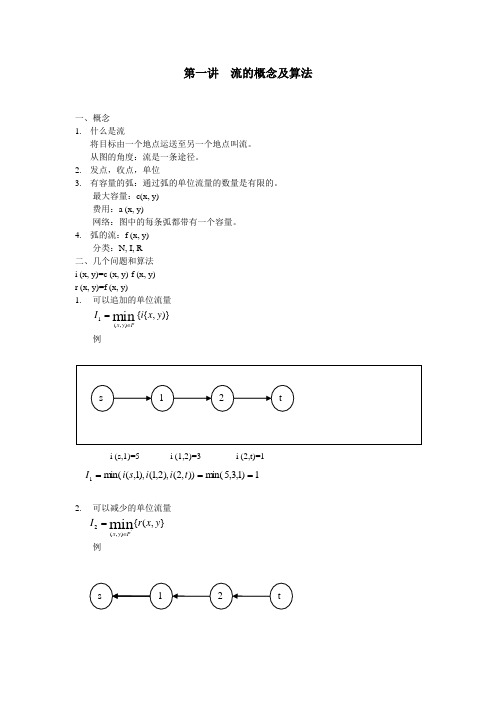
第一讲 流的概念及算法一、概念 1. 什么是流将目标由一个地点运送至另一个地点叫流。
从图的角度:流是一条途径。
2. 发点,收点,单位3. 有容量的弧:通过弧的单位流量的数量是有限的。
最大容量:c(x, y) 费用:a (x, y)网络:图中的每条弧都带有一个容量。
4. 弧的流:f (x, y)分类:N, I, R 二、几个问题和算法 i (x, y)=c (x, y)-f (x, y) r (x, y)=f (x, y)1. 可以追加的单位流量 )},{{min ),(1y x i I Py x ∈=例i (s,1)=5i (1,2)=3 i (2,t)=1 1)1,3,5m in()),2(),2,1(),1,(m in(1===t i i s i I2. 可以减少的单位流量 },({min '),(2y x r I P y x ∈=例r (1, s)=1 r (2, 1)=3 r (t, 2)=5 1}5,3,1m in{)}2,(),1,2(),,1(m in{2===t r r s r I3. 如何增加从s 至t 的净流前向弧,后向弧为后向弧,为前向弧),(:),(m in[]),(:),(m in{m in[3y x y x r y x y x i I =i (s, 1)=4 i (1, 2)=3 r (3, 2)=5 r (4, 3)=2 i (4, t)=33I =min{min[i (s, 1), i (1, 2), i (4, t)], min[r (3, 2), r (4, 3) ]}=min{min[4, 3, 3], min[5, 2]}=2流的增值链:可以运送追加单位流量的弧称为流的增值链。
4. 算法a) 主要思想:从发点s 生长出一棵由已着色的弧组成的树,追加的单位流量可以沿着这些弧从s 运出。
b) 增值算法:I. 确定集合N 、I 、R 中的元素,对s 着色。
数据结构中的的最大流问题与FordFulkerson算法

数据结构中的的最大流问题与FordFulkerson算法数据结构中的最大流问题与Ford-Fulkerson算法数据结构中的最大流问题(Maximum Flow Problem)是指在一个有向图中,给定源点和汇点,求解从源点到汇点的最大流量。
而Ford-Fulkerson算法是解决最大流问题的一种常用算法。
一、最大流问题描述最大流问题可以用一个有向图来表示,图中的每条边都有一个容量,表示该边所能承载的最大流量。
图中还有一个源点(source),表示流量的起始点,和一个汇点(sink),表示流量的终点。
最大流问题的目标是找到一条从源点到汇点的路径,使得路径上的边的流量之和最大。
二、Ford-Fulkerson算法原理Ford-Fulkerson算法基于增广路径的思想,通过不断寻找增广路径并更新路径上的边的流量,最终达到最大流量。
以下是Ford-Fulkerson算法的基本步骤:1. 初始化:将所有边的流量设为0;2. 寻找增广路径:使用深度优先搜索或广度优先搜索等方式,从源点到汇点找到一条增广路径;3. 计算路径上的最小剩余容量(即路径上的最小流量);4. 更新路径上的边的流量:将路径上的每条边的流量增加最小剩余容量;5. 重复步骤2至步骤4,直到无法找到增广路径为止;6. 输出最大流量。
三、Ford-Fulkerson算法示例为了更好地理解Ford-Fulkerson算法的应用过程,以下以一个简单的网络流问题为例进行演示。
假设有如下图所示的有向图,其中S表示源点,T表示汇点,A、B、C、D为其他节点。
边上的数字表示边的容量。
```(A)------3------>(B)/ | \ |3 4 2 |/ | \ |S 2 T 1\ | / |5 1 3 |\ | / |(C)------2------>(D)```首先,初始化所有边的流量为0。
然后,通过深度优先搜索或广度优先搜索寻找增广路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cut capacity = 30
2 9
Flow value 30
5
10
4
15
15
10
s A
5
3
8
6
10
t
15
4
6
15
10
4
30
7
Capacity = 30
15
Flows and Cuts
Weak duality. Let f be any flow. Then, for any s-t cut (A, B) we have v(f) cap(A, B). Pf.
Value of flow = 28 Cut capacity = 28
9 2 10 10 4 s 5 3 4 0 9 1 15 8 8 4 6 5 9
Flow value 28
15
0
10 9 10 10 10 t
A
15 14
4 0
6 14
15 0
4
30
7
17
Towards a Max Flow Algorithm
15 11
4 0
6 11
15 0
4
30
7
Value = 24
9
Maximum Flow Problem
Max flow problem. Find s-t flow of maximum value.
9 2 10 10 4 s 5 3 4 0 9 1 15 8 8 4 6 5 9
15
0
10 9 10 10 10 t
cap( A, B)
2 9
c(e)
e out ofA
5
s A
10
4
15
15
10
5
3
8
6
10
t
15
4
6
15
10
4
30
7
Capacity = 10 + 5 + 15 = 30
5
Cuts
Def. An s-t cut is a partition (A, B) of V with s A and t B. Def. The capacity of a cut (A, B) is:
Greedy algorithm. Start with f(e) = 0 for all edge e E. Find an s-t path P where each edge has f(e) < c(e). Augment flow along path P. Repeat until you get stuck.
f (e) f (e) v( f )
e out ofA
2 10
e in to A
6 9 0 15 8 5 6
s A
10 3 5
4 4
15
0
10 8
3
8 1
6
10 10 10
t
15 11
4 0
6 11
15 0
4
30
7
Value = 24
11
Flows and Cuts
Flow value lemma. Let f be any flow, and let (A, B) be any s-t cut. Then, the net flow sent across the cut is equal to the amount leaving s.
e in tov
e out ofv
Def. The value of a flow f is: v( f )
2 4 10 0 s 5 3 4 4 0 9 5
f (e) .
e out of s
0
4 8 0
0
15
15
0
10 4
6
10 0 10
t
capacity flow
15 0
e in tov
e out ofv
Def. The value of a flow f is: v( f )
2 10 10 3 s 5 3 4 4 6 9 5
f (e) .
e out of s
0
8 8 1
6
15
15
0
10 8
6
10 10 10
t
capacity flow
1
0 20
0 10
s
30 0
t
10 0
2
20 0
Flow value = 0
18
Towards a Max Flow Algorithm
Greedy algorithm. Start with f(e) = 0 for all edge e E. Find an s-t path P where each edge has f(e) < c(e). Augment flow along path P. Repeat until you get stuck.
e out ofs
by flow conservation
f (e) f (e) v A e out ofv e in to v f (e) f (e).
e out ofA e in to A
14
Flows and Cuts
Capacity = 10 + 8 + 10 = 28
2 9 5
10
4
15
15
10
s
5
3
8
6
10
t
A
15
4
6
15
7
Flows
Def. An s-t flow is a function that satisfies: For each e E: 0 f (e) c(e) [capacity] For each v V – {s, t}: f (e) f (e) [conservation]
Design and Analysis of Algorithms
3. Maximum Flow
Mingyu XIAO
School of Computer Science and Engineering University of Electronic Science and Technology of China
capacity flow
15 14
4 0
6 14
15 0
4
30
7
Value = 28
10
Flows and Cuts
Flow value lemma. Let f be any flow, and let (A, B) be any s-t cut. Then, the net flow sent across the cut is equal to the amount leaving s.
Flows and Cuts
Flow value lemma. Let f be any flow, and let (A, B) be any s-t cut. Then
f ( e) f (e ) v( f ) .
e out ofA e in toA
Pf.
v( f )
f (e)
Flows and Cuts
Flow value lemma. Let f be any flow, and let (A, B) be any s-t cut. Then, the net flow sent across the cut is equal to the amount leaving s.
A
4 8
v( f )
f (e ) f ( e)
e out ofA e in toA
s
B
t
f (e )
e out ofA
c( e )
e out ofA
7
6
▪
cap( A, B)
16
Certificate of Optimality
Corollary. Let f be any flow, and let (A, B) be any cut. If v(f) = cap(A, B), then f is a max flow and (A, B) is a min cut.
3
Minimum Cut Problem
Flow network. Abstraction for material flowing through the edges. G = (V, E) = directed graph, no parallel edges. Two distinguished nodes: s = source, t = sink. c(e) = capacity of edge e.
Nontrivial applications / reductions. Data mining. Network reliability. Open-pit mining. Distributed computing. Project selection. Egalitarian stable matching. Airline scheduling. Security of statistical data. Bipartite matching. Network intrusion detection. Baseball elimination. Multi-camera scene Image segmentation. reconstruction. Network connectivity. Many many more …
