90、30立方卧式罐液位高度对应容积
卧式储罐不同液位下的容积计算

卧式储罐不同液位下的容积计算卧式储罐是一种用于存储液体的设备,它的横向布置使得其在不同液位下的容积计算略有复杂。
在这篇文章中,我们将介绍如何计算卧式储罐在不同液位下的容积。
首先,我们需要了解卧式储罐的基本结构。
卧式储罐通常由圆筒形的罐体和两个半圆形的罩盖组成。
储罐的圆筒体积可以通过圆筒的高度和直径计算得到,罩盖的体积可以通过半球的体积公式计算得到。
卧式储罐在不同液位下的容积计算涉及到两个部分:液体位于圆筒部分的容积和液体位于罩盖部分的容积。
下面我们将逐步介绍如何计算这两个部分的容积。
液体位于圆筒部分的容积计算:液体位于圆筒部分的容积可以通过圆筒切割方法得到。
切割后的圆筒可以被视为一个高度为液位高度的小圆柱,其底面积等于卧式储罐的底面积。
因此,液体位于圆筒部分的容积等于卧式储罐的底面积乘以液位高度。
液体位于罩盖部分的容积计算:液体位于罩盖部分的容积可以通过罩盖切割方法得到。
根据切割后的罩盖形状,液体位于罩盖部分的容积可以分为顶圆锥体积和底椭球体积两部分。
顶圆锥体积可以通过圆锥体积公式计算得到。
圆锥体积的公式为V=(1/3)πr²h,其中V表示体积,r表示圆锥底面半径,h表示圆锥高度。
在这里,圆锥底面半径等于卧式储罐的直径,圆锥高度等于圆柱的高度减去液位高度。
底椭球体积可以通过椭球体积公式计算得到。
椭球体积的公式为V = (4/3)πabc,其中V表示体积,a,b和c分别表示椭球的半长轴、半短轴和半焦距。
在这里,半长轴等于卧式储罐的直径,半短轴等于圆柱的直径,半焦距等于半短轴减去液位高度。
最后,将液体位于圆筒部分的容积和液体位于罩盖部分的容积相加,即可得到卧式储罐在其中一液位下的总容积。
需要注意的是,以上计算方法均基于假设卧式储罐的罩盖为半圆形和圆柱体形状,实际情况可能会略有差异。
因此,在进行具体容积计算时,需要根据卧式储罐实际的罩盖形状进行相应的修正。
总之,卧式储罐在不同液位下的容积计算涉及到液体位于圆筒部分的容积和液体位于罩盖部分的容积。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积计算

椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l:椭圆封头直边长度(m);iL:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V:对应h高度卧罐内储液体积(m3);hm:对应h高度卧罐内储液重量(kg);h椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐体积与液位关系计算工具
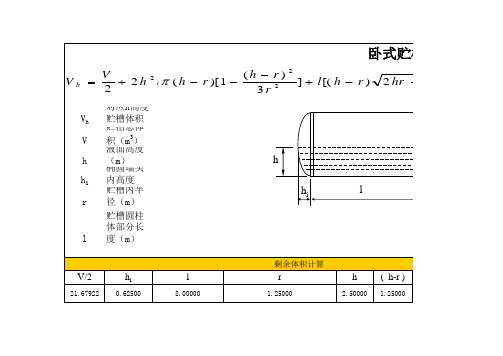
卧式贮槽体积计算公式
Vh V 2h 2
Vh [( h r ) i ( h r )[ 1 2 3r
2.50000
( h-r )
1.25000
卧式贮槽体积计算公式
2 hr h
2
r
2
arcsin(
h r )] r
剩余体积(M3) 43.35948
液位百分数
100.00000
注:设置好罐的参数,更改液位百分数即可计算出剩余体积,适合各种卧式罐
,适合各种卧式罐
2 hr h
2
r
2
arcsin
对应h高度贮槽体积(m3) 贮槽总体积(m3)=43.35844m³ 液面高度(m)
h hi
l
椭圆墙头内高度(不包括直边高度)(m) 贮槽内半径(m) 贮槽圆柱体部分长度(m)
剩余体积计算
V/2
21.67922
hi
0.62500
l
8.00000
r
1.25000
h
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
卧式容器不同液面高度的体积计算

化肥装置卧式容器不同液面高度的体积计算公式及运用(重庆建峰工业集团化肥分公司 乔华勇)摘要: 推导出尿素装置各种卧式容器不同液面高度的体积计算公式 。
并结合EXCEL软件实现便捷运算。
为装置运行过程中物料、蒸汽平衡计算以及即时成本计算 提供方便。
关键词:卧式容器;液面高度;体积;计算公式;EXCEL 。
重庆建峰工业集团化肥分公司于1993年建成投产,日产尿素1750吨。
工艺设备数量众多,包括塔、分解器、储罐等等。
其中,容器、储罐以卧式为主。
卧式容器的体积不像立式容器计算那样便捷,需运用较多数学知识才能实现。
所以每次系统的性能测试、成本计算都会因为容器液位变化问题而导致结果不精确。
因而,一套细致、准确的液面高度对应体积的数据参考,对于系统的各项测试和成本计算能够起到提高计算结果精确度的作用。
本文,笔者借助高等数学积分知识推导出卧式容器体积计算的通用公式,并在化肥尿素装置中加以运用。
1 计算公式容器分为两个部分:筒体、封头 。
公式推导过程中,将其二者分开讨论。
1.1 筒体部分筒体(图1)的横截面方程为:222t r y x =+故2122)(y r x t -=液面高度为h 时的体积:⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-=-=⎰--2arcsin12222πt tt t t t t y r h r t r r h r r h r r h Lr d y r LV ttr t :筒体内径,m h i :封头曲面深度,m L :筒体长度(含封头直边高度)V t :筒体体积,3mL图1 筒体1.2 封头部分尿素装置卧式容器的封头均为椭圆形封头(图2)。
所以,封头部分体积公式的推导按照椭圆球体积计算处理。
椭圆球面方程为:122222=++i th z r y x 故21222))(/(y x r r h z t t --=图2 封头当容器内的液面高度为h 时,封头的体积:()()⎥⎦⎤⎢⎣⎡+---=--==⎰⎰⎰⎰---32322332)(02222122t t t t ti r h r y r t s tif r r h r h r r h dx y x r dy r h zdxdy V ttt πh i :封头曲面深度,m V f :封头部分体积, 3m r t :筒体内径,m1.3 卧式容器卧式容器不同液面高度的体积为:ft V V V 2+=V :卧式容器体积, 3m V t :筒体部分体积, 3m V f :封头部分体积, 3m 2 尿素装置卧式容器不同液面高度的体积计算公式 2.1 容器的相关设计参数V05:原料氨储罐 V06:低压系统回收物料储罐 V10:系统蒸汽冷凝回收器设备位号L (m) t r (m)i h (m) 05300V8 1.35 0.868 06300V 12 2.385 1.165 10300V 5.921.50.752.2 容器的计算公式在化肥装置的实际运用 2.2.1 液面高度h 的计算λt r h 2=r t :筒体内径,m λ:容器液位计仪表显示值,1 2.2.2 05300V 不同液面高度对应体积计算公式f t V V V 2+==()()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯335.12335.135.135.135.18689.0235.135.1arcsin 35.135.1135.135.135.183322h h h h h ππ 2.2.3 06300V 不同液面高度对应体积计算公式f t V V V 2+==()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯3385.223385.2)385.2(385.2385.2165.12385.2385.2a r c s i n 385.2385.21385.2385.2385.2123322h h h h h ππ2.2.4 10300V 不同液面高度对应体积计算公式f t V V V 2+==()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯35.1235.1)5.1(5.15.175.025.15.1arcsin 5.15.115.15.15.192.53322h h h h h ππ3 EXCEL 计算从上述推导公式来看,式中使用的都是一些基本函数。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h :对应h 高度卧罐内储液重量(kg );椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下: 第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
