matlab遗传算法整数约束
matlab 约束条件

matlab 约束条件在MATLAB中,约束条件是一种限制条件,用于限定优化问题的解空间。
约束条件可以用于线性规划、非线性规划、整数规划等不同类型的优化问题。
在MATLAB中,可以使用不同的函数和工具箱来处理约束条件。
下面是一些常见的处理约束条件的方法:1. 线性规划约束条件:使用 linprog 函数进行线性规划求解,可以通过设置 A、b、Aeq、beq 参数来定义不等式约束和等式约束。
使用 fmincon 函数进行有约束的优化,可以通过设置 A、b、Aeq、beq 参数来定义不等式约束和等式约束。
2. 非线性规划约束条件:使用 fmincon 函数进行有约束的非线性优化,可以通过设置 nonlcon 参数来定义非线性约束函数。
使用 ga 函数进行遗传算法优化,可以通过设置 nonlcon参数来定义非线性约束函数。
3. 整数规划约束条件:使用 intlinprog 函数进行整数规划求解,可以通过设置 A、b、Aeq、beq 参数来定义不等式约束和等式约束。
使用 ga 函数进行遗传算法优化,可以通过设置 intcon 参数来定义整数变量。
除了上述方法外,还可以使用其他优化函数和工具箱来处理特定类型的约束条件,例如 quadprog 函数用于二次规划问题,bintprog 函数用于二进制整数规划问题等。
需要注意的是,在定义约束条件时,应确保约束条件的正确性和合理性,以避免产生无解或不可行解的情况。
此外,还可以使用可视化工具箱如 Optimization Toolbox 中的 Optimization App来直观地查看和调整约束条件。
总结起来,MATLAB提供了多种方法和工具箱来处理不同类型的约束条件,通过合理选择和设置约束条件,可以有效地求解各种优化问题。
使用Matlab进行多目标优化和约束优化

使用Matlab进行多目标优化和约束优化引言:多目标优化和约束优化是现代科学和工程领域中的重要问题。
在很多实际应用中,我们常常面对的是多个目标参数之间存在冲突的情况,同时还需要满足一定的约束条件。
这就需要我们采用适当的方法和工具进行多目标优化和约束优化。
本文将介绍如何使用Matlab进行多目标优化和约束优化。
一、多目标优化多目标优化是指在优化问题中存在多个目标函数,我们的目标是同时优化这些目标函数。
在Matlab中,可以使用多种方法进行多目标优化,其中常用的方法包括遗传算法、粒子群算法和模拟退火等。
1.1 遗传算法遗传算法是一种模拟生物进化过程的优化算法。
它模拟了遗传的过程,通过交叉、变异和选择等操作,利用群体中不断进化的个体来搜索最优解。
在多目标优化中,遗传算法常用于生成一组非支配解,即没有解能同时优于其他解的情况。
Matlab中提供了相关的工具箱,如Global Optimization Toolbox和Multiobjective Optimization Toolbox,可以方便地进行多目标优化。
1.2 粒子群算法粒子群算法是一种基于群体行为的优化算法。
它通过模拟鸟群或鱼群等群体的行为,寻找最优解。
在多目标优化中,粒子群算法也可以生成一组非支配解。
Matlab中的Particle Swarm Optimization Toolbox提供了相关函数和工具,可以实现多目标优化。
1.3 模拟退火模拟退火是一种模拟金属冶炼过程的优化算法。
它通过模拟金属在高温下退火的过程,通过温度控制来逃离局部最优解,最终达到全局最优解。
在多目标优化中,模拟退火算法可以通过调整温度参数来生成一组非支配解。
Matlab中也提供了相关的函数和工具,可以进行多目标优化。
二、约束优化约束优化是指在优化问题中存在一定的约束条件,我们的目标是在满足这些约束条件的前提下,使目标函数达到最优。
在Matlab中,也有多种方法可以进行约束优化,其中常用的方法包括罚函数法、惩罚函数法和内点法等。
MATLAB遗传算法工具使用教程

第八章使用MATLAB遗传算法工具最新发布的MA TLAB 7.0 Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱(Genetic Algorithm and Direct Search Toolbox,GADS)。
使用遗传算法与直接搜索工具箱,可以扩展MATLAB及其优化工具箱在处理优化问题方面的能力,可以处理传统的优化技术难以解决的问题,包括那些难以定义或不便于数学建模的问题,可以解决目标函数较复杂的问题,比如目标函数不连续、或具有高度非线性、随机性以及目标函数没有导数的情况。
本章8.1节首先介绍这个遗传算法与直接搜索工具箱,其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。
8.1 遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS(遗传算法与直接搜索)工具箱的特点、图形用户界面及运行要求,解释如何编写待优化函数的M文件,且通过举例加以阐明。
8.1.1 工具箱的特点GADS工具箱是一系列函数的集合,它们扩展了优化工具箱和MA TLAB数值计算环境的性能。
遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。
这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。
所有工具箱函数都是MATLAB的M文件,这些文件由实现特定优化算法的MATLAB语句所写成。
使用语句type function_name就可以看到这些函数的MATLAB代码。
我们也可以通过编写自己的M文件来实现来扩展遗传算法和直接搜索工具箱的性能,也可以将该工具箱与MATLAB的其他工具箱或Simulink结合使用,来求解优化问题。
工具箱函数可以通过图形界面或MA TLAB命令行来访问,它们是用MATLAB语言编写的,对用户开放,因此可以查看算法、修改源代码或生成用户函数。
遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题,譬如表查找问题等。
遗传算法与直接搜索工具箱有一个精心设计的图形用户界面,可以帮助我们直观、方便、快速地求解最优化问题。
用Matlab实现遗传算法

用GA找到函数最小值x = ga(fitnessfcn,nvars)局部无约束最小值,x是目标函数的适应度函数,nvars是适应度函数的尺寸(设计变量的数量)。
目标函数和适应度函数接受了1×N大小的x矢量,在x返回一个标量的计算值。
x = ga(fitnessfcn,nvars,A,b)在线性不等式约束下,适应度函数的局部最小值。
如果这个问题有m个线性不等式和n个变量,则A是m×n矩阵,b是m×1矩阵。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq)存在线性等式约束下,适应度函数的局部最小值。
如果没有不等式存在,设置A=[] 和 b=[]。
如果问题存在r个线性等式约束和n个变量,那么Aeq 是r ×n矩阵的大小,beq是r大小的矢量。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)定义了一系列设计变量x的最小和最大边界。
以至于在范围内找到一个解。
如果没有边界存在,LB 和 UB设置为空矩阵。
如果x(i)无下界,设置LB(i) = -Inf;如果x(i)无上界,设置UB(i) = Inf。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)服从在非线性约束条件下的最小值,非线性函数接收x,返回C和Ceq向量,分别代表非线性的不等式和等式。
GA最小化适应度函数,在C(x)≤0和Ceq(x)=0的条件下。
如果无边界存在,设置 LB=[] 和 UB=[]。
注意:当人口类型选项设置为“位串”或者“自定义”,非线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)用在结构选项中的值代替默认的优化参数来进行最小化,它也可以用gaoptimset函数来创建,具体参考gaoptimset的用法。
matlab工具箱遗传算法使用方法
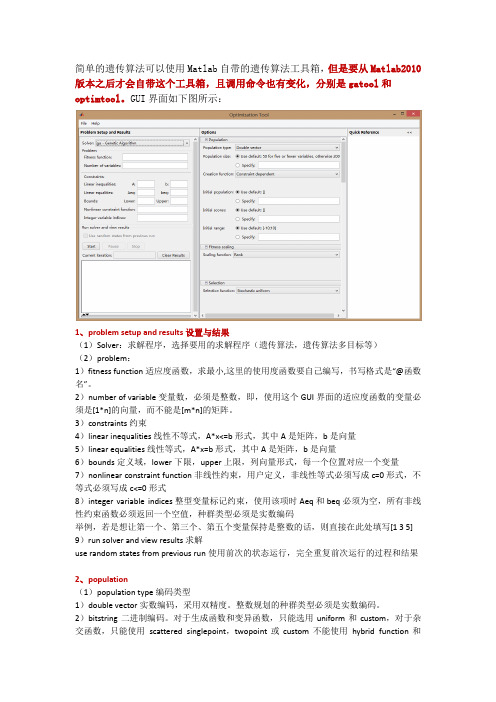
简单的遗传算法可以使用Matlab自带的遗传算法工具箱,但是要从Matlab2010版本之后才会自带这个工具箱,且调用命令也有变化,分别是gatool和optimtool。
GUI界面如下图所示:1、problem setup and results设置与结果(1)Solver:求解程序,选择要用的求解程序(遗传算法,遗传算法多目标等)(2)problem:1)fitness function适应度函数,求最小,这里的使用度函数要自己编写,书写格式是“@函数名”。
2)number of variable变量数,必须是整数,即,使用这个GUI界面的适应度函数的变量必须是[1*n]的向量,而不能是[m*n]的矩阵。
3)constraints约束4)linear inequalities线性不等式,A*x<=b形式,其中A是矩阵,b是向量5)linear equalities线性等式,A*x=b形式,其中A是矩阵,b是向量6)bounds定义域,lower下限,upper上限,列向量形式,每一个位置对应一个变量7)nonlinear constraint function非线性约束,用户定义,非线性等式必须写成c=0形式,不等式必须写成c<=0形式8)integer variable indices整型变量标记约束,使用该项时Aeq和beq必须为空,所有非线性约束函数必须返回一个空值,种群类型必须是实数编码举例,若是想让第一个、第三个、第五个变量保持是整数的话,则直接在此处填写[1 3 5] 9)run solver and view results求解use random states from previous run使用前次的状态运行,完全重复前次运行的过程和结果2、population(1)population type编码类型1)double vector实数编码,采用双精度。
整数规划的种群类型必须是实数编码。
matlab工具箱遗传算法使用方法

简单的遗传算法可以使用Matlab自带的遗传算法工具箱,但是要从Matlab2010版本之后才会自带这个工具箱,且调用命令也有变化,分别是gatool和optimtool。
GUI界面如下图所示:1、problem setup and results设置与结果(1)Solver:求解程序,选择要用的求解程序(遗传算法,遗传算法多目标等)(2)problem:1)fitness function适应度函数,求最小,这里的使用度函数要自己编写,书写格式是“@函数名”。
2)number of variable变量数,必须是整数,即,使用这个GUI界面的适应度函数的变量必须是[1*n]的向量,而不能是[m*n]的矩阵。
3)constraints约束4)linear inequalities线性不等式,A*x<=b形式,其中A是矩阵,b是向量5)linear equalities线性等式,A*x=b形式,其中A是矩阵,b是向量6)bounds定义域,lower下限,upper上限,列向量形式,每一个位置对应一个变量7)nonlinear constraint function非线性约束,用户定义,非线性等式必须写成c=0形式,不等式必须写成c<=0形式8)integer variable indices整型变量标记约束,使用该项时Aeq和beq必须为空,所有非线性约束函数必须返回一个空值,种群类型必须是实数编码举例,若是想让第一个、第三个、第五个变量保持是整数的话,则直接在此处填写[1 3 5] 9)run solver and view results求解use random states from previous run使用前次的状态运行,完全重复前次运行的过程和结果2、population(1)population type编码类型1)double vector实数编码,采用双精度。
整数规划的种群类型必须是实数编码。
matlab遗传算法求解约束问题

在MATLAB中使用遗传算法求解约束问题,你可以使用MATLAB的Global Optimization Toolbox,它包含一个名为ga的函数,可以用来求解无约束问题,而对于有约束问题,你可以使用conga函数。
conga函数是遗传算法的一种,专为求解约束优化问题而设计。
以下是一个简单的示例,用conga函数求解一个简单的约束问题:```Matlabfunction main% Objective functionfun = @(x) x(1)^2 + x(2)^2;% ConstraintsA = [1 1];b = [2];Aeq = [];beq = [];% Initial guessx0 = [0,0];% Call conga[x,fval] = conga(fun,2,A,b,Aeq,beq,x0);% Display resultsdisp('Solution')disp(x)disp('Objective function value at solution')disp(fval)end```这个示例中定义了目标函数为x(1)^2 + x(2)^2,想要找到使目标函数最小的x。
约束条件为x(1) + x(2) = 2。
这是一个等式约束问题。
在调用conga函数时,我们传入目标函数和约束条件等信息,并得到最优解和对应的函数值。
注意,你的问题和这个示例可能不完全一样,因此你需要根据实际情况调整目标函数、约束条件和初始猜测值等内容。
特别是约束条件,可能是等式约束也可能是不等式约束,甚至可能都有,你需要按实际情况提供。
遗传算法求解约束非线性规划及Matlab实现

第21卷第1期大 学 数 学Vol.21,№.1 2005年2月COLL EGE MA T H EMA TICS Feb.2005遗传算法求解约束非线性规划及Matlab实现倪金林(合肥工业大学理学院应用数学系,合肥230009) [摘 要]对于约束非线性规划问题,传统的方法:可行方向法、惩罚函数法计算烦琐且精度不高.用新兴的遗传算法来解决约束非线性规划,核心是惩罚函数的构造.以前的惩罚函数遗传算法有的精度较低,有的过于复杂.本文在两个定义的基础上构造了新的惩罚函数,并在新的惩罚函数的基础上,提出了一种解决约束非线性最优化问题的方法.通过两个例子应用Matlab说明了这个算法的可行性.[关键词]遗传算法;约束非线性规划;惩罚函数;交叉;变异[中图分类号]O22112 [文献标识码]A [文章编号]167221454(2005)01200912051 引 言约束非线性规划问题是运筹学中的一个重要分支,现实生活中许多实际问题都不能表达为容易解决的线性模型,如地下水调整系统和地下水污染来源识别问题中就不可避免非线性规划问题.解决约束非线性问题的方法也很多.一般方法,如可行方向法,惩罚函数法[1]都计算复杂且精度不高.遗传算法是一个新兴的方法,1975年Holland在他的著作《Adaptation in Nat ural and Artifical Systems》中首次提出遗传算法,很快就用遗传算法来解决非线性最优问题.而用遗传算法解决非线性等式与不等式约束最优化问题的核心问题是如何满足约束问题.如今用遗传算法解决非线性等式与不等式约束最优化有几种满足约束的策略:拒绝策略、改进策略、算子策略和惩罚策略[2].前三种策略不会产生不可行解,无法考虑可行域外的解,对于约束严的问题不可行解在种群中占的比例很大,因此将搜索限制在可行域内就很难找到可行解.惩罚策略不拒绝每代中的不可行解,其中一些个体可能提供关于最优解的更有用的信息,通过对不可行解的惩罚来将约束问题转换为无约束问题,任何对约束的违反都要在目标函数中添加惩罚项.因此,允许在搜索空间里的不可行域中进行搜索能实现更快更好的最终解.惩罚函数就是在遗传搜索中考虑不可行解的技术,给不可行解根据具体情况给予惩罚.如何设计一个好的惩罚函数就是关键.设计惩罚函数没有一般的指导性原则.Homaifar,Qi和Lai方法构造的惩罚函数简单,但不够精确. Joines和Houck设计的惩罚函数对参数太敏感.本文在两个定义基础上构造一个新的惩罚函数,并用两个例子说明该方法是有效可行的.2 遗传算法遗传算法是一种从适者生存概念和自然中抽象出来的基因运算,是基于自然选择机制和自然基因的相对较新的联合搜索方法.基因算法与其他的最优化方法相比有4点不同:1)遗传算法运算的是解集的编码,而不是解集本身. [收稿日期]2004201225 [基金项目]安徽省重点教学研究项目(2001011)2)遗传算法的搜索始于解的一种群,而不是单个解.3)遗传算法用的是目标函数本身,而不使用目标函数和约束函数的导数.4)遗传算法采用概率的,而不是确定的状态转移规则.遗传算法第一次是由Holland提出,自从提出以后,由于遗传算法不同于传统的最优化方法,有其灵活性和易变性.在基本的遗传算法中,许多文学中的变异,选择,交叉,平行计算被改进发展来加速方法的收敛和方法的有效性[4].遗传操作主要有三种:1)选择算子(Selection/rep roduction):选择算子从群体中按某一概率成对选择个体,某个体x被选择的概率Pi与其适应度值成正比.最通常的实现方法是轮盘赌(roulette wheel)模型.21交叉算子(Crossover):交叉算子将被选中的两个个体的基因链按概率Pc进行交叉,生成两个新的个体,交叉位置是随机的.其中Pc是一个系统参数.31变异算子(Mutation):变异算子将新个体的基因链的各位按概率Pm进行变异,对二值基因链(0,1编码)来说即是取反.对于遗传算法的收敛性一些研究人员对进化算法的运行机理进行过研究,Radolp h证明了一般的遗传算法不一定收敛,只有每代保存了最优个体时才收敛.对保存最优个体时遗传算法是收敛的结论的证明是通过对遗传算法构造马尔柯夫(Markov)链,因为遗传算法的进行过程是一个马尔柯夫过程.当遗传算法收敛时,求到的解通常只是所要解决问题的最优解的一个近似解,或者叫满意解.从数学分析的角度看,收敛过程是一个无限逼近过程,而计算过程是一个有限自动机,因此通过遗传算法程序求得的解总是一个近似解.近似解与问题真正的最优解的差是一个统计意义下的量,也就是说每次程序运行得到的解的质量可能是有较大的差别的.遗传算法一般采用二进制编码与实数编码.3 惩罚函数的改进及Matlab实现现在定义点x与可行域之间的距离d(x,Q)及非可行点可行度FD(x),在这两个定义的基础上提出了一种新的惩罚函数.一般形式的约束非线性规划问题为max f(x)=f(x1,x2,…,x n)s.t. x∈Q={x∈E n|g i(x)≤0,i=1,2,…,m1;h j(x)=0,j=1,2,…,m2}.定义d(x,Q)=max{0,g max(x),h max(x)},其中g max(x)=max{g i(x),i=1,2,…,m1}, h max(x)=max{|h j(x)|,j=1,2,…,m2}[5],d(x,Q)是点x与可行域Q之间为点超出约束的最大值,且反映了点x与可行域Q的关系.若d(x,Q) =0,则x∈Q;若d(x,Q)>0,则x|Q.d(x,Q)越大,表明x离可行域Q越远.定义FD(x)=∑m1i=1γi(x)+∑m2j=1λj(x)m1+m2,其中γi (x)=1,g i(x)≤0,1-g i(x)g max(x),0<g i(x)≤g max(x), λi(x)=1,h j(x)=0,1-|h j(x)|h max(x),其它.FD(x)也反映了x与可行域之间的关系.如果FD(x)=1,则x∈Q,若FD(x)=0,即g i(x)=g max(x), i=1,2,…,m1;h j(x)=h max(x),j=1,2,…,m2,则点完全不属于可行域.如果0<FD(x)<1,x|Q (记FD(x)为FD),且FD越大,突破约束越小.由上面的两个定义,可构造一个新的惩罚函数来处理x 在不可行域的适值函数.29大 学 数 学 第21卷eval (x )=f (x ),x ∈Q ,f (x )(d (x ,Q )+1/(FD +α))p ,f (x )≥0,x |Q ,f (x )3(d (x ,Q )+1/(FD +α))p ,f (x )<0,x |Q ,其中p ,α为参数,满足p ≥1,α>0.根据不同的情形,选择p ,α的值.上面的惩罚函数在处理极大化的问题时,若x 在可行域之内,等于目标函数值;不在可行域内,根据x 突破约束的程度来改变适值,脱离约束越大,d (x ,Q ),1/FD 越大,(d (x ,Q )+1/(FD +α))p 在p ≥1,α>0时也越大(d (x ,Q )+1/(FD +α))p .在p ≥1,α>0时恒大于1,所以求得的eval (x )越小于目标函数值.在遗传算法中被选取的概率越小,这也就达到了惩罚的目的.下面通过具体的例子来说明.先计算一个求约束非线性规划最小化问题例1 min F =x 31+2x 22x 3+2x 3,s.t. x 21+x 2+x 23=4,x 21-x 2+2x 3≤2,x 1,x 2,x 3≥0.对于上面的实例应用一般的遗传算法,序列二次规划(S Q P )方法及新的惩罚函数遗传算法(p =115,α=013)的结果如表1.表1变量一般GA 算法(α=10)一般GA 算法(α=100)SQ P 新算法精确解x 1015647011098010016010000010000x 2316549319849410000410000410000x 3010000010000010000010000010000F 0118035010026441194e -009010000010000 应用上面的惩罚函数在p =115,α=013时,得到的解为x 1=010000, x 2=410000, x 3=010000, f 1(x 1,x 2,x 3)=010000,且满足约束条件.上例用新惩罚函数的遗传算法的算法跟踪结果为图1.图1上面的例子说明在解非线性规划问题时,新构造的惩罚函数在遗传算法中可以得到更好的解.新的构造方法对于每代中根据具体的个体重新计算d (x ,Q ),1/FD ,让d (x ,Q ),1/FD 随着迭代进行而一直处于动态变化中.再举一个求最大化最优解的例子.39第1期 倪金林:遗传算法求解约束非线性规划及Matlab 实现例2 max f (x )=-2x 21+2x 1x 2-2x 22+4x 1+6x 2,s.t. 2x 1-x 2≤0,x 1+5x 2≤5,x 1,x 2≥0.对这个问题,应用可行方向法、惩罚函数法和上面新惩罚函数的遗传算法(p =115,α=011)的解对比结果如表2.表2变量可行方向法惩罚函数法基于权重GA Homairfar 的GA 新的算法x 1016300164501658016205016589x 2018740186901868017701018682F 6154461566616129616312616130上面的约束非线性最优化的实际最优解是x 1=01658,x 2=01868,F =616130.根据上表说明传统的解决约束非线性规划问题的方法可行方向法、惩罚函数法的方法的解比基于权重GA 差,Homaifar 的GA (r 1=019,r 2=1)得到的解结果也不是很好,而新的惩罚函数的遗传算法(p =115,α=011)的结果与基于权重的遗传算法[6]都相当于最优解.但是新的惩罚函数的遗传算法比基于权重的遗传算法简单.例2新惩罚函数的遗传算法的算法跟踪结果为图2.因为初始种群是随机产生,每次曲线可能不同,但最后的目标函数基本相同.图2新的惩罚函数的遗传算法应用在上面的两个例子:一个求最大化,一个求最小化得到的最优解比传统的解决约束非线性规划问题的方法、一般的遗传算法得到的结果都好,非常接近实际最优解.通过上述两个例子,参数p 在[1,6],α在[0101,015]内取值,容易得到比较好的解.由于遗传算法的初始的解是通过随机生成的,所以程序每次运行的结果可能不完全一样,但每次的结果误差都控制在一定的范围之内.可见,新的惩罚函数的遗传算法对于解决约束非线性规划问题是完全可行的,并且得到的结果优于传统的解决约束非线性规划问题的方法:可行方向法,惩罚函数法.比一般的遗传算法也要好.4 结 论解约束非线性规划问题一直是运筹学的一个难点.对于这个问题,已经有很多常规传统的解法,如可行方向法,惩罚函数法等.但这些方法计算复杂且结果不精确.遗传算法兴起以后,很快就应用到解决约束非线性规划问题.惩罚函数的选取一直是遗传算法的核心.本文根据两种脱离可行域程度函数d (x ,Q ),FD 来构造一种新的惩罚函数对突破可行域的x 进行惩罚.d (x ,Q ),FD 都是随着x 的变化而49大 学 数 学 第21卷动态地改变,因此能够更好地对每个具体的x 进行处理.用两种度量函数d (x ,Q ),FD 联合处理,互相补充,用两个参数调节解,能较好地得到最优解.通过两个实例,应用Matlab 进一步论证了这种方法的可操作性.[参 考 文 献][1] 运筹学教材编写组.运筹学[M ].北京:清华大学出版社,2000.180-189.[2] [日]玄光男,程润伟.遗传算法与工程设计[M ].北京:科学出版社,2000.36-38.[3] [日]玄光男,程润伟.遗传算法与工程设计[M ].北京:科学出版社,2000.39-40.[4] Guan Jiabao ,Mustafa M Aral.Progressive genetic algorithm for solution of optimization problems with nonlinearequality and inequality constraints[J ].Applied Mathematical Modelling ,1999,23:324-343.[5] 唐加福,汪定伟,许宝栋,李露.基于评价函数的遗传算法求解非线性规划问题[J ].控制与决策,2000,15(5):573-576.[6] 唐加福,汪定伟.一种求解非线性规划问题的改进遗传算法[J ].东北大学学报,1997,18(5):490-493.The Solution of Optimization with Nonliear Constraints Programmingwith G enetic Algorithm and Demonstration by MatlabN I J i n 2li n(Hefei University of Technology ,Hefei 230009,China )Abstract :To optimization with nonlinear constraints programming ,traditional method ,such as feasible direction ,penalty f unction ,is complicated and imprecise.Solving optimization with nonlinear constraints programming by genetic algorithm ,penalty f unction is core.The former genetic algorithm with penalty f unction is not perfect ,imprecise and complicated.Based on two definition ,the new penalty f unction is found.Throught new penalty f unction ,the article develops the new method of solution of optimization with nonliear constraints programming.Two examples show that the improved method is effective.K ey w ords :geneticalgorithm ;optimization with nonliear constraints programming ;penalty f unction ;mutation ;crossover 59第1期 倪金林:遗传算法求解约束非线性规划及Matlab 实现。
遗传算法在matlab中的实现

遗传算法是一种模拟自然选择与遗传机制的优化算法,它模拟了生物进化的过程,通过优化个体的基因型来达到解决问题的目的。
在工程和科学领域,遗传算法被广泛应用于求解优化问题、寻找最优解、参数优化等领域。
而MATLAB作为一款强大的科学计算软件,拥有丰富的工具箱和编程接口,为实现遗传算法提供了便利。
下面将通过以下步骤介绍如何在MATLAB中实现遗传算法:1. 引入遗传算法工具箱需要在MATLAB环境中引入遗传算法工具箱。
在MATLAB命令窗口输入"ver",可以查看当前已安装的工具箱。
如果遗传算法工具箱未安装,可以使用MATLAB提供的工具箱管理界面进行安装。
2. 定义优化问题在实现遗传算法前,需要清楚地定义优化问题:包括问题的目标函数、约束条件等。
在MATLAB中,可以通过定义一个函数来表示目标函数,并且可以采用匿名函数的形式来灵活定义。
对于约束条件,也需要进行明确定义,以便在遗传算法中进行约束处理。
3. 设置遗传算法参数在实现遗传算法时,需要对遗传算法的参数进行设置,包括种群大小、交叉概率、变异概率、迭代次数等。
这些参数的设置将会直接影响遗传算法的收敛速度和优化效果。
在MATLAB中,可以通过设置遗传算法工具箱中的相关函数来完成参数的设置。
4. 编写遗传算法主程序编写遗传算法的主程序,主要包括对适应度函数的计算、选择、交叉、变异等操作。
在MATLAB中,可以利用遗传算法工具箱提供的相关函数来实现这些操作,简化了遗传算法的实现过程。
5. 运行遗传算法将编写好的遗传算法主程序在MATLAB环境中运行,并观察优化结果。
在运行过程中,可以对结果进行实时监测和分析,以便对遗传算法的参数进行调整和优化。
通过以上步骤,可以在MATLAB中实现遗传算法,并应用于实际的优化问题与工程应用中。
遗传算法的实现将大大提高问题的求解效率与精度,为工程领域带来更多的便利与可能性。
总结:遗传算法在MATLAB中的实现涉及到了引入遗传算法工具箱、定义优化问题、设置算法参数、编写主程序和运行算法等步骤。
遗传算法GA的MATLAB代码

MATLAB实现算法代码:GA(遗传算法)——整数编码function [BestGene,aa] = GA(MaxGeneration,GeneSize,GeneNum,pcross,pmute,minGene,maxGene)Parent = Init(GeneSize,GeneNum,minGene,maxGene);[BestGene,Parent] = KeepBest(Parent);aa = [];for i = 1:MaxGeneration[i 1/value(BestGene)]Child = chose(Parent);Child = cross(Child,pcross);Child = mute(Child,pmute,maxGene);[BestGene,Parent] = KeepBest(Child);aa = [aa;value(BestGene)];endfunction GeneInit = Init(GeneSize,GeneNum,minGene,maxGene)GeneInit = [];for i = 1:GeneSizex = []; x = ceil(rand(1,GeneNum).*(maxGene-minGene)) + minGene;GeneInit = [GeneInit;x];endGeneInit = [GeneInit;x];function Child = chose(Parent)GeneSize = size(Parent,1);for i = 1:GeneSizex = Parent(i,:);val(i) = value(x);endValSum = sum(val);val = val / ValSum;for i = 2:GeneSizeval(i) = val(i) + val(i-1);endfor i = 1:GeneSizerandval = rand;if randval <= val(1)Child(i,:) = Parent(1,:);endfor j = 2:GeneSizeif randval > val(j-1) && randval <= val(j)Child(i,:) = Parent(j,:);break;endendendChild(end,:) = Parent(end,:);function Child = cross(Parent,pcross)[GeneSize,GeneNum] = size(Parent);GeneSize = GeneSize - 1;Child = Parent;for i = 1:GeneSize/2if rand < pcrossflag = 0;while( flag==0 )randval1 = floor((GeneNum-1)*rand) + 1;randval2 = floor((GeneNum-1)*rand) + 1;if randval1 ~= randval2flag = 1;endendtemp = Child(2*i-1,randval1:randval2);Child(2*i-1,randval1:randval2) = Child(2*i,randval1:randval2);Child(2*i,randval1:randval2) = temp;endendfunction Child = mute(Parent,pmute,maxGene)[GeneSize,GeneNum] = size(Parent);GeneSize = GeneSize - 1;Child = Parent;for i = 1:GeneSizeif rand < pmuterandval = ceil((GeneNum-1)*rand) + 1;Child(i,randval) = maxGene(randval) - Child(i,randval) + 1;endendfunction [BestGene,Parent] = KeepBest(Child)[GeneSize,GeneNum] = size(Child);for i = 1:GeneSizex = Child(i,:);val(i) = value(x);endBigVal = val(1);flag = 1;for i = 2:GeneSizeif BigVal < val(i)BigVal = val(i);flag = i;endendBestGene = Child(flag,:); Parent = Child;Parent(1,:) = BestGene; Parent(end,:) = BestGene;。
Matlab遗传算法,如何添加约束

Matlab 遗传算法,如何添加约束阿gen本人最近使用matlab 进行优化计算时,发现网络上有很多网友在寻求如何用遗传算法求解约束条件下的优化问题,本人现根据自己的摸索结果对如何求解该类问题做一简要说明,以求抛砖引玉。
例:目标函数2123-y x x x =+S.t. 2x 2+x 3≤1021212320101010101010x x x x x +≤-≤≤-≤≤-≤≤Matlab 遗传算法求解过程:1、在matlab 主面板command window 中输入gatool (或者OPTIMTOOL ),并按回车键执行命令,便可打开优化工具面板。
确保求解器为ga (遗传算法)。
2、优化工具面板说明:在打开的优化工具面板中,主要有problem setup and results (问题设置及结果显示)面板,options (选项)面板,Quick reference (快捷参考)面板。
解决非线性约束优化问题的关键点在于problem setup and results 中的设置。
以下按所给例子对其设置进行讲解。
3.在M 文件中编写目标函数,保存的文件名为“ex.m ”function y=ex(x)y=x(1)^2-x(2)+x(3)4. 在M 文件中编写非线性约束条件,保存的文件名为“tj.m ”function [c,cep]=tj(x)c(1)=2*x(1)+x(2)^2cep=[]5.按下图输入相应参数。
图中1为线性不等式约束条件,2为线性等式约束条件,3为各元素的上限和下限值,可依次填出。
4为非线性约束条件的方程,将所创建的约束条件方程的函数名填入即可。
(更详细的说明详见最右侧的Quick reference目录下的Constraints中的说明)6.在options中设置样本个数,终止条件等(一般默认即可),点击start,程序运行,可以看到大概运行到第4至第5代,便可得出优化结果。
基于Matlab工具的遗传算法求解有约束最优化问题概要

文章编号:1006-1576(2008 11-0043-02基于 Matlab 工具的遗传算法求解有约束最优化问题刘鲭洁,陈桂明,杨旗(第二炮兵工程学院 504教研室,陕西西安 710025摘要 :采用基于遗传算法的 Matlab 工具求解有约束的最优化问题,以函数 ga( 求解。
首先,编写求解的目标函数,再在编写的主程序中加入语句,运行主程序,最后的结果也给出运算寻优过程中,各代的进化信息中得出。
结果证明该工具是解决此类问题最有效工具之一。
关键词 :遗传算法; Matlab ;约束;优化中图分类号:TP311.1; O224 文献标识码:ASolving Constrained Optimization Through Genetic AlgorithmBased on Matlab ToolboxLIU Qing-jie, CHEN Gui-ming, YANG Qi(No. 504 Staff Room, The Second Artillery Engineering College, Xi’an 710025, ChinaAbstract: Matlab toolbox based on genetic algorithm (GA is used to solve constrainted optimization, and function ga( is the solving way. Firstly, the target function is compiled; then, the sentence is added into the main function, furthermore the main function is run; finally, eac h generation’s information is provided during the random-searching process. The result shows that this toolbox is one of the most effective ways to solve these questions.Keywords: Genetic algorithm; Matlab; Constraint; Optimization0 引言遗传算法的基本思想是从一个代表最优化问题解的一组初始值进行搜索,这组解称为一个群,种群由一定数量、通过基因编码的个体组成,其中每个个体称为染色体,不同个体通过染色体的复制、交叉或变异又生成新的个体,依照适者生存的规则,通过若干代的进化最终得出条件最优的个体。
matlab遗传算法整数约束

matlab遗传算法整数约束遗传算法是一种模拟自然界进化过程的优化算法,它通过模拟遗传操作和自然选择,逐步优化解空间中的解。
而在实际问题中,很多情况下需要对整数进行约束,即优化的解必须满足一定的整数条件。
本文将介绍如何在Matlab中使用遗传算法来解决整数约束问题。
我们需要明确整数约束的具体要求。
整数约束通常可以分为两种情况:一种是解的取值必须为整数,即优化的解必须是整数;另一种是解的取值范围限制在整数区间内,即优化的解只能在整数区间内取值。
接下来将分别介绍这两种情况下的处理方法。
对于解的取值必须为整数的情况,我们可以使用遗传算法的编码方式进行处理。
一种常用的编码方式是二进制编码,即将每个整数解转化为一个二进制串。
例如,假设我们要优化的解是一个3位整数,那么我们可以将解空间划分为8个区间,每个区间对应一个二进制串,如000表示0,001表示1,以此类推。
这样,在遗传算法的进化过程中,我们可以通过交叉、变异等遗传操作来生成新的二进制串,然后再将它们转化为整数解。
最后,通过适应度函数来评估每个解的优劣,并进行选择和进化,直至找到最优解。
对于解的取值范围限制在整数区间内的情况,我们可以通过调整遗传算法的参数来实现。
一种常用的方法是使用整数编码的实数遗传算法。
在实数遗传算法中,解空间中的每个解都用一个实数表示,然后通过适应度函数进行评估和选择。
在交叉和变异操作中,我们可以使用一些特定的方法来保证解的取值仍然在整数区间内。
例如,在交叉操作中,可以通过对两个解进行加权平均来生成新的解,然后再对新解进行四舍五入取整。
在变异操作中,可以对解进行微小的扰动,然后再进行四舍五入取整。
除了上述两种方法,还有一些其他的处理整数约束的方法。
例如,可以使用罚函数法来处理整数约束。
罚函数法通过给不符合整数约束的解增加一个罚函数值,从而惩罚这些解,使它们的适应度降低。
这样,在进化过程中,遗传算法会趋向于生成满足整数约束的解。
通过使用合适的编码方式、调整遗传算法参数或使用罚函数法,我们可以在Matlab中有效地处理整数约束问题。
遗传算法的Matlab实现讲解

Matlab函数调用实现GA
• Matlab的GA函数
[x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[], options);
fitnessfcn — Fitness function nvars — Number of variables for the problem Aineq — Matrix for inequality constraints Bineq — Vector for inequality constraints Aeq — Matrix for equality constraints Beq — Vector for equality constraints LB — Lower bound on x UB — Upper bound on x nonlcon — Nonlinear constraint Function options — Options structure
global Cmin;
Cmin=-10^6; popsize=50; %群体大小 Gene=20; chromlength=20; %字符串长 度(个体长度) pc=0.8; %交叉概率 pm=0.01; %变异概率 Xmax=10; Xmin=0;
[bestindividual,bestfit]=best(pop,fitvalue); %求出群体中适应值最大的 个体及其适应值
Matlab函数调用实现GA
• GA函数调用步骤
第一步:编写适应度函数; 第二步:对GA参数进行设置; options = gaoptimset(‘参数名’, 参数值, …, ‘参数名’, 参数值) 例:options = gaoptimset('PopulationSize', 100) 第三步:调用GA函数; [x fval] = ga(@fitnessfun, nvars) [x fval exitflag output population scores] = ga(@fitnessfcn, nvars) [x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[],options);
遗传算法整数约束

遗传算法整数约束遗传算法是一种模拟自然选择和自然遗传机制的优化算法。
在遗传算法中,一定数量的解称为一个种群,在每一代种群中,通过交叉、变异和选择等操作,产生下一代种群,直到达到满意的解。
这种算法在智能优化领域中应用广泛,因为它可以处理不同类型的问题,并且不需要太多的先验知识或数学模型。
然而,在遗传算法中,处理整数约束是一个常见的问题,有不同的方法可以解决这个问题。
第一步:编码在遗传算法中,问题的解可以通过染色体来表示。
对于数值问题,染色体中的基因表示问题中某个变量的值。
在处理整数约束时,可以将基因编码为整数,这样可以确保生成的解也是整数。
例如,对于一个需要确定非负整数x和y的问题,可以将它们的染色体编码为整数。
这种编码方式可以通过以下几种方法实现:1. 将基因直接编码为整数:将基因值映射为[0,MAX_VALUE],取整数部分作为整数基因。
2. 二进制编码:可以将整数转换为二进制字符串,然后在染色体中使用二进制字符串来表示整数基因。
第二步:适应度函数在遗传算法的每一代中,都会根据适应度函数来选择优良染色体。
适应度函数是评价染色体质量的函数。
根据问题的特点,可以设计合适的适应度函数来处理整数约束。
例如,对于需要求解非负整数问题的遗传算法,可以使用一个适应度函数,该函数用于评估一个解的质量。
适应度函数可以将不符合约束的解的适应度值设为0,以便选出仅包含符合约束的解。
然后,通过调整需要求解的函数来进行更好的适应度函数。
第三步:交叉和变异操作在遗传算法中,通过交叉和变异操作从父代染色体中产生新的子代染色体。
可以通过以下步骤来实现整数约束。
1. 交叉操作:根据交叉概率选择两个染色体,并选择一个位置进行交叉。
如果两个基因都是整数,那么它们可以直接交叉。
如果其中一个基因不是整数,则可以使用取整函数进行取整操作。
2. 变异操作:通过变异概率选择一个染色体,然后对其中的一个基因进行变异。
如果基因不是整数,则可以通过添加或减去一个整数来将其变为整数。
遗传算法约束条件matlab程序

遗传算法约束条件matlab程序遗传算法是一种模拟自然界遗传机制的优化算法,它通过模拟遗传的过程来搜索最优解。
在实际应用中,我们常常需要对遗传算法进行一些约束,以保证搜索结果符合特定的要求。
本文将介绍如何在Matlab中实现对遗传算法的约束条件。
我们需要明确遗传算法的基本流程。
遗传算法主要包括初始化种群、选择、交叉、变异和适应度评价等步骤。
在这个流程中,我们可以通过调整参数和添加约束条件来控制算法的搜索过程。
为了实现约束条件,我们首先需要定义适应度函数。
适应度函数用于评价每个个体的适应度,即其与最优解的接近程度。
在定义适应度函数时,我们可以根据具体问题的约束条件进行调整。
接下来,我们需要添加约束条件。
常见的约束条件包括线性约束、非线性约束、等式约束和不等式约束等。
在Matlab中,我们可以使用线性规划工具箱或非线性规划工具箱来添加约束条件。
这些工具箱提供了丰富的函数和方法,可以帮助我们实现约束条件。
在实际使用中,我们可以根据具体问题的特点来选择合适的约束条件。
例如,如果我们需要在一定的约束下求解某个函数的最优解,我们可以使用线性约束或非线性约束来限制搜索空间。
如果我们需要满足一些等式约束或不等式约束,我们可以使用等式约束或不等式约束来限制个体的取值范围。
除了添加约束条件,我们还可以通过调整遗传算法的参数来进一步控制搜索过程。
例如,我们可以调整种群大小、交叉率和变异率等参数来影响搜索的速度和精度。
此外,我们还可以使用遗传算法的改进方法,如精英保留策略、自适应参数和多目标优化等来提高搜索效果。
在实际使用中,我们还可以结合其他优化算法和技术来进一步改进遗传算法的性能。
例如,我们可以使用模拟退火算法、粒子群算法或遗传神经网络等方法来优化遗传算法的搜索过程。
遗传算法是一种强大的优化算法,可以应用于各种复杂的问题。
通过添加约束条件和调整参数,我们可以进一步提高遗传算法的搜索效果。
在Matlab中,我们可以使用丰富的工具和函数来实现对遗传算法的约束条件。
非线性整数规划的遗传算法matlab程序

非线性整数规划的遗传算法Matlab程序(附图)通常,非线性整数规划是一个具有指数复杂度的NP问题,如果约束较为复杂,Matlab优化工具箱和一些优化软件比如lingo等,常常无法应用,即使能应用也不能给出一个较为令人满意的解。
这时就需要针对问题设计专门的优化算法。
下面举一个遗传算法应用于非线性整数规划的编程实例,供大家参考!模型的形式和适应度函数定义如下:这是一个具有200个01决策变量的多目标非线性整数规划,编写优化的目标函数如下,其中将多目标转化为单目标采用简单的加权处理。
function Fitness=FITNESS(x,FARM,e,q,w)%% 适应度函数% 输入参数列表% x 决策变量构成的4×50的0-1矩阵% FARM 细胞结构存储的当前种群,它包含了个体x% e 4×50的系数矩阵% q 4×50的系数矩阵% w 1×50的系数矩阵%%gamma=0.98;N=length(FARM);%种群规模F1=zeros(1,N);F2=zeros(1,N);for i=1:Nxx=FARM{i};ppp=(1-xx)+(1-q).*xx;F1(i)=sum(w.*prod(ppp));F2(i)=sum(sum(e.*xx));endppp=(1-x)+(1-q).*x;f1=sum(w.*prod(ppp));f2=sum(sum(e.*x));Fitness=gamma*sum(min([sign(f1-F1);zeros(1,N)]))+(1-gamma)*sum(min([sign(f2-F2);zeros(1,N)]));针对问题设计的遗传算法如下,其中对模型约束的处理是重点考虑的地方function [Xp,LC1,LC2,LC3,LC4]=MYGA(M,N,Pm)%% 求解01整数规划的遗传算法%% 输入参数列表% M 遗传进化迭代次数% N 种群规模% Pm 变异概率%% 输出参数列表% Xp 最优个体% LC1 子目标1的收敛曲线% LC2 子目标2的收敛曲线% LC3 平均适应度函数的收敛曲线% LC4 最优适应度函数的收敛曲线%% 参考调用格式[Xp,LC1,LC2,LC3,LC4]=MYGA(50,40,0.3)%% 第一步:载入数据和变量初始化load eqw;%载入三个系数矩阵e,q,w%输出变量初始化Xp=zeros(4,50);LC1=zeros(1,M);LC2=zeros(1,M);LC3=zeros(1,M);LC4=zeros(1,M);Best=inf;%% 第二步:随机产生初始种群farm=cell(1,N);%用于存储种群的细胞结构k=0;while k %以下是一个合法个体的产生过程x=zeros(4,50);%x每一列的1的个数随机决定for i=1:50R=rand;Col=zeros(4,1);if R<0.7RP=randperm(4);%1的位置也是随机的Col(RP(1))=1;elseif R>0.9RP=randperm(4);Col(RP(1:2))=1;elseRP=randperm(4);Col(RP(1:3))=1;endx(:,i)=Col;end%下面是检查行和是否满足约束的过程,对于不满足约束的予以抛弃Temp1=sum(x,2);Temp2=find(Temp1>20);if length(Temp2)==0k=k+1;。
matlab遗传算法函数

matlab遗传算法函数MATLAB遗传算法函数是一种高效的优化算法,它基于生物学的遗传进程和自然选择机制建立数学模型,并利用进化算法中的遗传操作和适应度评估方法,搜索最优的解。
该算法广泛应用于多个领域,如工程优化、控制系统、机器学习、生物信息学、图象处理等。
本文将对常用的MATLAB遗传算法函数进行描述和介绍。
1. ga(遗传算法)ga是MATLAB中常用的遗传算法函数,用于寻找多目标函数的最优解。
这个函数可以用来解决最优化问题,包括线性优化、非线性优化、混合整数线性优化等。
例如,如果需要在约束条件下最小化一个多项式函数,可以使用以下代码:x = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options)其中,fun是目标函数,nvars是决策变量的数量,A和b是线性不等式限制条件,Aeq和beq是线性等式限制条件,lb和ub是变量的上下限非线性限制条件由nonlcon定义,options 是定义遗传算法的参数和配置的结构体数组。
3. gaoptimset(算法选项)gaoptimset函数是用于设置MATLAB遗传算法函数的选项和参数的函数。
通过修改选项,可以控制遗传算法的行为和表现。
常用的选项包括:PopulationSize:种群大小Generations:进化代数CrossoverFraction:交叉概率EliteCount:精英个数MutationFcn:变异函数SelectionFcn:选择函数例如,以下代码设置种群大小为50、进化代数为100、交叉概率为0.8、精英个数为2、变异函数为mutationuniform:options =gaoptimset('PopulationSize',50,'Generations',100,'CrossoverFraction',0.8,'Elit eCount',2,'MutationFcn',@mutationuniform);4. mutationgaussian(高斯变异)mutationgaussian是MATLAB中默认的变异函数之一,它可以引入随机扰动以增加解的多样性。
matlab有约束条件的遗传算法

matlab有约束条件的遗传算法Matlab中的遗传算法是一种超级有趣又很实用的优化算法呢!那要是再加上约束条件,就像是给这个算法加上了一些特殊的规则,让它在特定的范围内“玩耍”。
一、遗传算法基础。
遗传算法的灵感可是来源于生物的遗传进化哦。
就想象一下,有一群小生物(在算法里就是一个个可能的解啦),它们要通过不断地繁衍、变异、竞争,最后找到最适合生存(也就是最优解)的方式。
在Matlab里,我们可以很方便地创建初始种群。
比如说,我们可以用随机数来生成一些初始的个体,这些个体就像是一群懵懵懂懂的小生物,还不知道自己在这个算法世界里的命运呢。
每个个体都有自己的一组基因(在算法里就是一些参数值啦),这些基因决定了这个个体的“特性”。
二、约束条件的重要性。
那为啥要有约束条件呢?这就好比是在一个游戏里,你不能随便乱跑,得在规定的场地里活动。
在实际的优化问题中,约束条件是非常常见的。
比如说,你要设计一个产品,可能会受到成本的限制,或者是尺寸的限制。
在Matlab的遗传算法里,约束条件可以让我们的搜索范围更加合理。
如果没有约束条件,算法可能就会跑到一些不合理的区域,找到一些根本不符合实际情况的解。
这就像是你在找宝藏,结果跑到了外太空,那肯定是不对的呀。
三、Matlab里实现有约束条件的遗传算法。
在Matlab里实现这个算法可没有想象中那么难哦。
我们首先要定义目标函数,这个函数就像是一个裁判,它会告诉每个个体(解)是好是坏。
然后呢,就是要把约束条件给加进去。
这就有点像给小生物们画一个圈,告诉它们只能在这个圈里活动。
一种常见的方法是采用罚函数法。
简单来说,就是如果一个个体违反了约束条件,我们就给它一个惩罚,让它的“适应度”降低。
就像是小生物犯了错,要被扣分一样。
这样,随着算法的迭代,那些违反约束条件的个体就会逐渐被淘汰,最后留下来的就是符合约束条件的比较好的解啦。
四、实际应用的例子。
比如说,我们要优化一个生产流程,目标是最大化利润,但是有很多约束条件,像原材料的供应限制、设备的生产能力限制等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab遗传算法整数约束
遗传算法是一种通过模拟进化过程来解决优化问题的算法。
在许多实际问题中,我们需要找到满足一定约束条件的整数解。
本文将介绍如何使用MATLAB编程语言实现遗传算法,并给出一个整数约束的示例问题。
我们需要定义问题的目标函数和约束条件。
假设我们要求解的问题是在一定范围内找到使得目标函数取得最大值的整数解。
目标函数可以是任意的数学函数,如线性函数、非线性函数等。
约束条件可以包括等式约束和不等式约束,限制了解的取值范围。
接下来,我们需要定义遗传算法的基本元素,包括染色体表示、初始化种群、适应度评价、选择、交叉和变异等操作。
对于整数约束问题,染色体可以用一个整数数组表示,每个元素对应一个变量的取值。
种群可以由多个染色体组成,初始种群可以通过随机生成整数数组来实现。
适应度评价可以通过计算目标函数值来衡量染色体的优劣。
选择操作可以根据适应度值来确定优秀染色体的概率选择。
交叉操作可以通过交换染色体的某些片段来产生新的染色体。
变异操作可以通过改变染色体中的某个元素值来引入新的解。
在MATLAB中,我们可以使用遗传算法工具箱来实现遗传算法。
首先,我们需要定义一个函数来描述问题的目标函数和约束条件。
然后,我们可以使用`ga`函数来求解整数约束问题。
该函数的输入参
数包括目标函数、变量的取值范围、约束条件等。
通过设置适当的参数,我们可以控制遗传算法的执行过程。
下面,我们以一个简单的整数约束问题为例进行演示。
假设我们要求解的问题是在区间[0, 10]内找到使得函数f(x) = x^2取得最大值的整数解。
我们可以定义目标函数和约束条件如下:
```matlab
function y = myfun(x)
y = -x.^2; % 目标函数,取负号使得求解最大值问题
end
function [c, ceq] = mycon(x)
c = []; % 不等式约束条件
ceq = []; % 等式约束条件
end
```
然后,我们可以使用遗传算法工具箱中的`ga`函数来求解整数约束问题:
```matlab
lb = 0; % 变量下界
ub = 10; % 变量上界
intcon = 1; % 整数约束
[x, fval] = ga(@myfun, 1, [], [], [], [], lb, ub, @mycon, intcon); ```
以上代码中,`@myfun`表示目标函数,`1`表示变量的个数,`[]`表示不等式约束条件,`lb`和`ub`表示变量的下界和上界,`@mycon`表示约束条件,`intcon`表示整数约束。
通过运行以上代码,我们可以得到目标函数取得最大值的整数解。
在实际问题中,我们可以根据具体的需求来定义目标函数和约束条件,并使用遗传算法来求解整数约束问题。
本文介绍了如何使用MATLAB编程语言实现遗传算法来求解整数约束问题。
通过定义目标函数和约束条件,并使用遗传算法工具箱中的`ga`函数,我们可以有效地求解这类问题。
遗传算法在解决优化问题中具有广泛的应用,能够处理各种约束条件,包括整数约束。
希望本文能对读者理解和应用遗传算法有所帮助。
