2018年国考数量关系押题卷
粉笔2018年国考第11季行测数量模拟题

粉笔2018国考第11季行测模考数量关系(1)某公司准备在中秋前夕为单位员工发放月饼,要求尽量把月饼分完。
若全部平均分给甲部门则每人可得5个月饼且还剩余11个,若全部平均分给乙部门则每人可得6个月饼还剩3个,若尽量平均分给丙部门的12人,则每人至少会分得几个月饼:【粉笔模考】A.11 B.10 C.8 D.6楚香凝解析:每人5个还剩下11个,说明月饼数不少于(5*12)+11=71个;总月饼数除以5余11、除以6余3;除以5余11的有:11、16、21…其中满足除以6余3的是21,所以满足两个条件的通项公式为30n+21,n最小取2,月饼数最少81个,分给丙部门时,81/12=6…9,每人至少分6个,选D(2)某次球赛的门票为200元,由于开赛前一天未售完,主办方决定打折处理,最后一天又卖出了之前已售门票的1/5。
最后售出的门票数量比预计多了1/4,门票收入比预计多了1/6,问主办方最后一天将门票打几折出售:【粉笔模考】A.七折B.六折C.八五折D.八折楚香凝解析:假设之前已售门票为25份,最后一天又卖出5份,共售出30份,所以预计售出30/(1+ 1/4)=24份、预计收入为200*24=4800份,所以实际收入=4800*(1+ 1/6)=5600份,其中之前已售的25份收入为25*200=5000份,最后一天卖出的5份收入为5600-5000=600份,说明1份=120元,折扣=120/200=60%,选B(3)工匠计划在一块体积为1000cm3的正方体铁块上焊接一个长、宽、高分别为8cm、5cm、3cm的长方体铁块做成一个模具。
则焊接后的模具表面积最大为:【粉笔模考】A.710cm2B.728cm2C.743cm2D.758cm2楚香凝解析:假设在正方体的上方焊接一个长方体,焊接后增加了前后左右四个面,增加的面积最大=2*(8*5+8*3)=128cm2,原来正方体的表面积=6*10*10=600cm2,焊接后总的表面积=128+600=728cm2,选B(4)某书架有两层书籍,在第一层放入一些书后,此时第一层的书占书总数的2/7,再在第二层放入同样多的书,此时第一层与第二层的书的数量之比为1:3。
粉笔2018年国考第23季行测数量模拟题

粉笔2018年国考第23季行测数量模拟题第一篇:粉笔2018年国考第23季行测数量模拟题粉笔2018国考第23季行测模考数量关系(1)王师傅每周一、三、五在工厂值班,已知某年1月份王师傅共值班14天,则当年的元旦是星期几?【粉笔模考】A.星期一或星期三B.星期二或星期四C.星期一D.星期二楚香凝解析:每周值班三天,14=(3*4)+2,说明值班四周又两天,所以前三天里有两天值班,所以元旦为周一或周三,选A (2)某高校艺术学院分音乐系和美术系两个系别,去年共有学生940人。
今年音乐系学生人数增加1/6,美术系学生人数减少10%,总人数增加50人。
则该学院今年音乐系学生有多少人?【粉笔模考】A.400B.420C.540D.630 楚香凝解析:解法一:今年音乐系人数是7的倍数,排除AC;今年总人数是990、其中美术系人数是9的倍数,所以今年音乐系人数也是9的倍数,选D 解法二:鸡兔同笼,假设去年的940人都是美术系人数,则今年减少940*10%=94人,可得去年音乐系人数=(94+50)/(1/6 + 10%)=540,今年音乐系人数=540*(1+ 1/6)=630人,选D (3)现有同一种服装的A、B两个订单,已知甲车间完成A订单需要5天,乙车间完成A订单需要8天,丙车间完成B订单需要10天。
若甲、乙、丙三个车间同时工作,则完成A和B两个订单恰好需要4天,问乙车间单独完成B订单需要几天?【粉笔模考】A.3 B.4C.6D.8 楚香凝解析:假设A订单总任务量40,可得甲的效率为8、乙的效率为5,甲乙合作4天完成52的任务量,所以多出52-40=12的任务量需要丙单独做(10-4)=6天,可得B订单总任务量=(12/6)*10=20,乙单独完成需要20/5=4天,选B(4)一个高10厘米的圆柱形水杯,装有2/3的盐水溶液,加浓度为40%的盐水至水杯装满,充分混合后倒出一半,再加水至水杯8厘米高处,此时杯中盐水的浓度为15%,问最初水杯中盐水的浓度为多少?【粉笔模考】 A.8% B.16% C.18% D.24% 楚香凝解析:倒出5份后,剩余5份的溶液加了3份的水后浓度变为15%,所以之前充分混合后的浓度为(8*15%)/5=24%;假设水杯总容量为3份,(3*24%1/15)=300,选B(13)上午8点甲、乙二人同时匀速从A地出发开车前往B地,40分钟后甲到达B地,此时乙距离两地的中点处还有10分钟的车程,且乙车恰好发生故障。
2018年国家公务员考试数量关系备考习题及答案(一).

2018年国家公务员考试数量关系备考习题及答案(一1.3点19分时,时钟上的时针与分针所构成的锐角为几度?A. 14 度B. 14.5 度C. 15 度D. 15.5 度2. 某人银行账户今年底余额减去1500元后,正好比去年底余额减少了25%,去年底余额比前年底余额的120%少2000元。
则此人银行账户今年底余额一定比前年底余额:A. 多1000元B. 少1000元C多10%D.少10%3. 有70名学生参加数学、语文考试,数学考试得60分以上的有56人,语文考试得60分以上的有62人,都不及格的有4人,则两门考试都得60分以上的有多少人?A. 50B. 51C. 52D. 534. 某单位购买了10台新电脑,计划分配给甲、乙、丙3个部门使用。
已知每个部门都需要新电脑,且每个部门最多得到5台,那么电脑分配方法共有(种。
A. 9B. 12C. 18D. 275. 小明和姐姐用2013年的台历做游戏,他们将12个月每一天的日历一一揭下,背面朝上放在一个盒子里,姐姐让小明一次性帮她抽出一张任意月份的30号或者31 号。
问小明一次至少应抽出多少张日历,才能保证满足姐姐的要求?A. 346B. 347C. 348D. 3491. 【答案】B。
解析:从3点整到3点19分,分针走过6X19=114°,时针走过0.5 X9=9.5在3点整的时候时针、分针夹角为90°,所以在3点19分时的夹角为114-90-9.5=14.5。
°2. 【答案】D。
解析:设前年底的余额为x元,则去年底余额为(120%x-2000元,今年底余额为(120%X-2000X1-25%+1500=0.9X元,则今年底余额为前年底的90%,所以今年底余额一定比前年底余额少10%。
3. 【答案】C。
解析:由题意知,数学考试不及格的有70-56=14人,语文考试不及格的有70-62=8人,故至少有一门不及格的人数为14+8-4=18人,两门都及格的人数为70-18=52人。
粉笔2018年国考第18季行测数量模拟题

粉笔2018国考第18季行测模考数量关系(1)某公司销售部门和客服部门共有员工70人。
其中销售部门有2/3是男性,客服部门有3/5是女性。
则两个部门的男性比女性最多多()人:【粉笔模考】A.8B.12C.15D.18楚香凝解析:销售部门中男性占的比例比女性多1/3,客服部门中男性占的比例比女性少1/5,所以要使得销售部门的人数尽可能多,3和5的倍数,最大取60人,此时客服部门有10人,男性比女性多[60*(1/3)]-[10*(1/5)]=18人,选D(2)甲、乙两队合作做某项工程需要12天,甲、乙、丙三队合作做该项工程需要10天。
若甲队效率比乙队效率低1/3,则乙、丙两队合作所需天数比甲、丙两队合作少几天:【粉笔模考】A.6B.5C.3D.2楚香凝解析:假设总任务量60,可得效率甲+乙=5、甲+乙+丙=6,所以甲效率2、乙效率3,乙+丙=6-2=4、甲+丙=6-3=3,(60/3)-(60/4)=5,选B(3)小赵在一家服装店买了一件衬衣、一条裙子和一条裤子,参加了店铺“每满500元减100元”的优惠活动后共花费1550元。
几天后服装店的促销活动改为了“购满三件享折扣”,且折后价格仍高于1000元还可优惠100元。
小赵发现如果她此时才来购买同样的服装可再少花540元。
则服装店后面的促销活动为购买满三件打几折:【粉笔模考】A.六折B.六五折C.七折D.七五折楚香凝解析:花费1550说明优惠了300元,所以原价为1850元;打折后的价格为1550-540+100=1110元,1110/1850=0.6,选A(4)某慈善基金会发起给贫困山村学生捐赠书本的活动,且已有10人捐赠了129本书。
已知10人的捐赠数量都不相同,捐赠数量最少的三个人平均每人捐赠了5本书,则捐赠数量第四多的人,其捐赠书的数量最多为多少?【粉笔模考】A.21本B.22本C.33本D.34本楚香凝解析:要想使第四名数量最多,则其他人数量要尽可能的少;令后六名捐的书本数分别为4、5、6、7、8、9,可得前四名共捐了129-(4+9)*3=90本,构成等差数列,则第2.5名捐了90/4=22.5本,所以第四名捐了22.5-1.5=21本,选A(5)国考某岗位参考考生为100人,该岗位考试科目为《行政职业能力测试》、《申论》、专业测试。
粉笔2018年国考第16季行测数量模拟题

粉笔2018国考第16季行测模考数量关系(1)现有一杯浓度为20%的糖水,加入一定量的白糖后,糖水浓度变为25%,再加入若干白糖后变为浓度为40%的糖水,问前后两次加糖量之比为:【粉笔模考】A.1:2B.1:3C.1:4D.2:5楚香凝解析:加入白糖不影响水的质量,可得第一次加糖前后溶液的质量比=(1-25%):(1-20%)=15:16,所以第一次加了1份的白糖;同理可得第二次加糖前后溶液的质量比=(1-40%):(1-25%)=4:5=16:20,所以第二次加了4份的白糖;选C(2)某家庭中,父亲出生年份各数字之和与儿子出生年份各数字之和相同,且为9的整数倍;母亲与儿子的年龄之差为8的整数倍。
2017年,三人年龄之和为162,问母亲最有可能出生于下列哪个年份:【粉笔模考】A.1953B.1956C.1957D.1962楚香凝解析:2016年三人年龄之和为159、除以9余6;父亲出生年份为9的倍数,所以父亲2016年的年龄为9的倍数;同理儿子2016年的年龄为也9的倍数;可得母亲2016年的年龄除以9余6,则母亲的出生年份除以9余3,只有B满足;选B(3)某机关安排办公室工作人员工作日轮流值夜班,周五值夜班的人员需检查配电房。
已知小李每21天检查一次配电房,则办公室至少有多少名工作人员:【粉笔模考】A.2B.3C.4D.7楚香凝解析:21天里有15个工作日,所以人数为15的约数,选B(4)某商店若比上月少买60包A4纸、多买75包B5纸,购买这两种纸的成本与上月相当;若比上月多买30包A4纸、少买45包B5纸,成本比上月少1/25,则上月至多购买了多少包A4纸?【粉笔模考】A.188B.150C.125D.114楚香凝解析:60包A4的价格=75包B5的价格,假设每包A4纸5元、每包B5纸4元;本月比上月少花了(45*4)-(30*5)=30元,所以上月成本=30*25=750元;5x+4y=750,y最小为45,此时x最大为114,选D(5)小王口袋中有5枚1元硬币、3枚5角硬币、4枚1角硬币,硬币年份各不相同,现从中随机摸出4枚硬币,总额不少于2元6角的概率为:【粉笔模考】A.5/11B.7/12C.7/33D.5/14楚香凝解析:总额若要不少于26角,则1元硬币至少2枚;分类①2枚1元硬币,至少1枚5角,有C(5 2)*[C(3 1)*C(4 1)+C(3 2)]=150种;②3枚1元硬币,有C(5 3)*C(7 1)=70种;③4枚1元硬币,有C(5 4)=5种;概率=(150+70+5)/ C(12 4)=225/495=5/11,选A(6)2016年上半年,甲、乙、丙三人的收入之比为4:3:1,下半年,甲、乙、丙三人的收入均高于上半年,下半年总收入比上半年多16万元。
2018国考行测数量关系冲刺:预测题型之函数关系题
数量关系作为行测考试中的拉分板块,在临近考试的时候如果考生能够抓住高频考试题型,复习起来就会比较轻松,考试的时候也有可能有意想不到的收获。
在2015年至2017年连续三年的国家公务员考试中分别出现了三道类似的题目,它们的问法一般是“问以下哪个图形能反映…与…的关系?”,这是一种比较新颖的题目,虽然题目比较新颖,但是并不难,读懂题意、找出题目中所反映的函数关系即可。
》》更多、更全行测技巧、考点大全、行测每日一练尽在中公教育行测频道《《下面中公教育专家对2015副省级、2016年和2017年国家公务员考试中的题目做出解读,帮助我们考生去了解一下如何备考类似的题目。
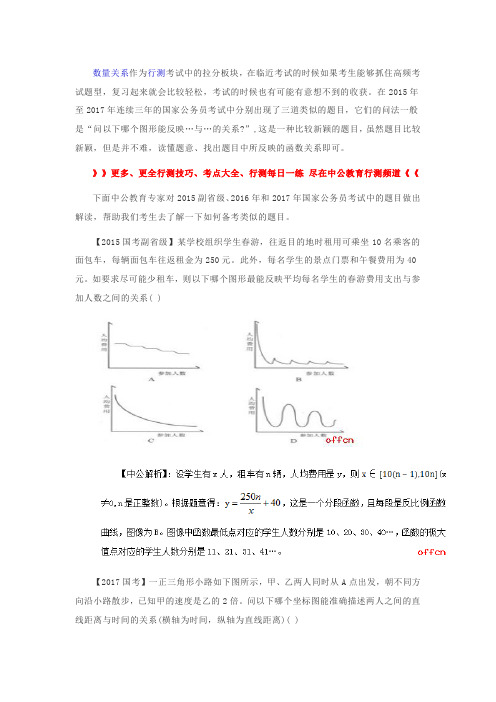
【2015国考副省级】某学校组织学生春游,往返目的地时租用可乘坐10名乘客的面包车,每辆面包车往返租金为250元。
此外,每名学生的景点门票和午餐费用为40元。
如要求尽可能少租车,则以下哪个图形最能反映平均每名学生的春游费用支出与参加人数之间的关系( )
【2017国考】一正三角形小路如下图所示,甲、乙两人同时从A点出发,朝不同方向沿小路散步,已知甲的速度是乙的2倍。
问以下哪个坐标图能准确描述两人之间的直线距离与时间的关系(横轴为时间,纵轴为直线距离)( )。
5.2018年国考地市级数量关系(2月14日)

7.枣园每年产枣2500公斤,每公斤固定盈利18元。 为了提高土地利用率,现决定明年在枣树下种植紫 薯(产量最大为10000公斤),每公斤固定盈利3 元。当紫薯产量大于400公斤时,其产量每增加n 公斤将导致枣的产量下降0.2n公斤。则该枣园明年 最多可能盈利多少元( )
2018年国考地市级数量关系
豆豆老爸
1.甲商店购入400件同款夏装。7月以进价的1.6 倍出售,共售出200件;8月以进价的1.3倍出售, 共售出100件;9月以进价的0.7倍将剩余的100件 全部售出,总共获利15000元。则这批夏装的单件 进价为多少元( )
A.125 B.144 C.100 D.120
A.46176 B.46200 C.46260 D.46380
8.某企业国庆放假期间,甲、乙和丙三人被安排 在10月1号到6号值班。要求每天安排且仅安排1人 值班,每人值班2天,且同一人不连续值班2天。则 有多少种不同的安排方式( )
A.15 B.24 C.30 D.36
9.某新能源汽车企业计划在A、B、C、D四 个城市建设72个充电站,其中在B市建设的充 电站数量占总数的1/3,在C市建设的充电站 数量比A市多6,在D市建设的充电站数量少于 其他任一城市。那么至少要在C市建设多少个65
4.将一块长24厘米、宽16厘米的木板分割成一 个正方形和两个相同的圆形,其余部分弃去不用。 在弃去不用的部分面积最小的情况下,圆的半径 为多少厘米( )
5.企业花费600万元升级生产线,升级后能耗 费用降低了10%,人工成本降低了30%。如每 天的产量不变,预计在400个工作日后收回成 本。若升级前人工成本为能耗费用的3倍,则升 级后每天的人工成本比能耗费用高多少万元( )
2018年国家公务员考试数量关系备考习题及答案(五)

2018年国家公务员考试数量关系备考习题及答案(五)1. 3,8,24,48,120,()A. 148B. 156C. 168D. 1782. 5,7,24,62,( ),468A. 152B. 172C. 192D. 2123. 13579,1358,136,14,1,( )A. 1B. 0C. -3D. -74. 222,193,166,141,( )A. 91B. 100C. 118D. 1225. 4,7,9,14,14,28,19,56,( ),( )A. 24,112B. 25,120C. 26,130D. 27,1401. 解析:本题考查多次方数列。
质数平方数列变式。
3=2的平方-1,8=3的平方-1,24=5的平方-1,48=7的平方-1,120=11的平方-1,故下一项为13的平方-1=168。
故答案为C。
2. 解析:本题属于和数列。
从第三项开始,每一项等于它前面两项之和的2倍。
故答案为B。
3. 解析:本题考查移动余数数列。
后项是前项除以10后对小数部分四舍五入的结果,所以最后一项为0。
故答案为B。
4. 解析:本题属于多次方数列。
222=15²-3,193=14²-3,166=13²-3,12²-3=141,因此空白处应以118=11²-3。
(或前一项减后一项得到29,27,25,公差为-2的二级等差数列)故答案为C。
5. 解析:本题属于积数列。
奇数项为等差数列4,9,14,19,(24),偶数项为积数列(后一项是前一项的2倍)数列7,14,28,56,(112)。
故答案为A。
粉笔2018年国考第2季行测数量模拟题

粉笔2018国考第2季行测模考数量关系(1)粉笔公考在2017年联考前举办了14次行测模考,小李参加了全部模考,小秦除了最后一次其余都参加,但小李行测模考得分之和比小秦还少5分,且小李所有模考的平均分比小秦少6分。
若小秦也参加了最后一次模考且得分为83.2,则小秦的平均分将变为:【粉笔模考】A、73B、75.5C、78D、79.3楚香凝解析:假设小李每次成绩都相同、小秦前13次每次成绩都比小李高6分,前13次小秦共比小李多13*6=78分,可得小李第14次成绩为78-5=73分,则小秦前13次每次成绩为73+6=79分、最后一次83.2分,则总平均分>79分,选D(2)旅行团每人均前往A、B、C三个景点中一个景点参观,已知前往A景点的人数比前往B景点的多5人,若计划前往C景点的人中有7人因特殊原因取消旅行计划,则前往C景点的人数恰好等于前往其余两个景点的人数之和。
则该旅行团原有人数可能为:【粉笔模考】A.27B.31C.37D.39楚香凝解析:假设前往B景点的有x人,则前往A景点的x+5人,计划前往C景点的x+x+5+7=2x+12,共x+(x+5)+(2x+12)=4x+17,除以4余1,选C(3)某工程交由四个队来完成,如果从这四个中任选三个队来做,最快需要15天,最慢需要18天,如果从这四个队中任选两个队来完成,最快需要20天,如果让一个队来做,最快需要36天,如果这项工程由两个队来完成,最慢需要多少天:【粉笔模考】A.20B.24C.26D.30楚香凝解析:假设总任务量180、四个队的效率甲>乙>丙>丁,可得甲+乙+丙=12、乙+丙+丁=10、甲+乙=9、甲=5,可得乙=9-5=4,丙+丁=10-4=6,丙丁合作需要180/6=30天,选D(4)某商场做促销活动,购买200元以内的商品九折优惠;如购买超过200元,低于500元,其中200元以内的九折优惠,超过200元,低于500元的部分八折优惠;如购买超过500元的商品,其中200元以内的九折优惠,200-500元的部分八折优惠,超过500元的部分七折优惠。
粉笔2018年国考第5季行测数量模拟题

粉笔2018国考第5季行测模考数量关系(1)若干老师一起批改行测与申论的模考试卷,需要批改的申论试卷是行测试卷的3/5。
如果每位老师批改6份行测试卷,则会有一位老师只需批改两份;如果每位老师批改3份申论试卷,则还剩余3份。
若批改一份行测或申论试卷均需12分钟,那么所有的试卷想在一小时之内批改完成,至少还需增加几位老师?【粉笔模考】A.16B.9C.8D.7楚香凝解析:申论试卷是行测的3/5,每人批3份申论、剩3份申论,转化为每人批5份行测、剩5份行测,每人批6份行测、缺4份行测,盈亏问题,可得总人数=(5+4)/(6-5)=9人,行测试卷共(9*5)+5=50份、申论试卷50*(3/5)=30份,共50+30=80份;每人1小时可以批改60/12=5份,则至少需要80/5=16人,需要增加16-9=7人,选D(2)某机关开展课题项目申报,共有450人参与。
提交研究报告的有190人,提交论文的有270人,提交专著的有134人,其中提交两种及两种以上成果的有87人,则只提交两种成果的有多少人?【粉笔模考】A.30B.40C.57D.20楚香凝解析:解法一:不包含的三容斥,450=190+270+134-87-三种的,可得三种的有57人,只两种的有87-57=30人,选A解法二:根据每个区域算的次数,可得(87*2)+450-190-270-134=30人,选A(3)一个公司在草地上举行庆新活动,用了白、蓝、绿、红四种颜色的旗帜围成了一个圆形场地。
其中正北方向的旗帜为四色旗,然后依次顺时针每隔三面旗有一枚双色旗,每隔六面旗有一面三色旗,每隔九枚旗有一面四色旗,每个位置只放一面旗帜,重叠处以颜色多者为准。
最终场地一共使用了81面旗帜,问共使用了多少面两种及两种以上颜色的旗帜?【粉笔模考】A.33B.35C.39D.40楚香凝解析:从正北方开始给81面旗帜分别编号0-80,则编号4的倍数为双色旗、编号7的倍数为三色旗、编号10的倍数为四色旗,1-80号中两种及以上的旗子有(80/4)+[80/7]+(80/10)-[80/28]-(80/20)-[80/70]=32面,加上0号、共33面,选A(4)有一个直径90公分、高150公分的圆柱形铁桶正好装满270公斤的墙漆,现将漆桶倾斜30°倒出部分油漆,若粉刷一平米墙面需要墙漆半公斤,问倒出的墙漆一共可粉刷多少平米?【粉笔模考】A.108√3B.90C.64D.54√3楚香凝解析:倒出水的体积占总体积的(30√3/2)/(150)=√3/10、有270*(√3/10)=27√3公斤,可以粉刷27√3*2=54√3平米,选D(5)水田中的水稻丰收,人工收割64小时可以完成,机械收割仅需8小时。
粉笔2018年国考第14季行测数量模拟题

粉笔2018国考第14季行测模考数量关系(1)随机对100名考生进行调查,其中有85人使用过粉笔行测,有68人使用过粉笔申论,有56人使用过粉笔教师,有45人三种都使用过,有1人没有使用过任何一种。
则有多少人只使用过其中一种?【粉笔模考】A.34B.25C.42D.39楚香凝解析:解法一:不包含的三容斥,100=85+68+56-x-(2*45)+1,恰好使用两次的人数x=20人,100-1-20-45=34人,选A解法二:三容斥,(100-1)*2+45-(85+68+56)=34人,选A(2)某旅行团共32人在景区购买纪念品,每人最多买3件。
已知购买1件纪念品的人数是购买多件纪念品的2倍。
后经统计,旅行团所有人共购买了48件纪念品。
则旅行团中有多少人没有购买纪念品?【粉笔模考】A.7B.5C.3D.2楚香凝解析:购买纪念品的人数为3的倍数,所以没有购买纪念品的人数除以3余2,排除AC;代入B项,此时购买多件纪念品的人数=(32-5)/3=9人、购买1件纪念品的人数为18人,最多共购买(9*3)+(18*1)=45件<48件,排除;选D(3)在一长木棍上每隔8cm标注一条红线,每隔10cm标注一条黄线,每隔12cm标注一条绿线,都能等分地将木棍分为几段,若用锯子在所有标注线处将木棍锯开,可得到28段小木棍,则长木棍长度为:【粉笔模考】A.120cmB.180cmC.240cmD.320cm楚香凝解析:8、10、12的最小公倍数为120,排除BD;代入A项,(120/8)+(120/10)+(120/12)-(120/40)-(120/24)-(120/60)+(120/120)=15+12+10-3-5-2+1=28段,满足,选A(4)某快餐品牌推出中杯可乐,容量为235.5ml,杯身为圆柱形,并配有一根吸管。
若将吸管垂直于杯底,吸管将会有4cm露出杯外。
若将吸管斜插入杯底,则吸管至少有3cm露出杯外。
粉笔2018年国考第13季行测数量模拟题

粉笔2018国考第13季行测模考数量关系(1)甲、乙、丙3个收割队各有若干台收割机,每台收割机效率相同,甲队的工效与乙、丙两队合作的工效相同,丙队工效不小于乙队。
现有一片麦地,三队合作5天可完成,如果甲队增加5台收割机后,三队合作4天可完成,则丙队至少有多少台收割机:【粉笔模考】A.4台B.5台C.6台D.10台楚香凝解析:时间比5:4,效率比4:5=20:25(差5台),所以原来三队共20台收割机,乙丙共10台,丙至少有5台,选B(2)小明与小红参加猜歌游戏,现播放5首歌分别让两人猜,假如两人猜中每首歌的概率均为0.5,则每首歌均只有1人猜对的概率为:【粉笔模考】A.1/1024B.1/32C.1/16D.1/2楚香凝解析:第一首歌恰有一人猜中的概率=C(2 1)*0.5*(1-0.5)=0.5=1/2,所以五首歌都恰有一人猜中的概率=(1/2)5 =1/32,选B(3)某公司三名销售人员2016年销售额如下:甲的销售额占三人销售总额的3/5,且比乙多17万元,丙的销售额比乙的3/5多2万元。
若甲、乙、丙的销售额均为整数,则甲的销售额比丙多:【粉笔模考】A.15万元B.17万元C.14万元D.19万元楚香凝解析:假设甲的销售额为3份,则乙的销售额为3份-17万元,乙丙的总销售额为2份,丙的销售额为17-1份=(3份-17)*(3/5)+2,可得1份=9万元,甲比丙多4份-17=19万元,选D(4)王、李、赵、周、杨五人到酒店后,发现只剩下1211号、1213号、1215号、1217号四间相邻的标准间,每间最多住两人。
所有人的入住满足以下条件:①周住在1211号②赵和周、杨均不住同一间③五人中只有王一人单独住一间,且王与其他人房间均不相邻则李住在:【粉笔模考】A.1211号B.1213号C.1215号D.1217号楚香凝解析:王与其他人房间不相邻,所以王自己住在1217号;赵和周、杨不住同一间,所以赵和李住在1213号,选B(5)把13棵同样的松树和7棵同样的柏树种植在道路两侧,每侧种植10棵,要求每侧柏树不相邻。
粉笔2018年国考第8季行测数量模拟题

粉笔2018国考第8季行测模考数量关系(1)某年级共有甲、乙、丙三个班级。
其中,丙班级学生人数是总人数的45%,且比乙班级多了18人,而乙班级的学生人数比甲班级多五分之一。
则该年级共有学生多少名?【粉笔模考】A.120B.130C.140D.150楚香凝解析:假设甲5份、乙6份,(甲+乙):丙=(1-45%):45%=11:9,可得丙9份,共20份;丙比乙多3份=18人,共20份=120人,选A(2)商店新进了一批商品,准备分三个阶段售卖。
第一阶段,按照50%的利润定价销售该批商品的三分之一;第二阶段,按照20%的利润定价销售,销量比第一阶段多一半;第三阶段,对剩余的商品进行亏本降价销售。
全部售出之后,最终这批商品的利润率为20%。
则第三阶段的商品在第一阶段定价的基础上打了几折?【粉笔模考】A.四折B.五折C.六折D.七五折楚香凝解析:第二阶段利润率为20%,总的利润率也为20%,可得第一阶段和第三阶段的混合利润率也为20%;假设进了6件、每件成本100元,第一阶段卖2件、第二阶段卖2*(1+50%)=3件、第三阶段卖6-2-3=1件,第一阶段和第三阶段的利润和=(2+1)*100*20%=60元,其中第一阶段利润为2*100*50%=100元,所以第三阶段利润为(-40)元,折数=(100-40)/150=40%,选A(3)小明的电脑密码原来是四个8,现决定在原四位数密码的基础上增加6和9两个数字,变为六位数密码,则小明电脑新密码的设置方式共有多少种?【粉笔模考】A.10B.20C.30D.45楚香凝解析:四个8之间有五个空,所以插6有五种选择,插完6后变为六个空,所以再插9有六种选择,共5*6=30种,选C(4)2016年小明与小庆的年龄之和是年龄之差的9倍,两人年龄之和介于50到60之间,小明比小庆大,小东的年龄是小明与小庆年龄之差的2倍,问小明年龄是小东年龄的3倍时,小明多少岁:【粉笔模考】A.24B.27C.30D.36楚香凝解析:(小明+小庆):(小明-小庆)=9:1,可得小明:小庆=(9+1):(9-1)=10:8=30:24,小东(30-24)*2=12岁,小明:小东=3:1,年龄差=30-12=18岁对应2份,小明3份对应27岁,选B(5)小龙有一块等边三角形的地,其边长为2a,现打算在这块地上修建一个圆形花圃,那么花圃的最大面积有多少:【粉笔模考】A.a2 πB.(a2 π)/3C.(a2 π)/4D.(a2 π)/8楚香凝解析:圆的半径=a/√3,可得圆的面积=π*(a/√3)2=(a2 π)/3,选B(6)一项工程A由10人去完成,完工时间将超出计划8天,若增派2人,则完成时间将超出计划4天。
粉笔2018年国考第17季行测数量模拟题

粉笔2018国考第17季行测模考数量关系(1)某次测验,7名同学的成绩都是整数且刚好呈等差数列,已知他们的平均成绩为82分。
若任意挑选两名同学的成绩,得到的最低平均成绩为72分。
则若任意挑选四名同学,得到的最高平均成绩为多少分?【粉笔模考】A.86B.88C.90D.94楚香凝解析:第4名的成绩为82分、第6.5名的成绩为72分,相差2.5名=82-72=10分,所以第2.5名和第4名相差1.5名=6分,则第2.5名为82+6=88分=前四名平均分,选B(2)一项工作,甲、乙两队合作完成。
若甲中途休息2天,则两队完成这项工作共需要10天。
若乙中途休息6天,则两队完成这项工作共需要11天。
现工作量提高了2倍,且乙中间请假2天,则两队完成共需要多少天?【粉笔模考】A.17B.19C.27D.25楚香凝解析:甲8天+乙10天=甲11天+乙5天,可得甲3天=乙5天;假设甲效率5、乙效率3,可得总工作量为(8*5)+(10*3)=70;假设乙不请假,可得总天数=(70*3 + 3*2)/(5+3)=27天,选C(3)有两份等量的浓度为20%的A溶液,其中一份与180克B溶液混合得到浓度为29%的C 溶液。
在C溶液中再加入另一份A溶液,此时新溶液的浓度为26%。
则B溶液的浓度为多少?【粉笔模考】A.30%B.32%C.38%D.40%楚香凝解析:解法一:29%的C溶液和20%的A溶液混合得到26%的溶液,十字交叉可得C溶液和A溶液的质量之比=(26-20):(29-26)=2:1,所以2份C溶液中包含1份的A溶液和1份的B溶液;即20%的A溶液和B溶液等质量混合得到29%的溶液,所以B溶液的浓度=(29*2)-20=38,选C解法二:以20%为基准,看作B溶液加入一些水后浓度变为9%,再加入等质量的水后浓度变为6%,调和平均数,假设溶质为1,1/(200/9 - 100/6)=18%,所以B溶液的初始浓度为18%+20%=38%,选C(4)某市党委决定在本周的工作日每天举办一场中央系列讲话学习活动,要求党校内254名党员每人至少参加一场。
粉笔2018年国考第12季行测数量模拟题

粉笔2018国考第12季行测模考数量关系(1)一项工程计划按4:3:5的工程量分给甲、乙、丙三个工程队,三队同时开工,8天后同时完工。
若三队同时开工3天后,乙队因事离开,甲、丙两队留下继续工作,问完成这项工程共用多少天?【粉笔模考】A.10B.9C.8D.7楚香凝解析:假设三队的效率分别为4、3、5,剩下五天的任务量=(4+3+5)*5=60,甲丙合作需要的天数=60/(4+5)≈7天,共3+7=10天,选A(2)有三个大小相同的杯子,分别装满浓度为10%、20%和40%的酒精溶液,如果依次将三杯酒精溶液的1/2、1/3和1/4倒入一足够大的空杯子中,则该杯子中的酒精溶液浓度是:【粉笔模考】A.15%B.25% D.20% D.30%楚香凝解析:假设三个杯子的容量都为12;混合浓度=(6*10% + 4*20% + 3*40%)/(6+4+3)=20%,选C(3)甲、乙两人从相距36千米的两地匀速相向而行,若甲先出发,2小时后乙再出发,则两人在乙动身2个半小时后相遇;若乙先出发,2小时后甲再出发,则在乙动身3个半小时后两人相遇。
问若甲、乙两人同时出发,则相遇时甲走了多少千米?【粉笔模考】A.9B.12C.18D.27楚香凝解析:甲4.5小时+乙2.5小时=乙3.5小时+甲1.5小时,可得甲3小时=乙1小时,则甲乙的速度比=1:3;同时出发,相遇时两人合走4份=36千米,甲走1份=9千米,选A(4)教师节将至,小莉花费320元从花店预定了一束鲜花,由玫瑰、康乃馨和百合共28枝鲜花包装而成。
已知玫瑰每枝15元,康乃馨每枝6元,百合每枝20元,包装及材料使用费共20元,问这束鲜花中康乃馨比百合多多少枝?【粉笔模考】A.3B.15C.10D.12楚香凝解析:28枝鲜花共花了300元,假设28枝都是百合花、共560元,多了260元;鸡兔同笼,5x+14y=260,y=15、x=10,说明有玫瑰10枝、康乃馨15枝、百合28-15-10=3枝,15-3=12,选D(5)2016年某瓷砖生产厂生产瓷砖总产量的1/4为抛光砖,1/7为仿古砖,生产的微晶石瓷砖是抛光砖和仿古砖产量之和的1/11,生产的全抛釉瓷砖是抛光砖和仿古砖产量之差的3倍,其他瓷砖产品产量比仿古砖多6万平方米。
粉笔2018年国考第19季行测数量模拟题

粉笔2018国考第19季行测模考数量关系(1)甲、乙、丙、丁四人投资一个项目,已知甲、乙、丙投资金额之和比乙、丙、丁投资金额之和多16%,甲、丁投资金额之和与乙、丙投资金额之和相等,甲比丁多投资4万元,那么四人共投资多少万元?【粉笔模考】A.36B.44C.56D.72楚香凝解析:假设乙丙丁共25份,则甲乙丙共29份,甲比丁多29-25=4份对应4万元,乙丙丁+甲乙丙=(甲丁)+2*(乙丙)=3(甲丁)=54份=54万元,(甲丁)+(乙丙)=(54/3)*2=36万,选A(2)有若干克浓度为10%的盐水,加入一定量的盐,浓度变为40%,再加入若干克浓度为20%的盐水,之后盐水浓度变为24%,质量变为300克,问最初盐水质量为多少克?【粉笔模考】A.20B.60C.40D.30楚香凝解析:浓度40%的盐水和20%的盐水十字交叉,(24-20):(40-24)=1:4=60:240,所以浓度40%的盐水有60克;最初加盐不改变水的质量,可得最初盐水质量=60*(1-40%)/(1-10%)=40克,选C(3)一项工程,甲工作了15天,乙工作了16天,此时恰好完工,最终甲、乙完成工作量之比为5:4,问此项工程若由乙单独工作需要多少天完工?【粉笔模考】A.27B.21C.36D.31楚香凝解析:解法一:甲乙的效率比=(5/15):(4/16)=4:3,所以甲15天工作量=乙15*4/3=20天的工作量,则乙单独做需要16+20=36天,选C解法二:甲乙的效率比=(5/15):(4/16)=4:3,所以乙单独做所需天数>15+16=31天,选C(4)小李每工作3天休息1天,7月他的第一个休息日是7月2日星期一,那么这一年的8月他最后一个工作日是星期几?【粉笔模考】A.星期五B.星期六C.星期三D.星期四楚香凝解析:7月2日→8月30日经过了60天=(7*8)+4,所以是星期五,且为休息日,则最后一个工作日是星期四,选D(5)某单位三个科室分别有3名、4名、1名同事报名参加大胃王比赛,领导打算从中选出4名同事作为最终参赛人员,若要求同一科室人数不得超过两人,问最终的参赛人员组合会有多少种情况?【粉笔模考】A.66B.54C.48D.32楚香凝解析:分类;2+2的情况有C(3 2)*C(4 2)=18种;2+1+1的情况有C(3 2)*C (4 1)+C(3 1)*C(4 2)=30种;共18+30=48种,选C(6)早上7:00,甲从A地出发去往B地,速度为9千米/小时,8:00乙从B地出发去往A 地,中途某个时刻两人相遇,之后甲到达B地后立即原路返回,11:00甲、乙两人同时到达A地,问中途两人相遇的时间是几点?【粉笔模考】A.9:40B.9:36C.8:40D.8:36楚香凝解析:甲4小时走了两个全程、乙3小时走了一个全程,所以甲乙的速度比=3:2=9:6,总路程=6*3=18千米,8点时甲先走了9千米,剩下的9千米甲乙合走需要[9/(9+6)]*60=36分钟,所以8:36相遇,选D(7)某商店里出售大、中、小三种规格的文具盒,单价分别为24元、13元、12元,已知小明购买了三种文具盒共20个,总计花费308元,问购买最多的一种文具盒有几个?【粉笔模考】A.7B.8C.9D.10楚香凝解析:假设20个都是12元的,共240元,还差308-240=68元;鸡兔同笼,每当有一个12元转化为13元,就增加1元;每当有一个12元转化为24元,就增加12元;x+12y=68,可得x=8、y=5,则大规格的有5个、中规格的有8个、小规格的有7个,选B(8)小明和3位同学玩一个游戏,把每个人的学号分别写在相同的卡片上,每局游戏中每人随机抽取一张卡片且每张卡片被抽中的概率相同,每局游戏结束后将卡片放回。
粉笔2018年国考第21季行测数量模拟题

粉笔2018国考第21季行测模考数量关系(1)小张在玩猜字母游戏,每局游戏设置的字母总数相同(字母的总数为猜中字母个数与猜不中字母个数之和),第一局他猜中的字母个数比没猜中字母个数的3倍少12个,第二局他猜中的字母个数比第一局猜中的个数增加了10个,且是没猜中的字母个数的4倍,则每局游戏设置的字母总数为多少个?【粉笔模考】A.112B.120C.136D.140楚香凝解析:解法一:由第二局可得字母总数=5的倍数,排除AC;代入B选项,第一局没猜中的个数有(120+12)/4=33个,则第二局没猜中的个数有33-10=23个、猜中的有120-23=97个,不满足4倍关系;选D解法二:第二局猜中的个数增加了10个,此时猜中的个数比没猜中个数的3倍多(3*10-12+10)=28个、猜中的个数是没猜中的4倍,盈亏可得没猜中的有28/(4-3)=28个,总个数28*5=140个,选D(2)一项工程由某工程队负责施工,工作10天后,完成了任务的1/3,之后,若在现有工人基础上再增加3人,可提前4天完工。
现要求提前5天完工,在原有工人人数不增加的情况下,每个工人的效率需要提高多少才能按时完工?(每个工人效率相同)【粉笔模考】A.1/2 B.1/3 C.1/4 D.1/6楚香凝解析:对于剩下2/3的任务量,提速前后时间比=20:16,效率比=16:20=12:15(差3人),可得原有12人;假设每人每天的效率为1,可得剩下的总任务量=12*20=240,若提前5天完成,可得每人每天效率=240/[(20-5)*12]=4/3,比原来提高了1/3,选B(3)有两杯质量均为300克的盐水,浓度分别为20%、12%,从两杯盐水中分别倒出一部分,配置了一杯400克、浓度为15%的盐水,问剩余两杯浓度20%与12%的盐水中,盐的质量之比为:【粉笔模考】A.3:1B.3:5C.25:9D.5:1楚香凝解析:十字交叉可得倒出的两杯盐水的质量比=(15-12):(20-15)=3:5=150:250(共400克),所以两杯盐水剩余的质量分别为150克和50克,盐的质量之比=(150*20%):(50*12%)=5:1,选D(4)为6个身高不同的人安排座位,前排1座,中排2座,后排3座,要求每人一座,且后排最高的人比中排最高的人更高,有多少种不同的排法?【粉笔模考】A.144B.216C.360D.432楚香凝解析:前排先安排一个人、有6种选择;剩下五人中最高的在后排、有3种坐法,其余四人随便坐、有A(4 4)种;共6*3*A(4 4)=432种,选D(5)小陈给自己制定了健身计划,跑步3天、游泳2天、跳健身操3天,前后不同的两项运动之间休息1天,如此依次循环,计划自9月1日开始执行,问本年最后一次游泳是在哪一天?【粉笔模考】A.12月23日B.12月24日C.12月25日D.12月26日楚香凝解析:(3+1+2+1+3+1)=11天一周期,9月1日→12月23日共30+31+30+23=114天=10个完整周期又四天,即从下一天开始游泳,所以最后一次游泳是12月25日,选C(6)商店购入一批商品,每件定价100元售出了15件,之后每件提价10元又售出10件,经计算,提价前销售商品所获总利润与提价后销售获利相同,问提价后卖出的每件商品的利润率为多少?【粉笔模考】A、25%B、30%C、37.5%D、40%楚香凝解析:解法一:提价前后的数量比=15:10,单件利润比=10:15=20:30(差10元),所以提价后的利润为30元、定价110元、成本110-30=80元,利润率=30/80=37.5%,选C解法二:提价后卖的10件比原来卖10件多赚了100元,等于原来卖5件的利润,所以原来每件的利润为20元,提价后每件的利润为30元、定价110元、成本110-30=80元,利润率=30/80=37.5%,选C(7)办公楼前设置了4级台阶,小明上台阶时每步迈1-3级台阶,下台阶时,每步迈1-2级台阶,那么他上四级台阶再走下去,有多少种不同的走法?【粉笔模考】A.35B.12C.25D.8楚香凝解析:标数法可得,上台阶时有(1+2+4)=7种走法,下台阶时有(2+3)=5种走法,共7*5=35种,选A(8)某人出生于20世纪40年代,1996年他的年龄各数字之和是其年龄的1/4,问他出生年份的各数字之和是多少?(出生当年算0岁)【粉笔模考】A.21B.22C.23D.24楚香凝解析:结合选项可得他的出生年份只能为1947、1948、1949,且1996年时他的年龄为4的倍数,所以出生年份只能是1948年,数字和为1+9+4+8=22,选B(9)甲、乙两人分别从A、B两地同时出发,匀速相向而行,甲在距离AB中点6千米处与乙相遇。
粉笔2018年国考第7季行测数量模拟题

粉笔2018国考第7季行测模考数量关系(1)一围棋棋盘上有若干黑子和白子,其中白子的数量占棋子总数的5/8。
现轮到小明执黑子行动,落一子后吃掉5个白子,此时棋盘上白子的数量占棋子总数的5/9。
则原棋盘上共有多少个棋子?【粉笔模考】A.36B.40C.72D.76楚香凝解析:解法一:总数为8的倍数,排除AD;总数+1-5后为9的倍数,排除C;选B解法二:黑:白=3:5,黑+1、白-5,黑:白=4份:5份;若黑-3、白-5,黑:白依然=3份:5份,黑子差4-3=1份对应4个,所以小明行动后共9份=36个,最初36+5-1=40个,选B(2)甲、乙、丙三个量筒内装有浓度不同的酒精溶液,其中酒精与水的体积比分别是2:1、3:1、4:1。
当把三个量筒的酒精溶液充分混合后,混合溶液的酒精与水的体积比是3:1。
若已知甲、乙两个量筒内的酒精溶液体积分别为81ml和32ml,那么丙量筒内的酒精溶液体积为多少毫升?【粉笔模考】A.81B.108C.113D.135楚香凝解析:三个混合后酒精:水=3:1,乙中酒精:水=3:1,所以甲丙混合后酒精:水=3:1,十字交叉可得甲和丙的水之比=(4-3):(3-2)=1:1,则甲和丙的总体积之比=(2+1):(4+1)=3:5=81:135,选D(3)有41颗珠子,6年前姐妹两人按年龄大小的比例分配,最后还剩下1颗珠子给妹妹;今年,她们再次按年龄的比例重新分配,最后还剩下1颗珠子给姐姐。
已知姐妹二人年龄相差2岁,那么,妹妹两次分得的珠子相差多少颗?【粉笔模考】A.2B.3C.4D.5楚香凝解析:6年前姐妹年龄和为41-1=40的约数,今年姐妹年龄和也为40的约数,40的约数中相差12的为8和20,所以6年前姐:妹=(8+2):(8-2)=5:3=25:15,今年姐:妹=(20+2):(20-2)=22:18,妹妹6年前分得15+1=16颗、今年分得18颗,差18-16=2颗,选A(4)某运动鞋店购进了一批品牌运动鞋,提价20%后全部卖出,用收入的一半又购进另一品牌运动鞋,提价25%后全部卖出又盈利3000元,问第一次购进的品牌运动鞋全部卖出后盈利多少元?【粉笔模考】A.2000B.3000C.4000D.5000楚香凝解析:购进另一运动鞋的成本=3000/25%=12000元,所以第一批运动鞋的收入=12000*2=24000元,成本24000/(1+20%)=20000元,利润24000-20000=4000元,选C(5)甲、乙二人以相同的速度同时从A地开车前往B地,甲花2小时10分钟到达,而乙行驶了一段时间后,由于发动机故障,停车维修花费了20分钟,修好后为了尽早到达B地,乙按原速度的1.5倍匀速行驶,恰好与甲同时到达。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年国考数量关系押题A卷
1、小布老师为新婚购置的别墅有一个6*24米花坛,若一个喷头可以覆盖半径为5米的面积,则需要安装多少喷头才可覆盖整个花坛:
A.3
B.4
C.5
D.6
2、7*7的队列方阵从左起第一排第一人开始报数(到队伍最末就从头重新开始),按照1、2、
3、4重复报数,报到4的战士摘掉帽子并不在参与报数,在五人未脱军帽时,一共报了多少个数:
A.176
B.44
C.132
D.144
3.甲、乙和丙三种不同浓度、不同规格的酒精溶液,单瓶重量分别为3公斤、7公斤和9公斤,如果将甲乙各一瓶、甲丙各一瓶和乙丙各一瓶分别混合,得到的酒精浓度分别为50%、50%和60%。
如果将三种酒精各一瓶混合,得到的酒精中要加入多少公斤纯净水后,其浓度正好是50%?
A.1.9
B.1.6
C.1.3
D.1
4.圈内求职有讲师和助教共17人,其中讲师11人。
现要从中选出4人到某大学组织一次宣讲会,要求其中必须包含讲师和助教,且讲师人数不多于助教人数。
问有多少种不同的选人方法:
A.750
B.1045
C.1225
D.1500
5.小布、小龙老师为同学批改作文,一共有125人上交作文,小布老师一小时可以批改三篇,但批改四小时需要休息一小时,小龙老师每小时可以批改两篇,但一直不休息,问多少小时后两人可以把作文批完:
A.28
B.25
C.30
D.24
6、有10元、20元、50元面值的钞票共10张,总额为250元。
问10元的钞票最多有多少张?
A.1
B.2
C.3
D.4
7、小布老师楼上邻居家漏水,家里积了很多水,并且还在匀速漏水。
如果13个同学帮他舀水,3小时可以舀完;如果6个同学帮他舀水,10小时可以舀完。
如果在2小时内舀完水,最少需要多少同学帮忙?
A.15
B.16
C.17
D.18
8、小明和姐姐用2015年的台历做游戏,他们将12个月每一天的日历——揭下,背面粘上放在一个盒子里、姐姐让小明一次性帮她抽出一张任意月份的30号或者31号。
问小明一次至少应抽出多少张日历,才能保证满足姐姐的要求?
A.346
B.347
C.348
D.349
C。
本题为抽屉原理问题,按照偏不原则,每个月都抽出29天,29*12-1(2015年为平
年,2月份28天),没有取到,再+1取到,所以29*12-1+1尾数8直接秒杀C。
9、甲、乙、丙三人匀速行驶在某条道路上。
某一时刻时,丙在甲之前,而乙刚好在甲、丙两人的正中间。
10分钟后,甲追上了乙,又过了5分钟,甲追上了丙。
问再过多少分钟,乙可以追上丙?
A5B15C20D30
10、小李和小王前往同一家教育机构应聘。
应聘流程包括两轮面试和一轮试讲,只有都通过后才会被录用。
已知小李通过每轮面试的概率都为0.5,通过试讲的概率为0.8;小王通过第一轮面试的概率为0.75,通过第二轮面试的概率为
0.8,通过试讲的概率为0.5。
问两人最终只有一人被录用的概率为多少?
A14%B24%C38%D50%
答案AABBA DDCBC
具体讲解视频请关注公众号:小布公考
2018年国考数量关系押题B卷
1.哥哥现在的年龄是弟弟当年年龄的3倍,哥哥当年的年龄与弟弟现在的年龄相同,哥哥与弟弟现在的年龄和是30岁。
问哥哥现在多少岁?
A.15
B.16
C.18
D.19
2.从前有个偏僻的小山村,对外联系只有一部公用电话。
某天有4个村民恰巧都想打电话,其中甲需要打25分钟,乙需要打35分钟,丙需要打18分钟,丁需要打5分钟,则四个人在此花的时间至少要多少分钟:
A.83
B.121
C.159
D.188
3.A、B两人同时从700米长的山坡坡底出发向上跑,跑到坡顶立即返回。
他们俩的上坡速度不同,下坡速度则是两人各自上坡速度的2倍。
A首先到达坡顶,立即沿原路返回,并且在离坡顶70米处与B相遇。
当A到达坡底时,那么B离坡底多少米:
A.210
B.240
C.300
D.400
4.某超市购进三种不同的糖,每种糖所用的费用相等,已知这三种糖每千克的费用分别为11元、12元、13.2元。
如果把这三种糖混在一起成为什锦糖,那么这种什锦糖每千克的成本是:
A12.6元B11.8元C12元D11.6元
5、8支足球队参加单循环比赛,胜者得2分,平者得1分,负者得0分,比赛结束后,8支足球队的得分各不相同,且第2名的得分与后4名的得分总和相等,第3名的得分是第5名的两倍,第4名的得分是第6名的两倍。
问第一名比第四名多拿了多少分?
A.6
B.5
C.4
D.3
6、有一只三层书架,若将最上层一半的书放到中间一层后,再将中间层的书放到最下层,则三层的书本数恰好相等。
问原来的三层书本数量之比为:A4:1:1B3:2:1C4:1:2D2:3:1
7、甲、乙、丙、丁、戊五人参加百米跑步比赛,比赛场共有五个平行的跑道,现要求甲不能在第一跑道、乙不能在第二跑道、丙不能在第三跑道、丁不能在第四跑道。
则有多少种不同的站位方法:
A9B24C44D53
8、小明家的挂钟每小时比标准时间快4分钟,某天中午12点,他将挂钟时间与标准时间调为一致后便外出,并恰好在标准时间下午四点整回家。
则在小明外出期间,他家挂钟的时针与分针垂直了多少次:
A6B7C8D9
9.、如图所示的四面体中,其中三个面均是腰长为2的等腰直角三角形。
一只蚂蚁从该四面体的任意一点沿着棱不重复的走。
问该蚂蚁能够走的路径最长为多少?
A B C D
10、某篮球队12个人的球衣号码是从4到15的自然数,如从中人选出3个人参加三对三篮球比赛.则选出的人中至少有两人的球衣号码是相邻自然数的概率为多少?
A.1/2
B.2/5
C.5/11
D.24/55
答案CCCCA ADCAC
具体讲解视频请关注公众号:小布公考。
