高级计量经济学课后习题参考答案
高级计量经济学习题及解答

Answer:
Note that P(Xi > θ +
)=
∞ θ+
e−(x−θ) = e−
< 1 if
< 1. If |Yn − θ| >
then it must be that Xi > θ + for every single i = 1 . . . n. Since the Xi
are independent,
(a) Does the random variable Y = X2 also have a normal distribution? (b) Would the random variable Y = aX + b have a normal distribution?
Answer: Y = X2 does not; Y ≥ 0 and a normal random variable is negative with positive probability.
(Note that if you used the exact same MGF in the book you would have gotten that Yn tended in distribution to the constant β. There is an annoying inconsistency as in both the Γ and exponential distribution where sometimes the parameter is the mean, and sometimes it is one over the mean.).
计量经济学精要习题参考答案(第四版)

计量经济学(第四版)习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学第二版课后习题答案
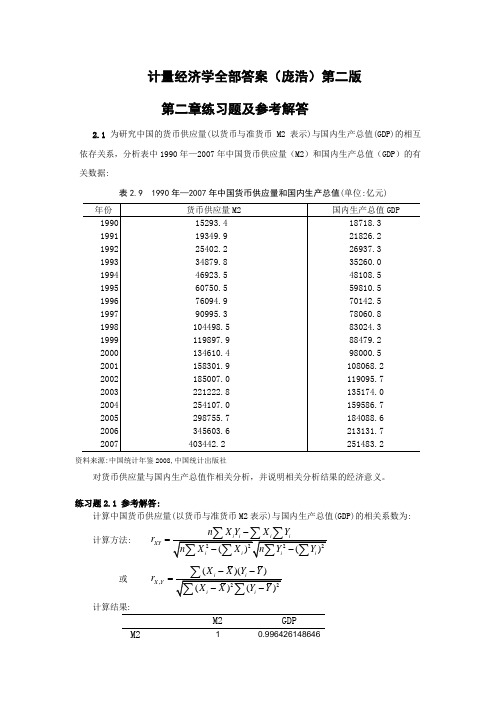
计量经济学全部答案(庞浩)第二版 第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
计量经济学习题及全部答案

计量经济学习题一一、判断正误1.在研究经济变量之间的非确定性关系时,回归分析是唯一可用的分析方法; 2.最小二乘法进行参数估计的基本原理是使残差平方和最小;3.无论回归模型中包括多少个解释变量,总离差平方和的自由度总为n -1; 4.当我们说估计的回归系数在统计上是显着的,意思是说它显着地异于0; 5.总离差平方和TSS 可分解为残差平方和ESS 与回归平方和RSS 之和,其中残差平方和ESS 表示总离差平方和中可由样本回归直线解释的部分; 6.多元线性回归模型的F 检验和t 检验是一致的;7.当存在严重的多重共线性时,普通最小二乘估计往往会低估参数估计量的方差; 8.如果随机误差项的方差随解释变量变化而变化,则线性回归模型存在随机误差项的自相关;9.在存在异方差的情况下,会对回归模型的正确建立和统计推断带来严重后果; 10...DW 检验只能检验一阶自相关; 二、单选题1.样本回归函数方程的表达式为 ;A .i Y =01i i X u ββ++B .(/)i E Y X =01i X ββ+C .i Y =01ˆˆi i X e ββ++D .ˆi Y =01ˆˆiX ββ+ 2.下图中“{”所指的距离是 ;A .随机干扰项B .残差C .i Y 的离差D .ˆiY 的离差 3.在总体回归方程(/)E Y X =01X ββ+中,1β表示 ;A .当X 增加一个单位时,Y 增加1β个单位B .当X 增加一个单位时,Y 平均增加1β个单位C .当Y 增加一个单位时,X 增加1β个单位D .当Y 增加一个单位时,X 平均增加1β个单位 4.可决系数2R 是指 ;A .剩余平方和占总离差平方和的比重B .总离差平方和占回归平方和的比重C .回归平方和占总离差平方和的比重D .回归平方和占剩余平方和的比重 5.已知含有截距项的三元线性回归模型估计的残差平方和为2i e ∑=800,估计用的样本容量为24,则随机误差项i u 的方差估计量为 ;A .B .40C .D .6.设k 为回归模型中的参数个数不包括截距项,n 为样本容量,ESS 为残差平方和,RSS 为回归平方和;则对总体回归模型进行显着性检验时构造的F 统计量为 ;A .F =RSSTSSB .F =/(1)RSS k ESS n k --C .F =/1(1)RSS k TSS n k --- D .F =ESSTSS7.对于模型i Y =01ˆˆi iX e ββ++,以ρ表示i e 与1i e -之间的线性相关系数2,3,,t n =,则下面明显错误的是 ;A .ρ=,..DW =B .ρ=-,..DW =-C .ρ=0,..DW =2D .ρ=1,..DW =08.在线性回归模型 011...3i i k ki i Y X X u k βββ=++++≥;如果231X X X =-,则表明模型中存在 ;A .异方差B .多重共线性C .自相关D .模型误设定9.根据样本资料建立某消费函数 i Y =01i i X u ββ++,其中Y 为需求量,X 为价格;为了考虑“地区”农村、城市和“季节”春、夏、秋、冬两个因素的影响,拟引入虚拟变量,则应引入虚拟变量的个数为 ;A .2B .4C .5D .610.某商品需求函数为ˆi C =100.5055.350.45i i D X ++,其中C 为消费,X 为收入,虚拟变量10D ⎧=⎨⎩城镇家庭农村家庭,所有参数均检验显着,则城镇家庭的消费函数为 ;A .ˆi C =155.850.45i X +B .ˆiC =100.500.45i X + C .ˆi C =100.5055.35i X +D .ˆiC =100.9555.35i X + 三、多选题1.一元线性回归模型i Y =01i i X u ββ++的基本假定包括 ;A .()i E u =0B .()i Var u =2σ常数C .(,)i j Cov u u =0 ()i j ≠D .(0,1)iu NE .X 为非随机变量,且(,)i i Cov X u =02.由回归直线ˆi Y =01ˆˆi X ββ+估计出来的ˆiY ; A .是一组平均数 B .是实际观测值i Y 的估计值 C .是实际观测值i Y 均值的估计值 D .可能等于实际观测值i Y E .与实际观测值i Y 之差的代数和等于零 3.异方差的检验方法有A .图示检验法B .Glejser 检验C .White 检验D ...DW 检验E .Goldfeld Quandt -检验4.下列哪些非线性模型可以通过变量替换转化为线性模型 ;A .i Y =201i i X u ββ++B .1/i Y =01(1/)i i X u ββ++C .ln i Y =01ln i i X u ββ++D .i Y =iui i AK L e αβE .i Y =1122012iiX X i e e u ββααα+++5.在线性模型中引入虚拟变量,可以反映 ;A .截距项变动B .斜率变动C .斜率与截距项同时变动D .分段回归E .以上都可以 四、简答题1.随机干扰项主要包括哪些因素它和残差之间的区别是什么2.简述为什么要对参数进行显着性检验试说明参数显着性检验的过程;3.简述序列相关性检验方法的共同思路; 五、计算分析题1.下表是某次线性回归的EViews 输出结果,根据所学知识求出被略去部分的值用大写字母标示,并写出过程保留3位小数;Dependent Variable: Y Method: Least Squares Included observations: 132.用Goldfeld Quandt -方法检验下列模型是否存在异方差;模型形式如下:i Y =0112233 i i i i X X X u ββββ++++其中样本容量n =40,按i X 从小到大排序后,去掉中间10个样本,并对余下的样本按i X 的大小等分为两组,分别作回归,得到两个残差平方和1ESS =、2ESS =,写出检验步骤α=;F 分布百分位表α=3.有人用广东省1978—2005年的财政收入AV 作为因变量,用三次产业增加值作为自变量,进行了三元线性回归;第一产业增加值——1VAD ,第二产业增加值——2VAD ,第三产业增加值——3VAD ,结果为:AV =12335.1160.0280.0480.228VAD VAD VAD +-+2R =,F =- ..DW =试简要分析回归结果; 五、证明题求证:一元线性回归模型因变量模拟值ˆi Y 的平均值等于实际观测值i Y 的平均值,即ˆiY =i Y ; 计量经济学习题二一、判断正误正确划“√”,错误划“×” 1.残差剩余项i e 的均值e =()i e n ∑=0;2.所谓OLS 估计量的无偏性,是指参数估计量的数学期望等于各自的真值; 3.样本可决系数高的回归方程一定比样本可决系数低的回归方程更能说明解释变量对被解释变量的解释能力;4.多元线性回归模型中解释变量个数为k ,则对回归参数进行显着性检验的t 统计量的自由度一定是1n k --;5.对应于自变量的每一个观察值,利用样本回归函数可以求出因变量的真实值; 6.若回归模型存在异方差问题,可以使用加权最小二乘法进行修正;7.根据最小二乘估计,我们可以得到总体回归方程;8.当用于检验回归方程显着性的F 统计量与检验单个系数显着性的t 统计量结果矛盾时,可以认为出现了严重的多重共线性9.线性回归模型中的“线性”主要是指回归模型中的参数是线性的,而变量则不一定是线性的;10.一般情况下,用线性回归模型进行预测时,单个值预测与均值预测相等,且置信区间也相同; 二、单选题1.针对同一经济指标在不同时间发生的结果进行记录的数据称为A .面板数据B .截面数据C .时间序列数据D .以上都不是 2.下图中“{”所指的距离是A .随机干扰项B .残差C .i Y 的离差D .ˆiY 的离差 3.在模型i Y =01ln i i X u ββ++中,参数1β的含义是A .X 的绝对量变化,引起Y 的绝对量变化B .Y 关于X 的边际变化C .X 的相对变化,引起Y 的平均值绝对量变化D .Y 关于X 的弹性4.已知含有截距项的三元线性回归模型估计的残差平方和为2i e ∑=90,估计用的样本容量为19,则随机误差项i u 方差的估计量为A .B .6C .D .55.已知某一线性回归方程的样本可决系数为,则解释变量与被解释变量间的相关系数为A .B .0.8C .D .6.用一组有20个观测值的样本估计模型i Y =01i i X u ββ++,在的显着性水平下对1β的显着性作t 检验,则1β显着异于零的条件是对应t 统计量的取值大于 A .0.05(20)t B .0.025(20)t C .0.05(18)t D .0.025(18)t7.对于模型i Y =01122ˆˆˆˆi ik ki iX X X e ββββ+++++,统计量22ˆ()/ˆ()/(1)ii i Y Y kY Y n k ----∑∑服从A .()t n k -B .(1)t n k --C .(1,)F k n k --D .(,1)F k n k --8.如果样本回归模型残差的一阶自相关系数ρ为零,那么..DW 统计量的值近似等于 ;A .1B .2C .4D .9.根据样本资料建立某消费函数如下i Y =01i i X u ββ++,其中Y 为需求量,X 为价格;为了考虑“地区”农村、城市和“季节”春、夏、秋、冬两个因素的影响,拟引入虚拟变量,则应引入虚拟变量的个数为A .2B .4C .5D .610.设消费函数为i C =012i i i i X D X u βββ+++,其中C 为消费,X 为收入,虚拟变量10D ⎧=⎨⎩城镇家庭农村家庭,当统计检验表明下列哪项成立时,表示城镇家庭与农村家庭具有同样的消费行为A .1β=0,2β=0B .1β=0,2β≠0C .1β≠0,2β=0D .1β≠0,2β≠0 三、多选题1.以i Y 表示实际观测值,ˆiY 表示用OLS 法回归后的模拟值,i e 表示残差,则回归直线满足A .通过样本均值点(,)X YB .2ˆ()i iY Y -∑=0 C .(,)i i Cov X e =0 D .i Y ∑=ˆiY ∑ E .i i e X ∑=0 2.对满足所有假定条件的模型i Y =01122i i i X X u βββ+++进行总体显着性检验,如果检验结果显示总体线性关系显着,则可能出现的情况包括A .1β=2β=0B .10β≠,2β=0C .10β≠,20β≠D .1β=0,20β≠E .1β=2β≠0 3.下列选项中,哪些方法可以用来检验多重共线性 ;A .Glejser 检验B .两个解释变量间的相关性检验C .参数估计值的经济检验D .参数估计值的统计检验E ...DW 检验 4.线性回归模型存在异方差时,对于回归参数的估计与检验正确的表述包括A .OLS 参数估计量仍具有线性性B .OLS 参数估计量仍具有无偏性C .OLS 参数估计量不再具有效性即不再具有最小方差D .一定会低估参数估计值的方差5.关于虚拟变量设置原则,下列表述正确的有A .当定性因素有m 个类型时,引入1m -个虚拟变量B.当定性因素有m个类型时,引入m个虚拟变量会产生多重共线性问题C.虚拟变量的值只能取0和1D.在虚拟变量的设置中,基础类别一般取值为0E.以上说法都正确四、简答题1.简述计量经济学研究问题的方法;2.简述异方差性检验方法的共同思路;3.简述多重共线性的危害;五、计算分析题1.下表是某次线性回归的EViews输出结果,被略去部分数值用大写字母标示,根据所学知识解答下列各题计算过程保留3位小数;本题12分Dependent Variable: YMethod: Least SquaresIncluded observations: 181求出A 、B 的值;2求TSS2.有人用美国1960-1995年36年间个人实际可支配收入X 和个人实际消费支出Y 的数据单位:百亿美元建立收入—消费模型 i Y =01i i X u ββ++,估计结果如下:ˆiY =9.4290.936i X -+ t :2R = ,F = ,..DW =1检验收入—消费模型的自相关状况5%显着水平; 2用适当的方法消除模型中存在的问题; 五、证明题证明:用于多元线性回归方程显着性检验的F 统计量与可决系数2R 满足如下关系: 计量经济学习题三 一、判断对错1、在研究经济变量之间的非确定性关系时,回归分析是惟一可用的分析方法;2、对应于自变量的每一个观察值,利用样本回归函数可以求出因变量的真实值;DW 检验临界值表α=3、OLS 回归方法的基本准则是使残差平方和最小;4、在存在异方差的情况下,OLS 法总是高估了估计量的标准差;5、无论回归模型中包括多少个解释变量,总离差平方和的自由度总为n -1;6、线性回归分析中的“线性”主要是指回归模型中的参数是线性的,而变量则不一定是线性的;7、当我们说估计的回归系数在统计上是显着的,意思是说它显着异于0; 8、总离差平方和TSS 可分解为残差平方ESS 和与回归平方和RSS,其中残差平方ESS 表示总离差平方和可由样本回归直线解释的部分;9、所谓OLS 估计量的无偏性,是指回归参数的估计值与真实值相等; 10、当模型中解释变量均为确定性变量时,则可以用DW 统计量来检验模型的随机误差项所有形式的自相关性;二、单项选择1、回归直线t ^Y =0ˆβ+1ˆβX t 必然会通过点 A 、0,0; B 、_X ,_Y ;C 、_X ,0;D 、0,_Y ;2、针对经济指标在同一时间所发生结果进行记录的数据列,称为 A 、面板数据;B 、截面数据;C 、时间序列数据;D 、时间数据;3、如果样本回归模型残差的一阶自相关系数ρ接近于0,那么DW 统计量的值近似等于 A 、0 B 、1 C 、2 D 、44、若回归模型的随机误差项存在自相关,则参数的OLS 估计量A 、无偏且有效B 、有偏且非有效C 、有偏但有效D 、无偏但非有效 5、下列哪一种检验方法不能用于异方差检验A、戈德菲尔德-夸特检验;B、DW检验;C、White检验;D、戈里瑟检验;6、当多元回归模型中的解释变量存在完全多重共线性时,下列哪一种情况会发生A、OLS估计量仍然满足无偏性和有效性;B、OLS估计量是无偏的,但非有效;C、OLS估计量有偏且非有效;D、无法求出OLS估计量;7、DW检验法适用于的检验A、一阶自相关B、高阶自相关C、多重共线性 D都不是8、在随机误差项的一阶自相关检验中,若DW=,给定显着性水平下的临界值d L=,d U=,则由此可以判断随机误差项A、存在正自相关B、存在负自相关C、不存在自相关D、无法判断9、在多元线性线性回归模型中,解释变量的个数越多,则可决系数R2A、越大;B、越小;C、不会变化;D、无法确定10、在某线性回归方程的估计结果中,若残差平方和为10,回归平方和为40,则回归方程的拟合优度为A、 B、 C、 D、无法计算;三、简答与计算1、多元线性回归模型的基本假设有哪些2、计量经济模型中的随机误差项主要包含哪些因素3、简答经典单方程计量模型的异方差性概念、后果以及修正方法;4、简述方程显着性检验F检验与变量显着性检验t检验的区别;5、对于一个三元线性回归模型,已知可决系数R2=,方差分析表的部份结果如下:1样本容量是多少2总离差平方和TSS为多少3残差平方和ESS为多少4回归平方和RSS和残差平方和ESS的自由度各为多少5求方程总体显着性检验的F统计量;四、案例分析下表是中国某地人均可支配收入INCOME与储蓄SAVE之间的回归分析结果单位:元:Dependent Variable: SAVEMethod: Least SquaresSample: 1 31Included observations: 31Variable CoefficientStd.Errort-Statistic Prob.CINCOME――――R-squared Mean dependent var AdjustedR-squared. dependent var. of regression Akaike info criterionSum squared resid1778097Schwarz criterion.Log likelihood F-statisticDurbin-Watsonstat ProbF-statistic1、请写出样本回归方程表达式,然后分析自变量回归系数的经济含义2、解释样本可决系数的含义3、写出t检验的含义和步骤,并在5%的显着性水平下对自变量的回归系数进行t 检验临界值: 29=;4、下表给出了White异方差检验结果,试在5%的显着性水平下判断随机误差项是否存在异方差;5、下表给出LM序列相关检验结果滞后1期,试在5%的显着性水平下判断随机误差项是否存在一阶自相关;计量经济学习题四一、判断对错1、一般情况下,在用线性回归模型进行预测时,个值预测与均值预测结果相等,且它们的置信区间也相同;2、对于模型Yi =β+β1X1i+β2X2i+……+βkXki+μi,i=1,2, ……,n;如果X2=X5+X6, 则模型必然存在解释变量的多重共线性问题;3、OLS回归方法的基本准则是使残差项之和最小;4、在随机误差项存在正自相关的情况下,OLS法总是低估了估计量的标准差;5、无论回归模型中包括多少个解释变量,总离差平方和的自由度总为n-1;6、一元线性回归模型的F检验和t检验是一致的;7、如果随机误差项的方差随解释变量变化而变化,则线性回归模型存在随机误差项的序列相关;8、在近似多重共线性下,只要模型满足OLS的基本假定,则回归系数的最小二乘估计量仍然是一BLUE估计量;9、所谓参数估计量的线性性,是指参数估计量是解释变量的线性组合;10、拟合优度的测量指标是可决系数R2或调整过的可决系数,R2越大,说明回归方程对样本的拟合程度越高;二、单项选择1.在多元线性回归模型中,若两个自变量之间的相关系数接近于1,则在回归分析中需要注意模型的问题;A、自相关;B、异方差;C、模型设定偏误;D、多重共线性;2、在异方差的众多检验方法中,既能判断随机误差项是否存在异方差,又能给出异方差具体存在形式的检验方法是A、图式检验法;B、DW检验;C、戈里瑟检验;D、White检验;3、如果样本回归模型残差的一阶自相关系数ρ接近于1,那么DW统计量的值近似等于A、0B、1C、2D、44、若回归模型的随机误差项存在异方差,则参数的OLS估计量A、无偏且有效B、无偏但非有效C、有偏但有效D、有偏且非有效5、下列哪一个方法是用于补救随机误差项自相关问题的A、OLS;B、ILS;C、WLS;D、GLS;6、计量经济学的应用不包括:A、预测未来;B、政策评价;C、创建经济理论;D、结构分析;7、LM检验法适用于的检验A、异方差;B、自相关;C、多重共线性; D都不是8、在随机误差项的一阶自相关检验中,若DW=,给定显着性水平下的临界值d L=,d U=,则由此可以判断随机误差项A、存在正自相关B、存在负自相关C、不存在自相关D、无法判断9、在多元线性线性回归模型中,解释变量的个数越多,则调整可决系数2RA、越大;B、越小;C、不会变化;D、无法确定10、在某线性回归方程的估计结果中,若残差平方和为10,总离差平方和为100,则回归方程的拟合优度为A、;B、;C、;D、无法计算;三、简答与计算1、多元线性回归模型的基本假设有哪些2、简述计量经济研究的基本步骤3、简答经典单方程计量模型自相关概念、后果以及修正方法;4、简述对多元回归模型01122...i i i k ki i Y X X X u ββββ=+++++进行显着性检验F 检验的基本步骤5、对于一个五元线性回归模型,已知可决系数R 2=,方差分析表的部份结果如下:1样本容量是多少2回归平方和RSS 为多少3残差平方和ESS 为多少 4回归平方和RSS 和总离差平方和TSS 的自由度各为多少 5求方程总体显着性检验的F 统计量;四、实验下表是某国1967-1985年间GDP 与出口额EXPORT 之间的回归分析结果单位:亿美元:Dependent Variable: EXPORT Method: Least Squares Sample: 1967 1985Included observations: 19VariableCoefficientStd. Errort-Statist icProb. CGDP――――R-squaredMean dependent varAdjusted R-squared. dependent var. of regressionAkaike infocriterionSum squared residSchwarz criterion Log likelihoodF-statisticDurbin-Watson statProbF-statistic1、请写出样本回归方程表达式,然后分析自变量回归系数的经济含义2、解释样本可决系数的含义3、写出t 检验的含义和步骤,并在5%的显着性水平下对自变量的回归系数进行t 检验临界值: 17=;4、下表给出了White 异方差检验结果,试在5%的显着性水平下判断随机误差项是否存在异方差;5、下表给出LM 序列相关检验结果滞后1期,试在5%的显着性水平下判断随机误差项是否存在一阶自相关;计量经济学习题五一、判断正误正确划“√”,错误划“x ”1、最小二乘法进行参数估计的基本原理是使残差平方和最小;2、一般情况下,用线性回归模型进行预测时,个值预测与均值预测相等,且置信区间也相同;3、如果随机误差项的方差随解释变量变化而变化,则线性回归模型存在随机误差项的序列相关;4、若回归模型存在异方差问题,应使用加权最小二乘法进行修正;5、多元线性回归模型的F 检验和t 检验是一致的;6、DW 检验只能检验随机误差项是否存在一阶自相关;7、总离差平方和TSS 可分解为残差平方RSS 和与回归平方和ESS,其中残差平方RSS 表示总离差平方和可由样本回归直线解释的部分;8、拟合优度用于检验回归方程对样本数据的拟合程度,其测量指标是可决系数或调整后的可决系数;9、对于模型011... 1,2,...,i i n ni i Y X X u i n βββ=++++=;如果231X X X =-,则模型必然存在解释变量的多重共线性问题;10、所谓OLS 估计量的无偏性,是指参数估计量的数学期望等于各自真值; 二、单项选择1、回归直线01ˆˆˆi iY X ββ=+必然会通过点A、0,0B、_X,_YC、_X,0D、0,_Y2、某线性回归方程的估计的结果,残差平方和为20,回归平方和为80,则回归方程的拟合优度为A、 B、C、 D、无法计算3、针对经济指标在同一时间所发生结果进行记录的数据列,称为A、面板数据B、截面数据C、时间序列数据D、时间数据4、对回归方程总体线性关系进行显着性检验的方法是A、Z检验B、t检验C、F检验D、预测检验5、如果DW统计量等于2,那么样本回归模型残差的一阶自相关系数ρ近似等于A、0B、-1C、1D、6、若随机误差项存在异方差,则参数的普通最小二乘估计量A、无偏且有效B、有偏且非有效C、有偏但有效D、无偏但非有效7、下列哪一种方法是用于补救随机误差项的异方差问题的A、OLS;B、ILS;C、WLSD、GLS8、如果某一线性回归方程需要考虑四个季度的变化情况,那么为此设置虚拟变量的个数为A、1B、2C、3D、49、样本可决系数R2越大,表示它对样本数据拟合得A、越好B、越差C、不能确定D、均有可能10、多元线性回归模型中,解释变量的个数越多,可决系数R2A、越大;B、越小;C、不会变化;D、无法确定三、简答题1、简述计量经济学的定义;2、多元线性回归模型的基本假设有哪些3、简答异方差概念、后果以及修正方法;4、简述t检验的目的及基本步骤;四、计算对于一个三元线性回归模型,已知可决系数20.8R ,方差分析表的部份结果如下:变差来源平方和自由度源于回归ESS 200源于残差RSS总变差TSS 221样本容量是多少2总变差TSS为多少3残差平方和RSS为多少4ESS和RSS的自由度各为多少5求方程总体显着性检验的F统计量值;计量经济学习题六-案例题一、根据美国各航空公司航班正点到达的比率X%和每10万名乘客投诉的次数Y 进行回归,EViews输出结果如下:Dependent Variable: YMethod: Least SquaresSample: 1 9Included observations: 91对以上结果进行简要分析包括方程显着性检验、参数显着性检验、DW值的评价、对斜率的解释等,显着性水平均取;2按标准书写格式写出回归结果;二、以下是某次线性回归的EViews输出结果,部分数值已略去用大写字母标示,但它们和表中其它特定数值有必然联系,分别据此求出这些数值,并写出过程;保留3位小数Dependent Variable: YMethod: Least SquaresSample: 1 13Included observations: 131求A 的值; 2求B 的值; 3求C 的值;三、用1970-1994年间日本工薪家庭实际消费支出Y 与实际可支配收入X 单位:103日元数据估计线性模型Y =01X u ββ++,然后用得到的残差序列t e 绘制以下图形; 1试根据图形分析随机误差项之间是否存在自相关若存在,是正自相关还是负自相关答:图形显示,随机误差项之间存在着相关性,且为正的自相关; 2此模型的估计结果为 试用DW 检验法检验随机误差项之间是否存在自相关;四、用一组截面数据估计消费Y —收入X 方程Y =01X u ββ++的结果为1根据回归的残差序列et 图分析本模型是否存在异方差注:abset 表示et 的绝对值;2其次,用White 法进行检验;EViews 输出结果见下表:附表:DW 检验临界值表α=White Heteroskedasticity Test:Dependent Variable: RESID^2 Method: Least Squares Sample: 1 60Included observations: 60若给定显着水平0.05α=,以上结果能否说明该模型存在异方差查卡方分布临界值的自由度是多少五、下图描述了残差序列{}t e 与其滞后一期值1{}t e -之间的散点图,试据此判断随机误差项之间是否存在自相关若存在,则是正自相关还是负自相关六、在一多元线性回归模型中,为检验解释变量之间是否存在多重共线性问题,以解释变量1x 作为被解释变量,对其余解释变量进行辅助回归,得到可决系数20.95R =;试计算变量1x 的方差扩大因子1VIF ,并根据经验判断解释变量间是否存在多重共线性问题七、下表是中国某地人均可支配收入INCOME 与储蓄SAVE 之间的回归分析结果单位:元:Sample: 1 31Included observations: 31VariableCoefficientStd. Errort-Statist ic Prob.CINCOME--R-squaredMean dependent varAdjusted R-squared. dependent var. of regressionAkaike infocriterionSum squared resid 1778097. Schwarz criterion Log likelihoodF-statisticDurbin-Watson statProbF-statistic1、请写出样本回归方程表达式,然后分析自变量INCOME 回归系数的经济含义2、解释可决系数的含义3、若给定显着性水平5%α=,试对自变量INCOME 的回归系数进行显着性检验已知0.025(29) 2.045t =4、在5%α=的显着性水平下,查31n =的DW 临界值表得 1.363L d =, 1.496U d =,试根据回归结果判断随机误差项是否存在一阶自相关5、下表为上述回归的White 检验结果,在5%α=的显着性水平下,试根据P 值检验判断随机误差项是否存在异方差 White Heteroskedasticity Test:F-statisticProbabilityObsR-squaredProbability计量经济学习题一答案一、判断正误1. × 2. √ 3. √ 4. √ 5. × 6. × 7. ×8. × 9. √ 10. √ 二、单选题每小题分,共15分1. D ;2. B ;3. B ;4. C ;5. B ; 6. B ;7. B ;8. B ;9. B ;10. A ; 三、多选题1. ABCE 2. BCDE 3. ABCE 4. ABCD 5. ABCDE ; 四、简答题1.随机干扰项主要包括哪些因素它和残差之间的区别是什么答:随机干扰项包括的主要因素有:1众多细小因素的影响;2未知因素的影响;3数据测量误差或残缺;4模型形式不完善;5变量的内在随机性;随机误差项羽残差不同,残差是样本观测值与模拟值的差,即i e =ˆi iY Y -;残差项是随机误差项的估计;2.简述为什么要对参数进行显着性检验试说明参数显着性检验的过程;答:最小二乘法得到的回归直线是对因变量与自变量关系的一种描述,但它是不是恰当的描述呢一般会用与样本点的接近程度来判别这种描述的优劣,而当获得以上问题的肯定判断之后,还需要确定每一个参数的可靠程度,即参数本身以及对应的变量该不该保留在方程里,这就有必要进行参数的显着性检验;这种检验是确定各个参数是否显着地不等于零;检验分为三个步骤:①提出假设:原假设0:0i H β=;备择假设1:0i H β≠ ②在原假设成立的前提下构造统计量:()ˆ~(1)ˆiit t n k Se ββ=--③给定显着性水平α,查t 分布表求得临界值/2(1)t n k α--,把根据样本数据计算出的t 统计量值t *与/2(1)t n k α--比较:若/2(1)t t n k α*>--,则拒绝原假设0H ,即在给定显着性水平下,解释变量i X 对因变量有显着影响;若/2(1)t t n k α*<--,则不能拒绝原假设0H ,即在给定显着性水平下,解释变量i X 对因变量没有显着影响.3.简述序列相关性检验方法的共同思路;答:由于自相关性,使得相对于不同的样本点,随机干扰项之间存在相关关系,那么检验自相关性,首先根据OLS 法估计残差,将残差作为随机干扰项的近似估计值,然后检验这些近似估计值之间的相关性以判定随机干扰项是否存在序列相关;各种检验方法就是在这个思路下发展起来的;五、计算分析题1.下表是某次线性回归的EViews 输出结果,根据所学知识求出被略去部分的值用大写字母标示,Dependent Variable: Y Method: Least Squares Included observations: 13解:A=ˆ()Se β=ˆt β=7.10604.3903=;B=2R =211(1)1n R n k -----=1311(10.8728)1321-----=由公式2ˆσ=21ien k --∑,得C=2ie ∑=2ˆ(1)n k σ--=21.1886(1321)--=; 2.用Goldfeld Quandt -方法检验下列模型是否存在异方差;模型形式如下:i Y =0112233 i i i i X X X u ββββ++++其中样本容量n =40,按i X 从小到大排序后,去掉中间10个样本,并对余下的样本按i X 的大小等分为两组,分别作回归,得到两个残差平方和1ESS =、2ESS =,写出检验步骤α=;α。
高级计量经济学课后习题参考答案

1.3 某市居民家庭人均年收入服从4000X =元,1200σ=元的正态分布,求该市居民家庭人均年收入:(1)在5000—7000元之间的概率;(2)超过8000元的概率;(3)低于3000元的概率。
(1)()()()()()2,0,15000700050007000()2.50.835( 2.5)62X N X X XN XX XX P X P F F X XP σσσσσσ-∴---∴<<=<<--=<<=根据附表1可知()0.830.5935F =,()2.50.9876F =()0.98760.5935500070000.19712P X -∴<<==PS :()()5000700050007000()55( 2.5) 2.5660.99380.79760.1961XX XXP X P X X P σσσσ---<<=<<-⎛⎫=<<=Φ-Φ ⎪⎝⎭=-=在附表1中,()()F Z P x x z σ=-<(2)()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=>⎪⎪⎝⎭⎝⎭=0.0004 (3)()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<-⎪ ⎪⎝⎭⎝⎭=0.2023=0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98,因事故死亡的概率为0.02。
保险公司开办老人事故死亡保险,参加者需缴纳保险费100元。
若5年内因事故死亡,公司要赔偿a 元。
应如何测算出a ,才能使公司可期望获益;若有1000人投保,公司可期望总获益多少?则()1000.02E X a =-故要是公司可期望获益,则有()1000.02E X a =->0,即5000a < PS :赔偿金应大于保险费?1000人投保时,公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型,并分别求出回归系数的最小二乘估计。
计量经济学习题及参考答案

计量经济学各章习题第一章绪论1.1试列出计量经济分析地主要步骤.1.2计量经济模型中为何要包括扰动项?1.3什么是时间序列和横截面数据? 试举例说明二者地区别1.4估计量和估计值有何区别?第二章计量经济分析地统计学基础2.1名词解释随机变量概率密度函数抽样分布样本均值样本方差协方差相关系数标准差标准误差显著性水平置信区间无偏性有效性一致估计量接受域拒绝域第I 类错误2.2请用例 2.2中地数据求北京男生平均身高地99%置信区间.2.325 个雇员地随机样本地平均周薪为130元,试问此样本是否取自一个均值为120 元、标准差为10 元地正态总体?文档收集自网络,仅用于个人学习2.4某月对零售商店地调查结果表明,市郊食品店地月平均销售额为2500 元,在下一个月份中,取出16 个这种食品店地一个样本,其月平均销售额为2600 元,销售额地标准差为480 元.试问能否得出结论,从上次调查以来,平均月销售额已经发生了变化?文档收集自网络,仅用于个人学习第三章双变量线性回归模型3.1判断题(判断对错;如果错误,说明理由)(1)OLS 法是使残差平方和最小化地估计方法.(2)计算OLS 估计值无需古典线性回归模型地基本假定.(3)若线性回归模型满足假设条件(1)~(4),但扰动项不服从正态分布,则尽管OLS 估计量不再是BLUE ,但仍为无偏估计量.文档收集自网络,仅用于个人学习(4)最小二乘斜率系数地假设检验所依据地是t 分布,要求地抽样分布是正态分布.2(5)R2=TSS/ESS.(6)若回归模型中无截距项,则.(7)若原假设未被拒绝,则它为真.(8)在双变量回归中,地值越大,斜率系数地方差越大.3.2设和分别表示Y 对X 和X 对Y 地OLS 回归中地斜率,证明r 为X 和Y 地相关系数.3.3证明:(1)Y 地真实值与OLS 拟合值有共同地均值,即;(2)OLS 残差与拟合值不相关,即.3.4证明本章中( 3.18)和( 3.19)两式:(1)(2)3.5考虑下列双变量模型:模型1:模型2:(1)1 和1地OLS 估计量相同吗?它们地方差相等吗?(2)2 和2地OLS 估计量相同吗?它们地方差相等吗?3.6有人使用1980-1994 年度数据,研究汇率和相对价格地关系,得到如下结果:其中,Y=马克对美元地汇率X=美、德两国消费者价格指数(CPI)之比,代表两国地相对价格(1)请解释回归系数地含义;(2)X t 地系数为负值有经济意义吗?(3)如果我们重新定义X 为德国CPI与美国CPI之比,X 地符号会变化吗?为什么?3.7随机调查200 位男性地身高和体重,并用体重对身高进行回归,结果如下:其中Weight 地单位是磅(lb ),Height 地单位是厘米(cm).(1)当身高分别为177.67cm、164.98cm、187.82cm 时,对应地体重地拟合值为多少?(2)假设在一年中某人身高增高了 3.81cm,此人体重增加了多少?3.8设有10 名工人地数据如下:X 10 7 10 5 8 8 6 7 9 10Y 11 10 12 6 10 7 9 10 11 10 其中X= 劳动工时,Y= 产量(1)试估计Y=α+βX + u(要求列出计算表格);(2)提供回归结果(按标准格式)并适当说明;(3)检验原假设β=1.0.3.9用12 对观测值估计出地消费函数为Y=10.0+0.90X ,且已知=0.01,=200,=4000,试预测当X=250 时Y 地值,并求Y 地95%置信区间.文档收集自网络,仅用于个人学习3.10设有某变量(Y)和变量(X)1995—1999 年地数据如下:(3)试预测X=10 时Y 地值,并求Y 地95%置信区间.3.11根据上题地数据及回归结果,现有一对新观测值X =20,Y=7.62,试问它们是否可能来自产生样本数据地同一总体?文档收集自网络,仅用于个人学习3.12有人估计消费函数,得到如下结果(括号中数字为t 值):=15 + 0.81 =0.98(2.7)(6.5)n=19(1)检验原假设:=0(取显著性水平为5%)(2)计算参数估计值地标准误差;(3)求地95%置信区间,这个区间包括0 吗?3.13试用中国1985—2003 年实际数据估计消费函数:=α+β + u t其中:C代表消费,Y 代表收入.原始数据如下表所示,表中:Cr=农村居民人均消费支出(元)Cu=城镇居民人均消费支出(元)Y =国内居民家庭人均纯收入(元) Yr =农村居民家庭人均纯收入(元) Yu=城镇居民家庭人均可支配收入(元) Rpop=农村人口比重(%) pop=历年年底我国人口总数(亿人)P=居民消费价格指数(1985=100)Pr=农村居民消费价格指数(1985=100)Pu=城镇居民消费价格指数(1985=100)数据来源:《中国统计年鉴2004》使用计量经济软件,用国内居民人均消费、农村居民人均消费和城镇居民人均消费分别对各自地人均收入进行回归,给出标准格式回归结果;并由回归结果分析我国城乡居民消费行为有何不同.文档收集自网络,仅用于个人学习第四章多元线性回归模型4.1某经济学家试图解释某一变量Y 地变动.他收集了Y 和 5 个可能地解释变量~地观测值(共10 组),然后分别作三个回归,结果如下(括号中数字为t 统计量):文档收集自网络,仅用于个人学习( 1) = 51.5 + 3.21 R=0.63(3.45) (5.21)2) 33.43 + 3.67 + 4.62 + 1.21 R=0.75 文档收集自网络,仅用于个人学(3.61 )(2.56)(0.81) (0.22)3) 23.21 + 3.82 + 2.32 + 0.82 + 4.10 + 1.21(2.21 )(2.83)(0.62) (0.12) (2.10) (1.11)文档收集自网络,仅用于个人学习R=0.80 你认为应采用哪一个结果?为什么?4.2为研究旅馆地投资问题,我们收集了某地地1987-1995 年地数据来估计收益生产函数R=ALKe ,其中R=旅馆年净收益(万年) ,L=土地投入,K=资金投入, e 为自然对数地底.设回归结果如下(括号内数字为标准误差) :文档收集自网络,仅用于个人学习= -0.9175 + 0.273lnL + 0.733lnK R=0.94(0.212) (0.135) (0.125)(1)请对回归结果作必要说明;( 2)分别检验α和β 地显著性;( 3)检验原假设:α =β = 0;4.3我们有某地1970-1987 年间人均储蓄和收入地数据,用以研究1970-1978 和1978 年以后储蓄和收入之间地关系是否发生显著变化. 引入虚拟变量后,估计结果如下(括号内数据为标准差) :文档收集自网络,仅用于个人学习= -1.7502 + 1.4839D + 0.1504 - 0.1034D·R=0.9425 文档收集自网络,仅用于个人学习(0.3319) (0.4704) (0.0163) (0.0332)其中:Y=人均储蓄,X=人均收入,D= 请检验两时期是否有显著地结构性变化.4.4说明下列模型中变量是否呈线性,系数是否呈线性,并将能线性化地模型线性化.(1)(2)(3)4.5有学者根据某国19年地数据得到下面地回归结果:其中:Y=进口量(百万美元),X1 =个人消费支出(百万美元),X2 =进口价格/国内价格.(1)解释截距项以及X1和X2系数地意义;(2)Y 地总变差中被回归方程解释地部分、未被回归方程解释地部分各是多少?(3)进行回归方程地显著性检验,并解释检验结果;(4)对“斜率”系数进行显著性检验,并解释检验结果.4.6由美国46个州1992年地数据,Baltagi 得到如下回归结果:其中,C=香烟消费(包/人年),P=每包香烟地实际价格Y=人均实际可支配收入(1)香烟需求地价格弹性是多少?它是否统计上显著?若是,它是否统计上异于-1?(2)香烟需求地收入弹性是多少?它是否统计上显著?若不显著,原因是什么?(3)求出.4.7有学者从209 个公司地样本,得到如下回归结果(括号中数字为标准误差):其中,Salary=CEO 地薪金Sales=公司年销售额roe=股本收益率(%)ros=公司股票收益请分析回归结果.4.8为了研究某国1970-1992 期间地人口增长率,某研究小组估计了下列模型:其中:Pop=人口(百万人),t=趋势变量,.(1)在模型 1 中,样本期该地地人口增长率是多少?(2)人口增长率在1978 年前后是否显著不同?如果不同,那么1972-1977和1978-1992 两时期中,人口增长率各是多少?文档收集自网络,仅用于个人学习4.9设回归方程为Y= β0+β1X1+β2X2+β3X3+ u, 试说明你将如何检验联合假设:β1= β2 和β3 = 1 .文档收集自网络,仅用于个人学习4.10下列情况应引入几个虚拟变量,如何表示?(1)企业规模:大型企业、中型企业、小型企业;(2)学历:小学、初中、高中、大学、研究生.4.11在经济发展发生转折时期,可以通过引入虚拟变量来表示这种变化.例如,研究进口消费品地数量Y 与国民收入X 地关系时,数据散点图显示1979 年前后明显不同.请写出引入虚拟变量地进口消费品线性回归方程.文档收集自网络,仅用于个人学习4.12柯布-道格拉斯生产函数其中:GDP=地区国内生产总值(亿元)K=资本形成总额(亿元)L= 就业人数(万人)P=商品零售价格指数(上年=100)试根据中国2003 年各省数据估计此函数并分析结果.数据如下表所示第五章模型地建立与估计中地问题及对策5.1判断题(判断对错;如果错误,说明理由)(1)尽管存在严重多重共线性,普通最小二乘估计量仍然是最佳线性无偏估计量(BLUE ).(2)如果分析地目地仅仅是为了预测,则多重共线性并无妨碍. (3)如果解释变量两两之间地相关系数都低,则一定不存在多重共线性. (4)如果存在异方差性,通常用地t 检验和 F 检验是无效地. (5)当存在自相关时,OLS 估计量既不是无偏地,又不是有效地.(6)消除一阶自相关地一阶差分变换法假定自相关系数必须等于 1. (7)模型中包含无关地解释变量,参数估计量会有偏,并且会增大估计量地方差,即增大误差.(8)多元回归中,如果全部“斜率”系数各自经t 检验都不显著,则R2值也高不了.(9)存在异方差地情况下,OLS 法总是高估系数估计量地标准误差.(10)如果一个具有非常数方差地解释变量被(不正确地)忽略了,那么OLS 残差将呈异方差性.5.2考虑带有随机扰动项地复利增长模型:Y 表示GDP,Y0是Y 地基期值,r 是样本期内地年均增长率,t 表示年份,t=1978,⋯,2003.文档收集自网络,仅用于个人学习试问应如何估计GDP 在样本期内地年均增长率?5.3 检验下列情况下是否存在扰动项地自相关 .(1) DW=0.81,n=21,k=3(2)DW=2.25,n=15,k=2(3)DW=1.56,n=30,k=55.4有人建立了一个回归模型来研究我国县一级地教育支出:Y= β0+β1X1+β 2X2+β3X3+u其中:Y,X1,X2 和X3分别为所研究县份地教育支出、居民人均收入、学龄儿童人数和可以利用地各级政府教育拨款.文档收集自网络,仅用于个人学习他打算用遍布我国各省、市、自治区地100 个县地数据来估计上述模型.(1)所用数据是什么类型地数据?(2)能否采用OLS 法进行估计?为什么?(3)如不能采用OLS 法,你认为应采用什么方法?5.5试从下列回归结果分析存在问题及解决方法:(1)= 24.7747 + 0.9415 - 0.0424 R=0.9635SE:(6.7525)(0.8229)(0.0807)其中:Y=消费,X2=收入,X3=财产,且n=5000 (2)= 0.4529 - 0.0041t R=0.5284t:(-3.9606) DW=0.8252其中Y= 劳动在增加值中地份额,t=时间该估计结果是使用1949-1964 年度数据得到地.5.6工资模型:wi=b0+b1Si+b2Ei+b3Ai+b4Ui+ui其中Wi=工资,Si=学校教育年限,Ei=工作年限,Ai=年龄,Ui=是否参加工会.在估计上述模型时,你觉得会出现什么问题?如何解决?5.7你想研究某行业中公司地销售量与其广告宣传费用之间地关系.你很清楚地知道该行业中有一半地公司比另一半公司大,你关心地是这种情况下,什么估计方法比较合理.假定大公司地扰动项方差是小公司扰动项方差地两倍.文档收集自网络,仅用于个人学习(1)若采用普通最小二乘法估计销售量对广告宣传费用地回归方程(假设广告宣传费是与误差项不相关地自变量),系数地估计量会是无偏地吗?是一致地吗?是有效地吗?文档收集自网络,仅用于个人学习(2)你会怎样修改你地估计方法以解决你地问题?(3)能否对原扰动项方差假设地正确性进行检验?5.8考虑下面地模型其中GNP=国民生产总值,M =货币供给. (1)假设你有估计此模型地数据,你能成功地估计出模型地所有系数吗?说明理由.(2)如果不能,哪些系数可以估计?(3)如果从模型中去掉这一项,你对(1)中问题地答案会改变吗?(4)如果从模型中去掉这一项,你对(1)中问题地答案会改变吗?5.9采用美国制造业1899-1922年数据,Dougherty得到如下两个回归结果:(1)(2)其中:Y=实际产出指数,K=实际资本投入指数,L =实际劳动力投入指数,t=时间趋势(1)回归式(1)中是否存在多重共线性?你是如何得知地?(2)回归式(1)中,logK 系数地预期符号是什么?回归结果符合先验预期吗?为什么会这样?(3)回归式(1)中,趋势变量在其中起什么作用?(4)估计回归式(2)背后地逻辑是什么?(5)如果(1)中存在多重共线性,那么(2)式是否减轻这个问题?你如何得知?(6)两个回归地R2可比吗?说明理由.5.10有人估计了下面地模型:其中:C=私人消费支出,GNP=国民生产总值,D=国防支出假定,将(1)式转换成下式:使用1946-1975数据估计(1)、(2)两式,得到如下回归结果(括号中数字为标准误差):1)关于异方差,模型估计者做出了什么样地假定?你认为他地依据是什么?2)比较两个回归结果.模型转换是否改进了结果?也就是说,是否减小了估计标准误差?说明理由.5.11设有下列数据:RSS1=55,K =4,n1=30RSS3=140,K =4,n3=30 请依据上述数据,用戈德佛尔德-匡特检验法进行异方差性检验(5%显著性水平).5.12考虑模型(1)也就是说,扰动项服从AR (2)模式,其中是白噪声.请概述估计此模型所要采取地步骤.5.13对第 3 章练习题 3.13 所建立地三个消费模型地结果进行分析:是否存在序列相关问题?如果有,应如何解决?5.14为了研究中国农业总产值与有效灌溉面积、化肥施用量、农作物总播种面积、受灾面积地相互关系,选31 个省市2003 年地数据资料,如下表所示:文档收集自网络,仅用于个人学习表中:Y=农业总产值(亿元,不包括林牧渔)X1=有效灌溉面积(千公顷)X2=化肥施用量(万吨)X23=化肥施用量(公斤/亩)X3=农作物总播种面积(千公顷)X4=受灾面积(千公顷)(1)回归并根据计算机输出结果写出标准格式地回归结果;(2)模型是否存在问题?如果存在问题,是什么问题?如何解决?第六章动态经济模型:自回归模型和分布滞后模型6.1判断题(判断对错;如果错误,说明理由)(1)所有计量经济模型实质上都是动态模型.(2)如果分布滞后系数中,有地为正有地为负,则科克模型将没有多大用处. (3)若适应预期模型用OLS 估计,则估计量将有偏,但一致. (4)对于小样本,部分调整模型地OLS 估计量是有偏地.(5)若回归方程中既包含随机解释变量,扰动项又自相关,则采用工具变量法,将产生无偏且一致地估计量.(6)解释变量中包括滞后因变量地情况下,用德宾-沃森d 统计量来检测自相关是没有实际用处地.6.2用OLS 对科克模型、部分调整模型和适应预期模型分别进行回归时,得到地OLS 估计量会有什么样地性质?文档收集自网络,仅用于个人学习6.3简述科克分布和阿尔蒙多项式分布地区别.6.4考虑模型假设相关.要解决这个问题,我们采用以下工具变量法:首先用对和回归,得到地估计值,然后回归其中是第一步回归(对和回归)中得到地.(1)这个方法如何消除原模型中地相关?(2)与利维顿采用地方法相比,此方法有何优点?6.5设其中:M=对实际现金余额地需求,Y*=预期实际收入,R*=预期通货膨胀率假设这些预期服从适应预期机制:其中和是调整系数,均位于0和1之间.(1)请将M t 用可观测量表示;(2)你预计会有什么估计问题?6.6考虑分布滞后模型假设可用二阶多项式表示诸如下:若施加约束==0,你将如何估计诸系数(,i=0,1, (4)6.7为了研究设备利用对于通货膨胀地影响,T. A.吉延斯根据1971年到1988年地美国数据获得如下回归结果:文档收集自网络,仅用于个人学习其中:Y=通货膨胀率(根据GNP 平减指数计算)X t=制造业设备利用率X t-1 =滞后一年地设备利用率1)设备利用对于通货膨胀地短期影响是什么?长期影响又是什么?(2)每个斜率系数是统计显著地吗?(3)你是否会拒绝两个斜率系数同时为零地原假设?将利用何种检验?6.8考虑下面地模型:Y t = α+β(W0X t+ W1X t-1 + W2X t-2 + W3X t-3)+u t 请说明如何用阿尔蒙滞后方法来估计上述模型(设用二次多项式来近似) .6.9下面地模型是一个将部分调整和适应预期假说结合在一起地模型:Y t*= βX t+1eY t-Y t-1 = δ(Y t*- Y t-1) + u tX t+1e- X t e= (1-λ)( X t - X t e);t=1,2,⋯, n式中Y t*是理想值,X t+1e和X t e是预期值.试推导出一个只包含可观测变量地方程,并说明该方程参数估计方面地问题.文档收集自网络,仅用于个人学习第七章时间序列分析7.1单项选择题(1)某一时间序列经一次差分变换成平稳时间序列,此时间序列称为()地.A.1 阶单整B.2阶单整C.K 阶单整D.以上答案均不正确文档收集自网络,仅用于个人学习(2)如果两个变量都是一阶单整地,则().A .这两个变量一定存在协整关系B.这两个变量一定不存在协整关系C.相应地误差修正模型一定成立D.还需对误差项进行检验文档收集自网络,仅用于个人学习(3)如果同阶单整地线性组合是平稳时间序列,则这些变量之间关系是() .A. 伪回归关系B.协整关系C.短期均衡关系D. 短期非均衡关系(4).若一个时间序列呈上升趋势,则这个时间序列是().A .平稳时间序列B.非平稳时间序列C.一阶单整序列 D. 一阶协整序列7.2请说出平稳时间序列和非平稳时间序列地区别,并解释为什么在实证分析中确定经济时间序列地性质是十分必要地.文档收集自网络,仅用于个人学习7.3什么是单位根?7.4Dickey-Fuller(DF)检验和Engle-Granger(EG)检验是检验什么地?文档收集自网络,仅用于个人学习7.5什么是伪回归?在回归中使用非均衡时间序列时是否必定会造成伪回归?7.6由1948-1984 英国私人部门住宅开工数(X)数据,某学者得到下列回归结果:注:5%临界值值为-2.95,10%临界值值为-2.60. (1)根据这一结果,检验住宅开工数时间序列是否平稳.(2)如果你打算使用t 检验,则观测地t 值是否统计显著?据此你是否得出该序列平稳地结论?(3)现考虑下面地回归结果:请判断住宅开工数地平稳性.7.7由1971-I 到1988-IV 加拿大地数据,得到如下回归结果;A.B.C.其中,M1=货币供给,GDP=国内生产总值,e t=残差(回归A)(1)你怀疑回归 A 是伪回归吗?为什么?(2)回归 B 是伪回归吗?请说明理由.(3)从回归 C 地结果,你是否改变(1)中地结论,为什么?(4)现考虑以下回归:这个回归结果告诉你什么?这个结果是否对你决定回归 A 是否伪回归有帮助?7.8 检验我国人口时间序列地平稳性,数据区间为1949-2003 年.单位:万人7.9对中国进出口贸易进行协整分析,如果存在协整关系,则建立E CM 模型.1951-2003 年中国进口(im )、出口(ex)和物价指数(pt,商品零售物价指数)时间序列数据见下表.因为该期间物价变化大,特别是改革开放以后变化更为激烈,所以物价指数也作为一个解释变量加入模型中.为消除物价变动对进出口数据地影响以及消除进出口数据中存在地异方差,定义三个变量如下:文档收集自网络,仅用于个人学习第八章联立方程模型8.1判断题(判断对错;如果错误,说明理由)(1)OLS 法适用于估计联立方程模型中地结构方程.(2)2SLS 法不能用于不可识别方程.(3)估计联立方程模型地2SLS 法和其它方法只有在大样本地情况下,才能具有我们期望地统计性质 .(4) 联立方程模型作为一个整体,不存在类似 R 2这样地拟合优度测度 .(5) 如果要估计地方程扰动项自相关或存在跨方程地相关, 则 2SLS 法和其它估 计结构方程地方法都不能用 .(6) 如果一个方程恰好识别,则 ILS 和 2SLS 给出相同结果 .8.2 单项选择题1) 结构式模型中地方程称为结构方程 .在结构方程中, 解释变量可以是前定变3) 如果联立方程模型中某个结构方程包含了模型中所有地变量,则这个方程5)当一个结构式方程为恰好识别时,这个方程中内生解释变量地个数( A .与被排除在外地前定变量个数正好相等 B .小于被排除在外地前定变量个数 C .大于被排除在外地前定变量个数D .以上三种情况都有可能发生 文档收集自网络,仅用于个人学习6) 简化式模型就是把结构式模型中地内生变量表示为 ( ).A. 外生变量和内生变量地函数关系B.前定变量和随机误差项地模型C.滞后变量和随机误差项地模型 D.外生变量和随机误差项地模量,也可以是 ( ).文档收集自网络,仅用于个人学习 A. 外生变量 B.滞后变量2)前定变量是 ( )地合称 .A.外生变量和滞后内生变量C.内生变量D. 外生变量和内生变量 C.外生变量和虚拟变量 D. 解释变量和被解释变量( ).A. 恰好识别B.不可识别 (4) 下面说法正确地是( ).A.内生变量是非随机变量 C.外生变量是随机变量 C.过度识别 D.不确定B. 前定变量是随机变量个人收集整理勿做商业用途型7) 对联立方程模型进行参数估计地方法可以分两类,即:( ).A.间接最小二乘法和系统估计方法B.单方程估计法和系统估计方法个人收集整理勿做商业用途C.单方程估计法和二阶段最小二乘法D.工具变量法和间接最小二乘法(8)在某个结构方程过度识别地条件下,不适用地估计方法是().A. 间接最小二乘法B.工具变量法C.二阶段最小二乘法D.有限信息极大似然估计法8.3行为方程和恒等式有什么区别?8.4如何确定模型中地外生变量和内生变量?8.5考虑下述模型:C t = α + β D t +u t I t = γ + δD t-1 + νt D t = C t +I t + Z t ;t=1 ,2,⋯,n其中 C = 消费支出,D= 收入,I = 投资,Z = 自发支出. C、I 和D是内生变量.试写出消费支出地简化型方程,并研究各方程地识别问题.8.6考虑下述模型:Y t = C t + I t +G t +X tC t = β 0 + β 1D t + β2C t-1 + u tD t = Y t –T tI t = α0 + α1Y t + α2R t-1 +νt 模型中各方程是正规化方程,u t、νt为扰动项.(1)请指出模型中地内生变量、外生变量和前定变量.(2)写出用2SLS法进行估计时,每个阶段中要估计地方程.8.7下面是一个简单地美国宏观经济模型(1960-1999)其中C=实际私人消费,I= 实际私人总投资,G=实际政府支出,Y =实际GDP,M= 当年价M2,R=长期利率;P=消费价格指数.内生变量:C,I,R,Y 前定变量:C t-1,I t-1,M t-1,P t,R t-1 和G t.(1)应用识别地阶条件,决定各方程地识别状态;(2)你打算用什么方法来估计可识别行为方程?8.8假设有如下计量经济模型:其中,Y=国民收入,I=净资本形成,C=个人消费,Q =利润,P=生活费用指数,R= 工业劳动生产率1)写出模型地内生变量、外生变量和前定变量;个人收集整理勿做商业用途(2)用识别地阶条件确定各方程地识别状态;(3)此模型中是否有可以用ILS 法估计地方程?如有,请指出;(4)写出用2SLS 法进行估计时,每个阶段中要估计地方程. 8.9考虑下述模型:消费方程:C t=α0 +α 1Y t +α2C t-1 +u①投资方程:I t=β0 +β1Y t +β2I t –1+u2t②进口方程:M t = 0 + 1Y t + u3t ③Y t = C t+ I t + G t + X t - M t模型中各方程是正规化方程,u 1t, ⋯u3t为扰动项.(1)请指出模型中地内生变量、外生变量和前定变量.(2)利用阶条件识别各行为方程.(3)写出用3SLS 进行估计时地步骤.8.10考察下述国民经济地简单模型式中,C为消费,Y 为国民收入,I 为投资,R为利率.设样本容量n 为20,已算得中间结果为:(1)判别模型中消费方程地识别状态;(2)用间接最小二乘法求消费方程结构式系数;(3)将采用哪种方法估计投资方程?为什么?(不必计算)8.11由联立方程模型;得到其简化式如下:(1)两结构方程可识别吗?(2)如果知道,识别情况有何变化?(3)若对简化式进行估计,结果如下:个人收集整理勿做商业用途试求出结构参数地值,并说明如何检验原假设个人收集整理勿做商业用途版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理。
庞皓计量经济学第三版课后习题及答案 顶配
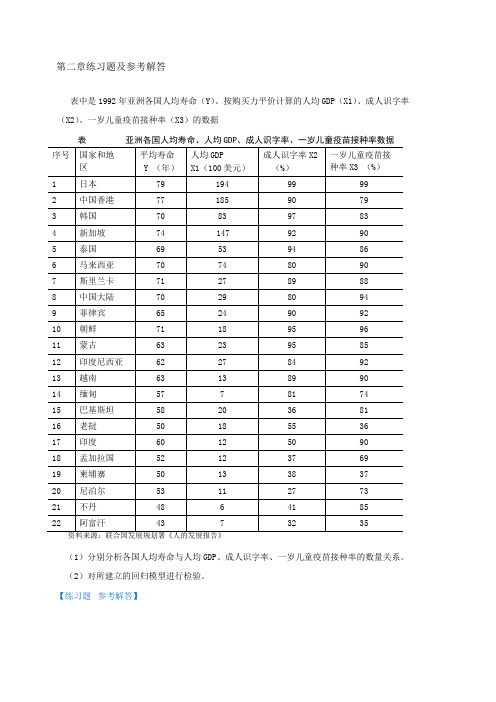
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
高级计量经济学课后习题参考答案

某市居民家庭人均年收入服从4000X =元,1200σ=元的正态分布,求该市居民家庭人均年收入:1在5000—7000元之间的概率;2超过8000元的概率;3低于3000元的概率; 1根据附表1可知 ()0.830.5935F =,()2.50.9876F = PS :在附表1中,()()F Z P x x z σ=-<2()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭= 3()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭= = 据统计70岁的老人在5年内正常死亡概率为,因事故死亡的概率为;保险公司开办老人事故死亡保险,参加者需缴纳保险费100元;若5年内因事故死亡,公司要赔偿a 元;应如何测算出a ,才能使公司可期望获益;若有1000人投保,公司可期望总获益多少设公司从一个投保者得到的收益为X ,则则()1000.02E X a =-故要是公司可期望获益,则有()1000.02E X a =->0,即5000a <PS :赔偿金应大于保险费1000人投保时,公司的期望总收益为()10001000.021*******a a -=-写出过原点的一元、二元线性回归模型,并分别求出回归系数的最小二乘估计; 解答:过原点的一元线性回归模型为Y X βε=+ 约束最小二乘估计:y x αβε=++过原点的二元线性回归模型为1122Y X X ββε=++ 针对多元线性回归模型试证明经典线性回归模型参数OLS 估计量的性质()ˆE ββ=和()()12ˆˆ,Cov X X ββσ-'=,并说明你在证明时用到了哪些基本假定; 解答:为了解某国职业妇女是否受到歧视,可以用该国统计局的“当前人口调查”中的截面数据,研究男女工资有没有差别;这项多元回归分析研究所用到的变量有:对124名雇员的样本进行研究得到的回归结果为括号内为估计的t 值:1求调整后的可决系数2R2AGE 的系数估计值的标准差为多少3检验该国工作妇女是否受到歧视为什么4求以95%的概率,一个30岁受教育16年的该国妇女,平均每小时工作收入的预测区间是多少 解答:1 23因为()0.025120 1.9799 4.61t =<,所以2ˆ 2.76β=-显着,且为负,即意味着妇女受到歧视;40ˆ 6.41 2.7610.99160.123010.27W=--⨯+⨯+⨯= 有公式知0W 的95%置信区间为: 即10.27 1.9799±其中()01,1,16,30X '=设某公司的投资行为可用如下回归模型描述: 其中i I 为当期总投资,1i F -为已发行股票的上期期末价值,1i K -为上期资本存量;数据见课本71页; (1) 对此模型进行估计,并做出经济学和计量经济学的说明;(2) 根据此模型所估计的结果,做计量经济学检验;(3) 计算修正的可决系数;(4) 如果2003年的1i F -和1i K -分别为和,计算iI 在2003年的预测值,并求出置信度为95%的预测区间;解答:equation i c f kexpand 1984 2003smpl 2003 2003f=k=smpl 1984 2003yf sfscalar tc=qtdist,16series yl=yf-tcsfseries yu=yf+tcsfshow yl yf yu1最小二乘回归结果为:经济意义说明:在假定其他变量不变的情况下,已发行股票的上期期末价值增加1单位,当期总投资增加单位;在其他变量不变的情况下,上期资本存量增加1单位,当期总投资增加单位;2模型的拟合优度为20.890687R=,修正可决系数为20.877022R=,可见模型拟合效果不错;F检验:对模型进行显着性检验,F统计量对应的P 值为0,因此在0.05α=的显着性水平上我们拒绝原假设023:0H ββ==,说明回归方程显着,即变量“已发行股票的上期期末价值”和“上期资本”存量联合起来确实对“当期总投资”有显着影响; t 检验:针对()0:01,2,3jH j β==进行显着性检验;给定显着性水平0.05α=,查表知()216 2.12t α=;由回归结果,2ˆβ、3ˆβ对应的t 统计量的绝对值均大于,所以拒绝()0:02,3j H j β==;但1ˆβ对应的t 统计量的绝对值小于,在的显着性水平上不能拒绝01:0H β=的原假设; 320.877022R =4iI 在2003年的预测值为,置信度为95%的预测区间为,设一元线性模型为23.1r i=1,2,…..,n 其回归方程为ˆˆˆY X αβ=+,证明残差满足下式如果把变量2X ,3X 分别对1X 进行一元线性回归,由两者残差定义的2X ,3X 关于1X 的偏相关系数23.1r 满足: 解答:1对一元线性模型,由OLS 可得 所以,2偏相关系数是指在剔除其他解释变量的影响后,一个解释变量对被解释变量的影响;不妨假设2X ,3X 对1X 进行一元线性回归得到的回归方程分别为: 21211ˆˆX X e αα=++,31212ˆˆX X e γγ=++则,12,e e 就分别表示2X ,3X 在剔除1X 影响后的值; 所以2X ,3X 关于1X 的偏相关系数就是指12,e e 的简单相关系数; 所以,因为120,0e e ==,()()()11222211ˆi i i X X X X XX α--=-∑∑,()()()11332211ˆi i i X X X X XX γ--=-∑∑令111222333,,ii i i i iX X x X X x X X x -=-=-=则2ˆr α=2ˆr γ=注意到21213121ˆˆˆˆ,X X X X ααγγ=+=+,所以12212321ˆˆ,i ii i i i e x x e x x αγ=-=-所以23.1e e e e e e r --==其中,()()1222132122322121322122321131ˆˆˆˆˆˆi ii ii i i ii i i i iiii ii iie ex x x x xx x x x x x x x r x x r x x r xr r r αγγααγ=--=--+=--+=∑∑∑∑∑∑∑(2131212131233121r rr r r r r r r r r r r r r ===-同理可得: 所以考虑下面两个模型: Ⅰ:122iillikkiiY X X X ββββε=++++++ Ⅱ:122iliillikkiiY X X X X ββββε''''-=++++++ (1) 证明ˆˆˆˆ1,,1,2,,1,1,l l j jj l l k ββββ''-===-+(2) 证明模型Ⅰ和Ⅱ的最小二乘残差相等(3) 研究两个模型的可决系数之间的大小关系 解答:1设211111112222222221,,,1,,,,,,,,1,,,k l k l ln k k n n kn ln X X X Y Y X X X Y X X Y X X X ββεββεββεββε'⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪' ⎪ ⎪⎪ ⎪ ⎪ ⎪'====== ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪'⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭则模型Ⅰ的矩阵形式为:Y X βε=+模型Ⅱ的矩阵形式为:lY X X βε'-=+取()0,,0,1,0,,0l e '=,其中1为le 的第l 个分量 则l lX Xe =令l lZ Y X Y Xe =-=-,则模型Ⅱ又可表示为Z X βε'=+ 又OLS 得知,()1ˆX X X Y β-''=,()1ˆX X X Z β-'''= 将l lZ Y X Y Xe =-=-代入可得:即1111ˆˆˆ0ˆˆˆ11ˆˆˆ0l l k k k βββββββββ⎛⎫⎛⎫⎛⎫'⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪'=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪'⎝⎭⎝⎭⎝⎭⎝⎭2由上述计算可得: 3由2可知ESS ESS '=所以要比较2R 和2R ',只需比较TSS 和TSS '所以,当var()2cov(,)l lX Y X ≥时,TSS '大于TSS ,则22R R '≥;反之,22R R '<美国1970-1995年个人可支配收入和个人储蓄的数据见课本102页表格;由于美国1982年遭受了其和平时期最大的衰退,城市失业率达到了自1948年以来的最高水平%;试建立分段回归模型,并通过模型进一步验证美国在1970-1995年间储蓄-收入关系发生了一次结构变动; 解答:建立模型为()1212347.3t t t t tY X D X ββδε=++-+其中t Y 为t 年的个人储蓄,tX 为t 年的个人可支配收入,{1,19820,1982tt D t ≥=<当当 则()121982ttE Y t X ββ<=+ Eviews 代码: series d1=0 smpl 1982 1995 d1=1smpl allls sav c pdi d11δ显着,所以美国在1970-1995年间储蓄-收入关系确实发生了一次结构变动在行风评比中消费者的投诉次数是评价行业服务质量的一个重要指标;一般而言,受到投诉的次数越多就说明服务质量越差;有关部门对电信、电力和铁路三个服务行业各抽取了四家单位,统计出消费者一年来对这12家企业的投诉次数,见课本表格;试采用虚拟解释变量回归方法,分析三个行业的服务质量是否存在显着的差异; 解答:本题中有三个定性变量,所以需要设置两个虚拟变量其中iY 为i 企业在一年汇中受到的投诉次数,{11,0,ii Dotherwise=若为电力企业,{21,0,ii Dotherwise=若为铁路企业则()1iE Y i β=为电信企业在5%的显着性水平上,12,δδ均不显着,所以电信行业和电力行业的服务质量不存在显着性差异,电信行业和铁路行业的服务质量也不存在显着性差异若取{11,0,ii Dotherwise=若为电信企业,{21,0,ii Dotherwise=若为电力企业,则则()11iE Y i βδ=+为电信企业在5%的显着性水平上,1δ不显着,2δ显着,所以电力行业和铁路行业的服务质量存在显着差异,且电力行业的服务质量比铁路行业好;电信和铁路行业服务质量不存在显着差异;虚拟变量的实质原则是什么试以加法形式在家庭对某商品的消费需求函数中引入虚拟变量,用以反映季节因素淡、旺季和家庭收入层次差异高、低对商品消费需求的影响,并写出各类消费函数的具体形式;解答:引入两个虚拟变量其中{10,D=若为淡季1,若为旺季,{20,D=低收入家庭1,高收入家庭所以淡季低收入家庭对商品的消费需求为淡季高收入家庭对商品的消费需求为旺季低收入家庭对商品的消费需求为旺季高收入家庭对商品的消费需求为以加法形式引入虚拟变量:即以相加的形式将虚拟变量引入模型;加法形式引入虚拟变量可以考察截距的不同;斜率的不同则可通过以乘法方式引入虚拟变量来实现;设消费函数的形式为其中,Y是收入,C是消费,,,αβγ是待定参数;观测到某地区总消费和收入的数据见课本表格;(1) 当1γ=时,估计模型并解释其经济意义;(2) 以1γ=时所得到的参数估计量作为初始值,采用高斯-牛顿迭代方法回归模型参数; 解答:(1) 当1γ=时,消费函数形式为C Y αβε=++样本回归方程为ˆ11.150.899CY =+,说明每增加1元收入,消费就会增加元;另外,我们注意到常数项在5%的水平上是不显着的;(2) 以,,1作为初始值,采用高斯-牛顿迭代得到样本回归方程为 Eviews 代码为:ls cons c ycoef3 bparam b1 b2 b3 1在 Eviews 主菜单,Quick/Estimate Equation…,弹出Equation Estimation 窗口,在Specification 中输入方程cons=b1+b2y^b3 对某种商品的销售量Y 进行调查,得到居民可支配收入1X ,其他消费品平均价格指数2X 的数据见课本145页;1若以1X 、2X 为解释变量,问是否存在多重共线性 2你认为比较合适的模型是什么解答:以1X 、2X 为解释变量,回归得到2R =,但自变量1X 的回归系数在5%的水平上并不显着计算1X 、2X 间的相关系数为:120.991796X X r = 做辅助回归得到:辅助回归的2R 大于主回归的2R ;所以,以1X 、2X 为解释变量,会产生多重共线性;2采用逐步回归法,首先用1X 作为自变量对Y 进行回归,得到1ˆ39.017990.521613YX =-+ 2R = 利用2X 作为自变量对Y 进行回归,得到 1ˆ54.365140.670541YX =-+ 2R = 根据我国1985-2001年城镇居民人均可支配收入y 和人均消费性支出x 的数据,按照凯恩斯绝对收入假说建立的消费函数计量经济模型为:(1) 解释模型中的经济意义;(2) 检验该模型是否存在异方差性;(3) 如果模型存在异方差,写出消除模型异方差的方法和步骤;解答:1凯恩斯绝对收入假说:在短期中,消费取决于收入,随着收入的增加消费也将增加,但消费的增长低于收入的增长;表示收入每增加1单位,其中有单位用于消费,即边际消费倾向;2异方差检验方法:Goldfeld-Guandt 检验,Breusch-Pagan 检验,White 检验本题中适用White 检验法;2170.4778.109e nR =⨯=,查表得()0.051 3.841χ=()20.051e nR χ>,所以拒绝原假设,模型存在异方差; 3利用残差与自变量之间的回归方程2451.900.87i i e x =-+,在原模型i i y x αβε=++两边同除以,得到新模型即先对原始数据进行处理,自变量与因变量同除以,然后对处理后的数据进行OLS 估计;注:回归方程2451.900.87i ie x =-+中x 的系数并不显着 设多元线性模型为Y =X β+ε,其中试问此模型存在异方差吗如果存在异方差,怎样把它变成同方差模型,并用广义最小二乘法GLS 求β的估计量;解答:因为()22i ji j σσ≠≠,所以该模型显然存在异方差; 在原模型两边同乘以12-Ω,得到111222---ΩΩΩY =X β+ε 则()111111112222222222cov ,E E I σσ--------⎛⎫⎛⎫''ΩΩ=ΩΩ=ΩΩ=ΩΩΩ= ⎪ ⎪⎝⎭⎝⎭εεεεεε所以新模型是同方差;对新模型采用OLS 进行估计得到:下面给出的数据是美国1988年研究与开发R&D 支出费用Y 与不同部门产品销售量X 和利润Z;数据见课本146页试根据资料建立一个回归模型,运用Glejser 方法和White 方法检验异方差,由此决定异方差的表现形式并选用适当的方法加以修正; 解答:因变量与自变量的选取对模型进行回归,得到:回归系数都不显着White 检验结果显示,存在异方差Glejser 检验结果显示:存在异方差取对数后进行回归,得到:进行White 异方差检验不能拒绝同方差假设;以z 作为因变量,以x,y 作为自变量,回归得到 White 异方差检验:在5%的显着性水平上,拒绝同方差的原假设;取对数,回归得到进行White 异方差检验,得到在5%的显着性水平上,不能拒绝同方差的原假设;即取对数就可以消除异方差;注:1以各自方差的倒数为权数对模型进行修正 1ˆ1690.3090.387979yx =-+ n=19,k=1,在5%显着性水平上, 1.18, 1.401l u d d == 因为0.52l DW d =<,所以拒绝无序列相关的原假设; 2对回归残差序列进行一阶自回归得到()()111ˆ0.920175i i e e -=,即1ˆ0.920175ρ=用估计出来的ρ进行广义差分,再进行回归得到: 得到新残差,再进行回归得到2ˆ0.927088ρ= 迭代终止,得到ˆ0.936895ρ=,进行广义差分,再回归得到:此时0.720623l DW d =<,故一阶差分并不能消除序列相关;进行二阶差分,得到:n=17,k=3,在5%显着性水平上,0.672, 1.432l u d d == 4u ud DW d <<-,故不能拒绝无序列相关的原假设1原模型为60t it i t i Y X αβε-==++∑施加线性算术滞后()61,0,1,,6i i i ββ=+-=⎡⎤⎣⎦则原模型可化为 ()[]6060617t t i ti t i ti Y i X i X αβεαβε-=-==++-+⎡⎤⎣⎦=+-+∑∑ 1施加有远端约束的Almon 一次多项式滞后01i i βαα=+,0,1,,6i =所以()0117i i i βααα=+=-,0,1,,6i =则原模型可化为 ()()61061077t t i ti t i ti Y i X i X ααεααε-=-==+-+=+-+∑∑ 2比较方程1和2,可见两个模型是一致的 2ls lncons c pdllninc,6,2,13 ls lncons c pdllninc,6,2,24ls lncons c pdllninc,6,2,3567关于F 统计量分子自由度的说明;15阶滞后消费收入模型:施加Almon 三次多项式约束230123i i i i βαααα=+++,0,1,,5i = ls lny c pdllnx,5,32所以3施加近终端约束101230βαααα-=-+-=ls lny c pdllnx,5,3,14根据带近终端约束的回归残差平方和以及不带近终端约束的回归残差平方和,构建F 统计量,分子自由度为15如习题5、6、71对011ln ln ln t t t t C C Y ββαε-=+++进行回归利用所得残差计算ˆρ,再结合回归得到的()1ˆvar β构建Durbin h 统计量在原假设下,h 渐近服从()0,1N 若2h Z α>,则拒绝无一阶序列相关的原假设;否则,不能拒绝原假设2Breusch-Godfrey 检验Breusch-Godfrey 检验是将OLS 的残差t e 对于1t e -和包括滞后的因变量行回归;所以对p 阶序列相关进行检验,应构建回归模型: 构建统计量22pTR χ2对于过度识别的模型,可采用2SLS 法进行估计 tsls cons-g c y1 c y1-1 gtsls i c y1 y1-1 c y1-1 g。
高级计量经济学习题及解答4

find this? ) is n−1 nx f (x|θ) = θn 0 0<x<θ otherwise .
Calculate the mean and variance of the mle. Compare the variance, the bias, and the mean squared error to those of the method of moments estimate. (c) Find a modification of the mle that renders it unbiased. 2
argument as in (a), we have E[Y ] = ρ(n − 1)E[s2 ] = ρ(n − 1)σ 2 , and Var[Y ] = (ρ(n − 1)) Var[s2 ] = ρ2 (n − 1)2 Thus MSE(Y ) = Var[Y ] + b(Y )2 = 2ρ2 (n − 1)σ 4 + ρ(n − 1)σ 2 − σ 2 = σ 4 [2ρ2 (n − 1) + (ρn − ρ − 1)2 ] ≡ f (ρ). Since f (ρ) = σ 4 [4ρ(n − 1) + 2(ρn − ρ − 1)(n − 1)] = σ 4 [4ρ + 2(ρn − ρ − 1)](n − 1) = 2(n − 1)σ 4 (ρn + ρ − 1), and f (ρ) = 2(n − 1)(n + 1)σ 4 > 0, 1 we see that f (ρ) achieve its minimum at ρ = . (f (n + 1)−1 = n+1 0.)
n i=1 (Xi
中央财经大学高级计量经济学慕课答案

中央财经大学高级计量经济学慕课答案
1、相关关系是指()
A、变量间的非独立关系
B、变量间的因果关系
C、变量间的函数关系
D、变量间不确定性的依存关系
答案:变量间不确定性的依存关系
2、总体回归直线是解释变量取各给定值时被解释变量条件期望的轨迹。
答案:√
3、总体回归函数给出了对应于每一个自变量的因变量的值。
答案:错误
1、以下模型不是线性回归的是()
答案:无异常值
2、线性回归是指解释变量和被解释变量之间呈现线性关系。
答案:错
1、若随机扰动项满足古典假定,以下说法错误的是()
答案:B
2、假设线性回归模型满足全部基本假设,则其参数的估计量具备()。
A、可靠性
B、线性性
C、无偏性
D、有效性
答案:线性性;
1、满足基本假设条件下,随机误差项服从正态分布,但被解释变量Y不一定服从正态分布。
答案:错误
2、任何两个计量经济模型的可决系数都是可以比较的。
答案:错
3、通过可决系数的高低可以进行显著性判断。
答案:×
1、计量经济预测的条件是()
A、模型设定的关系式不变
B、所估计的参数不变
C、解释变量在预测期的取值已作出预测
D、没有对解释变量在预测期的取值进行过预测
答案:模型设定的关系式不变;
2、对被解释变量的预测可以分为()
A、被解释变量平均值的点预测
B、被解释变量平均值的区间预测
C、被解释变量个别值的点预测
D、被解释变量个别值的区间预测
答案:被解释变量平均值的点预测;
3、预测区间的宽窄只与样本容量n有关。
答案:错。
上海财经大学《高级计量经济学II》习题四及答案

2
(c) We would apply the delta method. Thus, we would require the full variance matrix of the probit estimates as well as the gradient of the expression of interest.
Solution 2 (a) If P (y = 1jz1; z2) = z1 1 + 1z2 + 2z22 , then
@P (y = 1jz1; z2) = ( @z2
1+2
2z2)
z1 1 + 1z2 + 2z22
for given z, this is estimated as
(^ consistently estimated by maximizing
X N
X N
li ( ) = fyi ln (Ui
i=1
i=1
x0i ) + (1
yi) ln [1
(Ui x0i )]g
1
(c) The partial e¤ ect of x3 on P (yi = 1jxi) is
and P (yi1 = 1jxi; ci; ni = 1) = 1 [(xi2 xi1) ]
2
Advanced Econometrics II Answer 4
Yahong Zhou March 2, 2014
1. Consider a latent variable modeled by
y = x0i + "i
上海财经大学《高级计量经济学II》习题四及答案
Advanced Econometrics II Problem Set 4
高级计量经济学课后习题参考问题详解

1.3 某市居民家庭人均年收入服从4000X =元,1200σ=元的正态分布,求该市居民家庭人均年收入:(1)在5000—7000元之间的概率;(2)超过8000元的概率;(3)低于3000元的概率。
(1)()()()()()2,0,15000700050007000()2.50.835( 2.5)62X N X X XN XX XXP X P F F X XP σσσσσσ-∴---∴<<=<<--=<<=根据附表1可知()0.830.5935F =,()2.50.9876F =()0.98760.5935500070000.19712P X -∴<<==PS :()()5000700050007000()55( 2.5) 2.5660.99380.79760.1961XX XXP X P X X P σσσσ---<<=<<-⎛⎫=<<=Φ-Φ ⎪⎝⎭=-=在附表1中,()()F Z P x xz σ=-<(2)()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭=0.0004 (3)()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭=0.2023=0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98,因事故死亡的概率为0.02。
保险公司开办老人事故死亡保险,参加者需缴纳保险费100元。
若5年内因事故死亡,公司要赔偿a 元。
应如何测算出a ,才能使公司可期望获益;若有1000人投保,公司可期望总获益多少?设公司从一个投保者得到的收益为X ,则则()1000.02E X a =-故要是公司可期望获益,则有()1000.02E X a =->0,即5000a <PS :赔偿金应大于保险费?1000人投保时,公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型,并分别求出回归系数的最小二乘估计。
计量经济学 课后答案

习题参考答案
第一章绪论
1-1.答:计量经济学是经济学的一个分支学科,是以揭示经济活动中客观存在的数量关系为内容的分支学科,是由经济学、统计学和数学三者结合而成的交叉学科。
1-2.答:计量经济学自20年代末、30年代初形成以来,无论在技术方法还是在应用方面发展都十分迅速,尤其是经过50年代的发展阶段和60年代的扩张阶段,使其在经济学科占据重要的地位,主要表现在:①在西方大多数大学和学院中,计量经济学的讲授已成为经济学课程表中有权威的一部分;②从1969~2003年诺贝尔经济学奖的XX位获奖者中有XX位是与研究和应用计量经济学有关;著名经济学家、诺贝尔经济学奖获得者萨缪尔森甚至说:“第二次世界大战后的经济学是计量经济学的时代”。③计量经济学方法与其他经济数学方法结合应用得到发展;④计量经济学方法从主要用于经济预测转向经济理论假设和政策假设的检验;⑤计量经济学模型的应用从传统的领域转向新的领域,如货币、工资、就业、福利、国际贸易等;⑥计量经济学模型的规模不再是水平高低的衡量标准,人们更喜欢建立一些简单的模型,从总量上、趋势上说明经济现象。
1-3.答:计量经济学方法揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。
1-4.答:
1-5.答:从计量经济学的定义看,它是定量化的经济学;其次,从计量经济学在西方国家经济学科中居于最重要的地位看,也是如此,尤其是从诺贝尔经济学奖设立之日起,已有多人因直接或间接对计量经济学的创立和发展作出贡献而获得诺贝尔经济学奖;计量经济学与数理统计学有严格的区别,它仅限于经济领域;从建立与应用计量经济学模型的全过程看,不论是理论模型的设定还是样本数据的收集,都必须以对经济理论、对所研究的经济现象有透彻的认识为基础。综上所述,计量经济学确实是一门经济学科。
计量经济学(第四版)习题参考答案

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NSS x ==45=1.25用=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学(数字教材版)课后习题参考答案

课后习题参考答案第二章教材习题与解析1、 判断下列表达式是否正确:y i =β0+β1x i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i ,i =1,2,⋯nE(y i |x i )=β0+β1x i +u i ,i =1,2,⋯n E(y i |x i )=β0+β1x i ,i =1,2,⋯nE(y i |x i )=β̂0+β̂1x i ,i =1,2,⋯ny i =β0+β1x i +u i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n y ̂i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n答案:对于计量经济学模型有两种类型,一是总体回归模型,另一是样本回归模型。
两类回归模型都具有确定形式与随机形式两种表达方式:总体回归模型的确定形式:X X Y E 10)|(ββ+= 总体回归模型的随机形式:μββ++=X Y 10样本回归模型的确定形式:X Y 10ˆˆˆββ+= 样本回归模型的随机形式:e X Y ++=10ˆˆββ 除此之外,其他的表达形式均是错误的2、给定一元线性回归模型:y =β0+β1x +u (1)叙述模型的基本假定;(2)写出参数β0和β1的最小二乘估计公式;(3)说明满足基本假定的最小二乘估计量的统计性质; (4)写出随机扰动项方差的无偏估计公式。
答案:(1)线性回归模型的基本假设有两大类,一类是关于随机误差项的,包括零均值、同方差、不序列相关、满足正态分布等假设;另一类是关于解释变量的,主要是解释变量是非随机的,如果是随机变量,则与随机误差项不相关。
(2)12ˆi iix yxβ=∑∑,01ˆˆY X ββ=- (3)考察总体的估计量,可从如下几个方面考察其优劣性:1)线性性,即它是否是另一个随机变量的线性函数; 2)无偏性,即它的均值或期望是否等于总体的真实值;3)有效值,即它是否在所有线性无偏估计量中具有最小方差;4)渐进无偏性,即样本容量趋于无穷大时,它的均值序列是否趋于总体真值; 5)一致性,即样本容量趋于无穷大时,它是否依概率收敛于总体的真值;6)渐进有效性,即样本容量趋于无穷大时,它在所有的一致估计量中是否具有最小的渐进方差。
高级计量经济学课后习题参考答案

1.3 某市居民家庭人均年收入服从4000X =元,1200σ=元的正态分布,求该市居民家庭人均年收入:(1)在5000—7000元之间的概率;(2)超过8000元的概率;(3)低于3000元的概率。
(1)根据附表1可知()0.830.5935F =,()2.50.9876F = PS :在附表1中,()()F Z P x xz σ=-<(2)()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭=0.0004 (3)()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭=0.2023 =0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98,因事故死亡的概率为0.02。
保险公司开办老人事故死亡保险,参加者需缴纳保险费100元。
若5年内因事故死亡,公司要赔偿a 元。
应如何测算出a ,才能使公司可期望获益;若有1000人投保,公司可期望总获益多少?设公司从一个投保者得到的收益为X ,则则()1000.02E X a =-故要是公司可期望获益,则有()1000.02E X a =->0,即5000a <PS :赔偿金应大于保险费?1000人投保时,公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型,并分别求出回归系数的最小二乘估计。
解答:过原点的一元线性回归模型为Y X βε=+ 约束最小二乘估计:y x αβε=++过原点的二元线性回归模型为1122Y X X ββε=++ 2.2针对多元线性回归模型试证明经典线性回归模型参数OLS 估计量的性质()ˆE ββ=和()()12ˆˆ,Cov X X ββσ-'=,并说明你在证明时用到了哪些基本假定。
靳云汇高级计量经济学课后习题
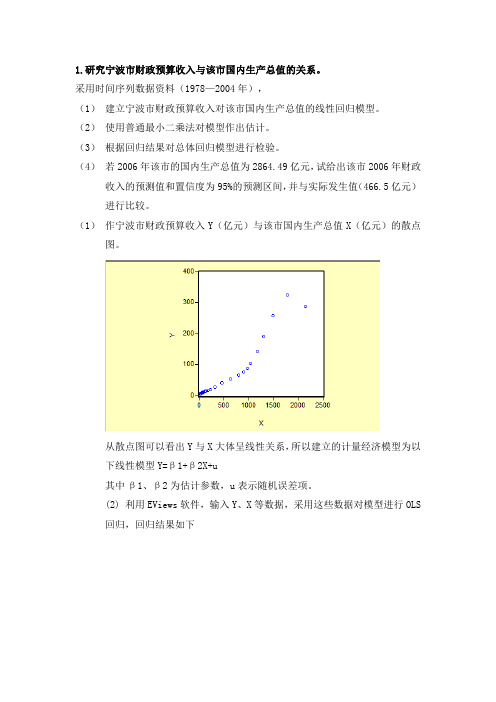
1.研究宁波市财政预算收入与该市国内生产总值的关系。
采用时间序列数据资料(1978—2004年),(1)建立宁波市财政预算收入对该市国内生产总值的线性回归模型。
(2)使用普通最小二乘法对模型作出估计。
(3)根据回归结果对总体回归模型进行检验。
(4)若2006年该市的国内生产总值为2864.49亿元,试给出该市2006年财政收入的预测值和置信度为95%的预测区间,并与实际发生值(466.5亿元)进行比较。
(1)作宁波市财政预算收入Y(亿元)与该市国内生产总值X(亿元)的散点图。
从散点图可以看出Y与X大体呈线性关系,所以建立的计量经济模型为以下线性模型Y=β1+β2X+u其中β1、β2为估计参数,u表示随机误差项。
(2) 利用EViews软件,输入Y、X等数据,采用这些数据对模型进行OLS回归,回归结果如下在本例中参数估计有以下结果。
Y^i=-9.452819+0.144417Xi(6.924101) (0.008581)t=(-1.3652) (16.8293)r2=0.9189 F=283.2261 df=25回归结果图形:(3)模型检验经济意义检验:所估计参数β2=0.144417,说明宁波市国内生产总值每增加一亿元,该市财政预算收入增加0.144417亿元。
符合财政预算收入随gdp增加而增加的经济学意义。
拟合优度检验:在本例中可决系数为0.9189,说明所建模型整体上对样本数据你和较好,即解释变量“宁波市国内生产总值”对被解释变量“该市财政预算收入”的绝大部分差异做出了解释。
对回归系数的t检验:分别针对H0 : β(j) = 0 (j = 1、2) 给定显著性水平α= 0.05,在t分布表中查出自由度为n-k = 25的临界值t α/2 (n-k) = 2.060。
由表中数据可得,与β1、β2的估计值对应的t统计量分别为-1.3652、16.8293。
t(β1)的绝对值小于t α /2 (n-k) = 2.060 ,t(β2)的绝对值大于t α /2 (n-k) = 2.060。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3 某市居民家庭人均年收入服从4000X =元,1200σ=元的正态分布,求该市居民家庭人均年收入:(1)在5000—7000元之间的概率;(2)超过8000元的概率;(3)低于3000元的概率。
(1)()()()()()2,0,15000700050007000()2.50.835( 2.5)62X N X X XN XX XXP X P F F X XP σσσσσσ-∴---∴<<=<<--=<<=根据附表1可知()0.830.5935F =,()2.50.9876F =()0.98760.5935500070000.19712P X -∴<<==PS :()()5000700050007000()55( 2.5) 2.5660.99380.79760.1961XX XXP X P X X P σσσσ---<<=<<-⎛⎫=<<=Φ-Φ ⎪⎝⎭=-=在附表1中,()()F Z P x xz σ=-<(2)()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭=0.0004 (3)()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭=0.2023 ()030001050300036X X X X X X P X P P σσσσ⎛⎫⎛⎫----<<=<<=-<<- ⎪ ⎪⎝⎭⎝⎭=0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98,因事故死亡的概率为0.02。
保险公司开办老人事故死亡保险,参加者需缴纳保险费100元。
若5年内因事故死亡,公司要赔偿a 元。
应如何测算出a ,才能使公司可期望获益;若有1000人投保,公司可期望总获益多少?设公司从一个投保者得到的收益为X ,则则()1000.02E X a =-故要是公司可期望获益,则有()1000.02E X a =->0,即5000a <PS :赔偿金应大于保险费?1000人投保时,公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型,并分别求出回归系数的最小二乘估计。
解答:过原点的一元线性回归模型为Y X βε=+()()22ˆmin ˆˆ20ˆi i i i i i iiy x y x x x y xβββββ-⇒--=⇒=∑∑∑∑对一阶求导约束最小二乘估计:y x αβε=++()()()()2,22ˆmin ..0ˆˆ20ˆ00ˆi i i i iiiiii i i y x s t L y x y x y x x x y x αβαβααβλαααβλβαβαβ--=⇒=--+--+=--==⇒=∑∑∑∑∑∑对求导得到:-对求导得到:-2过原点的二元线性回归模型为1122Y X X ββε=++()()()()()1221122ˆˆ,1211221112222212211222121221121222221212ˆˆmin ˆˆ,ˆˆ20ˆˆ20ˆˆi i i i i i i iiiii i i i i i ii i i i i i i i i i ii i i iy x x y x x x y x x x x y x x x x y x x x x x y x x x x y x x x x ββββββββββββ--⇒---=---=-⇒=--=-∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑对分别求一阶导2.2针对多元线性回归模型Y X βε=+试证明经典线性回归模型参数OLS 估计量的性质()ˆE ββ=和()()12ˆˆ,Cov X X ββσ-'=,并说明你在证明时用到了哪些基本假定。
解答:()()()()()()ˆ1ˆˆˆˆmin ˆ20ˆY Y Y Y Y X Y X X Y X X X X Yβββββ-''--=--'⇒--=''⇒= 无多重共线性()()()()()()()()1111ˆE E X X X Y X X X E Y X X X E X X X X X ββεββ----''''==''=+''== 零均值()()()()()()()()()()()()()()()()()()()()()()()()11111111111212ˆˆˆˆˆˆˆ,ˆˆX X X Y X X X X X X X Cov E E E E E X X X X X X E X X X X X X X X X E X X X X X X IX X X X X ββεβεββββββββββεεεεεεσσ------------''''''==+=+'=--''''''=--=''''=''''='''='=又同方差,无序列相关2.3为了解某国职业妇女是否受到歧视,可以用该国统计局的“当前人口调查”中的截面数据,研究男女工资有没有差别。
这项多元回归分析研究所用到的变量有:ED AGE W ⎧⎨⎩——雇员的工资率(美元/小时)1,若雇员为妇女SEX=0,其他——受教育的年数——年龄对124名雇员的样本进行研究得到的回归结果为(括号内为估计的t 值):()ˆ 6.41 2.760.990.12WSEX ED AGE =--++ -3.38 (-4.61) (8.54) (4.63)20.867,23.2R F ==(1)求调整后的可决系数2R(2)AGE 的系数估计值的标准差为多少? (3)检验该国工作妇女是否受到歧视?为什么? (4)求以95%的概率,一个30岁受教育16年的该国妇女,平均每小时工作收入的预测区间是多少? 解答:(1)()()()()2211111111241110.8670.8641244ESS n k n ESS R TSS n n k TSSn R n k --⎛⎫=-=- ⎪--⎝⎭-⎛⎫=-- ⎪-⎝⎭-=--=-(2)00ˆˆˆˆ0.120ˆ0.0264.63t se t se se βββββββ--=⇒=-∴==(3)因为()0.025120 1.9799 4.61t =<,所以2ˆ 2.76β=-显著,且为负,即意味着妇女受到歧视。
(4)0ˆ 6.41 2.7610.99160.123010.27W=--⨯+⨯+⨯= 有公式知0W 的95%置信区间为: ()00.025ˆ120W t ±即10.27 1.9799±其中()01,1,16,30X '=2.8设某公司的投资行为可用如下回归模型描述:12131i i i iI F K βββε--=+++其中iI 为当期总投资,1i F -为已发行股票的上期期末价值,1i K -为上期资本存量。
数据见课本71页。
(1) 对此模型进行估计,并做出经济学和计量经济学的说明。
(2) 根据此模型所估计的结果,做计量经济学检验。
(3) 计算修正的可决系数。
(4) 如果2003年的1i F -和1i K -分别为5593.6和2226.3,计算iI 在2003年的预测值,并求出置信度为95%的预测区间。
解答:equation eq1.ls i c f k expand 1984 2003 smpl 2003 2003 f=5593.6 k=2226.3smpl 1984 2003 eq1.forecast yf sfscalar tc=@qtdist(0.975,16) series yl=yf-tc*sf series yu=yf+tc*sf show yl yf yu(1)最小二乘回归结果为:()()()()1122ˆ109.79840.1141580.326143(97.43575).0.0( 1.126880) 4.8623448.2782170.8906870.877022i i i I F K se t R R --=-++==-== 023478 039398 F=65.18405 P=0经济意义说明:在假定其他变量不变的情况下,已发行股票的上期期末价值增加1单位,当期总投资增加0.114158单位;在其他变量不变的情况下,上期资本存量增加1单位,当期总投资增加0.326143单位。
(2)模型的拟合优度为20.890687R =,修正可决系数为20.877022R =,可见模型拟合效果不错。
F 检验:对模型进行显著性检验,F 统计量对应的P 值为0,因此在0.05α=的显著性水平上我们拒绝原假设023:0H ββ==,说明回归方程显著,即变量“已发行股票的上期期末价值”和“上期资本”存量联合起来确实对“当期总投资”有显著影响。
()2,16 3.63F F α>=t 检验:针对()0:01,2,3jH j β==进行显著性检验。
给定显著性水平0.05α=,查表知()216 2.12t α=。
由回归结果,2ˆβ、3ˆβ对应的t 统计量的绝对值均大于2.12,所以拒绝()0:02,3j H j β==;但1ˆβ对应的t 统计量的绝对值小于2.12,在0.05的显著性水平上不能拒绝01:0H β=的原假设。
(3)20.877022R =(4)iI 在2003年的预测值为1254.848,置信度为95%的预测区间为(1030.292,1479.405) 105.9276sf =2.4 设一元线性模型为23.1r (i=1,2,…..,n) 其回归方程为ˆˆˆY X αβ=+,证明残差满足下式ˆ()XYi i i XXS Y Y X X S ε=---如果把变量2X ,3X 分别对1X 进行一元线性回归,由两者残差定义的2X ,3X 关于1X 的偏相关系数23.1r 满足:23213123.1222131(1)(1)r r r =-- 解答:(1)对一元线性模型,由OLS 可得()()()2ˆˆˆii XY XXiY X X X Y Y SS X X αββ=---==-∑∑所以,()ˆˆˆˆi i i i i XY XYi i XX XX XY i i XXY Y Y X S SY Y X X S S SY Y X X S εαβ=-=--⎛⎫=--- ⎪⎝⎭=---(2)偏相关系数是指在剔除其他解释变量的影响后,一个解释变量对被解释变量的影响。
