深入浅出通信原理533-562
深入浅出通信原理

深入浅出通信原理通信原理是一门极具深刻性的学科,它的主要内容是研究信息的传播、发送和接收,以及从技术上讲如何实现这些任务。
通信技术的背景有许多,这使得学习通信原理变得复杂和有挑战性。
然而,有关通信原理的基础知识是基于物理学、数字信号处理、数据传输原理和信息理论等多重学科,所以学习它既可以具有专业性,也可以同时增强跨学科知识组合能力。
一、信息的传播原理信息是以信号的形式传播与传输的,而信号通过载波传输,这就要求信号必须能够抵达目标才能传输信息。
首先,我们需要知道信号的特性,以便产生特定的信号。
其次,我们需要知道信号的传播特性,以便知道如何传播信号。
这里涉及到单播、广播、准广播,多路复用等传播技术,以及信号路径衰落、信道噪声、多径效应等一系列现象,这是信息传播原理的核心。
二、数字信号处理从数字信号处理的角度来看,信息的传播可以表示为数字信号的流动,引入数字信号处理技术,可以提高信息的传播效率。
数字信号处理涉及的内容包括数字信号的分析、量化、压缩以及编码等,其目的是将信号的有用部分提取出来,以便发挥最大的效用。
三、数据传输原理数据传输原理是指传输数据的原理,它涉及到传输性能、传输延迟、传输距离、传输带宽等。
其目的是让数据可靠、快速地从一个位置到另一个位置,这里涉及到数据链路层、传输控制协议、数据交换协议等系统技术和协议。
四、信息理论信息理论是一种重要的概念,可以提供有关信息的语义、编码和传输的全面理解。
在信息理论的基础上,我们可以探究消息的内容,如何记录它并传输到接收端,以及用来控制传输的协议等。
信息的传播是一个复杂的过程,而信息理论是理解这一过程的重要工具。
本文介绍了关于通信原理的基本概念和基础知识,包括信息的传播原理、数字信号处理原理、数据传输原理和信息理论等。
虽然通信原理是一门复杂的学科,但它确实可以通过深入浅出的学习实现,从而有助于人们更全面地理解和运用通信技术。
深入浅出通信原理

深入浅出通信原理“通信原理”乃是电子技术最为基础的知识内容,它涵盖了现代通信工程的动力,也是推动人类技术进步的重要基础知识之一。
在现代的通信技术快速发展的今天,对于通信原理的深入理解,对于其中的技术细节和应用形式的了解,至关重要。
其实,通信原理将传输媒介、传输媒体、信号编码、信号处理、网络协议等一系列知识结合在一起,形成为完整的传输系统,这就是我们广泛所说的“通信原理”。
通信原理的基本知识其实并不复杂,只要对每个基本概念有所了解,就可以深入探究今天的通信技术了。
首先,我们来介绍传输媒介的基本概念,一般情况下,传输媒介是指用于传输数据的介质,分为“光纤”、“电缆”、“无线通信”、“卫星通信”、“网络”等。
它们在实际应用中表现出各自的特点,而对于不同的传输媒介,也有不同的信号处理方法,如电缆的信号处理会用到“放大”和“滤波”,而无线通信则会使用“天线”和“集中器”等来处理信号,而网络则依赖“路由”和“交换”等来进行信号处理。
其次,我们来介绍传输媒体的基本概念,传输媒体是指用于传输数据的介质,任何一种介质都可分为一种“短距离”和一种“长距离”,比如细铜线是一种短距离的传输媒体,它可以用来传输数据,但它的传输距离是有限的,而光缆通常就是一种长距离的传输媒体,它也可以用来传输数据,而且这个数据传输距离也可以比较远,其中最重要的一点就是光缆可以抵御“干扰”,比如电磁干扰,这样的传输才能达到更高的数据精确度。
再次,我们来介绍信号编码的基本概念,信号编码是指通信信号的压缩、编码与解码,它是为了缩短传输所需的带宽,也是为了提高信号传输质量,编码可以把一个完整的信号,编码成一种可以传输的少量位流,空域编码和频域编码分别是常用的两种编码方式,空域编码把信号编码成一组样本,而频域编码把信号编码成一定的频率。
此外,我们还要介绍信号处理的基本概念,信号处理可以把原有的信号处理成新的信号,以符合特定的使用要求,信号处理的方法有很多,比如可以使用“滤波”、“分离”、“预测”、“放大”等处理方法,它们可以把原有的信号改变成新的信号,从而使得信号更加接近实际应用的要求。
深入浅出通信原理

深入浅出通信原理通信原理是当今通信技术的基石,它是实现任何形式的信息传输的基本实现技术。
本文将重点介绍通信原理的基本概念,以及相关知识点,例如信号传输、信道模型、信息编码方法、网络传输和应用。
首先,让我们来了解一下什么是通信原理。
通信原理是一门研究信号传输的科学,它涉及到各种信号的传输机制,包括声音、视频、图像以及数据等。
它设计用于传输信号最有效和安全的方法,以确保信息准确地传输到目的地。
上面提到的信号传输是通信原理中的一个重要概念,这里我们简单地介绍它的一些基本概念。
信号传输是一种以模拟或数字形式传输信号的技术,可以将两个终端之间的信息传输到接收方。
它可以分为两个部分:信号的源和信号的接收。
在发送端,我们需要将原始的信号进行编码,然后通过某种形式的信道将其传输到目的地;而在接收端,则需要进行解码,将编码后的信号重新解码,并通过处理技术获得原始信号。
此外,信道模型是通信原理中的另一个重要概念,它描述了信号在信道中传输的过程,由此我们可以确定信号传输过程中会出现噪声等影响。
信道模型包括低阻抗信道、高阻抗信道和混合信道等。
信息编码是另一个重要的通信原理概念,它是指将原始的信息转换成更容易传输的形式的过程。
编码的主要目的是提高信息传输的准确性和可靠性,并为接收方更容易地解码信息。
主要有模拟编码、数字编码和线性编码等。
最后,我们要介绍的是网络传输和应用。
网络传输是指将信号在两个或多个网络中传输的过程,例如使用覆盖大范围的传输介质(如卫星和无线电),或使用有限范围的信号传输技术(如光缆和Wi-Fi)。
而应用则是指将信号进行加工和传输,以实现信息的有效传输,例如文件传输、图像处理等。
本文介绍了通信原理中的一些基本概念,包括信号传输、信道模型、信息编码方法、网络传输和应用等。
以上介绍的内容只是入门级的概念,如果要更深入地了解通信原理,还需要继续学习和实践。
深入浅出通信原理

深入浅出通信原理通信原理是指传递信息的基本原理和方法,是现代通信技术的基础。
深入了解通信原理,有助于我们更好地理解通信系统的工作原理,提高我们对通信技术的应用能力。
本文将深入浅出地介绍通信原理的相关知识,帮助读者更好地理解这一领域的知识。
首先,我们需要了解通信原理的基本概念。
通信原理是指信息的传输和交换过程,包括信号的产生、调制、传输、解调和处理等过程。
通信原理的基本要素包括信号、信道、调制解调器、编解码器等。
信号是指携带信息的载体,信道是信号传输的媒介,调制解调器用于将数字信号转换为模拟信号或者将模拟信号转换为数字信号,编解码器用于对信息进行编码和解码。
通信原理的基本原理是利用信号在信道中传输的特性,实现信息的传输和交换。
其次,我们需要了解通信原理的基本模型。
通信系统的基本模型包括发送端、信道和接收端。
发送端将信息转换为信号,并通过信道将信号传输给接收端,接收端将接收到的信号转换为信息。
通信系统的性能指标包括传输速率、误码率、带宽等。
传输速率是指单位时间内传输的信息量,误码率是指传输过程中出现错误的概率,带宽是指信号所占用的频率范围。
通信系统的设计需要考虑这些性能指标,以实现高效可靠的信息传输。
再次,我们需要了解通信原理的基本技术。
通信原理涉及到很多基本技术,包括调制解调技术、编解码技术、传输技术等。
调制解调技术是指将数字信号转换为模拟信号或者将模拟信号转换为数字信号的技术,编解码技术是指对信息进行编码和解码的技术,传输技术是指信号在信道中传输的技术。
这些基本技术是通信系统实现信息传输和交换的关键。
最后,我们需要了解通信原理的发展趋势。
随着信息技术的发展,通信原理也在不断地发展和演进。
未来的通信系统将更加智能化、高效化和可靠化,采用更加先进的调制解调技术、编解码技术和传输技术,实现更加高速、大容量、低延迟的信息传输。
同时,通信原理也将与其他技术领域相互融合,推动信息社会的发展。
总之,深入浅出地了解通信原理对我们理解通信系统的工作原理,提高我们对通信技术的应用能力具有重要意义。
深入浅出通信原理533-562
用前面的例子验证一下。
其中:u=U(:,1:3)表示截取矩阵U的前三列;s=S(1:3,:)表示截取矩阵S的前三行。
>> A=[4 4 5;4 5 5;3 3 2;4 5 4;4 4 4;3 5 4;4 4 3;2 4 4;5 5 5];A =4 4 54 5 53 3 24 5 44 4 43 5 44 4 32 4 45 5 5>> [U,S,V]=svd(A)U =-0.3549 0.0891 0.6351 0.0242 -0.3937 0.2366 -0.0899 0.0312 -0.4921-0.3842 0.1889 0.1027 -0.2271 0.0478 -0.5715 0.1054 -0.6410 0.0598-0.2181 -0.3960 -0.2809 -0.4417 -0.1458 -0.2550 -0.5919 0.2276 -0.1822-0.3568 -0.0756 -0.3300 0.8236 -0.0930 -0.1587 -0.1709 -0.0575 -0.1162-0.3274 -0.1754 0.2024 0.0195 0.8759 0.1294 -0.0595 0.0958 -0.1551-0.3318 0.3326 -0.4802 -0.2235 -0.0131 0.6394 -0.0832 -0.2872 -0.0164-0.2999 -0.4399 -0.2304 -0.1342 -0.1418 0.0108 0.7562 0.1483 -0.1773-0.2774 0.6410 -0.0981 -0.0747 0.0357 -0.2743 0.1160 0.6364 0.0446-0.4092 -0.2192 0.2530 0.0243 -0.1551 0.1618 -0.0743 0.1198 0.8061S =21.1167 0 00 2.0140 00 0 1.42390 0 00 0 00 0 00 0 00 0 00 0 0V =-0.5277 -0.8221 0.2139-0.6205 0.2010 -0.7580-0.5801 0.5327 0.6161>> U*S*V'ans =4.0000 4.00005.00004.00005.0000 5.00003.0000 3.0000 2.00004.00005.0000 4.00004.0000 4.0000 4.00003.0000 5.00004.00004.0000 4.0000 3.00002.0000 4.0000 4.00005.0000 5.0000 5.0000 >> u=U(:,1:3)u =-0.3549 0.0891 0.6351 -0.3842 0.1889 0.1027 -0.2181 -0.3960 -0.2809 -0.3568 -0.0756 -0.3300 -0.3274 -0.1754 0.2024 -0.3318 0.3326 -0.4802 -0.2999 -0.4399 -0.2304 -0.2774 0.6410 -0.0981 -0.4092 -0.2192 0.2530 >> s=S(1:3,:)s =21.1167 0 00 2.0140 00 0 1.4239>> u*s*V'ans =4.0000 4.00005.00004.00005.0000 5.00003.0000 3.0000 2.00004.00005.0000 4.00004.0000 4.0000 4.00003.0000 5.00004.00004.0000 4.0000 3.00002.0000 4.0000 4.00005.0000 5.0000 5.0000很明显,截取U的前3列和S的前3行后,U、S、V’相乘仍然可以得到矩阵A。
深入浅出通信原理

很多原理一旦上升为理论,常常伴随着繁杂的数学推导,很简单的本质反而被一大堆公式淹没,通信原理因此让很多人望而却步。
非常复杂的公式背后很可能隐藏了简单的道理。
真正学好通信原理,关键是要透过公式看本质。
以复傅立叶系数为例,很多人都只是会套公式计算,真正理解其含义的人不多。
对于经常出现的“负频率”,真正理解的人就更少了。
连载1:从多项式乘法说起多项式乘法相信我们每个人都会做:再合并同类项的方法得到的,要得到结果多项式中的某个系数,需要两步操作才行,有没有办法一步操作就可以得到一个系数呢?下面的计算方法就可以做到:这种计算方法总结起来就是:反褶:一般多项式都是按x的降幂排列,这里将其中一个多项式的各项按x的升幂排列。
平移:将按x的升幂排列的多项式每次向右平移一个项。
相乘:垂直对齐的项分别相乘。
求和:相乘的各结果相加。
反褶、平移、相乘、求和-这就是通信原理中最常用的一个概念“卷积”的计算过程。
连载2:卷积的表达式利用上面的计算方法,我们很容易得到:c(0)=a(0)b(0)c(1)=a(0)b(1)+a(1)b(0)c(2)=a(0)b(2)+a(1)b(1)+a(2)b(0)c(3)=a(0)b(3)+a(1)b(2)+a(2)b(1)+a(3)b(0)其中:a(3)=a(2)=b(3)=0在上面的基础上推广一下:假定两个多项式的系数分别为a(n),n=0~n1和b(n),n=0~n2,这两个多项式相乘所得的多项式系数为c(n),则:c(0)=a(0)b(0)c(1)=a(0)b(1)+a(1)b(0)c(2)=a(0)b(2)+a(1)b(1)+a(2)b(0)c(3)=a(0)b(3)+a(1)b(2)+a(2)b(1)+a(3)b(0)c(4)=a(0)b(4)+a(1)b(3)+a(2)b(2)+a(3)b(1)+a(4)b(0)以此类推可以得到:上面这个式子就是a(n)和b(n)的卷积表达式。
深入浅出通信原理

深入浅出通信原理深入浅出通信原理随着科技的不断发展,通信技术的应用越来越广泛。
而了解通信原理,则是学习和掌握通信技术的第一步。
深入浅出通信原理,要从以下几个方面进行阐述:一、信号传输信号传输是通信原理的核心,指数字或模拟信号在信道中的传输过程。
数字信号是由数值化的数字组成,可被计算机处理,并在过程中不会受到干扰或损失。
模拟信号是由连续的波形组成,比数字信号更接近真实的信号,但在传输过程中容易受到干扰和损失。
在信号传输过程中,还需要考虑信噪比和比特率等参数,以保证信号传输的质量。
二、调制与解调调制与解调是将数字信号转换为模拟信号和将模拟信号转换为数字信号的过程。
调制将数字信号嵌入在高频载波中,以便在信道中传输。
解调则将嵌入的数字信号解开,还原成原始信号。
常见的调制方式包括频移键控调制(FSK)、相移键控调制(PSK)和振幅键控调制(ASK)等。
解调方式则包括同步解调和非同步解调。
三、信道编码信道编码是在信道传输过程中对原始信号进行编码,使其具有更好的纠错能力和抗干扰能力。
其中涉及到的编码方式包括海明码、卷积码和交织码等。
编码能有效地保护信号免受误码和干扰的影响。
四、多路复用多路复用是指将多条信号通过同一信道同时传输的过程。
常见的多路复用方式包括时分多路复用(TDM)、频分多路复用(FDM)和码分多路复用(CDM)等。
多路复用的好处包括充分利用信道资源,提高传输效率。
五、网络协议网络协议是指计算机之间进行通信时的规矩和约定,包括物理层、数据链路层、网络层、传输层和应用层等。
网络协议的重要性在于协调计算机之间的通信和传输,以保证数据的可靠性和安全性。
六、无线通信无线通信是指通过无线电波进行传输的通信方式,包括蓝牙、WLAN、WIFI和移动通信等。
无线通信的优点在于免去了布线和距离限制,但同时也需要考虑距离衰减和信号干扰等问题。
以上是深入浅出的通信原理概述,了解和掌握通信原理对于理解和应用通信技术都非常重要。
深入浅出通信原理

8.3半波对称振子 8.4全向天线
8.5定向天线
8.6多天线技术
9.1 TDM/TDMA
9.2 FDM/FDMA
9.3 OFDM/OFDMA
9.4 CDM/CDMA
10.2模拟通信系统
10.1通信系统性能 指标
10.3数字通信系统
作者介绍
这是《深入浅出通信原理》的读书笔记模板,暂无该书作者的介绍。
感谢观看
读书笔记
花了大半天时间拉通看了一遍。 本书读完对学完的信号与系统认识有更进一步,书对一些知识点的解读非常好。 学生读起来会有课本不一样的感受,本来我是个游戏迷,但这本书都让我放弃了打游戏[呲牙][呲牙]。 一般,学这个专业的表示这本书的参考书目还不错,最爱奥本海姆了!。 非本专业,一部分概念讲的很清晰,也很有条理和逻辑性。 知识点内容讲的容易懂,作为入门了解一些通信概念还行,专业人士看的话,可能有些简单。 感觉还不错啊,通信工程专业已经学习了模电,数电,信号与系统,信息论与编码,电磁场与电磁波,,, 终于可以来一波大归纳了。 适合科普。 看第一章很happy,看到第我2章开始崩溃,读书学的全还给老师了[撇嘴]。 虽然说是深入浅出,读后才发现,是针对懂行的人说的。
精彩摘录
实现信息传递所需的一切技术设备和传输媒质被统称为通信系统。 天线尺寸为被辐射信号波长的十分之一或更大些,信号才能被有效地辐射。 只要在信号衰减到一定程度、波形失真还不是太严重时插入数字中继器,对数字信号进行放大,恢复理想脉 冲波形,再转发出去即可,这就是数字信号的再生 衰减快慢与电磁波的频率有关:在传播距离相同的情况下,频率越高,振幅衰减越快。 为了解决连续误码问题,需要将信道编码之后的数据顺序按照一定规律打乱,这就是交织。 和光分解成单色光类似,任何复杂的信号都可以分解成一系列不同频率的基本信号之和,一般用频谱来反映 构成信号的所有频率成分。 复信号的本质就是并行传输的2路实信号。之所以被称为复信号,只是因为这个信号可以用复数来表示而已。 模拟信号存在一个缺点,那就是抗干扰能力差,很容易在传输的过程中受到干扰影响而产生失真。 通过添加冗余信息,以便在接收端进行纠错处理,解决信道的噪声和干扰导致的误码问题,这就是信道编码。 发信机进行的信号处理:信源编码、信道编码、交织、脉冲成形、调制。
[原创连载]深入浅出通信原理(1...
![[原创连载]深入浅出通信原理(1...](https://img.taocdn.com/s3/m/da060ca570fe910ef12d2af90242a8956becaac7.png)
[原创连载]深入浅出通信原理(1...本帖最后由 chenaijun 于 2015-3-22 14:39 编辑利用上面的计算方法,我们很容易得到:c(0)=a(0)b(0)c(1)=a(0)b(1)+a(1)b(0)c(2)=a(0)b(2)+a(1)b(1)+a(2)b(0)c(3)=a(0)b(3)+a(1)b(2)+a(2)b(1)+a(3)b(0)其中:a(3)=a(2)=b(3)=0在上面的基础上推广一下:假定两个多项式的系数分别为a(n),n=0~n1和b(n),n=0~n2,这两个多项式相乘所得的多项式系数为c(n),则:c(0)=a(0)b(0)c(1)=a(0)b(1)+a(1)b(0)c(2)=a(0)b(2)+a(1)b(1)+a(2)b(0)c(3)=a(0)b(3)+a(1)b(2)+a(2)b(1)+a(3)b(0)c(4)=a(0)b(4)+a(1)b(3)+a(2)b(2)+a(3)b(1)+a(4)b(0)以此类推可以得到:上面这个式子就是a(n)和b(n)的卷积表达式。
通常我们把a(n)和b(n)的卷积记为:a(n)*b(n),其中的*表示卷积运算符。
连载总目录(二)连载201:什么是相位(二)连载202:如何计算相位(一)连载203:如何计算相位(二)连载204:如何理解同相和反相连载205:同相和反相情况下的相位差连载206:如何理解负相位连载207:如何确定零相位点连载208:如何确定初始相位(一)连载209:如何确定初始相位(二)连载210:什么是相位差连载211:什么是相移连载212:相位失真连载213:系统的相频特性连载214:什么是正交连载215:相位超前和滞后(一)连载216:相位超前和滞后(二)连载217:什么是相干连载218:什么是相干解调连载219:奈奎斯特第一准则(一)连载220:奈奎斯特第一准则(二)连载221:奈奎斯特第一准则(三)连载222:奈奎斯特第一准则(四)连载223:升余弦滚降滤波器连载224:脉冲成型滤波器连载225:BPSK调制的基带脉冲波形连载226:BPSK基带脉冲波形的解调连载227:什么是眼图连载228:眼图的形成原理连载229:频带利用率概念辨析连载230:基带系统与频带系统连载231:频带带宽与基带带宽的关系连载232:双边带调制信号带宽与基带带宽的关系连载233:单边带调制信号带宽与基带带宽的关系连载234:IQ调制信号带宽与基带带宽的关系连载235:数字调制系统的频带利用率连载236:增加信道编码后的频带利用率连载237:BPSK调制的频带信号波形连载238:QPSK调制的频带信号波形连载239:QPSK调制信号的包络连载240:利用旋转向量理解BBF+IQ调制连载241:旋转向量末端的三维立体轨迹图连载242:包络的严格定义(一)连载243:包络的严格定义(二)连载244:IQ信号的三维立体轨迹图连载245:IQ信号轨迹在复平面上的投影连载246:通过IQ平面信号轨迹分析包络变化连载247:IQ信号轨迹和星座图的关系连载248:相邻码元相同情况下的IQ信号轨迹连载249:QPSK调制的相位转移图连载250:为什么要研究信号的包络连载251:OQPSK调制的相位转移图连载252:OQPSK调制连载253:OQPSK调制原理框图连载254:OQPSK解调原理框图连载255:IQ解调原理回顾(一)连载256:IQ解调原理回顾(二)连载257:IQ解调原理回顾(三)连载258:IQ解调原理回顾(四)连载259:利用与冲激函数做卷积的性质理解IQ解调连载260:利用IQ调制解调系统传输复信号连载261:OFDM基带信号的传输连载262:OFDM射频信号的传输连载263:利用IQ调制传输OFDM基带信号连载264:只发送实部情况下的OFDM频谱连载265:实虚部都发送情况下的OFDM频谱(一)连载266:实虚部都发送情况下的OFDM频谱(二)连载267:实虚部都发送情况下的OFDM频谱(三)连载268:两种OFDM信号频谱对比(一)连载269:两种OFDM信号频谱对比(二)连载270:子载波频率取负值情况下的OFDM频谱(一)连载271:子载波频率取负值情况下的OFDM频谱(二)连载272:子载波频率取负值情况下的OFDM频谱(三)连载273:子载波频率取负值情况下的OFDM频谱(四)连载274:正负子载波频率各一半情况下的OFDM频谱连载275:正负子载波频率各一半情况下的OFDM调制(一)连载276:正负子载波频率各一半情况下的OFDM调制(二)连载277:正负子载波频率各一半情况下的OFDM调制(三)连载278:正负子载波频率各一半情况下的OFDM调制(四)连载279:正负子载波频率各一半情况下的OFDM调制(五)连载280:正负子载波频率各一半情况下的OFDM调制(六)连载281:多径效应连载282:码间串扰(一)连载283:码间串扰(二)连载284:码间串扰(三)连载285:码间串扰(四)连载286:码间串扰(五)连载287:OFDM解调(一)连载288:OFDM解调(二)连载289:OFDM解调(三)连载290:OFDM符号时长与子载波间隔的关系连载291:OFDM子载波间干扰(一)连载292:OFDM子载波间干扰(二)连载293:OFDM子载波间干扰(三)连载294:OFDM循环前缀(一)连载295:OFDM循环前缀(二)连载296:OFDM循环前缀(三)连载297:OFDM循环前缀(四)连载298:OFDM循环前缀(五)连载299:OFDM循环前缀(六)连载300:OFDM循环前缀(七)连载301:OFDM循环前缀(八)连载302:OFDM循环前缀(九)连载303:OFDM参数设计(一)连载304:OFDM参数设计(二)连载305:复信号的频谱(一)连载306:复信号的频谱(二)连载307:复信号的频谱(三)连载308:复信号的频谱(四)连载309:OFDM与复傅立叶级数展开(一)连载310:OFDM与复傅立叶级数展开(二)连载311:OFDM与复傅立叶级数展开(三)连载312:OFDM与离散傅立叶变换连载313:离散傅立叶变换(一)连载314:离散傅立叶变换(二)连载315:离散傅立叶变换(三)连载316:离散傅立叶变换(四)连载317:离散傅立叶变换(五)连载318:离散傅立叶变换(六)连载319:离散傅立叶变换(七)连载320:离散傅立叶变换(八)连载321:离散傅立叶变换(九)连载322:离散傅立叶变换(十)连载323:离散傅立叶变换(十一)连载324:离散傅立叶变换(十二)连载325:离散傅立叶变换(十三)连载326:离散傅立叶变换(十四)连载327:离散傅立叶变换(十五)连载328:离散傅立叶变换(十六)连载329:离散傅立叶变换(十七)连载330:离散傅立叶变换(十八)连载331:离散傅立叶变换(十九)连载332:离散傅立叶变换(二十)连载333:离散傅立叶变换(二一)连载334:离散傅立叶变换(二二)连载335:离散傅立叶变换(二三)连载336:离散傅立叶变换(二四)连载337:离散傅立叶变换(二五)连载338:离散傅立叶变换(二六)连载339:离散傅立叶变换(二七)连载340:离散傅立叶变换(二八)连载341:离散傅立叶变换(二九)连载342:离散傅立叶变换(三十)连载343:离散傅立叶变换(三一)连载344:离散傅立叶变换(三二)连载345:离散傅立叶变换(三三)连载346:离散傅立叶变换(三四)连载347:离散傅立叶变换(三五)连载348:离散傅立叶变换(三六)连载349:离散傅立叶变换(三七)连载350:离散傅立叶变换(三八)连载351:离散傅立叶变换(三九)连载352:离散傅立叶变换(四十)连载353:离散傅立叶变换(四一)连载354:利用DFT进行频谱分析连载355:如何提高频谱密度连载356:如何提高频谱分辨率(一)连载357:如何提高频谱分辨率(二)连载358:泄漏效应连载359:为什么会产生频谱泄漏(一)连载360:为什么会产生频谱泄漏(二)连载361:为什么会产生频谱泄漏(三)连载362:为什么会产生频谱泄漏(四)连载363:为什么会产生频谱泄漏(五)连载364:为什么会产生频谱泄漏(六)连载365:为什么会产生频谱泄漏(七)连载366:为什么会产生频谱泄漏(八)连载367:为什么会产生频谱泄漏(九)连载368:如何减小频谱泄漏连载369:频谱的主瓣和旁瓣连载370:为什么会出现主瓣和旁瓣(一)连载371:为什么会出现主瓣和旁瓣(二)连载372:循环卷积和卷积的区别连载373:循环卷积的计算过程连载374:形象图示循环卷积的计算过程连载375:利用matlab计算循环卷积连载376:时域相乘相当于频域做循环卷积连载377:验证频域循环卷积定理连载378:证明频域循环卷积定理之一连载379:证明频域循环卷积定理之二连载380:证明频域循环卷积定理之三连载381:证明频域循环卷积定理之四连载382:通过加窗减小旁瓣泄漏连载383:矩形窗连载384:汉宁窗连载385:汉明窗连载386:布莱克曼窗连载387:四种窗函数的波形比较连载388:四种窗函数的频谱比较连载389:窗函数的应用连载390:利用IDFT实现OFDM调制之一连载391:利用IDFT实现OFDM调制之二连载392:利用IDFT实现OFDM调制之三连载393:利用IDFT实现OFDM调制之四连载394:利用IDFT实现OFDM调制之五连载395:利用IDFT实现OFDM调制之六连载396:利用IDFT实现OFDM调制之七连载397:利用IDFT实现OFDM调制之八连载398:利用DFT实现OFDM解调之一连载399:利用DFT实现OFDM解调之二连载400:利用DFT实现OFDM解调之三连载401:利用DFT实现OFDM解调之四连载402:OFDM采样频率之一连载403:OFDM采样频率之二连载404:OFDM采样频率之三连载405:OFDM采样频率之四连载406:OFDM采样频率之五连载407:OFDM采样频率之六连载408:OFDM采样频率之七连载409:OFDM采样频率之八连载410:OFDM信号与周期信号连载411:傅立叶系数与DFT的关系之一连载412:傅立叶系数与DFT的关系之二连载413:傅立叶系数与DFT的关系之三连载414:傅立叶系数与DFT的关系之四连载415:傅立叶系数与DFT的关系之五连载416:傅立叶系数与DFT的关系之六连载417:OFDM信号的FT与DFT连载418:调制技术连载419:标准幅度调制(AM)连载420:AM解调连载421:AM信号的频谱连载422:AM的调制效率连载423:双边带调制(DSB)连载424:DSB的解调连载425:上边带和下边带连载426:单边带调制(SSB)连载427:SSB解调(一)连载428:SSB解调(二)连载429:IQ调制(一)连载430:IQ调制(二)连载431:IQ调制为什么被称为正交调制连载432:IQ调制信号的波形图连载433:IQ解调原理连载434:利用旋转向量理解IQ解调连载435:IQ调制解调三维频谱分析[本帖最后由 chenaijun 于 2012-3-23 22:21 编辑]。
深入浅出通信原理六

深入浅出通信原理六 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】连载251:OQPSK调制的相位转移图连载252:OQPSK调制% I路信号>> subplot(321);>> t=0::8;>> a=1/sqrt(2);>> x=;>> y1= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);>> x=;>> y2= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y3= - a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y4= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y5= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y6= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y7= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y8= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> y01= y1+y2+y3+y4+y5+y6+y7+y8;>> plot(t,y01);>> axis([0 8 -2 2]);>> grid on;% Q路信号>> subplot(323);>> t=0::8;>> a=1/sqrt(2);>> x=;>> y1= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y2= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y3= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y4= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y5= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y6= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y7= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y8= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> y02= y1+y2+y3+y4+y5+y6+y7+y8;>> plot(t,y02);>> axis([0 8 -2 2]);>> grid on;%QPSK调制信号>> subplot(325);>> t=0::8;>> s1=y01.*cos(2*pi*10*t) ;>> s2=y02.*sin(2*pi*10*t);>> plot(t,s1-s2) ;>> axis([0 8 -2 2]);% I路信号>> subplot(322);>> t=0::8;>> a=1/sqrt(2);>> x=;>> y1= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y2= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y3= - a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y4= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y5= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y6= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y7= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=;>> y8= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> y01= y1+y2+y3+y4+y5+y6+y7+y8;>> plot(t,y01);>> axis([0 8 -2 2]);>> grid on;% Q路信号>> subplot(324);>> t=0::8;>> a=1/sqrt(2);>> x=t-1;>> y1= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-2;>> y2= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-3;>> y3= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-4;>> y4= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-5;>> y5= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-6;>> y6= -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-7;>> y7= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> x=t-8;>> y8= a.*sinc(x).*cos(pi*x)./(1-4.*x.*x); >> y02= y1+y2+y3+y4+y5+y6+y7+y8;>> plot(t,y02);>> axis([0 8 -2 2]);>> grid on;%QPSK调制信号>> subplot(326);>> t=0::8;>> s1=y01.*cos(2*pi*10*t) ;>> s2=y02.*sin(2*pi*10*t);>> plot(t,s1-s2) ;>> axis([0 8 -2 2]);连载253:OQPSK调制原理框图连载254:OQPSK解调原理框图连载255:IQ解调原理回顾连载256:IQ解调原理回顾(二)连载257:IQ解调原理回顾(三)连载220:连载258:IQ解调原理回顾(四)连载259:利用与冲激函数做卷积的性质理解IQ解调在没讲余弦和正弦信号的傅立叶变换之前,信号与余弦信号相乘、信号与正弦信号相乘乘积的频谱可以这样得到:连载77:连载87:讲了余弦和正弦信号的傅立叶变换之后:连载100:连载101:可以借助频域卷积定理:连载133:和与冲激函数做卷积的性质:连载123:方便地得到信号与余弦信号相乘、信号与正弦信号相乘乘积的频谱。
深入浅出通信原理

深入浅出通信原理通信原理是指利用电磁波、电信号和其他信号传播的一种基本原理,是电信信号传播应用的基础。
它涉及到信号的传输、传输和接收复杂电信信号,以及完成信号处理的技术和原理。
它是物理和信号处理技术的基础,是运用电信技术实现通信的基础。
二、通信原理相关技术1. 信号发射信号发射是指将预定形式的电信信号通过特定的传输介质传输到接收方的一种技术。
它包括发射电路的设计和制造,发射架构的设计和安装,信号发射的误差控制和传输特性的测量,以及信号发射方式和编码技术等。
2. 信号接收信号接收是指传输介质中传播的信号被接收之后,在接收处被处理、数字化,从而获得原始信号的一种技术。
它要涉及接收处的架构设计,接收机的设计和制造,接收信号的特性测量,以及接收信号的信噪比、延时和抖动等综合性能的测量。
3. 信号处理信号处理是指接收后的信号,由解调器、转换器、分析仪等设备进行分析、处理,从而获得有效信息的一种技术。
它包括对信号进行分析和模拟,提取信号有效信息,信号模式识别,信号定位,以及多媒体信号处理等。
三、传播媒介1.中传播空中传播是指信号传播时,通过大气层中不同频率的电磁波进行传播的一种方式。
它可以提供大距离的信号传播,但存在较大的传播衰减,受气象影响,夜间传播不稳定等特点。
2.路传播线路传播指的是将信号传输到远处采用电缆作为载体的传播方式。
电缆传播信号的衰减比空中传输小,受气象的影响比较小,夜晚传播稳定,但架设成本较高。
四、综合应用综合应用指的是将上述三种技术综合应用,即通过空中、线路和其他传播媒介,将信号从发射方通过信号发射、传输和接收,最终处理成有用信息的一种方式。
综合应用不仅要熟练掌握信号发射、接收和处理的技术,而且还要熟悉各种传播媒介的特性,以便更好地实现信号传输。
总之,通信原理是实现信号传输的基础,包括信号发射、接收和处理,以及多种传播媒介的综合运用等技术。
通过对通信原理的准确掌握,可以更好地实现通信功能,使用户获得更高效、更便捷的通信服务。
陈爱军 深入浅出通信原理

很多原理一旦上升为理论,常常伴随着繁杂的数学推导,很简单的本质反而被一大堆公式淹没,通信原理因此让很多人望而却步。
非常复杂的公式背后很可能隐藏了简单的道理。
真正学好通信原理,关键是要透过公式看本质。
信号与系统、数字信号处理中很多复杂的公式其本质都是很简单的,我们可以通过图、动画等方式更好、更透彻地理解这些公式和原理,而不是仅仅局限于会套用这些公式(我大学毕业时就是这个水平,相信很多人和我一样)。
这个帖子面向的主要是非通信专业和通信专业在大学没真正学明白的人(我就是这样的人,不是我不想学明白,大学里老师讲的太抽象了,很难理解),大部分人对“希尔伯特空间”没有什么概念,所以虽然你能用上述理论将傅立叶级数讲得很简单,但大部分人无法理解和接受。
,“深入浅出通信原理”就是希望用尽可能少的公式推导和大量的图片,让大家真正理解通信原理。
虽然这样有时候会显得啰嗦,但对大部分读者来讲是只有好处没有坏处的。
以复傅立叶系数为例,很多人都只是会套公式计算,真正理解其含义的人不多。
对于经常出现的“负频率”,真正理解的人就更少了。
连载1:从多项式乘法讲起连载2:卷积的表达式连载3:利用matlab计算卷积连载4:将信号表示成多项式的形式连载5:著名的欧拉公式连载6:利用卷积计算两个信号的乘积连载7:信号的傅立叶级数展开连载8:时域信号相乘相当于频域卷积连载9:用余弦信号合成方波信号连载10:傅立叶级数展开的定义连载11:如何把信号展开成复指数信号之和?连载12:复傅立叶系数连载13:实信号频谱的共轭对称性连载14:复指数信号的物理意义-旋转向量连载15:余弦信号的三维频谱图连载16:正弦信号的三维频谱图连载17:两个旋转向量合成余弦信号的动画连载18:周期信号的三维频谱图连载19:复数乘法的几何意义连载20:用成对的旋转向量合成实信号连载21:利用李萨育图形认识复信号连载22:实信号和复信号的波形对比连载23:利用欧拉公式理解虚数连载24:IQ信号是不是复信号?连载25:IQ解调原理连载26:用复数运算实现正交解调连载27:为什么要对信号进行调制?连载28:IQ调制为什么被称为正交调制?连载29:三角函数的正交性连载30:OFDM正交频分复用连载31:OFDM解调连载32:CDMA中的正交码连载33:CDMA的最基本原理连载34:什么是PSK调制?连载35:如何用IQ调制实现QPSK调制?连载36:QPSK调制信号的时域波形连载37:QPSK调制的星座图连载38:QPSK的映射关系可以随意定吗?连载39:如何使用IQ调制实现8PSK?连载1:从多项式乘法说起多项式乘法相信我们每个人都会做:再合并同类项的方法得到的,要得到结果多项式中的某个系数,需要两步操作才行,有没有办法一步操作就可以得到一个系数呢?下面的计算方法就可以做到:这种计算方法总结起来就是:反褶:一般多项式都是按x的降幂排列,这里将其中一个多项式的各项按x的升幂排列。
精选-通信原理

精选-通信原理
通信原理是通信工程和电子工程中的重要组成部分,涵盖了信息传输的各个方面,包括信息编码、调制、解调、传输和接收等过程。
以下是一些关于通信原理的精选内容:
1.信息与信号
通信原理的基础是信息论,它研究信息的本质和传输规律。
信息是通信中传输的内容,而信号则是信息的载体。
信号可以是电信号、光信号、声信号等,它们携带着信息在信道中传输。
2.信道与噪声
信道是传输信号的媒介,它可以是无线信道或有线信道。
在信道中,信号可能会受到噪声的干扰,因此,噪声是通信中不可避免的因素。
为了提高通信系统的性能,需要研究和降低噪声的影响。
3.调制与解调
调制是将信息加载到载波上的过程,而解调则是从接收到的信号中提取出信息的过程。
调制和解调是通信系统中非常重要的技术之一,它们可以有效地提高信息的传输速率和降低噪声的影响。
4.信源编码与信道编码
信源编码是对原始信息进行压缩和编码的过程,以减少信息的冗余和提高传输效率。
信道编码是在信号传输过程中加入额外的冗余信息,以增强信号的可靠性,抵抗信道中的噪声干扰。
5.数字通信与模拟通信
数字通信是以数字信号为载体进行传输的通信方式,而模拟通信是以模拟信号为载体进行传输的通信方式。
数字通信具有更高的可靠性和灵活性,能够实现更高速的数据传输。
6.多路复用与多址接入
多路复用是一种将多个信号合并为一个复合信号的技术,以实现更高效的传输。
多址接入是一种允许多个用户同时访问信道的技术,以实现更广泛的网络覆盖和更高的网络容量。
以上是关于通信原理的一些精选内容,它们是理解和掌握通信原理的基础。
深入浅出通信原理

深入浅出通信原理现在的社会,我们与他人的交流方式可以说是越来越多样化了,从早期的来信和到访,到现在可以使用手机、网络、卫星等等通信方式,联络他人的方式也变得越来越容易。
这就是通信原理带来的好处,是当今社会不可缺少的重要功能。
通信原理是研究如何在时间、地点、环境以及噪声等多种因素下,将信息以及信息的传输方式进行综合分析,优化传输的能力。
它被应用于很多领域,如电信、科学研究、工业控制、娱乐、社会服务等等,是一门涉及非常广泛的学科。
通信原理主要包括信号与编码理论、控制理论、多媒体技术、无线通信以及信息安全等,它们之间是非常密切的。
信号与编码理论是针对发送信息时,信号的正确编码和解码,以及信号的加密和解密,而多媒体技术则关注于如何表现文字、图像、音频与视频等信息,以及如何将它们发送出去。
无线通信就是针对无线信息传输时收发端之间的配置,以及如何克服传输过程中的各种干扰,而信息安全则关注于如何保护传输信息的安全性和完整性。
传统的通信原理,以及大部分现代通信原理都是以通信和信息传输过程中的知识和技术为基础的。
它们涉及到传输过程、信号的加工、信号的重构、信号的压缩等多种技术,研究如何在通信过程中达到最优的效果。
除此之外,当今的通信原理也融合了计算机的技术,如网络安全与信息安全,以及最新的通信技术,如软件定义的网络、5G等,这些技术都是针对当今数字时代的需求而设计。
此外,还有诸如动态路由管理、保证服务质量、无线传感网络、多播技术以及无线定位等新技术,它们都是基于通信原理的理论,为网络的稳定性,以及更加高效的传输提供保障。
总之,随着通信技术的发展,通信原理也在不断演进,从信号处理到网络技术,从软件定义网络到5G,都是当今社会中不可或缺的重要组成部分,从深入浅出的角度看,它们之间的联系是非常重要的,唯有对其有深入的了解,才可以真正理解其中的内涵,并实现更加全面的应用。
通信原理

字频带(调制或载波)传输。
3
基带传输系统是指不使用调制和解调装置而直接传输 数字基带信号的系统。即在发端,首先将源符号进行信源
第n个码元为 un(t) =sn(t) −vn(t)。于是有:
u (t )
n
un
n
a n [ g 1 ( t n T s ) g 2 ( t n T s )]
an
1 P P
以概率P
以概率1-P
显然,u(t)是随机脉冲序列 ,图(c) 给出了u(t)的一个实现。
g 2 (t )e
j 2 fst
可见,交变波的的功率谱 Pu( f) 是连续谱,它与g1(t)
和g2(t)的频谱以及出现概率P有关。
29
3.s(t)=u(t)+v(t)的功率谱密度PS(f )
Ps
f
m
Pu
f Pv f
2 2
| C m | ( f m f s ) f s P (1 P ) | G 1 ( f ) G 2 ( f ) |
+A 表示。 0 -A
+A (a) 0 传号反转编码(CMI码)与数字双相码类似,也是一 -A
0”和“11”两位码组表示,而“0”则固定地用“01”
(b)
1
1
0 1
0
0
1 0
+A 0 -A
(c)
15
深入浅出通信原理

深入浅出通信原理
通信原理是指在信息传输过程中的基本原理和方法。
它涉及信息传输的各个环节,包括信息的产生、编码、调制、传输、解调、解码、接收和处理等过程。
首先,信息的产生是指将要传输的信息转化为适合传输的形式。
比如,人类语言可以通过音频或文本的方式传输;而图像、视频等多媒体信息需要通过图像或视频编码的方式进行转换。
接下来,编码是指将信息进行数字化处理,将其转化为二进制的信号序列。
这样可以使信息在传输过程中更加稳定可靠,减少信息传输过程中的干扰和失真。
调制是指将数字化的信号序列转换为可以在传输介质中传播的模拟信号。
常见的调制方式有幅移键控调制(ASK)、频移
键控调制(FSK)和相移键控调制(PSK)等。
传输是指将调制后的模拟信号通过传输介质传输到目标地点。
传输介质可以是空气、导线、光纤等。
在传输过程中,信号可能会因为传输介质的特性而出现衰减、噪声等问题。
解调是指将接收到的模拟信号转换为数字信号。
解调过程与调制过程相反,恢复出原始的数字信号序列。
解码是将数字信号序列转化为原始的信息形式。
解码过程与编码过程相反,将二进制信号转化为可理解的信息。
最后,接收和处理是指接收端对于解码后的信息进行接收和处理。
这包括对信息进行验证、检错、纠错以及进一步处理和存储等操作。
总体而言,通信原理是通过对信息的产生、编码、调制、传输、解调、解码、接收和处理等过程的控制,实现信息在传输过程中的稳定可靠传递。
了解通信原理可以帮助我们更好地理解和应用现代通信技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
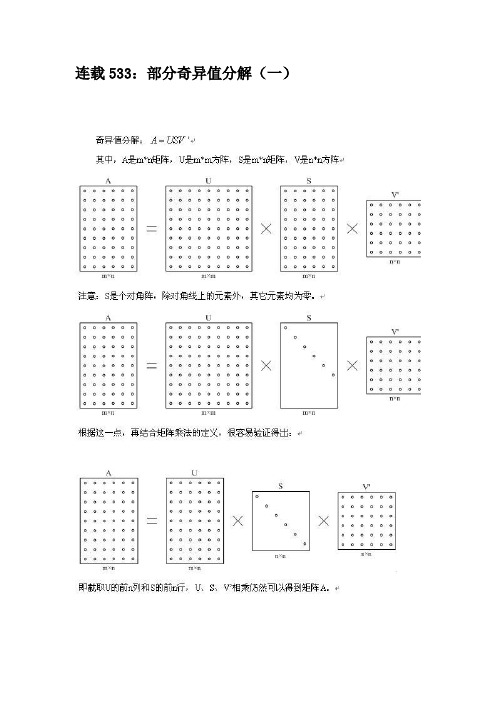
连载533:部分奇异值分解(一)连载534:部分奇异值分解(二)用前面的例子验证一下。
其中:u=U(:,1:3)表示截取矩阵U的前三列;s=S(1:3,:)表示截取矩阵S的前三行。
>> A=[4 4 5;4 5 5;3 3 2;4 5 4;4 4 4;3 5 4;4 4 3;2 4 4;5 5 5];A =4 4 54 5 53 3 24 5 44 4 43 5 44 4 32 4 45 5 5>> [U,S,V]=svd(A)U =-0.3549 0.0891 0.6351 0.0242 -0.3937 0.2366 -0.0899 0.0312 -0.4921 -0.3842 0.1889 0.1027 -0.2271 0.0478 -0.5715 0.1054 -0.6410 0.0598 -0.2181 -0.3960 -0.2809 -0.4417 -0.1458 -0.2550 -0.5919 0.2276 -0.1822 -0.3568 -0.0756 -0.3300 0.8236 -0.0930 -0.1587 -0.1709 -0.0575 -0.1162 -0.3274 -0.1754 0.2024 0.0195 0.8759 0.1294 -0.0595 0.0958 -0.1551 -0.3318 0.3326 -0.4802 -0.2235 -0.0131 0.6394 -0.0832 -0.2872 -0.0164 -0.2999 -0.4399 -0.2304 -0.1342 -0.1418 0.0108 0.7562 0.1483 -0.1773 -0.2774 0.6410 -0.0981 -0.0747 0.0357 -0.2743 0.1160 0.6364 0.0446 -0.4092 -0.2192 0.2530 0.0243 -0.1551 0.1618 -0.0743 0.1198 0.8061 S =21.1167 0 00 2.0140 00 0 1.42390 0 00 0 00 0 00 0 00 0 00 0 0V =-0.5277 -0.8221 0.2139-0.6205 0.2010 -0.7580-0.5801 0.5327 0.6161>> U*S*V'ans =4.0000 4.00005.00004.00005.0000 5.00003.0000 3.0000 2.00004.00005.0000 4.00004.0000 4.0000 4.00003.0000 5.00004.00004.0000 4.0000 3.00002.0000 4.0000 4.00005.0000 5.0000 5.0000>> u=U(:,1:3)u =-0.3549 0.0891 0.6351-0.3842 0.1889 0.1027-0.2181 -0.3960 -0.2809-0.3568 -0.0756 -0.3300-0.3274 -0.1754 0.2024-0.3318 0.3326 -0.4802-0.2999 -0.4399 -0.2304-0.2774 0.6410 -0.0981-0.4092 -0.2192 0.2530>> s=S(1:3,:)s =21.1167 0 00 2.0140 00 0 1.4239>> u*s*V'ans =4.0000 4.00005.00004.00005.0000 5.00003.0000 3.0000 2.00004.00005.0000 4.00004.0000 4.0000 4.00003.0000 5.00004.00004.0000 4.0000 3.00002.0000 4.0000 4.00005.0000 5.0000 5.0000很明显,截取U的前3列和S的前3行后,U、S、V’相乘仍然可以得到矩阵A。
连载535:部分奇异值分解(三)>> A=[0.6 0.7 0.8 0.2;0.3 0.5 0.1 0.9;0.0 0.15 -0.3 0.8;0.48 0.5 0.76 -0.16]A =0.6000 0.7000 0.8000 0.20000.3000 0.5000 0.1000 0.90000 0.1500 -0.3000 0.80000.4800 0.5000 0.7600 -0.1600>> rank(A)ans =2>> [U S V]=svd(A)U =-0.7103 0.1697 -0.0198 -0.6828-0.4541 -0.5911 0.5911 0.3083-0.0989 -0.6759 -0.7290 -0.0440-0.5287 0.4061 -0.3447 0.6609S =1.7152 0 0 00 1.2586 0 00 0 0.0000 00 0 0 0.0000V =-0.4758 0.0949 0.2159 -0.8473-0.5850 -0.0597 0.6462 0.4865-0.5747 0.4672 -0.6373 0.2127-0.3179 -0.8770 -0.3601 -0.0115>> u=U(:,1:2)u =-0.7103 0.1697-0.4541 -0.5911-0.0989 -0.6759-0.5287 0.4061>> s=S(1:2,1:2)s =1.7152 00 1.2586>> v=V(:,1:2)v =-0.4758 0.0949-0.5850 -0.0597-0.5747 0.4672-0.3179 -0.8770>> v'ans =-0.4758 -0.5850 -0.5747 -0.3179 0.0949 -0.0597 0.4672 -0.8770 >> u*s*v'ans =0.6000 0.7000 0.8000 0.20000.3000 0.5000 0.1000 0.90000.0000 0.1500 -0.3000 0.80000.4800 0.5000 0.7600 -0.1600连载536:部分奇异值分解(四)S矩阵中对角线上的元素从左上到右下快速减小,去掉S矩阵中最小的几项所在的行和列,U和V 也去掉对应的列,再将三个矩阵相乘,得到的矩阵约等于原矩阵。
注:其中的r小于矩阵的秩。
接着连载534那个例子。
去掉S矩阵中对角线上最小的那个值。
S =21.1167 0 00 2.0140 00 0 1.4239即取:s =21.1167 00 2.0140我们看一下u*s*v’是否约等于原矩阵。
>> A=[4 4 5;4 5 5;3 3 2;4 5 4;4 4 4;3 5 4;4 4 3;2 4 4;5 5 5]A =4 4 54 5 53 3 24 5 44 4 43 5 44 4 32 4 45 5 5>> [U,S,V]=svd(A)U =-0.3549 0.0891 0.6351 0.0242 -0.3937 0.2366 -0.0899 0.0312 -0.4921-0.3842 0.1889 0.1027 -0.2271 0.0478 -0.5715 0.1054 -0.6410 0.0598-0.2181 -0.3960 -0.2809 -0.4417 -0.1458 -0.2550 -0.5919 0.2276 -0.1822-0.3568 -0.0756 -0.3300 0.8236 -0.0930 -0.1587 -0.1709 -0.0575 -0.1162-0.3274 -0.1754 0.2024 0.0195 0.8759 0.1294 -0.0595 0.0958 -0.1551-0.3318 0.3326 -0.4802 -0.2235 -0.0131 0.6394 -0.0832 -0.2872 -0.0164-0.2999 -0.4399 -0.2304 -0.1342 -0.1418 0.0108 0.7562 0.1483 -0.1773-0.2774 0.6410 -0.0981 -0.0747 0.0357 -0.2743 0.1160 0.6364 0.0446-0.4092 -0.2192 0.2530 0.0243 -0.1551 0.1618 -0.0743 0.1198 0.8061S =21.1167 0 00 2.0140 00 0 1.42390 0 00 0 00 0 00 0 00 0 00 0 0V =-0.5277 -0.8221 0.2139-0.6205 0.2010 -0.7580-0.5801 0.5327 0.6161>> u=U(:,1:2)s=S(1:2,1:2)v=V(:,1:2)u =-0.3549 0.0891-0.3842 0.1889-0.2181 -0.3960-0.3568 -0.0756-0.3274 -0.1754-0.3318 0.3326-0.2999 -0.4399-0.2774 0.6410-0.4092 -0.2192s =21.1167 00 2.0140v =-0.5277 -0.8221-0.6205 0.2010-0.5801 0.5327>> u*s*v'ans =3.80664.6855 4.44283.9687 5.11094.90993.0856 2.6968 2.24654.1005 4.6438 4.28953.93844.2184 3.82253.14634.4817 4.42134.0702 3.7514 3.20212.02993.89414.08614.92295.2730 4.7781很显然,三个矩阵相乘得到的矩阵与原矩阵非常接近。
连载537:部分奇异值分解(五)连载538:利用部分奇异值分解进行数据压缩用0表示黑,1表示白,则上述图像可用下面这个矩阵来表示:这个矩阵23行,25列,共计575个元素。
下面我们对这个矩阵进行SVD分解。
>> M=[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];>> rank(M)ans =1该矩阵的秩为1,因此对角阵S应该只有对角线上左上角一个值不是零,其它值均为零。
